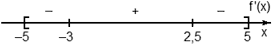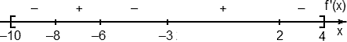15 марта 2011
В задаче 6 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x0,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x0, и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x1; y1) и B (x2; y2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x2 − x1 и приращение функции Δy = y2 − y1.
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
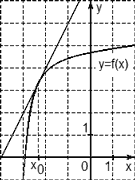
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x2 − x1 = −1 − (−3) = 2; Δy = y2 − y1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
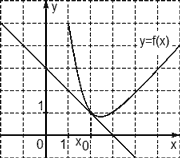
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x2 − x1 = 3 − 0 = 3; Δy = y2 − y1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
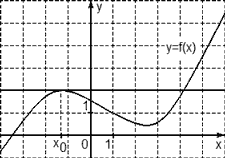
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x2 − x1 = 5 − 0 = 5; Δy = y2 − y1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≥ f(x).
- Точка x0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x0 известно, что f’(x0) ≠ 0, то возможны лишь два варианта: f’(x0) ≥ 0 или f’(x0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
- Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
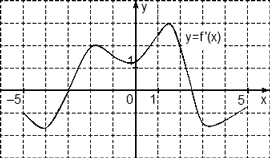
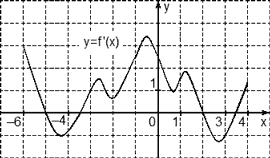
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
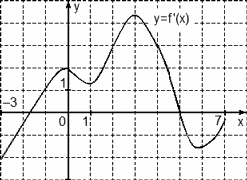
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется возрастающей на отрезке [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≤ f(x2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется убывающей на отрезке [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≥ f(x2). Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
- Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
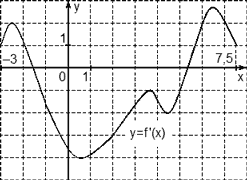
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
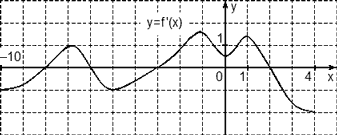
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l1 = − 6 − (−8) = 2;
l2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l2 = 5.
Смотрите также:
- ЕГЭ 2022, задание 6. Касательная к графику функции
- ЕГЭ 2022, задание 6. Касательная к графику функции
- Схема Бернулли. Примеры решения задач
- Решение задач B6: №362—377
- Четырехугольная пирамида: как найти координаты вершин
- Нестандартная задача B2: студенты, гонорары и налоги
Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).
Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.
Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.
Ответ: (11.)
Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.
7. Взаимосвязь функции и ее производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Связь производной с точками экстремума функции
В данных задачах речь идет о непрерывных функциях (простым языком, функция будет непрерывна на интервале, если ее график можно нарисовать на этом интервале, не отрывая ручку от листа).
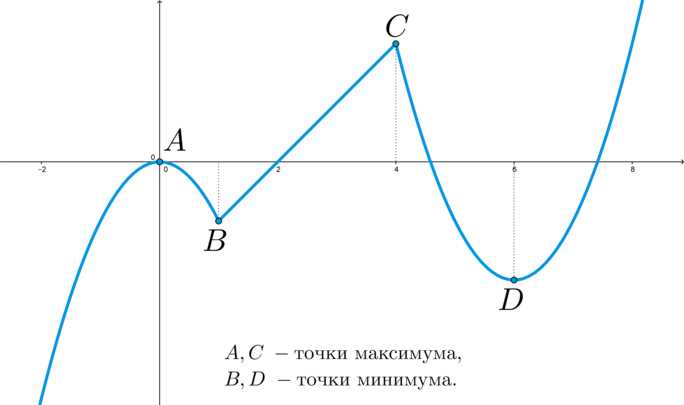
(blacktriangleright) (color{royalblue}{text{Точки}}) (локального) (color{royalblue}{text{экстремума}}) функции – это точки (локального) максимума и минимума.
Окрестность – это интервал вокруг точки некоторого радиуса. Например, окрестностью точки (x=0) можно назвать интервал ((-1;1)), или ((-0,1;0,1)), или ((-0,0000001;0,0000001)) и т.д.
(blacktriangleright) (color{royalblue}{text{Точка}}) (color{royalblue}{text{максимума}}) (x_{max}) – такая внутренняя точка области определения функции, для которой выполнено: (f(x)leqslant
f(x_{max})) для любого (x) из некоторой окрестности точки (x_{max}).
То есть можно найти такую окрестность, что для любой точки из этой окрестности будет выполнено данное неравенство.
Заметим, что, например, если функция определена на отрезке ([0;2]), то все точки интервала ((0;2)) будут внутренними, а вот точки (0) и (2) – граничными (то есть не внутренними).
(blacktriangleright) (color{royalblue}{text{Точка}}) (color{royalblue}{text{минимума}}) (x_{min}) – такая внутренняя точка области определения функции, для которой выполнено: (f(x)geqslant
f(x_{min})) для любого (x) из некоторой окрестности точки (x_{min}).
Например, для точки (C) за окрестность можно взять интервал ((3;5)) или даже ((2;6)), а можно совсем маленький — ((4-0,01;4+0,01)).
Следующие факты помогают искать точки экстремума функции.
(blacktriangleright) Если производная (f’) в точке (x) равна нулю и меняет свой знак слева направо с “(+)” на “(-)” , то эта точка является точкой максимума.
Заметим также, что если производная (f’) в точке (x) не существует и меняет свой знак слева направо с “(+)” на “(-)” (но (x) – внутренняя точка области определения функции (f,)!), то эта точка является точкой максимума.
Пример: в точке (A) производная равна нулю и эта точка является точкой максимума; в точке (C) производная не “равна нулю”, а не существует, при этом точка (C) также является точкой максимума.
(blacktriangleright) Если производная в точке (x) равна нулю и меняет свой знак слева направо с “(-)” на “(+)” , то эта точка является точкой минимума.
Также, если производная (f’) в точке (x) не существует и меняет свой знак слева направо с “(-)” на “(+)” (но (x) – внутренняя точка области определения функции (f,)!), то эта точка является точкой минимума.
(blacktriangleright) Заметим, что точки экстремума – это значение абсциссы (x).
(blacktriangleright) Заметим, что существует такое понятие, как критические точки — это все точки, в которых производная функции либо равна нулю, либо не существует.
Таким образом, только часть критических точек является точками экстремума.
Задание
1
#3107
Уровень задания: Равен ЕГЭ
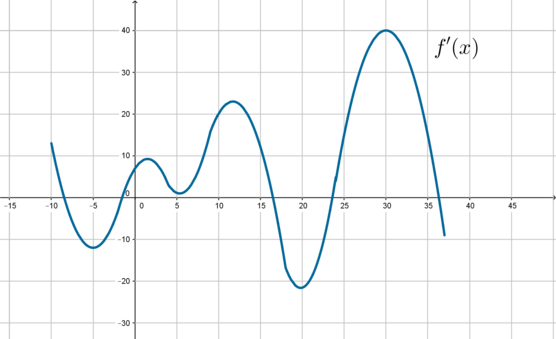
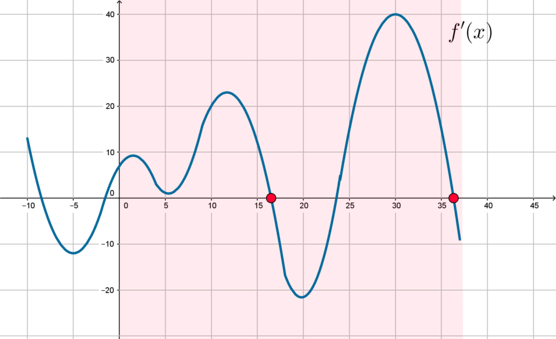
На рисунке изображен график производной функции (f(x)), определенной на отрезке ([-10;37]). Найдите количество точек максимума функции (f(x)) на отрезке ([0;37]).
Точка максимума – значение (x), в котором производная меняет свой знак с “(+)” на “(-)”. Следовательно, в этой точке ее график пересекает ось абсцисс “сверху вниз” (если двигаться по рисунку слева направо). Отметим отрезок ([0;37]) и увидим, что таких точек 2:
Ответ: 2
Задание
2
#2962
Уровень задания: Равен ЕГЭ
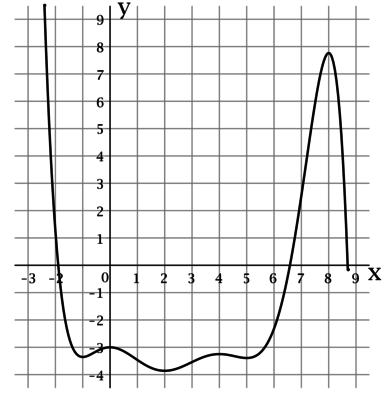
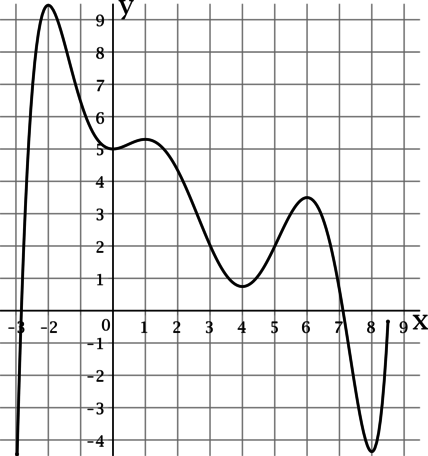
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-2,4; 8,7)). Найдите сумму точек экстремума этой функции на отрезке ([1;6]).
Так как на рисунке изображен график функции, то точки экстремума – это точки на графике, в которых функция меняется с возрастания на убывание или наоборот. Эти точки: (x=-1; 0; 2; 4; 5; 8.) Из них на отрезке ([1;6]) лежат только точки (2; 4; 5), следовательно, их сумма равна (2+4+5=11.)
Ответ: 11
Задание
3
#730
Уровень задания: Равен ЕГЭ
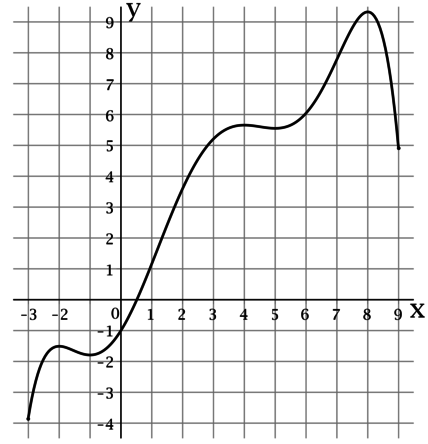
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-3; 8,5)). Найдите сумму точек экстремума этой функции.
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция (f(x)) достигает локально минимальные значения в точках (0), (4) и (8), а локально максимальные значения в точках (-2), (1) и (6). Таким образом, сумма точек экстремума этой функции равна (0 + 4 + 8 + (-2) + 1 + 6 = 17).
Ответ: 17
Задание
4
#731
Уровень задания: Равен ЕГЭ
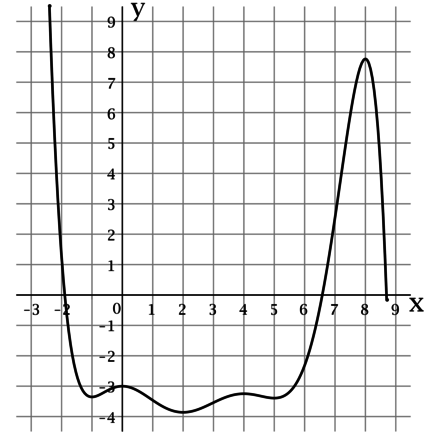
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-2,4; 8,7)). Найдите сумму точек экстремума этой функции.
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция (f(x)) достигает локально минимальные значения в точках (-1), (2) и (5), а локально максимальные значения в точках (0), (4) и (8). Таким образом, сумма точек экстремума этой функции равна (-1 + 2 + 5 + 0 + 4 + 8 = 18).
Ответ: 18
Задание
5
#732
Уровень задания: Равен ЕГЭ
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-3; 9)). Найдите произведение точек экстремума этой функции.
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция (f(x)) достигает локально минимальные значения в точках (-1) и (5), а локально максимальные значения в точках (-2), (4) и (8). Таким образом, произведение точек экстремума этой функции равно ((-1)cdot 5cdot (-2)cdot 4cdot 8 = 320).
Ответ: 320
Задание
6
#733
Уровень задания: Равен ЕГЭ
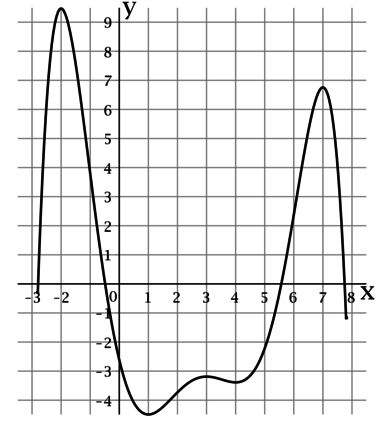
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-2.8; 7.8)). Найдите произведение точек экстремума этой функции.
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция (f(x)) достигает локально минимальные значения в точках (1) и (4), а локально максимальные значения в точках (-2), (3) и (7). Таким образом, произведение точек экстремума этой функции равно (1cdot 4cdot (-2)cdot 3cdot 7 = -168).
Ответ: -168
Задание
7
#734
Уровень задания: Равен ЕГЭ
На рисунке изображен график (y = f'(x)) – производной функции (y = f(x)), определенной на интервале ((-1; 8)). В какой точке отрезка ([2; 5]) функция (y = f(x)) принимает наибольшее значение?
По рисунку можно определить, что функция (y = f'(x)) на отрезке ([2; 5]) принимает неположительные значения, при этом (f'(2) = 0). Так как на полуинтервале ((2; 5]) производная функции (f(x)) отрицательна, то сама функция (f(x)) на ((2; 5]) убывает, тогда (y = f(x)) на отрезке ([2; 5]) принимает наибольшее значение при (x = 2).
Ответ: 2
Итоговый экзамен по математике для выпускников 11-х классов обязательно включает задания на поиск точек максимума и минимума функциональных зависимостей. Их решение проводится аналитически – методом дифференцирования. Применение производной для исследования функции на экстремум сокращает время анализа и позволяет представить общий вид графика зависимости еще до выполнения построений.
Обучающий ресурс «Школково» позволит учащимся освежить в памяти главные моменты темы – уточнить теоретические знания и отработать их в решении ряда задач. Наш подход к обучению в отношении поиска точек экстремума функции через производную в типовых заданиях ЕГЭ основан на принципе глубокой взаимосвязи теории и практики. Сначала ученик читает правила «Теоретической справки», потом смотрит видео с объяснениями учителя, а затем работает с реальным педагогом. В процессе просмотра предлагаемых на сайте вебинаров можно задать интересующие вопросы и получить помощь в решении конкретных задач.
В разделе «Каталог» имеются подборки тематических заданий на нахождение точек экстремума функции с помощью производной, а также нахождения производной угла наклона касательной. Каждый пример содержит готовое решение и правильный ответ, с которыми можно ознакомиться после окончания самостоятельной работы. «Конструктор» примерных вариантов ЕГЭ позволит провести исследование экстремумов функций с помощью производных в ходе пробного выполнения экзаменационной работы.

УСТАЛ? Просто отдохни
Задание 6. Геометрический смысл производной
В задаче 6 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x0,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x0, и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x1; y1) и B (x2; y2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x2 − x1 и приращение функции Δy = y2 − y1.
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x2 − x1 = −1 − (−3) = 2; Δy = y2 − y1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x2 − x1 = 3 − 0 = 3; Δy = y2 − y1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x2 − x1 = 5 − 0 = 5; Δy = y2 − y1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x0 называется функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≥ f(x).
- Точка x0 называется функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x0 известно, что f’(x0) ≠ 0, то возможны лишь два варианта: f’(x0) ≥ 0 или f’(x0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
- Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≤ f(x2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≥ f(x2). Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
- Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l1 = − 6 − (−8) = 2;
l2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l2 = 5.
Как найти значение производной функции в точке х0 уравнение
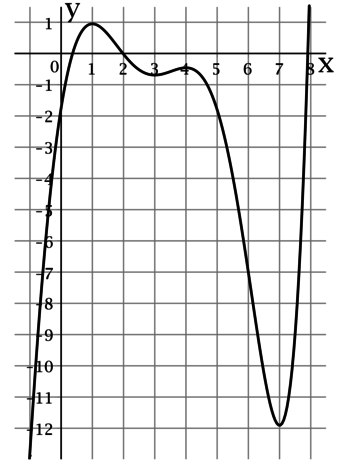
На рисунке изображен график функции y = f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
Поскольку касательная параллельна прямой y = 6 или совпадает с ней, их угловые коэффициенты равны 0. Угловой коэффициент касательной равен значению производной в точке касания. У данной функции производная равна нулю только в точках экстремума функции. На заданном интервале функция имеет 2 максимума и 2 минимума, итого 4 экстремума. Таким образом, касательная к графику функции параллельна прямой y = 6 или совпадает с ней в 4 точках.
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Найти (с решением) производную функции.
Этот математический калькулятор онлайн поможет вам если нужно найти производную функции. Программа решения производной не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения производной функции.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Вы можете посмотреть теорию о производной функции и правила дифференцирования и таблицу производных, т.е. список формул для нахождения производных от некоторых элементарных функций.
Если вам нужно найти уравнение касательной к графику функции, то для этого у нас есть задача Уравнение касательной к графику функции.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> –> Введите выражение функции Найти производную функции f(x)
Немного теории.
Определение производной
Определение. Пусть функция ( y = f(x) ) определена в некотором интервале, содержащем внутри себя точку ( x_0 ). Дадим аргументу приращение ( Delta x ) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции ( Delta y ) (при переходе от точки ( x_0 ) к точке ( x_0 + Delta x ) ) и составим отношение ( frac<Delta y> <Delta x>). Если существует предел этого отношения при ( Delta x rightarrow 0 ), то указанный предел называют производной функции ( y=f(x) ) в точке ( x_0 ) и обозначают ( f'(x_0) ).
Для обозначения производной часто используют символ ( y’ ). Отметим, что ( y’ = f(x) ) – это новая функция, но, естественно, связанная с функцией ( y = f(x) ), определенная во всех точках (x), в которых существует указанный выше предел. Эту функцию называют так: производная функции ( y = f(x) ).
Геометрический смысл производной состоит в следующем. Если к графику функции ( y = f(x) ) в точке с абсциссой ( x=a ) можно провести касательную, непараллельную оси (y), то ( f(a) ) выражает угловой коэффициент касательной:
( k = f'(a) )
Поскольку ( k = tg(a) ), то верно равенство ( f'(a) = tg(a) ) .
А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция ( y = f(x) ) имеет производную в конкретной точке ( x ):
$$ lim_ <Delta x to 0>frac<Delta y> <Delta x>= f'(x) $$
Это означает, что около точки (x) выполняется приближенное равенство ( frac<Delta y> <Delta x>approx f'(x) ), т.е. ( Delta y approx f'(x) cdot Delta x ).
Содержательный смысл полученного приближенного равенства заключается в следующем: приращение функции «почти пропорционально» приращению аргумента, причем коэффициентом пропорциональности является значение производной в заданной точке (x).
Например, для функции ( y = x^2 ) справедливо приближенное равенство ( Delta y approx 2x cdot Delta x ). Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение ( x ), найти ( f(x) )
2. Дать аргументу ( x ) приращение ( Delta x ), перейти в новую точку ( x+ Delta x ), найти ( f(x+ Delta x) )
3. Найти приращение функции: ( Delta y = f(x + Delta x) – f(x) )
4. Составить отношение ( frac<Delta y> <Delta x>)
5. Вычислить $$ lim_ <Delta x to 0>frac<Delta y> <Delta x>$$
Этот предел и есть производная функции в точке (x).
Если функция (y=f(x)) имеет производную в точке (x), то ее называют дифференцируемой в точке (x). Процедуру нахождения производной функции (y=f(x)) называют дифференцированием функции (y=f(x)).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция (y=f(x)) дифференцируема в точке (x). Тогда к графику функции в точке ( M(x; ; f(x)) ) можно провести касательную, причем, напомним, угловой коэффициент касательной равен ( f'(x) ). Такой график не может «разрываться» в точке (M), т. е. функция обязана быть непрерывной в точке (x).
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция (y=f(x)) дифференцируема в точке (x), то выполняется приближенное равенство ( Delta y approx f'(x) cdot Delta x ). Если в этом равенстве ( Delta x ) устремить к нулю, то и ( Delta y ) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке.
Обратное утверждение неверно. Например: функция ( y=|x|) непрерывна везде, в частности в точке (x=0), но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.
Еще один пример. Функция ( y=sqrt[3] ) непрерывна на всей числовой прямой, в том числе в точке (x=0). И касательная к графику функции существует в любой точке, в том числе в точке (x=0). Но в этой точке касательная совпадает с осью (y), т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид (x=0). Углового коэффициента у такой прямой нет, значит, не существует и ( f'(0) )
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу.
Если (C) — постоянное число и ( f=f(x), ; g=g(x) ) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
[spoiler title=”источники:”]
http://ege.sdamgia.ru/test?theme=68
http://www.math-solution.ru/math-task/derivative
[/spoiler]
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).


Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
(-7): минимум.
(3): максимум.
Все вышесказанное можно обобщить следующими выводами:
– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
– Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
– если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
– если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
– если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
Ответ. (-2).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов
Скачать статью