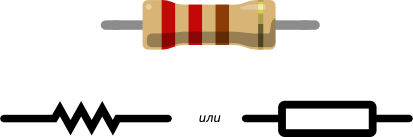
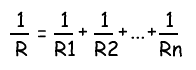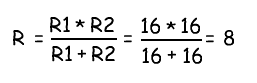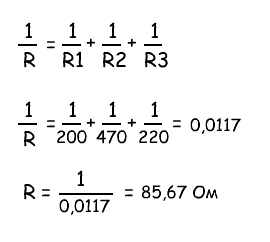Резистор и сопротивление
Теория
Резистор — искусственное «препятствие» для тока. Сопротивление в чистом виде. Резистор ограничивает силу тока, переводя часть электроэнергии в тепло. Сегодня невозможно изготовить ни одно, сколько-нибудь функциональное, электронное устройство без резисторов. Они используются везде: от компьютеров до систем охраны.
Сопротивление резистора — его основная характеристика. Основной единицей электрического сопротивления является Ом. На практике используются также производные единицы — килоом (кОм), мегаом (МОм), гигаом (ГОм), которые связаны с основной единицей следующими соотношениями:
1 кОм = 1000 Ом,
1 МОм = 1000 кОм,
1 ГОм = 1000 МОм
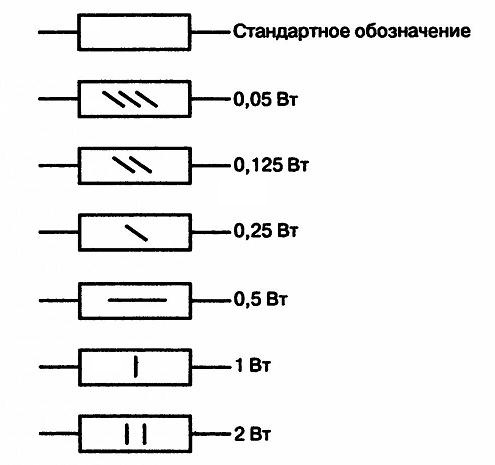
Ниже на рисунке видна маркировка резисторов на схемах:
Наклонные линии обозначают мощность резистора до 1 Вт. Вертикальные линии и знаки V и X (римские цифры), указывают на мощность резистора в несколько Ватт, в соответствии со значением римской цифры.
Для соединения резисторов в схемах используются три разных способа подключения: параллельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
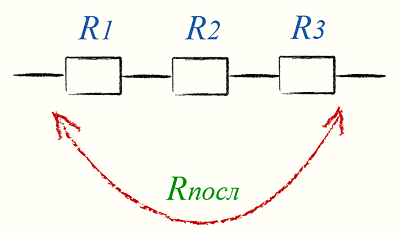
Последовательное соединение резисторов
Последовательное соединение резисторов применяется для увеличения сопротивления. Т.е. когда резисторы соединены последовательно, общее сопротивление равняется сумме сопротивлений каждого резистора. Например, если резисторы R1 и R2 соединены последовательно, их общее сопротивление высчитывается по формуле:
Rобщ = R1 + R2
Это справедливо и для большего количества соединённых последовательно резисторов:
Rобщ = R1 + R2 + R3 + … + Rn
Цепь из последовательно соединённых резисторов будет всегда иметь сопротивление большее, чем у любого резистора из этой цепи.
При последовательном соединении резисторов изменение сопротивления любого резистора из этой цепи влечёт за собой как изменение сопротивления всей цепи так и изменение силы тока в этой цепи.
Мощность при последовательном соединении
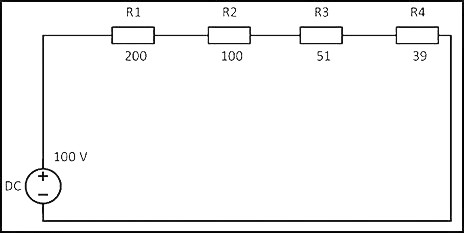
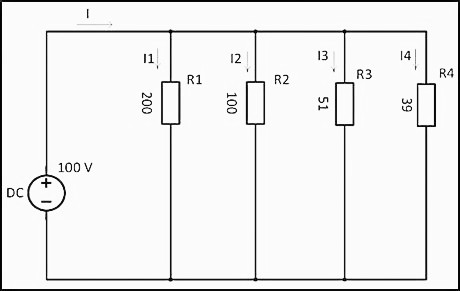
При соединении резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат:
R = 200 + 100 + 51 + 39 = 390 Ом
Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять
I = U/R = 100 В/390 Ом = 0,256 A
На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле:
P = I2 x R = 0,2562 x 390 = 25,55 Вт
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
P1 = I2 x R1 = 0,2562 x 200 = 13,11 Вт;
P2 = I2 x R2 = 0,2562 x 100 = 6,55 Вт;
P3 = I2 x R3 = 0,2562 x 51 = 3,34 Вт;
P4 = I2 x R4 = 0,2562 x 39 = 2,55 Вт.
Если сложить полученные мощности, то общая Р составит:
Робщ = 13,11 + 6,55 + 3,34 + 2,55 = 25,55 Вт
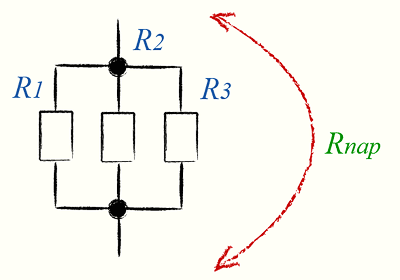
Параллельное соединение резисторов
Параллельное соединение резисторов необходимо для уменьшения общего сопротивления и, как вариант, для увеличения мощности нескольких резисторов по сравнению с одним.
Расчет параллельного сопротивления двух параллельно соединённых резисторов R1 и R2 производится по следующей формуле:
Rобщ = (R1 × R2) / (R1 + R2)
Параллельное соединение трёх и более резисторов требует более сложной формулы для вычисления общего сопротивления:
1 / Rобщ = 1 / R1 + 1 / R2 + … + 1 / Rn
Сопротивление параллельно соединённых резисторов будет всегда меньше, чем у любого из этих резисторов.
Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением. Общая мощность, в таком случае, вычисляется умножением мощности одного резистора на количество параллельно соединённых резисторов.
Мощность при параллельном соединении
При параллельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
1/R = 1/200 + 1/100 + 1/51 + 1/39 ≈ 0,06024 Ом
R = 1 / 0,06024 ≈ 16,6 Ом
Используя значение напряжения 100 В, по закону Ома рассчитывается сила тока
I = U/R = 100 В x 0,06024 Ом = 6,024 A
Зная силу тока, мощность резисторов, соединенных параллельно, определяется следующим образом
P = I2 x R = 6,0242 x 16,6 = 602,3 Вт
Расчет силы тока для каждого резистора выполняется по формулам:
I1 = U/R1 = 100/200 = 0,5 A;
I2 = U/R2 = 100/100 = 1 A;
I3 = U/R3 = 100/51 = 1,96 A;
I4 = U/R4 = 100/39 = 2,56 A
На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при параллельном подключении резисторов:
P1 = U2/R1 = 1002/200 = 50 Вт;
P2 = U2/R2 = 1002/100 = 100 Вт;
P3 = U22/R3 = 1002/51 = 195,9 Вт;
P4 = U22/R4 = 1002/39 = 256,4 Вт
Если сложить полученные мощности, то общая Р составит:
Робщ = 50 + 100 + 195,9 + 256,4 = 602,3 Вт
Калькулятор
Цветовая маркировка резисторов
Наносить номинал резистора на корпус числами — дорого и непрактично: они получаются очень мелкими. Поэтому номинал и допуск кодируют цветными полосками. Разные серии резисторов содержат разное количество полос, но принцип расшифровки одинаков. Цвет корпуса резистора может быть бежевым, голубым, белым. Это не играет роли. Если не уверены в том, что правильно прочитали полосы, можете проверить себя с помощью мультиметра или калькулятора цветовой маркировки.
Калькулятор цветовой маркировки резисторов
Основные характеристики
| Сопротивление (номинал) | R | Ом |
| Точность (допуск) | ± | % |
| Мощность | P | Ватт |
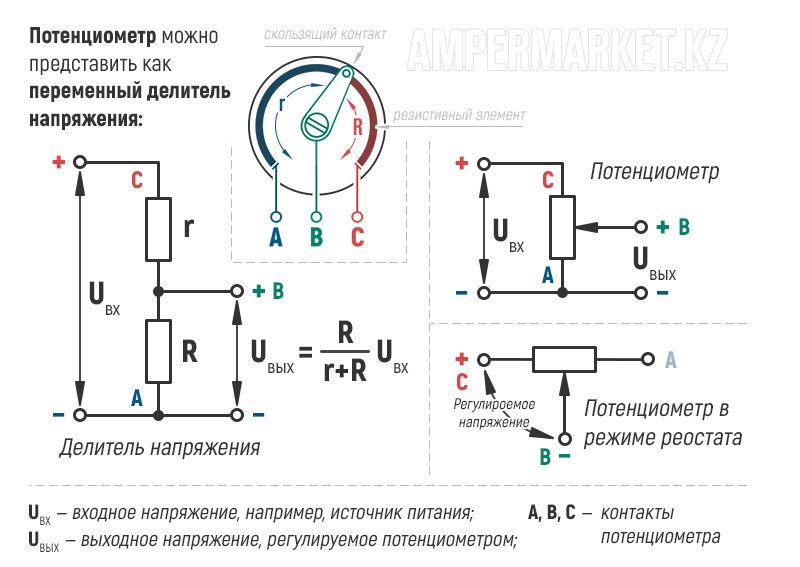
Переменный резистор
Переменный резистор — это резистор, у которого электрическое сопротивление между подвижным контактом и выводами резистивного элемента можно изменять механическим способом. Переменные резисторы (их также называют реостатами или потенциометрами) предназначены для постепенного регулирования силы тока и напряжения. Разница в том, что реостат регулирует силу тока в электрической цепи, а потенциометр — напряжение. Выглядят переменные резисторы так:
На радиосхемах переменные резисторы обозначаются прямоугольником с пририсованной к их корпусу стрелочкой.
Регулировать величину сопротивления переменных резисторов можно с помощью вращения специальной ручки. Те из резисторов, у которых регулировка сопротивления резистора может осуществляться только с помощью отвертки или специального ключа-шестигранника, называются подстроечными переменными резисторами.
Термисторы, варисторы и фоторезисторы
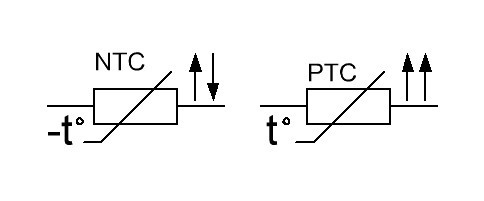
Кроме реостатов и потенциометров есть и другие виды резисторов: термисторы, варисторы и фоторезисторы. Термисторы, в свою очередь, делятся на термисторы и позисторы. Позистор – это термистор, у которого сопротивление возрастает вместе с ростом температуры окружающей среды. У термисторов, наоборот, чем выше температура вокруг, тем меньше сопротивление. Это свойство обозначают как ТКС – тепловой коэффициент сопротивления.
В зависимости от ТКС (отрицательный он или положительный) обозначают на схеме термисторы следующим образом:
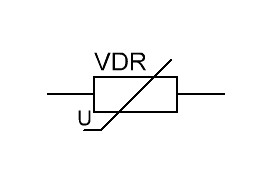
Следующий особый класс резисторов – это варисторы. Они изменяют силу сопротивления в зависимости от подаваемого на них напряжения. Зная свойства варистора, можно догадаться, что такой резистор защищает электрическую цепь от перенапряжения.
На схемах варисторы обозначаются так:
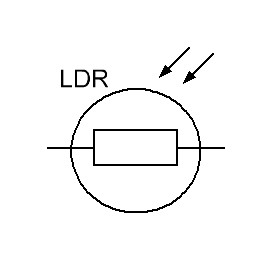
В зависимости от интенсивности освещения изменяет свое сопротивление еще один вид резисторов – фоторезисторы. Причем не важно, каков источник освещения: искусственный или естественный. Их особенность еще и в том, что ток в них протекает как в одном, так и в другом направлении, то есть еще говорят, что фоторезисторы не имеют p-n перехода.
А на схемах изображаются так:
Один из способов определения силы тока в резисторе – это ее прямое измерение мультиметром. Измерения следует проводить в разрыве цепи после резистора следующим образом:
– выставить на тестере максимально допустимый диапазон,
– присоединить щупы прибора к месту разрыва цепи.
Применив закон Ома, искомую величину можно также определить расчетным путем:
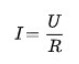
где I – сила тока, U – напряжение, R – сопротивление (единицы измерения ампер (А), вольт (В), ом (Ом) соответственно).
В приборостроении и электротехнике применяются различные типы соединения и подключения резисторов, что обеспечивает разнообразие электротехнических свойств электрических схем.
Типы соединений резисторов
Соединение элементов в одну цепь осуществляется следующими способами:
-
последовательно;
-
параллельно;
-
смешанно.
Общие схемы типов соединений представлены на рисунке 1.
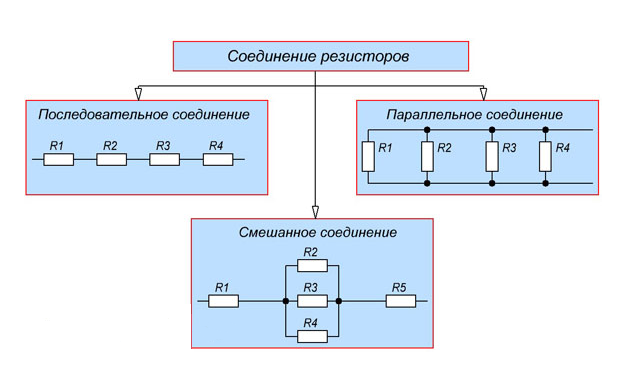
Рисунок 1. Типы соединений резисторов
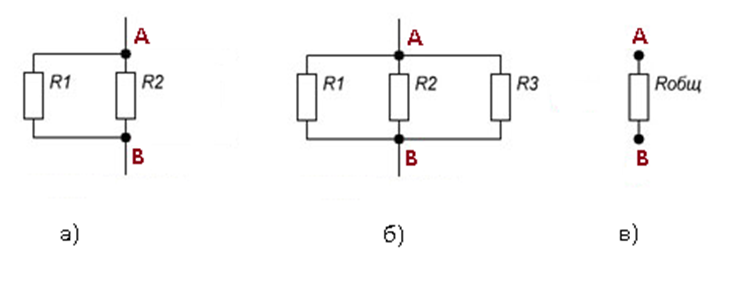
Параллельным соединением принято считать соединение, при котором элементы цепи соединены так, что их начала могут соединиться в одной точке, а концы – в другой (см.рис.2)
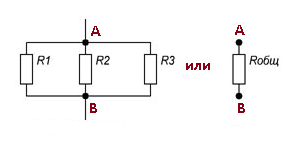
Рисунок 2. Параллельное соединение резисторов
Потоку заряженных частиц при прохождении участка АВ предоставлено несколько вариантов пути, поэтому на каждом участке с резистором будет протекать ток, величиной, обратно пропорциональной сопротивлению резистора.
При увеличении нагрузки параллельного соединения, в случае подключения большого числа резисторов способом параллельного соединения в электрическую цепь, общее сопротивление цепи значительно уменьшится, за счет увеличения числа путей, предоставленных потоку заряженных частиц. Увеличение количества возможных вариантов движения влечет за собой уменьшение противодействия движению тока.
Как найти сопротивление параллельно соединенных резисторов?
Общее сопротивление резисторов в случае параллельного соединения определено по закону Ома в следующем соотношении:
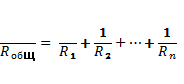
и рассчитывается по формуле:
Для примера произведем расчет общего сопротивления для цепи из двух резисторов, обладающих сопротивлением R1= R2=7Ом (см. рис.3а)
R12= 7*7/ (7+7) = 3,5Ом
Сопротивление на участке АВ
(1– 2) в 2 раза меньше R каждого из резисторов.
При параллельном подсоединении к рассматриваемой цепи еще одного резистора, также обладающего аналогичным сопротивлением R3=7Ом (см. рис.3б) общее сопротивление цепи рассчитывается с учетом предыдущих вычислений, где R12= 3,5Ом
Rобщ= 3,5*7/ (3,5+7) = 2,33 Ом
R123< R3
Рисунок 3. Увеличение цепи параллельного соединения резисторов
Из расчетов следует, что общее сопротивление (см. рис.3в) всегда будет меньше сопротивления любого параллельно включенного резистора. Такое условие обеспечивается равенством токов на входе и выходе узлов или групп параллельных резисторов и постоянством напряжения в сети.
Что такое последовательное соединение резисторов?
При последовательном соединении резисторы подсоединяются друг за другом, при этом конец предыдущего резистора соединен с началом последующего резистора (рисунок 4).
Рисунок 3. Последовательное соединение резисторов.
Потоку заряженных частиц при прохождении участка АВ предоставлен один путь, поэтому, чем больше резисторов подсоединено, тем большее сопротивление движущимся заряженным частицам они оказывают, то есть общее сопротивление участка цепи Rобщ возрастает.
Формула для расчета общего сопротивления при последовательном соединении имеет вид:
Как рассчитать напряжения на последовательно соединенных резисторах?
Последовательное соединение резисторов увеличивает общее сопротивление. Ток во всех частях схемы будет одинаковым, при этом будет определяться падение напряжения на каждом резисторе.
Общее напряжение питания на резисторах, соединенных последовательно, равно сумме разностей потенциалов на каждом резисторе:
URобщ =UR1+ UR2 + UR3+ UR4
Применив закон Ома, можно вычислить напряжение на каждом резисторе:
UR1=I*R1, UR2=I*R2, UR3=I*R3, UR4=I*R4
Напряжение на участке АВ рассчитывается по формуле:
UАВ=I* (R1
+ R2+R3+R4)
А ток в цепи:
Резисторы, соединенные последовательно, применяются в электротехнике в качестве делителя напряжения.
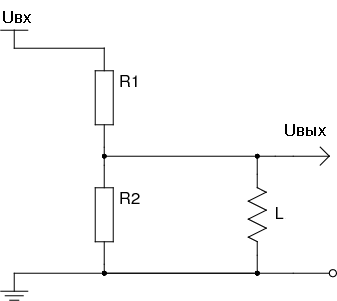
Рисунок 5. Схема простейшего делителя напряжения
Регулируя сопротивление обоих резисторов можно выделить требуемую часть входящего напряжения. При необходимости деления напряжения на несколько частей к источнику напряжения подключается несколько последовательно соединенных резисторов.
Смешанное соединение резисторов
В электротехнике наиболее распространено использование различных комбинаций параллельного и последовательного подключения. Силу тока при смешанном соединении резисторов определяют путем разделения цепи на последовательно соединенные части. Однако для определения общего сопротивления в случае параллельного сопротивления различных частей следует применять соответствующую формулу.
Алгоритм расчета смешанного подключения аналогичен правилу расчета базовой схемы последовательного и параллельного подключения резисторов. В этом нет ничего нового: нужно правильно разложить предложенное решение на пригодные для расчета части. Участки с элементами подключаются поочередно или параллельно. Гибридное резистивное соединение представляет собой комбинацию последовательного и параллельного. Эту комбинацию иногда называют последовательно-параллельным соединением.
На рисунке 6 представлена схема смешанного соединения резисторов.
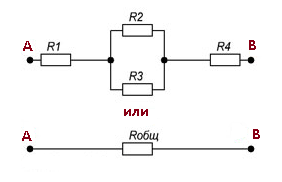
Рисунок 6. Смешанное соединение резисторов.
На рисунке показано, что резисторы R2 и R3
соединены параллельно, а R1, R23
и R4 последовательно.
Чтобы рассчитать сопротивление этого соединения, вся схема делится на простейшие части, начиная с параллельного или последовательного сопротивления. Тогда следующий алгоритм выглядит следующим образом:
1. Определите эквивалентное сопротивление части резистора, подключенной параллельно.
2. Если эти части содержат резисторы, включенные последовательно, сначала рассчитайте их сопротивление.
3. Вычислив эквивалентное сопротивление резистора, перерисовываем схему. Обычно схема получается из последовательного эквивалентного сопротивления.
4. Рассчитайте сопротивление цепи.
Другие способы подключения хорошо видны на примере, показанном на рисунке. Без специальных расчетов очевидно, что параллельное соединение резисторов создает несколько путей для тока. Следовательно, в одиночном контуре его сила будет меньше по сравнению с контрольными точками на входе и выходе. При этом напряжение на отметке остается неизменным.
Пример участка цепи для расчета сопротивления смешанного соединения показан на рисунке 5.
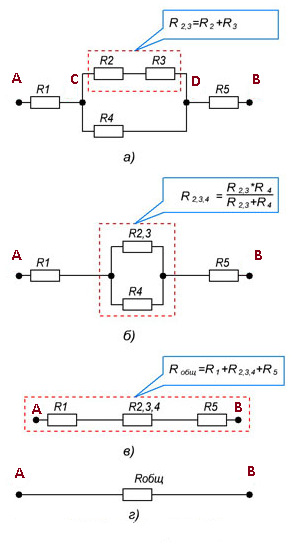
Рисунок 7. Общее сопротивление участка цепи со смешанным соединением резисторов.
Какие есть формулы для вычисления сопротивления резистора
Содержание
- 1 Что такое резистор
- 2 Сопротивление резистора
- 3 Последовательная цепь источника и сопротивлений
- 4 Параллельная схема элементов
- 5 Расчет смешанного соединения элементов схемы
- 6 Мощность рассеивания
- 7 Параметры резисторов
- 8 Определение параметров по маркировке и схеме
- 9 Видео по теме
Сопротивление направленному движению электронов (электрическому току) в проводах электроснабжения чаще всего провоцирует потери. Они зависят от площади сечения (S), длины (L), удельного сопротивления вещества провода (ρ). Однако, сопротивление послужило созданию самого распространенного элемента в электронике — резистора.
Что такое резистор
Деталь электрической или электронной схемы, сопротивляющаяся прохождению электрического тока, называется резистор (от латинского resisto — сопротивляюсь). Падение или изменение напряжения на этом элементе используется в схемотехнике для получения нужных процессов управления автоматикой или преобразования электричества в свет, тепло, звук или движение.
Наиболее удобно классифицировать резисторы по следующим признакам:
- назначение. Для различных сфер используют элементы с
общими свойствами или специфическими по частоте тока, точности изготовления или ограничения по напряжению;
- способ управления сопротивлением. Постоянные резисторы в определенном диапазоне напряжения и тока не меняют сопротивление. У переменных можно менять вручную данный параметр с целью управления процессами. Подстроечные используются для корректировки режимов при наладке и после ремонта;
- материал рабочей части резистора. Металлы, их окислы и сплавы, графитовые или композитные смеси;
- вид резистивных тел. Проволока, фольга или ленты из метала, напыление пленки на керамику, интегрированные каналы в микросхеме;
- способ размещения. Резисторы могут быть впаяны в электронную плату, устанавливаться отдельно на панели управления или закладываться при создании микросхемы внутри изделия;
- характер изменения падения напряжения на элементе от внешних условий (ВАХ). Вольт-амперная характеристика в рабочем диапазоне резистора может быть линейной или нелинейной.
Нелинейная ВАХ отражает изменение сопротивления компонента от внешних условий. Такие резисторы служат датчиками напряжения (варисторы), магнитного поля (магниторезисторы), уровня освещенности (фоторезисторы), перепада температуры (терморезисторы), изменения деформации (тензорезисторы).
Сопротивление резистора
У тех, кто только начинает изучать азы электротехники, часто возникает вопрос, а чем отличается резистор от сопротивления. Разница в том, что резистор является пассивным элементом электроцепи, а сопротивление — это характеристика данного элемента, которую можно рассчитать, определить по маркировке или измерить. Но зачастую сопротивление используется в качестве синонима слова «резистор».
Рассчитать внутреннее сопротивление резистора в сети постоянного тока помогает формула закона Ома для элемента цепи:
Эту формулу применяют также для расчета активного сопротивления в сети переменного тока, но используют действующий ток через элемент. Он равен постоянному току, при котором выделяется на резисторе столько же теплоты, сколько за одинаковое время при прохождении импульсного или синусоидального тока различной частоты.
Суммарное электрическое сопротивление в сетях переменного тока вычисляется при учете активной и реактивной составляющей участка цепи. Любой вид сопротивления измеряется в омах.
Одинокий резистор в схеме часто используется как ограничитель тока. На электронных платах этих элементов много. Друг с другом они соединяются в различных комбинациях: последовательно, параллельно или по смешанной системе.
Последовательная цепь источника и сопротивлений
В замкнутом контуре из последовательно соединенных резисторов и батареи ток в разных точках цепи имеет одинаковое значение. Показание вольтметра на отдельном резисторе будет отражать произведение его внутреннего сопротивления на ток в контуре. Суммарные показания вольтметров будут равны напряжению источника, а для определения общего сопротивления резисторов надо сложить сопротивления всех элементов.
Последовательную цепочку сопротивлений часто используют как делитель напряжения в маломощных измерительных или задающих ступенчатое управление параметрами устройствах. Сопротивление нагрузки Rн, подключенной параллельно R1 вместо вольтметра, должно быть немного больше, чтобы делитель работал стабильно.
Параллельная схема элементов
При параллельном соединении на каждом элементе присутствует напряжение источника, общий ток равен сумме токов резисторов. Расчет сопротивления участка цепи осуществляется по формуле R = (R1 • R2) / (R1 + R2).
Отличие параллельного соединения от последовательного заключается в том, что каждый резистор получает напряжение, которое равно напряжению источника, а общее сопротивление участка меньше меньшего из его составляющих.
Расчет смешанного соединения элементов схемы
Перед тем как рассчитать общее сопротивление схемы, состоящей из параллельных и последовательных участков, используют методы упрощения. На каждом шаге упрощенные эквивалентные схемы можно посчитать по уже известным формулам. Полученный в результате резистор будет обладать общим сопротивлением исходной схемы.
Мощность рассеивания
Для надежной работы электрической схемы нужно знать и сопротивление резистора, и мощность рассеивания, формула для вычисления последней имеет вид:
Правильно подобранный элемент схемы должен рассеять мощность Р (Вт) не разрушаясь и не нагревая другие детали.
Параметры резисторов
Выбор резисторов происходит чаще всего по следующим основным параметрам:
- номинальному сопротивлению. Подбирается или подгоняется ближайшее к расчетному;
- допуску — характеристика, отражающая точность при изготовлении номинального сопротивления. Она составляет 5–20%;
- номинальной мощности рассеивания. Наибольшая величина рассеянного тепла без изменения характеристик меньше номинала элемента;
- предельному рабочему напряжению. Приложенное к выводам резистора наибольшее напряжение, которое не разрушает его;
- температурный коэффициент. Показывает, как изменится сопротивление резистора при колебании на один градус температуры среды.
Для переменных резисторов учитывают ряд дополнительных характеристик:
- износоустойчивость — число циклов;
- функцию изменения сопротивления (линейная, логарифмическая, обратнологарифмическая);
- уровень шума при движении ползунка.
Определение параметров по маркировке и схеме
Некоторые из параметров наносятся непосредственно на резисторы, например, сопротивление и допуск. Раньше для информации о них использовали буквы и цифры. Номинальное сопротивление резисторов имеет диапазон от 0.01 Ом до 1 ГОм. Цифры в маркировке обозначают номинал, а буквы — множитель. Конкретная величина получается умножением или делением цифр.
Буквенно-цифровая маркировка предполагает использование букв Е и R для сопротивлений до 99 Ом, выше — К, а уровень мегаомов обозначается буквой М. В зависимости от того, какую позицию занимает буква в цифровом коде, определяются целые числа или дробные. Узнать, какому множителю соответствует определенная буква, поможет специальная таблица, которую можно найти в любом справочном пособии.
Элементы с цифро-буквенной маркировкой сейчас можно найти преимущественно в старой аппаратуре. В ходе ее ремонта часто приходится менять резисторы, поэтому необходимо уметь расшифровывать такое обозначение.
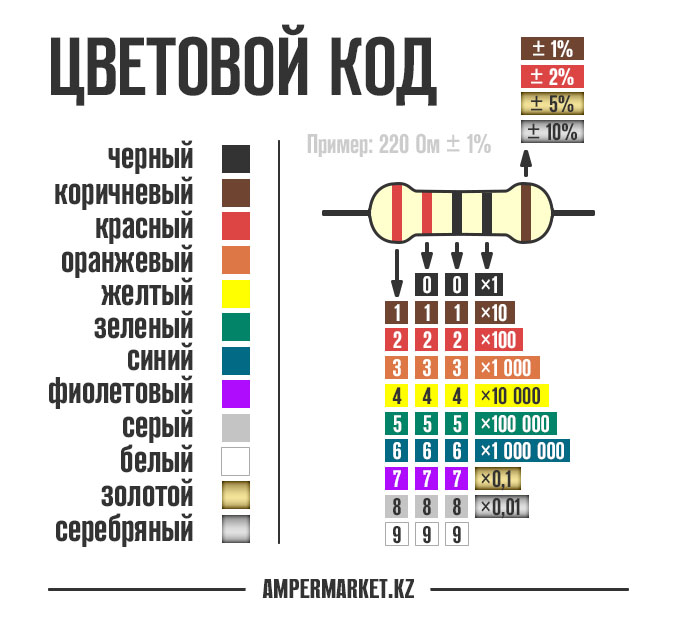
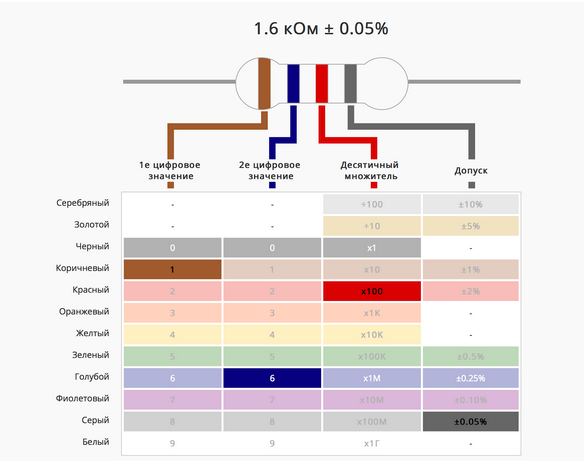
Сейчас в угоду минимизации отказались от буквенно-цифровых обозначений. На поверхность резисторов наносится маркировка кольцами или точками разных цветов. Чтобы определить по полоскам сопротивление резистора, следует начинать со смещенной к одному из выводов или самой широкой цветной полоски.
Набор цветов первых трех колец при 5 и 6-полосной раскраске означает шифр сопротивления резистора, цвет четвертого кольца обозначает определенное значение множителя для него. Цвет пятого кольца показывает точность изготовления резистора. При шестиполосной окраске цвет последнего кольца обозначает изменение сопротивления (процент) при перепаде температуры окружающей среды на 1 градус. Четырех и пятиполосная раскраска его не имеет.
При четырехполосной маркировке сопротивление резисторов определяется по цветам первых двух. Цвет третьей полосы — это множитель для точного определения сопротивления. Последняя полоса своей расцветкой говорит о допуске в процентах от номинала.
На электрической схеме резистор изображается в виде прямоугольника с размерами 4×10 мм. Рядом с изображением указывается буква R и цифра, обозначающая порядковый номер элемента на схеме, например, R1. Указывается также номинальное сопротивление. Как определить его по буквенно-цифровой маркировке, было рассказано выше.
Мощность рассеивания указывается на графическом изображении специальными метками, если этот параметр меньше 1 ватта. Как узнать мощность по ним подскажет таблица, приведенная ниже.
Если мощность рассеивания выше одного ватта, то внутри прямоугольника ставят римскую цифру. Например, V используется для мощности величиной 5 Вт, Х — 10 Вт и т. п.
Бывают случаи, когда нет возможности воспользоваться маркировкой, например, если она повреждена или стерта. В таком случае нужно знать, как измерить сопротивление специальным прибором. Это может быть омметр или мультиметр. Они мало чем отличаются, но последний является многофункциональным прибором. Принцип измерений основывается на законе Ома. Перед тем как проверить резистор, следует выставить рабочий режим и диапазон измеряемого сопротивления.
Алгоритм по измерению сопротивления используется такой:
Резистор является довольно простым элементом и по своему устройству, и по принципу работы. Поэтому его сопротивление определяется также довольно просто. Еще больше облегчают задачу онлайн-калькуляторы. Ими можно воспользоваться, если возникает необходимость рассчитывать сопротивление многих элементов, для соединения которых применяются разные способы, а также для расшифровки маркировки в виде цветных полос.
Видео по теме
Главная » Справочник » Параллельное соединение резисторов. Калькулятор для расчета
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Блок питания 0…30В/3A
Набор для сборки регулируемого блока питания…
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (закон Ома для участка цепи).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Правило Кирхгофа гласит: «Общий ток, входящий в цепь равен току выходящему из цепи».
Таким образом, протекающий общий ток в цепи можно определить как:
I = I1 + I2
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, входящего в параллельное соединение.

Инвертор 12 В/ 220 В
Инвертор с чистой синусоидой, может обеспечивать питание переменно…
Сопротивление
Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.
Сопротивление — физическая величина, которая показывает способность проводника пропускать электрический ток. Чем выше сопротивление, тем ниже эта способность.

Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.
Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.
Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.
Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала.
Эту закономерность можно описать следующей формулой:
Сопротивление
R = ρ · l/S
R — сопротивление [Ом]
l — длина проводника [м]
S — площадь поперечного сечения [мм2]
ρ — удельное сопротивление [Ом · мм2/м]
Единица измерения сопротивления — ом. Названа в честь физика Георга Ома.
Будьте внимательны!
Площадь поперечного сечения проводника и удельное сопротивление содержат в своих единицах измерения мм2. В таблице удельное сопротивление всегда дается в такой размерности, да и тонкий проводник проще измерять в мм2. При умножении мм2 сокращаются и мы получаем величину в СИ.
Но это не отменяет того, что каждую задачу нужно проверять на то, что там мм2 в обеих величинах! Если это не так, то нужно свести не соответствующую величину к мм2.
Знайте!
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
Удельное сопротивление проводника — это физическая величина, которая показывает способность материала пропускать электрический ток. Это табличная величина, она зависит только от материала.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Полезные подарки для родителей
В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!
Таблица удельных сопротивлений различных материалов
|
Материал |
Удельное сопротивление ρ, Ом · мм2/м |
|
Алюминий |
0,028 |
|
Бронза |
0,095–0,1 |
|
Висмут |
1,2 |
|
Вольфрам |
0,05 |
|
Железо |
0,1 |
|
Золото |
0,023 |
|
Иридий |
0,0474 |
|
Константан (сплав NiCu + Mn) |
0,5 |
|
Латунь |
0,025–0,108 |
|
Магний |
0,045 |
|
Манганин (сплав меди марганца и никеля — приборный) |
0,43–0,51 |
|
Медь |
0,0175 |
|
Молибден |
0,059 |
|
Нейзильбер (сплав меди, цинка и никеля) |
0,2 |
|
Натрий |
0,047 |
|
Никелин (сплав меди и никеля) |
0,42 |
|
Никель |
0,087 |
|
Нихром (сплав никеля, хрома, железа и марганца) |
1,05–1,4 |
|
Олово |
0,12 |
|
Платина |
0,107 |
|
Ртуть |
0,94 |
|
Свинец |
0,22 |
|
Серебро |
0,015 |
|
Сталь |
0,103–0,137 |
|
Титан |
0,6 |
|
Хромаль |
1,3–1,5 |
|
Цинк |
0,054 |
|
Чугун |
0,5–1,0 |
Резистор
Все реальные проводники имеют сопротивление, но его стараются сделать незначительным. В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.
Из-за того, что проводник у нас «кругом-бегом-такой-идеальный», чаще всего за сопротивление в цепи отвечает резистор. Это устройство, которое нагружает цепь сопротивлением.
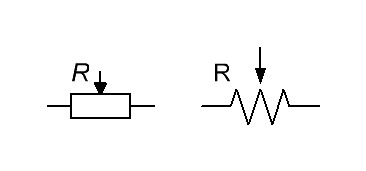
Вот так резистор изображается на схемах:
В школьном курсе физики используют европейское обозначение, поэтому запоминаем только его. Американское обозначение можно встретить, например, в программе Micro-Cap, в которой инженеры моделируют схемы.
Вот так резистор выглядит в естественной среде обитания:
Полосочки на нем показывают его сопротивление.
На сайте компании Ekits, которая занимается продажей электронных модулей, можно выбрать цвет резистора и узнать значение его сопротивления:
Источник: сайт компании Ekits
О том, зачем дополнительно нагружать сопротивлением цепь, мы поговорим в этой же статье чуть позже.
Реостат
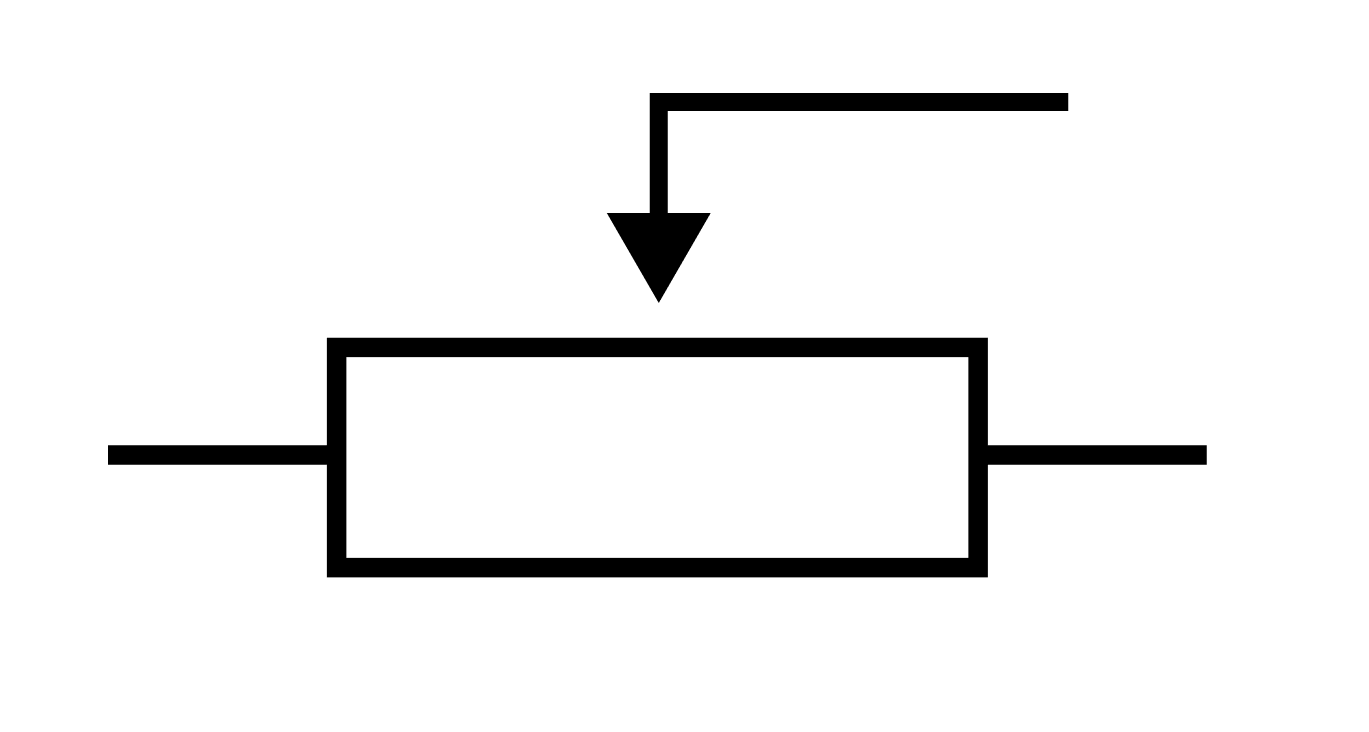
Есть такие выключатели, которые крутишь, а они делают свет ярче-тусклее. В такой выключатель спрятан резистор с переменным сопротивлением — реостат.
Стрелка сверху — это ползунок. По сути, он отсекает ту часть резистора, которая находится от него справа. То есть, если мы двигаем ползунок вправо — мы увеличиваем длину резистора, а значит и сопротивление. И наоборот — двигаем влево и уменьшаем.
По формуле сопротивления это очень хорошо видно, так как длина проводника находится в числителе:
Сопротивление
R = ρ · l/S
R — сопротивление [Ом]
l — длина проводника [м]
S — площадь поперечного сечения [мм2]
ρ — удельное сопротивление [Ом · мм2/м]
Закон Ома для участка цепи
С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит. Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.
Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. В результате этих реакций выделяется энергия, которая потом передается электрической цепи.
У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «−».
У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.
Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.
Математически его можно описать вот так:
Закон Ома для участка цепи
I = U/R
I — сила тока [A]
U — напряжение [В]
R — сопротивление [Ом]
Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее.
Сила тока измеряется в амперах, а подробнее о ней вы можете прочитать в нашей статье. 😇
Давайте решим несколько задач на закон Ома для участка цепи.
Задача раз
Найти силу тока в лампочке накаливания торшера, если его включили в сеть напряжением 220 В, а сопротивление нити накаливания равно 880 Ом.
Решение:
Возьмем закон Ома для участка цепи:
I = U/R
Подставим значения:
I = 220/880 = 0,25 А
Ответ: сила тока, проходящего через лампочку, равна 0,25 А
Давайте усложним задачу. И найдем силу тока, зная все параметры для вычисления сопротивления и напряжение.
Задача два
Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а длина нити накаливания равна 0,5 м, площадь поперечного сечения 0,01 мм2, а удельное сопротивление нити равно 1,05 Ом · мм2/м.
Решение:
Сначала найдем сопротивление проводника.
R = ρ · l/S
Площадь дана в мм2, а удельное сопротивления тоже содержит мм2 в размерности.
Это значит, что все величины уже даны в СИ и перевод не требуется:
R = 1,05 · 0,5/0,01 = 52,5 Ом
Теперь возьмем закон Ома для участка цепи:
I = U/R
Подставим значения:
I = 220/52,5 ≃ 4,2 А
Ответ: сила тока, проходящего через лампочку, приблизительно равна 4,2 А
А теперь совсем усложним! Определим материал, из которого изготовлена нить накаливания.
Задача три
Из какого материала изготовлена нить накаливания лампочки, если настольная лампа включена в сеть напряжением 220 В, длина нити равна 0,5 м, площадь ее поперечного сечения равна 0,01 мм2, а сила тока в цепи — 8,8 А
Решение:
Возьмем закон Ома для участка цепи и выразим из него сопротивление:
I = U/R
R = U/I
Подставим значения и найдем сопротивление нити:
R = 220/8,8 = 25 Ом
Теперь возьмем формулу сопротивления и выразим из нее удельное сопротивление материала:
R = ρ · l/S
ρ = RS/l
Подставим значения и получим:
ρ = 25 · 0,01/0,5 = 0,5 Ом · мм2/м
Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.
Ответ: нить накаливания сделана из константана.
Закон Ома для полной цепи
Мы разобрались с законом Ома для участка цепи. А теперь давайте узнаем, что происходит, если цепь полная: у нее есть источник, проводники, резисторы и другие элементы.
В таком случае вводится закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Так, стоп. Слишком много незнакомых слов — разбираемся по порядку.
Что такое ЭДС и откуда она берется
ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.
ЭДС — это сила, которая движет заряженные частицы в цепи. Она берется из источника тока. Например, из батарейки.
Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь. Именно эта энергия заставляет частицы двигаться по проводнику.
Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.
В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:
Закон Ома для полной цепи
I — сила тока [A]
ε — ЭДС [В]
R — сопротивление нагрузки [Ом]
r — внутреннее сопротивление источника [Ом]
Любой источник не идеален. В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.
Решим задачу на полную цепь.
Задачка
Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом
Решение:
Возьмем закон Ома для полной цепи:
Подставим значения:
A
Ответ: сила тока в цепи равна 1 А.
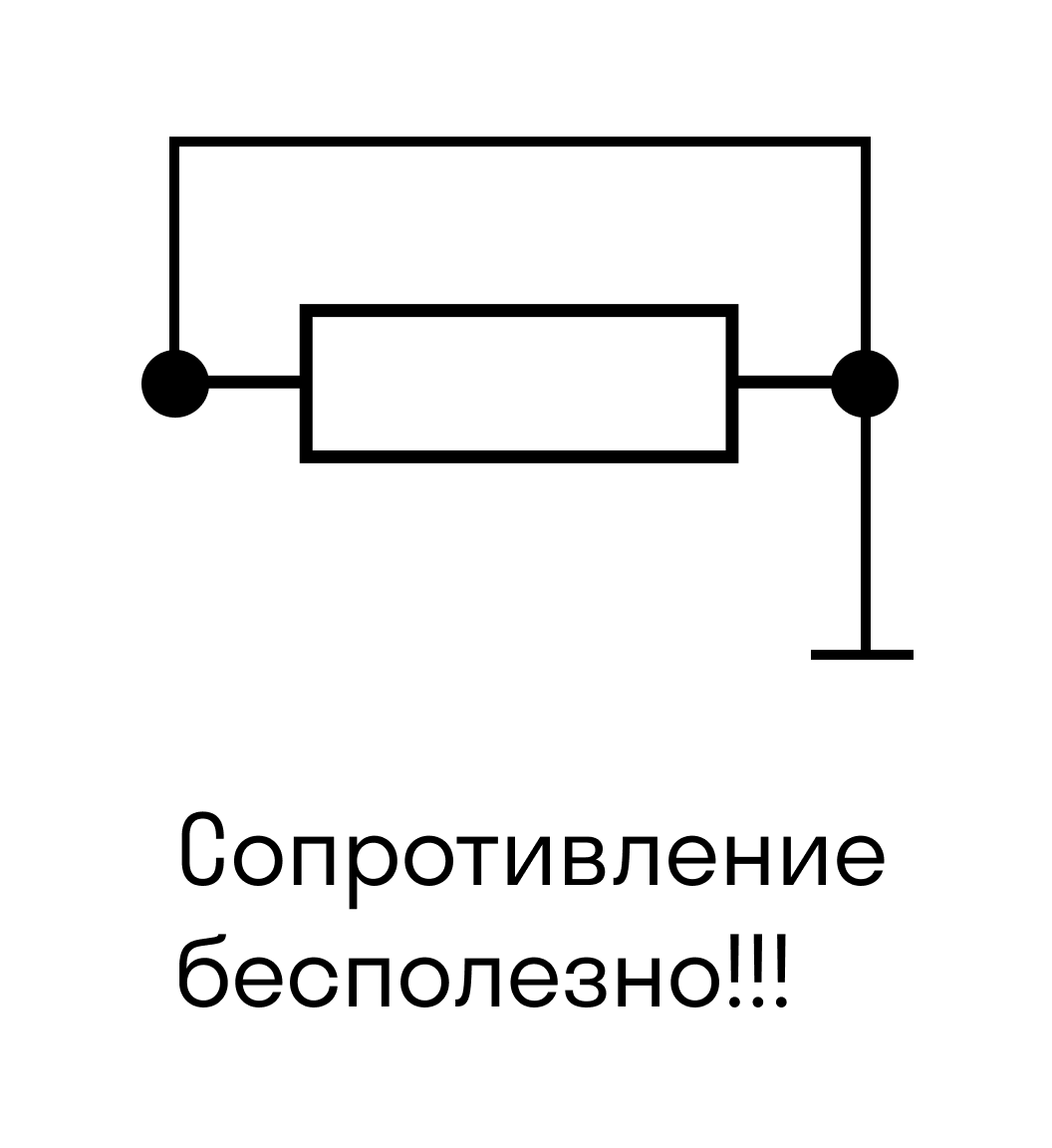
Когда «сопротивление бесполезно»
Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.
А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.
Ток идет по пути наименьшего сопротивления.
Теперь давайте посмотрим на закон Ома для участка цепи еще раз.
Закон Ома для участка цепи
I = U/R
I — сила тока [A]
U — напряжение [В]
R — сопротивление [Ом]
Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.
То есть:
I = U/0 = ∞
Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.
Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.
Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.
Параллельное и последовательное соединение
Все это время речь шла о цепях с одним резистором. Рассмотрим, что происходит, если их больше.
Зачем нужны эти соединения, если можно сразу взять резистор нужного номинала?
Начнем с того, что все электронные компоненты изготавливаются по ГОСТу. То есть есть определенные значения резисторов, от которых нельзя отойти при производстве. Это значит, что не всегда есть резистор нужного номинала и его нужно соорудить из других резисторов.
Параллельное соединение также используют, как «запасной аэродром»: когда на конечный результат общее сопротивление сильно не повлияет, но в случае отказа одного из резисторов, будет работать другой.
Признаемся честно: схемы, которые обычно дают в задачах (миллион параллельно соединенных резисторов, к ним еще последовательный, а к этому последовательному еще миллион параллельных) — в жизни не встречаются. Но навык расчета таких схем впоследствии упрощает подсчет схем реальных, потому что так вы невооруженным глазом отличаете последовательное соединение от параллельного.
Решим несколько задач на последовательное и параллельное соединение.
Задачка раз
Найти общее сопротивление цепи.
R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом, R4 = 4 Ом.
Решение:
Общее сопротивление при последовательном соединении рассчитывается по формуле:
R = R1 + R2 + R3 + R4 = 1 + 2 + 3 + 4 = 10 Ом
Ответ: общее сопротивление цепи равно 10 Ом
Задачка два
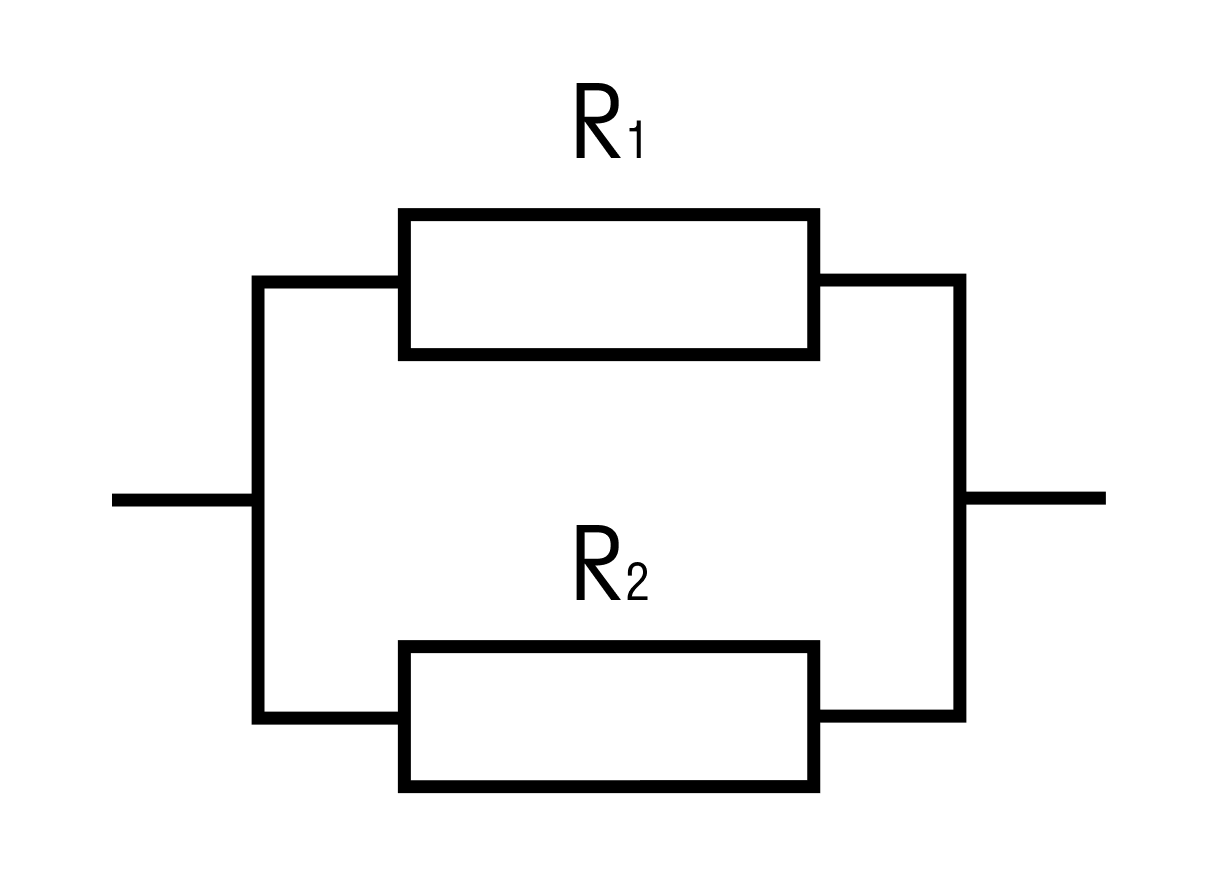
Найти общее сопротивление цепи.
R1 = 4 Ом, R2 = 2 Ом
Решение:
Общее сопротивление при параллельном соединении рассчитывается по формуле:
Ом
Ответ: общее сопротивление цепи равно
Ом
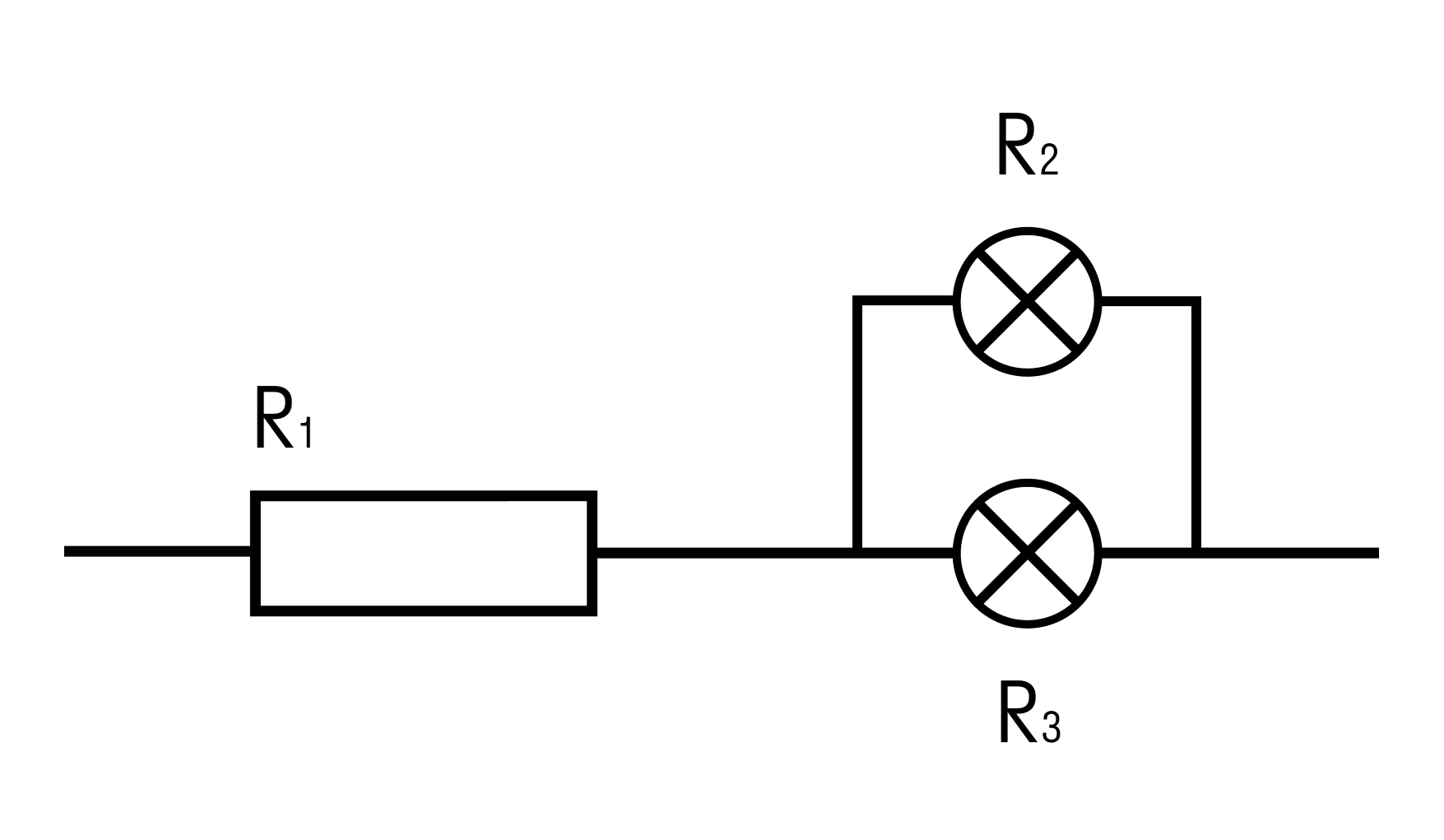
Задачка три
Найти общее сопротивление цепи, состоящей из резистора и двух ламп.
R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом
Решение:
Сначала обозначим, что лампы с точки зрения элемента электрической цепи не отличаются от резисторов. То есть у них тоже есть сопротивление, и они также влияют на цепь.
В данном случае соединение является смешанным. Лампы соединены параллельно, а последовательно к ним подключен резистор.
Сначала посчитаем общее сопротивление для ламп. Общее сопротивление при параллельном соединении рассчитывается по формуле:
Ом
Общее сопротивление при последовательном соединении рассчитывается по формуле:
R = R1 + Rламп = 1 + 1,2 = 2,2 Ом
Ответ: общее сопротивление цепи равно 2,2 Ом.
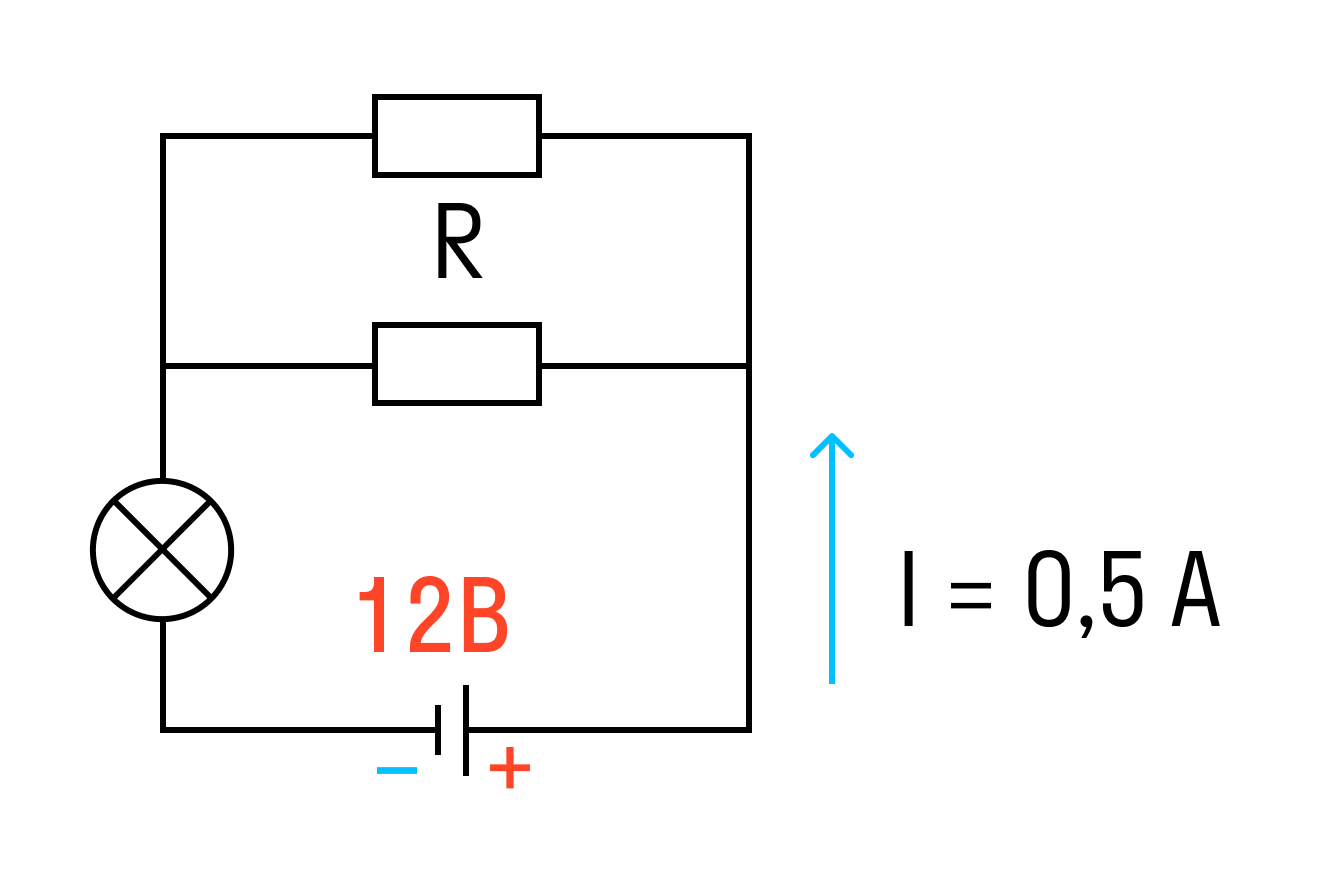
Наконец-то, последняя и самая сложная задача! В ней собрали все самое серьезное из этой статьи 💪.
Задачка четыре со звездочкой
К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.
Решение:
Найдем сначала сопротивление лампы.
Rлампы = R/2 = 10/2 = 5 Ом
Теперь найдем общее сопротивление двух параллельно соединенных резисторов.
Ом
И общее сопротивление цепи равно:
R = Rлампы + Rрезисторов = 5 + 5 = 10 Ом
Выразим внутреннее сопротивление источника из закона Ома для полной цепи.
R + r = ε/I
r = ε/I − R
Подставим значения:
r = 12/0,5 − 10 = 14 Ом
Ответ: внутреннее сопротивление источника равно 14 Ом.
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!