Синус 135 градусов найдем по формуле приведения для синуса тупого угла от 90 до 180 градусов.
Утверждение:
![]()
Доказательство:
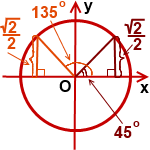
Синус угла альфа на единичной окружности — это ордината точки, полученной из точки (1;0) при повороте на угол альфа вокруг точки O.
Для синуса тупого угла (от 90º до 180º) имеет место следующая формула приведения:
![]()
Так как
![]()
то воспользовавшись этой формулой приведения и значением синуса 45º, получаем:
![]()
Что и требовалось доказать.
Если перевести 135 градусов в радианы:
![]()
то получим значение синуса 3П/4:
![]()
Лучший ответ
Наталья
Гений
(63507)
14 лет назад
sin135=sin(90+45)=cos45=корень (2)/2
Остальные ответы
ЛЮЛЯ
Профи
(987)
14 лет назад
0,7071
Включите в компьютере инженерную расклладку калькулятора
Ирина
Профи
(756)
14 лет назад
sin 135 = 0.707
М@SHUNY@
Профи
(792)
14 лет назад
по формулам приведения sin 135 = sin (90 + 45) = cos 45= (корень из 2 )/ 2
Shahlo
Профи
(922)
14 лет назад
cos45 или под корнем 2 на 2 🙂
ILuha KaNashKin
Ученик
(201)
14 лет назад
Вроде 0,7071
Trigonometry is a discipline of mathematics that studies the relationships between the lengths of the sides and angles of a right-angled triangle. Trigonometric functions, also known as goniometric functions, angle functions, or circular functions, are functions that establish the relationship between an angle to the ratio of two of the sides of a right-angled triangle. The six main trigonometric functions are sine, cosine, tangent, cotangent, secant, and cosecant.
Angles defined by the ratios of trigonometric functions are known as trigonometry angles. Trigonometric angles represent trigonometric functions. The value of the angle can be anywhere between 0-360°.

As given in the above figure in a right-angled triangle:
- Hypotenuse: The side opposite to the right angle is the hypotenuse, It is the longest side in a right-angled triangle and opposite to the 90° angle.
- Base: The side on which angle C lies is known as the base.
- Perpendicular: It is the side opposite to angle C in consideration.
Trigonometric Functions
Trigonometry has 6 basic trigonometric functions, they are sine, cosine, tangent, cosecant, secant, and cotangent. Now let’s look into the trigonometric functions. The six trigonometric functions are as follows,
sine: It is defined as the ratio of perpendicular and hypotenuse and It is represented as sin θ
cosine: It is defined as the ratio of base and hypotenuse and it is represented as cos θ
tangent: It is defined as the ratio of sine and cosine of an angle. Thus the definition of tangent comes out to be the ratio of perpendicular and base and is represented as tan θ
cosecant: It is the reciprocal of sin θ and is represented as cosec θ.
secant: It is the reciprocal of cos θ and is represented as sec θ.
cotangent: It is the reciprocal of tan θ and is represented as cot θ.
Trigonometric Identities of Complementary and Supplementary Angles
- Complementary Angles: Pair of angles whose sum is equal to 90°
- Supplementary Angles: Pair of angles whose sum is equal to 180°
Identities of Complementary angles are
sin (90° – θ) = cos θ
cos (90° – θ) = sin θ
tan (90° – θ) = cot θ
cot (90° – θ) = tan θ
sec (90° – θ) = cosec θ
cosec (90° – θ) = sec θ
Identities of supplementary angles
sin (180° – θ) = sin θ
cos (180° – θ) = – cos θ
tan (180° – θ) = – tan θ
cot (180° – θ) = – cot θ
sec (180° – θ) = – sec θ
cosec (180° – θ) = – cosec θ
Find the exact value of sin 135°.
Solution:
Since, we know that sin is positive in the 1st and 2nd Quadrant,
here, 135° lies in the 2nd Quadrant, then
By the Trigonometric Identity of Supplementary Angles,
We know that sin (180° – θ) = sin θ
Hence,
sin 135° = sin(180° – 45°)
= sin 45° {As given by Identity}
= 1/√2
Similar Questions
Question 1: What is the exact value of sin 150°?
Solution:
Here sin is positive only in the 1st and 2nd Quadrant.
150° lies in the 2nd Quadrant.
Therefore
sin (180° – θ) = sin θ
sin (150°) = sin (180° – 30°)
sin (150°) = sin (30°)
sin (150°) = 1/2
So the exact value of sin 150° is 1/2
Question 2: What is the Exact value of cos 150°?
Solution:
Here cos is positive only in 1st and 4th Quadrant.
150° lies in 2nd Quadrant.
Therefore cos(180° – θ) = – cos θ
cos(150°) = cos(180° – 30°)
cos(150°) = -cos(30°)
cos (150°) = -√3/2 { as per the trigonometry value table }
So the exact value of cos 150° is -√3/2
Last Updated :
01 Jan, 2022
Like Article
Save Article
Таблица синусов.
Таблица синусов – это записанные в таблицу посчитанные значения синусов углов от 0° до 360°. Используя таблицу синусов вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение синуса от нужного Вам угла достаточно найти его в таблице.
Калькулятор – синус угла
sin(°) = 0
Калькулятор – арксинус угла
arcsin() = 90°
Таблица синусов в радианах
| α | 0 | π6 | π4 | π3 | π2 | π | 3π2 | 2π |
| sin α | 0 | 12 | √22 | √32 | 1 | 0 | -1 | 0 |
Таблица синусов углов от 0° до 180°
| sin(0°) = 0 sin(1°) = 0.017452 sin(2°) = 0.034899 sin(3°) = 0.052336 sin(4°) = 0.069756 sin(5°) = 0.087156 sin(6°) = 0.104528 sin(7°) = 0.121869 sin(8°) = 0.139173 sin(9°) = 0.156434 sin(10°) = 0.173648 sin(11°) = 0.190809 sin(12°) = 0.207912 sin(13°) = 0.224951 sin(14°) = 0.241922 sin(15°) = 0.258819 sin(16°) = 0.275637 sin(17°) = 0.292372 sin(18°) = 0.309017 sin(19°) = 0.325568 sin(20°) = 0.34202 sin(21°) = 0.358368 sin(22°) = 0.374607 sin(23°) = 0.390731 sin(24°) = 0.406737 sin(25°) = 0.422618 sin(26°) = 0.438371 sin(27°) = 0.45399 sin(28°) = 0.469472 sin(29°) = 0.48481 sin(30°) = 0.5 sin(31°) = 0.515038 sin(32°) = 0.529919 sin(33°) = 0.544639 sin(34°) = 0.559193 sin(35°) = 0.573576 sin(36°) = 0.587785 sin(37°) = 0.601815 sin(38°) = 0.615661 sin(39°) = 0.62932 sin(40°) = 0.642788 sin(41°) = 0.656059 sin(42°) = 0.669131 sin(43°) = 0.681998 sin(44°) = 0.694658 sin(45°) = 0.707107 |
sin(46°) = 0.71934 sin(47°) = 0.731354 sin(48°) = 0.743145 sin(49°) = 0.75471 sin(50°) = 0.766044 sin(51°) = 0.777146 sin(52°) = 0.788011 sin(53°) = 0.798636 sin(54°) = 0.809017 sin(55°) = 0.819152 sin(56°) = 0.829038 sin(57°) = 0.838671 sin(58°) = 0.848048 sin(59°) = 0.857167 sin(60°) = 0.866025 sin(61°) = 0.87462 sin(62°) = 0.882948 sin(63°) = 0.891007 sin(64°) = 0.898794 sin(65°) = 0.906308 sin(66°) = 0.913545 sin(67°) = 0.920505 sin(68°) = 0.927184 sin(69°) = 0.93358 sin(70°) = 0.939693 sin(71°) = 0.945519 sin(72°) = 0.951057 sin(73°) = 0.956305 sin(74°) = 0.961262 sin(75°) = 0.965926 sin(76°) = 0.970296 sin(77°) = 0.97437 sin(78°) = 0.978148 sin(79°) = 0.981627 sin(80°) = 0.984808 sin(81°) = 0.987688 sin(82°) = 0.990268 sin(83°) = 0.992546 sin(84°) = 0.994522 sin(85°) = 0.996195 sin(86°) = 0.997564 sin(87°) = 0.99863 sin(88°) = 0.999391 sin(89°) = 0.999848 sin(90°) = 1 |
sin(91°) = 0.999848 sin(92°) = 0.999391 sin(93°) = 0.99863 sin(94°) = 0.997564 sin(95°) = 0.996195 sin(96°) = 0.994522 sin(97°) = 0.992546 sin(98°) = 0.990268 sin(99°) = 0.987688 sin(100°) = 0.984808 sin(101°) = 0.981627 sin(102°) = 0.978148 sin(103°) = 0.97437 sin(104°) = 0.970296 sin(105°) = 0.965926 sin(106°) = 0.961262 sin(107°) = 0.956305 sin(108°) = 0.951057 sin(109°) = 0.945519 sin(110°) = 0.939693 sin(111°) = 0.93358 sin(112°) = 0.927184 sin(113°) = 0.920505 sin(114°) = 0.913545 sin(115°) = 0.906308 sin(116°) = 0.898794 sin(117°) = 0.891007 sin(118°) = 0.882948 sin(119°) = 0.87462 sin(120°) = 0.866025 sin(121°) = 0.857167 sin(122°) = 0.848048 sin(123°) = 0.838671 sin(124°) = 0.829038 sin(125°) = 0.819152 sin(126°) = 0.809017 sin(127°) = 0.798636 sin(128°) = 0.788011 sin(129°) = 0.777146 sin(130°) = 0.766044 sin(131°) = 0.75471 sin(132°) = 0.743145 sin(133°) = 0.731354 sin(134°) = 0.71934 sin(135°) = 0.707107 |
sin(136°) = 0.694658 sin(137°) = 0.681998 sin(138°) = 0.669131 sin(139°) = 0.656059 sin(140°) = 0.642788 sin(141°) = 0.62932 sin(142°) = 0.615661 sin(143°) = 0.601815 sin(144°) = 0.587785 sin(145°) = 0.573576 sin(146°) = 0.559193 sin(147°) = 0.544639 sin(148°) = 0.529919 sin(149°) = 0.515038 sin(150°) = 0.5 sin(151°) = 0.48481 sin(152°) = 0.469472 sin(153°) = 0.45399 sin(154°) = 0.438371 sin(155°) = 0.422618 sin(156°) = 0.406737 sin(157°) = 0.390731 sin(158°) = 0.374607 sin(159°) = 0.358368 sin(160°) = 0.34202 sin(161°) = 0.325568 sin(162°) = 0.309017 sin(163°) = 0.292372 sin(164°) = 0.275637 sin(165°) = 0.258819 sin(166°) = 0.241922 sin(167°) = 0.224951 sin(168°) = 0.207912 sin(169°) = 0.190809 sin(170°) = 0.173648 sin(171°) = 0.156434 sin(172°) = 0.139173 sin(173°) = 0.121869 sin(174°) = 0.104528 sin(175°) = 0.087156 sin(176°) = 0.069756 sin(177°) = 0.052336 sin(178°) = 0.034899 sin(179°) = 0.017452 sin(180°) = 0 |
Таблица синусов углов от 181° до 360°
| sin(181°) = -0.017452 sin(182°) = -0.034899 sin(183°) = -0.052336 sin(184°) = -0.069756 sin(185°) = -0.087156 sin(186°) = -0.104528 sin(187°) = -0.121869 sin(188°) = -0.139173 sin(189°) = -0.156434 sin(190°) = -0.173648 sin(191°) = -0.190809 sin(192°) = -0.207912 sin(193°) = -0.224951 sin(194°) = -0.241922 sin(195°) = -0.258819 sin(196°) = -0.275637 sin(197°) = -0.292372 sin(198°) = -0.309017 sin(199°) = -0.325568 sin(200°) = -0.34202 sin(201°) = -0.358368 sin(202°) = -0.374607 sin(203°) = -0.390731 sin(204°) = -0.406737 sin(205°) = -0.422618 sin(206°) = -0.438371 sin(207°) = -0.45399 sin(208°) = -0.469472 sin(209°) = -0.48481 sin(210°) = -0.5 sin(211°) = -0.515038 sin(212°) = -0.529919 sin(213°) = -0.544639 sin(214°) = -0.559193 sin(215°) = -0.573576 sin(216°) = -0.587785 sin(217°) = -0.601815 sin(218°) = -0.615661 sin(219°) = -0.62932 sin(220°) = -0.642788 sin(221°) = -0.656059 sin(222°) = -0.669131 sin(223°) = -0.681998 sin(224°) = -0.694658 sin(225°) = -0.707107 |
sin(226°) = -0.71934 sin(227°) = -0.731354 sin(228°) = -0.743145 sin(229°) = -0.75471 sin(230°) = -0.766044 sin(231°) = -0.777146 sin(232°) = -0.788011 sin(233°) = -0.798636 sin(234°) = -0.809017 sin(235°) = -0.819152 sin(236°) = -0.829038 sin(237°) = -0.838671 sin(238°) = -0.848048 sin(239°) = -0.857167 sin(240°) = -0.866025 sin(241°) = -0.87462 sin(242°) = -0.882948 sin(243°) = -0.891007 sin(244°) = -0.898794 sin(245°) = -0.906308 sin(246°) = -0.913545 sin(247°) = -0.920505 sin(248°) = -0.927184 sin(249°) = -0.93358 sin(250°) = -0.939693 sin(251°) = -0.945519 sin(252°) = -0.951057 sin(253°) = -0.956305 sin(254°) = -0.961262 sin(255°) = -0.965926 sin(256°) = -0.970296 sin(257°) = -0.97437 sin(258°) = -0.978148 sin(259°) = -0.981627 sin(260°) = -0.984808 sin(261°) = -0.987688 sin(262°) = -0.990268 sin(263°) = -0.992546 sin(264°) = -0.994522 sin(265°) = -0.996195 sin(266°) = -0.997564 sin(267°) = -0.99863 sin(268°) = -0.999391 sin(269°) = -0.999848 sin(270°) = -1 |
sin(271°) = -0.999848 sin(272°) = -0.999391 sin(273°) = -0.99863 sin(274°) = -0.997564 sin(275°) = -0.996195 sin(276°) = -0.994522 sin(277°) = -0.992546 sin(278°) = -0.990268 sin(279°) = -0.987688 sin(280°) = -0.984808 sin(281°) = -0.981627 sin(282°) = -0.978148 sin(283°) = -0.97437 sin(284°) = -0.970296 sin(285°) = -0.965926 sin(286°) = -0.961262 sin(287°) = -0.956305 sin(288°) = -0.951057 sin(289°) = -0.945519 sin(290°) = -0.939693 sin(291°) = -0.93358 sin(292°) = -0.927184 sin(293°) = -0.920505 sin(294°) = -0.913545 sin(295°) = -0.906308 sin(296°) = -0.898794 sin(297°) = -0.891007 sin(298°) = -0.882948 sin(299°) = -0.87462 sin(300°) = -0.866025 sin(301°) = -0.857167 sin(302°) = -0.848048 sin(303°) = -0.838671 sin(304°) = -0.829038 sin(305°) = -0.819152 sin(306°) = -0.809017 sin(307°) = -0.798636 sin(308°) = -0.788011 sin(309°) = -0.777146 sin(310°) = -0.766044 sin(311°) = -0.75471 sin(312°) = -0.743145 sin(313°) = -0.731354 sin(314°) = -0.71934 sin(315°) = -0.707107 |
sin(316°) = -0.694658 sin(317°) = -0.681998 sin(318°) = -0.669131 sin(319°) = -0.656059 sin(320°) = -0.642788 sin(321°) = -0.62932 sin(322°) = -0.615661 sin(323°) = -0.601815 sin(324°) = -0.587785 sin(325°) = -0.573576 sin(326°) = -0.559193 sin(327°) = -0.544639 sin(328°) = -0.529919 sin(329°) = -0.515038 sin(330°) = -0.5 sin(331°) = -0.48481 sin(332°) = -0.469472 sin(333°) = -0.45399 sin(334°) = -0.438371 sin(335°) = -0.422618 sin(336°) = -0.406737 sin(337°) = -0.390731 sin(338°) = -0.374607 sin(339°) = -0.358368 sin(340°) = -0.34202 sin(341°) = -0.325568 sin(342°) = -0.309017 sin(343°) = -0.292372 sin(344°) = -0.275637 sin(345°) = -0.258819 sin(346°) = -0.241922 sin(347°) = -0.224951 sin(348°) = -0.207912 sin(349°) = -0.190809 sin(350°) = -0.173648 sin(351°) = -0.156434 sin(352°) = -0.139173 sin(353°) = -0.121869 sin(354°) = -0.104528 sin(355°) = -0.087156 sin(356°) = -0.069756 sin(357°) = -0.052336 sin(358°) = -0.034899 sin(359°) = -0.017452 sin(360°) = 0 |
Содержание
- – Сколько будет 135 градусов?
- – Как найти синус 150 градусов?
- – Чему равно значение тригонометрической функции синус 135 градусов?
- – Как найти тангенс угла 135 градусов?
- – Чему равен косинус 225 градусов?
- – Как вычислить тангенс 150 градусов?
- – Как найти синус 120 градусов?
- – Чему равен синус числа Пи?
- – Чему равен синус 90 градусов?
- – Чему равен косинус 135 градусов дробью?
- – Чему равен арктангенс от тангенса?
sin 135, используя формулы приведения, можно получить двумя различными способами: 1) sin (90 + A) = cos A. Вычислим А: 135 – 90 = 45.
COS 135 градусов равен:
Тангенс минус 135 градусов. Котангенс минус 135 градусов. Косинус 134 градусов. Косинус 136 градусов.
Как найти синус 150 градусов?
Ответ или решение1
Угол 150 градусов является тупым, для его вычисления воспользуемся формулой приведения : sin (180 – α) = sin α. Запишем 150 градусов как 180 градусов – 30 градусов и воспользуемся формулой : sin (180 – 30) = sin 30.
Чему равно значение тригонометрической функции синус 135 градусов?
По таблицам Брадиса для синуса значение синуса 135 градусов равно 0,7071, что соответствует полученному приближенному значению, которое вычислили аналитическим путем.
Как найти тангенс угла 135 градусов?
Ответ или решение1
tg=sin/cos; На единичной окружности найдём 135°- это точка 3*π/4, синус этого угла равен (√2)/2, косинус соответственно -(√2)/2. Отсюда получаем, что tg135°=((√2)/2)/-((√2)/2)=-1.
Чему равен косинус 225 градусов?
Точное значение cos(45) равно √22 .
Как вычислить тангенс 150 градусов?
tg 150 = tg (180 – 30) = tg (пи – 30) = -tg 30 = -√3/3. Ответ: tg 150 = -√3/3.
Как найти синус 120 градусов?
1) Чтобы сразу определить значение синуса 120 градусов, можно прибегнуть к помощи различных таблиц, ну а кто не может этого сделать, то необходимо угол 120 градусов расписать, как (90+30) или (180-60). 2) Далее нужно определить четверть, в которой будет находится синус: 90+30 / 180-60 – это вторая четверть.
Чему равен синус числа Пи?
Синус пи. таким образом, синус пи – это тоже самое, что синус 180 градусов и он равен нулю. 2. Косинус пи.
Чему равен синус 90 градусов?
sin (90°) = sin (π/2) = 1.
Чему равен косинус 135 градусов дробью?
Таблица углов от 0 до 179 градусов
| Угол (градусы) | Синус (Sin) | Косинус (Cos) |
|---|---|---|
| 132 | 0.74314483 | -0.66913061 |
| 133 | 0.7313537 | -0.68199836 |
| 134 | 0.7193398 | -0.69465837 |
| 135 | 0.70710678 | -0.70710678 |
Чему равен арктангенс от тангенса?
Чему равен arctg (tg x)
Функция арктангенс является обратной функцией к функции тангенс. Это значит, что если тангенс от первого числа равен второму числу, то арктангенс от второго числа равен первому числу.
Интересные материалы:
Почему зеленый фон при съемке?
Почему железные корабли не тонут?
Почему желтеет яблоко?
Почему желтые стены в психушке?
Почему жесткая педаль сцепления?
Почему животные так мало живут?
Почему животные видят в темноте?
Почему зимой день короче а летом длиннее?
Почему зимой день короче чем летом?
Почему зимой день короче?
