Как найти значение скользящей средней - Сайт, где вы сможете решить свои вопросы

График исходной функции (синий) и его скользящая средняя (красная) с шириной окна n = 2

Скользя́щая сре́дняя, скользя́щее сре́днее (англ. moving average, MA) — общее название для семейства функций, значения которых в каждой точке определения равны некоторому среднему значению исходной функции за предыдущий период.

Скользящие средние обычно используются с данными временных рядов для сглаживания краткосрочных колебаний и выделения основных тенденций или циклов^[1]^[2].

Математически скользящее среднее является одним из видов свёртки.

Применение[править | править код]

Скользящие средние используются:

В статистике и экономике для сглаживания числовых рядов (в первую очередь временных). Например, для оценки ВВП, показателей занятости или других макроэкономических индикаторов.
В технике, при обработке сигналов, анализе систем. См. Скользящая средняя (фильтр).
В техническом анализе, в качестве самостоятельного технического индикатора либо в составе других инструментов, см. Скользящая средняя (индикатор).

Этимология[править | править код]

Так как при расчёте скользящего среднего значение функции вычисляется каждый раз заново^[2], при этом учитывается конечное значимое^[3] множество предыдущих значений, скользящее среднее «перемещается» (движется), как бы «скользя» по временному ряду.

Виды скользящих средних[править | править код]

Общий случай[править | править код]

В общем случае, взвешенные скользящие средние вычисляются по формуле^[2]:

${textit {WWMA}}_{t}=sum _{{i=0}}^{{n-1}}w_{{t-i}}cdot p_{{t-i}},$

(WWMA 1)

где ${textit {WWMA}}_{t}$

— значение взвешенного скользящего среднего в точке

;

— количество значений исходной функции для расчёта скользящего среднего;

$w_{{t-i}}$

— нормированный вес (весовой коэффициент) t-i

-го значения исходной функции;

$p_{{t-i}}$

— значение исходной функции в момент времени, отдалённый от текущего на

интервалов.

Нормирование весовых коэффициентов означает, что^[2]:

$sum _{{i=0}}^{{n-1}}w_{{t-i}}=1.$

Указанную выше формулу с произвольными значениями весовых коэффициентов можно переписать в виде:

${textit {WWMA}}_{t}={frac {sum _{{i=0}}^{{n-1}}W_{{t-i}}cdot p_{{t-i}}}{sum _{{i=0}}^{{n-1}}W_{{t-i}}}},$

(WWMA 2)

где ${textit {WWMA}}_{t}$

— значение взвешенного скользящего среднего в точке

;

— количество значений исходной функции для расчёта скользящего среднего;

$W_{{t-i}}$

— вес (весовой коэффициент) t-i

-го значения исходной функции;

$p_{{t-i}}$

— значение исходной функции в момент времени, отдалённый от текущего на

интервалов.

Весовые коэффициенты в формулах (WWMA 1) и (WWMA 2) соотносятся как:

$w_{{t-i}}={frac {W_{{t-i}}}{sum _{{i=0}}^{{n-1}}W_{{t-i}}}}.$

Зачастую, в качестве веса используют либо 1 (для простого скользящего среднего — SMA), либо формальные ряды, например, арифметическая прогрессия (WMA) или экспоненциальная функция (EMA). Но в качестве весового коэффициента могут выступать и значения связанного временного ряда. Например, для взвешивания биржевых цен по объёмам сделки (VMA) в качестве $p_{{t-i}}$ следует рассматривать цену сделки по инструменту, а в качестве $W_{{t-i}}=V_{{t-i}}$ — объём в момент времени t-i :

${textit {VMA}}_{t}={frac {sum _{{i=0}}^{{n-1}}V_{{t-i}}cdot p_{{t-i}}}{sum _{{i=0}}^{{n-1}}V_{{t-i}}}}.$

Простое скользящее среднее[править | править код]

Исходная функция и её простые скользящие средние по четырём значениям (n = 4).
Зелёная линия — центрирование по середине интервала (истинное положение).
Красная линия — сдвиг графика вправо к последнему значению окна.

Простое скользящее среднее, или арифметическое скользящее среднее (англ. simple moving average, англ. SMA) численно равно среднему арифметическому значений исходной функции за установленный период^[1] и вычисляется по формуле^[2]:

${displaystyle {textit {SMA}}_{t}={frac {1}{n}}sum _{i=0}^{n-1}p_{t-i}=}$

${displaystyle ={frac {p_{t}+p_{t-1}+cdots +p_{t-i}+cdots +p_{t-n+2}+p_{t-n+1}}{n}},}$

где ${textit {SMA}}_{t}$

— значение простого скользящего среднего в точке

;

— количество значений исходной функции для расчёта скользящего среднего (сглаживающий интервал^[1]), чем шире сглаживающий интервал, тем более плавным получается график функции^[1];

$p_{{t-i}}$

— значение исходной функции в точке t-i

Полученное значение простой скользящей средней относится к середине выбранного интервала^[1], однако, традиционно его относят к последней точке интервала^[2].

Из предыдущего своего значения простое скользящее среднее может быть получено по следующей рекуррентной формуле^[2]:

${textit {SMA}}_{t}={textit {SMA}}_{{t-1}}-{frac {p_{{t-n}}}{n}}+{frac {p_{{t}}}{n}},$

где ${textit {SMA}}_{t}$

— значение простого скользящего среднего в точке

, ${textit {SMA}}_{{t-1}}$

— предыдущее значение простого скользящего среднего;

$p_{{t-n}}$

— значение исходной функции в точке t-n

(в случае временного ряда, самое «раннее» значение исходной функции, используемое для вычисления предыдущей скользящей средней);

$p_{{t}}$

— значение исследуемой функции в точке

(в случае временного ряда, текущее — последнее значение).

Данной формулой удобно пользоваться, чтобы избежать регулярного суммирования всех значений.

Например, простое скользящее среднее для временного ряда с количеством периодов равным 10 вычисляется как:

${displaystyle {textit {SMA}}_{t}={frac {p_{t}+p_{t-1}+p_{t-2}+p_{t-3}+p_{t-4}+p_{t-5}+p_{t-6}+p_{t-7}+p_{t-8}+p_{t-9}}{10}}=}$

${displaystyle ={textit {SMA}}_{t-1}-{frac {p_{t-10}}{10}}+{frac {p_{t}}{10}},}$

где ${textit {SMA}}_{t}$

— значение простого скользящего среднего в точке

;

$p_{{t-i}}$

— значение исходной функции в момент времени, отдалённый от текущего на

интервалов.

Выделяют следующие недостатки простого скользящего среднего^[2]:

Равенство весового коэффициента 1.
Двойная реакция на каждое значение (смотрите рекуррентную формулу): в момент входа в окно вычислений и в момент выхода из него.

Взвешенные скользящие средние[править | править код]

Общие положения[править | править код]

Иногда при построении скользящей средней некоторые значения исходной функции целесообразно сделать более значимыми.
Например, если предполагается, что внутри интервала сглаживания имеет место нелинейная тенденция^[1], или, в случае временных рядов, последние — более актуальные — данные могут быть весомее предыдущих.

Бывает, что исходная функция многомерна, то есть представлена сразу несколькими связанными рядами. В этом случае может возникнуть необходимость объединить в итоговой функции скользящей средней все полученные данные. Например, временные ряды биржевых цен обычно для каждого момента времени представлены как минимум двумя значениями — ценой сделки и её объёмом. Необходим инструмент для вычисления скользящей средней цены, взвешенной по объёму.

В этих и подобных случаях применяются взвешенные скользящие средние.

Взвешенное скользящее среднее[править | править код]

Веса значений исходной функции при вычислении WMA с n = 15

Взве́шенное скользящее среднее (англ. weighted moving average — англ. WMA), точнее линейно взвешенное скользящее среднее — скользящее среднее, при вычислении которого вес каждого члена исходной функции, начиная с меньшего, равен соответствующему члену арифметической прогрессии. То есть, при вычислении WMA для временного ряда, мы считаем последние значения исходной функции более значимыми чем предыдущие, причём функция значимости линейно убывающая.

Например, для арифметической прогрессии с начальным значением и шагом, равным 1, формула вычисления скользящей средней примет вид^[2]:

${displaystyle {textit {WMA}}_{t}={frac {ncdot p_{t}+(n-1)cdot p_{t-1}+cdots +(n-i)cdot p_{t-i}+cdots +2cdot p_{t-n+2}+1cdot p_{t-n+1}}{n+(n-1)+cdots +(n-i)+cdots +2+1}}=}$

${displaystyle ={frac {2}{ncdot (n+1)}}sum _{i=0}^{n-1}(n-i)cdot p_{t-i},}$

где ${textit {WMA}}_{t}$

— значение взвешенного скользящего среднего в точке

;

— количество значений исходной функции для расчёта скользящего среднего, : : $p_{{t-i}}$

— значение исходной функции в момент времени, отдалённый от текущего на

интервалов.

При этом знаменатель функции, в этом случае, равен треугольному числу — сумме членов арифметической прогрессии с начальным членом и шагом равными 1:

${frac {ncdot (n+1)}{2}}.$

Экспоненциально взвешенное скользящее среднее[править | править код]

Веса значений исходной функции при вычислении EMA с n = 15

Экспоненциально взвешенное скользящее среднее, экспоненциальное скользящее среднее (англ. exponentially weighted moving average — англ. EWMA, англ. exponential moving average — англ. EMA) — разновидность взвешенной скользящей средней, веса которой убывают экспоненциально и никогда не равны нулю^[3]. Определяется следующей формулой^[1]^[2]^[4]^[5]^[6]:

${textit {EMA}}_{t}=alpha cdot p_{t}+(1-alpha )cdot {textit {EMA}}_{{t-1}},$

где ${textit {EMA}}_{t}$

— значение экспоненциального скользящего среднего в точке

(последнее значение, в случае временного ряда);

${textit {EMA}}_{{t-1}}$

— значение экспоненциального скользящего среднего в точке t-1

(предыдущее значение в случае временного ряда);

$p_{t}$

— значение исходной функции в момент времени

(последнее значение, в случае временного ряда);

— (сглаживающая константа от англ. smoothing constant) коэффициент характеризующий скорость уменьшения весов, принимает значение от 0 и до 1, чем меньше его значение тем больше влияние предыдущих значений на текущую величину среднего.

Первое значение экспоненциального скользящего среднего, обычно принимается равным первому значению исходной функции:

${textit {EMA}}_{0}=p_{0}.$

Коэффициент alpha , может быть выбран произвольным образом, в пределах от 0 до 1. Например, он может быть выражен через величину окна усреднения:

$alpha ={frac {2}{n+1}}.$

Экспоненциальное скользящее среднее произвольного порядка[править | править код]

Веса экспоненциально взвешенной скользящей средней третьего порядка — TMA с окном n=10.

В обычном экспоненциальном скользящем среднем сглаживанию подвергаются значения исходной функции, однако, сглаживанию могут подвергаться и значения результирующей функции^[2].
Поэтому некоторые авторы определяют понятие экспоненциальные скользящее среднее произвольного порядка^[2], которые вычисляются по формуле:

${textit {EMA}}_{t}^{{(n)}}=alpha cdot {textit {EMA}}_{t}^{{(n-1)}}+(1-alpha )cdot {textit {EMA}}_{{t-1}}^{{(n)}},$

где ${textit {EMA}}_{t}^{{(n)}}$

— значение экспоненциального скользящего среднего

-го порядка в точке

(последнее значение, в случае временного ряда);

${textit {EMA}}_{{t-1}}^{{(n)}}$

— значение экспоненциального скользящего среднего

-го порядка в точке t-1

(предыдущее значение в случае временного ряда);

${EMA}_{t}^{{(n-1)}}$

— значение экспоненциального скользящего среднего (n-1)

-го порядка в точке

(последнее значение, в случае временного ряда);

— сглаживающая константа.

Экспоненциально взвешенные скользящие средние второго и третьего порядка обозначают иногда как, соответственно (от англ. double exponential moving average — двойное (двукратное) экспоненциальное скользящее среднее) и (от англ. triple exponential moving average — тройное (трёхкратное) экспоненциальное скользящее среднее)^[2]:

${textit {DMA}}_{t}=alpha cdot {textit {EMA}}_{t}+(1-alpha )cdot {textit {DMA}}_{{t-1}},$

${textit {TMA}}_{t}=alpha cdot {textit {DMA}}_{t}+(1-alpha )cdot {textit {TMA}}_{{t-1}}.$

Модифицированное скользящее среднее[править | править код]

Модифицированное скользящее среднее (от англ. modified moving average — англ. MMA; иногда называемое англ. running moving average — англ. RMA и англ. smoothed moving average) определятся как:

${text{MMA}}_{t}={frac {p_{t}+(n-1)cdot {text{MMA}}_{{t-1}}}{n}},$

где ${textit {MMA}}_{t}$

— значение модифицированного скользящего среднего в точке

(последнее значение, в случае временного ряда);

${textit {MMA}}_{{t-1}}$

— значение модифицированного скользящего среднего в точке t-1

(предыдущее значение в случае временного ряда);

— количество значений исходной функции для расчёта скользящего среднего (сглаживающий интервал).

Несложно заметить, что модифицированное скользящее среднее является частным случаем экспоненциального скользящего среднего, для которого сглаживающая константа равна обратному значению величины сглаживающего интервала:

$alpha ={frac {1}{n}}.$

Смежные функции[править | править код]

Скользящие на основе других усредняющих функций[править | править код]

По аналогии со скользящими средними значениями, построенными на основе арифметического среднего, можно использовать и другие усредняющие функции (среднее степенное: среднее квадратическое, среднее гармоническое и т. д.; среднее геометрическое; медиану и т. п.) и их взвешенные аналоги. Конкретный выбор зависит от природы исследуемой исходной функции.

Простая скользящая медиана[править | править код]

Простая скользящая медиана (англ. simple moving median — англ. SMM) — функция, значение которой в каждой точке определения численно равна медиане значений исходной функции за установленный период:

${textit {SMM}}_{t}={text{Median}}(p_{t},p_{{t-1}},ldots ,p_{{t-n+1}}),$

где ${textit {SMM}}_{t}$

— значение простой скользящей медианы в точке

;

— количество значений исходной функции для расчёта скользящей медианы (сглаживающий интервал);

$p_{{t-i}}$

— значение исходной функции в точке t-i

Динамические скользящие средние[править | править код]

В 1990-х годах был предложен ряд скользящих средних с динамически изменяемой шириной окна (или сглаживающим коэффициентом), смотрите, например, Адаптивная скользящая средняя Кауфмана.

Кумулятивное скользящее среднее[править | править код]

Кумулятивное скользящее среднее (англ. cumulative moving average) численно равно среднему арифметическому значений исходной функции за весь период наблюдений:

${textit {CA}}_{t}={frac {1}{t}}sum _{{i=1}}^{{t}}p_{i}={frac {p_{t}+p_{{t-1}}+cdots +p_{{2}}+p_{{1}}}{t}},$

где ${textit {CA}}_{t}$

— кумулятивное скользящее среднее в момент

;

— количество доступных для вычисления интервалов;

$p_{i}$

— значение исходной функции в точке

В реальных вычислениях, когда предыдущее значение кумулятивного скользящего среднего известны, применяются также следующие формулы:

${textit {CA}}_{t}={frac {p_{t}+(t-1)cdot {textit {CA}}_{{t-1}}}{t}}={textit {CA}}_{{t-1}}+{frac {p_{t}-{textit {CA}}_{{t-1}}}{t}},$

где ${textit {CA}}_{t}$

— кумулятивное скользящее среднее в момент

;

${textit {CA}}_{{t-1}}$

— кумулятивное скользящее среднее в момент t-1

(предыдущее значение, в случае временного ряда);

$p_{t}$

— значение исходной функции в момент времени

(в случае временного ряда — последнее значение);

— количество доступных, для вычисления интервалов, причём ${textit {CA}}_{0}=0.$

Кумулятивная сумма[править | править код]

Кумулятивное скользящее среднее не следует путать с кумулятивной суммой, которая вычисляется суммированием всех значений ряда нарастающим итогом:

${textit {Cumulative}}_{t}=p_{t}+{textit {Cumulative}}_{{t-1}}=sum _{{i=1}}^{{t}}p_{i}=p_{t}+p_{{t-1}}+cdots +p_{{2}}+p_{{1}},$

где ${textit {Cumulative}}_{t},{textit {Cumulative}}_{{t-1}}$

— текущее и предыдущее значения кумулятивной суммы;

$p_{i}$

— значение исходного ряда в момент

См. также[править | править код]

Авторегрессионная модель: Модель авторегрессии — скользящего среднего, Модель скользящего среднего
Окно (весовая функция)

Примечания[править | править код]

↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ Грешилов А. А., Стакун В. А., Стакун А. А. Математические методы построения прогнозов. — М.: Радио и связь, 1997. — 112 с. — ISBN 5-256-01352-1.
↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ¹⁰ ¹¹ ¹² ¹³ Булашев С. В. Статистика для трейдеров. — М.: Компания Спутник+, 2003. — 245 с.
↑ ¹ ² При расчёте экспоненциально взвешенного скользящего среднего теоретически учитываются все значения временного ряда, однако, на практике, начиная с какого-то вклад исходных значений ниже погрешности вычислений. Поэтому ими можно пренебречь и считать множество предыдущих значений конечным.
↑ В некоторых источниках используется «обратное» представление данной формулы:

${textit {EMA}}_{t}=(1-alpha )cdot p_{t}+alpha cdot {textit {EMA}}_{{t-1}},$

Математического смысла это не меняет, однако, при использовании и анализе следует внимательно отнестись к контекстному определению.
↑ Single Exponential Smoothing Архивная копия от 10 марта 2011 на Wayback Machine (англ.) на сайте Национального института стандартов и технологий США.
↑ EWMA Control Charts Архивная копия от 4 марта 2011 на Wayback Machine (англ.) на сайте Национального института стандартов и технологий США.

Источник

Практическое моделирование экономических ситуаций подразумевает разработку прогнозов. С помощью средств Excel можно реализовать такие эффективные способы прогнозирования, как: экспоненциальное сглаживание, построение регрессий, скользящее среднее. Рассмотрим подробнее использование метода скользящего среднего.

Использование скользящих средних в Excel

Метод скользящей средней – один из эмпирических методов для сглаживания и прогнозирования временных рядов. Суть: абсолютные значения ряда динамики меняются на средние арифметические значения в определенные интервалы. Выбор интервалов осуществляется способом скольжения: первые уровни постепенно убираются, последующие – включаются. В результате получается сглаженный динамический ряд значений, позволяющий четко проследить тенденцию изменений исследуемого параметра.

Временной ряд – это множество значений X и Y, связанных между собой. Х – интервалы времени, постоянная переменная. Y – характеристика исследуемого явления (цена, например, действующая в определенный период времени), зависимая переменная. С помощью скользящего среднего можно выявить характер изменений значения Y во времени и спрогнозировать данный параметр в будущем. Метод действует тогда, когда для значений четко прослеживается тенденция в динамике.

Например, нужно спрогнозировать продажи на ноябрь. Исследователь выбирает количество предыдущих месяцев для анализа (оптимальное число m членов скользящего среднего). Прогнозом на ноябрь будет среднее значение параметров за m предыдущих месяца.

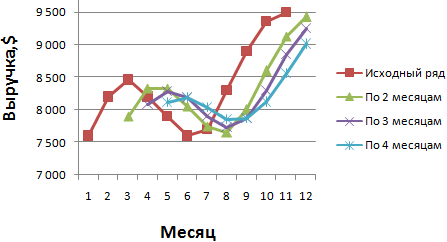
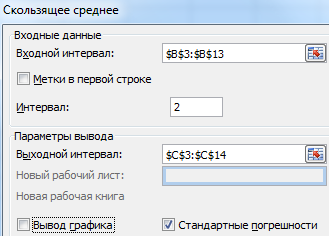
Задача. Проанализировать выручку предприятия за 11 месяцев и составить прогноз на 12 месяц.

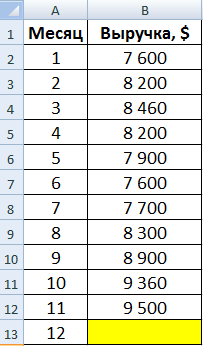
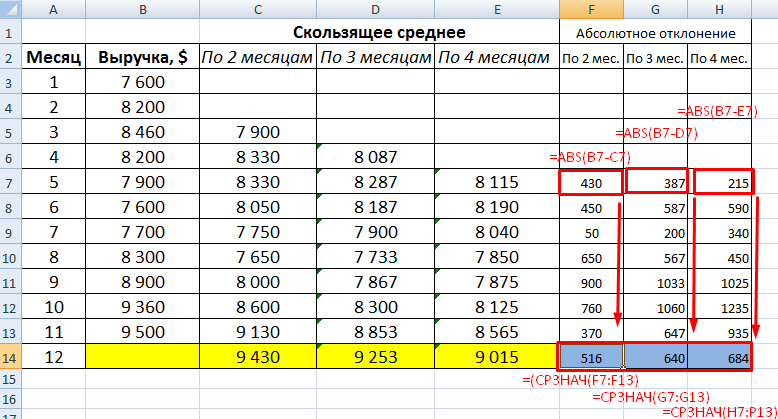
Сформируем сглаженные временные ряды методом скользящего среднего посредством функции СРЗНАЧ. Найдем средние отклонения сглаженных временных рядов от заданного временного ряда.

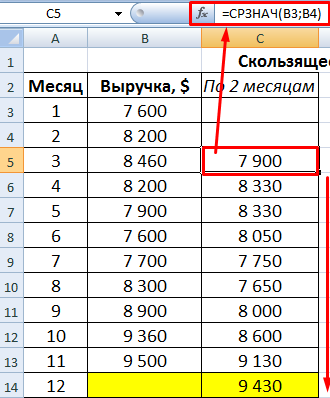
По значениям исходного временного ряда строим сглаженный временный ряд методом скользящего среднего по данным за 2 предыдущих месяца. Формула скользящей средней в Excel. Используя маркер автозаполнения, копируем формулу на диапазон ячеек С6:С14.

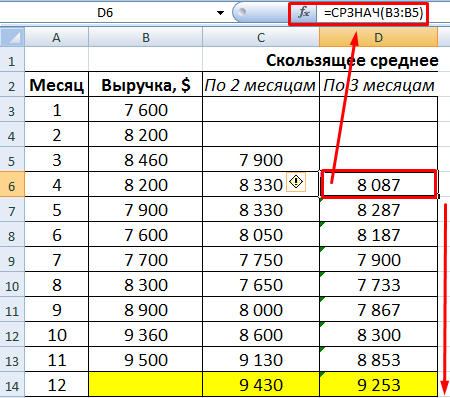
Аналогично строим ряд значений трехмесячного скользящего среднего. Формула:

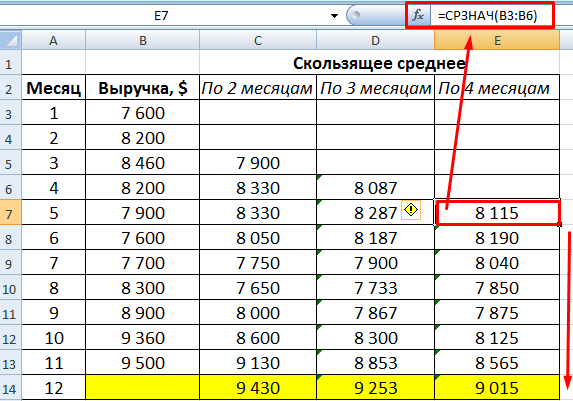
По такому же принципу формируем ряд значений четырехмесячного скользящего среднего.

Построим график заданного временного ряда и рассчитанные относительно его значений прогнозы по данному методу. На рисунке видно, что линии тренда скользящего среднего сдвинуты относительно линии исходного временного ряда. Это объясняется тем, что рассчитанные значения сглаженных временных рядов запаздывают по сравнению с соответствующими значениями заданного ряда. Ведь расчеты базировались на данных предыдущих наблюдений.

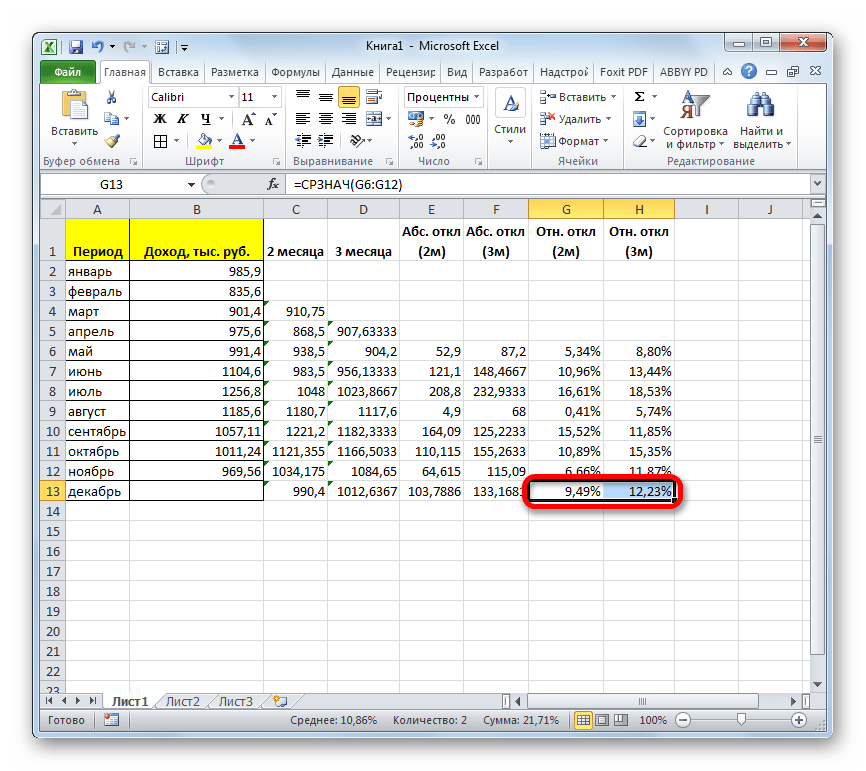
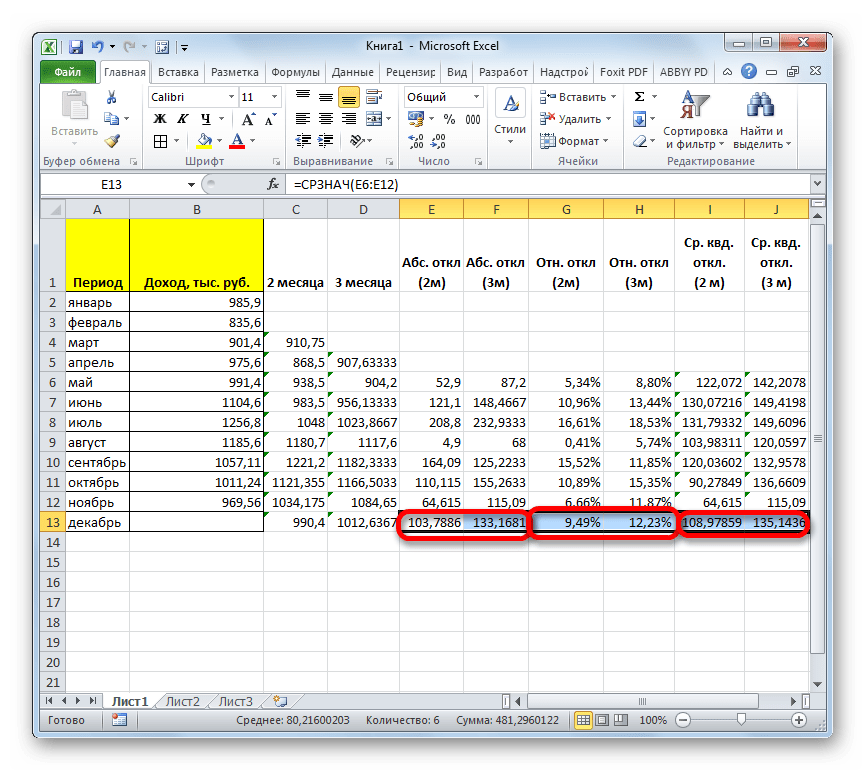
Рассчитаем абсолютные, относительные и средние квадратичные отклонения по сглаженным временным рядам. Абсолютные отклонения:

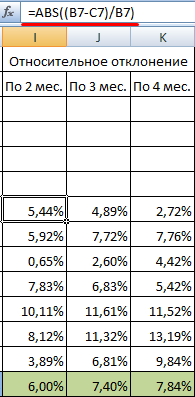
Относительные отклонения:

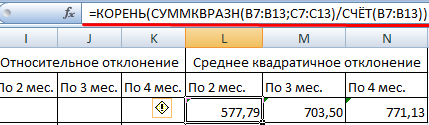
Средние квадратичные отклонения:

При расчете отклонений брали одинаковое число наблюдений. Это необходимо для того, чтобы провести сравнительный анализ погрешностей.

После сопоставления таблиц с отклонениями стало видно, что для составления прогноза по методу скользящей средней в Excel о тенденции изменения выручки предприятия предпочтительнее модель двухмесячного скользящего среднего. У нее минимальные ошибки прогнозирования (в сравнении с трех- и четырехмесячной).

Прогнозное значение выручки на 12 месяц – 9 430 у.е.

Применение надстройки «Пакет анализа»

Для примера возьмем ту же задачу.

На вкладке «Данные» находим команду «Анализ данных». В открывшемся диалоговом окне выбираем «Скользящее среднее»:

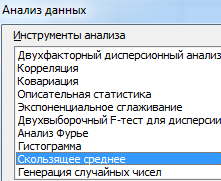
Заполняем. Входной интервал – исходные значения временного ряда. Интервал – число месяцев, включаемое в подсчет скользящего среднего. Так как сначала будем строить сглаженный временной ряд по данным двух предыдущих месяцев, в поле вводим цифру 2. Выходной интервал – диапазон ячеек для выведения полученных результатов.

Установив флажок в поле «Стандартные погрешности», мы автоматически добавляем в таблицу столбец со статистической оценкой погрешности.

Точно так же находим скользящее среднее по трем месяцам. Меняется только интервал (3) и выходной диапазон.

Сравнив стандартные погрешности, убеждаемся в том, что модель двухмесячного скользящего среднего больше подходит для сглаживания и прогнозирования. Она имеет меньшие стандартные погрешности. Прогнозное значение выручки на 12 месяц – 9 430 у.е.

Скачать расчет скользящей средней в Excel

Составлять прогнозы по методу скользящего среднего просто и эффективно. Инструмент точно отражает изменения основных параметров предыдущего периода. Но выйти за пределы известных данных нельзя. Поэтому для долгосрочного прогнозирования применяются другие способы.

Источник

Содержание

Применение скользящей средней
- Способ 1: Пакет анализа
- Способ 2: использование функции СРЗНАЧ
Вопросы и ответы

Метод скользящей средней – это статистический инструмент, с помощью которого можно решать различного рода задачи. В частности, он довольно часто используется при прогнозировании. В программе Excel для решения целого ряда задач также можно применять данный инструмент. Давайте разберемся, как используется скользящая средняя в Экселе.

Применение скользящей средней

Смысл данного метода состоит в том, что с его помощью происходит смена абсолютных динамических значений выбранного ряда на средние арифметические за определенный период путем сглаживания данных. Этот инструмент применяется для экономических расчетов, прогнозирования, в процессе торговли на бирже и т.д. Применять метод скользящей средней в Экселе лучше всего с помощью мощнейшего инструмента статистической обработки данных, который называется Пакетом анализа. Кроме того, в этих же целях можно использовать встроенную функцию Excel СРЗНАЧ.

Способ 1: Пакет анализа

Пакет анализа представляет собой надстройку Excel, которая по умолчанию отключена. Поэтому, прежде всего, требуется её включить.

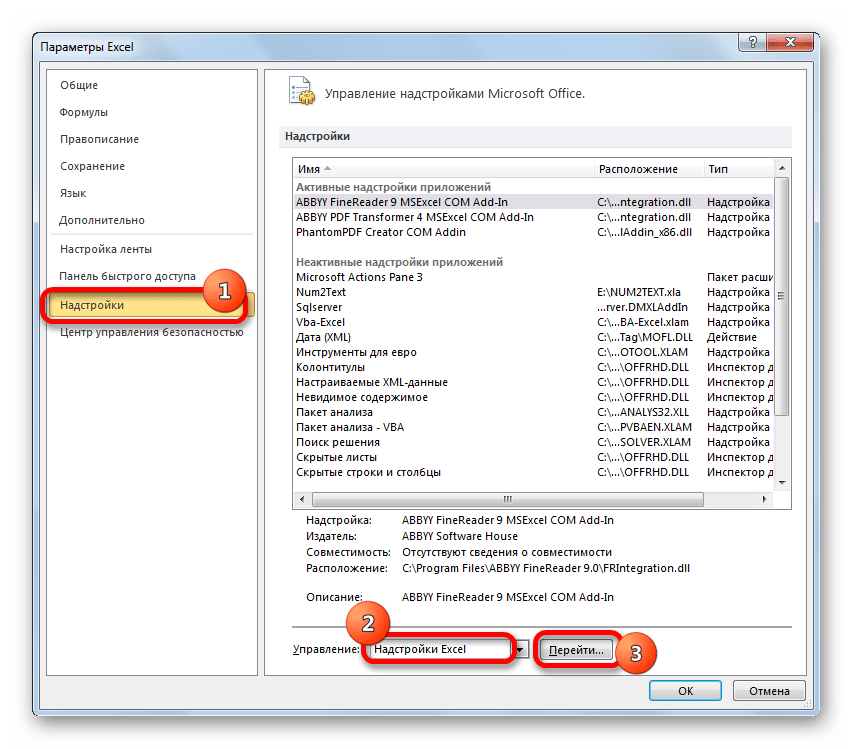
Перемещаемся во вкладку «Файл». Делаем щелчок по пункту «Параметры».

В запустившемся окне параметров следует перейти в раздел «Надстройки». В нижней части окна в поле «Управление» должен быть выставлен параметр «Надстройки Excel». Щелкаем по кнопке «Перейти».

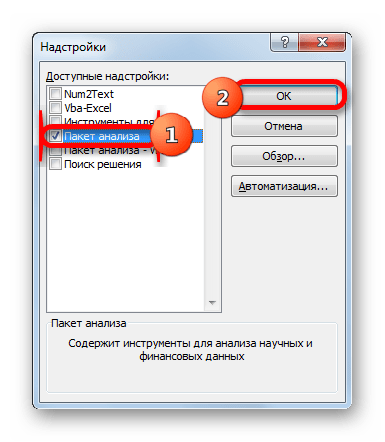
Мы попадаем в окно надстроек. Устанавливаем галочку около пункта «Пакет анализа» и щелкаем по кнопке «OK».

После этого действия пакет «Анализ данных» активирован, и соответствующая кнопка появилась на ленте во вкладке «Данные».

А теперь давайте рассмотрим, как непосредственно можно использовать возможности пакета Анализ данных для работы по методу скользящей средней. Давайте на основе информации о доходе фирмы за 11 предыдущих периодов составим прогноз на двенадцатый месяц. Для этого воспользуемся заполненной данными таблицей, а также инструментами Пакета анализа.

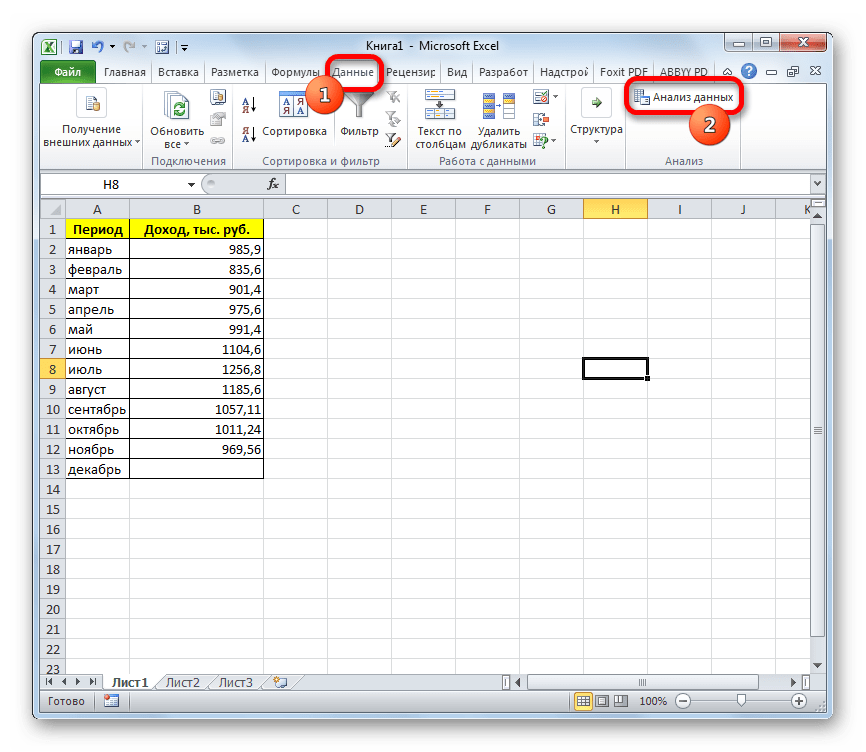
Переходим во вкладку «Данные» и жмем на кнопку «Анализ данных», которая размещена на ленте инструментов в блоке «Анализ».

Открывается перечень инструментов, которые доступны в Пакете анализа. Выбираем из них наименование «Скользящее среднее» и жмем на кнопку «OK».

Запускается окно ввода данных для прогнозирования методом скользящей средней.
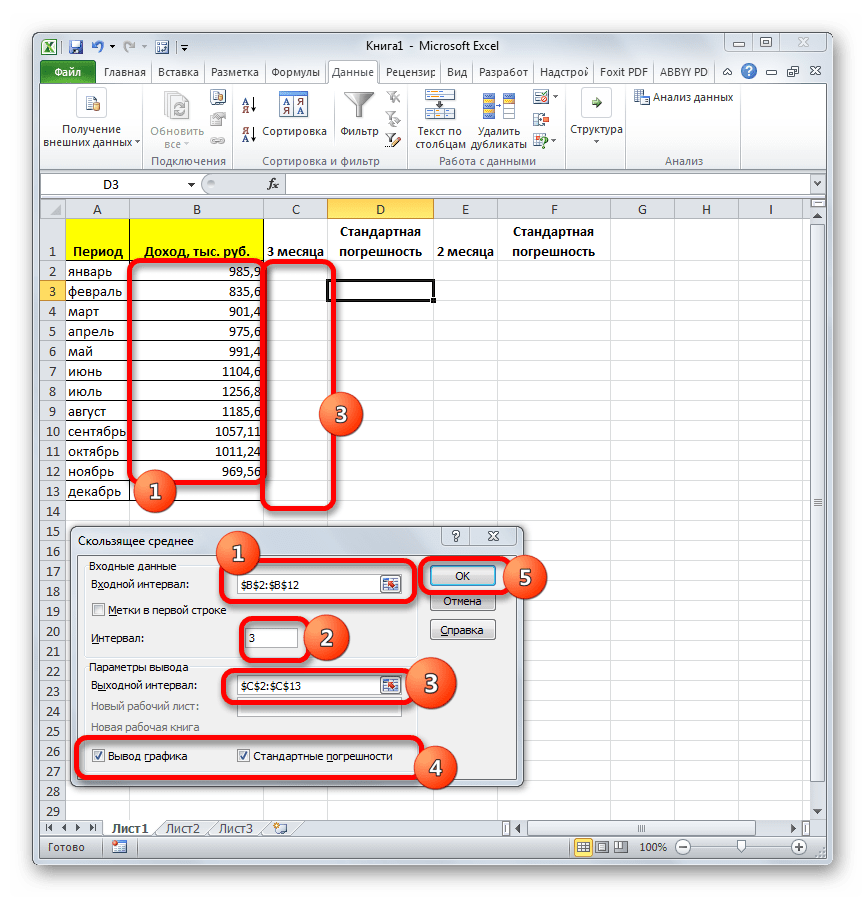
В поле «Входной интервал» указываем адрес диапазона, где расположена помесячно сумма выручки без ячейки, данные в которой следует рассчитать.

В поле «Интервал» следует указать интервал обработки значений методом сглаживания. Для начала давайте установим значение сглаживания в три месяца, а поэтому вписываем цифру «3».

В поле «Выходной интервал» нужно указать произвольный пустой диапазон на листе, где будут выводиться данные после их обработки, который должен быть на одну ячейку больше входного интервала.

Также следует установить галочку около параметра «Стандартные погрешности».

При необходимости, можно также установить галочку около пункта «Вывод графика» для визуальной демонстрации, хотя в нашем случае это и не обязательно.

После того, как все настройки внесены, жмем на кнопку «OK».

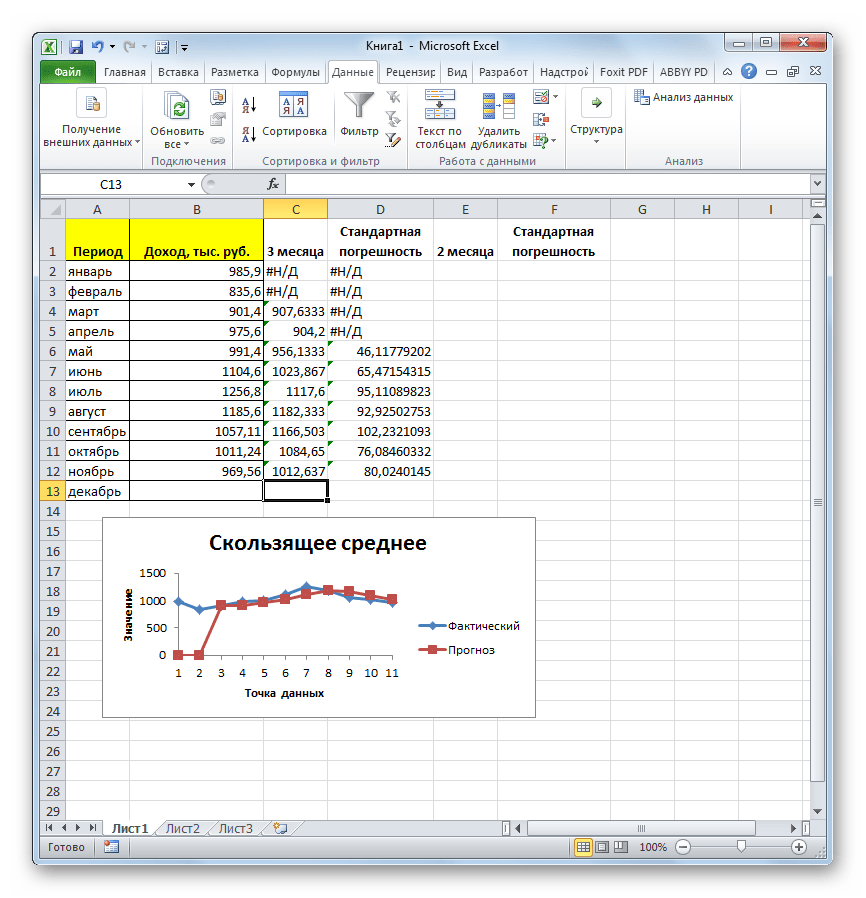
Программа выводит результат обработки.

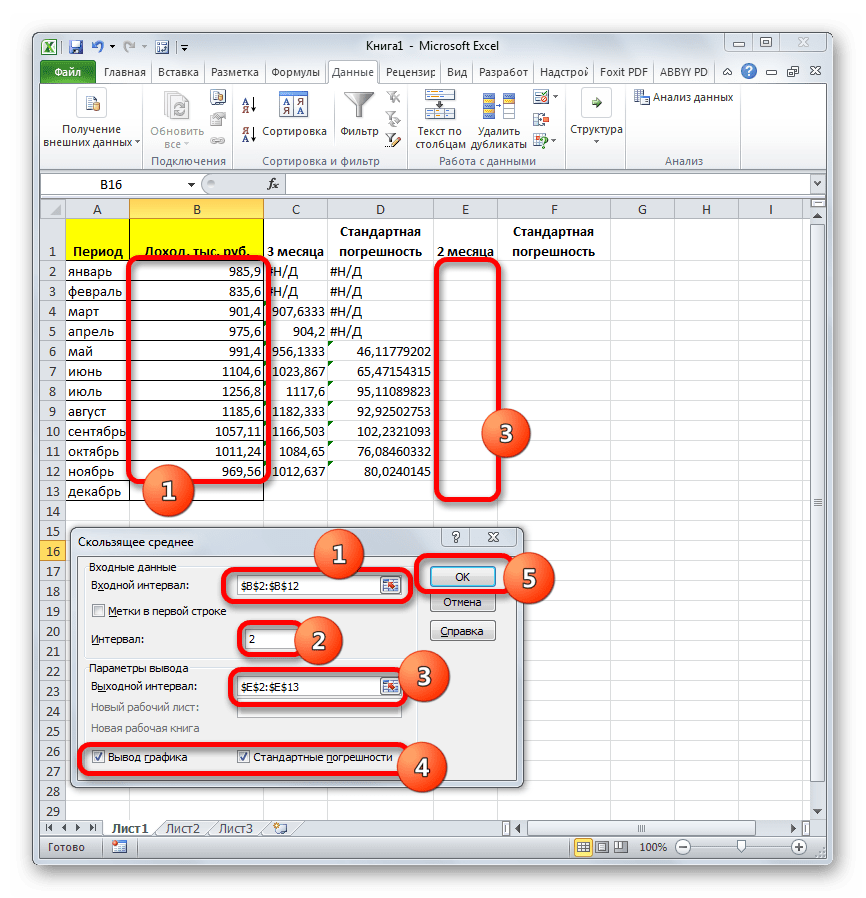
Теперь выполним сглаживание за период в два месяца, чтобы выявить, какой результат является более корректным. Для этих целей опять запускаем инструмент «Скользящее среднее» Пакета анализа.
В поле «Входной интервал» оставляем те же значения, что и в предыдущем случае.

В поле «Интервал» ставим цифру «2».

В поле «Выходной интервал» указываем адрес нового пустого диапазона, который, опять же, должен быть на одну ячейку больше входного интервала.

Остальные настройки оставляем прежними. После этого жмем на кнопку «OK».

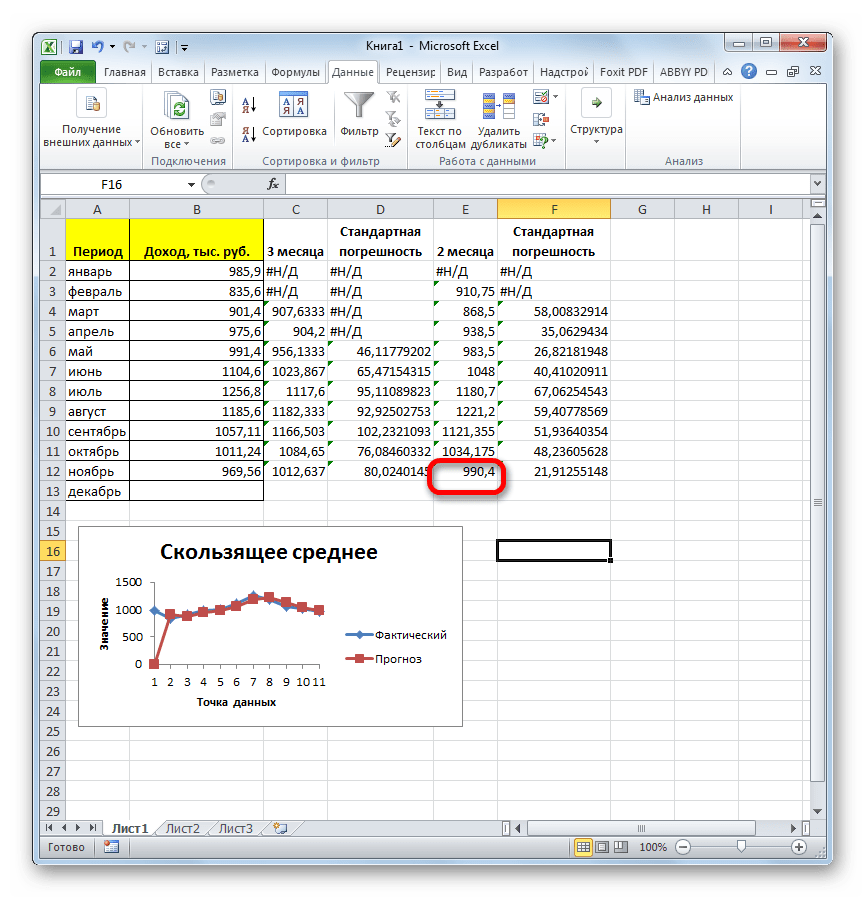
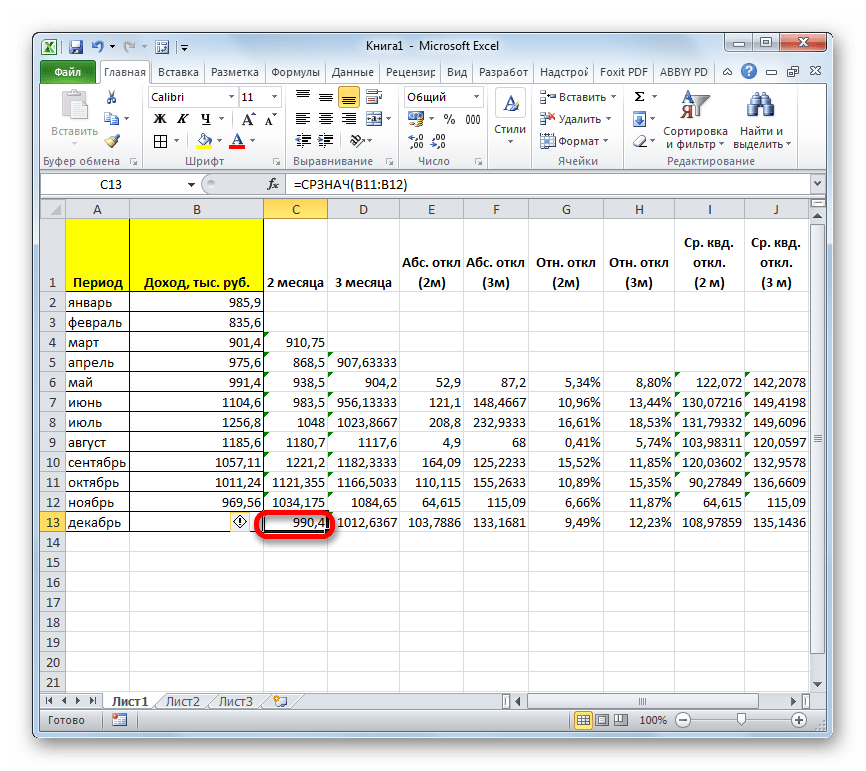
Вслед за этим программа производит расчет и выводит результат на экран. Для того, чтобы определить, какая из двух моделей более точная, нам нужно сравнить стандартные погрешности. Чем меньше данный показатель, тем выше вероятность точности полученного результата. Как видим, по всем значениям стандартная погрешность при расчете двухмесячной скользящей меньше, чем аналогичный показатель за 3 месяца. Таким образом, прогнозируемым значением на декабрь можно считать величину, рассчитанную методом скольжения за последний период. В нашем случае это значение 990,4 тыс. рублей.

Способ 2: использование функции СРЗНАЧ

В Экселе существует ещё один способ применения метода скользящей средней. Для его использования требуется применить целый ряд стандартных функций программы, базовой из которых для нашей цели является СРЗНАЧ. Для примера мы будем использовать все ту же таблицу доходов предприятия, что и в первом случае.

Как и в прошлый раз, нам нужно будет создать сглаженные временные ряды. Но на этот раз действия будут не настолько автоматизированы. Следует рассчитать среднее значение за каждые два, а потом три месяца, чтобы иметь возможность сравнить результаты.

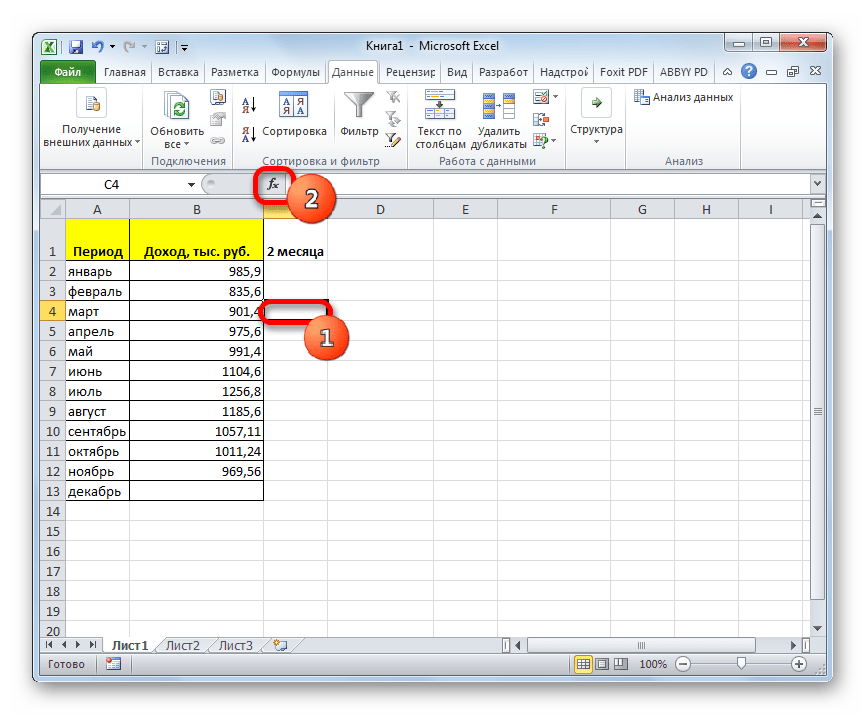
Прежде всего, рассчитаем средние значения за два предыдущих периода с помощью функции СРЗНАЧ. Сделать это мы можем, только начиная с марта, так как для более поздних дат идет обрыв значений.

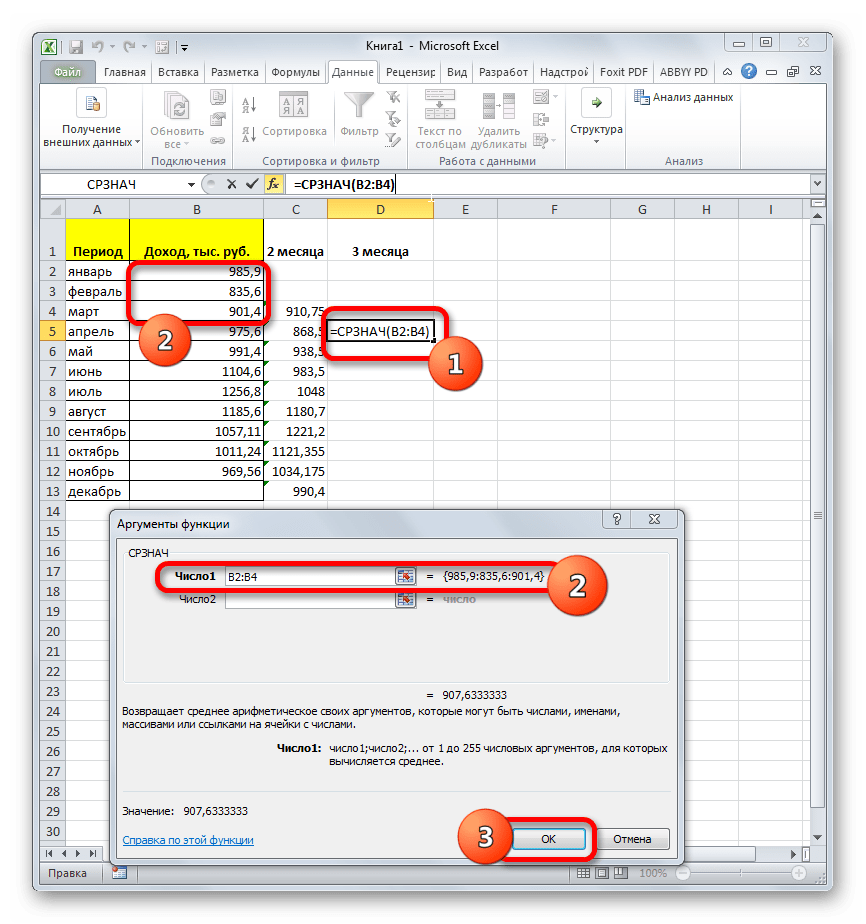
Выделяем ячейку в пустой колонке в строке за март. Далее жмем на значок «Вставить функцию», который размещен вблизи строки формул.

Активируется окно Мастера функций. В категории «Статистические» ищем значение «СРЗНАЧ», выделяем его и щелкаем по кнопке «OK».

Запускается окно аргументов оператора СРЗНАЧ. Синтаксис у него следующий:
=СРЗНАЧ(число1;число2;…)

Обязательным является только один аргумент.

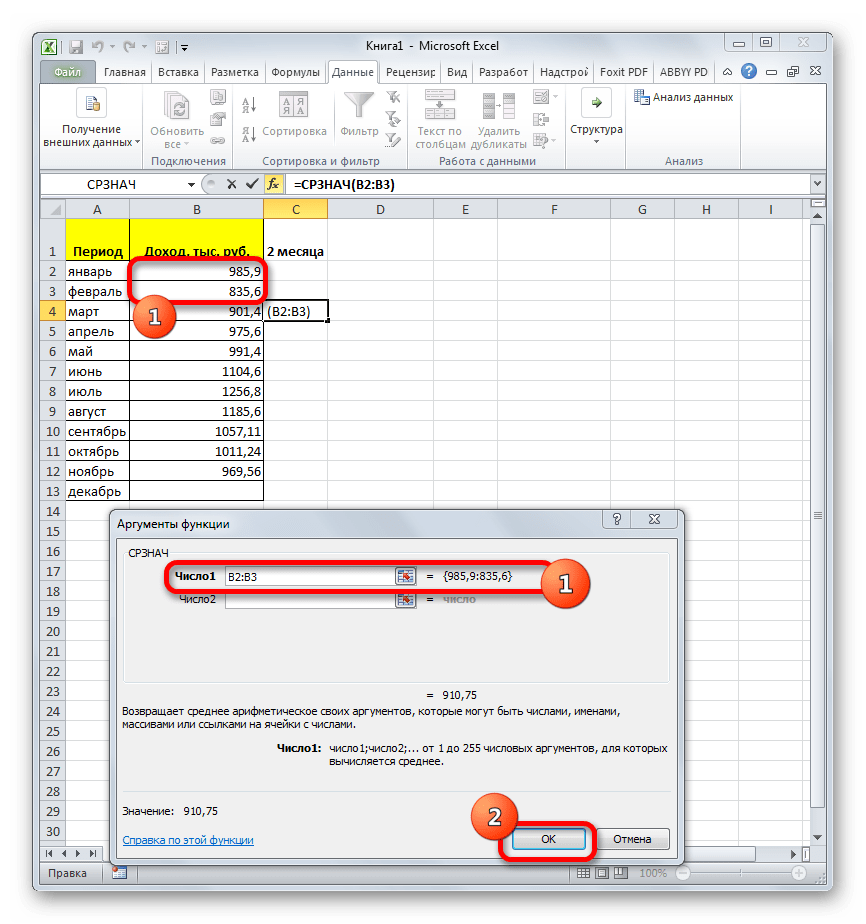
В нашем случае, в поле «Число1» мы должны указать ссылку на диапазон, где указан доход за два предыдущих периода (январь и февраль). Устанавливаем курсор в поле и выделяем соответствующие ячейки на листе в столбце «Доход». После этого жмем на кнопку «OK».

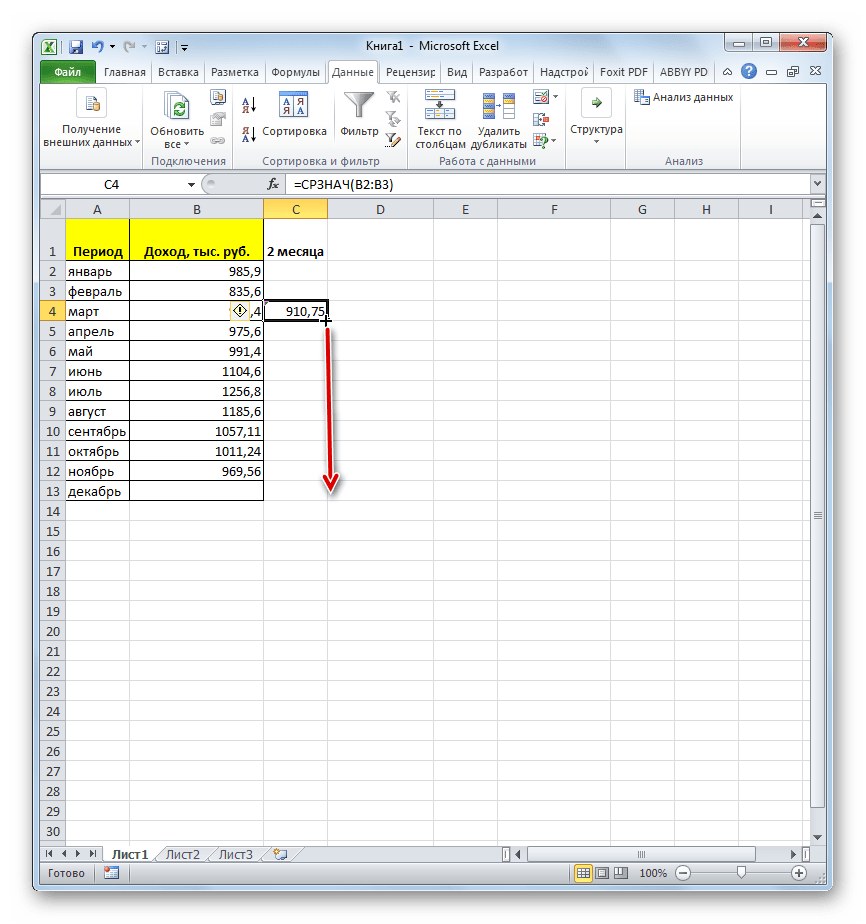
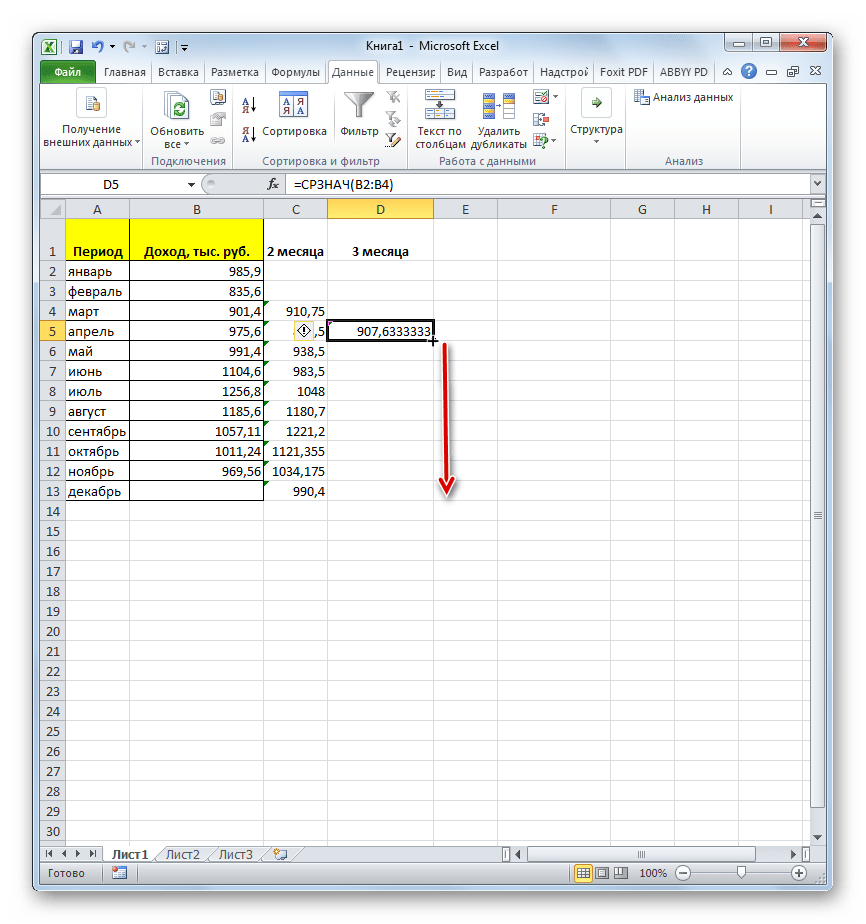
Как видим, результат расчета среднего значения за два предыдущих периода отобразился в ячейке. Для того, чтобы выполнить подобные вычисления для всех остальных месяцев периода, нам нужно скопировать данную формулу в другие ячейки. Для этого становимся курсором в нижний правый угол ячейки, содержащей функцию. Курсор преобразуется в маркер заполнения, который имеет вид крестика. Зажимаем левую кнопку мыши и протягиваем его вниз до самого конца столбца.

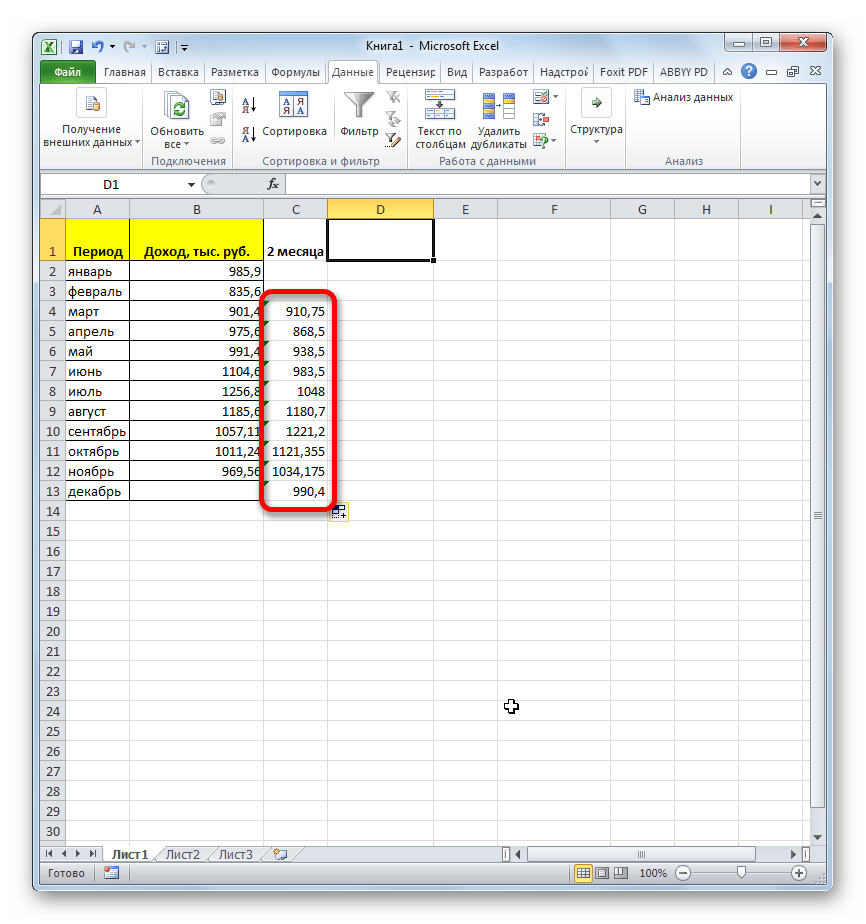
Получаем расчет результатов среднего значения за два предыдущих месяца до конца года.

Теперь выделяем ячейку в следующем пустом столбце в строке за апрель. Вызываем окно аргументов функции СРЗНАЧ тем же способом, который был описан ранее. В поле «Число1» вписываем координаты ячеек в столбце «Доход» с января по март. Затем жмем на кнопку «OK».

С помощью маркера заполнения копируем формулу в ячейки таблицы, расположенные ниже.

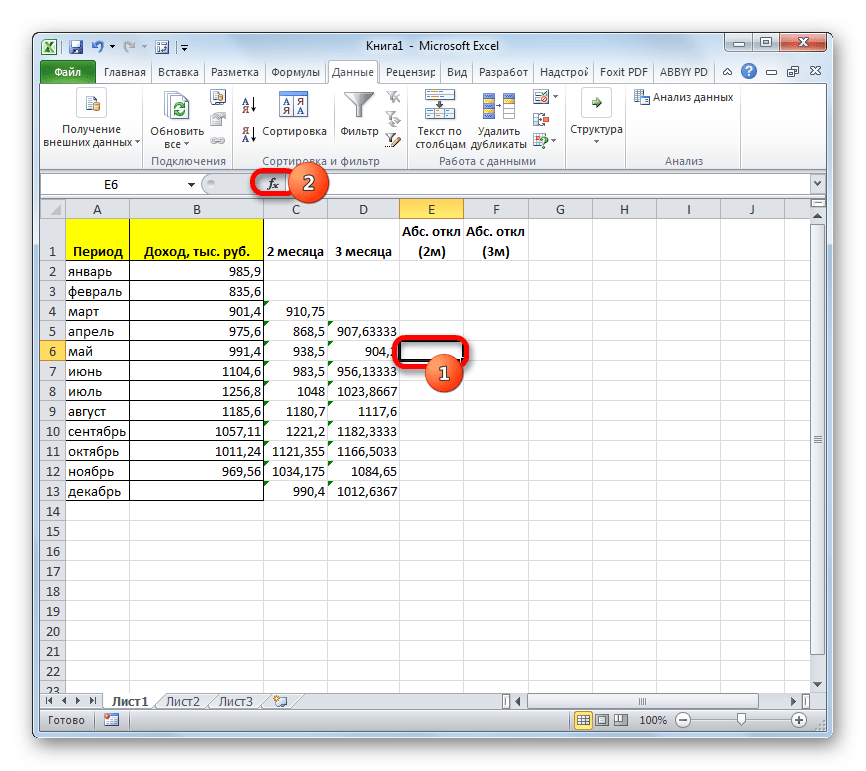
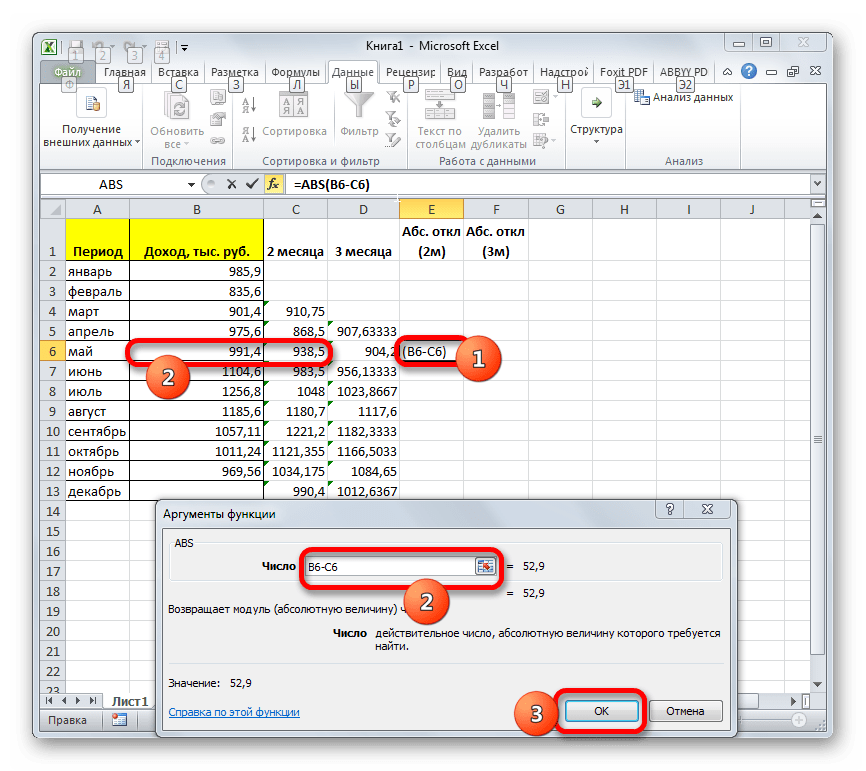
Итак, значения мы подсчитали. Теперь, как и в предыдущий раз, нам нужно будет выяснить, какой вид анализа более качественный: со сглаживанием в 2 или в 3 месяца. Для этого следует рассчитать среднее квадратичное отклонение и некоторые другие показатели. Для начала рассчитаем абсолютное отклонение, воспользовавшись стандартной функцией Excel ABS, которая вместо положительных или отрицательных чисел возвращает их модуль. Данное значение будет равно разности между реальным показателем выручки за выбранный месяц и прогнозируемым. Устанавливаем курсор в следующий пустой столбец в строку за май. Вызываем Мастер функций.

В категории «Математические» выделяем наименование функции «ABS». Жмем на кнопку «OK».

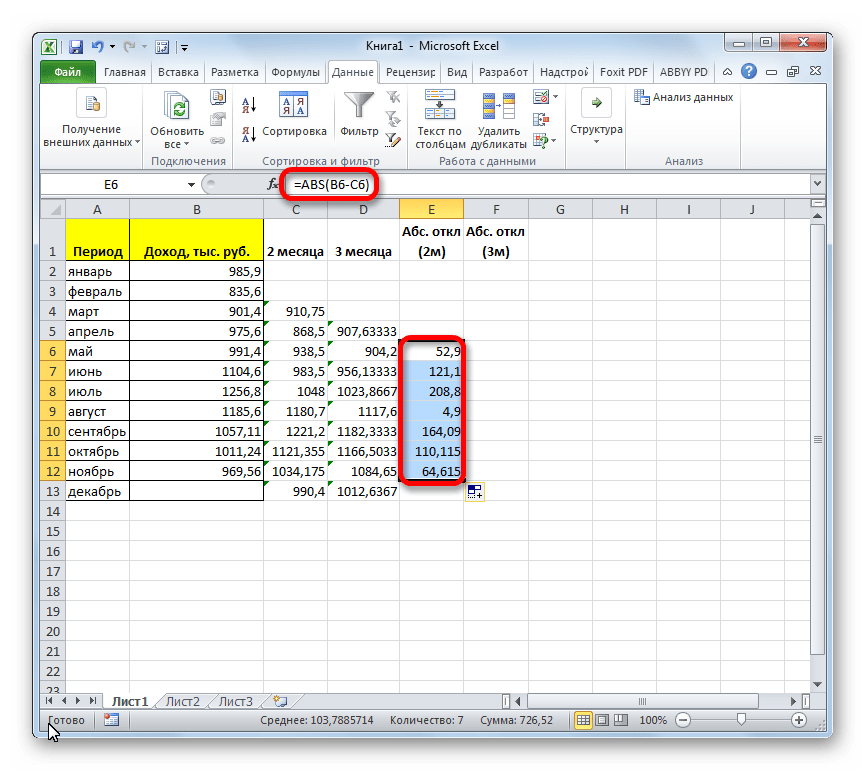
Запускается окно аргументов функции ABS. В единственном поле «Число» указываем разность между содержимым ячеек в столбцах «Доход» и «2 месяца» за май. Затем жмем на кнопку «OK».

С помощью маркера заполнений копируем данную формулу во все строки таблицы по ноябрь включительно.

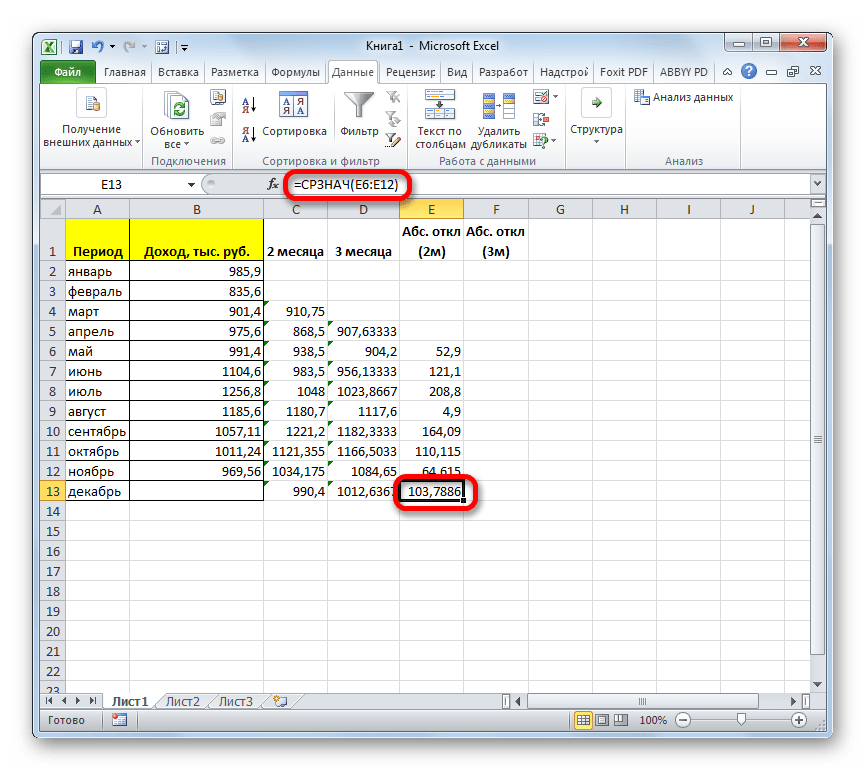
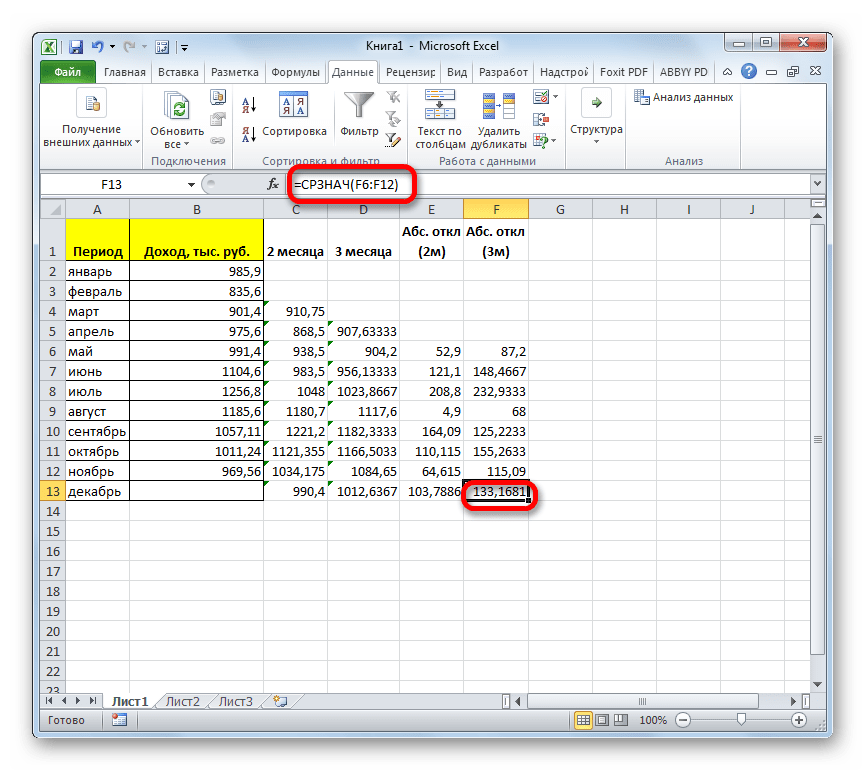
Рассчитываем среднее значение абсолютного отклонения за весь период с помощью уже знакомой нам функции СРЗНАЧ.

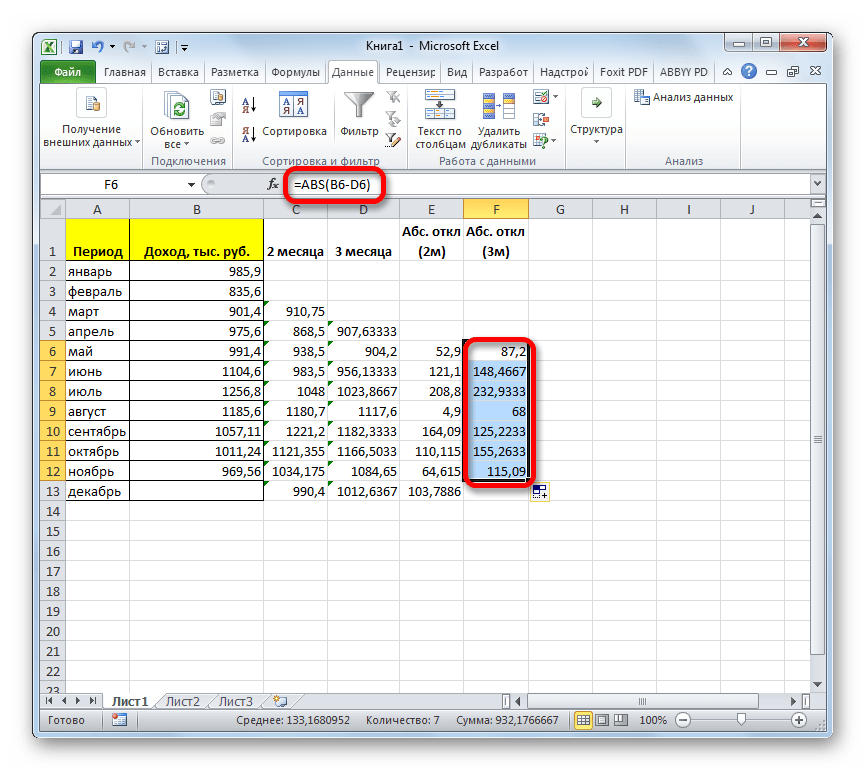
Аналогичную процедуру выполняем и для того, чтобы подсчитать абсолютное отклонение для скользящей за 3 месяца. Сначала применяем функцию ABS. Только на этот раз считаем разницу между содержимым ячеек с фактическим доходом и плановым, рассчитанным по методу скользящей средней за 3 месяца.

Далее рассчитываем среднее значение всех данных абсолютного отклонения с помощью функции СРЗНАЧ.

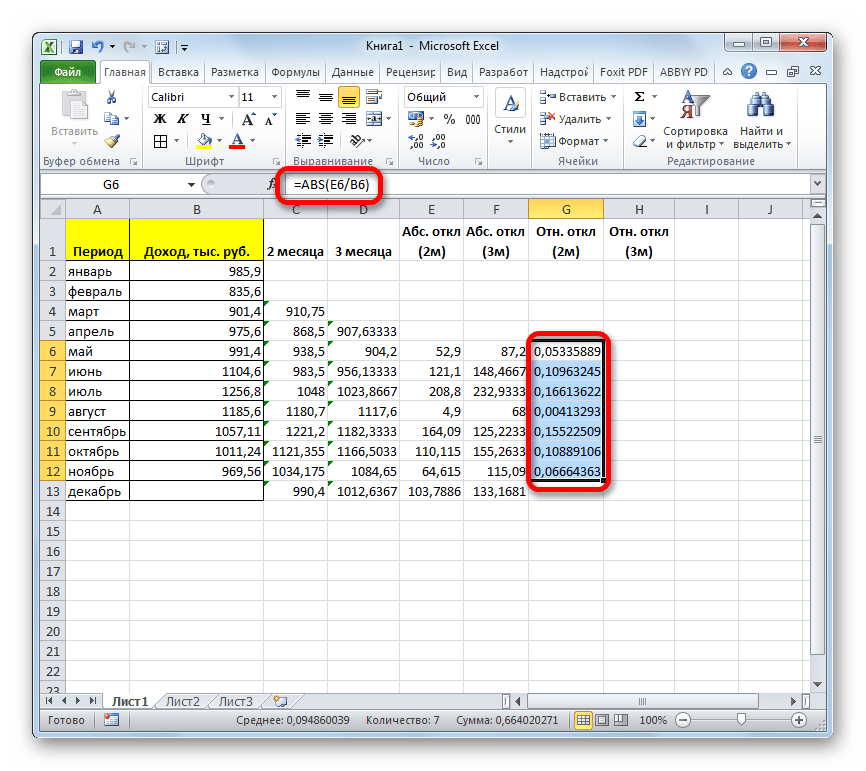
Следующим шагом является подсчет относительного отклонения. Оно равно отношению абсолютного отклонения к фактическому показателю. Для того чтобы избежать отрицательных значений, мы опять воспользуемся теми возможностями, которые предлагает оператор ABS. На этот раз с помощью данной функции делим значение абсолютного отклонения при использовании метода скользящей средней за 2 месяца на фактический доход за выбранный месяц.

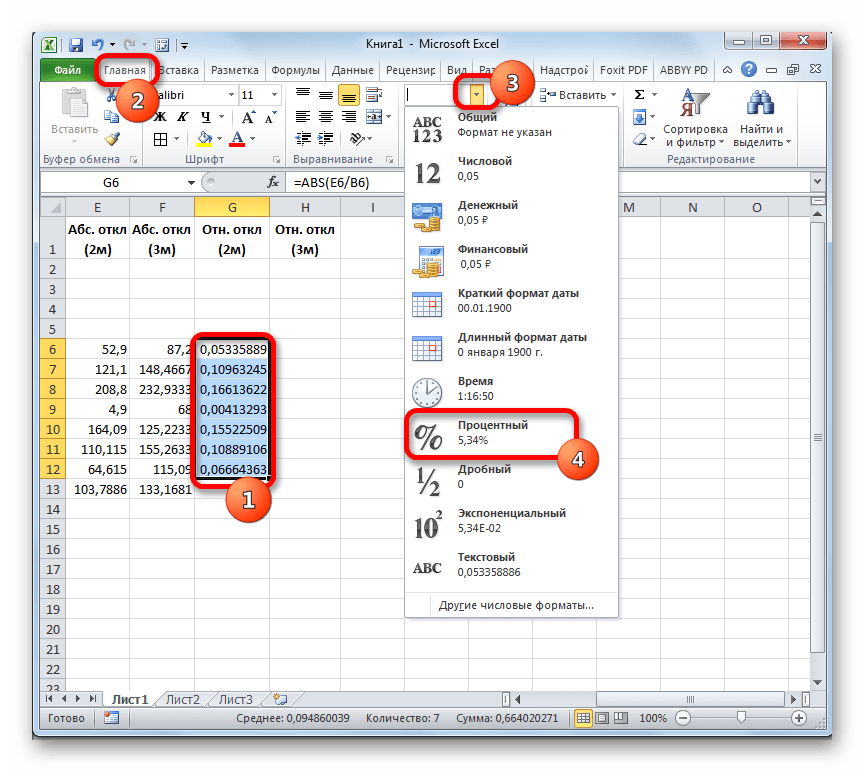
Но относительное отклонение принято отображать в процентном виде. Поэтому выделяем соответствующий диапазон на листе, переходим во вкладку «Главная», где в блоке инструментов «Число» в специальном поле форматирования выставляем процентный формат. После этого результат подсчета относительного отклонения отображается в процентах.

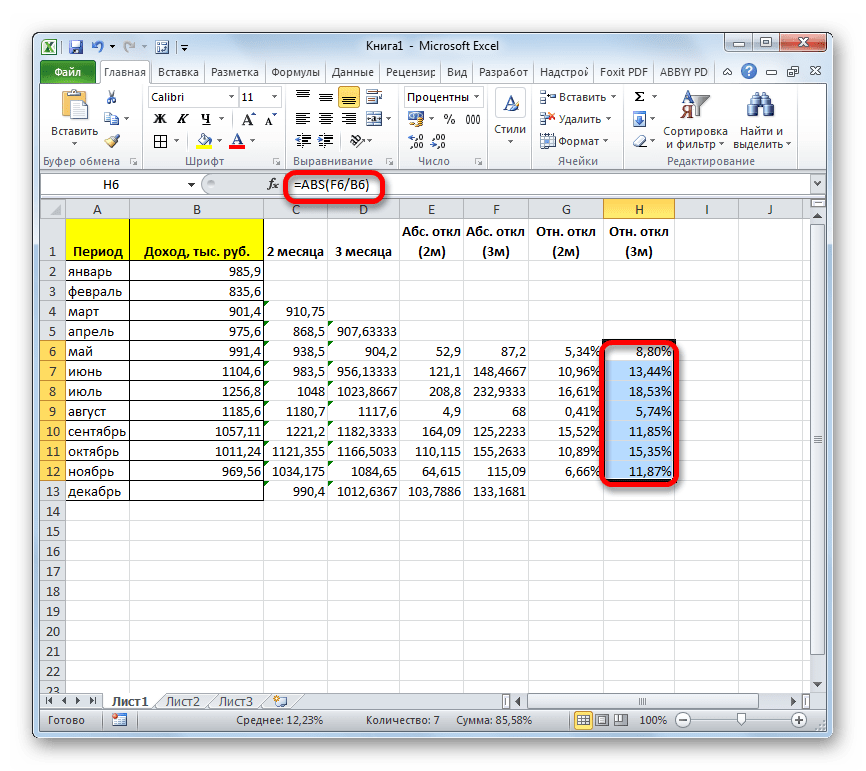
Аналогичную операцию по подсчету относительного отклонения проделываем и с данными с применением сглаживания за 3 месяца. Только в этом случае для расчета в качестве делимого используем другой столбец таблицы, который у нас имеет название «Абс. откл (3м)». Затем переводим числовые значения в процентный вид.

После этого высчитываем средние значения для обеих колонок с относительным отклонением, как и ранее используя для этого функцию СРЗНАЧ. Так как для расчета в качестве аргументов функции мы берем процентные величины, то дополнительную конвертацию производить не нужно. Оператор на выходе выдает результат уже в процентном формате.

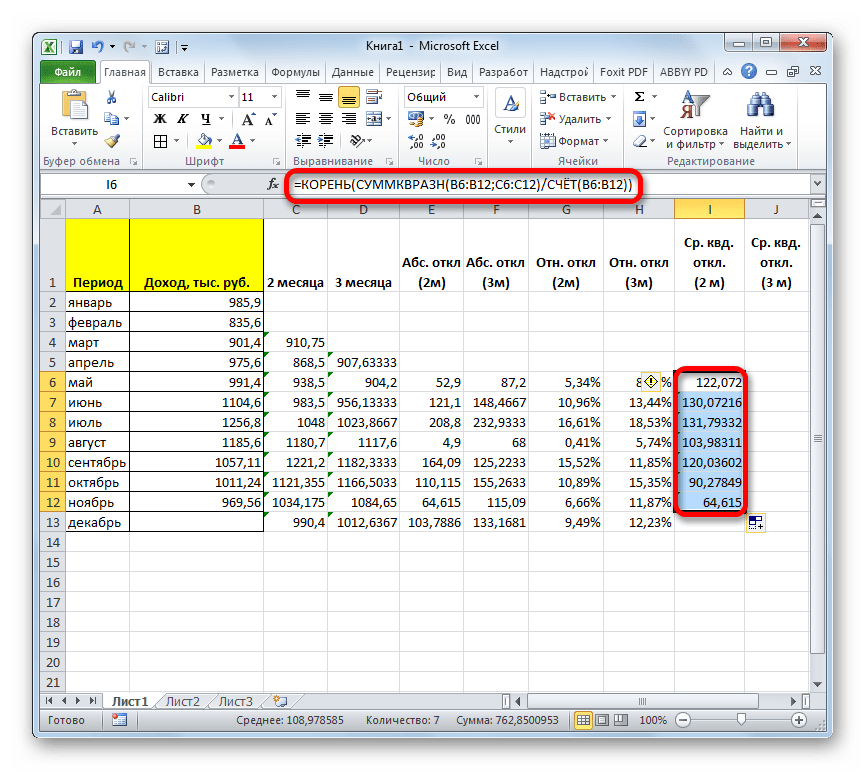
Теперь мы подошли к расчету среднего квадратичного отклонения. Этот показатель позволит нам непосредственно сравнить качество расчета при использовании сглаживания за два и за три месяца. В нашем случае среднее квадратичное отклонение будет равно корню квадратному из суммы квадратов разностей фактической выручки и скользящей средней, деленной на количество месяцев. Для того, чтобы произвести расчет в программе, нам предстоит воспользоваться целым рядом функций, в частности КОРЕНЬ, СУММКВРАЗН и СЧЁТ. Например, для расчета среднего квадратичного отклонения при использовании линии сглаживания за два месяца в мае будет в нашем случае применяться формула следующего вида:
=КОРЕНЬ(СУММКВРАЗН(B6:B12;C6:C12)/СЧЁТ(B6:B12))

Копируем её в другие ячейки столбца с расчетом среднего квадратичного отклонения посредством маркера заполнения.

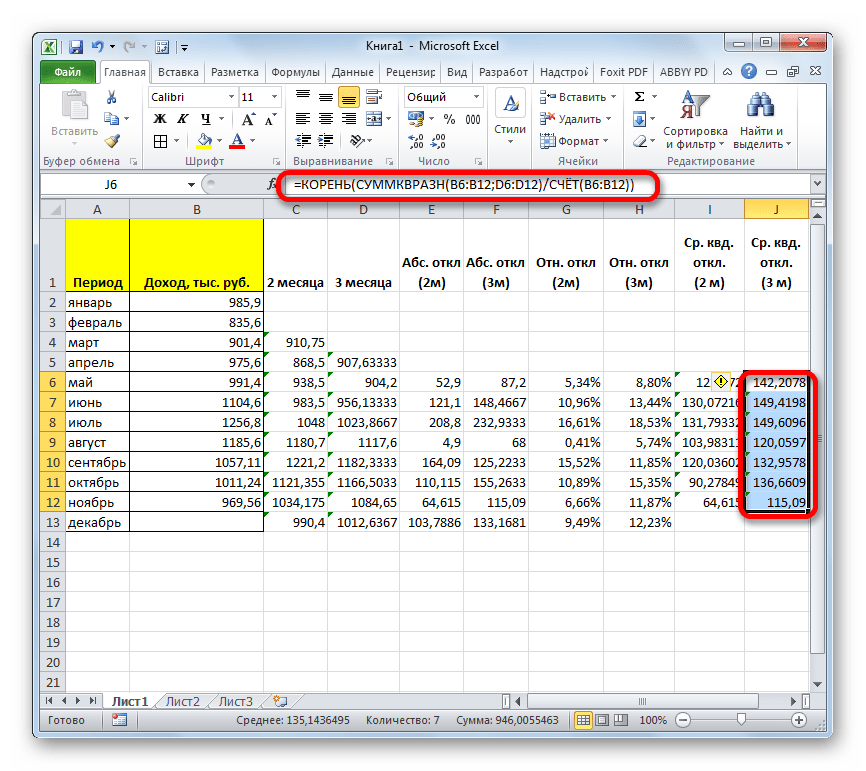
Аналогичную операцию по расчету среднего квадратичного отклонения выполняем и для скользящей средней за 3 месяца.

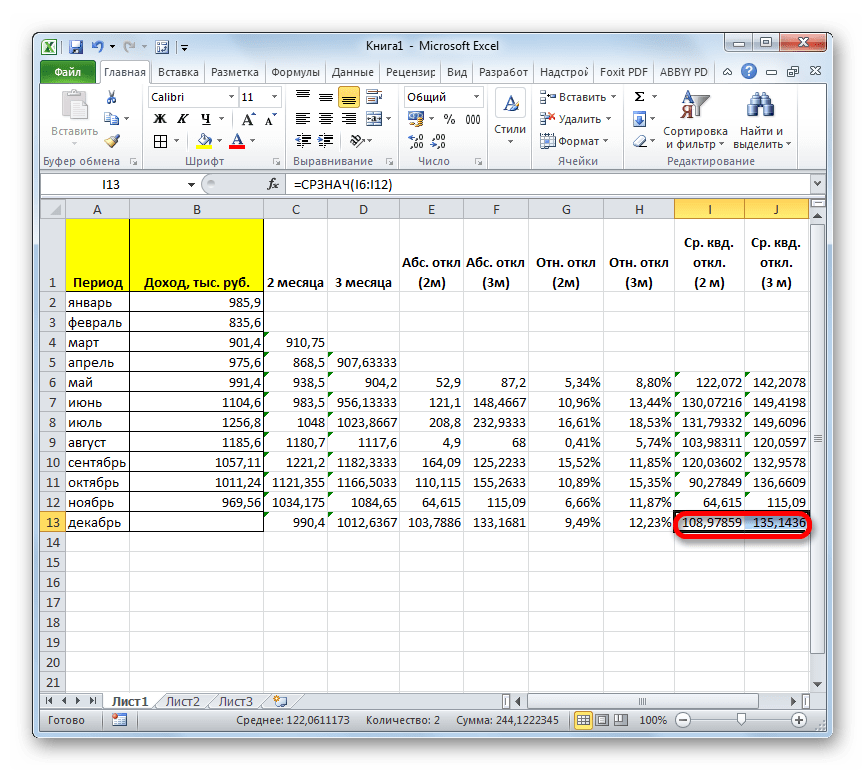
После этого рассчитываем среднее значение за весь период для обоих этих показателей, применив функцию СРЗНАЧ.

Произведя сравнение расчетов методом скользящей средней со сглаживанием в 2 и 3 месяца по таким показателям, как абсолютное отклонение, относительное отклонение и среднеквадратичное отклонение, можно с уверенностью сказать, что сглаживание за два месяца дает более достоверные результаты, чем применение сглаживания за три месяца. Об этом говорит то, что вышеуказанные показатели по двухмесячному скользящему среднему, меньше, чем по трехмесячному.

Таким образом, прогнозируемый показатель дохода предприятия за декабрь составит 990,4 тыс. рублей. Как видим, это значение полностью совпадает с тем, которое мы получили, производя расчет с помощью инструментов Пакета анализа.

Урок: Мастер функций в Экселе

Мы произвели расчет прогноза при помощи метода скользящей средней двумя способами. Как видим, данную процедуру намного проще выполнить с помощью инструментов Пакета анализа. Тем не менее некоторые пользователи не всегда доверяют автоматическому расчету и предпочитают для вычислений использовать функцию СРЗНАЧ и сопутствующие операторы для проверки наиболее достоверного варианта. Хотя, если все сделано правильно, на выходе результат расчетов должен получиться полностью одинаковым.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник

Для чего нужен метод скользящей средней и как его используют инвесторы

Один из основных индикаторов технического анализа, который помогает инвесторам определить тенденции на рынке ценных бумаг, — скользящая средняя. Что это такое и как ее правильно использовать — в статье.

Специальные индикаторы помогают правильно определить цель инвестирования и увеличить потенциальную прибыль. Сторонники технического анализа используют метод скользящей средней — Moving Average, или MA.

Что такое метод скользящей средней
Как рассчитать метод скользящей средней
Как применять метод скользящей средней
Насколько точен метод скользящей средней
Кратко

Что такое метод скользящей средней

Метод скользящей средней — усреднение цены акции или другого актива за определенный период времени. Это один из основных и наиболее простых инструментов технического анализа, который показывает тенденции на рынке и помогает инвесторам оценивать текущее состояние актива. Когда рынок растет — скользящая средняя увеличивается. Если он падает — индикатор снижается.

Как рассчитать метод скользящей средней

Существует два основных вида скользящей средней: простая (SMA) и экспоненциальная (EMA). От вида скользящей средней зависит формула расчета показателя.

Рассчитать простую скользящую среднюю. В этом случае данные за определенный период используются, чтобы получить среднее арифметическое. Каждая цена имеет такой же вес, как и все остальные. Этот способ придает всем ценам закрытия одинаковое значение и поэтому не учитывает потенциальную динамику цены актива.

Формула расчета простой скользящей средней:

Сумма цен за период времени / Период времени

Например, цены закрытия торгов для каждого из дней периода такие: 10 рублей, 15 рублей, 20 рублей, 15 рублей. Период времени соответствует количеству дней, то есть равен 4. В этом случае простая скользящая средняя: (10 + 15 + 20 + 15) / 4 = 15.

Рассчитать экспоненциальную скользящую среднюю. В отличии от SMA, этот способ придает больший вес последним ценам периода. Поэтому он чувствительнее к изменениям данных. График EMA более объективно отражает динамику актива.

Формула расчета экспоненциальной скользящей средней:

(Цена закрытия сегодня) * (2 / Период времени ─ 1) + Значение EMA вчера * (1 ─ (2 / Период времени ─ 1))

Простую или экспоненциальную скользящую среднюю не нужно рассчитывать самостоятельно. Готовые данные можно найти на любой аналитической платформе в разделе технического анализа.

На графике динамика акций компании. SMA — кривая фиолетового цвета, EMA — кривая желтого цвета. Видно, как EMA чувствительнее реагирует на спад цены акций в феврале. Она снижается быстрее, чем SMA, и дает более точные результаты. Источник: сервис Yahoo Finance

Как применять метод скользящей средней

Скользящие средние могут быть разной длины — это влияет на чувствительность к изменениям цены актива. Обычно длины скользящих средних составляют 10, 20, 50, 100 или 200 дней. Их можно применять на графике к любому периоду времени, который нужен инвестору. MA с короткой длиной будет реагировать на изменение цены актива быстрее, чем MA c более длинным периодом.

Скользящие средние с короткими периодами используют для краткосрочного трейдинга, чтобы видеть все скачки цены актива. Длинные скользящие средние помогают долгосрочным инвесторам следить за общим трендом актива и не отвлекаться на короткие колебания цены.

На графике динамика акций компании за последний год. Кривая зеленого цвета — EMA с длиной 50 дней. Кривая красного цвета — EMA с длиной 100 дней. Зеленая кривая чувствительнее реагирует на снижение цены акции и падает быстрее, чем красная кривая. Источник: сервис Yahoo Finance

Кроме того, технические аналитики считают, что если цена актива пересекла MA снизу вверх, актив стоит покупать. Если сверху вниз — актив стоит продавать.

На графике динамика акций компании Harrow health. Видно, как пересечение кривой EMA с графиком цены отражает рост или падение стоимости акции. Источник: Yahoo Finance

С помощью метода скользящей средней можно найти точку входа для покупки актива. Для этого нужно следить за пересечением графиков: наложите две скользящие средние разной длины, например 20 и 50 дней. Когда краткосрочная MA пересекает долгосрочную снизу вверх — тренд положительный, акцию можно покупать. Такое пересечение в трейдинге называется золотым крестом. Когда краткосрочная скользящая средняя пересекает более долгосрочную сверху вниз — тренд отрицательный, акцию стоит продать. Такое пересечение называется мертвым крестом.

На графике динамика акций Газпрома. Зеленая кривая — MA длиной 20 дней. Красная кривая — MA длиной 50 дней. Пересечения двух скользящих средних отражают падение и рост цены акции компании. Источник: Yahoo Finance

Насколько точен метод скользящей средней

Скользящие средние всегда рассчитываются на основе исторических данных, поэтому они показывают только текущую ситуацию на рынке и ничего не прогнозируют. Обычно в условиях кризиса или других экономических потрясений ситуация на рынке быстро меняется. В таких условиях метод скользящей средней не успевает отражать изменения и может давать необъективные результаты.

Допустим, в прошлом квартале компания по производству полупроводников показала плохие финансовые результаты. Инвесторам это не понравилось, и цена акций упала. Но после этого менеджмент объявил: компания заключила соглашение с Samsung на производство чипов. Такие новости часто становятся сигналом рынку, который корректирует ожидания, и в будущем цена акций может вырасти.

Метод скользящих средних не отразит перспективы роста и не поможет инвестору принять решение. Это слабая сторона технического анализа и метода скользящей средней. Чтобы повысить объективность оценки и снизить потенциальные риски, многие инвесторы применяют фундаментальный анализ. Они изучают отчетность компаний, читают мнения аналитиков и строят собственные прогнозы. Подробнее о том, что такое фундаментальный анализ, — в статье Фундаментальный анализ фондового рынка — минимум, который должен знать каждый инвестор.

Кратко

Существует два основных вида скользящей средней: простая (SMA) и экспоненциальная (EMA). В зависимости от вида индикатора меняется формула расчета. EMA учитывает вес последних показателей периода и поэтому дает более точный результат.
Чтобы правильно использовать метод скользящей средней, можно определять длину скользящей средней, следить за пересечением скользящей средней с графиком цены актива и наблюдать за пересечением одной MA c другой.
Метод скользящей средней учитывает только историческую динамику и поэтому не помогает строить прогнозы. Чтобы избежать рисков, инвесторы применяют фундаментальный анализ.

Данный справочный и аналитический материал подготовлен компанией ООО «Ньютон Инвестиции» исключительно в информационных целях. Оценки, прогнозы в отношении финансовых инструментов, изменении их стоимости являются выражением мнения, сформированного в результате аналитических исследований сотрудников ООО «Ньютон Инвестиции», не являются и не могут толковаться в качестве гарантий или обещаний получения дохода от инвестирования в упомянутые финансовые инструменты. Не является рекламой ценных бумаг. Не является индивидуальной инвестиционной рекомендацией и предложением финансовых инструментов. Несмотря на всю тщательность подготовки информационных материалов, ООО «Ньютон Инвестиции» не гарантирует и не несет ответственности за их точность, полноту и достоверность.

Какие бывают виды скользящих средних и каким образом они рассчитываются

По методу построения скользящие средние бывают следующих основных видов:

Простая
Взвешенная
Экспоненциальная

Простая скользящая средняя (SMA — Simple Moving Average) строится следующим образом: суммируются все значения цен за выбранный период (порядок средней) и делится на количество этих значений. Другими словами находится среднее арифметическое значение цены за период. В качестве цен могут браться цены открытия, цены закрытия или любые другие в зависимости от предпочтений трейдера.

Недостатком простой скользящей средней является тот факт, что она придает одинаковый вес всем значениям цены в выбранном периоде n. Т.е., например короткий восходящий тренд, который уже давно закончился, тем не менее, продолжает влиять на последнее значение простой скользящей средней наравне с более актуальными последними ценовыми тенденциями. Для того, чтобы нивелировать погрешность, вызванную этим фактом были созданы взвешенная и экспоненциальная скользящие средние рассмотренные ниже.

Формула для расчета простой скользящей средней имеет следующий вид:

SMA=(P1+P2+…+Pn)/n, где

P1…Pn — значения цены в периоде n;

n — Количество значений цены в периоде n.

Взвешенная скользящая средняя (WMA — Weighted Moving Average) рассчитывается по формуле:

WMA = Sum(Wn*Pn) / Sum(Wn), где

Pn — значение цены (P1. P2,…Pn);

Wn — вес цены, вычисляется таким образом, что чем ближе цена к ее нынешнему значению (к P1), тем больше ее вес: Wn=1/n

Таким образом, последние цены оказывают на значение взвешенной скользящей средней большее влияние, чем предыдущие.

Экспоненциальная скользящая средняя (EMA — Exponential Moving Average) вычисляется по формуле:

EMA = EMA(k-1) + (2/(n+1))*(Pk — EMA(k-1)), где

EMA(k-1) — предыдущее значение экспоненциальной скользящей средней;

n — Период скользящей средней;

Pk — текущая цена.

Как видно из формулы, экспоненциальная скользящая средняя учитывает свое предыдущее значение и придает больший вес последним ценам (Pk). Именно тот факт, что последние цены имеют больший вес, а влияние старых цен убывает экспоненциально, делает сглаживание более качественным. Некоторые трейдеры считают, что экспоненциальная скользящая средняя лучше предсказывает разворот тренда и дает меньше ложных сигналов.

Основные сигналы даваемые индикатором

Сигналы, даваемые всеми типами МА довольно просты и интерпретируются следующим образом:

— Скользящая средняя идущая вверх говорит о бычьем настроении рынка и дает сигнал к покупке;

— Скользящая средняя идущая вниз говорит о медвежьем настроении и дает сигнал к продаже;

— Пересечение ценой скользящей средней снизу вверх говорит об ускорении роста цены и дает сигнал к покупке;

— Пересечение ценой скользящей средней сверху вниз говорит об ускорении снижения цены и дает сигнал к продаже;

— Разворот скользящей средней снизу вверх при растущем графике цены — сигнал к покупке;

— Разворот скользящей средней сверху вниз при падающем графике цены является сигналом к продаже.

Резюмируя вышесказанное, стоит заметить, что не одна из описанных скользящих средних не является панацеей. Все они дают достаточно много ложных сигналов и требуют дополнительной фильтрации. Тем не менее, правильный выбор типа и периода индикатора скользящая средняя в применении к конкретным рыночным условиям, может заметно упростить трейдеру процесс принятия решений. Причем далеко не всегда сложное является лучшим и зачастую простая скользящая средняя является лучшим выбором для анализа ценового графика.

Настройка скользящей средней в терминале МТ4

Самый популярный среди российских трейдеров терминал MetaTrader4 (МТ4) располагает широким ассортиментом разного рода индикаторов среди которых, разумеется, нашлось место и для скользящих средних.

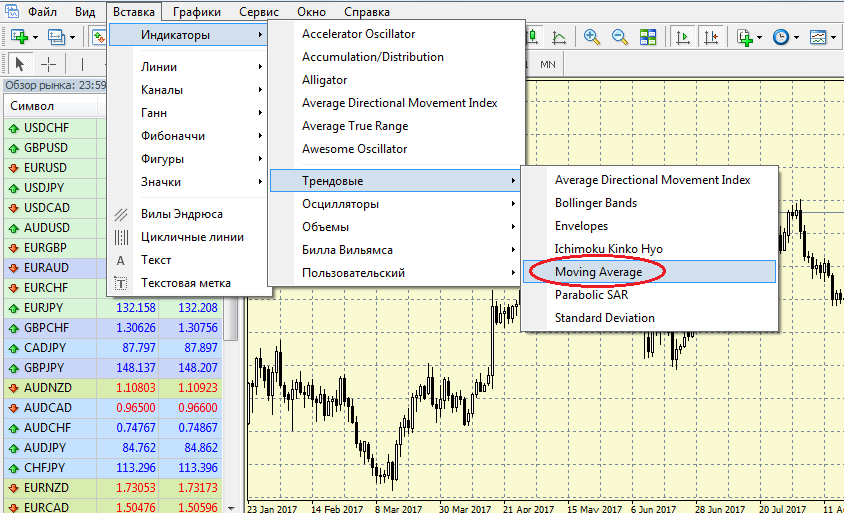
Для того чтобы прикрепить к графику скользящую среднюю, нужно перейти по следующему маршруту: Вставка -> Индикаторы -> Трендовые -> Moving Average.

Кликнув по вкладке Moving Average, вы увидите перед собой следующее окно:

Давайте рассмотрим все параметры по порядку. Начнем с параметра «Период», как вы уже, наверное, догадались, здесь устанавливается требуемый период скользящей средней. Параметр «Сдвиг», позволяет сдвинуть скользящую среднюю вправо относительно графика цены (в данном случае установлен сдвиг вправо на 30 свечей).

В окошке «Метод МА» можно выбрать один из четырёх типов скользящей средней:

Simple – простая скользящая средняя;
Exponential – экспоненциальная скользящая средняя;
Smoothed – сглаженная;
Linear Weigthed – линейно взвешенная;

Следующее окошко позволяет выбрать тип цены, по которому будет строиться индикатор. Можно выбрать из четырёх основных цен:

Close – индикатор будет построен по ценам закрытия свечей;
Open – Построение индикатора будет вестись по ценам открытия свечей;
High – Построение по наивысшим (максимальным) ценам свечей;
Low – Построение по минимальным ценам;

Кроме этого предлагаются к выбору усредненные значения цены такие как:

Median Price – среднеарифметическое значение цены между минимумом и максимумом: (High+Low)/2
Typical Price – среднеарифметическое значение от трех показателей High, Low и Close: (High+Low+Close)/3
Weighted Close — среднеарифметическое значение от четырех показателей High, Low, Open и Close: (High+Low+ Open+Close)/4

Наконец в группе параметров «Стиль» можно указать цвет, тип и толщину линии скользящей средней.

После установки необходимых настроек нажимаем кнопку «ОК» и наслаждаемся видом нанесенного на ценовой график индикатора 🙂

Нюансы которые необходимо учитывать при работе с МА

Для того чтобы получить от этого индикатора максимум пользы и вместе с тем не ждать от него невозможного, при работе с ним необходимо учитывать ряд нюансов:

В первую очередь всегда нужно отдавать себе отчёт в том, что скользящие средние не опережают рынок, а следуют вслед за ним. Соответственно сигналы получаемые на их основе всегда запаздывают по отношению к моменту начала движения рынка (и чем больше период МА, тем больше это запаздывание);
Если в процессе торговли вы увидите, что индикатор соприкоснулся с ценовым графиком, то не делайте из этого скороспелых выводов. Дело в том, что хотя сам индикатор и не подлежит перерисовке, но его “кончик” постоянно находится в движении, обретая свою окончательную форму только после закрытия очередной свечи;
Сам по себе индикатор МА не представляет из себя готовую торговую стратегию, не стоит торговать основываясь только на его сигналах. Но в сочетаниями с другими инструментами (в т.ч. с другими индикаторами технического анализа) он может стать надежным помощником трейдера;
Скользящие можно использовать в качестве динамического уровня поддержки/сопротивления. Для этого, в зависимости от текущей волатильности цены, подбирают такой период МА, чтобы большая ее часть находилась под ценой (для линии поддержки) или над ценой (при е использовании в качестве линии сопротивления);

Из последнего пункта вытекает возможность использовать МА для выставления уровней STOP LOSS в качестве хорошей альтернативы трейлинг-стопу. Для автоматизации этого процесса можно использовать скрипт или торговый робот. Стопы можно двигать вслед за ценой на небольшом расстоянии от скользящей, гарантируя, таким образом, их срабатывание только в тех случаях, когда цена действительно кардинально изменит вектор своего развития.

Стратегии торговли на основе скользящих средних

Поговорив о теории, давайте теперь перейдём непосредственно к практике использования этого индикатора технического анализа. На основе скользящих средних построено огромное множество торговых систем и стратегий. Все эти стратегии, пожалуй, не перечесть, да оно нам, собственно, и не нужно.Ведь в большинстве своём все они основаны на нескольких основных свойствах рассматриваемого индикатора и отличаются друг от друга лишь нюансами настройки и (или) разными наборами вспомогательных индикаторов.

Ниже, я предлагаю вашему вниманию те базовые стратегии торговли на основе скользящих средних, опираясь на которые, вы сможете создать свои собственные торговые системы. Их можно использовать подобно блокам конструктора, встраивая в свою торговую систему и меняя настройки и вспомогательный набор индикаторов.

Вспомогательными, я, называю такие индикаторы, которые используются исключительно для подтверждения сигнала подаваемого основным индикатором (в данном случае это — скользящие средние).

Итак, приступим.

Стратегия основанная на направлении движения скользящей средней

Это самое простое и очевидное применение MA. Ведь сама суть скользящей средней,как раз и состоит в том, чтобы максимально сгладить все «неровности» ценового графика, исключить случайные колебания цены и выдать в итоге её «чистое» направление.

При этом, помимо направления МА, смотрят ещё и на относительное положение ценового графика. Если график цены находится выше направленной вверх скользящей, то это говорит о текущем превосходстве быков (а, следовательно, о бычьем рынке и восходящем тренде). А если, наоборот, график цены находится под падающей скользящей средней, то это явный признак превосходства медведей.

На мой взгляд, наиболее оптимальным вариантом применения данной стратегии будет следующий:

1. Определяется основной тренд (возможно на графике с большим таймфреймом, чем тот который установлен на том графике, где ведётся торговля). Здесь нас интересуют только два варианта:

либо цена находится над восходящей МА и тренд, соответственно, восходящий;
либо цена находится под нисходящей МА и тренд — нисходящий.

2. Далее ищем точки входа только для длинных позиций (если тренд восходящий), или только для коротких позиций (в случае нисходящего тренда).

Как видите, при этом мы получаем уже не стратегию, построенную на скользящих средних в чистом виде, а некую систему из нескольких (как минимум двух** торговых стратегий).

** Вторая стратегия как раз призвана искать точки входа в обозначенном МА направлении (к слову, её тоже можно построить на скользящих средних, но только меньшего порядка).

При нисходящей МА ищем точки входа в продажи, при восходящей — в покупки (с помощью вспомогательного индикатора Stochastic)

Есть, конечно, ещё вариант, при котором трейдеры пытаются открыть позицию непосредственно в момент разворота скользящей средней, но он, на мой взгляд, не очень надёжен. Объясню почему. Дело здесь в том, что определить момент разворота МА достаточно сложно. Одно дело смотреть на ценовой график, и постфактум определять какие прекрасные моменты для входа в позицию были на разворотах МА, и совсем другое дело — определить этот самый момент разворота в реальном времени.

В силу того что текущая цена постоянно меняется, кончик линии МА также находится в постоянном рыскании. Он то поворачивается вверх, вслед за ростом цены, то клюёт вниз — вслед за её снижением. А кроме этого, ничто не мешает тому, чтобы развернувшаяся было скользящая средняя, вдруг опять не возобновила своего движения в прежнем направлении.

Стратегия основанная на пересечении скользящих средних

В данном случае речь идёт о пересечении, так называемых,быстрой и медленной линии МА. Из двух линий, быстрой называют ту, период которой меньше. А медленной, соответственно, ту скользящую среднюю у которой период расчёта больше. Дело здесь в том, что чем с меньшим периодом рассчитывается МА, тем более чутко она реагирует на каждое изменение цены.Большой же период, напротив, делает скользящую среднюю «неповоротливой» и нечувствительной к относительно небольшим ценовым перепадам.

Именно за счёт этой различной «чувствительности» индикатора к одним и тем же изменениям цены и возникает такое явление как взаимопересечение скользящих средних. Хотя, если быть более точным, то правильнее будет сказать, что быстрая линия пересекает линию медленную. Ну, это всё нюансы, а как же это использовать в торговле?

Иллюстрация стратегии основанной на пересечении быстрой и медленной МА

А используется данное явление следующим нехитрым образом:

Когда быстрая линия пересекает медленную снизу-вверх, то это является сигналом к покупке. Причём, если обе линии при этом направлены вверх, то это существенно усиливает подаваемый сигнал;
Когда же быстрая линия пересекает медленную сверху-вниз, то говорят о сигнале к продаже. При этом обоюдное направление линий вниз служит дополнительным подтверждением его (сигнала) истинности.

Некоторые трейдеры используют не две, а более скользящих средних с разными периодами. И для того, чтобы принять решение о покупке или продаже, они ждут, пока все эти линии выстроятся в определённом порядке (по возрастанию, либо по убыванию периода, соответственно).

Стратегия основанная на пересечении скользящей средней с ценовым графиком

В этом случае, сигналом к покупке либо к продаже является пересечение ценой линии МА. Причём для покупки мы ждём такого пересечения снизу-вверх, а для продажи — сверху-вниз, соответственно.

Когда цена пересекает своё среднее значение, то это говорит о том, что интенсивность её изменения возрастает. А это, в свою очередь, может быть свидетельством возросшего интереса к финансовому инструменту со стороны рыночных игроков (в том числе маркетмейкеров) и иметь своим следствием дальнейшее движение цены в том же направлении. На этом и построена данная стратегия.

Примеры сделок на пересечении ценой линии МА

Иногда, для дополнительной фильтрации сигнала, в этой стратегии используют не одну, а сразу две скользящие с разными периодами. В этом случае, пересечение ценой скользящей средней большего периода, будет предварительным сигналом, а пересечение скользящей меньшего периода — окончательным.

Основные недостатки стратегий на основе МА

Одним из главных недостатков всех вышеприведённых стратегий является большое запаздывание подаваемых МА сигналов. Ведь, по сути своей, МА — это лишь усреднённое значение всех ценовых значений на заданном временном интервале. А потому, перед тем как будет подан соответствующий сигнал (допустим- пересечение двух скользящих между собой), цена порой успевает проделать уже большую часть своего движения.

Отчасти эту проблему можно решать путём уменьшения периода МА. Ведь чем меньше будет период, тем чувствительнее она будет реагировать на каждое ценовое движение. В этом случае ценовое движение можно поймать у самых его истоков, однако здесь появляется другая проблема — большое количество ложных сигналов.

Масса ложных сигналов — это ещё один крупный недостаток стратегий на основе МА. И проявляется он, как уже сказано выше, тем сильнее, тем меньше периоды используемых скользящих средних. Для фильтрации такого рода ложных сигналов применяется целый ряд методов.

Методы фильтрации ложных сигналов

Для того чтобы отделить зёрна от плевел, или, в нашем случае
— истинные сигналы от ложных, трейдеры применяют три основных метода:

Фильтрация по минимальному ценовому диапазону;
Фильтрация по минимальному временному диапазону;
Фильтрация посредством применения
«конверта» скользящих средних.

Фильтрация сигнала по минимальному ценовому диапазону предполагает открытие соответствующей позиции только после того, как цена пройдёт некоторое заданное расстояние в»правильном» направлении после того, как этот сигнал будет получен.

Например, трейдер задал размер минимального ценового диапазона равным 5 пунктам. Тогда при пересечении ценой линии скользящей средней снизу-вверх, он совершит покупку не ранее того момента, когда цена отойдёт от точки этого пересечения вверх на заданные 5 пунктов.

Здесь важно не переборщить с размером этого самого минимального ценового диапазона. Здесь нужно найти золотую середину, чтобы и отложного сигнала застраховаться, и всю свою потенциальную прибыль при этом не упустить.

Фильтрация по минимальному временному диапазону подразумевает выжидание определённого времени с момента получения сигнала. Допустим, трейдер получил сигнал на продажу, но он не продаёт до тех пор, пока не пройдёт заданное количество времени. И только после этого, при условии, что полученный сигнал остался в силе (линии не развернулись в обратную сторону, не произошло их обратного пересечения, или то пересечение, которое послужило сигналом, осталось на графике), он совершает сделку.

Фильтрация посредством применения «конверта» предполагает изображение скользящей средней не в виде отдельной линии, а в виде полосы состоящей из двух линий отстоящих от основной в обе стороны на равные расстояния (обычно задаваемые посредством процента).

Суть метода состоит в том, что сигнал считается подтверждённым лишь после того, как цена прошла через всю полосу целиком. По сути своей, этот метод есть не что иное, как частный случай фильтрации сигнала по минимальному ценовому диапазону, только диапазон этот здесь задан неконкретным значением в пунктах, а в процентах.

Вы можете поделиться этой статьёй на своей странице в соцсетях:

Categories
Tags

Related Articles
Author

Источник

Применение[править | править код]

Этимология[править | править код]

Виды скользящих средних[править | править код]

Общий случай[править | править код]

Простое скользящее среднее[править | править код]

Взвешенные скользящие средние[править | править код]

Общие положения[править | править код]

Взвешенное скользящее среднее[править | править код]

Экспоненциально взвешенное скользящее среднее[править | править код]

Экспоненциальное скользящее среднее произвольного порядка[править | править код]

Модифицированное скользящее среднее[править | править код]

Смежные функции[править | править код]

Скользящие на основе других усредняющих функций[править | править код]

Простая скользящая медиана[править | править код]

Динамические скользящие средние[править | править код]

Кумулятивное скользящее среднее[править | править код]

Кумулятивная сумма[править | править код]

См. также[править | править код]

Примечания[править | править код]

Использование скользящих средних в Excel

Применение надстройки «Пакет анализа»

Применение скользящей средней

Способ 1: Пакет анализа

Способ 2: использование функции СРЗНАЧ

Еще статьи по данной теме:

Помогла ли Вам статья?

Что такое метод скользящей средней

Как рассчитать метод скользящей средней

Как применять метод скользящей средней

Насколько точен метод скользящей средней

Кратко

Читайте также

Какие бывают виды скользящих средних и каким образом они рассчитываются

Основные сигналы даваемые индикатором

Настройка скользящей средней в терминале МТ4

Нюансы которые необходимо учитывать при работе с МА

Стратегии торговли на основе скользящих средних

Стратегия основанная на направлении движения скользящей средней

Стратегия основанная на пересечении скользящих средних

Стратегия основанная на пересечении скользящей средней с ценовым графиком

Основные недостатки стратегий на основе МА

Методы фильтрации ложных сигналов

Вам также может понравиться

Как найти скорость движения кпд

Как найти разрешение экрана на телевизоре

Как найти лейкопластырь в террарии

Добавить комментарий Отменить ответ