Как найти значение степени алгебра 7 класс

Алгебра

7 класс

Урок № 2

Степень числа

Перечень вопросов, рассматриваемых в теме:

Понятие степени числа.

Свойства степеней.

Тезаурус

Степенью числа a с натуральным показателем n, бóльшим 1, называется произведение n одинаковых множителей, каждый из которых равен числу a.

Свойства степеней:

Произведение степеней с одним и тем же показателем равно степени с тем же показателем и основанием, равным произведению оснований.

Произведение степеней с одним и тем же основанием – это степень с тем же основанием и показателем, равным сумме показателей этих степеней.

Степень степени числа равна степени того же числа с показателем, равным произведению показателей этих степеней.

Основная литература:

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

Дополнительная литература:

1. Макарычев Ю. Н. Алгебра: 7 класс. // Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. – М.: Просвещение, 2019. – 256 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.

Произведение шести множителей, каждый из которых равен 8, называют шестой степенью числа 8 и обозначают 8⁶, т.е.

8 ∙ 8 ∙ 8 ∙ 8 ∙ 8 ∙ 8 = 8⁶.

При этом число 8 называют основанием степени, а число 6 – показателем степени.

А теперь давайте сформулируем общее определение степени числа, опираясь на предыдущий пример:

степенью числа a с натуральным показателем n, бóльшим 1, называется произведение n одинаковых множителей, каждый из которых равен числу a.

Запись aⁿ читается как: а в степени n, или n-ая степень числа a.

А вот следующие записи можно произносить по-разному:

a²– её можно произносить «а в квадрате» или «а во второй степени»;

a³ – её можно произносить «а в кубе» или «а в третьей степени».

Стоит отметить, что особые случаи возникают, если показатель степени равен нулю или единице:

степенью числа а с показателем n = 1 является само это число:

a¹ = a;

любое число в нулевой степени равно единице:

a⁰ = 1;

ноль в любой натуральной степени равен нулю:

0ⁿ = 0;

единица в любой степени равна 1:

1ⁿ = 1.

Выражение 0⁰ (ноль в нулевой степени) считают неопределенным.

Примеры. Возведём в степени:

(−91)⁰ = 1

0¹⁴⁴ = 0

1²³⁶ = 1.

При решении задач, нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.

Рассмотрим несколько примеров.

Возведём в степень

2⁵ = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 = 32

2,5³ = 2,5 ∙ 2,5 ∙ 2,5 = 15,625

Основание степени может быть любым числом – положительным, отрицательным или нулём.
При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа, в результате может получиться как положительное число, так и отрицательное число. Это зависит от того, чётным или нечётным числом был показатель степени.

Например, (-2)⁵. Ответ будет отрицательным, так как показатель степени, 5- нечётное число. (-2)⁵ = (-2) ∙ (-2) ∙ (-2) ∙ (-2) ∙ (-2) = -32.

(-5)⁴. А вот в этом примере ответ будет положительным, так как показатель степени, 4 – чётное число.

(-5)⁴ = (-5) ∙ (-5) ∙ (-5) ∙ (-5) = 625.

Рассмотрим такой пример: 4² ∙ 5² = 4 ∙ 4 ∙ 5 ∙ 5 = (4 ∙ 5) ∙ (4 ∙ 5) = (4 ∙ 5)² = 20² = 400.

Данный пример подтверждает справедливость следующего свойства степеней:

Произведение степеней с одним и тем же показателем равно степени с тем же показателем и основанием, равным произведению оснований:

aⁿ∙ bⁿ = (a ∙ b)ⁿ

Приведём еще такой пример: 5² ∙ 5⁵ = (5 ∙ 5) ∙ (5 ∙ 5 ∙ 5 ∙ 5 ∙ 5) = 5 ∙ 5 ∙ 5 ∙ 5 ∙ 5 ∙ 5 ∙ 5 = 5⁷.

Этот пример подтверждает справедливость следующего свойства степеней:

Произведение степеней с одним и тем же основанием это степень с тем же основанием и показателем, равным сумме показателей этих степеней, т.е.

aⁿ ∙ a^m = a^n+m

Наконец, рассмотрим равенство:

(7²)³ = (7 ∙ 7)³ = (7 ∙ 7) ∙ (7 ∙ 7) ∙ (7 ∙ 7) = 7 ∙ 7 ∙ 7 ∙ 7 ∙ 7 ∙ 7 = 7⁶.

Это равенство подтверждает справедливость следующего свойства степеней:

Степень степени числа равна степени того же числа с показателем, равным произведению показателей этих степеней, т.е.

(aⁿ)^m = a^n∙m

Разбор решения заданий тренировочного модуля

№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте

Заполните таблицу:

	Число	Основание	Показатель степени
1.	255
2.	1113
3.	1356

Для заполнения пропусков вспомним, что такое основание и показатель степени.

	Число	Основание	Показатель степени
1.	255	25	5
2.	1113	11	13
3.	1356	135	6

№2. Тип задания: Чему равно произведение 5⁴ ∙ 5¹¹ ∙ 4² ∙ 4¹³?

Варианты ответов:

(4 ∙ 5)¹⁵

4¹³ ∙ 5¹⁴

(4 ∙ 5)³⁰

4¹⁵ ∙ 5³⁰

Для решения задания, воспользуемся свойствами степеней: aⁿ∙a^m= a^n+m и aⁿ∙bⁿ= (a ∙ b)ⁿ

5⁴ ∙ 5¹¹ ∙ 4² ∙ 4¹³ = 5¹⁵ ∙ 4¹⁵ = (4 ∙ 5)¹⁵.

Верный ответ: (4 ∙ 5)¹⁵.

Напоминаем, что в данном уроке разбираются свойства степеней
с натуральными показателями и нулём.
Степени с рациональными показателями и их свойства будут рассмотрены в уроках
для 8 классов.

Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют
упрощать вычисления в примерах со степенями.

Свойство № 1
Произведение степеней

Данное свойство степеней также действует на произведение трёх и более степеней.

Примеры.

• Упростить выражение.
  
  b · b² · b³ · b⁴ · b⁵ =
  b ^{1 + 2 + 3 + 4 + 5} = b¹⁵
• Представить в виде степени.
  
  
  6¹⁵ · 36 = 6¹⁵ · 6² = 6¹⁵ · 6² =
  6¹⁷
• Представить в виде степени.
  
  
  (0,8)³ · (0,8)¹² = (0,8)^{3 + 12} = (0,8)¹⁵

Свойство № 2
Частное степеней

Примеры.

• Записать частное в виде степени
  
  (2b)⁵ : (2b)³ = (2b)^{5 − 3} = (2b)²
• Вычислить.
  

  =
  11^{3 − 2} · 4 ^{2 − 1} = 11 · 4 = 44

• Пример. Решить уравнение. Используем свойство частного степеней.
  
  
  3⁸ : t = 3⁴

  t = 3⁸ : 3⁴

  t = 3^{8 − 4}

  t = 3⁴

  
  Ответ: t = 3⁴ = 81

Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.

• Пример. Упростить выражение.
  
  
  4^{5m + 6} · 4^{m + 2} : 4^{4m + 3} =
  4^{5m + 6 + m + 2} : 4^{4m + 3} =
  4^{6m + 8 − 4m − 3} = 4^{2m + 5}
• Пример. Найти значение выражения, используя свойства степени.
  

  =
  =

  =

  =

  =

  2^{11 − 5} = 2 ⁶ = 64
  

Свойство № 3
Возведение степени в степень

• Пример.
  (a⁴)⁶ = a^{4 · 6} = a²⁴
• Пример. Представить 3²⁰ в виде степени с основанием
  3².

  По свойству возведения степени в степень известно, что при возведении
  в степень показатели перемножаются, значит: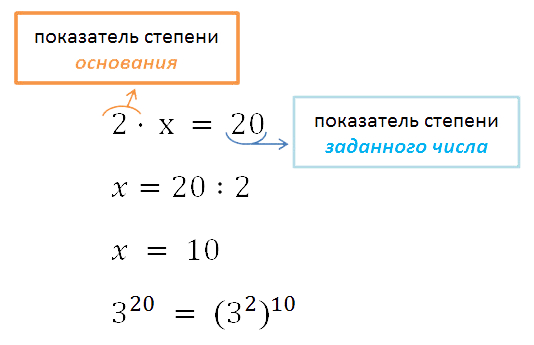

  

Свойства 4
Степень произведения

• Пример 1.
  (6 · a² · b³ · c )² =
  6² · a^{2 · 2} · b^{3 · 2}
  · с ^{1 · 2} = 36 a⁴ · b⁶
  · с ²
  
• Пример 2.
  
  (−x² · y)⁶ =

  ( (−1)⁶ · x^{2 · 6} · y^{1 · 6}) =

  x¹² · y⁶
  

То есть, чтобы перемножить степени с одинаковыми
показателями можно перемножить основания, а показатель степени оставить неизменным.

• Пример. Вычислить.
  2⁴ · 5⁴ = (2 · 5)⁴ =
  10⁴ = 10 000
• Пример. Вычислить.
  0,5¹⁶ · 2¹⁶ = (0,5 · 2)¹⁶ =
  1

В более сложных примерах могут встретиться случаи, когда умножение и деление
надо выполнить над степенями с разными основаниями и разными показателями.
В этом случае советуем поступать следующим образом.

Например,

4⁵ · 3² = 4³ ·
4² · 3² = 4³ · (4 · 3)² =

64 · 12² = 64 · 144 = 9216

Пример возведения в степень десятичной дроби.

4²¹ · (−0,25)²⁰ = 4 · 4 ²⁰ ·
(−0,25) ²⁰ = 4 · (4 · (−0,25))²⁰ = 4 · (−1)²⁰ =
4 · 1 = 4

Свойства 5
Степень частного (дроби)

• Пример. Представить выражение в виде частного степеней.
  
  (5 : 3)¹² = 5¹² : 3¹²

Напоминаем, что частное можно представить в виде дроби. Поэтому
на теме
возведение дроби в степень
мы остановимся более подробно на следующей странице.

---

Ваши комментарии

Оставить комментарий:

---

Математика – точная наука, и математический язык приветствует употребление более кратких записей.

Вместо записи 5 + 5 + 5 + 5 + 5 + 5, математик использует запись 5 · 6, потому что у нас шесть одинаковых слагаемых.

А запись 5 · 5 · 5 · 5 · 5 · 5 математик заменит записью 5⁶, потому что шесть одинаковых множителей.  Конечно, при необходимости можно использовать обратные записи.

Мы знаем, что 7⁶ есть произведение шести множителей, каждый из которых равен 7:

7⁶ = 7 · 7 · 7 · 7 · 7.

Число 7 – основание степени, число 6 – показатель степени, выражение 7⁶ – степень.

Дадим определение степени для любого основания и любого натурального показателя.

Степенью числа а с натуральным показателем n большим 1, называется произведение n множителей, каждый из которых равен а.

Для степени числа а с показателем n принято обозначение: аⁿ.

По определению  аⁿ = а · а · а · а… а. (n раз)

В определение не включён случай, когда показатель n = 1, так как не имеет смысла говорить о произведении, состоящем из одного множителя. Степень с показателем 1 определяется особо.

Степенью числа а с показателем 1 называется само число а: а¹ = а.

Вычисление значения степени называют действием возведения в степень. Это действие выполняется первым при вычислении значения выражения.

Рассмотрим примеры вычислений значений выражений, содержащих степени.

Пример 1. Найдём значение степеней  (-4)⁴  (-4)³.

(-4)⁴ = (-4) · (-4) · (-4) · (-4) = 256

(-4)³ = (-4) · (-4) · (-4) = -64

Обратим внимание, при возведении в степень отрицательного числа, положительное число получается, если число возводится в чётную степень, если же отрицательное число возводится в нечётную степень, то получается отрицательное число.

Пример 2. Вычислим (3/4)³.

(3/4)³ = 3/4 · 3/4 · 3/4 = 27/64.

Пример 3. Найдем значение выражения  6 · 3³.

Чтобы найти значение этого выражения, достаточно сначала найти значение степени 3³, а затем выполнить умножение:

1) 3³ = 3 · 3 · 3 = 27

2) 6 · 27 = 162.

Значение степени можно найти с помощью вычислительной техники, а можно воспользоваться таблицей степеней.

Пример 4. Рассмотрим ещё один пример. Найдём значение выражения 0,5 · 48².

0,5 · 48² = 0,5 · 2304 = 1152

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Свойства степени с натуральным показателем

Примеры

Пример 1. Запишите в виде степени с основанием 2

а) $ 2cdot4cdot16 = 2^1cdot2^2cdot2^4 = 2^{1+2+4} = 2^7 $

б) $4cdot 32^2 = 2^2 cdot (2^5)^2 = 2^2cdot2^{5cdot2} = 2^{2+10} = 2^{12}$

в) $4cdot8:32 = 2^2 cdot 2^3:2^5 = 2^{2+3-5} = 2^0$

г) $ frac{2^{10}}{(2^3)^2} = frac{2^{10}}{2^{3 cdot 2}} = 2^{10-6} = 2^4 $

Пример 2. Запишите в виде степени:

а) $ left(-frac{3}{7}right)^5 : left(-frac{3}{7}right)^3 = left(-frac{3}{7}right)^{5-3} = left(-frac{3}{7}right)^2 $

б) $ y^{22}: (y^2)^5 = y^{22}: y^{2cdot5} = y^{22-10} = y^{12} $

в) $ (a+2b)^14:(a+2b)^8 = (a+2b)^{14-8} = (a+2b)^6 $

г) $ (3a+5)^2cdot(3a+5)^7:(3a+5)^4 = (3a+5)^{2+7-4} = (3a+5)^5 $

Пример 3. Найдите значение выражения:

а) $ frac{7cdot3^3}{3^2} = 7cdot3^{3-2} = 7cdot3 = 21 $

б) $ frac{2^4cdot3^3}{4cdot9} = frac{2^4}{2^2} cdot frac{3^3}{3^2} = 2^{4-2}cdot3^{3-2} = 2^2cdot3^1 = 4cdot3 = 12$

в) $ frac{5^6cdot5}{25cdot125} = frac{5^{6+1}}{5^2cdot5^3} = frac{5^7}{5^5} = 5^{7-5} = 5^2 = 25 $

г) $ frac{11^3cdot4^7}{11^2cdot16cdot64} = frac{11^3}{11^2} cdot frac{4^7}{4^2cdot4^3} = 11^{3-2} cdot 4^{7-5} = 11^1cdot4^2 = 11cdot16 = 176 $

д) $ left(frac{3^5}{10^2}right)^2 cdot left(frac{2}{5}right)^5 cdot left(frac{5}{3}right)^4 = frac{(3^5 )^2}{((5cdot2)^2)^2}^2 cdot frac{2^5}{3^5} cdot frac{5^4}{3^4} = frac{3^{10}}{5^4 cdot 2^4} cdot frac{2^5 cdot 5^4}{3^{5+4}} = frac{3^{10}}{3^9} cdot frac{2^5}{2^4} cdot frac{5^4}{5^4} = frac{3^{10}}{3^9} cdot frac{2^5}{2^4} cdot frac{5^4}{5^4} = 3^1 cdot 2^1 cdot 5^0 = 6 $

е) $ left(frac{5}{3}right)^5 cdot left(1frac{4}{5}right)^2 cdot (1,5)^2 = frac{5^5}{3^5} cdot left(frac{9}{5}right)^2 cdot left(frac{3}{2}right)^2 = frac{5^5}{3^5} cdot frac{(3^2 )^2}{5^2} cdot frac{3^2}{2^2} = frac{5^5}{5^2} cdot frac{3^{4+2}}{3^5} cdot frac{1}{2^2} = frac{5^3cdot3}{2^2} = frac{725}{4} = 181 frac{1}{4} $

ж) $ frac{3^3cdot7{22}-3^2cdot7^{21}}{49^{10}} = frac{7{21}cdot3^2(3cdot7-1)}{(7^2)^{10}} = 7^{21-20}cdot3^2cdot20 = 7cdot9cdot20 = 1260 $

з) $ frac{(7^3cdot5^2-7^2cdot5^3 )cdot77}{(11cdot49)^2} = frac{7^2cdot5^2 (7-5)cdot11cdot7}{11^2cdot(7^2)^2} = frac{5^2cdot2}{11cdot7} = frac{50}{77} $

Пример 4. Возведите в степень выражение:

а) $ (a^2 b^3)^4 = (a^2)^4cdot(b^3)^4 = a^{2cdot4} cdot b^{3cdot4} = a^8 b^12 $

б) $ (-2x^5 y)^4 = (-2)^4 cdot (x^5)^4 cdot y^4 = 16x^{20}y^4 $

в) $ left(frac{10x^2}{y^3}right)^5 = left(frac{10^5cdot(x^2)^5}{(y^3 )^5}right)^5 = frac{100000x^{10}}{y^15} $

г) $ left(-frac{3y^8}{m^4 n}right)^3 = -frac{3^3cdot(y^8 )^3}{(m^4 )^3cdot n^3} = -frac{27y^{24}}{m^{12} n^3} $

Пример 5. Представьте в виде степени и вычислите:

а) $ frac{3^{10}cdot6^{10}}{2^{10}cdot9^{10}} = frac{(3cdot6)^{10}}{(2cdot9)^{10}} = frac{18^{10}}{18^{10}} = 1 $

б) $ 3^{n+2}:3^{n-1} = 3^{(n+2)-(n-1)} = 3^3 = 27 $

в) $ frac{4^{20}}{8^{13}} = frac{(2^2)^{20}}{(2^3)^{13}} = frac{2^{40}}{2^{39}} = 2^{40-39} = 2 $

г) $ 0,125^{10}cdot8^{10} = (0,125cdot8)^{10} = 1^{10} = 1 $

Пример 6. Сравните значения выражений:

а) $ 2,5^3 и 2,5^0 $

$ left. begin{array}{l} 2,5^3 = left(frac{5}{2}right)^3 = frac{125}{8} gt 1 \ 2,5^0 = 1 end{array} right} Rightarrow 2,5^3 gt 2,5^0 $

б) $ 0,7^3 и 0,7^0 $

$ left. begin{array}{l} 0,7^3 = left(frac{7}{10}right)^3 = frac{343}{1000} lt 1 \ 0,7^0 = 1 end{array} right} Rightarrow 0,7^3 gt 0,7^0 $

в) $ (-0,8)^5 и 0,8^0 $

$ left. begin{array}{l} (-0,8)^5 lt 0 \ 0,8^0 = 1 gt 0 end{array} right} Rightarrow (-0,8)^5 lt 0,8^0 $

Пример 7*. Какое из чисел больше?

а) $ 10^{20}$ или $ 20^{10} $

$ 10^{20} = (10^2)^{10} = 100^{10} $

$ 100 gt 20 Rightarrow 100^{10} gt 20^{10} Rightarrow 10^{20} gt 20^{10} $

б) $ 6^{20}$ или $2^{60} $

$2^{60} = (2^3)^{20} = 8^{20}$

$ 6 lt 8 Rightarrow 6^{20}lt 8^{20} Rightarrow 6^{20} lt 2^{60} $

в) $ 2^{300}$ или $3^{200} $

$ 2^{300} = (2^3)^{100} = 8^{100} $

$ 3^{200} = (3^2)^{100} = 9^{100} $

$ 8lt 9 Rightarrow 8^{100} lt 9^{100} Rightarrow 2^{300} lt 3^{200} $

Степени и их свойства

Данная тема очень легкая, если выучить все свойства степеней. Они, кстати, достаточно просты для запоминания.

Перед тем, как перейти в свойствам степеней, разберемся, что такое степень.

Степень – это произведение одинаковых множителей, состоящая из основания и показателя. Наглядно это можно рассмотреть на рисунке ниже.

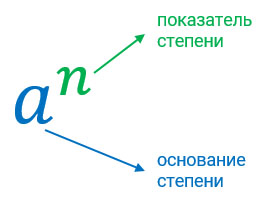
Показатель степени показывает (масло масляное) сколько раз мы умножаем основание на себя. Это очень хорошо проглядывается на следующих примерах:

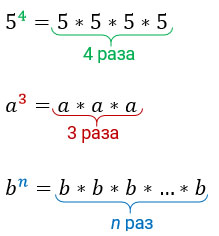
Вроде бы ничего сложного нет, правда?

Что ж, время перейти к свойствам.

Свойства степеней.

1. Любое число в первой степени равно самому себе: a¹ = a.

Сразу рассмотрим примеры.

2¹ = 2;

(-10)¹ = -10;

0¹ = 0.

2. Любое число в нулевой степени равно 1: а⁰ = 1.

Примеры:

2⁰ = 1;

(-3)⁰ = 1;

0⁰ = 1.

3. Единица в любой степени равна 1: 1ⁿ = 1.

4. При умножении степеней с одинаковыми основаниями показатели складываются: aⁿ · a^m = a^{n + m}.

Почему так?

Это свойство легко доказать на числовом примере.

2³ · 2² = 2 · 2 · 2 · 2 · 2 = 2⁵.

Конечно, так никто не расписывает, а сразу пользуется готовой формулой. Вот еще несколько примеров:

3⁴ · 3⁹ · 3¹⁵ = 3^{4 + 9 + 15} = 3²⁸;

(-2)³ · (-2)⁴ = (-2)^{3 + 4} = (-2)⁷.

5. При делении степеней с одинаковыми основаниями показатели вычитаются: aⁿ : a^m = a^{n – m} (a ≠ 0).

Доказывается эта формула тоже очень просто с помощью числового примера: три четверки из числителя сокращаем с тремя четверками из знаменателя и остаются две четверки в числителе, т.е. 4².

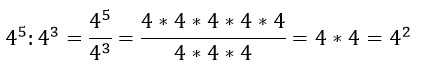
Еще парочка примеров:

15¹⁰ : 15³ : 15⁵ = 15^{10 – 3 – 5} = 10²;

(-3)¹¹ : (-3)⁵ = (-3)^{11 – 5} = (-3)⁶.

6. При возведении степени в степень показатели умножаются: (аⁿ)^m = a^nm.

Примеры:

(2²)³ = 2^{2 · 3} = 2⁶;

(5³)¹⁰ = 5^{3 · 10} = 5³⁰.

7. При возведении произведения в степень каждый множитель возводится в эту степень: (ab)ⁿ = aⁿbⁿ.

Примеры:

(5 · 4)² = 5² · 4²;

(2 · 3  · 4 · 5)^а = 2^а · 3^а · 4^а ·5^а.

8. Чтобы возвести дробь в степень надо и числитель, и знаменатель возвести в эту степень:.

Пример:

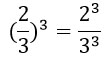
9. Степень с дробным показателем можно представить в виде корня некоторой степени по формуле (а > 0, n ≥ 2).

Пример:

10. Чтобы возвести число, отличное от нуля, в степень с отрицательным показателем надо взять число, обратное данному, и возвести его в ту же степень, только без минуса: (a ≠ 0).

Это же правило работает и для дробей:  (a ≠ 0, b ≠ 0).

Примеры:

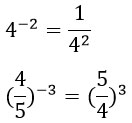
Все эти свойства срабатывают как в одну сторону, так и в другую. Соберем их в аккуратную табличку.

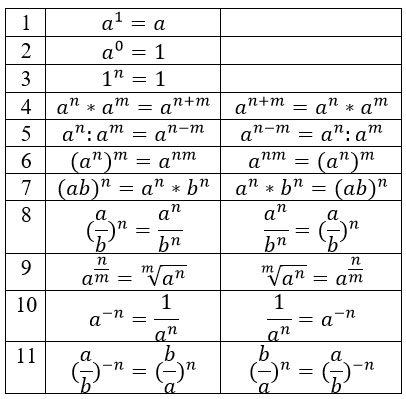
Напоследок, разберем пример, который может встретиться во второй части ОГЭ по математике. Он, конечно, не охватывает сразу все формулы – только несколько из них.

Нам нужно сократить такую дробь:

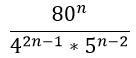
Преобразуем знаменатель дроби, дважды использовав формулу по номером 5 из второго столбика таблицы.

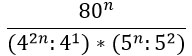
Получившиеся частные в знаменателе запишем в виде дробей.

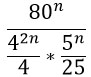
Получилась трехярусная дробь (можно произведение дробей в знаменателе переписать под одну черту). Нижний ярус этой дроби перейдет в верхний. Это не магия вне Хогвартса, но описывать эти преобразования текстом очень грустно. Если коротенько, то при делении на дробь мы ее переворачиваем и получается, что знаменатель заползает наверх 🙂

К тому же здесь можно воспользоваться свойством 6 из второго столбика и 4²ⁿ превратится в 16ⁿ.

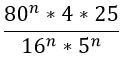
Переходим к финалу. Преобразуем знаменатель по свойству 7 из второго столбика таблицы (снова) и, наконец-таки, сокращаем дробь!

Успехов в учебе!

С уважением, Васильева Анна.