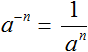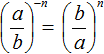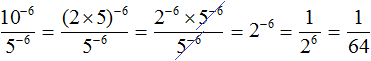Как найти значение степени отрицательного числа

Прежде чем перейти к изучению определения «отрицательная степень» рекомендуем повторно
прочитать урок
«Степень»
и «Свойства степеней».

Необходимо уверенно понимать, что такое положительная степень числа и уверенно использовать её свойства в решении
примеров.

Как возвести число в отрицательную степень

Примеры возведения в отрицательную степень.

• 6⁻² = =
• (−3)⁻³ = = = −
• 0,2⁻² = =

Примеры возведения в нулевую степень.

• ()⁰ = 1
• (−5)⁰ = 1
• d⁰ = 1

Как найти 10 в минус 1 степени

В уроке 8 класса «Стандартный вид числа» мы уже сталкивались с записью:

10⁻¹ = 0,1

Теперь, зная определение отрицательной степени, давайте разберемся, почему «10» в минус первой степени равно
«0,1».

Возведем «10⁻¹» по правилам отрицательной степени.

Перевернем «10» и запишем её в виде дроби
«

»
и заменим отрицательную степень
«−1» на
положительную степень «1».

Возведем «10» в «1» степень. Помним, что любое число в первой степени равно самому числу.

Теперь по определению десятичной дроби запишем обыкновенную дробь в виде десятичной.

По такому же принципу можно найти «10» в минус второй, третьей и т.д.

Проверим правило выше для «10⁻²».

Т.к. у нас степень «−2», значит, будет всего один ноль (положительное
значение степени «2 − 1 = 1». Сразу после запятой ставим один ноль и за ним «1».

Рассмотрим «10⁻¹».

Т.к. у нас степень «−1», значит, нулей после запятой не будет (положительное
значение степени «1 − 1 = 0». Сразу после запятой ставим «1».

То же самое правило работает и для «10⁻¹²». При переводе в десятичную дробь будет
«12 − 1 = 11 » нулей и «1» в конце.

10⁻¹² = 0,000 000 000 001

Как возвести в отрицательную степень дробь

Пример. Требуется возвести в отрицательную степень дробь.

Перевернем дробь «

»
и заменим отрицательную степень «−3» на положительную «3».

Возведем дробь в положительную степень по правилу возведения дроби в положительную степень.
Т.е. возведем и числитель «3», и знаменатель «10» в третью степень.

()⁻³ = ()³ =

=

Для более грамотного ответа запишем полученный результат в виде десятичной дроби.

()⁻³ = ()³ =

= = 0,027

Как возвести отрицательное число в отрицательную степень

Как и при возведении отрицательного числа в положительную степень, в первую
очередь необходимо определить конечный знак результата возведения в степень. Вспомним основные правила еще раз.

Пример.

(−5) ⁻² =

Перевернем число «−5» и заменим отрицательную степень
«−2»
на положительную
«2».

Так как степень «2» — четная, значит, результат возведения в степень будет
положительный. Поэтому
убираем знак минуса при раскрытии скобок.

Далее откроем скобки
и возведем во вторую степень и числитель «1»,
и знаменатель «5».

Как возвести отрицательную дробь в отрицательную степень

Конечный знак результата возведения в степень отрицательной дроби определяется по тем же правилам, что и для целого отрицательного числа.

Разберемся на примере. Задание: возвести отрицательную дробь
«(− )»
в «−3» степень.

По правилу возведения дроби в отрицательную степень перевернем дробь и заменим отрицательную степень «−3» на положительную
«3».

Теперь определим конечный знак результата возведения в «3» степень.

Степень «3» — нечетная, значит, по правилу возведения отрицательного числа в степень дробь
останется отрицательной.

Нам остается только раскрыть скобки и возвести в степень и числитель «3», и знаменатель
«2» в третью степень.

Для окончательного ответа выделим целую часть из дроби.

---

Рассмотрим другой пример возведения отрицательной дроби в отрицательную степень.

Правило возведения отрицательного числа в степень гласит: если степень четная, значит, результат возведения
будет положительным.

Свойства отрицательной степени

Все свойства степени, которые используются для положительной степени,
точно также применяются и для отрицательной степени.

В этом уроке мы не будем повторно подробно разбирать каждое свойство степени, но еще раз приведем основные формулы свойств степени
и покажем примеры их использования.

Примеры решений заданий с отрицательной
степенью

Разбор примера

Представить в виде степени.

Разбор примера

Записать в виде степени с отрицательным числом.

Разбор примера

Вычислить.

Разбор примера

Выполнить действия.

---

Ваши комментарии

Оставить комментарий:

---

Запись an означает что число a должно быть умножено n раз:

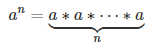Пример 1. 5³=5*5*5=125

Деление это обратная операция умножению. Отрицательная степень означает сколько раз нужно разделить число.

Число в отрицательной степени a-n может быть записано в виде:

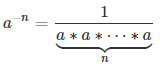Пример 2. 5^-3=1÷5÷5÷5=0,008

Пример 2 может быть записан в виде.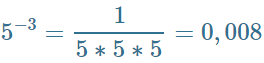

Определение. Если a≠0 и n – целое отрицательное число, то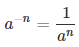

---

Для вычисления числа a^-n в отрицательной степени нужно:

1.Вычислить aⁿ

2.Затем разделить 1 на полученный результат, т.е.

В статье рассмотрим  степень с целым отрицательным показателем: определения, виды, вычисление степени, формулы для быстрого расчета.

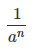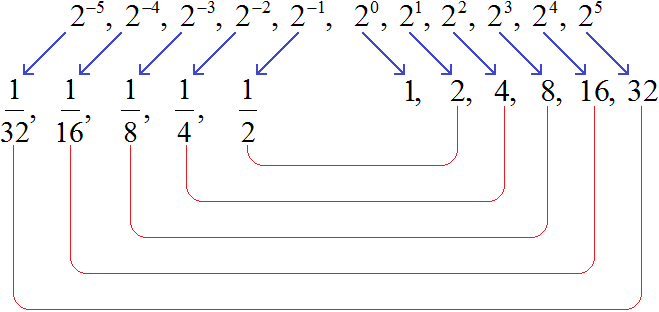
Примеры степени с целым отрицательным показателем выглядят следующим образом: 2⁻², 10⁻⁷, a⁻⁸.

Чтобы разобраться с ними, рассмотрим следующую последовательность степеней: 2⁻⁵, 2⁻⁴, 2⁻³, 2⁻², 2⁻¹, 2⁰, 2¹, 2², 2³, 2⁴, 2⁵.

• Степень с натуральным показателем в этой последовательности: 2¹, 2², 2³, 2⁴, 2⁵
• Нулевая степень в этой последовательности это степень 2⁰.
• Предыдущая степень с целым показателем будет уже с отрицательным показателем и выглядеть как 2⁻¹. Степень с целым отрицательным показателем в этой последовательности: 2⁻⁵, 2⁻⁴, 2⁻³, 2⁻², 2⁻¹.

Вычисление степени с целым отрицательным показателем

В отрицательную степень число возводится по-другому: если при возведении в положительную степень число увеличивается, то при возведении в отрицательную степень это число наоборот уменьшается.

Например, возьмём число 2 и возведем его  в неотрицательную степень:

• нулевая степень: 2⁰ =1
• степень с нутуральным показателем: 
  2¹=2,
  2²=2*2=4,
  2³=2*2*2=8,
  2⁴=2*2*2*2=16 и т.д.

Получили последовательность чисел, в которой каждое число больше следующего числа в 2 раза. Тогда логично предположить, что число, располагающееся до единицы, будет в два раза меньше единицы. Его можно получить, если 1 разделить на 2.

• Получается, что степень 2⁻¹ =1/2. 
• Предыдущее число 2⁻² должно быть в два раза меньше, чем 2⁻¹. Чтобы его получить разделим  на 2 и получим  2⁻² =1/(2*2)=1/4. 
• Предыдущее число 2⁻³ должно быть в два раза меньше, чем 2⁻². Чтобы его получить разделим  на 2 и получим  2⁻³ =1/(2-2*2)=1/8. 

Заметим, что в данной последовательности значения степеней с отрицательными показателями являются обратными числами к значениям степеней с натуральными показателями:

• Значение степени в 2² есть число 4, а значение степени 2⁻² есть число 1/4. Числа 4 и 1/4 являются обратными друг другу.
• Значение степени в 2³ есть число 8, а значение степени 2⁻³ есть число 1/8. Числа 8 и 1/8 являются обратными друг другу.

Можно сделать вывод, что для вычисления степени с отрицательным показателем, нужно записать дробь,  в числителе которой единица, а в знаменателе та же самая степень, но с противоположным показателем.

Данное правило можно доказать, используя правило деления степеней с одинаковыми основаниями. Допустим, нам нужно высислить степень в целым отрицательным показателем 2⁻². Использую правило деления степеней с одинаковыми основаниями записшем 2⁻² как  2^(3-5) = 2³ : 2⁵. Запишем это деление в виде дроби. Получим:

Пример 1. Найти значение выражения 3⁻³

Пример 2. Найти значение выражения (-2/3)⁻³

Желательно уметь возводить обыкновенную дробь в отрицательную степень как с помощью формулы, так и без неё.

Тождественные преобразования степеней с целым отрицательным показателем

Все тождественные преобразования, которые мы рассматривали при изучении степени с натуральным показателем, сохраняются и для степеней с целыми отрицательными показателями.

Пример 3. Найти значение выражения 2⁻¹ × 2⁻³.
Воспользуеся основным свойством степени:
2⁻¹ × 2⁻³ = 2^{−1 + (−3)} = 2⁻⁴=1/16 

Пример 4. Найти значение выражения 5⁻¹⁵ × 5¹⁶.
Воспользуемся основным свойством степени:
5⁻¹⁵ × 5¹⁶ = 5^{−15 + 16} = 5¹ = 5

Пример 5. Найти значение выражения (10⁻⁴)⁻¹
Воспользуемся правилом возведения степени в степень:
(10⁻⁴)⁻¹ = 10^{−4 × (−1)} = 10⁴ = 10000

Пример 6. Найти значение выражения (10⁻⁶)/(5⁻⁶)
Представим число основание 10 в виде произведения 2×5. Тогда числитель примет вид (2×5)⁻⁶

Возвести отрицательное число в степень

Отрицательное число в степени, теория и возведем отрицательное число в степень на калькуляторе. И степень отрицательного числа в четной и не четной степени будут противоположными по занку!

Возвести отрицательное число в степень

1. Отрицательное число в степени
   1. Возведение отрицательного числа в степень теория с примером.
   2. Возведение отрицательного числа в степень на калькуляторе
   3. Отрицательное число в нулевой степени чему равно
   4. Возведение отрицательных чисел в степень правила
   5. Как написать отрицательное число в степени
   6. Как написать отрицательное число в степени
   7. Возведение отрицательного числа в отрицательную степень
2. Число в отрицательной в степени
   1. Возведение числа в отрицательную степень теория с примером.
   2. Как посчитать отрицательную степень числа на калькуляторе

1. Отрицательное число в степени

   Очень похожее для робота два выражения:

   Отрицательное число в степени и …

   Число в отрицательной степени.

   Робот думает, что это одно и тоже… поэтому, две страницы объединяем в одну!

   Возведение отрицательного числа в степень теория с примером..

   Сперва разберем на простом примере, как возвести отрицательное число в степень возьмем опять 3 только с минусом, и далее мы видим, что если степень нечетная, то минус остается…,

   -3³ = -3*-3*-3 = -27

   Почему минус остался!?

   Если мы возьмем первые две тройки, то при умножении два минуса дадут плюс. А вот у третьей тройки минус остался! И когда мы умножим на тройку с минусом, то плюс на минус дает минус!

   но если мы сделаем степень четной, то все минусы уничтожатся(напоминаю, что если умножить два отрицательных числа, то минус на минус дает плюс.)

   -3⁴ = -3*-3*-3*-3 = 81

   Возведение отрицательного числа в степень на калькуляторе

   Теперь проделаем выше описанную теорию на калькуляторе

   Пример Возведения отрицательного числа в степень

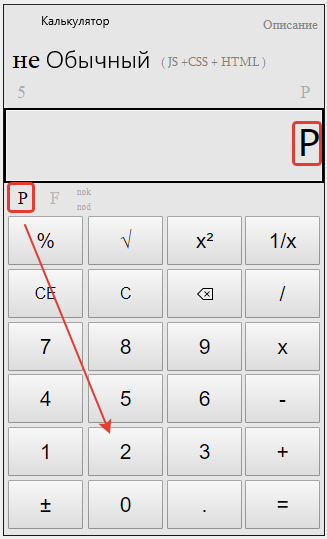
   Набираем число, которое требуется возвести в степень.

   После этого ставим минус, кнопкой плюс-минус

   
   После того, как мы получили отрицательное число, нам нужно нажать кнопку “

   P

   ” – знак степени. Знак степени после нажатия должен изменить цвет.

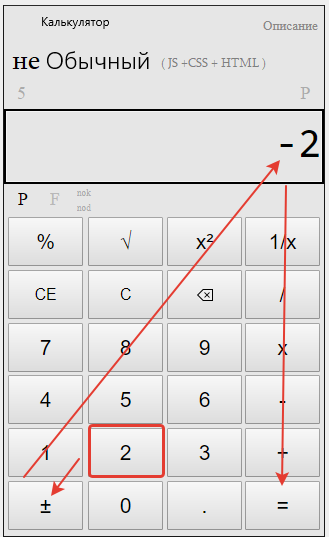
   Далее набираем степень, пусть это будут 3,

   и нажимаем равно:

   

   отрицательное число в нулевой степени чему равно

   Внимание!
   Любое число в нулевой степени – равно 1 !

   Возведение отрицательных чисел в степень правила

   Интересный поисковый запрос:

   “Возведение отрицательных чисел в степень правила“…
   смайлы

   О правилах возведения отрицательного числа в степень.

   Нет отдельного правила возведения отрицательного числа в степень.

   Для отрицательного числа в степени работают те же правила, что для обычного числа в степени.

   Единственное, что нужно добавить:

   что возведение отрицательного числа в четную степень дает положительный резельтат:

   -3⁴ = -3*-3*-3*-3 = 81

   а возведение отрицательного числа в нечетную степень дает число со знаком минус!

   -3⁴ = -3*-3*-3 = -27

   Как написать отрицательное число в степени

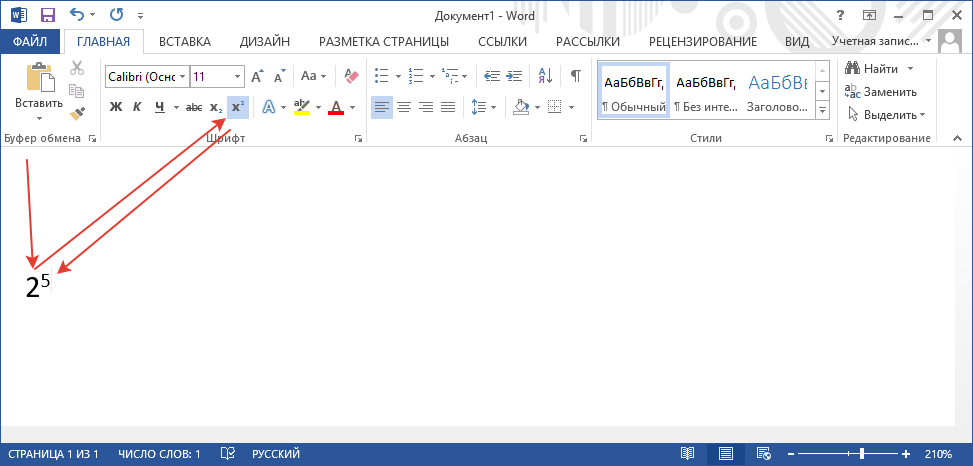
   Если вы хотите написать отрицательное число в степени в ворде, то поступаем так:

   Как написать отрицательное число в степени в ворде

   Набираем то число, которое хотим возвести в степень.

   Далее подымаем голову в меню ворда и ищем соответствующий значок, который обозначает степень – нажимаем.

   Возвращаемся к нашему числу и тут видим, что курсор стал находиться выше!

   Пишем число степени.

   

   Как написать отрицательное число в степени в html

   Для того, чтобы написать отрицательное число в степени в html нужно написать соответствующий тег, который отвечает за степень числа :

   2³

   Результат:

   2³

2. Число в отрицательной в степени

   Следующим пунктом разберемся с похожей по написанию, но отличной по содержанию формулировкой:

   Число в отрицательной в степени

   Возведение числа в отрицательную степень теория с примером.

   Далее разберемся как возводить число в отрицательную степень

   Чтобы разобраться нам потребуется схема преобразования отрицательной степени в обычную :

   

   Как мы видим из формулы, отрицательная степень числа, равна единице поделенной на число в положительной степени!

   И для полноты картины разберем пример.

   Пример как посчитать отрицательную степень числа!?

   В качестве примера возьмем два(чтобы легко можно было посчитать) в минус второй степени:

   2-2 = 12² = 14 = 0.25

   Два в минус второй степени будет равно единице деленное на два во второй степени, что равно 0.25

   Как посчитать отрицательную степень числа на калькуляторе!?

   Нам нужно какое-то число в качестве примера для иллюстрации того, как можно посчитать отрицательную степень на калькуляторе.

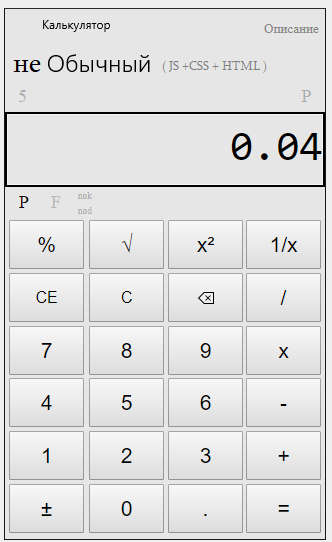
   Набираем число, которое будем возводить в отрицательную степень – пусть это будет 5.

   

   Нажимаем букву степени, после нажатия – она становится активной.

   

   Нажимаем число, степени и сделаем её отрицательной – нажимаем равно.

   

   Получаем результат возведения числа в отрицательную степень.

   

Не благодарите, но ссылкой можете поделиться!

COMMENTS+

 
BBcode

---

Отрицательная степень числа

• Степень с отрицательным показателем
• Действия над степенями с отрицательными показателями

Степень с отрицательным показателем

Число с отрицательным показателем степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем.

d -c =	1	;    7 -5 =	1	;    a -5 =	1	.
d c	7 5	a 5

Чтобы разобраться, почему число в отрицательной степени равно дроби, надо вспомнить правило деления степеней с одинаковыми основаниями:

При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя.

Следовательно, если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:

a ⁵ : a ⁸ = a^{5 – 8} = a ^-3.

Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:

Значит:

Действия над степенями с отрицательными показателями

При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются:

При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя:

Чтобы возвести произведение в отрицательную степень, надо возвести в эту степень каждый сомножитель отдельно:

Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:

При возведении одной степени (положительной или отрицательной) в степень (положительную или отрицательную) показатели степеней перемножаются: