Содержание
- Сумма и разность чисел
- Что такое сумма, и как ее найти
- Как найти разность чисел
- Сложение
- Как называются числа при сложении?
- Как найти неизвестное слагаемое
- Проверка сложения
- Перестановка слагаемых
- Сочетательный закон сложения
- Урок математики во 2-м классе по теме «Сложение двузначных чисел». Система Л.В. Занкова
Сумма и разность чисел
Что такое сумма, и как ее найти
Сумма – это результат складывания двух чисел (слагаемых), между которыми стоит знак +. Чтобы получить сумму, нужно к одному слагаемому прибавить второе слагаемое. В общем виде пример можно показать так: a + b = s, где а – первое слагаемое, b – второе слагаемое, а s – результат сложения этих двух слагаемых. При этом нужно знать, что от перестановки слагаемых сумма не меняется, — это одно из самых первых правил в математике, которое проходят в начальной школе.
Чтобы наглядно показать ребенку, как сложить числа, возьмите конфеты или любые другие вещи. Покажите ребенку две конфеты, а затем прибавьте к этим конфетам еще две. Пусть ребенок посчитает и скажет, что теперь конфет оказалось четыре. Объясните ему, что он только что сложил эти числа, то есть прибавил к одному числу другое число и в конечном итоге получил сумму.
Немного сложнее объяснить сложение разрядных слагаемых, эта тема может быть непонятна ребенку. Итак, существует множество разрядов: единицы, десятки, тысячи. Возьмите, к примеру, число 2564. Если разложить его на разряды, то получится: 2564 = 2000 + 500 + 60 + 4. Чтобы прибавить к этому числу, например, число 305, воспользуйтесь сложением в столбик. При таком сложении нужно прибавлять одни разряды к другим, начиная с конца: единицы к единицам, десятки к десяткам, тысячи к тысячам. То есть, для начала складываем 4 и 5, затем 6 и 0, после 5 и 3, и в конце 2 и 0. В конечном итоге получаем число 2869.
Как найти разность чисел
 Разность – результат вычитания одного числа из другого. В отличие от суммы, здесь мы не можем воспользоваться правилом «от перестановки слагаемых разность не меняется», так как в вычитании всегда есть уменьшаемое и вычитаемое. Чтобы найти вычитаемое и разность, для начала нужно разобраться с этими понятиями. Уменьшаемое – это то, из чего мы «вычитаем», то есть убираем, а вычитаемое – количество того, что мы у этого уменьшаемого вернем.
Разность – результат вычитания одного числа из другого. В отличие от суммы, здесь мы не можем воспользоваться правилом «от перестановки слагаемых разность не меняется», так как в вычитании всегда есть уменьшаемое и вычитаемое. Чтобы найти вычитаемое и разность, для начала нужно разобраться с этими понятиями. Уменьшаемое – это то, из чего мы «вычитаем», то есть убираем, а вычитаемое – количество того, что мы у этого уменьшаемого вернем.
В общем виде вычитание можно записать так: a — b = r.
Обратимся к тем же конфетам, с которыми мы разбирали сумму чисел. Чтобы помочь ребенку найти разность чисел, возьмите пять конфет. Пусть ребенок посчитает и убедится, что их пять. Затем заберите себе три конфеты. Ребенок скажет, что их осталось две. А сколько тогда забрали? Три.
А что касается разрядных слагаемых, то здесь мы делаем то же самое, что и с суммой, только теперь не прибавляем, а вычитаем. Возьмем число 6845 и вычтем из него 4231. Для этого мы вычитаем один разряд из другого разряда, производя вычитание с конца: 5-1 = 4, 4-3 = 1, 8-2 = 6, 6-4 = 2. В ответе получим 2614.
Источник
Сложение
Познакомимся со сложением.
Рассмотрим числовой ряд.

Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Посмотри на числовой ряд, по которому идёт заяц.

Какое действие выполняет заяц?
Прибавляет число 2.
К какому числу он прибавляет число 2?
К числу 4.
Наш зайчик стоит на числе 4 и думает, в какую сторону ему идти.
В какую сторону пойдёт зайчик?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает заяц?
2, потому что ему нужно прибавить 2.
На каком делении остановится заяц?
На числе 6.
Когда прибавляем, становится больше.
Чем правее, тем числа больше.
4 + 2 = 6
Рассмотрим еще один пример.

Какое действие выполняет заяц?
Прибавляет число 5.
К какому числу он прибавляет число 5?
К числу 3. Мы поставили зайчика на число 3.
В какую сторону он пойдёт?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает зайчик? 5.
На каком делении он остановится? На числе 8.
3 + 5 = 8
Как называются числа при сложении?
Первое слагаемое и второе слагаемое.
Результат называется суммой.

Представь части домика как слагаемые и сумму.

Как найти неизвестное слагаемое

Второе слагаемое неизвестно.
Рассмотри рисунок и догадайся, как его можно найти.
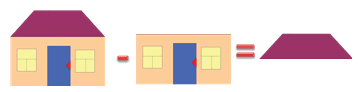
Нужно из суммы вычесть первое слагаемое.

Неизвестно первое слагаемое.
Как его можно найти?

Нужно из суммы вычесть второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Проверка сложения
Если из суммы двух слагаемых, вычесть одно из слагаемых, то получится второе слагаемое.
Именно эта связь между суммой и слагаемыми используют для проверки вычислений.
Например, 35 + 7 = 42.
Правильно ли произведено вычисление? Можно проверить так:
42 — 7 = 35, мы из суммы вычли одно из слагаемых и получили ВТОРОЕ слагаемое. Значит, вычисление произведено верно и пример решен правильно.
Перестановка слагаемых
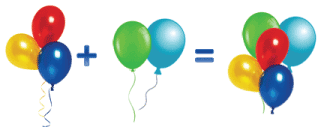
Сделаем запись к рисунку.
3 + 2 = 5
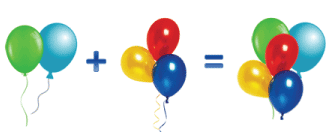
Сделаем запись к этому рисунку.
2 + 3 = 5
Теперь рассмотрим обе записи к рисункам:
3 + 2 = 5
3 — первое слагаемое
2 — второе слагаемое
2 + 3 = 5
2 — первое слагаемое
3 — второе слагаемое
Мы заметили, что сумма в обеих записях одинаковая, хотя слагаемые мы записывали по-разному.
Это переместительный закон сложения, который гласит:
От перестановки мест слагаемых сумма не меняется.
Сочетательный закон сложения
Рассмотрим пример: (37 + 29) + 1 = . (читаем: к сумме чисел 37 и 29 прибавить
1) Какие числа удобно сложить сначала, чтобы получился удобный способ? Числа 29 и 1.
Сумму чисел 29 и 1 возьмем в скобки.
37 + (29 + 1) = … (читаем: к 37 прибавить сумму чисел 29 и 1)
Решаем. Сначала выполним действие в скобках.
37 + 30 = 67, значит,
Вывод: два соседних слагаемых можно заменить их суммой.
Поделись с друзьями в социальных сетях:
Источник
Урок математики во 2-м классе по теме «Сложение двузначных чисел». Система Л.В. Занкова
Цель: Научиться находить значение выражений нового вида.
Тип урока: Урок сотрудничества и исследований.
Идея урока: Тему разбить на несколько небольших, но разных заданий, решение которых поручить отдельным группам учащихся.
Познавательные: поиск закономерностей и особенностей сложения двузначных чисел; систематическое поддержание интереса к предмету через творческое применение знаний; позитивная мотивация к дальнейшему овладению вычислительными навыками.
развитие универсальных учебных действий;
умение выделить проблему урока, провести рефлексию.
развитие коммуникативных навыков (умение вести диалог, договариваться в группе, отстаивать свое мнение и уважать чужое);
создание здоровьесберегающей среды через снятие напряжения и отрицательных эмоций.
Структура урока: урок состоит из восьми этапов, логически связанных между собой:
1.Психологический настрой на деятельность (упражнения на внимание)
2.Целеполагание (создание ситуации “знаю” — “не знаю”, определение проблемы урока).
3.Актуализация знаний через решение практических заданий, направленных на закрепление знания таблицы сложения.
4.Открытие нового знания в форме исследовательской работы, направленной на поиск закономерностей и особенностей сложения двузначных чисел;
6.Закрепление изученного материала.
7.Самостоятельная работа и взаимопроверка.
8.Рефлексия (физическая, интеллектуальная, сенсорная)
материал связан с несколькими разными исследовательскими заданиями, направленными на осознание общего принципа операции сложения двузначных чисел;
открытие нового знания идет через возникновение коллизий, побуждающих к поиску решения проблемы;
дети объединены в группы, пары.
1.Психологический настрой на деятельность.
2.Целеполагание: постановка темы и цели урока, мотивация.
1).Ритмический счет по 2, по 3, по 4.
2).На доске записаны числа: 70 18 22 9 46 83
У.Есть ли числа, которые отличаются от всех остальных?
Д. * число 9 – оно однозначное;
* число 70 – это круглые десятки;
*число 22 – десятки и единицы записаны одинаковыми цифрами;
У.Расположите эти числа в порядке возрастания.
Д. 9, 18, 22, 46, 70, 83.
У. Расположите эти числа в порядке убывания.
Д. 83, 70, 46, 22, 18, 9.
У. Молодцы! А теперь назовите слова из науки математики на букву “С”.
Д. *сложение *сумма *слагаемое *сантиметр *схема
У. Замечательно! Назовите слова из науки математики на букву “Р”.
Д. *равенство *разность *решение *разряд *равнобедренный …..
У. Как много вы уже знаете! Значит, вы взрослеете!
4.Открытие нового знания:
У. Прочитайте записи на доске. Что вы можете о них сказать?
| 80+5 | 40+20 | 70-30 |
| 16+1 | 73 — 3 | 29- 1 |
| 60+1 | 24+35 | 58-8 |
Д. Все эти записи – выражения. Это суммы и разности.
У. На какие группы можно распределить все эти выражения по способу нахождения их значения?
Д. Значения выражений 40+20 и 70-30 можно найти, используя таблицу сложения.
Д. Значения выражений 16+1, 60+1, 29-1 можно найти, используя натуральный ряд чисел.
Д. Значения выражений 73-3 и 58-8 можно найти, заменяя первое число суммой разрядных слагаемых.
Д.Здесь есть сумма 24+35, значение которой нельзя найти.
Д. Она не подходит ни к одному способу, который мы знаем.
У. Значит, нельзя к 24+35?
Д. Можно, но надо придумать какой-то другой способ.
У. Вот и придумайте, как можно найти значение этой суммы.
Д.-Я придумал, нужно каждое число заменить суммой разрядных слагаемых:
-А я увидел, что нам понадобятся строчки из таблицы сложения:
— А я уже догадался, что надо десятки прибавить к десяткам, а единицы к единицам и получится 59!
У.Хорошо. Давайте попробуем по способу, который вы придумали, найти сумму 46 и 21. Какой первый шаг? Какой второй шаг? Зачем мы это делаем? Где взяли число 7?
У. — Верно ли мое утверждение: “Для того чтобы найти сумму двузначных чисел, нужно десятки прибавить к десяткам, а единицы к единицам”?
Д. -Верно, потому что мы применили этот способ и смогли решить пример.
У. — А такой способ сложения можно применить ко всем двузначным числам?
Д. -Нет, если при сложении единиц получится больше 10, то мы не сможем посчитать.
Д. -Мы не сможем посчитать, если при сложении десятков тоже получится больше 10. (Возникает новая проблема и спор)
5.Физминутка: (под музыку, меняя темп)
Что такое, что мы слышим,
Это дождь стучит по крыше,
А потом пошел быстрей,
И по крыше бьет сильней.
6.Закрепление изученного материала: (дети работают в группах)
У.Чтобы узнать значение суммы 34+45 Вера и Боря сделали рисунки. Выбери, чей рисунок лучше поможет узнать значение суммы?
Подумай, какая математическая запись соответствует выбранному тобой рисунку. Сделай сам такую запись.
Сравни свою запись с записью Толи:
У тебя получилась такая же запись?
Какими суммами заменили слагаемые?
Как такие суммы называются?
Что обозначает запись (30+40) + (4+5)?
7.Самостоятельная работа и взаимопроверка:
У. Выполняем №117 с.48
— Сколько выражений приготовил автор?
54+32 63+24 73+16 27+42 56+30 46+31
— Чем похожи выражения? (Это суммы)
— Что необычного в суммах, которые мы находим? (Все слагаемые – двузначные числа)
-Какие знания нам пригодятся? (Таблица сложения, натуральный ряд чисел и замена слагаемых суммой разрядных слагаемых)
-Какие новые знания надо применить? (Десятки надо прибавить к десяткам, а единицы – к единицам)
(Дети самостоятельно находят значения сумм и выполняют взаимопроверку в парах.)
У. Я заметила, что в третьей сумме 73+16 у Оли и Тани разные ответы: 89 и 98. Почему? Кто прав?
(Новая проблема и спор).
Д. Кто-то из них посчитал неправильно.
Д. Давайте проверим последовательность вычислений.
Д. Таня в ответе поменяла местами десятки и единицы. Надо записать 89.
Д.Нельзя менять десятки и единицы местами, у каждого разряда свое место!
Какие новые знания мы получили сегодня? Какие старые знания нам пригодились? Что самое главное надо запомнить?
Д. -Десятки прибавить к десяткам, а единицы — к единицам.
Д. -Единицы надо писать на первом месте, а десятки — на втором.
У. Когда вам было трудно? Что мешало?
У.Назовите сумму, значение которой найти было легче остальных.
Д.Это сумма 56+30, потому что надо было сложить только десятки.
У. Дома придумайте еще несколько похожих сумм и найдите их значения.
Спасибо за урок. Мне очень приятно и интересно было работать с вами.
Для проверки знаний учащимся предложены такие задания:
1.Выполни подробную запись и найди значения сумм:
70+24 62+30 37+10 20+46 53+40
В каждой сумме измени одну цифру так, чтобы складывать числа стало труднее.
2.Найди значения сумм, сделав подробную запись:
35+43 24+41 63+24 54+35 76+20
Анализ работ показал, что все учащиеся поняли общий принцип операции сложения двузначных чисел через поразрядность выполнения операции и использование таблицы сложения в любом разряде, правильно находят результат, усвоили алгоритм выполнения подробной записи, заменяют двузначные числа суммой разрядных слагаемых. Формирование осознанного прочного навыка идет успешно.
Особый интерес вызывают задания, когда более легкие суммы надо заменить трудными, или придумать свои суммы, аналогичные данным.
Источник
Тема: Как найти неизвестное слагаемое.
Цель: создать необходимые условия для вывода обучающимися правила нахождения неизвестного слагаемого.
Задачи:
Образовательная: познакомить с правилом, позволяющим находить корень уравнения, если неизвестным является одно из двух слагаемых.
Развивающая: совершенствовать вычислительные навыки; развивать логическое мышление и внимание;
Воспитательная: воспитывать любовь к предмету, дисциплинированность во время урока;
Регулятивные: получают возможность контролировать свою деятельность, адекватно оценивать свои достижения. Познавательные: слушать и читать, извлекая нужную информацию, а также самостоятельно находить правильное решение примеров.
Личностные УУД: формировать положительное отношение к учению, к познавательной деятельности, желание приобретать новые знания, умения, совершенствовать имеющиеся, осваивать новые виды деятельности.
Содержание урока
|
Этапы урока |
Деятельность учителя |
Деятельность обучающихся |
УУД |
|
-Здравствуйте, ребята! Быстро, но тихо садитесь. |
Приветствуют учителя. |
Коммуникативные: Планирование учебного сотрудничества с педагогом и со сверстниками. |
|
-Постарайтесь все понять, Учитесь тайны открывать, Ответы полные давать, Чтоб за работу получать Только лишь отметку «пять»! |
Настраиваются на плодотворную и эффективную работу на уроке. |
Личностные: Выражать положительное отношение к процессу познания, проявлять желание проявлять новое. |
|
-Урок наш начнем с устного счета. -Найдите значение первого выражения. 43-17=26 -Найдите значение второго выражения. 57-46=11 -Найдите значение третьего выражения. 30-16=14 -Найдите значение четвертого выражения. 37+42=79 -Найдите значение пятого выражения. 25+18=43 -Найдите значение шестого выражения. 78-65=13 -Найдите значение седьмого выражения. 82-46=36 -Найдите значение восьмого выражения. 23+15=38 |
43-17=26 57-46=11 30-16=14 37+42=79 25+18=43 78-65=13 82-46=36 23+15=38 |
Познавательные: Самостоятельно выделять и формулировать познавательные задачи; с помощью деятельностного метода исследования. |
|
Решите следующую задачу. -Я прочитаю сейчас задачу, а вы внимательно слушайте. «Одна тыква легче другой на 2 кг и весит 8 кг. Сколько весят обе тыквы?» -Что известно в задаче? -Что нужно найти в задаче? -Решите задачу. -Объясните решение этой задачи. |
Известно, что одна тыква легче другой на 2 кг и весит 8 кг. В задаче нужно найти сколько весят обе тыквы. 1)8+2=10 (кг)-весит вторая тыква. 2)10+8=18 (кг)-весят обе тыквы. Ответ: 18 килограмм. |
Коммуникативные: Развивать умение использовать речь для решения примеров и задач, задавать вопросы. |
|
-Следующая задача логическая, слушайте внимательно. «Велосипедист проехал на двухколёсном велосипеде 14 км. Сколько километров проехало каждое колесо?» -Решите задачу. -Почему? |
Каждое колесо проехало 14 километров. Потому что колеса на одном транспорте, они едут одновременно с одинаковой скоростью. |
Регулятивные: Прогнозировать результат решения практической учебной задачи. |
|
–Разгадайте ребус. – Какое слово зашифровано? Как вы рассуждали? – Что такое уравнение? -Что такое корень? -Способом подбора найдите корень уравнения х+10=30 – Как называются числа при сложении? Какой компонент неизвестен в этом уравнении? |
Зашифровано слово уравнение. Равенство, содержащее неизвестное, называется уравнением. Корень уравнения – это число, чему равен х. Корнем уравнения является число 20. Первое слагаемое, второе слагаемое, значение суммы. Неизвестно первое слагаемое. |
|
|
-На устном счете активно работали … – Остальным желаю быть активнее! |
||
|
– Как вы думаете, открытию, какой закономерности будет посвящён урок? – Откройте учебник на странице 77 и прочитайте тему урока. -Определите цель урока. |
Нахождение неизвестного слагаемого. Научиться находить неизвестное слагаемое. Вывести правило для нахождения неизвестного слагаемого. |
Познавательные: Самостоятельно формулировать тему урока. |
|
-Откройте свои рабочие тетради и запишите число и классную работу. Сегодня 3 апреля. |
Записывают число и классную работу. |
|
|
-Найдите задание №1. Громко и четко прочитает задачу… -Что известно в задаче? -Что требуется узнать? -Составим краткую запись к этой задаче. -Сколько тетрадей было в I пачке? -Ставим 17 т. -Сколько тетрадей было во II пачке? -Обозначим число тетрадей во II пачке, т.к. неизвестно через х. -Что еще нам известно в задаче? -Объединяем 2 пачки фигурной скобкой и ставим 42 т. -Составим круговую схему по этой задаче. -Какое число поставим в синее окно? -Почему? -Какое число поставим в желтое окно? –Что нужно узнать? -В розовом окне какие будут тетради? -Мы знаем сколько тетрадей во II пачке? -Вместо вопроса мы поставим знак х. |
«В открытой пачке лежало 17 тетрадей, а число тетрадей во второй пачке неизвестно. Учительница сказала, что всего в двух пачках 42 тетради. Сколько тетрадей в двух пачках?» Известно, что в открытой пачке лежало 17 тетрадей, а всего в 2х пачках 42 тетради. Требуется узнать количество тетрадей во второй пачке. I пачка – 17 т. 42 т. II пачка – х т. Неизвестно. Известно, что всего было 42 тетради. 42 Потому что это сумма. 17 Сколько было тетрадей во II пачке. Которые находятся во II пачке. Нет. |
|
|
– Первое слагаемое 17, второе слагаемое – неизвестное число х, а значение суммы 42. Составьте и запишите соответствующее уравнение. -Какое запишем уравнение? |
17+х=42 х=42-17 х=25 |
|
|
-Знак какого действия стоит в уравнении между известным числом и неизвестным? |
Знак действия сложения. |
|
|
-Нам нужно найти неизвестное число. -Смотрим на круговую схему. -Как называются компоненты при сложении? -Определим каким знаком соединяет стрелка квадратики с известными числами. -Какой компонент нам неизвестен? -Записывают это так: второе слагаемое = из суммы 42 вычитаем первое слагаемое 17. Вычитаем. -42-17 сколько получаем? -25-это корень уравнения. -Ребята, как же найти неизвестное слагаемое? -Посмотрите на правило которое выделено розовым цветом на следующей странице. -Громко и четко правило прочитает… -Читаем все вместе хором. -Кто сможем повторить данное правило? |
Первое слагаемое, второе слагаемое, значение суммы. 17+… 42-… Второе слагаемое х 17+х=42 х=42-17 х=25 25 Из суммы вычесть известное слагаемое. |
|
|
Физминутка |
-Сейчас с вами немного отдохнем. Все встали. В уравненьях всё в порядке, Ну а нам нужна зарядка. Мы немножко отдохнём, Физкультминутку проведём. Мы семь раз в ладоши хлопнем, Восемь раз ногами топнем. Прибавляем три к семи Столько мы присесть должны. |
Повторяют движения за учителем. |
|
|
-Найдите задание №5, посмотрите на данную схему. -По данной схеме нам нужно составить и решить уравнение. -Назовите слагаемые и значение суммы. -Для нахождения неизвестного слагаемого составьте уравнение. -Как найди неизвестное слагаемое? -Найдите неизвестное слагаемое х + 25 = 60 используя новое правило. -К доске пойдет решить данное уравнение с объяснением пойдет… -Все остальные слушают внимательно и записывают решение уравнения в тетрадь. -Чтобы убедиться, что мы не ошиблись, нужно выполнить проверку. Для этого нужно вместо неизвестного числа подставить корень уравнения 35 и выполнить сложение. Если наша полученная сумма равняется сумме уравнения, то уравнение мы решили верно. Снизу записываем 60=60, знак равенства должно быть под знаком равенства. |
Слагаемые х и 25, значение суммы 60. х + 25 = 60 Из суммы вычесть известное слагаемое. х+25=60 х=60-25 х=35 35+25=60 60=60 |
|
|
-Найдите задание №6, громко и четко прочитает задание… -Какой компонент в первом уравнении нам неизвестен? -Как найти второе слагаемое? -К доске пойдет решать первое уравнение с объяснением пойдет… -На какие знания будем опираться? – Какое число можно назвать корнем уравнения? -Все остальные отступили 3 клеточки вправо и запишите уравнение. -Какой компонент неизвестен во втором уравнении? -Как найти первое слагаемое? – К доске пойдет решать следующее уравнение с объяснением пойдет… -Все остальные отступили 2 клеточки ниже и запишите уравнение. -Какой компонент неизвестен в последнем уравнении? -Как найти второе слагаемое? – К доске пойдет решать последнее уравнение с объяснением пойдет… -Все остальные отступили 3 клеточки вправо и запишите уравнение. |
Второе слагаемое. Из суммы вычесть первое слагаемое. Правило нахождения неизвестного слагаемого. Число является корнем уравнения, если при подстановке его вместо х в уравнение получаем верное равенство. 150+х=255 х=255-150 х=105 Первое слагаемое. Из суммы вычесть второе слагаемое. х+36=86 х=86-36 х=50 Второе слагаемое. Из суммы вычесть первое слагаемое. 10+х=20 х=20-10 х=10 |
|
|
-Найдите задание №7, громко и четко задание прочитает… -Выполнить данное задание к доске с объяснением пойдет… -Кто может рассказать нам правило нахождения неизвестного слагаемого? |
х+57=90 х=90-57 х=33 |
|
|
-Найдите задание №8, громко и четко задание прочитает… -Что известно в задании? -Какое действие выполняется? -Назовите компоненты действия сложения -Составить и решить уравнение пойдет к доске… -Что неизвестно в уравнении? -Как найти второе слагаемое? |
Что к 264 прибавили неизвестное число и получили 576. Действие сложения. Второе слагаемое. От суммы вычесть первое слагаемое. |
|
А) инструктаж по выполнению самостоятельной работы. |
-А сейчас проведём небольшую самостоятельную работу. Послушайте внимательно. -Работа по вариантам. Поднимите руки 1 варианта, опустите. Посмотрите внимательно на слайд. Вы решаете уравнение х + 18 = 93 вместе с проверкой. -Поднимите руки 2 варианта, опустите. -Посмотрите внимательно на слайд. Вы решаете уравнение 34 + х =60 вместе с проверкой. – Уравнение I варианта пойдет решать … – Уравнение II варианта пойдет решать … -Отступите 2 клеточки вниз и приступайте к работе. |
Слушают учителя. I вариант: х+18=93 х=93- 18 х=75 75+18=93 93=93 II вариант: 34+х=60 х=60-34 х=26 34+26=60 60=60 |
|
|
Б) проверка самостоятельной работы. |
-Проверим самостоятельную работу. – Ваше мнение, как выполнена самостоятельная работа? -У кого не так исправьте. -Молодцы, присаживайтесь. |
Проверяют как выполнили самостоятельную работу учащиеся у доски. |
Регулятивные: Совместно с учителем и одноклассниками давать оценку выполнения работы. |
|
– Подведём итог урока. – С каким правилом познакомились на уроке? – Где мы можем применить это правило? |
Научиться находить неизвестное слагаемое. Вывести правило для нахождения неизвестного слагаемого. Для решения уравнений. |
Регулятивные: Выделение и осознание обучающимися того, что уже усвоено. |
|
– Ребята, спасибо Вам за урок, за старание и стремление к знаниям, которые помогли нам сегодня вновь совершить новое открытие в математике. – Хочу поставить сегодня за урок оценку 5… |
Слушают учителя. |
Регулятивные: Совместно с учителем и одноклассниками давать оценку своей деятельности на уроке |
|
-Если вы считаете, что вы работали сегодня на уроке хорошо, все было ясно и понятно и чисто написано в тетради, то нарисуйте на полях простым карандашом веселый смайлик. -Если вы считаете, что вы не активно работали на уроке и у вас неопрятно в тетради, то нарисуйте на полях простым карандашом грустный смайлик. |
Самостоятельно оценивают себя на уроке. |
Личностные: рефлексия способов и условий действия, контроль и оценка процесса результатов деятельности. Регулятивные: Совместно с учителем и одноклассниками давать оценку своей деятельности на уроке |
|
-Запишите домашнее задание: тетрадь на печатной основе стр. 36 задания №1- №3. -Урок окончен, до свидания! |
Записывают домашнее задание. |
 В начальной школе ребенок впервые знакомится с математикой, и его первыми примерами являются такие простые действия, как складывание или вычитание. Но иногда ребенку сложно объяснить даже такие, казалось бы, несложные и привычные взрослым примеры. Как же научиться находить сумму и разность чисел?
В начальной школе ребенок впервые знакомится с математикой, и его первыми примерами являются такие простые действия, как складывание или вычитание. Но иногда ребенку сложно объяснить даже такие, казалось бы, несложные и привычные взрослым примеры. Как же научиться находить сумму и разность чисел?
Что такое сумма, и как ее найти
Сумма – это результат складывания двух чисел (слагаемых), между которыми стоит знак +. Чтобы получить сумму, нужно к одному слагаемому прибавить второе слагаемое. В общем виде пример можно показать так: a + b = s, где а – первое слагаемое, b – второе слагаемое, а s – результат сложения этих двух слагаемых. При этом нужно знать, что от перестановки слагаемых сумма не меняется, – это одно из самых первых правил в математике, которое проходят в начальной школе.
Чтобы наглядно показать ребенку, как сложить числа, возьмите конфеты или любые другие вещи. Покажите ребенку две конфеты, а затем прибавьте к этим конфетам еще две. Пусть ребенок посчитает и скажет, что теперь конфет оказалось четыре. Объясните ему, что он только что сложил эти числа, то есть прибавил к одному числу другое число и в конечном итоге получил сумму.
Немного сложнее объяснить сложение разрядных слагаемых, эта тема может быть непонятна ребенку. Итак, существует множество разрядов: единицы, десятки, тысячи. Возьмите, к примеру, число 2564. Если разложить его на разряды, то получится: 2564 = 2000 + 500 + 60 + 4. Чтобы прибавить к этому числу, например, число 305, воспользуйтесь сложением в столбик. При таком сложении нужно прибавлять одни разряды к другим, начиная с конца: единицы к единицам, десятки к десяткам, тысячи к тысячам. То есть, для начала складываем 4 и 5, затем 6 и 0, после 5 и 3, и в конце 2 и 0. В конечном итоге получаем число 2869.
Как найти разность чисел
 Разность – результат вычитания одного числа из другого. В отличие от суммы, здесь мы не можем воспользоваться правилом “от перестановки слагаемых разность не меняется”, так как в вычитании всегда есть уменьшаемое и вычитаемое. Чтобы найти вычитаемое и разность, для начала нужно разобраться с этими понятиями. Уменьшаемое – это то, из чего мы “вычитаем”, то есть убираем, а вычитаемое – количество того, что мы у этого уменьшаемого вернем.
Разность – результат вычитания одного числа из другого. В отличие от суммы, здесь мы не можем воспользоваться правилом “от перестановки слагаемых разность не меняется”, так как в вычитании всегда есть уменьшаемое и вычитаемое. Чтобы найти вычитаемое и разность, для начала нужно разобраться с этими понятиями. Уменьшаемое – это то, из чего мы “вычитаем”, то есть убираем, а вычитаемое – количество того, что мы у этого уменьшаемого вернем.
В общем виде вычитание можно записать так: a – b = r.
Обратимся к тем же конфетам, с которыми мы разбирали сумму чисел. Чтобы помочь ребенку найти разность чисел, возьмите пять конфет. Пусть ребенок посчитает и убедится, что их пять. Затем заберите себе три конфеты. Ребенок скажет, что их осталось две. А сколько тогда забрали? Три.
А что касается разрядных слагаемых, то здесь мы делаем то же самое, что и с суммой, только теперь не прибавляем, а вычитаем. Возьмем число 6845 и вычтем из него 4231. Для этого мы вычитаем один разряд из другого разряда, производя вычитание с конца: 5-1 = 4, 4-3 = 1, 8-2 = 6, 6-4 = 2. В ответе получим 2614.
Цель: Научиться находить значение
выражений нового вида.
Тип урока: Урок сотрудничества и
исследований.
Идея урока: Тему разбить на
несколько небольших, но разных заданий, решение
которых поручить отдельным группам учащихся.
Задачи:
Познавательные: поиск
закономерностей и особенностей сложения
двузначных чисел; систематическое поддержание
интереса к предмету через творческое применение
знаний; позитивная мотивация к дальнейшему
овладению вычислительными навыками.
Развивающие:
-
развитие универсальных учебных
действий; -
умение выделить проблему урока,
провести рефлексию.
Воспитательные:
-
развитие коммуникативных навыков
(умение вести диалог, договариваться в группе,
отстаивать свое мнение и уважать чужое); -
создание здоровьесберегающей среды
через снятие напряжения и отрицательных эмоций.
Структура урока: урок состоит из
восьми этапов, логически связанных между собой:
1.Психологический настрой на
деятельность (упражнения на внимание)
2.Целеполагание (создание ситуации
“знаю” – “не знаю”, определение проблемы урока).
3.Актуализация знаний через решение
практических заданий, направленных на
закрепление знания таблицы сложения.
4.Открытие нового знания в форме
исследовательской работы, направленной на поиск
закономерностей и особенностей сложения
двузначных чисел;
5.Физминутка.
6.Закрепление изученного материала.
7.Самостоятельная работа и
взаимопроверка.
8.Рефлексия (физическая,
интеллектуальная, сенсорная)
Особенности урока:
-
материал связан с несколькими
разными исследовательскими заданиями,
направленными на осознание общего принципа
операции сложения двузначных чисел; -
открытие нового знания идет через
возникновение коллизий, побуждающих к поиску
решения проблемы; -
дети объединены в группы, пары.
Ход урока
1.Психологический настрой на деятельность.
2.Целеполагание: постановка темы и цели урока,
мотивация.
3.Актуализация знаний:
1).Ритмический счет по 2, по 3, по 4.
2).На доске записаны числа: 70 18 22 9 46 83
У.Прочитайте числа;
У.Есть ли числа, которые отличаются от всех
остальных?
Д. * число 9 – оно однозначное;
* число 70 – это круглые десятки;
*число 22 – десятки и единицы записаны
одинаковыми цифрами;
У.Расположите эти числа в порядке возрастания.
Д. 9, 18, 22, 46, 70, 83.
У. Расположите эти числа в порядке убывания.
Д. 83, 70, 46, 22, 18, 9.
У. Молодцы! А теперь назовите слова из науки
математики на букву “С”.
Д. *сложение *сумма *слагаемое *сантиметр *схема
У. Замечательно! Назовите слова из науки
математики на букву “Р”.
Д. *равенство *разность *решение *разряд
*равнобедренный …..
У. Как много вы уже знаете! Значит, вы
взрослеете!
4.Открытие нового знания:
У. Прочитайте записи на доске. Что вы можете о
них сказать?
| 80+5 | 40+20 | 70-30 |
| 16+1 | 73 – 3 | 29- 1 |
| 60+1 | 24+35 | 58-8 |
Д. Все эти записи – выражения. Это суммы и
разности.
У. На какие группы можно распределить
все эти выражения по способу нахождения их
значения?
Д. Значения выражений 40+20 и 70-30 можно
найти, используя таблицу сложения.
Д. Значения выражений 16+1, 60+1, 29-1 можно
найти, используя натуральный ряд чисел.
Д. Значения выражений 73-3 и 58-8 можно
найти, заменяя первое число суммой разрядных
слагаемых.
Д.Здесь есть сумма 24+35, значение
которой нельзя найти.
У. Почему?
Д. Она не подходит ни к одному способу,
который мы знаем.
У. Значит, нельзя к 24+35?
Д. Можно, но надо придумать какой-то
другой способ.
У. Вот и придумайте, как можно найти
значение этой суммы.
Д.-Я придумал, нужно каждое число
заменить суммой разрядных слагаемых:
20+4 и 30+5
-А я увидел, что нам понадобятся
строчки из таблицы сложения:
2+3 и 4+5
– А я уже догадался, что надо десятки
прибавить к десяткам, а единицы к единицам и
получится 59!
У.Хорошо. Давайте попробуем по способу,
который вы придумали, найти сумму 46 и 21. Какой
первый шаг? Какой второй шаг? Зачем мы это делаем?
Где взяли число 7?
46+21=(40+6)+(20+1)=(40+20)+(6+1)=60+7=67
У. – Верно ли мое утверждение: “Для того
чтобы найти сумму двузначных чисел, нужно
десятки прибавить к десяткам, а единицы к
единицам”?
Д. -Верно, потому что мы применили этот
способ и смогли решить пример.
У. – А такой способ сложения можно
применить ко всем двузначным числам?
Д. -Нет, если при сложении единиц
получится больше 10, то мы не сможем посчитать.
Д. -Мы не сможем посчитать, если при
сложении десятков тоже получится больше 10.
(Возникает новая проблема и спор)
5.Физминутка: (под музыку, меняя
темп)
Что такое, что мы слышим,
Это дождь стучит по крыше,
А потом пошел быстрей,
И по крыше бьет сильней.
6.Закрепление изученного материала:
(дети работают в группах)
У.Чтобы узнать значение суммы 34+45 Вера
и Боря сделали рисунки. Выбери, чей рисунок лучше
поможет узнать значение суммы?
Подумай, какая математическая запись
соответствует выбранному тобой рисунку. Сделай
сам такую запись.
Сравни свою запись с записью Толи:
34+45=(30+4)+(40+5)=(30+40)+(4+5)=70+9=79
У тебя получилась такая же запись?
Какими суммами заменили слагаемые?
Как такие суммы называются?
Что обозначает запись (30+40) + (4+5)?
7.Самостоятельная работа и
взаимопроверка:
У. Выполняем №117 с.48
– Сколько выражений приготовил автор?
54+32 63+24 73+16 27+42 56+30 46+31
– Чем похожи выражения? (Это суммы)
– Что необычного в суммах, которые мы
находим? (Все слагаемые – двузначные числа)
-Какие знания нам пригодятся? (Таблица
сложения, натуральный ряд чисел и замена
слагаемых суммой разрядных слагаемых)
-Какие новые знания надо применить?
(Десятки надо прибавить к десяткам, а единицы – к
единицам)
(Дети самостоятельно находят значения
сумм и выполняют взаимопроверку в парах.)
У. Я заметила, что в третьей сумме 73+16 у
Оли и Тани разные ответы: 89 и 98. Почему? Кто прав?
(Новая проблема и спор).
Д. Кто-то из них посчитал неправильно.
Д. Давайте проверим
последовательность вычислений.
Д. Таня в ответе поменяла местами
десятки и единицы. Надо записать 89.
Д.Нельзя менять десятки и единицы
местами, у каждого разряда свое место!
8.Рефлексия:
Какие новые знания мы получили
сегодня? Какие старые знания нам пригодились? Что
самое главное надо запомнить?
Д. -Десятки прибавить к десяткам, а
единицы – к единицам.
Д. -Единицы надо писать на первом месте,
а десятки – на втором.
У. Когда вам было трудно? Что мешало?
У.Назовите сумму, значение которой
найти было легче остальных.
Д.Это сумма 56+30, потому что надо было
сложить только десятки.
У. Дома придумайте еще несколько
похожих сумм и найдите их значения.
Спасибо за урок. Мне очень приятно и
интересно было работать с вами.
Проверочная работа
Для проверки знаний учащимся предложены такие
задания:
1.Выполни подробную запись и найди значения
сумм:
70+24 62+30 37+10 20+46 53+40
В каждой сумме измени одну цифру так, чтобы
складывать числа стало труднее.
2.Найди значения сумм, сделав подробную запись:
35+43 24+41 63+24 54+35 76+20
Анализ работ показал, что все учащиеся поняли
общий принцип операции сложения двузначных
чисел через поразрядность выполнения операции и
использование таблицы сложения в любом разряде,
правильно находят результат, усвоили алгоритм
выполнения подробной записи, заменяют
двузначные числа суммой разрядных слагаемых.
Формирование осознанного прочного навыка идет
успешно.
Особый интерес вызывают задания, когда более
легкие суммы надо заменить трудными, или
придумать свои суммы, аналогичные данным.
- Главная
- Справочники
- Справочник по математике для начальной школы
- Сложение
Познакомимся со сложением.
Рассмотрим числовой ряд.

Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Посмотри на числовой ряд, по которому идёт заяц.

Какое действие выполняет заяц?
Прибавляет число 2.
К какому числу он прибавляет число 2?
К числу 4.
Наш зайчик стоит на числе 4 и думает, в какую сторону ему идти.
Подскажи ему.
В какую сторону пойдёт зайчик?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает заяц?
2, потому что ему нужно прибавить 2.
На каком делении остановится заяц?
На числе 6.
Когда прибавляем, становится больше.
Чем правее, тем числа больше.
4 + 2 = 6
Рассмотрим еще один пример.

Какое действие выполняет заяц?
Прибавляет число 5.
К какому числу он прибавляет число 5?
К числу 3. Мы поставили зайчика на число 3.
В какую сторону он пойдёт?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает зайчик? 5.
На каком делении он остановится? На числе 8.
3 + 5 = 8
Как называются числа при сложении?
Первое слагаемое и второе слагаемое.
Результат называется суммой.

Рассмотрите рисунок.
Представь части домика как слагаемые и сумму.

Как найти неизвестное слагаемое

Второе слагаемое неизвестно.
Рассмотри рисунок и догадайся, как его можно найти.
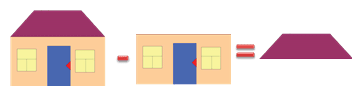
Нужно из суммы вычесть первое слагаемое.
Рассмотри рисунок.

Неизвестно первое слагаемое.
Как его можно найти?

Нужно из суммы вычесть второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Проверка сложения
Если из суммы двух слагаемых, вычесть одно из слагаемых, то получится второе слагаемое.
8 + 4 = 12
12 – 4 = 8
12 – 8 = 4
Именно эта связь между суммой и слагаемыми используют для проверки вычислений.
Например, 35 + 7 = 42.
Правильно ли произведено вычисление? Можно проверить так:
42 – 7 = 35, мы из суммы вычли одно из слагаемых и получили ВТОРОЕ слагаемое. Значит, вычисление произведено верно и пример решен правильно.
Перестановка слагаемых
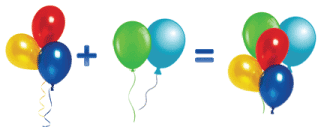
Сделаем запись к рисунку.
3 + 2 = 5
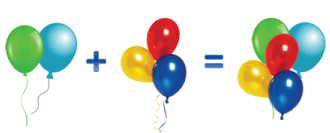
Сделаем запись к этому рисунку.
2 + 3 = 5
Теперь рассмотрим обе записи к рисункам:
3 + 2 = 5
3 – первое слагаемое
2 – второе слагаемое
5 сумма
2 + 3 = 5
2 – первое слагаемое
3 – второе слагаемое
5 – сумма
Мы заметили, что сумма в обеих записях одинаковая, хотя слагаемые мы записывали по-разному.
Это переместительный закон сложения, который гласит:
От перестановки мест слагаемых сумма не меняется.
Сочетательный закон сложения
Рассмотрим пример: (37 + 29) + 1 = …. (читаем: к сумме чисел 37 и 29 прибавить
1) Какие числа удобно сложить сначала, чтобы получился удобный способ? Числа 29 и 1.
Сумму чисел 29 и 1 возьмем в скобки.
37 + (29 + 1) = … (читаем: к 37 прибавить сумму чисел 29 и 1)
Решаем. Сначала выполним действие в скобках.
29 + 1 = 30
37 + 30 = 67, значит,
(37 + 29) + 1 = 67
Вывод: два соседних слагаемых можно заменить их суммой.
Советуем посмотреть:
Табличное сложение
Письменное сложение в столбик
Правило встречается в следующих упражнениях:
1 класс
Страница 102,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 103,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 32,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 19. Урок 12,
Петерсон, Учебник, часть 1
Страница 59. Урок 36,
Петерсон, Учебник, часть 1
Страница 28. Урок 15,
Петерсон, Учебник, часть 2
Страница 32. Урок 17,
Петерсон, Учебник, часть 2
Страница 55. Урок 28,
Петерсон, Учебник, часть 2
Страница 64,
Петерсон, Учебник, часть 2
Страница 89. Урок 35,
Петерсон, Учебник, часть 3
2 класс
Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 57,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 26,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 31,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 50. Тест. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 49,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 21,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 74,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 19. Урок 9,
Петерсон, Учебник, часть 1
Страница 28. Урок 14,
Петерсон, Учебник, часть 1
3 класс
Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 97,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 24,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 48,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 73. Урок 25,
Петерсон, Учебник, часть 1
Страница 23. Урок 10,
Петерсон, Учебник, часть 2
Страница 32. Урок 15,
Петерсон, Учебник, часть 3
Страница 37. Урок 17,
Петерсон, Учебник, часть 3
Страница 73. Повторение,
Петерсон, Учебник, часть 3
4 класс
Страница 20,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 62,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 95,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 9. ПР 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 12. Тест 1. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 84. Тест 3. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 90,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 92,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 94,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 16. Урок 6,
Петерсон, Учебник, часть 1
5 класс
Задание 219,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник






