Сложение и вычитание дробей
30 июля 2011
Дроби — это обычные числа, их тоже можно складывать и вычитать. Но из-за того, что в них присутствует знаменатель, здесь требуются более сложные правила, нежели для целых чисел.
Рассмотрим самый простой случай, когда есть две дроби с одинаковыми знаменателями. Тогда:
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений.
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.
Задача. Найдите значение выражения:
Внутри каждого выражения знаменатели дробей равны. По определению сложения и вычитания дробей получаем:
![]()
Как видите, ничего сложного: просто складываем или вычитаем числители — и все.
Но даже в таких простых действиях люди умудряются допускать ошибки. Чаще всего забывают, что знаменатель не меняется. Например, при сложении их тоже начинают складывать, а это в корне неправильно.
Избавиться от вредной привычки складывать знаменатели достаточно просто. Попробуйте сделать то же самое при вычитании. В результате в знаменателе получится ноль, и дробь (внезапно!) потеряет смысл.
Поэтому запомните раз и навсегда: при сложении и вычитании знаменатель не меняется!
Также многие допускают ошибки при сложении нескольких отрицательных дробей. Возникает путаница со знаками: где ставить минус, а где — плюс.
Эта проблема тоже решается очень просто. Достаточно вспомнить, что минус перед знаком дроби всегда можно перенести в числитель — и наоборот. Ну и конечно, не забывайте два простых правила:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
Разберем все это на конкретных примерах:
Задача. Найдите значение выражения:
В первом случае все просто, а во втором внесем минусы в числители дробей:
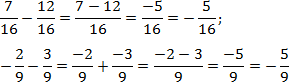
Что делать, если знаменатели разные
Напрямую складывать дроби с разными знаменателями нельзя. По крайней мере, мне такой способ неизвестен. Однако исходные дроби всегда можно переписать так, чтобы знаменатели стали одинаковыми.
Существует много способов преобразования дробей. Три из них рассмотрены в уроке «Приведение дробей к общему знаменателю», поэтому здесь мы не будем на них останавливаться. Лучше посмотрим на примеры:
Задача. Найдите значение выражения:
В первом случае приведем дроби к общему знаменателю методом «крест-накрест». Во втором будем искать НОК. Заметим, что 6 = 2 · 3; 9 = 3 · 3. Последние множители в этих разложениях равны, а первые взаимно просты. Следовательно, НОК(6; 9) = 2 · 3 · 3 = 18.
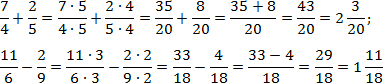
Что делать, если у дроби есть целая часть
Могу вас обрадовать: разные знаменатели у дробей — это еще не самое большое зло. Гораздо больше ошибок возникает тогда, когда в дробях-слагаемых выделена целая часть.
Безусловно, для таких дробей существуют собственные алгоритмы сложения и вычитания, но они довольно сложны и требуют долгого изучения. Лучше используйте простую схему, приведенную ниже:
- Перевести все дроби, содержащие целую часть, в неправильные. Получим нормальные слагаемые (пусть даже с разными знаменателями), которые считаются по правилам, рассмотренным выше;
- Собственно, вычислить сумму или разность полученных дробей. В результате мы практически найдем ответ;
- Если это все, что требовалось в задаче, выполняем обратное преобразование, т.е. избавляемся от неправильной дроби, выделяя в ней целую часть.
Правила перехода к неправильным дробям и выделения целой части подробно описаны в уроке «Что такое числовая дробь». Если не помните — обязательно повторите. Примеры:
Задача. Найдите значение выражения:
Здесь все просто. Знаменатели внутри каждого выражения равны, поэтому остается перевести все дроби в неправильные и сосчитать. Имеем:
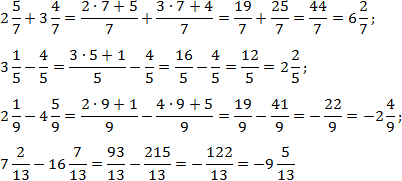
Чтобы упростить выкладки, я пропустил некоторые очевидные шаги в последних примерах.
Небольшое замечание к двум последним примерам, где вычитаются дроби с выделенной целой частью. Минус перед второй дробью означает, что вычитается именно вся дробь, а не только ее целая часть.
Перечитайте это предложение еще раз, взгляните на примеры — и задумайтесь. Именно здесь начинающие допускают огромное количество ошибок. Такие задачи обожают давать на контрольных работах. Вы также неоднократно встретитесь с ними в тестах к этому уроку, которые будут опубликованы в ближайшее время.
Резюме: общая схема вычислений
В заключение приведу общий алгоритм, который поможет найти сумму или разность двух и более дробей:
- Если в одной или нескольких дробях выделена целая часть, переведите эти дроби в неправильные;
- Приведите все дроби к общему знаменателю любым удобным для вас способом (если, конечно, этого не сделали составители задач);
- Сложите или вычтите полученные числа по правилам сложения и вычитания дробей с одинаковыми знаменателями;
- Если возможно, сократите полученный результат. Если дробь оказалась неправильной, выделите целую часть.
Помните, что выделять целую часть лучше в самом конце задачи, непосредственно перед записью ответа.
Смотрите также:
- Тест к уроку «Сложение и вычитание дробей» (легкий)

- Приведение дробей к общему знаменателю

- Тест к уроку «Десятичные дроби» (1 вариант)

- Метод узлов в задаче B5

- Задача B5: площадь кольца

- Сфера, вписанная в куб

Калькулятор дробей
- Главная
- /
- Математика
- /
- Арифметика
- /
- Калькулятор дробей
Если вам необходимо произвести математические операции с дробями воспользуйтесь нашим онлайн калькулятором:
Просто заполните необходимые поля и получите ответ и подробное решение.
Данный калькулятор может работать как с положительными, так и с отрицательными дробями.
При этом нужно помнить, что:
− ac = a− c = − ac
Всегда нужно использовать только последний вариант.
Сложение дробей
С одинаковыми знаменателями
При сложении дробей с одинаковыми знаменателями складываются только числители, а знаменатель остаётся прежним.
Формула
ac + bc = a + bc
Пример
Для примера сложим следующие дроби с равными знаменателями:
27 + 47 = 2 + 47 = 67
С разными знаменателями
При сложении дробей с разными знаменателями для начала необходимо привести дроби к общему знаменателю. А затем сложить числители.
Формула (универсальная)
ac + bd = a⋅d + b⋅cc⋅d
Пример №1
Для примера сложим следующие дроби с разными знаменателями:
12+13=1⋅32⋅3+1⋅23⋅2=36+26=3+26=56
Пример №2
Существуют также частные случаи, когда знаменатель одной дроби можно привести к знаменателю второй. Например:
12+14=1⋅22⋅2+14=24+14=2+14=34
Этот же пример можно решить и применяя вышеуказанную универсальную формулу:
12+14=1⋅42⋅4+1⋅24⋅2=48+28=4+28=68=34
Обратите внимание, что мы сократили дробь:
68=3 ⋅ 24 ⋅ 2=34
Сложение смешанных чисел
Смешанные числа – это такие числа, у которых есть как дробная часть, так и целая.
Преобразуя в неправильную дробь
Для начала смешанное число (дробь) нужно преобразовать в неправильную дробь, а потом можно складывать как в предыдущих примерах.
Формула
a bc + d ef = b + a ⋅ cc + e + d ⋅ ff
Пример
Для примера сложим два смешанных числа:
312+123=1+3⋅22+2+1⋅33=72+53=7⋅32⋅3+5⋅23⋅2=216+106=21+106=316=5⋅6+16=5⋅66 + 16=516
Обратите внимание, что из полученной неправильной дроби мы выделили целую часть:
316=5⋅6+16=5⋅66 + 16=516
Складывая целую и дробную части отдельно
Целую и дробную части смешанных чисел можно складывать по отдельности.
Формула
a bc + d ef = (a + d) + (bc + ef)
Пример
Решим предыдущий пример этим способом:
3 12 + 1 23 = (3+1)+(12+23) = 4+1⋅32⋅3+2⋅23⋅2=4+36+46=4+3+46=4+76=4+116 = 516
Вычитание дробей
Вычитание дробей происходит по тем же принципам, что и сложение.
С одинаковыми знаменателями
Формула
ac − bc = a − bc
Пример
Для примера вычтем одну дробь из другой с равными знаменателями:
35−25=3−25=15
С разными знаменателями
Тут также, как и при сложении, дроби нужно подвести под общий знаменатель, а затем вычитать.
Формула
ac − bd = a⋅d − b⋅cc⋅d
Пример
Для примера вычтем одну дробь из другой, с разными знаменателями:
34−13=3⋅34⋅3−1⋅43⋅4=912−412=9−412=512
Вычитание смешанных чисел
Для начала смешанные числа преобразуем в неправильные дроби, потом приводим полученные дроби к общему знаменателю, а затем вычтем одну из другой. Далее выделяем целую часть если она есть.
Формула
a bc − d ef = b + a ⋅ cc − e + d ⋅ ff
Пример
312−123=1+3⋅22−2+1⋅33=72−53=7⋅32⋅3−5⋅23⋅2=216−106=21−106=116=1⋅6+56=1⋅66 + 56=156
Умножение дробей
При умножении дробей неважно одинаковые или разные у них знаменатели. Числитель одной дроби умножается на числитель другой, а знаменатели тоже перемножаются между собой.
Формула
ac ⋅ be = a ⋅ bc ⋅ e
Давайте рассмотрим несколько примеров:
Пример №1
Умножим дроби с одинаковыми знаменателями:
13⋅23=1⋅23⋅3=29
Пример №2
Умножим дроби с разными знаменателями:
13⋅24=1⋅23⋅4=212=1⋅26⋅2=16
Пример №3
Умножим смешанные числа:
112⋅223=1+1⋅22⋅2+2⋅33=32⋅83=3⋅82⋅3=246=4
Деление дробей
При делении одной дроби на другую также неважно одинаковые или разные у них знаменатели. Чтобы разделить одну дробь на другую нужно перемножить числитель первой дроби и знаменатель второй, а знаменатель первой умножить на числитель второй.
Формула
ac : be = a ⋅ ec ⋅ b
Давайте рассмотрим несколько примеров:
Пример №1
Разделим одну дробь на другую с таким же знаменателем:
23:13=23⋅31=2⋅33⋅1=63=2
Пример №2
Делим дроби с разными знаменателями:
12:23=12⋅32=1⋅32⋅2=34
Пример №3
Деление смешанных чисел:
412:223=1+4⋅22:2+2⋅33=92:83=92⋅38=9⋅32⋅8=2716=1⋅16+1116=1⋅1616 + 1116=11116
См. также
Математика
6 класс
Урок № 40
Сложение и вычитание дробей
Перечень рассматриваемых вопросов:
- обобщение и систематизация знаний по теме «Сложение и вычитание дробей».
Тезаурус
Сумма дробей с одинаковыми положительными знаменателями есть дробь с тем же знаменателем и числителем, равным сумме числителей.
Разностью двух дробей называют такую дробь, которая в сумме с вычитаемым даёт уменьшаемое.
Наименьший общий положительный знаменатель – это наименьшее положительное число, кратное знаменателям данных дробей.
Наименьшее общее кратное двух чисел – наименьшее натуральное число, которое делится на заданные числа без остатка.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
На прошлых уроках мы с вами рассматривали, как выполняют сложение и вычитание дробей любого знака. Сегодня вспомним и закрепим эти правила.
Вспомним основные правила сложения и вычитания дробей любого знака.
Правило сложения дробей с одинаковыми знаменателями
Чтобы сложить две дроби с одинаковыми положительными знаменателями, надо сложить их числители, а знаменатель оставить прежним.

Правило сложения дробей с разными знаменателями
Чтобы сложить две дроби с разными знаменателями, надо привести их к общему положительному знаменателю и сложить полученные дроби.

Правило вычитания дробей с одинаковыми знаменателями
Чтобы вычесть две дроби с одинаковым положительными знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.

Правило вычитания дробей с разными знаменателями
Чтобы найти разность двух дробей с разными знаменателями, надо привести их к общему положительному знаменателю и выполнить вычитание дробей с одинаковыми знаменателями.

Разность дробей a и b равна сумме уменьшаемого и числа, противоположного вычитаемому.

Дроби можно складывать и вычитать по тем же правилам, что и целые числа, то есть сначала определять знак результата, потом выполнять действия с модулями.
Иногда сложение и вычитание дробей выполняется проще, если привести их к наименьшему общему положительному знаменателю.

Дополнительный материал
Решим задачу.

Какую часть пути прошли туристы за три дня?
Решение.

Найдём, какую часть пути туристы прошли в третий день.

Найдём, какую часть пути туристы прошли за три дня.
Для этого сложим все части.

Разбор заданий тренировочного модуля
№ 1. Разместите нужные подписи под изображениями.

Варианты ответов:
Сложение дробей с разными знаками и разными знаменателями.
Сложение отрицательных дробей с разными знаменателями
Вычитание дробей с одинаковыми знаменателями
Для ответа на вопрос задания вспомним действия с рациональными числами и внимательно посмотрим на знаки между предложенными дробями.
Правильный ответ:
- Вычитание дробей с одинаковыми знаменателями.
- Сложение дробей с разными знаками и разными знаменателями.
- Сложение отрицательных дробей с разными знаменателями
№ 2. Вставьте в текст нужные слова.
Чтобы сложить две дроби с разными …, надо привести их к общему положительному … и … полученные дроби.
Варианты слов для вставки:
знаменателями
числителями
знаменателю
числителю
сложить
вычесть
Для ответа на вопрос задания обратимся к теоретическому материалу урока.
Правильный ответ:
Чтобы сложить две дроби с разными знаменателями, надо привести их к общему положительному знаменателю и сложить полученные дроби.
Сложение и вычитание алгебраических дробей
- Сложение и вычитание с одинаковыми знаменателями
- Сложение и вычитание с разными знаменателями
Сложение и вычитание с одинаковыми знаменателями
Чтобы выполнить сложение или вычитание алгебраических дробей с одинаковыми знаменателями, надо найти сумму или разность числителей, а знаменатель оставить без изменений.
Пример 1. Выполните сложение алгебраических дробей:
| а) | a + 3 | + | a – 3 | ; |
| b | b |
| б) | 2b – 1 | + | b + 4 | . |
| 2 | 2 |
Решение: Складываем числители дробей и выполняем приведение подобных членов (если они есть):
| а) | a + 3 | + | a – 3 | = | (a + 3) + (a – 3) | = |
| b | b | b |
| = | a + 3 + a – 3 | = | 2a | ; | |
| b | b |
| б) | 2b – 1 | + | b + 4 | = | (2b – 1) + (b + 4) | = |
| 2 | 2 | 2 |
| = | 2b – 1 + b + 4 | = | 3b + 3 | . | |
| 2 | 2 |
Пример 2. Выполните вычитание алгебраических дробей:
| а) | x + 5 | – | 5x | ; |
| 3 | 3 |
| б) | a + b | – | a + 4 | . |
| a – 5 | a – 5 |
Решение: Вычитаем из числителя первой дроби числитель второй дроби и выполняем приведение подобных членов (если они есть):
| а) | x + 5 | – | 5x | = | x + 5 – 5x | = | 5 – 4x | ; |
| 3 | 3 | 3 | 3 |
| б) | a + b | – | a + 4 | = | (a + b) – (a + 4) | = |
| a – 5 | a – 5 | a – 5 |
| = | a + b – a – 4 | = | b – 4 | . |
| a – 5 | a – 5 |
Сложение и вычитание алгебраических дробей с одинаковыми знаменателями в виде общих формул:
| a | + | b | = | a + b | и | a | – | b | = | a – b | , |
| c | c | c | c | c | c |
где c≠0.
Если дроби имеют знаменатели, состоящие из противоположных выражений, то есть выражений, отличающихся только знаком, надо тождественно преобразовать одну из дробей, чтобы привести их к общему знаменателю. Преобразование выполняется в соответствии с правилами знаков:
Данное преобразование можно рассматривать как умножение числителя и знаменателя дроби на -1. Следовательно, если числитель и знаменатель алгебраической дроби заменить на противоположные выражения, то получится дробь, равная данной. Полученную дробь можно переписать, поставив один из минусов перед дробью:
| a | = | –a | = – | a | = – | –a | . |
| b | –b | –b | b |
Также, любую отрицательную дробь можно сделать положительной, перенеся минус, стоящий перед дробью, в числитель или знаменатель:
| – | a | = | –a | = | a | . |
| b | b | –b |
Пример 1. Найдите сумму дробей:
Решение: Чтобы выполнить сложение, поменяем знаки перед второй дробью и в её знаменателе на противоположные:
| 5a | + | 3a | = | 5a | – | 3a | = |
| b – c | c – b | b – c | -(c – b) |
| = | 5a | – | 3a | = | 2a | . |
| b – c | b – c | b – c |
Пример 2. Найдите разность дробей:
| n + 5 | – | 2n | . |
| n2 – m | m – n2 |
Решение: Чтобы выполнить вычитание, перенесём знак минус, стоящий перед второй дробью, в её знаменатель:
| n + 5 | – | 2n | = | n + 5 | + | 2n | = |
| n2 – m | m – n2 | n2 – m | -(m – n2) |
| = | n + 5 | + | 2n | = | 3n + 5 | . |
| n2 – m | n2 – m | n2 – m |
Сложение и вычитание с разными знаменателями
Чтобы найти сумму или разность алгебраических дробей с разными знаменателями, надо:
- найти общий знаменатель,
- привести алгебраические дроби к общему знаменателю,
- выполнить сложение или вычитание,
- сократить полученную дробь, если это возможно.
Пример 1. Выполните сложение дробей:
Решение: Находим общий знаменатель. Он будет равен произведению знаменателей данных дробей:
(a + b)(a – b).
Как находить общий знаменатель, Вы можете узнать на странице Приведение алгебраических дробей к общему знаменателю
. Далее умножаем числитель каждой дроби на дополнительный множитель:
2a(a – b) = 2a2 – 2ab;
b(a + b) = ab + b2.
Общий знаменатель можно свернуть в разность квадратов. В итоге у нас получится:
| 2a | + | b | = | 2a2 – 2ab | + | ab + b2 | = |
| a + b | a – b | a2 – b2 | a2 – b2 |
| = | 2a2 – 2ab + ab + b2 | = | 2a2 – ab + b2 | . |
| a2 – b2 | a2 – b2 |
Пример 2. Выполните вычитание дробей:
Решение: Разложим знаменатель первой дроби на множители:
a2 – ab = a(a – b).
Так как данное выражение делится на знаменатель второй дроби, то возьмём его в качестве общего знаменателя. Значит, теперь нам надо умножить числитель второй дроби на дополнительный множитель a:
2 · a = 2a.
Получаем:
| = | b | – | 2a | = | b – 2a | . |
| a(a – b) | a(a – b) | a(a – b) |
Пример 3. Выполните сложение:
Решение: Запишем первое слагаемое в виде дроби и приведём её к знаменателю 1 – x:
| x + | x2 | = | x | + | x2 | = |
| 1 – x | 1 | 1 – x |
| = | x(1 – x) | + | x2 | = | x – x2 | + | x2 | . |
| 1 – x | 1 – x | 1 – x | 1 – x |
Теперь можно выполнить сложение дробей с одинаковыми знаменателями:
| x – x2 | + | x2 | = | x – x2 + x2 | = | x | . |
| 1 – x | 1 – x | 1 – x | 1 – x |
Точно также можно выполнять сложение и вычитание алгебраических дробей с любыми многочленами.
Давайте разберемся, как складывать и вычитать обыкновенные дроби. Данный навык необходим для решения множества задач как и в школьном курсе, так и при сдаче ОГЭ или ЕГЭ по математике. Итак, перейдем к рассмотрению различных примеров.
Сложение и вычитание дробей с одинаковыми знаменателями
Начнем с рассмотрения самого простого примера – сложения и вычитания дробей с одинаковыми знаменателями. В данном случае необходимо просто произвести действия с числителями – сложить их или вычесть.
При сложении и вычитании дробей с одинаковыми знаменателями знаменатель не изменяется!
Главное не производить никакие операции сложения и вычитания в знаменателе, но некоторые школьники забывают об этом. Чтобы лучше понять это правило, прибегнем к принципу визуализации, или говоря простыми словами, рассмотрим жизненный пример:
У Вас есть половина яблока – это ½ от всего яблока. Вам дают еще одну половину, то есть еще ½. Очевидно, что теперь у Вас целое яблоко (не считая, что оно разрезано
). Поэтому ½ + ½ = 1, а не что-то другое, как, например, 2/4. Или же у Вас забирают эту половину: ½ – ½ = 0. В случае вычитания с одинаковыми знаменателями получается вообще особый случай – при вычитании одинаковых знаменателей, мы получим 0, а на 0 делить нельзя, и данная дробь не будет иметь смысла.
Приведем напоследок пример:
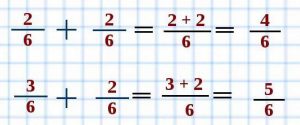
Сложение и вычитание дробей с разными знаменателями
Что же делать, если знаменатели разные? Для этого нам необходимо вначале привести дроби к одному знаменателю, а затем действовать как я указал выше.
Приводить дробь к общему знаменателю можно двумя способами. Во всех способах используется одно правило – при умножении числителя и знаменателя на одно и то же число дробь не изменяется.
Существует два способа. Первый – самый простой – так называемый “крест-накрест”. Он заключается в том, что первую дробь мы умножаем на знаменатель второй дроби (и числитель и знаменатель), а вторую дробь умножаем на знаменатель первой (аналогично и числитель и знаменатель). После этого действуем как в случае с одинаковыми знаменателями – теперь они действительно одинаковые!
Пример:
![]()
Предыдущий способ универсален, однако в большинстве случаев у дробей знаменателей можно найти наименьшее общее кратное – число, на которое делится и первый знаменатель и второй, причем самое маленькое. В данном методе нужно уметь видеть такие НОКи, потому что специальный поиск их достаточно ёмкий и уступает по скорости методу “крест-накрест”. Но в большинстве случаев НОКи довольно хороши видны, если набить глаз и достаточно тренироваться.
Пример:
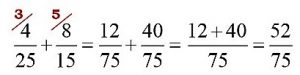
Надеюсь, что теперь Вы в совершенстве владеете методами сложения и вычитания дробей!
Даниил Романович | Просмотров: 2.5k
