Как найти значение суммы правило

Как найти значение суммы правило

Содержание:

  • § 1  Правило нахождения модуля суммы слагаемых с одинаковыми знаками
  • § 2  Правило нахождения модуля суммы слагаемых с разными знаками

§ 1  Правило нахождения модуля суммы слагаемых с одинаковыми знаками

В этом уроке рассмотрим правило вычисления алгебраической суммы двух чисел.

Найдем значения выражений: -4 – 10 и +4+10 с помощью координатной прямой.

Вспомним, что вычитание – это движение влево, а сложение – движение вправо по координатной прямой.

На координатной прямой отметим точки -4 и +4. От точки -4 отложим влево 10 единичных отрезков, получим координату -14. От точки +4 отложим вправо 10 единичных отрезков, получим координату +14.

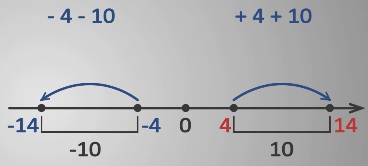
По рисунку видно, что -4-10 = -14; +4+10 = +14.

Проанализируем выражения. В каждом выражении слагаемые имеют одинаковые знаки: в первом знак минус, во втором знак плюс, значения суммы имеют тот же знак, что и слагаемые.

Найдем сумму модулей l-4l + l-10l = l-14l.

l -4l = 4

l-10l = 10

4+10 = 14, а 14 – модуль числа -14.

Аналогично l4l + l10l = l14l

l4l = 4

l10l = 10

4+10=14, а 14 – модуль и +14 тоже.

Можно сделать вывод:

Если слагаемые имеют одинаковые знаки, то значение суммы имеет тот же знак, что и слагаемые, а модуль суммы равен сумме модулей слагаемых.

Например:

В сумме -14-23 оба слагаемых имеют знак минус, значит, значение суммы тоже будет иметь знак минус, складываем модули 14+23=37, в итоге значение суммы -37.

§ 2  Правило нахождения модуля суммы слагаемых с разными знаками

Найдем значения выражений, в которых слагаемые имеют разные знаки.

Например, -4+10 и +4-10.

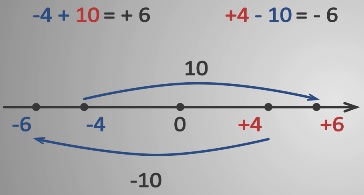
Отметим на координатной прямой точки -4 и +4. От координаты -4 отложим вправо 10 единичных отрезков, получим число +6. От координаты +4 отложим влево 10 единичных отрезков, получим точку -6. Таким образом, -4+10= +6 и +4-10 = -6.

Сделаем анализ выражений.

Сравним модули слагаемых l-4l < l10l; l+4l < l-10l,обратим внимание, результат суммы имеет знак слагаемого с большим модулем. Из большего модуля вычтем меньший:

l+10l – l-4l = 6 и l-10l – l+4l = 6, значит

-4+10= 6, а +4-10= -6.

Вывод:

Если слагаемые имеют разные знаки, то значение суммы имеет тот же знак, что и слагаемое с большим модулем, а модуль суммы равен разности модулей слагаемых при условии, что из большего модуля вычитается меньший модуль.

Например, найдем значение выражения 9 – 25, слагаемые имеют разные знаки +9 и -25, найдем модули слагаемых l+9l = 9, l-25l = 25.

Больший модуль 25, значит, знаком результата суммы будет знак минус. Найдем разность модулей 25 – 9 = 16. Значит значение суммы равно минус 16.

Вспомним, противоположные числа – это числа, которые отличаются знаками, их модули одинаковые. Следовательно, сумма противоположных чисел равна 0, так как разность одинаковых модулей равна 0.

Вывод:

Сумма противоположных чисел равна 0. Также можно утверждать, что если сумма двух чисел равна 0, то данные числа будут противоположными.

Если одно из слагаемых равно 0, то значение суммы равно другому слагаемому.

Например, -8,3 + 0, слагаемые с разными знаками, модуль -8,3 больше чем модуль 0, значит знак суммы – минус, найдем разность модулей l-8.3l – l0l = 8, 3, следовательно сумма равна -8,3.

Итак, на этом уроке Вы познакомились с правилом вычисления алгебраической суммы двух чисел.

Список использованной литературы:

  1. Математика.6 класс: поурочные планы к учебнику И.И. Зубаревой, А.Г. Мордковича //автор-составитель Л.А. Топилина. Мнемозина 2009.
  2. Математика. 6 класс: учебник для учащихся общеобразовательных учреждений. И.И. Зубарева, А.Г. Мордкович.- М.: Мнемозина, 2013.
  3. Математика. 6 класс: учебник для учащихся общеобразовательных учреждений. /Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Мнемозина, 2013.
  4. Справочник по математике – http://lyudmilanik.com.ua
  5. Справочник для учащихся в средней школе http://shkolo.ru
Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 декабря 2021 года; проверки требуют 9 правок.

У этого термина существуют и другие значения, см. сумма.

Су́мма (лат. summa — итог, общее количество) в математике — результат применения операции сложения величин (чисел, функций, векторов, матриц и т. д.), либо результат последовательного выполнения нескольких операций сложения (суммирования). Общими для всех случаев являются свойства коммутативности, ассоциативности, а также дистрибутивности по отношению к умножению (если для рассматриваемых величин умножение определено), то есть выполнение соотношений:

{displaystyle a+b=b+a,}
{displaystyle a+(b+c)=(a+b)+c,}
{displaystyle (a+b)cdot c=acdot c+bcdot c,}
{displaystyle ccdot (a+b)=ccdot a+ccdot b,}

В теории множеств суммой (или объединением) множеств называется множество, элементами которого являются все элементы объединяемых множеств, взятые без повторений.

Также сложение (нахождение суммы) может быть определено для более сложных алгебраических структур (сумма групп, сумма линейных пространств, сумма идеалов, и другие примеры). В теории категорий определяется понятие суммы объектов.

Сумма натуральных чисел[править | править код]

Пусть в множестве mathbb {N} находится a элементов, образующих подмножество A, и b элементов, образующих подмножество B ({displaystyle Asubset mathbb {N} ,Bsubset mathbb {N} }, a и b — натуральные числа). Тогда арифметической суммой a+b будет количество элементов c, образующих подмножество {displaystyle Csubset mathbb {N} }, полученное при дизъюнктном объединении двух исходных подмножеств {displaystyle C=Asqcup B.}

Алгебраическая сумма[править | править код]

Сумму математически обозначают заглавной греческой буквой Σ (сигма).

{displaystyle sum _{imathop {=} m}^{n}a_{i}=a_{m}+a_{m+1}+a_{m+2}+cdots +a_{n-1}+a_{n}}

где: i — индекс суммирования; ai — переменная, обозначающая каждый член в серии; m — нижняя граница суммирования, n — верхняя граница суммирования. Обозначение «i = m» под символом суммирования означает, что начальное (стартовое) значение индекса i эквивалентно m. Из этой записи следует, что индекс i инкрементируется на 1 в каждом члене выражения и остановится, когда i = n.[1]

В программировании данной процедуре соответствует цикл for.

Примеры записи
{displaystyle sum _{imathop {=} 1}^{100}i=1+2+3+4+{...}+99+100}
{displaystyle sum _{imathop {=} 3}^{6}i^{2}=3^{2}+4^{2}+5^{2}+6^{2}=86}

Границы могут опускаться из записи, если они ясны из контекста:

{displaystyle sum a_{i}^{2}=sum _{imathop {=} 1}^{n}a_{i}^{2}.}

Итератор может быть выражением — тогда переменная оформляется со скобками как функция «f()». Например, сумма всех f(k) при натуральных числах k в определённом диапазоне:

{displaystyle sum _{0leq k<100}f(k).}

Сумма f(x) элементов x множества S:

{displaystyle sum _{xmathop {in } S}f(x).}

Сумма {displaystyle mu (d)} всех положительных чисел d, являющихся делителями числа n:

{displaystyle sum _{d|n};mu (d).}

Под знаком итеративного суммирования может использоваться несколько индексов, например:

{displaystyle sum _{i,j}=sum _{i}sum _{j},}

причём набор из нескольких индексов можно сократить в виде так называемого мультииндекса.

Бесконечная сумма[править | править код]

В математическом анализе определяется понятие ряда — суммы бесконечного числа слагаемых.

Примеры последовательных сумм[править | править код]

1. Сумма арифметической прогрессии:

sum _{{i=0}}^{n}(a_{0}+bcdot i)=(n+1){frac {a_{0}+a_{n}}{2}}

2. Сумма геометрической прогрессии:

sum _{{i=0}}^{n}a_{0}cdot b^{i}=a_{0}cdot {frac {1-b^{{n+1}}}{1-b}}

3.sum limits _{{k=1}}^{n}k^{3}=left[{frac {n(n+1)}{2}}right]^{2}=left(sum limits _{{k=1}}^{n}kright)^{2}

4. sum _{{i=0}}^{n}{left({frac {1}{p}}right)}^{i}={frac {p}{p-1}}left(1-{frac {1}{p^{{n+1}}}}right),quad pneq 1,ngeq 0

Доказательство

sum _{{i=0}}^{n}{left({frac {1}{p}}right)}^{i}=sum _{{i=0}}^{n}{1cdot {{frac {1}{p^{i}}}}}=1cdot {frac {1-{left({frac {1}{p}}right)}^{{n+1}}}{1-{frac {1}{p}}}}={frac {{frac {p^{{n+1}}-1}{p^{{n+1}}}}}{{frac {p-1}{p}}}}={frac {p^{{n+1}}-1}{p^{n}(p-1)}}={frac {p}{p-1}}left(1-{frac {1}{p^{{n+1}}}}right)

5. sum _{{i=0}}^{n}ip^{i}={frac {np^{{n+2}}-(n+1)p^{{n+1}}+p}{(p-1)^{2}}},quad pneq 1

6. sum _{{i=0}}^{n}p^{i}=(p-1)sum _{{i=0}}^{{n-1}}((n-i)p^{i})+n+1,quad pneq 1

Например, при {displaystyle p=10} получается {textstyle sum _{i=0}^{n}10^{i}=9cdot sum _{i=0}^{n-1}((n-i)10^{i})+n+1}, а это последовательность равенств следующего вида:
1=9cdot 0+1,quad 11=9cdot 1+2,quad 111=9cdot 12+3,quad 1111=9cdot 123+4,quad 11111=9cdot 1234+5

Неопределённая сумма[править | править код]

Неопределённой суммой a_{i} по i называется такая функция f(i), обозначаемая
{textstyle sum _{i}^{}a_{i}},
что {textstyle forall i:f(i+1)-f(i)=a_{i}}.

«Дискретная» формула Ньютона — Лейбница[править | править код]

Если найдена «производная» {displaystyle a_{i}=f(i+1)-f(i)}, то {textstyle sum _{i=a}^{b}a_{i}=f(b+1)-f(a)}.

Этимология[править | править код]

Латинское слово summa переводится как «главный пункт», «сущность», «итог». С XV века слово начинает употребляться в современном смысле, а также появляется глагол «суммировать» (1489 год).

Это слово проникло во многие современные языки: сумма в русском, sum в английском, somme во французском.

Специальный символ для обозначения суммы (Σ) первым ввёл Леонард Эйлер в 1755 году, его поддержал Лагранж, однако долгое время с этим символом конкурировал знак S. Окончательно обозначение Σ для суммы утвердили уже в XVIII веке Фурье и Якоби[2].

Кодировка[править | править код]

В Юникоде есть символ суммы U+2211 ∑ n-ary summation (HTML ∑ • &sum;).

См. также[править | править код]

  • Сложение
  • Произведение

Примечания[править | править код]

  1. ↑ Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren. Chapter 2: Sums // Concrete Mathematics: A Foundation for Computer Science (2nd Edition) (англ.). — Addison-Wesley Professional, 1994. — ISBN 978-0201558029. (недоступная ссылка)
  2. ↑ Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. — 3-е изд. — СПб.: ЛКИ, 2008. — С. 175. — 248 с. — ISBN 978-5-382-00839-4.

Литература[править | править код]

  • Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — 7-е. — М.: Наука, 1969. — Т. 1. — 608 с. — 100 000 экз.
Источник

Содержание

  1. Сумма и разность чисел
  2. Что такое сумма, и как ее найти
  3. Как найти разность чисел
  4. Что такое сумма чисел
  5. Определение суммы чисел
  6. Свойства суммы чисел
  7. Математика. 2 класс
  8. Математика. 2 класс
  9. Математика 2 класс «Слагаемые,Сумма»
  10. Онлайн-конференция
  11. «Современная профориентация педагогов и родителей, перспективы рынка труда и особенности личности подростка»
  12. Свидетельство и скидка на обучение каждому участнику

Сумма и разность чисел

Что такое сумма, и как ее найти

Чтобы наглядно показать ребенку, как сложить числа, возьмите конфеты или любые другие вещи. Покажите ребенку две конфеты, а затем прибавьте к этим конфетам еще две. Пусть ребенок посчитает и скажет, что теперь конфет оказалось четыре. Объясните ему, что он только что сложил эти числа, то есть прибавил к одному числу другое число и в конечном итоге получил сумму.

Немного сложнее объяснить сложение разрядных слагаемых, эта тема может быть непонятна ребенку. Итак, существует множество разрядов: единицы, десятки, тысячи. Возьмите, к примеру, число 2564. Если разложить его на разряды, то получится: 2564 = 2000 + 500 + 60 + 4. Чтобы прибавить к этому числу, например, число 305, воспользуйтесь сложением в столбик. При таком сложении нужно прибавлять одни разряды к другим, начиная с конца: единицы к единицам, десятки к десяткам, тысячи к тысячам. То есть, для начала складываем 4 и 5, затем 6 и 0, после 5 и 3, и в конце 2 и 0. В конечном итоге получаем число 2869.

Как найти разность чисел

1533419760 vychitanie nayti raznostРазность – результат вычитания одного числа из другого. В отличие от суммы, здесь мы не можем воспользоваться правилом «от перестановки слагаемых разность не меняется», так как в вычитании всегда есть уменьшаемое и вычитаемое. Чтобы найти вычитаемое и разность, для начала нужно разобраться с этими понятиями. Уменьшаемое – это то, из чего мы «вычитаем», то есть убираем, а вычитаемое – количество того, что мы у этого уменьшаемого вернем.

А что касается разрядных слагаемых, то здесь мы делаем то же самое, что и с суммой, только теперь не прибавляем, а вычитаем. Возьмем число 6845 и вычтем из него 4231. Для этого мы вычитаем один разряд из другого разряда, производя вычитание с конца: 5-1 = 4, 4-3 = 1, 8-2 = 6, 6-4 = 2. В ответе получим 2614.

Источник

Что такое сумма чисел

Определение суммы чисел

formules 4195

Задание. Найти сумму чисел:

Ответ.

Свойства суммы чисел

На основании этих свойств можем заключить, что от перестановки мест слагаемых сумма не изменяется.

Дистрибутивность по отношению к умножению

$$(n+m) cdot k=n cdot k+m cdot k$$

Что такое сумма чисел не по зубам? Тебе ответит эксперт через 10 минут!

Задание. Найти сумму чисел удобным способом:

Решение. По свойствам сложения имеем

При сложении больших чисел или десятичных дробей используется сложение в столбик.

Задание. Найти сумму чисел удобным способом:

Решение. Складываем эти числа в столбик, для этого запишем их друг под другом, разряд под разрядом. В случае десятичных дробей ориентируемся на то, чтобы запятая первого числа стояла под запятой второго. Далее складываем числа стоящие друг под другом, двигаясь справа на лево и записывая результата под чертой дроби. Если сумма чисел в одном столбце превышает десять, то количество десятков прибавляем к числам стоящим в следующем столбце слева от этого столбца:

formules 4210

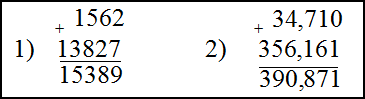
Сложение рациональных дробей производится по правилу

Задание. Найти сумму чисел:

Решение. Вычислим первую сумму используя правило сложения рациональных чисел

Числитель и знаменатель полученной дроби можно сократить на 2, тогда в ответе получим

Для вычисления второй суммы, преобразуем сначала второе слагаемое в неправильную дробь, для этого умножим целую часть на знаменатель и прибавим полученное число к числителю. Далее применим правило сложение рациональных дробей

Выделим в полученной дроби целую часть, для этого разделим числитель на знаменатель с остатком. Полученное частное запишем в целую часть, а остаток от деления в числитель.

Источник

Математика. 2 класс

Конспект урока

Математика, 2 класс

Урок № 14. Числовые выражения. Порядок действий в числовых выражениях. Скобки. Сравнение числовых выражений

Перечень вопросов, рассматриваемых в теме:

— Что такое числовые выражения?

— Как правильно читать и записывать числовые выражения?

— Как выполнять порядок действий, если есть скобки?

— Как сравнить два выражения?

Числовое выражение – это запись, состоящая из чисел и знаков действий между ними.

Значение выражения – это результат выполненных действий.

Сравнить числовые выражения – найти значение каждого из выражений и их сравнить.

Порядок выполнения действий – это последовательность проводимых вычислений в данном выражении.

Основная и дополнительная литература по теме:

1. Моро М. И., Бантова М. А., Бельтюкова Г. В.и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1. –8-е изд. – М.: Просвещение, 2017. – с.38-40

2. Волкова А. Д. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2017, с. 22-27

3. Глаголева Ю. И., Волкова А. Д. Математика. КИМы. 2 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, Учлит, 2017, с.16

Теоретический материал для самостоятельного изучения

Маша и Миша решали пример: из числа 12 вычесть сумму чисел 7 и 3. Они записали его по-разному и получили разные ответы. Маша сначала из 12 вычла 7 и получила 5, потом прибавила 3, получила 8.

Миша обвёл овалом сумму чисел 7 и 3 и сначала посчитал сумму, получил 10. Затем от 12 отнял 10, получил 2.

Кто из них вычислил верно? Решил верно, Миша.

Запишем пример, который решали дети правильно:

Вычислим. 7 + 3 равно 10, из 12 вычесть 10, получится 2. Запомните: действия, записанные в скобках, выполняются первыми.

Посмотрим на запись.

Запись, в которой разные числа (однозначные и двузначные) соединены знаками «+» и «–» в различных сочетаниях, называется числовым выражением и читается так: «из числа 9 вычесть сумму чисел 6 и 2».

Найти значение выражения – это значит, нужно выполнить все указанные действия в выражении. Значение данного выражения 1.

Теперь мы будем называть примеры числовыми выражениями, а ответы значениями числовых выражений.

К числу 10 прибавить разность чисел 8 и 3.

Как найти значение выражения? Нужно выполнить необходимые действия. Но с какого действия нужно начинать? С того, которое записано в скобках. Находим разность чисел 8 и 3, будет 5, к 10 прибавить 5, получится 15.

Давайте сравним значения двух выражений:

Сначала найдем значение каждого из выражений и их сравним.

Источник

Математика. 2 класс

Конспект урока

Математика, 2 класс

Урок № 16. Свойства сложения. Применение переместительного и сочетательного свойств сложения

Перечень вопросов, рассматриваемых в теме:

— Что такое сочетательное свойство сложения?

-В каких случаях можно использовать свойства сложения?

Переместительное свойство сложения: слагаемые можно переставлять местами, при этом значение суммы не изменится.

Сочетательное свойство сложения: результат сложения не изменится, если соседние слагаемые заменить их суммой.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.44-47

2. Математика. КИМы. 2 кл: учебное пособие для общеобразовательных организаций/ Глаголева Ю.И., Волкова А.Д.-М.: Просвещение, Учлит, 2017, с.18, 19

3. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017.- с.28, 29

Теоретический материал для самостоятельного изучения

Сравним выражения и их значения:

Сумма чисел шесть и девять равна сумме чисел девять и шесть.

Сумма чисел сорок пять и пять равна сумме чисел пять и сорок пять.

Значения выражений равны, так как от перестановки слагаемых значение суммы не меняется. Вспомним, как в математике называется данное свойство сложения?

Правильно, оно называется переместительным свойством сложения.

В школьном спортзале 3 волейбольных мяча, 5 баскетбольных мячей и 4 футбольных мяча. Сколько всего мячей в спортзале?

Первый способ решения.

Сначала узнаем, сколько волейбольных и баскетбольных мячей, затем прибавим число футбольных мячей. Запишем: к сумме чисел три и пять прибавить четыре, получится двенадцать.

Второй способ решения.

Прибавим к числу волейбольных мячей сумму баскетбольных и футбольных мячей. Запишем: к трем прибавить сумму чисел пять и четыре равно двенадцать.

В обоих случаях получили одинаковый результат, значит, выражения равны между собой. Можем записать так: (3+5)+4=3+(5+4)

Теперь ты знаешь еще одно свойство сложения: результат сложения не изменится, если соседние слагаемые заменить их суммой. Это свойство называется сочетательным свойством сложения.

Знание этих двух свойств сложения позволит нам решать примеры на сложение удобным способом.

Решим выражение: 1+7+9+3=?

Мы знаем, что слагаемые можно менять местами и соседние слагаемые заменять их суммой. Воспользуемся свойствами сложения и найдем сумму.

В данном случае удобно сложить попарно 1 и 9, 7 и 3. А затем сложить полученные результаты. Получим 20.

Делаем вывод: используя переместительное и сочетательное свойства сложения можно складывать числа в любом порядке, как удобнее.

1. Вычислите суммы удобным способом

30 + 3 + 7 + 40 = _________ 4 + 10 + 6 + 70=_______________

1. 30 + 3 + 7 + 40 = (3+7)+(30+40)=80 2. 4 + 10 + 6 + 70= (10+70)+(4+6)

2. Совместите название математического свойства с его значением и выражением

Результат сложения не изменится, если соседние слагаемые заменить их суммой.

Слагаемые можно переставлять местами, при этом значение суммы не изменится.

Результат сложения не изменится, если соседние слагаемые заменить их суммой.

Слагаемые можно переставлять местами, при этом значение суммы не изменится.

Источник

Математика 2 класс «Слагаемые,Сумма»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

image001

Открытый урок в МАОУ «СОШ №24» г. Пермь
Тема: Слагаемые. Сумма.

Цель: создать условия для ознакомления с математическими терминами «слагаемые», «сумма», использования этих терминов при чтении равенств.

1. познакомить с названием компонентов и результата в действии сложения;

2. учить устанавливать взаимосвязь между изменением компонентов и результатами действия сложения;

3. развивать навыки счета.

1. Организационный момент

— Посмотрите, друг другу в глаза, улыбнитесь, пожелайте удачи, хорошего настроения

— Какой у нас урок?
— А вы знаете, что математику называют царицей наук. Как вы думаете, почему? (Ответы детей)

— Нет такой профессии, где бы ни применялись знания по математике.

— Сегодня на уроке проверим ваши знания по математике: знаете ли вы цифры, умеете ли вы считать и решать задачи. Познакомимся с новыми математическими терминами.

1. Игра «Где мое место?»

(К доске вызываются 10 учащихся, каждый из которых получает карточку с числами от 7 до 20 (Дети строятся по порядку номеров у доски).

— Правильно ли построились ребята?
— Назовите соседей числа 12.
— Назовите предыдущее число по отношению к числу 8.
— Назовите следующее число числа 10.
— А теперь постройтесь, начиная с самого большого.
(Дети построились)
— Кто стоит перед Машей? Кто находится между Никитой и Тимофеем? Кто за Яной?
Кто стоит последним?

2. «Потерялось» число. Найдите его место в ряду чисел:

1 2 3 4 5 7 8 9 10

3. Минутка чистописания: 6.
Дети прописывают цифру в воздухе, а затем – в тетрадях.

1 ученик записывает выражения у доски, остальные – в тетрадях.

1) Дружно муравьи живут
И без дела не снуют.
5 несут травинку,
2 несут иголки. Сколько их под ёлкой? (7)

2) Ну-ка, сколько всех ребят
На горе катается?
Трое в саночках сидят,
Двое дожидаются. (5)

3) У котёнка 6 игрушек,
Две хозяйка принесла.
Вы игрушечки все эти
Сосчитайте скорей, дети. (8)
На доске: 15+2=17, 13+2=15, 6+12=18.
— Проверьте выражения. Прочитайте их по-разному.

— Эту запись ещё можно прочитать, используя математические термины. Прочитайте (ответа нет).

— Почему не получается? (Не хватает знаний)

— Значит, какая цель урока? (Познакомиться с новыми математическими терминами, узнать, как по-новому прочитать числовое равенство.)

— Верно, будучи внимательными на уроке в конце – вы сможете обязательно прочесть это числовое равенство.

3.Изучение нового материала.

Работа по учебнику.

Стр.86 (работа с рисунком)

– Сколько красных кубиков у девочки?image002
— Сколько синих кубиков у мальчика?
— Сколько всего?
— Как получили число 5?
— Какие 2 числа мы прибавили?
— Они тоже имеют свои имена. Числа, которые складывали, называются слагаемыми. Назовите первое слагаемое.
— Назовите второе слагаемое.
— В результате сложения мы получили сумму. Сумма сложения равна 5. Слева тоже записана сумма. Это сумма – выражение. А справа сумма – результат. Сумма чисел 3 и 2 равна 5.

Числа, которые складываются, называются слагаемыми, а результат сложения называется суммой.

1. (Вывешиваю таблицу)

Название чисел при сложении

image003

2. Чтение равенств с использованием новых терминов.

Упражнения в чтении примеров с использованием терминов «слагаемое», «сумма».

Например: первое слагаемое – 4, второе слагаемое – 2, сумма равна 6. Сумма чисел 5 и 2 равна 7.

Отработка с учащимися использования терминов «первое слагаемое», «второе слагаемое», «сумма чисел» проводится по заданию 1 (с. 86 учебника, часть 1).

3. Формирование навыков счета

Ученики выполняют с комментированием задание 2 (с. 86 учебника).

Дети при комментировании читают выражения по-разному. Например: «Первое слагаемое – один, второе слагаемое – один, значение суммы – два. Сумма чисел два и один равна трём. Два увеличить на два получится четыре. К трём прибавить один получится четыре». И т. д.

— Можно ли примеры на вычитание читать, используя слова «слагаемое», «сумма»? (Нет.)

Мы опять сидеть устали,

На зарядку дружно встали.

Руки в боки, смотрим вправо.

Поворот налево плавный (повороты корпуса в стороны)

Поднимем мы колени,

Занимаемся без лени.

Поднимаем их повыше.

Может быть, коснёмся крыши?

( По очереди поднимать ноги, согнутые в коленях)

Наклоняемся до пола,

Вправо-влево три наклона.

Повторяем снова дружно.

(Наклоны вперёд-назад, вправо-влево).

От души мы потянулись

(Потягивания – руки вверх и в стороны)

И за парты вновь вернулись. ( Дети садятся за парты).

— Пока вы делали зарядку, намело большой сугроб. Что это за обозначения на нем?

image004

— Что такое условие? Вопрос?

Один из учащихся читает задачу 3 (с. 87 учебника).

– О чем прочитанный рассказ? Что в рассказе известно? (Известно, что у Васи было 6 книг и ему подарили ещё 2 книги.)

– Что нужно узнать? (Сколько книг стало у Васи.)

– Какое арифметическое действие следует выполнить, чтобы ответить на поставленный вопрос? (Сложение.) Почему так считаете? (Потому что книг у Васи стало больше.)

Далее ученики записывают с комментированием решение задачи: 6 + 2 = 8 (кн.).

Аналогично разбирается задача 4 (с. 87 учебника).

5. Закрепление нового материала

— Белочке отдаём выражения, у которых сумма равна 7. Зайчику отдаем выражения, у которых слагаемое равно 2, а ёжику отдаём остальные выражения.

6. Самостоятельная работа

У каждого ученика карточка. Стрелочками надо соединить с названием компонента. Как называется пропущенное число: сумма или слагаемое?

7. Итоги урока. Рефлексия.

-Какие математические термины вы сегодня вспомнили? (слагаемые, сумма)

-Что называется слагаемым? (числа, которые складываем)

-Что называем суммой? (ответ и выражение)

— Ребята, давайте оценим свою работу. Кому на уроке было комфортно, всё понятно, получили новые знания- рисуем улыбающееся солнышко;

— кому не совсем понятно, кто затруднялся- солнышко, но оно не улыбается

— кому трудно было на уроке- тучку.

Учитель подводит итог урока, раздаёт детям улыбающиеся смайлики, а на обратной стороне смайлика написаны термины: слагаемое, слагаемое, сумма.

Самоанализ урока математики в 2 классе.

Представленный урок – урок повторение изученной темы и закрепление ранее изученного материала, на котором дети ставят перед собой цель, задачи. Повторить предыдущие темы способствует работа в парах, технология оценивания своих действий. В конце урока – рефлексивная оценка собственной деятельности учащихся.

Свой урок я строила в соответствии ФГОС. Данный урок представлен по ходу изучения раздела «Сложение и вычитание». На уроке были учтены возрастные и психологические особенности детей. В содержание урока включила элементы обучения школьников универсальным учебным действиям: цель урока определили ученики самостоятельно.

На всех этапах урока ученики были вовлечены в активную мыслительную и практическую деятельность исследовательского характера, обучающимся надо было не только использовать уже имеющиеся знания, но и найти новый способ выполнения уже известного им действия.

Этапы урока тесно взаимосвязаны между собой, чередовались различные виды деятельности. Умственные действия опирались и подкреплялись практическими. Учебный материал на протяжении всего урока работал на организацию посильного поиска и исследования первоклассников.

Для каждого ученика была создана ситуация успеха, что также способствовало повышению уровня мотивации и поддержанию познавательного интереса к учению.

Учебный материал урока соответствовал принципу научности, доступности и был посилен для учеников первого класса. Учебная информация была увлекательна для учеников. За счет привлекательности содержания заданий и подачи учебного материала, повысилась возможность учеников в достижении поставленных целей на уроке.

Учебное время на уроке использовалось эффективно, запланированный объем урока выполнен. Цель урока достигнута.

image005

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Источник

Источник

Содержание

  1. Сумма и разность чисел
  2. Что такое сумма, и как ее найти
  3. Как найти разность чисел
  4. 1-й класс Математика. «Сумма и значение суммы»
  5. Числовые и буквенные выражения
  6. Числовые выражения: что это
  7. Буквенные выражения
  8. Выражения с переменными
  9. Что такое сумма чисел
  10. Определение суммы чисел
  11. Свойства суммы чисел

Сумма и разность чисел

Что такое сумма, и как ее найти

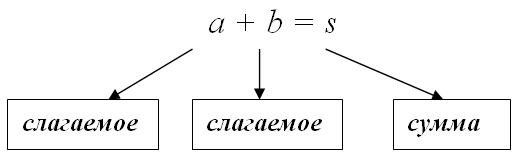
Сумма – это результат складывания двух чисел (слагаемых), между которыми стоит знак +. Чтобы получить сумму, нужно к одному слагаемому прибавить второе слагаемое. В общем виде пример можно показать так: a + b = s, где а – первое слагаемое, b – второе слагаемое, а s – результат сложения этих двух слагаемых. При этом нужно знать, что от перестановки слагаемых сумма не меняется, — это одно из самых первых правил в математике, которое проходят в начальной школе.

Чтобы наглядно показать ребенку, как сложить числа, возьмите конфеты или любые другие вещи. Покажите ребенку две конфеты, а затем прибавьте к этим конфетам еще две. Пусть ребенок посчитает и скажет, что теперь конфет оказалось четыре. Объясните ему, что он только что сложил эти числа, то есть прибавил к одному числу другое число и в конечном итоге получил сумму.

Немного сложнее объяснить сложение разрядных слагаемых, эта тема может быть непонятна ребенку. Итак, существует множество разрядов: единицы, десятки, тысячи. Возьмите, к примеру, число 2564. Если разложить его на разряды, то получится: 2564 = 2000 + 500 + 60 + 4. Чтобы прибавить к этому числу, например, число 305, воспользуйтесь сложением в столбик. При таком сложении нужно прибавлять одни разряды к другим, начиная с конца: единицы к единицам, десятки к десяткам, тысячи к тысячам. То есть, для начала складываем 4 и 5, затем 6 и 0, после 5 и 3, и в конце 2 и 0. В конечном итоге получаем число 2869.

Как найти разность чисел

Разность – результат вычитания одного числа из другого. В отличие от суммы, здесь мы не можем воспользоваться правилом «от перестановки слагаемых разность не меняется», так как в вычитании всегда есть уменьшаемое и вычитаемое. Чтобы найти вычитаемое и разность, для начала нужно разобраться с этими понятиями. Уменьшаемое – это то, из чего мы «вычитаем», то есть убираем, а вычитаемое – количество того, что мы у этого уменьшаемого вернем.

В общем виде вычитание можно записать так: a — b = r.
Обратимся к тем же конфетам, с которыми мы разбирали сумму чисел. Чтобы помочь ребенку найти разность чисел, возьмите пять конфет. Пусть ребенок посчитает и убедится, что их пять. Затем заберите себе три конфеты. Ребенок скажет, что их осталось две. А сколько тогда забрали? Три.

А что касается разрядных слагаемых, то здесь мы делаем то же самое, что и с суммой, только теперь не прибавляем, а вычитаем. Возьмем число 6845 и вычтем из него 4231. Для этого мы вычитаем один разряд из другого разряда, производя вычитание с конца: 5-1 = 4, 4-3 = 1, 8-2 = 6, 6-4 = 2. В ответе получим 2614.

Источник

1-й класс Математика. «Сумма и значение суммы»

Цели:

  • Познакомить и формировать умение пользоваться математическими терминами » сумма», » значение суммы». Совершенствовать вычислительные навыки.

  • Развивать умения сравнивать , анализировать, обобщать. Развивать математическую речь, интерес к математике.
  • Воспитывать самостоятельность, дисциплинированность, умение работать в коллективе.

    • Оборудование: Мел, доска, карточки, мультимедийная установка, презентация.

    1. Организация класса на урок.

    2. Сообщение темы и целей урока:

    Сегодня на уроке мы будем открывать и раскрывать тайны математики. Итак, в путь!

    3. Знакомство с новым материалом.

    Ребята, а вы любите сказки? А сказки Уолта Диснея? Сейчас я зачитаю отрывок из сказки, а вы попробуйте догадаться о ком идет речь.

    Просыпайся, друг Филин!- весело крикнул зайчонок Толстячок.- Новый принц родился!

    Радостная весть мгновенно облетела лес, и все лесные жители спешили посмотреть на новорожденного олененка. Они умилялись, глядя на то, как он пытается встать. Его ножки были еще слишком слабыми, и он все время падал.

    Кто его узнал? Это, действительно, олененок по имени Бемби. И вот однажды наступило время познакомить его с лесом Из сказки мы с вами знаем, что Бемби любознательный, поэтому он приходил в восторг от всего, что видел вокруг.

    Давайте мы с вами отправимся с олененком в необычный «лес-математики».

    Олененок попадает на полянку и видит множество цветов. Но присмотревшись поближе , он замечает, что цветы хранят в себе какую-то тайну.

    Помогите ему разгадать эту тайну.

    Посмотрите и скажите, что вы видите? Какие всевозможные математические записи мы можем составить?

    Источник

    Числовые и буквенные выражения

    О чем эта статья:

    Статья находится на проверке у методистов Skysmart.
    Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

    Числовые выражения: что это

    Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.

    Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.

    Например:

    • 23 + 5 = 28
    • 5 — 2 = 3
    • 52 * 3 = 156
    • 28 : 7 = 4

    Это простые числовые выражения.

    Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:

    • (5 * 3) — (5 * 2) = 5
    • 6 : (7 — 4) = 2
    • (45 + 45) : 9 = 10
    • 11 * (5 * 5) = 275

    Это сложные числовые выражения.

    Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».

    Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.

    Вспомним, какие виды арифметических действий есть.
    + — знак сложения, найти сумму.
    — — знак вычитания, найти разность.
    * — знак умножения, найти произведение.
    : — знак деления, найти частное.

    11 — значение числового выражения.
    6 * 8 = 48
    48 — значение числового выражения.

    При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:

    • Сначала выполняется действие, записанное в скобках.
    • Затем выполняется деление/умножение.
    • В последнюю очередь выполняется сложение/вычитание.

    Пример 1. Найдите значение числового выражения: 3 * (2 + 8) — 4

    Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)

    (6 + 7) * (13 + 2) = 195

    Часто бывает нужно сравнить два числовых выражения.

    Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.

    Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2

      Сначала находим значение первого выражения:

    6 + 8 = 14

    Затем находим значение второго выражения:

    2 * 2 = 4

    Сравниваем получившиеся результаты:

    14 больше 4
    14 > 4
    6 + 8 > 2 * 2

    Пример 2. Сравните следующие числовые выражения:
    5 * (12 — 2) — 7 и (115 + 9) — (7 — 3)

      Находим значение первого выражения, соблюдая порядок выполнения арифметических действий:

    12 — 2 = 10
    5 * 10 = 50
    50 — 7 = 43
    5 * (12 — 2) — 7 = 43

    Затем находим значение:

    115 + 9 = 124
    7 — 3 = 4
    124 — 4 = 120

    Сравниваем полученные результаты:

    43 меньше 120
    43

    Буквенные выражения

    Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.

    В буквенном выражение есть цифры, знаки арифметических действия и буквы.

    Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.

    Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.

    У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:

    • Сначала следует прочитать его полностью.
    • Затем оно записывается.
    • Третьим шагом идет подстановка значения неизвестного в выражение.
    • А затем производится вычисление, согласно очередности выполнения арифметических действий.

    Пример 1. Найдите значение выражения: 5 + x.

    1. Читаем: найдите сумму числа 5 и x.
    2. Подставляем вместо неизвестного x число 4.
    3. Вычисляем: 5 + 4 = 9.

    Пример 2. Найдите значение выражения: (4 + a) * (2 + x).

    1. Читаем: найдите произведение суммы числа 4 и а и суммы числа 2 и x.
    2. Подставляем вместо неизвестного a число 2.
    3. Вычисляем 4 + 2 = 6.
    4. Подставляем вместо неизвестного x число 5.
    5. Вычисляем 2 + 5 = 10.
    6. Находим произведение 6 * 10 = 60.
    7. Записываем результат: (4 + 2) * (2 + 5) = 60.

    Выражения с переменными

    Переменная — это значение буквы в буквенном выражении.

    • Например, в выражении x + a — 8
      x — переменная
      a — переменная

    Если вместо переменных подставить числа, то буквенное выражение x + a — 8 станет числовым выражением. Вот так:

    • подставляем вместо переменной x число 5, а вместо переменной a — число 10, получаем 5 + 10 — 8.

    Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.

    После подстановки значения переменных находим значение x + a — 8 = 5 + 10 — 8 = 7.

    Часто можно встретить буквенные выражения, записанные следующим образом:
    5x — 4a

    Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.

    5x — это произведение числа 5 и переменной x
    4a — это произведение числа 4 и переменной a

    Числа 4 и 5 называют коэффициентами.
    Коэффициент показывает, во сколько раз будет увеличена переменная.

    Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.

    Задание раз.

    1. Сумма 6 и a.
    2. Разность 8 и x.
    3. Сумма x — 2 и 6
    4. Разность 15 и x — y
    5. Сумма 45 + 5 и 12 — 6

    Задание два.

    Составьте буквенное выражение:

    Сумма разности b и 345 и суммы 180 и x.

    Ответ: (b — 345) + (180 + x).

    Задание три.
    Составьте буквенное выражение:
    Разность разности 30 и y и разности a и b.
    Ответ: (30 — y) — (a — b).

    Задание четыре.
    Составьте выражение для решения задачи и найдите его значение.
    Ролл «Калифорния» стоит 480 рублей — это на 40 рублей меньше, чем ролл «Филадельфия». Сколько будут стоить оба ролла?
    Как решаем:
    Калифорния — 480 рублей.
    Филадельфия — 480 + 40.
    Калифорния + Филадельфия = ?
    480 + (480 + 40).
    Мы помним, что выполнение арифметических действий в числовом выражении имеет строгую последовательность. Сначала — действие в скобках:
    480 + 520 = 1 000.

    Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.

    Задание пять.
    Составьте выражение для решения задачи и найдите его значение.
    Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?

    Маша — 150 видео.
    Лена — 150 + 13 видео.
    Маша + Лена = ? видео.

    150 + (150 + 13)
    Выполняем сначала действие в скобках: 150 + 13 = 163.
    150 + 163 = 313.

    Ответ: Маша и Лена посмотрели всего 313 видео.

    Задание шесть.
    Вычислите:
    (500 + 300) : a — 15,
    при условии, что a = 10.

    Подставляем число 10 (значение переменной) вместо переменной
    (500 + 300) : 10 — 15

    Затем выполняем сначала арифметическое действие в скобках: 500 + 300 = 800.
    Затем выполняем деление 800 : 10 = 80.
    Выполняем вычитание 80 — 15 = 65.

    Ответ: (500 + 300) : 10 — 15 = 65.

    Задание семь.
    Вычислите:
    (270 — 120) * (x — 10),
    при условии, что x = 45.

    Как решаем: подставляем число 45 (значение переменной) вместо переменной x
    (270 — 120) * (45 — 10).

    Затем выполняем сначала арифметическое действие в скобках: 270 — 120 = 150.
    Выполняем арифметическое действие во вторых скобках: 45 — 10 = 35.
    Затем выполняем умножение 150 * 35 = 5 250

    Ответ: (270 — 120) * (45 — 10) = 5 250.

    Задание восемь.
    Вычислите:
    (50 * x) — (3 * y)
    при условии, что x = 2; y = 10

    Подставляем число 2 вместо переменной x
    (50 * 2) — (3 * y).

    Подставляем число 10 вместо переменной y
    (50 * 2) — (3 * 10).

    Затем выполняем сначала арифметическое действие в скобках: 50 * 2 = 100.
    Выполняем арифметическое действие во вторых скобках: 3 * 10 = 30.
    Затем выполняем вычитание 100 — 30 = 70

    Источник

    Что такое сумма чисел

    Определение суммы чисел

    Суммой $s$ (лат. summa — итог, общее количество) чисел $a_<1>, a_<2>, dots, a_$ называется результат суммирования этих чисел: $s=a_<1>+a_<2>+ldots+a_$ . В частности, если складывается два числа $a$ и $b$, то

    Задание. Найти сумму чисел:

    1) $12$ и $15$ 2) $1,1 ; 2,2 ; 3,3$ и $4,4$

    Ответ.

    Свойства суммы чисел

    На основании этих свойств можем заключить, что от перестановки мест слагаемых сумма не изменяется.

    Дистрибутивность по отношению к умножению

    $$(n+m) cdot k=n cdot k+m cdot k$$

    Что такое сумма чисел не по зубам? Тебе ответит эксперт через 10 минут!

    Задание. Найти сумму чисел удобным способом:

    1) $15+17+13$ ; 2) $34+22+16+18$

    Решение. По свойствам сложения имеем

    Ответ. 1) $15+17+13=45$

    При сложении больших чисел или десятичных дробей используется сложение в столбик.

    Задание. Найти сумму чисел удобным способом:

    1) $1562+13827$ ; 2) $34,71+356,161$

    Решение. Складываем эти числа в столбик, для этого запишем их друг под другом, разряд под разрядом. В случае десятичных дробей ориентируемся на то, чтобы запятая первого числа стояла под запятой второго. Далее складываем числа стоящие друг под другом, двигаясь справа на лево и записывая результата под чертой дроби. Если сумма чисел в одном столбце превышает десять, то количество десятков прибавляем к числам стоящим в следующем столбце слева от этого столбца:

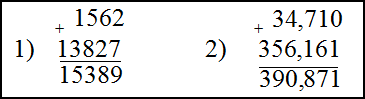
    Ответ. 1) $1562+13827=15389$

    Сложение рациональных дробей производится по правилу

    Задание. Найти сумму чисел:

    Решение. Вычислим первую сумму используя правило сложения рациональных чисел

    Числитель и знаменатель полученной дроби можно сократить на 2, тогда в ответе получим

    Для вычисления второй суммы, преобразуем сначала второе слагаемое в неправильную дробь, для этого умножим целую часть на знаменатель и прибавим полученное число к числителю. Далее применим правило сложение рациональных дробей

    Выделим в полученной дроби целую часть, для этого разделим числитель на знаменатель с остатком. Полученное частное запишем в целую часть, а остаток от деления в числитель.

    Источник

    Источник

    Математика

    6 класс

    Урок № 69

    Приближение суммы, разности, произведения и частного двух чисел

    Перечень рассматриваемых вопросов:

    – десятичная дробь, приближённое значение, округление;

    – значащая цифра десятичной дроби;

    – приближение суммы, разности, произведения и частного двух чисел.

    Тезаурус

    Округление десятичной дроби – замена десятичной дроби приближённым значением с меньшим количеством значащих цифр.

    Десятичная дробь – это дробь, записанная в десятичной форме.

    Значащая цифра десятичной дроби – это первая слева направо отличная от нуля цифра, а также все следующие за ней цифры.

    Список литературы

    Обязательная литература:

    1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

    Дополнительная литература:

    1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.

    2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

    Теоретический материал для самостоятельного изучения

    Зачастую необходимо быстро прикинуть результат, который получается при сложении, вычитании, умножении или делении двух десятичных дробей. Если дроби имеют много знаков после запятой, выполнить эти действия быстро довольно сложно. Для этого используют правила приближения суммы, разности, произведения и частного двух чисел.

    Сумма (разность, произведение, частное) двух чисел считается приближённо равной сумме (разности, произведению, частному) их приближений.

    Поясним на примере.

    1,45 + 2,32

    Округлим данные числа до десятых.

    1,45 ≈ 1,5

    2,32 ≈ 2,3

    Сложим приближённые значения дробей.

    1,5 + 2,3 = 3,8

    Проверим с исходными числами.

    1,45 + 2,32 = 3,77

    Округлим сумму до десятых.

    3,77 ≈ 3,8

    Получили тот же результат.

    Итак, чтобы вычислить приближённую сумму или разность двух чисел, надо округлить эти числа с одинаковой точностью, то есть до одного и того же разряда. Затем сложить или вычесть полученные приближения.

    Рассмотрим пример.

    23,184567 + 4,4486

    Округлим эти числа с точностью до одной сотой.

    23,184567 ≈ 23,18

    4,4486 ≈ 4,45

    Найдём сумму приближённых значений.

    23,18 + 4,45 = 27,63

    23,184567 + 4,4486 ≈ 27,63

    Теперь рассмотрим умножение и деление.

    Чтобы вычислить приближённое произведение или частное двух чисел, надо округлить эти числа с точностью до одной и той же значащей цифры, перемножить или разделить полученные приближения и результат округлить до той же значащей цифры.

    Пусть даны числа.

    246,76556 и 0,0078653

    Найдём их произведение и частное.

    Округлим числа до трёх значащих цифр.

    246,76556 ≈ 247

    0,0078653 ≈ 0,00787

    Вычислим произведение их приближений.

    247·0,00787 = 1,94389

    Округлим результат также до трёх значащих цифр.

    1,94389 ≈ 1,94

    Получаем, что

    246,76556 · 0,0078653 ≈ 1,94

    Вычислим частное приближений этих чисел и тоже округлим его до трёх значащих цифр.

    247 : 0,00787 = 31385,00635… ≈ 31400

    Получаем, что

    246,76556 : 0,0078653 ≈ 31400

    Точность вычислений находится в противоречии с простотой вычислений. Чем большим количеством цифр мы пользуемся, тем точнее наш результат.

    Пример

    Вычислить 2,26372.

    Для простоты вычислений округлим до одной значащей цифры.

    2,2637 ≈ 2

    Тогда 22 = 4.

    Округлим до двух значащих цифр.

    2,2637 ≈ 2,3

    Тогда 2,32 = 5,29

    Округлим до трёх значащих цифр.

    2,2637 ≈ 2,26

    2,262 = 5,1076

    Если же посчитать не приближённый, а реальный результат, то получается

    2,26372 = 5,12433769

    Видим, что наиболее приближённый к реальному результат дало нам округление до трёх значащих цифр. А самый далёкий от реального результат дало округление до одной значащей цифры.

    Разбор заданий тренировочного модуля

    Тип 1. Ввод с клавиатуры пропущенных элементов в тексте

    Вставьте вместо пропусков верные цифры.

    Задание. Вычислите приближённое значение произведения, округлив множители до двух значащих цифр.

    2,465·1,923 ≈ …

    Решение

    Округлим множители до двух значащих цифр.

    2,465≈ 2,5

    1,923≈1,9

    Найдём произведение приближённых значений.

    2,5·1,9=4,75

    Округлим произведение также до двух значащих цифр.

    4,75≈4,8

    Ответ:2,465·1,923 ≈4,8.

    Тип 2. Подстановка элементов в пропуски в тексте

    Нахождение приближённого значения частного десятичных дробей

    Задание. Вставьте вместо пропуска цифру, чтобы получилось верное равенство.

    3,_781 : 0,00494 ≈ 3,6 : 0,0049

    Решение. При нахождении приближённого значения частного, числа были округлены до двух значащих цифр. В делимом третья значимая цифра 7, значит, при округлении ко второй цифре прибавили единицу. Получилось 6, значит, исходная цифра – это 5.

    Ответ: 3,5781 : 0,00494 ≈ 3,6 : 0,0049

    Тип 3. Добавление подписей к изображениям

    Нахождение приближённого значения произведения и частного десятичных дробей

    Задание. Округлив числа a и b с точностью до двух значащих цифр, найдите и впишите результаты действий.

    a = 191,452; b = 0,004868

    a : b =

    a · b =

    Решение

    Округлим числа до двух значащих цифр.

    191,452 ≈ 190

    0,004868 ≈ 0,0049

    Найдём частное приближённых значений.

    190 : 0,0049 = 38775,5

    Округлим до двух значащих цифр.

    38775,5… ≈ 39000

    Найдём произведение приближённых значений.

    190 · 0,0049 = 0,931

    Округлим произведение также до двух значащих цифр.

    0,931 ≈ 0,93

    Ответ:

    a : b = 39000

    a · b = 0,93

    Источник

    Добавить комментарий