Как найти значение уклон i

Угол уклона в процентах и промилле

Уклон любой линии
на карте находим по формуле:

tgν
= h/d
= i, (1.8)

где
ν
– угол наклона линии к горизонту, в
градусах;

h
– разность отметок (превышение) концов
линии;

d
– горизонтальное проложение (проекция)
линии;

i
– уклон линии в тысячных долях.

Например,
найти уклон линии между точками S
и А (рис. 1.6). Уклон линии SА
определяем так:

h
= (H_A
– H_S)
= 141.3 – 151.1 = 9.8 м

d
= SA 
M = 3.8 x 100 = 380 м.

Здесь
SA
= 3,8 см,

М – знаменатель
масштаба, равный 100 м.

i
= tgν
= -9.8 
380 = – 0.026,

ν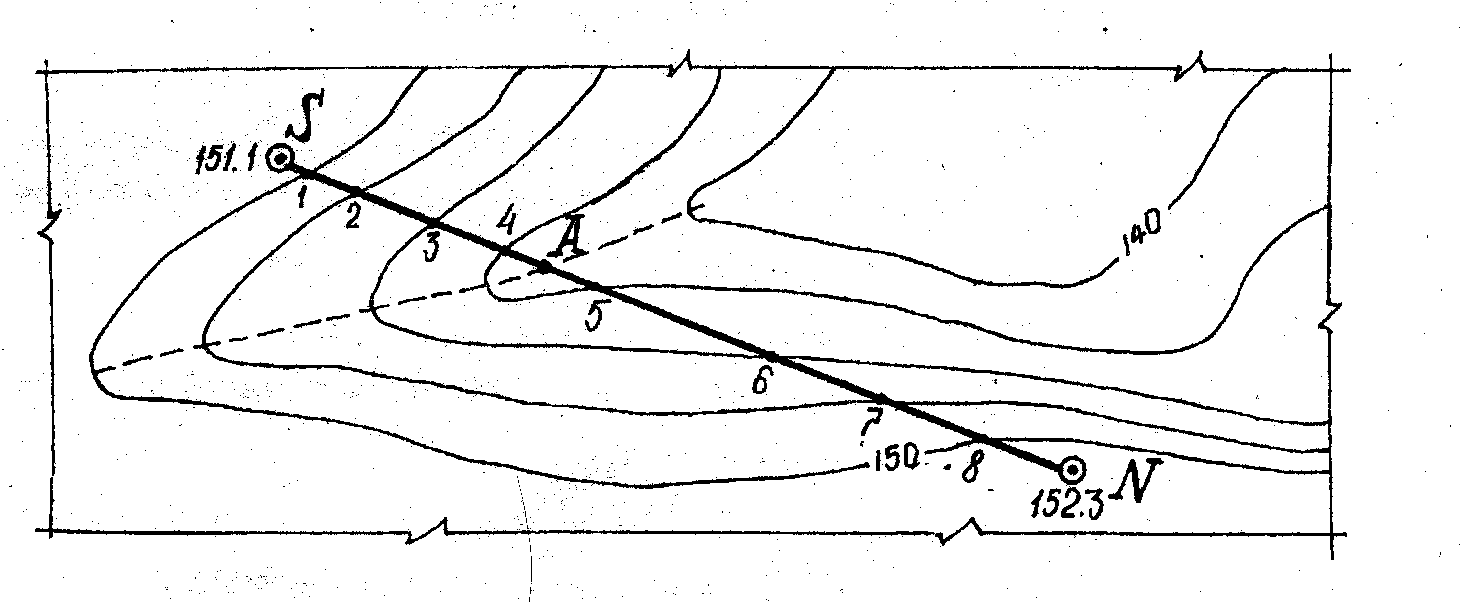
= 130.

Рисунок 1.6 –
Определение уклонов

1.5.7. Измерение угла наклона линии с помощью графиков «Масштаб заложения»

Графики
масштабов заложения (рис. 1.7а) строятся
по формулам, вытекающим из выражения
(1.8):

для
определения углов наклона: d
= h
/ tg
ν;
(1.9)

для
определения уклонов: d
= h/i.
(1.10)

Пользуясь
циркулем-измерителем, по построенным
графикам масштабов заложений находят
искомые ν
и i
для отрезков заданной линии SN

(рис. 1.7б).

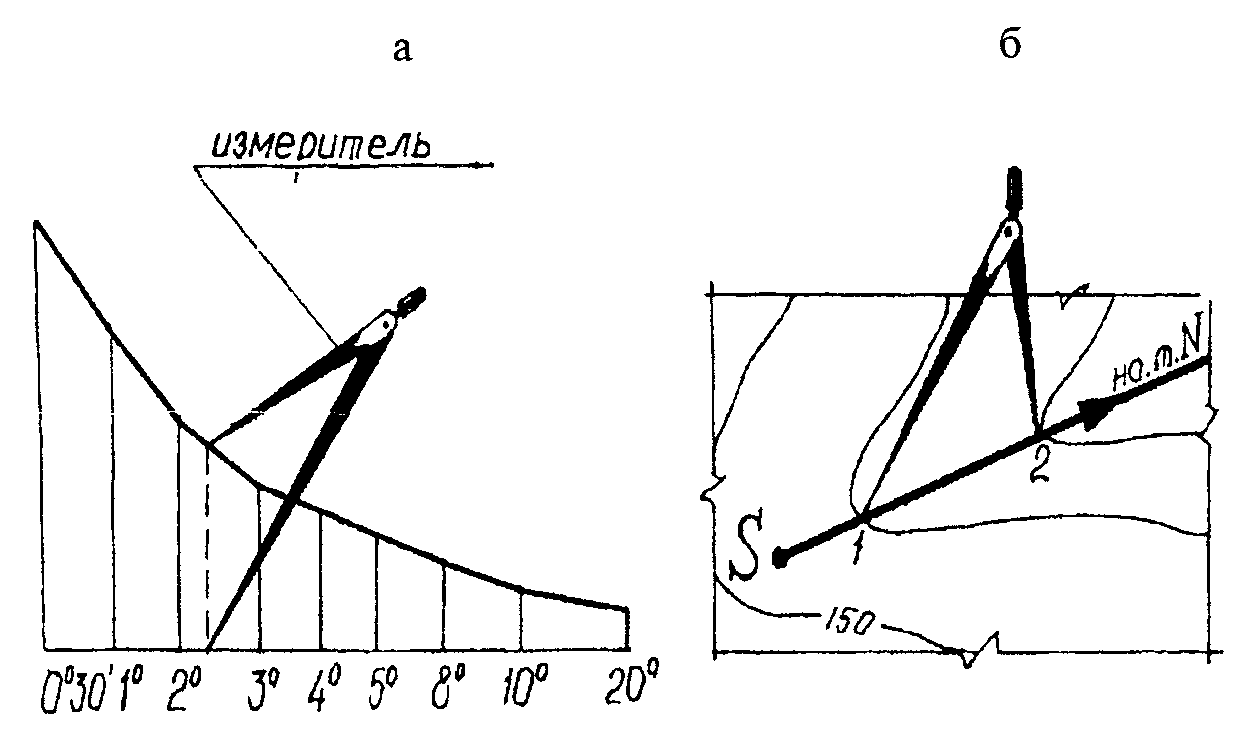
Рисунок
1.7 – Определение уклонов с помощью
графика масштаба заложения

1.5.8. Построение профиля местности

Профиль
местности (рис. 1.8) строят на миллиметровой
бумаге по заданной линии SN
в такой последовательности:

• к
  заданной профильной линии SN
  прикладывают лист миллиметровой бумаги
  и переносят на её край короткими
  черточками места пересечения горизонталей
  с профильной линией (выходы горизонталей);

• на
  листе миллиметровой бумаги слева у
  горизонтальных линий подписывают
  высоты, соответствующие высотам
  горизонталей на карте, приняв условно
  промежутки между этими линиями за
  высоту сечения;

• от
  всех черточек (выходов горизонталей)
  опускают перпендикуляры до пересечения
  их с соответствующими по отметкам
  параллельными линиями и отмечают
  полученные точки пересечения;

• соединяют
  точки пересечения плавной кривой,
  которая и изображает профиль местности.

Длины
отрезков S
– 1, 1 – 2 и т.д. измеряют по линейному
масштабу и подписывают под профилем
(рис. 1.8).

Вертикальный
масштаб (шкала высот) принимается в
десять раз крупнее горизонтального.

Отметку условного горизонта вычисляют
по формуле

УГ = Но – К 
М, (1.11)

где Но – минимальная отметка точки на
линии профиля, округлённая до значения,
кратного знаменателю вертикального
масштаба;

М – знаменатель вертикального масштаба
(м);

К – коэффициент, принимаемый равным 5
– 7.

Измеренные
и вычисленные значения отметок Н,
превышений h,
горизонтальных проложений d,
уклонов i
и углов наклона ν
для всех отрезков заданной профильной
линии SN
заносят в таблицу 1.2.

Таблица
1.2 – Расчет элементов продольного
профиля местности

№№ точек	Отметка точки Н, м	Расстояние между горизонталями, h, м	Горизонтальное проложение, d, м	Уклон i= h/d	Угол наклона, ν, 
S
1
2
…..
N

Р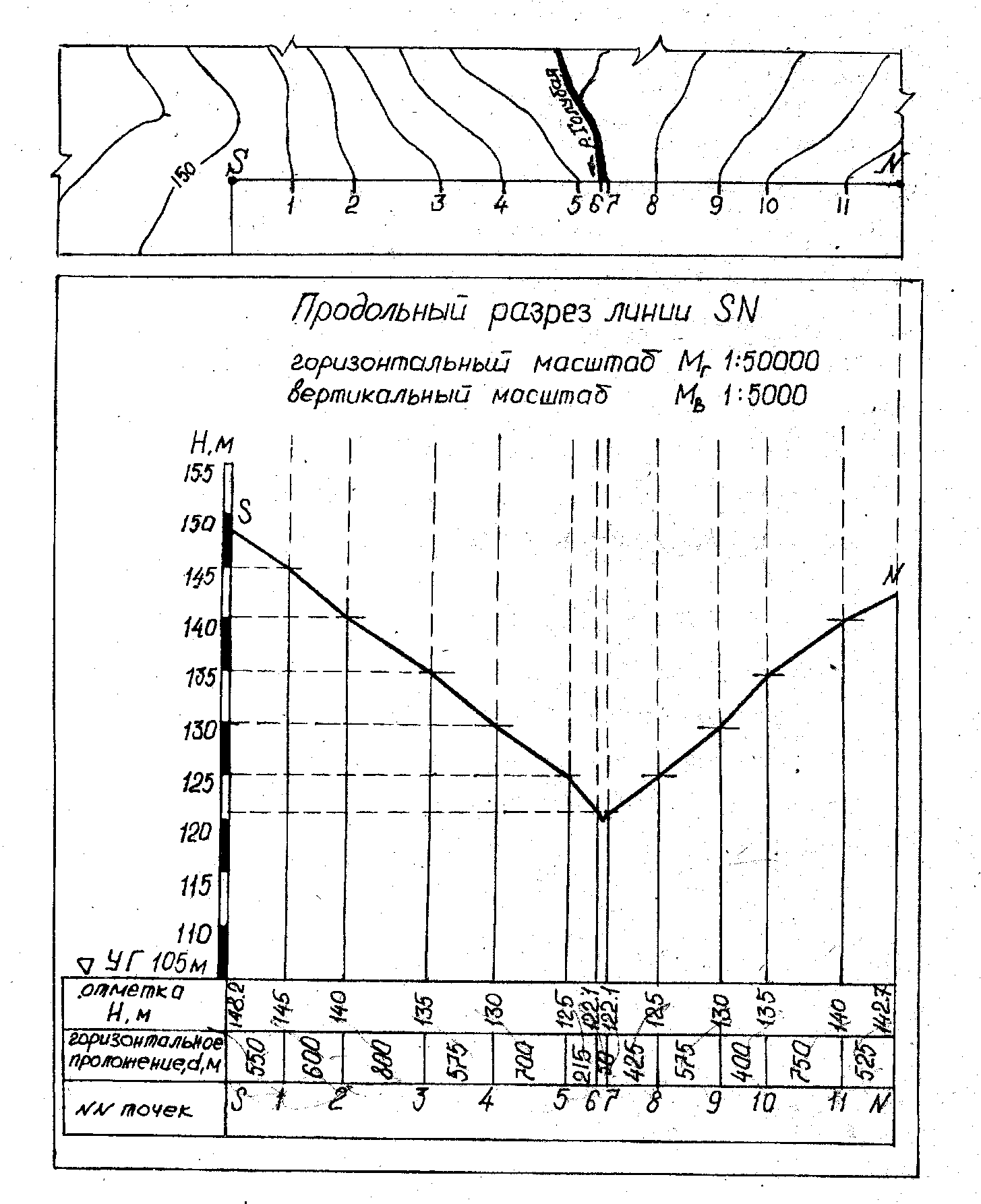исунок
1.8 – Продольный профиль местности

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Калькулятор уклонов

Чтобы посчитать уклон кровли, крыши, трубопровода, пандуса, лестницы, дороги, реки и т.п. воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Посчитать уклон

Посчитать превышение

Посчитать расстояние

Просто введите значения и выберите единицы измерения уклона.

Теория

Как посчитать уклон

Как посчитать превышение

Как посчитать расстояние

См. также

Что означает уклон в процентах, и как перевести его в градусы

Когда идет речь о кровле зданий, то под словом «уклон» подразумевают угол наклона оболочки крыши к горизонту. В геодезии данный параметр является показателем крутизны склона, а в проектной документации это степень отклонения прямых элементов от базовой линий. Уклон в градусах не вызывает ни у кого вопросов, а вот уклон в процентах порой вызывает замешательство. Пришла пора разобраться с этой единицей измерения, чтобы четко представлять себе, что это такое и, если потребуется, без особого труда переводить ее в другие единицы, например в те же градусы.

Расчет уклона в процентах

Попробуйте представить прямоугольный треугольник АВС, лежащей на одном из своих катетов АВ. Второй катет ВС будет направлен вертикально вверх, а гипотенуза АС образует с нижним катетом некий угол. Теперь нам предстоит немножко вспомнить тригонометрию и рассчитать его тангенс, который как раз и будет характеризовать уклон, образуемый гипотенузой треугольника с нижним катетом. Предположим, что катет АВ = 100 мм, а высота ВС = 36,4 мм. Тогда тангенс нашего угла будет равен 0,364, что по таблицам соответствует 20˚. Чему же тогда будет равен уклон в процентах? Чтоб перевести полученное значение в эти единицы измерения, мы просто умножаем значение тангенса на 100 и получаем 36,4%.

Как понимать угол уклона в процентах?

Если дорожный знак показывает 12%, то это означает, что на каждом километре такого подъема или спуска дорога будет подыматься (опускаться) на 120 метров. Чтобы перевести процентное значение в градусы, нужно попросту вычислить арктангенс этого значения и при необходимости перевести его из радиан в привычные градусы. То же самое касается и строительных чертежей. Если, к примеру, указывается, что угол уклона в процентах равен 1, то это означает, что соотношение одного катета к другому равно 0,01.

Почему не в градусах?

Многих наверняка интересует вопрос: «Зачем для уклона использовать еще какие-то проценты?» Действительно, почему бы просто не обойтись одними градусами. Дело в том, что при любых измерениях всегда имеет место некоторая погрешность. Если в проектной документации станут применять градусы, то неминуемо возникнут сложности с монтажом. Взять хотя бы ту же канализационную трубу. Погрешность в несколько градусов при длине в 4-5 метров может увести ее совершенно в другую от нужного положения сторону. Поэтому в инструкциях, рекомендациях и проектной документации обычно применяются проценты.

Применение на практике

Предположим, что проект строительства загородного дома предполагает устройство скатной кровли. Требуется проверить ее уклон в процентах и градусах, если известно, что высота конька составляет 3.45 метра, а ширина будущего жилища равна 10 метрам. Так как спереди крыша представляет собой равносторонний треугольник, то ее можно разделить на два прямоугольных треугольника, в которых высота конька будет являться одним из катетов. Второй катет находим, разделив ширину дома пополам.

Источник

Что значит проценты уклона

Угол уклона — показатель наклона какой либо поверхности (дороги, крыши, пандуса, лестничного марша и пр.) относительно уровня горизонта.

Угловые размеры указывают на чертежах в градусах, минутах и секундах с обозначением единицы измерения (ГОСТ 2.307-2011 «Единая система конструкторской документации (ЕСКД). Нанесение размеров и предельных отклонений«).

В соответствии с ГОСТ Р 21.1101-2013 «Система проектной документации для строительства (СПДС). Основные требования к проектной и рабочей документации», на планах направление уклона плоскостей указывают стрелкой, над которой при необходимости проставляют числовое значение уклона в процентах или в виде отношения единицы высоты плоскости к соответствующей горизонтальной проекции. Допускается числовое значение уклона указывать в промилле или в виде десятичной дроби с точностью до третьего знака.

На разрезах, сечениях и схемах перед размерным числом, определяющим числовое значение уклона, наносят знак,

острый угол которого должен быть направлен в сторону уклона (кроме крутизны откосов насыпей и выемок). Обозначение уклона наносят непосредственно над линией контура или на полке линии-выноски.

Также вместо знака угла, на чертежах встречается и буквенное обозначение уклона ( i ).

В процентах обычно обозначают углы уклонов крыш, пандусов, лестничных маршей и т.п.

В промилле обозначают углы уклонов плоскостных сооружений — спортивные игровые площадки, поля, беговые дорожки, а также линейные сооружения — автомобильные и железные дороги.

Процент ( % ) — одна сотая доля.
Промилле ( ‰ ) — одна тысячная доля.

Например: уклон при высоте 0,2 метра и протяженностью по горизонтали 4 метра будет равен 5 % (читается как — пять сотых) или 50 ‰ (читается как — пятьдесят тысячных), это значение также будет соответствовать приблизительно — 3 о .

Часто спрашивают, что означает уклон, на пример 0,05 — это соотношение высоты к длине горизонтального участка (0,2 м / 4 м = 0,05 — см. чертеж 1), которое при необходимости можно перевести в проценты или промилле, смотря что требуется.

Для определение угла уклона в процентах (%) (см. чертеж 1) необходимо: 0,2 м / 4 м х 100 = 5 %.

Для определение угла уклона в промилле (‰) необходимо: 0,2 м / 4 м х 1000 = 50 ‰.

Ту же величину уклона можно обозначить и как соотношение высоты к длине горизонтального участка — 1:20 (4 / 0,2 = 20).

Если требуется определить протяженность горизонтального участка, зная величину уклона в процентах и его высоту из чертежей, необходимо — 0,2 м / (5 % / 100) = 4 м.

Чтобы определить высоту уклона, зная величину уклона в процентах и протяженность участка из чертежей, необходимо — 5 % / 100 х 4 м = 0,2 м.

Аналогичным образом вычисляются размеры для угла уклона выраженного в промилле, только вместо деления на 100, выполняется деление на 1000.

Примечание: для того чтобы ввести на компьютере символ промилле (‰), необходимо включить NumLock, нажать клавишу Alt и удерживая ее набрать на цифровом блоке клавиатуры 0137, отпустить клавишу Alt после чего появится символ ‰.

Если требуется определить уклон с точностью до 1 градуса, нужно: 0,2 м / 4 м = 0,05. Полученное число — 0,05 необходимо найти в таблице tg (тангенсов) для углов. Приближенное значение в таблице — 0,0524, будет соответствовать углу 3 о (см. таблицу).

Источник

Калькулятор уклонов

Онлайн калькулятор

Посчитать уклон

Расстояние L =
Превышение h =

Посчитать превышение

Уклон α =
Расстояние L =

Посчитать расстояние

Уклон α =
Превышение h =

Теория

Как посчитать уклон

Для того чтобы посчитать уклон вам, для начала, необходимо знать расстояние (L) и превышение (h). Далее следуйте формулам:

В процентах:

Уклон в % = h / L ⋅ 100

В промилле:

Уклон в ‰ = h / L ⋅ 1000

В градусах:

Уклон в ° = arctg ( h /_L)

Пример

Для примера рассчитаем уклон дороги в процентах: на дистанции в L = 500 м дорога поднимается на h = 30 м:

Уклон дороги = 30/500 ⋅ 100 = 6%

Как посчитать превышение

Чтобы вычислить превышение (h), надо знать расстояние (L) и уклон (в процентах, в промилле или в градусах).

Если уклон в процентах (%):

h = L ⋅ Уклон в % /₁₀₀

Если уклон в промилле (‰):

h = L ⋅ Уклон в ‰ /₁₀₀₀

Если уклон в градусах (°):

h = L ⋅ tg(α) , где α — уклон в градусах

Пример

Для примера найдём превышение h, если расстояние L= 5м, а угол уклона α=45°:

h = 5 ⋅ tg(45) = 5 ⋅ 1 = 5 м

Как посчитать расстояние

Для того чтобы посчитать расстояние (L) необходимо знать превышение (h) и уклон (в процентах, в промилле или в градусах).

Если уклон в процентах (%):

L = h / _{Уклон в %} ⋅ 100

Если уклон в промилле (‰):

L = h / _{Уклон в ‰} ⋅ 1000

Если уклон в градусах (°):

L = h / tg(α) , где α — уклон в градусах

Пример

Для примера посчитаем расстояние (L), которое потребуется железной дороге, чтобы подняться на (h =) 6 м при угле подъёма 30‰:

Источник

О чём говорят проценты на дорожном знаке?

Тему для публикации я подобрал буквально на дороге.

Собирался написать об этом знаке каждый раз как ездил в соседний город к тёще, но все как-то забывал по прибытии домой, хотя видел его довольно часто, ведь город находится на возвышенности и там они встречаются постоянно.

Откровенно говоря, о том, что значат знаки 1.13 «Крутой спуск» и 1.14 «Крутой подъем» учат в автошколе, но если Вы не водитель или просто спали на занятиях, а эти проценты у Вас каждый раз вызывают недоумение, то узнать о них будет очень даже полезно.

На самом деле, все предельно просто. Проценты — тангенс угла подъема умноженный на 100.

Получается, это значение, на которое поднимется Ваше транспортное средство относительно линии горизонта, преодолев 100 метров.

Можно справедливо отметить:

А на кой нам проценты, если можно записать значение в градусах?

И есть 2 причины не использовать градусы:

1. Дорога редко представляет собой ровную линию, обычно есть небольшие углубления или там бугорок, а там впадина и действительно правильнее будет указать, на какую высоту в итоге поднимется Ваше ТС, а не показывать градусы.

2. Это — более веская причина. По счастливой случайности, проценты также означают коэффициент сцепления шин с дорожным покрытием.

Таким образом, цифры на знаке показывают, при каком коэффициенте сцепления с дорогой, Ваше транспортное средство станет неуправляемым.

Нашёл эти коэффициенты и вынес в табличку, надеюсь, Вам пригодится 🙂

Источник

Что значит проценты уклона

Войти

Авторизуясь в LiveJournal с помощью стороннего сервиса вы принимаете условия Пользовательского соглашения LiveJournal

Уклоны. Теория

Что такое уклон

Если брать небольшие расстояния, то это же будет означать перепад в сантиметрах на один метр . Так, если уклон, например трубы, i=0,02 (т.е. 2%), то на один метр по горизонтали труба поднимется (опустится) на 2 сантиметра.

Дорожные знаки. Интересное

Как было сказано ранее, по одному из определений уклон это тангенс угла. С большим интересом узнал, что он равен коэффициенту сцепления. Вот тут и начинает прояснятся тайный смысл предупреждающих дорожных знаков 1.13 и 1.14 (крутой спуск / подъём).

Коэффициентом сцепления называется отношение двух сил – силы, необходимой для сдвига машины с заблокированными колесами, и силы тяжести, прижимающей машину к дороге. Так мы легко можем получить коэффициенты сцепления для сухого асфальта – 7000/10000 = 0,7, для грязной дороги – 3000/10000 = 0,3, и для льда – 1000/10000 = 0,1.
Например, автомобиль, стоящий на сухом асфальтированном уклоне с коэффициентом сцепления 0,7, начнет сползать вниз, если тангенс угла наклона при этом будет равен 70% (это уклон около 35 градусов, вряд ли вы когда-нибудь встретите такой). Но, кроме дорог, существуют улочки старых городов, особенно приморских, с углами наклона, существенно превышающими всевозможные нормативы. [2]

И в чём практическая ценность этой информации? Вот в чём: если на дворе гололёд, то на дороге с уклоном в 10% и более остановившаяся машина не удержится, будет скатываться.
К тому же, «при движении в сырую погоду вниз по асфальтированному уклону крутизной 20% эффективность торможения падает наполовину. И очень часто вам придется двигаться по мокрому льду с коэффициентом сцепления 0,1 и менее. А это значит, что вы должны внимательно отслеживать предупреждающие дорожные знаки 1.13 и 1.14. Их устанавливают, когда тангенс угла уклона приближается к 10%. Если вы пренебрежете этими знаками и остановитесь на подъеме, то в лучшем случае – не сможете сдвинуться с места. А уж если затормозите на спуске, машину может занести. Старайтесь тормозить двигателем на длительных спусках.» [2]
Вот о чём предупреждают знаки.

Кстати, есть знаки и меньше 10%, поэтому стало интересно в каких случаях их устанавливают.
ГОСТ Р 52289-2004 «Правила применения дорожных знаков, разметки, светофоров, дорожных ограждений и направляющих устройств», п. 5.2.16:
4% — если длина участка дороги на спуске или подъёме больше 600 метров при данном уклоне.
5% если больше 450 метров
6% если больше 350 метров
7% если больше 300 метров
8% (и более) если больше 270 метров.
Там же указаны и другие случаи, как например расстояние видимости, но сейчас они нас не интересуют.

Причины: почему проценты?

При рассмотрении темы уклонов всегда возникает вопрос, а почему уклон измеряют в процентах, а не в привычных градусах? По этому поводу слышал несколько версий:

а) Карты
Так проще вычислять уклон рельефа на карте или на строительном плане. Рельеф на картах обозначается линиями — горизонталями. Это замкнутая линия, которая получается если мысленно сделать сечение на какой-либо высоте и посмотреть сверху. Проще это представить если вспомнить линию уреза воды реки или водоёма, это тоже своего рода горизонталь.
Горизонтали, т.е. горизонтальные сечения, проводятся через определённое постоянное расстояние по высоте, о чём указывается в примечаниях. Зная высоту сечения горизонталей и определив на карте расстояние между ними можно получить уклон. Чем ближе друг к другу на карте изображены горизонтали, тем рельеф круче.

б) Погрешность
Построить угол, заданный в градусах, так сказать «в натуре» на строительной площадке, задача не из простых, а построить точно и вовсе запредельная. Небольшие величины уклона в градусах имеют вид десятичных дробей, а ведь погрешность даже в 1° на 10 метров длины даст ошибочные 17 сантиметров высоты. Так же, проценты величина относительная, и потому уклон, выраженный в процентах, можно построить имея в распоряжении только рулетку (или иной инструмент для измерения длинны) и уровень.

в) Неравномерность
Дорога, на протяжении всего спуска (подъёма), имеет неравномерный уклон. В каждый отдельный момент угол разный, и поэтому проще посчитать сколько составляет горизонтальная длинна участка спуска (подъёма), и на сколько изменилась высота относительно начала спуска (подъёма).

Все эти версии вполне имеют право на жизнь. Общим для них является то, что для нахождения величины уклона используются меры длинны, которые всегда есть под рукой, а это практично. Что касается дорожных знаков, то более правдоподобной выглядит третья версия (неравномерность уклона), а для строительства дорог вторая (погрешность построений).
Есть ещё Международная Конвенция о дорожных знаках и сигналах за 1968 год, и Европейское соглашение 1971 года, дополняющее эту Конвенцию, по которой на предупреждающих знаках крутизна уклонов и подъемов указывается в процентах. [3]

Что стоит за цифрами, например 1/12 или 10%, много это или мало, как это выглядит и где применяется, рассмотрим в следующий раз на примерах из жизни.

1. Словари и энциклопедии на Академике © Академик
2. Материалы сайта «Школа жизни» © Shkolazhizni.ru
3. Википедия © Wikipedia
—

1‰ = 0,1% = 1/1000 = 0,001
10‰ = 1% = 1/100 = 0,01
100% = 45º = 1/1
1º — 1,7 %
1 % — 34′ 20″ Внимание! Это верно только для одного первого процента (0-1), но не верно для последнего (99-100), так как размер процентов в градусном выражении не равномерен!

1/4 0,25 25% 14°
1/2 0,50 50% 26,6°
1/6 0,17 17% 9,5°
1/8 0,13 13% 7,1°
1/10 0,10 10% 5,7°
1/12 0,08 8% 4,8°
1/14 0,07 7% 4,1°
1/16 0,06 6% 3,6°
1/18 0,06 6% 3,2°
1/20 0,05 5% 2,9°

Вертикальная планировка
1. При уклонах местности до 1% здания можно располагать независимо от направления горизонталей.
2. При уклонах от 1 до 3% поперек горизонталей можно располагать здания длиной не более 50 м. Более длинные здания следует размещать вдоль горизонталей.
3. При уклоне от 3 до 5% (слабо пересеченный рельеф) поперек горизонталей можно располагать здания длиной до 30м.
4. При уклоне от 5 до 8% (пересеченный рельеф) все здания располагают параллельно горизонталям или применяют ступенчатые здания, понижая отметку 1-го этажа каждой секции или блока.
5. При уклоне более 8% (сильно пересеченный рельеф) применяют только террасную застройку.

Чтобы избежать возможного застоя поверхностных вод на территории микрорайона и особенно на внутриквартальных проездах, не следует делать горизонтальных площадок. Подчиняясь общей форме поверхности территории, отдельные элементы ее должны иметь свои нормативные уклоны:
• продольные уклоны внутриквартальных проездов делают от 0,4 до 8%. В случае очень сложного рельефа допускается уклон до 10%;
• Поперечные уклоны делают 2—4%;
• пешеходные дорожки и аллеи должны иметь уклон от 0,5 до 6%;
• хозяйственные площадки, детские площадки, площадки для отдыха — 0,5-5%;
• спортивные площадки — 0,5—1%. Такие площадки лучше приподнимать над прилегающей территорией и по периметру устраивать озелененные откосы. Это будет способствовать более быстрому просыханию площадок после дождя; площадки, отводимые под зеленые насаждения, могут оставаться в естественном состоянии.
http://tehlib.com/arhitektura/vertikal-naya-planirovka/
—
Согласно требованиям, продольный уклон водоотводных канав должен быть не менее 5‰, а в исключительных случаях — 3‰, что объясняется необходимостью обеспечения своевременного и быстрого отвода поверхностных вод.

Б.Ф. Перевозников А.А. Ильина «СООРУЖЕНИЯ СИСТЕМЫ ВОДООТВОДА С ПРОЕЗЖЕЙ ЧАСТИ АВТОМОБИЛЬНЫХ ДОРОГ»; Обзорная информация; Выпуск 2; Москва 2002
http://www.gosthelp.ru/text/ObzornayainformaciyaAvtom10.html

Часть вторая — техническая, про моделирование уклонов в 3D программах (ArchiCAD и SketchUp)
Часть третья — практическая, примеры из жизни

Источник