Как найти значение вектора комплексного числа

Сегодня мне хочется рассказать про комплексные числа. Я не хочу перегружать статью формулами, а буду вставлять побольше анимированных картинок.

Идея

В комплексных числах есть своя красота и своя фишка. Чтобы мотивировать вас дочитать до конца, я хочу очень поверхностно пересказать основную идею, в чем я вишу фишку комплексных чисел.

Итак, изначально у нас есть действительные числа. На действительных числах определены операции сложения и умножения.

Мы берем и расширяем действительную ось до комплексной плоскости. Т.е. мы говорим, что любая точка (вектор) на этой плоскости это и есть комплексное число.

Далее для этих чисел нам нужно заново ввести операции сложения и умножения. И мы их вводим.

Но вводим их таким образом, чтобы они не противоречили нашим предыдущим операциям для вещественных чисел. Так, чтобы сложение и умножение вещественных чисел было все лишь частным случаем сложения и умножения комплексных чисел.

Затем мы получаем неожиданное свойство, что умножение комплексных чисел выражается через умножение модулей и сложение углов. Т.е. умножение связано с операциями растяжения и вращения.

А затем мы начинаем разбирать примеры и проверяем некоторые тождества, которые нам уже были известны для действительных чисел. И мы видим, как эти старые известные нам свойства выражаются через новую операцию умножения и тем самым связаны с вращением!

Если я вас заинтриговал, то давайте начнем.

Введение

Если представить, что действительное число – это вектор в одномерном пространстве,

тогда комплексное число – это вектор на, так называемой, комплексной плоскости.

Где горизонтальная ось – это действительная ось, а вертикальная – мнимая. Координаты вдоль этих осей называются действительной и мнимой частью комплексного числа.

Мнимая единица – это вертикальный вектор единичной длины.

Любое комплексные число можно записать в виде

Здесь a – это действительная часть числа, а b – комплексная.

Две функции Re() и Im() используются для извлечения действительной и мнимой частей по отдельности.

Далее нам нужно вывести операции сложения и умножения. Для этого мы будем использовать обычную алгебру. Но мы представим, что i – это тоже какое-то число, значение которого нам как бы не известно. Про мнимую единицу нам известно только то, что её квадрат равен -1.

Эта свойство и есть определение мнимой единицы. Забегая вперед, скажу, что от этого свойства будет зависеть вид операции умножения.

Сложение комплексных чисел

Сложение комплексных чисел выражается формулой

По сути, мы складываем отдельно действительную и мнимую части.

Это аналогично сложению двухмерных векторов.

Мы сразу можем заметить, что сложение двух действительных чисел – это частный случай сложения комплексных чисел. Когда мы складываем два действительных числа, мы получаем снова действительное число.

Сложение обладает свойством коммутативности (от перестановки слагаемых сумма не меняется).

Умножение комплексных чисел

Давайте выведем формулу для умножения.

Здесь желтым цветом помечено место, где мы использовали свойство мнимой единицы.

В движении умножение выглядит следующим образом.

Я уже писал выше, что умножение обладает одним интересным свойством. Но чтобы перейти к нему, нам нужно сначала ввести еще несколько операций.

Модуль и Аргумент комплексного числа

Если рассматривать комплексное число, как вектор, то мы можем найти его модуль, т.е. длину вектора. Для этого мы используем обычную теорему Пифагора.

Так же для комплексных чисел мы можем определить, так называемый, аргумент. Аргумент – это угол между положительным направлением действительной оси и вектором.

Если комплексное число расположено в верхней полуплоскости, то аргумент считается положительным, в противном случае – отрицательным. Таким образом аргумент принимает значения от -Pi до Pi радиан (или от -180 до 180 градусов).

По сути, модуль и аргумент – это еще одно представление комплексного числа. Это его полярные координаты. Если мы знаем модуль и аргумент, то это однозначно определяет само число.

Свойство операции умножения

Операция умножения обладает следующим не очевидным свойством.

Это значит, что при умножении двух чисел их аргументы (углы) складываются, а длины перемножаются.

Посмотрите еще раз внимательно на умножение. Я специально обозначил углы, чтобы было видно, что при умножении углы, действительно, складываются.

Допустим, у нас есть число X. Когда мы умножаем его на другое число Y, то мы тем самым растягиваем число X в |Y| раз и поворачиваем его на угол Arg(Y).

Кстати, операции вращение и растяжение коммутируют между собой. Т.е. не имеет значения, в каком порядке мы их выполняем. Они выполняются как бы одновременно.

В какую сторону отмерять углы?

В измерении углов есть некоторая неоднозначность. Например, аргумент числа на картинке равен -45 градусов. Но с тем же успехом мы могли бы сказать, что угол равен +315 градусов.

Фишка в том, что для операции умножения не имеет значения, как мы измеряем углы.

Например, при умножении двух чисел единичной длины с аргументом -45 мы получим угол в -90 градусов. Тем самым мы получим число равное минус мнимой единице.

Если откладывать углы в обратном направлении и считать, что аргументы этих чисел равны не -45, а +315. Тогда при сложении углов мы получим +630. Это то же самое, что и -90. И мы снова получаем минус мнимую единицу.

Таким образом, хоть у нас и имеется некоторая неопределенность в измерении углов, это никак не влияет на результат операции умножения. Умножение определено абсолютно однозначно.

Примеры

Лучший способ понять теорию – это рассмотреть достаточное количество примеров. Этим мы и займемся.

Все наши примеры будут связаны с операцией умножения, т.к. она наиболее интересная.

Умножение на нуль

Если модуль одного из аргументов равен нулю, то при перемножении модуль результата тоже будет равен нулю. В результате мы получаем привычное нам тождество

Умножение на действительное число

Я уже говорил, что умножение на комплексное число порождает сразу два эффекта: поворот и растяжение. Мы можем получить каждый из этих эффектов по отдельности.

Например, умножение любого числа X на действительное число Y (аргумент равен 0) просто растягивает число X в Y раз. И мы получаем операцию растяжение без поворота.

Умножение на число единичной длины

Напротив, мы можем получить операцию поворота без растяжения, если умножим число X на комплексное число Y единичной длины. Тогда число X просто поворачивается на угол, равный аргументу числа Y.

Умножение на мнимую единицу

Умножение на мнимую единицу дает поворот на 90 градусов.

А умножение на минус мнимую единицу дает поворот на 90 градусов в обратном направлении.

Умножение на действительную единицу

Самый тривиальный вариант – это умножение на действительную единицу. Мы должны повернуть число X на нулевой угол и растянуть в 1 раз. Другими словами, мы получим число X без изменений.

Это именно то, к чему мы привыкли со школы. Умножение любого числа на единицу должно давать то же самое число.

Умножение мнимой единицы на мнимую единицу

Аргумент мнимой единицы равен 90 градусов, а модуль равен единице. Значит при возведении в квадрат мнимой единицы мы получим число единичной длины, повернутое на 180 градусов. А именно -1.

Это свойство мы тоже уже знаем, потому что мы приняли его за определение мнимой единицы

Умножение отрицательного действительного числа на положительное действительное число

Отрицательное число имеет аргумент 180 градусов. А положительное – аргумент 0. При умножении аргументы складываются и получается угол в 180 градусов. В результате получаем снова отрицательное число.

Это правило известно нам, как “минус на плюс дает минус”.

Умножение двух отрицательных действительных чисел

Когда мы складываем аргументы двух отрицательных чисел (дважды по 180) мы получаем полный оборот на 360 градусов. В результате получаем положительное число.

А это правило мы знаем, как “минус на минус дает плюс”.

Мне кажется, это очень интересно, как вышеперечисленные правила выражаются через сложение углов :).

Заключение

Надеюсь вам понравились мои картинки :).

Спасибо за внимание.

Геометрический смысл комплексного числа

Комплексное
число
изображается в плоскоститочкойс координатамилибо вектором, начало которого находится
в точке,
а конец в точке(рис. 1.3).

Длина
вектораназываетсямодулем
комплексного числа и обозначается

(2.3)

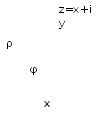
Рис.
2.1

Угол
,
образованный положительным направлением
оси ОХ и вектором,
называетсяаргументом
комплексного числа и обозначается

,
где
–главное
значение аргумента,
.
Главное значение аргумента комплексного
числа может быть найдено с помощью
формулы:

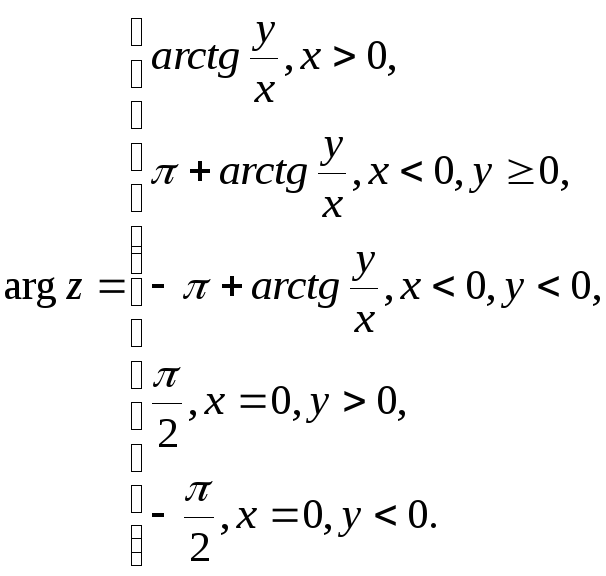(2.5)

Если
в алгебраической форме записи комплексного
числа вместо декартовых координат точки
подставить их полярное представление
(1.4), то получим тригонометрическое
представление комплексного числа.

Определение.
Каждое комплексное число, отличное от
нуля, можно записать в тригонометрической
форме

(2.6)

где
.

С
помощью формулы Эйлера:

(2.7)

каждое
комплексное число может быть записано
в показательной
форме

. (2.8)

Число
называетсясопряженным
комплексному
числу
.

Выполняются
следующие равенства:
;
;

;

Аналогично
доказывается, что
;;.

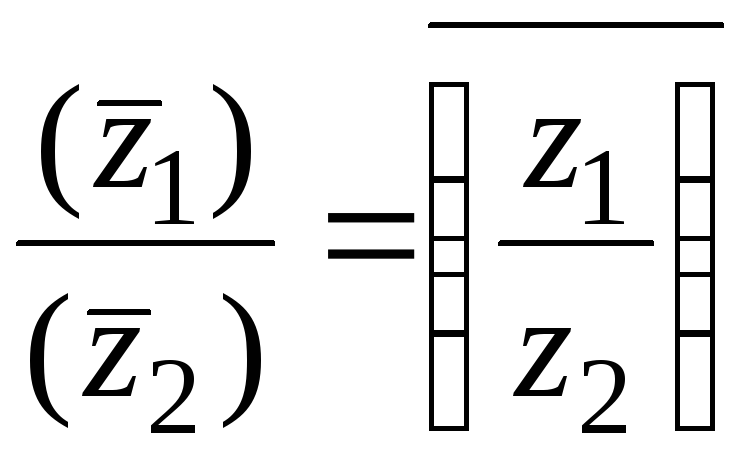Важно
знать, что (2.9)

Операции
над комплексными числами, заданными в

алгебраической форме

Определение.
Два
комплексных числа называются равными,
если у них совпадают действительные и
мнимые части, т.е.

,
еслии.

1. Сложение
   и вычитание

Действие
сложения и вычитания комплексных чисел
ипроизводится по правилу сложения и
вычитания двучленов

.

Группируя
отдельно действительную и мнимую части,
получим формулу:

(2.10)

1. Умножение.

Действие
умножение комплексных чисел
ипроизводится по правилу умножения
двучленов

раскроем
скобки

используя
формулу (2.2) и группируя действительные
и мнимые слагаемые, получим выражение:

(2.11)

1. Деление.

Чтобы
преобразовать дробь
в комплексное число, необходимо числитель
и знаменатель дроби умножить на число
сопряжённое к знаменателю, в числителе
произвести действие умножения, а для
знаменателя воспользоваться формулой
(2.9)

:

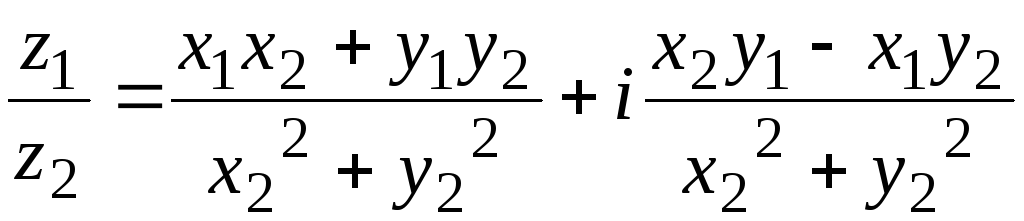(2.12)

Действия
над комплексными числами, заданными в
тригонометрической или в показательной
форме

1. Умножение:

При
умножении двух комплексных чисел
заданных в тригонометрической или
показательной формах их модули
перемножаются, а аргументы складываются:
.

(2.13)

(2.14)

Докажем
формулу (2.14). Пусть
,.

;

1. Деление:

При
делении двух комплексных чисел заданных
в тригонометрической или показательной
формах их модули делятся, а аргументы
вычитаются:
,.

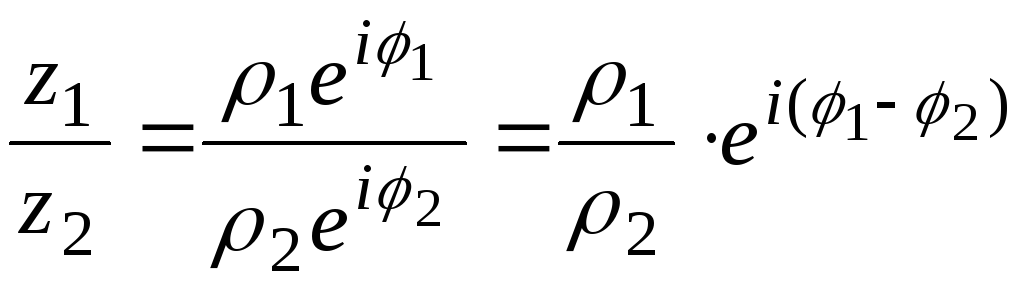(2.15)

(2.16)

Лекция
3

Понятие
многочлена, корни многочленов, кратность
корня, основные теоремы алгебры, следствия
из теорем.

1. Возведение
   в степень.

Для
возведения комплексного числа в целую
положительную степень
применяют формулу Муавра:

(3.1)

Данная
формула является следствием формулы
(2.14).

Пример.
Возвести комплексное число в степень:

1)
.

Решение.
1.
Пусть
,
тогда для комплексного числа в числителе
и знаменателе найдем модуль и аргумент
и перепишемв показательной форме, имеем,
значит,а,,,,
тогда получим

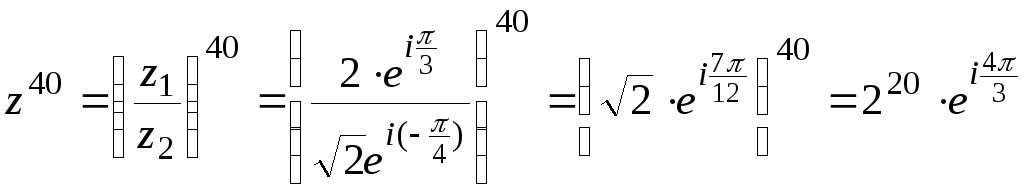
1. Извлечение
   корня порядка
   .

Определение.
Корнем
-й
степени
из комплексного числа
называется комплексное число,
такое что,
где–
натуральное число. Обычно используется
обозначение.

Корень
-й
степени из комплексного числа имеетразличных значений, которые находятся
по формуле Муавра-Лапласа:

(3.2)

Или
через показательную форму

(3.3)

Где

.

Точки,
соответствующие
являются вершинами правильного–
угольника, вписанного в окружность с
центром в начале координат и радиусом.

Способ
построения для
(рис.3.1):

1. Из
   начала координат описываем окружность
   радиуса
   .

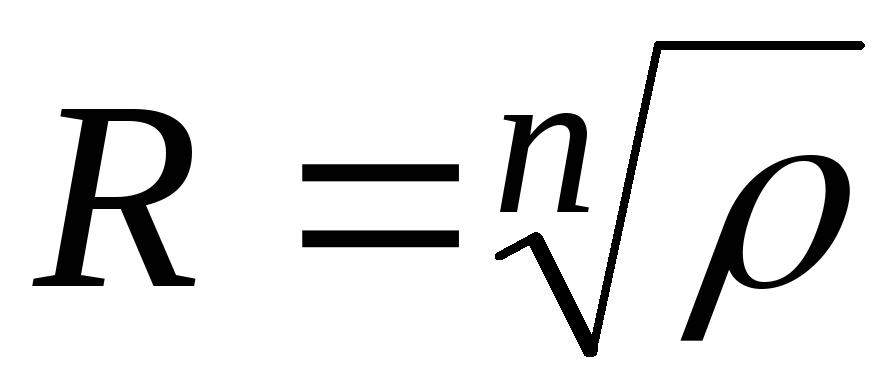2. Если
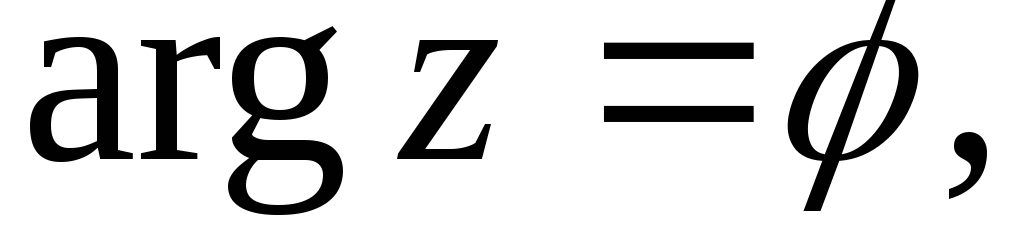   то из начала координат проводим луч
   под угломк положительному направлению.
   Пересечение луча с окружностью дает
   точку.

3. Вписываем
   в окружность правильный
   –
   угольник, одна из вершин которого
   найденная точка.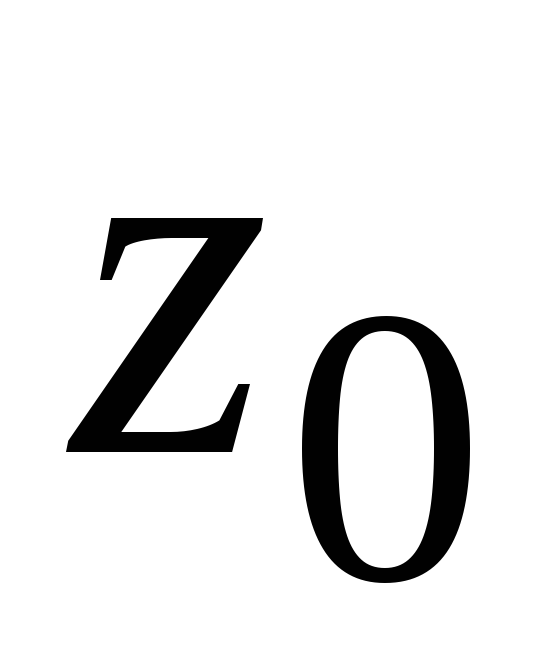
   Точки пересечения–
   угольника и окружности есть решения.

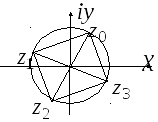
Рис.
2.2

Пример.
Найдем
все значения
.

Решение.
Тригонометрической формой числа 1
является:
.

Значениями
являются числа:,
различными будут лишь корни при следующих
значениях
,
;;.

Полученные
значения являются вершинами правильного
треугольника вписанного в окружность
радиуса
.

Пример.
Корни
-ой
степени из единицыесть вершины правильногоn-угольника,
вписанного в единичный круг.

Определение.
Многочленом
одной переменной
называется функция
,
где– действительные или комплексныекоэффициенты,
а
– целое неотрицательное число. Если,называютстепенью
многочлена и обозначают
,
а–старшим
коэффициентом. Многочлен
называетсянулевым,
если все его коэффициенты равны нулю.
Коэффициент
прив нулевой степени называютпостоянным
или свободным
членом.

Многочлены
степени
называются соответственнолинейными,
квадратичными
(или квадратными),
кубичными
и т.д. В дальнейшем рассматриваются
только действительные коэффициенты
.

Определение.
Корнем
многочлена
называется такое,
при котором
.

Основная
теорема алгебры.
Всякий многочлен положительной степени
имеет, по крайней мере, один корень
действительный или комплексный.

Деление
многочленов. Из
курса элементарной алгебры известен
метод деления уголком для целых чисел,
аналогичный алгоритм имеет место и для
многочленов.

Пусть
даны два многочлена:
и,
гдеи, тогда многочленусопоставляется одна и только одна пара
многочленов,
для которых,,называютчастным
деления, а
–остатком.

Если
,
тогда говорят, чтоделится
на
.

Если
многочлены имеют действительные
коэффициенты, то
итакже имеют действительные коэффициенты.

Пример.
Проверить, делится ли многочлен
на.

Решение.
Разделим многочлены столбиком, т.е.

_

_

_

:

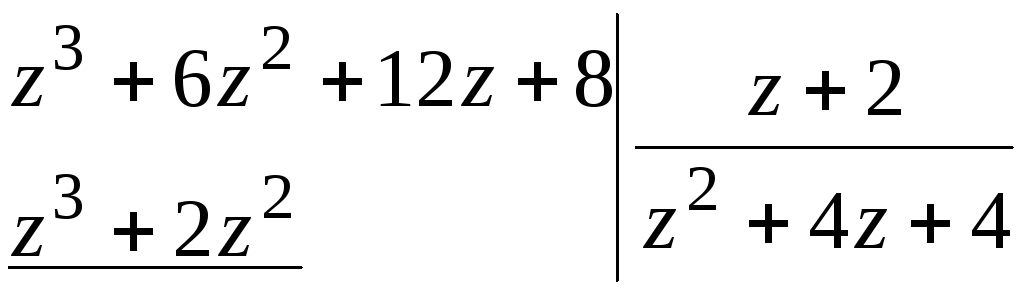
Итак,
многочлен
делится наи может быть представлен в виде.

Теорема
Безу.
Число
является корнем многочленатогда и только тогда, когдаделится на линейный многочлен ().

Доказательство.
В результате деления
на ()
имеем.
Степень,
значит
тогда
подставим
в,
получим,
следовательнои.

Теорема.
При делении
на,
остаток,
т.е..

Пример.
Проверить, делится ли многочлен
на.

Решение.
Разделим многочлены столбиком, т.е.

_

_

_

_

;

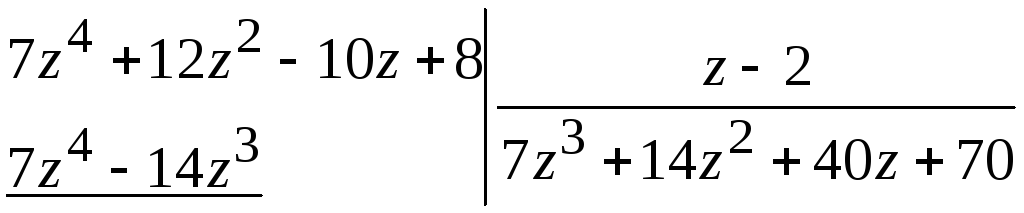
степень
остатка меньше степени делителя,
останавливаем деление.

Итак,
многочлен
не делится наи может быть представлен в виде.

Проверить,
правильно ли выполнено деление можно,
используя предыдущую теорему, согласно
которой
,
действительно,,
значит деление выполнено правильно.

Определение.
Число
называется–кратным
корнем многочлена
,
еслиделится на,
но не делится на.
Корень кратностиназываютпростым
корнем.

Теорема.
Если
– корни многочленастепени– кратностисоответственно и,
тогда,
где– многочлен степени (такой, что.

Доказательство
данной теоремы следует из теоремы Безу.

Правило
определения кратности корня

Пусть
–
корень кратностимногочленастепени,
тогда

,
где
и

,
где
,
продолжая вычислять производные на–
ом шаге получим,

,
т.к.
,
следовательно,
,тогда
можно предложить следующее правило для
вычисления кратности корня многочлена.

Для
того чтобы определить кратность корня
многочлена,
вычисляем значения производныхв точкеи как только,
тогда– кратность корня.

Лекция
4

Векторная
алгебра. Понятие вектора, координаты,
модуль вектора. Линейные операции над
векторами. Базис

Цель:
Изучить понятие вектора, равенства
векторов, как определяются координаты
вектора его модуль, линейные операции
над векторами и их свойства, понятие
базиса.

Определение.
Направленный отрезок (упорядочивающий
пару точек) будем называть вектором
и
обозначать

,,
где точкуназываютначалом
вектора, а
–
егоконцом

(рис.4.1).

Необходимо
знать, что в печатных изданиях часто
векторные величины и векторы обозначают
жирным шрифтом, без стрелки

В

В

ектор, у которого начало и конец
совпадают, будем называтьнулевым
вектором

А

Рис.
4.1

Расстояние
между началом и концом вектора называется
его длиной,
модулем
или абсолютной величиной вектора и
обозначают
,.

Векторы
называются коллинеарными,
если существует прямая, которой эти
векторы параллельны, пишут
.
Коллинеарные векторы могут быть
сонаправленными (направлены в одну
сторону), и противоположно направленными.
Обозначается соответственно,.

Векторы
называются компланарными,
если существует плоскость, которой они
параллельны.

Нулевой
вектор считается коллинеарным любому
вектору т.к. не имеет направления.

Свойство.
Если
вектор
коллинеарен ненулевому вектору,
то существует действительное числотакое, что.

Определение.
Два вектора
считаютсяравными,
если выполнено три условия: 1) их модули
равны, 2) они параллельны, 3) направлены
в одну сторону.

О
равенстве векторов стоит поговорить
отдельно, т.к. оно существенно отличается
от равенства чисел. Два равных числа
могут рассматриваться как одно и тоже.
С векторами все иначе.

Из
курса физики известно, что сила может
быть изображена вектором. Но, силы
изображаемые равными направленными
отрезками производят, вообще говоря
различные действия. Так сила действующая
на упругое тело изображается направленным
отрезком, который не может быть никуда
перенесен из данной точки. Т.е. он
характеризуется направлением и точкой
приложения и называется приложенным
вектором.

Сила
действуещая на абсолютно твердое тело,
изображается скользящим
вектором,
который может быть перенесен не в любую
точку пространства, а лишь вдоль прямой
на которой он лежит.

Все
остальные равные вектора (множество
направленных отрезков, равных данному)
называются свободными
векторами,
с которыми мы и будем работать.

Линейные
операции над векторами

Определение.
Суммой
называется вектор,
который может быть найден по следующим
правилам (рис.4.2).

Свойства
сложения векторов:

1)
,
(коммутативность);

2)
,
(ассоциативность);

3)
прибавление нулевого вектора к любому
другому не меняет последнего
;

4)
вектор, противоположный
вектору
,
обозначается.
Их сумма дает нулевой вектор.

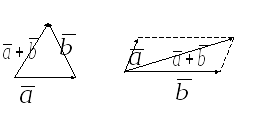
Правило
треугольника

Правило
параллелограмма

Рис.
4.2

Определение.
Разность
есть сумма(рис.4.3).

Рис.4.3

Определение.
Произведением вектора
на вещественное числоназывается любой вектор,
удовлетворяющий следующим условиям:

а)
вектор
коллинеарен вектору;

б)
;

в)
векторы
инаправлены одинаково еслии противоположно направлены если

Свойства
умножения вектора на число

1.
Для любых действительных чисел
и любого вектораверно равенство.(ассоциативность)

2.
Умножение
векторов на число дистрибутивно
относительно сложения чисел

(дистрибутивность).

3.
Умножение векторов на число дистрибутивно
относительно сложения векторов

4.
.

Применяя
линейные операции над векторами мы
можем составлять суммы векторов
умноженных на некоторые вещественные
числа.

Определение.
Выражение вида
,
где–
произвольные постоянные, называетсялинейной
комбинацией
векторов
.

С
помощью введенных выше линейных операций
мы можем преобразовать выражения,
составленные из линейных комбинаций:
раскрывать скобки, приводить подобные
члены, переносить некоторые слагаемые
в другую часть равенства с противоположным
знаком.

Свойства
линейной комбинации

1.
Если
–
параллельны, то каждая их линейная
комбинация параллельна им.

2.
Если
– компланарны, то каждая их линейная
комбинация компланарна с ними.

Определение.
Пусть дана линейная комбинация
,
еслитолько при условии, что,
тогда линейная комбинация векторов
называетсятривиальной
линейной
комбинацией, если
,
и существует хотя бы один,
то–нетривиальная
линейная
комбинация.

Определение.
Если существуют такие
,
что– нетривиальная линейная комбинация,
то говорят, что–линейно
зависимы.
В противном случае, т.е. если
– тривиальная линейная комбинация, то–линейно
независимы.

Теорема.
Векторы
линейно зависимы тогда и только тогда,
когда один из них является линейной
комбинацией остальных.

Доказательство.
Необходимость.
Докажем, что если векторы
линейно зависимы, то один из них является
линейной комбинацией остальных.
Поскольку векторы линейно зависимы,
то, согласно определению, существует,
при котором.

Пусть
,
тогда.
Т.е. векторявляется линейной комбинацией остальных.

Достаточность.
Докажем, что если один из векторов
является линейной комбинацией остальных,
то векторы линейно зависимы. Пусть– линейная комбинация остальных
векторов, тогда– линейно зависимы, посколькупри том, что.

Теорема.

1.
Если хотя бы один из векторов
,
является нулевым, то эти векторы линейно
зависимы.

2.
Любые два коллинеарных вектора линейно
зависимы, и наоборот, два линейно
зависимых вектора коллинеарные.

3.
Каждые три компланарных вектора линейно
зависимы, и наоборот, три линейно
зависимых вектора компланарны.

4.
Каждые четыре вектора линейно зависимы.

Доказательство.
(Приведем доказательство 1–го и 2–го
утверждений теоремы, остальные
доказываются аналогично).

1.
Поскольку среди векторов есть нулевой,
значит, в их линейной комбинации перед
нулевым вектором может стоять любой
ненулевой элемент, а перед остальными
векторами будут стоять нулевые элементы,
это и означает линейную зависимость
векторов.

2.
Докажем, что если два вектора
коллинеарны, то они линейно зависимы.
Если хотя бы один из векторовнулевой, то они линейно зависимы в силу
предыдущего утверждения теоремы.

Если
оба вектора ненулевые, то из свойства
коллинеарности векторов
следует, что существует действительное
числотакое, чтоили,
посколькуиотличны от нуляилинейно зависимы.

Докажем
теперь, что два линейно зависимых вектора
­-
иколлинеарны. Посколькуилинейно зависимы, следовательно, по
определению, существуют действительные
числаи,
хотя бы одно из них отлично от нуля,
такие, что,
пусть,
тогда,
пусть,
имеем,
согласно свойству произведения вектора
на число, это и означает коллинеарность
векторови.

Базис.

Определение.
Базисом
на прямой называется любой ненулевой
вектор лежащий на этой прямой или
коллинеарный с ней.

Определение.
Базисом на плоскости называются два
неколлинеарных вектора лежащих на этой
плоскости или параллельных ей, взятые
в определенном порядке.

Определение.
Базисом
в пространстве называют три некомпланарных
вектора, взятых в определенном порядке.

Определение.
Говорят, что три линейно независимых
вектора
образуютбазис
в пространстве
,
если каждый вектор этого пространства
можно представить как линейную комбинацию
этих векторов, т.е..
Числаназываются координатами векторав базисеи векторобычно записывают как.

Выражение
называется линейной комбинацией вектора
или разложением по базису.

Запись
называется координатной формой записи
вектора.

Равные
векторы в одном базисе имеют равные
компоненты.

При
умножении вектора на число каждая его
координата умножается на это число,
т.е. если
,
то=.

При
сложении двух векторов их координаты,
стоящие перед соответствующими базисными
векторами, складываются, т.е.
=.

Утверждение.
Любые три некомпланарных вектора, взятые
в определенном порядке, образуют базис
пространства.

Любые
два неколлинеарных вектора на плоскости,
взятые в определенном порядке, образуют
базис на этой плоскости.

Любой
ненулевой вектор, лежащий на прямой,
образует базис на этой прямой.

Теорема.

1. Каждый
   вектор, параллельный какой-либо прямой,
   может быть разложен по базису на этой
   прямой.

2. Каждый
   вектор, параллельный какой-либо
   плоскости, может быть разложен по базису
   на этой плоскости.

3. Каждый
   вектор может быть разложен по базису
   в пространстве.

4. Компоненты
   вектора в каждом случае определяются
   однозначно.

Доказательство.

1.
Поскольку вектор, параллельный прямой,
и вектор, лежащий на прямой, ненулевые,
существует число α такое, что
положим,
что.

2.
,
векторявляется диагональю параллелограмма,
построенного на векторах.

3.
,
векторявляется диагональю параллелепипеда,
построенного на векторах.

4.
Доказательство единственности разложения
вектора по определенному базису будем
вести от противного.

Пустьи,
тогда

.

П

усть– противоречие некомпланарности
векторов.

Определение.
Аффинные
координаты в пространстве определяются
заданием базиса
и некоторой точкой,
называемой началом координат.Аффинными
координатами
точки М называются координаты вектора
(относительно
базиса).

Определение.
В случае декартовой прямоугольной
системы координат базисом
являются векторы единичной длины,
лежащие на координатных осях и
сонаправленные с ними,,,.
Векторы взаимно ортогональныи их модули равны единице.

Т.е.
векторы
являются ортонормированным базисом
декартовой системы координат. Базисные
векторы имеют координаты,,.

Тогда
каждый вектор
может, и притом единственным образом,
быть разложен по декартовому прямоугольному
базису,
т.е. существует такая тройка чисел,
что справедливо равенство,– декартовы прямоугольные координаты,
где,тогда,,где– углы между вектороми осямисоответственно (рис. 4.5), а косинусы
называются направляющими косинусами
вектора.

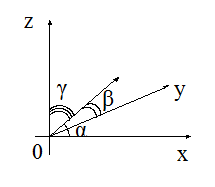
Рис.
4.5

Лекция
5

Проекция
вектора и ее свойства. Деление отрезка
в заданном отношении. Скалярное
произведение векторов

Цель:
Изучить понятие проекции и ее свойства,
методику деления отрезка в данном
отношении, скалярное произведение
векторов, его свойства, физическое
приложение.

Определение.
Проекцией
вектора
на вектор,
обозначаетсяназывается число, равноегде– угол между векторамии(рис.5.1).

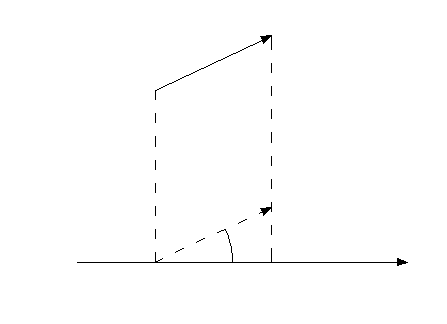
B

О

пр

Рис.
5.1.

Свойства
проекции

1. Проекция
   суммы векторов равна сумме проекций
   составляющих
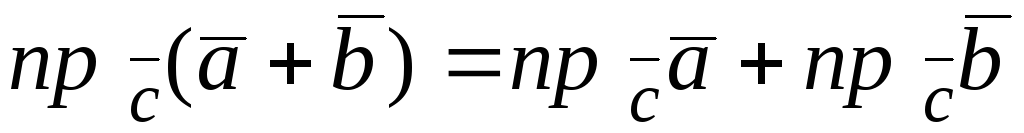   (рис. 5.2).

Рис.
5.2

2)
Проекция произведения вектора на число
равна произведению числа на проекцию
данного вектора
(рис. 5.3).

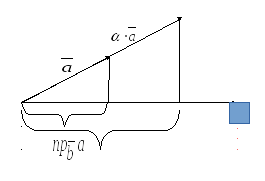Рис
5.3.

Теорема.
Чтобы найти компоненты вектора, нужно
из координат его конца вычесть координаты
его начала, т.е.

,
где

,(рис. 5.4).

Рис. 5.4

Найдем
координаты точки
,
которая делитв отношении().
Отношение,
в котором произвольная точкаделит отрезок(Рис. 5.5) удовлетворяет равенству.

Рис.5.5.

Пусть
,
а,
тогда разложим обе части равенства по
базису,
тогда,,

т.к.
,
следовательно

.

(5.1)

Когда
делит
отрезок пополам, имеем:

. (5.2)

Скалярное
произведение векторов

Определение.
Скалярным
произведением
двух векторов называется число (скаляр)
равное произведению длин этих векторов
на косинус угла между ними:

(5.3)

где
–
угол между векторами.
Обозначают скалярное произведение как.

Т.к.

,
то скалярное произведение можно вычислить
по формуле

или(5.4)

Физический
смысл скалярного произведения: работа
постоянной силы при прямолинейном
перемещении ее точки приложения.
.

Свойства
скалярного произведения

1)
(коммутативность).

Непосредственно
следует из коммутативности произведения
чисел;

2)
(дистрибутивность).

Для
доказательства этого свойства
воспользуемся линейным свойством
проекции и формулой, связывающей
скалярное произведение и проекцию.
Поскольку
и
,
тогда

=
;

1. Скалярный
   квадрат вектора равен квадрату модуля
   этого вектора:

(5.5)

Выполняется
для любого вектора
,
следует из определения, поскольку уголмежду векторомиравен нулю, тогда;

4)
Скалярный множитель можно выносить за
знак скалярного произведения

где
–
произвольное действительное число.

Доказывается
по аналогии со свойством 2. Поскольку
и
,
тогда
;

5)
Скалярное произведение равно нулю тогда
и только тогда, когда их скалярное
произведение равно нулю.

(5.6)

Доказательство.
Докажем,
что если векторы ортогональны, то их
скалярное произведение равно нулю.
Действительно, если
иортогональны, следовательно,–
угол между векторамиравен,
тогда,
тогда из определения следует, что.

Докажем
теперь, что если скалярное произведение
векторов
равно нулю, то они ортогональны. Пусть
оба вектора ненулевые, (т.к. в противоположном
случае доказательство тривиально,
поскольку нулевой вектор не имеет
определенного направления и его можно
считать ортогональным любому вектору).
Тогдаи,
поэтомутолько в том случае, если,
т.е. векторыдолжны быть ортогональны.

6)
векторы ортонормированного базиса
декартовой прямоугольной системы
координат

удовлетворяют соотношениям:

,

т.к. векторы попарно ортогональны
.

Если
базисные векторы

ортогональны, то для каждого вектора
координаты в данном базисе будут равны:,
поскольку
–
ортонормированный базис, тогда
.

Геометрический
смысл скалярного произведения: с
помощью скалярного произведения можно
вычислить проекцию вектора
на вектор,
и косинус угла между векторами:

(5.7)

(5.8)

Теорема.
Если базис ортонормированный и
,,
то

(5.9)

где
–
координаты векторов в ортонормированном
базисе.

Доказательство.
Поскольку
и,
тогда найдем скалярное произведение
векторов используя свойства дистрибутивности
и ассоциативности:

=

=

.

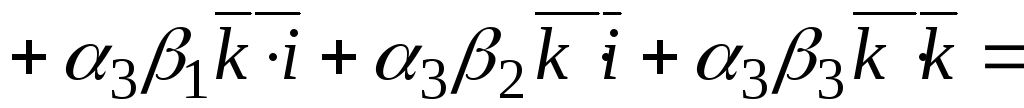
Следствие.
Необходимым
и достаточным условием ортогональности
векторов
иявляется условие.

Следствие.
Длина
(модуль) вектора
равна.

Следствие.

,
где–
угол между векторами.

Следствие.
Если
,
тогда:

.

Лекция
6

Векторное
произведение векторов, смешанное
произведение векторов, основные свойства.
Условия ортогональности, коллинеарности,
компланарности векторов.

Цель:
Изучить векторное и смешанное произведение
векторов, их свойства, методы вычисления,
условия ортогональности, компланарности
и коллинеарности векторов.

Определение.
Векторным
произведением
двух векторов
,
обозначаютназывается векторудовлетворяющий трем условиям:

1)
Модуль вектора равен площади
параллелограмма, построенного на этих
векторах

(6.1)

2)
Вектор ортогонален перемножаемым
векторам:
т.е. ортогонален плоскости построенного
на этих векторах параллелограмма

3)
составляют правую тройку векторов
(рис.6.1).

Рис.
6.1

Свойства
векторного произведения

1)
(антикоммутативность)

Свойство
следует из перемены ориентации векторов;

2)
Скалярный множитель можно вынести за
скобку
;

3)
(дистрибутивность);

4)
Векторный квадрат равен нуль-вектору:

(6.2)

Свойство
непосредственно вытекает из определения
векторного произведения

Теорема.
Чтобы
векторы
ибыли коллинеарны, необходимо и достаточно,
чтобы их векторное произведение равнялось
нулю.

(6.3)

Доказательство.
Докажем,
что если
векторы
коллинеарны, то их векторное произведение
равно нулю. Действительно, т.к. векторы

иколлинеарны, значит, уголмежду ними составляетлибо.
Тогда,
т.е. длина вектора, полученного в
результате перемножения коллинеарных
векторов, равна нулю, это возможно только
у нулевого вектора.

Докажем
теперь, что если векторное произведение
равно нулю, то векторы коллинеарны.
Пусть оба вектора
иненулевые (в противном случае доказательство
тривиально), тогдаи,
поэтомутолько в том случае, если,
т.е. векторыдолжны быть коллинеарны.

Теорема.
В ортонормированном базисе декартовой
прямоугольной системы координат
компоненты векторного произведения
могут быть вычислены по формуле:

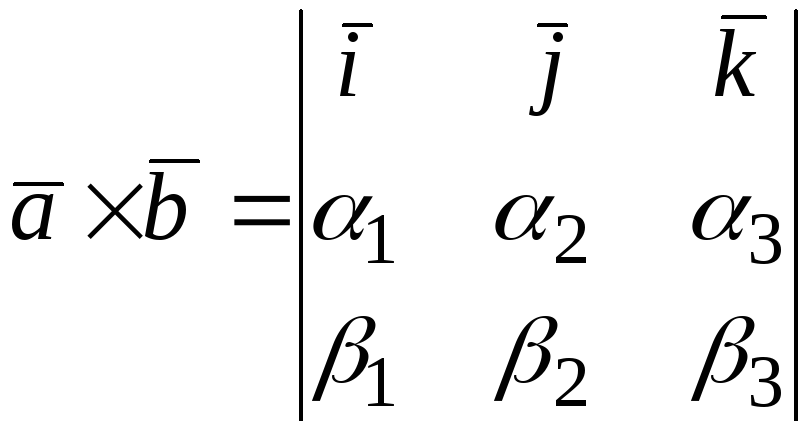(6.4)

где
,.

Доказательство.
Поскольку

и

,
,,,,

тогда

=(учитывая
выше записанные равенства, упрощаем
полученное выражение)

.

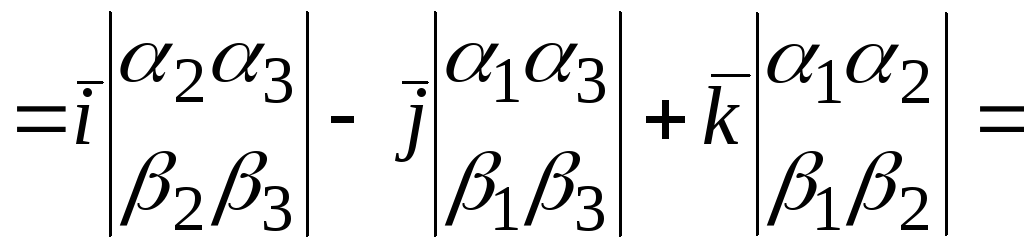
Вместо
можно взять любой ортонормированный
базис.

Теорема
(о
коллинеарных векторах). Если
два вектора коллинеарны, то их координаты
пропорциональны:

(6.5)

Доказательство.
Пусть
и,
т.к. вектор
коллинеарен

,
тогда
,согласно
предыдущей теореме, выполняются
равенства
,
получаем пропорцию
.

Геометрический
смысл векторного произведения

Поскольку

,
то значение длины векторного произведения
совпадает с значением площади
параллелограмма, построенного на
векторах
как на сторонах.– площадь параллелограмма, построенного
на векторахкак на сторонах.

–площадь
треугольника, построенного на векторах
.

Пример.
Найти площадь треугольникапостроенного на векторахи,
если;;.Решение.

Смешанное
произведение

Определение.
Под смешанным
произведением
векторов
подразумевают число обозначаемоеи получающееся в результате скалярного
произведения векторана векторное произведение.

Теорема

(геометрический
смысл смешанного произведения).
Смешанное произведение трех некомпланарных
векторов
по модулю равно объему параллелепипеда,
построенного на сомножителях.

,
причем
– имеет знак «»
еслиобразуют правую тройка и «»
если–
левая тройка.

Доказательство.

–объем
параллелепипеда, где
–
площадь основания,
–
высота параллелепипеда,
–
угол между вектороми вектором(рис.
6.2), тогда
.

Рис.
6.2

Следствие.
–
объем пирамиды.

Свойства
смешанного произведения

1)
,
данное свойство позволяет записывать
смешанное произведение в виде.
Действительно, из коммутативности
скалярного произведения следует, что,
докажем, что,
равенство очевидно, поскольку и справа,
и слева стоит объем параллелепипеда,
построенного на одних и тех же векторах,
знаки совпадают, поскольку векторы–
имеют одинаковую ориентацию;

2)
При перестановки местами двух соседних
множителей, смешанное произведение
меняет знак на противоположный

.

Данное
свойство следует из антикоммутативности
векторного произведения.

3)

.
Действительно, т.к. выполняется первое
свойство, тогда
,
согласно линейным свойствам скалярного
произведения, получаем равенство.

Теорема
(смешанное
произведение векторов в ортонормированном
базисе).
В ортонормированном базисе
смешанное произведение может быть
вычислено по формуле:

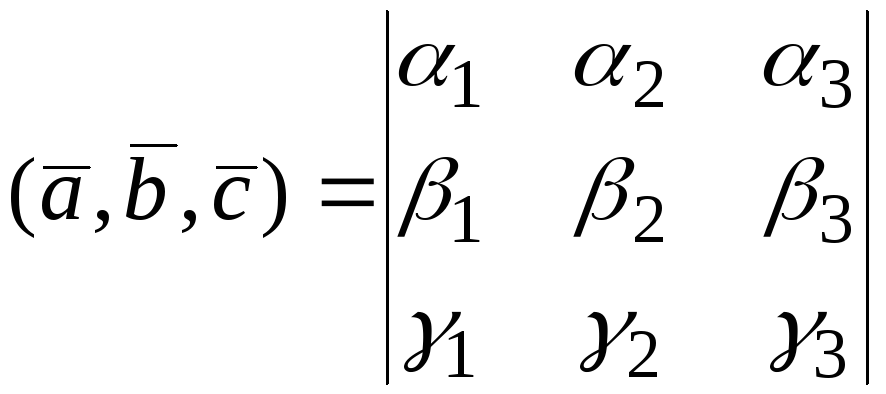(6.6)

Доказательство.
Действительно, смешанное произведение
равно скалярному произведению векторов
и,
поскольку координаты,
для скалярного произведения векторов
в координатах получим=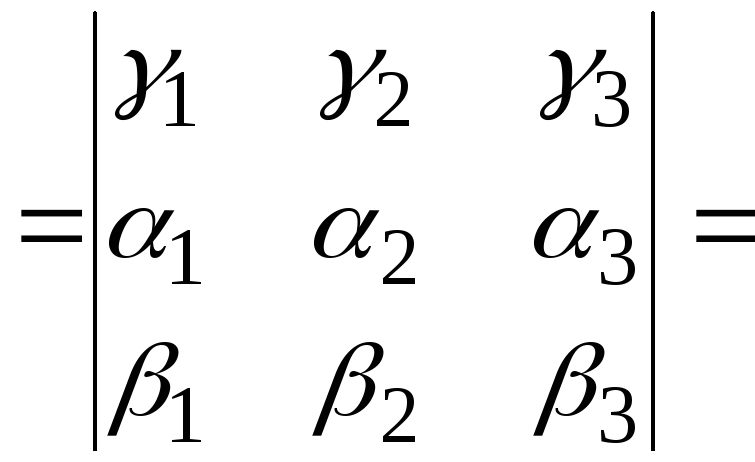(т.к.
четное число перестановок не меняет
знак определителя) =

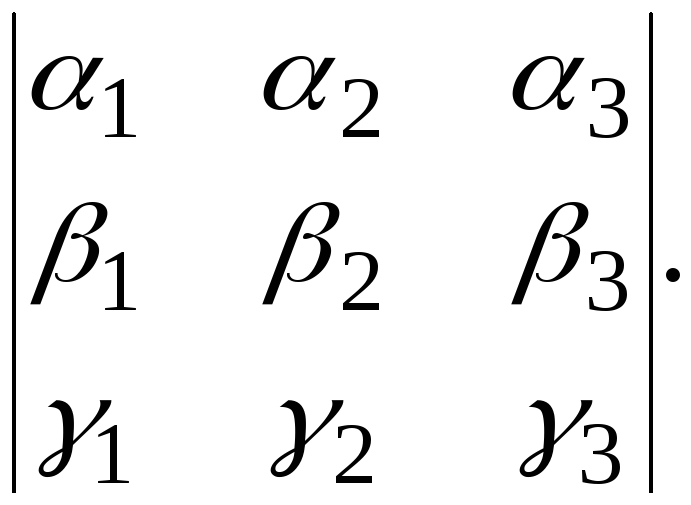
Теорема
(о
компланарных векторах). Для
того, чтобы
были компланарны, необходимо и достаточно,
чтобы их смешанное произведение равнялось
нулю, т.е. выполняется равенство:

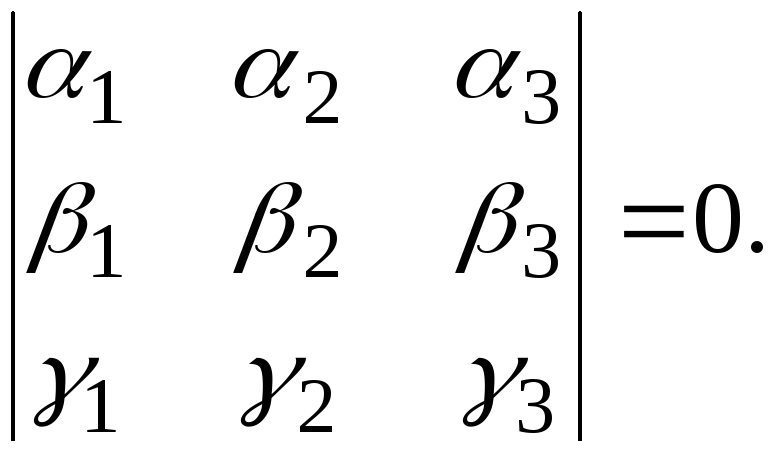(6.7)

В
самом деле, если векторы компланарны,
то они по определению лежат в одной
плоскости или в параллельных плоскостях,
следовательно, объем параллелепипеда,
построенного на этих векторах, будет
равен нулю, учитывая запись смешанного
произведения в координатной форме,
получаем требуемое равенство. В обратную
сторону доказательство аналогично.

Следствие.
Смешанное произведение трех векторов
два из которых совпадают, равно нулю,
например,
.

Действительно,
поскольку такие векторы заведомо
компланарны, их сшешанное произведение
будет равно нулю.

Определение.
Вектор
–
называетсядвойным
векторным произведением.

Комплексные числа в тригонометрической
и показательной формах

Тригонометрическая форма комплексного числа

Каждому комплексному числу геометрически соответствует точка на плоскости . Но положение точки на плоскости, кроме декартовых координат , можно зафиксировать другой парой — ее полярных координат в полярной системе (рис. 1.3,a).

Величина является неотрицательной и для данной точки определяется единственным образом, а угол может принимать бесчисленное множество значений (при этом ): если точке соответствует некоторое значение , то ей также соответствуют значения . Например, если для точки (см. рис. 1.1) выбрать , то ей соответствует любое , в частности при . Если же выбрать , то , а при получаем .

Используя связь декартовых и полярных координат точки (рис. 1.3,б), из алгебраической формы записи комплексного числа получаем тригонометрическую форму:

---

Показательная форма комплексного числа

Если обозначить комплексное число , у которого , а , через , то есть , то из (1.3) получим показательную форму записи комплексного числа:

Равенство называется формулой Эйлера.

Заметим, что геометрически задание комплексного числа равносильно заданию вектора , длина которого равна , то есть , а направление — под углом к оси (рис. 1.3,б).

---

Модуль комплексного числа

Число — длина радиуса-вектора точки называется модулем комплексного числа . Обозначение: .

Из рис. 1.3,б получаем формулу для нахождения модуля числа, заданного и алгебраической форме

Очевидно, что и только для числа .

С помощью правила вычитания запишем модуль числа , где и

А это, как известно, есть формула для расстояния между точками и .

Таким образом, число есть расстояние между точками и на комплексной плоскости.

Пример 1.13. Найти модули комплексных чисел:

Решение

---

Аргумент комплексного числа

Полярный угол точки называется аргументом комплексного числа . Обозначение: .

В дальнейшем, если нет специальных оговорок, под будем понимать значение , удовлетворяющее условию . Так, для точки (см. рис. 1.1) .

Формулу для нахождения аргумента комплексного числа , заданного в алгебраической форме, получаем, используя связь декартовых и полярных координат точки (см. рис. 1.3,б). Для точек, не лежащих на мнимой оси, т.е. для , у которых , получаем ; для точек мнимой положительной полуоси, т.е. для , у которых , имеем ; для точек мнимой отрицательной полуоси, т.е. для , у которых , соответственно .

Аргумент числа — величина неопределенная.

Нахождение аргумента при сводится к решению тригонометрического уравнения . При , т.е. когда — число действительное, имеем при и при . При решение уравнения зависит от четверти плоскости . Четверть, в которое расположена точка , определяется по знакам и . В результате получаем:

При решении примеров удобно пользоваться схемой, которая изображена на рис. 1.5.

Пример 1.14. Найти аргументы чисел из примера 1.13.

Решение

Пример 1.15. Найти модуль и аргумент числа .

Решение. Находим . Так как , т.е. точка расположена в четвертой четверти, то из равенства получаем (рис. 1.5).

---

Главное значение аргумента комплексного числа

Аргумент комплексного числа определяется неоднозначно. Это следует из неоднозначности задания величины угла для данной точки, а также из тригонометрической формы записи комплексного числа и свойства периодичности функций и .

Всякий угол, отличающийся от на слагаемое, кратное , обозначается и записывается равенством:

где — главное значение аргумента, .

Пример 1.16. Записать и для чисел .

Решение. Числа и — действительные, расположены на действительной оси (рис. 1.6), поэтому

числа и — чисто мнимые, расположены на мнимой оси (рис. 1.6), поэтому

Пример 1.17. Записать комплексные числа из примера 1.16:

а) в тригонометрической форме;

б) в показательной форме.

Решение

Пример 1.18. Записать в тригонометрической форме числа .

Решение

---

Равенство комплексных чисел в тригонометрической форме

Условия равенства комплексных чисел получаем, используя геометрический смысл модуля и аргумента комплексного числа, заданного в тригонометрической форме. Так, для чисел из условия . очевидно, следует:

или

Аргументы равных комплексных чисел либо равны (в частности равны главные значения), либо отличаются на слагаемое, кратное .

Для пары сопряженных комплексных чисел и справедливы следующие равенства:

---

Умножение комплексных чисел в тригонометрической форме

Зададим два комплексных числа в тригонометрической форме и и перемножим их по правилу умножения двучленов:

или

Получили новое число , записанное в тригонометрической форме: , для которого .

Правило умножения. При умножении комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются:

В результате умножения чисел может получиться аргумент произведения, не являющийся главным значением.

Пример 1.19. Найти модули и аргументы чисел:

Решение

---

Деление комплексных чисел в тригонометрической форме

Рассмотрим частное комплексных чисел , заданных в тригонометрической форме. Из определения частного имеем и, применяя к произведению правило умножения (формулы (1.10)), получаем .

Правило деления. Модуль частного, полученного в результате деления чисел, заданных в тригонометрической форме, равен частному от деления модуля числителя на модуль знаменателя, а аргумент частного равен разности аргументов делимого и делителя:

В результате деления чисел по формуле (1.11) может получиться аргумент честного, не являющийся главным значением.

Пример 1.20. Записать в тригонометрической форме комплексное число .

Решение. Обозначим . Для чисел и находим модули и аргументы: (см. пример 1.19). По формуле (1.11) получаем и

---

Возведение в степень комплексного числа в тригонометрической форме

Из определения степени и правила умножения чисел, записанных в тригонометрической форме (формула (1.10)), получаем

, где .

Правило возведения в степень. При возведении в степень комплексного числа в эту степень возводится модуль числа, а аргумент умножается на показатель степени:

Записывая число в тригонометрической форме , получаем формулу возведения в степень:

При это равенство принимает вид и называется формула Муавра

Пример 1.21. Найти модуль и аргумент комплексного числа .

Решение. Обозначим . Находим модуль и аргумент числа . Поэтому и . Так как по определению для главного значения аргумента выполняется условие , то .

Пример 1.22. Записать в тригонометрической форме число .

Решение

Пример 1.23. Используя формулу Муавра, найти выражения для и через тригонометрические функции угла .

Решение

---

Извлечение корня из комплексного числа в тригонометрической форме

Рассмотрим задачу извлечения корня из комплексного числа, заданного в показательной или тригонометрической форме , или . Искомое число также запишем в показательной форме: . Используя определение операции извлечения корня и условия (1.8), получаем соотношения

или

Правило извлечения корня. Чтобы извлечь корень из комплексного числа, нужно извлечь корень (арифметический) той же степени из модуля данного числа, а аргумент разделить на показатель корня:

Теперь можно записать число в показательной форме:

Если записать это соотношение в тригонометрической форме, то, учитывая периодичность тригонометрических функций, нетрудно убедиться, что выражение принимает только различных значений. Для их записи достаточно в формуле (1.15) взять последовательных значений , например . В результате получаем формулу извлечения корня из комплексного числа в тригонометрической форме, где :

---

Замечания 1.1

1. Рассмотренная задача извлечения корня степени из комплексного числа равносильна решению уравнения вида , где, очевидно, .

Для решения уравнения нужно найти значений , а для этого необходимо найти и использовать формулу извлечения корня.

2. Исследование формулы (1.17) показывает, что все комплексные числа (значения ) имеют равные модули, т.е. геометрически расположены на окружности радиуса . Аргументы двух последовательных чисел отличаются на , так как , т.е. каждое последующее значение может быть получено из предыдущего поворотом радиуса-вектора точки на .В этом заключается геометрический смысл формулы (1.17), что можно сформулировать следующим образом.

Точки, соответствующие значениям , расположены в вершинах правильного n-угольника, вписанного в окружность с центром в начале координат, радиус которой , причем аргумент одного из значений равен (рис. 1.7).

---

Алгоритм решения комплексных уравнений вида z^n-a=0

1. Найти модуль и аргумент числа .
2. Записать формулу (1.17) при заданном значении .
3. Выписать значения корней уравнения , придавая значения .

Пример 1.24. Решить уравнения: a) ; б) .

Решение

Пример 1.25. Найти корень уравнения , для которого .

Решение

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Содержание:

• Модуль комплексного числа
• Аргумент комплексного числа

Комплексные числа изображаются на так называемой комплексной плоскости. Ось, соответствующая в прямоугольной декартовой
системе координат оси абсцисс, называется действительной осью, а оси ординат – мнимой осью (рис. 1).

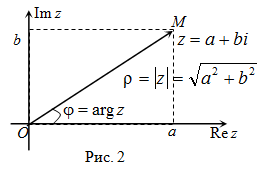
Комплексному числу $z=a+b i$ будет однозначно соответствовать
на комплексной плоскости точка
$(a ; b)$:
$z=a+b i leftrightarrow(a ; b)$ (рис. 2). То есть на действительной оси
откладывается действительная часть комплексного числа, а на мнимой – мнимая.

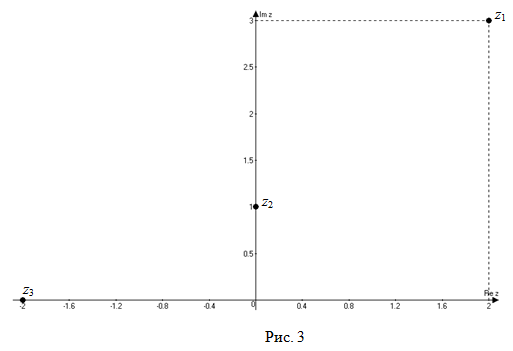
Например. На рисунке 3 на комплексной плоскости изображены числа
$z_{1}=2+3 i$,
$z_{2}=i$ и
$z_{3}=-2$ .

Модуль комплексного числа

Комплексное число также можно изображать радиус-вектором
$overline{O M}$ (рис. 2). Длина радиус-вектора, изображающего
комплексное число $z=a+b i$, называется модулем
этого комплексного числа.

Модуль любого ненулевого комплексного числа есть положительное число. Модули
комплексно сопряженных чисел равны.
Модуль произведения/частного двух комплексных чисел равен произведению/частному модулей каждого из чисел.

Модуль вычисляется по формуле:

То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа.

Аргумент комплексного числа

Угол $phi$ между положительным направлением
действительной оси и радиус-вектора $overline{O M}$, соответствующим
комплексному числу $z=a+b i$, называется аргументом
этого числа и обозначается $arg z$ .

Аргумент $phi$ комплексного числа
$z=a+b i$ связан с его
действительной и мнимой частями соотношениями:

$phi=operatorname{tg} frac{b}{a}, cos phi=frac{a}{sqrt{a^{2}+b^{2}}}, sin phi=frac{b}{sqrt{a^{2}+b^{2}}}$

На практике для вычисления аргумента комплексного числа обычно пользуются формулой:

$phi=arg z=arg (a+b i)=left{begin{array}{l}{operatorname{arctg} frac{b}{a}, a geq 0} \ {operatorname{arctg} frac{b}{a}+pi, a lt 0}end{array}right.$

Аргумент действительного положительного числа равен
$0^{circ}$, действительного отрицательного –
$pi$ или
$180^{circ}$. Чисто мнимые числа с положительной мнимой частью имеют
аргумент равный $frac{pi}{2}$, с отрицательной мнимой частью –
$frac{3 pi}{2}$ .

У комплексно сопряженных чисел аргументы отличаются знаком (рис. 3).

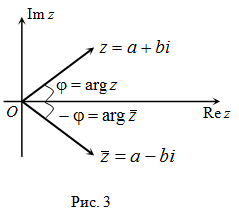
Читать дальше: комплексно сопряженные числа.