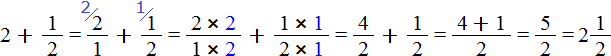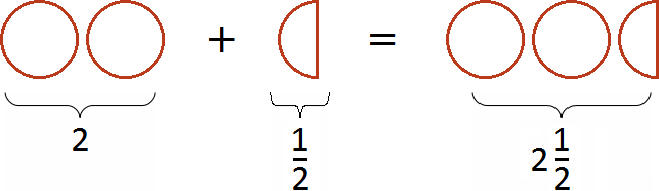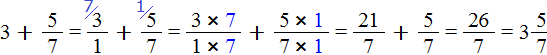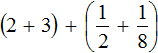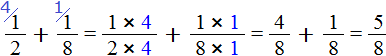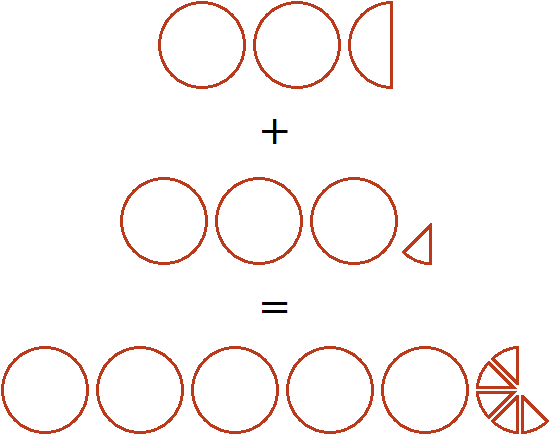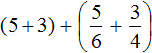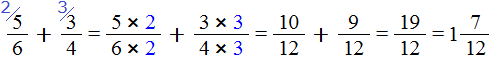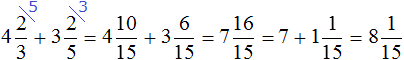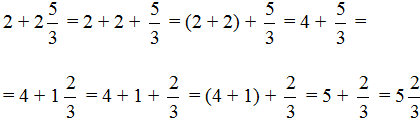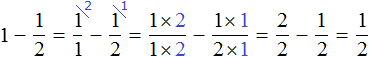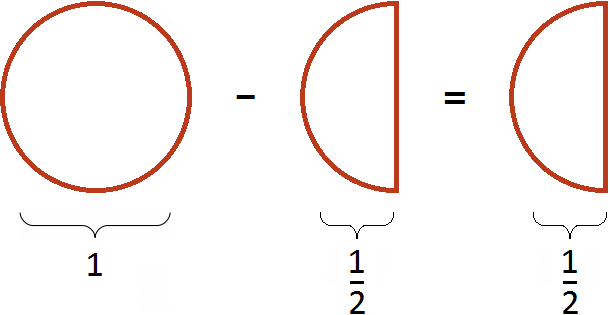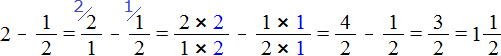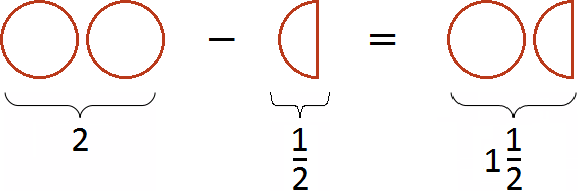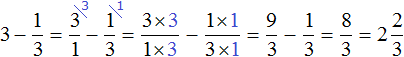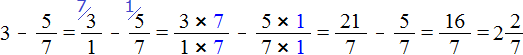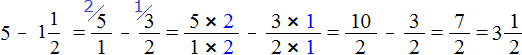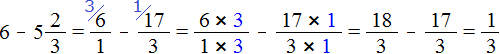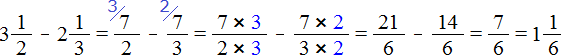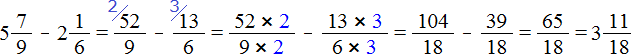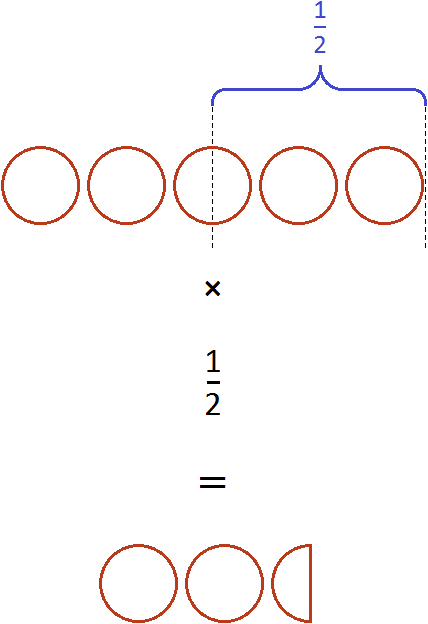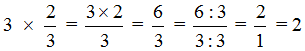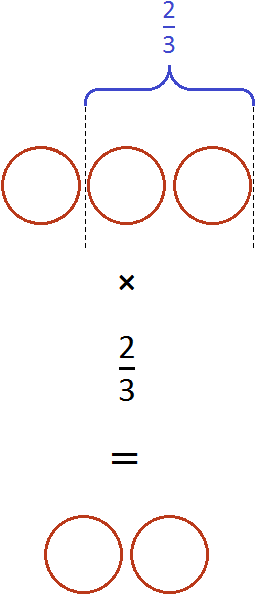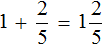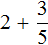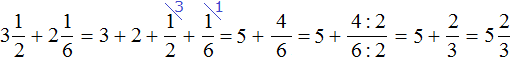Здравствуйте, дорогие читатели, подписчики и гости канала. В этой статье рассмотрим различные вычисления с дробями, которые встречаются в шестом задании ОГЭ по математике. В июле 2.07.2021 года состоится последняя пересдача по математике в основной этап. Дополнительный этап будет уже в сентябре.
Давайте начнем разбор заданий.
1) Умножение дробь на дробь. Чтобы умножить дробь на дробь, нужно числитель умножить на числитель, знаменатель на знаменатель, при возможности сократить.
2) Деление дроби на дробь. При делении дробь на дробь, первая дробь переписывается, вторая дробь переворачивается, а деление заменяется на умножение.
3) Вычитание и умножение дробей. Несколько действий.
Способ №1. Находим общий знаменатель при вычитании. Чтобы найти общий знаменатель, нужно найти такое число, которое будет делиться на первое и второе число. В нашем случае это числа 10 и 20. Общий знаменатель 20.
Способ №2. Распределительный закон умножения. Чтобы умножить число на сумму можно умножить это число на каждое слагаемое, и результат сложить. Также это действует и при вычитании.
Также встречаются выражения, в которых не стоит находить общий знаменатель, поскольку это будет сложно. Приведу два примера:
Пример №1
Пример №2
4) Умножение целого числа на дробь. При умножении целого числа на дробь, целое число умножается на числитель, а знаменатель остается без изменений.
5) Сложение, деление и умножение смешанных чисел.
При сложении, вычитании, умножении и делении смешанных чисел иногда легче перевести смешанное число в неправильную дробь. Чтобы смешанное число перевести в неправильную дробь, нужно целую часть умножить на знаменатель, к полученному значению прибавить числитель дробной части и записать это в числитель, а знаменатель оставить прежним.
6) Вынесение общего множителя за скобку.
7) Действия с десятичными дробями
В итоге у нас получилось, что числитель дроби умножили на 100 (10*10=100), значит и знаменатель дроби тоже умножаем на 100, чтобы значение дроби не изменилось.
И еще один пример:
8) Десятичные дроби и действия со степенями
При возведении отрицательного числа в четную степень, получится число положительное. При возведении отрицательного числа в нечетную степень, получится число отрицательное.
И последнее выражение
Для отработки этих примеров, можно воспользоваться сайтом. Там много аналогичных задания, а эта статья вам будет в помощь при их решений.
Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Если в выражении есть только числа и арифметические знаки “+”, “·”, “-“, “÷”, то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пусть нужно найти значения выражения 14-2·15÷6-3.
Выполним сначала умножение и деление. Получаем:
14-2·15÷6-3=14-30÷6-3=14-5-3.
Теперь проводим вычитание и получаем окончательный результат:
14-5-3=9-3=6.
Вычислим: 0,5-2·-7+23÷234·1112.
Сначала выполняем преобразование дробей, деление и умножение:
0,5-2·-7+23÷234·1112=12-(-14)+23÷114·1112
12-(-14)+23÷114·1112=12-(-14)+23·411·1112=12-(-14)+29.
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
12-(-14)+29=12+14+29=14+1318=141318.
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Найдем значение выражения 0,5·(0,76-0,06).
В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом – умножение.
0,5·(0,76-0,06)=0,5·0,7=0,35.
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Вычислим значение 1+2·1+2·1+2·1-14.
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
1+2·1+2·1+2·1-14=1+2·1+2·1+2·34
1+2·1+2·1+2·34=1+2·1+2·2,5=1+2·6=13.
В нахождении значений выражений со скобками главное – соблюдать последовательность действий.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Вычислим значение выражения с корнями -2·3-1+60÷43+3·2,2+0,1·0,5.
Сначала вычисляем подкоренные выражения.
-2·3-1+60÷43=-6-1+153=83=2
2,2+0,1·0,5=2,2+0,05=2,25=1,5.
Теперь можно вычислить значение всего выражения.
-2·3-1+60÷43+3·2,2+0,1·0,5=2+3·1,5=6,5
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Сколько будет 3+13-1-1
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
3+13-1=3-1.
Таким образом:
3+13-1-1=3-1-1=1.
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Найдем значение выражения 23·4-10+161-123,5-2·14.
Начинаем вычислять по порядку.
23·4-10=212-10=22=4
16·1-123,5-2·14=16*0,53=16·18=2.
Осталось только провести операцию сложение и узнать значение выражения:
23·4-10+161-123,5-2·14=4+2=6.
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Вычислим значение следующего выражения: 2-25·45-1+3136.
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
2-25·45-1+3136=2-25·225-1+313·6
2-25·225-1+313·6=2-25·22·5-2+32=22·5-2-25+32
22·5-2-25+32=2-2+3=14+3=314
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Найдем значение выражения, содержащего дроби: 3,22-3·7-2·36÷1+2+39-6÷2.
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
3,22=3,2÷2=1,6
7-2·36=7-66=16
1+2+39-6÷2=1+2+39-3=66=1.
Перепишем наше выражение и вычислим его значение:
1,6-3·16÷1=1,6-0,5÷1=1,1
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Вычислим выражение 25-1-25-74-3.
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
25-1=25+15-15+1=25+15-1=25+24
Исходное выражение принимает вид:
25-1-25-74-3=25+24-25-74-3.
Вычислим значение этого выражения:
25+24-25-74-3=25+2-25+74-3=94-3=-34.
Выражения с логарифмами
Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log24+2·4 можно сразу вместо log24 записать значение этого логарифма, а потом выполнить все действия. Получим: log24+2·4=2+2·4=2+8=10.
Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log5-6÷352+2+7. Имеем:
log5-6÷352+2+7=log327+7=3+7=10.
Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Найдем значение выражения log2log2256+log62+log63+log5729log0,227.
log2log2256=log28=3.
По свойству логарифмов:
log62+log63=log6(2·3)=log66=1.
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
log5729log0,227=log5729log1527=log5729-log527=-log27729=-log27272=-2.
Теперь можно переходить к вычислению значения исходного выражения.
log2log2256+log62+log63+log5729log0,227=3+1+-2=2.
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Найдите значение выражения: tg24π3-sin-5π2+cosπ.
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
tg4π3=3
sin-5π2=-1
cosπ=-1.
Подставляем значения в выражение и вычисляем его значение:
tg24π3-sin-5π2+cosπ=32-(-1)+(-1)=3+1-1=3.
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Нужно найти значение выражения cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1.
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1=cos2π8cos5π36+π9-1=cosπ4cosπ4-1=1-1=0.
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.
- Корни, степени, логарифмы и т.д. заменяются их значениями.
- Выполняются действия в скобках.
- Оставшиеся действия выполняются по порядку слева направо. Сначала – умножение и деление, затем – сложение и вычитание.
Разберем пример.
Вычислим, чему равно значение выражения -2·sinπ6+2·2π5+3π5+3 lne2+1+39.
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
Первым делом вычислим значение подкоренного выражения 2·sinπ6+2·2π5+3π5+3. Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.
π6+2·2π5+3π5=π6+2·2π+3π5=π6+2·5π5=π6+2π
Теперь можно узнать значение синуса:
sinπ6+2·2π5+3π5=sinπ6+2π=sinπ6=12.
Вычисляем значение подкоренного выражения:
2·sinπ6+2·2π5+3π5+3=2·12+3=4
Отсюда:
2·sinπ6+2·2π5+3π5+3=4=2.
Со знаменателем дроби все проще:
lne2=2.
Теперь мы можем записать значение всей дроби:
2·sinπ6+2·2π5+3π5+3 lne2=22=1.
С учетом этого, запишем все выражение:
-1+1+39=-1+1+33=-1+1+27=27.
Окончательный результат:
-2·sinπ6+2·2π5+3π5+3 lne2+1+39=27.
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56+8-3,789lne2-56+8-3,789lne2 также равно нулю.
Еще один прием, позволяющий ускорить процесс – использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями – сокращение одинаковых выражений в числителе и знаменателе.
Например, возьмем выражение 23-15+3·289·343·23-15+3·289·34. Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 13.
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.
Вычислить значение выражения 0,5x-y при заданных x=2,4 и y=5.
Подставляем значения переменных в выражение и вычисляем:
0,5x-y=0,5·2,4-5=1,2-5=-3,8.
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Например, выражение х+3-х, очевидно, имеет значение 3, и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.
Еще один пример. Значение выражения xx равно единице для всех положительных иксов.
В этом уроке мы познакомимся с понятием дробных выражений и с тем, как их считать. Узнаем интересные способы работы с дробями, в числителе или знаменателе которых стоят дроби.
Для начала определимся с определением дробного выражения.
Дробным выражением называется частное двух выражений или чисел, знак деления в котором обозначается чертой.
Пример:
$$mathbf{frac{1}{2}}$$
Мы привыкли называть такое выражение обыкновенной дробью. Она ничем не противоречит определению дробного выражения. Поэтому если вас спросят: “Является ли обыкновенная дробь дробным выражением?”, то можно смело ответить: “Да, является!”
$$mathbf{frac{1+2}{3+4}}$$
$$mathbf{frac{5cdot(1+2)}{(3+5)div2}}$$
Мы не накладываем никаких ограничений на то, что из себя представляют выражения; нужно только то, чтобы это было деление, записанное как дробь.
Также никто не запрещает записать в одну или даже в обе части выражения, содержащие дроби.
Примеры:
$$mathbf{frac{1}{1+frac{1}{8}}}$$
$$mathbf{frac{3+12frac{1}{2}}{7frac{1}{3}-2frac{3}{4}}}$$
$$mathbf{frac{(frac{1}{2}+frac{1}{4})cdotfrac{2}{3}}{frac{2}{7}cdot(frac{3}{8}-frac{1}{4})}}$$
Можем пойти дальше и записать так называемую многоэтажную дробь. Это дробь, в числителе или в знаменателе (а иногда и в числителе и в знаменателе) которой стоят дробные выражения.
Примеры:
$$mathbf{frac{frac{1}{2}}{3}}$$
$$mathbf{frac{1}{frac{12}{19}}}$$
$$mathbf{frac{frac{12}{89}}{frac{74}{99}}}$$
Помимо определения дробного выражения необходимо знать определения числителя и знаменателя дробного выражения.
Эта информация доступна зарегистрированным пользователям
Если мы считаем дробное выражение делением, то числителем будет являться делимое, а знаменателем делитель.
Например, существует следующее дробное выражение:
$$mathbf{frac{3+10cdot2}{2+frac{1}{2}}}$$
В данном случае (mathbf{3+10cdot2}) будет являться числителем, а (mathbf{2+frac{1}{2}})- знаменателем.
Также можно преобразовывать обычные выражения в дробные.
Это можно делать при условии, что выражение представляет из себя частное двух выражений или чисел, но пока что записанное через обычный знак деления.
Эта информация доступна зарегистрированным пользователям
Примеры преобразования обычного выражения в дробное:
(mathbf{(3+4)div(200+123)=frac{3+4}{200+123}})
(mathbf{(1247+523cdot(54+78))div((345+67)cdot56cdot87cdot(63+85))=})
(mathbf{=frac{1247+523cdot(54+78)}{(345+67)cdot56cdot87cdot(63+85)}})
(mathbf{(4+frac{1}{2})div(frac{3}{5}cdot8+2)=frac{4+frac{1}{2}}{frac{3}{5}cdot8+2}})
(mathbf{(452+789cdot(frac{7}{9}+frac{1}{2}))div(frac{4}{741}+582cdot741)=})
(mathbf{=frac{452+789cdot(frac{7}{9}+frac{1}{2})}{frac{4}{741}+582cdot741}})
Сформулируем правило: для того, чтобы преобразовать выражение, представляющее из себя частное двух выражений или чисел, необходимо делимое поместить в числитель дробного выражения, а делитель- в знаменатель.
Теперь вы видите, насколько большой класс формул покрывается понятием дробного выражения.
Давайте пройдем небольшой тест и перейдем к изучению того, как вычислять значения дробных выражений.
Эта информация доступна зарегистрированным пользователям
Начнем с самого простого способа вычисления значений дробных выражений.
Он заключается в том, чтобы отдельно посчитать значения числителя и знаменателя и получить дробное выражение, в знаменателе и числителе которого стоят числа.
Далее надо смотреть, что получилось:
- может получиться правильная дробь, тогда это будет готовым ответом
- может получиться дробь неправильная, тогда необходимо выделить целую часть
- в числителе и знаменателе дробного выражения могут получиться дробные числа; в таком случае нужно поделить числитель на знаменатель, это и будет ответом
Эта информация доступна зарегистрированным пользователям
Пример 1
Вычислим значение выражения (mathbf{frac{1+2cdot4}{5-2}})
Решение:
Для начала вычислим значения числителя и знаменателя:
(mathbf{frac{1+2cdot4}{5-2}=frac{1+8}{3}=frac{9}{3}})
В данном примере числитель делится на знаменатель, поэтому из дроби получится натуральное число.
(mathbf{frac{9}{3}=3})
Пример 2
Вычислим значение выражения (mathbf{frac{7+2cdot3cdot2}{2cdot9}})
Решение:
Сначала вычислим числитель и знаменатель:
(mathbf{frac{7+2cdot3cdot2}{2cdot9}=frac{7+12}{18}=frac{19}{18}})
В данном случае получилась неправильная дробь, выделим целую ее часть, чтобы получить в ответе смешанное число:
(mathbf{frac{19}{18}=frac{19}{18}=1frac{1}{18}})
Пока что были рассмотрены случаи, в которых выражения в числителе и знаменателе представляли из себя арифметические действия над натуральными числами. Но вас нисколько не должны смущать случаи, в которых выражения содержат в себе дроби как обыкновенные, так и десятичные.
Пример:
(mathbf{frac{3+frac{3}{4}}{1.2+0.3}})
Решение:
Наверное, вы уже догадываетесь, что мы сделаем дальше. Правильно! Вычислим числитель и знаменатель:
(mathbf{frac{3+frac{3}{4}}{1.2+0.3}=frac{frac{3cdot4+3}{4}}{1.5}=})
(mathbf{=frac{frac{12+3}{4}}{1.5}=frac{frac{15}{4}}{1.5}})
В данном случае мы получили неправильную дробь в числителе и десятичную дробь в знаменателе.
Чтобы получить окончательный результат разделим одно на другое:
(mathbf{frac{frac{15}{4}}{1.5}=frac{15}{4}div1.5=frac{15}{4}divfrac{15}{10}=})
(mathbf{=frac{15}{4}cdotfrac{10}{15}=frac{15cdot10}{4cdot15}=frac{10}{4}=frac{5}{2}=2frac{1}{2}})
Прежде чем перейти к дополнительным приемам работы с дробными выражениями, решим небольшой тест для закрепления навыка вычисления дробных выражений.
Эта информация доступна зарегистрированным пользователям
Пока что во всех предыдущих случаях мы находили значения дробных выражений «в лоб», по достаточно простому алгоритму.
Но, как это часто бывает в математике, в некоторых случаях можно упростить себе подсчеты, вовремя заметив определенные вещи.
Вы уже наверняка хорошо освоили сокращение дробей.
Напомним, в чем его суть: если числитель представляет из себя произведение, и знаменатель также является произведением, и в этих произведениях есть одинаковый множитель, то мы можем сократить дробь на этот множитель.
Как же это относится к дробным выражениям?
Дело в том, что в некоторых случаях числитель и знаменатель могут быть произведениями или же могут стать произведениями в процессе подсчетов.
Тогда почему бы не сокращать их по возможности?!
Эта информация доступна зарегистрированным пользователям
Пример:
(mathbf{frac{7cdot(123+4)}{3cdot(120+7)}})
Начнем считать выражение и посмотрим, что получается.
(mathbf{frac{7cdot(123+4)}{3cdot(120+7)}=frac{7cdot127}{3cdot127}})
Числитель и знаменатель дробного выражения после первых преобразований превратились в произведения.
Также можно заметить, что в этих произведениях есть общий множитель: 127
Тогда мы можем поделить числитель и знаменатель дробного выражения на это число, тем самым значительно упростив выражение.
(mathbf{frac{7cdot127}{3cdot127}=frac{7}{3}=2frac{1}{3}})
Это и будет значением этого выражения.
Также мы можем быть еще более хитрыми и внимательными.
Найдем значение выражения (mathbf{frac{2cdot(478569-145236)}{(478569-145236)cdot3}})
Конечно же, можно начать вычислять сначала числитель, потом знаменатель. Для этого мы будем вычислять разность шестизначных чисел.
Но можно сделать проще: заметим, что числитель и знаменатель являются произведениями.
Числитель является произведением 2-х и выражения (478569-145236)
Знаменатель же является произведением выражения (478569-145236) и 3-х.
Выражение (478569-145236) является множителем и можно утверждать, что это один и тот же множитель в числителе и в знаменателе.
Значит, мы можем уверенно сокращать дробное выражение на это выражение.
(mathbf{frac{2cdot(478569-145236)}{(478569-145236)cdot3}=frac{2}{3}})
В данном случае мы сразу получили правильную дробь, это и будет являться значением выражения.
Отдельно стоит упомянуть работу с многоэтажными дробями.
Мы всегда можем идти по алгоритму с последовательным вычислением числителя и знаменателя – это гарантированно дает результат.
Но также можно запомнить два правила, которые существенно экономят время.
Первое правило говорит о том, что, если в числителе дробного выражения находится дробь (или же дробное выражение), мы можем домножить дробное выражение на знаменатель дроби (или дробного выражения), стоящей в числителе, тем самым уменьшив «этажность» дробного выражения.
Эта информация доступна зарегистрированным пользователям
Парочка примеров:
(mathbf{frac{frac{2}{3}}{4}=frac{frac{2}{3}cdot3}{4cdot3}=frac{2}{12}=frac{1}{6}})
(mathbf{frac{frac{3}{7+13}}{5}=frac{frac{3}{7+13}cdot(7+13)}{5cdot(7+13)}=})
(mathbf{=frac{3}{5cdot20}=frac{3}{100}=0.03})
Второе правило рассматривает случай, когда дробь (или дробное выражение) находится в знаменателе дробного выражения.
В таком случае уменьшить «этажность» дробного выражения поможет домножение всего дробного выражения на знаменатель дроби (или дробного выражения), стоящей в знаменателе.
Эта информация доступна зарегистрированным пользователям
И парочка примеров на этот случай:
(mathbf{frac{3}{frac{2}{7}}=frac{3cdot7}{frac{2}{7}cdot7}=frac{21}{2}=10frac{1}{2}})
(mathbf{frac{11}{frac{3}{1+7}}=frac{11cdot(1+7)}{frac{3}{1+7}cdot(1+7)}=})
(mathbf{=frac{11cdot(1+7)}{3}=frac{11cdot8}{3}=frac{88}{3}=29frac{1}{3}})
И в завершение еще дам такой пример:
(mathbf{frac{frac{3}{4+1}}{frac{7-2}{4}}=frac{frac{3}{5}}{frac{5}{4}}=})
(mathbf{=frac{frac{3}{5}cdot5}{frac{5}{4}cdot5}=frac{3}{frac{25}{4}}=frac{3cdot4}{frac{25}{4}cdot4}=frac{12}{25}})
Эта информация доступна зарегистрированным пользователям
Десять интересных математических фактов:
1. Известные всем знаки сложения и вычитания впервые были использованы только около 500 лет назад
2. 2 и 5– единственные простые числа, которые оканчиваются на 2 или 5
3. Несмотря на то, что сохранилось много трудов древнегреческого ученого Евклида, о его биографии почти ничего не известно
4. В римской системе счисления не существует нуля
5. Знак равенства «=» появился только в XVI веке
6. Слово «миг» обозначает не только короткое мгновение, но и вполне конкретный временной промежуток: 0,01 секунды
7. У древних египтян отсутствовала таблицы умножения и прочие математические правила
8. В свое время заниматься математикой в высоких кругах было настолько популярно, что даже Наполеон Бонапарт оставил после себя научные труды
9. Самые древние математические записи были найдены написанными на костях
10. Ученый Муавр с помощью математики смог рассчитать дату своей смерти
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Нахождение числа по его дроби
Замечание 1
Чтобы найти число по данному значению его дроби нужно это значение разделить на дробь.
Пример 1
Антон за неделю учебы заработал три четверти отличных отметок. Сколько всего отметок получил Антон, если отличных отметок было 6.
Решение.
По условию задачи $6$ отметок – это $frac{3}{4}$.
Найдем количество всех отметок:
$6div frac{3}{4}=6 cdot frac{4}{3}=frac{6 cdot 4}{3}=frac{2 cdot 3 cdot 4}{3}=2 cdot 4=8$.
Ответ: всего $8$ отметок.
Пример 2
Выкосили $frac{4}{9}$ пшеницы на поле. Найти площадь поля, если было скошено $36$ га.
Решение.
По условию задачи $36$ га – это $frac{4}{9}$.
Найдем площадь всего поля:
$36div frac{4}{9}=36 cdot frac{9}{4}=frac{36 cdot 9}{4}=frac{4 cdot 9 cdot 9}{4}=81$.
Ответ: площадь всего поля $81$ га.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Пример 3
За один день автобус проехал $frac{2}{3}$ маршрута. Найти продолжительность намеченного маршрута, если за день автобус проехал $350$ км?
Решение.
По условию задачи $350$ км – это $frac{2}{3}$.
Найдем продолжительность всего маршрута автобуса:
$350div frac{2}{3}=350 cdot frac{3}{2}=frac{350 cdot 3}{2}=175 cdot 3=525$.
Ответ: продолжительность намеченного маршрута $525$ км.
Пример 4
Рабочий поднял производительность своего труда на $% $и сделал за такой же срок на $24$ детали больше, чем было запланировано. Найти количество деталей, запланированных для выполнения рабочим.
Решение.
По условию задачи $24$ детали = $8%$, а $8% = 0,08$.
Найдем количество деталей, запланированных для выполнения рабочим:
$24div 0,08=24div frac{8}{100}=24 cdot frac{100}{8}=frac{24 cdot 100}{8}=frac{3 cdot 8 cdot 100}{8}=300$.
Ответ: запланировано $300$ деталей для выполнения рабочим.
«Нахождение числа по его дроби, дробные выражения» 👇
Пример 5
В цехе отремонтировали $9$ станков, что составляет $18%$ всех станков цеха. Сколько станков находится в цехе?
Решение.
По условию задачи $9$ станков = $18%$, а $18% = 0,18.$
Найдем количество станков в цехе:
$9div 0,18=9div frac{18}{100}=9 cdot frac{100}{18}=frac{9 cdot 100}{18}=frac{9 cdot 100}{2 cdot 9}=frac{100}{2}=50$.
Ответ: в цехе $50$ станков.
Дробные выражения
Рассмотрим дробь $frac{a}{b}$, которая равна частному $adiv b$. В таком случае частное от деления одного выражения на другое удобно записывать также с помощью черты.
Пример 6
Например, выражение $(13,5–8,1)div (20,2+29,8)$ можно записать следующим образом:
$frac{13,5-8,1}{20,2+29,8}$.
После выполнение расчетов получим значение данного выражения:
$frac{13,5-8,1}{20,2+29,8}=frac{5,4}{50}=frac{10,8}{100}=0,108$.
Определение 1
Дробным выражением называется частное двух чисел или числовых выражений, в котором знак $«:»$ заменен дробной чертой.
Пример 7
$frac{2,4}{1,3 cdot 7,5}$, $frac{frac{5}{8}+frac{3}{11}}{2,7-1,5}$, $frac{2a-3b}{3a+2b}$, $frac{5,7}{ab}$ – дробные выражения.
Определение 2
Числовое выражение, которое записывается выше дробной черты, называется числителем, а числовое выражение, которое записывается ниже дробной черты, – знаменателем дробного выражения.
В числителе и знаменателе дробного выражения могут стоять числа, числовые или буквенные выражения.
Для дробных выражений могут применяться правила, которые справедливы для обыкновенных дробей.
Пример 8
Найти значение выражения $frac{5 frac{3}{11}}{3 frac{2}{7}}$.
Решение.
Умножим числитель и знаменатель данного дробного выражения на число $77$:
$frac{5 frac{3}{11}}{3 frac{2}{7}}=frac{5 frac{3}{11} cdot 77}{3 frac{2}{7} cdot 77}=frac{406}{253}=1,6047…$
Ответ: $frac{5 frac{3}{11}}{3 frac{2}{7}}=1,6047…$
Пример 9
Найти произведение двух дробных чисел $frac{16,4}{1,4}$ и $1 frac{3}{4}$.
Решение.
$frac{16,4}{1,4} cdot 1 frac{3}{4}=frac{16,4}{1,4} cdot frac{7}{4}=frac{4,1}{0,2}=frac{41}{2}=20,5$.
Ответ: $frac{16,4}{1,4} cdot 1 frac{3}{4}=20,5$.
Пример 10
Найти сумму двух дробей $frac{2}{0,7}+frac{3}{1,4}$.
Решение.
$frac{2}{0,7}+frac{3}{1,4}=frac{4+3}{1,4}=frac{7}{1,4}=frac{70}{14}=5$.
Ответ: $frac{2}{0,7}+frac{3}{1,4}=5$.
Для выполнения сложения дробных выражений удобно сразу их преобразовать к виду обыкновенных дробей, а затем выполнить сложение:
$frac{2}{0,7}+frac{3}{1,4}=frac{20}{7}+frac{30}{14}=frac{20}{7}+frac{15}{7}=frac{35}{7}=5$.
Пример 11
Найти значение выражения: $frac{frac{7}{11} cdot frac{33}{21}+1,23}{5,1-2,8}$.
Решение.
$frac{frac{7}{11} cdot frac{33}{21}+1,23}{5,1-2,8}=frac{frac{7 cdot 33}{11 cdot 21}+1,23}{2,3}=frac{1+1,23}{2,3}=frac{2,23}{2,3}=frac{9,79}{2,3}=0,96956…$
Ответ: $frac{frac{7}{11} cdot frac{33}{21}+1,23}{5,1-2,8}=0,96956…$
Пример 12
Найти значение выражения $frac{2,48+3 frac{5}{9} cdot 1 frac{1}{8}}{6,1-3,7}$.
Решение.
В числителе смешанные числа преобразуем к виду неправильных дробей и выполним вычисления:
$frac{2,48+3 frac{5}{9} cdot 1 frac{1}{8}}{6,1-3,7}=frac{2,48+frac{32}{9} cdot frac{9}{8}}{2,4}=frac{2,48+4}{2,4}=frac{6,48}{2,4}=2,7$.
Ответ: $2,7$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
В предыдущих уроках было сказано, что дробь, состоящая из целой и дробной части, называется смешанной.
Все дроби, имеющие целую и дробную часть, носят одно общее название — смешанные числа.
Смешанные числа так же как и обыкновенные дроби можно складывать, вычитать, умножать и делить. В данном уроке мы рассмотрим каждое из этих действий по отдельности.
Сложение целого числа и правильной дроби
Встречаются задачи, в которых требуется сложить целое число и правильную дробь. Например, сложить число 2 и дробь . Чтобы решить этот пример, нужно число 2 представить в виде дроби
. Затем сложить дроби с разными знаменателями:
А теперь внимательно посмотрим на этот пример. Смотрим на его начало и на его конец. Начало у него выглядит так: , а конец так:
. Различие в том, что в первом случае число 2 и дробь
соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что
это свёрнутая форма записи смешанного числа, а
— развёрнутая.
Когда перед нами смешанное число вида , мы должны понимать, что знак сложения опущен.
Какой можно сделать вывод? Если потребуется сложить целое число и правильную дробь, можно опустить плюс и записать целое число и дробь вместе.
Значит значение выражения равно
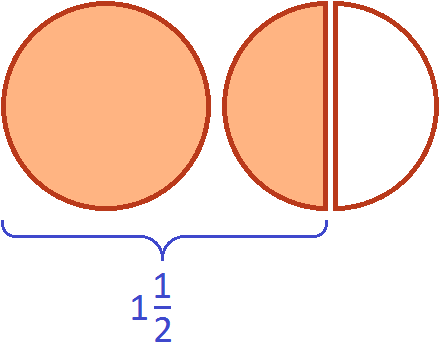
Если к двум целым пиццам прибавить половину пиццы, то получится две целые пиццы и ещё половина пиццы:
Пример 2. Найти значение выражения
Представим число 3 в виде дроби . Затем сложим дроби с разными знаменателями:
Это первый способ. Второй способ намного проще. Можно поставить знак равенства и записать целую и дробную часть вместе. То есть опустить знак сложения:
Пример 3. Найти значение выражения
Можно записать вместе число 2 и дробь , но этот ответ не будет окончательным, поскольку в дроби
можно выделить целую часть.
Поэтому в данном примере сначала нужно выделить целую часть в дроби . Пять вторых это две целых и одна вторая:
Теперь в главном выражении вместо дроби
запишем смешанное число
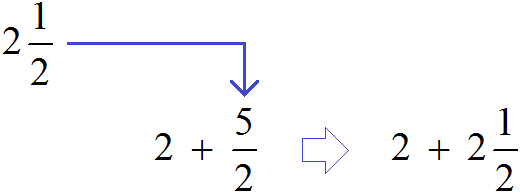
Получили новое выражение . В этом выражении смешанное число
запишем в развёрнутом виде:
Применим сочетательный закон сложения. Сложим две двойки, получим 4:
Теперь свернём полученное смешанное число:
Это окончательный ответ. Подробное решение этого примера можно записать следующим образом:
Сложение смешанных чисел
Встречаются задачи, в которых требуется сложить смешанные числа. Например, найти значение выражения . Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.
Для начала запишем смешанные числа в развёрнутом виде:
Применим сочетательный закон сложения. Сгруппируем целые и дробные части по отдельности:
Вычислим целые части: 2 + 3 = 5. В главном выражении заменяем выражение в скобках (2 + 3) на полученную пятёрку:
Теперь вычислим дробные части. Это сложение дробей с разными знаменателями. Как складывать такие дроби мы уже знаем:
Получили . Теперь в главном выражении
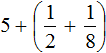
Теперь свернем полученное смешанное число:
Таким образом, значение выражения равно
. Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:
Подобные примеры нужно решать быстро, не останавливаясь на подробностях. Находясь в школе, нам пришлось бы записать решение этого примера следующим образом:
Если в будущем увидите такое короткое решение, не пугайтесь. Вы уже понимаете, что откуда взялось.
Пример 2. Найти значение выражения
Запишем смешанные числа в развёрнутом виде:
Сгруппируем целые и дробные части по отдельности:
Вычислим целые части: 5 + 3 = 8. В главном выражении заменяем выражение в скобках (5 + 3) на полученное число 8
Теперь вычислим дробные части:
Получили смешанное число . Теперь в главном выражении
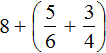
Получили выражение . В данном случае число 8 надо прибавить к целой части смешанного числа
. Для этого смешанное число
можно временно развернуть, чтобы было понятнее, что с чем складывать:
Сложим целые части. Получаем 9
Сворачиваем готовый ответ:
Таким образом, значение выражения равно
.
Полное решение этого примера выглядит следующим образом:
Для решения подобных примеров существует универсальное правило. Выглядит оно следующим образом:
Чтобы сложить смешанные числа, надо:
- привести дробные части этих чисел к общему знаменателю;
- отдельно выполнить сложение целых и дробных частей.
Если при сложении дробных частей получилась неправильная дробь, выделить целую часть в этой дроби и прибавить ее к полученной целой части.
Применение готовых правил допустимо в том случае, если суть темы полностью понятна. Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.
Пример 3. Найти значение выражения
Воспользуемся готовым правилом. Приведём дробные части к общему знаменателю, затем по отдельности сложим целые и дробные части:
Сложение целого и смешанного числа
Встречаются задачи, в которых нужно сложить целое и смешанное число. Например, сложить 2 и смешанное число . В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
Здесь смешанная дробь была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ
.
Попробуем изобразить это решение в виде рисунка. Если к двум целым пиццам прибавить три целые и треть пиццы, то получятся пять целых и треть пиццы:
Пример 2. Найти значение выражения
В этом примере, как и в предыдущем, нужно сложить целые части:
Осталось свернуть целую и дробную части, но дело в том, что дробная часть представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:
Вычитание дроби из целого числа
Встречаются задачи, в которых требуется вычесть дробь из целого числа. Например, вычесть из числа 1 дробь . Чтобы решить такой пример, нужно целое число 1 представить в виде дроби
, и выполнить вычитание дробей с разными знаменателями:
Если имеется одна целая пицца и мы вычтем из неё половину пиццы, то у нас получится половина пиццы:
Пример 2. Найти значение выражения .
Представим число 2 в виде дроби , и выполним вычитание дробей с разными знаменателями:
Если имеются две целые пиццы и мы вычтем из низ половину, то останется одна целая и половина пиццы:
Такие примеры можно решать в уме. Достаточно суметь воспроизвести их в своём воображении. К примеру, найдём значение выражения , не приводя на бумаге никаких вычислений.
Представим, что число 3 это три пиццы:
Нужно вычесть из них . Мы помним, что треть выглядит следующим образом:
Теперь представим, во что превратятся три пиццы, если отрезать от них эту треть
Получилось (две целых и две трети пиццы).
Чтобы убедиться в правильности решения, можно найти значение выражения обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:
Пример 3. Найти значение выражения
Представим число 3 в виде дроби . Затем выполним вычитание дробей с разными знаменателями:
Вычитание смешанного числа из целого числа
Теперь мы готовы к тому, чтобы вычесть смешанное число из целого числа. Найдём значение выражения .
Чтобы решить этот пример, число 5 нужно представить в виде дроби, а смешанное число перевести в неправильную дробь. После перевода смешанного числа
в неправильную дробь, получим дробь
. Теперь выполним вычитание дробей с разными знаменателями:
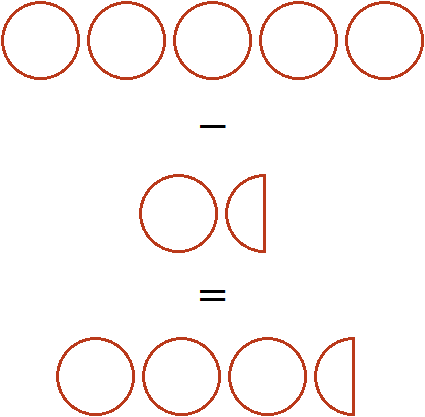
Если из пяти целых пицц вычесть одну целую и половину пиццы, то останутся три целые пиццы и половина пиццы:
Пример 2. Найти значение выражения
Представим 6 в виде дроби , а смешанное число
, в виде неправильной дроби. После перевода смешанного числа
в неправильную дробь, получим дробь
. Теперь выполним вычитание дробей с разными знаменателями:
Примеры на вычитание дроби из числа или вычитание смешанной дроби из числа опять же можно выполнять в уме. Этот процесс легко поддаётся воображению.
К примеру, если нужно быстро найти значение выражения , то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)
Тогда от той пиццы, от которой отрезали останется
пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:
Если на рисунке вы закроете рукой две третьих пиццы (она закрашена), то сразу всё поймёте.
Вычитание смешанных чисел
Встречаются задачи, в которых требуется вычесть из одного смешанного числа другое смешанное число. Например, найдём значение выражения:
Чтобы решить этот пример, нужно смешанные числа и
перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:
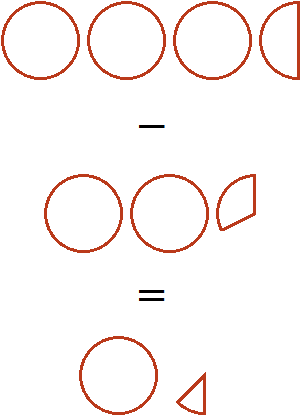
Если от трёх целых и половины пиццы вычесть две целые и треть пиццы, то останутся одна целая и одна шестая пиццы:
Пример 2. Найти значение выражения
Переводим смешанные числа и
в неправильные дроби и выполняем вычитание дробей с разными знаменателями:
К вычитанию смешанных чисел мы ещё вернёмся. В вычитании дробей есть немало тонкостей, которым новичок пока не готов. Например, возможен случай, когда уменьшаемое может оказаться меньше вычитаемого. Это может вывести нас в мир отрицательных чисел, которых мы ещё не изучали.
А пока изучим умножение смешанных чисел. Благо оно не такое сложное, как сложение и вычитание.
Умножение целого числа на дробь
Чтобы целое число умножить на дробь, достаточно умножить это целое число на числитель дроби, а знаменатель оставить без изменения.
Например, умножим число 5 на дробь . Чтобы решить этот пример, нужно число 5 умножить на числитель дроби
, а знаменатель оставить без изменения:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Если имеются пять целых пицц и мы возьмём от этого количества половину, то у нас окажется две целые пиццы и половина пиццы:
Пример 2. Найти значение выражения
Умножим число 3 на числитель дроби
В ответе получилась неправильная дробь , но мы выделили её целую часть и получили 2.
Также, можно было сократить эту дробь. Получился бы тот же результат. Выглядело бы это следующим образом:
Если имеются три целые пиццы и мы возьмём от этого количества две третьих, то у нас окажется две целые пиццы:
Пример 3. Найти значение выражения
Этот пример решается так же, как и предыдущие. Целое число и числитель дроби нужно перемножить:
Пример 4. Найти значение выражения
Умножим число 3 на числитель дроби
Умножение смешанного числа на дробь
Чтобы умножить смешанное число на дробь, нужно смешанное число перевести в неправильную дробь, затем выполнить перемножение обыкновенных дробей.
Пример 1. Найти значение выражения
Переведём смешанное число в неправильную дробь. После перевода это число превратится в дробь
. Затем можно будет умножить эту дробь на
Допустим, имеются одна целая и половина пиццы:
Умножить эти куски на означает взять от них две трети. Чтобы взять от них две трети, сначала разделим их на три равные части. Разделим пополам ту пиццу, которая слева. Тогда у нас получится три равных куска:
Теперь если мы возьмем (два куска из трёх имеющихся), то получим одну целую пиццу. Для наглядности закрасим эти два куска:
Поэтому значение выражения было равно 1
Умножение смешанных чисел
Встречаются задачи, в которых требуется перемножить смешанные числа. Например, перемножить и
. Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
Попробуем разобраться в этом примере с помощью рисунка. Допустим, имеются одна целая и половина пиццы:
Теперь разберемся со смешанным множителем . Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще
раза.
С множителем 2 всё понятно, он означает что одну целую и половину пиццы нужно взять два раза. Давайте возьмём два раза целую пиццу и половину:
Но ещё осталось взять от изначальной целой пиццы и половины, ведь множителем было смешанное число
. Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
Мы разделили нашу целую пиццу и половину на равные части, и теперь можем сказать, что является половиной от этих кусков. Половиной от этих кусков является пиццы. Это можно хорошо увидеть, если мы упорядочим наши равные кусочки следующим образом:
А если смотреть на изначальную целую пиццу и половину с точки зрения такого порядка, как на этом рисунке, то половиной от них является пиццы.
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Переводим смешанные числа в неправильные дроби и перемножаем эти неправильные дроби. Если в ответе получится неправильная дробь, выделим в ней целую часть:
Деление целого числа на дробь
Чтобы разделить целое число на дробь, нужно это целое число умножить на дробь, обратную делителю.
Например, разделим число 3 на дробь . Здесь число 3 — это делимое, а дробь
— делитель.
Чтобы решить этот пример, нужно число 3 умножить на дробь, обратную дроби . А обратная дробь для дроби
это дробь
. Поэтому умножаем число 3 на дробь
Допустим, имеются три целые пиццы:
Если мы зададим вопрос «cколько раз (половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».
Действительно, если мы разделим каждую пиццу пополам, то у нас получится шесть половинок:
Поэтому значение выражения равно 6.
Пример 2. Найти значение выражения
Чтобы решить этот пример, нужно число 2 умножить на дробь, обратную дроби . А обратная дробь для дроби
это дробь
Допустим, имеются две целые пиццы:
Зададим вопрос «Сколько раз пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби
. После выделения целой части в этой дроби получим
Теперь поставим вопрос так: «Сколько раз (одна целая и половина пиццы) содержится в двух пиццах?».
Чтобы ответить на этот вопрос, нужно найти в двух пиццах такое количество пиццы, которое изображено на следующем рисунке:
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:
А оставшаяся половина это треть от , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
Поэтому значение выражения равно
Пример 3. Найти значение выражения
Чтобы решить этот пример, нужно число 5 умножить на дробь, обратную дроби . А обратная дробь для дроби
это дробь
. Поэтому умножаем число 5 на
Дробь это 2 целых и
. Проще говоря, две целые и четверть пиццы:
А выражение определяет сколько раз
содержится в пяти целых пиццах. Ответом было смешанное число
.
То есть пиццы содержится в пяти целых пиццах
раза.
Давайте нащупаем в пяти пиццах два раза по
Белым цветом осталось не выделено две четверти. Эти две четверти представляют собой от
, которые не вместились. Двумя девятыми они являются по той причине, что в
пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:
Поэтому значение выражения равно
Деление дроби на целое число
Чтобы разделить дробь на целое число, нужно данную дробь умножить на число, обратное делителю. Таким делением мы занимались в прошлом уроке. Вспомним ещё раз.
Пример 1. Разделим дробь на число 2
Чтобы разделить дробь на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь
Пусть имеется половина пиццы:
Разделим её поровну на две части. Тогда каждая получившаяся часть будет одной четвертой пиццы:
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Чтобы решить этот пример, нужно дробь умножить на число, обратное числу 2. Обратное числу 2 это дробь
Пример 3. Найти значение выражения
Умножаем первую дробь на число, обратное числу 3. Обратное числу 3 это дробь
Деление целого числа на смешанное число
Встречаются задачи, в которых требуется разделить целое число на смешанное число. Например, разделим 2 на .
Чтобы решить этот пример, нужно делитель перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.
Переведём делитель в неправильную дробь, получим
. Затем умножим 2 на дробь, обратную дроби
. Обратная для дроби
это дробь
Допустим, имеются две целые пиццы:
Зададим вопрос «Сколько раз (одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:
А оставшаяся половина это треть от , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Переводим делитель в неправильную дробь, получаем
. Теперь умножаем число 5 на дробь, обратную дроби
. Обратная для дроби
это дробь
Сначала мы получили ответ , затем сократили эту дробь на 5, и получили
, но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ
Деление смешанного числа на целое число
Чтобы разделить смешанное число на целое число, нужно смешанное число перевести в неправильную дробь, затем умножить эту дробь на число, обратное делителю.
Например, разделим на 2. Чтобы решить этот пример, нужно делимое
перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
Переведём смешанное число в неправильную дробь, получим
.
Теперь умножаем на число, обратное числу 2. Обратное числу 2 это дробь
Допустим, имеется одна целая и половина пиццы:
Разделим это количество пиццы поровну на две части. Для этого сначала разделим на две части целую пиццу:
Затем разделим поровну на две части и половину:
Теперь если мы сгруппируем эти кусочки на две группы, то получим по пиццы в каждой группе:
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Переведём делимое в неправильную дробь, получим
. Теперь умножаем
на число, обратное числу 4. Обратное числу 4 это дробь
.
Деление смешанных чисел
Чтобы разделить смешанные числа, нужно перевести их в неправильные дроби, затем выполнить обычное деление дробей. То есть умножить первую дробь на дробь, обратную второй.
Пример 1. Найти значение выражения
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
Как решать дальше мы уже знаем. Первую дробь нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь
.
Дорешаем данный пример до конца:
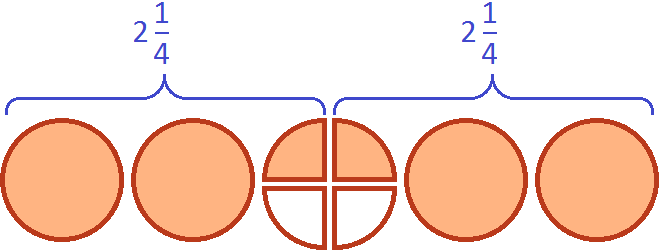
Допустим, имеются две целые и половина пиццы:
Если зададим вопрос «Сколько раз (одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:
Пример 2. Найти значение выражения
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
Теперь умножаем первую дробь на дробь, обратную второй. Обратная для дроби это дробь
Сначала мы получили дробь. Эту дробь мы сократили на 9. В результате получили дробь
, но такой ответ нас тоже не устроил и мы выделили в дроби
целую часть. В результате получили окончательный ответ
.
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
Решение:
Задание 2. Найдите значение выражения:
Решение:
Задание 3. Найдите значение выражения:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение выражения:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже