Как найти значение выражения егэ базовый уровень

Сайты, меню, вход, новости

---

Значение выражений

---

[su_box title=”Описание задания” style=”soft” box_color=”#c1e8cc” title_color=”#0c0a0a”]

В задании №5 ЕГЭ по математике базового уровня нам необходимо вычислить значение выражения, пользуясь различными правилами: формулами сокращенного умножения, знаниями тригонометрии, свойствами логарифмов и другими. Данное задание требует более глубоких знаний и значительно сложнее первого задания, где достаточно было знать элементарные математические операции.

Тематика заданий: значение выражений

Бал: 1 из 20

Сложность задания: ♦♦♦

Примерное время выполнения: 5-7 мин.

[/su_box]

Теория к заданию №5

В данном задании, кроме операций со степенями, о которых мы говорили в прошлых заданиях, необходимо помнить формулы сокращенного умножения:

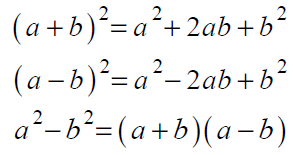
Кроме этого, очень часто встречаются задания на знания свойств логарифма:

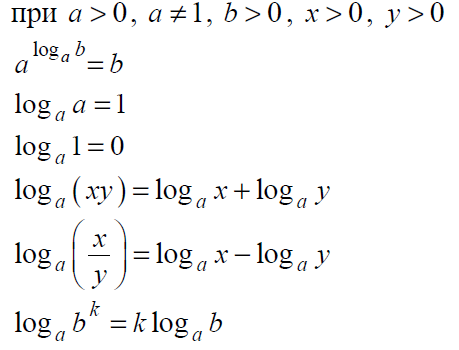
Полезными будут представления о тригонометрической окружности, по которой можно определять знаки тригонометрических функций:

---

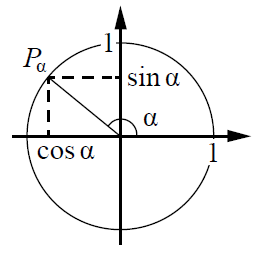
Разбор типовых вариантов заданий №5 ЕГЭ по математике базового уровня

---

Во всех заданиях необходимо найти значение выражения.

---

Вариант 5МБ1

Алгоритм выполнения

1. Представим угол 390° с учетом периодичности функции tg меньшим углом.
2. Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.
3. Выполним умножение.

Решение:

Функция tg является периодической с периодом 180°, то есть каждый раз при увеличении или уменьшении угла на 180° значение tg повторяется.

То есть tg α = tg (α + 180°) = tg (α – 180°)

tg 390° = tg (390° – 180°) = tg 210° = tg (210° – 180°) = tg 30°

Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.

tg 30° = √3/3

Подставим найденное значение в данное выражение.

20 · √3 · (√3/3) = (20 · √3 · √3)/3 = (20 · 3)/3 = 20

Решение в общем виде

Вычислим выражение, учитывая, что функция тангенс периодическая с периодом π радиан или 180°. Следовательно, угол 390° эквивалентен углу

и получаем выражение:

 

 

Ответ: 20.

---

Вариант 5МБ2

Алгоритм выполнения

1. Представим угол 420° с учетом периодичности функции tg меньшим углом.
2. Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.
3. Выполним умножение.

Решение №1:

Функция tg является периодической с периодом 180°, то есть каждый раз при увеличении или уменьшении угла на 180° значение tg повторяется.

То есть

tg α = tg (α + 180°) = tg (α – 180°)

tg 390° = tg (420° – 180°) = tg 240° tg (240° – 180°) = tg 60°

Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.

tg 60° = √3

Подставим найденное значение в данное выражение.

-50 · √3 · √3 = -50 · 3 = -150

Решение №2:

Заметим, что функция тангенс периодическая с периодом π радиан или 180°. Поэтому, тангенс угла 420° эквивалентен тангенсу угла в

,

получаем:

Ответ: -150.

---

Вариант 5МБ3

Алгоритм выполнения

1. Объединим подкоренные выражения под один корень.
2. Внесем под корень дробь.
3. Сократим дробь под корнем.
4. Представим произведение под корнем в виде произведения вторых степеней.
5. Вынесем из под корня множители.
6. Выполним умножение.

Решение:

Объединим подкоренные выражения под один корень. Имеем право так сделать использовав, свойство квадратного корня.

5/3 · √27 · √3 = 5/3 · √(27 · 3)

 

 

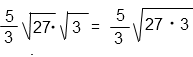
Внесем под корень дробь.

Корень квадратный, следовательно, чтобы внести дробь под знак корня нужно возвести ее в квадрат. То есть умножить сам на себя числитель и знаменатель.

(5/3)² = (5 · 5)/(3 · 3)

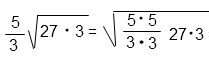
Сократим дробь под корнем на три дважды.

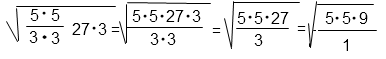
Представим произведение под корнем в виде произведения вторых степеней.

 

 

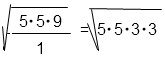
Вынесем из под корня множители и выполним умножение.

 

 

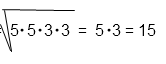
Решение в общем виде:

 

 

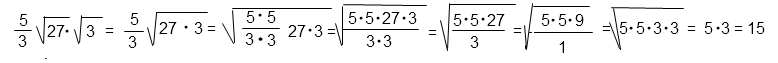
Ответ: 15.

---

Вариант 5МБ4

[su_note note_color=”#defae6″]

Найдите cos α, если sin α = 0,8 и 90° ‹ α ‹ 180°.

[/su_note]

Алгоритм выполнения

1. Запишем основное тригонометрическое тождество.
2. Подставим в основное тригонометрическое тождество все известные данные.
3. Решим полученное уравнение относительно cos α.
4. Выбрать корни, подходящие к условию задания.

Решение:

Запишем основное тригонометрическое тождество.

sin² α + cos² α = 1

Подставим в основное тригонометрическое тождество все известные данные.

0,8² + cos² α = 1

Решим полученное уравнение относительно cos α.

cos² α – неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.

cos² α = 1 – 0,8²

Чтобы найти вторую степень числа нужно число умножить само на себя.

0,8² = 0,8 · 0,8 = 0,64

cos² α = 1 – 0,8² 1 – 0,64 = 0,36

cos α = √0,36

cos α = 0,6 или -0,6

Условие 90° ‹ α ‹ 180° означает, что -1 ‹ соs α ‹ 0.

Следовательно данному условию удовлетворяет только один корень -0,6.

Ответ: -0,6.

---

Вариант 5МБ5

[su_note note_color=”#defae6″]

(2√13 −1)(2√13 +1).

[/su_note]

Алгоритм выполнения

В данном задании необходимо сразу заметить формулу сокращенного умножения – разность квадратов (последняя формула сокращенного умножения в теории выше).

Решение:

После этого, решение задания сводится к следующему:

(2√13 −1)(2√13 +1) = (2√13)² – 1²  = 4 • 13 – 1 = 51

Ответ: 51.

---

Вариант 5МБ6

[su_note note_color=”#defae6″]

5^log₅6+1 .

[/su_note]

Алгоритм выполнения

Сначала вспомним свойства степеней и разложим выражение следующим образом:

5^log₅6 • 5¹

Затем вспомним определение и свойство логарифма – это вторая строчка из нашей теории:

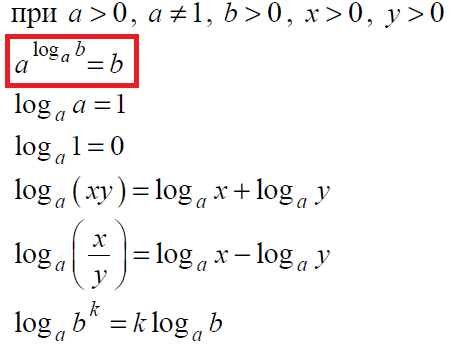
Решение:

 Получим:

6•5 = 30

Ответ: 30

---

Вариант 5МБ7

[su_note note_color=”#defae6″]

(√11-√3)(√11+√3)

[/su_note]

Алгоритм выполнения

1. Применяем формулу сокращенного умножения a²–b²=(a-b)(a+b).
2. Используем определение кв.корня: (√a)²=a.
3. Находим полученную разность целых чисел.

Решение:

Исходя из алгоритма, подставляем а=√11, а b=√3, тогда 11-3=8

Ответ: 8

---

Вариант 5МБ8

Алгоритм выполнения

1. Применяем тождество log_a(xy)=log_ax+log_ay.
2. Преобразовываем множители, стоящие под знаком логарифма, в степени.
3. Используем для выражения под знаком логарифма св-во степеней a^xb^x=(ab)^x.
4. Используем св-во логарифмов xlog_ab=log_ab^x.
5. Применяем тождество log_aa=1,.

Решение:

log₆27 + log₆8 = log₆27·8 = log₆3³·2³ = log₆(3·2)³ = log₆6³ = 3log₆6 = 3

Ответ:3

---

Вариант 5МБ9

Алгоритм выполнения

1. Вносим множитель √6 в скобки.
2. Выполняем умножение √24 и √6. Получим √144. Это число является полным квадратом: (√12)².
3. Перемножаем √6 и √6. Получаем (√6)².
4. Используя определение кв.корня (√а)²=а, находим, что (√12)²=12, а (√6)²=6.
5. Находим разность полученных целых чисел.

Решение:

Ответ: 6

---

Вариант 5МБ10

Найдите sinα, если

Алгоритм выполнения

1. Применим основное тригонометрическое тождество. В тождество подставим данное в условии числовое значение для косинуса.
2. Выполняем преобразование тождества, получаем числовой результат.
3. Определяем знак результата, исходя из величины угла α.

Решение: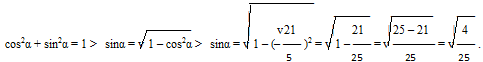

Ответ: 0,4

---

Вариант 5МБ11

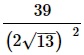
Алгоритм выполнения

1. Выполняем 1-ю по приоритетности операцию – возведение в степень (в знаменателе). Для этого используем св-во степеней (ab)²=a²·b². Далее для множителя (√13)² применяем формулу, определяющую понятие кв.корня: (√а)²=а.
2. Выполняем умножение в знаменателе.
3. Представляем число 39 в числителе как произведение 3·13.
4. Сокращаем дробь на 13.
5. Переводим полученную обыкновенную дробь в десятичную.

Решение: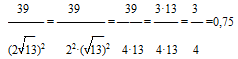

Ответ: 0,75

---

Вариант 5МБ12

Алгоритм выполнения

1. Применяем к показателю степени 2log₃7 св-во логарифмов log_b^ya^x=(x/y)log_ba. Получим log₃7².
2. Применяем св-во логарифмов a^log_a^b=b. В результате знак логарифма исчезает, остается только выражение 7², которое было под знаком логарифма.
3. Возводим 7 в квадрат.

Решение:

2log₃7 log₃7²

3 = 3 = 7² = 49

Ответ:49

---

Вариант 5МБ13

Алгоритм выполнения

1. Используем св-во корней √(a·b)=√a·√b. Таким способом √63 разложим на множители √9 и √7.
2. Сгруппируем одинаковые множители √7. Получим (√7)².
3. Основываясь на определении кв.корня (√а)²=а, представляем √9=(√3)².
4. Возводим полученные числа в квадрат.
5. Находим итоговое произведение.

Решение: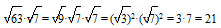

Ответ: 21

---

Вариант 5МБ14

Алгоритм выполнения

1. Используем св-во степеней x^a+b=x^a·x^b. Получим 2 множителя, первый из которых равен 7, а второй представляет собой степень с основанием 7 и показателем, содержащим логарифм.
2. Для второго множителя применим св-во логарифмов a^loga^b=b.
3. Находим результирующее произведение.

Решение:

Ответ: 21

---

Вариант 5МБ15

Алгоритм выполнения

1. Для cos 390⁰ используем ф-лу приведения cos (360⁰+α)=cos α. Получим cos 30⁰=√3/2. Записываем получившееся выражение в виде дроби со знаменателем 2.
2. Вычисляем произведение √3·√3 путем возведения в степень. Для этого используем определение кв.корня: (√а)²=а.
3. Сокращаем 20 в числителе и 2 в знаменателе на 2.
4. Находим конечное произведение.

Решение:

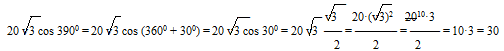
Ответ: 30

---

Вариант 5МБ16

Алгоритм выполнения

1. Преобразовываем часть выражения, взятую в скобки. Для этого представляем 49 как 7². Затем используем св-во логарифмов log_ba^x=xlog_ba, а далее св-во log_aa=1. Получаем 2.
2. Применяем св-во логарифмов log_aa=1.

Решение:

log₂(log₇49) = log₂(log₇7²) = log₂(2log₇7) = log₂2 = 1

Ответ: 1

Даниил Романович | Просмотров: 13.9k

Начиная с 2015 года, выпускники выбирают форму сдачи государственного экзамена по математике. ЕГЭ по данному предмету разделено на 2 уровня – базовый и профильный.

«Модель ЕГЭ по математике базового уровня предназначена для государственной итоговой аттестации выпускников, не планирующих продолжение образования в профессиях, предъявляющих специальные требования к уровню математической подготовки. Так как в настоящее время существенно возрастает роль общематематической подготовки в повседневной жизни, в массовых профессиях, в модели ЕГЭ по математике базового уровня, усилены акценты на контроль способности применять полученные знания на практике, развитие логического мышления, умения работать с информацией.

Выполнение заданий экзаменационной работы свидетельствует о наличии у участника экзамена общематематических умений, необходимых человеку в современном обществе. Задания проверяют базовые вычислительные и логические умения и навыки, умение анализировать информацию, представленную на графиках и в таблицах, использовать простейшие вероятностные и статистические модели, ориентироваться в простейших геометрических конструкциях. В работу включены задания базового уровня по всем основным предметным разделам: геометрия (планиметрия и стереометрия), алгебра, начала математического анализа, теория вероятностей и статистика.»¹

Задание №1, 2, 4, 5

Первое, второе, четвертое, пятое задания экзаменационной работы можно объединить, так как все они проверяют умения и навыки учащихся выполнять вычисления и преобразования. Первое задание предполагает действия с дробями, второе – со степенями, четвертое – на нахождение неизвестных компонент уравнения, пятое – решение уравнений. Причем, стоит отметить, что последнее из названных может включать в себя как линейное, квадратное, рациональное, так и показательное или логарифмическое выражения. Поэтому 1,2,4 задания посильны и ученикам 6-7 классов, а вот 5 – в зависимости от сложности уравнения может быть выполнено учеником 7-11 класса.

Приведем примеры заданий

1. Найдите значение выражения:  .

Пояснение.

Выполним преобразования: .

Ответ: −500.

1. Найдите значение выражения  .

Пояснение.

Преобразуем выражение, используя свойства степени:  .

Ответ: 40.

1. Найдите m из равенства F = ma, если F = 84 и a = 12.

Пояснение.

Подставляя значения F и a получаем: , откуда  . 

Ответ: 7.

1. Найдите значение выражения  .

Пояснение.

Выполним преобразования:

Ответ: -1.

Задание №3, 6

Третье и шестое задания экзаменационной работы – задачи, которые проверяют умение учащихся применять полученные знания в обыденных житейских ситуациях. Третье задание связано с процентами. В данных заданиях представлены задачи, посильные ученику 5-6 класса.

Примеры заданий.

Железнодорожный билет для взрослого стоит 720 рублей. Стоимость билета для школьника составляет 50% от стоимости билета для взрослого. Группа состоит из 15 школьников и 2 взрослых. Сколько рублей стоят билеты на всю группу? 

Пояснение.

1. Билет для ребенка стоит 720  0,5 = 360 руб. Стоимость билетов на 15 школьников и двух взрослых составляет 
   360  15 + 720  2 = 5400 + 1440 = 6840 руб.

Ответ: 6840.

1. Павел Иванович купил американский автомобиль, спидометр которого показывает скорость в милях в час. Американская миля равна 1609 м. Какова скорость автомобиля в километрах в час, если спидометр показывает 65 миль в час? Ответ округлите до целого числа. 

Пояснение.

Если спидометр показывает скорость 65 миль в час, значит, в километрах это будет 65  1,609 = 104,585 км в час. 

Ответ: 105.

Задание №7

Седьмое задание экзаменационной работы предполагает проверку умений учащихся решать уравнения, при этом в данном задании могут встретится:

• линейные, квадратные, кубические уравнения;

• рациональные уравнения;

• иррациональные уравнения ;

• показательные уравнения;

• логарифмические уравнения;

• тригонометрические уравнения.

Первые три типа уравнений изучаются в курсе основной школы, а вот последние – в курсе старшей школы.

Приведем пример задания.

Решите уравнение  . В ответе напишите наибольший отрицательный корень.

Пояснение.

Решим уравнение:  .

Значению k=0 соответствует x=-1. Положительным значениям параметра соответствуют положительные значения корней, отрицательным значениям параметра соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число −1. 

Ответ:  −1.

Задание №8

Данное задание представляет собой простейшую задачу геометрического содержания, для решения которых необходимо уметь описывать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем. Задание посильно ученику 7-9 класса.

Примеры заданий.

Два садовода, имеющие прямоугольные участки размерами 35 м на 40 м с общей границей, договорились и сделали общий прямоугольный пруд размером 20 м на 14 м (см. чертёж), причём граница участков проходит точно через центр. Какова площадь (в квадратных метрах) оставшейся части участка каждого садовода?

Пояснение.

Площадь каждого из участков равна 35 · 40 = 1400 кв. м, а площадь пруда равна 20 · 14 = 280 кв. м. На каждом участке находится половина пруда, занимая 140 кв. м. Поэтому площадь оставшейся части каждого из участков равна 1400 − 140 = 1260 кв. м. 

Ответ: 1260.

Задание №9, 11, 14

Данные задания связаны с анализом таблиц. Учащиеся должны уметь пользоваться основными единицами массы, длины, времени, скорости, площади и объема, выражать более крупные единицы через мелкие и наоборот. Такое задание посильно ученикам 5-6 классов.

Примеры заданий.

1. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. 

ВЕЛИЧИНЫ

ВОЗМОЖНЫЕ ЗНАЧЕНИЯ

А) рост ребёнка

Б) толщина листа бумаги

В) длина автобусного маршрута

Г) высота жилого дома

1) 32 км

2) 30 м

3) 0,2 мм

4) 110 см

Пояснение.

Рост ребёнка может быть равен 110 см, толщина листа бумаги может составлять 0,2 мм, длина автобусного маршрута — 32 км, высота жилого дома — 30 м. 

Ответ: 4312.

1. На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по 18 июля 1981 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линиями. Определите по рисунку, какой была наименьшая среднесуточная температура в период с 6 по 16 июля. Ответ дайте в градусах Цельсия. 

Пояснение.

Наименьшая температура с 6-го по 16-ое июля была 16-го июля и составила 16°С. 

Ответ: 16.

1. На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее с момента запуска двигателя, на оси ординат — температура двигателя в градусах Цельсия.

Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале. 

ИНТЕРВАЛЫ ВРЕМЕНИ

ХАРАКТЕРИСТИКИ ПРОЦЕССА

А) 0−2 мин.

Б) 2–4 мин.

В) 4–6 мин.

Г ) 8–10 мин.

1) температура росла медленнее всего

2) температура падала

3) температура росла быстрее всего

4) температура не превышала 40 °С

 В таблице под каждой буквой, соответствующей интервалу времени, укажите номер характеристики процесса. 

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: 

А

Б

В

Г

Пояснение.

На интервале 0−2 минуты температура возросла от примерно 18 °С до примерно 38 °С.

На интервале 2−4 минуты температура возросла от примерно 38 °С до примерно 45 °С.

На интервале 4−6 минут температура возросла от примерно 45 °С до примерно 74 °С.

На интервале 8−10 минут температура упала от 90 °С до примерно 78 °С.

Таким образом, получаем соответствие: A — 4, Б — 1, В — 3, Г — 2.

 Ответ: 4132.

Задание №10

Данное задание экзаменационной работы посвящено элементам комбинаторики, теории вероятности и статистики. Для успешного выполнения данного задания от учащихся требуется знание классического определения вероятности, теорем о вероятностях событий, и умение применять их на практике. Комбинаторика как отдельный, самостоятельный раздел не изучается в курсе основной школы. Умение решать комбинаторные задачи вырабатывается при изучении математики 5-6 классов, где комбинаторика представлена фрагментарно. Понятие вероятности и задачи, посвященные ее классическому определению, разбираются в курсе 9 класса, а вот теоремам о вероятностях событий отводится время в курсе изучения алгебры 11 класса. Целесообразнее данное задание разбирать с одиннадцатиклассниками, которые уже изучили начала теории вероятности в полном объеме школьной программы. Приведем примеры заданий:

Игральную кость с 6 гранями бросают дважды. Найдите вероятность того, что хотя бы раз выпало число, большее 3.

Пояснение.

Возможность появления числа в первом и втором броске не зависят друг от друга. Вероятность того, что на игральной кости выпадет число меньше, либо равное трёх: 1 − 0,5 =  0,5. Поэтому вероятность того, что ни разу оба раза число меньше либо равное трём равна 0,5 · 0,5 = 0,25. Следовательно, вероятность того, что хотя бы раз выпадет число большее трёх равна 1 − 0,25 = 0,75.

Ответ: 0,75.

Задание №12

Вычислительные навыки, умение работать с рациональными числами, анализировать, читать графики, формируемые в курсе математики 5-6 классов и алгебры 7 класса, — достаточная база, которая позволяет выполнить данное задание ЕГЭ. Приведем пример задания.

Для обслуживания международного семинара необходимо собрать группу переводчиков. Сведения о кандидатах представлены в таблице.

 Переводчики

Языки

Стоимость услуг

(рублей в день)

1

Немецкий, испанский

7000

2

Английский, немецкий

6000

3

Английский

3000

4

Английский, французский

6000

5

Французский

2000

6

Испанский

4000

Пользуясь таблицей, соберите хотя бы одну группу, в которой переводчики вместе владеют четырьмя иностранными языками: английским, немецким, французским и испанским, а суммарная стоимость их услуг не превышает 12 000 рублей в день. В ответе для собранной группы укажите номера переводчиков без пробелов, запятых и других дополнительных символов.

Пояснение.

Заметим, что стоимость услуг переводчиков, знающих только английский и французский языки меньше стоимости услуг переводчика, знающего одновременно английский и французский языки, поэтому при подборе вариантов четвёртого переводчика можно не учитывать. Переводчика, знающего только немецкий язык нет, поэтому в группу необходимо взять либо первого, либо второго переводчика.

В первом случае необходимо включить в группу переводчиков, знающих английский и французский языки; дешевле выбрать переводчиков 3 и 5, тогда стоимость услуг составит 12 000 рублей в день. Остальные варианты дороже.

Во втором случае необходимо включить в группу переводчиков, знающих французский и испанский языки; дешевле выбрать переводчиков 5 и 6, тогда стоимость услуг составит 12 000 рублей в день. Остальные варианты дороже.

Таким образом, группа переводчиков, удовлетворяющая всем условиям, может быть собрана из переводчиков 1, 3 и 5 или из переводчиков 2, 5 и 6. 

Ответ: 135 или 256.

Задание №13

Задание № 13 связано с умением решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов) и использовать при решении стереометрических задач планиметрические факты и методы. Эти умения вырабатываются в курсе изучения стереометрии 10-11 класса.

Пример задания.

В цилиндрический сосуд налили 2000 см³ воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см³.

Решение.

Объём детали равен объёму вытесненной ею жидкости. Объём вытесненной жидкости равен 9/12 исходного объёма: 

.

Ответ: 1500.

Задание №15

Пятнадцатое задание экзаменационной работы – планиметрическая задача. Для успешного выполнения данного номера учащемуся необходимо владеть основными геометрическими фактами, теоремами и аксиомами, изученными в 7-9 классах.

Пример задания.

 В треугольнике ABC угол A равен 30˚, CH – высота, угол BCH равен 22˚. Найдите угол ACB. Ответ дайте в градусах.

Пояснение. 

Ответ: 38.

Задание №16

Задание № 16 связано с умением решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов) и использовать при решении стереометрических задач планиметрические факты и методы. Эти умения вырабатываются в курсе изучения стереометрии 10-11 класса. Данное задание во многом схоже с №13, но более сложное. Приведем пример задания.

Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/π.

Пояснение.

Объем данной фигуры равен разности объемов цилиндра с радиусом основания 5 и высотой 5 и цилиндра с той же высотой и радиусом основания 2:

 Ответ: 105.

Задание №17

Это задание на сопоставление проверяет умение учащихся решать уравнения и неравенства. Согласно спецификации, в нем могут встретится линейные, квадратные, рациональные, показательные и логарифмические уравнения и неравенства, а также их системы. Изучаемые разделы -представлены в курсе алгебры 7-11 класса.

Пример задания.

На координатной прямой точками отмечены числа a, b, с, d и m. Установите соответствие между указанными точками и числами из правого столбца. 

ТОЧКИ

ЧИСЛА

1) 

2) 

3) 

4) 

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: 

a

b

с

d

Пояснение.

Заметим, что  примерно равно . Следовательно,  .  Таким образом, точка a соответствует числу 3m, b — числу  , c — числу  , d — числу 

Задание №18

В данном задании проверяется умение строить и исследовать простейшие математические модели. Здесь представлены задачи логического содержания. Их нельзя отнести к какому –либо классу, так как на протяжении всего изучения математики развивается логическое мышление учащихся.

Пример задания.

Пять жильцов многоквартирного дома — Андрей, Борис, Виктор, Денис и Егор — имеют различный возраст. При этом известно, что возраст Андрея больше, чем сумма возрастов Бориса и Виктора, Виктор старше Дениса, но младше Егора. Выберите утверждения, которые следуют из приведённых данных.

1) Андрей самый старший из жильцов

2) Егор старше Бориса

3) Андрей старше Дениса

4) Борис старше Егора 

В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Пояснение.

Пусть А, Б, В, Д и Е — соответственно возрасты Андрея, Бориса, Виктора, Дениса и Егора. Из условия получаем неравенства: А > Б + В,  В > Д,  В < Е. Откуда получаем: Д < В < Е, А > Б, А > В.

1) Из условия не следует, что Андрей старший из жильцов. Например, Егор может быть старше Андрея.

2) Из условия не следует, что Егор старше Бориса.

3) Из полученных уравнений следует, что Андрей старше Дениса.

4) Борис не обязательно старше Егора.

 Таким образом, верным является утверждение 3. 

Ответ: 3.

Задание №19

В данном задании проверяется умение строить и исследовать простейшие математические модели. Здесь представлены задачи логического содержания. Их нельзя отнести к какому –либо классу, так как на протяжении всего изучения математики развивается логическое мышление учащихся. Если ориентироваться на спецификацию и демоверсию 2015 года, данное задание больше ориентировано на знание признаков и свойств делимости чисел, которые изучаются в 5-6 классах. Приведем пример задания.

Найдите шестизначное натуральное число, которое записывается только цифрами 1 и 0 и делится на 24.

Пояснение.

Чтобы число делилось на 24 оно должно делится на 3 и на 8.

Число делится на 8, если три его последние цифры образуют число, делящееся на 8. Искомое число записывается только нулями и единицами, значит, оно заканчивается на 000.

Число делится на 3, если его сумма цифр числа делится на 3. Поскольку три последние цифры числа нули, первые три должны быть единицами.

Таким образом, единственное число, удовлетворяющее условию задачи, это число 111 000.

 Ответ: 111 000.

Задание №20

Последнее задание экзаменационной работы также проверяет умение учащихся строить и исследовать простейшие математические модели. Данный номер предполагает, что учащиеся умеют преобразовывать выражения, содержащие арифметические операции, степени корни, знакомы с арифметическими и геометрическими прогрессиями, что формируется к 9 классу основной школы. Приведем пример задания.

Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 3 капли, а в каждый следующий день — на 3 капли больше, чем в предыдущий. Приняв 30 капель, он ещё 3 дня пьёт по 30 капель лекарства, а потом ежедневно уменьшает приём на 3 капли. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?

Пояснение.

На первом этапе приёма капель число принимаемых капель в день представляет собой возрастающую арифметическую прогрессию с первым членом, равным 3, разностью, равной 3 и последним членом, равным 30. Следовательно,

этап, когда число капель в день возрастает продолжается дней. Суммарное число капель, принятых в этот период, представляет собой сумму арифметической прогрессии: капель.

 Затем в течение трёх дней пациент принимает ещё капель.  Последний этап приёма капель длится дней. Аналогично первому этапу: капель.

  Таким образом, за весь курс приёма пациенту нужно принять 165 + 90 + 135 = 390 капель. То есть нужно приобрести не меньше   пузырьков лекарства. Минимальное количество пузырьков лекарства — 2.

 Ответ: 2.

Общие выводы по базовому уровню ЕГЭ

Общие выводы по структуре ЕГЭ можно представить в таблице, где номеру задания соответствует класс, в котором данный тип изучается.

№ задания

Класс

№ задания

Класс

1

5-7

11

5-6

2

5-7

12

5-7

3

5-6

13

10-11

4

5-7

14

5-6

5

7-11

15

7-9

6

5-6

16

10-11

7

7-11

17

7-11

8

7-9

18

—

9

5-6

19

—

10

9-11

20

9

Из таблицы можно увидеть, что большая часть работы содержит задания, посильные для выпускника 9 класса. Пять заданий экзаменационной работы требуют знаний, полученных в старшей школе. И имеются два задания логического характера, аналоги которым либо не встречаются в школьных учебниках, либо освещены достаточно мало.

1Спецификация контрольных измерительных материалов для проведения в 2015 году единого государственного экзамена по математике. Базовый уровень

Итоговый экзамен по математике сдают все. Те, кто поступает на гуманитарные специальности (филология, юриспруденция, международные отношения) выбирают базовый уровень — вопросы в нем легче, а оценки «3» достаточно для получения аттестата. Профильный уровень сдают будущие экономисты, инженеры и программисты — на этих специальностях без знания математики не обойтись, ее обязательно изучают на первых курсах. Но это непростой предмет. Даже в профильных математических классах не всегда дают достаточно знаний. Если ваша цель — поступление в топовый вуз на техническую специальность, без курсов подготовки к ЕГЭ не обойтись. Это касается не только профильного уровня, но и ЕГЭ по математике базового. «Задание 2, как решать?» — часто спрашивают школьники, сдающие этот экзамен. В этой статье мы проведем разбор задания 2 из ЕГЭ по математике профильного и базового уровня. 

Теория

В задании 2 ЕГЭ по профильной математике теория достаточно простая. Это номер базового уровня сложности, он приносит 1 балл. Выпускникам дается график (иногда — диаграмма), нужно проанализировать его в соответствии с условием. Определение аргумента функции, поиск максимального и минимального значения — навыки, которые нужны для этого задания ЕГЭ. 2 часть математики профильного уровня тоже содержит номера с графиками, поэтому эта теория пригодится и там. То, что нужно знать для решения задания 2 ЕГЭ по математике профильного уровня: 

• функция и ее график;
• оси абсцисс и ординат;
• промежутки возрастания и убывания функции;
• области определения и значения функции;
• максимум и минимум функции;
• наибольшее и наименьшее значения на промежутке;
• диаграммы;
• цена деления на графике. 

Перечисленные понятия нужны для сдачи любого уровня ЕГЭ. Но задание 2 по базовой математике проверяет другие навыки. В нем выпускник должен произвести вычисления со степенями. Этот номер тоже считается легким, однако для его выполнения нужно знать куда больше теории. Формулы для ЕГЭ по базовой математике, к заданию 2:

• определение степени — an = a • a • a … • a, где n — натуральное число. a называют основанием степени, n — показателем. 
• a0 = 1.
• a1 = a.
• a-n = 1 / an.
• anm=man.
• an • am = an+m.
• an • bn = (a • b)n.
• an / am = an-m.
• an / bn = (a / b)n.

Разбор задания 2

Решение задания 2 по математике ЕГЭ мы начнем с профильного уровня. 

Задача. Замеры температуры проводились в течение 3 дней. Какой была минимальная температура 18 апреля? 

Решение. Подобное задание 2 на ЕГЭ по математике профильного уровня кажется очень простым, однако в нем легко ошибиться. Обратим внимание на два момента: «18 апреля» и «минимальная». Для начала отсекаем колонки, относящиеся к 19 и 20 апреля — про них ничего не спрашивают. После этого ищем самую низкую точку и находим ее ординату. 

Ответ: 6.

Задача. В помещении стоит кондиционер с датчиком температуры. Когда она достигает определенного максимального значения, кондиционер включается. Когда комната остужается до необходимой температуры, кондиционер автоматически выключается. На графике показана зависимость температуры от времени. Укажите, сколько минут кондиционер был выключен.

Решение. В этом номере важно умение логически рассуждать. Когда кондиционер отключен, температура увеличивается. На графике это показывается ростом функции вверх. Чтобы определить, сколько минут кондиционер был выключен, нужно найти область возрастания функции. Это промежуток между числами 6 и 9 на оси абсцисс. Теперь мы ищем время: 9 – 6 = 3.

Ответ: 3.

За выполнение такого простого номера можно получить 1 балл на экзамене по математике. Разбор задания 2 ЕГЭ мы продолжим базовым уровнем. Здесь встречаются несколько типов вопросов: степенные выражения с одинаковыми и разными основаниями, поиск частного, произведения и суммы. Чтобы посмотреть все существующие виды заданий, зайдите на «Решу ЕГЭ» по базовой математике. Задание 2 там представлено более чем 40 вариантами. А в рамках этой статьи мы разберем несколько примеров задания 2 из ЕГЭ по математике базового уровня. 

Найти значение выражения

Задача. 4 • 72 + 6 • 72.

Решение. У слагаемых есть общий множитель, который мы можем вынести за скобку. После этого считаем выражение в скобке, потом возводим число в степень и перемножаем: (4 + 6) • 72 = 10 • 72 = 10 • 49 = 490.

Ответ: 490.

Найти значение выражения (разные основания)

Задача. 8^0,76 • 64^0,12.

Решение. Нужно привести степени к одинаковому основанию, представив 64 как 82. После этого их можно перемножить: 8^0,76 • 64^0,12 = 8^0,76 • (8)^2*0,12 = 8^0,76+0,24 = 8¹ = 8.

Ответ: 8.

Найти значение выражения (одинаковые основания)

Задача. 26 • 2-2 / 22.

Решение. В данном примере расчеты можно провести сразу же. Умножение степеней с одинаковым основанием заменяем на сложение показателей, деление — на их вычитание: 26 + (-2) – 2 = 26 – 4 = 22 = 4.

Ответ: 4. 

Найти частное от деления

Задача. 1,6 • 102 : 4 • 10-2.

Решение. У степеней одинаковое основание, поэтому мы можем поделить их, найдя разность показателей. После этого мы делим числа без степеней и выполняем умножение: 1,6 : 4 • 102 – (-2) = 1,6 : 4 • 104 = 1,6 : 4 • 10000 = 0,4 • 10000 = 4000.

Ответ: 4000.

Найти произведение

Задача. 4 • 105 • 2,3 • 10-7.

Решение: Степени имеют одинаковые основания, поэтому мы можем умножить их, сложив показатели. После этого результат умножаем на остальные числа: 4 • 2,3 • 105 + (-7) = 4 • 2,3 • 10-2 = 4 • 2,3 • 0,01 = 9,2 • 0,01 = 0,092. 

Ответ: 0,092.

Найти сумму

Задача. 9,4 • 102 + 2,1 • 103.

Решение. Мы возводим числа в степень, затем выполняем умножение и сложение: 9,4 • 100 + 2,1 • 1000 = 940 + 2100 = 3040.

Ответ: 3040. 

Теперь вы знаете чуть больше теории для ЕГЭ по математике. Задание 2 из профильного уровня достаточно легкое (хотя без практики тут тоже не обойтись), а вот в базе придется рассуждать и выполнять вычисления. Но и его можно выполнить без труда, если должным образом подготовиться к ЕГЭ. Однако, лучший результат всегда дают занятия с опытными преподавателями, знающими специфику экзамена. Если нанимать репетитора для вас дорого, обратите внимание на курсы. Там разбирают не только задание 2 ЕГЭ по математике, но и многие другие номера, в том числе вторую часть. Грамотная подготовка — ключ к хорошим баллам, а значит, и месту на бюджете.