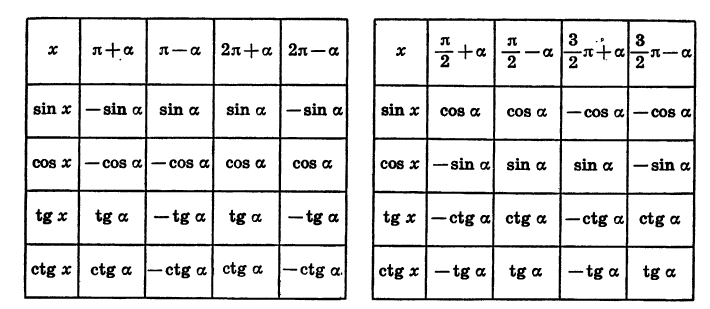
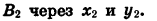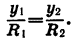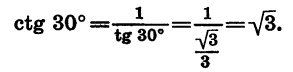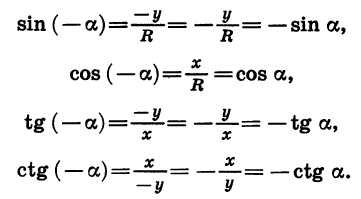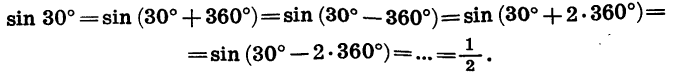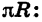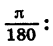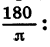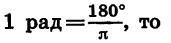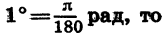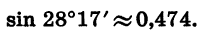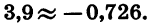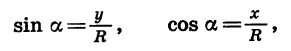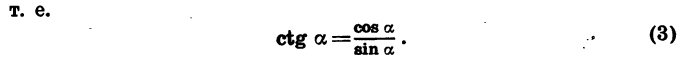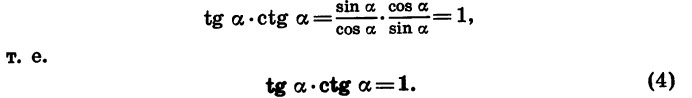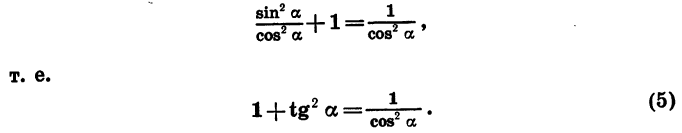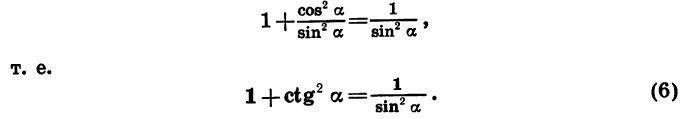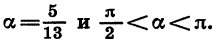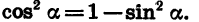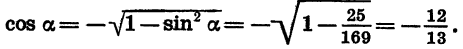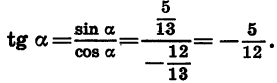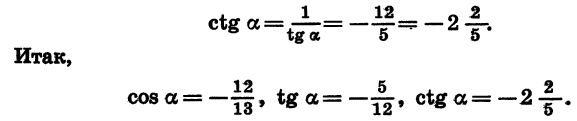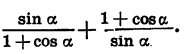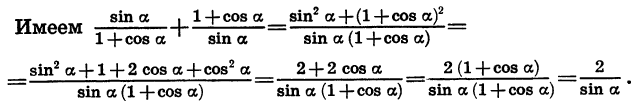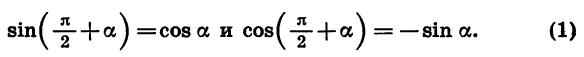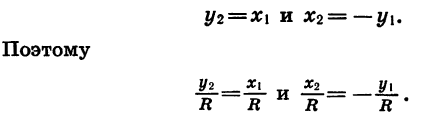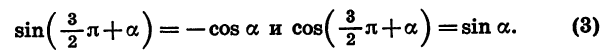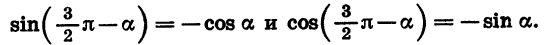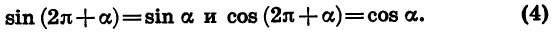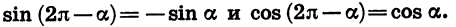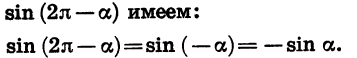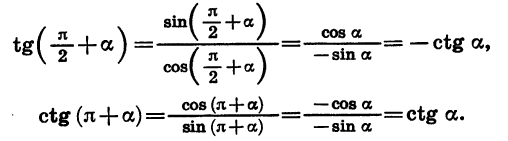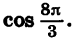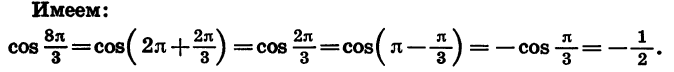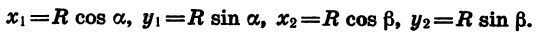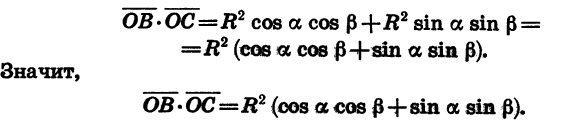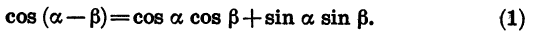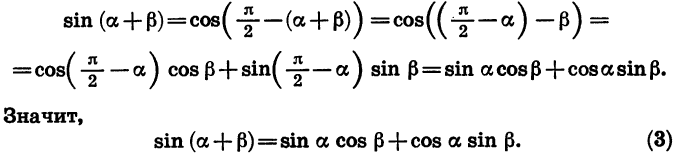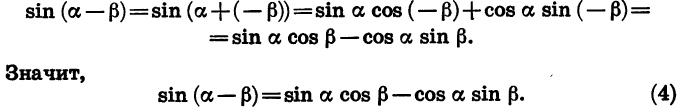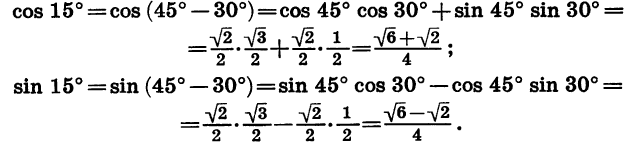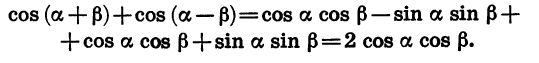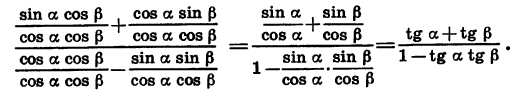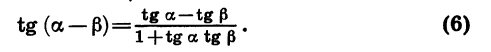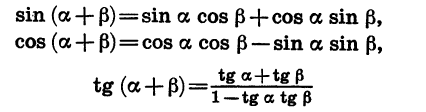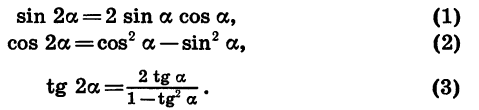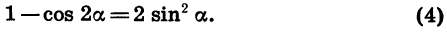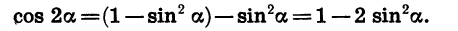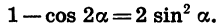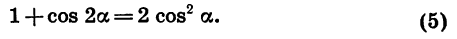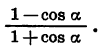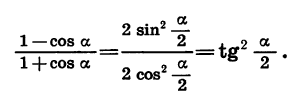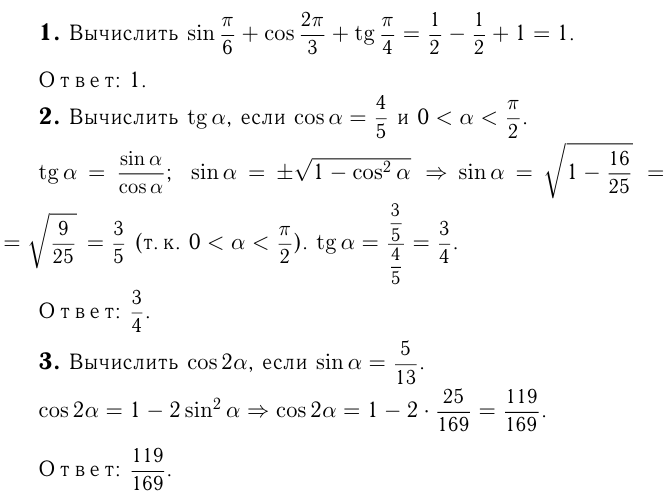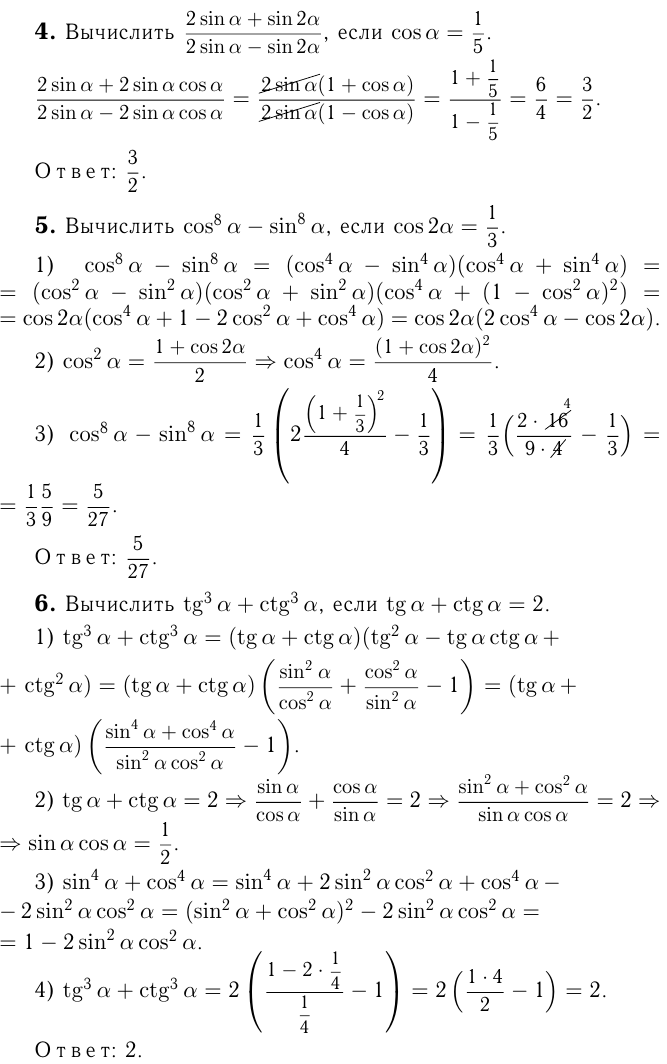Тригонометрические выражения
Тригонометрические выражения. Друзья! Для вас очередная статья с примерами на вычисление тригонометрических выражений. Примеры довольно простые, большинство из них, при определённом навыке, можно решить устно. Если вы основательно изучили тригонометрию и уяснили все важные и необходимые основы, то с решением не будет никаких трудностей.
Что используется в ходе решения данных выражений: формулы приведения, свойства периодичности тригонометрических функций, свойство чётности нечётности, формулы – синуса и косинуса двойного аргумента и, конечно же, основное тригонометрическое тождество.
— если в выражении видите, что один угол больше другого в два раза, то смело используйте соответствующую тригонометрическую формулу двойного аргумента;
— если вы видите, что сумма данных углов (или их разность) составляет 90, 180, 270, 360 градусов, то применяйте формулы приведения.
Последнюю статью с выражениями можно посмотреть здесь (там также использовались формулы функций двойного аргумента).
17289. Найдите значение выражения
Используем формулу синуса двойного аргумента:
Выражение в числителе «сворачиваем»:
*Второй путь: можно было использовать эту же формулу преобразовав знаменатель.
63139. Найдите значение выражения
Для решения этого примера достаточно знать формулу косинуса двойного аргумента:
63229. Найдите значение выражения
В данном случае 63 градуса представляем как разность 90 0 – 27 0
63763. Найдите значение выражения
63819. Найдите значение выражения
Используем формулу приведения косинуса. Представим 153 0 как разность 180 0 – 27 0 :
63875. Найдите значение выражения
Используем формулу приведения для тангенса. Представим 148 0 как разность 180 0 – 32 0 :
63929. Найдите значение выражения
63985. Найдите значение выражения
Используем формулы приведения:
*Применили формулу тригонометрии:
97369. Найдите значение выражения
Применяем формулу синуса двойного аргумента в числителе, и формулу приведения в знаменателе:
97967. Найдите значение выражения
Применяем формулу синуса двойного аргумента:
64097. Найдите значение выражения
64149. Найдите значение выражения
Используем формулы приведения и основное тригонометрическое тождество:
64205. Найдите значение выражения
Используем формулу приведения и основное тригонометрическое тождество:
63519. Найдите значение выражения
Косинус функция чётная, то есть
Её период равен 2Пn, то есть
Используем формулу приведения для косинуса:
63587. Найдите значение выражения
Период тангенса равен 180 градусам (Пи радиан), функция тангенса нечётная:
63651. Найдите значение выражения
Применяем свойство нечётности синуса, выделяем период и используем формулу приведения:
Источник
Найти значение выражения с косинусами и синусами и косинусами
Боковая сторона равнобедренного треугольника равна 7, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.
Сумма двух равных углов при основании треугольника равна 60°, поэтому каждый из них равен 30°. Тогда по теореме синусов
В равнобедренном треугольнике ABC с основанием AB боковая сторона равна Найдите длину высоты AH.
Проведем из вершины C высоту CK, и заметим, что Выразим косинус через синус:
откуда
Далее имеем: и тогда
Внимательный читатель заметит, что рисунок неверный! Действительно, синус угла при основании равен 0,25, значит, сам угол меньше 45°. Следовательно, угол при вершине больше 90° — треугольник тупоугольный. Тем не менее, решение верное: остроугольность треугольника в решении не использовалась, все рассуждения сохраняют свою силу.
Источник
Алгебра
Лучшие условия по продуктам от Тинькофф по этой ссылке
Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера
. 500 руб. на счет при заказе сим-карты по этой ссылке
Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке
План урока:
Основное тригонометрическое тождество
Несложно догадаться, что синус и косинус угла – это величины, связанные друг с другом. Отложим на единичной окружности произвольный угол α и опустим из точки А перпендикуляр на ось Ох, в некоторую точку В:
Изучим треугольник АОВ. Он прямоугольный, а потому для него можно записать теорему Пифагора:
Мы рассматриваем единичную окружность, а потому ОА = 1, ОВ = соsα, AB = sinα. Подставив эти величины в равенство, получим тождество:
sin 2 α + соs 2 α = 1
Его называют основным тригонометрическим тождеством, ведь именно оно связывает значение двух прямых тригонометрических ф-ций – синуса и косинуса.
Задание. В прямоугольном треугольнике есть угол α. Известно, что sin α = 0,8. Чему равен соsα?
Решение. Подставим в основное тригон-кое тождество значение sinα = 0,8 и получим уравнение:
sin 2 α + соs 2 α = 1
соsα = – 0,6 или соsα = 0,6
Нашли два возможных значения косинуса. Но по условию α – это острый угол, ведь в прямоугольном треугольнике угол не может быть больше 90°. То есть угол α относится к первой четверти, а потому его косинус положителен. Значит, соsα = 0,6.
Рассмотренный пример показал, что одному заданному значению синуса соответствует сразу два противоположных друг другу значения косинуса. Верно и обратное. Действительно, отложим по оси Ох некоторую величину соsα и проведем вертикальную линию, чтобы найти соответствующие ему значения синуса. Она пересечет единичную окружность в двух точках с противоположными ординатами:
По этой причине при решении задач на использование основного тригон-кого тождества обычно указывают, к какой четверти относится угол α.
Задание. Вычислите sinα, если соsα = 0,28 и α принадлежит IV четверти.
sin 2 α + соs 2 α = 1
sin α = –0,96 или sin α = 0,96
Так как α принадлежит IV четверти, то sinα должен быть отрицательным, поэтому sinα = – 0,96.Напомним, что в IV четверти значение косинуса положительно, ведь соответствующая ей дуга единичной окружности располагается правее оси Оу, то есть абсциссы точек, принадлежащих ей, положительны.
Задание. Найдите tgα, если sinα = 5/13 и π/2 2 α + соs 2 α = 1
соs 2 α = 1 – sin 2 α = 1 – (5/13) 2 = 169/169 – 25/169 = 144/169
соsα = – 12/13 или соsα = 12/13
Условие π/2 2 α + соs 2 α = 1
Далее поделим его на величину соs 2 α:
Крайнее левое слагаемое – это величина tg 2 α, а следующая дробь равна единице, так как у неё совпадают числитель и знаменатель:
В итоге нам удалось получить ф-лу, которая связывает значение тангенса и косинуса угла. Есть такая формула и для котангенса. Для ее получения необходимо поделить основное тригон-кое тождество на sin 2 α:
Задание. Известно, что tgα = 0,75. Найдите соsα и sinα, если угол α принадлежит III четверти.
Просто подставляем в ф-лу известное значение тангенса и решаем получившееся уравнение. Для простоты вычислении заменим десятичную дробь 0,75 на обычную 3/4:
Так как угол относится к III четверти, где косинус отрицателен, то
Синус угла найдем, используя основное тригон-кое тождество:
sin 2 α + соs 2 α = 1
sin 2 α = 1 – соs 2 α = 1 – (– 0,8) 2 = 1 – 0,64 = 0,36
sinα = – 0,6 или sinα = 0,6
С учетом того, что в III четверти синус становится отрицательным, следует выбрать вариант sinα = – 0,6
Ответ: sinα = – 0,6; соsα = – 0,8.
Иногда ф-лы используют не для вычисления значений тригон-ких выражений, а для упрощения выражений. Из тождества sin 2 α + соs 2 α = 1 несложно получить из выражения
sin 2 α = 1 – соs 2 α
соs 2 α = 1 – sin 2 α
которые помогают в работе с длинными ф-лами.
Задание. Упростите выражение
4sin 2 α + 9соs 2 α – 6
таким образом, чтобы в нем не содержалось синуса.
Решение. Произведем замену sin 2 α = 1 – соs 2 α:
4sin 2 α+ 9соs 2 α – 6 = 4(1 – соs 2 α)+ 9соs 2 α – 6 =
= 4 – 4 соs 2 α + 9соs 2 α – 6 = 5соs 2 α – 2
Видим, что получилось значительно более простое выражение.
Задание. Избавьтесь от синуса в выражении
sin 4 α – соs 4 α
Решение. Воспользуемся ф-лой разности квадратов:
sin 4 α – соs 4 α = (sin 2 α – соs 2 α)(sin 2 α + соs 2 α) = (sin 2 α – соs 2 α)•1 =
= 1 – соs 2 α– соs 2 α = 1 – 2 соs 2 α
Задание. Упростите дробь
Тригонометрические функции суммы и разности
Легко проводить вычисления, когда все тригонометрические действия выполняются над одним углом α. Однако иногда в задачах добавляется ещё один угол, который обычно обозначают как β. Существуют ф-лы, с помощью которых можно вычислять тригон-кие ф-ции от суммы и разности углов α и β.
Вывод этих ф-л достаточно сложен, поэтому сначала мы просто без доказательства приведем две из них, позволяющие вычислять синус суммы и косинус суммы:
Достаточно запомнить их, а далее следующие формулы можно выводить из них. Так, если вместо β подставить угол (–β), то получим формулы для разности. При этом мы используем тот факт, что синус – нечетная ф-ция, то естьsin (– β) = – sinβ, а косинус – четная ф-ция, то есть соs (– β) = соsβ:
Теперь поступим также с ф-лой для косинуса разности:
Итак, нам удалось получить ф-лы для нахождения синуса и косинуса суммы и разности углов.
С помощью этих формул возможно вычислить значение тригон-ких ф-ций для некоторых нестандартных углов. (Стандартными считаются углы в 0°, 30°, 45°, 60° и 90°, ведь для них значение тригон-ких ф-ций можно узнать из таблички.)
Задание. Вычислите соs 150°.
Решение. В табличке стандартных углов есть углы, равные 90° и 60°. Их сумма как раз равна 150°. Поэтому запишем:
Задание. Вычислите синус, косинус и тангенс для угла 15°.
Решение. Угол в 15° можно представить как разность 45° – 30°. Тогда синус будет вычисляться так:
Далее вычислим косинус:
Можно выполнить проверку. Полученные значения должны удовлетворять основному тригон-кому тождеству. И действительно:
Проверка пройдена: сумма квадратов синуса и косинуса оказалась равной единице. Теперь посчитаем tg 15°, используя определение тангенса:
Задание. Вычислите значение тригонометрического выражения
sinπ/7 соsπ/42 + sinπ/42 соsπ/7
Решение: Значение тригон-ких ф-ций для углов π/7 и π/42 мы не знаем, однако это не помешает вычислениям. Можно заметить, что исходное выражение представляет собой синус суммы π/7 и π/42:
sinπ/7 соsπ/42 + sinπ/42 соsπ/7 = sin (π/7 + π/42) = sinπ/6 = 1/2
Задание. Упростите выражение
Вынесем за скобки множитель 2:
Теперь произведем замену:
C учетом этого можно переписать выражение и использовать ф-лу суммы косинусов:
Формулы двойного угла
Что будет, если формулу синуса суммы подставить не два различных угла α и β, а два одинаковых угла α и α? Получится ф-ла для синуса двойного угла:
Аналогично можно составить ф-лу и для косинуса двойного угла:
Итак, справедливы следующие ф-лы:
Задание. Вычислите sin 120° и соs 120°.
Задание. Упростите выражение
соs 2 t – соs 2t = соs 2 t – (соs 2 t – sin 2 t) = соs 2 t – соs 2 t + sin 2 t = sin 2 t
Задание. Докажите, что функция
является периодической и имеет период, равный π.
Решение. Используем ф-лу квадрата суммы:
Таким образом, исходную ф-цию можно переписать в виде
По определению, ф-ция является периодической с периодом Т, если выполняется условие у(х + Т) = у(х). Поэтому подставим в нашу ф-цию величину х + π:
Получили, что у(х + π) = y(x), то есть ф-ция имеет период, равный π.
Задание. Выведите формулы синуса и косинуса тройного угла.
Решение. Для их получения следует использовать ф-лу синуса суммы углов, в которую подставляют вместо β величину 2α:
Аналогично можно получить и ф-лу для косинуса тройного угла:
Формулы понижения степени
Если нам необходимо узнать косинус угла, который вдвое больше табличного, мы используем ф-лу:
соs 2α = соs 2 α – sin 2 α
А что делать, если нам надо вычислить косинус угла, который вдвое меньше известного? Попробуем преобразовать ф-лу косинуса двойного угла:
В результате нам удалось получить тождество, позволяющее по косинусу удвоенного угла найти косинус самого угла! Однако значительно чаще в тригонометрии это равенство записывают в обратном порядке:
и называют ф-лой понижения степени. Действительно, в левой части стоит косинус в квадрате, а справа – косинус без квадрата, но вычисляется он от угла 2α, а не α.
Попробуем получить аналогичную ф-лу и для синуса. Для этого используем основное тригон-кое тождество:
С помощью этих ф-л можно вычислять тригон-кие ф-ции для некоторых малых углов. Так, ранее мы с использованием ф-лу разности синусов определили, что
При этом мы представляли угол 15° как разность 45° – 30°. Но как посчитать соs 7,5°? Этот угол невозможно представить как разницу или сумму известных нам табличных углов (0°, 30°; 45°; 60° и 90°). Однако поможет ф-ла понижения степени. Действительно, ведь 2•7,5° = 15°. Тогда можно записать:
Мы нашли соs 2 7,5°. Чтобы узнать соs 7,5°, необходимо извлечь квадратный корень:
Так как угол 7,5° принадлежит I четверти, то его косинус должен быть положительным, поэтому можно записать:
Видно, что получается довольно громоздкое выражение. Используя ф-лу понижения степени, можно найти косинус и угла, который ещё вдвое меньше, то есть равен 3,75°, но в результате получится ещё более громоздкое выражение.
Задание. Вычислите sinπ/8.
Решение. Угол π/4 является табличным (его градусная мера составляет 45°). Поэтому можно записать:
Эти примеры показывают, что тригон-кие ф-ции многих нестандартных углов можно выразить, используя квадратные корни. Возникает вопрос – а любую ли тригонометрическую ф-цию можно выразить таким способом? Оказывается, что нет. Например, sin 10° невозможно найти ни в одной, даже самой подробной тригонометрической таблице. Мы не будем это доказывать, но эту величину невозможно представить в виде выражения, используя арифметические операции и корни. Однако существуют приближенные методы, позволяющие с любой наперед заданной точностью вычислять значение тригонометрических ф-ций.
Формулы приведения
Возможно, вы уже заметили, что синусы и косинусы принимают одинаковые значения в углах, чья сумма равна 90°. Например, sin30° = соs60° = 1/2, и при этом 30° + 60° = 90°. Также мы знаем, что sin 45° = соs 45° (45° + 45° = 90°) и sin60° = соs30° (60° + 30°). В чем причина такой закономерности и справедлива ли она для нестандартных углов?
Используя ф-лу синуса разности, мы можем записать, что
Полученная ф-ла sin (90° – α) = соsα называется формулой приведения. При ее выводе мы использовали тот факт, что sin 90° = 1, а соs 90° = 0, поэтому формула получилась очень простой. Однако синусы и косинусы других углов, кратных 90° (или кратных π/2, если измерять углы в радианах), также равны 0, 1 или – 1, поэтому для них тоже можно получить подобные простые ф-лы, например:
Похожих ф-л можно написать несколько десятков! Все их запоминать не надо, так как существует особое мнемоническое правило, позволяющее записать необходимую ф-лу.
Пусть есть некоторое тригон-кое выражение вида
где f – тригонометрическая ф-ция (sin; соs; tg; ctg)
k– угол, кратный π/2 (π/2, π, 3π/2, 2π)
Мы хотим заменить ее другой ф-цией, только от угла α. На первом шаге мы смотрим на слагаемое k. Если оно кратно π (– π, π, 2π), то ф-ция f остается неизменной. Если же слагаемое k – это число π/2 или 3π/2, то ф-цию f надо поменять на так называемую кофункцию (синус меняем на косинус, тангенс на котангенс и наоборот).
Далее надо определить знак, стоящий перед новой ф-цией. Для этого мы предполагаем, что α – это острый угол, то есть он принадлежит I четверти. Далее с учетом этого предположения смотрим, в какую четверть попадает угол k ± α, и какое значение принимает там исходная тригонометрическая ф-ция. Если она отрицательна, то перед новой тригонометрической ф-цией надо поставить минус. В противном случае ничего ставить не надо.
Лучше всего изучить это алгоритм на примерах.
Задание. Упростите выражение соs (π/2 + α).
Решение. Первый шаг – смотрим на слагаемое под знаком косинуса. Это число π/2. Оно НЕ кратно π, а потому мы должны поменять косинус на синус:
Второй шаг – надо определить, надо ли ставить минус перед синусом. Если α – это острый угол, то угол (π/2 + α) попадет во II четверть:
Во второй четверти косинус отрицателен, а потому перед синусом следует поставить минус:
Важное примечание. В этом примере для составления формулы приведения мы «предположили», что угол α является острым. В результате нам удалось получить формулу соs (π/2 + α) = – sinα. Однако отметим, что полученная нами формула выполняется для абсолютно любых значений угла α, а не только для 0° 1 2 + 3 соs2x
Источник
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение тригонометрических уравнений.
Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение. Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Немного теории.
Тригонометрические уравнения
Уравнение cos(х) = а
Уравнение cos x = а, где ( |a| leqslant 1 ), имеет на отрезке ( 0 leqslant x leqslant pi ) только один корень. Если ( a geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac<pi> <2>right] ); если a
Уравнение sin(х) = а
Уравнение tg(х) = а
Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.
Решение тригонометрических уравнений
Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а. К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.
Уравнения, сводящиеся к квадратным
Уравнение вида a sin(x) + b cos(x) = c
Используя формулы ( sin(x) = 2sinfrac <2>cosfrac<2>, ; cos(x) = cos^2 frac <2>-sin^2 frac <2>) и записывая правую часть уравпения в виде ( 2 = 2 cdot 1 = 2 left( sin^2 frac <2>+ cos^2 frac <2>right) ) получаем
В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях ( a neq 0, ; b neq 0, ; c neq 0, ; c^2 leqslant b^2+c^2 ) можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на ( sqrt ):
Решить уравнение 4 sin(x) + 3 cos(x) = 5
Здесь a = 4, b = 3, ( sqrt = 5 ). Поделим обе части уравнения на 5:
Уравнения, решаемые разложением левой части на множители
Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.
Источник
Тригонометрические функции любого угла и определение синуса, косинуса, тангенса и котангенса:
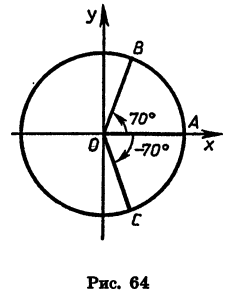
Отметим на оси х справа от начала координат точку А и проведем через нее окружность с центром в точке О (рис. 64). Радиус OA будем называть начальным радиусом.
Повернем начальный радиус около точки О на 70° против часовой стрелки. При этом он перейдет в радиус ОВ. Говорят, что угол поворота равен 70°. Если повернуть начальный радиус около точки О на 70° по часовой стрелке, то он перейдет в радиус ОС. В этом случае говорят, что угол поворота равен —70°. Углы поворота в 70° и —70° показаны стрелками на рисунке 64.
Вообще при повороте против часовой стрелки угол поворота считают положительным, а при повороте по часовой стрелке — отрицательным.
Из курса геометрии известно, что мера угла в градусах выражается числом от 0 до 180. Что касается угла поворота, то он может выражаться в градусах каким угодно действительным числом от 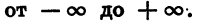
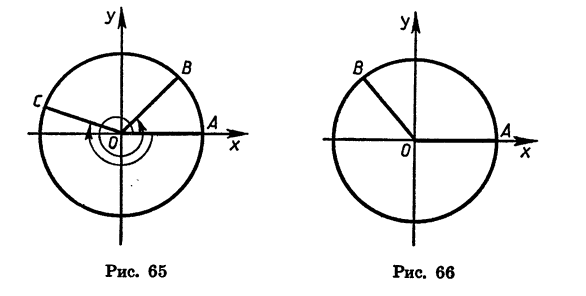
радиус повернуть против часовой стрелки на 180°, а потом еще на 30°, то угол поворота будет равен 210°. Если начальный радиус сделает полный оборот против часовой стрелки, то угол поворота будет равен 360°; если он сделает полтора оборота в том же направлении, то угол поворота будет равен 540° и т. д. На рисунке 65 стрелками показаны углы поворота в 405° и -200°.
Рассмотрим радиусы OA и ОВ (рис. 66). Существует бесконечно много углов поворота, при которых начальный радиус OA переходит в радиус ОВ. Так, если 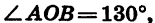
Пусть при повороте на угол а начальный радиус OA переходит в радиус ОВ. В зависимости от того, в какой координатной четверти окажется радиус ОВ, угол а называют углом этой четверти. Так, если 0° < а < 90°, то а — угол I четверти; если 90° < а <180°, то а — угол II четверти; если 180° < а < 270°, то а — угол III четверти; если 270° < а < 360°, то а — угол IV четверти. Очевидно, что при прибавлении к углу целого числа оборотов получается угол той же четверти. Например, угол в 430° является углом I четверти, так как 430° = 360°+ 70° и 0°<70°<90°; угол в 920° является углом III четверти, так как 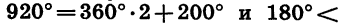
Углы 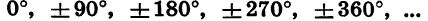
В курсе геометрии были определены синус, косинус и тангенс угла а при 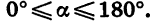
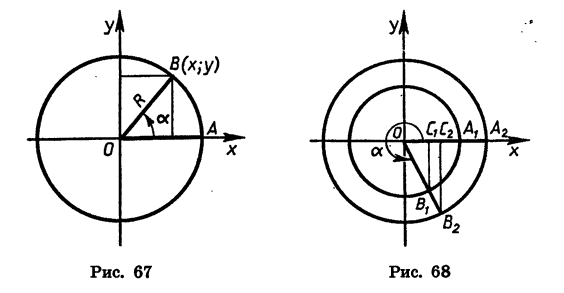
Пусть при повороте около точки О на угол а начальный радиус OA переходит в радиус ОВ (рис. 67).
Синусом угла а называется отношение ординаты точки В к длине радиуса.
Косинусом утла а называется отношение абсциссы точки В к длине радиуса.
Тангенсом угла а называется отношение ординаты точки В к ее абсциссе.
Котангенсом угла а называется отношение абсциссы точки В к ее ординате.
Если координаты точки В равны х и у, а длина начального радиуса равна R, то
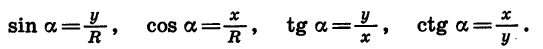
В курсе геометрии было показано, что значения синуса, косинуса и тангенса угла а, где 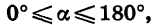
Покажем, например, что sin а не зависит от R.
Пусть при повороте луча 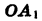
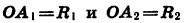
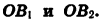
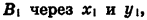
Опустим перпендикуляры из точек 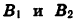
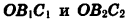
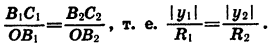
Так как точки 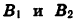
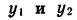
Заметим, что это равенство верно и в том случае, когда точки 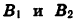
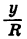
Выражения sin а и cos а определены при любом а, так как для любого угла поворота можно найти соответствующие значения дробей 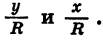
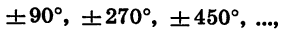
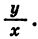
Каждому допустимому значению а соответствует единственное значение sin a, cos а, tg а и ctg а. Поэтому синус, косинус, тангенс и котангенс являются функциями угла а. Их называют тригонометрическими функциями.
Можно доказать, что областью значений синуса и косинуса является промежуток [—1; 1], а областью значений тангенса и котангенса — множество всех действительных чисел.
Приведем примеры вычисления значений тригонометрических функций.
Пример:
Найдем с помощью чертежа приближенные значения sin 110°, cos 110°, tg 110° и ctg 110°.
Начертим окружность с центром в начале координат и радиусом OA = R = 3 (рис. 69). Повернем радиус OA на 110°. Получим радиус ОВ. Найдем по рисунку координаты х и у точки В: 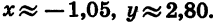
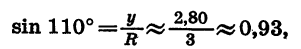
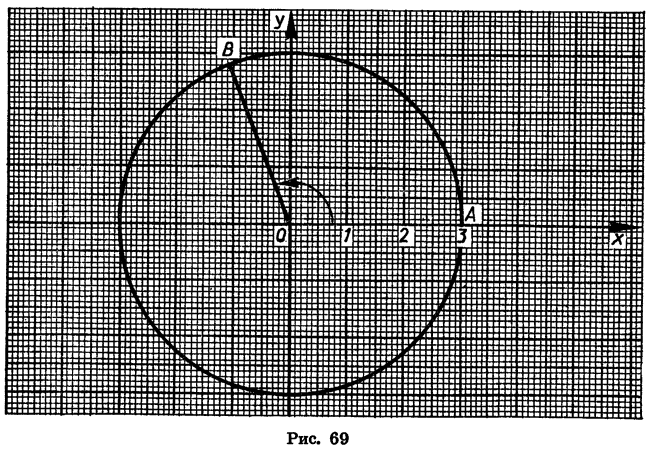
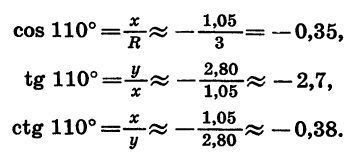
В таблице приведены известные из курса геометрии значения синуса, косинуса и тангенса углов 0°, 30°, 45°, 60° и 90°. Прочерк сделан в том случае, когда выражение не имеет смысла.
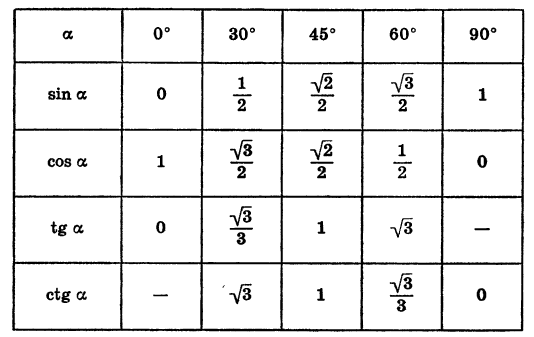
Значения котангенса могут быть получены из значений тангенса, так как котангенс угла является числом, обратным тангенсу этого же угла. Поэтому, например,
Пример:
Найдем синус, косинус, тангенс и котангенс углов 180° и 270°.
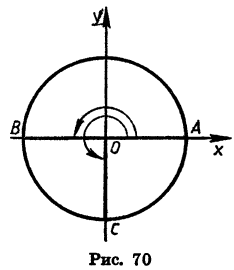
При повороте на 180° около точки О радиус OA, равный 1, (рис. 70) переходит в радиус ОВ, а при повороте на 270° — в радиус ОС.
Так как точка В имеет координаты х = — 1 и у = 0, то
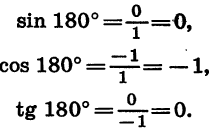
Так как точка С имеет координаты х = 0 и у = —1, то

Напомним, что выражения ctg 180° и tg 270° не имеют смысла.
Свойства синуса, косинуса, тангенса и котангенса
Рассмотрим некоторые свойства тригонометрических функций.
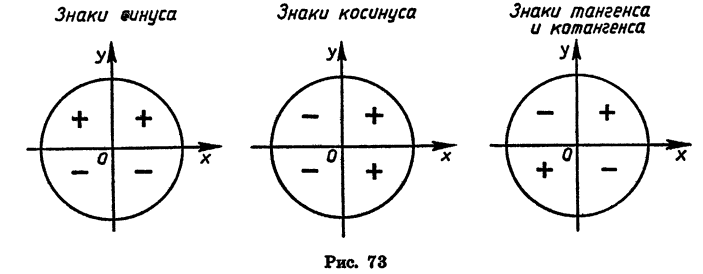
Выясним сначала, какие знаки имеют синус, косинус, тангенс и котангенс в каждой из координатных четвертей.
Пусть при повороте радиуса OA, равного R, на угол а точка А перешла в точку В с координатами х и у (см. рис. 67).
Так как 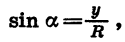
В I и II четвертях у > 0, а в III и IV четвертях у < 0. Значит, sin a > 0, если а является углом I или II четверти, и sin a < 0, если а является углом III или IV четверти.
Знак cos а зависит от знака х, так как 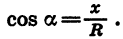
Так как 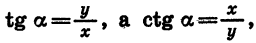
Знаки синуса, косинуса, тангенса и котангенса в каждой из четвертей показаны на рисунке 73.
Выясним теперь вопрос о четности и нечетности тригонометрических функций.
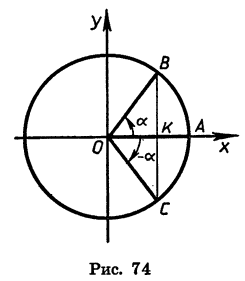
Пусть при повороте на угол а радиус OA переходит в радиус ОВ, а при повороте на угол — а в радиус ОС х (рис. 74). Соединив отрезком точки В и С, получим равнобедренный треугольник ВОС. Луч OA является биссектрисой угла ВОС. Значит, отрезок ОК является медианой и высотой треугольника ВОС. Отсюда следует, что точки В и С симметричны относительно оси абсцисс.
Пусть координаты точки В равны х и у, тогда координаты точки С равны х и -у. Пользуясь этим, найдем, что
Мы получили формулы, выражающие зависимость между синусами, косинусами, тангенсами и котангенсами противоположных углов:
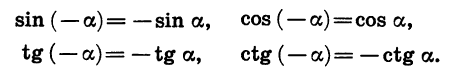
Например:
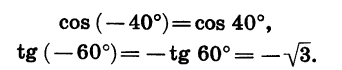
Итак, синус, тангенс и котангенс являются нечетными функциями, а косинус является четной функцией.
Рассмотрим еще одно свойство тригонометрических функций.
Если при повороте радиуса OA на угол а получен радиус ОВ (см. рис. 67), то тот же радиус получится и при повороте OA на угол, отличающийся от а на целое число оборотов. Отсюда следует, что при изменении угла на целое число оборотов значения синуса, косинуса, тангенса и котангенса не изменяются.
Например:
Рассмотренные свойства позволяют свести нахождение значений синуса, косинуса, тангенса и котангенса любого угла к нахождению их значений для неотрицательного угла, меньшего 360°.
Пример:
Найдем sin 765° и cos ( — 1170°). Имеем:
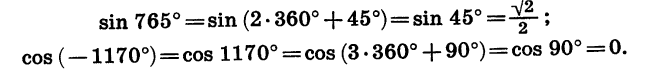
Радианная мера угла. Вычисление значении тригонометрических функции с помощью микрокалькулятора
Как известно, углы измеряются в градусах, минутах, секундах. Эти единицы измерения связаны между собой соотношениями
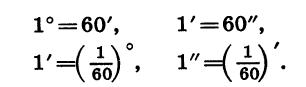
Кроме указанных, используется также единица измерения углов, называемая радианом.
Углом в один радиан называют центральный угол, которому соответствует длина дуги, равная длине радиуса окружности.
Угол, равный 1 рад, изображен на рисунке 75.
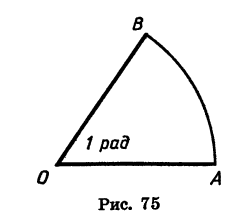
Радианная мера угла, т. е. величина угла, выраженная в радианах, не зависит О А от длины радиуса. Это следует из того, что фигуры, ограниченные углом и дугой окружности с центром в вершине этого угла, подобны между собой (рис. 76).
Установим связь между радиан-ным и градусным измерениями углов.
Углу, равному 180°, соответствует полуокружность, т. е. дуга, длина l которой равна
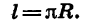
Чтобы найти радианную меру этого угла, надо длину дуги l разделить на длину радиуса R. Получим:
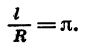
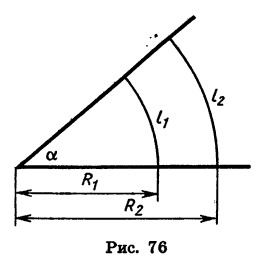
Следовательно, радианная мера угла в 180° равна
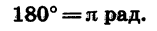
Отсюда получаем, что радианная мера угла в 1° равна
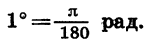
Приближенно 1° равен 0,017 рад.
Из равенства 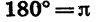
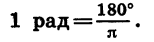
Приближенно 1 рад равен 57°.
Рассмотрим примеры перехода от радианной меры к градусной и от градусной меры к радианной.
Пример:
Выразим в градусах 4,5 рад.
Так как
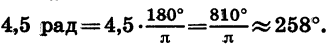
Пример:
Найдем радианную меру угла в 72°.
Так как
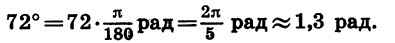
При записи радианной меры угла обозначение «рад» часто опускают. Например, вместо равенства 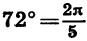
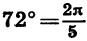
Выразим в радианной мере углы 30°, 45°, 60°, 90°, 270° и 360°. Получим:
Радианная мера угла часто используется в тригонометрических выражениях. Так, запись sirfl означает синус угла в 1 радиан, запись sin ( — 2,5) означает синус угла в —2,5 радиана, запись 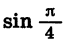
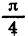
Значения тригонометрических функций для углов, выраженных как в градусах, так и в радианах, можно находить, используя микрокалькулятор. Так, с помощью микрокалькулятора «Электроника БЗ-З6» значения синуса, косинуса и тангенса вычисляют следующим образом. Переводят переключатель «ГРАД — РАД», находящийся в нижней части корпуса, в положение «ГРАД», если угол задан в градусах, или в положение «РАД», если угол задан в радианах. Вводят угол, нажимают клавишу 
Пример:
Найдем с помощью микрокалькулятора значение выражения с точностью до 0,001:
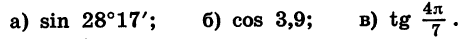
а) Установим переключатель в положение «ГРАД», затем выразим 28°17′ в градусах и нажмем «последовательно клавиши 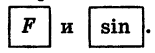
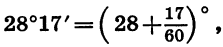

Получаем, что
б) Устанавливаем переключатель в положение «РАД» и находим значение cos 3,9 по программе:
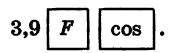
Получаем, что cos
в) Переключатель устанавливаем в положение «РАД». При нахождении значения выражения 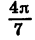
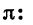
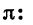
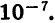

Получаем, что
Отметим, что для вычисления котангенса угла надо сначала найти значение тангенса этого угла, а потом обратное число, нажав клавиши
Основные тригонометрические формулы
Соотношения между тригонометрическими функциями одного и того же угла:
Рассмотрим, как связаны между собой синус и косинус одного и того же угла.
Пусть при повороте радиуса OA вокруг точки О на угол а получен радиус ОВ (рис. 77). По определению
где х — абсцисса точки В, у — ее ордината, a R — длина радиуса OA. Отсюда

Так как точка В принадлежит окружности с центром в начале координат, радиус которой равен R, то ее координаты удовлетворяют уравнению
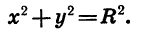
Подставив в это уравнение вместо х и у выражения R cos а и R sin а, получим:
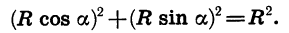
Разделив обе части последнего равенства на 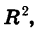

Равенство (1) верно при любых значениях а. Выясним теперь, как связаны между собой тангенс, синус и косинус одного и того же угла.
По определению 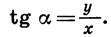
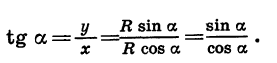
Таким образом,
Аналогично
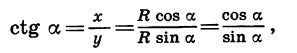
Равенство (2) верно при всех значениях а, при которых cos 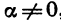
С помощью формул (1) — (3) можно получить другие формулы, выражающие соотношения между тригонометрическими функциями одного и того же угла.
Из равенств (2) и (3) получим:
Равенство (4) показывает, как связаны между собой тангенс и котангенс угла а. Оно верно при всех значениях а, при которых tg а и ctg а имеют смысл.
Заметим, что формулу (4) можно получить и непосредственно из определения тангенса и котангенса.
Выведем теперь формулы, выражающие соотношения между тангенсом и косинусом, а также между котангенсом и синусом одного и того же угла.
Разделив обе части равенства (1) на 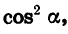
Если обе части равенства (1) разделить на 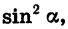
т. е.
Равенство (5) верно, когда cos 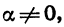
Равенства (1) — (6) являются тождествами. Их называют основными тригонометрическими тождествами. Рассмотрим примеры использования этих тождеств для нахождения значений тригонометрических функций по известному значению одной из них.
Пример:
Найдем cos a, tg а и ctg а, если известно, что sin
Найдем сначала cos а. Из формулы 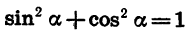
Так как а является углом II четверти, то его косинус отрицателен. Значит,
Зная синус и косинус угла а, можно найти его тангенс:
Для отыскания котангенса угла а удобно воспользоваться формулой tg a • ctg a = 1. Имеем:
Пример:
Известно, что 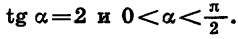
Воспользовавшись формулой 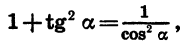
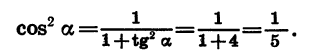
По условию угол a является углом I четверти, поэтому его косинус положителен. Значит,
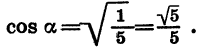
Зная cos а и tg а, можно найти sin а. Из формулы 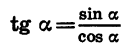
По известному tg а легко найти ctga:
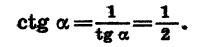
Итак,
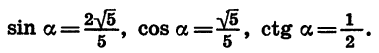
Применение основных тригонометрических формул к преобразованию выражении
Мы уже встречались с некоторыми простейшими преобразованиями тригонометрических выражений. Рассмотрим более сложные примеры.
Пример:
Упростим выражение
Воспользовавшись формулами 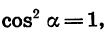
Пример:
Упростим выражение
Пример:
Докажем тождество
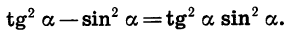
Преобразуем левую часть данного равенства:
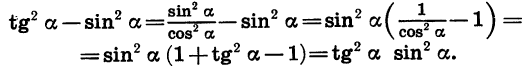
Мы получили выражение, стоящее в правой части равенства. Таким образом, тождество доказано.
Формулы приведения
Тригонометрические функции углов вида 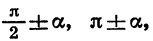
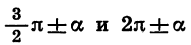
Выведем сначала формулы приведения для синуса и косинуса.
Докажем, что для любого а
Повернем радиус OA, длина которого равна R, на угол а и на угол 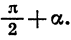
Опустим из точки В1 перпендикуляры 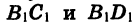
Повернем прямоугольник 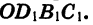
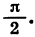
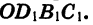
Отсюда следует, что ордината точки В2 равна абсциссе точки В1, а абсцисса точки В2 равна числу, противоположному ординате точки В1. Обозначим координаты точки B1 через 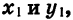
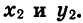
Значит,
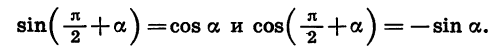
Из формул (1) следует, что
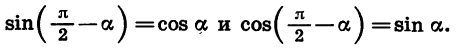
Действительно, представим разность 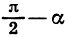
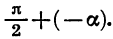
Формулы приведения для синуса и косинуса угла 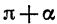
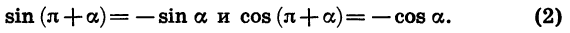
Для доказательства достаточно представить 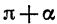
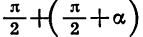
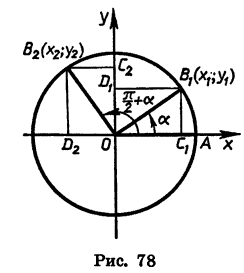
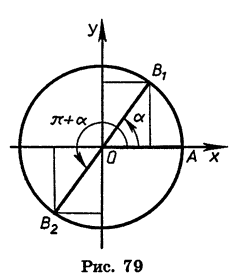
Заметим, что к формулам (2) легко прийти и из геометрических соображений (рис. 79). При повороте радиуса OA на угол а и на угол 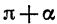
начала координат точек равны по модулю и противоположны по знаку. Отсюда следует, что 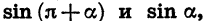
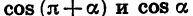
Из формул (2) следует, что
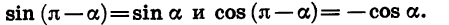
Для доказательства достаточно представить 
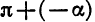
Формулы приведения для синуса и косинуса угла 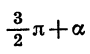
Чтобы доказать формулы (3), достаточно представить 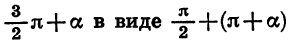
Из формул (3) нетрудно получить, что
Наконец, формулы приведения для синуса и косинуса угла 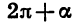
Справедливы также формулы
Например, для
Формулы приведения для тангенса и котангенса можно получить с помощью формул приведения для синуса и косинуса. Например:
Все формулы приведения сведем в две таблицы, поместив в первой из них формулы для углов 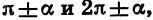
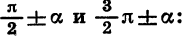
Цо таблицам легко проследить закономерности, имеющие место для формул приведения. Эти закономерности позволяют сформулировать правило, с помощью которого можно записать любую формулу приведения, не прибегая к таблице:
Функция в правой части равенства берется с тем же знаком, какой имеет исходная функция, если считать, что угол а является углом 1 четверти;
для углов 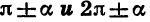
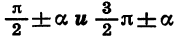
Пример:
Выразим 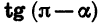
Если считать, что a — угол I четверти, то 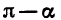
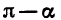
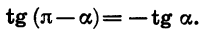
С помощью формул приведения нахождение значений тригонометрических функций любого угла можно свести к нахождению значений тригонометрических функций угла от 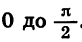
Пример:
Найдем значение
Пример:
Найдем значение sin (— 585°).
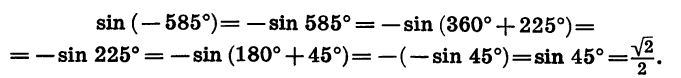
Формулы сложения и их следствия
Выведем формулы, выражающие тригонометрические функции суммы и разности двух углов через тригонометрические функции этих углов.
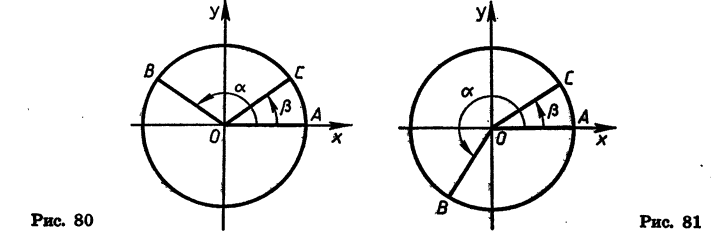
Повернем радиус OA, равный R, около точки О на угол а и на угол 
Найдем скалярное произведение векторов 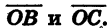
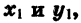
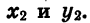
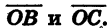
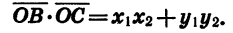
Выразим скалярное произведение 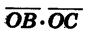

Подставив значения 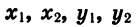
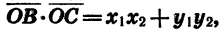
С другой стороны, по теореме о скалярном произведении векторов имеем:

Угол ВОС между векторами 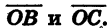

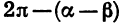
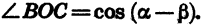
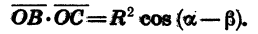
Так как 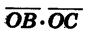
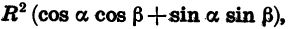
Формулу (1) называют формулой косинуса разности.
Косинус разности двух углов равен произведению косинусов этих углов плюс произведение синусов этих углов.
С помощью формулы (1) легко получить формулу косинуса суммы:
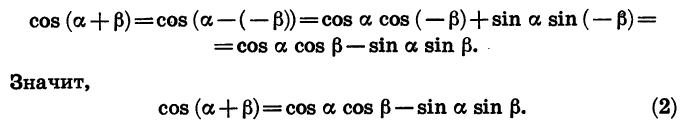
Косинус суммы двух углов равен произведению косинусов этих углов минус произведение синусов этих углов.
Выведем теперь формулы синуса суммы и синуса разности. Используя формулы приведения и формулу (1), получим:
Синус суммы двух углов равен произведению синуса первого угла на косинус второго плюс произведение косинуса первого угла на синус второго.
Для синуса разности имеем:
Синус разности двух углов равен произведению синуса первого угла на косинус второго минус произведение косинуса первого угла на синус второго.
Формулы (1) — (4) называют формулами сложения для синуса и косинуса.
Приведем примеры использования формул сложения.
Пример:
Вычислим cos 15° и sin 15°. Представим 15° в виде разности 45° — 30°. Тогда
Пример:
Упростим выражение 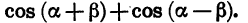
Используя формулы (1) — (4), можно вывести формулы сложения для тангенса и котангенса. Выведем, например, формулу тангенса суммы:
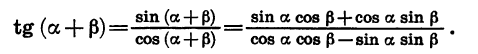
Разделим числитель и знаменатель полученной дроби на произведение cos a cos 
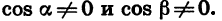
Значит,
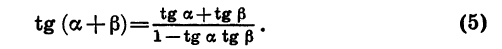
Аналогично можно доказать, что
Формулы двойного угла
Формулы сложения позволяют выразить sin 2a, cos 2a и tg 2a через тригонометрические функции угла a. Положим в формулах

Эти тождества называют формулами двойного угла.
Приведем примеры применения формул двойного угла для нахождения значений тригонометрических функций и преобразования тригонометрических выражений.
Пример:
Найдем значение sin 2а, зная, что cosa = — 0,8 и a — угол III четверти.
Сначала вычислим sin а. Так как a — угол III четверти, то sin а < 0. Поэтому
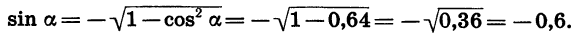
По формуле синуса двойного угла
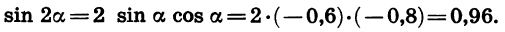
Пример:
Упростим выражение
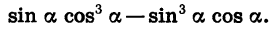
Вынесем за скобки sin a cos a и воспользуемся формулами двойного угла:
Из формулы (2) следует, что
Действительно, выразив cos 2a через sin a, получим:
Отсюда
Аналогично, выразив cos 2a через cos a, получим:
Формулы (4) и (5) используются в вычислениях и преобразованиях.
Пример:
Упростим выражение
Применим формулы (4) и (5) к выражениям 1 — cos а и 1 + cos а, представив а в виде произведения 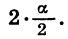
Формулы суммы и разности тригонометрических функции
Сумму и разность синусов или косинусов можно представить в виде произведения тригонометрических функций. Формулы, на которых основано такое преобразование, могут быть получены из формул сложения.
Чтобы представить в виде произведения сумму sin a + sin 
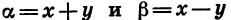
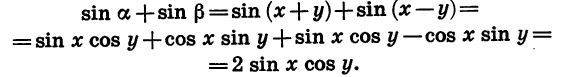
Из равенств a = x + y и 
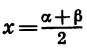
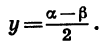
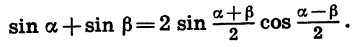
Мы получили формулу суммы синусов двух углов.
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус их полуразности.
Аналогично можно вывести формулы разности синусов, суммы и разности косинусов.
Формула разности синусов:
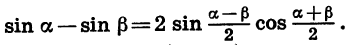
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус их полусуммы.
Формула суммы косинусов:
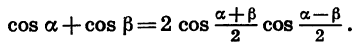
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы, этих углов на косинус их полуразности.
Формула разности косинусов:
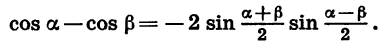
Разность косинусов двух углов равна взятому со знаком *минус» удвоенному произведению синуса полусуммы этих углов на синус их полуразности.
Учитывая, что 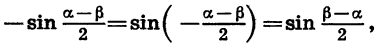
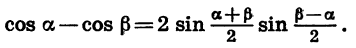
Приведем примеры применения полученных формул.
Пример:
Упростим сумму sin 10° + sin 50°.
Воспользовавшись формулой суммы синусов, получим:
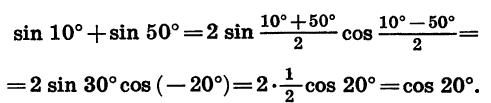
Пример:
Представим в виде произведения разность
Воспользовавшись формулой приведения, представим данное выражение в виде разности косинусов и преобразуем ее в произведение. Тогда
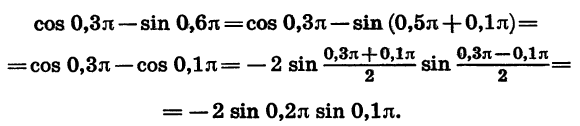
Пример:
Представим в виде произведения выражение 1 — sin а.
Так как 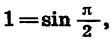
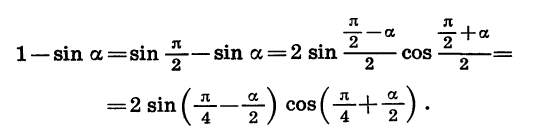
Эту задачу можно решить иначе:
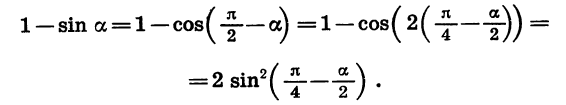
С помощью формул приведения первое из полученных выражений можно преобразовать во второе и наоборот.
Вычисление значений тригонометрических выражений
Возможно вам будут полезны эти страницы:
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Для решения задачи следует воспользоваться основным тригонометрическим тождеством: сумма квадратов синуса и косинуса одного и того же угла равна 1.
Отсюда синус угла равен плюс минус корню квадратному из разности 1 и квадрата косинуса угла.
Какой знак перед корнем квадратным брать зависит от того, где находится угол, косинус которого известен.
Если в условии задачи значение косинуса больше нуля (равенство нулю рассмотрено, как частный случай, ниже, хотя применимы рассуждения и для нуля), то угол находится либо в 1-й, либо в 4-й четверти.
Для определенности в условии задачи обычно дается ограничение для угла.
Если указано, что 0< a< 90 (1 четверть), то значение синуса тоже следует брать со знаком плюс.
Если же 270< a< 360 (4 четверть), то значение синуса следует брать со знаком минус.
Если значение косинуса угла меньше нуля, то это означает, что угол может находиться во 2-й или 3-й четверти.
1) 90< a< 180 (2 четверть).
Тогда синус угла будет положительным и равняется корню квадратному из разности 1 и квадрата косинуса угла.
2) 180< a< 270 (3 четверть).
В этом случае синус угла будет отрицательным и равняется тому же значению, что и в первом случае, только со знаком минус.
Частные случаи: Если cos a = 0, то sina=1; если cos a = 1, то sina=0; cos a = -1, то sina=0. Эти значения также легко находятся из основного тригонометрического тождества.
Приведем примеры.
Пример 1. Найти синус угла, если cos a = -0,8. 180<a<270 (в градусах)
Решение. Находим разность 1 и квадрата значения cos a, т.е. квадрата (-0,8).
-0,8 возводим в квадрат, получим (-0,8)*(-0,8) = 0, 64. Подставим его в искомую разность:
1-0,64=0,36
Получили квадрат значения синуса. Для нахождения значения самого синуса, извлечем корень квадратный из 0,36 и возьмем его со знаком + и со знаком – (см. картинку). Получим 0,6 или -0,6.
Так как по условию угол находится в 3 четверти, то искомое значение синуса будет отрицательным. Значит выбираем -0,6.
Ответ: sina=-0,6.
Рассмотрим для краткости изложения этот же пример для случая, когда угол находится во второй четверти:
Пример 2. Найти синус угла, если cos a = -0,8. 90<a<180 (в градусах)
Решение будет точно таким же, как для примера 1.
Изменится лишь выбор ответа. Рассуждения будут следующими:
Так как по условию угол находится во 2 четверти, то искомое значение синуса будет положительным. Значит выбираем 0,6.
Ответ: sina=0,6.
9. Преобразование числовых и буквенных выражений
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Числовые тригонометрические выражения
(blacktriangleright) Алгоритм применения формул приведения:
Шаг 1: определить, меняется ли функция на кофункцию: [sin
longleftrightarrow cos] [mathrm{tg} longleftrightarrow mathrm{ctg}]
Шаг 2: определить знак, который имеет изначальная функция, поняв, в какой четверти тригонометрической окружности находится изначальный угол (предполагая, что (alpha) – острый)
(blacktriangleright) Если угол можно представить в виде ((pi npm
alpha)), где (n) – натуральное, то функция на кофункцию не меняется.
Пример: (sin (pi npm alpha)=bigodot sin alpha), где на месте (bigodot) должен стоять знак синуса для угла ((pi npm alpha))
(blacktriangleright) Если угол можно представить в виде (left(dfrac{pi}2npm alpharight)), где (n) – нечетное число, то функция на кофункцию меняется
Пример: (sin left(dfrac{pi}2npm alpharight)=bigodot cos
alpha), где на месте (bigodot) должен стоять знак синуса для угла (left(dfrac{pi}2npm alpharight))
(blacktriangleright) Основные формулы:
[begin{array}{|ccc|}
hline sin^2 alpha+cos^2 alpha =1&& mathrm{tg} alpha cdot
mathrm{ctg}alpha
=1\ &&\
mathrm{tg} alpha=dfrac{sin alpha}{cos alpha}&&mathrm{ctg}
alpha
=dfrac{cos alpha}{sin alpha}\&&\
cos {2alpha}=cos^2 alpha – sin^2 alpha&&cos
{2alpha}=1-2sin^2
alpha\&&\
cos {2alpha}=2cos^2alpha -1&&sin {2alpha}=2sin alpha cos
alpha\
hline
end{array}]
Задание
1
#573
Уровень задания: Легче ЕГЭ
Найдите значение выражения (2sin^2 30^circ + cos^2 30^circ).
Используя основное тригонометрическое тождество, исходное выражение можно преобразовать следующим образом: [2sin^2 30^circ + cos^2 30^circ = sin^2 30^circ + (sin^2 30^circ + cos^2 30^circ) = sin^2 30^circ + 1.] Так как (sin 30^circ = 0,5), то значение исходного выражения равно (0,5^2 + 1 = 1,25).
Ответ: 1,25
Задание
2
#2958
Уровень задания: Равен ЕГЭ
Найдите значение выражения [dfrac{24}{sin^2127^circ+1+sin^2217^circ}]
Заметим, что (217^circ=90^circ+127^circ). Так как по формуле приведения (sin(90^circ+alpha)=cos alpha), то [sin
217^circ=sin (90^circ+127^circ)=cos 127^circ] Следовательно, выражение можно переписать в виде: [dfrac{24}{sin^2127^circ+cos^2127^circ+1}=dfrac{24}{1+1}=12,] так как по основному тригонометрическому тождеству (sin^2alpha+cos^2alpha=1) для любого угла (alpha).
Ответ: 12
Задание
3
#2626
Уровень задания: Равен ЕГЭ
Найдите значение выражения
[sqrt{48}-sqrt{192}sin^2dfrac{19pi}{12}]
(Задача от подписчиков.)
Заметим, что (192=48cdot 4), следовательно, (sqrt{192}=2sqrt{48}). Таким образом, выражение примет вид (по формуле косинуса двойного угла (cos2x=1-2sin^2x)):
[sqrt{48}left(1-2sin^2dfrac{19pi}{12}right)=
sqrt{48}cdot cosdfrac{19pi}6]
Т.к. (dfrac{19pi}6=dfrac{18pi+pi}6=3pi+dfrac{pi}6), то по формуле приведения:
[sqrt{48}cosleft(3pi+dfrac{pi}6right)=
sqrt{48}cdot left(-cosdfrac{pi}6right)=-sqrt{48}cdot
dfrac{sqrt3}2=-4sqrt3cdot dfrac{sqrt3}2=-6.]
Ответ: -6
Задание
4
#2434
Уровень задания: Равен ЕГЭ
Найдите значение выражения
[8left(sindfrac{pi}{12}cosdfrac{pi}{12}-1right)]
По формуле синуса двойного угла (sin2alpha=2sinalphacosalpha) имеем: (sinalphacosalpha=frac12sin2alpha). Следовательно,
[8left(dfrac12sin2cdotdfrac{pi}{12}-1right)=8left(dfrac12sindfrac{pi}6-1right)=
8left(dfrac12cdot dfrac12-1right)=-6.]
Ответ: -6
Задание
5
#2625
Уровень задания: Равен ЕГЭ
Найдите значение выражения
[dfrac{32}{sinleft(-dfrac{35pi}4right)cdot cos dfrac{25pi}4}]
(Задача от подписчиков.)
Т.к. синус — нечетная функция, то есть (sin (-alpha)=-sin
alpha), то (sinleft(-frac{35pi}4right)=-sin frac{35pi}4).
Заметим, что :
(dfrac{35pi}4=dfrac{36pi
-pi}4=9pi-dfrac{pi}4);
(dfrac{25pi}4=dfrac{24pi+pi}4=6pi+dfrac{pi}4).
Таким образом, по формулам приведения:
(sin
dfrac{35pi}4=sinleft(9pi-dfrac{pi}4right)=sindfrac{pi}4);
(cos
dfrac{25pi}4=cosleft(6pi+dfrac{pi}4right)=cosdfrac{pi}4).
Следовательно, выражение принимает вид:
[dfrac{32}{-sindfrac{pi}4cosdfrac{pi}4}=
-dfrac{32}{dfrac{sqrt2}2cdot dfrac{sqrt2}2}=-64.]
Ответ: -64
Задание
6
#581
Уровень задания: Равен ЕГЭ
Найдите значение выражения (dfrac{7sin{11^circ}}{cos{79^circ}}).
Используя формулу приведения (sin(90^circ pm alpha) = cos alpha), исходное выражение можно преобразовать следующим образом: [dfrac{7sin{11^circ}}{cos{79^circ}} = dfrac{7sin{(90^circ – 79^circ)}}{cos{79^circ}} = dfrac{7cos{79^circ}}{cos{79^circ}} = 7.]
Ответ: 7
Задание
7
#1841
Уровень задания: Равен ЕГЭ
Найдите значение выражения (dfrac{15}{sin{(-frac{20pi}{3})}
cdot cos{(-frac{43pi}{6})}}).
Используя формулы приведения, а также четность косинуса и нечетность синуса, исходное выражение можно преобразовать следующим образом: [dfrac{15}{-sin{left(6pi + frac{2pi}{3}right)} cdot
cos{left(7pi + frac{pi}{6}right)}} =
dfrac{15}{-sin{left(frac{2pi}{3}right)} cdot
(-cos{left(frac{pi}{6}right)})} =
dfrac{15}{-frac{sqrt{3}}{2} cdot ({-frac{sqrt{3}}{2})}} = 20.]
Ответ: 20

УСТАЛ? Просто отдохни

Внимание! Эти формулы работают только если аргументы у тригонометрических функций одинаковые, т.е.
(sin^2 776^° +cos^2 776^° =1)
(tg, 3xcdot ctg, 3x=1)
Но:
(sin^2x+cos^23x≠1)
(tg, xcdot ctg, y≠1)
Все формулы связи тригонометрических функций учить не надо, потому что они достаточно легко получаются друг из друга несложными преобразованиями (подробности в этих видео). Кроме того, при частом использовании они постепенно запоминаются сами.
Примеры применения формул связи
Зачем нужны формулы связи? Они позволяют найти все тригонометрические функции угла, если известна лишь одна из них, а также дают возможность упрощать выражения, доказывать тождества, решать тригонометрические уравнения, заменяя одну функцию другой и так далее.
Пример. Найдите (5sin,α), если (cos,α=frac{2sqrt{6}}{5}) и (α∈(frac{3π}{2};2π)).
Решение. Нам известен косинус, найти надо синус. А что связывает синус и косинус? Основное тригонометрическое тождество:
(sin^2α+cos^2α=1).
Подставим вместо косинуса его значение:
(sin^2α+)((frac{2sqrt{6}}{5}))(^2=1)
(sin^2α+)(frac{4cdot 6}{25})(=1)
(sin^2α+)(frac{24}{25})(=1)
(sin^2α=1-)(frac{24}{25})
(sin^2α=)(frac{1}{25})
(sinα=±)(frac{1}{5})
Внимание! Последняя строчка – место, где теряется огромное количество баллов на ЕГЭ! Это одна из самых популярных ошибок – забыть отрицательный корень. Пожалуйста, раз и навсегда запомните, что у неполного квадратного уравнения вида (x^2=a) (при (a>0)) два корня (x_1=sqrt{a}) и (x_2=-sqrt{a}). Пусть двойка над иксом (та которая «квадрат») будет вам вечным маяком, сигнализирующим: «тут ДВА корня! Два! Не забудь!»
Вернемся к задаче. Получилось, что синус может иметь значение (frac{1}{5}), а может (-)(frac{1}{5}). И какое значение нам надо выбрать – с минусом или плюсом? Тут нам на помощь приходит информация, что (α∈(frac{3π}{2};2π)). Давайте нарисуем числовую окружность и отметим отрезок ((frac{3π}{2};2π)).

Обратите внимание – в этой четверти синус принимает только отрицательные значения (можно провести перпендикуляры до оси синусов и убедиться, что это так).

Значит, в нашем случае (sin,α=-frac{1}{5}) т.е. (5sin,α=5cdot(-frac{1}{5})=-1).
Ответ: (-1).
Пример.Найдите (tg,α), если (cos,α=)(frac{sqrt{10}}{10}) и (α∈(frac{3π}{2};2π)).
Решение. Есть 2 пути решения этой задачи:
– напрямую вычислить тангенс через формулу (tg^2α+1=)(frac{1}{cos^2α});
– сначала с помощью тождества (sin^2α+cos^2α=1) найти (sin,α), а потом через формулу (tg,α=)(frac{sin,α}{cos,α}) получить тангенс.
В учебниках обычно идут первым путем, поэтому мы пойдем вторым.
Вычисляем синус:
(sin^2α+)((frac{sqrt{10}}{10})^2)(=1)
(sin^2α+)(frac{10}{100})(=1)
(sin^2α+)(frac{1}{10})(=1)
(sin^2α=1-)(frac{1}{10})
(sin^2α=)(frac{9}{10});
(sin,α=±)(frac{3}{sqrt{10}})
Опять (α∈(frac{3π}{2};2π)), значит в итоге синус может быть только отрицательным. То есть, (sin,α=-)(frac{3}{sqrt{10}}).
А теперь вычисляем тангенс: (tg,α=-)(frac{3}{sqrt{10}})(:)(frac{sqrt{10}}{10})(=)(-frac{3}{sqrt{10}}cdotfrac{10}{sqrt{10}})(=-)(frac{30}{10})(=-3).
Ответ: (-3).
Пример. Известно, что (tg,α=-frac{3}{4}) и (frac{π}{2}<α<π). Найдите значения трех других тригонометрических функций угла (α).
Решение. Проще всего из тангенса найти котангенс:
(ctg, α=)(frac{1}{tg, α})
(ctg,α=1:(-frac{3}{4})=1cdot(-frac{4}{3})=-frac{4}{3}).
Теперь вычислим косинус по упомянутой выше формуле:
(tg^2 α+1=)(frac{1}{cos^2α})
((-)(frac{3}{4}))(^2+1=)(frac{1}{cos^2α})
(frac{9}{16})(+1=)(frac{1}{cos^2α})
(frac{9+16}{16})(=)(frac{1}{cos^2α})
(frac{25}{16})(=)(frac{1}{cos^2α})
(cos^2α=)(frac{16}{25})
(cosα=±)(frac{4}{5})
Опять перед нами стоит выбор плюс или минус. Отметим отрезок ((frac{π}{2};π)) на тригонометрической окружности и посмотрим какие значения принимает косинус в этой четверти, чтобы определится со знаком.

Очевидно, что косинус отрицателен в этой четверти, а значит (cos,α=-)(frac{4}{5}).
Осталось найти синус:
(sin^2α+cos^2α=1)
(sin^2α+(-)(frac{4}{5})()^2=1)
(sin^2α+)(frac{16}{25})(=1)
(sin^2α=1-)(frac{16}{25})
(sin^2α=)(frac{9}{25})
(sin,α=±)(frac{3}{5})
Опять используем круг, чтобы определить знак.

Получается, что (sin,α=)(frac{3}{5}).
Ответ: (ctg,α=-)(frac{4}{3}); (cos,α=-)(frac{4}{5}); (sin,α=)(frac{3}{5}).
Пример (ЕГЭ). Найдите (tg^2 α), если (5 sin^2α+13 cos^2α=6).
Решение. Давайте пойдем от того, что известно. В равенстве (5 sin^2α+13 cos^2α=6) синус заменим на косинус:
(5(1-cos^2α)+13 cos^2α=6)
(5-5 cos^2α+13 cos^2α=6)
(5+8 cos^2α=6)
(8 cos^2α=1)
(cos^2α=)(frac{1}{8})
Поняли почему именно синус заменили на косинус, а не наоборот? И почему не надо извлекать корень, досчитывая до «чистого» косинуса? Потому что для нахождения (tg^2α) хорошо подходит формула (tg^2α+1=)(frac{1}{cos^2α}) :
(tg^2 α+1=1:)(frac{1}{8})
(tg^2 α+1=1cdot)(frac{8}{1})
(tg^2 α+1=8)
(tg^2 α=7)
Ответ: (7).
Теперь еще одна задача из ЕГЭ, для наглядности мы ее решение оформили картинкой.

Пример. Упростите выражение (frac{1}{sin^2 α})(-ctg^2 α-cos^2 β).
Решение.
|
(frac{1}{sin^2 α})(-ctg^2 α-cos^2 β) |
Самое очевидное, что можно сделать – это представить котангенс как отношение косинуса к синусу. |
|
|
(=)(frac{1}{sin^2 α})(-)(frac{cos^2α}{sin^2 α})(-cos^2 β=) |
Приводим дроби к общему знаменателю. |
|
|
(=)(frac{1-cos^2α}{sin^2 α})(-cos^2 β=) |
(1-cos^2α) можно заменить на (sin^2 α). |
|
|
(=)(frac{sin^2 α}{sin^2 α})(-cos^2 β=) |
Сокращаем синусы. |
|
|
(=1-cos^2 β=sin^2 β). |
Пример. Докажите тождество (frac{cos^4α-sin^4α}{(1-sinα)(1+sinα)})(+2tg^2 α=)(frac{1}{cos^2 α}).
Решение.
|
(frac{cos^4α-sin^4α}{(1-sinα)(1+sinα)})(+2tg^2 α=)(frac{1}{cos^2 α}) |
Чтобы доказать это тождество, будем преобразовывать левую часть, пытаясь свести ее к правой. Поехали. Разложим числитель левой дроби по формуле разности квадратов, а знаменатель, наоборот, соберем по ней же. |
|
|
(frac{(cos^2α-sin^2α )(cos^2 α+sin^2α)}{1-sin^2α})(+2tg^2 α=)(frac{1}{cos^2 α}) |
Очевидно, что вторая скобка числителя равна (1) (по основному тригонометрическому тождеству), а знаменатель можно заменить на (cos^2 α). |
|
|
(frac{cos^2α-sin^2α}{cos^2 α})(+2tg^2 α=)(frac{1}{cos^2 α}) |
Теперь разложим тангенс по формуле (tg, α=)(frac{sin,α}{cos,α}). |
|
|
(frac{cos^2α-sin^2α}{cos^2 α})(+2)(frac{sin^2α}{cos^2α})(=)(frac{1}{cos^2 α}) |
Приводим дроби к общему знаменателю. |
|
|
(frac{cos^2α-sin^2α+2 sin^2α}{cos^2 α})(=)(frac{1}{cos^2 α}) |
Приводим подобные слагаемые. |
|
|
(frac{cos^2α+sin^2α}{cos^2 α})(=)(frac{1}{cos^2 α}) |
И вновь нас выручает основное тригонометрическое тождество |
|
|
(frac{1}{cos^2 α}) (=)(frac{1}{cos^2 α}) |
Левая часть полностью идентична правой, то есть тождество доказано.