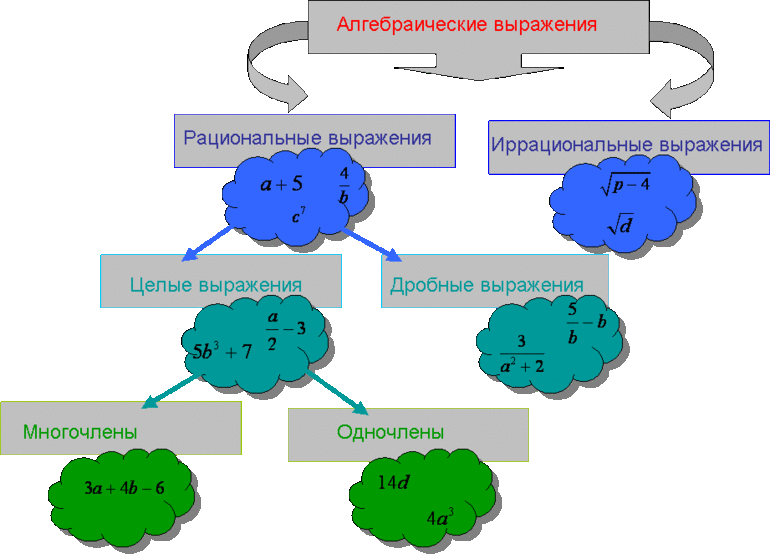
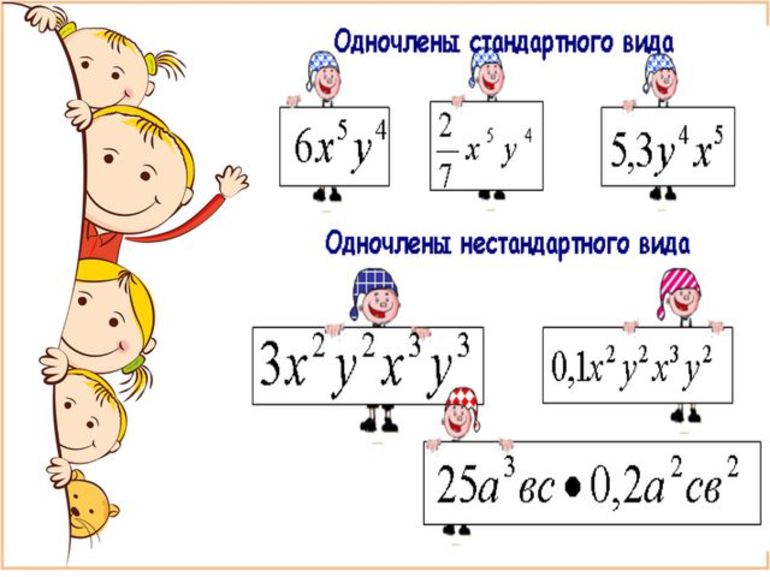
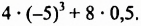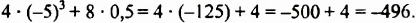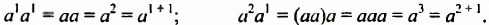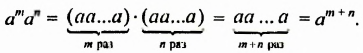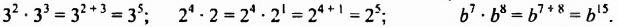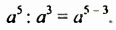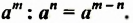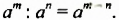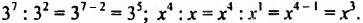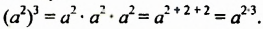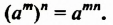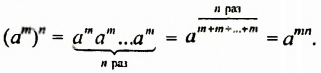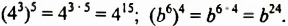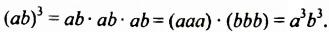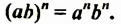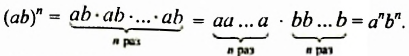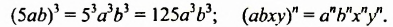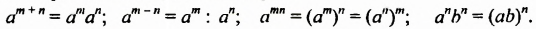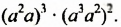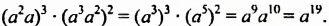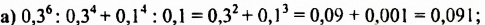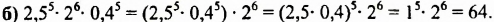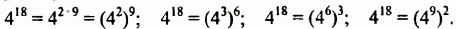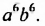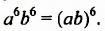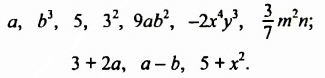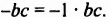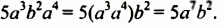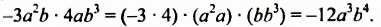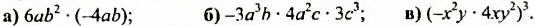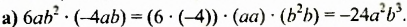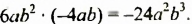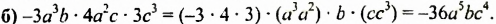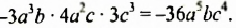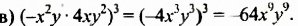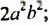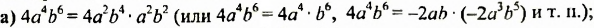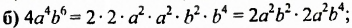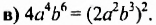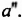Определения и примеры
Одночлен — это произведение чисел, переменных и степеней. Например, выражения 5a, 3ab2 и −62aa2b3 являются одночленами.
Приведём ещё примеры одночленов:
Одночленом также является любое отдельное число, любая переменная или любая степень. Например, число 9 является одночленом, переменная x является одночленом, степень 52 является одночленом.
Приведение одночлена к стандартному виду
Рассмотрим следующий одночлен:
Этот одночлен выглядит не очень аккуратно. Чтобы сделать его проще, нужно привести его к так называемому стандартному виду.
Приведение одночлена к стандартному виду заключается в перемножении однотипных сомножителей, входящих в этот одночлен. То есть числа нужно перемножать с числами, переменные с переменными, степени со степенями. В результате этих действий получается упрощённый одночлен, который тождественно равен предыдущему.
Ещё один нюанс заключается в том, что в одночлене степени можно перемножать только в том случае, если они имеют одинаковые основания.
Итак, приведём одночлен 3a25a3b2 к стандартному виду. В этом одночлене содержатся числа 3 и 5. Перемножим их, получим число 15. Записываем его:
15
Далее в одночлене 3a25a3b2 содержатся степени a2 и a3, которые имеют одинаковое основание a. Из тождественных преобразований со степенями известно, что при перемножении степеней с одинаковыми основаниями, основание оставляют без изменений, а показатели складывают. Тогда перемножение степеней a2 и a3 даст в результате a5. Записываем a5 рядом с числом 15
15a5
Далее в одночлене 3a25a3b2 содержится степень b2. Её не с чем перемножать, поэтому она остаётся без изменений. Записываем её как есть к новому одночлену:
15a5b2
Мы привели одночлен 3a25a3b2 к стандартному виду. В результате получили одночлен 15a5b2
3a25a3b2 = 15a5b2
Числовой сомножитель 15 называют коэффициентом одночлена. Приводя одночлен к стандартному виду, коэффициент нужно записывать в первую очередь, и только потом переменные и степени.
Если коэффициент в одночлене отсутствует, то говорят, что коэффициент равен единице. Так, коэффициентом одночлена abc является 1, поскольку abc это произведение единицы и abc
abc = 1 × abc
А коэффициентом одночлена −abc будет −1, поскольку −abc это произведение минус единицы и abc
−abc = −1 × abc
Степенью одночлена называют сумму показателей всех переменных входящих в этот одночлен.
Например, степенью одночлена 15a5b2 является 7. Это потому что переменная a имеет показатель 5, а переменная b имеет показатель 2. Отсюда 5 + 2 = 7. Показатель числового сомножителя 15 считать не нужно, поскольку нас интересуют только показатели переменных.
Ещё пример. Степенью одночлена 7ab2 является 3. Здесь переменная a имеет показатель 1, а переменная b имеет показатель 2. Отсюда 1 + 2 = 3.
Если одночлен не содержит переменных или степеней, а состоит из числа, то говорят, что степень такого одночлена равна нулю. Например, степень одночлена 11 равна нулю.
Не следует путать степень одночлена и степень числа. Степень числа это произведение из нескольких одинаковых множителей, тогда как степень одночлена это сумма показателей всех переменных входящих в этот одночлен. В одночлене 11 нет переменных, поэтому его степень равна нулю.
Пример 1. Привести одночлен 5xx3ya2 к стандартному виду
Перемножим числа 5 и 3, получим 15. Это будет коэффициент одночлена:
15
Далее в одночлене 5xx3ya2 содержатся переменные x и x. Перемножим их, получим x2.
15x2
Далее в одночлене 5xx3ya2 содержится переменная y, которую не с чем перемножать. Записываем её без изменений:
15x2y
Далее в одночлене 5xx3ya2 содержится степень a2, которую тоже не с чем перемножать. Её также оставляем без изменений:
15x2ya2
Получили одночлен 15x2ya2, который приведён к стандартному виду. Буквенные сомножители принято записывать в алфавитном порядке. Тогда одночлен 15x2ya2 примет вид 15a2x2y.
Поэтому, 5xx3ya2 = 15a2x2y.
Пример 2. Привести одночлен 2m3n × 0,4mn к стандартному виду
Перемножим числа, переменные и степени по отдельности.
2m3n × 0,4mn = 2 × 0,4 × m3 × m × n × n = 0,8m4n2
Числа, переменные и степени при перемножении разрешается заключать в скобки. Делается это для удобства. Так, в данном примере перемножение чисел 2 и 0,4 можно заключить в скобки. Также в скобки можно заключить перемножение m3 × m и n × n
2m3n × 0,4mn = (2 × 0,4) × (m3 × m) × (n × n) = 0,8m4n2
Но желательно выполнять все элементарные действия в уме. Так, решение можно записать значительно короче:
2m3n × 0,4mn = 0,8m4n2
Но чтобы в уме приводить одночлен к стандартному виду, тема умножения целых чисел и умножения степеней должна быть изучена на хорошем уровне.
Сложение и вычитание одночленов
Одночлены можно складывать и вычитать. Чтобы это было возможно, они должны иметь одинаковую буквенную часть. Коэффициенты могут быть любыми. Сложение и вычитание одночленов это по сути приведение подобных слагаемых, которое мы рассматривали при изучении буквенных выражений.
Чтобы сложить (вычесть) одночлены, нужно сложить (вычесть) их коэффициенты, а буквенную часть оставить без изменений.
Пример 1. Сложить одночлены 6a2b и 2a2b
6a2b + 2a2b
Сложим коэффициенты 6 и 2, а буквенную часть 6a2b оставим без изменений
6a2b + 2a2b = 8a2b
Пример 2. Вычесть из одночлена 5a2b3 одночлен 2a2b3
5a2b3 − 2a2b3
Можно заменить вычитание сложением, и сложить коэффициенты одночленов, оставив буквенную часть без изменения:
5a2b3 − 2a2b3 = 5a2b3 + (−2a2b3) = 3a2b3
Либо сразу из коэффициента первого одночлена вычесть коэффициент второго одночлена, а буквенную часть оставить без изменения:
5a2b3 − 2a2b3 = 3a2b3
Умножение одночленов
Одночлены можно перемножать. Чтобы перемножить одночлены, нужно перемножить их числовые и буквенные части.
Пример 1. Перемножить одночлены 5x и 8y
Перемножим числовые и буквенные части по отдельности. Для удобства перемножаемые сомножители будем заключать в скобки:
5x × 8y = (5 × 8) × (x × y) = 40xy
Пример 2. Перемножить одночлены 5x2y3 и 7x3y2c
Перемножим числовые и буквенные части по отдельности. В процессе умножения будем применять правило перемножения степеней с одинаковыми основаниями. Перемножаемые сомножители будем заключать в скобки:
5x2y3 × 7x3y2c = (5 × 7) × (x2x3) × (y3y2) × c = 35x5y5c
Пример 3. Перемножить одночлены −5a2bc и 2a2b4
−5a2bc × 2a2b4 = (−5 × 2) × (a2a2) × (bb4) × c = −10a4b5c
Пример 4. Перемножить одночлены x2y5 и (−6xy2)
x2y5 × (−6xy2) = −6 × (x2x) × (y5y2) = −6x3y7
Пример 5. Найти значение выражения
Деление одночленов
Одночлен можно разделить на другой одночлен. Для этого нужно коэффициент первого одночлена разделить на коэффициент второго одночлена, а буквенную часть первого одночлена разделить на буквенную часть второго одночлена. При этом используется правило деления степеней.
Например, разделим одночлен 8a2b2 на одночлен 4ab. Запишем это деление в виде дроби:
Первый одночлен 8a2b2 будем называть делимым, а второй 4ab — делителем. А одночлен, который получится в результате, назовём частным.
Разделим коэффициент делимого на коэффициент делителя, получим 8 : 4 = 2. В исходном выражении ставим знак равенства и записываем этот коэффициент частного:
Теперь делим буквенную часть. В делимом содержится a2, в делителе — просто a. Делим a2 на a, получаем a, поскольку a2 : a = a2 − 1 = a. Записываем в частном a после 2
Далее в делимом содержится b2, в делителе — просто b. Делим b2 на b, получаем b, поскольку b2 : b = b2 − 1 = b. Записываем в частном b после a
Значит, при делении одночлена 8a2b2 на одночлен 4ab получается одночлен 2ab.
Сразу можно выполнить проверку. При умножении частного на делитель должно получаться делимое. В нашем случае, если 2ab умножить на 4ab, должно получиться 8a2b2
2ab × 4ab = (2 × 4) × (aa) × (bb) = 8a2b2
Не всегда можно первый одночлен разделить на второй одночлен. Например, если в делителе окажется переменная, которой нет в делимом, то говорят, что деление невозможно.
К примеру, одночлен 6xy2 нельзя разделить на одночлен 3xyz. В делителе 3xyz содержится переменная z, которая не содержится в делимом 6xy2.
Проще говоря, мы не сможем найти частное, которое при умножении на делитель 3xyz дало бы делимое 6xy2, поскольку такое умножение обязательно будет содержать переменную z, которой нет в 6xy2.
Но если в делимом содержится переменная, которая не содержится в делителе, то деление будет возможным. В этом случае переменная, которая отсутствовала в делителе, будет перенесена в частное без изменений.
Например, при делении одночлена 4x2y2z на 2xy, получается 2xyz. Сначала разделили 4 на 2 получили 2, затем x2 разделили на x, получили x, затем y2 разделили на y, получили y. Затем приступили к делению переменной z на такую же переменную в делителе, но обнаружили, что такой переменной в делителе нет. Поэтому перенесли переменную z в частное без изменений:
Для проверки умножим частное 2xyz на делитель 2xy. В результате должен получиться одночлен 4x2y2z
2xyz × 2xy = (2 × 2) × (xx) × (yy) × z = 4x2y2z
Но в некоторых дробях, если невозможно выполнить деление, бывает возможным выполнить сокращение. Делается это с целью упростить выражение.
Так, в предыдущем примере нельзя было разделить одночлен 6xy2 на одночлен 3xyz. Но можно сократить эту дробь на одночлен 3xy. Напомним, что сокращение дроби это деление числителя и знаменателя на одно и то же число (в нашем случае на одночлен 3xy). В результате сокращения дробь становится проще, но её значение не меняется:
В числителе и знаменателе мы пришли к делению одночленов, которое можно выполнить:
Процесс деления обычно выполняется в уме, записывая над числителем и знаменателем получившийся результат:
Пример 2. Разделить одночлен 12a2b3c3 на одночлен 4a2bc
Пример 3. Разделить одночлен x2y3z на одночлен xy2
Дополнительно упомянем, что деление одночлена на одночлен также невозможно, если одна из степеней, входящая в делимое, имеет показатель меньший, чем показатель той же степени из делителя.
Например, разделить одночлен 2x на одночлен x2 нельзя, поскольку степень x, входящая в делимое, имеет показатель 1, тогда как степень x2, входящая в делитель, имеет показатель 2. Мы не сможем найти частное, которое при перемножении с делителем x2 даст в результате делимое 2x.
Конечно, мы можем выполнить деление x на x2, воспользовавшись свойством степени с целым показателем:
и такое частное при перемножении с делителем x2 будет давать в результате делимое 2x
Но нас пока интересуют только те частные, которые являются так называемыми целыми выражениями. Целые выражения это те выражения, которые не являются дробями, в знаменателе которых содержится буквенное выражение. А частное целым выражением не является. Это дробное выражение, в знаменателе которого содержится буквенное выражение.
Возведение одночлена в степень
Одночлен можно возвести в степень. Для этого используют правило возведения степени в степень.
Пример 1. Возвести одночлен xy во вторую степень.
Чтобы возвести одночлен xy во вторую степень, нужно возвести во вторую степень каждый сомножитель этого одночлена
(xy)2 = x2y2
Пример 2. Возвести одночлен −5a3b во вторую степень.
(−5a3b)2 = (−5)2 × (a3)2 × b2 = 25a6b2
Пример 3. Возвести одночлен −a2bc3 в пятую степень.
В данном примере коэффициентом одночлена является −1. Этот коэффициент тоже нужно возвести в пятую степень:
(−a2bc3)5 = (−1)5 × (a2)5 × b5 × (c3)5 = −1a10b5c15 = −a10b5c15
Когда коэффициент равен −1, то саму единицу не записывают. Записывают только минус и потом остальные сомножители одночлена. В приведенном примере сначала получился одночлен −1a10b5c15, затем он был заменён на тождественно равный ему одночлен −a10b5c15.
Пример 4. Представить одночлен 4x2 в виде одночлена, возведённого в квадрат.
В данном примере нужно найти произведение, которое во второй степени будет равно выражению 4x2. Очевидно, что это произведение 2x. Если это произведение возвести во вторую степень (в квадрат), то получится 4x2
(2x)2 = 22x2 = 4x2
Значит, 4x2 = (2x)2. Выражение (2x)2 это и есть одночлен, возведённый в квадрат.
Пример 5. Представить одночлен 121a6 в виде одночлена, возведённого в квадрат.
Попробуем найти произведение, которое во второй степени будет равно выражению 121a6.
Прежде всего заметим, что число 121 получается, если число 11 возвести в квадрат. То есть первый сомножитель будущего произведения мы нашли. А степень a6 получается в том случае, если возвести в квадрат степень a3. Значит вторым сомножителем будущего произведения будет a3.
Таким образом, если произведение 11a3 возвести во вторую степень, то получится 121a6
(11a3)2 = 112 × (a3)2 = 121a6
Значит, 121a6 = (11a3)2. Выражение (11a3)2 это и есть одночлен, возведённый в квадрат.
Разложение одночлена на множители
Поскольку одночлен является произведением чисел, переменных и степеней, то он может быть разложен на множители, из которых состоит.
Пример 1. Разложить одночлен 3a3b2 на множители
Данный одночлен можно разложить на множители 3, a, a, a, b, b
3a3b2 = 3aaabb
Либо степень b2 можно не раскладывать на множители b и b
3a3b2 = 3aaab2
Либо степень b2 разложить на множители b и b, а степень a3 оставить без изменений
3a3b2 = 3a3bb
В каком виде представлять одночлен зависит от решаемой задачи. Главное, чтобы разложение было тождественно равно исходному одночлену.
Пример 2. Разложить одночлен 10a2b3c4 на множители.
Разложим коэффициент 10 на множители 2 и 5, степень a2 разложим на множители aa, степень b3 — на множители bbb, степень c4 — на множители cccc
10a2b3c4 = 2 × 5 × aabbbcccc
Задания для самостоятельного решения
Задание 1. Приведите одночлен −2aba к стандартному виду.
Задание 2. Приведите одночлен 0,5m × 2n к стандартному виду.
Решение:
0,5m × 2n = (0,5 × 2)(mn) = 1mn = mn
Задание 3. Приведите одночлен −8ab(−2,5)b2 к стандартному виду.
Решение:
−8ab(−2,5)b2 = −8 × (−2,5) × a × (b × b2) = 20ab3
Задание 4. Приведите одночлен 0,15pq × 4pq2 к стандартному виду.
Решение:
Задание 5. Приведите одночлен −2x3 × 0,5xy2 к стандартному виду.
Решение:
Задание 6. Приведите одночлен 2m3n × 0,4mn к стандартному виду.
Решение:
Задание 7. Приведите одночлен 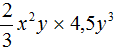
Решение:
Задание 8. Приведите одночлен 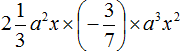
Решение:
Задание 9. Перемножьте одночлены 2x и 2y
Задание 10. Перемножьте одночлены 6x, 5x и y
Решение:
6x × 5x × y = 30x2y
Задание 11. Перемножьте одночлены 2x2, 2x3 и y2
Решение:
2x2 × 2x3 × y2 = (2 × 2) × (x2x3) × y2 = 4x5y2
Задание 12. Перемножьте одночлены −8x и 5x3
Решение:
−8x × 5x3 = (−8 × 5)×(xx3) = −40x4
Задание 13. Перемножьте одночлены x2y5 и (−6xy2)
Решение:
x2y5 × (−6xy2) = −6 × (x2x) × (y5y2) = −6x3y7
Задание 14. Выполните умножение:
Решение:
Задание 15. Выполните умножение:
Решение:
Задание 16. Возведите одночлен x2y2z2 в третью степень
Решение:
(x2y2z2)3 = (x2)3 × (y2)3 × (z2)3 = x6y6z6
Задание 17. Возведите одночлен xy2z3 в пятую степень.
Решение:
(xy2z3)5 = x5 × (y2)5 × (z3)5 = x5y10z15
Задание 18. Возведите одночлен 4x во вторую степень.
Решение:
(4x)2 = 42 × x2 = 16x2
Задание 19. Возведите одночлен 2y3 в третью степень.
Решение:
(2y3)3 = 23 × (y3)3 = 8y9
Задание 20. Возведите одночлен −0,6x3y2 в третью степень.
Решение:
(−0,6x3y2)3 = (−0,6)3 × (x3)3 × (y2)3= −0,216x9y6
Задание 21. Возведите одночлен −x2yz3 в пятую степень.
Решение:
(−x2yz3)5 = (−x2)5 × y5 × (z3)5= −x10y5z15
Задание 22. Возведите одночлен −x3y2z во вторую степень.
Решение:
(−x3y2z)2 = (−x3)2 × (y2)2 × z2 = x6y4z2
Задание 23. Представьте одночлен −27x6y9 в виде одночлена, возведённого в куб.
Решение:
−27x6y9 = (−3x2y3)3
Задание 24. Представьте одночлен −a3b6 в виде одночлена, возведённого в куб.
Задание 25. Выполните деление
Решение:
Задание 26. Выполните деление
Решение:
Задание 27. Выполните деление
Решение:
Задание 28. Выполните деление
Решение:
Задание 29. Выполните деление
Решение:
Задание 30. Выполните деление
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Важность понятия
Пик развития математики пришёлся на XVI век, когда учёные разных стран начали обобщать известные сведения и формулировать различные теоремы и доказательства. Но перед этим появились такие понятия, как одночлен и многочлен. Запись уравнения или любой другой формулы, в которой не использовалось сложение или вычитание, получило название одночлен. А суммирование нескольких таких выражений или их разность назвали многочленом.
Карл Фридрих Гаусс, считающийся королём математиков, утверждал, что коэффициенты многочлена могут быть не только вещественными, но и комплексными. Свои доказательства этому он привёл в основной теореме алгебры. Из-за этого роль неизвестных в выражениях начала меняться. Буквенные обозначения стали не только символами, подменяющими числовые значения, но и начали заменять функции.
Таким образом, было принято, что любое математическое выражение состоит из совокупности одночленов. Ими могут быть:
- единственные числа;
- буквы;
- буквенно-числовые произведения.
Изучение уравнений и равенств, состоящих из нескольких одночленов, стало главным объектом в развитии классической алгебры. С их преобразованием связаны такие разделы, как теория групп, анализ функций, изучение комплексных чисел, алгебраическая геометрия.
Над одночленами можно выполнять различные действия. Их можно возводить в корень с разным основанием, перемножать или делить между собой, возводить в степень. Это позволяет выполнять упрощения и приведения выражений к стандартной форме, что впоследствии облегчает вычисление многочленов.
Впервые с понятием «одночлен» знакомят учеников в среднеобразовательной школе в седьмом классе на уроке алгебры. Изучение видов одночленов и правил действий над ними является стартовой площадкой для понимания сущности многочлена, то есть фактически основ алгебры.
С помощью одночлена можно описать простые события, при которых происходит умножение. Это могут быть как количественно известные параметры, так и переменные или неизвестные. Для того чтобы понять важность введения в математике термина «одночлен», лучше всего провести аналогию с фруктами. Яблоко и груши — это отдельный вид деревьев, но их всех объединяет одинаковое свойство, поэтому их называют «фруктами». Так и с формулами: они хотя и разные, но обладают общими свойствами. Поэтому и придумали название — одночлен.
Общие сведения
Алгебраическое выражение, в состав которого входит переменная и постоянная часть, объединённая произведением, принято называть одночленом. Фактически эта запись представляет умножение чисел и степеней неизвестных с натуральным показателем. Каждое неопределённое или известное число занимает одну позицию. Количество таких позиций неограниченно.
Если перед буквенным значением стоит цифра, то её называют коэффициентом одночлена. Он может быть как положительным, так и отрицательным. Когда коэффициент не указан, в зависимости от знака он принимается равным единице или минус единице. При этом понятие коэффициент зачастую применительно и к числу. Например, считают, что у числа девять он равен девяти.
Наиболее типичные записи рассматриваемого вида выражений имеют следующий вид:
- 23 — это обыкновенный одночлен, в составе которого нет переменных;
- 12 * f — выражение, состоящее из буквенного и цифрового числа;
- -5 * d2 — запись, содержащая степень;
- 12 * 3 5/6 * x2 * y4 — пример сложного порядка;
- x * y — формула, в которой все коэффициенты равны единице.
Это всё стандартные виды одночлена, то есть выражения записаны в таком состоянии, что их упростить уже невозможно. Например, формула a3 * 1*3 * b * 3 * а * b3 хоть и является одночленом, но не считается записью стандартного вида. Всё дело в том, что её можно упростить. Кроме этого, её нужно переписать таким образом, чтобы числовой множитель стоял на первом месте, затем неизвестные и основания со степенными показателями. После преобразования получится выражение: 9 * a4 * b4. Этот вид записи уже является стандартным. В нём одночленами считаются числа, переменные и степени.
В алгебре часто используется понятие «степень одночлена». Под ним понимают сумму показателей переменных значений, входящих в состав выражения. Примечательно что нуль, входящий в состав одночлена, степени не имеет, при этом если степень не указана, то она принимается нулевой. Когда выражения похожи друг на друга, они считаются подробными. Например, 5 * d2* k10 и 1/8 * d2 * k10 — подобны.
Действия над выражениями
После умножения одночленов получается также одночлен, указываемый в стандартной записи. Для того чтобы выполнить операцию произведения, используют свойства умножения, а также правила действия со степенями. Умножить одно выражение на другое, значит, определить сумму слагаемых множителя, каждое из которых равно умножаемому.
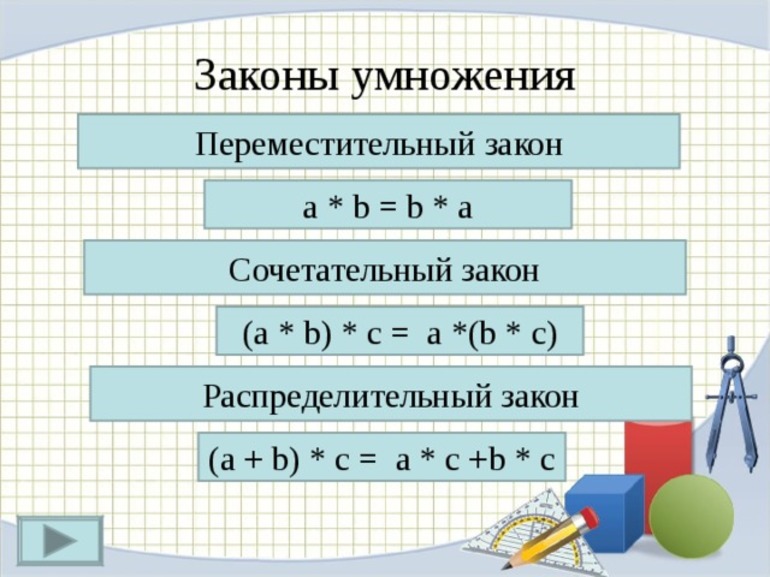
Существует три закона умножения:
- Сочетательный. Если нужно умножить два одночлена на третий, то можно сначала посчитать произведение первого на третий, а после результат умножить на второй член.
- Переместительный. От перестановки множителей итог не изменится.
- Распределительный. Для того чтобы умножить одночлен на сумму, нужно его отдельно перемножить с каждым суммирующимся членом, а после сложить результат. То есть одночлен превратится в многочлен. При этом этот закон справедлив и для разницы.
При умножении сложных выражений типовой операцией является упрощение записи. Но преобразовать возможно не все выражения. Например, пусть необходимо выполнить умножение одночленов: 2 * c * p3 * s5 (-7 * c3 * p2) = -14 * с2 * p5 * s5.
Деление происходит аналогичным образом. При этом действует правило, согласно которому частное одночленов можно упростить, но лишь в том случае, если делимое и делитель содержат одинаковые буквенные или числовые коэффициенты. В этом случае из показателя делителя отнимается значение степени делимого, коэффициент которого делят на количественный показатель делителя. Например, 12 * p3 * d4 * r6: 4 * p * d2 * r3 = 3 * p2 * d2 * r3.
Возведение в степень выполняют согласно правилам свойств степеней. Так как операция возведения это не что иное, как умножение члена самого на себя столько раз, сколько показывает число в показателе. Например, (3*с)3 = (3*с) * (3*с) *(3*с). Используя правило умножения, выражение можно представить как (3 * 3 * 3) * (с * с * с). Последнюю запись же можно упростить до вида: (3 * 3 * 3) * (с * с * с) = 33 * c3 = 9 * c * p3.
Таким образом, для того чтобы возвести выражение в степень, необходимо каждый множитель отдельно возвести в степень, а затем результаты перемножить. Это правило действует и для любых степеней, показатель которых натуральный. Закон применим и для дробного отношения, только после возведения числитель делят на знаменатель.
Принцип преобразования
Пусть имеется сложный одночлен, состоящий из ненулевых степеней, квадратов, дробных чисел и букв следующего вида: 5 * 7 * a * m * c7 * 3 *2/9 * 2 (1/7) * am * bn * c * x5 * 120. Тут следует обратить внимание, что дроби в выражении могут быть любого типа, кроме случая, когда в знаменателе будет стоять буква. Такая запись неудобна для восприятия и дальнейшего использования из-за хаотично расставленных подобных членов. Поэтому нужно преобразовать её к стандартному виду.
В основе способа упрощения одночлена лежат следующие принципы:
- Если в записи встречается число, то оно обязательно пишется впереди и должно быть единственным в выражении.
- Каждая буква, встречающаяся в формуле, должна повторяться только один раз, записанная в своей степени.
- Буквы в одночлене записывают в алфавитном порядке.
При этом математиками было решено не писать знак умножения между числовым и буквенным множителем, а также между буквенными множителями, перемножающимися между собой.
Решения одночленов
Примеры для самостоятельной работы по преобразованию многочленов помогут понять, как правильно выполняются простые арифметические действия, что важно для решения последующих задач, связанных с многочленами.
Можно выделить следующие виды типовых заданий:
- Пусть дан многочлен: 14 a7b13mt. Нужно определить степень одночлена, то есть сумму степеней входящих в выражение. Для рассматриваемого примера она будет равна: 7 + 13 + 1 + 6 = 20.
- Необходимо записать результат перемножения двух выражений: 12a7c5d * 3b9c6d7k. Решение задания будет следующим: 12a7c5d * 3b9c6d7k = 36a7b9c11d8k.
-
Нужно найти ответ, получающийся после деления 16 a7b5k14m на 8 a5bk3. Итак, при делении получится следующее: 16 a7b5k14m / 8 a5bk3 = 2a2b4k11m.
-
Сложение и вычитание одночленов допускается только в том случае, если буквенная часть у них одинаковая, включая степени. Например, 2 a7b5ck + 7a7b5ck = 9 a7b5ck или 9 p5 — 3p5 = 6p5. То есть действие выполняется только над коэффициентами.
-
Дан многочлен вида: 2a7b5kz3. Нужно возвести его в пятую степень. Согласно правилу, каждый член выражения возводится в степень отдельно. При этом следует помнить правило, что при возведении степени в степень показатели перемножаются. Ответ будет выглядеть следующим образом: (2a7b5kz3)5 = 32a35 b25k5z15.
При выполнении различных действий с одночленом нужно знать всего лишь несколько правил и быть предельно аккуратным при вычислении. Особенно это важно для длинных выражений, состоящих из различного вида членов.
Упрощение на онлайн-калькуляторе
Привести одночлены к удобному виду, значит, упростить их до стандартной записи. Однако зачастую приходится иметь дело с выражениями большого порядка. При этом они могут включать в себя одновременно различные арифметические операции. Выполнять тождественные преобразования самостоятельно бывает довольно трудно, причём возникает вероятность допущения ошибки.
Поэтому использовать специализированные сайты, которые умеют быстро и безошибочно упрощать одночлены любого вида, не зазорно. Порталы предлагают свои услуги бесплатно и для решения примеров не требуют даже регистрации. Что интересно, кроме быстрого расчёта, пользователь, зашедший на такой ресурс, сможет увидеть всю цепочку упрощения, а при желании на страницах онлайн-калькулятора ознакомиться с теорией и основными определениями.
Из всего множества сайтов можно выделить следующие три:
- Kontrolnaya-rabota. Сервис хоть и ориентирован на учащихся старших классов, но по своим возможностям довольно функционален. Так, с его помощью можно преобразовать даже комплексные выражения. Всё, что требуется от пользователя, это правильно ввести выражение и нажать кнопку «Упростить».
- Umath. Программа даёт возможность упростить любое алгебраическое выражение. На сайте можно найти всю необходимую теорию. Ограничений в размере формулы нет.
- Mathforyou. Используя этот онлайн-калькулятор, пользователь сможет выполнить различные действия над выражением, содержащим числовое и символьное обозначение. Для правильного вычисления нужно предварительно ознакомиться с правилами ввода математической формулы, указанными тут же на сайте.
Рекомендованные сайты имеют российский домен, а программы написаны русскими программистами. Поэтому проблем с пониманием, как пользоваться приложениями, возникнуть не должно. Интерфейс онлайн-калькуляторов не содержит нагромождения ненужной информации и интуитивно понятен. Ответ вычисляется буквально за несколько секунд, а используемые алгоритмы исключают возникновение ошибки.
Содержание:
Одночлены
Степень с натуральным показателем
Напомним, что произведение двух или трех одинаковых множителей, каждый из которых равен
Квадрат числа 5 называют еще второй степенью этого числа, а куб — третьей степенью.
Соответственно произведение 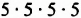
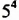
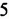
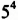
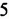
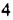
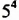
Определение:
Степенью числа 
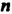
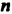



Степень с основанием 
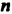
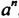

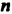
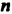

Итак, по определению
Выясним знак степени с натуральным показателем.
тогда
— любая натуральная степень числа 0 равна 0.
, тогда
— любая натуральная степень положительного числа есть положительное число.
тогда
. Степень отрицательного числа с четным показателем является положительным числом, поскольку произведение четного количества отрицательных чисел положительно. Степень отрицательного числа с нечетным показателем является отрицательным числом, поскольку произведение нечетного количества отрицательных чисел отрицательно.
Возводить числа в степень с натуральным показателем можно с помощью микрокалькулятора. Вычислить, например, значение 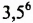
или по более удобной схеме:
Получим значение степени: 1838,265625.
Возведение в степень — действие третьей ступени. Напомним, что если выражение без скобок содержит действия разных ступеней, то сначала выполняют действия высшей ступени, а потом — низшей. Так, чтобы найти значение выражения 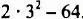
Примеры выполнения заданий:
Пример №110
Вычислить
Решение:
Выполняя вычисления, можно:
а) записывать каждое действие в отдельности:
б) записывать вычисления в строчку:
Ответ. 496.
Свойства степени с натуральным показателем
Умножение степеней с одинаковыми основаниями
Рассмотрим произведения двух степеней с основанием 
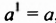
Следовательно, 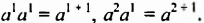
Свойство 1. Для любого числа 

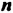
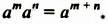
Из свойства 1, которое еще называют основным свойством степени, следует правило умножения степеней:
Чтобы умножить степени с одинаковыми основаниями, нужно основание оставить прежним, а показатели степеней сложить.
Например:
Правило умножения степеней распространяется на произведение трех и более степеней. Например:
Деление степеней с одинаковыми основаниями
Рассмотрим равенство 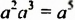
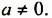
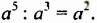
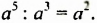
В этом примере частное степеней с одинаковыми основаниями равно степени с тем же основанием и показателем, который равен разности показателя степени делимого и показателя степени делителя. Сформулируем и докажем соответствующее свойство в общем случае.
Свойство 2. Для любого числа 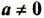
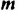
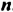
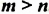
Доказательство. Поскольку 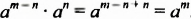
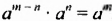
Из доказанного свойства следует правило деления степеней:
Чтобы разделить степени с одинаковыми основаниями, нужно основание оставить прежним, а из показателя степени делимого вычесть показатель степени делителя.
Например:
Возведение степени в степень
! Возведем степень 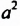
Итак, 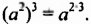
Свойство 3. Для любого числа 
Доказательство.
Из свойства 3 следует правило возведения степени в степень:
Чтобы возвести степень в степень, нужно основание оставить прежним, а показатели степеней перемножить.
Например:
Возведение произведения в степень
Возведем произведение 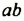
Итак, 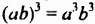
Свойство 4. Для любых чисел 
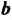
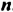
Доказательство.
Имеем такое правило:
Чтобы возвести в степень произведение, нужно возвести в эту степень каждый множитель и результаты перемножить.
Это правило распространяется на произведение трех и более множителей. Например:
Примечание. Доказанные тождества 
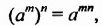
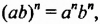
- Заказать решение задач по высшей математике
Примеры выполнения заданий:
Пример №111
Упростить выражение
Решение:
Пример №112
Вычислить:
Пример №113
Представить 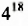
Решение:
Пример №114
Представить в виде степени произведение
Решение:
Одночлен и его стандартный вид
Рассмотрим две группы выражений:
Какова особенность выражений первой группы? Чем они отличаются от выражений второй группы?
Выражения первой группы — это переменные, числа, их степени и произведения. Такие выражения называют одночленами. В общем виде одночлен — это произведение чисел, переменных и их степеней.
Выражения второй группы не являются одночленами, поскольку содержат действия сложения или вычитания.
Рассмотрим одночлен 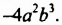
Одночленом стандартного вида называют такой одночлен, который содержит только один числовой множитель, находящийся на первом месте, ч степени разных переменных.
Числовой множитель одночлена стандартного вида называют коэффициентом одночлена. Коэффициент одночлена 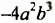
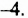
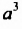
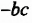

Одночлен 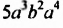
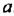
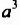
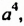
Умножение одночленов
Перемножим одночлены 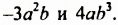
-3а2Ь • 4aby = (-3 • 4) • (а2а) • (ЬЬг) = -12аъЬ
Итак, произведением одночленов -Ъа2Ь и 4аЬъ является одночлен -12а3Ь*. Вообще, произведением любых одночленов является одночлен.
Возведение одночлена в степень
Возведем одночлен -5а2Ь в куб. Используя свойства степени, получим:
Итак, кубом одночлена 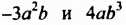
Степень одночлена
В одночлене 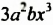
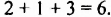
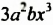
Степенью одночлена называют сумму показателей степеней всех переменных, которые в него входят. Если одночленом является число, отличное от нуля, то считают, что степень такого одночлена равна нулю.
Например: 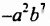
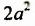
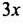
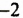
Примеры выполнения заданий:
Пример №115
Записать выражение в виде одночлена стандартного вида:
Сокращенная запись:
Сокращенная запись:
Пример №116
Представить одночлен 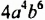
а) произведения двух одночленов стандартного вида;
б) произведения двух одночленов, одним из которых является
в) квадрата одночлена стандартного вида.
Решение:
Интересно знать
Понятие степени с натуральным показателем возникло в античные времена в связи с вычислением площадей и объемов. Толкование степеней 
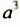
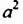
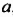
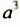
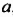
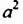
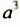
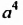
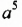
Только в XVII в. французский математик Рене Декарт (1596-1650) дал геометрическое толкование произведения любого числа множителей после чего и произведение 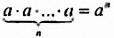
Декарт же ввел и современное обозначение степени с натуральным показателем в виде
- Многочлены
- Формулы сокращенного умножения
- Разложение многочленов на множители
- Системы линейных уравнений с двумя переменными
- Делимость натуральных чисел
- Выражения и уравнения
- Линейное уравнение с одной переменной
- Целые выражения
План урока:
Определение степени с натуральным показателем
Сравнение степеней
Умножение и деление степеней
Одночлен. Умножение одночленов
Возведение одночлена в степень
Тождества
Определение степени с натуральным показателем
Периодически в математике приходится умножать число на само себя несколько раз. Пусть нам надо записать произведение десяти множителей, каждый из которых равен 2. Эта запись будет выглядеть так:
2*2*2*2*2*2*2*2*2*2
Однако существует и более компактная и удобная запись:
2*2*2*2*2*2*2*2*2*2 = 210
Говорят, что число 2 возвели в десятую степень. В данном случае двойка – это основание степени, а 10 – показатель степени:
Если показатель равен единице, то в произведении должен быть только один множитель, а потому само число не меняется:
21 = 2
Теперь сформулируем определение степени числа с натуральным показателем:
Важно понимать, что такое определение может использоваться только в том случае, если n – натуральное число. В старших классах будут рассматриваться примеры с дробными и отрицательными показателями, однако в таких случаях потребуются и более сложные определения этого понятия.
Отметим, что основание может быть любым числом – целым, дробным, положительным, отрицательным.
Рассмотрим несколько простейших заданий.
- Возведите в 5-ую степень число 3.
Решение:
35 = 3*3*3*3*3 = 9*3*3*3 = 27*3*3 = 81*3 = 243
- Возведите во 2-ю степень число 0,7.
Решение:
0,72 = 0,7*0,7 = 0,49
- Возведите в 3-ю степень дробь 3/4.
Решение:
- Возведите в 4-ую степень число – 4.
Решение:
(-4)4 = (-4)*(-4)*(-4)*(-4) = 16*(-4)*(-4) = (-64)*(-4) = 256
- Возведите в третью степень – 5.
Решение:
(-5)3 = (-5)*(-5)*(-5) = 25*(-5) = -125
Обратите внимание, что при возведении отрицательного числа можно получить как отрицательное, так и положительное число. Здесь всё зависит от значения показателя. Если он четный, то получится положительное число, а если нечетный, то отрицательное.
- Сравните выражения (–1,365)106 и (– 2,512)75.
Решение:
Число 106 – четное, поэтому при вычислении (–1,365)106 должно получиться положительное число:
(–1,365)106> 0.
Число 75 – нечетное, поэтому (– 2,512)75 – это отрицательное число:
(– 2,512)75<0.
Следовательно, можно записать следующее
(– 2,512)75< 0 <(–1,365)106, откуда
(– 2,512)75< (–1,365)106.
Ответ: (– 2,512)75< (–1,365)106.
Очевидно, что, сколько бы мы не умножали ноль на самого себя, в результате всегда будет получаться снова 0. Поэтому при любом натуральном значении n выражение 0n равно нулю.
Исторически сложилось, что для некоторых степеней в математике есть особое название. Квадратом числа называют его произведение на само себя. Например, квадрат шести (ещё говорят «шесть в квадрате») равен 36:
62 = 6*6 = 36
Кубом числа называют его третью степень. Так, куб пяти (ещё говорят «пять в кубе») равен 125:
53 = 5*5*5 = 25*5 = 125
Пример. Найдите сумму квадратов чисел (натуральных) от 1 до 5.
Решение:
12+22+32+42+52 = 1+4+9+16+25 = 55
Ответ: 55.
Такие названия связаны с тем, что, площадь квадрата со стороной, равной a, составляет a2, а объем куба с такой же длиной ребра равен a3. Квадраты и кубы чисел обладают множеством интересных свойств. Например, квадрат натурального числа n равен сумме первых n нечетных чисел:
12 = 1
22 = 1 + 3 = 4
32 = 1 + 3 + 5 = 9
42 = 1 + 3 + 5 + 7 = 16
Попытайтесь привести доказательство этого факта. Если не получается, то просто посмотрите на следующую картинку:
Количество клеточек под каждым числом соответствует его квадрату. Видно, что для получения каждого следующего квадрата нужно добавить к предыдущему нечетное количество клеточек (выделены зеленым цветом), чтобы «достроить» его до «полного» квадрата.
Важно отметить, что в арифметических выражениях операция возведения в степень выполняется до умножения и сложения. Рассмотрим пример. Пусть надо вычислить значение выражения:
-52 + 54/(-3)3
Решение:
Поставим последовательность выполнения операций:
Выполним арифметические операции:
1) 52 = 5*5 = 25
2) (-3)3 = (-3)*(-3)*(-3) = -27
3) 54/(-27) = -2
4) -25+(-2) = -27
Ответ: – 27.
Обратите внимание, что самый первый минус в выражении относится не к пятерке, которую возводят в квадрат, а ко всему квадрату. То есть здесь сначала надо возвести 5 в квадрат, а потом изменить знак выражения
Если бы в этом примере была запись
(-5)2 + 54/(-3)3
то тогда в первом действии мы получили бы
(-5)*(-5) = 25
А в четвертом выполняли бы сложение
25 + (-2) = 23
То есть, если необходимо возвести в степень отрицательное число, то его следует записать в скобках:
(-2)4 = (-2)*(-2)*(-2)*(-2) = 16
-24 = -2*2*2*2 = -16
Сравнение степеней
Можно заметить несколько очевидных правил, которые помогают сравнивать степени положительных чисел, не вычисляя напрямую их значения.
Правило 1. Каждая следующая степень числа, большего единицы, больше предыдущей:
21<22<23<24<25<26 …
31<32<33<34<35<36 …
1.11<1.12<1.13<1.14<1.15<1.16 …
Правило 2. Каждая следующая степень положительного числа, меньшего единицы, меньше предыдущей:
Правило 3. Все степени единицы равны друг другу:
11 = 12 =13 =14 =15 =16 …
Правило 4. Если две степени имеют одинаковый показатель, но различающееся основание (положительное), то больше та, у которой больше основание:
12<22<32<42…
0,172<0,182<0,192<0,22…
Рассмотрим примеры:
- Необходимо сравнить числа 56100 и 56102.
Решение:
Число 56 больше единицы, а 100 < 102. Поэтому и 56100< 56102.
Ответ: 56100< 56102.
- Сравните числа 0,91000 и 0,99500.
Решение: Сравнить напрямую эти числа друг с другом не получится, так как у них отличаются и показатель, и основание. Однако оба эти выражения можно сравнить с другим числом 0,991000:
0,91000<0,991000, по правилу 4, так как показатели равны, а основание у 0,91000 меньше(0,9 < 0,99).
0,991000< 0,99500, по правилу 2, так как основания этих чисел равны и меньше единицы, а показатель больше у 0,991000
На основании этих двух неравенств можно записать двойное неравенство
0,91000<0,91000< 0,99500,
Из него следует, что 0,91000< 0,99500.
Ответ: 0,91000< 0,99500.
Умножение и деление степеней
Пусть нам надо перемножить две выражения с одинаковым основанием, например, 54 и 53. Для этого представим их как произведение множителей:
54 = 5*5*5*5
53 = 5*5*5
Тогда их произведение можно записать как:
54*53 = (5*5*5*5)(5*5*5) = 5*5*5*5*5*5*5 = 57
Получается, что если перемножаются степени с одинаковым основанием, то в результате получается ещё одна степень с таким же основанием, чей показатель равен сумме показателей перемножаемых степеней. В виде формулы это записывается так:
an*am = an+m
Это правило умножения степеней называют основным свойством степени. Доказывается оно так:
Аналогично можно перемножить и более двух чисел. Например,
32*33*34 = 32+3+4 = 39
Теперь попробуем понять, как делить степени с одинаковыми основаниями.
Для этого запишем произведение чисел am–n и an:
am–n * an = am–n+n = am+(n-n) = am+0 = am
Получили, что am–n * an = am. Теперь поделим правую и левую часть равенства этого равенства на an:
Для наглядности рассмотрим случай с конкретными числами. Пусть надо надо вычислить 210:26. Можно записать, что
210-6*26 = 210-6+6 = 210
Поделим правую и левую часть этого равенства на 26:
Получается, что верно следующее правило деления степеней:
Данные правила действуют и в том случае, когда вместо показателя и/или основания используется переменная. Например:
Если в выражении есть и умножение, и деление, то следует сначала сложить показатели перемножаемых чисел, а потом вычесть из нее показатели делителей:
Теперь введем понятие нулевой степени числа. Для этого поделим an на само себя, учитывая уже сформулированные правила деления:
an : an = an-n = a0
С другой стороны, любое число (кроме нуля), при делении на само себя дает единицу:
an : an = 1
Из этих двух равенств можно составить третье равенство:
a0 = 1
Получается, что любое число в нулевой степени равно единице.
К выражению 00 подобная логика неприменима, так как деление на ноль не допускается в алгебре. Поэтому считается, что выражение 00 не имеет смысла, так же как и деление на ноль.
Иногда приходится возводить в степень другую степень. Попытаемся вычислить выражение (23)4:
(23)4 = 23 * 23 * 23 * 23 = 23+3+3+3 = 23*4 = 212
Видно, что нам пришлось перемножить показатели. Верно следующее правило возведения степени в степень:
(an)m = anm
Рассмотрим пример. Необходимо вычислить значение выражения 910:318.
Решение. У делимого и делителя разные основания, поэтому сразу произвести деление не получится. Однако число 9 можно представить как квадрат тройки:
9 = 32
Тогда и выражение можно переписать:
910 : 318 = (32)10 : 318
Далее последовательно выполняем математические операции:
(32)10 : 318 = 32*10 : 318 = 320 : 318 = 320-18 = 32 = 9
Ответ: 9.
Ещё один пример. Необходимо сравнить числа 5300 и 3500.
Решение.
5300 = 53•100 =(53)100 =125100.
3500 =35•100 =(35)100 =243100.
125100<243100, значит, 5300< 3500.
Ответ: 5300< 3500.
Иногда приходится выполнять операции над степенями с разными основаниями, но одинаковыми показателями. Перемножим числа 24 и 34:
24*34 = (2*2*2*2)*(3*3*3*3)
Поменяем местами множители:
(2*2*2*2)*(3*3*3*3) = (2*3)*(2*3)*(2*3)*(2*3) = 6*6*6*6 = 64
Получается, что
24*34 = (2*3)4
Аналогичным образом для любых a и b, а также для любого натурального n справедливым будет равенство:
an•bn = (ab)n.
Такие же рассуждения помогают найти формулу и для деления чисел с одинаковыми показателями:
an:bn = (a:b)n.
Далее решим несколько примеров:
- Вычислите 56•26.
Решение: 56•26 = (5*2)6 = 106 = 1 000 000
Ответ: 1 000 000.
- Вычислите 4100•16150•0,5795.
Решение: Перепишем выражение с учетом того факта, что 4 = 22, а 16 = 24:
Заметим, что
а потому можно провести замену:
Ответ: 32.
Одночлен. Умножение одночленов
В алгебраических выражениях могут встречаться переменные, возведенные в степень, например, z4 или d3. Одночленом называют произведение нескольких таких переменных, а также действительных чисел.
Также может использоваться термин «моном», который является синонимом одночлена.
Приведем примеры мономов:
- 15L8F4;
- 4bc;
- – 9s17t21;
- 1,563b3h2r10.
Между переменными можно было бы поставить знак умножения, но почти всегда его опускают. Отдельно отметим, что мономом также считается выражение, в котором отсутствует числовой множитель, присутствует только одна переменная или вовсе нет переменных:
- 15a2;
- c5;
- 456.
То есть обычное число также считается мономом. Смысл в том, что для вычисления значения монома достаточно использовать операцию умножения.
Так как множители в произведении можно переставлять местами, то выражения 4•abc и a•4•bc идентичны друг другу. Для удобства принято записывать их в так называемом стандартном виде одночлена, когда числовой множитель располагается на первом месте. Сам этот множитель называют коэффициентом одночлена:
Коэффициент есть у всех мономов. Если он не указан, то считают, что перед переменными стоит единица:
с2а2 = 1с2а2.
Соответственно, в таком случае коэффициентом является единица. Если же перед мономом стоит только знак минус, то его коэффициентом является –1:
– с2а2 = –1с2а2.
Следующее важное понятие – степень одночлена. Она равна сумме степеней, стоящих у переменных в мономе. Найдем степени у некоторых одночленов:
- 9a2b3– степень одночлена равна 2+3=5, так как у переменных они равны 2 и 3;
- 7c4– степень равна 4, так как у единственной переменной в мономе степень равна 4;
- 56v8n3– степень равна 11=(8+3).
Если у переменной в мономе нет степени, то на самом деле она равна единице, так как любое число в 1-ой степени равно самому себе:
a1 = a.
Если моном представляет собой отдельное число, то есть не содержит переменных, то его степень равна нулю.
При умножении одночленов всегда получается моном. Посмотрим на примере, как выполняется эта операция. Пусть надо перемножить одночлены 5a3b4и 6a5b7. Для этого сначала поменяем местами множители в произведении:
5a3b4*6a5b7 = 5*a3*b4*6*a5*b7 = 5*6*a3*a5*b4*b7
Продолжим вычисление, учитывая правила умножения чисел с одинаковыми основаниями:
5*6*a3*a5*b4*b7 = (5*6)*(a3*a5)*(b4*b7) = 30*a3+5*b4+7 = 30a8b11
Получается, что мы просто перемножили коэффициенты мономов, а у одинаковых переменных сложили степени.
Здесь важно не перепутать такие две операции, как нахождение степени монома и умножение одночленов. В первом случае мы складываем степени, стоящие у разных переменных в одном мономе. Во втором случае мы складываем степени, стоящие у одинаковых переменных, но в разных (перемножаемых) мономах.
Рассмотрим несколько примеров.
- Перемножьте одночлены 8d2v и 9d3v4 и найдите степень получившегося произведения.
Решение:
8d2v•9d3v4 = (8•9) d2+3v1+4 = 72 d5v5.
Степень получившегося монома равна 5 + 5 = 10
- Перемножьте – 4a2b3с и – 3 b2с3.
Решение:
– 4a2b3с •(– 3b2с3) = (– 4)•(– 3)a2b3+2с1+3 = 12a2b5с4.
- Приведите одночлен к стандартному виду: 19t4• (– 2)t2d3.
Решение. В данном случае приведение к стандартному виду значит тоже самое, что и перемножение одночленов:
19t4 • (– 2)t2d3 = 19•(–2)•t4+2d3 = – 38t6d3.
Возведение одночлена в степень
Периодически в ходе вычислений возникает необходимость возведения одночлена в степень. Посмотрим, как выполняется подобная операция. Пусть надо возвести 2a3b2c в четвертую степень:
Видно, что каждый множитель монома мы по отдельности возвели в 4-ую степень. Можно сформулировать следующее правило:
Рассмотрим ещё несколько примеров:
- (3v3b2n4)3 = 33(v3)3(b2)3(n4)3 = 27v3•3b2•3n4•3 = 27v9b6n12;
- (4t5u7g9)2 = 42t5•2u7•2g9•2 = 16t10u14g18.
Тождества
Рассмотрим равенство
a+(a+5)=2a+5.
В данном случае переменная a, содержащаяся в равенстве, может принимать любое значение. Подставим значение a, равное 1:
1+(1+5)=2•1+5;
1+6=2+5;
7=7.
Получили верное равенство. Подставим другое значение переменной, например, а=2, снова получим верное равенство (9=9). Вообще при любом допустимом значении переменной a всегда будет получаться верное равенство. Такое равенство называют тождеством.
Иногда в тождествах вместо знака равенства используют особый значок «≡». Основные тождества алгебры, которые вы уже встречали ранее – это переместительные законы сложения и умножения:
- a+b=b+a;
- ab=b•a;
сочетательные законы сложения и умножения:
(a+b)+c = a+(b+c);
(a•b)•c = a•(b•c);
а также распределительный закон, позволяющий раскрывать скобки:
(a+b)•c = a•c+b•c.
Иногда в понятие тождества включают также и равенства, вовсе не содержащие никаких переменных, например:
62 =36.
В качестве примера равенства, не являющегося тождеством, можно привести 5d+10 = 50. Оно будет выполняться только при значении переменной, равной 8, а при всех остальных значениях не выполняться.
Если два выражения равны друг другу при любых значениях переменных, то их называют тождественно равными.Тождественным преобразованием называют замену выражения на другое, тождественно ему равное. В качестве примера тождественного преобразования можно привести запись:
a5+a6 =a11.
Определение одночлена
Одночлен – это алгебраическое выражение, которое является произведением чисел, переменных и их степеней.
Одночленами также считают все числа, любые переменные и их степени.
Например:
Являются одночленами
Не являются одночленами
$ 5m^2 n $
$ left(frac{3}{4}right)^2 k $
$8^3$
$ -34m^7 pm^4 z$
abcde
$a^2 b+1$
$ 4(k+n)^2 $
$ 500-m^4+2m^2 $
$ 10p^2+k $
Стандартный вид одночлена – представление одночлена в виде произведения, в котором на первом месте стоит числовой множитель (коэффициент одночлена), а все остальные множители являются степенями различных переменных.
Степень одночлена – это сумма показателей всех переменных, в него входящих.
Например:
$x^2cdot23xy$ – одночлен нестандартного вида, с коэффициентом 23 и степенью 4 (x в кубе и y в первой степени);
$-frac{3}{15}a^3 b^2$ – одночлен стандартного вида, с коэффициентом $left(-frac{3}{15}right)$ и степенью 5 (a в кубе и b в квадрате);
9 – одночлен стандартного вида, с коэффициентом 9 и степенью 0;
a – одночлен стандартного вида, с коэффициентом 1 и степенью 1.
Число 0, а также одночлены, тождественно равные нулю (например, $0 cdot x^3, 0cdot mn$), называются нуль-одночленами. Считают, что нуль-одночлен степени не имеет. Одночлены с одинаковой буквенной частью (например, $2ab^3 c^2 и -frac{7}{5}ab^3 c^2$) называются подобными.
Приведение одночлена к стандартному виду
Любой одночлен можно преобразовать так, чтобы получился одночлен стандартного вида.
Алгоритм приведения одночлена к стандартному виду
- Определить коэффициент одночлена: перемножить все числовые множители и записать результат первым множителем.
- Используя свойства степеней, найти общую степень для каждой из переменных одночлена.
Если в одночлен в качестве множителей входят несколько переменных, их принято записывать по алфавиту. Но это не является обязательным.
Примеры
Пример 1. Преобразуйте выражение в одночлен стандартного вида, найдите его коэффициент и степень:
а) $ frac{1}{2}x^5y^4c cdot (-5xy^2 c^3) = frac{1}{2} cdot (-5) cdot c^{1+3} cdot x^{5+1} cdot y^{4+2} = -2,5c^4 x^6 y^6 $
коэффициент (-2,5), степень 4+6+6 = 16
б) $ -(3m^4)^2 cdot (-m^3 kp)^3 = -3^2 cdot (-1)^3 cdot k^3 cdot m^{8+9} cdot p^3 = 9k^3 m^17 p^3 $
коэффициент 9, степень 3+17+3 = 23
в) $ (-2)^3 xy cdot 1,5(x^4 y)^2 = -8 cdot 1,5 cdot x^{1+8} cdot y^{1+2} = -12x^9 y^3 $
г) $ (8m^3 )^2 n^3 cdot frac{1}{(4mn)^3} = frac{8^2 m^6 n^3}{4^3 m^3 n^3} = frac{(2^3)^2}{(2^2)^3} cdot frac{m^6}{m^3} cdot frac{n^3}{n^3} = m^3$
коэффициент 1, степень 3
Пример 2. Запишите одночлен в стандартном виде и найдите его числовое значение:
а) $ frac{1}{2} xycdot frac{1}{4}x^2 при x = 2, y = 3 $
$ frac{1}{2}xy cdot frac{1}{4}x^2 = frac{1}{2} cdot frac{1}{4} cdot x^{1+2}cdot y = frac{1}{8} x^3 y $
Подставляем: $ frac{1}{8}cdot2^3cdot3 = 3 $
б) $ (-2a^2 b^3) cdot left(frac{0,5}{ab}right)^2 при a = 73,b = 3 $
$ (-2a^2 b^3) cdot left(frac{0,5}{ab}right)^2 = -2 cdot frac{1}{2}^2 cdot frac{a^2}{a^2} cdot frac{b^3}{b^2} = -frac{1}{2}b $
Подставляем: $ -frac{1}{2}cdot3 = -1,5 $
Пример 3. Представьте выражение в виде квадрата одночлена:
а) $ 16x^4 y^2 z^6 = 4^2cdot(x^2 )^2cdot y^2cdot(z^3 )^2 = (4x^2 yz^3 )^2 $
б) $ frac{49}{64}x^{12} y^4 z^{16} = (frac{7}{8} x^6 y^2 z^8 )^2 $
Пример 4*. Известно, что $ 5a^2 b^3 = 7$. Найдите значение выражения $ -frac{4}{49} a^6 b^9 $
Выразим произведение переменных через число: $ a^2 b^3 = frac{7}{5} $
Преобразуем выражение:
$$ -frac{4}{49} a^6 b^9 = -frac{4}{49} left(underbrace{a^2 b^3}_{=7/5text{}}right)^3 = -frac{4}{7^2} cdot left(frac{7}{5}right)^3 = -frac{4}{5^3} cdot frac{7^3}{7^2} = -frac{28}{125} $$
Ответ: $ -frac{28}{125} $
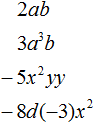
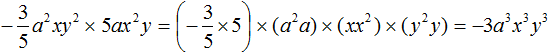
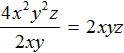
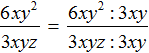
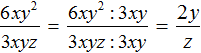
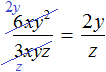
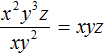
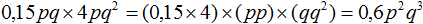
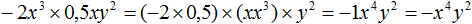

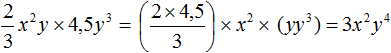
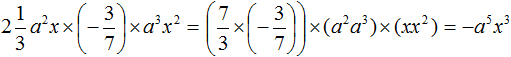
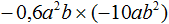

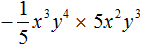
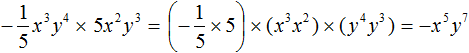
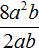
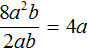
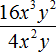
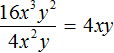
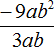

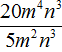
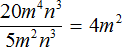
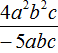
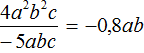
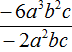
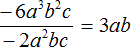





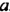
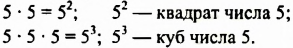
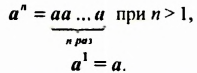
 тогда
тогда 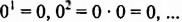 — любая натуральная степень числа 0 равна 0.
— любая натуральная степень числа 0 равна 0.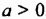 , тогда
, тогда 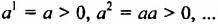 — любая натуральная степень положительного числа есть положительное число.
— любая натуральная степень положительного числа есть положительное число.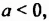 тогда
тогда  . Степень отрицательного числа с четным показателем является положительным числом, поскольку произведение четного количества отрицательных чисел положительно. Степень отрицательного числа с нечетным показателем является отрицательным числом, поскольку произведение нечетного количества отрицательных чисел отрицательно.
. Степень отрицательного числа с четным показателем является положительным числом, поскольку произведение четного количества отрицательных чисел положительно. Степень отрицательного числа с нечетным показателем является отрицательным числом, поскольку произведение нечетного количества отрицательных чисел отрицательно.