В предыдущих уроках было сказано, что дробь, состоящая из целой и дробной части, называется смешанной.
Все дроби, имеющие целую и дробную часть, носят одно общее название — смешанные числа.
Смешанные числа так же как и обыкновенные дроби можно складывать, вычитать, умножать и делить. В данном уроке мы рассмотрим каждое из этих действий по отдельности.
Сложение целого числа и правильной дроби
Встречаются задачи, в которых требуется сложить целое число и правильную дробь. Например, сложить число 2 и дробь ![]() . Чтобы решить этот пример, нужно число 2 представить в виде дроби
. Чтобы решить этот пример, нужно число 2 представить в виде дроби ![]() . Затем сложить дроби с разными знаменателями:
. Затем сложить дроби с разными знаменателями:
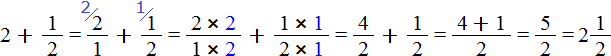
А теперь внимательно посмотрим на этот пример. Смотрим на его начало и на его конец. Начало у него выглядит так: ![]() , а конец так:
, а конец так: ![]() . Различие в том, что в первом случае число 2 и дробь
. Различие в том, что в первом случае число 2 и дробь ![]() соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что
соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что ![]() это свёрнутая форма записи смешанного числа, а
это свёрнутая форма записи смешанного числа, а ![]() — развёрнутая.
— развёрнутая.
Когда перед нами смешанное число вида ![]() , мы должны понимать, что знак сложения опущен.
, мы должны понимать, что знак сложения опущен.
Какой можно сделать вывод? Если потребуется сложить целое число и правильную дробь, можно опустить плюс и записать целое число и дробь вместе.
Значит значение выражения ![]() равно
равно ![]()
![]()
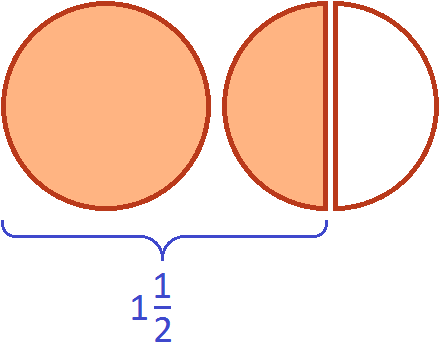
Если к двум целым пиццам прибавить половину пиццы, то получится две целые пиццы и ещё половина пиццы:
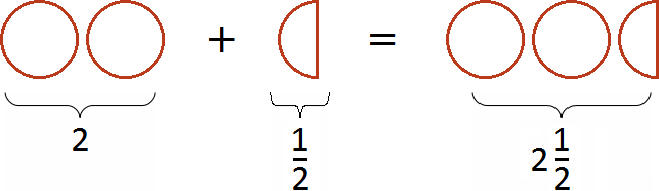
Пример 2. Найти значение выражения ![]()
Представим число 3 в виде дроби ![]() . Затем сложим дроби с разными знаменателями:
. Затем сложим дроби с разными знаменателями:
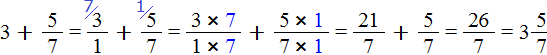
Это первый способ. Второй способ намного проще. Можно поставить знак равенства и записать целую и дробную часть вместе. То есть опустить знак сложения:
![]()
Пример 3. Найти значение выражения ![]()
Можно записать вместе число 2 и дробь ![]() , но этот ответ не будет окончательным, поскольку в дроби
, но этот ответ не будет окончательным, поскольку в дроби ![]() можно выделить целую часть.
можно выделить целую часть.
Поэтому в данном примере сначала нужно выделить целую часть в дроби ![]() . Пять вторых это две целых и одна вторая:
. Пять вторых это две целых и одна вторая:
![]()
Теперь в главном выражении ![]() вместо дроби
вместо дроби ![]() запишем смешанное число
запишем смешанное число ![]()
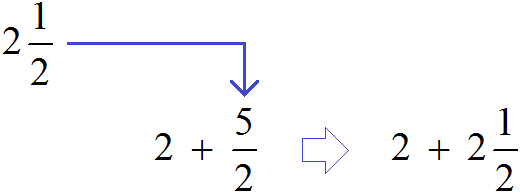
Получили новое выражение ![]() . В этом выражении смешанное число
. В этом выражении смешанное число ![]() запишем в развёрнутом виде:
запишем в развёрнутом виде:
![]()
Применим сочетательный закон сложения. Сложим две двойки, получим 4:
![]()
Теперь свернём полученное смешанное число:
![]()
Это окончательный ответ. Подробное решение этого примера можно записать следующим образом:
![]()
Сложение смешанных чисел
Встречаются задачи, в которых требуется сложить смешанные числа. Например, найти значение выражения ![]() . Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.
. Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.
Для начала запишем смешанные числа в развёрнутом виде:
![]()
Применим сочетательный закон сложения. Сгруппируем целые и дробные части по отдельности:
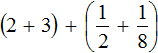
Вычислим целые части: 2 + 3 = 5. В главном выражении заменяем выражение в скобках (2 + 3) на полученную пятёрку:
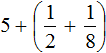
Теперь вычислим дробные части. Это сложение дробей с разными знаменателями. Как складывать такие дроби мы уже знаем:
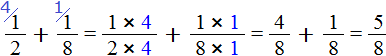
Получили ![]() . Теперь в главном выражении
. Теперь в главном выражении 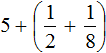 заменяем дробные части на полученную дробь
заменяем дробные части на полученную дробь ![]()
![]()
Теперь свернем полученное смешанное число:
![]()
Таким образом, значение выражения ![]() равно
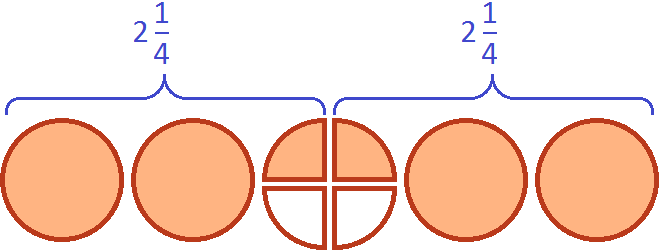
равно ![]() . Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:
. Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:
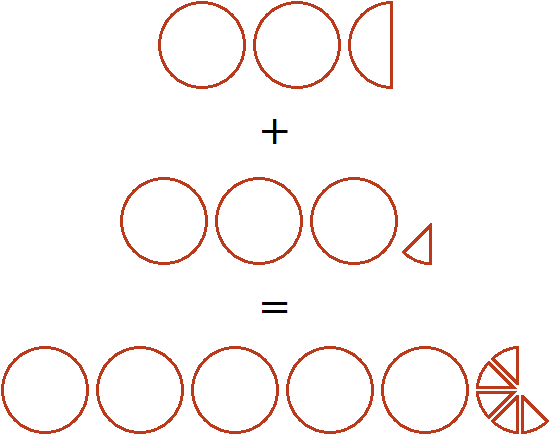
Подобные примеры нужно решать быстро, не останавливаясь на подробностях. Находясь в школе, нам пришлось бы записать решение этого примера следующим образом:
![]()
Если в будущем увидите такое короткое решение, не пугайтесь. Вы уже понимаете, что откуда взялось.
Пример 2. Найти значение выражения
Запишем смешанные числа в развёрнутом виде:
![]()
Сгруппируем целые и дробные части по отдельности:
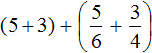
Вычислим целые части: 5 + 3 = 8. В главном выражении заменяем выражение в скобках (5 + 3) на полученное число 8
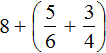
Теперь вычислим дробные части:
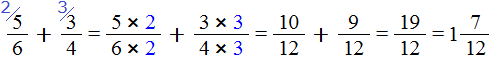
Получили смешанное число ![]() . Теперь в главном выражении
. Теперь в главном выражении 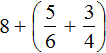 заменяем выражение в скобках на полученное смешанное число
заменяем выражение в скобках на полученное смешанное число ![]()
![]()
Получили выражение ![]() . В данном случае число 8 надо прибавить к целой части смешанного числа
. В данном случае число 8 надо прибавить к целой части смешанного числа ![]() . Для этого смешанное число
. Для этого смешанное число ![]() можно временно развернуть, чтобы было понятнее, что с чем складывать:
можно временно развернуть, чтобы было понятнее, что с чем складывать:
![]()
Сложим целые части. Получаем 9
![]()
Сворачиваем готовый ответ:
![]()
Таким образом, значение выражения равно
![]() .
.
Полное решение этого примера выглядит следующим образом:
![]()
Для решения подобных примеров существует универсальное правило. Выглядит оно следующим образом:
Чтобы сложить смешанные числа, надо:
- привести дробные части этих чисел к общему знаменателю;
- отдельно выполнить сложение целых и дробных частей.
Если при сложении дробных частей получилась неправильная дробь, выделить целую часть в этой дроби и прибавить ее к полученной целой части.
Применение готовых правил допустимо в том случае, если суть темы полностью понятна. Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.
Пример 3. Найти значение выражения ![]()
Воспользуемся готовым правилом. Приведём дробные части к общему знаменателю, затем по отдельности сложим целые и дробные части:
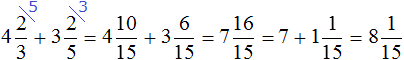
Сложение целого и смешанного числа
Встречаются задачи, в которых нужно сложить целое и смешанное число. Например, сложить 2 и смешанное число ![]() . В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
. В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
![]()
Здесь смешанная дробь ![]() была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ
была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ ![]() .
.
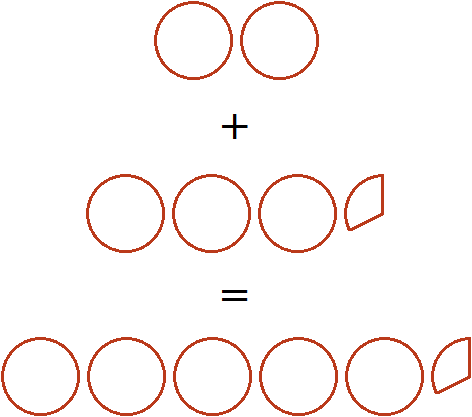
Попробуем изобразить это решение в виде рисунка. Если к двум целым пиццам прибавить три целые и треть пиццы, то получятся пять целых и треть пиццы:
Пример 2. Найти значение выражения ![]()
В этом примере, как и в предыдущем, нужно сложить целые части:
![]()
Осталось свернуть целую и дробную части, но дело в том, что дробная часть ![]() представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:
представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:
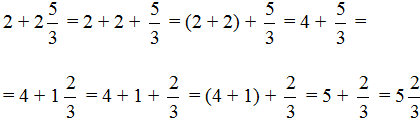
Вычитание дроби из целого числа
Встречаются задачи, в которых требуется вычесть дробь из целого числа. Например, вычесть из числа 1 дробь ![]() . Чтобы решить такой пример, нужно целое число 1 представить в виде дроби
. Чтобы решить такой пример, нужно целое число 1 представить в виде дроби ![]() , и выполнить вычитание дробей с разными знаменателями:
, и выполнить вычитание дробей с разными знаменателями:
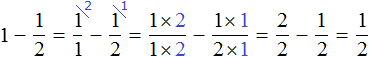
Если имеется одна целая пицца и мы вычтем из неё половину пиццы, то у нас получится половина пиццы:
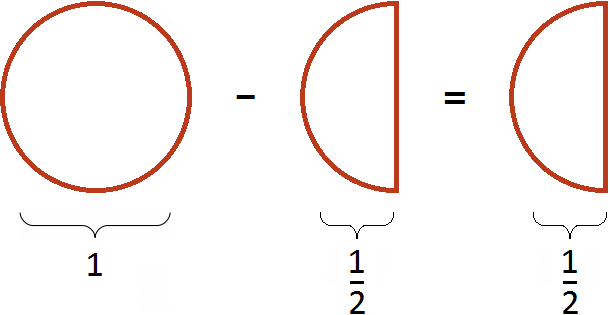
Пример 2. Найти значение выражения ![]() .
.
Представим число 2 в виде дроби ![]() , и выполним вычитание дробей с разными знаменателями:
, и выполним вычитание дробей с разными знаменателями:
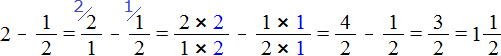
Если имеются две целые пиццы и мы вычтем из низ половину, то останется одна целая и половина пиццы:
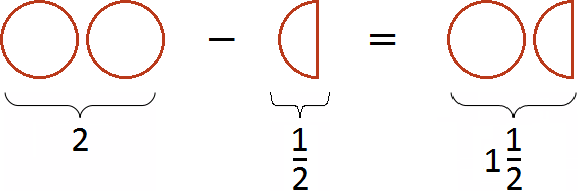
Такие примеры можно решать в уме. Достаточно суметь воспроизвести их в своём воображении. К примеру, найдём значение выражения ![]() , не приводя на бумаге никаких вычислений.
, не приводя на бумаге никаких вычислений.
Представим, что число 3 это три пиццы:

Нужно вычесть из них ![]() . Мы помним, что треть выглядит следующим образом:
. Мы помним, что треть выглядит следующим образом:

Теперь представим, во что превратятся три пиццы, если отрезать от них эту треть

Получилось ![]() (две целых и две трети пиццы).
(две целых и две трети пиццы).
Чтобы убедиться в правильности решения, можно найти значение выражения ![]() обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:
обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:
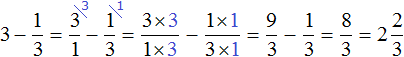
Пример 3. Найти значение выражения ![]()
Представим число 3 в виде дроби ![]() . Затем выполним вычитание дробей с разными знаменателями:
. Затем выполним вычитание дробей с разными знаменателями:
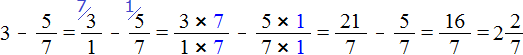
Вычитание смешанного числа из целого числа
Теперь мы готовы к тому, чтобы вычесть смешанное число из целого числа. Найдём значение выражения .
Чтобы решить этот пример, число 5 нужно представить в виде дроби, а смешанное число перевести в неправильную дробь. После перевода смешанного числа
в неправильную дробь, получим дробь
![]() . Теперь выполним вычитание дробей с разными знаменателями:
. Теперь выполним вычитание дробей с разными знаменателями:
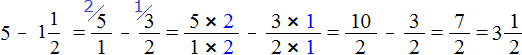
Если из пяти целых пицц вычесть одну целую и половину пиццы, то останутся три целые пиццы и половина пиццы:
Пример 2. Найти значение выражения ![]()
Представим 6 в виде дроби ![]() , а смешанное число
, а смешанное число ![]() , в виде неправильной дроби. После перевода смешанного числа
, в виде неправильной дроби. После перевода смешанного числа ![]() в неправильную дробь, получим дробь
в неправильную дробь, получим дробь ![]() . Теперь выполним вычитание дробей с разными знаменателями:
. Теперь выполним вычитание дробей с разными знаменателями:
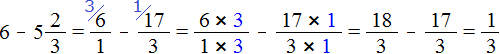
Примеры на вычитание дроби из числа или вычитание смешанной дроби из числа опять же можно выполнять в уме. Этот процесс легко поддаётся воображению.
К примеру, если нужно быстро найти значение выражения ![]() , то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)
, то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)

Тогда от той пиццы, от которой отрезали останется
![]() пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:
пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:
![]()
Если на рисунке вы закроете рукой две третьих пиццы (она закрашена), то сразу всё поймёте.
Вычитание смешанных чисел
Встречаются задачи, в которых требуется вычесть из одного смешанного числа другое смешанное число. Например, найдём значение выражения: ![]()
Чтобы решить этот пример, нужно смешанные числа ![]() и
и ![]() перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:
перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:
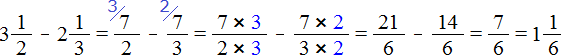
Если от трёх целых и половины пиццы вычесть две целые и треть пиццы, то останутся одна целая и одна шестая пиццы:
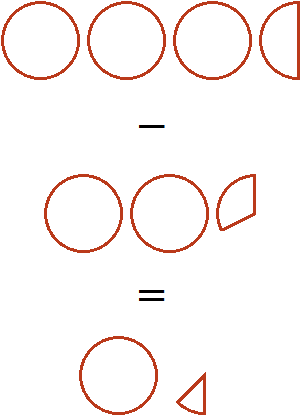
Пример 2. Найти значение выражения ![]()
Переводим смешанные числа ![]() и
и ![]() в неправильные дроби и выполняем вычитание дробей с разными знаменателями:
в неправильные дроби и выполняем вычитание дробей с разными знаменателями:
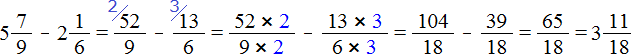
К вычитанию смешанных чисел мы ещё вернёмся. В вычитании дробей есть немало тонкостей, которым новичок пока не готов. Например, возможен случай, когда уменьшаемое может оказаться меньше вычитаемого. Это может вывести нас в мир отрицательных чисел, которых мы ещё не изучали.
А пока изучим умножение смешанных чисел. Благо оно не такое сложное, как сложение и вычитание.
Умножение целого числа на дробь
Чтобы целое число умножить на дробь, достаточно умножить это целое число на числитель дроби, а знаменатель оставить без изменения.
Например, умножим число 5 на дробь ![]() . Чтобы решить этот пример, нужно число 5 умножить на числитель дроби
. Чтобы решить этот пример, нужно число 5 умножить на числитель дроби ![]() , а знаменатель оставить без изменения:
, а знаменатель оставить без изменения:
![]()
В ответе получилась неправильная дробь. Выделим в ней целую часть:
![]()
Если имеются пять целых пицц и мы возьмём от этого количества половину, то у нас окажется две целые пиццы и половина пиццы:
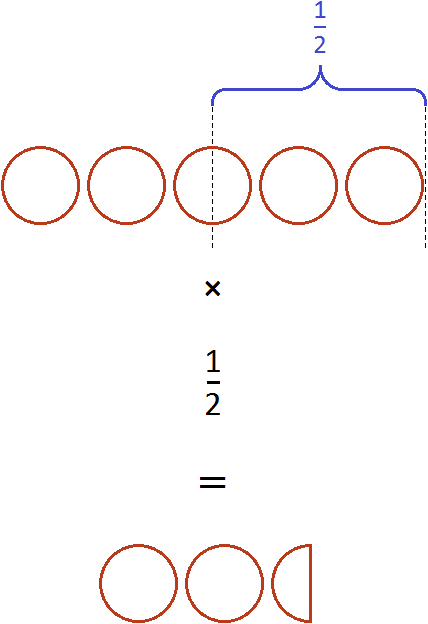
Пример 2. Найти значение выражения ![]()
Умножим число 3 на числитель дроби ![]()
![]()
В ответе получилась неправильная дробь ![]() , но мы выделили её целую часть и получили 2.
, но мы выделили её целую часть и получили 2.
Также, можно было сократить эту дробь. Получился бы тот же результат. Выглядело бы это следующим образом:
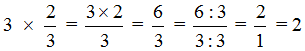
Если имеются три целые пиццы и мы возьмём от этого количества две третьих, то у нас окажется две целые пиццы:
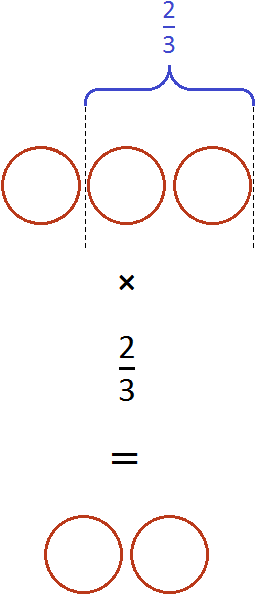
Пример 3. Найти значение выражения ![]()
Этот пример решается так же, как и предыдущие. Целое число и числитель дроби нужно перемножить:
![]()
Пример 4. Найти значение выражения ![]()
Умножим число 3 на числитель дроби ![]()
![]()
Умножение смешанного числа на дробь
Чтобы умножить смешанное число на дробь, нужно смешанное число перевести в неправильную дробь, затем выполнить перемножение обыкновенных дробей.
Пример 1. Найти значение выражения ![]()
Переведём смешанное число ![]() в неправильную дробь. После перевода это число превратится в дробь
в неправильную дробь. После перевода это число превратится в дробь ![]() . Затем можно будет умножить эту дробь на
. Затем можно будет умножить эту дробь на
![]()
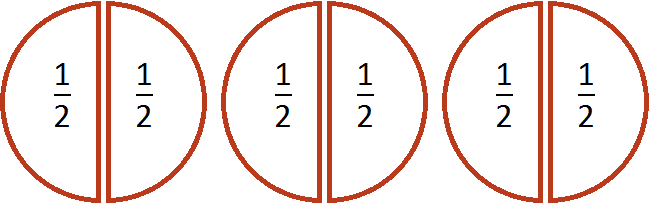
Допустим, имеются одна целая и половина пиццы:

Умножить эти куски на означает взять от них две трети. Чтобы взять от них две трети, сначала разделим их на три равные части. Разделим пополам ту пиццу, которая слева. Тогда у нас получится три равных куска:
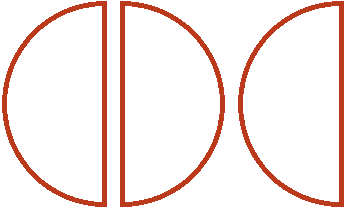
Теперь если мы возьмем (два куска из трёх имеющихся), то получим одну целую пиццу. Для наглядности закрасим эти два куска:
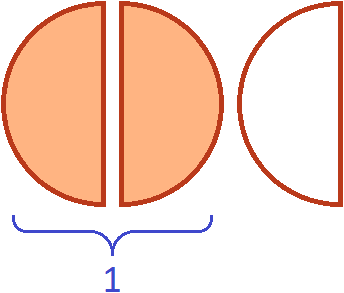
Поэтому значение выражения ![]() было равно 1
было равно 1
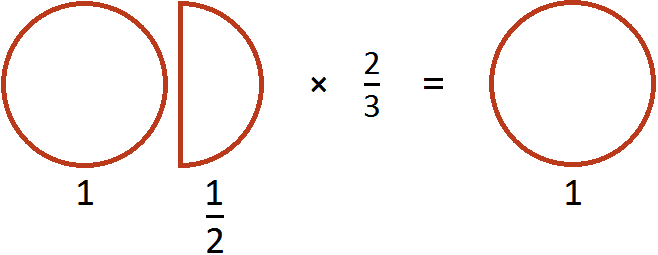
Умножение смешанных чисел
Встречаются задачи, в которых требуется перемножить смешанные числа. Например, перемножить ![]() и
и ![]() . Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
. Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
![]()
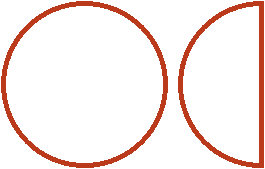
Попробуем разобраться в этом примере с помощью рисунка. Допустим, имеются одна целая и половина пиццы:
Теперь разберемся со смешанным множителем ![]() . Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще
. Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще ![]() раза.
раза.
С множителем 2 всё понятно, он означает что одну целую и половину пиццы нужно взять два раза. Давайте возьмём два раза целую пиццу и половину:
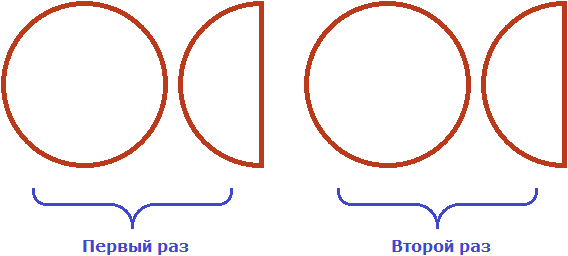
Но ещё осталось взять ![]() от изначальной целой пиццы и половины, ведь множителем было смешанное число
от изначальной целой пиццы и половины, ведь множителем было смешанное число ![]() . Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
. Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
Мы разделили нашу целую пиццу и половину на равные части, и теперь можем сказать, что является половиной от этих кусков. Половиной от этих кусков является пиццы. Это можно хорошо увидеть, если мы упорядочим наши равные кусочки следующим образом:
А если смотреть на изначальную целую пиццу и половину с точки зрения такого порядка, как на этом рисунке, то половиной от них является пиццы.
Поэтому значение выражения ![]() равно
равно ![]()
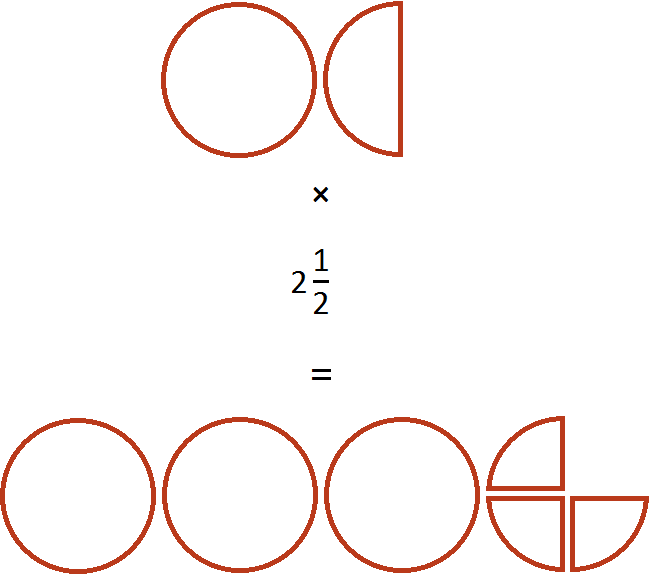
Пример 2. Найти значение выражения ![]()
Переводим смешанные числа в неправильные дроби и перемножаем эти неправильные дроби. Если в ответе получится неправильная дробь, выделим в ней целую часть:
![]()
Деление целого числа на дробь
Чтобы разделить целое число на дробь, нужно это целое число умножить на дробь, обратную делителю.
Например, разделим число 3 на дробь ![]() . Здесь число 3 — это делимое, а дробь
. Здесь число 3 — это делимое, а дробь ![]() — делитель.
— делитель.
Чтобы решить этот пример, нужно число 3 умножить на дробь, обратную дроби ![]() . А обратная дробь для дроби
. А обратная дробь для дроби ![]() это дробь
это дробь ![]() . Поэтому умножаем число 3 на дробь
. Поэтому умножаем число 3 на дробь ![]()
![]()
Допустим, имеются три целые пиццы:

Если мы зададим вопрос «cколько раз ![]() (половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».
(половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».
Действительно, если мы разделим каждую пиццу пополам, то у нас получится шесть половинок:
Поэтому значение выражения ![]() равно 6.
равно 6.
Пример 2. Найти значение выражения ![]()
Чтобы решить этот пример, нужно число 2 умножить на дробь, обратную дроби ![]() . А обратная дробь для дроби
. А обратная дробь для дроби ![]() это дробь
это дробь
![]()
Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз ![]() пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби
пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби ![]() . После выделения целой части в этой дроби получим
. После выделения целой части в этой дроби получим ![]()
Теперь поставим вопрос так: «Сколько раз ![]() (одна целая и половина пиццы) содержится в двух пиццах?».
(одна целая и половина пиццы) содержится в двух пиццах?».
Чтобы ответить на этот вопрос, нужно найти в двух пиццах такое количество пиццы, которое изображено на следующем рисунке:

В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:
А оставшаяся половина это треть от ![]() , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
, которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
Поэтому значение выражения ![]() равно
равно ![]()
Пример 3. Найти значение выражения ![]()
Чтобы решить этот пример, нужно число 5 умножить на дробь, обратную дроби ![]() . А обратная дробь для дроби
. А обратная дробь для дроби ![]() это дробь
это дробь ![]() . Поэтому умножаем число 5 на
. Поэтому умножаем число 5 на ![]()
![]()
Дробь ![]() это 2 целых и
это 2 целых и ![]() . Проще говоря, две целые и четверть пиццы:
. Проще говоря, две целые и четверть пиццы:

А выражение ![]() определяет сколько раз
определяет сколько раз ![]() содержится в пяти целых пиццах. Ответом было смешанное число
содержится в пяти целых пиццах. Ответом было смешанное число ![]() .
.
То есть ![]() пиццы содержится в пяти целых пиццах
пиццы содержится в пяти целых пиццах ![]() раза.
раза.
Давайте нащупаем в пяти пиццах два раза по ![]()
Белым цветом осталось не выделено две четверти. Эти две четверти представляют собой ![]() от
от ![]() , которые не вместились. Двумя девятыми они являются по той причине, что в
, которые не вместились. Двумя девятыми они являются по той причине, что в ![]() пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:
пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:
Поэтому значение выражения ![]() равно
равно ![]()
Деление дроби на целое число
Чтобы разделить дробь на целое число, нужно данную дробь умножить на число, обратное делителю. Таким делением мы занимались в прошлом уроке. Вспомним ещё раз.
Пример 1. Разделим дробь ![]() на число 2
на число 2
Чтобы разделить дробь ![]() на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь
на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь ![]()
![]()
Пусть имеется половина пиццы:

Разделим её поровну на две части. Тогда каждая получившаяся часть будет одной четвертой пиццы:
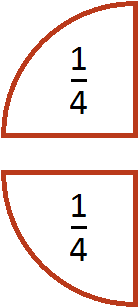
Поэтому значение выражения ![]() равно
равно ![]()
Пример 2. Найти значение выражения ![]()
Чтобы решить этот пример, нужно дробь ![]() умножить на число, обратное числу 2. Обратное числу 2 это дробь
умножить на число, обратное числу 2. Обратное числу 2 это дробь ![]()
![]()
Пример 3. Найти значение выражения ![]()
Умножаем первую дробь ![]() на число, обратное числу 3. Обратное числу 3 это дробь
на число, обратное числу 3. Обратное числу 3 это дробь ![]()
![]()
Деление целого числа на смешанное число
Встречаются задачи, в которых требуется разделить целое число на смешанное число. Например, разделим 2 на ![]() .
.
Чтобы решить этот пример, нужно делитель ![]() перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.
перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.
Переведём делитель ![]() в неправильную дробь, получим
в неправильную дробь, получим ![]() . Затем умножим 2 на дробь, обратную дроби
. Затем умножим 2 на дробь, обратную дроби ![]() . Обратная для дроби
. Обратная для дроби ![]() это дробь
это дробь
![]()
Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз ![]() (одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.
(одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:

А оставшаяся половина это треть от ![]() , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
, которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:

Поэтому значение выражения ![]() равно
равно ![]()
Пример 2. Найти значение выражения ![]()
Переводим делитель ![]() в неправильную дробь, получаем
в неправильную дробь, получаем ![]() . Теперь умножаем число 5 на дробь, обратную дроби
. Теперь умножаем число 5 на дробь, обратную дроби ![]() . Обратная для дроби
. Обратная для дроби ![]() это дробь
это дробь ![]()
![]()
Сначала мы получили ответ ![]() , затем сократили эту дробь на 5, и получили
, затем сократили эту дробь на 5, и получили ![]() , но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ
, но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ ![]()
Деление смешанного числа на целое число
Чтобы разделить смешанное число на целое число, нужно смешанное число перевести в неправильную дробь, затем умножить эту дробь на число, обратное делителю.
Например, разделим ![]() на 2. Чтобы решить этот пример, нужно делимое
на 2. Чтобы решить этот пример, нужно делимое ![]() перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
Переведём смешанное число ![]() в неправильную дробь, получим
в неправильную дробь, получим ![]() .
.
Теперь умножаем ![]() на число, обратное числу 2. Обратное числу 2 это дробь
на число, обратное числу 2. Обратное числу 2 это дробь ![]()
![]()
Допустим, имеется одна целая и половина пиццы:

Разделим это количество пиццы поровну на две части. Для этого сначала разделим на две части целую пиццу:

Затем разделим поровну на две части и половину:

Теперь если мы сгруппируем эти кусочки на две группы, то получим по пиццы в каждой группе:
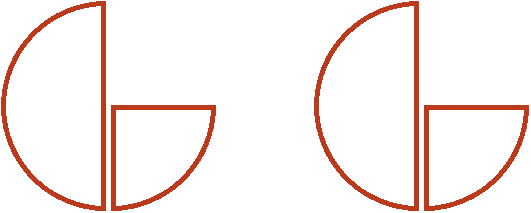
Поэтому значение выражения ![]() равно
равно
Пример 2. Найти значение выражения ![]()
Переведём делимое ![]() в неправильную дробь, получим
в неправильную дробь, получим ![]() . Теперь умножаем
. Теперь умножаем ![]() на число, обратное числу 4. Обратное числу 4 это дробь
на число, обратное числу 4. Обратное числу 4 это дробь ![]() .
.
![]()
Деление смешанных чисел
Чтобы разделить смешанные числа, нужно перевести их в неправильные дроби, затем выполнить обычное деление дробей. То есть умножить первую дробь на дробь, обратную второй.
Пример 1. Найти значение выражения ![]()
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
![]()
Как решать дальше мы уже знаем. Первую дробь ![]() нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь
нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь ![]() .
.
Дорешаем данный пример до конца:
![]()
Допустим, имеются две целые и половина пиццы:
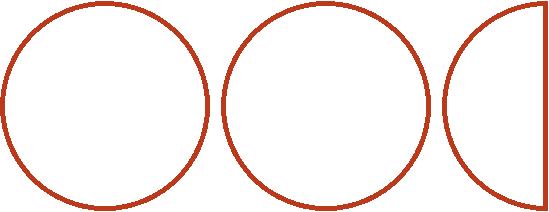
Если зададим вопрос «Сколько раз ![]() (одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:
(одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:
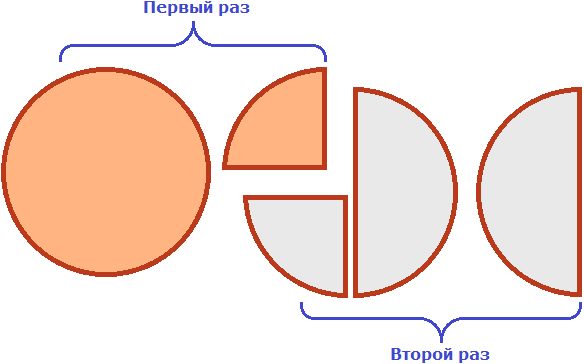
Пример 2. Найти значение выражения ![]()
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
![]()
Теперь умножаем первую дробь на дробь, обратную второй. Обратная для дроби это дробь ![]()
![]()
Сначала мы получили дробь![]() . Эту дробь мы сократили на 9. В результате получили дробь
. Эту дробь мы сократили на 9. В результате получили дробь ![]() , но такой ответ нас тоже не устроил и мы выделили в дроби
, но такой ответ нас тоже не устроил и мы выделили в дроби ![]() целую часть. В результате получили окончательный ответ
целую часть. В результате получили окончательный ответ ![]() .
.
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:

Решение:
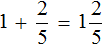
Задание 2. Найдите значение выражения:
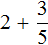
Решение:

Задание 3. Найдите значение выражения:

Решение:

Задание 4. Найдите значение выражения:

Решение:
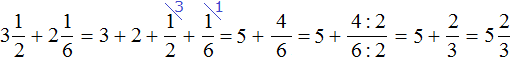
Задание 5. Найдите значение выражения:

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Поиск значений выражений — основное математическое действие. Им сопровождается каждый пример, задача. Поэтому чтобы вам было проще работать с различными математическими выражениями, подробно разберем способы и правила их решения в данной статье. Правила представлены в порядке увеличения сложности: от простейших выражений до выражений с функциями. Для лучшего понимания каждый пункт сопровождается подробным пояснением и расписанными примерами.
Поиск значения числовых выражений
Числовые выражения представляют собой математические задачи, состоящие, преимущественно, из чисел. Они подразделяются на несколько групп в зависимости от своей сложности: простейшие, со скобками, корнями, дробями и т.д. Каждый тип выражений подразумевает свои правила нахождения значения, порядок действий. Рассмотрим каждый случай подробнее.
Простейшие числовые выражения. К простейшим числовым выражениям относятся примеры, состоящие из двух элементов:
- Числа (целые, дробные и т.д.);
- Знаки: «+», «—», «•» и «÷».
Чтобы найти значение выражения в данном случае, необходимо выполнить все арифметические действия (которые подразумевают конкретные знаки). В случае отсутствия скобок решение примера производится слева направо. Первыми выполняются действия деления и умножения. Вторыми — сложение и вычитание.
Пример 1. Решение числового выражения
Задача. Решить:
20 — 2 • 10 ÷ 5 — 4 = ?
Решение. Чтобы решить выражение, нам необходимо выполнить все арифметические действия в соответствии с установленными правилами. Поиск значения начинается с решения деления и умножения. В первую очередь находим произведение цифр 2 и 10 (если рассматривать с левой стороны, данное действие является первым по значимости). Получаем 20. Теперь это число делим на 5. Итог — 4. Когда известно значение основных действий, можем подставить его в наш пример:
20 — 4 — 4 = ?
Упрощенный пример также решаем слева направо: 20 — 4 = 16. Второе действие: 16 — 4 = 12. Ответ 12.
Решение без пояснений. 20 — 2 • 10 ÷ 5 — 4 = 20 — (2 • 10 ÷ 5) — 4 = 20 — 4 — 4 = 12.
Ответ. 12
Пример 2. Решение числового выражения
Задача. Решить:
0,2 — 5 • (— 4) + 1/2 • 5 • 4 = ?
Решение. Начинаем решение с умножения и деления. Умножая 5 на (— 4) получаем (— 20), т.к. производное сохраняет знак множителя. Далее умножаем 1/2 на 5. Для этого преобразуем дробь: 1/2 = 5/10 = 0,5. 0,5 умножаем на 5. Ответ — 2,5. Далее умножаем полученное число на 4. 2,5 • 4 = 10. Получаем следующее выражение:
0,2 — (— 20) + 10
Теперь нам остается решить сложение и вычитание. В первую очередь раскрываем скобку и получаем:
0,2 + 20 + 10 = 30,2
Решение без пояснений. 0,2 — 5 • (— 4) + 1/2 • 5 • 4 = 0,2 — (— 20) + 10 = 0,2 + 20 + 10 = 30,2
Ответ. 30,2
Находим значение выражения со скобками
Скобки определяют порядок действий при решении примера. Выражения, находящиеся внутри скобок «()» имеют первостепенную значимость, независимо от того, какое математическое действие в них выполняется.
Пример 3. Значение числового выражения со скобками
Задача. Решить:
5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = ?
Решение. Начинаем нахождение значения выражения с решения скобок. Порядок действий определяется слева направо. При этом не забываем, что после раскрытия скобок в первую очередь решаем умножение и деление и лишь потом — вычитание и сложение:
- 7 — 2 • 3 = 7 — 6 = 1
- 6 — 4 = 2
Когда скобки решены, подставляем полученные значения в наш пример:
5 + 1 • 2 ÷ 2
Снова решаем все по порядку, не забывая о том, что деление и умножение выполняется в первую очередь:
- 1 • 2 = 2
- 2 ÷ 2 = 1
Упрощенное выражение выглядит следующим образом:
5 + 1 = 6
Решение без пояснений. 5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = 5 + (7 — 6) • 2 ÷ 2 = 5+ 1 • 2 ÷ 2 = 5 + 1 = 6
Ответ. 6
Значение числового выражения со скобками
Задача. Решить:
4 + (3 + 1 + 4 • (2+3)) = ?
Решение. Подобные примеры решаются поэтапно. Помним, что поиск выражения со скобками начинается с решения скобок. Поэтому в первую очередь решаем:
3 + 1 + 4 • (2+3)
В уже упрощенном примере снова встречаются скобки. Их будем решать в первую очередь:
2 + 3 = 5
Теперь можем подставить определенное значение в общую скобку:
3 + 1 + 4 • 5
Начинаем решение с умножения и далее слева направо:
- 4 • 5 = 20
- 3 + 1 = 4
- 4 + 20 = 24
Далее подставляем полученный ответ вместо большой скобки и получаем:
4 + 24 = 28
Решение без пояснений. 4 + (3 + 1 + 4 • (2+3)) = 4 + (3 + 1 + 4 • 5) = 4 + (3 + 1 + 20) = 4 + 24 = 28
Ответ. 28
Важно: Чтобы правильно определить значение числового выражения с множественными скобками, необходимо выполнять все действия постепенно. Скобки читаются слева направо. Приоритет в решении внутри скобок остается за делением и умножением.
Поиск значения выражения с корнями
Часто алгебраические задания основываются на нахождении значений из-под корня. И если определить √4 несложно (напомним, это будет 2), то с примерами, которые полностью расположены под корнем, возникает ряд вопросов. На самом деле в таких заданиях нет ничего сложного. В данном случае порядок действий следующий:
- Решаем все выражение, которое находится под корнем (не забываем о правильной последовательности: сперва скобки, деление и умножение, а лишь потом — сложение и вычитание);
- Извлекаем корень из числа, которое получили в результате решения обычного примера.
Если же и под корнем имеется корень (например: √ 4 + 8 — √4), то начинаем решение примера с его извлечения (в нашем примере это будет: √ 4 + 8 — 2). Если подкоренные числа возведены во вторую степень, то их квадратный корень будет равняться модулю подкоренного выражения.
Значение числового выражения с корнями
Задача. Решить:
√ 2² • 2² • 3² = ?
Решение. Все действия под корнем одинаковы — умножение. Это дает нам право разделить выражение на множители. Получаем:
√2² • √2² • √3² = ?
Т.к. под квадратным корнем у нас числа, возведенные во вторую степень, получаем:
2 • 2 • 3 = 12
Решение без пояснений. √ 2² • 2² • 3² = √2² • √2² • √3² = 2 • 2 • 3 = 12
Ответ. 12
Нет времени решать самому?
Наши эксперты помогут!
Находим значение числовых выражений со степенями
Следующий математический знак, который имеет приоритет в процессе решения, — степени. Они представляют собой результат многократного умножения числа на себя. Само число является основанием степени. А количество операций умножения — ее показателем. Причем выражен он может быть не только целым числом, но и дробью, полноценным числовым выражением.
Начинается решение выражения со степенями с вычисления самих степеней. Если они представляют собой полноценное выражение (например: [3^{3 cdot 4-10}]), то его необходимо решить в нашем примере это будет: [3^{12-10}=3^{2}=9].
Задача. Решите:
[
3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=?
]
Решение. Чтобы решить это выражение со степенями, воспользуемся равенством:
[(a cdot b)^{r}=a^{r} cdot b^{r}]
Рассматривая пример слева направо, видим, что у первых двух множителей одинаковые степени. Это позволяет нам упростить выражение:
[
(3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3}
]
Зная, что при умножении степени с одинаковыми показателями складываются, получаем следующее выражение:
[
21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21
]
Решение без пояснений: [3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=(3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21]
Ответ. 21
Интересно: Этот же пример можно решить и другим способом, преобразовав число 21 в степени ⅔ в два множителя. В данном случае решение будет выглядеть следующим образом:
[3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot(3 cdot 7)^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot 3^{2 / 3} cdot 7^{2 / 3}=3^{1 / 3+2 / 3} cdot 7^{1 / 3+2 / 3}=3^{1}+7^{1}=21]
Ответ. 21
Задача. Решить:
[
2^{-2 sqrt{5}} cdot 4^{sqrt{5}-1}+left((sqrt{3})^{1 / 3}right)^{6}
]
Решение. В данном случает получить точные числовые значения показателей степеней не удастся. Поэтому искать значение выражения с дробями в виде степени будем снова через упрощение:

Ответ. 3,25
Выражения с дробями
Поиск значения выражения дробей начинается с их приведения к общему виду. В большинстве случаев проще представить все значения в виде обыкновенной дроби с числителем и знаменателем. После преобразования всех чисел необходимо привести все дроби к общему знаменателю.
Важно: Прежде чем найти выражение дробей, необходимо провести вычисления в их знаменателе и числителе отдельно. В данном случае действуют стандартные правила решения.
Когда дроби приведены к единому знаменателю можно переходить к решению. Вычисление значений верхней строки (числителя) и нижней (знаменателя) производятся параллельно.
Задача. Решить:
[
6 frac{2}{13}+4 frac{1}{13}=?
]
Решение. Действуя по главному правилу, прежде чем найти значение числового выражения, преобразуем всего его части в простую дробь. Получаем:
[
frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13}
]
Теперь выполняем вычисления в знаменателе и числителе и находим ответ:
[
frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13}=frac{80}{13}+frac{53}{13}=frac{133}{13}=10 frac{3}{13}
]
Ответ. [10 frac{3}{13}]
Примеры(2):

Задача. Решить:
[
frac{2}{sqrt{5}-1}-frac{2 sqrt{5}-7}{4}-3=?
]
Решение. В данном примере мы не можем извлечь корень из пятерки. Но мы можем воспользоваться формулой разложения корней:
[
frac{2}{sqrt{5}-1}=frac{2(sqrt{5}+1)}{(sqrt{5}-1)(sqrt{5}+1)}=frac{2(sqrt{5}+1)}{5-1}=frac{2 sqrt{5}+2}{4}
]
Теперь можем придать нашему первоначальному выражению следующий вид:
[
frac{2 sqrt{5}+2}{4} frac{2 sqrt{5}-7}{4}-3=frac{2 sqrt{5}+2-2 sqrt{5}+7}{4}-3=frac{9}{4} 3=-frac{3}{4}
]
Ответ. [-frac{3}{4}].
Выражения с логарифмами
Как и степени, логарифмы (log), имеющиеся в выражении, вычисляются (если это возможно) в первую очередь. К примеру, зная, что [log _{2} 4=2] мы можем сразу упростить выражение [log _{2} 4+5 cdot 6] до простого и понятного 2 + 5*6 = 32.
Со степенями логарифмы объединяет и порядок выполнения действий. Прежде чем искать значение выражения логарифмов, необходимо вычислить его основание (если оно представлено математическим выражением).
В случаях, когда полное вычисление логарифма невозможно, производится упрощение примера.
Задача. Решить:
[log _{27} 81+log _{27} 9=?]
Решение. Чтобы найти логарифм выражения, воспользуемся свойствами логарифмов и представим значение логарифмов со степенями:
![]()
Это позволит нам решить пример следующим образом:

Ответ. 2
Решаем выражения с тригонометрической функцией
Часто в выражениях встречаются тригонометрические функции. Всего их в математике шесть:
- Синус;
- Косинус;
- Котангенс;
- Тангенс;
- Секанс;
- Косеканс.
Изучение тригонометрии начинается в 9-м классе, когда ученики уже подготовлены к сложным задачам. Большинство заданий представляются с sin и cos. Остальные функции встречаются значительно реже.
В математических примерах, которые содержат sin, cos, tg и др. функции, вычисление тригонометрической функции производится в первую очередь. Если это невозможно — осуществляется упрощение выражения до получения краткой формулы.
Задача. Решить:
[
frac{24}{sin ^{2} 127+1+sin ^{2} 217}
]
Решение. Разложим 217 на 90 и 127. Т.к. по формуле приведения sin(90 + a) = cosa, получаем:
sin217 — sin (90 + 127) = cos127
Теперь заменяем полученной формулой наше слагаемое в знаменателе дроби:
[
frac{24}{sin ^{2} 127+cos ^{2} 127+1}
]
Вспоминаем, что по тригонометрическому тождеству sin2a+ cos2 a= 1 (независимо от значения угла a). Поэтому одну часть слагаемого знаменателя (sin2127+ cos2127) преобразуем в единицу и получаем:
[
frac{24}{sin ^{2} 127+cos ^{2} 127+1}=frac{24}{1+1}=frac{24}{2}=2
]
Ответ. 2

Важно: Не стоит бояться буквенных тригонометрических значений. Большинство примеров построено таким образом, чтобы функции можно было заменить более удобной для вычисления формулой. Поэтому вместо того, чтобы пытаться сразу решить пример, стоит обратить внимание на особенности функций и возможность их приведения к подходящей формуле.
Задача. Решить:
[
sqrt{4} 8-sqrt{1} 92 sin ^{2} frac{19 pi}{12}=?
]
Решение. Начинаем решение с разбора второй дроби. Обращаем внимание, что 192 = 48 • 2. А значит, корень этого числа можно представить в виде 2√48. Зная это и используя формулу косинуса двойного угла, преобразим наше выражение:

Теперь по формуле приведения решаем наш пример:
[
sqrt{4} 8 cos left(3 pi+frac{pi}{6}right)=sqrt{4} 8left(-cos frac{pi}{6}right)=-sqrt{4} 8 cdot frac{sqrt{3}}{2}=-4 sqrt{3} cdot frac{sqrt{3}}{2}=-6
]
Ответ. — 6.
Общий случай: находим значения выражений с дробями, функциями, степенями и не только
Самым сложным считается поиск числовых выражений общих случаев. Они представляют собой тригонометрические примеры, которые могут содержать:
- Степени;
- Скобки;
- Корни;
- Функции и т.д.
Общие числовые выражения сложны только длительностью решения. В остальном же они ничуть не сложнее, чем решение каждого примера (со скобкой, степенями, функциями и т.д.) по отдельности.
Чтобы найти значение выражения с логарифмами, тригонометрическими функциями, скобками и/или другими действиями, необходимо помнить три основных правила:
- Упрощение. Прежде чем приступать к решению внимательно изучите выражение. Особенно — его степени, корни, логарифмы, функции. В большинстве случаев их можно сократить или заменить простым числовым значением еще до решения.
- Скобки. Независимо от типа выражения, действий, начинать решение всегда необходимо со скобок. Часто именно игнорирование этого правила приводит к получению неверного ответа или отсутствию решения в принципе.
- Общий вид. Старайтесь привести выражение к общему виду. Особенно это касается дробей. Смешанные и десятичные дроби преобразуйте в обычные.
- Последовательность. Действия в скобках и действия после их решения выполняются слева направо. В первую очередь необходимо совершать умножение и деление. Когда все произведения и частные найдены, можно переходить к сложению и вычитанию.
Для удобства решения и устранения возможных ошибок рекомендуем расставлять порядок действий непосредственно над математическими знаками.
Задача. Решить:
[
-frac{sqrt{2} sin left(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)right)+3}{operatorname{Ln} e^{2}}+left(1+3^{sqrt{9}}right)=?
]
Решение. Чтобы решить этот пример, сначала найдем значение выражения числителя дроби, а точнее — подкоренного выражения. Для этого необходимо вычислить значение sin и общего выражения. Начинаем с раскрытия скобок в числителе:

Полученное значение можем подставить в подкоренное выражение для вычисления числителя дроби:
[
sqrt{2} sin cdotleft(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)+3=sqrt{4}=2right.
]
Со знаменателем дела обстоят куда проще:
[
ln e^{2}=2
]
Числитель и знаменатель у нас одинаковые, что позволяет нам их сократить:

Теперь остается решить следующее выражение:

Ответ. 27
Как видите, при последовательном решении примеров с большим количеством действий нет ничего сложного. Главное — верно обозначить последовательность шагов и четко ей следовать.
Как найти значение выражения числителя дроби, подкорневого значения рационально?
Независимо от типа выражения решать его необходимо последовательно, руководствуясь стандартными правилами (описаны ранее). Но не стоит забывать, что во многих случаях поиск ответа может быть значительно упрощен за счет рационального подхода к решению. Основывается он на нескольких правилах.
Правило 1. Когда произведение равно нулю
Производное равно нулю в том случае, если хотя бы один из его сомножителей равен нулю. Если вы решаете пример из нескольких сомножителей, одним из которых является «0», то проводить многочисленные вычислительные действия не стоит.
Например, выражение [3 cdotleft(451+4+frac{18}{3}right)left(1-sin left(frac{3 pi}{4}right)right) cdot 0] будет равняться нулю.
Правило 2. Группировка и вынесение чисел
Ускорить процесс поиска ответа можно за счет группировки множителей, слагаемых или вынесения единого множителя за скобки. Также не стоит забывать о возможности сокращения дроби.
Например, выражение [frac{left(451+4+frac{18}{3}right)}{4left(451+4+frac{18}{3}right)}] решать не надо. Достаточно сократить скобки, чтобы получить ответ [=frac{1}{4}]
Решение примеров с переменными
Примеры с переменными отличаются от числовых только формой предоставления. В данном случае значения предоставляются дополнительно к выражению.
Пример задания: Найдите значение выражения 2x — y, если x = 2,5, а y = 2. В данном случае решение будет выглядеть следующим образом:
2x — y = 2 • 2,5 — 2 = 3
При этом в таких примерах сохраняются все описанные выше правила. Касается это и советов по рациональному решению примеров. Так, решать дробь [frac{sqrt{y}}{sqrt{y}}] бессмысленно, т.к. при любых значениях «y» ответ будет одинаковым — 1.
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Если в выражении есть только числа и арифметические знаки “+”, “·”, “-“, “÷”, то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пусть нужно найти значения выражения 14-2·15÷6-3.
Выполним сначала умножение и деление. Получаем:
14-2·15÷6-3=14-30÷6-3=14-5-3.
Теперь проводим вычитание и получаем окончательный результат:
14-5-3=9-3=6.
Вычислим: 0,5-2·-7+23÷234·1112.
Сначала выполняем преобразование дробей, деление и умножение:
0,5-2·-7+23÷234·1112=12-(-14)+23÷114·1112
12-(-14)+23÷114·1112=12-(-14)+23·411·1112=12-(-14)+29.
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
12-(-14)+29=12+14+29=14+1318=141318.
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Найдем значение выражения 0,5·(0,76-0,06).
В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом – умножение.
0,5·(0,76-0,06)=0,5·0,7=0,35.
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Вычислим значение 1+2·1+2·1+2·1-14.
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
1+2·1+2·1+2·1-14=1+2·1+2·1+2·34
1+2·1+2·1+2·34=1+2·1+2·2,5=1+2·6=13.
В нахождении значений выражений со скобками главное – соблюдать последовательность действий.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Вычислим значение выражения с корнями -2·3-1+60÷43+3·2,2+0,1·0,5.
Сначала вычисляем подкоренные выражения.
-2·3-1+60÷43=-6-1+153=83=2
2,2+0,1·0,5=2,2+0,05=2,25=1,5.
Теперь можно вычислить значение всего выражения.
-2·3-1+60÷43+3·2,2+0,1·0,5=2+3·1,5=6,5
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Сколько будет 3+13-1-1
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
3+13-1=3-1.
Таким образом:
3+13-1-1=3-1-1=1.
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Найдем значение выражения 23·4-10+161-123,5-2·14.
Начинаем вычислять по порядку.
23·4-10=212-10=22=4
16·1-123,5-2·14=16*0,53=16·18=2.
Осталось только провести операцию сложение и узнать значение выражения:
23·4-10+161-123,5-2·14=4+2=6.
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Вычислим значение следующего выражения: 2-25·45-1+3136.
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
2-25·45-1+3136=2-25·225-1+313·6
2-25·225-1+313·6=2-25·22·5-2+32=22·5-2-25+32
22·5-2-25+32=2-2+3=14+3=314
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Найдем значение выражения, содержащего дроби: 3,22-3·7-2·36÷1+2+39-6÷2.
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
3,22=3,2÷2=1,6
7-2·36=7-66=16
1+2+39-6÷2=1+2+39-3=66=1.
Перепишем наше выражение и вычислим его значение:
1,6-3·16÷1=1,6-0,5÷1=1,1
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Вычислим выражение 25-1-25-74-3.
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
25-1=25+15-15+1=25+15-1=25+24
Исходное выражение принимает вид:
25-1-25-74-3=25+24-25-74-3.
Вычислим значение этого выражения:
25+24-25-74-3=25+2-25+74-3=94-3=-34.
Выражения с логарифмами
Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log24+2·4 можно сразу вместо log24 записать значение этого логарифма, а потом выполнить все действия. Получим: log24+2·4=2+2·4=2+8=10.
Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log5-6÷352+2+7. Имеем:
log5-6÷352+2+7=log327+7=3+7=10.
Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Найдем значение выражения log2log2256+log62+log63+log5729log0,227.
log2log2256=log28=3.
По свойству логарифмов:
log62+log63=log6(2·3)=log66=1.
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
log5729log0,227=log5729log1527=log5729-log527=-log27729=-log27272=-2.
Теперь можно переходить к вычислению значения исходного выражения.
log2log2256+log62+log63+log5729log0,227=3+1+-2=2.
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Найдите значение выражения: tg24π3-sin-5π2+cosπ.
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
tg4π3=3
sin-5π2=-1
cosπ=-1.
Подставляем значения в выражение и вычисляем его значение:
tg24π3-sin-5π2+cosπ=32-(-1)+(-1)=3+1-1=3.
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Нужно найти значение выражения cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1.
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1=cos2π8cos5π36+π9-1=cosπ4cosπ4-1=1-1=0.
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.
- Корни, степени, логарифмы и т.д. заменяются их значениями.
- Выполняются действия в скобках.
- Оставшиеся действия выполняются по порядку слева направо. Сначала – умножение и деление, затем – сложение и вычитание.
Разберем пример.
Вычислим, чему равно значение выражения -2·sinπ6+2·2π5+3π5+3 lne2+1+39.
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
Первым делом вычислим значение подкоренного выражения 2·sinπ6+2·2π5+3π5+3. Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.
π6+2·2π5+3π5=π6+2·2π+3π5=π6+2·5π5=π6+2π
Теперь можно узнать значение синуса:
sinπ6+2·2π5+3π5=sinπ6+2π=sinπ6=12.
Вычисляем значение подкоренного выражения:
2·sinπ6+2·2π5+3π5+3=2·12+3=4
Отсюда:
2·sinπ6+2·2π5+3π5+3=4=2.
Со знаменателем дроби все проще:
lne2=2.
Теперь мы можем записать значение всей дроби:
2·sinπ6+2·2π5+3π5+3 lne2=22=1.
С учетом этого, запишем все выражение:
-1+1+39=-1+1+33=-1+1+27=27.
Окончательный результат:
-2·sinπ6+2·2π5+3π5+3 lne2+1+39=27.
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56+8-3,789lne2-56+8-3,789lne2 также равно нулю.
Еще один прием, позволяющий ускорить процесс – использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями – сокращение одинаковых выражений в числителе и знаменателе.
Например, возьмем выражение 23-15+3·289·343·23-15+3·289·34. Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 13.
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.
Вычислить значение выражения 0,5x-y при заданных x=2,4 и y=5.
Подставляем значения переменных в выражение и вычисляем:
0,5x-y=0,5·2,4-5=1,2-5=-3,8.
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Например, выражение х+3-х, очевидно, имеет значение 3, и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.
Еще один пример. Значение выражения xx равно единице для всех положительных иксов.
Содержание:
Целые выражения
Выражения в математике играют приблизительно такую же роль, как слова в языке или как отдельные кирпичи в сооружении. Математический язык — это язык выражений. Чтобы овладеть им, надо научиться оперировать математическими выражениями, понимать их содержание, уметь записывать в удобном виде. Существуют разные виды математических выражений. В этой главе вы узнаете о:
- выражениях с переменными;
- выражениях со степенями;
- одночленах;
- многочленах;
- действиях над многочленами.
Выражения с переменными
Рассмотрим, например, уравнение:
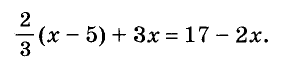
Левая и правая его части — выражения:
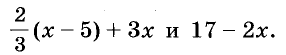
Каждое из этих выражений содержит одну переменную х. Но бывают выражения с двумя, тремя и большим количеством переменных. Например, выражение 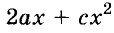 содержит три переменных: а, с и х.
содержит три переменных: а, с и х.
В математике выражения с переменными играют очень важную роль. Математический язык — это язык выражений. Неслучайно значительная часть школьного курса алгебры посвящена изучению выражений.
Бывают выражения и без переменных, например:
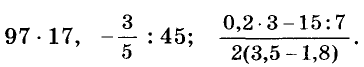
Такие выражения называют числовыми.
Итак, выражения бывают числовые и с переменными (рис. 23). Далее мы будем рассматривать преимущественно выражения с переменными.
Каждое числовое выражение (не содержащее деления на 0) имеет одно значение. А выражение с переменными при разных значениях этих переменных может принимать разные значения.
Для примера найдём значения выражения 3a + 5, если а равно 1, 2, 3 и -4. 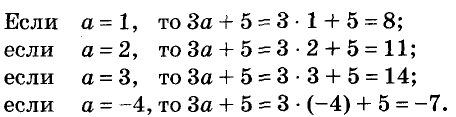 Результаты вычислений запишем в таблицу.
Результаты вычислений запишем в таблицу. 
Если выражение содержит несколько переменных, например 2a – 3x, то для нахождения его числовых значений следует давать значение каждой переменной. Например, если a = 7 и x = 5, то 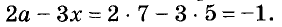
Если выражение не содержит никаких других действий, кроме сложения, вычитания, умножения, возведения в степень и деления, его называют рациональным выражением. Примеры рациональных выражений:
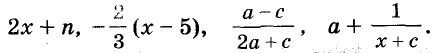
Рациональное выражение, не содержащее деления на выражение с переменной, называют целым. Два первых из указанных выше выражений — целые, другие — дробные. В этой главе мы будем рассматривать только целые выражения.
Выражения 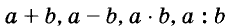 — соответственно сумма, разность, произведение и частное переменных а и b. Читают их и так: «сумма чисел а и b», «разность чисел а и b» и т. д.
— соответственно сумма, разность, произведение и частное переменных а и b. Читают их и так: «сумма чисел а и b», «разность чисел а и b» и т. д.
Математическими выражениями считаются также отдельные числа или переменные, например 2, 0, х, -а. А записи, содержащие знаки равенства или неравенства, например
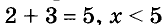 — не выражения.
— не выражения.
Раньше вы различали числовые выражения и буквенные выражения, однако в современной математике буквами обозначают не только неизвестные числа. Например, буква 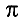 обозначает отношение длины окружности к её диаметру, его приближённое значение равно 3,14. Поэтому выражение
обозначает отношение длины окружности к её диаметру, его приближённое значение равно 3,14. Поэтому выражение 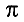 + 2,5, хотя и содержит букву
+ 2,5, хотя и содержит букву 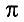 , является числовым выражением. Со временем вы ознакомитесь с выражениями
, является числовым выражением. Со временем вы ознакомитесь с выражениями 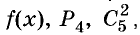
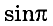 и многими другими, содержащими буквы, вместо которых не нужно подставлять числа. Поэтому дальше те буквы, вместо которых можно подставлять разные числа, мы будем называть переменными, понимая, что их значения могут изменяться. А выражения, содержащие такие переменные, будем называть выражениями с переменными.
и многими другими, содержащими буквы, вместо которых не нужно подставлять числа. Поэтому дальше те буквы, вместо которых можно подставлять разные числа, мы будем называть переменными, понимая, что их значения могут изменяться. А выражения, содержащие такие переменные, будем называть выражениями с переменными.
Словом выражение часто называют и высказывание (например, крылатое выражение), и проявление расположения духа (выражение лица) и т. п. В математике этим словом коротко называют математическое выражение. Математическое выражение — это написанные в определённом порядке математические символы, включающие числа, буквы, знаки действий, скобки, знаки процентов, модуля и т. п. Например, старшеклассники кроме всех прочих рассматривают и такие выражения: 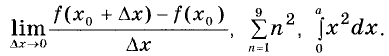
Что они означают, вы со временем узнаете.
Пример:
Запишите в виде выражения число, которое имеет:
а) а сотен, b десятков и с единиц; б) m тысяч и n десятков.
Решение:
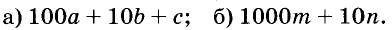
Пример:
Известно, что а + b = 35. Найдите значение выражения 7а + 7 + 7b.
Решение:
Воспользуемся переместительным, сочетательным и распределительным законами:
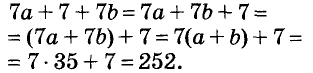
Пример:
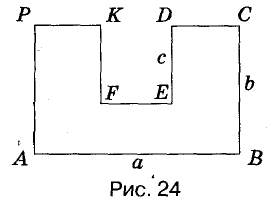
Найдите периметр многоугольника, изображённого на рисунке 24, если АВ = а, ВС = b, DE = с.
Решение:
Поскольку CD+EF+KP=AB, то AB+BC+CD+DE+EF+FK+KP+PA=2AB+2BC+2FK=2a+2b+2c
Тождественные выражения
Два выражения, соответствующие значения которых равны при любых значениях переменных, называют тождественно равными, или тождественными.
Например, тождественно равными являются выражения 5a + 8a и 13a, так как при каждом значении переменной а эти выражения имеют равные значения (следует из распределительного закона умножения).
Два тождественно равных выражения, соединённые знаком равенства, образуют тождество.
Примеры.
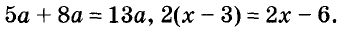
Тождеством является каждое равенство, выражающее законы действий: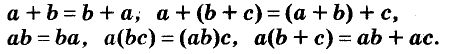
Тождествами также принято считать верные числовые равенства, например 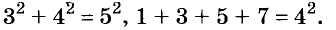 Замена данного выражения другим, тождественным ему, называется тождественным преобразованием выражения.
Замена данного выражения другим, тождественным ему, называется тождественным преобразованием выражения.
Каждое равенство — это утверждение, которое может быть верным или неверным. Говоря «тождество», понимают, что оно верное. Чтобы убедиться в этом, его доказывают, как в геометрии — теоремы. Чтобы доказать истинность числового тождества, например 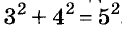 , достаточно вычислить его левую и правую части и показать, что они равны:
, достаточно вычислить его левую и правую части и показать, что они равны: 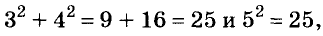 значит,
значит, 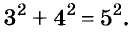 .
.
Тождества, содержащие переменные, чаще всего доказывают, ссылаясь на законы действий и на уже известные правила приведения подобных слагаемых, раскрытие скобок и т. п. Чтобы доказать тождество, как правило, одну из его частей (левую или правую) преобразовывают так, чтобы получить другую её часть.
Пример:
Докажите тождество:
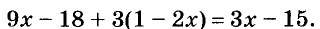
Доказательство:
Упростим левую часть тождества.
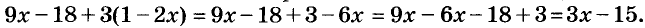
Левая часть доказываемого равенства тождественно равна правой. Итак, тождество доказано.
Иногда для доказательства тождества целесообразно преобразовать каждую из его частей.
Пример:
Докажите тождество:
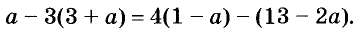
Доказательство:
Упростим каждую из частей тождества. 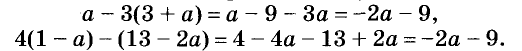
Правая и левая части тождества равны одному и тому же выражению  Тождество доказано.
Тождество доказано.
Существуют и другие способы доказательства тождеств. С ними вы ознакомитесь позднее.
Говоря, что какое-либо выражение тождественно, обязательно следует отметить, какому именно выражению оно тождественно. Речь идёт об отношении тождественности двух выражений (как об отношении перпендикулярности прямых, отношении равенства углов и т. п.).
Отношение тождественности выражений имеет такие свойства:
- каждое выражение тождественно самому себе;
- если выражение А тождественно выражению В, то и выражение В тождественно выражению А;
- если выражение А тождественно выражению В, а выражение В тождественно выражению С, то и выражение А тождественно выражению С.
Подобные свойства имеют также отношения равенства чисел или фигур, параллельности прямых и т. п.
Если в тождестве вместо переменной везде написать одно и то же выражение, получим новое тождество. Например, если в тождестве 4(а – 2) + 8 = 4 а переменную а заменить выражением z + 3, то получим равенство  , которое также является тождеством.
, которое также является тождеством.
Пример:
Докажите тождество 
Доказательство:
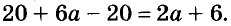 Правая часть равенства тождественно равна левой, поэтому это равенство — тождество.
Правая часть равенства тождественно равна левой, поэтому это равенство — тождество.
Пример:
Всегда ли верно равенство 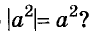
Решение:
Каким бы не было значение а, значение выражения а2 положительно или равно нулю. Модуль неотрицательного числа равен этому же числу. Итак, равенство 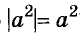 верно для каждого значения а.
верно для каждого значения а.
Выражения со степенями
В алгебре часто приходится иметь дело с выражениями, содержащими степени чисел или переменных.
Степенью называется произведение нескольких равных множителей.
Например,
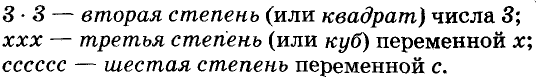
Эти степени обозначают: 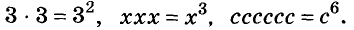
Возвести число 2 в десятую степень — это означает перемножить десять двоек:
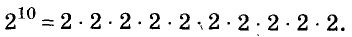
Значит, 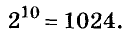 Здесь 2 — основание степени, 10 — показатель степени, а 1024, или
Здесь 2 — основание степени, 10 — показатель степени, а 1024, или  — десятая степень числа 2.
— десятая степень числа 2.
Число, возводимое в степень, называют основанием степени.
Число, показывающее, в какую степень возводят основание, называют показателем степени.

Степени 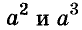 называют квадратом и кубом потому, что для вычисления площади квадрата длину его стороны возводят во вторую степень, а для вычисления объёма куба длину его ребра возводят в третью степень.
называют квадратом и кубом потому, что для вычисления площади квадрата длину его стороны возводят во вторую степень, а для вычисления объёма куба длину его ребра возводят в третью степень.
Первой степенью любого числа считают само это число: 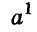 — то же самое, что и а. Показатель степени 1 не принято писать.
— то же самое, что и а. Показатель степени 1 не принято писать.
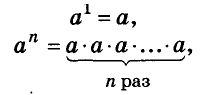
где n — натуральное число, 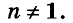
Основанием степени может быть и дробное число, и отрицательное. Например,
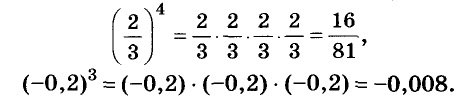
Чтобы возвести в степень отрицательное число, надо возвести в эту степень модуль этого числа и перед результатом поставить знак «плюс», если показатель степени чётный, или «минус» — если показатель степени нечётный.
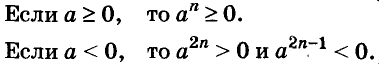
Не путайте слова «степень» и «ступень». Сложение и вычитание считаются действиями первой ступени, умножение и деление — второй ступени, возведение в степень — действие третьей ступени. Вычисляя значение выражения, сначала выполняют действия высшей ступени, потом — низшей. Действия одной и той же ступени выполняют в том порядке, в котором они записаны. Но когда выражение содержит деление на одночлен, то сначала находят значение одночлена, например если 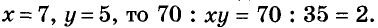 Если выражение содержит скобки, сначала находят значение выражения в скобках.
Если выражение содержит скобки, сначала находят значение выражения в скобках.
Пример:
Найдите значение выражения
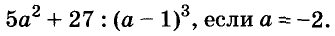
Решение:
Подставим вместо а его значение -2 и выполним действия в соответствии с их ступенью. Первый способ. 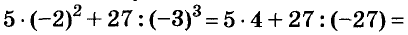
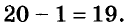
Второй способ. 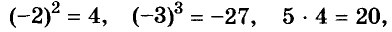
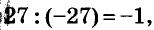 значит,
значит, 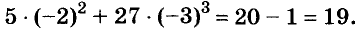 С помощью калькулятора можно возводить число в степень, умножив это число на себя несколько раз. Например, пятую степень числа 3,7 можно вычислить по такой программе:
С помощью калькулятора можно возводить число в степень, умножив это число на себя несколько раз. Например, пятую степень числа 3,7 можно вычислить по такой программе: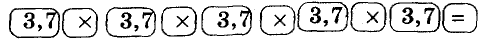 Или короче:
Или короче: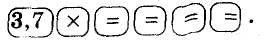
Калькуляторы, имеющие клавиши  и
и  , дают возможность упростить вычисление — 20-ю степень числа 1,2 можно вычислить по такой программе:
, дают возможность упростить вычисление — 20-ю степень числа 1,2 можно вычислить по такой программе: 
В математике, физике, астрономии, биологии и других науках часто используются степени 10 для записи чисел в стандартном виде.
Любое число А, большее 10, можно записать в виде 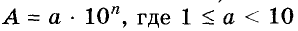 и n — натуральное число. Такая запись числа А называется стандартной, а показатель п называют порядком числа А.
и n — натуральное число. Такая запись числа А называется стандартной, а показатель п называют порядком числа А.
Например, в астрономии за единицу длины принимается 1 парсек (сокращенно — пк).
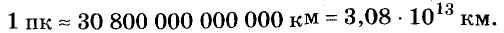
Вы уже знаете, как записывать в стандартном виде большие числа. Чтобы записать в стандартном виде маленькие положительные числа, например скорость движения улитки (0,000003 м/с), используют степени числа 10 с целыми отрицательными показателями. Покажем, как: следует понимать степени числа 10 с целым показателем: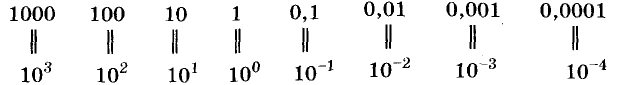
А вообще считают, что 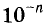 , где n — число натуральное, обозначает десятичную дробь 0,0000 … 01 с n десятичными знаками.
, где n — число натуральное, обозначает десятичную дробь 0,0000 … 01 с n десятичными знаками.
Например, 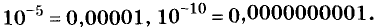
Используя степени числа 10 с целым показателем, в стандартном виде можно записать любое число:
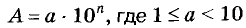 и n -целое число
и n -целое число
Скорость движения улитки в стандартном виде записывают так: 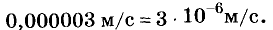
Если число А большое, его порядок — положительное число, а если положительное число А очень маленькое, то его порядок — отрицательное число.
Пример:
Запишите число 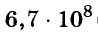 без показателя степени.
без показателя степени.
Решение:
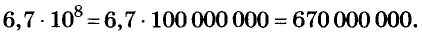
Пример:
Запишите число 2 000 000 000 в стандартном виде.
Решение:
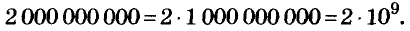
Пример:
Найдите значение выражения: 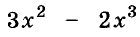 , если х = -0,2.
, если х = -0,2.
Решение:
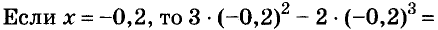
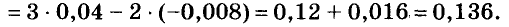
4. Докажите, что:
а) 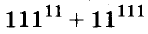 делится на 2;
делится на 2;
б) 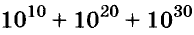 делится на 3.
делится на 3.
Доказательство, а) Последние цифры чисел 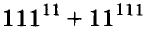 — единицы, а потому последняя цифра суммы этих чисел — два. Значит, число
— единицы, а потому последняя цифра суммы этих чисел — два. Значит, число 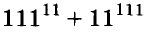 делится на 2.
делится на 2.
б) Каждое из слагаемых — это число, которое можно записать в виде единицы с последующими нулями. Сумма цифр трёх таких чисел равна трём, поэтому само число делится на три.
Пример:
Сколько корней имеет уравнение 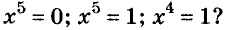
Решение:
Только один: х = 0, так как
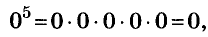 и не существует такого числа х, отличного от 0, чтобы выполнялось равенство
и не существует такого числа х, отличного от 0, чтобы выполнялось равенство 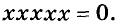
Так же можно убедиться, что уравнение 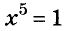 .имеет только один корень х = 1, а уравнение
.имеет только один корень х = 1, а уравнение 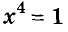 имеет два корня: х=1 и х = -1.
имеет два корня: х=1 и х = -1.
Свойства степеней
Далее рассмотрим важнейшие тождественные преобразования выражений со степенями. Начнём с основного свойства степени.
Для любого числа а и произвольных натуральных показателей m и n всегда
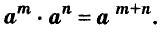
Доказательство.
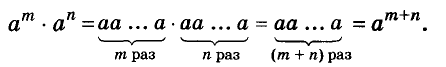
Тождество 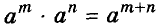 называют основным свойством степени. Из него следует, что при умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают. Например
называют основным свойством степени. Из него следует, что при умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают. Например
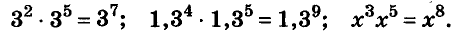
Для любого числа  и произвольных натуральных показателей степеней
и произвольных натуральных показателей степеней 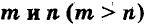 всегда
всегда
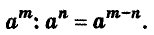
Доказательство. По правилу умножения степеней
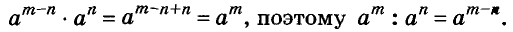
При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
Например,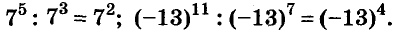
Для любого числа а и произвольных натуральных показателей степеней m и n всегда 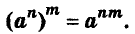
Доказательство.
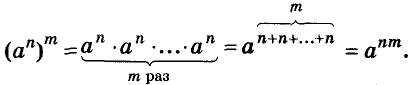
При возведении степени в степень нужно показатели степеней перемножить, а основание оставить прежним. Например,
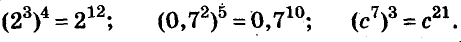
Для любых чисел а и b и произвольного натурального показателя степени n
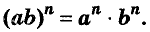
Доказательство.
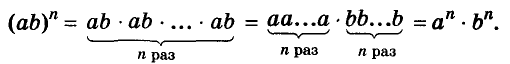
Значит,
n-я степень произведения равна произведению n-х степеней множителей.
Например,
 Можно доказать (попробуйте сделать это самостоятельно), что для любых чисел
Можно доказать (попробуйте сделать это самостоятельно), что для любых чисел  и натурального показателя степени п справедливо равенство:
и натурального показателя степени п справедливо равенство:
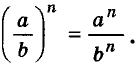 Итак, при указанных условиях:
Итак, при указанных условиях: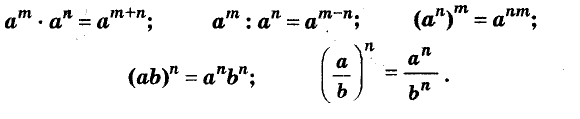
Рассмотренные свойства степеней с натуральными показателями можно применить и к степеням с целыми отрицательными показателями. Например,
Используя свойства степеней с целыми показателями, можно упростить выполнение действий с любыми числами, записанными в стандартном виде. Найдём, для примера, произведение и частное чисел а и b, если 
Пример:
Вычислите: а)  б)
б) 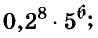 в)
в) 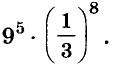
Решение:
а) 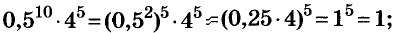
б)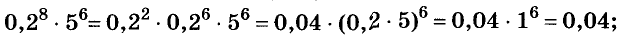
в)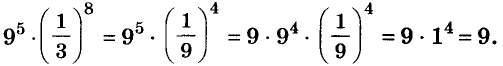
Ответ, а) 1; 6)0,04; в) 9.
Пример:
Решите уравнение 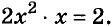
Решение:
Поделим обе части уравнения на 2 и представим левую часть в виде степени с основанием х:
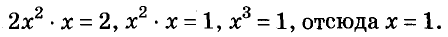
Ответ. х= 1.
Пример:
Запишите в виде степени выражение:
а) 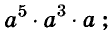 б)
б)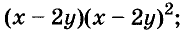 в)
в)
Решение:
а)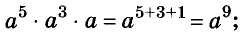
б)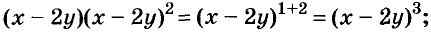
в)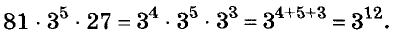
Ответ: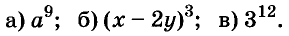
Пример:
Найдите сумму, разность, произведение и частное чисел
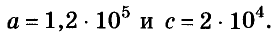
Решение:
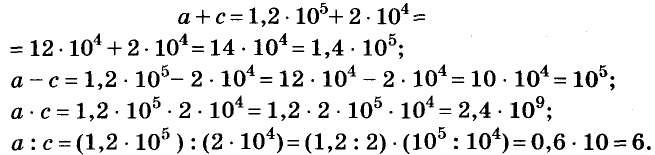
Ответ: 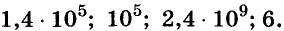
Одночлены
Простейшие выражения — числа, переменные, их степени и произведения, например 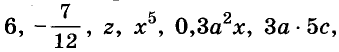 называют одночленами.
называют одночленами.
Если одночлен содержит только один числовой множитель, и к тому же стоящий на первом месте, и если каждая переменная входит только в один множитель, такой одночлен называется одночленом стандартного вида. Такими являются, например, все приведённые выше одночлены, кроме последнего. Одночлены 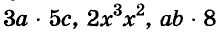 записаны в нестандартном виде:
записаны в нестандартном виде:
- первый содержит два числовых множителя 3 и 5, второй — два множителя
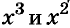 с одной и той же переменной х, в третьем числовой множитель 8 стоит не на первом месте.
с одной и той же переменной х, в третьем числовой множитель 8 стоит не на первом месте.
Пользуясь переместительным и сочетательным законами умножения, каждый одночлен можно записать в стандартном виде.
Например,
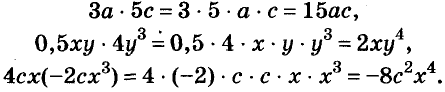
Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом этого одночлена. Например, коэффициенты одночленов 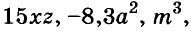 равны соответственно
равны соответственно 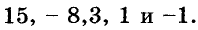 Коэффициенты 1 и -1 писать не принято.
Коэффициенты 1 и -1 писать не принято.
Приведение одночлена к стандартному виду часто состоит в умножении двух или нескольких одночленов.
Чтобы перемножить одночлены, числовые множители перемножают, а к буквенным применяют правило умножения степеней с одинаковыми основаниями.
Если возникает потребность перемножить несколько одночленов, то их соединяют знаком умножения, а полученный таким способом одночлен приводят к стандартному виду.
Например, найдём произведение одночленов 
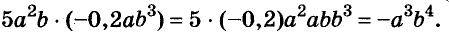
В одночлене 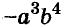 сумма показателей переменных равна 7. Эту сумму называют степенью одночлена
сумма показателей переменных равна 7. Эту сумму называют степенью одночлена 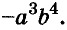 Степень одночлена
Степень одночлена 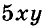 равна 2.
равна 2.
Вообще, степень одночлена — это сумма показателей всех входящих в него переменных. Если одночлен — число, считают, что его степень равна нулю.
Например, одночлены 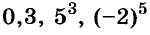 имеют нулевую степень.
имеют нулевую степень.
Одночлены можно возводить в степень. Для примера возведём в третью степень одночлен 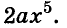
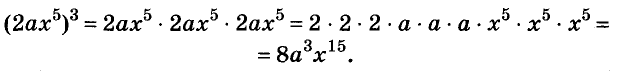
Из тождества 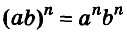 следует такое правило.
следует такое правило.
Чтобы возвести в степень одночлен, нужно возвести в эту степень каждый множитель одночлена и найденные степени перемножить.
Пример:
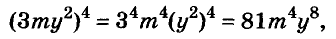
Решение:
Одночлены, как и числа, можно складывать, вычитать, умножать и делить. Однако сумма, разность и частное двух одночленов не всегда является одночленом. Например, сумма и разность одночленов 6х и 2х равны соответственно одночленам 8х и 4х. Но сумма и разность одночленов 8ах и 4ау равны выражениям 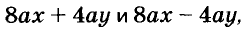 а эти два выражения — не одночлены.
а эти два выражения — не одночлены.
Частное одночленов  равно одночлену
равно одночлену  (так как
(так как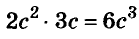 ). Но частное от деления
). Но частное от деления 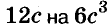 —не одночлен.
—не одночлен.
Пример:
Запишите одночлен в стандартном виде:
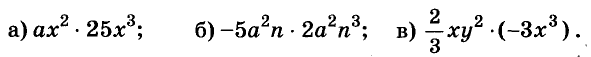
Решение:
а)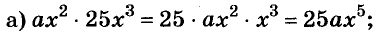
б) 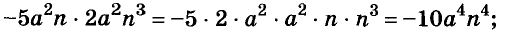
в) 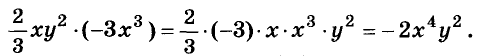
Ответ. 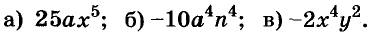
Пример:
Возведите в квадрат и куб одночлен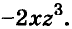
Решение:
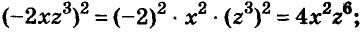
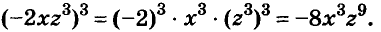
Ответ.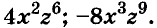
Многочлены
В математике часто приходится складывать или вычитать одночлены. Например,7х + 2а — сумма, а 7х – 2а — разность одночленов 7х и 2а. Выражение 7х – 2а можно считать также суммой одночленов 7х и -2а, так как 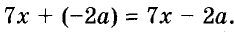 Выражение
Выражение 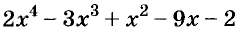 — сумма одночленов
— сумма одночленов 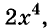
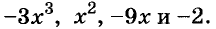
Сумму нескольких одночленов называют многочленом.
Каждое слагаемое многочлена называется его членом . Например, многочлен  содержит три члена:
содержит три члена: 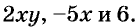
Если многочлен содержит два слагаемых, он называется двучленом, три — трёхчленом. Одночлен также считается отдельным видом многочлена.
Существуют целые выражения, не являющиеся многочленами.
Например, выражения целые, но не являются многочленами. Связи между упоминавшимися выражениями иллюстрирует рис. 31.
целые, но не являются многочленами. Связи между упоминавшимися выражениями иллюстрирует рис. 31.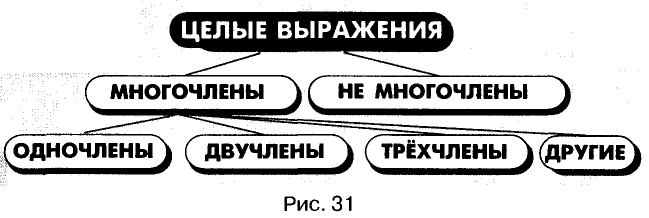
Многочлен может иметь подобные члены, т. е. такие слагаемые, которые отличаются только коэффициентами или совсем не отличаются. Например, в трёхчлене  первые два члена подобны. Приведя их, получим двучлен
первые два члена подобны. Приведя их, получим двучлен 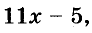 который тождественно равен данному трёхчлену.
который тождественно равен данному трёхчлену.
Считают, что многочлен записан в стандартном виде, если все его члены — одночлены стандартного вида и среди них нет подобных.
Например, среди многочленов
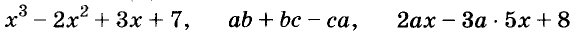
два первых выражения — многочлены стандартного вида, а третий — нет. На основе законов действий (см. с. 52) каждый многочлен можно представить в стандартном виде, например:
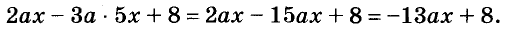
Члены многочлена можно записывать в разной последовательности. В основном их упорядочивают по убывающим показателям степени той или другой переменной. Например,упорядочив многочлен 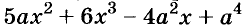 по убывающим степеням переменной х, получим
по убывающим степеням переменной х, получим 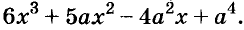 Наибольший показатель степени переменной х равен трём, поэтому такой многочлен называют многочленом третьей степени относительно х. Его можно упорядочить и по убывающим степеням переменной а:
Наибольший показатель степени переменной х равен трём, поэтому такой многочлен называют многочленом третьей степени относительно х. Его можно упорядочить и по убывающим степеням переменной а: 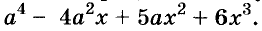 Тогда это будет многочлен четвёртой степени относительно переменной а.
Тогда это будет многочлен четвёртой степени относительно переменной а.
Является ли многочленом выражение  Иногда отвечают на этот вопрос утвердительно, так как согласно распределительному закону умножения данное выражение тождественно равно двучлену
Иногда отвечают на этот вопрос утвердительно, так как согласно распределительному закону умножения данное выражение тождественно равно двучлену  а значит, и оно является двучленом. Это неправильно. В алгебре выражения принято называть в зависимости от того, как они записаны, а не от того, как их можно записать.
а значит, и оно является двучленом. Это неправильно. В алгебре выражения принято называть в зависимости от того, как они записаны, а не от того, как их можно записать.
Рассмотрим пример. Выражение 8а можно представить в виде суммы двух, трёх или любого другого количества слагаемых:
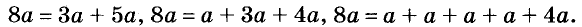
Если, исходя из этого, выражение 8а называть и одночленом, и двучленом, и трёхчленом и т. п., то это будет очень неудобно. Поэтому в алгебре договорились выражения называть так, как они записаны, а не так, как их можно записать, выполнив те или другие тождественные преобразования.
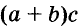 — не одночлен, не многочлен.
— не одночлен, не многочлен.
Пример:
Запишите многочлен в стандартном виде:
а) 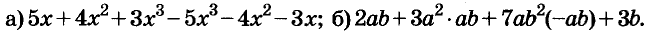
Решение:
а) Приведём подобные слагаемые и упорядочим члены многочлена:
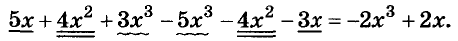
б) Приведём к стандартному виду каждый одночлен заданного многочлена и упорядочим его члены по степеням переменной :
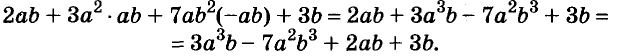
Ответ. 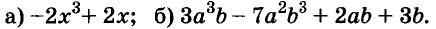
Пример:
Вычислите значение многочлена
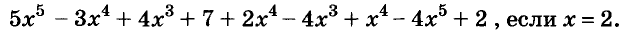
Решение:
Приведём многочлен к стандартному виду:
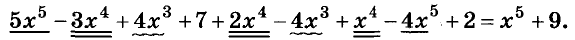
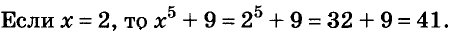
Ответ. 41.
Пример:
Два велосипедиста одновременно выехали из пунктов А и В навстречу друг другу. Найдите расстояние между А и В, если они ехали со скоростями  и встретились через t ч.
и встретились через t ч.
Решение:
Первый способ. За t ч первый велосипедист проехал at км, а второй — bt км. Итак, всё расстояние равно 
Второй способ. За 1 ч велосипедисты приблизились на (а + b) км, к моменту встречи через t ч они проехали (а + b)t км. Это и есть искомое расстояние. Ответ. (а + b)t км.
Сложение и вычитание многочленов
Чтобы сложить два многочлена, то есть найти сумму многочленов, достаточно соединить их знаком «плюс».
Например, суммой многочленов 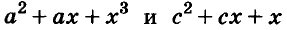 является многочлен
является многочлен 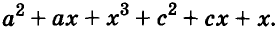 Если в найденной сумме есть подобные члены, их следует привести. Так же складывают три и более многочленов.
Если в найденной сумме есть подобные члены, их следует привести. Так же складывают три и более многочленов.
Пример:
Сложите многочлены
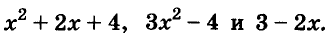
Решение:
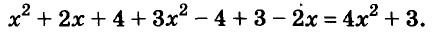
Сложение многочленов подчиняется переместительному и сочетательному законам: какие бы не были многочлены А, В и С, всегда
А + В = В+А и (А + В) + С = А + (В + С).
Чтобы найти разность двух многочленов, надо из первого многочлена вычесть второй.
Выполняя такое задание, после первого многочлена пишут знак «минус», а второй берут в скобки.
Раскрывая скобки, перед которыми стоит знак «минус», знаки всех членов, заключённых в этих скобках, изменяют на противоположные.
Пример:
Найдите разность многочленов 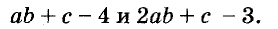
Решение:
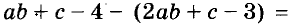
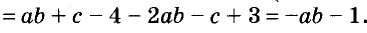
Сумма и разность произвольных многочленов — многочлены.
Какой может быть сумма двух двучленов? Она может иметь несколько членов, быть равной любому числу, в частности и нулю. Прибавьте, например, двучлену 4с – 5х последовательно двучлены 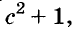
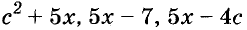 и убедитесь в этом.
и убедитесь в этом.
Так как многочленами считают и одночлены, и любые числа, в том числе нуль, то сумма любых многочленов является многочленом. Поэтому говорят, что во множестве многочленов сложение и вычитание всегда возможно.
Пример:
Найдите сумму и разность многочленов
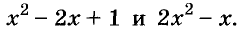
Решение:
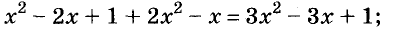
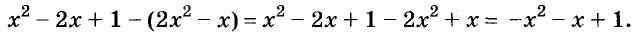
Ответ. 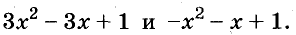
Пример:
Докажите, что сумма трёх последовательных натуральных чисел всегда делится на 3.
Доказательство:
Первый способ. Обозначим произвольное натуральное число буквой n. Тогда следующие за ним натуральные числа будут n + 1 и n + 2. Их сумма равна:
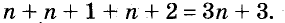
Числа 3 и Зn при каждом натуральном n делятся на 3. Итак, какое бы ни было натуральное число n, сумма 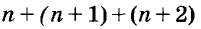 всегда делится на 3. Что и требовалось доказать.
всегда делится на 3. Что и требовалось доказать.
Второй способ. Если n — второе из трёх последовательных целых чисел, то первое из них n – 1, а третье — n + 1. Тогда 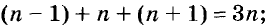 число 3n делится на 3.
число 3n делится на 3.
Пример:
Докажите, что разность чисел  делится на 99.
делится на 99.
Запись 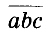 означает трёхзначное число, содержащее а сотен, 6 десятков и с единиц
означает трёхзначное число, содержащее а сотен, 6 десятков и с единиц
Доказательство:
Запишем каждое из чисел в виде многочлена, найдём их разность и приведём подобные слагаемые.
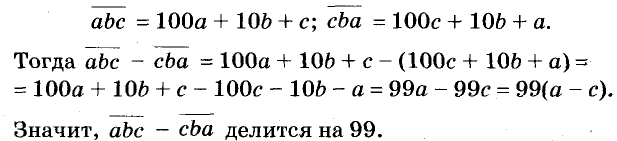
Умножение многочлена на одночлен
Умножим двучлен а + b на одночлен m. По распределительному закону умножения
Так же можно умножить произвольный многочлен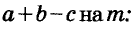
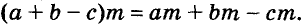
Каждое из этих равенств — тождество. Если в любое из них вместо любой переменной написать то же самое выражение, то снова получим тождество:
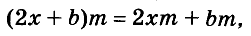
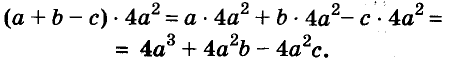
Чтобы умножить многочлен на одночлен, нужно каждый член .многочлена умножить на данный одночлен и результаты сложить.
По этому правилу можно также умножить одночлен на многочлен, так как множители можно менять местами.
Пример:
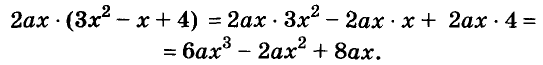
При положительных значениях а, b, m равенство 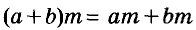 можно проиллюстрировать геометрически (рис. 38). Площадь прямоугольника с основанием m и высотой а + b равна сумме площадей двух прямоугольников, основания которых а и b, а высота — m.
можно проиллюстрировать геометрически (рис. 38). Площадь прямоугольника с основанием m и высотой а + b равна сумме площадей двух прямоугольников, основания которых а и b, а высота — m.
В алгебре равенство 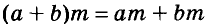 считается верным не только для положительных чисел а, b, m, но и для отрицательных и любых других чисел и даже выражений. В частности, если вместо переменной b подставить выражение -с или с – d, то будем иметь:
считается верным не только для положительных чисел а, b, m, но и для отрицательных и любых других чисел и даже выражений. В частности, если вместо переменной b подставить выражение -с или с – d, то будем иметь:
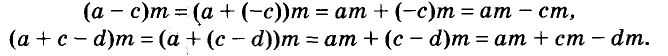
Значит, 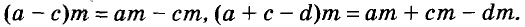
Каждое из этих равенств — тождество, то есть равенство верно для произвольных чисел и выражений а, b, с, d, m.
Пример:
Выполните умножение 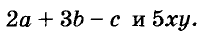
Решение:
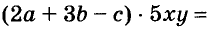
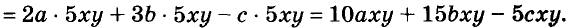
Пример:
Решите уравнение: 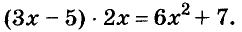
Решение:
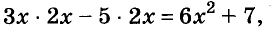

Ответ.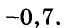
Пример:
Один брат старше второго на 6 лет, а 3 года назад он был вдвое старше брата. Сколько лет каждому из них?
Решение:
Если младшему брату х лет, то старшему — (x + 6) лет. Три года назад младшему было (х – 3), а старшему — (х + 6 – 3) года. Тогда старший брат был вдвое старше младшего, значит,
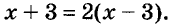
Решим это уравнение:
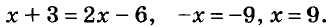
Если младшему брату 9 лет, то старшему — 9 + 6 = 15.
Ответ. 9 лет и 15 лет.
Умножение многочленов
Умножим многочлен a + b-с на х + у. Если обозначим многочлен х + у одной буквой m, то будем иметь:
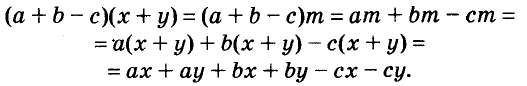
Значит, 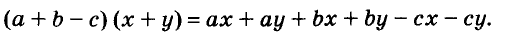
Если бы мы сначала умножили а на х и у, потом b на х и у, наконец — с на х и у, то есть каждый член первого многочлена на каждый член второго многочлена, и полученные произведения сложили, то имели бы тот же результат: ax + ay + bx + by-cx- су.
Чтобы умножить многочлен на многочлен, надо каждый член первого многочлена умножить на каждый член второго многочлена и полученные произведения сложить.
Пример.
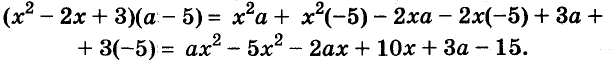
Умножать многочлены можно двумя способами, которые соответствуют таким схемам:
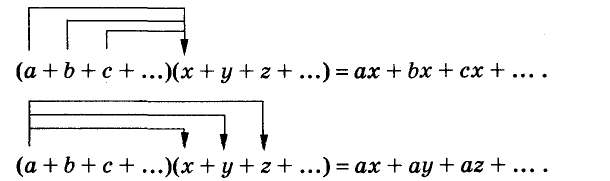
Если нужно выполнить умножение более двух многочленов, то сначала умножают первые два из них, потом полученный результат умножают на третий многочлен и т. д. Для примера выполним умножение многочленов 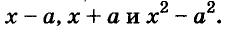
Следовательно, 
Тождество 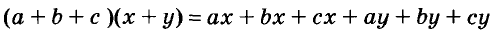 для положительных значений переменных соответствует рисунку 40. Ведь если стороны прямоугольника соответственно равны
для положительных значений переменных соответствует рисунку 40. Ведь если стороны прямоугольника соответственно равны 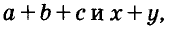 то его площадь будет равна:
то его площадь будет равна:
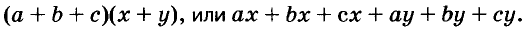
Итак, эти два выражения тождественно равны.
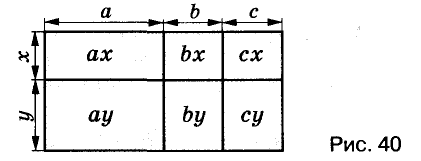
В алгебре равенство 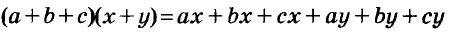 считается верным при условии, что его буквы обозначают не только положительные числа, но и любые числа или выражения.
считается верным при условии, что его буквы обозначают не только положительные числа, но и любые числа или выражения.
Обратите внимание: если трёхчлен умножить на двучлен, то в результате будем иметь шестичлен. Если умножить многочлены, в которых соответственно k и р членов, то получим многочлен, имеющий 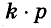 членов. Только после приведения подобных слагаемых количество членов произведения может уменьшиться. Например,
членов. Только после приведения подобных слагаемых количество членов произведения может уменьшиться. Например,
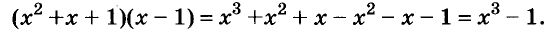
Пример:
Выполните умножение многочленов 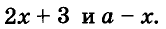
Решение:
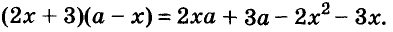
Пример:
Упростите выражение: 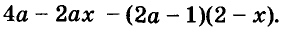
Решение:
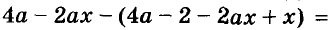
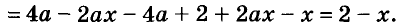
Исторические сведения:
Выражения с переменными появились тогда, когда числа начали обозначать не только цифрами, но и буквами. Первые такие обозначения встречаются у Диофанта (III в.), но они не получили широкого распространения. Не сразу установились для общего употребления и знаки действий. Египтяне действия сложения и вычитания обозначали рисунком, подобным двум ногам, идущим в разных направлениях. Они писали справа налево.
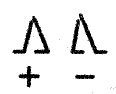
Степени чисел и выражений раньше называли, пользуясь словами квадрат и куб. Например:

Некоторые европейские математики XV в. «плюс» и «минус» обозначали буквами p и m — первыми буквами латинских слов plus и minus. Знаки «+» и «-» ввёл в 1489 г. И. Вид-ман, знак умножения  — У. Оутред. Знаки умножения
— У. Оутред. Знаки умножения  и и деления
и и деления  ввёл Г. Лейбниц.
ввёл Г. Лейбниц.
Первая книга по математике, напечатанная в России,— «Арифметика» JI. Магницкого (1703 г.). В ней двучлены, которые теперь принято писать 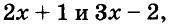 записывались так:
записывались так: 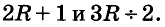 Квадрат переменной обозначался буквой q, коэффициент 1 не опускался. Умножать такие выражения предлагалось столбиком.
Квадрат переменной обозначался буквой q, коэффициент 1 не опускался. Умножать такие выражения предлагалось столбиком.
Скобки для записи математических выражений европейские математики начали употреблять в XVI в. Сначала ввели квадратные скобки, позже — круглые и фигурные.
Ещё до середины XX в. для записи выражений использовали не только круглые скобки, но и квадратные и фигурные. Писали, например, так:
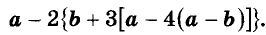 Современные математические термины и символы хорошо упорядочены намного удобнее прежних.
Современные математические термины и символы хорошо упорядочены намного удобнее прежних.
Напомню:
Произведение нескольких одинаковых множителей называют степенью.
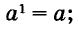
Если 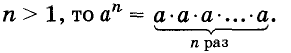
Свойства степеней для натуральных m и n:
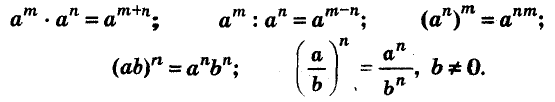
Выражения бывают числовые и с переменными. Если выражение не содержит никаких других действий, кроме сложения, вычитания, умножения, возведения в степень и деления, его называют рациональным выражением. Рациональное выражение, не содержащее действия деления на выражение с переменной, называют целым выражением.
Два целых выражения, соответствующие значения которых равны при любых значениях переменных, называют тождественно равными, или тождественными. Два тождественно равных выражения, соединённые знаком равенства, образовывают тождество.
Простейшие выражения — числа, переменные, их степени или произведения. Их называют одночленами.
Чтобы выполнить умножение одночленов, между ними ставят знак умножения и полученное произведение приводят к одночлену стандартного вида. Чтобы возвести одночлен в степень, нужно возвести в эту степень каждый множитель одночлена и найденные степени перемножить.
Сумму нескольких одночленов называют многочленом. Для удобства каждый одночлен также считают многочленом.
Складывая многочлены, пользуются правилом раскрытия скобок.
Чтобы умножить многочлен на одночлен, нужно каждый член многочлена умножить на данный одночлен и результаты сложить. Чтобы умножить многочлен на многочлен, нужно каждый член первого многочлена умножить на каждый член второго и полученные произведения сложить.
Целые выражения
- В этом параграфе вы научитесь упрощать выражения, познакомитесь с формулами и приемами, помогающими облегчить работу по преобразованию выражений. Вы узнаете, что возведение числа в квадрат и куб – частные случаи нового арифметического действия. Вы научитесь классифицировать алгебраические выражения.
- Слова «определение» и «теорема» станут для вас привычными и понятными.
Тождественно равные выражения. Тождества
Рассмотрим две пары выражений:

В следующих таблицах приведены значения этих выражений при некоторых значениях переменной 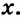
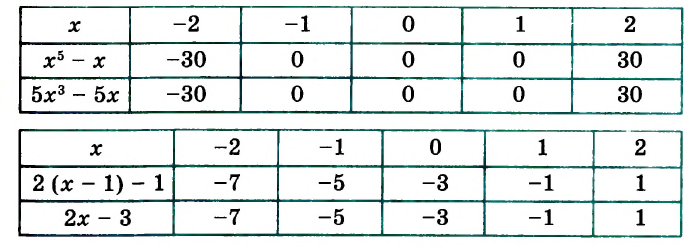
Мы видим, что эти значения совпадают для каждой отдельно взятой пары выражений.
Сохранится ли подмеченная закономерность при любых других значениях 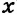 ?
?
Для выражений, записанных в первой таблице, ответ на этот вопрос отрицательный: если, например,  то
то 
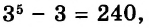 а
а 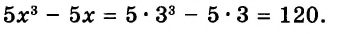
А вот значения выражений, записанных во второй таблице, совпадают при любых значениях 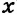 . Покажем это.
. Покажем это. 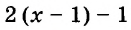 то есть после упрощения выражение 2 (jc — 1) — 1 «превратилось» в выражение
то есть после упрощения выражение 2 (jc — 1) — 1 «превратилось» в выражение
Определение. Выражения, соответственные значения которых равны при любых значениях переменных, называют тождественно равными.
Например, выражения 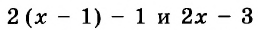 — тождественно равные, а выражения
— тождественно равные, а выражения  тождественно равными не являются.
тождественно равными не являются.
Вот еще примеры тождественно равных выражений:
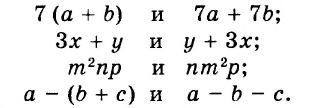
Рассмотрим равенство 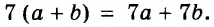 В силу распределительного свойства умножения оно верно при любых значениях переменных
В силу распределительного свойства умножения оно верно при любых значениях переменных 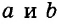 .
.
Определение. Равенство, верное при любых значениях переменных, входящих в него, называют тождеством.
Из пары тождественно равных выражений легко конструируется тождество.
Например, все равенства
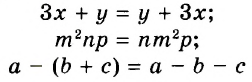
являются тождествами.
Заметим, что с тождествами вы встречались и раньше. Так, равенства, выражающие свойства сложения и умножения чисел, являются примерами тождеств:
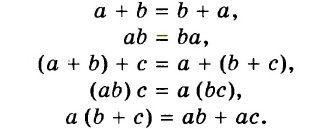
Найдем значение выражения 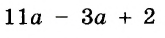 при
при 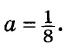
Конечно, можно сразу в это выражение вместо а подставить число 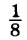 и найти значение числового выражения
и найти значение числового выражения 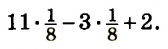 Однако гораздо удобнее вначале привести подобные слагаемые, заменив данное выражение
Однако гораздо удобнее вначале привести подобные слагаемые, заменив данное выражение 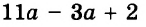 на тождественно равное:
на тождественно равное: 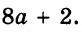 . При
. При 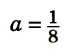 имеем:
имеем: 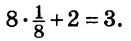
Замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения.
Приведение подобных слагаемых и раскрытие скобок — примеры тождественных преобразований выражений. Упрощая выражение, мы фактически заменяем его на более простое, тождественно равное ему.
Доказать тождество — это значит доказать, что данное равенство является тождеством.
Для доказательства тождеств используют такие приемы (методы):
- тождественно преобразуют одну из частей данного равенства, получая другую часть;
- тождественно преобразуют каждую из частей данного равенства, получая одно и то же выражение;
- показывают, что разность левой и правой частей данного равенства тождественно равна нулю.
Пример:
Докажите тождество:
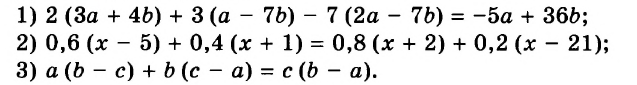
Решение:
1) Упростим левую часть тождества, которое требуется доказать:
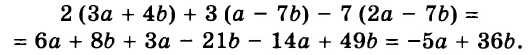
Тождество доказано.
2) Упростим левую и правую части тождества, которое требуется доказать:
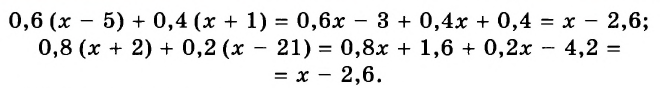
Тождество доказано.
3) Рассмотрим разность левой и правой частей тождества, которое требуется доказать:
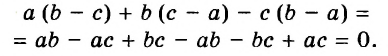
Тождество доказано.
Пример:
Докажите, что равенство 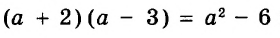 не является тождеством.
не является тождеством.
Решение:
Чтобы доказать, что равенство не является тождеством, достаточно привести контрпример: указать такое значение переменной (переменных), при котором данное равенство не выполняется.
Например, при 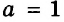 имеем:
имеем:
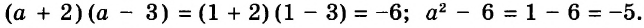
Следовательно, данное равенство не является тождеством.
Степень с натуральным показателем
Как вы знаете, в математике придумали способ коротко записывать произведение, все множители которого равны.
Например, 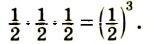
Выражение 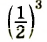 называют степенью, число
называют степенью, число 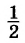 — основанием степени, а число 3 — показателем степени.
— основанием степени, а число 3 — показателем степени.
Определение. Степенью числа 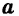 с натуральным показателем
с натуральным показателем  , большим 1, называют произведение
, большим 1, называют произведение  множителей, каждый из которых равен
множителей, каждый из которых равен 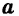 .
.
Степень с основанием 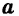 и показателем
и показателем 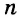 обозначают
обозначают 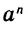 и читают: «
и читают: «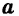 в
в 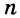 -й степени».
-й степени».
Степени с показателями 2 и 3 можно прочитать иначе: запись 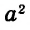 читают «
читают «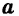 в квадрате», запись
в квадрате», запись 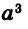 — «
— «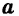 в кубе».
в кубе».
Обратите внимание, что в определении степени на показатель 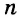 наложено ограничение
наложено ограничение 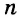 > 1. И это понятно: ведь не принято рассматривать произведение, состоящее из одного множителя.
> 1. И это понятно: ведь не принято рассматривать произведение, состоящее из одного множителя.
А может ли показатель степени быть равным 1? Ответ на этот вопрос дает следующее
Определение. Степенью числа 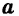 с показателем 1 называют само это число.
с показателем 1 называют само это число.
Замечание. Это определение позволяет любое число считать степенью с показателем 1.
Итак, из приведенных определений следует, что
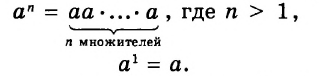
Легко подсчитать, что, например, 25 = 32. В таких случаях говорят, что число 2 возвели в пятую степень и получили 32. Также можно сказать, что выполнили действие возведения в пятую степень числа 2.
Равенство (-3)2 = 9 означает, что число -3 возвели в квадрат и получили 9, а равенство (-3)3 = -27 означает, что число -3 возвели в куб и получили -27.
Заметим, что алгебраическое выражение может быть сконструировано не только с помощью действий сложения, вычитания, умножения и деления, но и действия возведения в степень.
Очевидно, что если  то
то  если
если 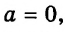 то
то 
Итак, при возведении неотрицательного числа в степень получаем, неотрицательное число.
При возведении отрицательного числа в степень возможны два случая.
Если показатель степени — четное число, то при возведении в степень множители можно разбить на пары.
Например, 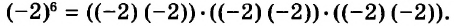
Если же показатель степени — число нечетное, то один множитель останется без пары.
Например, 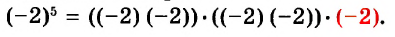
Поскольку каждые два отрицательных множителя в произведении дают положительное число, то верно следующее утверждение:
при возведении отрицательного числа в степень с четным показателем получаем положительное число, а при возведении отрицательного числа в степень с нечетным показателем получаем отрицательное число.
Можно ли, например, число 5 возвести в степень 0 или в степень -2? Можно. Как это сделать, вы узнаете в следующем учебном году.
Пример:
Решите уравнение 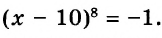
Решение:
Так как при возведении в степень с четным показателем любого числа, кроме 0, получаем положительное число, то данное уравнение не имеет корней.
Ответ: корней нет.
Пример:
Докажите, что значение выражения  делится нацело на 3.
делится нацело на 3.
Решение:
Запись значения выражения 10200 состоит из цифры 1 и двухсот цифр 0, а запись значения выражения 10200 + 2 — из цифры 1, цифры 2 и ста девяноста девяти цифр 0. Следовательно, сумма цифр числа равна 3 и само число делится нацело на 3.
Пример:
Докажите, что значение выражения  делится нацело на 10 при любом четном значении
делится нацело на 10 при любом четном значении  .
.
Решение:
Если 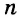 — четное число, то последней цифрой выражения
— четное число, то последней цифрой выражения 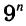 является единица, а последней цифрой значения выражения
является единица, а последней цифрой значения выражения 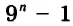 — нуль. Следовательно, значение выражения
— нуль. Следовательно, значение выражения 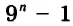 делится нацело на 10 при любом четном значении
делится нацело на 10 при любом четном значении 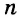 .
.
Свойства степени с натуральным показателем
Рассмотрим произведение двух степеней с одинаковыми основаниями, например, 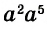 . Это выражение можно представить в виде степени с основанием
. Это выражение можно представить в виде степени с основанием  :
:
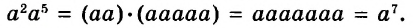
Значит, 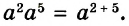
Аналогично легко убедиться в том, что, например,
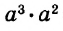
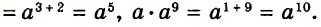
Прослеживается закономерность: 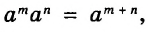 , где
, где 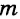 и
и 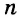 — произвольные натуральные числа.
— произвольные натуральные числа.
Однако никакое количество конкретных примеров не может гарантировать, что приведенное равенство верно для любых натуральных  Истинность его можно установить только путем доказательства.
Истинность его можно установить только путем доказательства.
В математике утверждение, справедливость которого устанавливается с помощью доказательства, называют теоремой.
Теорема 1. Для любого числа а и любых натуральных чисел  справедливо равенство:
справедливо равенство:
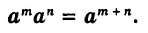
Доказательство. Для  и
и  имеем:
имеем:
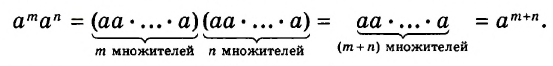
Если, например,  и
и  , то
, то
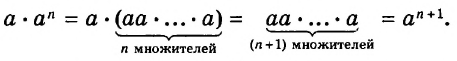
Случаи, когда  и
и 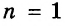 или когда
или когда 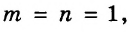 рассмотрите самостоятельно.
рассмотрите самостоятельно.
Тождество 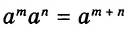 выражает основное свойство степени.
выражает основное свойство степени.
Аналогичное свойство имеет место для произведения трех и более степеней. Например,
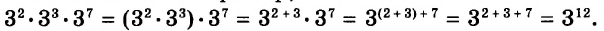
Итак, при умножении степеней с одинаковыми основаниями показатели складывают, а основание оставляют прежним.
Рассмотрим выражение 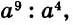 где
где  Оно является частным двух степеней с одинаковыми основаниями. Так как
Оно является частным двух степеней с одинаковыми основаниями. Так как 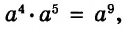 то по определению частного
то по определению частного 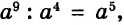 то есть
то есть 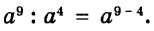 Этот пример подсказывает, что имеет место такая
Этот пример подсказывает, что имеет место такая
Теорема 2. Для любого числа  , отличного от нуля, и любых натуральных чисел
, отличного от нуля, и любых натуральных чисел  таких, что
таких, что  справедливо равенство:
справедливо равенство:
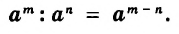
Доказательство. Рассмотрим произведение степеней 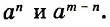 Используя основное свойство степени, имеем:
Используя основное свойство степени, имеем:
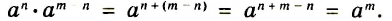
Тогда по определению частного
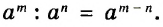
Из этой теоремы следует такое правило:
при делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя, а основание оставляют прежним.
Рассмотрим выражение 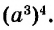 . Оно является степенью с основанием
. Оно является степенью с основанием 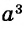 и показателем 4. Поэтому
и показателем 4. Поэтому
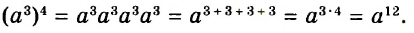
Этот пример подсказывает, что справедлива следующая
Теорема 3. Для любого числа а и любых натуральных чисел тип справедливо равенство:
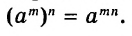
Доказательство. Очевидно, что для 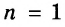 доказываемое равенство верно.
доказываемое равенство верно.
Для 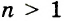 имеем:
имеем:
Из этой теоремы следует такое правило:
при возведении степени в степень показатели перемножают, а основание оставляют прежним.
Например, 
Покажем, как можно преобразовать степень произведения, например, выражение 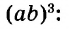
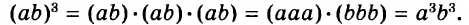
В общем случае справедлива следующая
Теорема 4. Для любых чисел  и любого натурального числа
и любого натурального числа  справедливо равенство:
справедливо равенство:
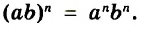
Доказательство. Очевидно, что для  доказываемое равенство верно. Для
доказываемое равенство верно. Для  имеем:
имеем:
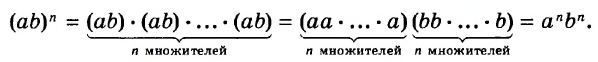
Аналогичное свойство имеет место и для произведения трех или более множителей. Например, 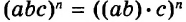
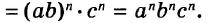
Итак, при возведении произведения в степень каждый множитель возводят в степень и полученные результаты перемножают.
Пример:
Упростите выражение: 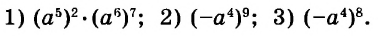
Решение:
1) Применив последовательно правило возведения степени в степень и правило умножения степеней с одинаковыми основаниями, имеем:
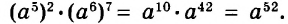
2) Так как 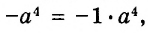 то, применив правило возведения произведения в степень, получим:
то, применив правило возведения произведения в степень, получим:
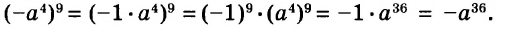
3) Аналогично предыдущему примеру, учитывая, что 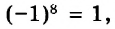 получаем
получаем 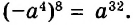
Пример:
Представьте в виде степени выражение 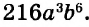
Решение:
Имеем: 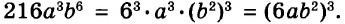
Пример:
Найдите значение выражения 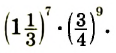
Решение:
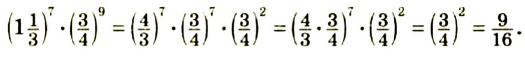
Пример:
Сравните значения выражений:
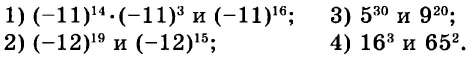
Решение:
1) Имеем: 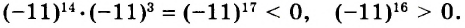
Следовательно, 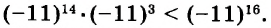
2) Так как 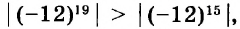 а сравниваемые числа отрицательные, то
а сравниваемые числа отрицательные, то 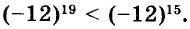
3) Так как 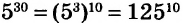 и
и 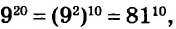 то
то 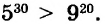
4) Имеем: 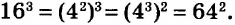 Следовательно,
Следовательно, 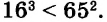
Пример:
Какой цифрой оканчивается значение выражения 
Решение:
Имеем: 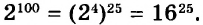
Если число оканчивается цифрой 6, то любая его степень оканчивается цифрой 6.
Одночлены
Рассмотрим выражения:
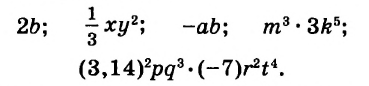
Каждое из них представляет собой произведение чисел, переменных и их степеней. Такие выражения называют одночленами.
Договорились также считать одночленами все числа, любые переменные и их степени. Например, одночленами являются:
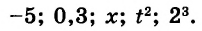
Заметим, что, например, выражения
одночленами не являются, так как они, кроме умножения и возведения в степень, содержат и другие действия.
При взгляде на одночлен  возникает естественное желание его упростить. Имеем:
возникает естественное желание его упростить. Имеем:
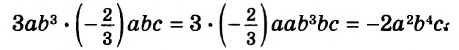
Полученный одночлен содержит только один числовой множитель, отличный от нуля, который стоит на первом месте. Все остальные множители — это степени с различными основаниями. Такой вид одночлена называют стандартным видом одночлена.
Приведем еще примеры одночленов стандартного вида:
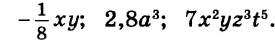
Отметим, что, например, выражения 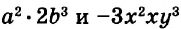 не являются одночленами стандартного вида. Действительно, хотя первое из них и имеет единственный числовой множитель, но он не стоит на первом месте. Во втором выражении степень с основанием
не являются одночленами стандартного вида. Действительно, хотя первое из них и имеет единственный числовой множитель, но он не стоит на первом месте. Во втором выражении степень с основанием 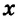 встречается дважды.
встречается дважды.
Однако эти одночлены легко привести (преобразовать) к стандартному виду:
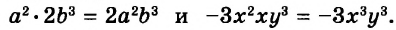
К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени. Так, 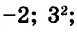
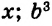 — одночлены стандартного вида.
— одночлены стандартного вида.
Число 0, а также одночлены, тождественно равные нулю, например, 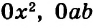 и т. д., называют нуль-одночленами. Их не относят к одночленам стандартного вида.
и т. д., называют нуль-одночленами. Их не относят к одночленам стандартного вида.
Определение. Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
Например, коэффициенты одночленов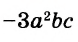 и
и 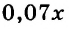 соответственно равны -3 и 0,07.
соответственно равны -3 и 0,07.
Вообще, любой одночлен стандартного вида имеет коэффициент. И даже, например, у одночленов 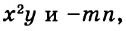 при записи которых числовой множитель не используется, коэффициентами являются числа 1 и -1 соответственно. И это понятно, ведь
при записи которых числовой множитель не используется, коэффициентами являются числа 1 и -1 соответственно. И это понятно, ведь 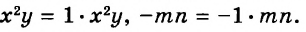
Рассмотрим одночлены 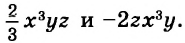 У них одинаковые буквенные части. Такие одночлены называют подобными. К подобным одночленам также относят и числа. Например, 7 и -5 — подобные одночлены.
У них одинаковые буквенные части. Такие одночлены называют подобными. К подобным одночленам также относят и числа. Например, 7 и -5 — подобные одночлены.
Обратим внимание на то, что, например, у одночленов 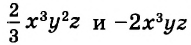 буквенные части неодинаковы, хотя и состоят из одних и тех же переменных. Поэтому они не являются подобными.
буквенные части неодинаковы, хотя и состоят из одних и тех же переменных. Поэтому они не являются подобными.
Определение. Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него. Степень одночлена, который является числом, отличным от нуля, считают равной нулю.
Считают, что нуль-одночлен степени не имеет.
Например, степень одночлена 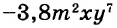 равна 10, а степени одночленов
равна 10, а степени одночленов 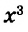 и 9 равны соответственно 3 и 0.
и 9 равны соответственно 3 и 0.
Рассмотрим два одночлена 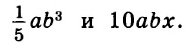 Одночлен
Одночлен 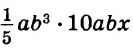 является их произведением. Упростим его:
является их произведением. Упростим его:
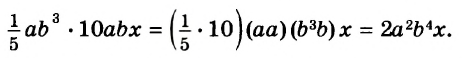
Итак, произведение двух одночленов — это одночлен. Его, как правило, записывают в стандартном виде.
При возведении одночлена в степень также получают одночлен. Возведем, например, в четвертую степень одночлен 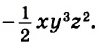 Имеем:
Имеем:
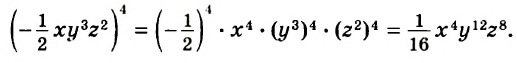
Пример:
Упростите выражение 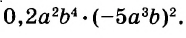
Решение:
Имеем:
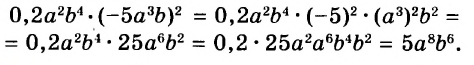
Пример:
Значения переменных  и
и 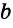 таковы, что
таковы, что 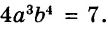 Найдите значение выражения
Найдите значение выражения 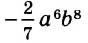 при этих же значениях переменных.
при этих же значениях переменных.
Решение:
Имеем:
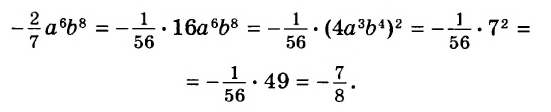
Многочлены
В предыдущем пункте вы узнали, что произведение одночленов является одночленом. Иначе обстоит дело с суммой и разностью одночленов. Например, выражения 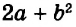 и
и 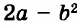 не являются одночленами. Они представляют собой соответственно сумму и разность одночленов
не являются одночленами. Они представляют собой соответственно сумму и разность одночленов 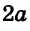 и
и 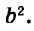 Кстати, выражение
Кстати, выражение 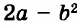 можно представить в виде
можно представить в виде 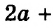
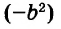 и считать суммой одночленов
и считать суммой одночленов 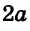 и
и 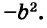
Определение. Выражение, которое является суммой нескольких одночленов, называют многочленом.
Приведем еще примеры многочленов: 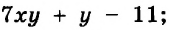
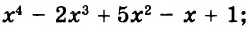
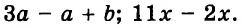
Одночлены, из которых составлен многочлен, называют членами многочлена. Так, членами многочлена 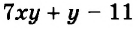 являются одночлены
являются одночлены 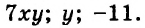
Многочлен, состоящий из двух членов, называют двучленом, а состоящий из трех членов — трехчленом. Договорились рассматривать одночлен как частный случай многочлена. Считают, что такой многочлен состоит из одного члена.
Связи между многочленами, одночленами и их частным видом — числами иллюстрирует схема, изображенная на рисунке 3.
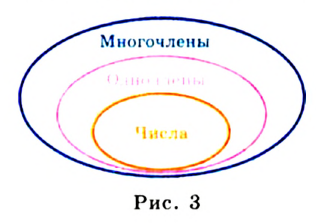
Если среди одночленов, составляющих многочлен, есть подобные, то их называют подобными членами многочлена.
Например, в многочлене  подобные члены подчеркнуты одинаковым количеством черточек.
подобные члены подчеркнуты одинаковым количеством черточек.
Используя правило приведения подобных слагаемых, упростим этот многочлен:
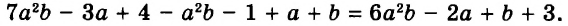
Такое упрощение называют приведением подобных членов многочлена. Это преобразование позволяет заменить многочлен на тождественно равный ему, но более простой — с меньшим количеством членов.
Сложение и вычитание многочленов
Пусть надо сложить два многочлена
 и
и  Для этого возьмем их в скобки и поставим между ними знак «плюс». Затем раскроем скобки и приведем подобные слагаемые (если таковые имеются).
Для этого возьмем их в скобки и поставим между ними знак «плюс». Затем раскроем скобки и приведем подобные слагаемые (если таковые имеются).
Имеем:
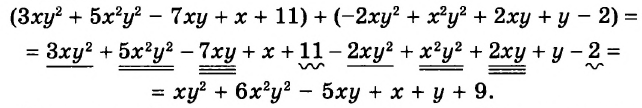
Полученный многочлен является суммой двух данных многочленов.
Пусть теперь требуется из первого данного многочлена вычесть второй. Для этого каждый из многочленов возьмем в скобки и поставим перед вычитаемым знак «минус». Затем раскроем скобки и приведем подобные слагаемые.
Имеем:
Полученный многочлен является разностью двух данных многочленов.
Вообще, при сложении и вычитании многочленов всегда получается многочлен.
Пример:
Докажите, что разность двузначного числа и числа, записанного теми же цифрами, но в обратном порядке, делится надело на 9.
Решение:
Пусть данное число содержит  десятков и
десятков и  единиц. Тогда оно равно
единиц. Тогда оно равно 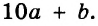
Число, записанное теми же цифрами в обратном порядке, равно 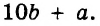
Рассмотрим разность 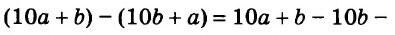
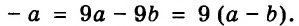
Очевидно, что число 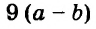 делится нацело на 9.
делится нацело на 9.
Отметим, что запись 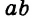 является обозначением двузначного числа, содержащего
является обозначением двузначного числа, содержащего 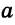 десятков и
десятков и 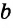 единиц, то есть
единиц, то есть 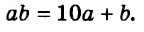
Пример:
Докажите, что разность 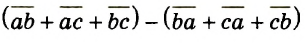 делится нацело на 18. Решение:
делится нацело на 18. Решение:
Имеем:
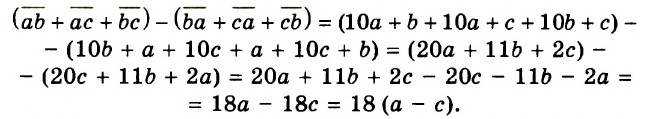
Очевидно, что число 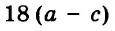 делится нацело на 18.
делится нацело на 18.
Пример:
Докажите, что сумма четырех последовательных четных натуральных чисел не делится нацело на 8.
Решение:
Пусть первое из этих чисел равно 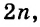 где
где 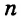 — произвольное натуральное число. Тогда следующими тремя числами являются
— произвольное натуральное число. Тогда следующими тремя числами являются 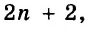
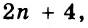
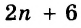 соответственно.
соответственно.
Рассматриваемая сумма имеет вид
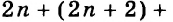
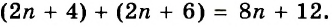
Первое слагаемое 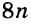 суммы
суммы 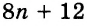 делится нацело на 8, а второе слагаемое 12 — не делится. Следовательно, сумма
делится нацело на 8, а второе слагаемое 12 — не делится. Следовательно, сумма 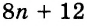 не делится нацело на 8.
не делится нацело на 8.
- Заказать решение задач по высшей математике
Умножение одночлена на многочлен
Умножим одночлен 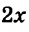 на многочлен
на многочлен 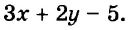 Для этого запишем произведение
Для этого запишем произведение 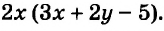 Раскроем скобки, применив распределительное свойство умножения. Имеем:
Раскроем скобки, применив распределительное свойство умножения. Имеем:
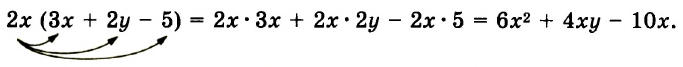
Полученный многочлен 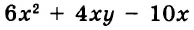 является произведением одночлена
является произведением одночлена 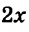 и многочлена
и многочлена 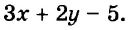
Вообще, произведение одночлена и многочлена всегда можно представить в виде многочлена.
Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить.
Для произведения одночлена и многочлена справедливо переместительное свойство умножения. Поэтому приведенное правило позволяет умножать многочлен на одночлен.
Пример:
Упростите выражение 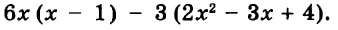
Решение:
Имеем:
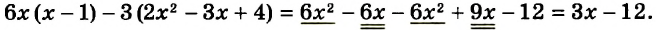
Пример:
Решите уравнение 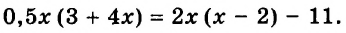
Решение:
Имеем:
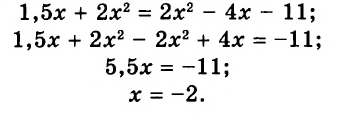
Ответ: -2.
Пример:
Решите уравнение 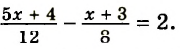
Решение:
Умножив обе части данного уравнения на число 24, являющееся наименьшим общим знаменателем дробей, содержащихся в этом уравнении, получаем:
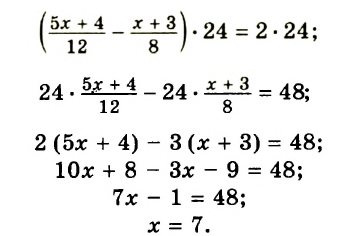
Ответ: 7.
Пример:
Докажите, что при любом значении переменной 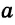 значение выражения
значение выражения 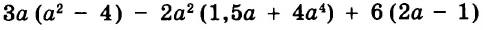 является отрицательным числом.
является отрицательным числом.
Решение:
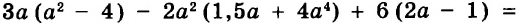
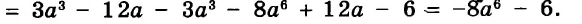
Выражение 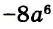 при любом значении
при любом значении 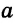 принимает неположительное значение. Следовательно, значение выражения
принимает неположительное значение. Следовательно, значение выражения 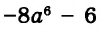 является отрицательным числом при любом значении
является отрицательным числом при любом значении  .
.
Пример:
Остаток при делении натурального числа  на 6 равен 5, а остаток при делении натурального числа
на 6 равен 5, а остаток при делении натурального числа 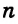 на 4 равен 2. Докажите, что значение выражения
на 4 равен 2. Докажите, что значение выражения 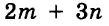 делится нацело на 4 и не делится нацело на 12.
делится нацело на 4 и не делится нацело на 12.
Решение:
Пусть неполное частное от деления 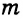 на 6 равно
на 6 равно 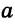 , а от деления
, а от деления 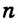 на 4 равно
на 4 равно 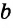 . Тогда
. Тогда 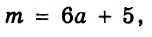
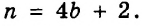 Следовательно,
Следовательно,
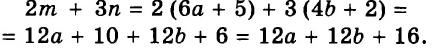
Каждое слагаемое полученной суммы делится нацело на 4, поэтому и сумма делится нацело на 4.
Первые два слагаемых делятся нацело на 12, а третье — не делится. Поэтому и сумма не делится нацело на 12.
Умножение многочлена на многочлен
Научимся умножать два многочлена на примере произведения 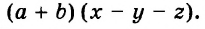 Обозначим второй множитель буквой
Обозначим второй множитель буквой  . Тогда
. Тогда
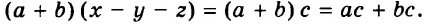
Теперь в выражение 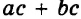 подставим вместо
подставим вместо 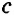 многочлен
многочлен 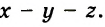 Запишем:
Запишем:
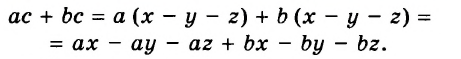
Полученный многочлен и является искомым произведением.
Этот же результат можно получить, если произведение находить по схеме: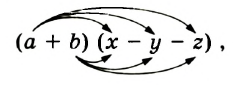
которая разъясняет следующее правило:
чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.
Таким образом, при умножении многочлена на многочлен всегда получаем многочлен.
Пример:
Упростите выражение 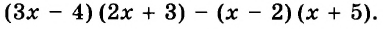
Решение:
Имеем:
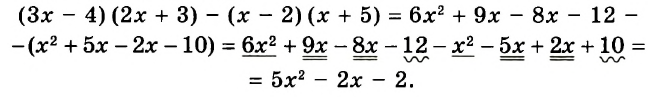
Пример:
Представьте в виде многочлена выражение: 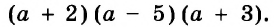
Решение:
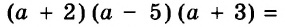
Пример:
Найдите четыре последовательных натуральных числа таких, что произведение третьего и четвертого из них на 38 больше произведения второго и первого.
Решение:
Пусть меньшее из этих чисел равно 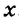 , тогда три следующие за ним числа будут равны
, тогда три следующие за ним числа будут равны 
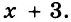 Так как по условию произведение
Так как по условию произведение 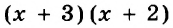 на 38 больше, чем произведение
на 38 больше, чем произведение 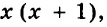 то:
то:
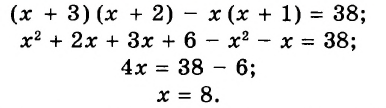
Следовательно, искомыми числами являются 8, 9, 10 и 11.
Ответ: 8, 9, 10, 11.
Пример:
Докажите, что значение выражения 
кратно 7 при всех натуральных значениях 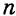 .
.
Решение:
Выполним преобразование:
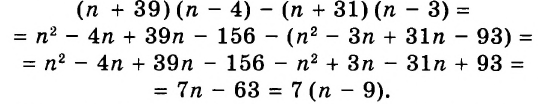
Следовательно, данное выражение можно представить в виде произведения двух множителей, один из которых равен 7, а второй принимает только целые значения. Этот факт доказывает утверждение задачи.
Разложение многочленов на множители. Вынесение общего множителя за скобки
Умножим два многочлена 
Имеем: 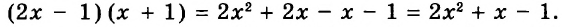
Получили тождество 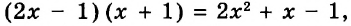 которое можно записать и так:
которое можно записать и так: 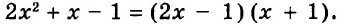
О такой записи говорят, что многочлен 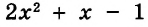 разложили на множители
разложили на множители 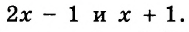
Вообще, представление многочлена в виде произведения нескольких многочленов называют разложением многочлена на множители.
Разложение многочлена на множители является ключом к решению многих задач. Например, каждое из уравнений 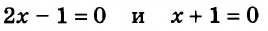 решить очень легко, а вот уравнение
решить очень легко, а вот уравнение 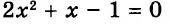 вы пока решать не умеете. Однако, если воспользоваться разложением многочлена
вы пока решать не умеете. Однако, если воспользоваться разложением многочлена 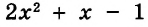 на множители, то можно записать:
на множители, то можно записать: 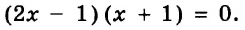
Отсюда 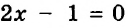 или
или 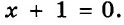 Искомыми корнями являются числа 0,5 и -1.
Искомыми корнями являются числа 0,5 и -1.
Таким образом, разложение многочлена на множители позволило свести решение сложного уравнения к решению двух более простых.
Существует немало приемов разложения многочлена на множители. Самый простой из них — вынесение общего множителя за скобки.
Это преобразование вам уже знакомо. Например, значение выражения 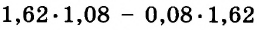 находили так:
находили так: 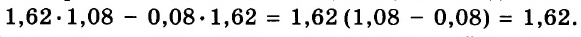
Здесь использовано распределительное свойство умножения 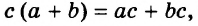 прочитанное справа налево:
прочитанное справа налево: 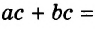
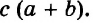
Воспользуемся этой идеей в следующих примерах.
Пример:
Разложите на множители:
Решение:
1) Одночлены 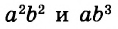 содержат такие общие множители:
содержат такие общие множители: 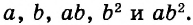 Любой из этих множителей можно вынести за скобки. Но обычно выбирают такой общий множитель, чтобы члены многочлена, остающегося в скобках, не имели общего буквенного множителя. Такие соображения подсказывают, что надо вынести за скобки общий множитель
Любой из этих множителей можно вынести за скобки. Но обычно выбирают такой общий множитель, чтобы члены многочлена, остающегося в скобках, не имели общего буквенного множителя. Такие соображения подсказывают, что надо вынести за скобки общий множитель 
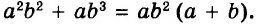
Чтобы проверить, правильно ли разложили многочлен на множители, надо эти множители перемножить.
2) Если коэффициенты многочлена — целые числа, то за скобки обычно выносят наибольший общий делитель модулей этих коэффициентов (в нашем примере это число 4:
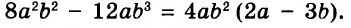
3) Имеем: 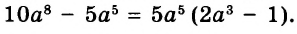
Пример:
Представьте в виде произведения многочленов выражение:

Решение:
1) В данном случае общим множителем является многочлен 
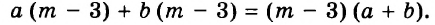
2) Имеем:
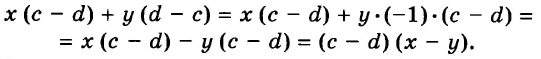
3) Имеем:
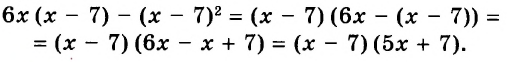
Пример:
Вынесите за скобки общий множитель в выражении
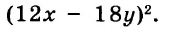
Решение:
Имеем:
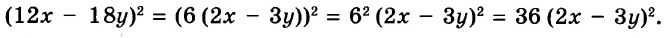
Пример:
Решите уравнение:
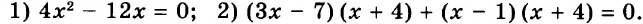
Решение:
1) Разложив левую часть уравнения на множители и применив условие, согласно которому произведение равно нулю, имеем:
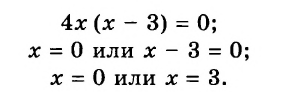
Ответ: 0; 3.
2) Имеем:
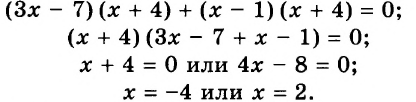
Ответ: -4; 2.
Пример:
Докажите, что значение выражения:
1)  делится надело на 14; 2 )
делится надело на 14; 2 ) 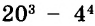 делится надело на 121.
делится надело на 121.
Решение:
1) Представим выражения  в виде степеней с основанием 2 и вынесем за скобки общий множитель. Получим:
в виде степеней с основанием 2 и вынесем за скобки общий множитель. Получим:
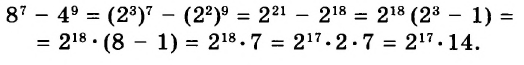
Данное выражение равно произведению двух натуральных чисел, одним из которых является 14. Отсюда следует, что значение выражения  делится нацело на 14.
делится нацело на 14.
2) Имеем:
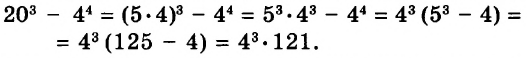
Следовательно, значение данного выражения делится нацело на 121.
Пример:
При каком значении 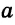 уравнение
уравнение 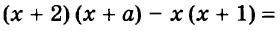
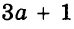 имеет бесконечно много корней?
имеет бесконечно много корней?
Решение:
Имеем:
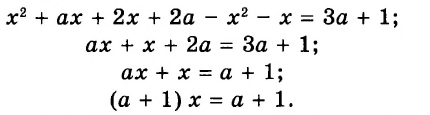
Только при 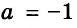 последнее уравнение принимает вид
последнее уравнение принимает вид  и имеет бесконечно много корней.
и имеет бесконечно много корней.
Ответ: при 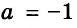 .
.
Разложение многочленов на множители. Метод группировки
Многочлен 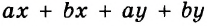 не удастся разложить на множители методом вынесения за скобки общего множителя, так как множителя, общего для всех слагаемых, нет. Однако члены этого многочлена можно объединить в группы так, что слагаемые каждой группы будут иметь общий множитель:
не удастся разложить на множители методом вынесения за скобки общего множителя, так как множителя, общего для всех слагаемых, нет. Однако члены этого многочлена можно объединить в группы так, что слагаемые каждой группы будут иметь общий множитель:
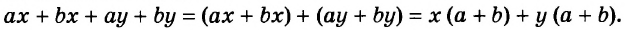
Мы получили выражение, в котором оба слагаемых имеют множитель  Вынесем его за скобки:
Вынесем его за скобки:
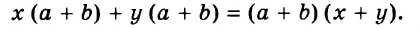
Исходный многочлен удалось разложить на множители благодаря тому, что мы выгодным способом объединили в группы его члены. Поэтому описанный прием называют методом группировки.
Пример:
Разложите на множители многочлен:
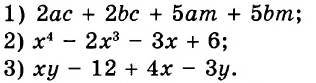
Решение:
1) Сгруппировав члены данного многочлена так, чтобы слагаемые в каждой группе имели общий множитель, получим:
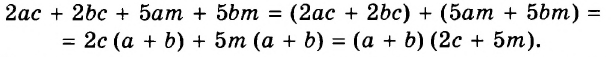
Этот же результат можно получить, если слагаемые сгруппировать другим способом:
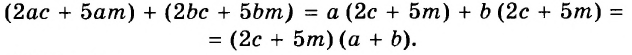
2) Имеем:
3) Имеем:
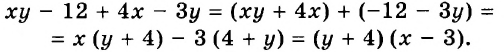
Пример:
Разложите на множители трехчлен 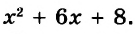
Решение:
Представив слагаемое 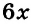 в виде суммы
в виде суммы 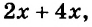 применим метод группировки:
применим метод группировки:
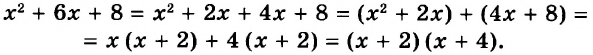
Произведение разности и суммы двух выражений
Нередко в математике помимо знания общего закона (теоремы) удобно пользоваться правилами, применимыми в частных (особых) случаях.
Например, если надо умножить десятичную дробь на 10, 100, 1000 и т. д., то нет необходимости использовать общий алгоритм умножения в столбик, а гораздо выгоднее применить правило переноса запятой.
Особые ситуации встречаются и при умножении многочленов.
Рассмотрим частный случай, когда в произведении двух многочленов один из них представляет собой разность двух выражений, а другой — их сумму.
Имеем:
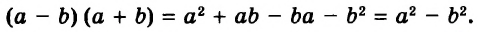
Получили тождество
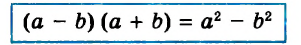
Теперь при умножении разности выражений на их сумму можно сократить работу, сразу записав результат — разность квадратов этих выражений. Поэтому это тождество называют формулой сокращенного умножения:
- произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
Пример:
Выполните умножение многочленов:
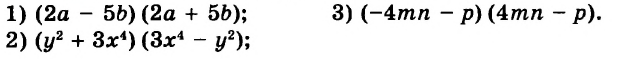
Решение:
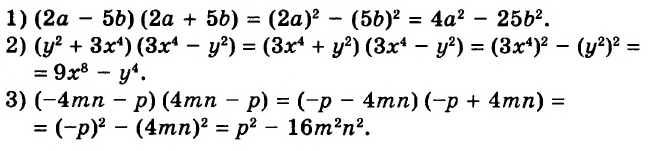
Пример:
Упростите выражение:
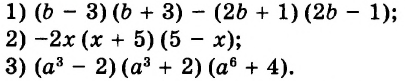
Решение:
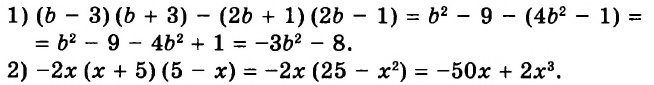
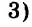 Применив дважды формулу произведения суммы и разности двух выражений, получим:
Применив дважды формулу произведения суммы и разности двух выражений, получим:
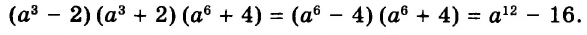
Разность квадратов двух выражений
Вы уже знаете два способа разложения многочленов на множители: вынесение общего множителя за скобки и метод группировки. Рассмотрим еще один способ. Формулу 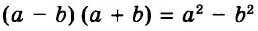 запишем так:
запишем так:
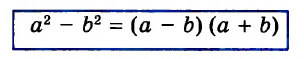
Это тождество называют формулой разности квадратов.
Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.
Приведем примеры применения этой формулы для разложения многочленов на множители.
Пример:
Разложите на множители:
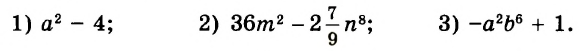
Решение:
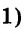 Имеем:
Имеем: 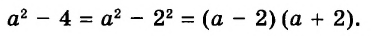
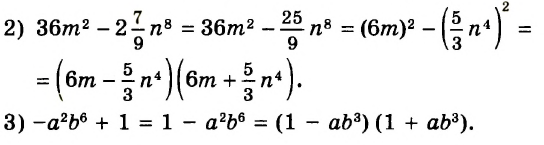
Пример:
Разложите на множители, используя формулу разности квадратов:
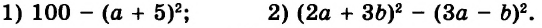
Решение:
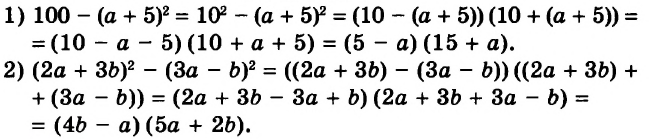
Пример:
Решите уравнение:
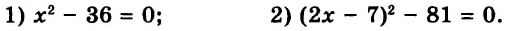
Решение:
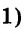 Применив формулу разности квадратов и условие равенства произведения нулю, получим:
Применив формулу разности квадратов и условие равенства произведения нулю, получим:
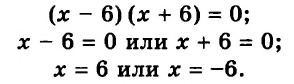
Ответ: 6; -6.
 Имеем:
Имеем:
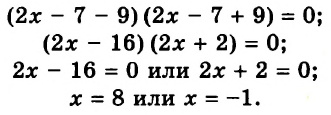
Ответ: 8; -1.
Пример:
Докажите, что при любом натуральном 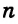 значение выражения
значение выражения 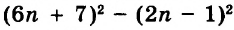 делится нацело на 8.
делится нацело на 8.
Решение:
Имеем:
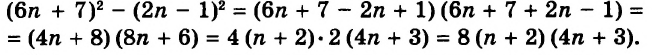
Следовательно, независимо от значения 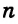 данное выражение можно представить в виде произведения трех множителей, один из которых равен 8, а два других — натуральные числа. Отсюда следует, что значение данного выражения делится нацело на 8 при любом натуральном
данное выражение можно представить в виде произведения трех множителей, один из которых равен 8, а два других — натуральные числа. Отсюда следует, что значение данного выражения делится нацело на 8 при любом натуральном 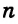 .
.
Квадрат суммы и квадрат разности двух выражений
Преобразуем в многочлен выражение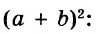
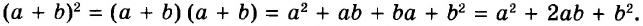
Итак,
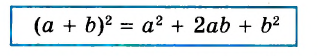
Это тождество называют формулой квадрата суммы и формулируют:
квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения.
Преобразуем в многочлен выражение 
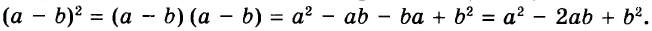
Мы получили формулу квадрата разности:
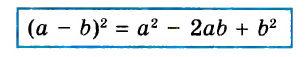
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения.
Заметим, что формулу квадрата разности можно получить с помощью формулы квадрата суммы:
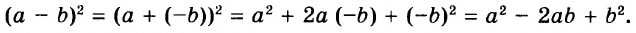
С помощью полученных формул можно проще возводить в квадрат сумму либо разность любых двух выражений, не используя правило умножения двух многочленов. Поэтому их относят к формулам сокращенного умножения.
Пример:
Представьте в виде многочлена выражение:

Решение:
1) По формуле квадрата разности получаем:
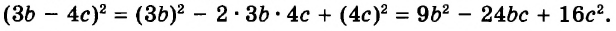
2) По формуле квадрата суммы получаем:
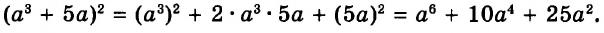
Пример:
Преобразуйте в многочлен выражение:

Решение:
1) Имеем: 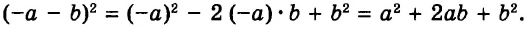
Этот пример можно решить иначе.
Так как 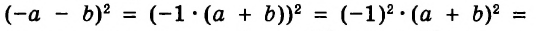
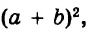 то есть выражения
то есть выражения 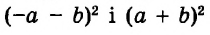 тождественно равны, то:
тождественно равны, то: 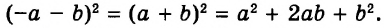
2) 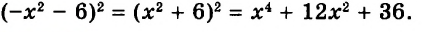
Пример:
Решите уравнение 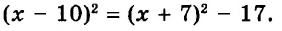
Решение:
Имеем:
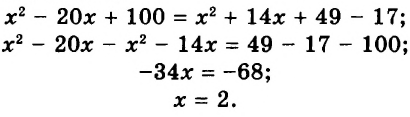
Пример:
Докажите, что остаток при делении квадрата натурального числа на число 3 равен 0 или 1.
Доказательство:
Пусть 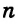 — некоторое натуральное число. Рассмотрим три случая.
— некоторое натуральное число. Рассмотрим три случая.
1) Число 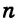 кратно 3. Тогда
кратно 3. Тогда 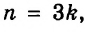 где
где 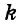 — натуральное число.
— натуральное число.
Имеем: 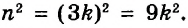 Значение выражения
Значение выражения 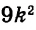 кратно 3, то есть остаток при делении
кратно 3, то есть остаток при делении 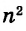 на 3 равен 0.
на 3 равен 0.
2) Остаток при делении на 3 числа 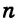 равен 1. Тогда
равен 1. Тогда 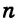 можно представить в виде
можно представить в виде 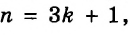 где
где 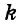 — натуральное число.
— натуральное число.
Имеем:
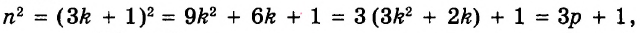 где
где 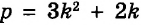 — неполное частное от деления
— неполное частное от деления 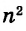 на 3, а остаток при этом равен 1.
на 3, а остаток при этом равен 1.
3) Остаток при делении на 3 числа 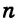 равен 2. Тогда
равен 2. Тогда 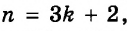 где
где 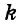 — натуральное число;
— натуральное число; 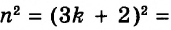
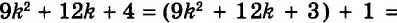
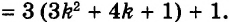 Очевидно, что и в этом случае остаток при делении
Очевидно, что и в этом случае остаток при делении 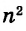 на 3 равен 1.
на 3 равен 1.
Преобразование многочлена в квадрат суммы или разности двух выражении
Перепишем формулы квадрата суммы и квадрата разности, поменяв местами их левые и правые части:
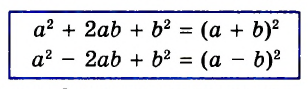
В таком виде эти формулы позволяют «свернуть» трехчлен в квадрат двучлена.
Трехчлен, который можно представить в виде квадрата двучлена, называют полным квадратом.
Пример:
Представьте трехчлен в виде квадрата двучлена:
Решение:
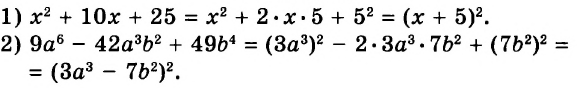
Пример:
Найдите, пользуясь преобразованием выражения в квадрат двучлена, значение суммы 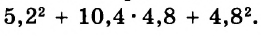
Решение:
Имеем:
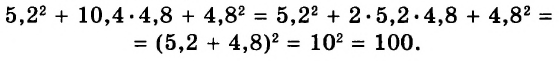
Пример:
Решите уравнение 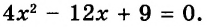
Решение:
Представим левую часть уравнения в виде квадрата разности:
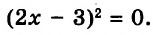
Так как значение квадрата равно нулю тогда и только тогда, когда его основание равно нулю, то получаем:
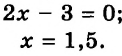
Ответ: 1,5.
Пример:
Докажите, что значение выражения 
 не зависит от значения переменной.
не зависит от значения переменной.
Решение:
Имеем:
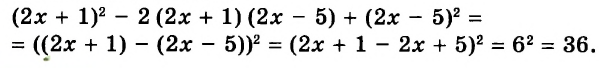
Пример:
Докажите, что выражение 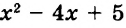 принимает положительные значения при любых значениях
принимает положительные значения при любых значениях  . Какое наименьшее значение принимает выражение и при каком значении
. Какое наименьшее значение принимает выражение и при каком значении  ?
?
Решение:
Преобразуем данное выражение:
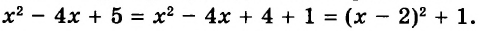
Представление выражения 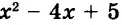 в виде
в виде 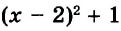 называют выделением полного квадрата из трехчлена.
называют выделением полного квадрата из трехчлена.
Так как 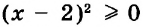 при любых значениях
при любых значениях  , то выражение
, то выражение 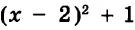 принимает только положительные значения. Также понятно, что
принимает только положительные значения. Также понятно, что 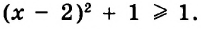 Отсюда наименьшее значение, равное 1, данное выражение принимает при
Отсюда наименьшее значение, равное 1, данное выражение принимает при 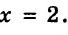
Пример:
При каких значениях 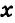 и
и 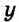 значение многочлена
значение многочлена 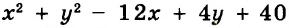 равно нулю?
равно нулю?
Решение:
Имеем:
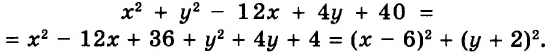
Мы представили данный многочлен в виде суммы двух слагаемых, которые могут принимать только неотрицательные значения. Их сумма, а следовательно, и данный многочлен будут принимать нулевое значение тогда и только тогда, когда каждое из слагаемых будет равно нулю, то есть когда 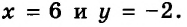
Ответ: 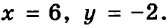
Сумма и разность кубов двух выражений
Умножим двучлен 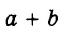 на трехчлен
на трехчлен 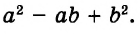 Получим:
Получим:
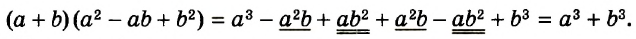
Таким образом, мы доказали тождество
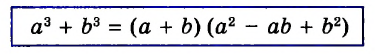
Это тождество называют формулой суммы кубов.
Многочлен 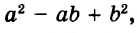 стоящий в правой части формулы, называют неполным квадратом разности. Такое название объясняется его внешним сходством с многочленом
стоящий в правой части формулы, называют неполным квадратом разности. Такое название объясняется его внешним сходством с многочленом 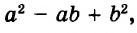 который равен квадрату разности
который равен квадрату разности 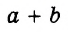 .
.
Теперь можно сказать, что сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
Разложим на множители выражение 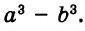 Имеем:
Имеем:
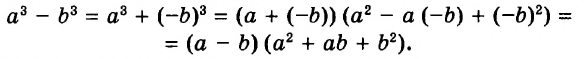
Мы доказали тождество
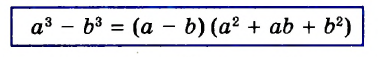
Это тождество называют формулой разности кубов.
Многочлен 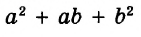 называют неполным квадратом суммы.
называют неполным квадратом суммы.
Итак, разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
Заметим, что эту формулу также можно доказать, перемножив многочлены, стоящие в правой части.
Пример:
Разложите на множители: 
Решение:
1) Представив данный многочлен в виде суммы кубов двух выражений, получим:
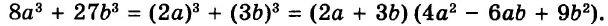
2) Представив данный многочлен в виде разности кубов двух выражений, получим:
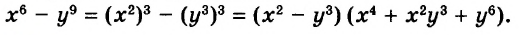
Пример:
Упростите выражение 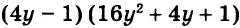 и найдите
и найдите
его значение при 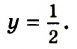
Решение:
Имеем:
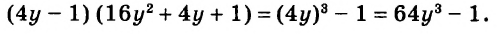
При 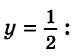
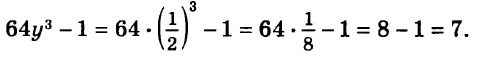
Пример:
Представьте в виде произведения выражение 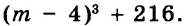
Решение:
Применив формулу суммы кубов, получим:
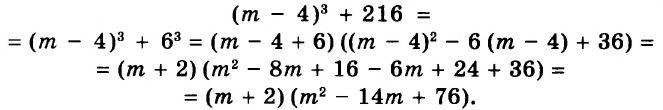
Пример:
Докажите, что значение выражения 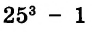 делится нацело на 24.
делится нацело на 24.
Решение:
Применив формулу разности кубов, получим:
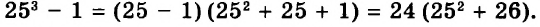
Данное выражение можно представить в виде произведения, один из множителей которого равен 24, а другой — натуральное число. Следовательно, значение этого выражения делится нацело на 24.
Применение различных способов разложения многочлена на множители
В предыдущих пунктах мы рассмотрели такие способы разложения многочлена на множители:
- вынесение общего множителя за скобки;
- метод группировки;
- применение формул сокращенного умножения.
Однако в математике при решении многих задач часто приходится использовать несколько приемов, применяя их в некоторой последовательности. В частности, есть много многочленов, для разложения которых на множители надо применить несколько способов.
Возникает естественный вопрос: какие способы и в какой последовательности надо применять при разложении многочлена на множители? Универсальных рекомендаций не существует, все зависит от конкретного многочлена. И все же дадим несколько общих советов:
- если это возможно, то разложение надо начинать с вынесения общего множителя за скобки;
- проверить, можно ли применить формулы сокращенного умножения;
- если не удается применить формулы сокращенного умножения, то надо попробовать воспользоваться методом группировки.
Пример:
Разложите на множители многочлен:

Решение:
1) Применив последовательно вынесение общего множителя за скобки и формулу разности квадратов, получим:
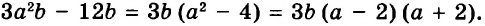
2) Применив последовательно вынесение общего множителя за скобки и формулу квадрата разности, получим:
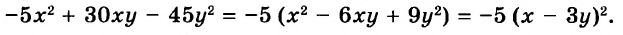
3) Вынесем общий множитель за скобки и применим формулу суммы кубов:
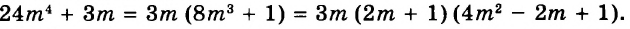
4) Комбинируя метод вынесения общего множителя за скобки и метод группировки, получим:
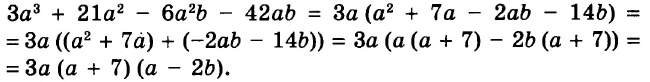
Пример:
Представьте в виде произведения многочленов: 
Решение:
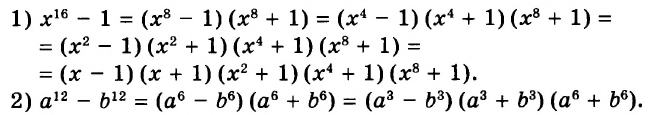
Мы получили три множителя, один из которых является разностью кубов, а два других — суммой кубов. Используя соответствующие формулы, окончательно получим:
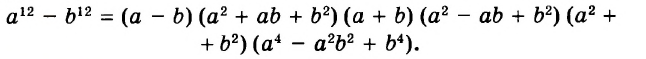
Пример:
Разложите на множители:

Решение:
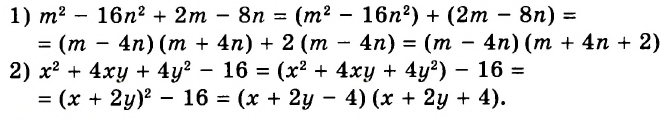
Пример:
Решите уравнение 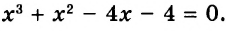
Решение:
Имеем:
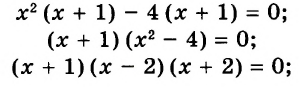
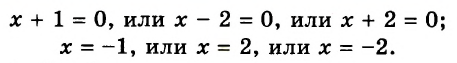
Пример:
Разложите на множители трехчлен 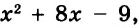 выделив предварительно квадрат двучлена.
выделив предварительно квадрат двучлена.
Решение:
Если к сумме 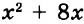 прибавить число 16, то полученное выражение
прибавить число 16, то полученное выражение 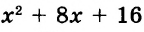 можно «свернуть» по формуле квадрата суммы. Поэтому, прибавив к данному трехчлену число 16 и вычтя из него 16, получим:
можно «свернуть» по формуле квадрата суммы. Поэтому, прибавив к данному трехчлену число 16 и вычтя из него 16, получим:
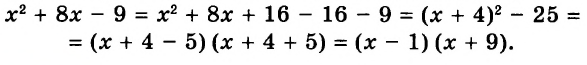
Пример:
Разложите на множители многочлен 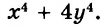
Решение:
Так как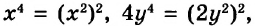 то, прибавляя к данному многочлену
то, прибавляя к данному многочлену 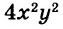 (удвоенное произведение одночленов
(удвоенное произведение одночленов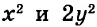 ) и вычитая из него такой же одночлен, получим:
) и вычитая из него такой же одночлен, получим:
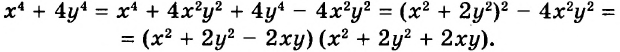
Язык, понятный всем
Здесь на трех восточных языках — арабском, китайском и иврите — записано хорошо известное вам переместительное свойство сложения: от перемены мест слагаемых сумма не меняется.

Но человек, не владеющий этими языками, это простое предложение не поймет.
Тогда на помощь приходит интернациональный математический язык. На нем перевод выглядит так:
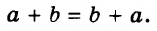
Как и любой другой язык, он имеет свой алфавит — математические символы. Это цифры, буквы, знаки математических действий и т. д. Из них составляют «слова» математического языка, например, выражения.
Казалось бы, чего проще — использовать математическую фразу 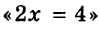 для записи линейного уравнения. Однако даже великий аль-Хорезми записывал это предложение громоздко: «Два корня равны 4 дирхемам». Это связано с тем, что аль-Хорезми вообще не использовал в своих работах математическую символику.
для записи линейного уравнения. Однако даже великий аль-Хорезми записывал это предложение громоздко: «Два корня равны 4 дирхемам». Это связано с тем, что аль-Хорезми вообще не использовал в своих работах математическую символику.
Сказанное совершенно не означает, что до IX века ученые не предпринимали попыток создать математический язык.
Еще в I веке греческий математик Герон Александрийский начал обозначать неизвестную величину буквой 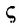 (сигма). Следующий шаг в создании символики сделал в III веке Диофант Александрийский. В своем знаменитом труде «Арифметика» он ввел обозначение не только для неизвестной величины, но и для некоторых ее степеней:
(сигма). Следующий шаг в создании символики сделал в III веке Диофант Александрийский. В своем знаменитом труде «Арифметика» он ввел обозначение не только для неизвестной величины, но и для некоторых ее степеней:
первая степень — 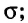
вторая степень —  (от
(от  —
— 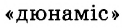 , что означает сила, степень);
, что означает сила, степень);
третья степень — 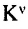 (от
(от 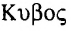 — «кубос», т. е. куб).
— «кубос», т. е. куб).
Для равенства Диофант применял знак 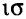 — первые две буквы слова
— первые две буквы слова  — «исос», то есть равный.
— «исос», то есть равный.
Вряд ли символику Диофанта можно считать удобной и наглядной. Например, он не ввел никаких специальных символов для обозначения действий сложения и умножения. Обозначение всех неизвестных величин одной буквой  также сильно затрудняло запись решения задач, в которых фигурировали несколько переменных.
также сильно затрудняло запись решения задач, в которых фигурировали несколько переменных.
С закатом эпохи античности алгебраическая символика Диофанта практически была забыта.
Возрождение процесса создания алгебраической символики связано с трудами талантливого немецкого ученого XIII века Иордана Неморария, который внес в европейскую математику идею буквенной символики.
В XV веке широкое распространение получили символы, применявшиеся выдающимся итальянским математиком Лукой Паччоли (ок. 1445 — ок. 1515).
Немало сделали для совершенствования математического языка немецкие математики XVI века Ян Видман и Адам Ризе.
Создателем буквенной символики по праву считается крупнейший французский математик XVI века Франсуа Виет (1540—1603). Он первый обозначил буквами не только неизвестные, но и данные величины. Виет предложил: «Искомые величины будем обозначать буквой А или другой гласной, Е, I, О, U, а данные — буквами В, D, G и другими согласными». Такие обозначения позволили Виету не только решать отдельные уравнения, но и исследовать процесс решения сразу целого класса уравнений. Например, благодаря символике Виета все линейные уравнения можно записать в виде 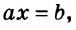 а следовательно, построить процесс решения уравнения в общем виде так, как мы это сделали в п. 2.
а следовательно, построить процесс решения уравнения в общем виде так, как мы это сделали в п. 2.

Языки многих народов продолжают развиваться. Не составляет исключения и математический язык. Новые открытия приносят в математику новые символы и термины.
Большой вклад в развитие и систематизацию математической терминологии внес профессор физико-математического факультета Львовского университета Владимир Иосифович Левицкий (1872 — 1956).

Его научно-методические труды в значительной мере способствовали становлению и развитию математической школы.
Основателем математической культуры по праву считается ученый с европейским именем, доктор философии, профессор Мирон Онуфриевич Зарицкий (1889—1961). Его научные труды и педагогические разработки хорошо известны во многих странах мира.

——
Целые выражения
Решение многих задач по математике, физике, химии связано с необходимостью проводить определенные преобразования выражений.
В данном разделе мы выясним, что такое выражение, целое выражение, что такое тождественное преобразование выражения, изучим основные формулы, на основании которых можно выполнять преобразования выражений.
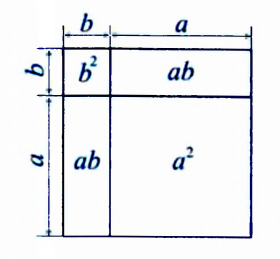
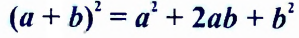
Выражения с переменными
Рассмотрим несколько задач.
Пример №98
Длина прямоугольного участка 42 м, а ширина на b м меньше. Записать площадь участка в виде выражения.
Решение:
Ширина участка  м, а площадь —
м, а площадь —  .
.
Ответ.  . •
. •
Выражение 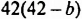 содержит букву b. Такое выражение мы называли буквенным выражением.
содержит букву b. Такое выражение мы называли буквенным выражением.
Буква b может принимать разные значения: b может равняться, например, 0,8; 5; 7,2; 10 и т. п., то есть значение b можно изменять. Поэтому b называют переменной, а выражение 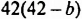 — выражением с переменной.
— выражением с переменной.
Пример №99
Длина прямоугольною участка 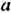 м, а ширина на b м меньше. Записать площадь участка в виде выражения.
м, а ширина на b м меньше. Записать площадь участка в виде выражения.
Решение:
Ширина участка 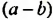 м, а площадь —
м, а площадь — 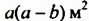 .
.
Буквы 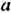 и b также могут принимать разные значения, поэтому
и b также могут принимать разные значения, поэтому 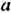 и b — переменные, а выражение
и b — переменные, а выражение 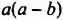 — выражение с двумя переменными.
— выражение с двумя переменными.
Выражение с переменными составляют из переменных, чисел, знаков действий и скобок. Выражением с переменной считают и отдельную переменную.
Если в выражении 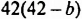 вместо переменной подставить определенное число, например, число 12, то получим числовое выражение
вместо переменной подставить определенное число, например, число 12, то получим числовое выражение 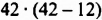 , значение которого равно:
, значение которого равно: 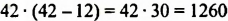 . Полученное число 1260 называют значением выражения
. Полученное число 1260 называют значением выражения 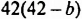 для значения переменной
для значения переменной 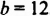 .
.
Значение выражения 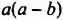 для
для 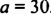 ,
, 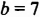 равно:
равно:
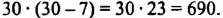
Рассмотрим выражение с переменной: 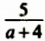 . Значение этого выражения можно найти для любого значения
. Значение этого выражения можно найти для любого значения  , кроме
, кроме 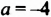 . Если
. Если 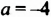 , то делитель (знаменатель)
, то делитель (знаменатель) 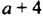 равен нулю, а на ноль делить нельзя. Говорят, что при
равен нулю, а на ноль делить нельзя. Говорят, что при 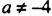 , выражение
, выражение 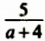 имеет смысл, а при
имеет смысл, а при 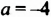 оно не имеет смысла.
оно не имеет смысла.
Целые выражения
Сравним выражения
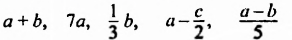
с выражениями
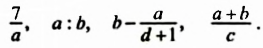
Выражения первой группы не содержат действия деления на выражение с переменными. Такие выражения называют целыми.
Выражения второй группы содержат действие деления на выражение с переменными. Такие выражения называют дробными. Мы будем изучать их в восьмом классе, а в седьмом будем рассматривать только целые выражения.
Формулы
Выражения с переменными используют для записи формул. Например:
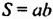 — формула для нахождения площади прямоугольника;
— формула для нахождения площади прямоугольника;
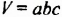 — формула для нахождения объема прямоугольного параллелепипеда.
— формула для нахождения объема прямоугольного параллелепипеда.
Формулой 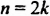 (где
(где  — целое число) задаются четные числа, а формулой
— целое число) задаются четные числа, а формулой 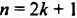 — нечетные числа.
— нечетные числа.
Для тех, кто хочет знать больше
Формулами можно задавать все целые числа, которые при делении на заданное натуральное число дают один и тот же остаток.
Рассмотрим сначала пример деления двух натуральных чисел. Разделим 48 на 5 с остатком:
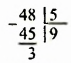
Получили: 9 — неполное частное, 3 — остаток.
Натуральные числа, не кратные числу 5, при делении на 5 могут давать в остатке 1, 2, 3 или 4. Числа, кратные числу 5, делятся (нацело) на 5. Еще говорят, что такие числа при делении на 5 дают в остатке 0.
Разделив 48 на 5, мы нашли два числа 9 и 3 (неполное частное и остаток), используя которые число 48 можно записать в виде
 .
.
Деление любого целого числа на натуральное с остатком сводится к отысканию подобного равенства.
Разделить целое число  на натуральное число
на натуральное число  с остатком значит найти такие целые числа
с остатком значит найти такие целые числа 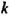 и
и 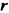 , чтобы выполнялось равенство
, чтобы выполнялось равенство
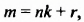 где
где 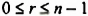 .
.
При этих условиях число 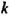 называют неполным частным, а
называют неполным частным, а 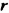 — остатком от деления
— остатком от деления 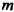 на
на 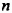 .
.
Остатков от деления целых чисел на натуральное число  может быть
может быть  :
:
0, 1, 2…..  -2,
-2,  -1.
-1.
Найдем для примера остаток от деления числа -17 на число 3. Для этого запишем число -17 в виде 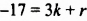 , где
, где  и
и  — целые числа, причем
— целые числа, причем  . Чтобы число
. Чтобы число 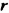 было в пределах от 0 до 2, нужно взять
было в пределах от 0 до 2, нужно взять 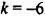 . Тогда легко найти, что
. Тогда легко найти, что  . Получили верное равенство
. Получили верное равенство 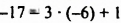 . Таким образом, число -17 при делении на 3 даст в остатке 1.
. Таким образом, число -17 при делении на 3 даст в остатке 1.
Целые числа при делении на 3 могут давать в остатке 0, 1 или 2. В соответствии с этим их можно разделить на 3 группы.
| Целые числа | Остаток от деления на 3 | Вид чисел |
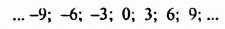 |
0 | 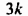 |
 |
1 | 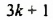 |
 |
2 | 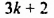 |
Следовательно, формулами 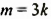 ,
, 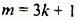 и
и 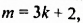 где
где 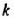 — произвольное целое число, задаются все целые числа, которые при делении на 3 дают в остатке соответственно 0, 1, 2. О числах вида
— произвольное целое число, задаются все целые числа, которые при делении на 3 дают в остатке соответственно 0, 1, 2. О числах вида 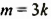 еще говорят, что они делятся (нацело) на 3. Так, -9 делится на 3.
еще говорят, что они делятся (нацело) на 3. Так, -9 делится на 3.
Примеры решения упражнений:
Пример №100
Записать в виде выражения:
а) произведение числа  и суммы чисел
и суммы чисел  и
и 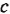 ;
;
б) частное разности чисел 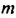 и
и 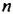 и числа 7;
и числа 7;
в) разность числа а и произведения чисел 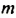 и
и 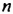 .
.
а) 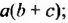 б)
б) 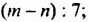 в)
в) 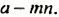
Примечание. Читая словами числовые выражения или выражения с переменными, первым называют последнее по порядку выполнения действие, далее — предпоследнее и т. д.
Пример №101
Найти значение выражения 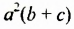 при
при 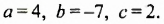
Решение:
При 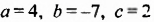 получим:
получим:
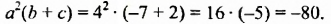
Ответ. -80.
Пример №102
Найти значение выражения 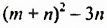 при
при 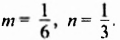
Решение:
Если 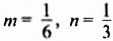 , то
, то
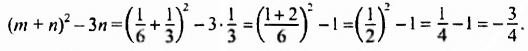
Ответ. 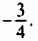
Пример №103
Записать в виде выражения число, в котором 9 сотен, с десятков, d единиц.
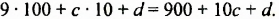
Тождественно равные выражения
Найдем значения выражений 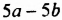 и
и 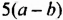 при
при 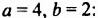
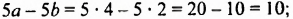
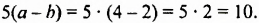
Значения этих выражений при данных значениях переменных равны (говорят, что при  соответствующие значения выражений равны). Из распределительного свойства умножения относительно вычитания следует, что и при любых других значениях переменных соответствующие значения выражений
соответствующие значения выражений равны). Из распределительного свойства умножения относительно вычитания следует, что и при любых других значениях переменных соответствующие значения выражений 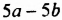 и
и 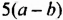 также равны. Такие выражения называют тождественно равными.
также равны. Такие выражения называют тождественно равными.
Определение:
Два выражения называют тождественно равными, если при любых значениях переменных соответствующие значения этих выражений равны.
Рассмотрим теперь выражения  и
и  . При
. При 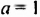 и
и 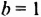 соответствующие значения этих выражений равны:
соответствующие значения этих выражений равны:
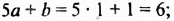
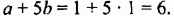
При 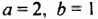 соответствующие значения этих выражений разные:
соответствующие значения этих выражений разные:
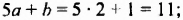
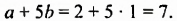
Итак, значения выражений 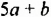 и
и 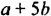 при одних значениях переменных равны, а при других — нет. Такие выражения не являются тождественно равными.
при одних значениях переменных равны, а при других — нет. Такие выражения не являются тождественно равными.
Тождества
Если два тождественно равные выражения 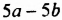 и
и 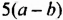 соединить знаком «=», то получим равенство
соединить знаком «=», то получим равенство 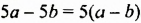 , являющееся верным при любых значениях переменных. Такое равенство называют тождеством.
, являющееся верным при любых значениях переменных. Такое равенство называют тождеством.
Определение:
Равенство, верное при всех значений переменных, называют тождеством.
Примерами тождеств являются равенства, выражающие основные свойства сложения и умножения чисел:
переместительное свойство: 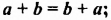
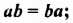
сочетательное свойство: 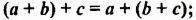
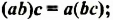
распределительное свойство: 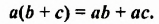
Тождествами являются также равенства, выражающие правила раскрытия скобок:
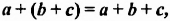
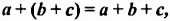
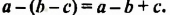
Тождествами являются и такие равенства:
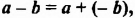
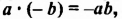
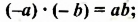
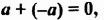
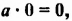
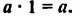
Тождественные преобразования выражений
В выражении 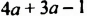 приведем подобные слагаемые
приведем подобные слагаемые 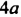 и
и 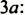
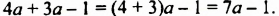
Выражение 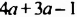 заменили тождественно равным ему выражением
заменили тождественно равным ему выражением 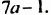 Замену одного выражения тождественно равным ему выражением называют тождественным преобразованием выражения.
Замену одного выражения тождественно равным ему выражением называют тождественным преобразованием выражения.
В математике часто приходится упрощать выражение, то есть заменять его тождественно равным выражением, имеющим более короткую запись или, как говорят, являющимся «более компактным». Рассмотрим примеры.
Пример №104
Упростить выражение 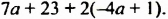
Решение:
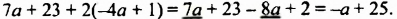
Пример №105
Упростить выражение 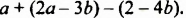
Решение:
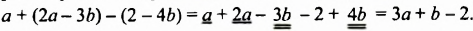
Тождественные преобразования используют и при доказательстве тождеств.
Чтобы доказать тождество, можно использовать один из способов:
- левую часть тождества путем тождественных преобразований привести к правой части;
- правую часть привести к левой части;
- обе части привести к одному и тому же выражению;
- образовать разность левой и правой частей и доказать, что она равна нулю.
Рассмотрим примеры.
Пример №106
Доказать тождество 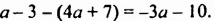
Решение:
Преобразуем левую часть равенства:
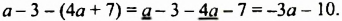
Путем тождественных преобразований левую часть равенства привели к правой части. Поэтому это равенство является тождеством.
Пример №107
Доказать тождество 15 = (27 – 5а) – (12 – За – 2а).
Решение:
Преобразуем правую часть равенства:
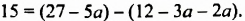
Путем тождественных преобразований правую часть равенства привели к левой части. Поэтому это равенство является тождеством.
Пример №108
Доказать тождество 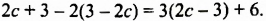
Решение:
Преобразуем левую и правую части равенства:
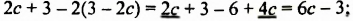
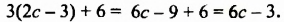
Путем тождественных преобразований левую и правую части равенства привели к одному и тому же выражению 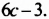 Поэтому это равенство является тождеством.
Поэтому это равенство является тождеством.
Пример №109
Доказать тождество 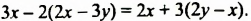
Решение:
Образуем разность левой и правой частей и упростим ее:
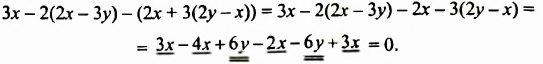 Разность левой и правой частей равенства равна нулю, поэтому данное равенство является тождеством.
Разность левой и правой частей равенства равна нулю, поэтому данное равенство является тождеством.
Интересно знать
Записывая выражения, уравнения, неравенства, мы используем математические символы  и многие другие. Такая система условных знаков, которой мы пользуемся сейчас, сложилась в алгебре постепенно.
и многие другие. Такая система условных знаков, которой мы пользуемся сейчас, сложилась в алгебре постепенно.
Еще в III в. древнегреческий математик Диофант вместо слова «равный» использовал отдельный знак — букву i, первую букву слова isos, то есть равный. Аналогичные сокращения использовали и другие математики, но предложенные ими символы не стали общепризнанными.
Современная символика была создана в XIV-XVIU в. Большую роль- в этом процессе сыграл французский математик Франсуа Виет, который впервые с помощью символов начал записывать уравнения.

Юрист по образованию, Виет был советником французских королей Генриха III и Генриха IV, прославился как талантливый дешифровщик. Во время войны с Испанией Виет нашел ключ к очень важному шифру. Расшифровка французами секретных сообщений испанцев привела к тому, что Испания начала терпеть поражения одно за другим. За это испанская инквизиция приговорила Виета к сожжению на костре, но, к счастью, приговор не был приведен в исполнение.
Несмотря на занятость на службе, Виет написал много математических трудов, главным из которых является «Введение в аналитическое искусство» (1591).
Важнейшим результатом научной деятельности Ф. Виета было то, что благодаря его трудам алгебра стала наукой об алгебраических уравнениях, базирующейся на использовании символов (букв).
- Одночлены
- Многочлены
- Формулы сокращенного умножения
- Разложение многочленов на множители
- Рациональные числа и действия над ними
- Делимость натуральных чисел
- Выражения и уравнения
- Линейное уравнение с одной переменной
Арифметические действия с целыми числами
Найдите значение выражения: ( 7 cdot 3 – 105:(-5)).
( 7 cdot 3 – 105:(-5) = 21 – (-21) = 42).
Ответ: 42
Найдите значение выражения: ((42 cdot 406 + 42 cdot 320 ): 11^2 ).
((42 cdot 406 + 42 cdot 320 ): 11^2 = 42 cdot (406 + 320) : 121 = 42 cdot 726 : 121 = 42 cdot 6 = 252).
Ответ: 252
Найдите значение выражения: ( 5 cdot 10^6 + 4 cdot 10^4 + 2 cdot 10^3 + 1cdot 10).
( 5 cdot 10^6 + 4 cdot 10^4 + 2 cdot 10^3 + 1cdot 10 = 5 cdot 1000000 + 4 cdot 10000 + 2 cdot 1000 + 10 = 5042010).
Ответ: 5042010
Найдите значение выражения: ( 3 cdot 10^4 + 4 cdot 10^2 + 3 cdot 10 + 5).
( 3 cdot 10^4 + 4 cdot 10^2 + 3 cdot 10 + 5 = 30000 + 400 + 30 +5 = 30435).
Ответ: 30435
Найдите значение выражения: ( 8 cdot 10^3 + 3 cdot 10^2 + 2 cdot 5 cdot 10 + 6).
( 8 cdot 10^3 + 3 cdot 10^2 + 5 cdot 10 + 6 = 8000 + 300 + 50 + 6 = 8356).
Ответ: 8356
Найдите значение выражения: ((122 cdot 12 – 132 cdot 12) : 60 cdot (-2) ).
((122 cdot 12 – 132 cdot 12) : 60 cdot (-2) = (122 – 132) cdot 12 : (-120) = 120 : (-120) = -1).
Ответ: -1
Найдите значение выражения: ( (255 cdot 25 – 254 cdot 25 ) cdot 28 : 7).
( (255 cdot 25 – 254 cdot 25 ) cdot 28 : 7 = 25 cdot (255 – 254) cdot 4 = 10).
Ответ: 100

