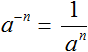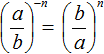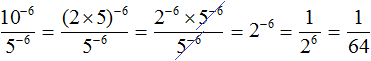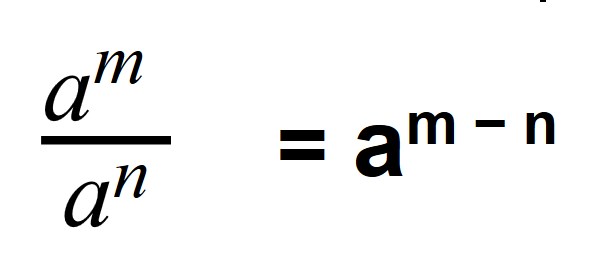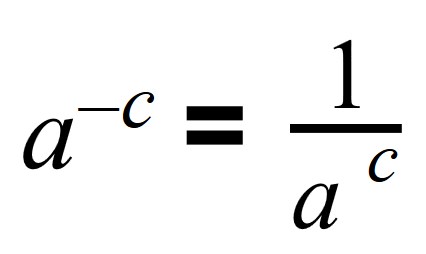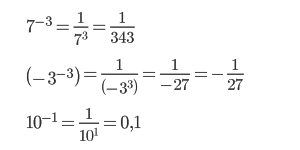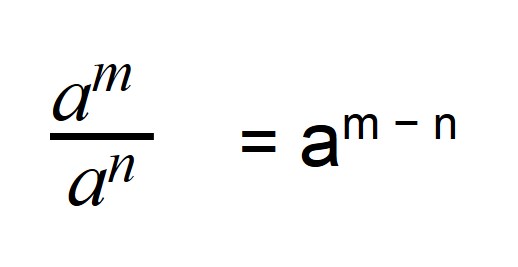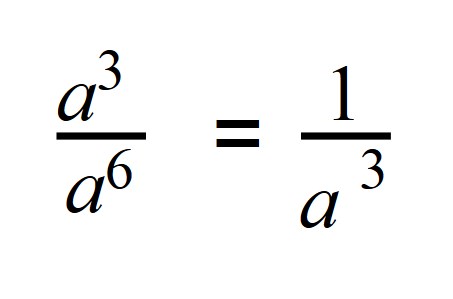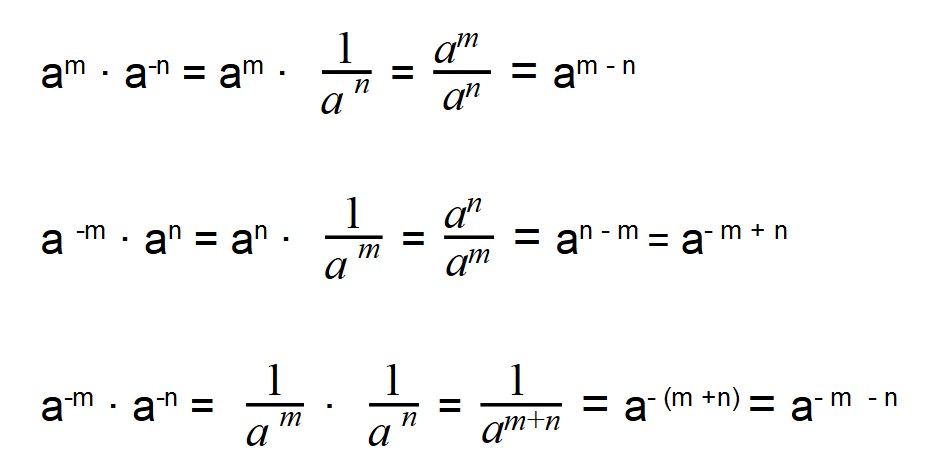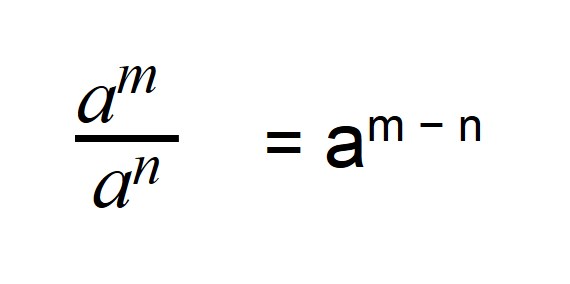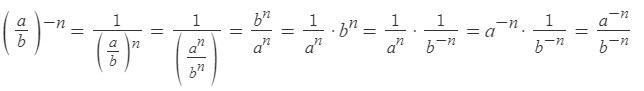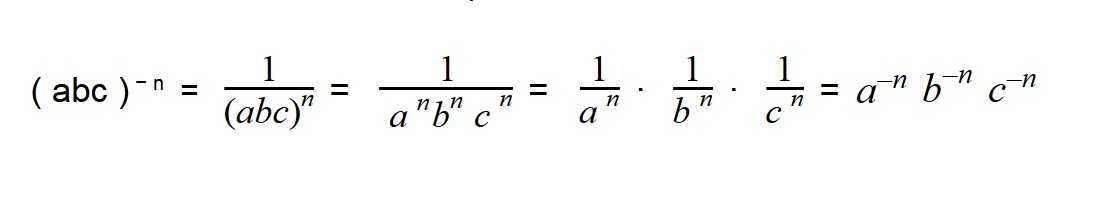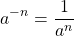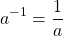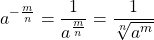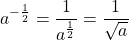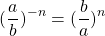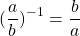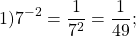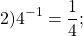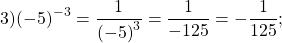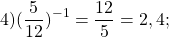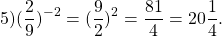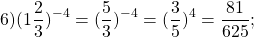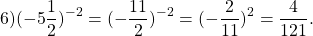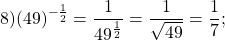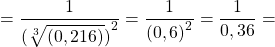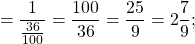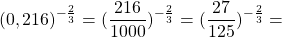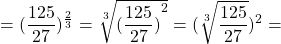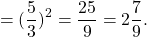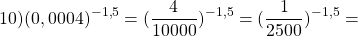|
Запись an означает что число a должно быть умножено n раз: |
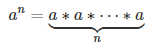 |
Пример 1. 53=5*5*5=125
Деление это обратная операция умножению. Отрицательная степень означает сколько раз нужно разделить число.
|
Число в отрицательной степени a-n может быть записано в виде: |
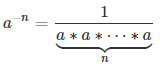 |
Пример 2. 5-3=1÷5÷5÷5=0,008
| Пример 2 может быть записан в виде. | 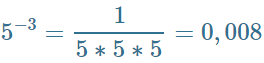 |
| Определение. Если a≠0 и n – целое отрицательное число, то | 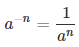 |
Для вычисления числа a-n в отрицательной степени нужно:
1.Вычислить an
|
2.Затем разделить 1 на полученный результат, т.е. |
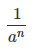 |

Примеры степени с целым отрицательным показателем выглядят следующим образом: 2−2, 10−7, a−8.
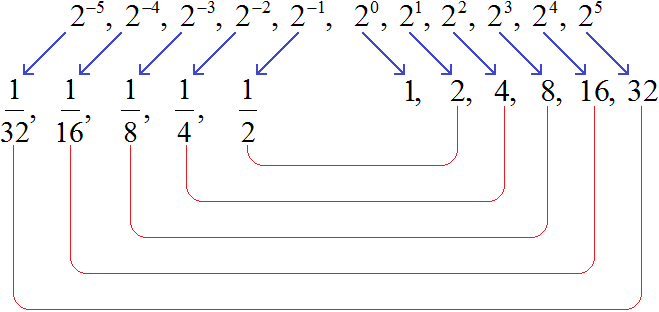
Чтобы разобраться с ними, рассмотрим следующую последовательность степеней: 2−5, 2−4, 2−3, 2−2, 2−1, 20, 21, 22, 23, 24, 25.
- Степень с натуральным показателем в этой последовательности: 21, 22, 23, 24, 25
- Нулевая степень в этой последовательности это степень 20.
- Предыдущая степень с целым показателем будет уже с отрицательным показателем и выглядеть как 2−1. Степень с целым отрицательным показателем в этой последовательности: 2−5, 2−4, 2−3, 2−2, 2−1.
Вычисление степени с целым отрицательным показателем
В отрицательную степень число возводится по-другому: если при возведении в положительную степень число увеличивается, то при возведении в отрицательную степень это число наоборот уменьшается.
Например, возьмём число 2 и возведем его в неотрицательную степень:
- нулевая степень: 20 =1
- степень с нутуральным показателем:
21=2,
22=2*2=4,
23=2*2*2=8,
24=2*2*2*2=16 и т.д.
Получили последовательность чисел, в которой каждое число больше следующего числа в 2 раза. Тогда логично предположить, что число, располагающееся до единицы, будет в два раза меньше единицы. Его можно получить, если 1 разделить на 2.
- Получается, что степень 2−1 =1/2.
- Предыдущее число 2−2 должно быть в два раза меньше, чем 2−1. Чтобы его получить разделим на 2 и получим 2−2 =1/(2*2)=1/4.
- Предыдущее число 2−3 должно быть в два раза меньше, чем 2−2. Чтобы его получить разделим на 2 и получим 2−3 =1/(2-2*2)=1/8.
Заметим, что в данной последовательности значения степеней с отрицательными показателями являются обратными числами к значениям степеней с натуральными показателями:
- Значение степени в 22 есть число 4, а значение степени 2−2 есть число 1/4. Числа 4 и 1/4 являются обратными друг другу.
- Значение степени в 23 есть число 8, а значение степени 2−3 есть число 1/8. Числа 8 и 1/8 являются обратными друг другу.
Можно сделать вывод, что для вычисления степени с отрицательным показателем, нужно записать дробь, в числителе которой единица, а в знаменателе та же самая степень, но с противоположным показателем.
Таким образом, чтобы вычислить степень вида 2−n , можно воспользоваться следующим правилом:
Правило работает только тогда, когда a ≠ 0. Если a будет равным нулю, то в знаменателе получим 0, а на нуль делить нельзя.
Данное правило можно доказать, используя правило деления степеней с одинаковыми основаниями. Допустим, нам нужно высислить степень в целым отрицательным показателем 2−2. Использую правило деления степеней с одинаковыми основаниями записшем 2−2 как 2(3-5) = 23 : 25. Запишем это деление в виде дроби. Получим:
Пример 1. Найти значение выражения 3−3
Пример 2. Найти значение выражения (-2/3)−3
Формула для возведения обыкновенных дробей в отрицательную степень:
Желательно уметь возводить обыкновенную дробь в отрицательную степень как с помощью формулы, так и без неё.
Тождественные преобразования степеней с целым отрицательным показателем
Все тождественные преобразования, которые мы рассматривали при изучении степени с натуральным показателем, сохраняются и для степеней с целыми отрицательными показателями.
Пример 3. Найти значение выражения 2−1 × 2−3.
Воспользуеся основным свойством степени:
2−1 × 2−3 = 2−1 + (−3) = 2−4=1/16
Пример 4. Найти значение выражения 5−15 × 516.
Воспользуемся основным свойством степени:
5−15 × 516 = 5−15 + 16 = 51 = 5
Пример 5. Найти значение выражения (10−4)−1
Воспользуемся правилом возведения степени в степень:
(10−4)−1 = 10−4 × (−1) = 104 = 10000
Пример 6. Найти значение выражения (10−6)/(5−6)
Представим число основание 10 в виде произведения 2×5. Тогда числитель примет вид (2×5)−6
Отрицательная степень числа
Степень с отрицательным показателем
Число с отрицательным показателем степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем.
Чтобы разобраться, почему число в отрицательной степени равно дроби, надо вспомнить правило деления степеней с одинаковыми основаниями:
При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя.
Следовательно, если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Пример 1. Замените дробь степенью с отрицательным показателем:
Пример 2. Представьте в виде степени с отрицательным показателем:
Действия над степенями с отрицательными показателями
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются:
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя:
Чтобы возвести произведение в отрицательную степень, надо возвести в эту степень каждый сомножитель отдельно:
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
При возведении одной степени (положительной или отрицательной) в степень (положительную или отрицательную) показатели степеней перемножаются:
Источник
Отрицательная степень числа: правила возведения и примеры
В одной из предыдущих статей мы уже упоминали о степени числа. Сегодня мы постараемся сориентироваться в процессе нахождения ее значения. Научно говоря, мы будем выяснять, как правильно возводить в степень. Мы разберемся, как производится этот процесс, одновременно затронем все вероятные показатели степени: натуральный, иррациональный, рациональный, целый.
Итак, давайте подробно рассмотрим решения примеров и выясним, что значит:
Определение понятия
Вот точно отражающее смысл определение: «Возведением в степень называют определение значения степени числа».
Соответственно, возведение числа a в ст. r и процесс нахождения значения степени a с показателем r — это идентичные понятия. К примеру, если стоит задача вычислить значение степени (0,6)6″, то ее можно упростить до выражения «Возвести число 0,6 в степень 6».
После этого можно приступать напрямую к правилам возведения.
Возведение в отрицательную степень
Минусовая степень обозначает, что число множат на него самого такое количество раз, какое значится в ст., а после этого единицу делят на вычисленный результат.
Для наглядности следует обратить внимание на такую цепочку выражений:
110=0,1=1* 10 в минус 1 ст.,
1100=0,01=1*10 в минус 2 степ.,
11000=0,0001=1*10 в минус 3 ст.,
110000=0,00001=1*10 в минус 4 степeни.
Благодаря данным примерам можно четко просмотреть возможность моментально вычислить 10 в любой минусовой степени. Для этой цели достаточно банально сдвигать десятичную составляющую:
Так же легко понять по данной схеме, сколько будет составлять 10 в минус 5 ст. —
Как возвести число в натуральную степeнь
Вспоминая определение, учитываем, что натуральное число a в ст. n равняется произведению из n множителей, при этом каждый из них равняется a. Проиллюстрируем: (а*а*…а)n, где n — это количество чисел, которые умножаются. Соответственно, чтобы a возвести в n, необходимо рассчитать произведение следующего вида: а*а*…а разделить на n раз.
Отсюда становится очевидно, что возведение в натуральную ст. опирается на умение осуществлять умножение (этот материал освещен в разделе про умножение действительных чисел). Давайте рассмотрим задачу:
Мы имеем дело с натуральным показателем. Соответственно, ход решения будет следующим: (-2) в cт. 4 = (-2)*(-2)*(-2)*(-2). Теперь осталось только осуществить умножение целых численностей:(-2)*(-2)*(-2)*(-2). Получаем 16.
Пример:
Вычислите значение: три целых две седьмых в квадрате.
Данный пример равняется следующему произведению: три целых две седьмых умножить на три целых две седьмых. Припомнив, как осуществляется умножение смешанных чисел, завершаем возведение:
Возведение в иррациональную стeпeнь
Касаемо вопроса возведения в иррациональный показатель, следует отметить что расчеты начинают проводить после завершения предварительного округления основы степени до какого-либо разряда, который позволил бы получить величину с заданной точностью. К примеру, нам необходимо возвести число П (пи) в квадрат.
Начинаем с того, что округляем П до сотых и получаем:
П в квадрате = (3,14)2=9,8596. Однако если сократить П до десятитысячных, получим П=3,14159. Тогда возведение в квадрат получает совсем другое чиcло: 9,8695877281.
Здесь следует отметить, что во многих задачах нет надобности возводить иррациональные числа в cтeпeнь. Как правило, ответ вписывается или в виде, собственно, степени, к примеру, корень из 6 в степени 3, либо, если позволит выражение, проводится его преобразование: корень из 5 в 7 cтепeни = 125 корень из 5.
Как возвести чиcло в целую степень
Эту алгебраическую манипуляцию уместно принимать во внимание для следующих случаев:
Поскольку практически все целые положительные числа совпадают с массой чисел натуральных, то постановка в положительную целую степень — это тот же процесс, что и постановка в ст. натуральную. Данный процесс мы описали в предшествующем пункте.
Теперь поговорим о вычислении ст. нулевой. Мы уже выяснили выше, что нулевую степень числа a можно определить для любого отличного от нуля a (действительного), при этом a в ст. 0 будет равно 1.
Соответственно, возведение какого угодно действительного числа в нулевую ст. будет давать единицу.
К примеру, 10 в ст.0=1, (-3,65)0=1, а 0 в ст. 0 нельзя определить.
Пример:
Вычислить значение числа 2 в кубе с целым отрицательным показателем.
Согласно определению стeпeни с отрицательным показателем обозначаем: два в минус 3 ст. равняется один к двум в третьей cтепeни.
Знаменатель рассчитывается просто: два в кубе;
Ответ: два в минус 3-й ст. = одна восьмая.
Видео
Из этого видео вы узнаете, что делать, если степень с отрицательным показателем.
Источник
Отрицательная степень
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n раз подряд»
Например, a n — степень, где:
Читается такое выражение как a в степени n.
Если говорить проще, то степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить данное число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).
Свойства степеней
Степень с натуральным показателем в математике имеет несколько важных свойств, которые позволяют упрощать вычисления. Всего их пять штук — ниже мы их рассмотрим.
Свойство 1: произведение степеней
При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:
Свойство 2: частное степеней
Когда мы делим степени с одинаковыми основаниями, то основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.
Свойство 3: возведение степени в квадрат
Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.
Свойство 4: степень произведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
Свойство 5: степень частного
Чтобы возвести в степень частное, можно возвести в эту степень сначала делимое, потом делитель, и первый результат разделить на второй.
Степень с показателем 0
Любое целое a ≠ 0 в степени 0 равно 1.
Выражение 0 в степени 0 многие математики считают лишенным смысла, так график функции f (x, у) = xy прерывается в точке (0; 0).
Степень с отрицательным показателем
Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:
Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Действия с отрицательными степенями
Умножение отрицательных степеней
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:
Деление отрицательных степеней
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:
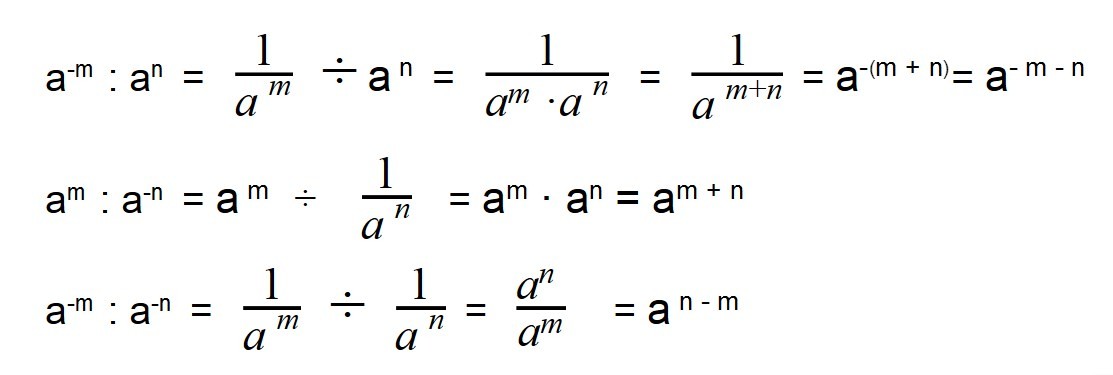
Возведение дроби в отрицательную степень
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
Возведение произведения в отрицательную степень
Чтобы возвести произведение в отрицательную степень, необходимо возвести в эту степень каждый множитель произведения отдельно:
Источник
Степень с отрицательным показателем
Что такое степень с отрицательным показателем (отрицательная степень)? Как выполнить возведение числа в отрицательную степень? Как возвести в отрицательную степень дробь?
В частности, число в степени минус один — это число, обратное данному:
Если n — целое число, то речь идет о степени с целым отрицательным показателем и равенство верно для любого a, отличного от нуля (т.е. при a≠0).
Если n — дробное число, то речь идет о степени с рациональным показателем:
(m — целое число, n — натуральное число). Степень с дробным показателем определена только для положительных a (a>0).
Дробь в степени с отрицательным показателем равна обратному этой дроби числу в степени с показателем, противоположным данному:
Другими словами, чтобы возвести дробь в отрицательную степень, надо эту дробь «перевернуть»(числитель и знаменатель поменять местами) и изменить знак в показателе степени.
Дробь в минус первой степени — это «перевернутая» дробь.
Рассмотрим примеры возведения чисел в степень с отрицательным показателем.
Для ускорения вычислений используем таблицу степеней.
Чтобы возвести в отрицательную степень смешанное число, надо сначала перевести его в неправильную дробь:
Возведем числа в степень с дробным отрицательным показателем:
При возведении в отрицательную степень десятичной дроби можно сначала перевести ее в обыкновенную и, если возможно, сократить:
Если в показателе степени стоит десятичная дробь, нужно перевести ее в обыкновенную:
Возведение в степень с отрицательным показателем в алгебре встречается достаточно часто, поэтому важно вовремя усвоить эту тему.
14 комментариев
Спасибо! врубился) жаль, что в школе не учился(
Что ж, учиться никогда не поздно). Но всё же лучше вовремя.
Забавно, что за время работы встречал множество коллег, кому приходилось на внутренних курсах разжёвывать какие вещи начального уровня и все сокрушались: «Что же я в школе-то (институте) не учил это? Это же так просто, понятно, полезно и ИНТЕРЕСНО. »
А вся проблема в том, что ни в школе, ни в институте перед тем, как что-то начать рассказывать не проводят красочные, завлекательные, познавательные, весёлые и игровые презентации будущего курса, чтобы было понятно, а где же то, что будем скоро изучать, применяется в жизни? Каким профессиям и в каких житейских ситуациях это может быть полезно?
Учат каким-то абстрактным формулам вместо того, чтобы рассказать, что это пригодится на кухне, при разделе земли, при строительстве сарая на даче, при стрельбе из пушки, при запуске спутника и т. д.
При разбавлении спирта водой, в конце концов! :))
Ведь часто женщины встают в ступор от элементарной задачи:
В рецепте указано «1 ст. ложка 3 %-го уксуса», а у неё на кухне только 9 % или («О, БОЖЕ! Крах! Провал!») вообще уксусная эссенция! А по сути та же кислота, но в концентрации 70 %…
Вообще-то знание и умение решать примеры с отрицательной степенью никак не поможет в задаче с разными процентами уксуса. Просто заговор против большинства людей))
Источник
Свойства степеней. Действия со степенями
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n-раз подряд»
a — основание степени
n — показатель степени
Соответственно, a n = a·a·a·a. ·a
Читается такое выражение, как a в степени n
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) на само себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 — она решается довольно просто:
2 — основание степени
3 — показатель степени
Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.
Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.
Задачка про миллион: представьте, что у вас есть миллион рублей. В начале каждого года вы зарабатываете на нем еще два. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.
Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:
Математики заскучали и решили все упростить:
Ответ: через четыре года у вас будет 81 миллион.
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).
Источник
Отрицательная степень числа
- Степень с отрицательным показателем
- Действия над степенями с отрицательными показателями
Степень с отрицательным показателем
Число с отрицательным показателем степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем.
| d -c = | 1 | ; 7 -5 = | 1 | ; a -5 = | 1 | . |
| d c | 7 5 | a 5 |
Чтобы разобраться, почему число в отрицательной степени равно дроби, надо вспомнить правило деления степеней с одинаковыми основаниями:
При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя.
Следовательно, если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
a 5 : a 8 = a5 – 8 = a -3.
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Значит:
Пример 1. Замените дробь степенью с отрицательным показателем:
Решение:
Пример 2. Представьте в виде степени с отрицательным показателем:
Решение:
| 1 | = (m + n) -2. |
| (m + n) 2 |
Действия над степенями с отрицательными показателями
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются:
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя:
Чтобы возвести произведение в отрицательную степень, надо возвести в эту степень каждый сомножитель отдельно:
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
При возведении одной степени (положительной или отрицательной) в степень (положительную или отрицательную) показатели степеней перемножаются:
Как считать примеры с отрицательной степенью?
При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя. Следовательно, если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью: a 5 : a 8 = a5 — 8 = a -3….Решение:
| 1 | = (m + n) -2. |
|---|---|
| (m + n) 2 |
3 июн. 2021 г.
Как умножать в отрицательной степени?
1. Степень с отрицательным показателем
- При умножении степеней с одинаковыми основаниями показатели нужно сложить: a s ⋅ a t = a s + t .
- При делении степеней с одинаковыми основаниями показатели нужно вычесть a s : a t = a s − t .
- При возведении степени в степень показатели нужно перемножить: a s t = a s ⋅ t .
Что означает минус в степени?
Степень с отрицательным показателем К примеру, 4 в минус 2 степени — это 1/42, 2 в минус 3 степени — это 1/23, 3 в минус 1 степени — это 1/3, 10 в минус первой степени — это 1/10 или 0,1. Степени с отрицательным показателям помогают компактно записывать крайне малые или постоянно уменьшающиеся величины.
Как посчитать на калькуляторе число в отрицательной степени?
Чтобы возвести отличное от нуля число в отрицательную степень, нужно вычислить значение этого числа в той же положительной степени и разделить единицу на полученный результат.
Как считать отрицательные числа?
Чтобы сложить положительное и отрицательное число, нужно:
- Найти модули слагаемых — то есть этих чисел.
- Сравнить полученные числа. …
- Из большего модуля вычесть меньший.
- Перед полученным числом поставить знак того слагаемого, модуль которого больше.
29 дек. 2020 г.
Как считать дроби в степенях?
Правило возведения рациональной дроби в степень: Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.
Сколько будет 10 в минус пятой степени?
Сколько будет 10 в минус пятой степени?? И вообще расскажите пожалуйста, что значит минусовая степень… 1*10 в пятой степени означает, что запятую надо передвинуть на 5 позиций вправо, получится 100000. 1*10 в минус пятой — на 5 позиций влево: 0,00001.
Как умножать отрицательные десятичные дроби?
Правило умножения отрицательных чисел заключается в том, что для того, чтобы умножить два отрицательных числа, необходимо перемножить их модули. Данное правило записывается так: для любых отрицательных чисел –a, −b данное равенство считается верным. (−а)⋅(−b)=a⋅b. ( — а ) · ( — b ) = a · b .
Сколько будет 4 в минус третьей степени?
4 в минус3 степени =1/4 в 3 степени и равно 1/64. Степень с отрицательным показателем.
Как на инженерном калькуляторе посчитать число в степени?
Для ввода знака возведения в степень используйте клавишу [xy] или [^], в зависимости от типа аппарата. После нажатия клавиши [=] результат отобразится в нижней строке. При отсутствии калькулятора для возведения в степень можно использовать компьютер.
Как решить число в степени?
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем.
Как сложить плюс и минус?
Чтобы сложить положительное и отрицательное число, нужно:
- Найти модули слагаемых — то есть этих чисел.
- Сравнить полученные числа. …
- Из большего модуля вычесть меньший.
- Перед полученным числом поставить знак того слагаемого, модуль которого больше.
29 дек. 2020 г.
Как от отрицательного числа отнять число?
Таким образом, при вычитании отрицательного числа из отрицательного мы действуем по правилу сложения чисел с разными знаками, и у нас может получиться как положительное, так и отрицательное число. Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.
Как упростить дробное выражение со степенями?
Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель….Сокращение дробей с буквами и степенями проходит в три этапа:
- Определите общий множитель.
- Сократите коэффициенты.
- Поделите все числители и все знаменатели на общий множитель.
9 дек. 2020 г.
Как правильно считать дроби?
привести дроби к наименьшему общему знаменателю; сложить числители дробей, а знаменатель оставить без изменений; сократить полученную дробь; если получилась неправильная дробь преобразовать неправильную дробь в смешанную.
Как найти 10 в минус 3 степени?
10 в минус 3 степени=110 в 3 степени=1(10*10*10)=0.001.
Сколько будет 10 в минус первой степени?
Теперь, зная определение отрицательной степени, давайте разберемся, почему «10» в минус первой степени равно «0,1».