В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Если в выражении есть только числа и арифметические знаки “+”, “·”, “-“, “÷”, то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пусть нужно найти значения выражения 14-2·15÷6-3.
Выполним сначала умножение и деление. Получаем:
14-2·15÷6-3=14-30÷6-3=14-5-3.
Теперь проводим вычитание и получаем окончательный результат:
14-5-3=9-3=6.
Вычислим: 0,5-2·-7+23÷234·1112.
Сначала выполняем преобразование дробей, деление и умножение:
0,5-2·-7+23÷234·1112=12-(-14)+23÷114·1112
12-(-14)+23÷114·1112=12-(-14)+23·411·1112=12-(-14)+29.
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
12-(-14)+29=12+14+29=14+1318=141318.
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Найдем значение выражения 0,5·(0,76-0,06).
В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом – умножение.
0,5·(0,76-0,06)=0,5·0,7=0,35.
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Вычислим значение 1+2·1+2·1+2·1-14.
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
1+2·1+2·1+2·1-14=1+2·1+2·1+2·34
1+2·1+2·1+2·34=1+2·1+2·2,5=1+2·6=13.
В нахождении значений выражений со скобками главное – соблюдать последовательность действий.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Вычислим значение выражения с корнями -2·3-1+60÷43+3·2,2+0,1·0,5.
Сначала вычисляем подкоренные выражения.
-2·3-1+60÷43=-6-1+153=83=2
2,2+0,1·0,5=2,2+0,05=2,25=1,5.
Теперь можно вычислить значение всего выражения.
-2·3-1+60÷43+3·2,2+0,1·0,5=2+3·1,5=6,5
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Сколько будет 3+13-1-1
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
3+13-1=3-1.
Таким образом:
3+13-1-1=3-1-1=1.
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Найдем значение выражения 23·4-10+161-123,5-2·14.
Начинаем вычислять по порядку.
23·4-10=212-10=22=4
16·1-123,5-2·14=16*0,53=16·18=2.
Осталось только провести операцию сложение и узнать значение выражения:
23·4-10+161-123,5-2·14=4+2=6.
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Вычислим значение следующего выражения: 2-25·45-1+3136.
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
2-25·45-1+3136=2-25·225-1+313·6
2-25·225-1+313·6=2-25·22·5-2+32=22·5-2-25+32
22·5-2-25+32=2-2+3=14+3=314
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Найдем значение выражения, содержащего дроби: 3,22-3·7-2·36÷1+2+39-6÷2.
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
3,22=3,2÷2=1,6
7-2·36=7-66=16
1+2+39-6÷2=1+2+39-3=66=1.
Перепишем наше выражение и вычислим его значение:
1,6-3·16÷1=1,6-0,5÷1=1,1
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Вычислим выражение 25-1-25-74-3.
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
25-1=25+15-15+1=25+15-1=25+24
Исходное выражение принимает вид:
25-1-25-74-3=25+24-25-74-3.
Вычислим значение этого выражения:
25+24-25-74-3=25+2-25+74-3=94-3=-34.
Выражения с логарифмами
Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log24+2·4 можно сразу вместо log24 записать значение этого логарифма, а потом выполнить все действия. Получим: log24+2·4=2+2·4=2+8=10.
Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log5-6÷352+2+7. Имеем:
log5-6÷352+2+7=log327+7=3+7=10.
Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Найдем значение выражения log2log2256+log62+log63+log5729log0,227.
log2log2256=log28=3.
По свойству логарифмов:
log62+log63=log6(2·3)=log66=1.
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
log5729log0,227=log5729log1527=log5729-log527=-log27729=-log27272=-2.
Теперь можно переходить к вычислению значения исходного выражения.
log2log2256+log62+log63+log5729log0,227=3+1+-2=2.
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Найдите значение выражения: tg24π3-sin-5π2+cosπ.
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
tg4π3=3
sin-5π2=-1
cosπ=-1.
Подставляем значения в выражение и вычисляем его значение:
tg24π3-sin-5π2+cosπ=32-(-1)+(-1)=3+1-1=3.
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Нужно найти значение выражения cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1.
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1=cos2π8cos5π36+π9-1=cosπ4cosπ4-1=1-1=0.
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.
- Корни, степени, логарифмы и т.д. заменяются их значениями.
- Выполняются действия в скобках.
- Оставшиеся действия выполняются по порядку слева направо. Сначала – умножение и деление, затем – сложение и вычитание.
Разберем пример.
Вычислим, чему равно значение выражения -2·sinπ6+2·2π5+3π5+3 lne2+1+39.
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
Первым делом вычислим значение подкоренного выражения 2·sinπ6+2·2π5+3π5+3. Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.
π6+2·2π5+3π5=π6+2·2π+3π5=π6+2·5π5=π6+2π
Теперь можно узнать значение синуса:
sinπ6+2·2π5+3π5=sinπ6+2π=sinπ6=12.
Вычисляем значение подкоренного выражения:
2·sinπ6+2·2π5+3π5+3=2·12+3=4
Отсюда:
2·sinπ6+2·2π5+3π5+3=4=2.
Со знаменателем дроби все проще:
lne2=2.
Теперь мы можем записать значение всей дроби:
2·sinπ6+2·2π5+3π5+3 lne2=22=1.
С учетом этого, запишем все выражение:
-1+1+39=-1+1+33=-1+1+27=27.
Окончательный результат:
-2·sinπ6+2·2π5+3π5+3 lne2+1+39=27.
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56+8-3,789lne2-56+8-3,789lne2 также равно нулю.
Еще один прием, позволяющий ускорить процесс – использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями – сокращение одинаковых выражений в числителе и знаменателе.
Например, возьмем выражение 23-15+3·289·343·23-15+3·289·34. Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 13.
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.
Вычислить значение выражения 0,5x-y при заданных x=2,4 и y=5.
Подставляем значения переменных в выражение и вычисляем:
0,5x-y=0,5·2,4-5=1,2-5=-3,8.
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Например, выражение х+3-х, очевидно, имеет значение 3, и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.
Еще один пример. Значение выражения xx равно единице для всех положительных иксов.
План урока:
Сложение отрицательных чисел
Сложение чисел с разными знаками
Вычитание отрицательных чисел и чисел с разными знаками
В субботу, ученики 6 класса договорились встретиться и погулять в парке. Утром Юля выглянула в окошко, ярко светит солнышко, но при этом морозно. Девочка взглянула на термометр. Он показывал -10˚C. Мама попросила Юлю пойти на улицу немного позже, когда на улице потеплеет. Юля расстроилась и стала ждать. Через два часа девочка снова взглянула на термометр. Он показал -3. Ого! Всего два часа, а так потеплело – обрадовалась девочка и стала одеваться, чтобы идти гулять. В это время в комнату вошла мама и удивленно спросила «Уже потеплело? На сколько градусов?» Дочь не знала, что сказать и как правильно узнать, на сколько градусов стало теплее. Мама пришла на помощь и сообщила, что достаточно от -10 отнять -3, и мы узнаем, на сколько градусов изменилась температура воздуха за окном. Иначе, можно сказать, что шкала термометра поднялась вверх на 7 делений, значит, на улице стало теплее на 7 градусов. Запомнив все, что рассказала мама, Юля побежала в парк делиться новыми знаниями с друзьями.
Сложение и вычитание отрицательных чисел
Давайте вспомним любимую многими сказку «Буратино» и разберем задачу с участием любимых персонажей.
В театре Карабаса-Барабаса актерам жилось очень сложно, все куклы мечтали жить на свободе. Актеры тяжело работали, но долги перед хозяином росли с каждым днем. Злой владелец пообещал отпустить Буратино и Мальвину из своего театра только тогда, когда кукольные герои вернут ему долг. Сколько монет нужно собрать героям, чтобы оказаться на свободе, если у Буратино было -15 монет, а у Мальвины -6?

Чтобы ответить на главный вопрос задачи, нам нужно понимать, о чем идет речь. Изучив условие, возникает вопрос «Как может быть -15 и -6 монет?». В данном случае выходит, что Буратино и Мальвина должны вернуть Карабасу-Барабасу 15 и 6 монет, поэтому перед данными числами и стоит знак «минус». Получается, кукольные персонажи смогут покинуть театр, когда полностью вернут долг. Для этого необходимо узнать общий размер долга Буратино и Мальвины. Чтобы узнать размер долга, суммируем монеты персонажей -15 и -6. Но как их сложить, когда перед слагаемыми стоит «минус»? В подобных ситуациях применяют правило сложения отрицательных чисел.

Возвращаемся к решению задачи.
Теперь, правильно запишем и суммируем известные данные.

Получается, что герои имеют -21 монету, следовательно, они должны собрать 21 монету и вернуть долг, только тогда появится возможность покинуть театр Карабаса-Барабаса.

Источник
Рассмотрим еще одно задание.
Найдите результат сложения -24 и -16.
Чтобы вычислить сумму двух значений со знаком «минус», достаточно суммировать их модули, и перед полученной цифрой записать «-».
-24+(-16)=-(24+16)=-40.
Запомни! Если складываем два отрицательных числа, то суммируем их модули, а перед результатом сложения записываем «-».
Сложение чисел с разными знаками
Рассмотрим ситуацию.
Мишин папа навещал бабушку в деревне, обещал привезти гостинец сыну – яблоки. Во дворе Миша рассказал мальчишкам про папино обещание, и решил угостить яблоком, каждого из трех друзей, то есть, у него уже стало -3 яблока. Папа привез сыну 10 яблок и мальчик с радостью поделился фруктами с друзьями. Сколько яблок осталось у мальчика?
Чтобы найти количество яблок у мальчика, нам нужно узнать, чему равна сумма яблок –тех которые были у мальчика(-3), и тех, которые дал папа(10). То есть, чтобы ответить на главный вопрос задачи, достаточно сложить -3 и 10. Но слагаемые имеют разные знаки «+» и «-». Как же выполнить сложение положительного и отрицательного чисел? Запомнив алгоритм сложения положительных и отрицательных чисел сделать это, будет очень просто.

Используем рассмотренный алгоритм при выполнении действий.
Суммируем-3 и 10. Для этого:
- определяем модули: -3=|3|, 10=|10|;
- сравниваем модули, определяя больший: |3|<|10|;
- от большего отнимаем меньший: 10 – 3=7;
- так как по условию 10 – число положительное, то и результат будет числом положительным.
Записывается в таком виде:
-3+10=10 – 3=7.
Выходит, у мальчика стало 7 яблок.

Рассмотрим еще один пример сложения чисел с разными знаками.
Вычислите сумму -28 и 11.
Известные слагаемые имеют разные знаки, то есть -28 является значением отрицательным, а 11–положительным. Чтобы суммировать слагаемые, необходимо воспользоваться ранее рассмотренным алгоритмом. Вначале, определяем модули и сравниваем их.
-28=|28|;
11=|11|;
28>11.
Помним, что большее значение модуля имеет отрицательное слагаемое (-28), поэтому перед результатом нужно будет поставить знак «минус». Теперь, находим разность большего и меньшего значения модуля (28-17) и записываем математическое выражение:
-28+11=-(28-11)=-17.
Учитывая рассмотренные примеры, можно сказать, что:
любое числовое значение от прибавления к нему положительного числа, всегда становится больше, а от прибавления отрицательного числа только меньше.
Докажем справедливость данного правила, вычислив выражение и сравнив уменьшаемое с полученной суммой:-150+50.
Чтобы найти значение выражения нужно определить модули (150 и 50), оставив знак«-» модуля большего слагаемого, от большего значения отнимаем меньшее:
-150+50=-(150-50)=-100.
Сравним найденное значение выражения (-100) с уменьшаемым (-150), используя правило сравнения чисел с отрицательным знаком:
При сравнении цифровых значений со знаком «минус», меньшим будет то, чей модуль больше.
-150=|150|;
-100=|100|.
150>100;
-150<-100.
Действительно, при сложении с отрицательным числом уменьшаемое стало только меньше.
Вычитание отрицательных чисел и чисел с разными знаками
Мы уже знаем, как выполнять сложение и вычитание положительных и отрицательных чисел, но хочется сказать, что именно в этом разделе математики, большую роль играют противоположные числа. Для тех, кто забыл, напоминаем, какие числовые значения называются противоположными:
Если два числа отличаются только знаком, то они являются противоположными:-13 и 13, 141 и -141, 1000 и -1000.
Чтобы понять, какие правила необходимо соблюдать при выполнении вычитания чисел с разными знаками, давайте разберем задание.
Определите, чему будет равно значение выражения: от -510 отнять +210.
На первый взгляд задание очень простое и не вызывает никаких проблем. Но стоит записать разность в виде выражения:
-510-(+210)
Сразу возникает вопрос «Как вычитать, если уменьшаемое со знаком «минус», а вычитаемое со знаком «плюс»?».Чтобы решение подобных выражений не вызывало у вас трудностей, возьмите на заметку правило:
Чтобы выполнить вычитание чисел с разными знаками, нужно уменьшаемое оставить без изменений и прибавить к нему число, противоположное вычитаемому.
Например: -5-(+2).
Минус пять оставляем без изменений. Вычитаемое +2, а противоположное ему -2. Складываем уменьшаемое(-5) и число противоположное вычитаемому(-2): -5+(-2).
По правилу сложения отрицательных чисел, складываем модули(5+2) и ставим знак «-»:
-5+(-2)=-(5+2)=-7
Учитывая данное правило, получается, что к уменьшаемому(-510) необходимо прибавить значение,противоположное вычитаемому(210), таким числом будет -210:
Запишем выражение:
-510-(+210)=-510+(-210). Чтобы вычислить полученное выражение нужно сложить отрицательные значения, согласно правилу сложения отрицательных чисел:
-510-(+210)=-510+(-210)=-(510+210)=-720.
Вычисления окончены.

Источник
Рассмотрим следующее задание.
Найдите значение выражения: -248+248.
Используем правило сложения значений с разными знаками.
-248=|248|;
248=|248|;
248 – 248=0.
Следовательно, при сложении противоположных числовых значений в результате всегда будет 0.
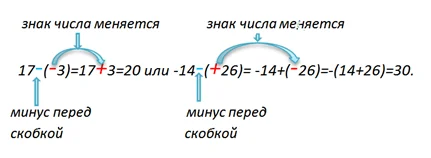
Зная правило вычитания отрицательных чисел, можем сделать вывод, что знаки, стоящие перед скобками, могут менять знак числа, находящегося в скобках.
К примеру, в выражении 19-(-4), при вычислении используем правило, согласно которого, к уменьшаемому прибавляем, число противоположное вычитаемому, то есть знак вычитаемого «-» меняем на противоположный «+». Получим:

Запомни! Если перед скобкой в математическом выражении стоит знак «минус», то знак числа в скобках меняется на противоположный.
Ну а сейчас, разберем задание, в котором перед скобкой стоит знак «плюс».
Вычисли: -36+(-7).
В этом задании воспользуемся правилом сложения отрицательных чисел– сложим модули числовых значений, а перед суммой поставим знак «минус»:

Мы видим, что «плюс» перед скобкой никак не повлиял на знак числа, стоящего в скобках. Запомни! Если перед скобками стоит «плюс», то знак числового значения, стоящего в скобках никак не меняется.
В выполнении рассматриваемых действий нет ничего сложного. Главное запомнить основные требования и придерживаться их в процессе любых вычислений! Если сразу запомнить все правила не получается, заходи на сайт 100уроков.ru и мы всегда с удовольствием напомним нужное правило или алгоритм.
Минутка истории
История математики утверждает, что человечество длительное время не принимало ряд отрицательных числовых значений. Данный вид чисел, казался непонятным и ненужным. Привычных нам знаков «плюс» и «минус» просто не существовало. Если возникала необходимость в записи отрицательно числа, то его записывали следующим образом «долг в 30 монет». И лишь математики Древней Индии и Китая, выполняли записи отрицательных чисел без употребления слова «долг», а просто использовали черные чернила, вместо синих.
Только в 3 веке греческий ученый Диофант, стал обозначать знак «минус» вот таким символом .
Привычные нам знаки «+» и «-» появились в Германии в конце 15 века. Чешский ученый Ян Видман, отразил данные знаки в своей книге-пособии, помогающей подсчитывать прибыль и убытки чешским купцам. Стоит заметить, что данная книга была написана от руки и имела огромную популярность среди богатых людей того времени.
Поиск значений выражений — основное математическое действие. Им сопровождается каждый пример, задача. Поэтому чтобы вам было проще работать с различными математическими выражениями, подробно разберем способы и правила их решения в данной статье. Правила представлены в порядке увеличения сложности: от простейших выражений до выражений с функциями. Для лучшего понимания каждый пункт сопровождается подробным пояснением и расписанными примерами.
Поиск значения числовых выражений
Числовые выражения представляют собой математические задачи, состоящие, преимущественно, из чисел. Они подразделяются на несколько групп в зависимости от своей сложности: простейшие, со скобками, корнями, дробями и т.д. Каждый тип выражений подразумевает свои правила нахождения значения, порядок действий. Рассмотрим каждый случай подробнее.
Простейшие числовые выражения. К простейшим числовым выражениям относятся примеры, состоящие из двух элементов:
- Числа (целые, дробные и т.д.);
- Знаки: «+», «—», «•» и «÷».
Чтобы найти значение выражения в данном случае, необходимо выполнить все арифметические действия (которые подразумевают конкретные знаки). В случае отсутствия скобок решение примера производится слева направо. Первыми выполняются действия деления и умножения. Вторыми — сложение и вычитание.
Пример 1. Решение числового выражения
Задача. Решить:
20 — 2 • 10 ÷ 5 — 4 = ?
Решение. Чтобы решить выражение, нам необходимо выполнить все арифметические действия в соответствии с установленными правилами. Поиск значения начинается с решения деления и умножения. В первую очередь находим произведение цифр 2 и 10 (если рассматривать с левой стороны, данное действие является первым по значимости). Получаем 20. Теперь это число делим на 5. Итог — 4. Когда известно значение основных действий, можем подставить его в наш пример:
20 — 4 — 4 = ?
Упрощенный пример также решаем слева направо: 20 — 4 = 16. Второе действие: 16 — 4 = 12. Ответ 12.
Решение без пояснений. 20 — 2 • 10 ÷ 5 — 4 = 20 — (2 • 10 ÷ 5) — 4 = 20 — 4 — 4 = 12.
Ответ. 12
Пример 2. Решение числового выражения
Задача. Решить:
0,2 — 5 • (— 4) + 1/2 • 5 • 4 = ?
Решение. Начинаем решение с умножения и деления. Умножая 5 на (— 4) получаем (— 20), т.к. производное сохраняет знак множителя. Далее умножаем 1/2 на 5. Для этого преобразуем дробь: 1/2 = 5/10 = 0,5. 0,5 умножаем на 5. Ответ — 2,5. Далее умножаем полученное число на 4. 2,5 • 4 = 10. Получаем следующее выражение:
0,2 — (— 20) + 10
Теперь нам остается решить сложение и вычитание. В первую очередь раскрываем скобку и получаем:
0,2 + 20 + 10 = 30,2
Решение без пояснений. 0,2 — 5 • (— 4) + 1/2 • 5 • 4 = 0,2 — (— 20) + 10 = 0,2 + 20 + 10 = 30,2
Ответ. 30,2
Находим значение выражения со скобками
Скобки определяют порядок действий при решении примера. Выражения, находящиеся внутри скобок «()» имеют первостепенную значимость, независимо от того, какое математическое действие в них выполняется.
Пример 3. Значение числового выражения со скобками
Задача. Решить:
5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = ?
Решение. Начинаем нахождение значения выражения с решения скобок. Порядок действий определяется слева направо. При этом не забываем, что после раскрытия скобок в первую очередь решаем умножение и деление и лишь потом — вычитание и сложение:
- 7 — 2 • 3 = 7 — 6 = 1
- 6 — 4 = 2
Когда скобки решены, подставляем полученные значения в наш пример:
5 + 1 • 2 ÷ 2
Снова решаем все по порядку, не забывая о том, что деление и умножение выполняется в первую очередь:
- 1 • 2 = 2
- 2 ÷ 2 = 1
Упрощенное выражение выглядит следующим образом:
5 + 1 = 6
Решение без пояснений. 5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = 5 + (7 — 6) • 2 ÷ 2 = 5+ 1 • 2 ÷ 2 = 5 + 1 = 6
Ответ. 6
Значение числового выражения со скобками
Задача. Решить:
4 + (3 + 1 + 4 • (2+3)) = ?
Решение. Подобные примеры решаются поэтапно. Помним, что поиск выражения со скобками начинается с решения скобок. Поэтому в первую очередь решаем:
3 + 1 + 4 • (2+3)
В уже упрощенном примере снова встречаются скобки. Их будем решать в первую очередь:
2 + 3 = 5
Теперь можем подставить определенное значение в общую скобку:
3 + 1 + 4 • 5
Начинаем решение с умножения и далее слева направо:
- 4 • 5 = 20
- 3 + 1 = 4
- 4 + 20 = 24
Далее подставляем полученный ответ вместо большой скобки и получаем:
4 + 24 = 28
Решение без пояснений. 4 + (3 + 1 + 4 • (2+3)) = 4 + (3 + 1 + 4 • 5) = 4 + (3 + 1 + 20) = 4 + 24 = 28
Ответ. 28
Важно: Чтобы правильно определить значение числового выражения с множественными скобками, необходимо выполнять все действия постепенно. Скобки читаются слева направо. Приоритет в решении внутри скобок остается за делением и умножением.
Поиск значения выражения с корнями
Часто алгебраические задания основываются на нахождении значений из-под корня. И если определить √4 несложно (напомним, это будет 2), то с примерами, которые полностью расположены под корнем, возникает ряд вопросов. На самом деле в таких заданиях нет ничего сложного. В данном случае порядок действий следующий:
- Решаем все выражение, которое находится под корнем (не забываем о правильной последовательности: сперва скобки, деление и умножение, а лишь потом — сложение и вычитание);
- Извлекаем корень из числа, которое получили в результате решения обычного примера.
Если же и под корнем имеется корень (например: √ 4 + 8 — √4), то начинаем решение примера с его извлечения (в нашем примере это будет: √ 4 + 8 — 2). Если подкоренные числа возведены во вторую степень, то их квадратный корень будет равняться модулю подкоренного выражения.
Значение числового выражения с корнями
Задача. Решить:
√ 2² • 2² • 3² = ?
Решение. Все действия под корнем одинаковы — умножение. Это дает нам право разделить выражение на множители. Получаем:
√2² • √2² • √3² = ?
Т.к. под квадратным корнем у нас числа, возведенные во вторую степень, получаем:
2 • 2 • 3 = 12
Решение без пояснений. √ 2² • 2² • 3² = √2² • √2² • √3² = 2 • 2 • 3 = 12
Ответ. 12
Нет времени решать самому?
Наши эксперты помогут!
Находим значение числовых выражений со степенями
Следующий математический знак, который имеет приоритет в процессе решения, — степени. Они представляют собой результат многократного умножения числа на себя. Само число является основанием степени. А количество операций умножения — ее показателем. Причем выражен он может быть не только целым числом, но и дробью, полноценным числовым выражением.
Начинается решение выражения со степенями с вычисления самих степеней. Если они представляют собой полноценное выражение (например: [3^{3 cdot 4-10}]), то его необходимо решить в нашем примере это будет: [3^{12-10}=3^{2}=9].
Задача. Решите:
[ 3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=? ]
Решение. Чтобы решить это выражение со степенями, воспользуемся равенством:
[(a cdot b)^{r}=a^{r} cdot b^{r}]
Рассматривая пример слева направо, видим, что у первых двух множителей одинаковые степени. Это позволяет нам упростить выражение:
[ (3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3} ]
Зная, что при умножении степени с одинаковыми показателями складываются, получаем следующее выражение:
[ 21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21 ]
Решение без пояснений: [3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=(3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21]
Ответ. 21
Интересно: Этот же пример можно решить и другим способом, преобразовав число 21 в степени ⅔ в два множителя. В данном случае решение будет выглядеть следующим образом:
[3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot(3 cdot 7)^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot 3^{2 / 3} cdot 7^{2 / 3}=3^{1 / 3+2 / 3} cdot 7^{1 / 3+2 / 3}=3^{1}+7^{1}=21]
Ответ. 21
Задача. Решить:
[ 2^{-2 sqrt{5}} cdot 4^{sqrt{5}-1}+left((sqrt{3})^{1 / 3}right)^{6} ]
Решение. В данном случает получить точные числовые значения показателей степеней не удастся. Поэтому искать значение выражения с дробями в виде степени будем снова через упрощение:

Ответ. 3,25
Выражения с дробями
Поиск значения выражения дробей начинается с их приведения к общему виду. В большинстве случаев проще представить все значения в виде обыкновенной дроби с числителем и знаменателем. После преобразования всех чисел необходимо привести все дроби к общему знаменателю.
Важно: Прежде чем найти выражение дробей, необходимо провести вычисления в их знаменателе и числителе отдельно. В данном случае действуют стандартные правила решения.
Когда дроби приведены к единому знаменателю можно переходить к решению. Вычисление значений верхней строки (числителя) и нижней (знаменателя) производятся параллельно.
Задача. Решить:
[ 6 frac{2}{13}+4 frac{1}{13}=? ]
Решение. Действуя по главному правилу, прежде чем найти значение числового выражения, преобразуем всего его части в простую дробь. Получаем:
[ frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13} ]
Теперь выполняем вычисления в знаменателе и числителе и находим ответ:
[ frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13}=frac{80}{13}+frac{53}{13}=frac{133}{13}=10 frac{3}{13} ]
Ответ. [10 frac{3}{13}]
Примеры(2):

Задача. Решить:
[ frac{2}{sqrt{5}-1}-frac{2 sqrt{5}-7}{4}-3=? ]
Решение. В данном примере мы не можем извлечь корень из пятерки. Но мы можем воспользоваться формулой разложения корней:
[ frac{2}{sqrt{5}-1}=frac{2(sqrt{5}+1)}{(sqrt{5}-1)(sqrt{5}+1)}=frac{2(sqrt{5}+1)}{5-1}=frac{2 sqrt{5}+2}{4} ]
Теперь можем придать нашему первоначальному выражению следующий вид:
[ frac{2 sqrt{5}+2}{4} frac{2 sqrt{5}-7}{4}-3=frac{2 sqrt{5}+2-2 sqrt{5}+7}{4}-3=frac{9}{4} 3=-frac{3}{4} ]
Ответ. [-frac{3}{4}].
Выражения с логарифмами
Как и степени, логарифмы (log), имеющиеся в выражении, вычисляются (если это возможно) в первую очередь. К примеру, зная, что [log _{2} 4=2] мы можем сразу упростить выражение [log _{2} 4+5 cdot 6] до простого и понятного 2 + 5*6 = 32.
Со степенями логарифмы объединяет и порядок выполнения действий. Прежде чем искать значение выражения логарифмов, необходимо вычислить его основание (если оно представлено математическим выражением).
В случаях, когда полное вычисление логарифма невозможно, производится упрощение примера.
Задача. Решить:
[log _{27} 81+log _{27} 9=?]
Решение. Чтобы найти логарифм выражения, воспользуемся свойствами логарифмов и представим значение логарифмов со степенями:
![]()
Это позволит нам решить пример следующим образом:

Ответ. 2
Решаем выражения с тригонометрической функцией
Часто в выражениях встречаются тригонометрические функции. Всего их в математике шесть:
- Синус;
- Косинус;
- Котангенс;
- Тангенс;
- Секанс;
- Косеканс.
Изучение тригонометрии начинается в 9-м классе, когда ученики уже подготовлены к сложным задачам. Большинство заданий представляются с sin и cos. Остальные функции встречаются значительно реже.
В математических примерах, которые содержат sin, cos, tg и др. функции, вычисление тригонометрической функции производится в первую очередь. Если это невозможно — осуществляется упрощение выражения до получения краткой формулы.
Задача. Решить:
[ frac{24}{sin ^{2} 127+1+sin ^{2} 217} ]
Решение. Разложим 217 на 90 и 127. Т.к. по формуле приведения sin(90 + a) = cosa, получаем:
sin217 — sin (90 + 127) = cos127
Теперь заменяем полученной формулой наше слагаемое в знаменателе дроби:
[ frac{24}{sin ^{2} 127+cos ^{2} 127+1} ]
Вспоминаем, что по тригонометрическому тождеству sin2a+ cos2 a= 1 (независимо от значения угла a). Поэтому одну часть слагаемого знаменателя (sin2127+ cos2127) преобразуем в единицу и получаем:
[ frac{24}{sin ^{2} 127+cos ^{2} 127+1}=frac{24}{1+1}=frac{24}{2}=2 ]
Ответ. 2

Важно: Не стоит бояться буквенных тригонометрических значений. Большинство примеров построено таким образом, чтобы функции можно было заменить более удобной для вычисления формулой. Поэтому вместо того, чтобы пытаться сразу решить пример, стоит обратить внимание на особенности функций и возможность их приведения к подходящей формуле.
Задача. Решить:
[ sqrt{4} 8-sqrt{1} 92 sin ^{2} frac{19 pi}{12}=? ]
Решение. Начинаем решение с разбора второй дроби. Обращаем внимание, что 192 = 48 • 2. А значит, корень этого числа можно представить в виде 2√48. Зная это и используя формулу косинуса двойного угла, преобразим наше выражение:

Теперь по формуле приведения решаем наш пример:
[ sqrt{4} 8 cos left(3 pi+frac{pi}{6}right)=sqrt{4} 8left(-cos frac{pi}{6}right)=-sqrt{4} 8 cdot frac{sqrt{3}}{2}=-4 sqrt{3} cdot frac{sqrt{3}}{2}=-6 ]
Ответ. — 6.
Общий случай: находим значения выражений с дробями, функциями, степенями и не только
Самым сложным считается поиск числовых выражений общих случаев. Они представляют собой тригонометрические примеры, которые могут содержать:
- Степени;
- Скобки;
- Корни;
- Функции и т.д.
Общие числовые выражения сложны только длительностью решения. В остальном же они ничуть не сложнее, чем решение каждого примера (со скобкой, степенями, функциями и т.д.) по отдельности.
Чтобы найти значение выражения с логарифмами, тригонометрическими функциями, скобками и/или другими действиями, необходимо помнить три основных правила:
- Упрощение. Прежде чем приступать к решению внимательно изучите выражение. Особенно — его степени, корни, логарифмы, функции. В большинстве случаев их можно сократить или заменить простым числовым значением еще до решения.
- Скобки. Независимо от типа выражения, действий, начинать решение всегда необходимо со скобок. Часто именно игнорирование этого правила приводит к получению неверного ответа или отсутствию решения в принципе.
- Общий вид. Старайтесь привести выражение к общему виду. Особенно это касается дробей. Смешанные и десятичные дроби преобразуйте в обычные.
- Последовательность. Действия в скобках и действия после их решения выполняются слева направо. В первую очередь необходимо совершать умножение и деление. Когда все произведения и частные найдены, можно переходить к сложению и вычитанию.
Для удобства решения и устранения возможных ошибок рекомендуем расставлять порядок действий непосредственно над математическими знаками.
Задача. Решить:
[ -frac{sqrt{2} sin left(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)right)+3}{operatorname{Ln} e^{2}}+left(1+3^{sqrt{9}}right)=? ]
Решение. Чтобы решить этот пример, сначала найдем значение выражения числителя дроби, а точнее — подкоренного выражения. Для этого необходимо вычислить значение sin и общего выражения. Начинаем с раскрытия скобок в числителе:

Полученное значение можем подставить в подкоренное выражение для вычисления числителя дроби:
[ sqrt{2} sin cdotleft(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)+3=sqrt{4}=2right. ]
Со знаменателем дела обстоят куда проще:
[ ln e^{2}=2 ]
Числитель и знаменатель у нас одинаковые, что позволяет нам их сократить:

Теперь остается решить следующее выражение:

Ответ. 27
Как видите, при последовательном решении примеров с большим количеством действий нет ничего сложного. Главное — верно обозначить последовательность шагов и четко ей следовать.
Как найти значение выражения числителя дроби, подкорневого значения рационально?
Независимо от типа выражения решать его необходимо последовательно, руководствуясь стандартными правилами (описаны ранее). Но не стоит забывать, что во многих случаях поиск ответа может быть значительно упрощен за счет рационального подхода к решению. Основывается он на нескольких правилах.
Правило 1. Когда произведение равно нулю
Производное равно нулю в том случае, если хотя бы один из его сомножителей равен нулю. Если вы решаете пример из нескольких сомножителей, одним из которых является «0», то проводить многочисленные вычислительные действия не стоит.
Например, выражение [3 cdotleft(451+4+frac{18}{3}right)left(1-sin left(frac{3 pi}{4}right)right) cdot 0] будет равняться нулю.
Правило 2. Группировка и вынесение чисел
Ускорить процесс поиска ответа можно за счет группировки множителей, слагаемых или вынесения единого множителя за скобки. Также не стоит забывать о возможности сокращения дроби.
Например, выражение [frac{left(451+4+frac{18}{3}right)}{4left(451+4+frac{18}{3}right)}] решать не надо. Достаточно сократить скобки, чтобы получить ответ [=frac{1}{4}]
Решение примеров с переменными
Примеры с переменными отличаются от числовых только формой предоставления. В данном случае значения предоставляются дополнительно к выражению.
Пример задания: Найдите значение выражения 2x — y, если x = 2,5, а y = 2. В данном случае решение будет выглядеть следующим образом:
2x — y = 2 • 2,5 — 2 = 3
При этом в таких примерах сохраняются все описанные выше правила. Касается это и советов по рациональному решению примеров. Так, решать дробь [frac{sqrt{y}}{sqrt{y}}] бессмысленно, т.к. при любых значениях «y» ответ будет одинаковым — 1.
Сложение и вычитание целых чисел с разными знаками
Сложение
При сложении двух целых чисел с одинаковым знаком складываются их абсолютные величины и перед суммой ставится их общий знак.
Примеры:
(+3) + (+7) = 10,
(-3) + (-7) = -10.
Из данных примеров следует, что в результате сложения двух положительных чисел получится положительное число, а в результате сложения двух отрицательных чисел – отрицательное число.
При сложении двух целых чисел с разными знаками нужно взять их абсолютные величины и из большей вычесть меньшую, в результате ставится знак того числа, у которого абсолютная величина больше.
Другими словами, можно просто, не обращая внимания на знаки, вычесть из большего числа меньшее и у получившегося результата поставить знак большего числа:
Примеры:
(-4) + (+11) = 7, так как 11 — 4 = 7;
(-5) + (+2) = -3, так как 5 — 2 = 3.
Из данных примеров следует, что в результате сложения двух чисел с разными знаками может получится как положительное, так и отрицательное число.
Сумма двух противоположных чисел равна нулю.
Примеры:
(-7) + 7 = 0,
(+12) + (-12) = 0.
Вычитание
Вычитание одного целого числа из другого можно заменить сложением, при этом уменьшаемое берётся со своим знаком, а вычитаемое с противоположным.
Примеры:
(+6) — (+5) = (+6) + (-5) = 1,
(+6) — (-5) = (+6) + (+5) = 11,
(-6) — (-5) = (-6) + (+5) = -1,
(-6) — (+5) = (-6) + (-5) = -11.
Из данных примеров следует, что, чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.
При решении выражений, содержащих и сложение, и вычитание, можно сначала заменить вычитание сложением, затем отдельно сложить положительные и отрицательные слагаемые, а потом найти сумму получившихся чисел.
Пример.
12 — 18 + 41 — 9.
Решение: Заменим вычитание на сложение:
12 + (-18) + 41 + (-9),
сгруппируем слагаемые по их знакам и сложим отдельно положительные и отрицательные числа:
(12 + 41) + ((-18) + (-9)) = 53 + (-27).
Теперь осталось только найти сумму двух получившихся результатов:
53 + (-27) = 26, значит 12 — 18 + 41 — 9 = 26.
Сложение и вычитание целых чисел
В данном уроке мы изýчим сложение и вычитание целых чисел.
Напомним, что целые числа — это все положительные и отрицательные числа, а также число 0. Например, следующие числа являются целыми:
−3, −2, −1, 0, 1, 2, 3
Положительные числа легко складываются и вычитаются, умножаются и делятся. К сожалению, этого нельзя сказать об отрицательных числах, которые смущают многих новичков своими минусами перед каждой цифрой.
Примеры сложения и вычитания целых чисел
Первое чему следует научиться это складывать и вычитать целые числа с помощью координатной прямой. Совсем необязательно рисовать координатную прямую. Достаточно воображать её в своих мыслях и видеть, где располагаются отрицательные числа и где положительные.
Совсем необязательно рисовать координатную прямую. Достаточно воображать её в своих мыслях и видеть, где располагаются отрицательные числа и где положительные.
Рассмотрим следующее простейшее выражение
1 + 3
Значение данного выражения равно 4
1 + 3 = 4
Этот пример можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1, нужно сдвинуться вправо на три шага. В результате мы окажемся в точке, где располагается число 4. На рисунке можно увидеть, как это происходит:
Знак плюса в выражении 1 + 3 указывает нам, что нужно двигаться вправо в сторону увеличения чисел.
Пример 2. Найдём значение выражения 1 − 3
Значение данного выражения равно −2
1 − 3 = −2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −2. На рисунке можно увидеть, как это происходит:
На рисунке можно увидеть, как это происходит:
Знак минуса в выражении 1 − 3 указывает нам, что нужно двигаться влево в сторону уменьшения чисел.
Вообще, если осуществляется сложение, то нужно двигаться вправо в сторону увеличения. Если же осуществляется вычитание, то нужно двигаться влево в сторону уменьшения.
Пример 3. Найти значение выражения −2 + 4
Значение данного выражения равно 2
−2 + 4 = 2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на четыре шага. В результате мы окажемся в точке, где располагается положительное число 2
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на четыре шага, и оказались в точке, где располагается положительное число 2.
Пример 4. Найти значение выражения −1 − 3
Значение данного выражения равно −4
−1 − 3 = −4
Этот пример опять же можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −4
Для этого из точки, где располагается отрицательное число −1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −4
Видно, что мы сдвинулись из точки где располагается отрицательное число −1 в левую сторону на три шага, и оказались в точке, где располагается отрицательное число −4.
Пример 5. Найти значение выражения −2 + 2
Значение данного выражения равно 0
−2 + 2 = 0
Этот пример можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на два шага и оказались в точке, где располагается число 0.
Правила сложения и вычитания целых чисел
Чтобы сложить или вычесть целые числа, вовсе необязательно каждый раз воображать координатную прямую, и тем более рисовать её. Можно воспользоваться готовыми правилами.
Можно воспользоваться готовыми правилами.
Применяя правила, нужно обращать внимания на знак операции и знаки чисел, которые нужно сложить или вычесть. От этого будет зависеть какое правило применять.
Пример 1. Найти значение выражения −2 + 5
Здесь к отрицательному числу прибавляется положительное число. Другими словами, осуществляется сложение чисел с разными знаками, потому что −2 это отрицательное число, а 5 — положительное. Для таких случаев применяется следующее правило:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.
Итак, посмотрим какой модуль больше:
Модуль числа 5 больше, чем модуль числа −2. Правило требует из большего модуля вычесть меньший. Поэтому мы должны из 5 вычесть 2, и перед полученным ответом поставить знак того числа, модуль которого больше.
У числа 5 модуль больше, поэтому знак этого числа и будет в ответе. То есть ответ будет положительным:
То есть ответ будет положительным:
−2 + 5 = 5 − 2 = 3
Обычно записывают покороче: −2 + 5 = 3
Пример 2. Найти значение выражения 3 + (−2)
Здесь как и в предыдущем примере, осуществляется сложение чисел с разными знаками. 3 это положительное число, а −2 — отрицательное. Обратите внимание, что число −2 заключено в скобки, чтобы сделать выражение понятнее. Это выражение намного проще для восприятия, чем выражение 3 + −2.
Итак, применим правило сложения чисел с разными знаками. Как и в прошлом примере, из большего модуля вычитаем меньший модуль и перед ответом ставим знак того числа, модуль которого больше:
3 + (−2) = |3| − |−2| = 3 − 2 = 1
Модуль числа 3 больше, чем модуль числа −2, поэтому мы из 3 вычли 2, и перед полученным ответом поставили знак того числа, модуль которого больше. У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть ответ положительный.
Обычно записывают покороче 3 + (−2) = 1
Пример 3.
Найти значение выражения 3 − 7
В этом выражении из меньшего числа вычитается большее. Для такого случая применяется следующее правило:
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее, и перед полученным ответом поставить минус.
3 − 7 = 7 − 3 = −4
В этом выражении есть небольшая загвоздка. Вспомним, что знак равенства (=) ставится между величинами и выражениями тогда, когда они равны между собой.
Значение выражения 3 − 7 как мы узнали равно −4. Это означает, что любые преобразования которые мы будем совершать в данном выражении, должны быть равны −4
Но мы видим, что на втором этапе располагается выражение 7 − 3, которое не равно −4.
Чтобы исправить эту ситуацию, выражение 7 − 3 нужно взять в скобки и перед этой скобкой поставить минус:
3 − 7 = − (7 − 3) = − (4) = −4
В этом случае равенство будет соблюдаться на каждом этапе:
После того, как выражение вычислено, скобки можно убрать, что мы и сделали.
Поэтому, чтобы быть более точным, решение должно выглядеть так:
3 − 7 = − (7 − 3) = − (4) = − 4
Данное правило можно записать с помощью переменных. Выглядеть оно будет следующим образом:
a − b = − (b − a)
Большое количество скобок и знаков операций могут усложнять решение, казалось бы совсем простой задачи, поэтому целесообразнее научиться записывать такие примеры коротко, например 3 − 7 = − 4.
На самом деле сложение и вычитание целых чисел сводится только к сложению. Это означает, что если требуется осуществить вычитание чисел, эту операцию можно заменить сложением.
Итак, знакомимся с новым правилом:
Вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
Например, рассмотрим простейшее выражение 5 − 3. На начальных этапах изучения математики мы ставили знак равенства и записывали ответ:
5 − 3 = 2
Но сейчас мы прогрессируем в изучении, поэтому надо приспосабливаться к новым правилам. Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
На примере выражения 5 − 3 попробуем понять это правило. Уменьшаемое в данном выражении это 5, а вычитаемое это 3. Правило говорит, что для того, чтобы из 5 вычесть 3 , нужно к 5 прибавить такое число, которое будет противоположно 3. Противоположное для числа 3 это число −3. Записываем новое выражение:
5 + (−3)
А как находить значения для таких выражений мы уже знаем. Это сложение чисел с разными знаками, которое мы рассмотрели ранее. Чтобы сложить числа с разными знаками, мы из большего модуля вычитаем меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше:
5 + (−3) = |5| − |−3| = 5 − 3 = 2
Модуль числа 5 больше, чем модуль числа −3. Поэтому мы из 5 вычли 3 и получили 2. У числа 5 модуль больше, поэтому знак этого числа и поставили в ответе. То есть ответ положителен.
Поначалу быстро заменять вычитание сложением удаётся не всем. Это связано с тем, что положительные числа записываются без знака плюс.
Это связано с тем, что положительные числа записываются без знака плюс.
Например, в выражении 3 − 1 знак минуса, указывающий на вычитание, является знаком операции и не относится к единице. Единица в данном случае является положительным числом, и у неё есть свой знак плюса, но мы его не видим, поскольку плюс перед положительными числами не записывают.
А стало быть, для наглядности данное выражение можно записать следующим образом:
(+3) − (+1)
Для удобства числа со своим знаками заключают в скобки. В таком случае заменить вычитание сложением намного проще.
В выражении (+3) − (+1) вычитаемое это число (+1), а противоположное ему число это (−1).
Заменим вычитание сложением и вместо вычитаемого (+1) записываем противоположное ему число (−1)
(+3) − (+1) = (+3) + (−1)
Дальнейшее вычисление не составит особого труда.
(+3) − (+1) = (+3) + (−1) = |3| − |−1| = 3 − 1 = 2
На первый взгляд покажется, какой смысл в этих лишних телодвижениях, если можно старым добрым методом поставить знак равенства и сразу записать ответ 2. На самом деле это правило ещё не раз нас выручит.
На самом деле это правило ещё не раз нас выручит.
Решим предыдущий пример 3 − 7, используя правило вычитания. Сначала приведём выражение к понятному виду, расставив каждому числу свои знаки.
У тройки знак плюса, поскольку она является положительным числом. Минус, указывающий на вычитание не относится к семёрке. У семёрки знак плюса, поскольку она является положительным числом:
(+3) − (+7)
Заменим вычитание сложением:
(+3) − (+7) = (+3) + (−7)
Дальнейшее вычисление не составляет труда:
(+3) − (−7) = (+3) + (-7) = −(|−7| − |+3|) = −(7 − 3) = −(4) = −4
Пример 7. Найти значение выражения −4 − 5
Приведём выражение к понятному виду:
(−4) − (+5)
Перед нами снова операция вычитания. Эту операцию нужно заменить сложением. К уменьшаемому (−4) прибавим число, противоположное вычитаемому (+5). Противоположное число для вычитаемого (+5) это число (−5).
(−4) − (+5) = (−4) + (−5)
Мы пришли к ситуации, где нужно сложить отрицательные числа. Для таких случаев применяется следующее правило:
Для таких случаев применяется следующее правило:
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.
Итак, сложим модули чисел, как от нас требует правило, и поставим перед полученным ответом минус:
(−4) − (+5) = (−4) + (−5) = |−4| + |−5| = 4 + 5 = −9
Запись с модулями необходимо заключить в скобки и перед этими скобками поставить минус. Так мы обеспечим минус, который должен стоять перед ответом:
(−4) − (+5) = (−4) + (−5) = −(|−4| + |−5|) = −(4 + 5) = −(9) = −9
Решение для данного примера можно записать покороче:
−4 − 5 = −(4 + 5) = −9
или ещё короче:
−4 − 5 = −9
Пример 8. Найти значение выражения −3 − 5 − 7 − 9
Приведём выражение к понятному виду. Здесь все числа, кроме числа −3 являются положительными, поэтому у них будут знаки плюса:
(−3) − (+5) − (+7) − (+9)
Заменим вычитания сложениями. Все минусы, кроме минуса, стоящего перед тройкой, поменяются на плюсы, и все положительные числа поменяются на противоположные:
(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9)
Теперь применим правило сложения отрицательных чисел. Чтобы сложить отрицательные числа, нужно сложить их модули и перед полученным ответом поставить минус:
Чтобы сложить отрицательные числа, нужно сложить их модули и перед полученным ответом поставить минус:
(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9) =
= −( |−3| + |−5| + |−7| + |−9| ) = −(3 + 5 + 7 + 9) = −(24) = −24
Решение данного примера можно записать покороче:
−3 − 5 − 7 − 9 = −(3 + 5 + 7 + 9) = −24
или ещё короче:
−3 − 5 − 7 − 9 = −24
Пример 9. Найти значение выражения −10 + 6 − 15 + 11 − 7
Приведём выражение к понятному виду:
(−10) + (+6) − (+15) + (+11) − (+7)
Здесь сразу две операции: сложение и вычитание. Сложение оставляем без изменения, а вычитание заменяем сложением:
(−10) + (+6) − (+15) + (+11) − (+7) = (−10) + (+6) + (−15) + (+11) + (−7)
Соблюдая порядок действий, выполним поочерёдно каждое действие, опираясь на ранее изученные правила. Записи с модулями можно пропустить:
Первое действие:
(−10) + (+6) = − (10 − 6) = − (4) = − 4
Второе действие:
(−4) + (−15) = − (4 + 15) = − (19) = − 19
Третье действие:
(−19) + (+11) = − (19 − 11) = − (8) = −8
Четвёртое действие:
(−8) + (−7) = − (8 + 7) = − (15) = − 15
Таким образом, значение выражения −10 + 6 − 15 + 11 − 7 равно −15
Примечание. Приводить выражение к понятному виду, заключая числа в скобки, вовсе необязательно. Когда происходит привыкание к отрицательным числам, это действие можно пропустить, поскольку оно отнимает время и может запутать.
Приводить выражение к понятному виду, заключая числа в скобки, вовсе необязательно. Когда происходит привыкание к отрицательным числам, это действие можно пропустить, поскольку оно отнимает время и может запутать.
Итак, для сложения и вычитания целых чисел необходимо запомнить следующие правила:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее и перед полученным ответом поставить минус.
Вычесть одно число из другого означает, прибавить к уменьшаемому такое число, которое противоположно вычитаемому.
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
−50 + 40
Решение
−50 + 40 = −10
Задание 2. Найдите значение выражения:
Найдите значение выражения:
25 + (−5)
Решение
25 + (−5) = 20
Задание 3. Найдите значение выражения:
−20 + 60
Решение
−20 + 60 = 40
Задание 4. Найдите значение выражения:
20 + (−8)
Решение
20 + (−8) = 12
Задание 5. Найдите значение выражения:
30 + (−50)
Решение
30 + (−50) = −20
Задание 6. Найдите значение выражения:
27 + (−19)
Решение
27 + (−19) = 8
Задание 7. Найдите значение выражения:
−17 + (−12) + (−8)
Решение
Задание 8. Найдите значение выражения:
−6 − 4
Решение
−6 − 4 = −6 + (−4) = −10
Задание 9. Найдите значение выражения:
−6 − (−4)
Решение
−6 − (−4) = −6 + 4 = −2
Задание 10. Найдите значение выражения:
−15 − (−15)
Решение
−15 − (−15) = −15 + 15 = 0
Задание 11. Найдите значение выражения:
−11 − (−14)
Решение
−11 − (−14) = −11 + 14 = 3
Задание 12. Найдите значение выражения:
Найдите значение выражения:
−3 + 2 − (−1)
Решение
Задание 13. Найдите значение выражения:
−5 − 6 − 3
Решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
правила, примеры, вычитание и сложение с разными знаками
Данная статья посвящена числам с разными знаками. Мы будем разбирать материал и пытаться выполнять вычитание между этими числами. В параграфе мы познакомимся с основными понятиями и правилами, которые пригодятся во время решения упражнений и задач. Также в статье представлены подробно разобранные примеры, которые помогут лучше понять материал.
Как правильно выполнять вычитание
Для того, чтобы лучше понять процесс вычитания, следует начать с основных определений.
Определение 1
Если вычесть из числа a число b, то это можно преобразовать как сложение числа a и -b, где b и −b – числа с противоположными знаками.
Если выразить данное правило буквами, то оно выглядит так a−b=a+(−b), где a и b – любые действительные числа.
Данное правило вычитания чисел с разными знаками работает для действительных, рациональных и целых чисел. Его можно доказать на основании свойств действий с действительными числами. Благодаря им мы может представить числа как несколько равенства (a+(−b))+b=a+((−b)+b)=a+0=a. Так как сложение и вычитание тесно связаны, то равным также будет выражение a−b=a+(−b). Это значит, что рассматриваемое правило вычитания также верно.
Данное правило, которое применяется для вычитания чисел с разными знаками, позволяет работать как с положительными, так и с отрицательными числами. Также можно производить процесс вычитания из отрицательного числа из положительного, которое переходит в сложение.
Для того, чтобы закрепить полученную информацию, мы рассмотрим типичные примеры и на практике рассмотрим правило вычитания для чисел с разными знаками.
Примеры упражнений на вычитание
Закрепим материал, рассмотрев типичные примеры.
Пример 1
Необходимо выполнить вычитание 4 из −16.
Для того, чтобы выполнить вычитание, следует взять число, противоположное вычитаемому 4, есть −4. Согласно рассмотренному выше правилу вычитания (−16) −4=(−16) +(−4). Далее мы должны сложить получившиеся отрицательные числа. Получаем: (−16) +(−4) =−(16+4) =−20. (−16)−4=−20.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Для того, чтобы выполнять вычитание дробей, необходимо представлять числа в виде обыкновенных или десятичных дробей. Это зависит от того, с числами какого вида будет удобнее проводить вычисления.
Пример 2
Необходимо выполнить вычитание −0,7 от 37.
Прибегаем к правилу вычитания чисел. Заменяем вычитание на сложение: 37-(-0,7)=37+0,7.
Мы складываем дроби и получаем ответ в виде дробного числа. 37-(-0,7)=1970.
Когда какое-либо число представлено в виде квадратного корня, логарифма, основной и тригонометрических функций, то зачастую результат вычитания может быть записан в виде числового выражения. Чтобы пояснить данное правило, рассмотрим следующий пример.
Пример 3
Необходимо выполнить вычитание числа 5 из числа -2.
Воспользуемся описанным выше правилом вычитания. Возьмем противоположное число вычитаемому 5 – это −5. Согласно работы с числами с разными знаками -2-5=-2+(-5).
Теперь выполним сложение: получаем -2+(-5)=2+5.
Полученное выражение и является результатом вычитания исходных чисел с разными знаками: -2+5.
Значение полученного выражения может быть вычислено максимально точно только в том случае, если это необходимо. Для подробной информации можно изучить другие разделы, связанные с данной темой.
Сложение и вычитание степеней ⬅️
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n-раз подряд»
где
a — основание степени
n — показатель степени
Соответственно, an= a·a·a·a. ..·a
..·a
Читается такое выражение, как a в степени n.
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить данное число (основание степени) на само себя. А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например число 2, то решается она довольно просто:
2 — основание степени
3 — показатель степени
Действия, конечно, можно выполнять и в онлайн калькуляторе — вот несколько подходящих:
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).
|
Число |
Вторая степень |
Третья степень |
|
1 |
1 |
1 |
|
2 |
4 |
8 |
|
3 |
9 |
27 |
|
4 |
16 |
64 |
|
5 |
25 |
125 |
|
6 |
36 |
216 |
|
7 |
49 |
343 |
|
8 |
64 |
512 |
|
9 |
81 |
729 |
|
10 |
100 |
1000 |
Свойства степеней: когда складывать, а когда вычитать
Степень в математике с натуральным показателем имеет несколько важных свойств, которые позволяют упрощать вычисления. Всего их пять штук — давайте их рассмотрим.
Всего их пять штук — давайте их рассмотрим.
Свойство 1: произведение степеней
При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:
a — основание степени
m, n — показатели степени, любые натуральные числа.
Свойство 2: частное степеней
Когда мы делим степени с одинаковыми основаниями, то основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.
a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n
Свойство 3: возведение степени в квадрат
Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.
a — основание степени (не равное нулю)
m, n — показатели степени, натуральное число
Свойство 4: степень возведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
Затем полученные результаты перемножаются.
a, b — основание степени (не равное нулю)
n — показатели степени, натуральное число
Записывайся на онлайн курсы по математике для учеников с 1 по 11 классы!
Свойство 5: степень частного
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
a, b — основание степени (не равное нулю), любые рациональные числа, b ≠ 0,
n — показатель степени, натуральное число
Сложение и вычитание степеней
Как складывать числа со степенями и как вычитать степени — очень просто. Основной принцип такой: выполняется сначала возведение в степень, а уже потом действия сложения и вычитания. Примеры:
- 23+ 34= 8 + 81= 89
- 63— 33= 216 — 27 = 189
И еще несколько правил:
- при наличии скобок — начинать вычисления нужно внутри них
- только потом возведение производим в степень
- затем выполняем остальные действия: сначала умножение и деление
- после — сложение и вычитание
Сложение степеней с разными показателями
В таком случае действуем согласно общему правилу: сначала выполняем возведение в степень каждого числа, затем — производим сложение.
Сложение степеней с разными основаниями
В целом, это ничем не отличается от предыдущего пункта. Могут быть разные основания, но одинаковые степени. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим сложение.
- 34+ 54=81 + 625 = 706
- 14+ 72= 1+ 49 = 50
Как складывать числа с одинаковыми степенями
Точно также, как и в предыдущем примере. Если степени одинаковые, а основания разные, то нельзя сложить основания и затем эту сумму возводить в степень.
Сначала возводим каждое число в степень и затем выполняем сложение.
В уравнениях это будет происходить немного иначе. Если показатель и основание степени одинаковые (тогда это называется переменная, a2, например) — их коэффициенты можно складывать. Коэффициент — это число перед переменной a2.
2, 3, 5 — коэффициенты
a2 — переменная
Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.
Вычитание степеней с одинаковым основанием
Здесь принцип тот же, что и со сложением: возводим в степень числа и только потом вычитаем их.
Вычитание степеней с разными основаниями
Могут быть разные основания, но одинаковые степени. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим вычитание.
- 54— 44= 625 — 256 = 369
- 74— 32= 2401 — 9 = 2392
Вычитание чисел с одинаковыми степенями
Все точно также, как и со сложением. Если степени одинаковые, а основания разные, то нельзя вычесть основания и затем эту разницу возводить в степень. Сначала возводим каждое число в степень и затем выполняем вычитание.
И та же история с коэффициентами: если показатель степени и основание степени одинаковые (тогда это называется переменная, a2) — их коэффициенты можно вычитать. Коэффициент — это число перед переменной a2.
6, 3, 2 — коэффициенты
a2 — переменная
Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.
Подготовиться к сложной контрольной ребенку помогут в детской онлайн-школе Skysmart. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Запишите вашего ребенка на бесплатный вводный урок математики и начните заниматься ей с удовольствием уже завтра.
Вычитание чисел с разными знаками
В курсе арифметики установлено, что вычитание есть действие, обратное сложению, при помощи которого по данной сумме и по одному слагаемому находят другое слагаемое.
Пользуясь этим определением, мы должны разобрать, как надо выполнять вычитание относительных чисел.
Пусть надо из (+8) вычесть (–3), т. е. пусть надо
Первое данное число выражает данную сумму, второе – данное слагаемое, а над найти другое слагаемое (для него оставлено место после знака равенства), т. е. надо решить вопрос: какое число надо сложить с (–3), чтобы в сумме получилось (+8)? Этот вопрос запишем в такой форме:
е. надо решить вопрос: какое число надо сложить с (–3), чтобы в сумме получилось (+8)? Этот вопрос запишем в такой форме:
(?) + (–3) = +8.
Но сразу этот вопрос решить трудно, а поэтому сначала решим более простой, вспомогательный вопрос: какое число надо сложить с (–3), чтобы в сумме получился нуль ?, т. е.
(?) + (–3) = 0.
На этот вопрос ответ ясен: надо взять для неизвестного слагаемого число, имеющее ту же абсолютную величину, как и данное слагаемое, но обратный знак, – в данном случае надо для неизвестного слагаемого взять число +3. Теперь перейдем к решению главного вопроса: мы взяли для неизвестного слагаемого число + 3 и в сумме получился нуль, но нам надо получить в сумме число +8, поэтому надо чтобы и в другое слагаемое вошло это же число +8. Следовательно, неизвестное слагаемое должно состоять: 1) из +3, чтобы в сумме получился нуль и 2) из +8, чтобы эту сумму «нуль» довести до требуемой +8. Поэтому на месте неизвестного слагаемого пишем + 3 + 8:
(+ 8) – (– 3) = + 3 + 8 = + 11.
Последнее (= + 11) написано на том основании, что числа + 3 и + 8 надо соединить в одно или сложить.
Вот еще примеры:
(– 7) – (+ 5) = – 5 – 7 = – 12.
Искомое слагаемое должно состоять: 1) из –5, чтобы в сумме получился нуль и 2) из –7, чтобы дополнить этот нуль до требуемой суммы, до –7. Сложив числа –5 и –7, получим –12.
(– 3) – (– 8) = + 8 – 3 = + 5.
Искомое слагаемое должно состоять: 1) из +8, чтобы в сумме получился нуль и 2) из –3, чтобы дополнить этот нуль до требуемой суммы, до –3. Сложив числа +8 и –3, получим +5.
(+7) – (+9) = –9 + 7 = –2.
Искомое слагаемое должно состоять: 1) из –9, чтобы в сумме получился нуль и 2) +7, чтобы дополнить этот нуль до требуемой суммы, до +7; сложив числа –9 и +7, получим –2.
Из этих примеров видим, что вычитание в алгебре состоит лишь в умении раскрывать скобки: надо второе число (данное слагаемое или вычитаемое) написать с обратным знаком, а первое число (данную сумму или уменьшаемое) написать с тем же знаком. После того, как это сделано, т. е., когда скобки раскрыты, дело сводится к сложению, так как написаны числа рядом с их знаками, напр., в последнем примере: – 9 + 7.
После того, как это сделано, т. е., когда скобки раскрыты, дело сводится к сложению, так как написаны числа рядом с их знаками, напр., в последнем примере: – 9 + 7.
Так как сумма не изменяется от перестановки слагаемых, то можно числа, полученные в разобранных примерах после раскрытия скобок, переставить, чтобы порядок был согласен с порядком данных чисел:
(+ 8) – (– 3) = + 8 + 3; (– 7) – (+ 5) = – 7 – 5;
– 3 – (– 8) = – 3 + 8; (+ 7) – (+ 9) = + 7 – 9.
Итак,
чтобы раскрыть скобки при вычитании, надо первое число (уменьшаемое) написать без изменения и приписать к нему второе число (вычитаемое) с обратным знаком.
Заметим еще, что при обозначении вычитания первое число пишется часто без скобок, а если оно положительное, то, как уже известно, знак + можно впереди не писать.
Например,
– 3 – (– 5) = – 3 + 5 = + 2; 1 – (– 6) = 1 + 6 = 7;
3 – (+ 3) = 3 – 3 = 0.
14. Примеры на сложение и вычитание. Пусть требуется вычислить:
1 – {3 + [5 – (3 – 5 – 6)]}.
Мы станем руководствоваться следующим порядком: если внутри какой-либо пары скобок нет других скобок и нет действия, то эти скобки можно раскрыть; если же внутри этих скобок есть действие (сложение), то надо сначала его выполнить. В нашем примере такой порядок: сначала выполним сложение чисел, написанных внутри маленьких скобок, потом надо эти скобки раскрыт, выполнить сложение внутри квадратных скобок, раскрыть квадратные скобки, выполнить сложение внутри витых скобок, раскрыть эти скобки и, наконец, сложить полученные числа:
1 – {3 + [5 – (3 – 5 – 6)]} = 1 – {3 + [5 – (– 8)]} = 1 – {3 + [5 + 8]} =
= 1 – {3 + [+13]} = 1 – {3 + 13} = 1 – {+ 16} = 1 – 16 = – 15.
Конечно, при навыке можно сразу выполнять несколько действий и, следовательно, укоротить вычисление.
Еще пример:
Пусть еще требуется вычислить выражение:
a – {(b – c) – [d + (e + f)]} при a = – 3; b = 1; c = 4; d = – 5; e = – 7; f = 2.
Выполним вычисления по действиям:
1) b – c = + 1 – (+ 4) = 1 – 4 = – 3;
2) e + f = (– 7) + (+ 2) = – 7 + 2 = – 5;
3) d + (– 5) = – 5 + (– 5) = – 5 – 5 = – 10;
4) (– 3) – (– 10) = – 3 + 10 = + 7;
5) – 3 – (+ 7) = – 3 – 7 = – 10.
Примеры для упражнений:
Если взять число нуль и прибавлять к нему по +1, то получим ряд постепенно увеличивающихся целых чисел:
0, +1, +2, +3, +4, +5, …..
Этот ряд совпадает (см. конец п. 10) с натуральным рядом чисел, т. е. с
0, 1, 2, 3, 4, 5 …..
Если мы, взяв число нуль, вычтем из него (+1), затем еще раз вычтем (+1) и т. д., то, согласно с тем, как мы это понимали в арифметике по отношению к натуральному ряду чисел, мы теперь признаем, что и здесь станем получать все уменьшающиеся целые числа:
1) 0 – (+ 1) = – 1; 2) (– 1) – (+ 1) = – 1 – 1 = – 2;
3) (– 2) – (+ 1) = – 3 и т. д.
Получим, идя от нуля налево, ряд уменьшающихся относительных чисел:
….., – 5, – 4, – 3, – 2, – 1, 0.
Соединяя этот ряд с предыдущим, получим полный ряд относительных чисел:
….., – 6, – 5, – 4, – 3, – 2, – 1, 0, +1, +2, +3, +4, +5, +6 …..
Этот ряд и вправо и влево идет без конца.
Всякое число в этом ряду больше другого, которое стоит левее и меньше любого, стоящего правее его. Так +1 > –3; 0 > –6; –5 < 0; –3 < +2 и т. д.
Так +1 > –3; 0 > –6; –5 < 0; –3 < +2 и т. д.
В промежутках между целыми числами этого ряда можно вставить бесконечно много дробных чисел.
Урок 28. частное целых чисел. часть 2 — Математика — 6 класс
Математика
6 класс
Урок № 28
Частное целых чисел. Часть 2.
Перечень рассматриваемых вопросов:
- Деление рациональных чисел.
- Правила знаков при делении.
Глоссарий по теме
Чтобы разделить (или умножить) два числа с разными знаками, надо разделить (или перемножить) модули этих чисел и поставить перед полученным частным (или произведением) знак «минус».
Чтобы разделить (или умножить) два числа с одинаковыми знаками, надо разделить (или перемножить) модули этих чисел и поставить перед полученным частным (или произведением) знак «плюс»
В выражениях, где есть только действия умножения и деления чисел с разными знаками, знак можно определить по числу сомножителей. Если число знаков «минус» чётное, то значение выражения будет положительным, а если нечётное, то отрицательным.
Если число знаков «минус» чётное, то значение выражения будет положительным, а если нечётное, то отрицательным.
Чтобы сложить два числа одинакового знака, надо сложить их модули и поставить перед суммой знак слагаемых.
Чтобы сложить два числа с разными знаками, надо из большего модуля вычесть меньший и перед разностью поставить знак слагаемого с большим модулем.
Основная литература
Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
Дополнительная литература
Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения.
На предыдущем занятии мы узнали правило нахождения частного двух чисел одного знака и двух чисел разных знаков. Но таких выражений, содержащих только одно действие деления, на самом деле очень мало. Чаще всего встречаются более громоздкие выражения, которые содержат несколько действий.
Но таких выражений, содержащих только одно действие деления, на самом деле очень мало. Чаще всего встречаются более громоздкие выражения, которые содержат несколько действий.
Сегодня мы поговорим о вычислительной операции деления в таких случаях.
Для начала давайте вспомним все правила деления чисел с одинаковым и разными знаками. Стоит отметить, что аналогичное правило есть и при умножении.
Чтобы разделить (или умножить) два числа с разными знаками, надо разделить (или перемножить) модули этих чисел и поставить перед полученным частным (или произведением) знак «минус».
45 : (– 5) = – 9
Чтобы разделить (или умножить) два числа с одинаковыми знаками, надо разделить (или перемножить) модули этих чисел и поставить перед полученным частным (или произведением) знак «плюс».
– 35 : (– 7) = 5
В выражениях, где есть только действия умножения и деления чисел с разными знаками, знак можно определить по числу сомножителей. Если число знаков «минус» чётное, то значение выражения будет положительным, а если нечётное, то отрицательным.
Например:
– 5 ∙ 6 : (– 10) ∙ (– 4) = ?
В данном выражении сначала можно посчитать число знаков «минус», их оказалось 3, следовательно, ответ будет отрицательный. Далее выполним вычисления, взяв числа по модулю. В результате, объединив оба рассуждения (о знаке результата и сами вычисления), получаем ответ:
- 5 ∙ 6 : 10 ∙ 4 = 12
- – 5 ∙ 6 : (– 10) ∙ (– 4) = – 12
Обратите внимание, что если отрицательное число стоит после какого-либо знака, то его надо заключать в скобки, как и было представлено в наших примерах.
Если в вычислениях содержится не только умножение и деление, но и сложение с вычитанием, то нужно воспользоваться еще правилами сложения целых чисел.
Вспомним их.
Чтобы сложить два числа одинакового знака, надо сложить их модули и поставить перед суммой знак слагаемых.
Чтобы сложить два числа с разными знаками, надо из большего модуля вычесть меньший и перед разностью поставить знак слагаемого с большим модулем.
Вычислим значение выражения, состоящего из нескольких действий.
25 : (– 5) + 16 ∙ (– 2) = ?
В данном выражении 3 действия.
Первое действие деление, второе умножение, третье сложение.
Выполним первое действие:
1) 25 : (– 5) = – 5, ответ в этом действии будет с минусом так как «плюс» на «минус» даст знак «минус» и при делении модулей чисел получим ответ пять, следовательно, в этом действии ответ минус пять.
Выполним второе действие:
2) 16 ∙ (– 2) = – 32
Здесь знак определим по тому же правилу, это будет «минус» и умножим модули чисел, в итоге получим минус 32.
И последним действием сложим минус 5 и минус 32. Так как числа с одним знаком, следовательно, будем складывать результаты, но в ответе запишем «минус», следуя правилу сложения чисел, рассмотренному ранее. Получаем ответ данного выражения минус 37.
3) – 5 + (– 32) = – 37
25 : (– 5) + 16 ∙ (– 2) = – 37
Итак, сегодня мы получили представление о применении свойств деления для чисел с одинаковыми и разными знаками при вычислении значений выражений, содержащих разные действия.
Сравним значения выражений, не вычисляя их.
38 : (– 19) ? 52 · (– 4) : (– 13)
– 35 + (– 18) : 2 ? – 735 : (– 5)
Решение:
Для сравнения данных выражений достаточно посмотреть на знаки, которые будут получаться при вычислениях.
Сравним выражения в первой строке. В первом выражении, знак будет минус, т. к. число отрицательных знаков в нём нечётное. Во втором выражении ответ будет иметь положительное значение, т. к. число отрицательных знаков в нём чётное. Следовательно, первое выражение меньше второго.
Сравним выражения во второй строке. Сначала рассмотрим первое выражение по действиям. При делении у частного получается знак «минус» т. к. число отрицательных знаков в первом действии нечётное. Во втором действии при сложении двух чисел с одинаковым знаком получается результат с таким же знаком, следовательно, в ответе будет отрицательное число. Во втором выражении ответ будет иметь положительное значение, т. к. число отрицательных знаков в нём чётное. Следовательно, первое выражение меньше второго.
Следовательно, первое выражение меньше второго.
38 : (– 19) < 52 · (– 4) : (– 13)
– 35 + (– 18) : 2 < – 735 : (– 5)
Тренировочные задания
Какой знак имеет выражение?
28 : (– 4) · 8
Решение: Для нахождения знака используем правило нахождения частного (произведения) чисел с разными знаками. Если число знаков «минус» чётное, то значение выражения будет положительным, а если нечётное, то отрицательным.
Следовательно, в нашем примере ответ будет со знаком минус, т. к. число знаков «минус» нечётное – равное единице.
Решите уравнение
5 · х + 8 · х = – 65
Решение:
Вначале найдём, сколько x содержится в левой части уравнения: сложим 5x и 8x, получается 13x. Далее найдём x, как частное (– 65) от 13. Далее находим знак, используя правило нахождения частного двух чисел с разными знаками. Частное чисел а и b равно частному их модулей, со знаком «минус», если они разных знаков. Следовательно, частное будет со знаком минус. Далее выполним деление данных чисел по модулю, результат равен 5, но с учетом знака:
Далее выполним деление данных чисел по модулю, результат равен 5, но с учетом знака:
x = – 5
Сложение рациональных чисел
Сложение рациональных чисел — это сложение целых и дробных положительных и отрицательных чисел. Сложение положительных (натуральных) чисел и дробей нами изучено, поэтому рассмотрим подробно сложение положительных и отрицательных чисел и дробей с одинаковыми и разными знаками.
При сложении рациональных чисел с разными знаками можно подразумевать, что положительное число — это ваш «доход», а отрицательное число — это ваш «долг». Результатом вычисления будет то, что у вас останется от «дохода», когда вы отдадите «долг».
Правило. При сложении двух чисел с разными знаками из большего модуля вычитают меньший и перед полученным числом ставят знак того слагаемого, модуль которого больше.
Два знака подряд в арифметических действиях не ставятся, их нужно разделять скобками, значит, отрицательное число в сумме чисел после знака «+» нужно всегда брать в скобки.
При сложении чисел с разными знаками и результате возможны такие варианты:
-
Число положительное больше числа отрицательного (ваш «доход» больше вашего «долга»), тогда сумма будет со знаком «плюс» («+»).
-
Число положительное меньше числа отрицательного (ваш «доход» меньше вашего «долга»), тогда сумма будет со знаком «минус» («-»).
Правило. При сложении двух чисел с одинаковыми знаками складывают их модули и перед полученным числом ставят их общий знак.
При сложении чисел с одинаковыми знаками в результате возможны такие варианты:
-
Числа положительные (ваш «доход» увеличивается еще на некоторый «доход»), тогда сумма будет со знаком «плюс» («+»).
-
Числа отрицательные (ваш «долг» увеличивается еще на величину некоторого вашего «долга»), тогда сумма будет со знаком «минус» («-»).
При вычислении числовых и буквенных выражений действия с положительными и отрицательными числами можно выполнять «шаг за шагом» (по порядку записи слагаемых), тогда используются предыдущие два правила. Можно также производить вычисления с помощью законов сложения (переместительного и сочетательного).
Можно также производить вычисления с помощью законов сложения (переместительного и сочетательного).
Правило. Чтобы вычислить сумму рациональных чисел, нужно отдельно сложить все положительные числа (заключив в скобки и поставив перед скобкой знак «+») и отдельно сложить все отрицательные числа (заключив в скобки и поставив перед скобкой знак «-»). Затем из большей по модулю суммы вычесть меньшую по модулю сумму, а перед полученным результатом поставить знак той суммы, модуль которой больше.
Особенности сложения рациональных чисел с 0
Нуль — это отсутствие у вас «дохода» и «долга».
-
Если с 0 складывается положительное число, то сумма равна вашему «доходу» (со знаком «+»). Например: 0 + 17 — 17.
-
Если с 0 складывается отрицательное число, то сумма равна вашему «долгу» (со знаком «-»). Например: 0 + (- 29) = -29.
-
Если два слагаемых — нули, то и сумма равна 0. Например: 0 + 0 = 0.
вещественных чисел | Начальная алгебра
Результаты обучения
- Сложить и вычесть действительные числа
- Сложить действительные числа с одинаковыми и разными знаками
- Вычесть действительные числа с одинаковыми и разными знаками
- Упростите комбинации, требующие как сложения, так и вычитания действительных чисел.

- Умножать и делить действительные числа
- Умножение двух или более действительных чисел.
- Разделить действительные числа
- Упростите выражения умножением и делением
- Упростите выражения с помощью действительных чисел
- Распознавать и комбинировать похожие термины в выражении
- Используйте порядок операций для упрощения выражений
- Упростите составные выражения с помощью действительных чисел
- Упростите выражения с помощью дробных черт, скобок и круглых скобок
- Используйте свойство распределения для упрощения выражений с помощью символов группировки
- Упростить выражения, содержащие абсолютные значения
Перед тем, как мы начнем, следует запомнить важную терминологию:
- целых чисел: подсчет чисел, таких как 1, 2, 3 и т. Д., включая негативы и ноль
- вещественное число: дроби, отрицательные числа, десятичные дроби, целые числа и ноль — все действительные числа
- абсолютное значение: расстояние от нуля до числа; это всегда положительно.
 [латекс] | -7 | = 7 [/ латекс]
[латекс] | -7 | = 7 [/ латекс] - sign: это относится к положительному или отрицательному числу, мы используем [latex] + [/ latex] для положительного (справа от нуля в числовой строке) и [latex] — [/ latex] для отрицательного. (слева от нуля в числовой строке)
- разница: результат вычитания
- сумма: результат сложения
Умение комфортно работать с отрицательными числами необходимо для успеха в алгебре.По этой причине мы сделаем краткий обзор сложения, вычитания, умножения и деления целых чисел. Целые числа — это целые положительные числа, ноль и их противоположности (отрицательные). Поскольку это обзор целых чисел, описания и примеры не будут такими подробными, как на обычном уроке.
Сложение и вычитание действительных чисел
При сложении целых чисел необходимо рассмотреть два случая. Первый случай — совпадают ли знаки (положительные или отрицательные). Если знаки совпадают, мы сложим числа и сохраним знак.
Если знаки не совпадают (одно положительное и одно отрицательное число), мы вычтем числа (как если бы все они были положительными), а затем используем знак из большего числа. Это означает, что если большее число положительно, ответ будет положительным. Если большее число отрицательно, ответ отрицательный.
Для сложения двух чисел с одинаковым знаком (положительных или отрицательных)
- Добавьте их абсолютных значений (без знака [latex] + [/ latex] или [latex] — [/ latex])
- Поставьте сумму тем же знаком.
Чтобы сложить два числа с разными знаками (одно положительное и одно отрицательное)
- Найдите разницу из их абсолютных значений. (Обратите внимание, что когда вы обнаруживаете разницу абсолютных значений, вы всегда вычитаете меньшее абсолютное значение из большего.)
- Укажите для суммы тот же знак, что и у числа с большим абсолютным значением.
Пример
Найдите [латекс] 23–73 [/ латекс].
Показать решение
Вы не можете использовать свой обычный метод вычитания, потому что 73 больше 23.Перепишите вычитание как добавление противоположного.
[латекс] 23+ слева (-73 справа) [/ латекс]
Слагаемые имеют разные знаки, поэтому найдите разницу их абсолютных значений.
[латекс] begin {array} {c} left | 23 right | = 23 , , , text {and} , , , left | −73 right | = 73 \ 73-23 = 50 end {array} [/ latex]
Поскольку [latex] left | −73 right |> left | 23 right | [/ latex], окончательный ответ отрицательный.
Ответ
[латекс] 23–73 = −50 [/ латекс]
Другой способ подумать о вычитании — это подумать о расстоянии между двумя числами на числовой прямой.В приведенном ниже примере [latex] 382 [/ latex] соответствует правому 0 единицам [latex] 382 [/ latex], а [latex] -93 [/ latex] соответствует левому 0 на 93 ед. Расстояние между ними — это сумма расстояний до 0: [латекс] 382 + 93 [/ латекс].
Пример
Найдите [латекс] 382– left (−93 right) [/ latex].
Показать решение
Вы убираете отрицательный знак, поэтому думайте об этом как об удалении отрицательного знака. Это становится дополнительной проблемой. [латекс] -93 [/ латекс] становится [латекс] +93 [/ латекс]
[латекс] 382 + 93 = 475 [/ латекс]
Ответ
[латекс] 382 — (- 93) = 475 [/ латекс]
В следующем видео объясняется, как вычесть два целых числа со знаком.
Пример
Найдите [латекс] — frac {3} {7} — frac {6} {7} + frac {2} {7} [/ latex]
Показать решение
Сложите первые два и дайте результату знак минус:
Так как знаки у первых двух одинаковые, найти сумму абсолютных значений дробей
Поскольку оба числа отрицательны, сумма отрицательная. Если вы должны деньги, то занимайте больше, и сумма вашей задолженности становится больше.
[латекс] левый | — frac {3} {7} right | = frac {3} {7} [/ latex] и [latex] left | — frac {6} {7} right | = frac {6} {7} [/ латекс]
[латекс] begin {array} {c} frac {3} {7} + frac {6} {7} = frac {9} {7} \\ — frac {3} {7 } — frac {6} {7} = — frac {9} {7} end {array} [/ latex]
Теперь добавьте третье число.Знаки разные, поэтому найдите разницы их абсолютных значений.
[латекс] левый | — frac {9} {7} right | = frac {9} {7} [/ latex] и [latex] left | frac {2} {7} right | = frac {2} {7} [/ латекс]
[латекс] frac {9} {7} — frac {2} {7} = frac {7} {7} [/ latex]
Поскольку [latex] left | frac {-9} {7} right |> left | frac {2} {7} right | [/ latex], знак окончательной суммы такой же, как знак [латекс] — frac {9} {7} [/ латекс].
[латекс] — frac {9} {7} + frac {2} {7} = — frac {7} {7} [/ латекс]
Ответ
[латекс] — frac {3} {7} + left (- frac {6} {7} right) + frac {2} {7} = — frac {7} {7} [/ латекс]
В следующем видео вы увидите пример того, как сложить три дроби с общим знаменателем и разными знаками.
Пример
Оценить [латекс] 27,832 + (- 3,06) [/ латекс]. Когда вы добавляете десятичные дроби, не забудьте выровнять десятичные дроби так, чтобы вы добавляли десятые доли к десятым, сотые к сотым и т. Д.
Показать решение
Поскольку слагаемые имеют разные знаки, вычтите их абсолютные значения.
[латекс] begin {array} {r} underline { begin {array} {r} 27.832 \ — text {} 3.06 , , , end {array}} \ 24.772 end { array} [/ latex]
[латекс] влево | -3,06 вправо | = 3.06 [/ латекс]
Сумма имеет тот же знак, что и 27,832, абсолютное значение которого больше.
Ответ
[латекс] 27,832+ слева (-3,06 справа) = 24,772 [/ латекс]
В следующем видео приведены примеры сложения и вычитания десятичных знаков с разными знаками.
Произведение двух чисел с одинаковым знаком (как положительных, так и отрицательных)
Чтобы умножить два положительных числа на , умножьте их абсолютные значения. Продукт положительный .
Чтобы умножить два отрицательных числа на , умножьте их абсолютные значения.Продукт положительный .
Пример
Найдите [латекс] ~ left (- frac {3} {4} right) left (- frac {2} {5} right) [/ latex]
Показать решение
Умножьте абсолютные значения чисел. Сначала умножьте числители, чтобы получить числитель произведения. Затем умножьте знаменатели, чтобы получить знаменатель произведения. Если нужно, перепишите в наименьших терминах.
[латекс] left ( frac {3} {4} right) left ( frac {2} {5} right) = frac {6} {20} = frac {3} {10} [/ латекс]
Произведение двух отрицательных чисел положительно.
Ответ
[латекс] left (- frac {3} {4} right) left (- frac {2} {5} right) = frac {3} {10} [/ latex]
В следующем видео показаны примеры умножения двух дробей со знаком, включая упрощение ответа.
Суммируем:
- положительный [латекс] cdot [/ latex] положительный : Продукт положительный .
- отрицательный [латекс] cdot [/ latex] отрицательный : Продукт положительный .
- негатив [латекс] cdot [/ latex] позитив : Продукт негатив .
- положительный [латекс] cdot [/ latex] отрицательный : Продукт отрицательный .

Как видите, произведение двух отрицательных чисел является положительным числом. Итак, если вы умножаете более двух чисел, вы можете подсчитать количество отрицательных множителей.
Умножение более двух отрицательных чисел
Если есть четных числа (0, 2, 4,…) отрицательных множителей для умножения, произведение будет положительным .
Если имеется нечетное число (1, 3, 5,…) отрицательных множителей, произведение отрицательное .
Пример
Найдите [латекс] 3 (−6) (2) (- 3) (- 1) [/ latex].
Показать решение
Умножьте абсолютные значения чисел.
[латекс] begin {array} {l} 3 (6) (2) (3) (1) \ 18 (2) (3) (1) \ 36 (3) (1) \ 108 ( 1) \ 108 end {array} [/ latex]
Подсчитайте количество отрицательных факторов. Есть три [латекса] left (−6, −3, −1 right) [/ latex].
[латекс] 3 (−6) (2) (- 3) (- 1) [/ латекс]
Поскольку существует нечетное количество отрицательных факторов, произведение отрицательное.
Ответ
[латекс] 3 (−6) (2) (- 3) (- 1) = — 108 [/ латекс]
Следующее видео содержит примеры умножения более двух целых чисел со знаком.
Разделить действительные числа
Вы можете помнить, что когда вы делили дроби, вы умножали на обратную величину . Обратный — это другое название мультипликативного обратного (точно так же, как напротив — другое название аддитивного обратного).
Самый простой способ найти обратное умножение — просто «перевернуть» числитель и знаменатель, как вы это делали, чтобы найти обратное.Вот несколько примеров:
- Обратное значение [latex] frac {4} {9} [/ latex] равно [latex] frac {9} {4} [/ latex], потому что [latex] frac {4} {9} left ( frac {9} {4} right) = frac {36} {36} = 1 [/ латекс].

- Обратное значение 3 равно [latex] frac {1} {3} [/ latex], потому что [latex] frac {3} {1} left ( frac {1} {3} right) = frac {3} {3} = 1 [/ латекс].
- Обратное значение [latex] — frac {5} {6} [/ latex] равно [latex] frac {-6} {5} [/ latex], потому что [latex] — frac {5} {6} left (- frac {6} {5} right) = frac {30} {30} = 1 [/ latex].
- Обратное значение 1 равно 1, поскольку [латекс] 1 (1) = 1 [/ латекс].
Когда вы делите на положительные дроби, вы научились умножать на обратную. Вы также делаете это, чтобы разделить вещественных чисел на .
Подумайте о том, чтобы разделить мешок из 26 шариков на два мешка меньшего размера с одинаковым количеством шариков в каждом. Вы также можете сказать, что в каждой сумке меньшего размера находится , половина — шариков.
[латекс] 26 div 2 = 26 left ( frac {1} {2} right) = 13 [/ latex]
Обратите внимание, что 2 и [latex] frac {1} {2} [/ latex] являются обратными величинами.
Попробуйте еще раз, разделив мешок из 36 шариков на мешочки поменьше.
| Количество мешков | Деление на количество мешков | Умножение на обратное |
|---|---|---|
| 3 | [латекс] frac {36} {3} = 12 [/ латекс] | [латекс] 36 left ( frac {1} {3} right) = frac {36} {3} = frac {12 (3)} {3} = 12 [/ latex] |
| 4 | [латекс] frac {36} {4} = 9 [/ латекс] | [латекс] 36 left ( frac {1} {4} right) = frac {36} {4} = frac {9 left (4 right)} {4} = 9 [/ latex] |
| 6 | [латекс] frac {36} {6} = 6 [/ латекс] | [латекс] 36 left ( frac {1} {6} right) = frac {36} {6} = frac {6 left (6 right)} {6} = 6 [/ латекс] |
Деление на число аналогично умножению на обратную величину.(То есть вы используете обратную величину делителя , второго числа в задаче деления. )
)
Пример
Найдите [латекс] 28 div frac {4} {3} [/ latex]
Показать решение
Перепишите деление как умножение на обратную. Аналог [latex] frac {4} {3} [/ latex] — это [latex] frac {3} {4} [/ latex].
[латекс] 28 div frac {4} {3} = 28 left ( frac {3} {4} right) [/ latex]
Умножить.
[латекс] frac {28} {1} left ( frac {3} {4} right) = frac {28 left (3 right)} {4} = frac {4 left ( 7 right) left (3 right)} {4} = 7 left (3 right) = 21 [/ латекс]
Ответ
[латекс] 28 div frac {4} {3} = 21 [/ латекс]
Теперь давайте посмотрим, что это означает, когда одно или несколько чисел отрицательны.Число и его обратная величина имеют один и тот же знак. Поскольку деление переписывается как умножение с использованием обратной величины делителя, а взятие обратной величины не меняет никаких знаков, деление следует тем же правилам, что и умножение.
Правила раздела
При делении перепишите задачу как умножение, используя обратную величину делителя в качестве второго множителя.
Когда одно число — положительное , а другое — отрицательное , частное равно отрицательному .
Когда оба числа — отрицательные , частное будет положительным .
Когда оба числа — положительные , частное будет положительным .
Пример
Найдите [латекс] 24 div left (- frac {5} {6} right) [/ latex].
Показать решение
Перепишите деление как умножение на обратную.
[латекс] 24 div left (- frac {5} {6} right) = 24 left (- frac {6} {5} right) [/ latex]
Умножить.Поскольку одно число положительное, а другое отрицательное, произведение отрицательное.
[латекс] frac {24} {1} left (- frac {6} {5} right) = — frac {144} {5} [/ latex]
Ответ
[латекс] 24 div left (- frac {5} {6} right) = — frac {144} {5} [/ latex]
Пример
Найдите [латекс] 4 , left (- frac {2} {3} right) , div left (-6 right) [/ latex]
Показать решение
Перепишите деление как умножение на обратную.
[латекс] frac {4} {1} left (- frac {2} {3} right) left (- frac {1} {6} right) [/ latex]
Умножить.Число отрицательных чисел четное, значит, произведение положительное.
[латекс] frac {4 left (2 right) left (1 right)} {3 left (6 right)} = frac {8} {18} [/ latex]
Запишите дробь наименьшим числом.
Ответ
[латекс] 4 left (- frac {2} {3} right) div left (-6 right) = frac {4} {9} [/ latex]
В следующем видео объясняется, как делить дроби со знаком.
Помните, что черта дроби также указывает на деление, поэтому отрицательный знак перед дробью идет вместе с числителем, знаменателем или целой дробью: [latex] — frac {3} {4} = frac {-3 } {4} = frac {3} {- 4} [/ latex].
В каждом случае общая дробь отрицательная, потому что при делении есть только одно отрицательное значение.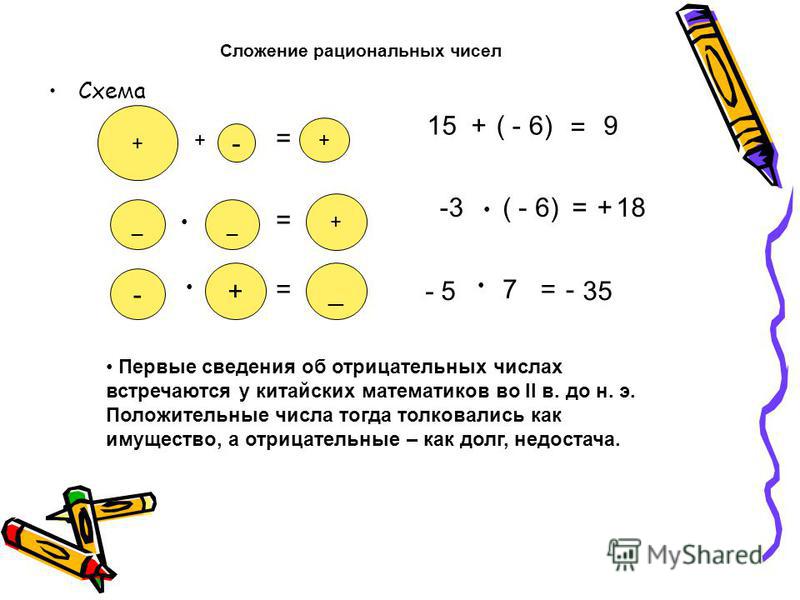
В следующем видео объясняется, как делить дроби со знаком.
Упростить выражения действительными числами
Прежде чем мы начнем, немного важной терминологии:
- операций / операторов: В математике мы называем такие вещи, как операции умножения, деления, сложения и вычитания. Это глаголы математического мира, выполняющие работу с числами и переменными.2b [/ латекс] или [латекс] -3 [/ латекс] и [латекс] 8 [/ латекс]. Если у нас есть одинаковые термины, нам разрешено складывать (или вычитать) числа перед переменными, а затем оставлять переменные такими же. Когда мы комбинируем одинаковые термины, нам нужно интерпретировать знаки вычитания как часть следующего термина. Это означает, что если мы видим знак вычитания, мы рассматриваем следующий термин как отрицательный.
 Знак всегда соответствует сроку.
Знак всегда соответствует сроку.
Это показано в следующих примерах:
Пример
Объедините похожие термины: [латекс] 5x-2y-8x + 7y [/ латекс]
Показать решение
Подобные термины в этом выражении:
[латекс] 5x [/ латекс] и [латекс] -8x [/ латекс]
[латекс] -2y [/ латекс] и [латекс] -7y [/ латекс]
Обратите внимание, как мы держали табличку перед каждым термином.
Объедините похожие термины:
[латекс] 5x-8x = -3x [/ латекс]
[латекс] -2y-7y = -9y [/ латекс]
Обратите внимание, как знаки становятся операциями, когда вы объединяете одинаковые термины.
Упрощенное выражение:
[латекс] 5x-2y-8x + 7y = -3x-9y [/ латекс]
В следующем видео вам будет показано, как комбинировать похожие термины, используя идею распределительного свойства. Обратите внимание, что это другой метод, чем показан в письменных примерах на этой странице, но он дает тот же результат.2 \ — 3x + 3x = 0 , , , , , , , , , , , \ 9-1 = 8 , , , , , , , , , , , end {array} [/ latex]
В следующем видео вам будет показан еще один пример объединения похожих терминов.
 Обратите внимание, почему вы не можете объединить все три термина в примере.
Обратите внимание, почему вы не можете объединить все три термина в примере. Порядок действий
Вы можете вспомнить или не вспомнить порядок операций для применения нескольких математических операций к одному выражению. Так же, как для нас принято ездить по правой стороне дороги, порядок операций — это набор соглашений, используемых для обеспечения порядка, когда вам необходимо использовать несколько математических операций для одного выражения.На приведенном ниже рисунке показан порядок выполнения математических операций.
Порядок работы
Пример
Упростить [латекс] 7–5 + 3 cdot8 [/ latex].
Показать решение
Согласно порядку операций умножение предшествует сложению и вычитанию.Умножение [латекс] 3 cdot8 [/ латекс].
[латекс] begin {array} {c} 7–5 + 3 cdot8 \ 7–5 + 24 end {array} [/ latex]
Теперь сложите и вычтите слева направо.
 [латекс] 7–5 [/ латекс] на первом месте.
[латекс] 7–5 [/ латекс] на первом месте.[латекс] 2 + 24 [/ латекс].
Наконец, доп.
[латекс] 2 + 24 = 26 [/ латекс]
Ответ
[латекс] 7–5 + 3 cdot8 = 26 [/ латекс]
В следующем примере вам будет показано, как упростить выражение, которое содержит как умножение, так и вычитание, используя порядок операций.
Когда вы применяете порядок операций к выражениям, содержащим дроби, десятичные дроби и отрицательные числа, вам также необходимо вспомнить, как выполнять эти вычисления.
Пример
Упростите [латекс] 3 cdot frac {1} {3} -8 div frac {1} {4} [/ latex].
Показать решение
Согласно порядку операций умножение и деление предшествуют сложению и вычитанию. Иногда полезно добавить круглые скобки, чтобы вы знали, что идет первым, поэтому давайте заключим в скобки умножение и деление, поскольку оно будет стоять перед вычитанием.
[латекс] 3 cdot frac {1} {3} -8 div frac {1} {4} [/ латекс]
Сначала умножьте [latex] 3 cdot frac {1} {3} [/ latex].
[латекс] begin {array} {c} left (3 cdot frac {1} {3} right) — left (8 div frac {1} {4} right) \ текст {} \ = left (1 right) — left (8 div frac {1} {4} right) end {array} [/ latex]
Теперь разделите [латекс] на 8 div frac {1} {4} [/ latex].
[латекс] begin {array} {c} 8 div frac {1} {4} = frac {8} {1} cdot frac {4} {1} = 32 \ text {} \ 1-32 end {array} [/ latex]
Вычесть.
[латекс] 1–32 = −31 [/ латекс]
Ответ
[латекс] 3 cdot frac {1} {3} -8 div frac {1} {4} = — 31 [/ латекс]
В следующем видео показано, как использовать порядок операций для упрощения выражения, содержащего умножение, деление и вычитание, с помощью членов, содержащих дроби.{3}} = 72 [/ латекс]
В следующем видео выражение с показателями степени упрощено с использованием порядка операций.

Группировка символов
Группирующие символы, такие как круглые скобки (), квадратные скобки [], фигурные скобки [латекс] displaystyle left {{} right } [/ latex] и дробные черты, могут использоваться для дальнейшего управления порядком четырех арифметических операций. . Правила порядка операций требуют, чтобы сначала были выполнены вычисления внутри символов группировки, даже если вы добавляете или вычитаете внутри символов группировки и у вас есть умножение вне символов группировки.После вычисления внутри символов группировки разделите или умножьте слева направо, а затем вычтите или сложите слева направо. Если символы группировки находятся внутри символов группировки, выполняйте расчет от внутренней части к внешней. То есть сначала начните упрощать внутри самых внутренних символов группировки.

Помните, что скобки также могут использоваться для обозначения умножения. В следующем примере показаны оба использования круглых скобок — как способ представления группы, так и способ выражения умножения.{3}} cdot 32 = frac {3} {4} [/ латекс]
Упростите составные выражения действительными числами
В этом разделе мы будем использовать навыки из последнего раздела, чтобы упростить математические выражения, которые содержат множество символов группировки и множество операций. Мы используем термин составной для описания выражений, которые имеют много операций и много группирующих символов. При применении порядка операций с этими выражениями требуется больше внимания. Кроме того, вы увидите, как обрабатывать абсолютные значения при упрощении выражений.{2}} + 2} [/ латекс]
Показать решение
В этой задаче есть скобки, круглые скобки, дроби, показатели, умножение, вычитание и сложение.Сначала обрабатываются символы группировки. Скобки вокруг [latex] -6 [/ latex] не являются символом группировки; они просто дают понять, что отрицательный знак принадлежит цифре 6.
 Начните с самого внутреннего набора круглых скобок, которые являются символом группировки. В этом примере самые внутренние круглые скобки будут в числителе дроби, [latex] (2 cdot (−6)) [/ latex].{2} +2} = frac {14} {11} [/ latex]
Начните с самого внутреннего набора круглых скобок, которые являются символом группировки. В этом примере самые внутренние круглые скобки будут в числителе дроби, [latex] (2 cdot (−6)) [/ latex].{2} +2} = frac {14} {11} [/ latex] Следующее видео содержит пример, аналогичный написанному выше. Обратите внимание, как числитель и знаменатель дроби упрощаются по отдельности.
Распределительная собственность
Круглые скобки используются для группировки или объединения выражений и терминов в математике. Вы можете увидеть, как они используются, когда вы работаете с формулами, и когда вы переводите реальную ситуацию в математическую задачу, чтобы найти количественное решение.
Распределительная собственность Combo Meal
Например, вы собираетесь пообщаться с друзьями и звоните им, чтобы спросить, не хотят ли они чего-нибудь из вашего любимого проезда.
 Три человека хотят одно и то же комбинированное блюдо из 2 тако и одного напитка. Вы можете использовать свойство distributive, чтобы узнать, сколько всего тако и сколько всего напитков вы должны им принести.
Три человека хотят одно и то же комбинированное блюдо из 2 тако и одного напитка. Вы можете использовать свойство distributive, чтобы узнать, сколько всего тако и сколько всего напитков вы должны им принести. [латекс] begin {array} {c} , , , 3 left (2 text {tacos} + 1 text {drink} right) \ = 3 cdot {2} text { тако} +3 текст {напитки} \, , = 6 текст {тако} +3 текст {напитки} end {массив} [/ латекс]
Свойство распределенности позволяет нам явно описать сумму, которая является результатом группы групп.В случае комбинированных блюд у нас есть три группы (два тако плюс один напиток). Следующее определение описывает, как использовать свойство распределения в общих чертах.
Распределительное свойство умножения
Для всех действительных чисел a, b, и c , [латекс] a (b + c) = ab + ac [/ латекс].
Это означает, что когда число в скобках умножает выражение, вы можете распределить умножение на каждый член выражения индивидуально.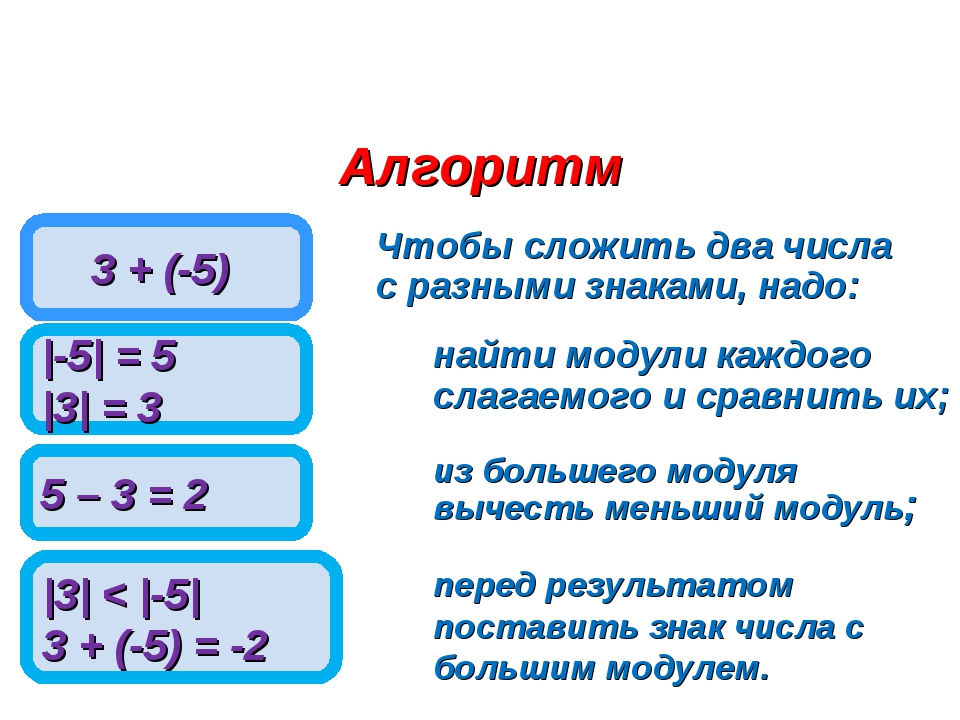
Чтобы упростить [латекс] 3 left (3 + y right) -y + 9 [/ latex], может быть полезно увидеть выражение, переведенное словами:
умножьте три на (сумму трех и y), затем вычтите y, затем прибавьте 9
Чтобы умножить три на сумму трех и y, вы используете свойство распределения —
[латекс] begin {array} {c} , , , , , , , , , 3 left (3 + y right) -y + 9 \, , , , , , , , , = underbrace {3 cdot {3}} + underbrace {3 cdot {y}} — y + 9 \ = 9 + 3y-y + 9 end {array} [/ latex]
Теперь вы можете вычесть y из 3y и прибавить 9 к 9.
[латекс] begin {array} {c} 9 + 3y-y + 9 \ = 18 + 2y end {array} [/ latex]
В следующем примере показано, как использовать свойство распределения, когда один из задействованных терминов отрицательный.
Пример
Упростить [латекс] a + 2 left (5-a right) +3 left (a + 4 right) [/ latex]
Показать решение
Это выражение содержит два набора круглых скобок с заблокированными в них переменными.
 Мы будем использовать свойство distributive, чтобы убрать круглые скобки.
Мы будем использовать свойство distributive, чтобы убрать круглые скобки. [латекс] begin {array} {c} a + 2 left (5-a right) +3 left (a + 4 right) \ = a + 2 cdot {5} -2 cdot {a} +3 cdot {a} +3 cdot {4} end {array} [/ latex]
Обратите внимание, как мы поместили отрицательный знак, который был на b, перед 2, когда мы применили свойство распределения.Когда вы умножаете отрицательный результат на положительный, результат будет отрицательным, поэтому [latex] 2 cdot {-a} = — 2a [/ latex]. При использовании распределительного свойства важно быть осторожным с отрицательными знаками.
[латекс] begin {array} {c} a + 2 cdot {5} -2 cdot {a} +3 cdot {a} +3 cdot {4} \ = a + 10-2a + 3a + 12 \ = 2a + 22 end {array} [/ latex]
Мы объединили все возможные условия, чтобы получить окончательный результат.
Ответ
[латекс] a + 2 left (5-a right) +3 left (a + 4 right) = 2a + 22 [/ латекс]
Абсолютное значение
Выражения абсолютного значения — это последний метод группировки, который вы можете увидеть.
 Напомним, что абсолютное значение количества всегда положительно или равно 0.
Напомним, что абсолютное значение количества всегда положительно или равно 0. Когда вы видите выражение абсолютного значения, включенное в большее выражение, относитесь к абсолютному значению как к символу группировки и сначала оцените выражение внутри знака абсолютного значения. Затем возьмите абсолютное значение этого выражения. Пример ниже показывает, как это делается.
Пример
Упростите [латекс] frac {3+ left | 2-6 right |} {2 left | 3 cdot1.5 right | — left (-3 right)} [/ latex].
Показать решение
В этой задаче есть абсолютные значения, десятичные дроби, умножение, вычитание и сложение.Сначала обрабатываются символы группировки, включая абсолютное значение. Упростите числитель, а затем знаменатель.
Оцените [латекс] left | 2–6 right | [/ latex].
[латекс] begin {array} {c} frac {3+ left | 2-6 right |} {2 left | 3 cdot1.5 right | — left (-3 right)} \\ frac {3+ left | -4 right |} {2 left | 3 cdot1.
 5 right | — left (-3 right)} end {array} [/ latex]
5 right | — left (-3 right)} end {array} [/ latex] Возьмите абсолютное значение [латекс] left | −4 right | [/ latex].
[латекс] begin {array} {c} frac {3+ left | -4 right |} {2 left | 3 cdot1.5 right | — left (-3 right)} \\ frac {3 + 4} {2 left | 3 cdot1.5 right | — left (-3 right)} end {array} [/ latex]
Сложите числа в числителе.
[латекс] begin {array} {c} frac {3 + 4} {2 left | 3 cdot1.5 right | — left (-3 right)} \\ frac {7 } {2 left | 3 cdot 1.5 right | — (- 3)} end {array} [/ latex]
Теперь, когда числитель упростился, обратимся к знаменателю.
Сначала вычислите выражение абсолютного значения. [латекс] 3 cdot 1,5 = 4,5 [/ латекс], что дает
[латекс] begin {array} {c} frac {7} {2 left | {3 cdot {1.5}} right | — (- 3)} \\ frac {7} {2 left | {4.5} right | — (- 3)} end {array} [/ latex]
Выражение «[латекс] 2 left | 4.5 right | [/ latex]» читается как «двойное абсолютное значение 4,5».
 Умножить 2 раза на 4,5.
Умножить 2 раза на 4,5. [латекс] begin {array} {c} frac {7} {2 left | 4.5 right | — left (-3 right)} \\ frac {7} {9- left (-3 справа)} end {array} [/ latex]
Вычесть.
[латекс] begin {array} {c} frac {7} {9- left (-3 right)} \\ frac {7} {12} end {array} [/ latex]
Ответ
[латекс] frac {3+ left | 2-6 right |} {2 left | 3 cdot1.5 right | -3 left (-3 right)} = frac {7} {12} [/ латекс]
В следующем видео порядок операций используется для упрощения выражения в форме дроби, которое содержит элементы абсолютного значения. Обратите внимание, как абсолютные значения обрабатываются как круглые и квадратные скобки при использовании порядка операций.
Сложение и вычитание положительных и отрицательных чисел
Числа могут быть положительными или отрицательными
Это числовая строка:
Отрицательные числа (-) Положительные числа (+) «-» — отрицательный знак. 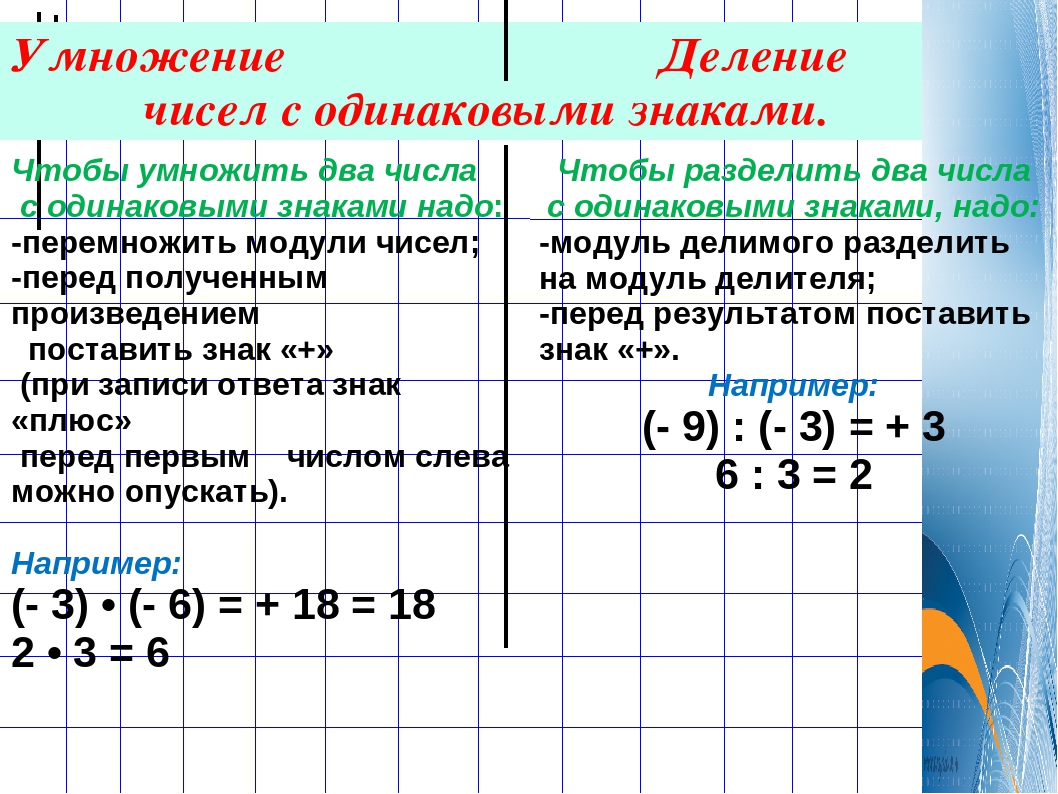
«+» — положительный знак Нет знака означает положительный
Если число имеет без знака , это обычно означает, что это положительное число .
Воздушные шары и гири
Давайте представим числа как воздушные шары (положительные) и веса (отрицательные):
К этой корзине привязаны воздушные шары и гирьки:
Добавление положительного числа
Сложение положительных чисел — это просто сложение.
Мы можем добавить воздушные шары (мы добавляем положительное значение )
корзина поднимается вверх (положительно)
Пример: 2 + 3 = 5
действительно говорит
«Положительное 2 плюс Положительное 3 равно Положительное 5»
Мы могли бы записать это как (+2) + (+3) = (+5)
Вычитание положительного числа
Вычитание положительных чисел — это просто вычитание.

Мы можем забрать воздушные шары (мы вычитаем положительное значение )
корзина тянется вниз (минус)
Пример: 6 — 3 = 3
действительно говорит
«Положительное 6 минус Положительное 3 равно Положительное 3»
Мы могли бы записать это как (+6) — (+3) = (+3)
Добавление отрицательного числа
Теперь посмотрим, как выглядит сложение и вычитание отрицательных чисел :
Мы можем добавлять веса (мы добавляем отрицательные значения )
корзина тянется вниз (минус)
Пример: 6 + (−3) = 3
действительно говорит
«Положительные 6 плюс отрицательные 3 равны положительным 3»
Мы могли бы записать это как (+6) + (−3) = (+3)
Последние два примера показали нам, что удаление воздушных шаров (вычитание положительного значения) или прибавление веса (добавление отрицательного значения) заставляют корзину опускаться.

Итак, у них тот же результат :
- (+6) — (+3) = (+3)
- (+6) + (−3) = (+3)
Другими словами вычитание положительного то же самое, что добавление отрицательного .
Вычитание отрицательного числа
Наконец, мы можем убрать веса (мы вычитаем отрицательных значений )
корзина поднимается вверх (положительно)
Пример: Что такое 6 — (−3)?
6 — (- 3) = 6 + 3 = 9
Да, действительно! Вычесть отрицание — это то же самое, что и сложить!
Два отрицательных результата дают положительный результат
Что мы нашли?
Добавление положительного числа — это простое сложение…
Добавление плюс Добавление
Положительное и отрицательное вместе …
Вычитание положительного
или
Сложение отрицательного
равно
ВычитаниеПример: Что такое 6 — (+3)?
6 — (+ 3) = 6 — 3 = 3
Пример: Что такое 5 + (−7)?
5 + (- 7) = 5 — 7 = −2
Вычитание негатива.
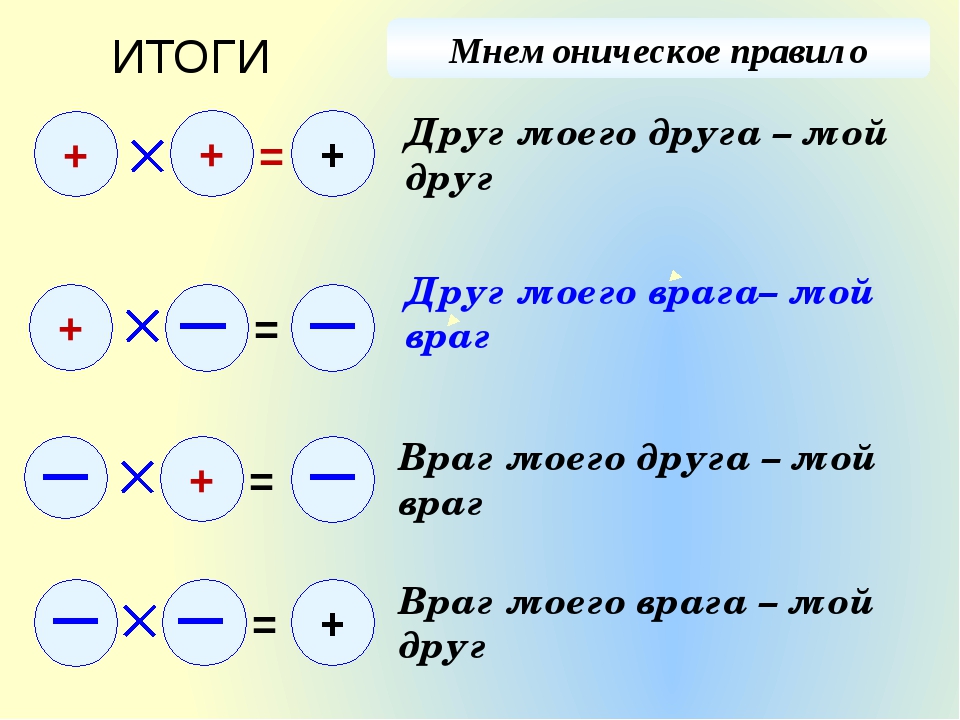 ..
.. Вычитание отрицательного числа аналогично Добавление
Пример: Что такое 14 — (−4)?
14 — (- 4) = 14 + 4 = 18
Правила:
Все это можно поместить в два правила :
Правило Пример + (+) Два одинаковых знака становятся положительным знаком 3 + (+ 2) = 3 + 2 = 5 — (-) 6 — (- 3) = 6 + 3 = 9 + (-) Два непохожих знака превращаются в знак минуса 7 + (- 2) = 7 — 2 = 5 — (+) 8 — (+ 2) = 8 — 2 = 6 Они «как знаки», когда они похожи друг на друга (другими словами: одинаковые).
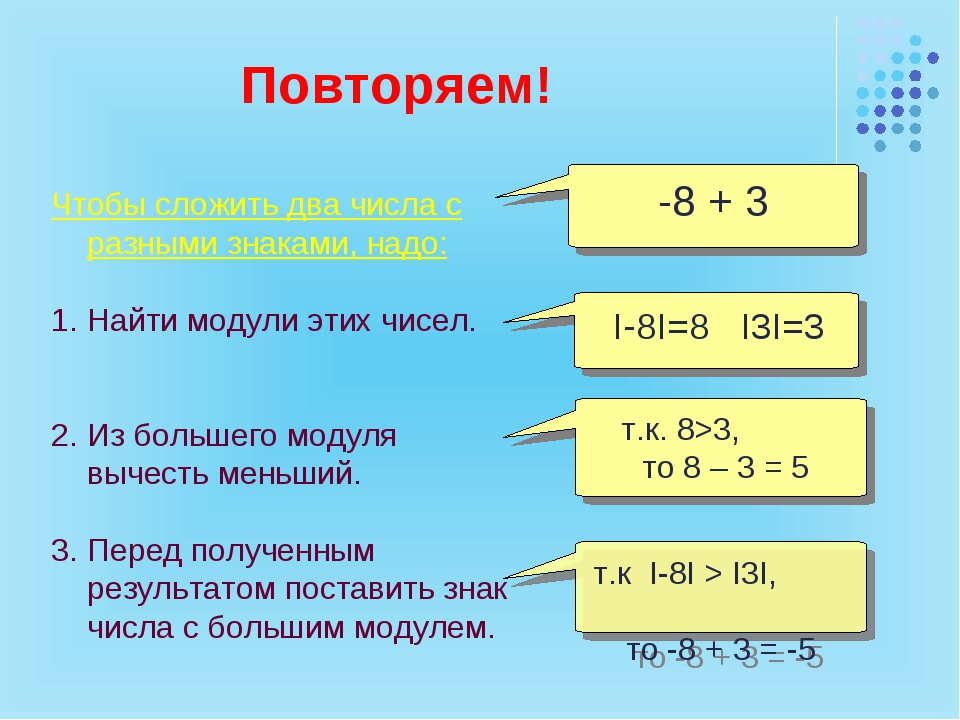
Итак, все, что вам нужно запомнить, это:
Два знака типа становятся положительным знаком
Два знака , отличных от , становятся отрицательным знаком
Пример: Что такое 5 + (- 2)?
+ (-) — это , в отличие от знаков (они не совпадают), поэтому они становятся отрицательным знаком .
5 + (- 2) = 5 — 2 = 3
Пример: Что такое 25 — (- 4)?
— (-) — это , как знаки , поэтому они становятся положительным знаком .
25 — (- 4) = 25 + 4 = 29
Пример: Что такое −6 + (+ 3)?
+ (+) — это , как знаки , поэтому они становятся положительным знаком .
−6 + (+ 3) = −6 + 3 = −3
Начните с −6 на числовой прямой, двигайтесь вперед на 3, и вы получите −3
А теперь поиграйся!
Попробуйте сыграть в Casey Runner, вам нужно знать правила положительного и отрицательного, чтобы добиться успеха! Объяснение здравого смысла
И есть объяснение «здравого смысла»:
Если я скажу «Ешь!» Я призываю вас поесть (позитив)
Если я скажу «Не ешьте!» Я говорю об обратном (отрицательном).

Теперь, если я скажу « НЕ не ешь!», Я говорю, что не
хочу, чтобы вы умерли с голоду, поэтому я снова говорю: «Ешь!» (положительный).Итак, два отрицания дают положительный результат, и если это вас устраивает, то
вы сделали!Другое объяснение здравого смысла
Друг +, враг —
.
.+ + ⇒ + друг друга мой друг + — ⇒ — друг врага — мой враг — + ⇒ — враг друга — мой враг — — ⇒ + враг врага — мой друг Пример банка
Пример. В прошлом году банк по ошибке снял с вашего счета 10 долларов, и они хотят это исправить.
Итак, банк должен забрать отрицательные 10 долларов.
Допустим, ваш текущий баланс составляет 80 долларов США, поэтому у вас будет:
80 долларов — (- 10 долларов) = 80 долларов + 10 долларов = 90 долларов
Таким образом, вы получаете на 10 долларов еще на свой счет.

Длинный пример, который вам может понравиться
Очки союзников
Элли может быть непослушным или милым. Итак, родители Элли сказали
«Если вы будете любезны, мы добавим 3 балла (+3).
Если вы непослушны, снимаем 3 балла (−3).
Когда вы набираете 30 очков, вы получаете игрушку.Союзник начинает день с 9 очками: 9 Мама Элли обнаруживает пролитое молоко: 9–3 = 6 Тогда папа признается, что пролил молоко и пишет «отменить».
Как «отменить» минус 3?
Мы добавляем 3 снова!Итак, мама вычисляет: 6 — (−3) = 6 + 3 = 9 Итак, когда мы вычитаем отрицательное, мы получаем
балла (т. е.е. так же, как добавление очков).
е.е. так же, как добавление очков). Таким образом, вычитание отрицательного числа аналогично Добавление
Несколько дней спустя. У Элли 12 очков. Мама добавляет 3 очка, потому что комната Элли чистая. 12 + 3 = 15 Папа говорит: «Я убрал эту комнату» и пишет «отменить» на диаграмме.Мама считает: 15 — (+3) = 12 Папа видит, как Элли чистит собаку.  Пишет на графике «+3». Мама считает:
Пишет на графике «+3». Мама считает: 12 + (+3) = 15 Элли бросает камень в окно. Папа пишет на диаграмме «−3».Мама считает: 15 + (−3) = 12 См .: как « 15 — (+3) », так и « 15 + (−3) » дают 12.
Итак:
Неважно, вычтите ли вы положительные баллы
или добавите отрицательные,
вы все равно потеряете баллы.Итак, вычитание положительного
или
Добавление отрицательного
— это
ВычитаниеПопробуйте эти упражнения…
Теперь попробуйте этот рабочий лист и посмотрите, как у вас получится.
А также попробуйте эти вопросы:
12 интересных способов попрактиковаться в сложении целых чисел
Вашим ученикам сложно вспомнить, как складывать и вычитать целые числа? Разве это не сводит с ума? Я мог бы залезть в свою мыльницу и продолжать и продолжать о том, как мы должны учить целым числам или как мы должны начинать с отрицательных чисел в детском саду, но это не что-то вроде мыльницы.
 Поэтому я постараюсь составить список удивительных занятий, которые дадут вашим ученикам целую лодку практики с добавлением и вычитанием целых чисел
Поэтому я постараюсь составить список удивительных занятий, которые дадут вашим ученикам целую лодку практики с добавлением и вычитанием целых чисел Когда мы практикуем такие навыки, как сложение и вычитание целых чисел, мне нравится быть уверенным, что существует множество видов практики и что мы выполняем их в течение длительного периода времени. В прошлом году я обучал 12 семиклассников, у которых был уровень математических навыков с 4-го по 5-й класс. К концу нескольких месяцев небольшой ежедневной практики все они стали экспертами в сложении и вычитании целых чисел.Было так приятно видеть. Но тренировка одних и тех же навыков день за днем иногда может показаться немного устаревшей, поэтому мы практиковались с помощью множества разных игр и занятий. В этом списке есть некоторые, которые мы использовали, а некоторые я планирую использовать в следующем году. *** Обновлено, чтобы включить еще больше действий по добавлению целых чисел в цифровом формате 8/2020 ***
Перечень работ:
- Целочисленные лабиринты (печатные и цифровые в Google Slides ™)
- Викторина
- Целые числа Digital Escape Room
- Карточная игра с целыми числами
- Доски
- Бинго
- Kahoot
- Строка в натуральную величину
- Карточки заданий (для печати ИЛИ в цифровом формате в Google Slides ™)
- Рабочие листы БЕСПЛАТНОЙ практики
- Сумка на молнии, номер строки
- Круги беглости
- Онлайн-игры
Я использую лабиринты много в моем классе (вы можете прочитать немного больше о многих способах их использования здесь).
 Каждый урок моих студентов математической лаборатории мы начинали с лабиринта. Я использовал эти три лабиринта за 3 дня в неделю, а через пару месяцев снова использовал те же 3 лабиринта. По пути в комнату студенты схватились за лабиринт, а затем работали над ним самостоятельно. Мне пришлось напомнить им, чтобы они не использовали калькулятор. Я также напомнил студентам, что они должны обратиться к своим интерактивным блокнотам о правилах сложения и вычитания целых чисел при решении этих задач.
Каждый урок моих студентов математической лаборатории мы начинали с лабиринта. Я использовал эти три лабиринта за 3 дня в неделю, а через пару месяцев снова использовал те же 3 лабиринта. По пути в комнату студенты схватились за лабиринт, а затем работали над ним самостоятельно. Мне пришлось напомнить им, чтобы они не использовали калькулятор. Я также напомнил студентам, что они должны обратиться к своим интерактивным блокнотам о правилах сложения и вычитания целых чисел при решении этих задач. Когда ученики закончили свой лабиринт, они принесли свой лабиринт и свою работу за задний стол, где я проверил их лабиринт.Это дало мне прекрасную возможность для конкретных и своевременных отзывов всех студентов. Когда они были закончены и все задачи были решены правильно, они переходили к следующему занятию.
Лабиринты
— это отличные занятия с низким уровнем подготовки и высоким уровнем вовлеченности, позволяющие студентам тренироваться. Но что, если вы преподаете онлайн или индивидуально? Независимо от того, в каком формате вы преподаете, ученикам действительно нравятся лабиринты.
 Итак, я создал цифровую версию этих трех целочисленных лабиринтов в Google Slides ™.
Итак, я создал цифровую версию этих трех целочисленных лабиринтов в Google Slides ™. Эти цифровые лабиринты легко назначить в Google Classroom ™, чтобы студенты могли практиковаться.Учащиеся показывают свой путь, перетаскивая изображения стрелок по мере решения задач.
Эти лабиринты были обновлены и теперь включают как печатную, так и цифровую версии. Таким образом, независимо от того, что вы преподаете, эти ресурсы — отличный способ для студентов больше попрактиковаться в целых числах.
Хотите получить больше бесплатных эксклюзивных лабиринтов? Когда вы присоединитесь к клубу «Лабиринт месяца», вы получите бесплатный лабиринт с целыми числами сегодня (печатную И цифровую версию), а также математический лабиринт для средней школы по различным темам, который будет отправляться вам на почту каждый месяц.
Да! Зарегистрируйся в клубе «Лабиринт месяца»!
Не могу дождаться встречи с вами там!
Мы начали использовать Quizizz как способ научиться бегло говорить в школе.
 Викторина — это онлайн-игра, в которой доступно множество игр, которые другие учителя сделали для своих классов, или вы можете создать свои собственные. Затем учащиеся могут работать над ними в своем собственном темпе в режиме «домашнего задания». Если вы знакомы с Kahoot, он похож на то, как ученики задают вопросы.
Викторина — это онлайн-игра, в которой доступно множество игр, которые другие учителя сделали для своих классов, или вы можете создать свои собственные. Затем учащиеся могут работать над ними в своем собственном темпе в режиме «домашнего задания». Если вы знакомы с Kahoot, он похож на то, как ученики задают вопросы. Мы потратили много дней, работая над играми-викторинами с добавлением и вычитанием целых чисел.Я задавал вопросы викторины или позаимствовал их у другого учителя в общественном банке в рамках викторины для каждого ежедневного задания. Затем я получил код активности на день и поделился им. Например, все классы 8-го класса использовали один и тот же код. Это помогло нам как ученику увидеть, как у нас дела, и помочь ученикам стать лучше. (Еще раз напомните студентам, чтобы они не использовали калькулятор.)
Одна из замечательных особенностей Quizizz заключается в том, что здесь проводятся небольшие дружеские соревнования, и дети любят решать их каждый день.Я прошу студентов записывать, как они делают, в задней части своей записной книжки.
 Я прошу их посмотреть на свою точность и убедиться, что они улучшаются день ото дня. Использование Quizizz, чтобы получить больше практики с целыми числами, требует относительно небольшой подготовки и может иметь большое влияние на беглость сложения и вычитания целых чисел.
Я прошу их посмотреть на свою точность и убедиться, что они улучшаются день ото дня. Использование Quizizz, чтобы получить больше практики с целыми числами, требует относительно небольшой подготовки и может иметь большое влияние на беглость сложения и вычитания целых чисел. Квесты — отличный способ научить студентов практиковаться по-новому. Они побуждают учеников не только применять свои математические навыки, но и решать проблемы, открывая коды и разгадывая загадки.
Этот квест полностью представлен в Google Slides. Учащиеся могут проверять свои ответы, чтобы убедиться, что они правильно решили задачи.
Это безумие, как можно превратить что-то в «игру», и люди вдруг захотят принять в ней участие. В этой карточной игре с целыми числами игральные карты используются для тренировки сложения и вычитания целых чисел (см. Источник вдохновения в этом посте). Вот правила:
- Красные карточки — отрицательные, черные — положительные
- Каждому игроку раздается по 6 карт.

- Остальная часть колоды размещается в центре стола.
- Вы переворачиваете карту, а затем каждый игрок пытается составить комбинацию карт, равную этому числу. (См. Пример ниже)
- Каждый, кто составляет комбинацию, которая работает, получает балл. Затем они сбрасывают использованные карты и заменяют их двумя новыми.
Есть определенно другие способы сыграть в эту карточную игру. Я думаю, что дело в том, что студенты одновременно играют и практикуют целые числа.У меня есть набор огромных игральных карт, и я люблю использовать их с классом, потому что они думают, что они забавные и нелепые. И все знают, что старшеклассники любят смешное.
Доски
Практика целых чисел — отличный навык, который нужно практиковать на доске. В моем классе мы используем доски почти ежедневно, и вы можете быстро проверить свои навыки работы с досками. Обычно я показываю на проекторе целочисленное выражение, и они должны его скопировать, упростить и показать мне.
 Поскольку это практика беглости, им не нужно показывать свою работу. Это дает учителю прекрасную возможность увидеть, насколько быстро ученики овладевают навыками. Это может занять менее 3 минут, и каждый получит небольшое подкрепление.
Поскольку это практика беглости, им не нужно показывать свою работу. Это дает учителю прекрасную возможность увидеть, насколько быстро ученики овладевают навыками. Это может занять менее 3 минут, и каждый получит небольшое подкрепление. Иногда вы хотите попрактиковаться в каком-то навыке в игре для всего класса. Бинго довольно хорошо работает в качестве обзорной игры. В моей игре в бинго 36 уникальных игровых карт. Я прошу учащихся пометить свою карточку игры в бинго на половину листа разными символами для каждого раунда, который мы проводим, что позволяет играть в несколько игр с одной и той же игровой доской.Обычно у меня есть небольшие призы для победителей, такие как наклейки, конфеты или безделушки. Это одно из моих любимых занятий с губкой, и дети всегда приходят в восторг, когда слышат, что мы собираемся сыграть в бинго.
Еще одна замечательная игра для обзора всего класса — Kahoot. Если вы еще не играли в нее раньше, вам стоит полностью попробовать ее с этой темой.
 Студенты отвечают на вопросы независимо, поскольку они отображаются на проекторе для всего класса. Они получают баллы за скорость и точность.В игре есть музыка и таймер, и ученики действительно увлекаются этим. Вот пример Kahoot, который вы можете использовать для тренировки целых чисел. Если вы будете искать в Kahoot, вы найдете гораздо больше на выбор.
Студенты отвечают на вопросы независимо, поскольку они отображаются на проекторе для всего класса. Они получают баллы за скорость и точность.В игре есть музыка и таймер, и ученики действительно увлекаются этим. Вот пример Kahoot, который вы можете использовать для тренировки целых чисел. Если вы будете искать в Kahoot, вы найдете гораздо больше на выбор. Числовая строка в натуральную величину
В конечном счете, мы хотим, чтобы учащиеся могли автоматически складывать и вычитать целые числа. Это не означает, что мы не хотим, чтобы они могли мысленно видеть, что происходит, когда они складывают и вычитают целые числа. Создание числовой линии в натуральную величину — отличный способ конкретизировать эту концепцию для учащихся.(Кроме того, я одержим малярной лентой на полу или стенах, особенно для нанесения числовых линий. Так что это идеальный способ развить эту одержимость)
Если у вас в классе или в холле проведено несколько числовых линий, тогда вы можете попросить учащихся попрактиковаться в перемещении по числовой линии вверх и вниз.
 Кроме того, это дает им небольшой фон в числовых линиях, который позже можно перенести на координатную диаграмму.
Кроме того, это дает им небольшой фон в числовых линиях, который позже можно перенести на координатную диаграмму. Конечно же, в этом списке есть карточки задач! Это отличный способ для студентов практиковаться самостоятельно.Карточки с заданиями можно использовать по-разному, чтобы дать студентам больше практики. Я использую карточки с ответами на обратной стороне для самопроверки. Вы должны научить студентов самоконтролю, а не просто правильному ответу. Акцент должен быть сделан на поиске и исправлении ошибок.
Я считаю, что эти карточки с целочисленными задачами очень нравятся студентам, и рекомендую использовать их после того, как студенты немного овладеют этим навыком. Это еще одно упражнение, которое вы можете снова использовать несколько месяцев спустя в качестве средства проверки.Если вы будете систематизировать карточки с задачами, тогда у вас будет отличное упражнение для проверки, которое вы можете просто взять и уйти, когда оно вам понадобится.
Карточки с заданиями — отличный способ попрактиковаться, если вы тоже преподаете онлайн! Я также создал цифровую версию этих карточек с заданиями. Вы можете получить их здесь: Добавление целочисленных цифровых карточек задач. В этом наборе цифровых карточек с заданиями учащиеся получают ту же практику добавления положительных и отрицательных целых чисел с помощью Google Slides. Эти карточки с задачами включают слайды с вопросами и ответами, чтобы студенты могли сразу же получить обратную связь.
Ну, иногда вам просто нужно вернуться к старому листу. Это все, что представляют собой эти рабочие листы, но я использовал их, чтобы укрепить эту концепцию на бесчисленном количестве студентов, и они работают. Они могут быть не блестящими и захватывающими, но они заставляют детей сосредоточиться на том, что они делают.
Эта серия из 3 листов (щелкните, чтобы загрузить бесплатно) становится все сложнее. Кроме того, эти рабочие листы включают некоторые переменные и комбинируют аналогичные термины практики с добавлением и вычитанием целых чисел.Надеюсь, они будут полезны вашим ученикам.
Zip-Lock Baggie Number Line
Изготовление числовой линии с помощью мешочка с застежкой-молнией — это для меня новое занятие, которое я не пробовал в классе, но я хочу попробовать в этом году. Вы берете лист бумаги, помещаете числовую линию вверху и вставляете его в сумку с замком Zip-Lock с ползунком вверху. Затем вы используете ползунок как способ показать, что происходит с целыми числами, когда вы их складываете и вычитаете (см. Источник вдохновения здесь).
Мне нравится визуальный аспект этого и то, что ученики могут манипулировать числовой линией.На мой взгляд, студенты просто не могут получить слишком много практики с числовыми линиями.
Когда я увидел круги беглости на Pinterest из блога My Math Imagination, это сразу привлекло мое внимание. Такой подход отлично подойдет для рукавов SmartPal. Кроме того, это новый способ научить студентов владеть языком. Они не знают, какая проблема будет следующей. У вас может быть двухсторонний пустой шаблон, ожидающий, когда ученики будут использовать его, когда он вам понадобится. Круги беглости кажутся идеальными для быстрого завершения и упражнений с губкой, а также отличным набором упреждений, когда вы вводите целые числа в новую тему.
Онлайн игры
За прошедшие годы в Интернете было собрано большое количество разнообразных математических игр. Конечно, качество игр разное, но есть много детей, которые любят играть в такие игры. Они добавляют новизны в отработку навыка. Это то, что вы можете разместить в своем классе Google или на веб-сайте, чтобы учащиеся могли выполнять домашнее задание, быстро заканчивать или звякнуть. Вот несколько игр, которые, как я обнаружил, могут вам понравиться в классе:
- Spider Math Integer — Мне нравится, как эта игра дает учащимся возможность поиграть с целыми числами и развить в себе чувство числа, связанное с ними.
- Fruit Splat Integer Addition — В этой игре есть множество вариантов скорости и сложности, поэтому в нее может сыграть даже новичок. К тому же это что-то вроде Fruit Ninja, одной из моих любимых игр.
- Line Jumper — это игра от FunBrain, которая включает числовые линии в практику, которую выполняют ученики. По мере продвижения вы можете увеличивать сложность.
Итак, этот пост представляет множество идей о том, как практиковать сложение и вычитание целых чисел.Я надеюсь, что некоторые из них являются новыми идеями для вас, и что вы с нетерпением ждете возможности попробовать что-то новое. Попробуйте одну из этих идей со своими учениками и расскажите нам, как все прошло. Вовлеките своих учеников и помогите им стать экспертами в области целых чисел. Спасибо за прочтение! До скорого.
Связанные
Деменция — ранние признаки — Better Health Channel
Ранние признаки деменции очень малозаметны и расплывчаты и могут быть не сразу очевидны. Ранние симптомы также зависят от типа деменции и сильно различаются от человека к человеку.
Ранние симптомы деменции
Хотя ранние признаки различаются, общие ранние симптомы деменции включают:
- проблемы с памятью, особенно вспоминание недавних событий
- растущее замешательство
- снижение концентрации
- изменения личности или поведения
- апатия и ломка или депрессия
- потеря способности выполнять повседневные задачи.
Иногда люди не понимают, что эти симптомы указывают на то, что что-то не так.Они могут ошибочно полагать, что такое поведение — нормальная часть процесса старения. Симптомы также могут развиваться постепенно и долгое время оставаться незамеченными. Кроме того, некоторые люди могут отказываться действовать, даже если знают, что что-то не так.
Десять предупреждающих признаков деменции
Просмотрите следующий контрольный список общих симптомов деменции. Если у пострадавшего есть несколько из этих признаков, проконсультируйтесь с врачом для полной оценки.
Деменция и потеря памяти
Иногда можно забыть о назначенных встречах и вспомнить их позже.Человек с деменцией может чаще что-то забывать или совсем не помнить.
Деменция и трудности с заданиями
Люди могут отвлекаться и забывать подавать часть еды. У человека с деменцией могут быть проблемы со всеми этапами приготовления еды.
Деменция и дезориентация
Человек с деменцией может испытывать трудности с поиском пути в знакомое место, не понимает, где находится, или думает, что вернулся в какой-то прошлый период своей жизни.
Деменция и языковые проблемы
У всех иногда возникают проблемы с поиском нужного слова, но человек с деменцией может забывать простые слова или подставлять неподходящие слова, что затрудняет понимание предложений. У них также могут быть проблемы с пониманием других.
Деменция и изменения в абстрактном мышлении
Управление финансами может быть трудным для любого, но человеку с деменцией может быть трудно понять, что означают цифры или что с ними делать.
Деменция и плохое суждение
Многие виды деятельности требуют здравого смысла. Когда на эту способность влияет слабоумие, человеку может быть трудно принять правильное решение, например, что надеть в холодную погоду.
Деменция и плохие пространственные навыки
Человек с деменцией может испытывать трудности с определением расстояния или направления при вождении автомобиля.
Деменция и потеря вещей
Кто угодно может временно потерять бумажник или ключи.Человек с деменцией может не знать, для чего нужны ключи.
Деменция и изменения настроения, личности или поведения
Все время от времени грустят или унывают. У человека с деменцией могут быть быстрые перепады настроения без видимой причины. Они могут запутаться, стать подозрительными или замкнутыми. Некоторые могут стать расторможенными или более общительными.
Деменция и потеря инициативы
Утомление от некоторых видов деятельности — это нормально. Деменция может привести к тому, что человек потеряет интерес к ранее полученным занятиям или потребует подсказок, побуждающих его к участию.
Состояния с симптомами, похожими на деменцию
Помните, что многие состояния имеют симптомы, похожие на деменцию, поэтому важно не предполагать, что у кого-то есть деменция только потому, что присутствуют некоторые из вышеперечисленных симптомов. Инсульты, депрессия, чрезмерное длительное употребление алкоголя, инфекции, гормональные нарушения, дефицит питательных веществ и опухоли головного мозга могут вызывать симптомы, похожие на слабоумие. Многие из этих состояний поддаются лечению.
Диагностика деменции
Лучшее место для начала диагностического процесса — это поговорить с местным врачом или в клинике службы когнитивной деменции и памяти (CDAMS) по поводу постановки диагноза на ранней стадии.Только врач может диагностировать деменцию. Правильный диагноз деменции на ранней стадии важен для раннего лечения, поддержки и планирования на будущее.
Полное медицинское обследование может выявить излечимое состояние и убедиться, что оно лечится правильно, или оно может подтвердить наличие деменции и то, является ли это болезнью Альцгеймера или другим типом деменции. Шесть типов оценки могут помочь подтвердить или исключить диагноз деменции.История болезни
Врач спросит о прошлых и текущих проблемах со здоровьем, семейной истории болезни, принимаемых лекарствах и проблемах с памятью, мышлением или поведением, которые вызывают беспокойство.Врач также может пожелать поговорить с близким членом семьи, который может помочь предоставить всю необходимую информацию.
Физикальное обследование
Чтобы исключить другие состояния, медицинский осмотр может включать в себя проверку чувств, движений, а также функции сердца и легких.
Лабораторные анализы
Они будут включать различные анализы крови и мочи для выявления любого возможного заболевания, которое может быть причиной симптомов. В некоторых случаях для исследования может быть взят небольшой образец спинномозговой жидкости.
Когнитивное тестирование
Для оценки мыслительных способностей, включая память, язык, внимание и решение проблем, используются различные тесты. Это может помочь выявить конкретные проблемные области, что, в свою очередь, поможет определить первопричину или тип деменции.
Визуализация головного мозга
Существуют определенные виды сканирования, которые изучают структуру мозга и используются для исключения опухолей головного мозга или сгустков крови в головном мозге как причины симптомов.
Некоторые сканирования могут также выявить паттерны потери мозговой ткани, которые могут различать разные типы деменции.Другие типы сканирования показывают, насколько активны определенные части мозга, а также могут помочь определить тип деменции.Психиатрическая экспертиза
Психиатрическая экспертиза помогает выявить излечимые расстройства, такие как депрессия, и управлять любыми психиатрическими симптомами, такими как тревога или бред, которые могут возникать вместе с деменцией.
Разговор с врачом
После рассмотрения симптомов пациента и назначения скрининговых тестов врач может предложить предварительный диагноз или направить человека в клинику службы когнитивной деменции и памяти (CDAMS), неврологу, гериатру или психиатру.
Некоторые люди могут сопротивляться идее посещения врача. В некоторых случаях люди не осознают или отрицают, что с ними что-то не так. Это может быть связано с изменениями мозга при деменции, которые мешают способности распознавать или оценивать происходящие изменения. Другие понимают изменения, но могут бояться подтверждения своих опасений.
Один из действенных способов преодолеть эту проблему — найти еще один повод для визита к врачу.Возможно, порекомендуйте пройти обследование для выявления симптома, который человек готов признать, например, артериального давления, или порекомендовать пересмотр долгосрочного состояния или приема лекарств.
Другой способ — предложить вам обоим пройти медицинский осмотр. Любое выраженное человеком беспокойство — отличный повод предложить визит к врачу. Обязательно предоставьте много уверений. Спокойное, заботливое отношение в это время может помочь преодолеть вполне реальные заботы и страхи человека.
Иногда ваш друг или член семьи может отказаться посетить врача, чтобы спросить о своих симптомах. Чтобы получить поддержку, вы можете предпринять ряд действий, в том числе:
- поговорить с другими опекунами, которые, возможно, столкнулись с аналогичными ситуациями
- , связавшись с вашей местной группой оценки ухода за престарелыми (ACAT)
- , позвонив на национальную горячую линию по деменции.
Где получить помощь
- Ваш врач
- Ваш местный совет
- Ваш местный общественный медицинский центр
- Национальная телефонная линия помощи при деменции — Dementia Australia Тел.1800 100 500
- Услуги по оценке ухода за престарелыми тел. 1300 135 090
- My Aged Care (информационная линия правительства Австралии) 1800 200 422
- Клиники службы когнитивной деменции и памяти (CDAMS) Тел. 1300 135 090
- Сиделки Виктория Тел. 1800 242 636 (также известная как Консультативная и консультационная служба по уходу)
- Центры помощи и временного ухода Commonwealth — Правительство Австралии Тел. 1800 052 222
- Консультативная служба по управлению поведением при деменции (DBMAS) Тел.1800 699 799 — для круглосуточной консультации по телефону для лиц, осуществляющих уход, и работников по уходу
Что следует помнить
- Ранние признаки деменции очень малозаметны и неопределенны и могут быть не сразу очевидны.
- Хотя ранние признаки деменции различаются, есть некоторые общие ранние симптомы.
- Если у пострадавшего есть несколько из десяти предупреждающих признаков деменции, проконсультируйтесь с врачом для полной оценки.
- Ваш врач может использовать шесть основных типов медицинского обследования, чтобы помочь подтвердить или исключить диагноз деменции.
- Некоторые люди могут сопротивляться посещению врача для медицинского осмотра, но есть несколько стратегий, которые могут помочь облегчить этот процесс.
Знайте предупреждающие знаки | НАМИ: Национальный альянс по психическим заболеваниям
Пытаться определить разницу между ожидаемым поведением и признаками психического заболевания не всегда легко. Нет простого теста, который позволил бы кому-то узнать, есть ли у него психическое заболевание, могут ли действия и мысли быть типичным поведением человека или результатом физического заболевания.
У каждого заболевания есть свои симптомы, но общие признаки психического заболевания у взрослых и подростков могут включать следующие:
- Чрезмерное беспокойство или страх
- Чувство чрезмерной грусти или подавленности
- Спутанность мышления или проблемы с концентрацией и обучением
- Резкие перепады настроения, включая неконтролируемые «подъемы» или чувство эйфории
- Продолжительное или сильное чувство раздражительности или гнева
- Избегание друзей и общественных мероприятий
- Трудности в понимании или отношениях с другими людьми
- Изменения в привычках сна или чувство усталости и упадка энергии
- Изменения в привычках питания, такие как усиление голода или отсутствие аппетита
- Изменения полового влечения
- Затруднение восприятия реальности (бред или галлюцинации, при которых человек переживает и ощущает вещи, которых не существует в объективной реальности)
- Неспособность воспринимать изменения в собственных чувствах, поведении или личности («недостаток понимания» или анозогнозия)
- Чрезмерное употребление таких веществ, как алкоголь или наркотики
- Множественные физические недомогания без очевидных причин (например, головные боли, боли в животе, неопределенные и постоянные «боли и боли»)
- Думаю о самоубийстве
- Неспособность заниматься повседневными делами или справляться с повседневными проблемами и стрессом
- Сильный страх набора веса или беспокойство о внешности
Психические расстройства могут также начать развиваться у маленьких детей.Поскольку они все еще учатся определять мысли и эмоции и говорить о них, их самые очевидные симптомы — поведенческие. Симптомы у детей могут включать следующие:
- Изменения в успеваемости в школе
- Чрезмерное беспокойство или беспокойство, например, борьба за уклонение от постели или школы
- Гиперактивное поведение
- Частые кошмары
- Частое неповиновение или агрессия
- Частые истерики
Куда обратиться за помощью
Не бойтесь обратиться, если вам или кому-то из ваших знакомых нужна помощь.Узнавать все, что можно о психическом здоровье, — важный первый шаг.
Обратитесь в свою медицинскую страховку, к врачу первичной медико-санитарной помощи или в орган психиатрической помощи штата / округа, чтобы получить дополнительные ресурсы.
Обратитесь в службу поддержки NAMI, чтобы узнать, какие услуги и поддержка доступны в вашем районе.
Если вам или кому-то из ваших знакомых сейчас нужна помощь, вам следует немедленно позвонить в Национальную линию помощи по предотвращению самоубийств по телефону 1-800-273-8255 или позвонить 911.
Получение диагноза
Предупреждающие знаки могут помочь вам узнать, если вам нужно поговорить со специалистом.Для многих людей постановка точного диагноза является первым шагом в плане лечения.
В отличие от диабета или рака, не существует медицинского теста, который мог бы точно диагностировать психическое заболевание. Специалист в области психического здоровья будет использовать Руководство по диагностике и статистике психических расстройств , опубликованное Американской психиатрической ассоциацией, для оценки симптомов и постановки диагноза. В руководстве перечислены критерии, включая чувства и поведение, а также временные рамки, чтобы быть официально классифицированным как состояние психического здоровья.
После постановки диагноза врач может помочь разработать план лечения, который может включать прием лекарств, терапию или другие изменения образа жизни.
Поиск лечения
Диагноз — это только первый шаг; также важно знать свои собственные предпочтения и цели. Лечение психических заболеваний зависит от диагноза и человека. Не существует универсального подхода. Варианты лечения могут включать лекарства, консультирование (терапию), социальную поддержку и образование.
17 способов, которыми Вселенная общается с вами (знаки духа) — Следуйте своему собственному ритму
Вселенная говорит с нами. Он пытается привлечь наше внимание. Он пытается направить нас, установить с нами связь и разбудить нас .
Знаков предостаточно, но ищем ли мы? Мы слушаем? И знаем ли мы, что искать?
Сколько раз вы хотели, чтобы у вас был знак, в каком направлении вам следует двигаться в жизни?
Сколько раз вы просили ответ, но не знали, как его получить?
Как часто вы чувствуете себя одиноким и лишенным поддержки в жизни?
Когда вы настраиваетесь на , как вселенная общается с вами, жизнь становится намного менее запутанной, и вы начинаете чувствовать себя более согласованным и связанным.
(Примечание: я использую термины Универсальный Дух, Универсальная Истина, Вселенная, Источник, Божественное, Дух, Любовь, Жизнь, Бог как синонимы).
Однако, поскольку мы живем в физическом мире, мы также испытываем физические ограничения. Эти физические ограничения не позволяют Духу похлопать вас по плечу и сказать: «Да, я думаю, вам следует заняться этой работой», поэтому мы должны обратить внимание на более тонкие и творческие способы, которые Дух использует для отправки нам сообщения.
Ключ в том, чтобы ЗАМЕДЛИТЬ, поскольку в целом просто живите в более медленном темпе, и БУДЬТЕ НАСКОЛЬКО НАСТОЯЩИМ, чтобы вы могли настроиться на любой знак, появляющийся в вашей жизни.
Если вы застряли в своей голове, беспокоясь, слишком много думая, чрезмерно анализируя, торопясь и будучи занятым, осуждающим и сердитым, вы никогда не поймете, когда Дух пытается привлечь ваше внимание. Вы должны быть открыты и готовы получать ответы.
Ощущение чудес
Каждый знак, который я когда-либо получаю, я считаю чудом, потому что он напрямую связан с Источником.Я знаю, что когда я вижу знак, Источник находится прямо там, общается со мной, направляет меня, и я знаю, что я окружен чистой Любовью. Это действительно чудесное переживание.
Однако дело в том, что эти чудеса не такие, как вы представляете или как их изображают в фильмах. Нет ангелов, падающих с неба (по крайней мере, не буквально и физически), и нет лица в небе, говорящего с вами и направляющего вас.
Знаки менее эфирны и как бы включены в структуру и распорядок повседневной жизни.Знаки тонкие, косвенные, могут быть очень мягкими и тихими, хотя иногда и довольно громкими и очевидными.
Универсальный Дух не где-то там, он во всем и во всех; все вокруг нас, и поэтому переплетается в обычные моменты жизни.
Это означает, что вы можете получить знак в душе, пока вы моете посуду, спорите с партнером или застряли в пробке. Момент не обязательно должен быть гламурным, чтобы появилась вывеска, но если вы увидите вывеску в эти неприглядные моменты, это, несомненно, сделает этот момент более гламурным.
Кроме того, каждый знак, который приходит к вам, содержит сообщение , которое уникально для вас, и вашей конкретной ситуации, и вы видите знаки в том месте и в то время, когда вы должны их видеть.
Из-за этого знаки не подходят для всех, и поэтому вы должны интерпретировать их на интуитивном уровне и с более осознанной точки зрения. Важно убрать с дороги свое эго и страхи и позволить интуиции вести вас.
С учетом всего сказанного, давайте рассмотрим некоторые способы, которыми Универсальный Дух общается с нами!
17 СПОСОБОВ ВСЕЛЕННАЯ ОБЩАЕТСЯ С ВАМИ 1.Через людей
Универсальный Дух приходит к нам в форме людей. Не спрашивайте меня, , как это происходит, , но вселенная использует людей в качестве средств передачи определенных сообщений.
Это может быть встреча со случайным человеком, который, возможно, говорит вам что-то или делает что-то, что зажигает что-то внутри вас или вызывает глубокое знание внутри вас, предлагает вам возможность, получение текстового или телефонного звонка от кого-то, прослушивание сообщения на радио или подслушивать разговор.
Очевидно, что не все, что вы слышите, является знаком, но это знак, когда вы специально ищете ответ, на который кто-то случайно скажет вам что-то, что связано с вашим вопросом. Вы интуитивно почувствуете, что это слишком случайно, чтобы не быть признаком вселенной. Ключ тогда состоит в том, чтобы ПОСЛЕДОВАТЬ за ним.
Например, если вы подумываете о сохранении или увольнении с нынешней работы, на которой вам предлагают повышение, и вы паникуете и впадаете в панику, потому что вам нужно принять решение в течение короткого периода времени, а затем внезапно из ниоткуда вы получаете текстовое сообщение от одного из ваших коллег, в котором говорится: «Я ненавижу эту работу, они полностью обманули меня, они солгали о моем повышении», тогда я бы сказал, что это была вселенная, проходящая через этого человека, чтобы сказать вам оставить работу.На самом деле это реальная история того, что совсем недавно случилось со мной и моим мужем. Это было действительно чудо.
2. Синхронность
Синхронность — это случайное возникновение событий, которые кажутся случайными, случайными и связанными, но не связаны между собой ни одной вещью.
Например, вы едете на работу и видите ребенка с красным воздушным шариком, затем вы идете на работу, и кто-то подарил вашей коллеге красные воздушные шарики на ее день рождения, затем, когда вы едете домой, вы видите еще один красный шарик на «день открытых дверей» » знак.Совпадение? Думаю, нет.
Синхронности — это один из самых мощных способов, которыми Вселенная общается с вами, и вы начинаете испытывать их все больше и больше, чем больше вы начинаете пробуждаться. И иногда вам даже не нужно глубоко вникать в синхронность, это просто вопрос осознания того, что за кулисами происходит что-то НАМНОГО БОЛЬШЕ; нечто более глубокое, чем мы можем себе представить.
Синхронистичность — это прямая связь с Духом и знак того, что вы на правильном пути.
3. Числа
Видя определенный образец или последовательность чисел, например, на номерных знаках, или встречая тот же образец номера или номера, например, в адресе или номере телефона, или видя время 11:11, 2:22, 3:33, 12:34 и т. Д. Могут иметь скрытое значение.
Например, если вы видите повторяющиеся числа, такие как 1111, 333, 444, 555 и т. Д., Это все знаки Вселенной, что вы на правильном пути. Каждая числовая последовательность может иметь более конкретное значение, если вы проанализируете, что означают числа в нумерологии.
Вы также можете увидеть случайные числа, которые означают что-то особенное для вас, например, ваш любимый номер, счастливое число или ваш день рождения. Например, я всегда вижу 6:21 на часах, так как мой день рождения 21 июня, и я всегда вижу день рождения моего мужа 10:11 (11 октября). Для меня это всегда знаки того, что я связана с Вселенским Духом и одухотворенно связана с моим мужем.
4. Песни
Вы когда-нибудь замечали, что у вас в голове всплывает случайная песня? Или по радио звучит какая-то песня? Или вы подслушиваете определенный набор текстов из чужого радио? Или слышите, как кто-то проходит мимо поет песню?
Когда эти вещи случайны и вы чувствуете сильную связь с песней, которую слышите, вероятно, вам следует изучить это дальше.
Обратите внимание на конкретные слова, которые вы слышите, так как там может быть сообщение для вас. Если это знакомая песня, такая как ваша свадебная песня, или песня, которая напоминает вам об отпуске, или песня, которая вам нравилась в старшей школе, тогда интерпретируйте значение знака с этой точки зрения.
5. Случайная мысль
Вам может прийти в голову мысль из ниоткуда. Это может быть случайная идея, решение проблемы или что-то, что вас вдохновляет.Обязательно обратите на это внимание и посмотрите, что это может значить для и .
Например, если вам в голову приходит случайная мысль «Интересно, как дела у моего брата», это, вероятно, знак того, что вам следует позвонить своему брату, поскольку он, вероятно, нуждается в вашей любви и поддержке прямо сейчас.
6. Слово или физический знак
Знак может быть буквальным знаком со словами или изображениями на нем, например, дорожный знак, рекламный щит или сообщение в Instagram, пытающееся передать вам сообщение.
Например, если вы в последнее время были в действительно темном месте и видите сообщение в Instagram, в котором говорится, что «самый темный час незадолго до рассвета», я бы определенно воспринял это как знак того, что все будет лучше. скоро.
Или, если вы видите рекламный щит с пальмой, на котором написано: «Пора в отпуск», сразу после размышлений, стоит ли вам сделать перерыв в работе, я бы воспринял это как знак того, что нужно сделать перерыв.
Или, может быть, вы видите дорожный знак с надписью «Притормози», и по какой-то причине он действительно находит отклик у вас, это может быть признаком того, что вам нужно сбавить темп в жизни и быть более внимательным.
Опять же, существует так много разных способов интерпретации знаков, главное — следовать своей интуиции, а не зацикливаться на ней.
7. Сны
Сообщения, указания и ответы могут приходить к нам через наши сны. У вас был сильный сон, который казался сверхреальным? Кого ты встретил? Что они сказали? Что случилось? Как вы себя чувствуете? Какие идеи вы получили?
Вам снова и снова снятся одни и те же сны? О чем они? Вы постоянно встречаетесь с одним и тем же человеком, посещаете одни и те же места, испытываете одинаковые переживания? Посмотрите на «значение снов», чтобы понять, что это может означать.
Вам постоянно снятся кошмары? О чем они? Может быть, это основано на более глубоком страхе, который нужно исцелить.
Вы часто мечтаете о каком-то периоде жизни или о том, чтобы быть с определенными людьми из вашего прошлого? Что это значит для тебя? Есть ли здесь нерешенный вопрос, который нужно решить?
8. Символы природы
Цвета, цветы, животные, перья, камни и кристаллы имеют определенное значение. Обращайте внимание на то, что вы видите, с чем вступаете в контакт, что снова и снова появляется в вашей жизни и к чему вас тянет.
Например, ястребы олицетворяют возросшее духовное осознание и время, чтобы летать высоко, красный цвет представляет безопасность, стабильность и удачу, а перо, падающее вам на колени, — это «привет» от Вселенной и знак того, что ваши ангелы возле.
9. Глубокое чувство или знание
Когда вы чувствуете, что «это правильно», или «что-то не так», или «каждая часть меня хочет это сделать», это явный признак Вселенной.
Кроме того, когда вы слышите сообщение или читаете что-то в книге, которая глубоко резонирует с вами, и вы не знаете, почему, но кажется, что правильно, а кажется, что правда, это пробуждает вашу внутреннюю истину.
Внутри нас есть глубокая истина, связанная с Универсальной Истиной, и когда вы слышите эту Истину, она начинает пробуждать что-то глубоко внутри вас, что заставляет вас чувствовать к ней действительно влечение. Обратите на это внимание и следуйте!
10. Объекты
Вселенная может общаться с вами через объекты, например, когда вы находите то, что искали, когда предметы падают с полок или из шкафов, или когда вы натыкаетесь на объект, который что-то запускает. из прошлого, поддерживает вашу новую идею или действует как ответ на вопрос.
Например, кто-то дает вам книгу о финансовой свободе, когда вы решаете выбраться из долгов. Или вы гуляете на природе и видите на земле случайную детскую игрушку. Или вы найдете фотографию своей сестры, с которой не разговаривали много лет. Или случайная книга падает с книжной полки в книжном магазине. Это все способы, которыми Дух пытается вам что-то сказать, вам решать, что именно.
11. Технологические сбои или сбои
Может быть, у вас отключился интернет, нет сервиса или Wi-Fi, ваше текстовое сообщение не отправляется, ваш компьютер выключается, ваш фильм не загружается или ваш ТВ не работает.Эти знаки можно трактовать по-разному.
Например, если у вас нет службы, но вы хотите отправить электронное письмо, возможно, это способ вселенной сказать вам, что сейчас не подходящее время для работы и что вы должны наслаждаться настоящим моментом. Когда текстовое сообщение не нужно отправлять, возможно, это знак того, что вам не следует отправлять сообщение или что вам следует переосмыслить / перефразировать то, что вы написали. Если ваш телевизор не работает, возможно, это признак того, что вы слишком много смотрите телевизор.
12.Проблемы в вашем теле
Физическая боль, симптомы, недомогания и болезни — все это способы, которыми Вселенная сообщает вам, что что-то не так. Ваш образ жизни и привычки могут стать причиной таких проблем, как боль в спине из-за слишком долгого сидения. Это может быть признаком того, что вам нужно изменить образ жизни и начать вести активный образ жизни.
Однако болезни могут иметь духовные причины, проявляющиеся в физических недугах. Например, у вас может появиться сыпь из-за желания выйти из ситуации или отношений, которые вам не нравятся.
Разумно изучить образ жизни, а также духовные и эмоциональные причины того или иного симптома, чтобы понять, что на самом деле его вызывает. Часто, когда вы исцеляете эмоциональный аспект, физические симптомы исчезают естественным образом.
13. Неудачи, препятствия, объезды и задержки
Когда неожиданно ваш рейс задерживается, ваше собеседование отменяется, вы заболеете и т. Д., Жизнь может подтолкнуть вас в другом направлении.
Эти вещи обычно находятся вне нашего контроля, поэтому лучше не бороться и не сопротивляться этому, а принять это как знак. Вселенная может управлять повреждениями, чтобы направить вас на правильный путь. Это также может быть признаком того, что ваша энергия имеет низкую вибрацию и фактически создает эти неудачи, поэтому вам нужно сместить свою энергию и изменить свое мышление, чтобы согласоваться с более высокой вибрацией.
«Будьте благодарны за закрытые двери, объезды и заграждения. Они защищают вас от путей и мест, не предназначенных для вас.Сюзанна Хейн
14. Все рушится
Бывают моменты в жизни, когда кажется, что все рушится, и когда вы думали, что жизнь не может стать хуже, это происходит. Ваша машина ломается, ваша крыша начинает протекать, вы теряете работу, ваш ребенок вступает в драку, ваш партнер расстается с вами или умирает кто-то, кого вы любите.
Часто, когда все в нашей жизни рушится, это приглашение научиться отпускать и отстраняться от мира форм. Это возможность проснуться.
Это также прекрасная возможность переосмыслить и переосмыслить то, как мы прожили свою жизнь, увидеть, что нужно изменить, и начать все заново, чтобы соответствовать тому, кем мы являемся на самом деле.
15. Все в вашей жизни течет и выравнивается
Это противоположно тому, что все разваливается на части, и здесь вы чувствуете вдохновение, чувствуете себя хорошо, вы в зоне, возможности появляются слева и справа , ваши желания проявляются, вы чувствуете себя связанным и выровненным, все как-то получается, и в вашей жизни есть ощущение потока.Это прекрасный знак того, что вы согласны со своей истиной и идете по правильному пути.
16. Во время медитации
Когда вы находитесь в состоянии присутствия и входите внутрь, чтобы соединиться с самим собой, открывается великая мудрость. Это открывает врата наводнения для Духа, чтобы общаться с вами, чтобы вы могли получать знаки, руководство и ответы.
Если вы хотите научиться некоторым медитативным упражнениям, чтобы настроиться на свою внутреннюю систему руководства, подпишитесь на мой бесплатный курс электронной почты «Восстановите связь с собой за 4 дня.
17. Все вокруг вас делают то, что вы собираетесь делать или знаете, что глубоко внутри вы должны сделать
Глубоко внутри вы знаете, что вам следует бросить употреблять алкоголь и вести более здоровый образ жизни. Внезапно вы навещаете своего лучшего друга, и он говорит, что только что бросил пить. Завтра ваш брат и его жена начнут «не пить». Ваш коллега говорит вам, как хорошо он себя чувствует, когда не пил целый год. Все это явные признаки из вселенной, что «да, вам обязательно нужно бросить пить и сосредоточиться на своем здоровье!»
Типы, признаки и сообщения о возможном насилии
Жестокое обращение с детьми относится к любому эмоциональному, сексуальному или физическому жестокому обращению или пренебрежению взрослым, исполняющим обязанности по отношению к кому-то младше 18 лет.
Это относится к любому виду действия или бездействия, которое приводит к причинению вреда или возможному вреду для ребенка. Взрослый может быть родителем или другим членом семьи или другим опекуном, включая спортивных тренеров, учителей и так далее.
Центры по контролю и профилактике заболеваний (CDC) классифицируют типы жестокого обращения с детьми как физическое насилие, сексуальное насилие, эмоциональное насилие или пренебрежение.
Злоупотребления часто связаны с одним или несколькими из этих типов. Издевательства не включены в эти категории, но это способ совершения различных видов насилия.
Действие может быть или не быть насильственным.
Это может произойти дома или где-либо еще, и это происходит во всех культурах, странах и экономических классах. Обычно в нем участвует член семьи или друг, а не незнакомец.
Это также может произойти по разным причинам, например, из-за проблем с психическим здоровьем человека, совершившего насилие.
В этой статье рассматриваются типы злоупотреблений, которые они включают, и некоторые признаки, на которые следует обратить внимание.
Поделиться на PinterestМногие дети сталкиваются с каким-либо насилием в процессе взросления.Это может привести к чувству страха и изоляции.
В Соединенных Штатах службы защиты детей (CPS) получили 676 000 сообщений о лицах, подвергшихся жестокому обращению или пренебрежению в 2016 году. Одно исследование показало, что каждый четвертый ребенок в какой-то момент испытывал какое-либо пренебрежение или жестокое обращение.
Жестокое обращение с детьми — серьезная проблема, которая привела к гибели 1750 детей в США в 2016 году.
Наблюдатели могут не захотеть вмешиваться, если они не уверены или не знают всей истории.
Иногда люди боятся высказаться из-за существующего баланса сил.
Ребенок может бояться, что человек, который злоупотребляет им, слишком важен или могущественен. Они также могут бояться, что им не поверят. Им также может быть стыдно, смущаться или беспокоиться о том, что они виноваты.
Злоупотребление бывает трудно обнаружить. Некоторые из признаков, например синяки, могут быть частью нормального взросления.
Иногда жестокое обращение частично является результатом проблем, с которыми сталкиваются родители или опекуны, которые также требуют решения.Это может быть финансовое давление, безработица, проблемы с психическим здоровьем или проблемы со злоупотреблением психоактивными веществами. Они тоже, возможно, испытали насилие в детстве.
Сообщение о признаках того, что что-то не так, может помочь детям, но также может помочь их опекунам.
Физическое насилие может включать в себя умышленное:
Поделиться на Pinterest Умышленное нанесение ударов ребенку или иным образом причинение ему физического вреда считается жестоким обращением, в том числе, во многих странах, в качестве наказания.
- жжение или ошпаривание
- удушье или утопление, например, удерживание ребенка под водой
- отравление
- тряска, бросание, удары, укусы
- щекотка без согласия
- чрезмерное ущемление, шлепок или спотыкание
- любое другое физическое нанесение вреда
- привязывание или принуждение ребенка к стрессовому положению
- отказ от сна, еды или лекарств
Это также может включать сфабрикование симптома или преднамеренное индуцирование болезни у ребенка, как в случае синдрома Мюнхгаузена по доверенности, теперь известного как фиктивное расстройство, навязанное другому (FDAI).
Во многих странах телесные наказания все чаще рассматриваются как форма физического насилия над детьми.
Признаки физического насилия
Признаки того, что физическое насилие может иметь место, включают следующее, но важно отметить, что это не обязательно признаки жестокого обращения, и они могут иметь место по другим причинам.
- необъяснимые черные глаза, сломанные кости, синяки, укусы или ожоги
- травм, которые могут выявить характерную картину, например, более одного ожога или ранка на руке
- протестовать или плакать, когда пора идти в больницу конкретное место, будь то дом или школа, или другое место, где могло произойти насилие
- выглядело так, как будто боялись конкретного человека
- проявляли бдительность, как будто ожидали чего-то неприятного
- вздрагивая при прикосновении
- , например, в неподходящей одежде , длинные рукава летом, чтобы скрыть травмы
- говорить о травмах, причиненных родителем, опекуном или другим лицом
Если взрослый совершает жестокое обращение, они могут:
- казаться слишком серьезными и суровыми, когда ребенок
- ведет себя непредсказуемым образом, без четких границ и правил
- набрасывается в гневе, когда ребенок делает что-то не так, вместо того, чтобы объяснять 900 08
- использовать страх физического наказания, а не обучение правилам, как способ контролировать поведение ребенка
Эмоциональное насилие происходит, когда люди постоянно говорят вещи и ведут себя таким образом, который демонстрирует ребенку, что они неадекватны, нелюбимы, никчемны , или ценится только в том, что касается потребностей другого человека.
Это может иметь глубокое и долгосрочное воздействие на ребенка.
Примеры включают:
- не позволять детям выражать свои взгляды и мнения
- высмеивать то, что они говорят
- заставлять их замолчать
- часто кричать или угрожать им
- высмеивать то, как они или как они пытаются общаться
- «молчаливое обращение» с ребенком в качестве наказания
- ограничение физического контакта
- сообщение им о том, что они «плохие» или «ошибка»
- предотвращение нормального социального взаимодействия со сверстниками и другими людьми
- жестокое обращение с другим человеком впереди ребенка, например, в результате домашнего насилия
- запугивания, включая запугивание в Интернете
- «эмоциональный шантаж»
Все виды жестокого обращения включают некоторый уровень эмоционального насилия, но также могут происходить сами по себе.
Признаки эмоционального насилия
Некоторые из этих признаков могут указывать на то, что ребенок переживает эмоциональное насилие:
- выглядит замкнутым, тревожным или испуганным
- демонстрирует крайности в поведении, например, уступчивость, пассивность или агрессивность
- отсутствие привязанности к родителю или опекуну
- неподходящее по возрасту поведение, например, сосание пальца
Сексуальное насилие определяется как любое действие, которое вынуждает или побуждает ребенка или молодого человека к участию в сексуальной деятельности.
Это сексуальное насилие, даже если ребенок не понимает, что происходит, и нет силы, насилия или даже контакта.
Если ребенка принуждают или приглашают к участию в какой-либо деятельности, которая вызывает возбуждение у другого, это считается сексуальным насилием.
Такие действия могут включать:
- нападение путем проникновения, такое как изнасилование или оральный секс
- непроникающие сексуальные действия, такие как прикосновения вне одежды, трение, поцелуи и мастурбация
- наблюдение за другими, совершающими сексуальные действия или получение ребенок наблюдать за такими действиями
- просмотр, демонстрация или обмен сексуальными изображениями, видео, игрушками или другими материалами
- рассказывание грязных анекдотов или историй
- принуждение или приглашение ребенка раздеться для сексуального удовлетворения
- «мигает» или демонстрация гениталий ребенку
- поощрение ребенка к сексуально неприемлемому поведению
- уход за телом или подготовка к насилию или активности в будущем
Лицо, совершающее насилие, может быть взрослым мужчиной, взрослой женщиной, или другой ребенок, обычно подросток, который уже достиг половой зрелости, хотя дети младшего возраста также могут подвергаться насилию.
Признаки сексуального насилия
Признаки у ребенка, которые могут указывать на сексуальное насилие, включают:
- разговоры о сексуальном насилии
- демонстрацию сексуальных знаний или поведения не по годам, странное или необычное
- отказ от друзей и другие
- бегство из дома
- уклонение от конкретного человека
- кошмары
- мочиться в постель после того, как не сделали этого до
- изменения настроения или аппетита
- беременность или заболевание, передающееся половым путем (ЗППП), особенно до 14 лет
Физические признаки, которые могут указывать на сексуальное насилие, включают трудности при ходьбе или сидении.
Сексуальное насилие обычно касается кого-то, кого ребенок знает. Часто ребенку говорят держать отношения в секрете. Им могут угрожать что-то плохое, если они кому-нибудь расскажут.
Взрослый, совершающий сексуальное насилие по отношению к ребенку, возможно, подвергался такому же обращению в прошлом. Нарушение цикла может помочь предотвратить его передачу следующему поколению.
Поделиться на Pinterest Долгосрочные последствия жестокого обращения включают одиночество, изоляцию и низкую самооценку.
Безнадзорность ребенка — это когда родитель или опекун постоянно не удовлетворяет основные физические и психологические потребности ребенка, что приводит к ухудшению здоровья или развития ребенка.
Это может включать:
- отсутствие надлежащего питания, одежды или медицинской помощи
- запирание ребенка в комнате или туалете
- не предоставление надлежащего жилья, в том числе отказ от ребенка или исключение его из семейного дома
- размещение или оставить ребенка в ситуации, в которой он может испытать эмоциональную или физическую опасность или причинить вред
- Оставить ребенка одного на долгое время или так, чтобы ему был причинен вред
Пренебрежение или невыполнение основных эмоциональных потребностей ребенка может представлять собой пренебрежение .
Признаки и симптомы пренебрежения
Если родитель или опекун ведет себя небрежно, ребенок может:
- иметь медицинские или стоматологические потребности, которые не удовлетворяются
- иметь немытую одежду, кожу или волосы
- употреблять наркотики или алкоголь
- не хватать еды или денег в необычное время, например, на обед или проезд на автобусе домой
- носить одну и ту же одежду все время или постоянно быть одеты неподходящим для времени года
- пропустить школа часто
- нуждаются в очках, но никогда не носят их
- говорят, что никто не присматривает за ними дома
Признаки того, что родитель пренебрегает ребенком, включают отсутствие интереса к его прогрессу и благополучию, но родитель тоже может испытывать трудности.
Им может потребоваться помощь, например, с:
- нелеченным психическим заболеванием
- злоупотреблением психоактивными веществами или алкоголем
- стрессом
- отсутствием поддержки
- незнанием лучшего способа заботиться о своих детях
Не замужем, не замужем, родители-подростки и те, кто испытывал трудности в собственном детстве, могут испытывать трудности как родители.
В некоторых случаях выявление родителей, нуждающихся в помощи, а также их поддержка и обучение могут помочь родителям избежать жестокого обращения при воспитании своих детей.
Лицо, которое подозревает или считает, что ребенок подвергается жестокому обращению, должно принять меры для немедленной и долгосрочной безопасности ребенка. Вам не нужно быть уверенным в том, что происходит злоупотребление, или знать, какой тип.
В долгосрочной перспективе жестокое обращение может привести к проблемам с доверием и трудностям во взаимоотношениях, чувству собственной никчемности и трудностям с регулированием эмоций. В некоторых случаях ребенок может вырасти во взрослого, который жестоко обращается с детьми, находящимися на его попечении.
Если это ваш собственный ребенок, вам следует убрать ребенка из присутствия человека, например, временно или, возможно, навсегда отказавшись от няни, если опасения кажутся обоснованными.
Один из признаков, который может указывать на то, что имело место насилие, — это рисование детьми рисунков, отражающих их опыт, или разыгрывание того, что произошло с ними в игре.
Исследователи заявили, что не хватает объективных мер, которые можно было бы использовать для подтверждения использования рисунков в качестве доказательства для использования в судебном деле. Однако если ребенок рисует необычные изображения, на них стоит обратить внимание, особенно если есть другие знаки.
Стоит отметить, что двух одинаковых корпусов не будет.Знаки тоже могут перекрываться. Например, агрессивные изменения поведения могут быть признаком физического или эмоционального насилия.
Кроме того, подобные симптомы могут вызывать и другие факторы. Потеря любимого человека, разлука или развод, помимо прочего, также могут вызывать признаки эмоционального стресса.
Детям, которые могли подвергнуться насилию, следует посетить врача или больницу, поскольку может потребоваться физическая медицинская помощь или консультация.
Любой, кто считает, что он оскорблял, оскорблял или мог оскорбить ребенка, должен отделиться от ребенка и поместить его в безопасное место, например, попросив кого-нибудь присмотреть за ним, а затем найти кого-нибудь, кому можно довериться.Может потребоваться консультация.
Есть телефоны доверия, и местная полиция или медицинские службы могут помочь. Звонки можно совершать анонимно. Соответствующие люди примут меры для расследования.
Чтобы сообщить о предполагаемом случае жестокого обращения, вы можете позвонить по телефону 9-1-1 или по этому номеру: (1-800) 4-A-CHILD или (1-800) 422-4453.
Разговор с детьми может повысить их осведомленность и подготовить их к распознаванию и, возможно, предотвращению будущих проблем.
Советы включают:
- поговорить с вашим ребенком о подходящем и несоответствующем поведении, а также о безопасных и небезопасных ситуациях
- ролевые игры, что делать, если кто-то ведет себя ненадлежащим образом, и как получить помощь
- поощрять открытое общение с вашим ребенком, поскольку это упростит обнаружение каких-либо необычных событий
- Убедитесь, что ваш собственный дом и двор в безопасности, и планируйте заранее, чтобы никогда не оставлять маленьких детей одних
- всегда знать, где находится ваш ребенок, когда его нет
Построение отношений с людьми, которые заботятся о ваших детях, включая учителей, няни и родителей друзей, может помочь по-разному.
Уравнение чисел с разными знаками
Математику уж затем учить надо, что она ум в порядок приводит
Основные правила математики с примерами. 6 класс. Часть 2.
Содержание
Умножение. Свойства умножения
Произведением числа на натуральное число не равное 1, называют сумму, состоящую из слагаемых, каждое из которых равно а:
a · b = a + a + a + . . . + a ⏟ b
Если один из двух множителей равен 1, то произведение равно второму множителю:
Если один из множителей равен нулю, то произведение равно нулю:
Если произведение равно нулю, то хотя бы один из множителей равен нулю.
!Важное правило. Помогает решать уравнения
( x — a ) ( x — b ) = 0 ; И л и x — a = 0 , и л и x — b = 0 ; 2 к о р н я x = a и x = b . ( x — 5 ) ( x + 2 ) = 0 ; И л и x — 5 = 0 , и л и x + 2 = 0 ; 2 к о р н я x = 5 и x = — 2 .
Умножение обыкновенных дробей
Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения:
Чтобы умножить смешанные числа, надо сначала записать их в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Умножение рациональных чисел
Чтобы умножить два числа с разными знаками, надо умножить их модули и перед полученным произведением поставить знак «-».
Чтобы умножить два отрицательных числа, надо умножить их модули.
Для любого рационального числа :
Если произведение • — отрицательное, то числа и имеют разные знаки.
Деление обыкновенных дробей
Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю:
a b : c d = a b · d c
Деление рациональных чисел
Чтобы найти частное двух чисел с разными знаками, надо модуль делимого разделить на модуль делителя и перед полученным числом поставить знак «-».
Чтобы найти частное двух отрицательных чисел, надо модуль делимого разделить на модуль делителя.
Нахождение дроби от числа
Чтобы найти дробь от числа, можно число умножить на эту дробь.
Чтобы найти проценты от числа, можно представить проценты в виде дроби и умножить число на эту дробь.
Нахождение числа по его дроби
Чтобы найти число по значению его дроби, можно это значение разделить на эту дробь.
Найти число, если известно, что
е г о д р о б ь 5 7 с о с т а в л я е т ч и с л о 15 : 15 : 5 7 = 15 · 7 5 = 15 3 · 7 5 1 = 21
Чтобы найти число по его процентам, можно представить проценты в виде дроби и разделить значение процентов на эту дробь.
Найти число, если известно, что
24 % э т о г о ч и с л а р а в н ы 48 . 24 % = 24 100 ; 48 : 24 100 = 48 · 100 24 = 48 2 · 100 24 1 = 200
Степень числа
Степенью числа с натуральным показателем , большим , называют произведение множителей, каждый из которых равен :
a n = a · a · a · … · a ⏟ n
Число при этом называют основанием степени.
Степенью числа с показателем называют само число
Вторую степень числа называют также квадратом числа. Например, запись читают: « в квадрате».
Третью степень называют кубом числа, а запись читают: « в кубе».
Если в числовое выражение входит степень, то сначала выполняют возведение в степень, а затем производят другие действия.
Найти значение выражения
5 · 2 3 + 15 5 · 2 2 3 1 + 3 15 = 5 · 8 + 15 = 40 + 15 = 55
Числовые и буквенные выражения
Запись, составленную из чисел, знаков арифметических действий и скобок, называют числовым выражением.
Запись, составленную из чисел, букв, знаков арифметических действий и скобок, называют буквенным выражением.
Приведение подобных слагаемых
Чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на общую буквенную часть.
Раскрытие скобок
Если перед скобками стоит знак «-», то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, изменить на противоположные.
Если перед скобками стоит знак « + », то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, оставить без изменений.
Свойства уравнений
- Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, имеющее те же корни, что и данное.
- Если данное уравнение не имеет корней, то, прибавив к обеим его частям одно и то же число, получим уравнение, тоже не имеющее корней.
- Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, имеющее те же корни, что и данное.
- Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, имеющее те же корни, что и данное.
Отношения
- Частное двух чисел и , не равных нулю, еще называют отношением чисел и , или отношением числа к числу .
- Отношение положительных чисел и показывает, во сколько раз число больше числа , или какую часть число составляет число .
показывает, что число 10 в 5 раз больше числа 2 или число 2 в 5 раз меньше числа 10.
- Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
Пропорции
Равенство двух отношений называют пропорцией. В буквенном виде пропорцию можно записать так:
a : b = c : d и л и a b = c d
Числа и называют крайними членами пропорции, а числа и — средними членами пропорции.
Основное свойство пропорции
Произведение крайних членов пропорции равно произведению ее средних членов:
a b = c d ⇒ a d = b c
Если , , и числа, не равные нулю, и • = • , то отношения
могут образовывать пропорцию
Процентное отношение двух чисел
Процентное отношение двух чисел — это их отношение, выраженное в процентах. Оно показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.
Прямая и обратная пропорциональная зависимость
Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Если величины и обратно пропорциональны, то их соответствующие значения удовлетворяют равенству
, где -число, постоянное для данных величин.
Действия с числами, имеющими разные знаки. 6-й класс
Разделы: Математика
Класс: 6
Тип урока: игра “Математический поезд”
Цели:
– систематизация знаний по данной теме;
– повторение правил сложения и вычитания чисел с одинаковыми и разными знаками;
– повторение правил умножения и деления сложения и вычитания чисел с одинаковыми и разными знаками;
– повторение алгоритма решения уравнения;
– умение применять их при решении различных задач.
Оборудование:
– цветные жетоны;
– интерактивный комплекс.
– жетоны;
– карточки;
– схема маршрута.
“Математический поезд” состоит из 3-х вагонов: мягкого, купейного, плацкартного.
В кассовом зале каждый ученик получает посадочный талон с заданиями и 6 жетонов.
Решив все задачи, ученик обращается за получением билета.
Если ученик не может решить какое-либо задание, то он обращается в справочное бюро. В зависимости от содержания справки определяется “плата”.
2. Справочное бюро.
Проверка правильности решения задачи и указание ошибки проводится бесплатно;
За наводящий вопрос, помогающий найти путь решения, платится 1 жетон;
За подсказку пути решения – 2 жетона;
За решение – 3 жетона.
3. Получения билета.
В мягкий вагон – при правильном решении всех заданий и предъявлении в кассу более 3-х жетонов;
В купейный вагон – при решении всех заданий и предъявлении в кассу 3-х жетонов;
В плацкартный вагон – при решении всех заданий и предъявлении в кассу 1 или 2-х жетонов.
I. Разминка.
Прочитать правила сложения и вычитания чисел с одинаковыми и разными знаками.
| Устно -6 – 3,5 2,8 – 1,2 8,1 + 1,9 1 – 0,25 0,6 – 1,6 |
Письменно 12,3 – 43, -33,3 + 14,8 -16,7 – 19,14 1,324 – 5,18 -36,6 + 13,4 |
При сложении двух чисел отрицательны
Надо модули сложить их обязательно.
И поставить минус перед суммой,
Только минус, обязательно подумай!
При сложении с разными знаками чисел
Надо меньший из большего модуля вычесть
И поставить того знак числа в результате,
Модуль больше которого, знай математик!
(Н. Зайцева).
Прочитать правила умножения чисел с одинаковыми и разными знаками.
| Устно 6*0,8 -4*0,7 -6,2*(-1) -0,52*100 52*0,01 |
Письменно 0,4*(-5,2) -25,3*0,1 -0,14*(-20) -4*3,5 24*15 |
Прочитать правила деления чисел с одинаковыми и разными знаками.
| Устно 4:0,4 2,4: (-12) -2,5:(-5) -3: 0,01 -0,2:0,1 |
Письменно 0,2: (-4) -56: (-0,7) -2,6: 13 763: 0,1 -0,15: 0,01 |
Не на шутку в самом деле,
Если Оля, Таня, Зина…
Умножают или делят
Два числа со знаком минус,
Получают, спора нет,
Положительный ответ.
Даже сказочный Емеля,
Чтобы спорились дела,
Умножает или делит
Разных знаков два числа.
Получает, не секрет,
Отрицательный ответ.
(Н. Зайцева).
Проверка письменных заданий проводится на интерактивной доске.
II. Выдаются посадочные талоны и жетоны.
Письменно в тетрадях.
а) раскрыть скобки
а – (с + х + у – в)
а + (-х – у + в + с)
б) привести подобные слагаемые
8х + 12а – 2х – 6а
-7х – (-4х – 3а) + 6а
7*(-2х + 3) – 4*(3х + 2)
III. После проверки выдаются “посадочные билеты”:
– желтый – в мягкий вагон;
– зеленый – в купейный вагон;
– красный – в плацкартный вагон
Голос диктора: “Внимание! Внимание! Прослушайте объявление! Математический поезд отправляется от станции “Школьная” и следует до станции “Решай-ка”. (Звучит бодрая музыка.)
Голос диктора: “Внимание! Внимание! Прослушайте объявление! Наш поезд прибывает на станцию “Решай-ка”. Вас встречает кандидат математических наук “Уравнение”.
“Уравнение” – “Здравствуйте, дорогие друзья. Очень радо встрече с вами. Ответьте, пожалуйста, на мои следующие вопросы:
– что называется уравнением?
– что называется корнем уравнения?
– что значит решить уравнение?
– какие уравнения называются равносильными?
– назвать алгоритм решения уравнения”.
Самостоятельная работа по вариантам.
-27х + 220 = – 5х
0,8*(9 + 2х) = 0,5*(2 – 3х)
2-й в.
7х = -310 + 3а
0,5*(х + 3) = 0,8*(10 – х)
Проверка – на интерактивной доске.
“Уравнение”: “Дорогие друзья! Вы все знаете об уравнении и умеете решать уравнения. Поэтому можете продолжить свое путешествие дальше”.
За правильное решение учащиеся получают карточку.
Голос диктора: “Внимание! Внимание! Прослушайте объявление! Математический поезд отправляется от станции “Школьная”.
Голос диктора: “Внимание! Внимание! Прослушайте объявление! Наш поезд прибывает на станцию “Весенняя”. Здесь вас встречает
Задача: (решаем на доске).
Из одной скворечни одновременно в противоположные стороны вылетели 2 скворца. Скорость одного из них на 25 кмч. больше скорости другого. Через 0,3 часа расстояние между ними стало 37,5 км. Найдите скорость каждого скворца.
Пусть х кмч. скорость первого скворца, тогда (х + 25) кмч. – скорость второго скворца, (х + х + 25)*0,3 = 0,6х + 7,5 км. Расстояние между ними.
Уравнение: 0,6х + 7,5 = 37,5
0,6х = 30
х = 50
50 + 25 = 75(кмч.) скорость второго скворца.
Ответ. 50кмч., 75кмч.
Дано уравнение: 3х – 20 = х + 20.
Составьте по нему задачу и решите ее.
За правильное решение учащиеся получают карточку.
Голос диктора: “Внимание! Внимание! Прослушайте объявление! Математический поезд отправляется от станции “Весенняя”.
Голос диктора: “Внимание! Внимание! Прослушайте объявление! Наш поезд прибывает на станцию “Угадай-ка”. Здесь вас встречает Емеля.
Проверьте, верно ли решены уравнения:
(Решают самостоятельно за партой, затем – на доске.)
3х + 8= -17
3х = -17 + 8
3х = 9
Х = 3
Ответ. 3.
14х – 19 = 4х – 10
14х – 4х = -10 + 19
10х = 9
Х = 10:9
Х =1 19
Ответ. 1 19
3х – 6 = 2х – 4
3х – 2х = -4 + 6
Х = 2
Ответ. 2.
За правильное решение учащиеся получают карточку.
- Уравнение – это равенство, содержащее букву, значение которой надо найти.
- Чтобы найти неизвестное слагаемое, надо к сумме прибавить известное слагаемое.
- Решить уравнение – это найти все его корни, или убедиться, что их нет.
- Корень уравнения 0х = 0 равен 0.
- Корнем уравнения называется значение буквы, при котором оно обращается в верное равенство.
- Корни уравнения не изменяются, если обе части уравнения умножить или разделить на отличное от нуля число.
(1, 0, 1, 1, 1, 1 – ответ на интерактивной доске.)
За правильное решение учащиеся получают карточку.
Голос диктора: “Внимание! Внимание! Прослушайте объявление! Математический поезд отправляется от станции “Угадай-ка”.
В вагоне работают контролеры, предъявите цветные карточки, полученные за верные решения заданий во время путешествия. Наш поезд возвращается на станцию “Школьная”.
№ № 1318(в), 1319 (ж,з), 1347.
- Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбург. Математика 6, МНЕМОЗИНА, Москва, 2005.
- В.В. Выговская. Поурочные разработки по математике. “ВАКО”, Москва, 2008.
- О.В. Панишева. Математика в стихах. “Учитель”, Волгоград.2009.
Решение простых линейных уравнений

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
-
Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | : (−4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.

Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
-
Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
-
Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
- 4х + 8 = 6 − 7х
- 4х + 7х = 6 − 8
- 11х = −2
- х = −2 : 11
- х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = – 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
[spoiler title=”источники:”]
http://urok.1sept.ru/articles/605684
http://skysmart.ru/articles/mathematic/reshenie-prostyh-linejnyh-uravnenij
[/spoiler]

