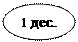План урока:
Буквенные выражения
Уравнение. Решение уравнений методом подбора
Проверка сложения и вычитания
Письменные вычисления. Запись столбиком
Здравствуйте, ребята! Начнем урок с интересной загадки:
Отгадайте без подсказки
Вы героев этой сказки:
Трое братьев до чего же
Друг на друга все похожи!
(Три поросенка)
Буквенные выражения
Три весёлых поросёнка Ниф-Ниф, Наф-Наф и Нуф-Нуф приглашают нас с вами, ребята, в гости. Посмотрите, какие дома они построили!
Как вы думаете, можно ли вставить в окошки карточки с цифрами? Почему?
В домике Ниф-Нифа в открытом окошке может быть карточка с цифрой 5? Какое выражение можно записать?
5 + 4
А какое выражение запишем, если в доме Нуф-Нуфа в окошке будет цифра 2?
6 + 2
Можно ли в окошке Наф-Нафа увидеть цифру 1? А цифру 3?
С цифрой 1 запишем выражение: 1 – 1.
А вот цифра 3 не подходит, потому что из 1 нельзя вычесть 3.
Запишите получившиеся выражения и найдите их значения.
Проверь себя.
5 + 4= 9
6 + 2= 8
1 – 1= 0
Мы записали числовые выражения, ведь они содержат только числа.
Ребята, как вы думаете, можно ли в окошко вставить карточку с буквой?
В математике принято использовать латинские буквы. Может быть, вы уже знаете некоторые из них? Давайте, правильно назовем латинские буквы.
В окошки домиков поросят подставим карточки с буквами: x, y, d.
Запишем выражения: x + 4, 6 + y, 1 – d.
У нас получились буквенные выражения.
Найдём значение следующих буквенных выражений: 8 + а, d – 6, x + 5, y – 1.
Для этого вместо буквы подставим число: а = 12, d = 9, x = 14, y = 20.
|
8 + a d – 6 x + 5 y – 1 |
8 + 12 = 20 9 – 6 = 3 14 + 5 = 19 20 – 1 = 19 |
Найдите значение выражения: k + 20, если k = 3, k = 5, k = 9.
Проверь себя.
3 + 20 = 23
5 + 20 = 25
9 + 20 = 29
Уравнение. Решение уравнений методом подбора
Ребята, внимательно посмотрите на карточки с цифрами трех поросят. Чья карточка подходит для записи в рамке? Почему?
Подходит карточка с цифрой 8, потому что 8 + 2 = 10.
Вместо окошка запишем латинскую букву х (икс).
Получится запись: х + 2 = 10.
Это уравнение.
Ниф-Ниф просит из чисел 6, 5, 2, 1 подобрать для каждого уравнения такое значение у (игрек), при котором получится верное равенство:
8 + у = 9 12 – у= 10 у + 7 = 12 у – 5 = 1
Мы решили уравнения методом подбора. Обязательно нужно сделать проверку. Для этого вместо у (игрек) подставим в уравнение нужное число и убедимся, что равенство верное.
|
8 + у = 9 у = 1 8 + 1 = 9 9 = 9 |
у + 7 = 12 у = 5 5+7=12 12 = 12 |
12 – у = 10 у = 2 12 – 2 = 10 10 = 10 |
у – 5 = 1 у = 6 6 – 5 = 1 1 = 1 |
А теперь задание от Наф-Нафа. Ребята, найдите среди этих записей уравнение и решите его методом подбора.
3 + у 10 – х 14 – 2 b < 3 у – 6 = 2 а + 5
Проверь себя.
у – 6 = 2
у = 8
8 – 6 = 2
2 = 2
Проверка сложения и вычитания
Ребята, по примеру на сложение составьте два примера на вычитание по образцу:
2 + 3 = 5 6 + 1 = 7 9 + 7 = 16
5 – 2 = 3 ……….. …………
5 – 3 = 2 ……….. …………
Проверь себя:
Молодцы! Вспомните, как называются числа при сложении!
Это правило пригодится нам для проверки правильности вычислений.
Например, 2 + 1 = 3
Проверку выполним вычитанием: 3 – 1 = 2 или 3 – 2 = 1.
Выполните самостоятельно сложение и сделайте проверку вычитанием:
17 + 3 76 + 4 20 + 19
Проверь себя.
|
17 + 3 = 20 20 – 3 = 17 |
76+ 4 = 80 80 – 4 = 76 |
20 + 19 = 39 39 – 20 = 19 |
Задание от Нуф-Нуфа. Ребята, вспомните, как называются числа при вычитании?
Ребята, выполните вычитание и сделайте проверку сложением:
30 – 9 100 – 40
Проверь себя.
30 – 9 = 21
21 + 9 = 30
100 – 40 = 60
60 + 40 = 100
Выполните вычитание и сделайте проверку, пользуясь правилом:
72 – 30 60 – 20
Проверь себя.
72 – 30 = 42
72 – 42 = 30
60 – 20 = 40
60 – 40 = 20
Письменное сложение и вычитание. Запись столбиком
Ребята. Помогите трем поросятам посчитать!
Веселым поросятам для строительства прочного каменного дома нужно ещё 36 камней. У них уже есть 53 камня. Сколько всего камней нужно для строительства дома?
В этом примере мы к единицам прибавляли единицы, к десяткам прибавляли десятки.
Гораздо удобнее этот пример записать столбиком:
Алгоритм сложения
- Пишу десятки под десятками, а единицы под единицами.
- Складываю единицы: 6 плюс 3 будет 9.
- Пишу под единицами – 9.
- Складываю десятки: 3 плюс 5 будет 8.
- Пишу под десятками – 8.
- Читаю ответ: 89.
Вычитание тоже можно выполнять столбиком:
Алгоритм вычитания
- Пишу десятки под десятками, а единицы под единицами.
- Вычитаю единицы: 9 минус 4 будет 5.
- Пишу под единицами – 5.
- Вычитаю десятки: 6 минус 3 будет 3.
- Пишу под десятками – 3.
- Читаю ответ: 35.
Ребята, веселые поросята записали для вас примеры столбиком. Используя алгоритмы, спишите примеры правильно и вычислите с устным объяснением:
Пока мы с вами решали примеры, в записях наших сказочных поросят кто-то стер некоторые цифры. Помогите восстановить примеры на сложение столбиком. Узнайте, какие числа складывали, какие результаты получились. Подумайте, какая цифра должна стоять на месте звездочки.
Правильный ответ вы найдете в конце урока со значком
Ребята, все ли задания этого урока давались вам легко? Выберите мордочку одного из трёх поросят: Ниф-Нифа, Нуф-Нуфа или Наф-Нафа по своему настроению.
А вы помните, чем закончилась сказка про трех веселых поросят? Они спрятались от волка в крепком каменном доме Наф-Нафа. Крепким бывает не только дом, крепкой бывает дружба! Сообща можно многого добиться, даже если бывает очень трудно.
Напоследок три веселых задачки на смекалку от наших сказочных героев.
Задача от Ниф-Нифа.
Сколько лап и сколько ушей у трех зайцев?
Задача от Нуф-Нуфа.
Сколько клювов и сколько лапок у трех цыплят?
Задача от Наф-Нафа.
Сколько хвостов и сколько ушей у трех котов?
Проверь себя.
У трех зайцев 12 лап и 6 ушей.
У трех цыплят 3 клюва и 6 лапок.
У трех котов 3 хвоста и 6 ушей.

Ниф-Ниф, Наф-Наф и Нуф-Нуф прощаются с вами, ребята. До новых встреч! Проверьте свои знания, подумайте, что еще не очень хорошо у вас получается.
Выберите подписку для получения дополнительных возможностей Kalk.Pro
Любая активная подписка отключает
рекламу на сайте
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.
Подробнее с подписками можно ознакомиться здесь.
Онлайн калькулятор. Сложение, вычитание, умножение и деление столбиком.
Калькулятор вычисления суммы, разности, произведения и частного столбиком отобразит все этапы решения примера и даст подробное решение. Калькулятор может сложить, вычесть, умножить и разделить столбиком десятичные дроби и целые числа. Для записи десятичной дроби используйте точку либо запятую (например, 1.12 или 1,12).
Как складывать столбиком
Для того, чтобы сложит два числа столбиком, необходимо записать большее число над меньшим и выполнить последовательное сложение справа на лево, например, сложим столбиком 345 и 67.
1) 5 + 7 = 12; 2 пишем, число 1 запишем над числом 4.
2) 4 + 6 = 10; 10 + 1 = 11; 1 пишем, 1 запишем над числом 3.
3) Под числом 3 нет слагаемого, поэтому просто прибавим 3 + 1 = 4
Получилось 412
Приведем еще один пример: 1567 + 761
1) 7 + 1 = 8, запишем 8.
2) 6 + 6 = 12; 2 пишем, 1 запишем над числом 5.
3) 5 + 7 = 12; 12 + 1 = 13; 3 пишем, 1 запишем над числом 1.
4) Под числом 1 нет слагаемого, поэтому просто прибавим 1 + 1 = 2
Как складывать столбиком десятичные дроби
Для того, чтобы сложить две десятичные дроби, необходимо записать одну десятичную дробь над другой, совместив их точки. Приведем пример: 123.345 + 46.02
123.345 + 46.02 = 169.365
1) Запишем число 123.345 над числом 46.02
2) Под числом 5 нет слагаемого, поэтому просто запишем его внизу.
2) Далее сложим 2 и 4; 2 + 4 = 6; запишем 6 внизу.
3) 3 + 0 = 3; записываем 3.
4) Ставим точку
5) 3 + 6 = 9; записываем 9 внизу.
6) 2 + 4 = 6; записываем 6 внизу.
7) Так как под числом 1 нет слагаемого, просто сносим его вниз. Запишем число 1 внизу.
Итак, у нас получилось 169.365
Приведем следующий пример: 123.99 + 12.99
1) 9 + 9 = 18; 8 пишем, 1 запишем над числом 9.
2) 9 + 9 = 18; 18 + 1 = 19; 9 пишем, 1 запишем над числом 3.
3) Ставим точку.
4) 2 + 3 = 5; 5 + 1 = 6; 6 запишем внизу
5) 2 + 1 = 3; 3 запишем внизу.
6) Так как под числом 1 нет слагаемого, просто сносим его вниз. Запишем число 1 внизу.
Ответ: 136.98
Для того чтобы сложить десятичную дробь с целым числом, необходимо сложить целую часть десятичной дроби с целым числом. Сложим, например, 23 и 0.34. У числа 23, после точки поставим столько нолей, сколько чисел после точки у десятичной дроби.
1) 0 + 4 = 4. Запишем 4.
2) 0 + 3 = 3. Запишем 3.
3) Ставим точку
4) 3 + 0 = 3. Запишем 3
5) Под числом 2 нет слагаемого, поэтому просто сносим его вниз.
Ответ: 23.34
Как вычитать столбиком
Для того, чтобы вычесть два числа столбиком, необходимо записать большее число над меньшим и выполнить последовательное вычитание, например, вычтем столбиком 456 и 89.
1) Из 6-ти вычесть число 9 не получится, так как 6 меньше девяти, поэтому займем 1 у числа 5 и поставим над ним точку, получим вместо числа 6 число 16. Отнимем от 16 число 9; 16 – 9 = 7; запишем 7.
2) Так как мы заняли число 1 у числа 5, то теперь осталось число 4. Из числа 4 вычесть число 8 не получится, поэтому займем 1 у соседнего числа 4 и поставим над ним точку, получим вместо числа 4 число 14. Отнимем от числа 14 число 8 = 6. Запишем 6.
3) Под числом 4 нет вычитаемого, поэтому отнимем от числа 4 число 1 (так как мы занимали 1-цу): 4 -1 = 3; запишем число 3.
Получилось 367.
Приведем еще один пример: 307 – 58
1) Из числа 7 вычесть число 8 не получится, так как 7 меньше 8, поэтому займем 1 у ноля. Поставим над нолем точку. Когда мы занимаем 1-цу у нуля, ноль становится числом 9! получим вместо 0 число 9. Однако у ноля не получится взять единицу, поэтому двигаемся влево и занимаем единицу у числа 3 и ставим над ним точку; отнимем от 17 число 8; 17 – 8 = 9; запишем 9.
2) Так как мы заняли число 1 у ноля, то теперь осталось число 9. Отнимем от числа 9 число 5 = 4. Запишем 4.
3) Под числом 3 нет вычитаемого, но мы помним, что мы заняли единицу у числа 3, поэтому 3-1 = 2. Запишем число 2.
Получилось 249.
Как вычитать столбиком десятичные дроби
Для того, чтобы отнять из десятичной дроби целое число, либо из целого числа вычесть десятичную дробь нужно у целого числа после точки записать столько нолей, сколько чисел после точки у десятичной дроби, затем записать большее число над меньшим.
Например вычтем столбиком из десятичной дроби 123.478 целое число 56
123.478 – 56 = 67.478
..00000
–123.478
56.000
67.478
Начинаем последовательно вычитать справа налево
1) 8 – 0 = 8. Запишем 8.
2) 7 – 0 = 7. Запишем 7.
3) 4 – 0 = 4. Запишем 4.
4) Ставим точку.
5) Из числа 3 не вычесть число 6, поэтому занимаем единицу у числа 2 и ставим над ним точку. 13 – 6 = 7. Запишем число 7.
6) Над числом 2 стоит точка, значит теперь там уже не число 2, а число 1. Из единицы число 5 не вычесть, поэтому занимаем единицу у числа 1 и ставим над ним точку. 11 – 5 = 6. Запишем число 6.
7) Над числом 1 стоит точка, следовательно, 1 – 1 = 0, поэтому на этом решение законченно.
Ответ: 67.478
Еще один пример на вычитание столбиком десятичной дроби из целого числа.
432 – 2.95
1) Из ноля число 5 не вычесть, поэтому займем единицу у ноля и поставим над ним точку, далее, как мы уже знаем ставим точку над числом 2 и занимаем единицу. 10 – 5 = 5. Запишем число 5.
2) Над числом 0 стоим точка, следовательно, 0 превратился в число 9. 9 – 9 = 0. Запишем 0.
3) Над числом два стоит точка значит 2-1 = 1. Из числа 1 число 2 не отнять, поэтому занимаем единицу у числа 3 и ставим над ним точку. 11 – 2 = 9. Запишем число 9.
4) Над числом 3 стоит точка, 3 – 1 = 2. Так как нет вычитаемого, просто сносим число 2 вниз, тоже делаем и с числом 4.
Ответ: 429.05
Правила вычитания десятичной дроби из десятичной дроби, такие же как при сложении. Нам так же необходимо сначала совместить точки десятичных дробей и затем выполнить последовательное вычитание справа налево. Вот несколько примеров на вычитание десятичных дробей:
378.326 – 26.57 = 351.756
00.0.00
–378.326
26.570
351.756
Как умножать столбиком
Для того, чтобы умножить одно число на другое необходимо записать первый множитель над вторым, причем не важно какой множитель больше первый или второй, но удобнее чтобы записать более компактное решение записать большее число над меньшим. Затем необходимо каждое число нижнего множителя умножить на каждое число верхнего справа налево, затем суммировать произведения.
На примере будет намного понятнее. Итак, умножим 367 на 12
367 × 12 = 4404
×367
12
734
3670
4404
1. Умножим число 2 на 367 и результат запишем с справа налево от числа 2.
1) 2 × 7 = 14. Запишем число 4, число 1 в уме.
2) 2 × 6 = 12; 12 + 1 = 13. Запишем 3, число 1 в уме.
3) 2 × 3 = 6; 6 + 1 = 7. Запишем число 7. На этом этапе мы получили число 734.
2. Умножим число 1 на 367 и результат запишем справа на лево начиная уже от числа 1 под первой строкой.
1) 1 × 7 = 7. Запишем число 7.
2) 1 × 6 = 6. Запишем число 6.
3) 1 × 3 = 3. Запишем число 3. На этом этапе мы получили число 367
3. Теперь нам необходимо сложить получившиеся два числа 734 и 367
1) Под числом 4 нет слагаемого, поэтом просто снесем его вниз. Запишем число 4.
2) 3 + 7 = 10. Запишем 0 и запомним число 1.
3) 7 + 6 + 1 = 14. Запишем число 4, число 1 в уме.
4) У числа три нет слагаемого, поэтому просто запишет число 3.
На этом решение закончено, получилось 4404.
Как умножать столбиком десятичные дроби
Десятичные дроби столбиком умножать очень просто. Прежде всего, уберем точки из десятичных дробей. Затем произведем умножение уже получившихся целых чисел, далее посчитаем количество чисел в первом и во втором множителе, сложим эти значения, результатом будет число равное количеству чисел после точки в получившемся произведении. На примерах все станет намного понятнее.
Умножим 0.2354 на 12.3997
Уберем точки из десятичных дробей, чтобы было удобной умножать.
×123997
2354
495988
6199850
37199100
247994000
291888938
Теперь добавим точку в получившейся ответ. Так как в первом множителе 12.3997 после точки стоит 4 числа, и во втором множителе 0.2354 стоит 4 числа, тогда 4 + 4 = 8. Сдедовательно в ответе после точки будет 8 чисел.
2.91888938
×12.3997
0.2354
2.91888938
Умножим 49.265 на 0.0045
Уберем точки из десятичных дробей, чтобы было удобной умножать.
×49265
45
246325
1970600
2216925
Теперь добавим точку в получившейся ответ. Так как в первом множителе 49.265 после точки стоит 3 числа, а во втором множителе 0.0045 стоит 4 числа, тогда 3 + 4 = 7. Сдедовательно в ответе после точки будет 7 чисел.
0.2216925
×49.265
0.0045
0.2216925
Как делить столбиком
Как делить столбиком целые числа.
Деление столбиком с остатком, в данном материале рассматриваться не будет, если интересно, есть много информации по остатку от деления тут.
Разберем для начала как разделить большее число на меньшее в столбик (когда делимое больше делителя).
На примере будет намного нагляднее изучить данную тему. Итак, разделим 12 на 5
12 : 5 = 2.4
01205
01002.4
0020
0020
0000
При делении числа 12 на число 5 у нас получится конечная десятичная дробь. Кому интересно почитать что такое десятичные дроби — это можно сделать здесь.
1) Сколько раз число 5 помещается в числе 12? Правильно 2 раза. Поэтому первым делом умножим 2 на 5 получим 10.
2) Теперь отнимем из числа 12 число 10; 12 – 10 = 2. Запишем число 2.
3) В числе 12 нет больше чисел, поэтому поле числа 2 в ответе необходимо поставить точку. Целую часть ответа мы уже нашли! Двигаемся дальше.
4) Теперь будем находить дробную часть нашей десятичной дроби. Поставим ноль рядом с разностью. Получим число 20. Теперь снова думаем, сколько раз число 5 содержится в числе 20? Правильно 4 раза. 5 × 4 = 20.
5) Отнимем от числа 20 число 20; 20 – 20 = 0. Разность равна нулю, следовательно, результатом деления является конечная десятичная дробь.
Ответ: 2.4
Возьмем другой пример, где уже ответом будет являться бесконечная периодическая десятичная дробь. Разделим 7 на 3
7 : 3 = 2.(3)
0703
0602.3
010
009
001
1) В числе 7 число 3 содержится 2 раза. То есть неполное частное деления числа 7 на число 3 равно числу 2. Умножим число 2 на делитель. 2 × 3 = 6.
2) Отнимем от числа 7 число 6; 7 – 6 = 1; В делимом больше нет чисел, поэтому ставим точку.
3) Начинаем вычислять ответ для дробной части. Для этого к получившейся разности добавим ноль, получим число 10. Неполное частное деления числа 10 на число 3 равно числу 3. Запишем число 3 после точки.
4) 3 × 3 = 9. Из числа 10 отнимем число 9; 10 – 9 = 1. На этом этапе необходимо завершить деление, так как мы уже получали число 1 при вычитании числа 6 из числа 7, следовательно, при дальнейшем решении примера мы снова и снова будем получать число три в виде неполного частного и этот процесс будет продолжаться бесконечно (2.333333333333333333333333333…). Такое повторение называется периодом бесконечной периодической десятичной дроби. Для краткости период записывают в скобках 2.(3)
Деление десятичных дробей в столбик примеры
Разделим 3.12 на 3.6
Если числитель и знаменатель дроби умножить на одно и тоже число, то значение дроби не изменится, поэтому, чтобы было проще разделить одно число на другое, уберем запятую, домножив оба числа на 100
07120360
036001.97
03520
03240
002800
002520
000280
Разделим 9.4 на 45.1
Если числитель и знаменатель дроби умножить на одно и тоже число, то значение дроби не изменится, поэтому, чтобы было проще разделить одно число на другое, уберем запятую, домножив оба числа на 10
0940451
00000.2084257206
0940
0902
003800
003608
0001920
0001804
00001160
00000902
000002580
000002255
0000003250
0000003157
00000000930
00000000902
0000000002800
0000000002706
0000000000094
| Вам могут также быть полезны следующие сервисы |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер по математике |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Показать больше |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
|
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
|
Оптика |
| Калькулятор отражения и преломления света |
|
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
|
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Деление столбиком
Деление десятичных дробей столбиком
Если при делении столбиком делимое или делитель десятичная дробь, то для упрощения расчётов необходимо делитель и делимое преобразовать в целые числа.
Разберём пример
Разделим 0.125 на 0.05 для этого умножим оба числа на 1000.
0.125×1000=125
0.05×1000=50.
В итоге наш пример сведётся к делению 125 на 50.
| – | 1 | 2 | 5 | 5 | 0 | ||
| 1 | 0 | 0 | 2 | . | 5 | 50 × 2 = 100 | |
| – | 2 | 5 | 0 | 125 – 100 = 25 | |||
| 2 | 5 | 0 | 50 × 5 = 250 | ||||
| 0 | 250 – 250 = 0 |
Деление дробей в столбик
Разделим 5220 на 36
| – | 5 | 2 | 2 | 0 | 3 | 6 | ||
| 3 | 6 | 1 | 4 | 5 | 36 × 1 = 36 | |||
| – | 1 | 6 | 2 | 52 – 36 = 16 | ||||
| 1 | 4 | 4 | 36 × 4 = 144 | |||||
| – | 1 | 8 | 0 | 162 – 144 = 18 | ||||
| 1 | 8 | 0 | 36 × 5 = 180 | |||||
| 0 | 180 – 180 = 0 |
Выделим первое полное делимое 52
Делим 52 на 36.
Получится 1 с остатком
Под чертой в ответе пишем цифру 1.
Проверяем умножением 36х1=36.
Вычитаем и сравниваем, разница должна быть меньше делителя.
52-36=16, 16<36
Сносим 2
Делим 162 на 36
Получится 4 с остатком
Под чертой в ответе пишем цифру 4.
Проверяем умножением 36х4=144.
Вычитаем и сравниваем, разница должна быть меньше делителя.
162-144=18, 18<36
Сносим 0
Делим 180 на 36
Получится 5 без остатка
Под чертой в ответе пишем цифру 5.
Проверяем умножением 36х5=180.
Вычитаем и сравниваем
180-180=0
Сносить больше нечего
Расчёт окончен.
Алгоритм деления в столбик
- Если делимое или делитель являются десятичными дробями преобразуем их в целые числа.
- Если делитель и делимое целые числа и на концах есть нули, необходимо их сократить для упрощения.
- Записываем пример в столбик.
- Ищем первое неполное делимое.
- Делим неполное делимое.
- Проверяем умножением.
- Записываем в ответ первую цифру.
- Ищем остаток, он должен быть меньше делителя.
- Сносим следующую цифру и повторяем всё заново.
Что может калькулятор
Делить десятичные дроби столбиком
Делить в столбик натуральные числа
Разделить уголком десятичную дробь на натуральное число
Разделить столбиком натуральное число на десятичную дробь
Похожие калькуляторы
Содержание
- Способы письменных вычислений ( в столбик)
- Вычитание столбиком
- Основные понятия
- Свойства вычитания
- Алгоритм вычитания в столбик
- Деление в столбик
- Как правильно делить в столбик
- Как выглядит деление в столбик с остатком
- Примеры на деление в столбик
- Математика
- Буквенные выражения
- Уравнение. Решение уравнений методом подбора
- Проверка сложения и вычитания
- Письменное сложение и вычитание. Запись столбиком
Способы письменных вычислений ( в столбик)
Способы письменных вычислений
( в столбик)
В основе выполнения письменных способов вычислений лежит использование правила сложения суммы с суммой. В явном виде в современных учебниках математики для начальных классов данное правило не изучается, оно заменено упрощенным вариантом правила поразрядного сложения: единицы складываются с единицами, десятки с десятками.
Письменный алгоритм сложения содержит:
1. Правило записи слагаемых при письменном сложении: разряд записывается под соответствующим разрядом.
2. Указание на порядок выполнения действий: сложение начинаем с разряда единиц (справа налево).
3. Прием добавления накапливающихся единиц старших разрядов в соответствующий разряд после выполнения основного сложения.
Алгоритм письменного сложения и вычитания в начальной школе вводится во 2 классе на примере сложения и вычитания двузначных чисел в пределах сотни.
На самом же деле, уже при знакомстве со случаями вида 45 + 23, учитель знакомит детей со способами записи вычислительных действий «в столбик» и приемом поразрядного сложения, применяемым при письменных вычислениях:
Сначала предлагается устный способ вычислений:

Затем отмечается, что удобно записать этот пример столбиком:
Далее в учебнике приводятся подробные объяснения приема вычислений:
1. Пишу десятки под десятками, а единицы под единицами.
2. Складываю единицы: 5 + 3 = 8. Пишу 8 под единицами.
3. Складываю десятки: 4 + 2 = 6. Пишу 6 под десятками.
4. Читаю ответ: сумма равна 68.
Главным отличием письменных вычислений от устных является порядок складывания (или вычитания) разрядных единиц. При устных вычислениях всегда начинают со старших разрядов (в данном случае – с разряда десятков) и выполняют действие, двигаясь слева направо. При письменных вычислениях всегда начинают с разряда единиц и выполняют действие, двигаясь справа налево.
Методическое обоснование знакомства детей со способами письменных вычислений при формировании вычислительной деятельности в пределах 100:
1. Многие дети с большим трудом осваивают устные вычислительные действия с двузначными числами. Письменный прием вычислений облегчает им вычислительную деятельность.
2. Полноценное освоение устной вычислительной деятельности требует от ребенка свободного владения результатами табличных вычислений в пределах 10 и 20, свободного владения разрядным составом чисел, десятичным составом чисел, умением гибко и свободно применять разнообразные вычислительные действия, выбирая способ вычислений в каждом случае. Далеко не все дети могут это делать. Письменный способ вычислений требует более простых вычислительных действий, выполняемых по единому жесткому правилу (называемому «алгоритмом письменных вычислений»).
3. Знакомство со способами оформления вычислений «в столбик» при изучении вычислений в пределах 100 рассматривается как подготовка к использованию этой вычислительной технологии в дальнейшем (при вычислениях с трехзначными и многозначными числами).
Запись и способ вычисления « в столбик» для многих детей, с трудом усваивающих устные приемы сложения и вычитания (особенно с переходом через десяток), является более легким и доступным. Запись «в столбик» и применяемые при этом вычислительные приемы позволяет создать для ребенка «систему промежуточных опор», так как на каждом шаге вычислений ребенок фактически действует не более чем в пределах второго десятка, что значительно облегчает вычисления.
| 1) 217 +439 | 2) 217 +439  56 1 дес. + 3.дес. = 4дес. 56 1 дес. + 3.дес. = 4дес.
|
3) 217 2сот. + 4дес. = 6сот. +439  656 656 |
В основе письменного сложения и вычитания лежат:
1) прочное знание таблицы сложения и соответствующих случаев вычитания в пределах 10;
2) умение складывать и вычитать в пределах 20 (с переходом через десяток);
3) знание разрядного состава чисел и соотношение разрядных единиц;
Алгоритм письменного вычитания строится на тех же принципах. Сначала детей знакомят со способом записи чисел при выполнении письменных вычислений и определяют порядок выполнения вычислений (справа налево, начиная с разряда единиц).
1. Пишу десятки под десятками, а единицы под единицами.
2. Вычитаю единицы из единиц: 6 – 2 = 4. Пишу 4 под единицами.
3. Вычитаю десятки из десятков: 5дес. – 4дес. = 1дес. Пишу 1 под десятками.
4. Читаю ответ: разность равна 14.
Наиболее трудны для многих детей, как и при устных вычислениях, случаи вида 50 – 24 и 52 — 24, где для выполнения вычислений необходимо выполнить «заем» десятка из старшего разряда.
Например: 5дес. = 4дес. + 1дес.
1. Пишу единицы под единицами, десятки под десятками.
2. Вычитаю единицы. Из 0 нельзя вычесть 4. Занимаю 1дес. из 5дес.
1дес. = 10; 10 – 4 = 6.Пишу под единицами 6.
3. Вычитаю десятки. Было 5 дес., но 1дес. занятии при вычитании единиц. Осталось 4дес. 4дес. – 2 дес. = 2дес. Пишу 2 под десятками.
4. Читаю ответ: разность равна 26.
Для того чтобы не забывать о заемной единице, над разрядом десятков можно ставить точку, черточку, или подписывать число оставшихся после заема разрядных единиц.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Вычитание столбиком
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.
Название числа напрямую зависит от количества знаков. Однозначное — состоит из одного знака. Двузначное — из двух. Трехзначное — из трех и так далее.
Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитываются с конца.
- Разряд единиц — то, чем заканчивается любое число.
- Разряд десятков — то, что находится перед разрядом единиц.
- Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.
Вычитание — это арифметическое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее — вычитаемым. Результат их вычитания — разностью.
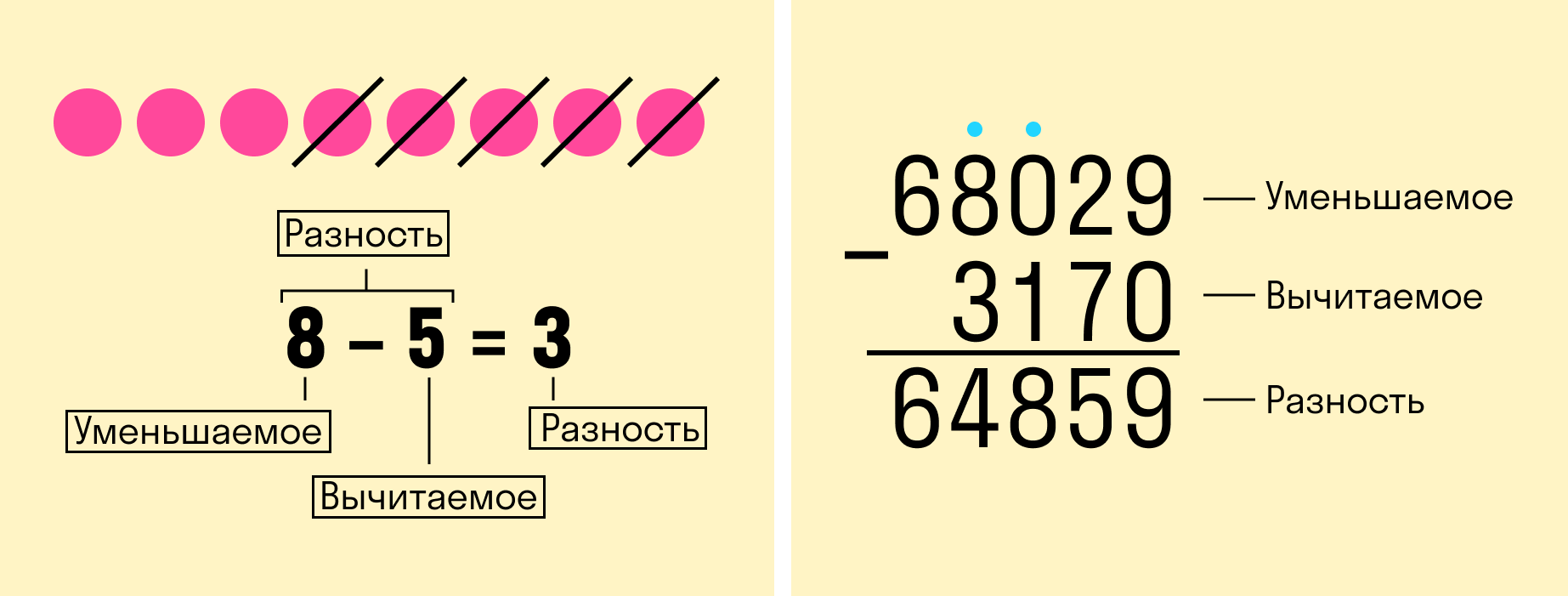
Свойства вычитания
- Вычитание нуля из числа не изменяет этого числа.
Если из числа вычесть само это число, то разность равна нулю.
Чтобы вычесть сумму из числа, можно вычесть из этого числа одно слагаемое, из полученной разности — второе слагаемое.
a — (b + c) = a — b — c
Чтобы вычесть число из суммы, можно вычесть это число из одного слагаемого и полученную разность прибавить к сумме остальных слагаемых.
(a + b) — c = (a — c) + b = a + (b — c)
Чтобы прибавить разность к числу, можно прибавить к нему уменьшаемое и из полученной суммы вычесть вычитаемое.
а + (b — c) = a + b — c
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Алгоритм вычитания в столбик
Вычитать столбиком проще, чем считать в уме, особенно при действиях с большими числами. Этот способ наглядный — помогает держать во внимании каждый шаг.
Рассмотрим алгоритм вычитания в столбик на примере: 4312 — 901.
Шаг 1. При вычитании столбиком самое главное — правильно записать исходные данные, чтобы самая правая цифра первого числа была под правой цифрой второго числа.
Большее число (уменьшаемое) записываем сверху. Слева между числами ставим знак минус. Вот так:
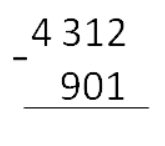
Шаг 2. Вычитание столбиком начинаем с самой правой цифры. Вычитаем по цифре (знаку). Результат записываем под чертой.
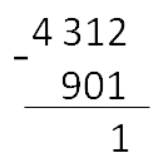
Шаг 3. Далее вычитаем из второй цифры справа: из «1» ноль.
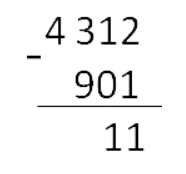
Шаг 4. Теперь нам нужно вычесть из «3» девять. Это сделать невозможно. Поэтому займем десятку у соседа слева от тройки. Это цифра «4». Поставим над четверкой точку. Занятый десяток прибавим к «3»: 10 + 3 = 13.
Из «13» вычтем девять: 13 − 9 = 4.
Так как мы заняли десяток у «4», значит четверка уменьшилось на единицу. Об этом нам напоминает точка над «4»: 4 − 1 = 3. Вот, как это выглядит:
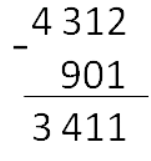
Рассмотрим пример вычитания в столбик чисел с нулями: 1009 — 423.
Шаг 1. Запишем числа в столбик. Большее число ставим сверху.
Вычитаем справа налево по одной цифре.
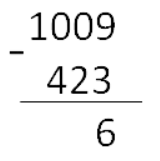
Шаг 2. Так как из нуля нельзя вычесть «2», занимаем у соседней цифры слева (ноль). Поставим над «0» точку. У нуля занять нельзя, поэтому смотрим на следующую цифру. Занимаем у «1» и ставим над ней точку. Теперь вычитаем не из нуля двойку, а из «10». Вот так:
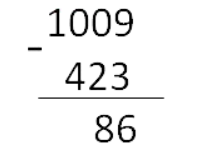
Шаг 3. Над нулем стоит точка, поэтому нуль превращается в «9». Вычитаем из «9» четыре: 9 − 4 = 5.
Над «1» стоит точка. Единица уменьшается на «1»: 1 − 1 = 0. Если в результате разности левее всех цифр стоит ноль, то его записывать не надо.
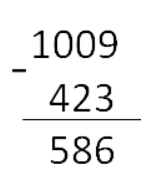
Так выглядит алгоритм вычитания в столбик. Во 2 классе школьники могут сделать себе подсказку в виде таблички. А позже алгоритм запомнится и будет срабатывать автоматически, как «дважды два четыре».
Источник
Деление в столбик
О чем эта статья:
3 класс, 4 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Как правильно делить в столбик
Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который впоследствии будет срабатывать автоматически.
Рассмотрим пример деления трехзначного числа на однозначное 322 : 7. Для начала определимся с терминами:
- 322 — делимое или то, что необходимо поделить;
- 7 — делитель или то, на что нужно поделить:
- частное — результат действия.
Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.
Шаг 2. Смотрим на делимое слева направо и находим ту часть, которая больше делителя. 3, 32 или 322? Нам подходит 32. Теперь нужно определить сколько раз наш делитель 7 содержится в числе 32. Похоже, что четыре раза.
Проверяем: 4 × 7 = 28, а 28
Шаг 3. Остаток равен 4. Для продолжения решения его нужно увеличить. Мы сделаем это за счет следующей цифры делимого. Приписываем к четверке оставшуюся двойку и продолжаем размышлять.
Шаг 4. Сколько раз делитель 7 содержится в числе 42? Кажется, шесть раз. Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем полученное число к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.
Мы закончили решать пример и в результате получили целое число 46.
Как выглядит деление в столбик с остатком
Это такое же деление, только в результате получается неровное число, как получилось в примере выше.
- Например, делим 19 на 5. Наибольшее число, делящееся на 5 до 19 это 15. Проверяем 5*3=15, 19-15=4. Ответ: 3 и остаток 4. Записываем так: 19:5=3(4).
- Еще пример: делим 29 на 6. Также определяем максимальное число, делящееся на 6 до 29. Подходит 24. Ответом будет: 4 и остаток 5. А записываем: 29:6=4(5).
Примеры на деление в столбик
Давайте закрепим знания на практике. Для этого разделите столбиком примеры ниже, а после проверьте полученные цифры — чур, не подглядывать!
Источник
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
План урока:
Здравствуйте, ребята! Начнем урок с интересной загадки:
Отгадайте без подсказки
Вы героев этой сказки:
Трое братьев до чего же
Друг на друга все похожи!
Буквенные выражения
Три весёлых поросёнка Ниф-Ниф, Наф-Наф и Нуф-Нуф приглашают нас с вами, ребята, в гости. Посмотрите, какие дома они построили!
Как вы думаете, можно ли вставить в окошки карточки с цифрами? Почему?
В домике Ниф-Нифа в открытом окошке может быть карточка с цифрой 5? Какое выражение можно записать?
А какое выражение запишем, если в доме Нуф-Нуфа в окошке будет цифра 2?
Можно ли в окошке Наф-Нафа увидеть цифру 1? А цифру 3?
С цифрой 1 запишем выражение: 1 – 1.
А вот цифра 3 не подходит, потому что из 1 нельзя вычесть 3.
Запишите получившиеся выражения и найдите их значения.
Мы записали числовые выражения, ведь они содержат только числа.
Ребята, как вы думаете, можно ли в окошко вставить карточку с буквой?
В математике принято использовать латинские буквы. Может быть, вы уже знаете некоторые из них? Давайте, правильно назовем латинские буквы.
В окошки домиков поросят подставим карточки с буквами: x, y, d.
Запишем выражения: x + 4, 6 + y, 1 – d.
У нас получились буквенные выражения.
Найдём значение следующих буквенных выражений: 8 + а, d – 6, x + 5, y – 1.
Для этого вместо буквы подставим число: а = 12, d = 9, x = 14, y = 20.
Найдите значение выражения: k + 20, если k = 3, k = 5, k = 9.
Уравнение. Решение уравнений методом подбора
Ребята, внимательно посмотрите на карточки с цифрами трех поросят. Чья карточка подходит для записи в рамке? Почему?
Подходит карточка с цифрой 8, потому что 8 + 2 = 10.
Вместо окошка запишем латинскую букву х (икс).
Получится запись: х + 2 = 10.
Это уравнение.
Ниф-Ниф просит из чисел 6, 5, 2, 1 подобрать для каждого уравнения такое значение у (игрек), при котором получится верное равенство:
8 + у = 9 12 – у= 10 у + 7 = 12 у – 5 = 1
Мы решили уравнения методом подбора. Обязательно нужно сделать проверку. Для этого вместо у (игрек) подставим в уравнение нужное число и убедимся, что равенство верное.
А теперь задание от Наф-Нафа. Ребята, найдите среди этих записей уравнение и решите его методом подбора.
3 + у 10 – х 14 – 2 b у = 8
Проверка сложения и вычитания
Ребята, по примеру на сложение составьте два примера на вычитание по образцу:
2 + 3 = 5 6 + 1 = 7 9 + 7 = 16
Молодцы! Вспомните, как называются числа при сложении!
Это правило пригодится нам для проверки правильности вычислений.
Например, 2 + 1 = 3
Проверку выполним вычитанием: 3 – 1 = 2 или 3 – 2 = 1.
Выполните самостоятельно сложение и сделайте проверку вычитанием:
17 + 3 76 + 4 20 + 19
Задание от Нуф-Нуфа. Ребята, вспомните, как называются числа при вычитании?
Ребята, выполните вычитание и сделайте проверку сложением:
Выполните вычитание и сделайте проверку, пользуясь правилом:
Письменное сложение и вычитание. Запись столбиком
Ребята. Помогите трем поросятам посчитать!
Веселым поросятам для строительства прочного каменного дома нужно ещё 36 камней. У них уже есть 53 камня. Сколько всего камней нужно для строительства дома?
В этом примере мы к единицам прибавляли единицы, к десяткам прибавляли десятки.
Гораздо удобнее этот пример записать столбиком:
Алгоритм сложения
- Пишу десятки под десятками, а единицы под единицами.
- Складываю единицы: 6 плюс 3 будет 9.
- Пишу под единицами – 9.
- Складываю десятки: 3 плюс 5 будет 8.
- Пишу под десятками – 8.
- Читаю ответ: 89.
Вычитание тоже можно выполнять столбиком:
Алгоритм вычитания
- Пишу десятки под десятками, а единицы под единицами.
- Вычитаю единицы: 9 минус 4 будет 5.
- Пишу под единицами – 5.
- Вычитаю десятки: 6 минус 3 будет 3.
- Пишу под десятками – 3.
- Читаю ответ: 35.
Ребята, веселые поросята записали для вас примеры столбиком. Используя алгоритмы, спишите примеры правильно и вычислите с устным объяснением:
Пока мы с вами решали примеры, в записях наших сказочных поросят кто-то стер некоторые цифры. Помогите восстановить примеры на сложение столбиком. Узнайте, какие числа складывали, какие результаты получились. Подумайте, какая цифра должна стоять на месте звездочки.
Правильный ответ вы найдете в конце урока со значком
Ребята, все ли задания этого урока давались вам легко? Выберите мордочку одного из трёх поросят: Ниф-Нифа, Нуф-Нуфа или Наф-Нафа по своему настроению.
А вы помните, чем закончилась сказка про трех веселых поросят? Они спрятались от волка в крепком каменном доме Наф-Нафа. Крепким бывает не только дом, крепкой бывает дружба! Сообща можно многого добиться, даже если бывает очень трудно.
Напоследок три веселых задачки на смекалку от наших сказочных героев.
Задача от Ниф-Нифа.
Сколько лап и сколько ушей у трех зайцев?
Задача от Нуф-Нуфа.
Сколько клювов и сколько лапок у трех цыплят?
Задача от Наф-Нафа.
Сколько хвостов и сколько ушей у трех котов?
У трех зайцев 12 лап и 6 ушей.
У трех цыплят 3 клюва и 6 лапок.
У трех котов 3 хвоста и 6 ушей.
А вот и правильный ответ!
Ниф-Ниф, Наф-Наф и Нуф-Нуф прощаются с вами, ребята. До новых встреч! Проверьте свои знания, подумайте, что еще не очень хорошо у вас получается.
Источник
Adblock
detector