Как найти значение выражения вариант 14 - Сайт, где вы сможете решить свои вопросы

Решение заданий варианта №14 из сборника ОГЭ 2023 по математике И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.

ЧАСТЬ 1

Задание 1-5.
Володя летом отдыхает у дедушки в деревне Ёлочки. В воскресенье они собираются съездить на машине в село Кленовое. Из деревни Ёлочки в село Кленовое можно проехать по прямой грунтовой дороге. Есть более длинный путь: по прямолинейному шоссе через деревню Сосенки до деревни Жуки, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в село Кленовое. Есть и третий маршрут: в деревне Сосенки можно свернуть на прямую грунтовую дорогу в село Кленовое, которая идёт мимо пруда.

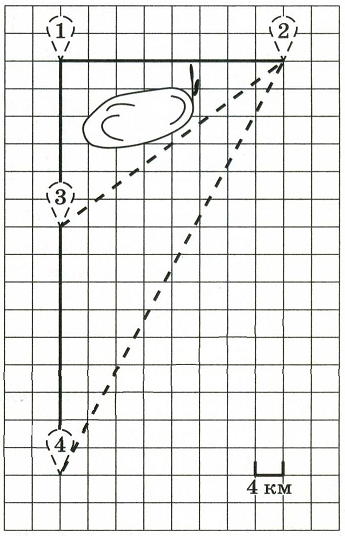
Шоссе и грунтовые дороги образуют прямоугольные треугольники.
По шоссе Володя с дедушкой едут со скоростью 80 км/ч, а по грунтовой дороге – со скоростью 40 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 4 км.

Задание 6.
Найдите значение выражения frac{5,6cdot 0,3}{0,8}.

Задание 7.
Какое из следующих чисел заключено между числами 3√2 и 2√3?

1) 2
2) 3
3) 4
4) 5

В ответ запишите номер выбранного варианта.

Задание 8.
Найдите значение выражения а⁶·а¹⁹:а²² при а = 3.

Задание 9.
Найдите корень уравнения 2x + 7 = frac{x}{3}.

Задание 10.
На тарелке лежат одинаковые на вид пирожки: 4 с мясом, 5 с рисом и 21 с повидлом. Андрей наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с повидлом.

Задание 11.
На рисунках изображены графики функций вида у = kх + b. Установите соответствие между знаками коэффициентов k и b и графиками функций.

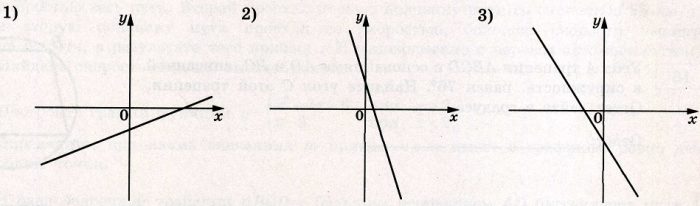
КОЭФФИЦИЕНТЫ

А) k < 0, b < 0
Б) k < 0, b > 0
В) k > 0, b < 0

ГРАФИКИ

В таблице под каждой буквой укажите соответствующий ответ.

Задание 12.
В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) длительностью более 5 минут рассчитывается по формуле С = 180 + 15·(t – 5), где t – длительность поездки (в минутах). Пользуясь этой формулой, рассчитайте стоимость 16-минутной поездки. Ответ дайте в рублях.

Задание 13.
Укажите решение неравенства 4х – х² ≤ 0.

Задание 14.
У Юли есть теннисный мячик. Она со всей силы бросила его об асфальт. После первого отскока мячик подлетел на высоту 450 см, а после каждого следующего отскока от асфальта подлетал на высоту в три раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит мячик, станет меньше 20 см?

Задание 15.
В треугольнике АВС угол С равен 90°, ВС = 15, АС = 3. Найдите tgВ.

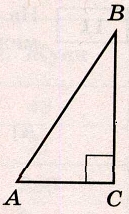
Задание 16.
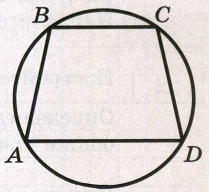
Угол А трапеции АВСD с основаниями АD и ВС, вписанной в окружность, равен 76º. Найдите угол C этой трапеции. Ответ дайте в градусах.

Задание 17.
Две стороны параллелограмма равны 7 и 12, а один из углов этого параллелограмма равен 30°. Найдите площадь этого параллелограмма.

Задание 18.
На клетчатой бумаге с размером клетки 1 х 1 изображён прямоугольный треугольник. Найдите длину его большего катета.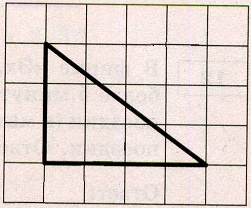

Задание 19.
Какие из следующих утверждений верны?

1) Один из углов треугольника всегда не превышает 60 градусов.
2) Средняя линия трапеции равна сумме её оснований.
3) Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

ЧАСТЬ 2

Задание 20.
Решите неравенство (2х – 5)² ≤ (5х – 2)².

Задание 21.
Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 55 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого на 6 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста.

Задание 22.
Постройте график функции

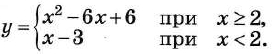
Определите, при каких значениях m прямая у = m имеет с графиком ровно две общие точки.

Задание 23.
В равнобедренной трапеции ABCD с большим основанием AD биссектриса угла А пересекается с биссектрисой угла С в точке F, а также пересекает сторону CD в точке К. Известно, что прямые АВ и CF параллельны. Найдите CF, если FK = 4√3.

Задание 24.
В выпуклом четырёхугольнике АВСD углы DAC и DBC равны. Докажите, что углы CDB и CAB также равны.

Задание 25.
Найдите площадь трапеции, диагонали которой равны 17 и 15, а средняя линия равна 4.

Источник варианта: Сборник ОГЭ 2023 по математике. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.8 / 5. Количество оценок: 6

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Володя летом отдыхает у дедушки в деревне Ёлочки. В воскресенье они собираются съездить на машине в село Кленовое. Из деревни Ёлочки в село Кленовое можно проехать по прямой грунтовой дороге. Есть более длинный путь: по прямолинейному шоссе через деревню Сосенки до деревни Жуки, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в село Кленовое. Есть и третий маршрут: в деревне Сосенки можно свернуть на прямую грунтовую дорогу в село Кленовое, которая идёт мимо пруда.

Шоссе и грунтовые дороги образуют прямоугольные треугольники. По шоссе Володя с дедушкой едут со скоростью 80 км/ч, а по грунтовой дороге – со скоростью 40 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 4 км.

1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.

Насел. пункты	д. Ёлочки	с. Кленовое	д. Жуки
Цифры

2. Сколько километров проедут Володя с дедушкой от деревни Ёлочки до села Кленового, если они поедут по шоссе через деревню Жуки?

3. Найдите расстояние от деревни Сосенки до села Кленового по прямой. Ответ дайте в километрах.

4. Сколько минут затратят на дорогу из деревни Ёлочки в село Кленовое Володя с дедушкой, если поедут через деревню Жуки?

5. В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Ёлочки, селе Кленовом, деревне Сосенки и деревне Жуки.

Наименование продукта	д. Ёлочки	с. Кленовое	д. Сосенки	д. Жуки
Молоко (1л)	42	45	38	43
Хлеб (1 батон)	22	25	23	27
Сыр «Российский» (1 кг)	320	290	270	280
Говядина (1 кг)	410	420	450	430
Картофель (1 кг)	26	18	24	16

Володя с дедушкой хотят купить 5 л молока, 3 кг сыра «Российский» и 4 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего?

В ответ запишите стоимость данного набора в этом магазине.

Источник

ВПР по математике за 4 класс 2022 – 2023 года — Вариант 14 (25 вариантов)

Внимание! Перед Вами ответы на ВПР с 25 варинтами работ. На нашем сайте Вы также можете найти ответы на ВПР с 10 варинтами работ здесь. Некоторые задания у них ОДИНАКОВЫЕ, но могут отличаться КОЛИЧЕСТВОМ ЗАДАНИЙ

VPR-mat-4-klass-2017-14-variant-1

Задание №1

Найди значение выражения 27 + 26.

Ответ:

Задание №2

Найди значение выражения (17 + 6) * 3 — 6.

Решение:

(17 + 6) * 3 — 6 = 23 * 3 — 6 = 69 — 6 = 63

Ответ:

Задание №3

По правилам авиаперевозок, если багаж весит больше 20 кг, то за перевес нужно доплатить. Рассмотри рисунок с багажом туриста и ответь на вопрос: за сколько килограммов туристу придется доплатить?

Решение:

11 + 5 + 6 = 22 (кг) — вес всего багажа

22 — 20 = 2 (кг) — вес, за который придется доплатить

Ответ:

Туристу придется доплатить за 2 килограмма.

VPR-mat-4-klass-2017-14-variant-2

Задание №4

Катя родилась в сентябре 2005 года. Сколько полных лет было Кате в марте 2015 года?

Решение:

2015 — 2005 = 10 лет

Так как речь идет о марте, то 10 год еще не наступил, следовательно Кате было полных 9 лет.

Ответ:

9 лет

Задание №5

Нарисуй по клеточкам прямоугольник так, чтобы его стороны проходили через все отмеченные точки.

Решение:

Смотри рисунок выше (красный квадрат)

Найди периметр этого прямоугольника, если сторона клетки — 1 см.

Решение:

сторона a = 5 клеткам, а значит 5 * 1 = 5 см

сторона b = 2 клеткам, а значит 2 * 1 = 2 см

Р = (a + b) * 2 = (5 + 2) * 2 = 7 * 2 = 14

Ответ:

Периметр прямоугольника равен 14 см

Задание №6

В таблице приведены данные о численности населения трёх областей России в разные годы (в тыс. человек). Используя эти данные, ответь на вопросы.

В каком году численность населения Омской области была наибольшей?

Ответ:

В 1990 году.

В какой области численность населения за период с 1970 по 2010 год выросла больше, чем в двух других?

Решение:

2665 — 2505 = 160 (чел.) — Новосибирская обл.

1975 — 1825 = 150 (чел.) — Омская обл.

2430 — 2315 = 115 (чел) — Иркутская обл.

Ответ:

В Новосибирской области.

Задание №7

Найди значение выражения 4004 ^. 5 — 540 : 6.

Решение:

4004 ^. 5 — 540 : 6 = 20020 — 90 = 19930

Ответ:

19930

Задание №8

Аня и Таня договорились встретиться у четвертого вагона поезда. Аня отсчитывает вагоны с «головы» состава, а Таня — с «хвоста» состава, Тем не менее они подошли к одному и тому же вагону. Сколько вагонов в поезде?

Решение:

С «головы» состава Аня отсчитал 3 вагона, а Таня отсчитала с «хвоста» 3 вагона, один вагон оказался общим (4-ый).

Получается 3 + 3 + 1 = 7 вагонов

Ответ:

В поезде 7 вагонов.

Задание №9

Аня делает открытки к Восьмому марта для родственников: мамы, бабушки и тёти, Сначала она сделала открытку оранжевого цвета, затем — розового, а потом — фиолетового. Известно, что мамин любимый цвет фиолетовый, а бабушка не любит розовый цвет.

Открытка какого цвета досталась тёте?

Решение:

1 открытка — оранжевая — бабушка не любит розовый цвет, значит эта открытка для неё

2 открытка — розовая — открытка для тёти

3 открытка — фиолетовая — мамин любимый цвет фиолетовый — эта открытка для мамы

Ответ: розовая

Для кого Аня сделала открытку сразу после открытки для бабушки?

Ответ: для тёти

Задание №10

Родственные связи можно представить в виде схемы. Например, на схеме ниже представлена семья с двумя детьми. Такую схему ещё называют родословное или семейное дерево.

Пример

Прочитай текст и изобрази семейное дерево, включающее всех перечисленных в тексте родственников. Впиши в прямоугольники на схеме имена или имена и отчества родственников.

Меня зовут Тамара. У меня большая и дружная семья: мама Ольга Ивановна, папа Николай Станиславович, я, сестра и брат. Моя мама домохозяйка, на её плечах держится весь дом. Мой папа механизатор. Это одна из самых сложных профессий на селе.

Есть в нашей семье и старшее поколение. Дедушка и бабушка с папиной стороны (Станислав Максимович и Ольга Васильевна) живут в селе Дальнее. А мамины родители (Нина Матвеевна и Иван Дмитриевич) живут в селе Светлое. Они уже на пенсии. Мы их очень любим и всегда прислушиваемся к их советам. Бабушки учат нас с сестрой Катей готовить, шить, вязать. Дедушки тоже дают советы, помогают нам.Они учат моего брата Матвея тому, что умеют сами.

Схема для заполнения

Заполним схему, использую информацию из текста.

Задание №11

На столбе висел знак (см. рис. 1). Верхний болт, державший знак, отвалился, и знак перевернулся. Нарисуй, как будет выглядеть знак (рис. 2).

VPR-mat-4-klass-2017-14-variant-3

Задание №12

Петя говорит Васе: «Я легче тебя в три раза». А Вася говорит Пете: «А я тяжелее тебя на 30 килограммов». Оба говорят правду. Сколько весит Петя?

Решение:

Если Петя = х кг, то уравнивая вес обоих ребят получим:

x + 30 = x * 3 — здесь левая сторона — вес Васи (он в три раза тяжелее Пети), а правая сторона — вес Пети + 30 кг

30 = x * 3 — x

30 = x * 2

x = 30 : 2 = 15 (кг.) — вес Пети

x *3 = 15 * 3 = 45 (кг.) — вес Васи

Ответ:

Петя весит 15 килограммов.

Источник

ОГЭ по математике 9 класс 2019 года под редакцией И. В. Ященко (14 вариантов) – Вариант 14

При написании данной работы “ОГЭ по математике 2019. ТТЗ Ященко. 14 вариантов. Вариант 14” было использовано пособие “ОГЭ 2019. Математика. 14 вариантов. Типовые тестовые задания от разработчиков ОГЭ И. Р. Высоцкий, Л. О. Рослова, Л. В. Кузнецова, В. А. Смирнов, А. В. Хачатурян, С. А. Шестаков, Р. К. Гордин, А. С. Трепалин, А. В. Семенов, П. И. Захаров; под редакцией И. В. Ященко. – М.: Издательство “Экзамен”, МЦНМО, 2019″.

Часть 1

Модуль “Алгебра”

Найдите значение выражения

$[ 15 * (frac{1}{5})^2 - 8 * frac{1}{5} ]$

Решение

$[ 15 * (frac{1}{5})^2 - 8 * frac{1}{5} = 15 * frac{1}{25} - frac{8}{5} = 3 * frac{1}{5} - frac{8}{5} = ]$

$[ = frac{3}{5} - frac{8}{5} = frac{3 - 8}{5} = frac{-5}{5} = -1 ]$

Ответ:

-1

В таблице приведены результаты группового этапа Лиги Чемпионов* 2016/2017 в группе А.

Команда	Победы	Ничьи	Поражения
“Арсенал”	4	2	0
“Базель”	0	2	4
“Лудогорец”	0	3	3
“ПСЖ”	3	3	0

За победу начисляется 3 очка, за ничью – 1 очко, за поражение – 0 очков. Первое место в группе занимает команда, набравшая наибольшее число очков. Какая команда заняла последнее место в группе?

“Арсенал”
“Базель”
“Лудогорец”
“ПСЖ”

*Лига Чемпионов – футбольный турнир

Решение

Посчитаем количество очков, набранное каждой командой:

“Арсенал”

4 * 3 + 2 * 1 + 0 = 12 + 2 = 14

“Базель”

0 + 2 * 1 + 0 = 2

“Лудогорец”

0 + 3 * 1 + 0 = 3

“ПСЖ”

3 * 3 + 3 * 1 + 0 = 9 + 3 = 12

Последнее место в группе заняла команда “Базель”

Ответ:

Между какими числами заключено число √56

55 и 57
3 и 4
19 и 21
7 и 8

Решение

Ответы 1 и 3 сразу отпадают, поскольку квадраты этих чисел очень большие.

Ответ 2 тоже не подходит, поскольку квадраты этих числе очень малы: 9 и 16

Правильный ответ – 4, поскольку квадраты числе 7 и 8 соответственно равны 49 и 64.

Ответ:

Найдите значение выражения 25 * 5^-1

Решение

$[ 25 * 5^{-1} = 5^2 * 5^{-1} = 5^{2 + (-1)} = 5^{2 - 1} = 5^1 = 5 ]$

Ответ:

На рисунке жирными точками показано суточное количество осадков, выпавших в Мурманске с 7 по 22 ноября 1995 года. По горизонтали указываются числа месяца, по вертикали – количество осадков, выпавших в соответствующий день, в миллиметрах. Определите по рисунку, сколько дней из данного периода в Мурманске выпало более 3 миллиметра осадков.

Решение

На графике видно два пиковых значения, превышающих отметку 3 миллиметра осадков – 13 и 16 ноября.

2 дня в Мурманске выпадало более 3 миллиметра осадков.

Ответ:

Найдите корень уравнения 4 * (x + 10) = -1

Решение

4 * (x + 10) = -1

4x + 40 = -1

4x = -1 – 40

4x = -41

x = -41 : 4

x = -10,25

Ответ:

-10,25

Стоимость проезда в электропоезде составляет 131 рубль. Школьникам предоставляется скидка 50%. Сколько рублей будет стоить проезд для 3 взрослых и 6 школьников?

Решение

131 руб – 100%

Найдём стоимость проезда для школьника

131 : 2 = 65,5

Найдём стоимость проезда для 3 взрослых и 6 школьников

131 * 3 + 65,5 * 6 = 393 + 393 = 786

Ответ:

786

На диаграммах показано распределение земель по категориям Уральского, Приволжского, Южного и Сибирского федеральных округов. Определите по диаграмме, в каких округах доля земель сельскохозяйственного назначения превышает 50%.

*Прочие земли – это земли поселений; земли промышленности и иного социального назначения; земли особо охраняемых территорий и объектов.

Уральский ФО
Приволжский ФО
Южный ФО
Сибирский ФО

Решение

50% – это половина круга

На диаграмме хорошо видно, что доля земель сельскохозяйственного назначения превышает 50% в двух ФО: Приволжском и Южном.

Ответ:

Датчик измеряет уровень воды в водохранилище по отношению к ординару (нормальному уровню). Расположите события в порядке возрастания их вероятностей:

1) “уровень воды не ниже ординара”
2) “уровень между отметками 1,2 и 1,9 м выше ординара”
3) “уровень выше отметки “0,9 м выше ординара”
4) “уровень выше отметки “0,4 м выше ординара”

В ответе запишите последовательность цифр без пробелов и посторонних знаков.

Решение

Данная задача не решается путем каких-либо формул, она решается путём обычного рассуждения.

Из всех предложенных вероятностей на первом месте стоит вероятность 1) – она возникнет даже при малейшем отклонении уровня воды выше ординара.

Следующей из предложенных вероятностей стоит вероятность 4) – поскольку отметка 0,4 м более близка к ординару. И уж если вода начнет подниматься, то достигнет данной отметки быстрее чем другие отметки.

По такому же принципу рассматривается вероятность 3) – поскольку отметка 0,9 следует за отметкой 0,4 м

И последней вероятностью стоит 2) – это наиболее удалённая отметка от ординара.

Получаем последовательность вероятностей: 1, 4, 3, 2.

Однако, по условию задачи их необходимо расположить в порядке возрастания, получаем: 2, 3, 4, 1.

Ответ:

2341

Установите соответствие между графиками функций и формулами, которые их задают.

Формулы:

$[ y = -frac{2}{x} ]$

Графики:

В таблице под каждой буквой укажите соответсвующий номер.

Решение

Графику А соответсвует функция 3, поскольку функция представлена параболой (поскольку перед нами квадратное уравнение). Выполним проверку: a) при х = -2, y = 2; б) при х = 0, y = -2; г) при х = 2, y = 2;
Графику Б соответсвует функция 2, поскольку функция представлена прямой. Выполним проверку: a) при х = 0, y = 0; б) при х = 2, y = 4; в) при х = -2, y = -4
Графику В соответсвует функция 1, поскольку функция представлена гиперболой – х находится в знаменателе дроби.

Ответ:

А – 3 ; Б – 2 ; В – 1

Дана арифметическая прогрессия (a_n), разность которой равна 5,5 и а₁ = -6,9. Найдите а₆

Решение

Дано

d = 5,5
а₁ = -6,9

Для арифметической прогрессии существует формула:

a_n = a₁ + d(n-1)

Отсюда получим

a₆ = a₁ + d(6-1) = (-6,9) + 5,5 * 5 = -6,9 + 27,5 = 20,6

a₆ = 20,6

Ответ:

a₆ = 20,6

Найдите значение выражения

при

Решение

Выполним преобразование дроби:

подставим значения a и b в полученное выражение

$[ 4a^2 + 49b^2 = 4(sqrt{15})^2 + 49(sqrt{8})^2 = 4 * 15 + 49 * 8 = 60 + 392 = 452 ]$

Ответ:

452

Центростремительное ускорение движения по окружности (в м/с²) вычисляется по формуле a = w²R, где w – угловая скорость (в с^-1), R – радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 8 с^-1, а центростремительное ускорение равно 128 м/с². Ответ дайте в метрах.

Решение

Исходная формула

Отсюда R будет равно

$[ R = frac{a}{w^2} ]$

По условию задачи известно:

w = 8 с^-1a = 128 м/с²

Подставим значения в формулу:

$[ R = frac{a}{w^2} = frac{128}{8^2} = frac{128}{64} = 2 ]$

Радиус R равен 2

Ответ:

Укажите решение неравенства (x + 8) (x – 3) < 0

Решение

Преобразуем уравнение

Перед нами квадратное уравнение, графиком которой является парабола с ветвями направленными вверх (так как коэффициент “а” положительный). Уже на этом этапе ясно, что правильный ответ 1.

Решим квадратное уравнение.

Найдём дискриминант:

Дискриминант больше нуля, D>0, значит уравнение имеет два корня

$[ x_1 = frac{-b + sqrt{D}}{2a} = frac{-5 + sqrt{121}}{2 * 1} = frac{-5 + 11}{2} = frac{6}{2} = 3 ]$

$[ x_2 = frac{-b - sqrt{D}}{2a} = frac{-5 - sqrt{121}}{2 * 1} = frac{-5 - 11}{2} = frac{-16}{2} = -8 ]$

Решением данного уравнения будет множество точек в интервале [-8; 3]

Правильный ответ 1

Ответ:

Модуль “Геометрия”

Очиститель заднего стекла автомобиля состоит из поводка и щётки, расположенных на одной прямой. Середина щётки крепится к концу поводка. Когда поводок поворачивается вправо-влево, щётка очищает стекло. Найдите площадь очищенной части стекла, если длина поводка 35 см, длина щётки 25 см, а угол поворота 180°. Значение 𝜋 считается равным 3,14. Ответ дайте в квадратных сантиметрах.

Решение

Фигура, которую описывает очиститель заднего стекла выглядет следующим образом:

Чтобы найти площадь фигуры, образованной очистителем заднего стекла, необходим от площади сектора круга с большим радиусом R отнять площадь сектора круга с меньшим радиусом r.

Площадь сектора круга с дугой n° равна произведению площади окружности с радиусом r на отношение угла сектора n° к углу полной окружности, т.е. 360°

$[ S = pi r^2 frac{n}{360} ]$

Дано:

𝜋 = 3,14
n° = 180°
R = 35 + (25 : 2) = 35 + 12,5 = 47,5
r = 35 – (25 : 2) = 35 – 12,5 = 22,5

Подставим данные значения в формулу и найдём площадь большего сектора, образованного радиусом R:

$[ S_1 = pi R^2 frac{n}{360} = 3,14 * 47,5^2 * frac{180}{360} = 3,14 * 2256,25 * frac{1}{2} = frac{7084,625}{2} ]$

Подставим данные значения в формулу и найдём площадь меньшего сектора, образованного радиусом r:

$[ S_2 = pi r^2 frac{n}{360} = 3,14 * 22,5^2 * frac{180}{360} = 3,14 * 506,25* frac{1}{2} = frac{1589,625}{2} ]$

Отсюда искомая площадь будет равна:

$[ S = S_1 - S_2 = frac{7084,625}{2} - frac{1589,625}{2} = frac{7084,625 - 1589,625}{2} = frac{5495}{2} = 2747,5 ]$

Площадь очищенной части стекла равна 2747,5 см²

Ответ:

2747,5 см²

В треугольнике ABC угол C равен 90°, AC = 11, AB = 20. Найдите sin B.

Решение

По условию задачи дано:

C = 90°
AC = b = 11
AB = c = 20

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

$[ sinB = frac{b}{c} = frac{11}{20} =0,55 ]$

sin B = 0,55

Ответ:

sin B = 0,55

Периметр треугольника равен 140, а одна из сторон равна 56, а радиус вписанной в него окружности равен 9. Найдите площадь этого треугольника.

Решение

Определение: Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:

где p – это полупериметр, r – радиус вписанной окружности

$[ p = frac{a + b + c}{2} = frac{140}{2} = 70 ]$

Подставляем значения в первую формулу

Площадь треугольника равна 630

Ответ:

630

Сторона квадрата равна 6√2. Найдите диагональ этого квадрата.

Решение

Диагональ квадрата вычисляется по формуле

где d – длина диагонали квадрата, s – длина стороны квадрата

Длина диагонали квадрата равна 12

Также диагональ квадрата можно найти по Теореме Пифагора, поскольку диагональ делит квадрат на 2 равных прямоугольных треугольника. Нам известны длины двух катетов и требуется найти длину гипотенузы (диагонали).

$[ с^2 = a^2 + b^2 = (6sqrt{2})^2 + (6sqrt{2})^2 = 36 * 2 + 36 * 2 = 72 + 72 = 144 ]$

Ответ:

На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину ее средней линии.

Решение

Определение: Длина средней линии трапеции равна полусумме ее оснований.

Из чертежа видно, что длина меньшего основания трапеции равна 3, а длина большего основания трапеции равна 9.

$[ frac{a + b }{2} = frac{3 + 9 }{2} = frac{12 }{2} =6 ]$

Длина средней линии трапеции равна 6

Ответ:

Какое из следующих утверждений верно?

Тангенс любого острого угла меньше единицы.
Если диагонали параллелограмма равны, то этот параллелограмм называется ромбом.
Точка, лежащая на серединном перпендикуляре к отрезку, равно удалена от концов этого отрезка.

Решение

Данное задание не является задачей. Вопросы, перечисленные здесь необходимо знать наизусть и уметь на них отвечать.

Неверно – тангенс острого угла бывает и больше единицы (например, тангенс 60 градусов равен √3)
Неверно – Если диагонали параллелограмма равны, то этот параллелограмм называется прямоугольником.
Верно – это свойство серединного перпендикуляра

Ответ:

Часть 2

Модуль “Алгебра”

Решите систему уравнений

$[ left{begin{matrix} 7x^2 - 5x = y\ 7x - 5 = y end{matrix}right. ]$

Решение

Приравняем данные уравнения

Решим полученное квадратное уравнение.

Найдём дискриминант:

Дискриминант больше нуля D>0, уравнение имеет два корня:

$[ x_1 = frac{-b + sqrt{D}}{2a} = frac{-(-12) + sqrt{4}}{2 * 7} = frac{12 + 2}{14} = frac{14}{14} = 1 ]$

$[ x_2 = frac{-b - sqrt{D}}{2a} = frac{-(-12) - sqrt{4}}{2 * 7} = frac{12 - 2}{14} = frac{10}{14} = frac{5}{7} ]$

Найдём значение y для каждого x

$[ y_2 = 7x - 5 = 7 * frac{5}{7} - 5 = 5 - 5 = 0 ]$

Решением данной системы уравнений является (1; 2); (5/7; 0)

Ответ:

(1; 2); (5/7; 0)

Первую половину пути автомобиль проехал со скоростью 54 км/ч, а вторую – со скоростью 90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Решение

Определение: Средняя скорость равна отношению расстояния к затраченному времени на преодоление данного расстояния.

$[ v = frac{S}{t} ]$

По условию задачи дано

v1 = 54 км/ч
v2 = 90 км/ч
S – длина всего пути в км

Половина пути равна = S/2

Время потраченное на первую половину пути:

$[ t_1 = frac{frac{S}{2}}{v_1} = frac{frac{S}{2}}{54} = frac{S}{2 * 54} = frac{S}{108} ]$

Время потраченное на вторую половину пути:

$[ t_2 = frac{frac{S}{2}}{v_2} = frac{frac{S}{2}}{90} = frac{S}{2 * 90} = frac{S}{180} ]$

Средняя скорость автомобиля будет равна:

$[ v = frac{S}{t} = frac{S}{t_1 + t_2} = frac{S}{frac{S}{108} + frac{S}{180}} = frac{S}{S * (frac{1}{108} + frac{1}{180})} = ]$

$[ = frac{1}{frac{1}{108} + frac{1}{180}} = frac{1}{frac{5}{540} + frac{3}{540}} = frac{1}{frac{8}{540}} = ]$

$[ = frac{540}{8} = 67,5 ]$

Средняя скорость автомобиля будет равна 67,5 км/ч

Ответ:

67,5 км/ч

Постройте график функции

$[ y = frac{(x^2 + 0,25) (x + 1)}{-1 - x} ]$

и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.

Решение

Определим область допустимых значений

Так как делить на ноль нельзя, знаменатель не может равняться 0

-1 -x ≠ 0

– x ≠ 1

x ≠ -1

Упростим выражение

$[ y = frac{(x^2 + 0,25) (x + 1)}{-1 - x} = frac{(x^2 + 0,25) (-1 - x) (-1)}{-1 - x} = (x^2 + 0,25) (-1) = ]$

Найдем при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.

Для этого надо составить систему из данных функций:

$[ left{begin{matrix} y = -x^2 - 0,25 \ y = kx end{matrix}right. ]$

Решим, полученное квадратное уравнение.

Найдём дискриминант:

По условию задачи необходимо найти значения k при которых прямая y=kx имеет с графиком ровно одну общую точку, следовательно корень этой системы должен быть только один. Значит дискриминант должен быть равен нулю.

Учитывая то, что k представлена в квадрате, значит k может принимать как положительные, так и отрицательные значения -1; 1

Заметим, что в нашем графике есть “выколотая” точка при x=-1, через которую может пройти искомая прямая. Найдем координату “y” этой точки:

Итак, точка (-1; -1,25) является “выколотой”. Подставим данные значения x и y в заданное уравнение прямой:

$[ k = frac{-1,25}{-1} = 1,25 ]$

y=kx имеет с графиком ровно одну общую точку при следующие значениях k: 1,25; -1; 1

Ответ:

1,25; -1; 1

Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответсвенно и проходит через вершины B и C. Найдите длину отрезка KP, если AK = 6, а сторона AC в 1,5 раза больше стороны BC.

Решение

Выполним чертёж, согласно заданного условия:

Соединив точки пересечения K и P треугольника ABC с кругом, мы получили вписанный четырёхугольник KBCP.

Поскольку четырёхугольник KBCP вписан в окружность, сумма его противоположных углов равна 180°, следовательно:

∠KBC (1) + ∠KPC(2) = 180°

Углы ∠APK (3) и ∠KPC (2) являются смежными углами, следовательно их сумма также равна 180°

∠APK (3) + ∠KPC (2) = 180°

Исходя из приведённых равенств углов получаем, что углы ∠KBC (1) и ∠APK (3) равны.

Аналогичная ситуация с углами ∠BCP (5) и ∠PKB (4)

∠BCP (5) + ∠PKB (4) = 180°

Углы ∠PKB (4) и ∠AKP (6) являются смежными углами, следовательно их сумма также равна 180°

∠PKB (4) + ∠AKP (6) = 180°

Исходя из приведённых равенств углов получаем, что углы ∠BCP (5) и ∠AKP (6) равны.

Рассмотрим треугольники ∆ABC и ∆AKP

Данные треугольники подобны по третьему признаку подобия треугольников.

Следовательно

$[ frac{KP}{BC} = frac{AK}{AC} = frac{AP}{AB} ]$

Рассмотрим равенство

$[ frac{KP}{BC} = frac{AK}{AC} ]$

Найдём отсюда чему равен KP

$[ KP = frac{AK * BC}{AC} ]$

По условию задачи сторона AC в 1,5 раза больше стороны BC

AC = 1,5 * BC

Подставим значение AC и AK = 6 в формулу

$[ KP = frac{AK * BC}{AC} = frac{AK * BC}{1,5 * BC} = frac{AK}{1,5} = frac{6}{1,5} = 4 ]$

Длина отрезка KP равна 4

Ответ:

В треугольнике ABC с тупым углом BAC проведены высоты AA1 и BB1. докажите, что треугольники A1CB1 и ABC подобны.

Решение

Выполним чертёж, согласно заданного условия:

Определение: Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противоположную сторону.

Следовательно, углы ∠AA1C и ∠BB1C являются прямыми.

Рассмотрим треугольники ∆AA1C и ∆BB1C

Данные треугольники являются прямоугольными, поскольку углы ∠AA1C и ∠BB1C прямые.

Углы ∠A1CA и ∠B1CB равны, как вертикальные.

Углы ∠A1AC и ∠B1BC также равны по двум признакам:

1) Сумма углов треугольника составляет 180°. Из выше сказанного будет верным равенство:

∠A1AC = ∠B1BC = 180° – ∠A1CA – ∠A1AC = 180° – ∠B1CB – ∠B1BC

2) Углы ∠A1AC и ∠B1BC равны как углы с взаимно перпендикулярными сторонами

Следовательно треугольники ∆AA1C и ∆BB1C подобны. Для подобных треугольников справедливо следующее отношение:

$[ frac{CA}{CB} = frac{AA1}{BB1} = frac{CA1}{CB1} ]$

Рассмотрим треугольники ∆A1CB1 и ∆ABC

Углы ∠A1CB1 и ∠ACB равны, как вертикальные.

Ранее мы установили, что

$[ frac{CA}{CB} = frac{CA1}{CB1} ]$

Следовательно данные треугольники подобны.

Утверждение доказано.

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC = 7, а расстояние от точки K до стороны AB равно 4.

Решение

Выполним чертёж согласно условия: