Карточки по математике в 3 классе «Порядок действий»
Карточка 1
92 – (31 + 19) +58
73 + (61 – 45) – 26
(63 + 17) – (100 – 24)
(81 – 35) + (48 – 19)
Карточка 2
40 : 5 + 8 • 3
12 :3 – 28 :7
39 : 9 + 45 : 5
8 • 4 – 16 : 2
6 • 9 – 7 • 5
27 : 3 + 48 : 8
36 : 4 + 7 • 6
Карточка 3
(53 – 29) + (28 +48) – 55
72 – (100 – 47) + 81
(27 + 36) – (74 – 58) + 16
(57 + 34) – (25 +48)
(69 + 18) – (92 – 39) +66
(80 – 56) + (100 – 72)
Карточка 4
100 – (50 – 38) – (25 + 13)
(49 +11 – 16) – (92 – 76)
(51 – 17) + (85 – 46) + (43 – 24)
(29 + 64 – 72) – (35 + 35 – 49)
86 – 79 + 64 – (18 + 35)
Карточка 5
27 + (9 • 6 – 25) + 72 : 8
100 – (63 + 27 – 58) : 4
(31 – 30) • (63 : 7 + 64 : 8)
(6 • 4 + 3 • 8) : (70 – 69)
(42 – 18) : (60 – 36) + 99
Карточка 6
(63 – 23) • 2 – (45 + 45) : 30 – (72 + 28) : 10
(71 – 45) + (62 – 34) + (83 – 57)
(27 + 27) : 6 + (54 + 27) : 9 + (80 – 32) : 8
(56 : 8 + 81 : 9 + 4 • 1) • 4 : 40
(68 – 19) : 7 + (72 – 48) : 4
Карточка 7
24 : 2 + 30 : 2 + 50 : 2
72 : 18 + 95 : 19 + 80 : 16
100 – 55 : 11 – 85 : 17
45 : 15 + 51 : 17 + 66 : 11
76 : 19 + 40 : 2 – 57 : 19
Карточка 1.
42 : 6 + ( 19 + 6 ) : 5 – 6 • 2
( 27 – 19 ) • 4 + 18 : 3 + ( 8 + 27 ) : 5 – 17
60 – (13 + 22 ) : 5 – 6 • 4 + 25
Карточка 2.
( 82 – 74) : 2 • 7 + 7 • 4 – 19 + ( 63 – 27 ) : 4
( 91 – 83 ) • 3 : 4 + 12 : 6
32 : 8 + ( 27 + 15 ) : 6 + 8 • 5
Карточка 3.
9 • 5 – 36 : 6 : 2 – ( 38 – 23 ) : 5
90 – ( 40 – 24 : 3) : 4 • 6 + 3 • 5
3 • 4 + 9 • 6 – (27 + 9) : 4 • 5
Карточка 4.
(50 – 23 ) : 3 + 8 • 5 – 6 • 5 – (26 – 16 ) • 6
( 5 • 6 – 3 • 4 + 48 : 6) + ( 82 – 78 ) • 7 – 13
(69 – 45) : 3 • 2 + ( 43 – 34 ) • 2
Карточка 5.
9 • 6 – 6 • 4 : ( 33 – 25 ) • 7
( 5 • 9 – 25 ) : 4 • 8 – 4 • 7 – 13
3 • ( 12 – 8 ) : 2 + 6 • 9 – 33
Карточка 6.
( 76 – (27 + 9) + 8 ) : 6 • 4
9 • ( 2 • 3 ) – 48 : 8 • 3 + 7 • 6 – 34
( 7 • 4 + 33 ) – 3 • 6 : 2
Карточка 7.
( 9 • 4 – 6 • 5 ) • 4 – 42 : 7 + (60 – 11 )
7 • 6 + 9 • 4 – ( 2 • 7 + 54 : 6 • 5 )
(37 + 7 • 4 – 17 ) : 6 + 7 • 5
33 + 9 • 3 – ( 85 – 67 ) : 2 • 6
Карточка 8.
28 : 4 + 27 : 3 – (17 + 31 ) : 6
54 : 9 + ( 8 + 19 ) : 3 – 32 :4
( 8 • 6 – 36 : 6 ) : 6 • 3 + 5 • 9
21 : 7 + (42 – 14 ) : 4 – ( 44 – 14 ) : 5
Карточка 9.
8 • 5 – (60 – 42 ) : 3 + 9 • 2
5 • 7 + (18 +14) : 4 – (26 – 8 ) : 3 • 2
(58 – 31 ) : 3 – 2 + (58 – 16) : 6
( 9 • 7 + 56 : 7) – ( 2 • 6 – 4 ) • 3 + 54 : 9
1. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
45 : 5 + 36 : 4 – 6=
27 + 7 · 8 – 35 : 35=
42 : 6 + 28 – 3 · 6=
9 · 7 – 3 · 7 + 29 – 24 : 4=
2. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
48 : 6 + 33 – 54 : 9 + 7 · 4=
15 + 21 : 21 · 5 – 27 : 9 · 2=
6 · 5 : 3 + 48 : 6 : 4 · 6 + 3 · 9=
100 – 6 · 4 : 3 · 9 – 19 + 7 · 5=
3. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
100 – 21 : 7 · 0 + 5 · 4=
2 · 5 + 24 : 6 + 18 : 3 · 9=
9 · 5 – 19 + 6 · 6 – 3 · 4=
7 · 6 + 35 : 7 · 5 – 16 : 2 : 4 · 5=
4. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
32 : 4 · 6 : 8 + 6 · 3 – 17=
5 · 8 + 4 · 6 + 15 – 14=
36 : 6 + 18 : 9 + 20 – 12 + 6 · 4=
27 : 3 – 35 : 7 + 8 · 0 + 5 · 5=
5. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
42 : 6 · 3 + 11 + 24 : 4 – 7 =
6 · 9 + 30 : 5 : 2 · 7 – 27=
90 – 7 · 5 – 24 : 8 · 5=
6 · 5 – 12 : 6 · 3 + 49=
6. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
32 : 8 · 5 + 48 : 6 : 2 · 5=
50 – 45 : 9 · 3 + 16 : 8 · 9=
1 · 8 + 25 – 24 : 4 · 2 + 14=
48 : 6 · 4 + 6 · 7 – 23 + 16=
7. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
42 : 7 + (19 + 11) : 5 – 2 · 6=
60 – (23 + 22) : 5 – 6 · 3 + 35=
(23 – 19) · 4 + 18 : 3 + (8 + 22) =
(82 – 82) : 2 · 7 + 7 · 7 – (63 – 27)=
8. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
(50 – 23) : 3 + 8 · 5 – 6 · 5 =
3 · 4 + 9 · 6 – (27 + 9) : 4 · 5= (5 · 6 – 3 · 4 – 48 : 6) · 7 – 13=
9. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
9 · 4 – 6 · 4 : (33 – 25) · 5=
3 · (12 – 8) : 2 + 8 · 9 – 38=
(5 · 9 – 25) : 4 · 8 – 4 · 7 =
9 · (2 · 5) – 48 : 48 · 3 + 7 · 6 =
10. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
(8 · 6 – 36 : 36) – 6 · 3 + 5 · 1=
7 · 4 + 9 · 4 – (2 · 7 + 54 : 6)=
(75 – 27 : 9 + 8) : 8 · 4=
(7 · 4 + 33) – 3 · 6 : 9=
11. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
( 7 · 4 – 16) : 6 + 7 · 5 – (85 – 85) : 2 · 5=
5 · 7 + (18 + 14) : 4 – 28 : 4 + 27 : 3 – (17 + 31) : 6=
12. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
(58 – 31) : 3 – 2 + (58 – 16) : 6 + 8 · 5 – (60 – 42) : 3 =
(9 · 7 + 56 : 7) – (2 · 6 – 4) · 3 + 0 : 9=
13. РЕШИ Я, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
(8 · 5 + 28 : 7) + 12 : 2 – 6 · 5 + (13 – 5) · 4 + 5 · 4=
(7 · 8 – 14 : 14) + (7 · 4 + 12 : 6) – 10 : 5 + 63 : 9=
14. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
(7 · 4 + 28 : 7) + 14 : 2 – 6 · 6 + (18 – 9) · 3 + 2 · 6=
(3 · 8 – 24 : 6) + (5 · 3 + 12 : 12) – 15 : 5 + 54 : 6=
(5 ∙ 9 + 36 – 27) – (51 – 10 · 4) =
35 + (7 ∙ 4 + 47 – 25) : 10 =
18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =
80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =
(64 – 26) + (35 : 7 + 45) : 10 =
70 – (32 + 19) + 24 – (60 : 10 + 28) =
24 : 6 + 42 : 7 =
56 : 8 – 35 : 5 =
40 – 24 : 8 =
21 : 3 + 28 :7 =
18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =
80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =
(64 – 26) + (35 : 7 + 45) : 10 =
70 – (32 + 19) + 24 – (60 : 10 + 28) =
24 : 6 + 42 : 7 =
56 : 8 – 35 : 5 =
40 – 24 : 8 =
21 : 3 + 28 :7 =
18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =
80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =
(64 – 26) + (35 : 7 + 45) : 10 =
70 – (32 + 19) + 24 – (60 : 10 + 28) =
24 : 6 + 42 : 7 =
56 : 8 – 35 : 5 =
40 – 24 : 8 =
21 : 3 + 28 :7 =
18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =
80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =
(64 – 26) + (35 : 7 + 45) : 10 =
70 – (32 + 19) + 24 – (60 : 10 + 28) =
24 : 6 + 42 : 7 =
56 : 8 – 35 : 5 =
40 – 24 : 8 =
21 : 3 + 28 :7 =
18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =
80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =
(64 – 26) + (35 : 7 + 45) : 10 =
70 – (32 + 19) + 24 – (60 : 10 + 28) =
24 : 6 + 42 : 7 =
56 : 8 – 35 : 5 =
40 – 24 : 8 =
21 : 3 + 28 :7 =
70 : 7 + 6 · 8 – 42 : 7 =
24 : 6 · 3 : 2 · 5 : 3 · 7 =
92 – (40 – 21 + 37) + 46 =
72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 =
35 : 5 · 4 : 7 · 9 : 6 =
9 · 4 : 6 · 7 : 42 · 64 : 8 =
(4 ∙ 9 + 28) – (27 : 3 + 15) =
82 – 44 · 0 – 82 =
(31 + 61 – 47) · 0 =
18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 =
|
24 : 6 · 3 : 2 · 5 : 3 · 7 = |
|
92 – (40 – 21 + 37) + 46 = |
|
72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 = |
|
35 : 5 · 4 : 7 · 9 : 6 = |
|
9 · 4 : 6 · 7 : 42 · 64 : 8 = |
|
(4 ∙ 9 + 28) – (27 : 3 + 15) = |
|
82 – 44 · 0 – 82 = |
|
(31 + 61 – 47) · 0 = |
|
18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 = |
|
24 : 6 · 3 : 2 · 5 : 3 · 7 = |
|
92 – (40 – 21 + 37) + 46 = |
|
72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 = |
|
35 : 5 · 4 : 7 · 9 : 6 = |
|
9 · 4 : 6 · 7 : 42 · 64 : 8 = |
|
(4 ∙ 9 + 28) – (27 : 3 + 15) = |
|
82 – 44 · 0 – 82 = |
|
(31 + 61 – 47) · 0 = |
|
18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 = |
|
24 : 6 · 3 : 2 · 5 : 3 · 7 = |
|
92 – (40 – 21 + 37) + 46 = |
|
72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 = |
|
35 : 5 · 4 : 7 · 9 : 6 = |
|
9 · 4 : 6 · 7 : 42 · 64 : 8 = |
|
(4 ∙ 9 + 28) – (27 : 3 + 15) = |
|
82 – 44 · 0 – 82 = |
|
(31 + 61 – 47) · 0 = |
|
18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 = |
|
24 : 6 · 3 : 2 · 5 : 3 · 7 = |
|
92 – (40 – 21 + 37) + 46 = |
|
72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 = |
|
35 : 5 · 4 : 7 · 9 : 6 = |
|
9 · 4 : 6 · 7 : 42 · 64 : 8 = |
|
(4 ∙ 9 + 28) – (27 : 3 + 15) = |
|
82 – 44 · 0 – 82 = |
|
(31 + 61 – 47) · 0 = |
|
18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 = |
|
34 · 2 – 48 : 8 = |
|
56 : 7 + 42 : 6 = |
|
5 · (18 : 3) + 58 = |
|
8 ∙ 9 + (70 – 56) = |
|
48 : 6 + 24 : 6 = |
|
9 · (12 : 6) + 47 = |
|
6 · 2 + (90 – 73) = |
|
63 : 7 + 28 : 7 = |
|
48 : 8 · 2 : 3 · 0 : = |
|
56 : 8 + 7 · 7 = |
45 : (33 – 24) ∙ 6 =
63 + 27 : (30 : 10) =
60 – 54 : 6 =
60 – 18 : 2 ∙ 3 =
96 – (35 – 5) : 6 =
49 : 6 ∙ 3 : 0 =
72 : 8 + 63 : 7 + 81 : 9 =
60 : 2 + 60 : 3 + 100 : 2 =
27 : 3 ∙ 2 : 6 ∙ 3 ∙ 4 =
|
54 : 6 – 15 : 15 = |
|
0 : 12 + 13 ∙ 2 = |
|
18 : 1 ∙ 0 + 99 = |
|
56 : (24 : 4 · 3 : 9) + (40 – 25 : 25) = |
|
64 – (80 – 38 – 29) + (90 – 46 + 17) = |
|
4 · (71 – 58) – (60 – 40 : 4) = |
|
46 + (91 – 76) + 19 – (63 – 38) = |
|
35 + 57 – (62 – 29) – (71 – 48) = |
|
56 – 8 – 9 – ( 7 + 24) = |
56 : (15 – 7) + 4 =
9 ∙ (5 + 4) : 9 =
13 + (60 – 6) : 9 =
42 : 6 + 7 ∙ 4 =
72 + (40 – 4) : 9 =
63 : 7 + (20 – 5) – (9 + 6) =
18 + 36 : 9 + 6 ∙ 8 – 50 =
5 ∙ (4 + 3) + 19 – 10 =
(18 + 36) : 9 + 6 ∙ 8 – 40 =
7 · (18 : 3) – 32 : 4 =
67 – 9 : 3 · 9 + 28 =
45 : 5 + 12 : 4 ∙ 6 =
16 + 560 : 7 – 21 =
72 : (44 – 8) + 5 =
49 : 7 + 18 – 9 =
98 – 6 ∙ 4 + 17 =
630 : 7 + 40 : (4 ∙ 2) =
6 ∙ 4 : ( 560 : 70) ∙ 5 =
85 – 6 ∙ 8 : 4 =
(26 – 6) ∙ 5 : 4 =
7 ∙ 4 : 2 – 8 =
54 : 9 ∙ 7 – 20 =
420 : 7 · 8 – 24 : 6 =
47 – 30 : 5 + 7 · 7 =
20 : 4 ∙ 8 + 28 : 4 ∙ 7 =
14 + 12 : 6 · 8 – 45 : 5 =
6 · 2 : 3 · 7 – 81 : 9 =
18 + 27 : 3 · 8 – 8 · 8 =
|
4 ∙ (18 : 9) ·7 – 64 : 8 = |
|
7 · 3 + (28 + 8) : 6 · 5 = |
|
80 – (25 : 5 + 9) : 2 – 13 = |
|
2 · 9 – 36 : (3 · 8 : 6) = |
|
4 · 4 : 2 + (30 – 15) : 3 = |
|
(12 + 9 · 4) : 6 – 5 = |
|
20 – 3 · 3 · 2 + 48 : 8 · 5 = |
|
4 · 9 – 6 · 6 + 56 : 8 · 6 = |
|
12 + (9 · 4 : 6 – 5) = |
2 · 2 · 5 – 72 : 8 + 9 · 9 =
12 + 9 · 4 : (6 – 5) =
9 · 8 – (5 · 2 – 8) – 6 · 6 : 4 =
40 : 8 + 3 · 2 · 6 : 4 – 7 =
5 · (9 – 6) + 14 : 2 =
(5 · 5 – 7) : 9 + 7 · 8 – 81 : 9 =
3 · 3 · 7 – (7 · 2 – 1) + 28 : 7 =
5 · 9 – (6 + 14) : 2 =
5 · 3 + 5 · 6 + 5 · 7 =
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Если в выражении есть только числа и арифметические знаки “+”, “·”, “-“, “÷”, то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пусть нужно найти значения выражения 14-2·15÷6-3.
Выполним сначала умножение и деление. Получаем:
14-2·15÷6-3=14-30÷6-3=14-5-3.
Теперь проводим вычитание и получаем окончательный результат:
14-5-3=9-3=6.
Вычислим: 0,5-2·-7+23÷234·1112.
Сначала выполняем преобразование дробей, деление и умножение:
0,5-2·-7+23÷234·1112=12-(-14)+23÷114·1112
12-(-14)+23÷114·1112=12-(-14)+23·411·1112=12-(-14)+29.
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
12-(-14)+29=12+14+29=14+1318=141318.
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Найдем значение выражения 0,5·(0,76-0,06).
В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом – умножение.
0,5·(0,76-0,06)=0,5·0,7=0,35.
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Вычислим значение 1+2·1+2·1+2·1-14.
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
1+2·1+2·1+2·1-14=1+2·1+2·1+2·34
1+2·1+2·1+2·34=1+2·1+2·2,5=1+2·6=13.
В нахождении значений выражений со скобками главное – соблюдать последовательность действий.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Вычислим значение выражения с корнями -2·3-1+60÷43+3·2,2+0,1·0,5.
Сначала вычисляем подкоренные выражения.
-2·3-1+60÷43=-6-1+153=83=2
2,2+0,1·0,5=2,2+0,05=2,25=1,5.
Теперь можно вычислить значение всего выражения.
-2·3-1+60÷43+3·2,2+0,1·0,5=2+3·1,5=6,5
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Сколько будет 3+13-1-1
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
3+13-1=3-1.
Таким образом:
3+13-1-1=3-1-1=1.
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Найдем значение выражения 23·4-10+161-123,5-2·14.
Начинаем вычислять по порядку.
23·4-10=212-10=22=4
16·1-123,5-2·14=16*0,53=16·18=2.
Осталось только провести операцию сложение и узнать значение выражения:
23·4-10+161-123,5-2·14=4+2=6.
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Вычислим значение следующего выражения: 2-25·45-1+3136.
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
2-25·45-1+3136=2-25·225-1+313·6
2-25·225-1+313·6=2-25·22·5-2+32=22·5-2-25+32
22·5-2-25+32=2-2+3=14+3=314
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Найдем значение выражения, содержащего дроби: 3,22-3·7-2·36÷1+2+39-6÷2.
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
3,22=3,2÷2=1,6
7-2·36=7-66=16
1+2+39-6÷2=1+2+39-3=66=1.
Перепишем наше выражение и вычислим его значение:
1,6-3·16÷1=1,6-0,5÷1=1,1
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Вычислим выражение 25-1-25-74-3.
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
25-1=25+15-15+1=25+15-1=25+24
Исходное выражение принимает вид:
25-1-25-74-3=25+24-25-74-3.
Вычислим значение этого выражения:
25+24-25-74-3=25+2-25+74-3=94-3=-34.
Выражения с логарифмами
Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log24+2·4 можно сразу вместо log24 записать значение этого логарифма, а потом выполнить все действия. Получим: log24+2·4=2+2·4=2+8=10.
Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log5-6÷352+2+7. Имеем:
log5-6÷352+2+7=log327+7=3+7=10.
Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Найдем значение выражения log2log2256+log62+log63+log5729log0,227.
log2log2256=log28=3.
По свойству логарифмов:
log62+log63=log6(2·3)=log66=1.
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
log5729log0,227=log5729log1527=log5729-log527=-log27729=-log27272=-2.
Теперь можно переходить к вычислению значения исходного выражения.
log2log2256+log62+log63+log5729log0,227=3+1+-2=2.
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Найдите значение выражения: tg24π3-sin-5π2+cosπ.
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
tg4π3=3
sin-5π2=-1
cosπ=-1.
Подставляем значения в выражение и вычисляем его значение:
tg24π3-sin-5π2+cosπ=32-(-1)+(-1)=3+1-1=3.
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Нужно найти значение выражения cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1.
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1=cos2π8cos5π36+π9-1=cosπ4cosπ4-1=1-1=0.
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.
- Корни, степени, логарифмы и т.д. заменяются их значениями.
- Выполняются действия в скобках.
- Оставшиеся действия выполняются по порядку слева направо. Сначала – умножение и деление, затем – сложение и вычитание.
Разберем пример.
Вычислим, чему равно значение выражения -2·sinπ6+2·2π5+3π5+3 lne2+1+39.
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
Первым делом вычислим значение подкоренного выражения 2·sinπ6+2·2π5+3π5+3. Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.
π6+2·2π5+3π5=π6+2·2π+3π5=π6+2·5π5=π6+2π
Теперь можно узнать значение синуса:
sinπ6+2·2π5+3π5=sinπ6+2π=sinπ6=12.
Вычисляем значение подкоренного выражения:
2·sinπ6+2·2π5+3π5+3=2·12+3=4
Отсюда:
2·sinπ6+2·2π5+3π5+3=4=2.
Со знаменателем дроби все проще:
lne2=2.
Теперь мы можем записать значение всей дроби:
2·sinπ6+2·2π5+3π5+3 lne2=22=1.
С учетом этого, запишем все выражение:
-1+1+39=-1+1+33=-1+1+27=27.
Окончательный результат:
-2·sinπ6+2·2π5+3π5+3 lne2+1+39=27.
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56+8-3,789lne2-56+8-3,789lne2 также равно нулю.
Еще один прием, позволяющий ускорить процесс – использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями – сокращение одинаковых выражений в числителе и знаменателе.
Например, возьмем выражение 23-15+3·289·343·23-15+3·289·34. Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 13.
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.
Вычислить значение выражения 0,5x-y при заданных x=2,4 и y=5.
Подставляем значения переменных в выражение и вычисляем:
0,5x-y=0,5·2,4-5=1,2-5=-3,8.
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Например, выражение х+3-х, очевидно, имеет значение 3, и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.
Еще один пример. Значение выражения xx равно единице для всех положительных иксов.
- Главная
- Справочники
- Справочник по математике для начальной школы
- Числовые и буквенные выражения
Числовые выражения
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
Числовое выражение – это запись , состоящая из чисел и знаков действий между ними.
Например, 44 + 32
Значение выражения – это результат выполненных действий.
Например, в записи 44 + 32 = 76, значение выражения – это 76.
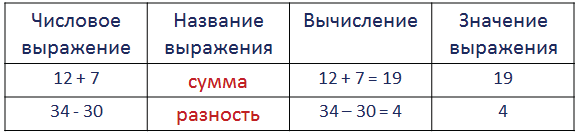
Чтение числовых выражений
12 + 9 – сумма
49 – 20 – разность
34 – (8 + 21) – из 34 вычесть сумму чисел 8 и 21
13 + (26 – 8) – к 13 прибавить разность чисел 26 и 8
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Давай сравним значения двух выражений: 14 – 6 и 18 – 9.
Для этого найдем значения каждого из них:
14 – 6 = 8
18 – 9 = 9
8 < 9, значит,
14 – 6 < 18 – 9
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
В этих выражениях буквы могут обозначать различные числа. Число, которым заменяют букву, называют значением.
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.
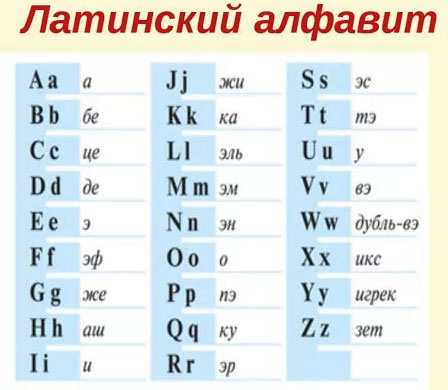
Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
Алгоритм – значит, порядок, план выполнения команд.
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Например, 28 – с
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
Подставим вместо неизвестного «с» число 4.
У нас получается выражение: 28 – 4
Вычисляем результат:
28 – 4 = 24
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
c = 2, x = 3
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
2 + 3 + 2
Теперь мы можем найти значение этого выражения:
с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7
Советуем посмотреть:
Уравнения
Правило встречается в следующих упражнениях:
1 класс
Страница 18. Урок 11,
Петерсон, Учебник, часть 1
Страница 8. Урок 5,
Петерсон, Учебник, часть 2
Страница 10. Урок 6,
Петерсон, Учебник, часть 2
Страница 45. Урок 23,
Петерсон, Учебник, часть 2
Страница 49. Урок 25,
Петерсон, Учебник, часть 2
Страница 51. Урок 26,
Петерсон, Учебник, часть 2
Страница 57. Урок 29,
Петерсон, Учебник, часть 2
Страница 9. Урок 5,
Петерсон, Учебник, часть 3
Страница 29. Урок 15,
Петерсон, Учебник, часть 3
Страница 37. Урок 19,
Петерсон, Учебник, часть 3
2 класс
Страница 40,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 53,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 73,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 52,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 8. Урок 2,
Петерсон, Учебник, часть 2
Страница 20. Урок 6,
Петерсон, Учебник, часть 2
Страница 63. Урок 25,
Петерсон, Учебник, часть 2
Страница 108. Урок 44,
Петерсон, Учебник, часть 2
Страница 57. Урок 20,
Петерсон, Учебник, часть 3
Страница 71. Урок 26,
Петерсон, Учебник, часть 3
3 класс
Страница 25,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 100,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 108,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 28,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 16,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 27. Урок 9,
Петерсон, Учебник, часть 1
Страница 84. Урок 30,
Петерсон, Учебник, часть 1
Страница 9. Урок 4,
Петерсон, Учебник, часть 2
Страница 12. Урок 5,
Петерсон, Учебник, часть 3
4 класс
Страница 94,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 20,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 21,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 22,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 50,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 67,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 16,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 31,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 48,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 4. Урок 2,
Петерсон, Учебник, часть 1
5 класс
Задание 936,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 939,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 255,
Мерзляк, Полонский, Якир, Учебник
Номер 258,
Мерзляк, Полонский, Якир, Учебник
Номер 260,
Мерзляк, Полонский, Якир, Учебник
Номер 291,
Мерзляк, Полонский, Якир, Учебник
Номер 929,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 1006,
Мерзляк, Полонский, Якир, Учебник
Номер 1100,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Задание 699,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 705,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1127,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1153,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 4,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 259,
Мерзляк, Полонский, Якир, Учебник
Номер 316,
Мерзляк, Полонский, Якир, Учебник
Номер 480,
Мерзляк, Полонский, Якир, Учебник
Номер 481,
Мерзляк, Полонский, Якир, Учебник
Номер 906,
Мерзляк, Полонский, Якир, Учебник
Номер 1040,
Мерзляк, Полонский, Якир, Учебник
Номер 1071,
Мерзляк, Полонский, Якир, Учебник
Номер 1139,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 46,
Мерзляк, Полонский, Якир, Учебник
Номер 47,
Мерзляк, Полонский, Якир, Учебник
Номер 229,
Мерзляк, Полонский, Якир, Учебник
Номер 391,
Мерзляк, Полонский, Якир, Учебник
Номер 392,
Мерзляк, Полонский, Якир, Учебник
Муниципальное бюджетное образовательное
учреждение
средняя общеобразовательная школа № 37
Урок
математики по теме
«
Вычисление значений выражений.
Решение
задач»
(3
класс)
Разработала
Каплун Анна Ивановна,
учитель
начальных классов
Смоленск,
2013
Урок разработан с учётом требований
Федерального государственного стандарта нового поколения по учебнику Н.Б.
Истоминой «Математика» образовательной системы «Гармония».
На протяжении всего урока с учащимися ведётся работа по усвоению правил порядка
выполнения действий в числовых выражениях, совершенствованию умения решать
задачи, записывать решение задач выражением, применяя правила порядка
выполнения действий. 4 вида заданий было дано
дифференцированно, с учётом подготовленности учащихся. Учащиеся имели
возможность выбора. Задания были ориентированы на формирование у учащихся УУД
(личностных, познавательных, регулятивных, коммуникативных).
Реализовать поставленные цели урока помогает активное использование средств
ИКТ (компьютера, медиа – проектора, презентации Power Point со слайдами).
Деятельность
учащихся
Находить сходство и
различие в числовых выражениях.
Выбирать числовые
выражения, соответствующие правилу, и правило, соответствующее числовому
выражению.
Вычислять значения числовых
выражений.
Расставлять порядок выполнения
действий в схеме числового выражения.
Вставлять пропущенные числа
в схему числовых выражений.
Применять полученные знания
для решения задач
Планируемые результаты
Планировать свои действия в соответствии с
поставленной задачей (Р)
Вносить необходимые коррективы в действие
после его завершения на основе его оценки и учёта характера сделанных ошибок
(Р)
Ставить новые учебные задачи в
сотрудничестве с учителем (Р)
Выделять существенную информацию из
текстов задач, из формулировок учебных заданий (П)
Осуществлять анализ объектов с выделением
существенных и несущественных признаков (П)
Осуществлять синтез как составление целого
из частей (П)
Проводить сравнение и классификацию по
заданным критериям (П)
Строить рассуждение в форме связи простых
суждений об объекте (П)
Обобщать (П)
Устанавливать соответствие предметной и
символической модели (П)
Допускать возможность различных точек
зрения (К)
Учитывать разные мнения и стремиться к
координации различных позиций в сотрудничестве (К)
Формулировать собственное мнение и позицию
(К)
Строить понятные для партнёра высказывания
(К)
Задавать вопросы (К)
Контролировать действия партнёра (К)
Использовать речь для регуляции своего
действия (К)
Пробудить
познавательную активность (Л)
Воспитывать толерантное отношение друг к другу
(Л)
Тема:
Вычисление значений выражений. Решение задач
Тип урока:
урок комплексного применения знаний и умений (урок закрепления)
ТДЦ:
-продолжить
работу по усвоению правил порядка выполнения действий в числовых выражениях;
-совершенствовать
умение решать задачи, записывать решение задач выражением, применяя правила
порядка выполнения действий;
-строить
рассуждения, устанавливать причинно-следственные связи, обобщать;
-формировать
любознательность, трудолюбие и познавательный интерес к учебному предмету
«Математика»
Оборудование: учебник, рабочая
тетрадь, часть 1, тетрадь «Учимся решать задачи», компьютер, медиа – проектор,
презентация Power Point со слайдами, карточки «Математическое лото», карточки –
схемы выражений
Ход
урока.
I.
Организация класса, эмоциональный настрой на урок
Цель: создать на уроке рабочую,
психологически комфортную
обстановку.
Громко
прозвенел звонок —
Начинается урок.
Наши ушки на макушке,
Глазки широко открыты.
Слушаем, запоминаем,
Ни минуты не теряем.
Давайте
улыбнёмся друг другу. Пусть сегодняшний урок принесёт всем радость общения друг
с другом!
II.
Актуализация опорных знаний и умений
Цель:
организовать актуализацию изученных способов действий, достаточных для
осуществления последующей деятельности учащихся на уроке, мотивировать к
выполнению учебного действия
-Поиграем в математическое лото, повторим
ранее изученные понятия и способы действий. Постарайтесь их запомнить, они
помогут нам определить тему сегодняшнего урока.
|
10 лет |
Какое математическое выражение |
|
Выражение, в котором несколько |
12 : 4 и 12 : 4 + 8 Выбери сложное выражение |
|
12 : 4 + 8 (к |
Как выражение превратить в равенство? |
|
Добавить знак (=) равно |
В выражениях без скобок, |
|
По порядку слева направо |
В выражениях без скобок, |
|
В выражениях без скобок сначала слева направо выполняются по |
В выражениях со скобками, |
|
В выражениях со скобками сначала вычисляют значения в скобках. |
Какое арифметическое действие надо 3 + 16 : 8? (к |
|
Деление |
Какое арифметическое действие надо |
|
Умножение |
Уменьшить 75 на 25, значит … |
|
Найти разницу между числами (75 – 25) |
Увеличить 7 |
|
Повторить 7 три раза (7 · 3) |
Уменьшить 40 в |
|
40 разделить на 8 равных частей и взять одну часть |
Как |
|
Нужно узнать, сколько раз меньшее число |
Уменьши 48 в |
|
Получится 8 |
Уменьши |
|
Получится 2 дм |
Увеличь 34 на 6 |
|
Получится 40 |
Увеличь 10 в 5 раз. |
|
Получится 50 |
Какое |
|
32 |
Во сколько раз 27 больше 9? |
|
В 3раза |
Увеличь 0 в 9 раз |
|
Получится 0 |
60 увеличь на 3 десятка |
|
Получится 90 |
На сколько 12 меньше 70? |
|
На 58 |
В первом слове букв столько же, сколько |
|
9 букв |
Папа старше сына в 4 раза. Сколько лет |
III. Сообщение темы, цели урока
Цель:
организация деятельности учащихся по определению темы урока и постановки
учебных задач
–
Какие математические понятия встретились? (сложное выражение, порядок
действий, правила порядка выполнения действий, отношения…, задача). Как вы
думаете, какова же тема нашего сегодняшнего урока?
Тема:
Вычисление значений выражений. Решение задач (Слайд 1)
Какие
учебные задачи мы с вами поставим? Чему будем сегодня учиться? (Слайд 2)
учиться
вычислять значения сложных числовых выражений, опираясь на правила; проверить
себя
учиться
решению задач
совершенствовать
вычислительные навыки
учиться
трудиться вместе, оценивать себя и своего товарища
–
Задачи серьёзные, но решаемые. Приступим
IV.
Закрепление изученного материал
Цель:
включение учащихся в деятельность не только по воспроизведению, но и по
оперированию знаниями, включение новых знаний в систему ранее изученного
а)
Откройте учебники, с.108, №327, прочитайте глазами задание до схемы и выполните
его на карточке:
![]()
![]()
![]()
![]()
![]() 1) · · + ( ( + ) –
1) · · + ( ( + ) –
2) 3)
1) 4)
2)
Читайте задание 1-го синего кружка, у кого есть вариант ответа? Запишите его в
рабочую тетрадь и вычислите значение
20
42 22
3)
5 ·
4
+ (3 + 19) – 10 = 32 (запишите в тетрадь)
2) 3) 1) 4)
4) Обменяйтесь
тетрадями, проверьте правильность выполнения задания,
оцените на полях (Слайд 3)
5) Прочитайте задание второго синего
кружка. Всем ли понятно? Выполняйте
на карточке, можно несколько
вариантов
6) Кто справится первым пойдёт к доске и
запишет свой вариант.
Кто затрудняется, вычислите значение
выражения за скобкой 1) = 44
б)
Продолжим учиться вычислять значения сложных выражений
1) Откройте печатную
тетрадь, с.73, №134, прочитайте глазами задание,
включая задание синего кружка,
выполнять будем по вариантам.
Пометьте галочкой: 1в. – а), б) 22, 65 (ответы на доске,
закрыты)
2в.
– в), г) 65. 44
2) Дополнительно: д), е) 302, 16
3) Обменяйтесь тетрадями, проверьте
правильность выполнения задания,
оцените
в) физкультминутка
г)
Вспомните учебную задачу: проверить себя. Думаю, вы достаточно
поупражнялись для того, чтобы справиться с самостоятельной работой. Задание
№329 учебника
Пометьте галочкой: 1в. – 1)
2в. – 2)
Ребятам 1–й группы необходимо найти
значение выражения 3)
д)
Итак, вспомните все выполненные задания. Какие учебные задачи решали? учиться
вычислять значения сложных числовых выражений, опираясь на правила
совершенствовать вычислительные навыки
учиться трудиться вместе, оценивать себя и
своего товарища
е)
Какую ещё важную учебную задачу ставили в начале урока? (Учиться решать
задачи)
Задание №328 учебника, схема 1. Почему не
2? (Слайд 4)
Ребята 1-й группы, записывайте решение
задачи любой формой (по действиям или выражением). После записи решения
выполняйте задание под схемами, записывайте решение других задач, устно
рассказы сюжетов задач мы послушаем позже)
Ребята 2-й группы побеседуют со мной. Кто
пойдёт к доске, закончит рисунок схемы? (на доске)
(Что значит в 3 раза больше? Сколько ? на
чертеже знаков ?, сколько действий в задаче?, на какой первый вопрос ответим?
Что он обозначает?, запишите, что напишем в пояснении?, какое действие
отображается фигурной скобкой?, запишите
Кто запишет решение выражением?
1) 7
· 3 = 21 (с.) – за 2 день.
2) 7
+ 21 = 28 (с.)
7 + 7 · 3 = 28 (с.) Ответ: 28
страниц он прочитал за 2 дня.
– Ребята 1-й группы можете сверить решение
основной задачи
– Кто записал решение задачи в форме
выражения?
– Кто решил задачу другим способом? 7·
(1+3) = 28(с.)
Сюжеты других задач (устно)
ж) физкультминутка (Слайд 5)
з)
Задание №331 учебника, схема 1. Почему не 2? Кто знает как решить задачу?
Почему 24 : 3? Откуда вы взяли число 3? Его же нет в данных? (24 года это 3
равные части, тогда 1 – 24 : 3= 8. И эта 1 часть равна возрасту дочери, значит
ей 8 лет.
24 : 3 = 8 (л.)
Ответ: 8 лет дочери.
и) Ребята 1-й группы с. 38 № 55 задачника «Учимся решать задачи»
Ребята 2- группы с.109 учебника, №330
Прочитайте задачу, нарисуйте схему
(схема в одну линию или в три?)
Во сколько раз 1-е слово короче 3-его?,
2-е 3-его? Почему в 2 раза? (Чтобы найти во сколько раз одно число больше или
меньше другого, нужно посмотреть сколько раз меньшее число укладывается в
большем, т.е. надо большее число разделить на меньшее). Это поможет вам решить
задачу дома
Ребята первой группы сдадут на проверку
задачники
к)
Итак, какую учебную задачу решали?
учились решать задачи (учились читать
задачи, выбирать схемы к условию задачи, записывать пояснения, выбирать форму
записи решения, учились составлять текст задачи по заданной схеме, упражнялись
в вычислениях)
V. Подведение итогов
урока, домашнее задание
Цель:
сообщение результата решения учебных задач урока, организация обсуждения и
записи домашнего задания
– Тема урока…, задачи урока…, Удалось ли
их решить?
Я согласна, удалось!
Дом. задание: С.109, №330 (у.), с.74 №135
(т) (Слайд 6)
VI. Рефлексия
Цель:
осознание учащимся личного вклада в общую деятельность
Мне на уроке было… (Слайд 7)
Я трудился (лась)…
Я доволен (льна) собой!
Спасибо за урок! (Слайд 8)
![]()
Математика. 3-й класс. Задание:
Где это возможно вычисли выражения другим способом.
(36+34):7=10
(30+24):9=6
(40+16):8=7
(42+24):6=11
(30+26):8=7
(23+22):5=9
Как вычислить выражения другим способом?
![]()
В этом задании лишь третье и четвертое выражение можно вычислить другим способом, а именно раскрыв скобки, так как оба слагаемых в скобках делятся на делитель.
Ответ:
(36+34):7=49 здесь мы можем исправить лишь неверный ответ на верный: (36+34):7=10
(30+24):9=81 и здесь мы можем исправить лишь неверный ответ на верный: (30+24):9=6
(40+16):8=7 решаем другим способом: (40+16):8= 40:8+16:8= 5+2=7
(42+24):6=11 решаем другим способом: (42+24):6= 42:6+24:6= 7+4=11
(30+26):8=7 оставляем без изменений
(23+22):5=9
автор вопроса выбрал этот ответ лучшим
Rafail
[136K]
4 года назад
Непонятно, чего же хочет автор вопроса?
Я например, под “другим способом” понимаю что нужно что-то изменить, чтобы легче было считать, меньше вычислений. Ну и, предполагаю, что таблица умножения школьником усвоена “назубок”.
Рассмотрим первый пример с подробными комментариями:
Если мы 36 представим как 35+1, а затем 1+34 как 35, то получается намного быстрее и проще считать “в уме”.
(36+34):7=10;
(35+1+34):7=10;
(35+(1+34)):7=10;
(35+35):7=10;
5+5=10;
(30+24):9=6;
(27+3+24):9=6;
(27+27):9=6;
3+3=6;
Ну, и аналогично с остальными заданиями. Смысл в том, что вместо представленного в исходных заданиях разложения суммы на “неудобные числа” можно путём несложных вычислений разложить эти суммы на “удобные числа”, т.е. кратные делителю.
Озермас
[335]
4 года назад
Смотря где вам это нужно. В первых 2 выражениях нет ответа, августа дальнейших смотря на то,что вам нужно найти. В вопросе не уточняется что нужно вычислитт другим способом,поэтому покажу так,как меня учили.
1)Если ваше равенство справедливо, то скорее всего вам нужно найти один из неизвестных членов выражения. Пусть это будет “(40+16)”.
Тогда:
Используя таблицу умножения мы находим его. Т.е. нам нужно 7*8. Получим 56. Если сложить 40 и 16 ,то тоже будет 56,но я показал другим способом. Следовательно:
Берём выражение:
(40+16):8=7
Найдём 40+16:
40+16=7*8
40+16=56
56=56(верно)
Если я неправильно понял, то объясните, пожалуйста, а так пользуйтесь этим аналогично для других примеров
Викторина Рассказова
[97.7K]
4 года назад
Если это задание для 3его класса, то дроби наверняка еще не проходят. Но детям объяснили, что если каждое слагаемое в скобках разделить на делитель, а потом сложить, то так можно тоже получить правильный ответ.
пример № 3: (40+16):8=7 или так 40:8=5, 16:8=2 в сумме 5+2=7; пример №4 (42+24):6=11 или так 42:6=7, 24:6=4 в сумме 7+4=11.
Все остальные примеры без дробей не решаются.
Валентина МД
[33.2K]
4 года назад
В вопросе указано, где возможно вычисли выражения другим способом.
Другим способом можно вычислить только два выражения из указанных в вопросе (под №3 и №4):
(40 + 16):8 =7 другой способ 40:8 + 16:8 =7;
(42 = 24):6 =11 другой способ 42:6 + 24:6 =11.
Другие выражения нельзя вычислить другим способом.
Лембит
[54.5K]
4 года назад
Другим способом, это как, особенно с учётом того, что ответы в первых двух выражениях у вас неправильные.?
Если не заниматься откровенными извращениями, то единственный “другой способ”, это только раскрыть скобки. Но тогда придётся складывать иррациональные числа. Откройте учебник математики и почитайте, что же от вас требуют и что это за “другой способ”. А нам остаётся только гадать
Знаете ответ?
