Электрон ( ) ) |
|
|---|---|
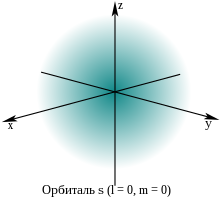
 Вероятностная картина местоположения единственного электрона в атоме на s-орбитали |
|
| Состав | фундаментальная частица |
| Семья | Фермион |
| Группа | Лептон |
| Участвует во взаимодействиях | гравитационное[1], слабое и электромагнитное |
| Античастица | Позитрон |
| Масса |
9,1093837015(28)⋅10−31 кг[2], 5,48579909065(16)⋅10-4 а.е.м.[2] |
| Время жизни | ∞ (не менее 6,6⋅1028 лет[3][4]) |
| Квантовые числа | |
| Электрический заряд | −1,602176634⋅10−19 Кл[2] |
| Барионное число | 0 |
| Лептонное число | +1 |
| Спин | 1/2 ħ |
| Магнитный момент | −9,2847647043(28)⋅10−24 Дж/Тл[2] |
| Внутренняя чётность | +1 |
| Изотопический спин | 0 |
Электро́н (от др.-греч. ἤλεκτρον «янтарь»[5]) — субатомная частица (обозначается символом e−
или β−
), чей электрический заряд отрицателен и равен по модулю одному элементарному электрическому заряду[6]. Электроны принадлежат к первому поколению лептонных частиц[7] и обычно считаются фундаментальными частицами, поскольку у них нет известных компонентов или субструктур[8]. Электрон имеет массу, которая составляет приблизительно 1/1836[en] массы протона[9]. Квантово-механические свойства электрона включают собственный угловой момент (спин) полуцелого значения, выраженного в единицах приведённой постоянной Планка, ħ, что делает их фермионами. В связи с этим никакие два электрона не могут занимать одно и то же квантовое состояние в соответствии с принципом запрета Паули[7]. Как и все элементарные частицы, электроны обладают свойствами как частиц, так и волн: они могут сталкиваться с другими частицами и могут дифрагировать как свет. Волновые свойства электронов легче наблюдать экспериментально, чем свойства других частиц, таких как нейтроны и протоны, потому что электроны имеют меньшую массу и, следовательно, большую длину волны де Бройля для равных энергий.
Электроны играют существенную роль во многих физических явлениях, таких как электричество, магнетизм, химия и теплопроводность, а также участвуют в гравитационных, электромагнитных и слабых взаимодействиях. Поскольку электрон имеет заряд, его окружает электрическое поле, и если этот электрон движется относительно наблюдателя, то наблюдатель увидит также магнитное поле. Электромагнитные поля, создаваемые другими источниками, будут влиять на движение электрона в соответствии с законом Лоренца. Электроны излучают или поглощают энергию в виде фотонов при ускоренном движении. Лабораторные приборы способны улавливать отдельные электроны, а также электронную плазму с помощью электромагнитных полей. Специальные телескопы наблюдают электронную плазму в космическом пространстве. Свойства электронов используются во многих технологических процессах, приборах и устройствах, таких как трибология, электролиз, электрохимия, аккумуляторные технологии, электроника, сварка, электронно-лучевые трубки, фотоэлектричество, солнечные панели, электронные микроскопы, лучевая терапия, лазеры, детекторы на основе ионизации газов[en] и ускорители частиц.
Взаимодействия электронов с другими субатомными частицами представляют интерес в химии и ядерной физике. Кулоновское взаимодействие между положительно заряженными протонами внутри атомных ядер и отрицательно заряженными электронами позволяет образовать из них атомы. Ионизация или различия в пропорциях отрицательного заряда электронов по сравнению с положительными зарядами ядер изменяют энергию связи атомной системы. Обмен или совместное использование электронов между двумя или более атомами является основной причиной химической связи[10]. В 1838 году британский естествоиспытатель Ричард Лэминг[en] впервые выдвинул гипотезу о неделимом количестве электрического заряда для объяснения химических свойств атомов[11]. Ирландский физик Джордж Джонстон Стони назвал этот заряд «электроном» в 1891 году, а Дж. Дж. Томсон и его команда британских физиков идентифицировали его как частицу в 1897 году во время эксперимента с электронно-лучевой трубкой. Электроны также могут участвовать в ядерных реакциях при нуклеосинтезе в звёздах, где они известны как бета-частицы. Электроны могут образовываться в результате бета-распада радиоактивных изотопов и при высокоэнергетических столкновениях, например, когда космические лучи попадают в атмосферу. Античастица электрона называется позитроном; он идентичен электрону, за исключением того, что несёт положительный электрический заряд. Когда электрон сталкивается с позитроном[en], обе частицы могут аннигилировать, создавая фотоны гамма-излучения.
История[править | править код]
Открытие эффекта электрической силы[править | править код]
Древние греки заметили, что янтарь притягивает мелкие предметы, когда его натирают мехом. Наряду с молнией, это явление оказалось одним из самых ранних зарегистрированных опытов человечества с электричеством. В своём трактате 1600 г. De Magnete[en], английский учёный Уильям Гилберт ввёл новый латинский термин electrica, для обозначения тех веществ, которые обладают свойствами, подобными янтарю, которые притягивают мелкие предметы после трения[12]. Слова электрический, и электричество происходят от латинского ēlectrum (также корень одноимённого сплава), который произошёл от греческого слова для янтаря, ἤλεκτρον (ēlektron)[5].
Открытие двух видов зарядов[править | править код]
В начале 1700-х годов французский химик Шарль Франсуа Дюфе обнаружил, что если заряженный лист золота отталкивается стеклом, натёртым шёлком, то такой же заряженный лист золота притягивается янтарём, натёртым шерстью. Из этого и других результатов подобных экспериментов Дюфе сделал вывод, что электричество состоит из двух электрических жидкостей: стекловидного тела из стекла, натёртого шёлком, и смолистого флюида из янтаря, натёртого шерстью. Эти две жидкости могут нейтрализовать друг друга при объединении[12][13]. Американский ученый Эбенезер Киннерсли позже независимо пришёл к такому же выводу[14]:118. Десять лет спустя Бенджамин Франклин предположил, что электричество происходит не из разных типов электрической жидкости, а из одной электрической жидкости, демонстрирующей избыток (+) или дефицит (-). Он дал им современную номенклатуру зарядов положительных и отрицательных соответственно[15]. Франклин считал носитель заряда положительным, но он неправильно определил, в какой ситуации был избыток носителя заряда, а в какой — дефицит[16].
Между 1838 и 1851 годами британский естествоиспытатель Ричард Лэминг разработал идею о том, что атом состоит из ядра материи, окружённого субатомными частицами, имеющими единичный электрический заряд[17]. Начиная с 1846 года немецкий физик Вильгельм Эдуард Вебер предположил, что электричество состоит из положительно и отрицательно заряженных жидкостей, а их взаимодействие регулируется законом обратных квадратов. Изучив явление электролиза в 1874 году, ирландский физик Джордж Стони предположил, что существует «одно определённое количество электричества» — заряд одновалентного иона. Он смог оценить значение этого элементарного заряда e с помощью законов электролиза Фарадея[18]. Однако Стони считал, что эти заряды постоянно связаны и неотделимы от атомов. В 1881 году немецкий физик Герман фон Гельмгольц утверждал, что как положительные, так и отрицательные заряды делятся на элементарные части, каждая из которых «ведёт себя как атомы электричества»[11].
Стони впервые ввёл термин «электролион» в 1881 году. Десять лет спустя он стал использовать термин электрон, чтобы описать эти элементарные заряды, написав в 1894 году: «…была сделана фактическая оценка значения этой наиболее замечательной фундаментальной единицы электричества, для которой я с тех пор осмелился предложить название электрон». Предложение 1906 года перейти на электрион не прижилось, потому что Хендрик Лоренц предпочёл сохранить название электрон[19][20]. Слово электрон представляет собой сочетание английских слов electric и ion[21]. Суффикс -on в настоящее время также используется для обозначения других субатомных частиц, таких как протон или нейтрон[22][23].
Открытие свободных электронов вне материи[править | править код]
Пучок электронов, отклоняемый по окружности магнитным полем<[24].
Изучая электропроводность в разреженных газах в 1859 году, немецкий физик Юлиус Плюккер заметил, что излучение, испускаемое катодом, вызывает появление фосфоресцентного света на стенке трубки возле катода; а пятно излучения можно перемещать с помощью магнитного поля[25]. В 1869 году ученик Плюккера Иоганн Вильгельм Гитторф обнаружил, что твёрдое тело, помещённое между катодом и фосфоресценцирущей поверхностью, будет отбрасывать тень на эту область трубки. Гитторф предположил, что катод испускает прямые лучи и, что фосфоресценция вызвана лучами, падающими на стенки трубки. В 1876 году немецкий физик Ойген Гольдштейн показал, что лучи испускаются перпендикулярно поверхности катода, что отличает их от света лампы накаливания. Гольдштейн назвал эти лучи катодными лучами[26][27]:393.
В 1870-х годах английский химик и физик сэр Уильям Крукс разработал первую электронно-лучевую трубку с высоким вакуумом внутри[28]. Затем в 1874 году он показал, что катодные лучи могут вращать маленькое гребное колесо, когда оно находится на их пути. Поэтому он пришёл к выводу, что лучи несут импульс. Более того, приложив магнитное поле, он смог отклонить лучи, тем самым продемонстрировав, что луч ведёт себя так, как если бы он был заряжен отрицательно[26]. В 1879 году он предложил объяснение этих наблюдений, рассматривая катодные лучи как состоящие из отрицательно заряженных газообразных молекул в четвёртом состоянии вещества, при котором длина свободного пробега частиц настолько велика, что столкновениями можно пренебречь[27]:394–395.
Британский физик немецкого происхождения Артур Шустер расширил эксперименты Крукса, поместив металлические пластины параллельно катодным лучам и приложив электрический потенциал между пластинами[29]. Поле отклоняло лучи к положительно заряженной пластине, что ещё раз свидетельствовало о том, что лучи несут отрицательный заряд. Измерив величину отклонения для заданного уровня тока, в 1890 году Шустер смог оценить отношение заряда к массе[en][a] компонент луча. Однако это дало значение, которое более чем в тысячу раз превышало ожидаемое, поэтому в то время его расчётам не доверяли[26]. Это связано с тем, что предполагалось, что носителями заряда являются гораздо более тяжёлые атомы водорода или азота[29].
В 1892 году Хендрик Лоренц предположил, что масса этих частиц (электронов) может быть следствием их электрического заряда[30].
Изучая естественно флуоресцирующие минералы в 1896 году, французский физик Анри Беккерель обнаружил, что они испускают излучение без какого-либо воздействия внешнего источника энергии. Эти радиоактивные материалы стали предметом большого интереса учёных, в том числе новозеландского физика Эрнеста Резерфорда, обнаружившего, что они испускают частицы. Он назвал эти частицы альфа и бета на основании их способности проникать сквозь материю[31]. В 1900 году Беккерель показал, что бета-лучи, испускаемые радием, отклоняются электрическим полем, и что отношение их массы к заряду такое же как и у катодных лучей[32]. Это свидетельство укрепило мнение о том, что электроны входят в состав атомов[33][34].
Десятилетия экспериментальных и теоретических исследований с использованием катодных лучей сыграли важную роль в окончательном открытии Дж. Дж. Томсоном электронов[11]. В 1897 году Томсон вместе со своими коллегами Джоном С. Таунсендом и Х. А. Уилсоном[en] провёл опыты, показавшие, что катодные лучи действительно представляют собой новые частицы, а не волны, атомы или молекулы, как считалось ранее. Томсон дал хорошие оценки как заряда e, так и массы m, обнаружив, что частицы электронных лучей, которые он назвал «корпускулами», имеют, возможно, одну тысячную часть массы наименее массивного из известных ионов: иона водорода. Он показал, что их отношение заряда к массе, e/m, не зависит от материала катода. Далее он показал, что отрицательно заряженные частицы, создаваемые радиоактивными материалами, нагретыми материалами и освещёнными материалами, обладали универсальностью[35]. Название «электрон» было принято для этих частиц научным сообществом, в основном благодаря поддержке Дж. Фитцджеральда, Дж. Лармора и Х. А. Лоренца[36]:273. В том же году Эмиль Вихерт и Вальтер Кауфманн также рассчитали отношение e/m, но им не удалось интерпретировать свои результаты, в то время как Дж. Дж. Томсон впоследствии в 1899 году дал оценки также для заряда и массы электрона: e ~ 6,8⋅10-10 Фр. и m ~ 3⋅10-26 г[37][38].
Заряд электрона более тщательно измерили американские физики Роберт Милликен и Харви Флетчер[en] в их эксперименте с каплей масла в 1909 году, результаты которого были опубликованы в 1911 году. В этом эксперименте использовалось электрическое поле, чтобы скомпенсировать падение заряженной капли масла под действием силы тяжести. Их установка позволяла измерять электрический заряд от 1 до 150 ионов с погрешностью менее 0,3 %. Сопоставимые эксперименты были проведены ранее группой Томсона с использованием облаков из заряженных водных капель, полученных электролизом, и в 1911 году Абрамом Иоффе, который независимо получил тот же результат, что и Милликен, используя заряженные микрочастицы металлов, а затем опубликовал свои результаты в 1913 году[39]. Однако капли масла были более стабильны, чем капли воды, из-за их более низкой скорости испарения и, следовательно, больше подходили для точных экспериментов в течение более длительного времени[40].
Примерно в начале XX века выяснилось, что быстро движущаяся заряженная частица при определённых условиях вызывает на своём пути конденсацию пересыщенного водяного пара. В 1911 году Чарльз Вильсон использовал этот принцип для разработки своей камеры Вильсона для фотографирования следов заряженных частиц, таких как быстро движущиеся электроны[41].
Атомная теория[править | править код]
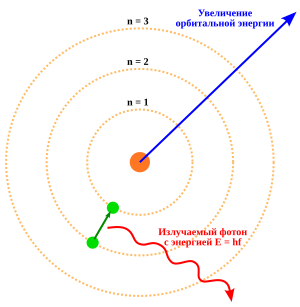
Модель атома Бора, показывающая состояния электрона с энергией, квантованной согласно натуральному числу n. Электрон, переходящий на более низкую орбиту, излучает фотон, равный разности энергий между орбитами.
К 1914 году эксперименты физиков Эрнеста Резерфорда, Генри Мозли, Джеймса Франка и Густава Герца в значительной степени установили структуру атома как плотного ядра с положительным зарядом, окружённого электронами меньшей массы[42]. В 1913 году датский физик Нильс Бор постулировал, что электроны находятся в квантованных энергетических состояниях, а их энергия определяется угловым моментом орбиты электрона вокруг ядра. Электроны могут перемещаться между этими состояниями или орбитам, испуская или поглощая фотоны определённых частот. С помощью этих квантованных орбит он точно объяснил спектральные линии атома водорода[43]. Однако модель Бора не смогла учесть относительную интенсивность спектральных линий и не смогла объяснить спектры более сложных атомов[42].
Химические связи между атомами были объяснены Гилбертом Ньютоном Льюисом, который в 1916 году предположил, что ковалентная связь между двумя атомами поддерживается парой общих электронов[44]. Позже, в 1927 году, Вальтер Гайтлер и Фриц Лондон дали полное объяснение образования электронной пары и химической связи с точки зрения квантовой механики[45]. В 1919 году американский химик Ирвинг Ленгмюр разработал статическую модель атома Льюиса и предположил, что все электроны распределены в последовательных «концентрических (почти) сферических оболочках одинаковой толщины»[46]. В свою очередь, он разделил оболочки на ряд ячеек, каждая из которых содержала по одной паре электронов. С помощью этой модели Ленгмюр смог качественно объяснить химические свойства всех элементов периодической таблицы[45], которые, как известно, в значительной степени повторяются в соответствии с периодическим законом[47].
В 1924 году австрийский физик Вольфганг Паули заметил, что оболочечную структуру атома можно объяснить набором четырёх параметров, определяющих каждое квантовое энергетическое состояние, если каждое состояние занято не более чем одним электроном. Этот запрет на нахождение более чем одного электрона в одном и том же квантовом состоянии стал известен как принцип запрета Паули[48]. Физический механизм для объяснения четвёртого параметра, который имел два различных возможных значения, был предложен голландскими физиками Сэмюэлем Гаудсмитом и Джорджем Уленбеком. В 1925 году они предположили, что электрон, помимо углового момента своей орбиты, обладает собственным угловым моментом и магнитным дипольным моментом[en][42][49]. Это аналогично вращению Земли вокруг своей оси, когда она вращается вокруг Солнца. Собственный угловой момент стал известен как спин и объяснил ранее загадочное расщепление спектральных линий, наблюдаемое с помощью спектрографа высокого разрешения; это явление известно как расщепление тонкой структуры[50].
Квантовая механика[править | править код]
В своей диссертации 1924 года Recherches sur la théorie des quanta (Исследования по квантовой теории) французский физик Луи де Бройль выдвинул гипотезу, что вся материя может быть представлена в виде волны, названную позже волной де Бройля на манер света[51]. То есть при соответствующих условиях электроны и другая материя проявляли бы свойства либо частиц, либо волн. Корпускулярные свойства частицы демонстрируются, когда показано, что она имеет локализованное положение в пространстве вдоль своей траектории в любой данный момент времени[52]. Волнообразная природа света проявляется, например, когда луч света проходит через параллельные щели, создавая интерференционные картины. В 1927 году Джордж Пэджет Томсон обнаружил, что эффект интерференции возникает, когда пучок электронов проходит через тонкую металлическую фольгу, а американские физики Клинтон Дэвиссон и Лестер Джермер — путём отражения электронов от монокристалла никеля[53].
В квантовой механике поведение электрона в атоме описывается орбиталью, которая представляет собой распределение вероятностей, а не орбиту. На рисунке штриховка указывает на относительную вероятность «найти» электрон, имеющий энергию, соответствующую данным квантовым числам, в этой точке.
Предсказание де Бройля о волновой природе электронов привело Эрвина Шрёдингера к постулированию волнового уравнения для электронов, движущихся под влиянием ядра в атоме. В 1926 году его уравнение, уравнение Шредингера, успешно описало, как распространяются электронные волны[54]. Волновое уравнение не даёт решение в виде зависимости положения электрона от времени, но предсказывает вероятности нахождения электрона в окрестности точки, особенно для систем, где электрон привязан к пространству посредством потенциальной ямы, для которой электронные волновые уравнения не меняются во времени. Этот подход привёл ко второй формулировке квантовой механики (первая формулировка квантовой теории в виде матричной механики предложена Гейзенбергом в 1925 году), а решения уравнения Шрёдингера, как и уравнения Гейзенберга, позволяют получить энергетические состояния электрона в атоме водорода, которые оказались эквивалентны впервые полученным Бором в 1913 году выражениям и воспроизводили спектр атома водорода[55]. Как только стало возможно описать спин и взаимодействие между несколькими электронами, квантовая механика позволила предсказать конфигурацию электронов в атомах с атомными номерами больше, чем у водорода[56].
В 1928 году, основываясь на работе Вольфганга Паули, Поль Дирак создал модель электрона — уравнение Дирака, согласующуюся с принципом относительности, путём применения соображений специальной теории относительности и симметрии к гамильтоновой формулировке квантовой механики электромагнитного поля[57]. Чтобы решить некоторые проблемы в рамках своего релятивистского уравнения, Дирак разработал в 1930 году модель вакуума как бесконечного моря частиц с отрицательной энергией, позже названного морем Дирака. Это привело его к предсказанию существования позитрона, аналога электрона из антивещества[58]. Эта частица была открыта в 1932 году Карлом Андерсоном[59].
В 1947 году Уиллис Лэмб, работая в сотрудничестве с аспирантом Робертом Резерфордом, обнаружил, что определённые квантовые состояния атома водорода, которые должны иметь одинаковую энергию, сдвинуты по отношению друг к другу; эта разница стала называться лэмбовским сдвигом. Примерно в то же время Поликарп Куш, работая с Генри Фоли[en], обнаружил, что магнитный момент электрона несколько больше, чем предсказывает теория Дирака. Эта небольшая разница позже была названа аномальным магнитным дипольным моментом электрона. Это различие вскоре было объяснено теорией квантовой электродинамики, разработанной Синъитиро Томонагой, Джулианом Швингером и Ричардом Фейнманом в конце 1940-х годов[60].
Ускорители частиц[править | править код]
С развитием ускорителей частиц в первой половине двадцатого века физики начали глубже вникать в свойства субатомных частиц[61]. Первую успешную попытку ускорить электроны с помощью электромагнитной индукции предпринял в 1942 году Дональд Керст. Его первоначальный бетатрон достиг энергии 2,3 МэВ, а последующие бетатроны достигли 300 МэВ. В 1947 году в электронном синхротроне компании General Electric было открыто синхротронное излучение с длиной волны 70 МэВ. Это излучение было вызвано ускорением электронов в магнитном поле, когда они двигались со скоростью, близкой к скорости света[62].
При энергии луча 1,5 ГэВ, первым коллайдером частиц высокой энергии был ADONE, который начал работу в 1968 году[63]. Это устройство ускоряло электроны и позитроны в противоположных направлениях, фактически удваивая энергию их столкновения по сравнению с ударом электрона по статической цели[64]. Большой электрон-позитронный коллайдер (LEP) в ЦЕРНе, который работал с 1989 по 2000 год, достиг энергии столкновения 209 ГэВ и сделал важные измерения для Стандартной модели физики элементарных частиц[65][66].
Удержание отдельных электронов[править | править код]
Отдельные электроны теперь можно легко удерживать в сверхмалых (L = 20 нм, W = 20 нм) КМОП-транзисторах, работающих при криогенных температурах в диапазоне −269 °С (4 К) до примерно −258 °С (15 К)[67]. Волновая функция электрона распространяется в решётке полупроводника и незначительно взаимодействует с электронами валентной зоны, поэтому её можно рассматривать в формализме одной частицы, заменяя её массу тензором эффективной массы[68].
Характеристики[править | править код]
Классификация[править | править код]
Стандартная модель элементарных частиц. Электрон (символ e) находится слева.
В Стандартной модели физики элементарных частиц электроны принадлежат к группе субатомных частиц, называемых лептонами, которые считаются фундаментальными или элементарными частицами. Электроны имеют наименьшую массу среди всех заряженных лептонов (или электрически заряженных частиц любого типа) и принадлежат к первому поколению фундаментальных частиц[69]. Второе и третье поколения содержат заряженные лептоны, мюон и тау-лептон, которые идентичны электрону по заряду, спину и взаимодействиям, но более массивны. Лептоны отличаются от других основных составляющих материи, кварков, отсутствием сильного взаимодействия. Все члены лептонной группы — фермионы, потому что все они имеют полуцелый спин; электрон имеет спин 12[70].
Основные свойства[править | править код]
Инвариантная масса электрона составляет примерно 9,109×10−31[en] кг[71] или 5,489⋅10-4 а. е. м. Согласно принципу эквивалентности массы и энергии, это соответствует энергии покоя 0,511 МэВ[en]. Отношение массы протона к массе электрона составляет около 1836[9][72]. Астрономические измерения показывают, что отношение массы протона к массе электрона[en] сохраняло то же значение, как и предсказывает стандартная модель, по крайней мере, в течение половины возраста Вселенной[73].
Электроны имеют электрический заряд −1,602176634⋅10-19 Кл[71], который используется в качестве стандартной единицы заряда для субатомных частиц и также называется элементарным электрическим зарядом. В пределах экспериментальной точности заряд электрона идентичен заряду протона, но с обратным знаком[74]. Поскольку символ e используется для обозначения элементарного заряда, электрон обычно обозначается как e−
, где знак минус указывает на отрицательный заряд. Позитрон обозначается символом e+
, потому что он имеет те же свойства, что и электрон, но с положительным, а не отрицательным электрическим зарядом[70][71].
Электрон имеет собственный угловой момент или спин 12[71]. Это свойство обычно формулируют, называя электрон спин-12[en] частицей[70]. Для таких частиц величина спина равна ħ2[b][75], а результат измерения проекции спина на любую ось может принимать значения только ±ħ2. В дополнение к спину, электрон обладает собственным магнитным моментом, сонаправленным спину[71]. Он приблизительно равен одному магнетону Бора[76][c], что является физической константой, равной (9,27400915 ± (23))⋅10-24 Дж/Т[71]. Ориентация спина по отношению к импульсу электрона (для релятивистских частиц) определяет свойство элементарных частиц, известное как спиральность[77].
Электрон не имеет известной субструктуры[8][78]. Вопрос о радиусе электрона является сложной проблемой современной физики. В экспериментах по рассеянию электронов на позитронах не наблюдается никакого отличия от точечного характера частиц[79]. Внутренняя структура электрона отражалась бы в существовании у него электрического дипольного момента, но такого не было обнаружено[80]. Допущение о конечном радиусе электрона несовместимо с положениями специальной теории относительности. С другой стороны, точечный электрон (нулевой радиус) порождает серьёзные математические трудности из-за стремления собственной энергии[en] электрона к бесконечности[81]. Наблюдение одиночного электрона в ловушке Пеннинга предполагает, что верхний предел радиуса частицы составляет 10−22 метров[82]. Верхнюю границу электронного радиуса 10−18 метров[83] можно получить, используя соотношение неопределённостей с энергией. Существует также физическая константа называемая «классический радиус электрона», с гораздо большим значением 2,8179⋅10-15 м, больше радиуса протона. Однако терминология исходит из упрощённого расчёта, который игнорирует эффекты квантовой механики; в действительности так называемый классический радиус электрона имеет мало общего с истинной фундаментальной структурой электрона[84][d].
Существуют элементарные частицы, которые самопроизвольно распадаются[en] на менее массивные частицы. Примером может служить мюон со средним временем жизни 2,2⋅10-6 секунд, который распадается на электрон, мюонное нейтрино и электронное антинейтрино. С другой стороны, электрон считается стабильным по теоретическим соображениям: электрон является наименее массивной частицей с ненулевым электрическим зарядом, поэтому его распад нарушил бы закон сохранения заряда[85]. Экспериментальная нижняя граница среднего времени жизни электрона составляет 6,6⋅1028 лет при уровне достоверности 90 %[3][86][87].
Квазичастицы[править | править код]
В физике конденсированного состояния, которая имеет дело не с элементарными частицами, а с квазичастичными возбуждениями, в некоторых материалах может происходить разделение спина и заряда. В таких случаях электроны «расщепляются» на три независимые частицы: орбитон, спинон и холон. Электрон всегда можно теоретически рассматривать как связанное состояние из трёх — с орбитоном, несущим орбитальную степень свободы, спиноном, несущим спин электрона и холоном, несущим заряд, но при определённых условиях они могут вести себя как независимые квазичастицы[88][89][90]. В физике твёрдого тела состояние в почти полностью заполненной валентной зоне называется дыркой и несёт положительный заряд. В некотором смысле поведение дырки в полупроводнике похоже на поведение пузырька в полной бутылке с водой[91]. Коллективные колебания свободного электронного газа, отвечающая квантованию плазменных колебаний в металлах и полупроводниках, образуют другие квазичастицы — плазмоны[92].
Квантовые свойства[править | править код]
Как и все частицы, электроны могут вести себя как волны. Это явление называется корпускулярно-волновым дуализмом и его можно продемонстрировать с помощью эксперимента с двумя щелями[93].
Волновая природа электрона позволяет ему проходить через две параллельные щели одновременно, а не только через одну щель, как в случае классической частицы. В квантовой механике волновое свойство одной частицы может быть описано математически как комплекснозначная функция, волновая функция, обычно обозначаемая греческой буквой psi (ψ). Когда абсолютное значение этой функции возводится в квадрат, это даёт вероятность того, что частица будет наблюдаться вблизи определённого места — плотность вероятности[94]:162–218.
Электроны являются неразличимыми частицами, потому что их нельзя отличить друг от друга по присущим им физическим свойствам. В квантовой механике это означает, что пара взаимодействующих электронов должна иметь возможность менять местами без видимого изменения состояния системы. Волновая функция фермионов, включая электроны, антисимметрична, что означает, что она меняет знак, когда два электрона меняются местами; то есть ψ(r1, r2) = −ψ(r2, r1), где переменные r1 и r2 соответствуют первому и второму электронам. Поскольку абсолютное значение не изменяется при замене знака, это соответствует равным вероятностям. Бозоны, такие как фотон, вместо этого имеют симметричные волновые функции[94]:162–218.
В случае антисимметрии решения волнового уравнения для взаимодействующих электронов приводят к нулевой вероятности того, что каждая пара будет занимать одно и то же место или состояние. Это отвечает за принцип запрета Паули, который не позволяет любым двум электронам занимать одно и то же квантовое состояние. Этот принцип объясняет многие свойства электронов. Например, это заставляет группы связанных электронов занимать разные орбитали в атоме, а не перекрывать друг друга, находясь на одной и той же орбите[94]:162–218.
Виртуальные частицы[править | править код]
В упрощённой картине, которая часто имеет тенденцию давать неверное представление, но может служить иллюстрацией некоторых качественных аспектов, каждый фотон проводит некоторое время как комбинация виртуального электрона и его античастицы, виртуального позитрона, которые вскоре после этого быстро аннигилируют друг друга[95]. Комбинация изменения энергии, необходимой для создания этих частиц, и времени, в течение которого они существуют, находятся ниже порога обнаруживаемости, выраженного соотношением неопределённостей Гейзенберга, ΔE · Δт ≥ ħ. По сути, энергию, необходимую для создания этих виртуальных частиц, ΔE, можно «одолжить» у вакуума на период времени Δt, так что их произведение не превышает приведённую постоянную Планка, ħ ≈ 6,6⋅10-16 эВ·с . Таким образом, для виртуального электрона Δt не превышает 1,3⋅10-21 с[96].
Схематическое изображение виртуальных пар электрон-позитрон, случайным образом появляющихся рядом с электроном (внизу слева).
Пока существует виртуальная пара электрон-позитрон, кулоновская сила окружающего электрического поля, вокруг электрона, заставляет созданный позитрон притягиваться к исходному электрону, в то время как созданный электрон испытывает отталкивание. Это вызывает так называемую поляризацию вакуума. Фактически вакуум ведёт себя как среда с диэлектрической проницаемостью больше единицы. Таким образом, эффективный заряд электрона на самом деле меньше его истинного значения, и заряд уменьшается по мере удаления от электрона[97][98]. Эта поляризация была подтверждена экспериментально в 1997 году на японском ускорителе частиц TRISTAN[99]. Виртуальные частицы вызывают эффект экранирования[en], сравнимый с массой электрона[100].
Взаимодействием с виртуальными частицами объясняется также небольшое (около 0,1 %) отклонение собственного магнитного момента электрона от магнетона Бора (аномальный магнитный момент)[76][101]. Чрезвычайно точное совпадение этой предсказанной разницы с экспериментально определённой величиной рассматривается как одно из главных достижений квантовой электродинамики[102].
Кажущийся в классической физике парадокс представления электрона как точечной частицы, обладающий собственным угловым моментом и магнитным моментом, можно объяснить свойствами динамики электрона в электромагнитном поле при переходе к нерелятивистскому пределу, когда электрон смещается в дрожащей манере (zitterbewegung), что приводит к среднему круговому движению с прецессией[103]. Это движение создаёт как спин, так и магнитный момент электрона представляемого как некий протяжённый объект размером с длиной волны Комптона[7][104]. В атомах виртуальные фотоны объясняют лэмбовский сдвиг, наблюдаемый в спектральных линиях. Длина волны Комптона показывает, что рядом с элементарными частицами, такими как электрон, соотношение неопределённости энергии-времени позволяет создавать виртуальные частицы в окрестности электрона. Эта длина волны объясняет «статичность» виртуальных частиц вокруг элементарных частиц на близком расстоянии[97].
Взаимодействие[править | править код]
Электрон создаёт электрическое поле, которое оказывает притяжение на частицу с положительным зарядом, например протон, и вызывает силу отталкивания на частицу с отрицательным зарядом. Величина этой силы в нерелятивистском приближении определяется законом обратных квадратов Кулона[105]: 58-61. Когда электрон движется, он создаёт магнитное поле[94]: 140. Закон Ампера — Максвелла связывает магнитное поле с массовым движением электронов (током) относительно наблюдателя. Это свойство индукции создаёт магнитное поле, которое приводит в движение электродвигатель[106]. Электромагнитное поле произвольно движущейся заряженной частицы выражается потенциалами Льенара — Вихерта, которые правильны, даже когда скорость частицы близка к скорости света (релятивистская)[105]: 429—434.
Частица с зарядом q (слева) движется со скоростью v через магнитное поле B, ориентированное на наблюдателя. Для электрона q отрицательно, поэтому он движется по изогнутой траектории вверх.
Когда электрон движется через пространство в магнитном поле, на него действует сила Лоренца, направленная перпендикулярно плоскости, определяемой магнитным полем и скоростью электрона. Эта центростремительная сила заставляет электрон следовать по винтовой траектории с радиусом, называемым ларморовским радиусом. Ускорение от этого криволинейного движения заставляет электрон излучать энергию в виде синхротронного излучения[107][e][94]: 160. Излучение энергии, в свою очередь, вызывает отдачу электрона, известную как сила Абрахама — Лоренца — Дирака, создающая замедляющее электрон трение. Эта сила вызвана действием собственного поля электрона на самого себя[108].
Здесь тормозное излучение создаётся электроном e, отклоняемым электрическим полем атомного ядра. Изменение энергии E2 − E1 определяет частоту f излучаемого фотона.
Фотоны являются переносчиками электромагнитного взаимодействия между частицами в квантовой электродинамике. Изолированный электрон с постоянной скоростью не может излучать или поглощать реальный фотон; это нарушило бы закон сохранения энергии и импульса. Вместо этого виртуальные фотоны могут передавать импульс между двумя заряженными частицами. Такой обмен виртуальными фотонами порождает кулоновскую силу[109]. Излучение энергии может происходить, когда движущийся электрон отклоняется заряженной частицей, такой как протон. Ускорение электрона приводит к испусканию тормозного излучения[110].
Неупругое столкновение между фотоном (светом) и уединённым (свободным) электроном называется комптоновским рассеянием. Это столкновение приводит к передаче импульса и энергии между частицами, что изменяет длину волны фотона на величину, называемую комптоновским сдвигом. Максимальная величина этого сдвига длины волны равнаh/me c, что известно как длина волны Комптона[111]. Для электрона она имеет значение 2,43⋅10-12 м[71]. Когда длина волны света велика (например, длина волны видимого света составляет 0,4-0,7 мкм) сдвиг длины волны становится незначительным. Такое взаимодействие между светом и свободными электронами называется томсоновским рассеянием или линейным томсоновским рассеянием[112].
Относительная сила электромагнитного взаимодействия между двумя заряженными частицами, такими как электрон и протон, определяется постоянной тонкой структуры. Эта величина представляет собой безразмерную величину, образованную соотношением двух энергий: электростатической энергии притяжения (или отталкивания) на расстоянии одной комптоновской длины волны и энергии покоя заряда. Она определяется как α ≈ 7,297353⋅10-3, что примерно равно 1137[71].
Когда электроны и позитроны сталкиваются, они аннигилируют друг друга, давая два или более фотонов гамма-излучения с энергией в сумме 1,022 МэВ. Если электрон и позитрон имеют незначительный импульс, то перед аннигиляцией может образоваться атом позитрония[113][114]. С другой стороны, высокоэнергетический фотон может превратиться в электрон и позитрон в результате процесса, называемого образованием пар, но только в присутствии поблизости заряженной частицы, такой как ядро атома[115][116].
В теории электрослабого взаимодействия левая составляющая волновой функции электрона образует слабый изоспиновый дублет с электронным нейтрино. Это означает, что при слабых взаимодействиях электронные нейтрино ведут себя как электроны. Любой член этого дублета может взаимодействовать с заряженным током, излучая или поглощая W-бозон и превратиться в другую частицу. Заряд сохраняется во время этой реакции, потому что W-бозон также несёт заряд, отменяя любые суммарные изменения заряда во время трансмутации. Взаимодействия заряженных токов ответственны за явление бета-распада в радиоактивном атоме. Как электрон, так и электронное нейтрино могут подвергаться взаимодействию с нейтральным током через обмен Z0
, и этот процесс ответственен за упругое рассеяние нейтрино и электронов[117].
Атомы и молекулы[править | править код]
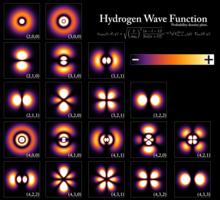
Плотности вероятности для первых нескольких орбиталей атома водорода в поперечном сечении. Энергетический уровень связанного электрона определяет занимаемую им орбиталь, а цвет отражает вероятность нахождения электрона в окрестности данной точки.
Электрон может быть связан с ядром атома кулоновской силой притяжения. Система из одного или нескольких электронов, связанных с ядром, называется атомом. Если число электронов отличается от электрического заряда ядра, такой атом называется ионом. Волновое поведение связанного электрона описывается функцией, называемой атомной орбиталью. Каждая орбиталь имеет свой собственный набор квантовых чисел, таких как энергия, угловой момент и проекция углового момента на выбранную ось, и вокруг ядра существует только определённый набор этих орбиталей, отвечающих дискретным квантовым числам. Согласно принципу запрета Паули, каждая орбиталь может быть занята двумя электронами, которые должны различаться своим спиновым квантовым числом[118].
Электроны могут перемещаться между разными орбиталями путём испускания или поглощения фотонов с энергией, соответствующей разнице потенциалов[119]:159–160. Другие способы смены орбитали включают столкновения с частицами, такими как электроны, и эффект Оже[120]. Чтобы оторваться от ядра атома, энергия электрона должна быть больше энергии его связи с атомом. Это происходит, например, при фотоэлектрическом эффекте, когда энергия падающего фотона, превышающая энергию ионизации атома, поглощается электроном[119]:127–132.
Орбитальный угловой момент электронов квантуется[en]. Поскольку электрон заряжен, его движение создаёт также орбитальный магнитный момент, пропорциональный угловому моменту. Суммарный магнитный момент атома равен векторной сумме орбитальных и спиновых магнитных моментов всех электронов и ядра. Магнитный момент ядра пренебрежимо мал по сравнению с магнитным моментом электрона. Магнитные моменты электронов, занимающих одну и ту же орбиталь (так называемые спаренные электроны), компенсируют друг друга[121].
Химическая связь между атомами возникает в результате электромагнитных взаимодействий, описываемых законами квантовой механики[122]. Самые прочные связи образуются путём обмена или передачи электронов между атомами, что позволяет образовывать молекулы[10]. Внутри молекулы электроны движутся под влиянием нескольких ядер и занимают молекулярные орбитали; частично они могут занимать атомные орбитали в изолированных атомах[123]. Фундаментальным фактором, определяющим существование молекулярных структур, является наличие электронных пар — электронов с противоположно ориентированными спинами, которые занимают одну и ту же молекулярную орбиталь не нарушая принципа запрета Паули (аналогично атомам). Различные молекулярные орбитали имеют различное пространственное распределение электронной плотности. Например, в связанных парах (то есть в тех парах, которые реально связывают атомы между собой) электроны с максимальной вероятностью могут находиться в сравнительно небольшом объёме пространства между ядрами. Напротив, в несвязанных парах электроны распределены в большом объёме вокруг ядер[124].
Проводимость[править | править код]
Разряд молнии состоит в основном из потока электронов[125]. Электрический потенциал, необходимый для молнии получается за счёт трибоэлектрического эффекта[126][127].
Если в теле больше или меньше электронов, чем требуется для уравновешивания положительного заряда ядер, то этот объект имеет суммарный электрический заряд. Когда есть избыток электронов, говорят, что объект заряжен отрицательно. Когда электронов меньше, чем число протонов в ядрах, говорят, что объект заряжен положительно. Когда количество электронов и количество протонов равны, их заряды компенсируют друг друга, и говорят, что объект электрически нейтрален. Макроскопическое тело может приобретать электрический заряд при трении за счёт трибоэлектрического эффекта[128].
Независимые электроны без кулоновского взаимодействия между ними или с ядрами, называются свободными электронами. Электроны в металлах также ведут себя так, как будто они свободны. В действительности частицы, которые обычно называют электронами в металлах и других твёрдых телах, являются квазиэлектронами — квазичастицами, которые имеют тот же электрический заряд, спин и магнитный момент, что и настоящие электроны, но могут иметь другую кажущуюся или эффективную массу[129]. Когда свободные электроны — как в вакууме, так и в металлах — движутся, они создают суммарный поток заряда, называемый электрическим током, который создаёт магнитное поле. Точно так же ток может быть создан изменяющимся магнитным полем. Эти взаимодействия математически описываются уравнениями Максвелла[130].
При данной температуре каждый материал обладает электрической проводимостью, которая определяет величину электрического тока при приложении электрического напряжения. Примеры хороших проводников включают такие металлы, как медь и золото, тогда как стекло и тефлон являются плохими проводниками. В любом диэлектрическом материале электроны остаются связанными со своими соответствующими атомами, и материал ведёт себя как изолятор. Большинство полупроводников имеют переменный уровень проводимости, который находится между крайними значениями проводимости и изоляции[131]. С другой стороны, металлы имеют электронную зонную структуру, содержащую частично заполненные электронные зоны. Наличие таких зон позволяет электронам в металлах вести себя так, как если бы они были свободными или делокализованными электронами. Эти электроны не связаны с конкретными атомами, поэтому при приложении электрического поля они могут свободно перемещаться, как газ (называемый ферми-газом)[132] через материал, как и свободные электроны[132].
Из-за столкновений между электронами и дефектами решётки дрейфовая скорость электронов в проводнике составляет порядка миллиметров в секунду. Однако скорость, с которой изменение тока в одной точке материала вызывает изменения токов в других частях материала, скорость распространения обычно составляет около 75 % скорости света[133]. Это происходит потому, что электрические сигналы распространяются в виде волны, скорость которой зависит от диэлектрической проницаемости материала[134].
Металлы являются относительно хорошими проводниками тепла, прежде всего потому, что делокализованные электроны могут свободно переносить тепловую энергию между атомами. Однако, в отличие от электропроводности, теплопроводность металла почти не зависит от температуры. Математически это выражается законом Видемана — Франца[132], который утверждает, что отношение теплопроводности к электропроводности пропорционально температуре. Тепловой беспорядок в металлической решетке увеличивает электрическое сопротивление материала, создавая зависимость электрического тока от температуры при данном напряжении[135].
При охлаждении ниже точки, называемой критической температурой, материалы могут подвергнуться фазовому переходу, при котором они полностью теряют сопротивление электрическому току при явлении, известном как сверхпроводимость. В теории БКШ пары электронов, называемые куперовскими парами, связаны своим движением с близлежащим веществом через колебания кристаллической решётки, называемые фононами, тем самым избегая столкновений с дефектами, которые обычно создают электрическое сопротивление[136]. Куперовские пары имеют радиус примерно 100 нм, поэтому они могут перекрываться друг другом[137]. Однако механизм действия высокотемпературных сверхпроводников остаётся неясным[138][139].
Электроны внутри проводящих твёрдых тел, которые сами являются квазичастицами, при тесном ограничении при температурах, близких к абсолютному нулю, ведут себя так, как если бы они разделились на три другие квазичастицы: орбитоны, спиноны и холоны[140]. Первая несёт спин и магнитный момент, следующая несёт своё орбитальное положение, а последняя — электрический заряд[141].
Движение и энергия[править | править код]
Согласно специальной теории относительности при приближении скорости электрона к скорости света, с точки зрения наблюдателя его релятивистская масса увеличивается, тем самым затрудняя его последующее ускорение в системе отсчёта наблюдателя. Скорость электрона может приближаться, но никогда не достигать скорости света в вакууме c. Однако когда релятивистские электроны, то есть электроны, движущиеся со скоростью, близкой к с, попадают в диэлектрическую среду, такую как вода, где локальная скорость света меньше с, электроны временно движутся быстрее света в среде. При их взаимодействии со средой, они генерируют слабый свет, называемый черенковским излучением[142].
Лоренц-фактор как функция скорости. Начинаясь со значения 1, он уходит в бесконечность при стремлении v к c.
Эффекты специальной теории относительности основаны на величине, известной как Лоренц-фактор, определяемой как 
где me — масса электрона. Например, линейный ускоритель Стэнфорда может ускорить электрон примерно до 51 ГэВ[143]. Поскольку электрон ведёт себя как волна, при заданной скорости ему ставят в соответствие характерную длину волны де Бройля. Она определяется выражением λ e = h/p, где h — постоянная Планка, а p — импульс частицы[51]. Для энергии электрона 51 ГэВ, длина волны составляет около 2,4⋅10-17 м, достаточно малая, для исследования структур намного меньших чем размер атомного ядра[144].
Образование[править | править код]
Парное рождение электрона и позитрона, вызванное тесным сближением фотона с ядром атома. Символ молнии представляет собой обмен виртуальным фотоном, при этом действует электрическая сила. Угол между частицами очень мал[145].
Теория Большого взрыва — наиболее широко принятая научная теория, объясняющая ранние этапы эволюции Вселенной[146]. В первую миллисекунду Большого взрыва температура превышала 10 миллиард Кельвин и фотоны имели среднюю энергию более миллиона электронвольт. Эти фотоны были достаточно энергичны, чтобы реагировать друг с другом, образуя пары электронов и позитронов. Точно так же пары позитрон-электрон аннигилировали друг друга и испускали фотоны высоких энергий — гамма-квантов:
- γ + γ ↔ e+
+ e−
На этом этапе эволюции Вселенной поддерживалось равновесие между электронами, позитронами и фотонами. Однако по прошествии 15 секунд температура Вселенной упала ниже порога, при котором могло произойти образование электронов и позитронов. Большинство выживших электронов и позитронов аннигилировали друг друга, испустив гамма-излучение, которое ненадолго вновь нагрело Вселенную[147].
По причинам, которые остаются невыясненными, в процессе аннигиляции имело место превышение числа частиц над числом античастиц. Следовательно, выживал примерно один электрон на каждый миллиард электрон-позитронных пар. Этот избыток соответствовал избытку протонов над антипротонами в состоянии, известном как барионная асимметрия, что привело к нулевому суммарному заряду Вселенной[148][149]. Уцелевшие протоны и нейтроны начали вступать в реакции друг с другом — в процессе, известном как нуклеосинтез, с образованием изотопов водорода и гелия со следовыми количествами лития. Этот процесс достиг своего пика примерно через пять минут[150]. Любые оставшиеся нейтроны подверглись отрицательному бета-распаду с периодом полураспада около тысячи секунд, высвобождая при этом протон и электрон.
- n → p + e−
+ ν
e
Примерно на следующие 300 000 — 400 000 лет избыточные электроны оставались слишком энергичными, чтобы связываться с атомными ядрами[151]. За этим последовал период, известный как рекомбинация, когда образовались нейтральные атомы и расширяющаяся Вселенная стала прозрачной для излучения[152].
Примерно через миллион лет после Большого взрыва начало формироваться первое поколение звёзд[152]. Внутри звезды звёздный нуклеосинтез приводит к образованию позитронов в результате слияния атомных ядер. Эти частицы антивещества немедленно аннигилируют с электронами, испуская гамма-кванты. Конечным результатом является постоянное уменьшение числа электронов и соответствующее увеличение числа нейтронов. Однако процесс эволюции звёзд может привести к синтезу радиоактивных изотопов. Выбранные изотопы могут впоследствии подвергаться отрицательному бета-распаду, испуская из ядра электрон и антинейтрино[153]. Примером может служить изотоп кобальта-60 (60Co), который распадается с образованием никеля-60 (60
Ni)[154].
Протяжённый воздушный ливень, вызванный энергетическим космическим лучом, проникающим в атмосферу Земли.
В конце своей жизни звезда с массой более 20 масс Солнца подвергается гравитационному коллапсу с образованием чёрной дыры[155]. Согласно классической физике, эти массивные звёздные объекты обладают гравитационным притяжением, которое достаточно сильно, чтобы предотвратить выход чего-либо, даже электромагнитного излучения, за пределы радиуса Шварцшильда[156]. Однако считается, что квантово-механические эффекты потенциально позволяют испускать излучение Хокинга на этом расстоянии. Считается, что электрон-позитронные пары создаются на горизонте событий этих звёздных остатков[157][158].
Когда пара виртуальных частиц (таких как электрон и позитрон) создаётся вблизи горизонта событий, случайное пространственное позиционирование может привести к тому, что одна из них появится снаружи; этот процесс называется квантовым туннелированием. Затем гравитационный потенциал чёрной дыры предоставляет энергию, превращающую эту виртуальную частицу в реальную частицу, позволяя ей излучаться в космос[159]. Взамен другой член пары получает отрицательную энергию, что приводит к чистой потере массы-энергии чёрной дырой. Скорость излучения Хокинга увеличивается с уменьшением массы, что в конечном итоге приводит к тому, что чёрная дыра испаряется, пока, наконец, не взорвётся[160].
Космические лучи — это частицы, путешествующие в космосе с высокими энергиями. Были зарегистрированы события с энергией до 3,0⋅1020 эВ[161]. Когда эти частицы сталкиваются с нуклонами в атмосфере Земли, генерируется поток частиц, в том числе пионов[162]. Более половины космического излучения, наблюдаемого с поверхности Земли, состоит из мюонов, которые представляют собой лептоны, возникающие в верхних слоях атмосферы при распаде пиона
- π−
→ μ−
+ ν
μ
Мюон, в свою очередь, может распасться с образованием электрона или позитрона[163]
- μ−
→ e−
+ ν
e + ν
μ
Наблюдение[править | править код]
Дистанционное наблюдение электронов требует регистрации их излучаемой энергии. Например, в высокоэнергетических средах, таких как корона звезды, свободные электроны образуют плазму, излучающую энергию за счет тормозного излучения. Электронный газ подвержен плазменным колебаниям, которые представляют собой волны, вызванные изменениями электронной плотности, и они производят выбросы энергии, которые можно обнаружить с помощью радиотелескопов[165].
Частота фотона пропорциональна его энергии. Когда связанный электрон переходит между различными энергетическими уровнями атома, он поглощает или излучает фотоны с характерными частотами. Например, при облучении атомов источником с широким спектром в спектре прошедшего излучения появляются отчётливые тёмные линии в местах поглощения соответствующей частоты электронами атома. Каждый элемент или молекула отображает характерный набор спектральных линий, таких как спектральные серии водорода. При спектроскопических измерениях интенсивности и ширины этих линий позволяют определить состав и физические свойства вещества[166][167].
В лабораторных условиях взаимодействия отдельных электронов можно наблюдать с помощью детекторов частиц, которые позволяют измерять определённые свойства, такие как энергия, спин и заряд[168]. Разработка ловушек Пауля[en] и ловушки Пеннинга позволяет удерживать заряженные частицы в небольшой области в течение длительного времени. Это позволяет точно измерять свойства частиц. Например, в одном случае ловушка Пеннинга использовалась для удержания одного электрона в течение 10 месяцев[169]. Магнитный момент электрона был измерен с точностью до одиннадцати знаков, что в 1980 году оказалось наибольшей точностью среди любых физических констант[170].
Первые видеоизображения распределения энергии электрона были сняты командой Лундского университета в Швеции в феврале 2008 года. Учёные использовали чрезвычайно короткие вспышки света, называемые аттосекундными импульсами, которые впервые позволили наблюдать за движением электрона[171][172].
Распределение электронов в твёрдых материалах можно визуализировать с помощью фотоэмиссионной спектроскопии с угловым разрешением (ARPES). Этот метод использует фотоэлектрический эффект для измерения их свойств в обратном пространстве, которое удобно для математического представления периодических структур, используемое для установления исходной решётки. ARPES можно использовать для определения направления, скорости и рассеяния электронов в материале[173].
Плазменные технологии[править | править код]
Пучки частиц[править | править код]
Электронные пучки используются при сварке[175]. Они позволяют достигать плотность энергии до 107 Вт·см−2 в фокусе диаметром 0.1—1.3 мм и обычно не требуют присадок[en]. Этот метод сварки должен выполняться в вакууме, чтобы электроны не взаимодействовали с остаточными газами до достижения поверхности. Его можно использовать для соединения проводящих материалов, которые в противном случае считались бы непригодными для сварки[176][177].
Электронно-лучевая литография (ЭЛЛ) — это метод литографии используемый для создания масок в электронном резисте с субмикронным разрешением[178]. Этот метод ограничен высокой стоимостью, низкой производительностью, необходимостью работы с пучком в высоком вакууме и рассеянием электронов в твёрдых телах. Последняя проблема ограничивает разрешение примерно 10 нм. По этой причине ЭЛЛ в основном используется для производства небольшого количества специализированных интегральных схем и научных исследований[179].
Электронно-лучевая обработка используется для облучения материалов с целью изменения их физических свойств или стерилизации медицинских и пищевых продуктов[180]. Электронные лучи разжижают или квазиплавят стекла без существенного повышения температуры при интенсивном облучении: например, интенсивное электронное облучение вызывает уменьшение вязкости на много порядков и ступенчатое уменьшение энергии её активации[181]. Электронно-лучевой нагрев используется для получения высокой концентрации энергии в малой области облучаемого материала при относительно малых токах, что может приводить к физико-химическим реакциям на поверхности. При определённых условиях можно достичь проплавления материала с образованием сквозных отверстий[182], что позволяет резать листы материалов толщиной до нескольких сантиметров[183]. Для получения особо чистых материалов используют электронно-лучевую плавку. При достаточно высокой температуре электронный пучок нагревает поверхность материала, что приводит к его быстрому испарению — это принцип используется в тонкоплёночных технологиях для создания пучков частиц с последующим напылением на подложку[184][185].
Среди циклических ускорителей выделяют циклотрон[186], бетатрон[187], синхротрон[188]. Линейные ускорители частиц генерируют электронные пучки для лечения поверхностных опухолей при лучевой терапии. Электронная терапия[en] может удалять такие поражения кожи, как базально-клеточная карцинома, потому что электронный пучок проникает только на ограниченную глубину, до полного поглощения, обычно до 5 см для энергий электронов в диапазоне 5—20 МэВ. Электронный пучок можно использовать для лечения областей, подвергшихся облучению рентгеновскими лучами[189][190].
Ускорители частиц используют электрические поля для разгона электронов и их античастиц до высоких энергий. Эти частицы излучают синхротронное излучение при движении в магнитных полях. Зависимость интенсивности этого излучения от спина поляризует электронный пучок — процесс, известный как эффект Соколова — Тернова[f]. Поляризованные электронные пучки могут быть полезны для различных экспериментов. Синхротронное излучение также может охлаждать электронные пучки, чтобы уменьшить разброс частиц по импульсу. Пучки электронов и позитронов сталкиваются при ускорении частиц до требуемых энергий; детекторы частиц наблюдают за результирующим излучением энергии, которое изучает физика элементарных частиц[192].
Визуализация[править | править код]
Дифракция медленных электронов (ДМЭ) — это метод исследования кристаллического материала коллимированным пучком электронов с последующим наблюдением полученных дифракционных картин для определения структуры материала. Требуемая энергия электронов обычно находится в диапазоне 20—200 эВ[193]. Метод дифракции быстрых электронов на отражение (ДБЭО) использует отражение пучка электронов, падающих на поверхность образца под различными малыми углами, для характеристики поверхности кристаллических материалов. Энергия пучка обычно находится в диапазоне 8—20 кэВ и угол падения составляет 1—4°[194][195].
Электронный микроскоп направляет сфокусированный пучок электронов на образец. Некоторые электроны изменяют свои свойства при рассеивании, среди которых направление движения, угол, относительная фаза и энергия, когда луч взаимодействует с материалом. Детекторы микроскопа могут регистрировать эти изменения для получения изображения материала с атомарным разрешением[196]. В синем свете обычные оптические микроскопы имеют дифракционно-ограниченное разрешение около 200 нм[197]. Для сравнения, электронные микроскопы теоретически ограничены длиной волны де Бройля электрона. Эта длина волны, например, равна 0,0037 нм для электронов, ускоренных при потенциале 100 000 В[198]. Просвечивающий электронный микроскоп с коррекцией аберраций[en] способен измерять расстояния менее 0,05 нм, что более чем достаточно для разрешения отдельных атомов[199]. Эта возможность делает электронный микроскоп полезным лабораторным инструментом для получения изображений с высоким разрешением. Однако электронные микроскопы являются дорогими приборами, обслуживание которых требует больших затрат[200].
В рентгенографии используется рентгеновские трубки, где катод при нагревании испускает электроны, которые ускоряются в вакуумном промежутке между катодом и анодом при большой разности потенциалов. Полученный ускоренный пучок электронов попадает на положительно заряженный анод, где электроны испытывают резкое торможение, благодаря чему возникает тормозное излучение рентгеновского диапазона. В процессе торможения лишь около 1% кинетической энергии электрона идёт на рентгеновское излучение, 99% энергии превращается в тепло[201].
Существуют два основных типа электронных микроскопов: просвечивающие и сканирующие. Просвечивающие электронные микроскопы работают как диапроекторы: пучок электронов проходит через срез материала, а затем проецируется линзами на предметное стекло или прибор с зарядовой связью. Сканирующие электронные микроскопы растрируют тонко сфокусированный электронный пучок, как в электронно-лучевой трубке телевизора, исследуемый образец для получения изображения. Увеличение варьируется от 100× до 1 000 000× или выше для обоих типов микроскопов. Сканирующий туннельный микроскоп использует квантовое туннелирование электронов между острым металлическим остриём (иглой) и атомами исследуемого материала и создаёт изображение его поверхности с атомарным разрешением[202][203][204].
Другие приложения[править | править код]
В лазере на свободных электронах (ЛСЭ) пучок релятивистских электронов проходит через пару ондуляторов, содержащих массивы дипольных магнитов, поля которых разнонаправленны. Электроны испускают синхротронное излучение, которое когерентно взаимодействует с теми же электронами, сильно усиливая поле излучения на резонансной частоте. ЛСЭ может излучать когерентный пучок электромагнитного излучения с высокой яркостью и в широком диапазоне частот, от микроволн до мягкого рентгеновского излучения. Эти устройства используются в производстве, связи и с медицинскими целями, такими как хирургия мягких тканей[205].
Электроны играют важную роль в электронно-лучевых трубках, которые широко использовались в качестве устройств отображения в лабораторных приборах, компьютерных мониторах и телевизорах[206]. В фотоумножителе каждый фотон, падающий на фотокатод, инициирует лавину электронов, которая создаёт регистрируемый импульс тока[207]. Вакуумные лампы используют поток электронов для управления электрическими сигналами, и они сыграли решающую роль в развитии электронных технологий. Однако впоследствии они были в значительной степени вытеснены твердотельными устройствами, такими как транзистор[208].
Примечания[править | править код]
Комментарии[править | править код]
- ↑ Обратите внимание, что в более старых источниках указывается отношение заряда к массе, а не современное соглашение об отношении массы к заряду.
- ↑ Эта величина получается из спинового квантового числа как
для квантового числа s = 12.
- ↑ магнетон Бора:
- ↑ Классический радиус электрона находится следующим образом. Предположим, что заряд электрона равномерно распределён по сферическому объёму. Поскольку одна часть сферы будет отталкивать другие части, сфера содержит электростатическую потенциальную энергию. Предполагается, что эта энергия равна энергии покоя электрона, определяемой специальной теорией относительности (E = mc2).
Из теории электростатики потенциальная энергия равномерно заряженной сферы радиусом r и зарядом e определяется выражением:
где ε0 — диэлектрическая проницаемость вакуума. Для электрона с массой покоя m0, энергия покоя равна:
где c — скорость света в вакууме. Приравняв их и найдя r, мы получим классический радиус электрона.
См.: Haken, Wolf, & Brewer (2005). - ↑ Излучение нерелятивистских электронов иногда называют циклотронным излучением.
- ↑ Поляризация электронного пучка означает, что спины всех электронов направлены в одном направлении. Другими словами, проекции спинов всех электронов на их вектор импульса имеют одинаковый знак[191].
Источники[править | править код]
- ↑ Иванов И. Удивительный мир внутри атомного ядра: Научно-популярная лекция для школьников. ФИАН, 11 сентября 2007 года.
- ↑ 1 2 3 4 5 Fundamental Physical Constants — Complete Listing. CODATA. NIST.
- ↑ 1 2 Agostini M. et al. (Borexino Coll.). Test of Electric Charge Conservation with Borexino (англ.) // Physical Review Letters. — 2015. — Vol. 115, iss. 23. — P. 231802. — doi:10.1103/PhysRevLett.115.231802. — arXiv:1509.01223.
- ↑ Back H. O. et al. (Borexino Coll.). Search for electron decay mode e → γ + ν with prototype of Borexino detector (англ.) // Phys. Lett. B. — 2002. — Vol. 525, iss. 1—2. — P. 29—40. — doi:10.1016/S0370-2693(01)01440-X. — Bibcode: 2002PhLB..525…29B.
- ↑ 1 2 Также то же, что и электрум: «янтарного цвета сплав золота (80 %) с серебром (20 %)» (Черных П. Я. Историко-этимологический словарь).
- ↑ Jerry Coffey. What Is An Electron (10 сентября 2010). Дата обращения: 3 сентября 2022.
- ↑ 1 2 3
Curtis, L.J. Atomic Structure and Lifetimes: A Conceptual Approach. — ISBN 978-0-521-53635-6. - ↑ 1 2
Eichten, E.J. (1983). “New Tests for Quark and Lepton Substructure”. Physical Review Letters. 50 (11): 811—814. Bibcode:1983PhRvL..50..811E. DOI:10.1103/PhysRevLett.50.811. - ↑ 1 2
CODATA value: proton-electron mass ratio. 2006 CODATA recommended values. National Institute of Standards and Technology. Дата обращения: 18 июля 2009. - ↑ 1 2
Pauling, L.C. The Nature of the Chemical Bond and the Structure of Molecules and Crystals: an introduction to modern structural chemistry. — 3rd. — Cornell University Press, 1960. — P. 4–10. — ISBN 978-0-8014-0333-0. - ↑ 1 2 3
Arabatzis, T. Representing Electrons: A Biographical Approach to Theoretical Entities. — University of Chicago Press, 2006. — P. 70–74, 96. — ISBN 978-0-226-02421-9. - ↑ 1 2 Benjamin, Park (1898), A history of electricity (The intellectual rise in electricity) from antiquity to the days of Benjamin Franklin, New York: J. Wiley, с. 315, 484–5, ISBN 978-1-313-10605-4, <https://archive.org/details/cu31924004128686/page/n10>
- ↑
Keithley, J. F. The Story of Electrical and Magnetic Measurements: From 500 B.C. to the 1940s. — IEEE Press, 1999. — P. 19–20. — ISBN 978-0-7803-1193-0. - ↑ Cajori, Florian. A History of Physics in Its Elementary Branches: Including the Evolution of Physical Laboratories. — Macmillan, 1917.
- ↑
Benjamin Franklin (1706–1790). Eric Weisstein’s World of Biography. Wolfram Research. Дата обращения: 16 декабря 2010. - ↑
Myers, R. L. The Basics of Physics. — Greenwood Publishing Group, 2006. — P. 242. — ISBN 978-0-313-32857-2. - ↑
Farrar, W. V. (1969). “Richard Laming and the Coal-Gas Industry, with His Views on the Structure of Matter”. Annals of Science. 25 (3): 243—254. DOI:10.1080/00033796900200141. - ↑
Barrow, J. D. (1983). “Natural Units Before Planck”. Quarterly Journal of the Royal Astronomical Society. 24: 24—26. Bibcode:1983QJRAS..24…24B. - ↑
Okamura, Sōgo. History of Electron Tubes. — IOS Press, 1994. — P. 11. — «In 1881, Stoney named this electromagnetic . It came to be called ‘electron’ from 1891. […] In 1906, the suggestion to call cathode ray particles ‘electrions’ was brought up but through the opinion of Lorentz of Holland ‘electrons’ came to be widely used. В 1881 году Стоуни назвал это электромагнитное явление «электролионом». С 1891 года он стал называться «электроном». […] В 1906 году было выдвинуто предложение называть частицы катодных лучей «электрионами», но, по после Лоренца название «электроны» стало широко использоваться.». — ISBN 978-90-5199-145-1. - ↑
Stoney, G. J. (1894). “Of the “Electron,” or Atom of Electricity”. Philosophical Magazine. 38 (5): 418—420. DOI:10.1080/14786449408620653. - ↑ «electron, n.2». OED Online. March 2013. Oxford University Press. Accessed 12 April 2013
- ↑
Word Mysteries & Histories. — Houghton Mifflin, 1986. — P. 73. — ISBN 978-0-395-40265-8. - ↑
Webster’s New World Dictionary. — Prentice Hall, 1970. — P. 450. - ↑
Born, M. Atomic Physics / M. Born, R.J. Blin-Stoyle, J.M. Radcliffe. — Courier Dover, 1989. — P. 26. — ISBN 978-0-486-65984-8. - ↑ Plücker, M. (1858-12-01). “XLVI. Observations on the electrical discharge through rarefied gases”. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 16 (109): 408—418. DOI:10.1080/14786445808642591. ISSN 1941-5982.
- ↑ 1 2 3
Leicester, H.M. The Historical Background of Chemistry. — Courier Dover, 1971. — P. 221–222. — ISBN 978-0-486-61053-5. - ↑ 1 2 Whittaker, E.T. A History of the Theories of Aether and Electricity. — Nelson, 1951. — Vol. 1.
- ↑
DeKosky, R.K. (1983). “William Crookes and the quest for absolute vacuum in the 1870s”. Annals of Science. 40 (1): 1—18. DOI:10.1080/00033798300200101. - ↑ 1 2 Schuster, Arthur (1890). “The discharge of electricity through gases”. Proceedings of the Royal Society of London. 47: 526—559. DOI:10.1098/rspl.1889.0111.
- ↑ Wilczek, Frank (June 2012). “Happy birthday, electron”. Scientific American.
- ↑
Trenn, T.J. (1976). “Rutherford on the Alpha-Beta-Gamma Classification of Radioactive Rays”. Isis. 67 (1): 61—75. DOI:10.1086/351545. - ↑
Becquerel, H. (1900). “Déviation du Rayonnement du Radium dans un Champ Électrique”. Comptes rendus de l’Académie des sciences [фр.]. 130: 809—815. - ↑ Buchwald and Warwick (2001:90-91).
- ↑
Myers, W.G. (1976). “Becquerel’s Discovery of Radioactivity in 1896”. Journal of Nuclear Medicine. 17 (7): 579—582. PMID 775027. - ↑ Thomson. Nobel Lecture: Carriers of Negative Electricity. The Nobel Foundation. Дата обращения: 25 августа 2008. Архивировано 10 октября 2008 года.
- ↑ O’Hara, J. G. (March 1975). “George Johnstone Stoney, F.R.S., and the Concept of the Electron”. Notes and Records of the Royal Society of London. Royal Society. 29 (2): 265—276. DOI:10.1098/rsnr.1975.0018.
- ↑ Abraham Pais (1997). “The discovery of the electron – 100 years of elementary particles” (PDF). Beam Line. 1: 4—16.
- ↑ Kaufmann, W. (1897). “Die magnetische Ablenkbarkeit der Kathodenstrahlen und ihre Abhängigkeit vom Entladungspotential”. Annalen der Physik und Chemie. 297 (7): 544—552. Bibcode:1897AnP…297..544K. DOI:10.1002/andp.18972970709. ISSN 0003-3804.
- ↑
Kikoin, I.K. (1961). “Abram Fedorovich Ioffe (on his eightieth birthday)”. Soviet Physics Uspekhi. 3 (5): 798—809. Bibcode:1961SvPhU…3..798K. DOI:10.1070/PU1961v003n05ABEH005812. Original publication in Russian: Кикоин, И.К. (1960). “Академик А.Ф. Иоффе”. Успехи Физических Наук. 72 (10): 303—321. DOI:10.3367/UFNr.0072.196010e.0307. - ↑
Millikan, R.A. (1911). “The Isolation of an Ion, a Precision Measurement of its Charge, and the Correction of Stokes’s Law” (PDF). Physical Review. 32 (2): 349—397. Bibcode:1911PhRvI..32..349M. DOI:10.1103/PhysRevSeriesI.32.349. - ↑ Das Gupta, N.N. (1999). “A Report on the Wilson Cloud Chamber and Its Applications in Physics”. Reviews of Modern Physics. 18 (2): 225—290. Bibcode:1946RvMP…18..225G. DOI:10.1103/RevModPhys.18.225.
- ↑ 1 2 3
Smirnov, B.M. Physics of Atoms and Ions. — Springer, 2003. — P. 14–21. — ISBN 978-0-387-95550-6. - ↑
Bohr. Nobel Lecture: The Structure of the Atom. The Nobel Foundation. Дата обращения: 3 декабря 2008. - ↑
Lewis, G.N. (1916). “The Atom and the Molecule”. Journal of the American Chemical Society. 38 (4): 762—786. DOI:10.1021/ja02261a002. - ↑ 1 2
Arabatzis, T. (1997). “The chemists’ electron” (PDF). European Journal of Physics. 18 (3): 150—163. Bibcode:1997EJPh…18..150A. DOI:10.1088/0143-0807/18/3/005. - ↑
Langmuir, I. (1919). “The Arrangement of Electrons in Atoms and Molecules”. Journal of the American Chemical Society. 41 (6): 868—934. DOI:10.1021/ja02227a002. - ↑
Scerri, E.R. The Periodic Table. — ISBN 978-0-19-530573-9. - ↑
Massimi, M. Pauli’s Exclusion Principle, The Origin and Validation of a Scientific Principle. — ISBN 978-0-521-83911-2. - ↑
Uhlenbeck, G.E. (1925). “Ersetzung der Hypothese vom unmechanischen Zwang durch eine Forderung bezüglich des inneren Verhaltens jedes einzelnen Elektrons”. Die Naturwissenschaften [нем.]. 13 (47): 953—954. Bibcode:1925NW…..13..953E. DOI:10.1007/BF01558878. - ↑
Pauli, W. (1923). “Über die Gesetzmäßigkeiten des anomalen Zeemaneffektes”. Zeitschrift für Physik [нем.]. 16 (1): 155—164. Bibcode:1923ZPhy…16..155P. DOI:10.1007/BF01327386. - ↑ 1 2
de Broglie. Nobel Lecture: The Wave Nature of the Electron. The Nobel Foundation. Дата обращения: 30 августа 2008. - ↑
Falkenburg, B. Particle Metaphysics: A Critical Account of Subatomic Reality. — Springer, 2007. — P. 85. — ISBN 978-3-540-33731-7. - ↑
Davisson. Nobel Lecture: The Discovery of Electron Waves. The Nobel Foundation. Дата обращения: 30 августа 2008. - ↑
Schrödinger, E. (1926). “Quantisierung als Eigenwertproblem”. Annalen der Physik [нем.]. 385 (13): 437—490. Bibcode:1926AnP…385..437S. DOI:10.1002/andp.19263851302. - ↑
Rigden, J.S. Hydrogen. — Harvard University Press, 2003. — P. 59–86. — ISBN 978-0-674-01252-3. - ↑
Reed, B.C. Quantum Mechanics. — Jones & Bartlett Publishers, 2007. — P. 275–350. — ISBN 978-0-7637-4451-9. - ↑
Dirac, P.A.M. (1928). “The Quantum Theory of the Electron” (PDF). Proceedings of the Royal Society A. 117 (778): 610—624. Bibcode:1928RSPSA.117..610D. DOI:10.1098/rspa.1928.0023. - ↑
Dirac. Nobel Lecture: Theory of Electrons and Positrons. The Nobel Foundation. Дата обращения: 1 ноября 2008. - ↑ Anderson, C. D. (1933). “The Positive Electron”. Physical Review. 43 (6): 491—494. Bibcode:1933PhRv…43..491A. DOI:10.1103/PhysRev.43.491.
- ↑
The Nobel Prize in Physics 1965. The Nobel Foundation. Дата обращения: 4 ноября 2008. - ↑
Panofsky, W.K.H. (1997). “The Evolution of Particle Accelerators & Colliders” (PDF). Beam Line. 27 (1): 36—44. Дата обращения 2008-09-15. - ↑
Elder, F.R. (1947). “Radiation from Electrons in a Synchrotron”. Physical Review. 71 (11): 829—830. Bibcode:1947PhRv…71..829E. DOI:10.1103/PhysRev.71.829.5. - ↑
Hoddeson, L. The Rise of the Standard Model: Particle Physics in the 1960s and 1970s. — Cambridge University Press, 1997. — P. 25–26. — ISBN 978-0-521-57816-5. - ↑
Bernardini, C. (2004). “AdA: The First Electron–Positron Collider”. Physics in Perspective. 6 (2): 156—183. Bibcode:2004PhP…..6..156B. DOI:10.1007/s00016-003-0202-y. - ↑
Testing the Standard Model: The LEP experiments. CERN. Дата обращения: 15 сентября 2008. - ↑
“LEP reaps a final harvest”. CERN Courier. 40 (10). 2000. - ↑ Prati, E. (2012). “Few electron limit of n-type metal oxide semiconductor single electron transistors”. Nanotechnology. 23 (21): 215204. arXiv:1203.4811. Bibcode:2012Nanot..23u5204P. DOI:10.1088/0957-4484/23/21/215204. PMID 22552118.
- ↑ Green, M. A. (1990). “Intrinsic concentration, effective densities of states, and effective mass in silicon”. Journal of Applied Physics. 67 (6): 2944—2954. Bibcode:1990JAP….67.2944G. DOI:10.1063/1.345414.
- ↑
Frampton, P.H. (2000). “Quarks and Leptons Beyond the Third Generation”. Physics Reports. 330 (5—6): 263—348. arXiv:hep-ph/9903387. Bibcode:2000PhR…330..263F. DOI:10.1016/S0370-1573(99)00095-2. - ↑ 1 2 3
Raith, W. Constituents of Matter: Atoms, Molecules, Nuclei and Particles / W. Raith, T. Mulvey. — CRC Press, 2001. — P. 777–781. — ISBN 978-0-8493-1202-1. - ↑ 1 2 3 4 5 6 7 8 The original source for CODATA is Mohr, P.J. (2008). “CODATA recommended values of the fundamental physical constants”. Reviews of Modern Physics. 80 (2): 633—730. arXiv:0801.0028. Bibcode:2008RvMP…80..633M. DOI:10.1103/RevModPhys.80.633.
- ↑
Zombeck, M. V. Handbook of Space Astronomy and Astrophysics. — 3rd. — Cambridge University Press, 2007. — P. 14. — ISBN 978-0-521-78242-5. - ↑
Murphy, M. T. (2008). “Strong Limit on a Variable Proton-to-Electron Mass Ratio from Molecules in the Distant Universe”. Science. 320 (5883): 1611—1613. arXiv:0806.3081. Bibcode:2008Sci…320.1611M. DOI:10.1126/science.1156352. PMID 18566280. - ↑
Zorn, J.C. (1963). “Experimental Limits for the Electron-Proton Charge Difference and for the Charge of the Neutron”. Physical Review. 129 (6): 2566—2576. Bibcode:1963PhRv..129.2566Z. DOI:10.1103/PhysRev.129.2566. - ↑ Gupta, M. C. Atomic and Molecular Spectroscopy. — New Age Publishers, 2001. — P. 81. — ISBN 978-81-224-1300-7.
- ↑ 1 2
Odom, B. (2006). “New Measurement of the Electron Magnetic Moment Using a One-Electron Quantum Cyclotron”. Physical Review Letters. 97 (3): 030801. Bibcode:2006PhRvL..97c0801O. DOI:10.1103/PhysRevLett.97.030801. PMID 16907490. - ↑
Anastopoulos, C. Particle Or Wave: The Evolution of the Concept of Matter in Modern Physics. — Princeton University Press, 2008. — P. 261–262. — ISBN 978-0-691-13512-0. - ↑
Gabrielse, G. (2006). “New Determination of the Fine Structure Constant from the Electron g Value and QED”. Physical Review Letters. 97 (3): 030802(1–4). Bibcode:2006PhRvL..97c0802G. DOI:10.1103/PhysRevLett.97.030802. PMID 16907491. - ↑ Комар, А. А. Электрон // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1999. — Т. 5: Стробоскопические приборы — Яркость. — 692 с. — 20 000 экз. — ISBN 5-85270-101-7.
- ↑ Petrov, Alexey A. David vs. Goliath: What a tiny electron can tell us about the structure of the universe (англ.). https://theconversation.com. The Conversation (20 декабря 2018). Дата обращения: 18 июля 2022.
- ↑ Шпольский, Эдуард Владимирович, Atomic physics (Atomnaia fizika), second edition, 1951
- ↑
Dehmelt, H. (1988). “A Single Atomic Particle Forever Floating at Rest in Free Space: New Value for Electron Radius”. Physica Scripta. T22: 102—110. Bibcode:1988PhST…22..102D. DOI:10.1088/0031-8949/1988/T22/016. - ↑ Gabrielse, Gerald Electron Substructure. Harvard University. Дата обращения: 21 июня 2016. Архивировано 10 апреля 2019 года.
- ↑ Meschede, D. Optics, light and lasers: The Practical Approach to Modern Aspects of Photonics and Laser Physics. — Wiley-VCH, 2004. — P. 168. — ISBN 978-3-527-40364-6.
- ↑
Steinberg, R. I. (1999). “Experimental test of charge conservation and the stability of the electron”. Physical Review D. 61 (2): 2582—2586. Bibcode:1975PhRvD..12.2582S. DOI:10.1103/PhysRevD.12.2582. - ↑
Beringer, J. (2012). “Review of Particle Physics: [electron properties]” (PDF). Physical Review D. 86 (1): 010001. Bibcode:2012PhRvD..86a0001B. DOI:10.1103/PhysRevD.86.010001. - ↑
Back, H.O. (2002). “Search for electron decay mode e → γ + ν with prototype of Borexino detector”. Physics Letters B. 525 (1—2): 29—40. Bibcode:2002PhLB..525…29B. DOI:10.1016/S0370-2693(01)01440-X. - ↑ UK | England | Physicists ‘make electrons split’. BBC News (28 августа 2009). Дата обращения: 11 июля 2016.
- ↑ Discovery About Behavior Of Building Block Of Nature Could Lead To Computer Revolution. Science Daily (July 31, 2009)
- ↑ Yarris, Lynn. First Direct Observations of Spinons and Holons. Lbl.gov (13 июля 2006). Дата обращения: 11 июля 2016.
- ↑ Weller, Paul F. An analogy for elementary band theory concepts in solids (англ.) // J. Chem. Educ : journal. — 1967. — Vol. 44, no. 7. — P. 391. — doi:10.1021/ed044p391.
- ↑ Слюсар, В.И. Наноантенны: подходы и перспективы. – C. 58 – 65. Электроника: наука, технология, бизнес. – 2009. – № 2. C. 63 (2009). Дата обращения: 3 июня 2021. Архивировано 3 июня 2021 года.
- ↑ Eibenberger, Sandra; et al. (2013). “Matter-wave interference with particles selected from a molecular library with masses exceeding 10000 amu”. Physical Chemistry Chemical Physics. 15 (35): 14696—14700. arXiv:1310.8343. Bibcode:2013PCCP…1514696E. DOI:10.1039/C3CP51500A. PMID 23900710. S2CID 3944699.
- ↑ 1 2 3 4 5
Munowitz, M. Knowing the Nature of Physical Law. — Oxford University Press, 2005. — P. 162. — ISBN 978-0-19-516737-5. - ↑ Kane, G. (9 October 2006). “Are virtual particles really constantly popping in and out of existence? Or are they merely a mathematical bookkeeping device for quantum mechanics?”. Scientific American. Дата обращения 19 September 2008.
- ↑
Taylor, J. The New Physics. — Cambridge University Press, 1989. — ISBN 978-0-521-43831-5. - ↑ 1 2
Genz, H. Nothingness: The Science of Empty Space. — Da Capo Press, 2001. — P. 241–243, 245–247. — ISBN 978-0-7382-0610-3. - ↑
Gribbin. More to electrons than meets the eye, New Scientist (January 25, 1997). Дата обращения: 17 сентября 2008. - ↑
Levine, I. (1997). “Measurement of the Electromagnetic Coupling at Large Momentum Transfer”. Physical Review Letters. 78 (3): 424—427. Bibcode:1997PhRvL..78..424L. DOI:10.1103/PhysRevLett.78.424. - ↑ Murayama, H. (10–17 March 2006). Supersymmetry Breaking Made Easy, Viable and Generic. Proceedings of the XLIInd Rencontres de Moriond on Electroweak Interactions and Unified Theories. La Thuile, Italy. arXiv:0709.3041. Bibcode:2007arXiv0709.3041M. — lists a 9 % mass difference for an electron that is the size of the Planck distance.
- ↑
Schwinger, J. (1948). “On Quantum-Electrodynamics and the Magnetic Moment of the Electron”. Physical Review. 73 (4): 416—417. Bibcode:1948PhRv…73..416S. DOI:10.1103/PhysRev.73.416. - ↑
Huang, K. Fundamental Forces of Nature: The Story of Gauge Fields. — World Scientific, 2007. — P. 123–125. — ISBN 978-981-270-645-4. - ↑
Foldy, L.L. (1950). “On the Dirac Theory of Spin 1/2 Particles and Its Non-Relativistic Limit”. Physical Review. 78 (1): 29—36. Bibcode:1950PhRv…78…29F. DOI:10.1103/PhysRev.78.29. - ↑ Foldy, 1950, p. 32.
- ↑ 1 2
Griffiths, David J. Introduction to Electrodynamics. — 3rd. — Prentice Hall, 1998. — ISBN 978-0-13-805326-0. - ↑
Crowell, B. Electricity and Magnetism. — Light and Matter, 2000. — P. 129–152. — ISBN 978-0-9704670-4-1. - ↑
Mahadevan, R. (1996). “Harmony in Electrons: Cyclotron and Synchrotron Emission by Thermal Electrons in a Magnetic Field”. The Astrophysical Journal. 465: 327—337. arXiv:astro-ph/9601073. Bibcode:1996ApJ…465..327M. DOI:10.1086/177422. - ↑
Rohrlich, F. (1999). “The Self-Force and Radiation Reaction”. American Journal of Physics. 68 (12): 1109—1112. Bibcode:2000AmJPh..68.1109R. DOI:10.1119/1.1286430. - ↑ Georgi, H. Grand Unified Theories // The New Physics / Davies, Paul. — Cambridge University Press, 1989. — P. 427. — ISBN 978-0-521-43831-5.
- ↑ Blumenthal, G.J. (1970). “Bremsstrahlung, Synchrotron Radiation, and Compton Scattering of High-Energy Electrons Traversing Dilute Gases”. Reviews of Modern Physics. 42 (2): 237—270. Bibcode:1970RvMP…42..237B. DOI:10.1103/RevModPhys.42.237.
- ↑ The Nobel Prize in Physics 1927. The Nobel Foundation. Дата обращения: 28 сентября 2008.
- ↑
Chen, S.-Y. (1998). “Experimental observation of relativistic nonlinear Thomson scattering”. Nature. 396 (6712): 653—655. arXiv:physics/9810036. Bibcode:1998Natur.396..653C. DOI:10.1038/25303. - ↑
Beringer, R. (1942). “The Angular Distribution of Positron Annihilation Radiation”. Physical Review. 61 (5—6): 222—224. Bibcode:1942PhRv…61..222B. DOI:10.1103/PhysRev.61.222. - ↑
Buffa, A. College Physics. — 4th. — Prentice Hall, 2000. — P. 888. — ISBN 978-0-13-082444-8. - ↑
Eichler, J. (2005). “Electron–positron pair production in relativistic ion–atom collisions”. Physics Letters A. 347 (1—3): 67—72. Bibcode:2005PhLA..347…67E. DOI:10.1016/j.physleta.2005.06.105. - ↑
Hubbell, J.H. (2006). “Electron positron pair production by photons: A historical overview”. Radiation Physics and Chemistry. 75 (6): 614—623. Bibcode:2006RaPC…75..614H. DOI:10.1016/j.radphyschem.2005.10.008. - ↑
Quigg, C. The Electroweak Theory. - ↑ Ельяшевич, M. А. Атом // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — 707 с. — 100 000 экз.
- ↑ 1 2
Tipler, Paul. Modern Physics. — 2003. — ISBN 978-0-7167-4345-3. - ↑
Burhop, E.H.S. The Auger Effect and Other Radiationless Transitions. — ISBN 978-0-88275-966-1. - ↑
Jiles, D. Introduction to Magnetism and Magnetic Materials. — CRC Press, 1998. — P. 280–287. — ISBN 978-0-412-79860-3. - ↑
Löwdin, P.O. Fundamental World of Quantum Chemistry: A Tribute to the Memory of Per-Olov Löwdin. — Springer Science+Business Media, 2003. — P. 393–394. — ISBN 978-1-4020-1290-7. - ↑
McQuarrie, D.A. Physical Chemistry: A Molecular Approach. — University Science Books, 1997. — P. 325–361. — ISBN 978-0-935702-99-6. - ↑
Daudel, R. (1974). “The Electron Pair in Chemistry”. Canadian Journal of Chemistry. 52 (8): 1310—1320. DOI:10.1139/v74-201. - ↑
Rakov, V. A. Lightning: Physics and Effects / V. A. Rakov, M. A. Uman. — Cambridge University Press, 2007. — P. 4. — ISBN 978-0-521-03541-5. - ↑
Freeman, G. R. (1999). “Triboelectricity and some associated phenomena”. Materials Science and Technology. 15 (12): 1454—1458. DOI:10.1179/026708399101505464. - ↑
Forward, K. M. (2009). “Methodology for studying particle–particle triboelectrification in granular materials”. Journal of Electrostatics. 67 (2—3): 178—183. DOI:10.1016/j.elstat.2008.12.002. - ↑
Weinberg, S. The Discovery of Subatomic Particles. — ISBN 978-0-521-82351-7. - ↑
Lou, L.-F. Introduction to phonons and electrons. — World Scientific, 2003. — P. 162, 164. — ISBN 978-981-238-461-4. - ↑
Guru, B.S. Electromagnetic Field Theory. — Cambridge University Press, 2004. — P. 138, 276. — ISBN 978-0-521-83016-4. - ↑
Achuthan, M. K. Fundamentals of Semiconductor Devices / M. K. Achuthan, K. N. Bhat. — Tata McGraw-Hill, 2007. — P. 49–67. — ISBN 978-0-07-061220-4. - ↑ 1 2 3
Ziman, J. M. Electrons and Phonons: The Theory of Transport Phenomena in Solids. — Oxford University Press, 2001. — P. 260. — ISBN 978-0-19-850779-6. - ↑
Main, P. (June 12, 1993). “When electrons go with the flow: Remove the obstacles that create electrical resistance, and you get ballistic electrons and a quantum surprise”. New Scientist. 1887. Дата обращения 2008-10-09. - ↑
Blackwell, G. R. The Electronic Packaging Handbook. — CRC Press, 2000. — P. 6.39–6.40. — ISBN 978-0-8493-8591-9. - ↑
Durrant, A. Quantum Physics of Matter: The Physical World. — CRC Press, 2000. — P. 43, 71–78. — ISBN 978-0-7503-0721-5. - ↑
The Nobel Prize in Physics 1972. The Nobel Foundation. Дата обращения: 13 октября 2008. - ↑
Kadin, A. M. (2007). “Spatial Structure of the Cooper Pair”. Journal of Superconductivity and Novel Magnetism. 20 (4): 285—292. arXiv:cond-mat/0510279. DOI:10.1007/s10948-006-0198-z. - ↑ P. Monthoux; Balatsky, A.; Pines, D.; et al. (1992). “Weak-coupling theory of high-temperature superconductivity in the antiferromagnetically correlated copper oxides”. Phys. Rev. B. 46 (22): 14803—14817. Bibcode:1992PhRvB..4614803M. DOI:10.1103/PhysRevB.46.14803. PMID 10003579.
- ↑ S. Chakravarty; Sudbo, A.; Anderson, P. W.; Strong, S.; et al. (1993). “Interlayer Tunneling and Gap Anisotropy in High-Temperature Superconductors”. Science. 261 (5119): 337—40. Bibcode:1993Sci…261..337C. DOI:10.1126/science.261.5119.337. PMID 17836845. S2CID 41404478.
- ↑
Jompol, Y. (2009). “Probing Spin-Charge Separation in a Tomonaga-Luttinger Liquid”. Science. 325 (5940): 597—601. arXiv:1002.2782. Bibcode:2009Sci…325..597J. DOI:10.1126/science.1171769. PMID 19644117. - ↑
Discovery about behavior of building block of nature could lead to computer revolution. ScienceDaily (31 июля 2009). Дата обращения: 1 августа 2009. - ↑
The Nobel Prize in Physics 1958, for the discovery and the interpretation of the Cherenkov effect. The Nobel Foundation. Дата обращения: 25 сентября 2008. - ↑
Special Relativity. Stanford Linear Accelerator Center (26 августа 2008). Дата обращения: 25 сентября 2008. - ↑
Adams, S. Frontiers: Twentieth Century Physics. — CRC Press, 2000. — ISBN 978-0-7484-0840-5. - ↑
Bianchini, Lorenzo. Selected Exercises in Particle and Nuclear Physics. — Springer, 2017. — P. 79. — ISBN 978-3-319-70494-4. - ↑
Lurquin, P. F. The Origins of Life and the Universe. — Columbia University Press, 2003. — P. 2. — ISBN 978-0-231-12655-7. - ↑
Silk, J. The Big Bang: The Creation and Evolution of the Universe. — 3rd. — Macmillan, 2000. — P. 110–112, 134–137. — ISBN 978-0-8050-7256-3. - ↑
Kolb, E.W. (1980). “The Development of Baryon Asymmetry in the Early Universe” (PDF). Physics Letters B. 91 (2): 217—221. Bibcode:1980PhLB…91..217K. DOI:10.1016/0370-2693(80)90435-9. - ↑
Sather. The Mystery of Matter Asymmetry. Stanford University (Spring–Summer 1996). Дата обращения: 1 ноября 2008. - ↑
Burles, S.; Nollett, K. M. & Turner, M. S. (1999), Big-Bang Nucleosynthesis: Linking Inner Space and Outer Space, arΧiv:astro-ph/9903300. - ↑
Boesgaard, A.M. (1985). “Big bang nucleosynthesis – Theories and observations”. Annual Review of Astronomy and Astrophysics. 23 (2): 319—378. Bibcode:1985ARA&A..23..319B. DOI:10.1146/annurev.aa.23.090185.001535. - ↑ 1 2
Barkana, R. (2006). “The First Stars in the Universe and Cosmic Reionization”. Science. 313 (5789): 931—934. arXiv:astro-ph/0608450. Bibcode:2006Sci…313..931B. DOI:10.1126/science.1125644. PMID 16917052. - ↑
Burbidge, E.M. (1957). “Synthesis of Elements in Stars” (PDF). Reviews of Modern Physics. 29 (4): 548—647. Bibcode:1957RvMP…29..547B. DOI:10.1103/RevModPhys.29.547. - ↑
Rodberg, L.S. (1957). “Fall of Parity: Recent Discoveries Related to Symmetry of Laws of Nature”. Science. 125 (3249): 627—633. Bibcode:1957Sci…125..627R. DOI:10.1126/science.125.3249.627. PMID 17810563. - ↑
Fryer, C.L. (1999). “Mass Limits For Black Hole Formation”. The Astrophysical Journal. 522 (1): 413—418. arXiv:astro-ph/9902315. Bibcode:1999ApJ…522..413F. DOI:10.1086/307647. - ↑ Wald, Robert M. General Relativity. — University of Chicago Press, 1984. — P. 299–300. — ISBN 978-0-226-87033-5.
- ↑ Visser, Matt (2003). “Essential and inessential features of Hawking radiation” (PDF). International Journal of Modern Physics D. 12 (4): 649—661. arXiv:hep-th/0106111. Bibcode:2003IJMPD..12..649V. DOI:10.1142/S0218271803003190. S2CID 16261173.
- ↑ Laurent, Philippe; Titarchuk, Lev. Electron–Positron Pair Creation Close to a Black Hole Horizon: Redshifted Annihilation Line in the Emergent X-Ray Spectra of a Black Hole. I. // The Astrophysical Journal. — 2018. — Т. 859:89. — doi:10.3847/1538-4357/aac090.
- ↑ Parikh, M.K. (2000). “Hawking Radiation As Tunneling”. Physical Review Letters. 85 (24): 5042—5045. arXiv:hep-th/9907001. Bibcode:2000PhRvL..85.5042P. DOI:10.1103/PhysRevLett.85.5042. PMID 11102182.
- ↑
Hawking, S.W. (1974). “Black hole explosions?”. Nature. 248 (5443): 30—31. Bibcode:1974Natur.248…30H. DOI:10.1038/248030a0. - ↑
Halzen, F. (2002). “High-energy neutrino astronomy: the cosmic ray connection”. Reports on Progress in Physics. 66 (7): 1025—1078. arXiv:astro-ph/0204527. Bibcode:2002RPPh…65.1025H. DOI:10.1088/0034-4885/65/7/201. - ↑
Ziegler, J.F. (1998). “Terrestrial cosmic ray intensities”. IBM Journal of Research and Development. 42 (1): 117—139. Bibcode:1998IBMJ…42..117Z. DOI:10.1147/rd.421.0117. - ↑
Sutton. Muons, pions and other strange particles, New Scientist (August 4, 1990). Дата обращения: 28 августа 2008. - ↑
(July 24, 2008). Scientists solve 30 year-old aurora borealis mystery. Пресс-релиз. - ↑
Gurnett, D.A. (1976). “Electron Plasma Oscillations Associated with Type III Radio Bursts”. Science. 194 (4270): 1159—1162. Bibcode:1976Sci…194.1159G. DOI:10.1126/science.194.4270.1159. PMID 17790910. - ↑
Martin. Atomic Spectroscopy: A compendium of basic ideas, notation, data, and formulas. National Institute of Standards and Technology. Дата обращения: 8 января 2007. - ↑
Fowles, G.R. Introduction to Modern Optics. — Courier Dover, 1989. — P. 227–233. — ISBN 978-0-486-65957-2. - ↑
Grupen, C. (2000). “Physics of Particle Detection”. AIP Conference Proceedings. 536: 3—34. arXiv:physics/9906063. Bibcode:2000AIPC..536….3G. DOI:10.1063/1.1361756. - ↑
The Nobel Prize in Physics 1989. The Nobel Foundation. Дата обращения: 24 сентября 2008. - ↑
Ekstrom, P. (1980). “The isolated Electron” (PDF). Scientific American. 243 (2): 91—101. Bibcode:1980SciAm.243b.104E. DOI:10.1038/scientificamerican0880-104. Дата обращения 2008-09-24. - ↑
Mauritsson. Electron filmed for the first time ever. Lund University. Дата обращения: 17 сентября 2008. Архивировано 25 марта 2009 года. - ↑
Mauritsson, J. (2008). “Coherent Electron Scattering Captured by an Attosecond Quantum Stroboscope”. Physical Review Letters. 100 (7). arXiv:0708.1060. Bibcode:2008PhRvL.100g3003M. DOI:10.1103/PhysRevLett.100.073003. PMID 18352546. - ↑
Damascelli, A. (2004). “Probing the Electronic Structure of Complex Systems by ARPES”. Physica Scripta. T109: 61—74. arXiv:cond-mat/0307085. Bibcode:2004PhST..109…61D. DOI:10.1238/Physica.Topical.109a00061. - ↑
Image # L-1975-02972. NASA (4 апреля 1975). Дата обращения: 20 сентября 2008. Архивировано 7 декабря 2008 года. - ↑ Elmer. Standardizing the Art of Electron-Beam Welding. Lawrence Livermore National Laboratory (3 марта 2008). Дата обращения: 16 октября 2008. Архивировано 20 сентября 2008 года.
- ↑
Schultz, H. Electron Beam Welding. — Woodhead Publishing, 1993. — P. 2–3. — ISBN 978-1-85573-050-2. - ↑
Benedict, G. F. Nontraditional Manufacturing Processes. — CRC Press, 1987. — Vol. 19. — P. 273. — ISBN 978-0-8247-7352-6. - ↑
Ozdemir, F. S. (June 25–27, 1979). Electron beam lithography. Proceedings of the 16th Conference on Design automation. San Diego, CA: IEEE Press. pp. 383—391. Дата обращения 16 October 2008. - ↑
Madou, M. J. Fundamentals of Microfabrication: the Science of Miniaturization. — 2nd. — CRC Press, 2002. — P. 53–54. — ISBN 978-0-8493-0826-0. - ↑ Jongen, Y.; Herer, A. (2–5 May 1996). [no title cited]. APS/AAPT Joint Meeting. Electron Beam Scanning in Industrial Applications. American Physical Society. Bibcode:1996APS..MAY.H9902J.
- ↑
Mobus, G. (2010). “Nano-scale quasi-melting of alkali-borosilicate glasses under electron irradiatio”. Journal of Nuclear Materials. 396 (2—3): 264—271. Bibcode:2010JNuM..396..264M. DOI:10.1016/j.jnucmat.2009.11.020. - ↑ Гасанов, 2007, с. 78.
- ↑ Гасанов, 2007, с. 82.
- ↑ Гасанов, 2007, с. 83.
- ↑ Гасанов, 2007, с. 150.
- ↑ Гасанов, И. С. Плазменная и пучковая технология. — Баку: Элм, 2007. — С. 51. — 174 с.
- ↑ Гасанов, 2007, с. 53.
- ↑ Гасанов, 2007, с. 54.
- ↑
Beddar, A. S. (2001). “Mobile linear accelerators for intraoperative radiation therapy”. AORN Journal. 74 (5): 700—705. DOI:10.1016/S0001-2092(06)61769-9. PMID 11725448. - ↑
Gazda, M. J. Principles of Radiation Therapy (1 июня 2007). Дата обращения: 31 октября 2013. - ↑ Соколов, А. А.; Тернов, И. М. О поляризационных и спиновых эффектах в теории синхротронного излучения // Доклады Академии Наук СССР : журнал. — 1963. — Т. 153. — С. 1053.
- ↑ Chao, A. W. Handbook of Accelerator Physics and Engineering. — World Scientific, 1999. — P. 155, 188. — ISBN 978-981-02-3500-0.
- ↑
Oura, K. Surface Science: An Introduction. — Springer Science+Business Media, 2003. — P. 1–45. — ISBN 978-3-540-00545-2. - ↑
Ichimiya, A. Reflection High-energy Electron Diffraction / A. Ichimiya, P. I. Cohen. — Cambridge University Press, 2004. — P. 1. — ISBN 978-0-521-45373-8. - ↑
Heppell, T. A. (1967). “A combined low energy and reflection high energy electron diffraction apparatus”. Journal of Scientific Instruments. 44 (9): 686—688. Bibcode:1967JScI…44..686H. DOI:10.1088/0950-7671/44/9/311. - ↑
McMullan, D. Scanning Electron Microscopy: 1928–1965. University of Cambridge (1993). Дата обращения: 23 марта 2009. - ↑
Slayter, H. S. Light and electron microscopy. — Cambridge University Press, 1992. — P. 1. — ISBN 978-0-521-33948-3. - ↑
Cember, H. Introduction to Health Physics. — McGraw-Hill Professional, 1996. — P. 42–43. — ISBN 978-0-07-105461-4. - ↑
Erni, R.; et al. (2009). “Atomic-Resolution Imaging with a Sub-50-pm Electron Probe”. Physical Review Letters. 102 (9): 096101. Bibcode:2009PhRvL.102i6101E. DOI:10.1103/PhysRevLett.102.096101. PMID 19392535. - ↑ Shiloh, Roy; et al. Spherical aberration correction in a scanning transmission electron microscope using a sculpted thin film // Ultramicroscopy. — 2018. — Т. 189. — С. 46—53. — doi:10.1016/j.ultramic.2018.03.016.
- ↑ Кишковский, А. Н.; Тютин, Л. А. Медицинская рентгенотехника. — Л.: Медицина, Ленингр. отд-ние, 1983.
- ↑
Bozzola, J. J. Electron Microscopy: Principles and Techniques for Biologists / J. J. Bozzola, L. D. Russell. — Jones & Bartlett Publishers, 1999. — P. 12, 197–199. — ISBN 978-0-7637-0192-5. - ↑
Flegler, S. L. Scanning and Transmission Electron Microscopy: An Introduction / S. L. Flegler, J. W. Heckman Jr., K. L. Klomparens. — Reprint. — Oxford University Press, 1995. — P. 43–45. — ISBN 978-0-19-510751-7. - ↑
Bozzola, J. J. Electron Microscopy: Principles and Techniques for Biologists / J. J. Bozzola, L. D. Russell. — 2nd. — Jones & Bartlett Publishers, 1999. — P. 9. — ISBN 978-0-7637-0192-5. - ↑
Freund, H. P. Principles of Free-Electron Lasers / H. P. Freund, T. Antonsen. — Springer, 1996. — P. 1–30. — ISBN 978-0-412-72540-1. - ↑
Kitzmiller, J. W. Television Picture Tubes and Other Cathode-Ray Tubes: Industry and Trade Summary. — Diane Publishing, 1995. — P. 3–5. — ISBN 978-0-7881-2100-5. - ↑
Sclater, N. Electronic Technology Handbook. — McGraw-Hill Professional, 1999. — P. 227–228. — ISBN 978-0-07-058048-0. - ↑
The History of the Integrated Circuit. The Nobel Foundation (2008). Дата обращения: 18 октября 2008.
Литература на русском языке[править | править код]
- Бронштейн М. П. Атомы и электроны. — М.: Наука. — 1980. — 152 с., Библиотечка «Квант», вып. 1. Тир. 150000 экз.
- Дмитриев И.С. Электрон глазами химика / 2-е изд., испр.. — Л.: Химия, 1986. — 225 с.
- Широков Ю. М., Юдин Н. П. Ядерная физика. — М.: Наука, 1972. — 670 с.
- Буравихин В. А., Егоров В. А. Биография электрона. — М.: Знание, 1985. — 136 с.
- Китайгородский А. И. Электроны. — М.: Наука, 1979. — 206 с.
- Соколов А. А., Тернов И. М. Релятивистский электрон. — М.: Наука, 1974. — 391 с.
Ссылки[править | править код]
- Все известные свойства электрона систематизированы в обзоре Particle Data Group [1] (англ.).
- The Discovery of the Electron. American Institute of Physics.
- Particle Data Group. University of California.
- Bock, R.K. The Particle Detector BriefBook / R.K. Bock, A. Vasilescu. — 14th. — Springer, 1998. — ISBN 978-3-540-64120-9.
- Copeland, Ed Spherical Electron. Sixty Symbols. Brady Haran for the University of Nottingham.
|
|
Макеты страниц
Удельный заряд электрона (т. е. отношение 
Подавая напряжение на пластины конденсатора, можно было воздействовать на пучок практически однородным электрическим полем. Трубка помещалась между полюсами электромагнита, с помощью которого можно было создавать на том же участке пути электронов перпендикулярное к электрическому однородное магнитное поле (область этого поля обведена на рис. 74.1 пунктирной окружностью). При выключенных полях пучок попадал на экран в точке О. Каждое из полей в отдельности вызывало смещение пучка в вертикальном направлении. Величины смещений определяются полученными в предыдущем параграфе формулами (73.3) и (73.4).
Включив магнитное поле и измерив вызванное им смещение следа пучка

Томсон включал также электрическое поле и подбирал его значение так, чтобы пучок снова попадал в точку О. В этом случае электрическое и магнитное поля действовали на электроны пучка одновременно с одинаковыми по величине, но противоположно направленными силами. При этом выполнялось условие

Решая совместно уравнения (74.1) и (74.2), Томсон вычислял 
Буш применил для определения удельного заряда электронов метод магнитной фокусировки. Суть этого метода заключается в следующем. Допустим, что в однородном магнитном поле вылетает из некоторой точки слегка расходящийся симметричный относительно направления поля пучок электронов, имеющих одинаковую по величине скорость v. Направления, по которым вылетают электроны, образуют с направлением В небольшие углы а. В § 72 было выяснено, что электроны движутся в этом случае по спиральным траекториям, совершая за одинаковое время

полный оборот и смещаясь вдоль направления поля на расстояние 


Рис. 74.1.
Вследствие малости угла а расстояния (74.3) для разных электронов оказываются практически одинаковыми и равными 


В опыте Буша электроны, испущенные раскаленным катодом К (рис. 74.2), ускоряются, проходя разность потенциалов U, приложенную между катодом К и анодом А. В результате они приобретают скорость и, значение которой может быть найдено из соотношения

Вылетев затем из отверстия в аноде, электроны образуют узкий пучок, направленный вдоль оси эвакуированной трубки, вставленной внутрь соленоида. На входе в соленоид помещается конденсатор, на который подается переменное напряжение. Поле, создаваемое конденсатором, отклоняет электроны пучка от оси прибора на небольшие изменяющиеся со временем углы а. Это приводит к «завихрению» пучка — электроны начинают двигаться по различным спиральным траекториям. На выходе из соленоида ставится флуоресцирующий экран. Если подобрать магнитную индукцию В так, чтобы расстояние Г от конденсатора до экрана удовлетворяло условию

(l — шаг спирали, 

Наиболее точное значение удельного заряда электрона, установленное с учетом результатов, полученных разными методами, равно

Величина (74.7) дает отношение заряда электрона к его массе покоя 


Рис. 74.2
В опытах Томсона скорость электронов составляла примерно 0,1 с. При такой скорости релятивистская масса превышает массу покоя на 0,5%. В последующих опытах скорость электронов достигала очень больших значений. Во всех случаях было обнаружено уменьшение измеряемых значений 
Заряд электрона был определен с большой точностью Милликеном в 1909 г. В закрытое пространство между горизонтально расположенными пластинами конденсатора (рис. 74.3) Милликен вводил мельчайшие капельки масла. При разбрызгивании капельки электризовались, и их можно было устанавливать неподвижно, подбирая величину и знак напряжения на конденсаторе.
Равновесие наступало при условии

здесь 

(









Движение капельки наблюдалось с помощью микроскопа. Для измерения 
Точно зафиксировать равновесие капельки очень трудно. Поэтому вместо поля, отвечающего условию (74.9), включалось такое поле, под действием которого капелька начинала двигаться с небольшой скоростью вверх. Установившаяся скорость подъема 



Исключив из уравнения (74.10), (74.11) и (74.12) Р и 


(в эту формулу Милликен вносил поправку, учитывающую, что размеры капелек были сравнимы с длиной свободного пробега молекул воздуха).

Рис. 74.3.
Итак, измерив скорость свободного падения капельки 





Измеренные Милликеном изменения заряда капельки 


Значение элементарного заряда, установленное с учетом измерений Милликена и данных, полученных другими методами, равно

Такую же величину имеет заряд электрона.
Из (74.7) и (74.13) получается для массы покоя электрона значение

приблизительно в 1840 раз меньшее массы самого легкого из атомов — атома водорода.
В обнаружении дискретной природы электричества сыграли большую роль законы электролиза, установленные экспериментально Фарадеем в 1836 г. Согласно этим законам масса 


Здесь М — масса моля выделяющегося вещества, 

Разделив обе части равенства (74.15) на массу иона, получим




Следовательно, заряд иона оказывается целым кратным величины

«угорая представляет собой элементарный заряд.
Таким образом, из анализа законов электролиза вытекает дискретность зарядов, которыми могут обладать ионы в электролитах.
Подстановка в (74.17) значения (74.16) для F и найденного из зпытов Перрена (см. § 


Поскольку точность, с которой определяется постоянная Фарадея F, и точность значения 


Оглавление
- ПРЕДИСЛОВИЕ
- МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
- ЧАСТЬ 1. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
- § 1. Электрический заряд
- § 2. Закон Кулона
- § 3. Системы единиц
- § 4. Рационализованная запись формул
- § 5. Электрическое поле. Напряженность поля
- § 6. Потенциал
- § 7. Энергия взаимодействия системы зарядов
- § 8. Связь между напряженностью электрического поля и потенциалом
- § 9. Диполь
- § 10. Поле системы зарядов на больших расстояниях
- § 11. Описание свойств векторных полей
- Дивергенция.
- Циркуляция.
- Теорема Стокса.
- § 12. Циркуляция и ротор электростатического поля
- § 13. Теорема Гаусса
- § 14. Вычисление полей с помощью теоремы Гаусса
- Поле двух разноименно заряженных плоскостей.
- Поле заряженной сферической поверхности.
- Поле объемно-заряженного шара.
- ГЛАВА II. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКАХ
- § 15. Полярные и неполярные молекулы
- § 16. Поляризация диэлектриков
- § 17. Поле внутри диэлектрика
- § 18. Объемные и поверхностные связанные заряды
- § 19. Вектор электрического смешения
- § 20. Примеры на вычисление поля в диэлектриках
- § 21. Условия на границе двух диэлектриков
- § 22. Силы, действующие на заряд в диэлектрике
- § 23. Сегнетоэлектрики
- ГЛАВА III. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 24. Равновесие зарядов на проводнике
- § 25. Проводник во внешнем электрическом поле
- § 26. Электроемкость
- § 27. Конденсаторы
- ГЛАВА IV. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
- § 28. Энергия заряженного проводника
- § 29. Энергия заряженного конденсатора
- § 30. Энергия электрического поля
- ГЛАВА V. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 31. Электрический ток
- § 32. Уравнение непрерывности
- § 33. Электродвижущая сила
- § 34. Закон Ома. Сопротивление проводников
- § 35. Закон Ома для неоднородного участка цепи
- § 36. Разветвленные цепи. Правила Кирхгофа
- § 37. Мощность тока
- § 38. Закон Джоуля — Ленца
- ГЛАВА VI. МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ
- § 39. Взаимодействие токов
- § 40. Магнитное поле
- § 41. Поле движущегося заряда
- § 42. Закон Био — Савара
- § 43. Сила Лоренца
- § 44. Закон Ампера
- § 45. Магнитное взаимодействие как релятивистский эффект
- § 46. Контур с током в магнитном поле
- § 47. Магнитное поле контура с током
- § 48. Работа, совершаемая при перемещении тока в магнитном
- § 49. Дивергенция и ротор магнитного поля
- § 50. Поле соленоида и тороида
- ГЛАВА VII. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ
- § 51. Намагничение магнетика
- § 52. Напряженность магнитного поля
- § 53. Вычисление поля в магнетиках
- § 54. Условия на границе двух магнетиков
- § 55. Виды магнетиков
- § 56. Магнитомеханические явления
- § 57. Диамагнетизм
- § 58. Парамагнетизм
- § 59. Ферромагнетизм
- ГЛАВА VIII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
- § 60. Явление электромагнитной индукции
- § 61. Электродвижущая сила индукции
- § 62. Методы измерения магнитной индукции
- § 63. Токи Фуко
- § 64. Явление самоиндукции
- § 65. Ток при замыкании и размыкании цепи
- § 66. Взаимная индукция
- § 67. Энергия магнитного поля
- § 68. Работа перемагничивания ферромагнетика
- ГЛАВА IX. УРАВНЕНИЯ МАКСВЕЛЛА
- § 69. Вихревое электрическое поле
- § 70. Ток смещения
- § 71. Уравнения Максвелла
- ГЛАВА X. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ПОЛЯХ
- § 72. Движение заряженной частицы в однородном магнитном поле
- § 73. Отклонение движущихся заряженных частиц электрическим и магнитным полями
- § 74. Определение заряда и массы электрона
- § 75. Определение удельного заряда ионов. Масс-спектрографы
- § 76. Ускорители заряженных частиц
- ГЛАВА XI. КЛАССИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОПРОВОДНОСТИ МЕТАЛЛОВ
- § 77. Природа носителей тока в металлах
- § 78. Элементарная классическая теория металлов
- § 79. Эффект Холла
- ГЛАВА XII. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ
- § 80. Несамостоятельная и самостоятельная проводимость
- § 81. Несамостоятельный газовый разряд
- § 82. Ионизационные камеры и счетчики
- § 83. Процессы, приводящие к появлению носителей тока при самостоятельном разряде
- § 84. Газоразрядная плазма
- § 85. Тлеющий разряд
- § 86. Дуговой разряд
- § 87. Искровой и коронный разряды
- ГЛАВА XIII. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
- § 88. Квазистационарные токи
- § 89. Свободные колебания в контуре без активного сопротивления
- § 90. Свободные затухающие колебания
- § 91. Вынужденные электрические колебания
- § 92. Переменный ток
- ЧАСТЬ 2. ВОЛНЫ
- § 93. Распространение волн в упругой среде
- § 94. Уравнения плоской и сферической волн
- § 95. Уравнение плоской волны, распространяющейся в произвольном направлении
- § 96. Волновое уравнение
- § 97. Скорость упругих волн в твердой среде
- § 98. Энергия упругой волны
- § 99. Стоячие волны
- § 100. Колебания струны
- § 101. Звук
- § 102. Скорость звука в газах
- § 103. Эффект Доплера для звуковых волн
- ГЛАВА XV. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- § 104. Волновое уравнение для электромагнитного поля
- § 105. Плоская электромагнитная волна
- § 106. Экспериментальное исследование электромагнитных волн
- § 107. Энергия электромагнитных волн
- § 108. Импульс электромагнитного поля
- § 109. Излучение диполя
- ЧАСТЬ 3. ОПТИКА
- § 110. Световая волна
- § 111. Представление гармонических функций с помощью экспонент
- § 112. Отражение и преломление плоской волны на границе двух диэлектриков
- § 113. Световой поток
- § 114. Фотометрические величины и единицы
- § 115. Геометрическая оптика
- § 116. Центрированная оптическая система
- § 117. Тонкая линза
- § 118. Принцип Гюйгенса
- ГЛАВА XVII. ИНТЕРФЕРЕНЦИЯ СВЕТА
- § 119. Интерференция световых волн
- § 120. Когерентность
- § 121. Способы наблюдения интерференции света
- § 122. Интерференция света при отражении от тонких пластинок
- § 123. Интерферометр Майкельсона
- § 124. Многолучевая интерференция
- ГЛАВА XVIII. ДИФРАКЦИЯ СВЕТА
- § 126. Принцип Гюйгенса—Френеля
- § 127. Зоны Френеля
- § 128. Дифракция Френеля от простейших преград
- § 129. Дифракция Фраунгофера от щели
- § 130. Дифракционная решетка
- § 131. Дифракция рентгеновских лучей
- § 132. Разрешающая сила объектива
- § 133. Голография
- ГЛАВА XIX. ПОЛЯРИЗАЦИЯ СВЕТА
- § 134. Естественный и поляризованный свет
- § 135. Поляризация при отражении и преломлении
- § 136. Поляризация при двойном лучепреломлении
- § 137. Интерференция поляризованных лучей
- § 138. Прохождение плоскополяризованного света через кристаллическую пластинку
- § 139. Кристаллическая пластинка между двумя поляризаторами
- § 140. Искусственное двойное лучепреломление
- § 141. Вращение плоскости поляризации
- ГЛАВА XX. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН С ВЕЩЕСТВОМ
- § 142. Дисперсия света
- § 143. Групповая скорость
- § 144. Элементарная теория дисперсии
- § 145. Поглощение света
- § 146. Рассеяние света
- § 147. Эффект Вавилова — Черенкова
- ГЛАВА XXI. ОПТИКА ДВИЖУЩИХСЯ СРЕД
- § 148. Скорость света
- § 149. Опыт Физо
- § 150. Опыт Майкельсона
- § 151. Эффект Доплера
- ПРИЛОЖЕНИЯ
- I. Единицы электрических и магнитных величин в СИ и в гауссовой системе
- Приложение II. Основные формулы электромагнетизма в СИ и в гауссовой системе
- Приложение III. Векторный потенциал
Электрон — это стабильная отрицательно заряженная элементарная частица.
Электроны играют важную роль почти во всех физических эффектах. Поскольку электроны несут заряд, они также генерируют электрическое поле. Если привести электрон в движение, то возникнет магнитное поле. Если электрон проходит через другое внешнее электрическое поле, его путь изменяется под действием силы Лоренца.
Электрон принадлежит к лептонному семейству частиц. Существует несколько различных семейств частиц, перечисленных в стандартной модели физики частиц.
Спин электрона и магнитный момент электрона.
Согласно современному уровню знаний, лептоны являются элементарными частицами. По сравнению с другими лептонами, электрон имеет самую низкую массу среди лептонов, несущих заряд. Он принадлежит к первому поколению лептонов. Второе и третье поколения — мюон и тауон. Эти две частицы имеют одинаковые с электроном заряды и спин, но отличаются от него большей массой.
Лептоны отличаются от других фундаментальных частиц, таких как кварки, отсутствием сильного взаимодействия. Все лептоны принадлежат к семейству фермионов, поэтому электрон имеет собственный вращательный момент ( спин ) s = ½ в единицах ℏ, где ℏ — приведённая постоянная Планка).
« Как и любая заряженная частица со спином, электрон обладает магнитным моментом, причём магнитный момент делится на нормальную часть и аномальный магнитный момент (добавка примерно 0,116 %). Магнитный момент электрона μe = -9,2847647043(28)⋅10−24 Дж/Тл. »
Википедия
Атомы и молекулы.
Электроны связаны с ядрами атомов «притягивающей» кулоновской силой. Такой состав из атомного ядра и одного или нескольких электронов называется атомом. Электроны движутся вокруг ядра атома. Если число электронов отличается от заряда ядра, то это ион.
Волновая природа связанных электронов описывается атомными орбиталями. Каждая из этих орбиталей имеет ряд квантовых чисел, таких как энергия и момент. Кроме того, у атома может быть только дискретное число орбиталей. В силу принципа Паули на орбитали может находиться максимум два электрона, спин которых имеет разные знаки.
Химическая связь между атомами возникает благодаря электромагнитным взаимодействиям, которые описываются с помощью квантовой физики. Самые прочные связи создаются путем обмена или передачи электронов. Это позволяет образовывать молекулы. В молекулах электроны движутся аналогично атомам и занимают молекулярные орбитали. Однако фундаментальным отличием является образование пар электронов с разными спинами. Это позволяет нескольким электронам занимать одну орбиталь без нарушения принципа Паули.
Делимость электрического заряда
Хорошо известно, что молекулы и атомы в их нормальном состоянии не имеют электрического заряда. Поэтому мы не можем объяснить электризацию их движением. Однако если мы предположим, что частицы с электрическим зарядом существуют в природе, то мы должны обнаружить, что существует предел деления электрического заряда.
Согласно различным экспериментам, проведенным советским ученым Абрамом Федоровичем Иоффе и американским ученым Робертом Милликеном, было обнаружено, что существует заряженная частица с минимальным зарядом, который невозможно разделить.
В своих экспериментах они электризовали маленькие частицы цинковой пыли. Заряд пылинок меняли и вычисляли. Это было проделано несколько раз. При этом заряд оказывался каждый раз другим. Однако все изменения были кратны целому числу, большему, чем некоторый минимальный заряд (т.е. 2, 3, 4 и т.д.). Этот результат можно интерпретировать только следующим образом. Только наименьший заряд (или целое число таких зарядов) присоединяется к пылинке цинка или отсоединяется от нее. Этот заряд дальше уже не делится. Частица с наименьшим зарядом называется электроном.
Также в ходе опытов было установлено, что любая частица вещества либо электрически нейтральна, либо имеет заряд, кратный по модулю заряду электрона.
Свойства электрона
Электрон характеризуется и другими важными свойствами, помимо спина и магнитного момента. Рассмотрим их.
Масса электрона
Электроны очень малы. Масса электрона составляет me = 9,109 • 10-31 кг или 5, 489 • 10-4 атомных единиц массы (а. е. м). Эта масса примерно в 3700 раз меньше массы молекулы водорода, которая является самой маленькой из всех молекул. Из-за эквивалентности массы и энергии в соответствии с принципом относительности это приводит к энергии покоя 0,511 МэВ (мегаэлектронвольт).
Отношение массы протона к массе электрона равно 1836, то есть протон в 1836 раз «тяжелее» электрона.
Заряд электрона
Электрический заряд — одно из основных свойств электрона. Невозможно представить, что с электронов можно снять заряд. Они неотделимы друг от друга.
Электрический заряд — это физическая величина. Она обозначается буквой q. Единицей электрического заряда является кулон (Кл). Эта единица названа в честь французского физика Шарля Кулона. Электрон — это частица с наименьшим отрицательным зарядом. Его заряд равен e0 = — 1,6 • 10-19 Кл.
Модуль заряда электрона назвали элементарным электрическим зарядом. Его обозначают е. Измерения показали, что e = 1,6 • 1019 Кл.
Обратите внимание, что любой, даже самый малый, заряд тела содержит целое число элементарных зарядов. Так как заряд тела обозначается буквой q, то получаем: q = eN, где N — целое число (N = 1, 2, 3, … ).
Элементарный заряд может показаться очень малым, однако вспомним: в любом теле, видимом невооружённым глазом, содержится невообразимо большое число заряженных частиц. Так, суммарный заряд электронов в одной столовой ложке воды равен по модулю примерно миллиону кулонов (а вы уже знаете, как велик заряд всего в 1 Кл).
Важно! Термин элементарный заряд был придуман, когда предположили, что этот заряд является наименьшим электрическим зарядом в природе. Сегодня мы знаем, что 1/3 элементарного заряда также приходится на кварки.
Энергия покоя электрона
Энергия электрона рассчитывается из эквивалентности массы и энергии. Вы знаете это как формулу из теории относительности E=mc2. E означает энергию, m — массу, а c — скорость света. Как было уже сказано выше в этой статье: «из-за эквивалентности массы и энергии в соответствии с принципом относительности это приводит к энергии покоя 0,511 МэВ (мегаэлектронвольт)».
В формуле это можно рассчитать следующим образом: E = mec2 = 9,109 • 10-31 • (3 • 108 )2 = 8,2 • 10-14 Дж = 0,511 • 106 эВ ≈ 0,511 МэВ
Список литературы
Список литературы
- Тихомирова С. А., Яворский Б. М. Физика (базовый уровень) – М.: Мнемозина, 2012.
- Перышкин А. В. Физика 8. – М.: Дрофа, 2010.
- Бронштейн М. П. Атомы и электроны. — М.: Наука. — 1980. — 152 с., Библиотечка «Квант», вып. 1. Тир. 150000 экз.
Создание работы лабораторного практикума «Определение заряда электрона»
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Кувайцев Д.А. 1
1Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа № 19 имени Героя Советского Союза Ивана Петровича Мытарева города Димитровграда Ульяновской области»
Хайруллова Е.В. 1
1Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа № 19 имени Героя Советского Союза Ивана Петровича Мытарева города Димитровграда Ульяновской области
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
ВВЕДЕНИЕ
Изучая физику, я столкнулся с такой постоянной величиной, как заряд электрона. Он равен: . Заряд электрона был определен в 1874 году. Я задумался, как такую маленькую величину смогли определить более чем сто лет назад? В то время не существовало компьютеров и мощных вычислительных машин. Значит и сегодня можно повторить эти рассуждения и эксперименты в школьном кабинете физики на уроках лабораторного практикума. И показать одноклассникам, что компьютер это не единственное средство в изучении нашего мира.
Цель моей работы: Создать для кабинета физики школы работу лабораторного практикума по теме: «Определение заряда электрона»
Задачи, которые стояли передо мной были следующие:
1) Изучить закон Фарадея.
2) Познакомиться с процессом электролиза.
3) Изучить метод определение заряда электрона через закон Фарадея и подобрать к нему оборудование.
4)Экспериментальным путем определить заряд электрона.
5)Разработать описание лабораторной работы по теме: «Определение заряда электрона».
Проблема, стоящая передо мной, заключалась в следующем: Выяснить, можно ли на экспериментальной установке из доступных приборов определить заряд электрона.
Объект изучения: Закон Фарадея и процесс электролиза. Предмет изучения: Заряд электрона. Продукт проекта: Лабораторная работа по теме: «Определение заряда электрона»
Явление электролиза было открыто в начале 19 века. Законы электролиза сформулированы Майклом Фарадеем в 1833 году. С тех пор были обнаружены с помощью электролиза такие элементы как галлий, фтор. Электролиз широко применяют в технике для различных целей. Электролитическим способом покрывают поверхность металла тонким слоем другого металла для защиты от коррозии. При помощи электролиза осуществляют очистку металла от примесей. С помощью электролиза получают электронные платы для различных электронных изделий. Я изучил явление электролиза и на его основе создал установку по определению заряда электрона для лабораторного практикума по физике в старших классах.
ОСНОВНАЯ ЧАСТЬ
Электрический ток в жидкостях
Жидкости, как и твердые тела, могут быть проводниками электрического тока. В растворах и расплавах солей происходит распад молекул соли на ионы под действием молекул воды. Молекулу воды можно представить диполем. В той части молекулы, где находится атом кислорода, скапливается отрицательный заряд, так как атомы водорода отдают валентные электроны кислороду. А в той части молекулы воды, где находятся атомы водорода, скапливается положительный заряд. (Рис.1)
Рис.1.
Диполи воды своим положительным краем подходят к отрицательному иону кислотного остатка, а отрицательным краем к положительному иону металла соли. В результате теплового движения диполи воды растаскивают молекулы соли на катионы металла и анионы кислотного остатка. Таким образом, в растворе соли всегда имеются её положительные и отрицательные ионы. (Рис.2)
Рис. 2.
В моем случае происходит диссоциация молекулы сульфата меди на анионы сульфатного остатка SO4 и катионы меди Cu.
Наряду с процессом диссоциации молекул в растворах электролитов происходит и обратный процесс, объединение разных ионов в одну молекулу при их сближении, который называется рекомбинацией. При создании в электролите внешнего электрического поля путем опускания в раствор медного купороса CuSO4 разноименно заряженных электродов, возникает направленное движение ионов. Положительные ионы меди движутся к отрицательному электроду, а отрицательные ионы кислотного остатка к положительному электроду. (Рис.3)
Рис.3.
Д остигнув катода, ионы меди нейтрализуются избыточными электронами, находящимися на катоде. Образовавшиеся в результате реакции нейтральные атомы меди оседают на катоде.
Таким образом, прохождение тока через раствор соли сопровождается явлением электролиза, то есть выделением на электродах веществ, входящих в состав электролита, при протекании через его раствор электрического тока. Явление электролиза было открыто в 1800г. Английскими учеными: У. Никольсоном и А. Карлейлем.
Законы Фарадея
Масса вещества, выделившегося на электроде, прямо пропорциональна заряду, прошедшему через раствор электролита.
Найдем массу вещества, выделяющегося на электроде за определенный промежуток времени t. Эта масса равна массе всех ионов, осевших на электроде за это время:
где mi-масса одного иона.
Полный заряд Q всех ионов, прошедших через раствор на электрод, пропорционален заряду qi каждого иона:
Из этой формулы получаем
Тогда масса выделившегося на электроде вещества
Коэффициент пропорциональности , учитывая, что и , где n– валентность вещества. Из первого закона Фарадея получаем второй
Определение заряда электрона
Из второго закона Фарадея получаем формулу для расчета элементарного заряда:
Учитывая, что молярная масса меди 0,06355 кг/моль и валентность меди равна 2 необходимо в эксперименте измерить силу тока в цепи, время его протекания и массу выделившейся на электроде меди .
Электрическая цепь установки для определения заряда электрона должна содержать амперметр, для измерения силы тока, электроды, опущенные в раствор медного купороса, ключ и источник постоянного тока. Все элементы цепи должны быть соединены последовательно. Так же необходимы весы для измерения массы меди и часы для измерения времени протекания тока через раствор медного купороса. (Рис. 4)
(Рис. 4.)
Экспериментальная часть
В первой попытке создания установки источником тока служил гальванический элемент « Крона 9V», в качестве электродов были выбраны два гвоздя. (Приложение 1) После многочисленных попыток, я понял, что оба электрода темнеют, и на них не остается медь, следовательно, в качестве электродов нужно было использовать другой металл. (Приложение 2) Я решил изменить опыт. Заменил электроды медными пластинками, источник тока оставил «Крону 9V», убрал амперметр и добавил в цепь реостат и вольтметр для определения силы тока. (Приложение 3). В результате опыта я заметил, что один электрод стал оранжевым, что свидетельствовало о том, что на нем выделилась медь, а другой остался без изменений. (Приложение 4) Опыт получился, но т. к. я использовал весы с точностью 0.1г, то не смог обнаружить увеличение массы пластины из-за выделения на ней меди. Я несколько раз повторил опыт, но разницы в массах электрода так и не заметил. Перед постановкой следующего эксперимента сначала изучил он-лайн модель установки, представленной в интернете. (Определение заряда электрона и числа Фарадея.4.) (Приложение 5) Она состояла из того же оборудования, что и моя принципиальная схема, но в качестве источника питания использовался лабораторный выпрямитель, который давал силу тока в 2А. Поэтому следующий эксперимент был поставлен с лабораторным выпрямителем. При силе тока в 2А и времени протекания 600с изменение массы электрода составило 0,4 г (Приложение 6) . По второму закону Фарадея я рассчитал заряд электрона. (Приложение 7) Выполнив измерения и вычисления, получил данные, представленные в приложении 8. Я провел эксперимент три раза и по результатам трех опытов вычислил среднее значение заряда электрона. (Приложение 8) . Оно совпало с табличным значением:
ЗАКЛЮЧЕНИЕ
Выводы
В ходе работы над проектом я работы я получил следующие результаты:
Познакомился с процессом электролиза и законом Фарадея;
Изучил метод определение заряда электрона через закон Фарадея и подобрал к нему оборудование;
Выяснил наилучшие условия постановки эксперимента;
Экспериментальным путем определил заряд электрона.
Разработал описание лабораторной работы по теме: «Определение заряда электрона».
Описание работы передано моему руководителю для проведения этой работы на уроках практикума. Хотя эксперимент лабораторной работы кажется простым с первого взгляда, но для получения результата необходимо знать наилучшие условия для его проведения. Я сделал множество попыток, имея в распоряжении справочные материалы, пока не добился результата. Поэтому вызывает особое уважение труд первооткрывателей научных знаний и их мастерство экспериментаторов. Проект будет интересен не только мне, но и ученикам нашей школы и ученикам других школ. Для реализации проекта нужны приборы, которые имеются в кабинете физики любой школы. Для реализации проекта участники должны иметь базовое знание физики и иметь навыки работы с электрическим оборудованием.
Результаты
Продуктом моего проекта является описание работы лабораторного практикума.
Работа лабораторного практикума по теме: «Определение заряда электрона»
Цель работы: Научиться определять заряд электрона экспериментальным путем.
Теоретическое обоснование: Масса вещества, выделившегося на электроде, прямо пропорциональна заряду, прошедшему через раствор электролита.
Найдем массу вещества, выделяющегося на электроде за определенный промежуток времени t. Эта масса равна массе всех ионов, осевших на электроде за это время:
, где mi-масса одного иона.
Полный заряд Q всех ионов, прошедших через раствор на электрод, пропорционален заряду qi каждого иона:
Тогда масса выделившегося на электроде вещества .
Коэффициент пропорциональности , учитывая, что и , где n– валентность вещества. Из первого закона Фарадея получаем второй
Из второго закона Фарадея получаем формулу для расчета элементарного заряда:
Учитывая, что молярная масс меди 0,06355 кг/моль и валентность меди равна 2, необходимо в эксперименте измерить силу тока в цепи, время его протекания и массу выделившейся на электроде меди.
Оборудование: источник тока, ключ, амперметр, раствор медного купороса, анод и катод (медные пластинки), соединительные провода, емкость, электронные весы, секундомер
Порядок выполнения работы:
Подготовьте таблицу для записи результатов измерений.
|
Время t, с |
Сила тока I,А |
m0нач.,г |
m1конеч.,г |
m=m1-m0, кг |
Взвесьте на весах катод (m0)
Соберите электрическую цепь.
Наполните сосуд насыщенным раствором медного купороса.
Замкните цепь. Наблюдайте на протяжении опыта в течении 10-15 минут за показаниями амперметра. Так как показания амперметра могут изменяться, то регулируйте значение тока ручкой выпрямителя.
Разомкните цепь, извлеките из сосуда с медным купоросом катод и взвесьте его на весах. (m1) Полученный результат запишите в таблицу
Найдите разницу массы катода до начала опыта и после его окончания. (m) Полученный результат запишите в таблицу. Это значение показывает массу налипшей на катод меди.
Подставьте данные значения в формулугде M-молярная масса, I- -сила тока в электролите, NА– постоянная Авогадро, m -изменение массы катода, t- время прохождения тока через электролит.
Рассчитайте значение заряда электрона. Сравните полученное значение заряда с табличным значением. Ваше показание и табличные данные расходятся? Если да, то запишите почему.
Запишите вывод.
ЛИТЕРАТУРА
Касьянов В.А. Физика 10 класс. Углубленный уровень, Москва, «Дрофа», 2018 год.
Библиотека по физике. http://physiclib.ru/books/item/f00/s00/z0000058/st033.shtml
Мякишев Г. Я., Буховцев Б. Б., Сотский Н.Н. Физика 10 класс. Учебник для общеобразовательных учреждений, Москва, «Просвещение», 2011 год.
Определение заряда электрона и числа Фарадея. Видеоуроки. https://www.youtube.com/watch?v=phzGQXi4Hys
Электролиз. Статья из Википедии. https://ru.wikipedia.org/wiki/%D0%AD%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%BE%D0%BB%D0%B8%D0%B7
Электролиз. Статья. http://electricity-automation.com/page/elektroliz-bazovoye-predstavleniye
ПРИЛОЖЕНИЯ
Приложение 1
Электрическая схема опыта №1
Приложение 2
Результат опыта №1
Приложение 3
Электрическая схема опыта №2
Приложение 4
Результат опыта №2
Приложение 5
Вид установки эксперимента из интернета
Приложение 6
Фотография установки для определения заряда электрона
Приложение 7
Фотографии выполнения эксперимента по определению заряда электрона
Приложение 8
Таблица результатов экспериментов
|
№ |
I, A |
t, c |
m0, г |
m1, г |
m,кг |
Q, 10-19Кл |
Q10-19ср |
|
1 |
2 |
600 |
11.3 |
11.7 |
0.0004 |
1.58 |
|
|
2 |
2 |
602 |
11.3 |
11.701 |
0.0004 |
1.58 |
1,583 |
|
3 |
2 |
615 |
11.3 |
11.73 |
0.00043 |
1.59 |
Просмотров работы: 2574
Исследовательская работа
«Определение заряда
электрона»
Выполнил: ученик Стариков
Артём
Учитель физики: Сенчик
Максим Максимович
Школа физиков «Спектр»
МБОУ «Богашевская СОШ им. А.
И. Фёдорова» Томского района
2018 год
Введение
Заряд электрона (e) – одна из фундаментальных постоянных, которая определяет
наименьшее значение электрического заряда, наблюдаемое у элементарных частиц.
Заряд любого тела кратен элементарному заряду ().
Используя закон Фарадея, ирландский физик Джордж Стони рассчитал
значение заряда электрона Кл и
предложил назвать эту величину электроном.
В 1897 году, исследуя катодные лучи, английский физик Джозеф
Томсон открыл первую элементарную частицу, обладающую отрицательным зарядом. В
1909 году американский физик Роберт Милликен на основе этого эксперимента точно
определил заряд этой элементарной частицы, и он оказался равен заряду,
высчитанному Стони. Элементарная частица получила название электрона.
Изучение электрона, явлений, связанных с ним и его движением,
позволило не только объяснить многие явления как электричество, магнетизм и
свет, но и предсказать новые явления, свойства, что привело к появлению в 20
веке квантовой физики.
Электролиз
Электрический ток в металлах не сопровождается никакими
химическими процессами, что объясняется тем, что ток в металлах переносят
электроны. Но в некоторых проводниках — растворах электролитов и расплавах —
ток сопровождается определёнными химическими изменениями.
Соединим последовательно с источником тока лампу и электрическую
ванну с дистиллированной водой, в которую опустим угольные электроды. Замкнув
цепь, мы увидим, что лампа не загорится — химически чистая вода практически не
проводит ток. Но если мы растворим в воде какую-либо соль, например, медный
купорос, то лампа загорится, а на катоде выделится медь из раствора (рис. 1).
Рис. 1
Когда через раствор протекает электрический ток, с зарядом всегда
переносится вещество — это явление называется электролизом. Соответственно, в
этих проводниках носителями тока являются ионы.
Когда в воде растворяют соли, кислоты или щелочь, нейтральные молекулы
этих веществ расщепляются на положительные и отрицательные ионы. Растворы
электролитов всегда имеют какое-нибудь количество катионов — положительных
ионов — и анионов — отрицательных ионов. Они передвигаются беспорядочно, пока
отсутствует электрическое поле. Но когда оно появляется, катионы начинают
двигаться к катоду, а анионы — к аноду (рис. 2).
Рис. 2
Закон Фарадея
С помощью электронной теории можно вычислить массу веществ, выделившихся
на электроде при электролизе. Эта масса m равна произведению массы
одного электрона m0 на число ионов n, которые осели на
электроде, то есть . Масса
одного иона , где M —
молярная масса вещества, NA — постоянная Авогадро. Число
осевших на электроде ионов можно выразить через заряд Q, прошедший через
электролит, и заряд одного иона q0: .
Соответственно,
.
Заряд любого иона равен заряду одновалентного иона e,
умноженного на валентность иона n: . Таким образом,
. (1)
Из формулы (1) следует, что масса вещества, выделившегося на
электроде, пропорциональна заряду, прошедшему через раствор. Эту зависимость
экспериментально установил Майкл Фарадей в 1930-х годах, поэтому формула (1)
стала носить название закона Фарадея.
Вычисление заряда электрона
Пользуясь законом Фарадея, можно вычислить заряд электрона. Из
формулы (1) получаем:
.
Чтобы определить заряд электрона, нужно в опыте с электролизом какого-нибудь
раствора, например медного купороса, определить массу выделившейся меди,
продолжительность опыта и силу тока. Тогда можно вычислить заряд электрона,
зная молярную массу меди и ее валентность.
Проведение экспериментов
Я решил экспериментально определить заряд электрона. Для этого
была нарисована схема электрической цепи (рис. 3). Собранная схема показана на
фотографии 1. Отдельно элементы цепочки показаны на фотографиях 2, 3 и 4.
Рис. 3
Фотография 1 Фотография 2
Фотография 3 Фотография 4

График 2

После того как в кюветку (фотография 2) налили раствор медного
купороса и собрали электрическую цепь, подключают источник тока (ВСШ-6).
Изменение тока, протекающего через раствор, показано на графике 1. Поскольку в
процессе эксперимента сила тока менялась (см. график 1), использовали его
среднее значение. Эксперимент проводили в течение 10 минут. На основании
проведенных измерений определяем значение заряда электрона по формуле . Постоянные
значения внесены в таблицу 1.
|
M (кг/моль) |
n |
NA (моль-1) |
t (с) |
|
|
2 |
|
600 |
Таблица 1
Было проведено 8 экспериментов, результаты 2 экспериментов ближе
всего к табличному значению e. Значения, полученные во время более экспериментов,
внесены в таблицу 2.
|
№ |
m1 (10-3 |
m2 (10-3 |
m (10-3 кг) |
Iср (A) |
e (Кл) |
|
1 |
4,37 |
4,45 |
|
0,423 |
|
|
2 |
4,68 |
4,77 |
|
0,438 |
|
|
3 |
4,46 |
4,54 |
|
0,384 |
|
|
4 |
4,60 |
4,65 |
|
0,438 |
|
|
5 |
4,74 |
4,88 |
|
0,311 |
0, |
|
6 |
4,33 |
4,43 |
|
0,4 |
|
|
7 |
4,52 |
4,60 |
|
0,361 |
|
|
8 |
4,59 |
4,66 |
|
0,275 |
|
Таблица 2
Вычислим среднее значение заряда электрона:
Получили
, что близко
к табличному значению .
Вычислим
погрешность вычислений:
Соответственно,