Так
как выборочный коэффициент
вычисляется по выборочным данным, то
он является случайной величиной.
Если
,
то возникает вопрос: объясняется ли это
действительно существующей линейной
связью между
и
или вызвано случайными факторами?
Проверим
нулевую
гипотезу
о том, что в генеральной совокупности
отсутствует корреляция
:
,
а отличие от нуля выборочного коэффициента
корреляции объясняется только случайностью
выборки.
Альтернативная
гипотеза
может быть одной из видов: двусторонней
:
(если не известен знак корреляции); или
односторонней
:
или
:
(если знак корреляции может быть заранее
определен).
Способ
1. Для проверки
гипотезы используется
–критерий
Стьюдента.
Вычисляется эмпирическое значение
-критерия
Стьюдента по формуле
,
где
– выборочный коэффициент корреляции,
– объем выборки.
Вычисленное
эмпирическое значение
сравнивается с найденным по таблице
критическим значением
при выбранном уровне значимости
и числе степеней свободы
для двустороннего критерия.
Критическая
область задается неравенством
.
Если
,
то принимается нулевая гипотеза. Значит,
в генеральной совокупностиотсутствует
значимая корреляция,
а отличие от нуля выборочного коэффициента
корреляции объясняется только случайностью
выборки.
Если
,
то нулевая гипотеза отклоняется. Делаем
выводы:
-
для
двусторонней альтернативной гипотезы
– коэффициент корреляции значимо
отличается от нуля; -
для
односторонней гипотезы – существует
статистически значимая положительная
(или отрицательная) корреляция.
Способ
2. Можно
воспользоваться также
таблицей критических значений коэффициента
корреляции,
из которой находим
величину критического значения
коэффициента корреляции
по числу степеней свободы
и уровню значимости
.
Если
,
то в генеральной совокупностиотсутствует
значимая корреляция между исследуемыми
признаками,
а отличие от нуля выборочного коэффициента
корреляции объясняется только случайностью
выборки либо объем выборки недостаточен
для выявления линейной связи.
Если
же
,
то делается вывод, что коэффициент
корреляции значимо отличатся от 0 исуществует
статистически значимая корреляция.
Так,
одни явления могут одновременно, но
независимо друг от друга (совместные
события) происходить или изменяться
(ложная
регрессия). Другие – находиться в
причинной зависимости не друг с другом,
а по более сложной причинно-следственной
связи (косвенная
регрессия). Таким образом, при значимом
коэффициенте корреляции окончательный
вывод о наличии причинно-следственной
связи можно сделать только с учетом
специфики исследуемой проблемы.
Пример
2. Определить
значимость выборочного коэффициента
корреляции, вычисленного
в примере 1.
Решение.
Выдвинем
гипотезу
:
о том, что в генеральной совокупности
отсутствует корреляция. Так как знак
корреляции в результате решения примера
1 определен – корреляция положительна,
то альтернативная гипотеза является
односторонней вида
:
.
Найдем
эмпирическое значение
-критерия:
Число
степеней свободы равно
,
уровень
значимости выберем равным
.
По таблице «Критические значения
-критерия
Стьюдента при различных уровнях
значимости» находим критическое значение
.
Так
как
,
то между уровнем
и средним уровнем успеваемости по
математике существует статистически
значимая корреляция.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Савельева А.С.
1
Черненко Н.А.
1
1 ФГБОУ ВО «Ставропольский государственный аграрный университет»
Исследователя нередко интересует, как связаны между собой две или большее количество переменных в одной или нескольких изучаемых выборках. Например, может ли рост влиять на вес человека или может ли давление влиять на качество продукции? Такого рода зависимость между переменными величинами называется корреляционной, или корреляцией. Задача корреляционного анализа сводится к установлению направления (положительное или отрицательное) и формы (линейная, нелинейная) связи между варьирующими признаками, измерению ее тесноты, и, наконец, к проверке уровня значимости полученных коэффициентов корреляции. В статье рассматривается применение корреляционного анализа с расчетом коэффициентов корреляции Стьюдента. Изложенный материал дает общие сведения об оценке степени тесноты взаимосвязи между переменными.
корреляционный анализ
коэффициенты корреляции
выборка
переменные
случайные колебания
генеральная совокупность
1. Бондаренко В.А., Донец З.Г., Цыплакова О.Н. Теория игр и финансовые рынки // Финансово-экономические и учетно-аналитические проблемы развития региона: материалы Ежегодной 78-й научно-практической конференции. – 2014. – С. 231–236.
2. Бондаренко В.А., Мамаев И.И., Сахнюк П.А., Сахнюк Т.И. Решение задачи планирования посевов с использованием теории игр // Экономические, инновационные и информационные проблемы развития региона: материалы Международной научно-практической конференции. – 2014. – С. 56–62.
3. Бондаренко Д.В., Бражнев С.М., Литвин Д.Б., Варнавский А.А. Метод повышения точности измерения векторных величин // Наука Парк. – 2013. № 6 (16). – С. 66–69.
4. Гулай Т.А., Литвин Д.Б., Попова С.В., Мелешко С.В. Прогнозирование в регрессионном анализе при построении статистических моделей экономических задач с помощью программы Microsoft excel // Экономика и предпринимательство. – 2017. – № 8–2 (85–2). – С. 688–692.
5. Долгополова А.Ф., Гулай Т.А., Литвин Д.Б. Финансовая математика в инвестиционном проектировании (учебное пособие) // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 8–2. – С. 178–179.
6. Долгополова А.Ф., Гулай Т.А., Литвин Д.Б. Совершенствование экономических механизмов для решения проблем экологической безопасности // Информационные системы и технологии как фактор развития экономики региона. II Международная научно-практическая конференция, 2013. – С. 68–71.
7. Литвин Д.Б. Дифференциальное исчисление в исследовании производственных моделей. // В сборнике: экономические приоритеты и информационный механизм устойчивого развития регионов России: Сборник научных статей Всероссийской научно-практической конференции, 2017. – С. 102–105.
8. Литвин Д.Б., Гулай Т.А., Жукова В.А., Мамаев И.И. Модель экономического роста с распределенным запаздыванием в инвестиционной сфере. // Вестник АПК Ставрополья. – 2017. № 2 (26). – С. 225–228.
9. Литвин Д.Б., Шепеть И.П. Моделирование роста производства с учетом инвестиций и выбытием фондов. // Социально-экономические и информационные проблемы устойчивого развития региона: Международная научно-практическая конференция. – 2015. – С. 114–116.
10. Литвин Д.Б., Шепеть И.П., Бондарев В.Г., Литвина Е.Д. Применение дифференциального исчисления функций нескольких переменных к разработке алгоритма определения координат объекта. // Финансово-экономические и учетно-аналитические проблемы развития региона: Материалы Ежегодной 78-й научно-практической конференции, 2014. – С. 242–246.
Как неоднократно отмечалось, для статистического вывода о наличии или отсутствии корреляционной связи между исследуемыми переменными необходимо произвести проверку значимости выборочного коэффициента корреляции. В связи с тем что надежность статистических характеристик, в том числе и коэффициента корреляции, зависит от объема выборки, может сложиться такая ситуация, когда величина коэффициента корреляции будет целиком обусловлена случайными колебаниями в выборке, на основании которой он вычислен. При существенной связи между переменными коэффициент корреляции должен значимо отличаться от нуля. Если корреляционная связь между исследуемыми переменными отсутствует, то коэффициент корреляции генеральной совокупности ρ равен нулю [9].
Как всякая статистическая характеристика, выборочный коэффициент корреляции является случайной величиной, т.е. его значения случайно рассеиваются вокруг одноименного параметра генеральной совокупности (истинного значения коэффициента корреляции) [1].
При отсутствии корреляционной связи между переменными у и х коэффициент корре ляции в генеральной совокупности равен нулю. Но из-за случайного характера рассеяния принципиально возможны ситуации, когда некоторые коэффициенты корреляции, вычисленные по выборкам из этой совокупности, будут отличны от нуля [5].
Процедура проверки значимости начинается с формулировки нулевой гипотезы H0. В общем виде она заключается в том, что между параметром выборки и параметром гене ральной совокупности нет каких-либо существенных различий. Альтернативная гипотеза H1 состоит в том, что между этими параметрами имеются существенные различия. Например, при проверке наличия корреляции в генеральной совокупности нулевая гипотеза заключается в том, что истинный коэффициент корреляции равен нулю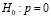 
. Если в результате проверки окажется, что нулевая гипотеза не приемлема, то выборочный коэффициент корреляции 
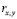значимо отличается от нуля (нулевая гипотеза отвергается и принимается альтернативная Н1) [7, 10].
При проверке значимости исследователь устанавливает уровень значимости α, который дает определенную практическую уверенность в том, что ошибочные заключения будут сделаны только в очень редких случаях. Уровень значимости выражает вероятность того, что нулевая гипотеза Н0 отвергается в то время, когда она в действительности верна. Ясно, что имеет смысл выбирать эту вероятность как можно меньшей [2].
Пусть известно распределение выборочной характеристики, являющейся несмещенной оценкой параметра генеральной совокупности. Выбранному уровню значимости α соответствуют под кривой этого распределения заштрихованные площади (см. рис. 1). Незаштрихованная площадь под кривой распределения определяет вероятность
.
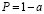Границы отрезков на оси абсцисс под заштрихованными площадями называют критическими значениями, а сами отрезки образуют критическую область, или область отклонения гипотезы [3].
Когда же надо убедиться в том, что одна величина в среднем строго больше или мень ше другой, используется односторонняя критическая область. Если распределение выборочной характеристики симметрично, то уровень значимости двусторонней критической области равен α, а односторонней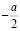 
(см. рис. 1). Далее мы лишь укажем критерии значимости для различных процедур, не останавливаясь на их построении [6].
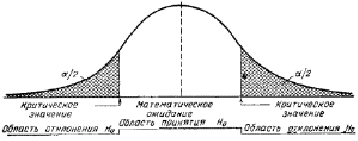
Рис. 1 Проверка нулевой гипотезы H0
Проверяя значимость коэффициента парной корреляции, устанавливают наличие или отсутствие корреляционной связи между исследуемыми явлениями. При отсутствии связи коэффициент корреляции генеральной совокупности равен нулю (p=0). Процедура проверки начинается с формулировки нулевой и альтернативной гипотез [8]:
Н0: различие между выборочным коэффициентом корреляции r и ρ = 0 незначимо,
Н1: различие между r и p=0 значимо, и следовательно, между переменными у и х имеется существенная связь. Из альтернативной гипотезы следует, что нужно воспользоваться двусторонней критической областью.
Выборочный коэффициент корреляции при определенных предпосылках связан со случайной величиной t, подчиняющейся распределению Стьюдента с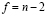 
степенями свободы [4].
Вычисленная по результатам выборки статистика
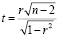(1)
сравнивается с критическим значением, определяемым по таблице распределения Стьюдента при заданном уровне значимости α и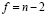 
степенях свободы. Правило применения критерия заключается в следующем: если 
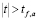, то нулевая гипотеза на уровне значимости α отвергается, т. е. связь между переменными значима; если
,
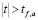то нулевая гипотеза на уровне значимости α принимается. Отклонение значения r от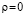 
можно приписать случайной вариации. Данные выборки характеризуют рассматриваемую гипотезу как весьма возможную и правдоподобную, т. е. гипотеза об отсутствии связи не вызывает возражений.
Рассмотрим на конкретном примере проверку гипотезы о значимости выборочного коэффициента корреляции.
Для 15 пар порядковых переменных (x, y) был вычислен коэффициент корреляции Спирмена, который оказался равным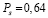 
. При уровне значимости 
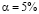проверить гипотезу H0 о равенстве генерального коэффициента ранговой корреляции нулю 
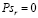при конкурирующей гипотезе 
.
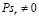Решение:
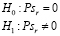
Постановка задачи:
Найдем наблюдаемое значение критерия:
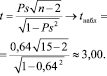
Найдем значения границ двусторонней критической области из условия, что при малых объемах выборок критерий t распределен (при справедливости нулевой гипотезы) по закону распределения Стьюдента с числом степеней свободы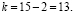 
На основе таблицы «Критические точки распределения Стьюдента» найдем границы двусторонней критической области на основе
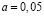и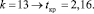 
Полученные результаты покажем графически (рис. 2).
Поскольку наблюдаемое значение критерия попало в критическую область, то следует отклонить нулевую гипотезу в пользу альтернативной гипотезы. Это означает, что коэффициент ранговой корреляции значим: между двумя порядковыми случайными величинами X и Y в генеральной совокупности имеется значимая связь, которая говорит о наличии связи этих двух случайных величин.
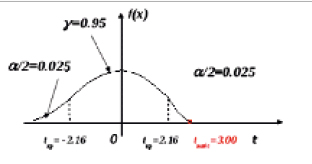
Рис. 2
Библиографическая ссылка
Савельева А.С.,Черненко Н.А. ПРОВЕРКА ЗНАЧИМОСТИ ДЛЯ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ // Международный студенческий научный вестник. – 2018. – № 3-1.
;
URL: https://eduherald.ru/ru/article/view?id=18221 (дата обращения: 20.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Корреляционный анализ
Корреляционный анализ – раздел математической статистики, исследующий зависимости между двумя или более случайными величинами. Термин «Correlation» означает взаимосвязь, взаимоотношение.
История разработки корреляционного анализа
Термин «корреляция» был впервые применил французский палеонтолог Ж.Кювье в 1806 году. Этот ученый вывел «закон корреляции частей и органов животных», позволяющий восстанавливать по найденным частям тела облик всего животного. Математическое обоснование метода предложено О. Браве в 1846 году, а применительно к биомедицинским исследованиям (речь идет о коэффициенте корреляции Пирсона) — Ф. Гальтоном в 1886 году (Г.Ф. Лакин, 1990).
Функциональная зависимость и корреляция
Еще Гиппократ обратил внимание на то, что между телосложением и темпераментом людей, между строением их тела и предрасположенностью к заболеваниям существует определенная взаимосвязь.
В области физической культуры и спорта можно привести много примеров такой взаимосвязи. Например, от уровня силы во многом зависит результат, показанный спортсменом в таких видах спорта, как тяжелая атлетика, пауэрлифтинг, гиревой спорт, метание диска и толкание ядра и т.д. Результат в беге на 100 м во многом зависит от процента содержания в мышцах спортсменов быстрых мышечных волокон (II типа). Доказано, что у выдающихся спринтеров этот показатель превышает 80%. Чтобы определить, насколько сильна взаимосвязь между переменными (признаками) используется корреляционный анализ.
Две случайные величины X и Y могут быть:
- связаны функциональной зависимостью (жестко, как зависимость переменных в математическом анализе);
- независимыми;
- связаны стохастической (вероятностной зависимостью) при которой изменение одной величины влечет изменение распределения другой.
В качестве меры связи между случайными величинами используется коэффициент корреляции. Коэффициент корреляции для генеральной совокупности обозначается ρ. Однако, как правило, он неизвестен. Поэтому он оценивается по экспериментальным данным, представляющим выборку объема n, полученную при совместном измерении двух переменных (признаков) X и Y. Коэффициент корреляции, определяемый по выборочным данным называется выборочным коэффициентом корреляции (или просто коэффициентом корреляции). Его принято обозначать символом r. Наиболее часто в качестве оценок генерального коэффициента корреляции используется коэффициент корреляции Пирсона (r) и коэффициент корреляции Спирмена (rs).
Коэффициент корреляции Пирсона (r)
Чтобы правильно применять корреляционный анализ в научных исследованиях, нужно учитывать условия применения этого метода.
Условия, при которых возможен расчет коэффициента корреляции Пирсона:
- Экспериментальные данные должны быть представлены в только в интервальной шкале или шкале отношений.
- Распределение экспериментальных данных подчиняется нормальному закону.
- Предполагается линейная зависимость между случайными величинами X и Y.
Коэффициент корреляции Спирмена (rS)
При расчете коэффициента корреляции Спирмена требования к исходным данным менее строгие, а именно:
- Данные могут быть представлены в порядковой, интервальной шкале или шкале отношений.
- Допускается любой закон распределения случайных величин X и Y.
- Между случайными величинами X и Y должна существовать монотонно-возрастающая или монотонно-убывающая зависимость.
Свойства оценок коэффициентов корреляции
Рассчитанные коэффициенты корреляции могут принимать значения от -1 до +1.
- Если коэффициент корреляции равен: r =+1 и r = -1, это означает, что случайные величины X и Y связаны жесткой линейной зависимостью.
- Если r ≠ 0, то чем ближе |r| к единице, тем сильнее линейная зависимость случайных величин X и Y.
- Если коэффициент корреляции положительный (r > 0) – это означает, что между случайными величинами X и Y существует положительная корреляция (или другими словами положительная корреляционная зависимость). Примером положительной корреляционной зависимости является увеличение результата прыжка в длину с увеличением силы мышц ног (рис.1А).
- Eсли коэффициент корреляции отрицательный (r < 0) – это означает, что между случайными величинами X и Y существует отрицательная корреляция (или другими словами отрицательная корреляционная зависимость). Примером отрицательной корреляционной зависимости является уменьшение результата пробегания 100 м с увеличением силы мышц ног (рис. 1Б)
- Если коэффициент корреляции равен нулю (r = 0) – это означает, что корреляции нет; случайные величины X и Y некоррелированы (рис. 1В). Другими словами, это означает, что между случайными величинами X и Y нет взаимосвязи.
Геометрическая интерпретация коэффициента корреляции
Корреляция считается положительной, если график имеет выраженное направление из левого нижнего угла в правый верхний угол и с увеличением значений одной переменной другая также увеличивается;
Корреляция считается отрицательной, если график имеет направление из левого верхнего угла в правый нижний, и с увеличением одной переменной, другая уменьшается;
Корреляция отсутствует, когда у корреляционного облака нет четко выраженного направления, точки рассеиваются далеко от воображаемой прямой и нельзя сказать, что с увеличением одной переменной другая уменьшается или увеличивается.
Значимость коэффициента корреляции
Коэффициент корреляции между случайными величинами X и Y для генеральной совокупности как правило, неизвестен. Однако его можно оценить, рассчитав выборочный коэффициент корреляции (коэффициент корреляции Пирсона или Спирмена). Но при заменяя генеральную совокупность выборкой при оценке коэффициента корреляции допускается ошибка. Поэтому важно оценить значимость (достоверность) рассчитанного коэффициента корреляции.
Например, в эксперименте участвовало 10 человек. Оценивалась взаимосвязь между результатами в беге на 30 м и 100 м. Получен коэффициент корреляции r = 0,611. Чтобы оценить значимость коэффициента корреляции нужно сравнить его с критическим, величина которого зависит от объема выборки и уровня значимости. Если фактическое значение коэффициента корреляции больше, чем критическое, это означает, что коэффициент корреляции достоверен (значим). В нашем случае критическое значение коэффициента корреляции при n= 10 и α = 0,05 составляет r0,05 =0,632 (в таблице 1 это значение выделено жирным шрифтом). Из этого следует, что рассчитанный коэффициент корреляции статистически недостоверен. Приводить его в своих исследованиях нежелательно.
Таблица 1 — Критические значения коэффициента корреляции Пирсона
| n | 0,05 | 0,01 | 0,001 |
| 3 | 0,9969 | 0,999877 | 0,99999877 |
| 4 | 0,950 | 0,9900 | 0,9990 |
| 5 | 0,878 | 0,9597 | 0,99114 |
| 6 | 0,811 | 0,9172 | 0,9741 |
| 7 | 0,754 | 0,875 | 0,9509 |
| 8 | 0,707 | 0,834 | 0,9244 |
| 9 | 0,666 | 0,798 | 0,898 |
| 10 | 0,632 | 0,765 | 0,872 |
| 20 | 0,444 | 0,561 | 0,679 |
| 30 | 0,361 | 0,463 | 0,570 |
| 40 | 0,312 | 0,402 | 0,501 |
| 50 | 0,279 | 0,361 | 0,451 |
В итоговой таблице необходимо указать объем выборки, чтобы читающий мог оценить значимость (достоверность) вычисленных коэффициентов корреляции. Иногда в публикациях приводятся только значимые коэффициенты корреляции, а вместо незначимых ставится прочерк. В таблице 2 авторы указали, что объем выборки равен n = 32. Критическое значение коэффициента корреляции при n = 32 и a = 0,05 составляет r0,05 = 0,349 (В.С.Иванов, 1990). Следовательно, все коэффициенты корреляции достоверны.
Таблица 2 — Значения коэффициентов корреляции между результатами в скоростно-силовых тестах и результатом в толкании ядра с разгоном n=32, спортивный результат группы варьировал от 12,00 м до 20,50. Критическое значение коэффициента корреляции при n = 32 и a = 0,05 составляет r0,05 = 0,349 (по: Я.Е.Ланка, Ан.А.Шалманов, 1982).
| Упражнение | 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | Толкание ядра с разгона | 1 | 0,97 | 0,84 | 0,83 | 0,73 | 0,73 |
| 2 | Толкание ядра с места | 1 | 0,84 | 0,82 | 0,74 | 0,76 | |
| 3 | Бросок ядра назад | 1 | 0,85 | 0,71 | 0,66 | ||
| 4 | Бросок ядра вперед | 1 | 0,66 | 0,62 | |||
| 5 | Приседание со штангой | 1 | 0,58 | ||||
| 6 | Жим штанги лежа | 1 |
Литература
- Боровиков В.П., Боровиков И.П. STATISTICA Статистический анализ и обработка данных в среде Windows.– М.: Филинъ, 1995.– 608 с.
- Дюк В. Обработка данных на ПК в примерах.– СПб: Питер, 1997.– 240 с.
- Ежевская К.А. Особенности динамики показателей скоростных способностей детей 4-6 лет в условиях стандартной тестовой тренировочной программы в детском саду //Теория и практика физической культуры, 1995.– № 3 .–С.15-18.
- Жданов Л.Н. Возраст спортивных достижений //Теория и практика физической культуры, 1996.– № 6 .– С. 59-60.
- Зациорский В.М. Осторожно: статистика! // Теория и практика физической культуры, 1989.– № 2.– С. 52-55.
- Катранов, А.Г. Компьютерная обработка данных экспериментальных исследований / А.Г. Катранов, А.В. Самсонова /Учебное пособие.– СПб: СПбГАФК им. П.Ф. Лесгафта, 2005.– 132 с.
- Лакин Г.Ф. Биометрия .- М.: Высшая школа, 1990.- 350 с.
- Ланка Я.Е., Шалманов Ан. А. Биомеханика толкания ядра. – М: Физкультура и спорт, 1982.- 72 с.
- Лапшина Г.Г. Особенности физического состояния студенток гуманитарного факультета // Теория и практика физической культуры, 1989.–№ 4.– С. 18-20
- Марченко В.В., Дворкин Л.С., Рогозян В.Н. Анализ силовой подготовки тяжелоатлета в нескольких макроциклах //Теория и практика физической культуры, 1998.– № 8.– С. 18–22.
- Основы математической статистики: Учебное пособие для ин-тов физ. культ./ /Под ред. В.С.Иванова. М.: Физкультура и спорт, 1990.– 176 с.
- Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере.– М.: Финансы и статистика, 1995.– 384 с.
