На этой странице вы узнаете
- Как мы ежедневно расставляем знаки неравенства в жизни?
- Как быстро определить верное обозначение точки на прямой?
- Как правильно чередовать знаки на числовой прямой?
Решая уравнение, мы стремимся к тому, чтобы обе части были равны. Но существуют такие примеры, где мы заведомо знаем, что два выражения не могут быть равны между собой. Они называются неравенствами.
Метод интервалов
Неравенство — это алгебраическое выражение, в котором одна сторона имеет отличное от другой значение. В неравенствах обычно одна сторона больше другой.
Для записи неравенств используют знаки > , < , ≥ , ≤ .
При этом “>” и “<” — это строгие знаки неравенства, а “≥” и “≤” — нестрогие знаки неравенства.
Их отличие в том, что нестрогие знаки неравенства включают граничные точки в итоговый промежуток, а строгие — нет.
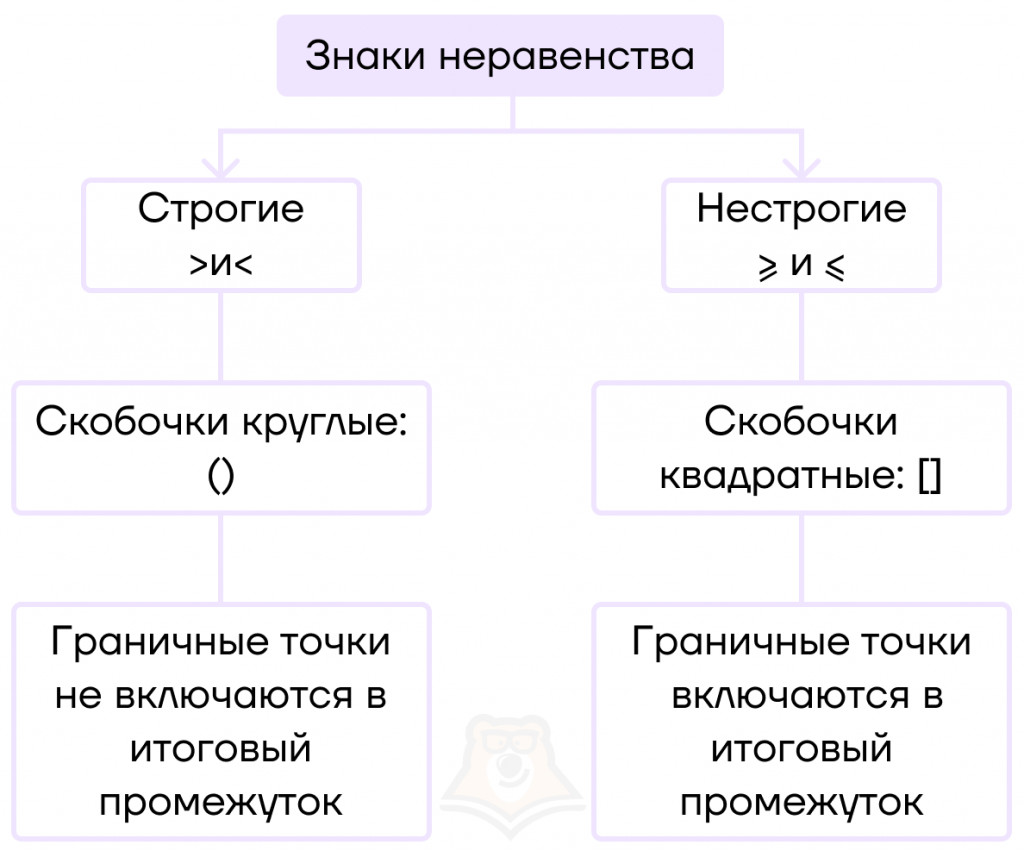
Посмотрим на привычные ситуации с точки зрения строгости знаков неравенства.
Например, возьмем известную игру “Камень, ножницы, бумага”.
Правила игры говорят нам, что камень всегда побеждает ножницы, а бумага побеждает камень. Если перенести это на язык неравенства, то получится:
Теперь зайдем в магазин цифровой техники и попробуем выбрать себе новый мобильный телефон. Задачка непростая, не так ли? Две разные модели могут настолько незначительно отличаться друг от друга своими характеристиками, что будут казаться почти одинаковыми. Тогда мы можем сказать, что они практически равны между собой, то есть неравенство нестрогое. Но один из них всё-таки понравился нам больше.
И каждый наш выбор, каждый шаг – это расстановка знака неравенства в настоящей жизни. Просто по бокам от него не цифры и переменные, а существующие ситуации и вещи.
Рассмотрим пример неравенства (х — 10)(х + 21) > 0.

Его можно решить несколькими способами. Например, вспомним, что положительным будет произведение двух положительных или двух отрицательных множителей, тогда получается совокупность из двух систем.
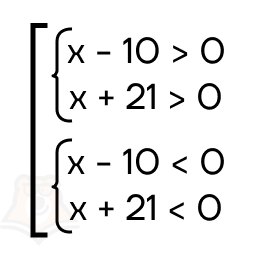
Однако этот способ решения очень трудоемкий и требует много времени. А если множителей будет больше, например, три или четыре, то время на решение в разы увеличивается.
Небольшой секрет тайм-менеджмента: как сократить время при решении неравенств? В таких случаях на помощь приходит метод интервалов.
Метод интервалов — специальный алгоритм решения для сложных неравенств вида f(x) > 0. При этом знак неравенства может быть любым.
Интервал — это промежуток на числовой прямой, ограниченный двумя различными числами.
Алгоритм решения неравенств методом интервалов
1 шаг. Перенести все части неравенства в одну сторону так, чтобы с другой остался только 0.
2 шаг. Найти нули функции, для этого необходимо решить уравнение f(x) = 0.
3 шаг. Начертить числовую прямую и отметить на ней все полученные корни. Таким образом, числовая прямая разобьется на интервалы.
4 шаг. Определить знаки на каждом интервале. Для этого необходимо подставить любое удобное значение в f(x) и определить, какой знак будет иметь функция на данном интервале.
Расставляя полученные корни на прямой, необходимо отмечать их точками. При этом от того, какая отмечена точка (выколотая или закрашенная), будет зависеть ответ.
- Если в неравенстве стоит строгий знак неравенства, то все точки на прямой должны быть выколотыми.
Таким образом, граничные точки не будут включены в итоговый промежуток. Для записи таких точек используют круглые скобочки. Например, в промежуток (2;3) включаются все значения от 2 до 3, но не включаются граничные точки.
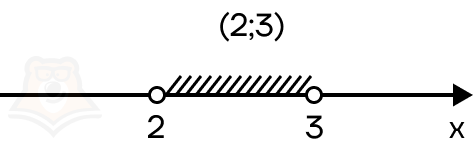
- Если в неравенстве стоит нестрогий знак неравенства, то найденные корни должны быть отмечены закрашенными точками.
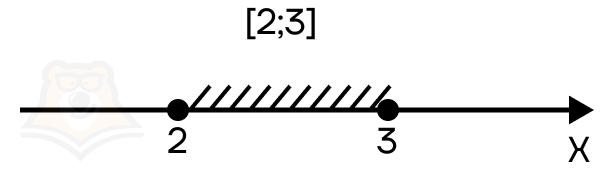
Это означает, что мы включаем их в итоговый промежуток. Для записи таких точек используют квадратные скобочки. Например, в промежуток [2;3] включаются все значения от 2 до 3, в том числе и граничные точки.
- Если в неравенстве появляются ограничения и некоторые точки нельзя взять в ответ, то такие точки должны быть выколотыми на числовой прямой, при этом знак самого неравенства может быть как строгим, так и нестрогим.
Например, если необходимо решить неравенство с дробью, то нули знаменателя на числовой прямой обязательно должны быть обозначены выколотыми точками.
В случае сомнений мы всегда можем проверить себя по простой схеме.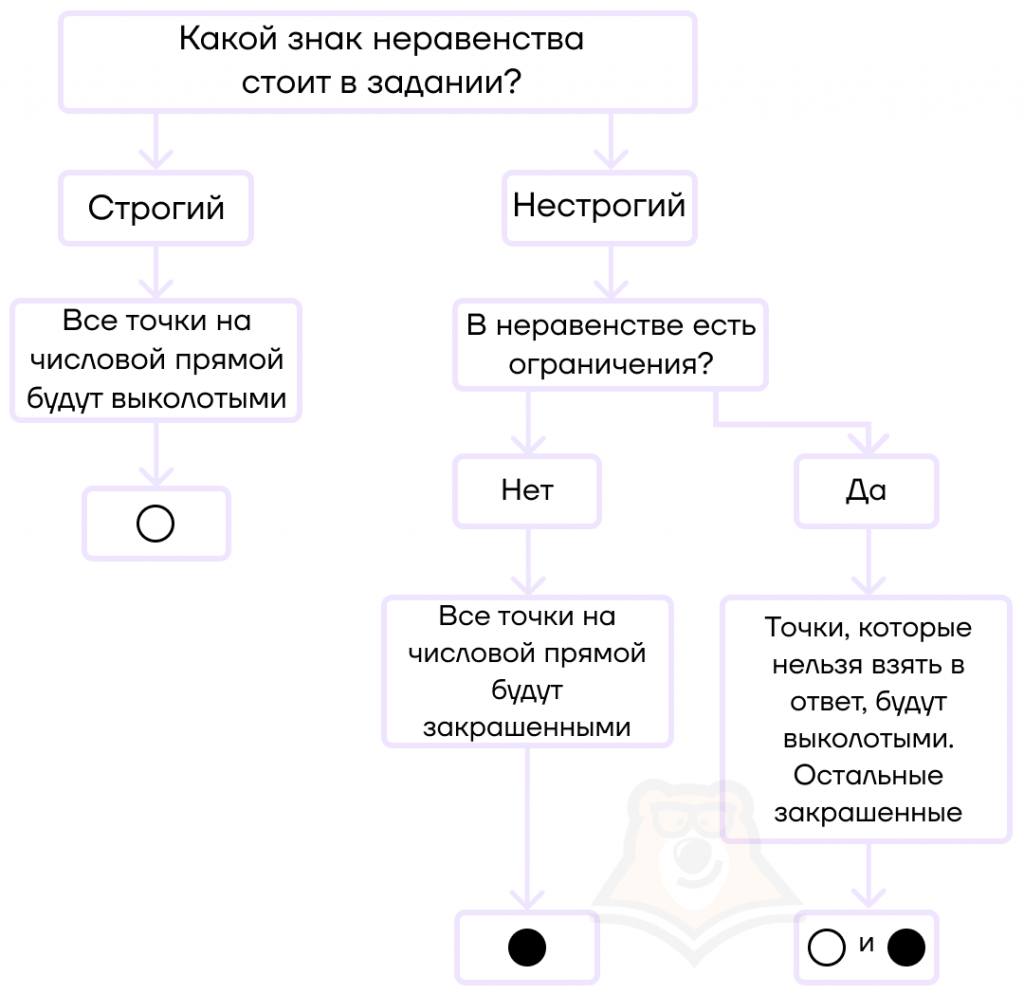
Вывод:
— если знак неравенства строгий, то все точки будут выколотыми;
— если знак неравенства нестрогий, то точки будут закрашенными, кроме тех точек, которые нельзя взять в ответ (например, они не удовлетворяют ОДЗ).
Стоит отметить, что непрерывная функция будет менять знак только в точках, в которых она равна 0. Подробнее узнать про смену знака функции можно в статье «Определение и график функции». Именно поэтому в методе интервалов мы ищем и отмечаем нули функции на прямой — только при переходе через них будет меняться знак функции.
При этом существует способ, с помощью которого можно быстро расставить знаки на прямой. Достаточно определить знак на одном из интервалов, а дальше чередовать знаки при переходе через каждую точку на прямой.
Правила чередования знаков:
- Если корень повторяется нечетное количество раз (то есть его степень нечетная), то знак при переходе на следующий интервал меняется.
- Если корень повторяется четное количество раз (его степень четная), то знак при переходе на следующий интервал не меняется.
Всегда будет нелишним перепроверить знак на каждом интервале, подставив значения в функцию, и убедиться в правильности расстановки знаков на прямой.
Но при расстановке можно пользоваться следующим алгоритмом, что значительно сократит время расстановки знаков. 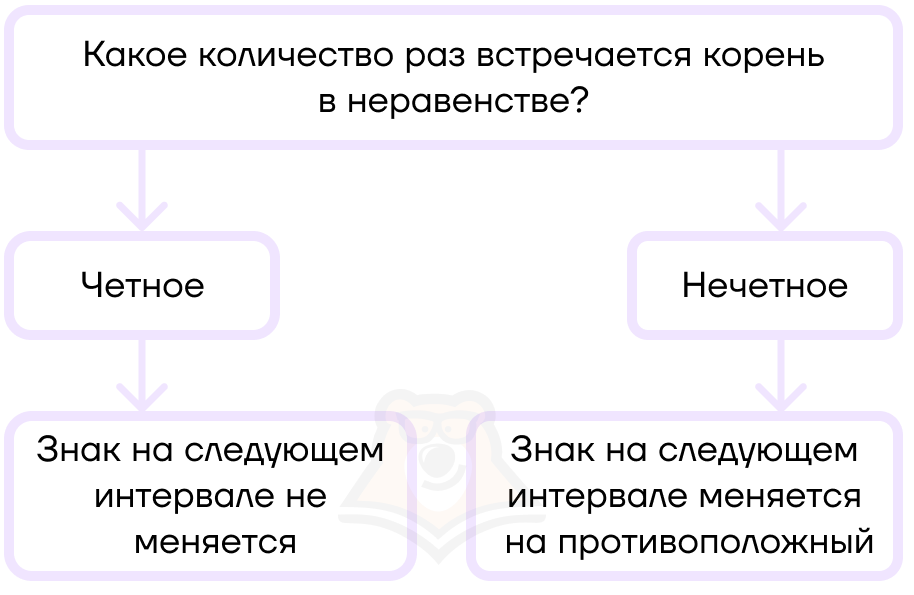
Методом интервалов можно решить практически любое неравенство в задании 14 из ЕГЭ по профильной математике, также он может понадобиться в заданиях 8, 11 и 17 «профиля» или в задании 17 ЕГЭ по базовой математике.
На ОГЭ данным методом можно воспользоваться при решении неравенств из первой и второй частей — №13 и №20.
Так что осваивайте метод и 2 балла ЕГЭ или 3 балла ОГЭ будут у вас в кармане. Обязательно следуйте алгоритму решения неравенств методом интервалов, тогда вы точно решите неравенство верно.
Практика
Рассмотрим несколько примеров, чтобы на практике разобрать применение метода интервалов для решения неравенств.
Пример 1. Решить неравенство x2 + 8x — 33 > 0.
Шаг 1. Первым шагом необходимо найти нули функции, для этого приравниваем выражение слева к 0: x2 + 8x — 33 = 0.
Шаг 2. Находим корни уравнения, получаем х = 3 и х = -11.
Шаг 3. Расставляем полученные корни на числовой прямой. Поскольку знак неравенства строгий, то точки должны быть выколотыми:

Шаг 4. Дальше необходимо определить знаки на каждом интервале. Для этого подставим х = -12 в x2 + 8x — 33. Получаем:
(-12)2 + 8*(-12) — 33 = 144 — 96 — 33 = 15.
Получается положительное число, следовательно, интервал от минус бесконечности до -11 положительный. Поскольку все корни в неравенстве повторяются нечетное количество раз (по одному разу), то знаки чередуются.
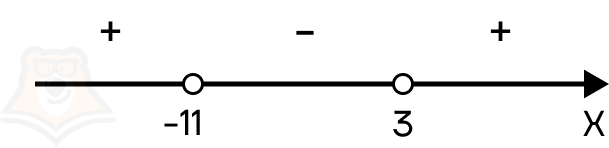
В ответ необходимо записать промежутки с положительным знаком, следовательно, ответом будет х ∈ (-∞; -11) U (3; +∞).
Пример 2. Решить неравенство (frac{2х^2 + 22х — 204}{(х-3)(х+5)} ≤ 0).
1. Находим нули функции.
Нули числителя: 2х2 + 22х — 204 = 0. Решая уравнение, получаем х = 6 и х = -17.
Нули знаменателя: (х — 3)(х + 5) = 0, следовательно, х = 3 и х = -5.
2. Расставляем полученные корни на числовой прямой. Нули числителя будут обозначены закрашенными точками, поскольку знак неравенства нестрогий. А вот нули знаменателя — выколотыми, поскольку знаменатель не может равняться 0, следовательно, и нули знаменателя не должны входить в итоговый промежуток.

3. Определяем знак на крайнем левом промежутке, подставляя х=-20 в дробь:
(frac{2(-20)^2 + 22(-20) — 204}{(-20 -3)(-20 +5)} = frac{2 * 400 — 440 — 204}{(-23) * (-15)} = 156345. )
Следовательно, промежуток положительный.
4. Поскольку каждый корень встречается один раз, то есть нечетное количество раз, то знаки будут чередоваться.

В ответ необходимо включить отрицательные промежутки. Следовательно, ответом будет х ∈ [-17; -5) U (3; 6].
Пример 3. Решить неравенство (frac{1}{х^2} ≥ frac{1}{х+2})
1. Первым делом следует отметить, что знаменатели не могут быть равны 0, следовательно, х2 ≠ 0 и х + 2 ≠ 0, отсюда получаем х ≠ 0 и х ≠ -2.
2. Теперь перенесем все части неравенства влево:
(frac{1}{х^2} — frac{1}{х+2} ≥ 0).
Приведем к общему знаменателю:
(frac{х + 2 — х^2}{х^2 (х + 2)} ≥ 0).
Для решения неравенства будет удобнее, если перед х2 в числителе будет стоять положительный знак, для этого умножим неравенство на -1.
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Получаем:
(frac{х^2 — х — 2}{х^2 (х + 2)} ≤ 0).
Теперь найдем нули функции.
Нули числителя: х2 — х — 2 = 0. Тогда х = -1 и х = 2.
Нули знаменателя: х = 0 и х = -2.
2. Расставим корни на числовой прямой, при этом нули числителя будут обозначены закрашенными точками, а нули знаменателя — выколотыми.

3. Определим знак на крайнем левом промежутке, подставив для этого х = -3 в дробь:
(frac{(-3)^2 — (-3) — 2}{(-3)^2 ((-3) + 2)} = frac{9 + 3 — 2}{9 * (-1)} = frac{10}{-9})
Промежуток отрицательный.
4. Дальше расставляем знаки, чередуя их. При этом следует заметить, что х = 0 — корень, повторяющийся четное количество раз (поскольку у х2 четная степень). Следовательно, при переходе через эту точку знак функции меняться не будет.

В ответ необходимо включить отрицательные промежутки, следовательно: х ∈ (-∞; -2) U [-1; 0) U (0; 2].
Давайте подведем итог. Для чего мы это изучили?
Конечно же, эти знания пригодятся на экзаменах, а также в решении школьных примеров с 8 класса по 11 класс.
Советуем после прочтения этой статьи попрактиковаться в рубрике «Проверь себя», чтобы закрепить полученные знания. После чего можете приступить к решению заданий посложнее, чтобы на экзамене у вас точно получилось решить подобные задания и набрать за них максимум баллов.
Фактчек
- Метод интервалов позволяет упростить решение любого неравенства, а также экономит время, которое ограничено на экзамене.
- Чтобы решить неравенство с помощью метода интервалов необходимо найти нули функции, расставить их на числовой прямой, а после определить знак каждого полученного интервала.
- Нули функции на прямой обозначаются точками, при этом закрашенные точки включают граничные значения в итоговый промежуток, а незакрашенные, напротив, исключают их из промежутка.
- Для определения знака на каждом интервале необходимо подставить любое значение из этого интервала в функцию.
- Для упрощения расстановки знаков можно пользоваться правилами чередования, определив знак только на одном интервале, а дальше менять знаки на каждом следующем. При этом если корень встречается в функции нечетное количество раз, то знак при переходе через эту точку на следующий интервал меняется, а если корень встречается четное количество раз, то знак на следующем интервале не меняется.
Проверь себя
Задание 1.
Какие знаки неравенства существуют?
- Строгие
- Нестрогие
- Строгие и нестрогие
- Больше и меньше
Задание 2.
Какой знак неравенства может встретиться в методе интервалов?
- Только больше или меньше.
- Только “больше или равно” или “меньше или равно”.
- Только “больше” и “больше или равно” или только “меньше” и “меньше или равно”.
- Любой.
Задание 3.
Какое утверждение верное?
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой закрашены.
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой выколоты.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой закрашены, даже если в неравенстве есть ограничения.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой выколоты.
Задание 4.
Какое утверждение верное?
- При переходе на числовой прямой на следующий интервал, знак на интервале всегда будет меняться.
- Если корень встречается в неравенстве четное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Если корень встречается в неравенстве нечетное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Невозможно определить правильное чередование знаков на прямой, не подставляя значение из каждого интервала в функцию.
Задание 5.
Если в неравенстве строгий знак неравенства, то какие скобочки могут встретиться в ответе?
- Круглые
- Квадратные
- И круглые, и квадратные
- Ни один из перечисленных вариантов
Ответы: 1. — 3 2. — 4 3. — 2 4. — 2 5. — 1
Метод интервалов: решение простейших строгих неравенств
12 ноября 2017
- Домашнее задание
- Ответы
Для начала — немного лирики, чтобы почувствовать проблему, которую решает метод интервалов. Допустим, нам надо решить вот такое неравенство:
(x − 5)(x + 3) > 0
Какие есть варианты? Первое, что приходит в голову большинству учеников — это правила «плюс на плюс дает плюс» и «минус на минус дает плюс». Поэтому достаточно рассмотреть случай, когда обе скобки положительны: x − 5 > 0 и x + 3 > 0. Затем также рассмотрим случай, когда обе скобки отрицательны: x − 5 < 0 и x + 3 < 0. Таким образом, наше неравенство свелось к совокупности двух систем, которая, впрочем, легко решается:
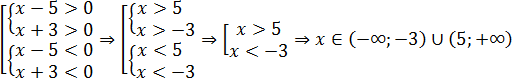
Более продвинутые ученики вспомнят (может быть), что слева стоит квадратичная функция, график которой — парабола. Причем эта парабола пересекает ось OX в точках x = 5 и x = −3. Для дальнейшей работы надо раскрыть скобки. Имеем:
x2 − 2x − 15 > 0
Теперь понятно, что ветви параболы направлены вверх, т.к. коэффициент a = 1 > 0. Попробуем нарисовать схему этой параболы:
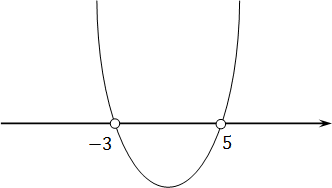
Функция больше нуля там, где она проходит выше оси OX. В нашем случае это интервалы (−∞ −3) и (5; +∞) — это и есть ответ.
Обратите внимание: на рисунке изображена именно схема функции, а не ее график. Потому что для настоящего графика надо считать координаты, рассчитывать смещения и прочую хрень, которая нам сейчас совершенно ни к чему.
Почему эти методы неэффективны?
Итак, мы рассмотрели два решения одного и того же неравенства. Оба они оказались весьма громоздкими. В первом решении возникает — вы только вдумайтесь! — совокупность систем неравенств. Второе решение тоже не особо легкое: нужно помнить график параболы и еще кучу мелких фактов.
Это было очень простое неравенство. В нем всего 2 множителя. А теперь представьте, что множителей будет не 2, а хотя бы 4. Например:
(x − 7)(x − 1)(x + 4)(x + 9) < 0
Как решать такое неравенство? Перебирать все возможные комбинации плюсов и минусов? Да мы уснем быстрее, чем найдем решение. Рисовать график — тоже не вариант, поскольку непонятно, как ведет себя такая функция на координатной плоскости.
Для таких неравенств нужен специальный алгоритм решения, который мы сегодня и рассмотрим.
Что такое метод интервалов
Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f (x) > 0 и f (x) < 0. Алгоритм состоит из 4 шагов:
- Решить уравнение f (x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
- Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
- Выяснить знак (плюс или минус) функции f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней;
- Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется.
Вот и все! После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f (x) > 0, или знаком «−», если неравенство имеет вид f (x) < 0.
На первый взгляд может показаться, что метод интервалов — это какая-то жесть. Но на практике все будет очень просто. Стоит чуть-чуть потренироваться — и все станет понятно. Взгляните на примеры — и убедитесь в этом сами:
Задача. Решите неравенство:
(x − 2)(x + 7) < 0
Работаем по методу интервалов. Шаг 1: заменяем неравенство уравнением и решаем его:
(x − 2)(x + 7) = 0
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:
x − 2 = 0 ⇒ x = 2;
x + 7 = 0 ⇒ x = −7.
Получили два корня. Переходим к шагу 2: отмечаем эти корни на координатной прямой. Имеем:
![]()
Теперь шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000). Получим:
f (x) = (x − 2)(x + 7);
x = 3;
f (3) = (3 − 2)(3 + 7) = 1 · 10 = 10;
Получаем, что f(3) = 10 > 0, поэтому в самом правом интервале ставим знак плюс.
Переходим к последнему пункту — надо отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус.
Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси. Имеем:
![]()
Вернемся к исходному неравенству, которое имело вид:
(x − 2)(x + 7) < 0
Итак, функция должна быть меньше нуля. Значит, нас интересует знак минус, который возникает лишь на одном интервале: (−7; 2). Это и будет ответ.
Задача. Решите неравенство:
(x + 9)(x − 3)(1 − x) < 0
Шаг 1: приравниваем левую часть к нулю:
(x + 9)(x − 3)(1 − x) = 0;
x + 9 = 0 ⇒ x = −9;
x − 3 = 0 ⇒ x = 3;
1 − x = 0 ⇒ x = 1.
Помните: произведение равно нулю, когда хотя бы один из множителей равен нулю. Именно поэтому мы вправе приравнять к нулю каждую отдельную скобку.
Шаг 2: отмечаем все корни на координатной прямой:
![]()
Шаг 3: выясняем знак самого правого промежутка. Берем любое число, которое больше, чем x = 1. Например, можно взять x = 10. Имеем:
f (x) = (x + 9)(x − 3)(1 − x);
x = 10;
f (10) = (10 + 9)(10 − 3)(1 − 10) = 19 · 7 · (−9) = − 1197;
f (10) = −1197 < 0.
Шаг 4: расставляем остальные знаки. Помним, что при переходе через каждый корень знак меняется. В итоге наша картинка будет выглядеть следующим образом:
![]()
Вот и все. Осталось лишь выписать ответ. Взгляните еще раз на исходное неравенство:
(x + 9)(x − 3)(1 − x) < 0
Это неравенство вида f (x) < 0, т.е. нас интересуют интервалы, отмеченные знаком минус. А именно:
x ∈ (−9; 1) ∪ (3; +∞)
Это и есть ответ.
Замечание по поводу знаков функции
Практика показывает, что наибольшие трудности в методе интервалов возникают на последних двух шагах, т.е. при расстановке знаков. Многие ученики начинают путаться: какие надо брать числа и где ставить знаки.
Чтобы окончательно разобраться в методе интервалов, рассмотрим два замечания, на которых он построен:
- Непрерывная функция меняет знак только в тех точках, где она равна нулю. Такие точки разбивают координатную ось на куски, внутри которых знак функции никогда не меняется. Вот зачем мы решаем уравнение f (x) = 0 и отмечаем найденные корни на прямой. Найденные числа — это «пограничные» точки, отделяющие плюсы от минусов.
- Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала. Например, для интервала (−5; 6) мы вправе брать x = −4, x = 0, x = 4 и даже x = 1,29374, если нам захочется. Почему это важно? Да потому что многих учеников начинают грызть сомнения. Мол, что если для x = −4 мы получим плюс, а для x = 0 — минус? А ничего — такого никогда не будет. Все точки на одном интервале дают один и тот же знак. Помните об этом.
Вот и все, что нужно знать про метод интервалов. Конечно, мы разобрали его в самом простом варианте. Существуют более сложные неравенства — нестрогие, дробные и с повторяющимися корнями. Для них тоже можно применять метод интервалов, но это тема для отдельного большого урока.
Теперь хотел бы разобрать продвинутый прием, который резко упрощает метод интервалов. Точнее, упрощение затрагивает только третий шаг — вычисление знака на самом правом куске прямой. По каким-то причинам этот прием не проходят в школах (по крайней мере, мне никто такого не объяснял). А зря — ведь на самом деле этот алгоритм очень прост.
Итак, знак функции на правом куске числовой оси. Этот кусок имеет вид (a; +∞), где a — самый большой корень уравнения f (x) = 0. Чтобы не взрывать мозг, рассмотрим конкретный пример:
(x − 1)(2 + x)(7 − x) < 0;
f (x) = (x − 1)(2 + x)(7 − x);
(x − 1)(2 + x)(7 − x) = 0;
x − 1 = 0 ⇒ x = 1;
2 + x = 0 ⇒ x = −2;
7 − x = 0 ⇒ x = 7;
Мы получили 3 корня. Перечислим их в порядке возрастания: x = −2, x = 1 и x = 7. Очевидно, что наибольший корень — это x = 7.
Для тех, кому легче рассуждать графически, я отмечу эти корни на координатной прямой. Посмотрим, что получится:
![]()
Требуется найти знак функции f (x) на самом правом интервале, т.е. на (7; +∞). Но как мы уже отмечали, для определения знака можно взять любое число из этого интервала. Например, можно взять x = 8, x = 150 и т.д. А теперь — тот самый прием, который не проходят в школах: давайте в качестве числа возьмем бесконечность. Точнее, плюс бесконечность, т.е. +∞.
«Ты че, обкурился? Как можно подставить в функцию бесконечность?» — возможно, спросите вы. Но задумайтесь: нам ведь не нужно само значение функции, нам нужен только знак. Поэтому, например, значения f (x) = −1 и f (x) = −938 740 576 215 значат одно и то же: функция на данном интервале отрицательна. Поэтому все, что от вас требуется — найти знак, который возникает на бесконечности, а не значение функции.
На самом деле, подставлять бесконечность очень просто. Вернемся к нашей функции:
f (x) = (x − 1)(2 + x)(7 − x)
Представьте, что x — это очень большое число. Миллиард или даже триллион. Теперь посмотрим, что будет происходить в каждой скобке.
Первая скобка: (x − 1). Что будет, если из миллиарда вычесть единицу? Получится число, не особо отличающееся от миллиарда, и это число будет положительным. Аналогично со второй скобкой: (2 + x). Если к двойке прибавить миллиард, по получим миллиард с копейками — это положительное число. Наконец, третья скобка: (7 − x). Здесь будет минус миллиард, от которого «отгрызли» жалкий кусочек в виде семерки. Т.е. полученное число мало чем будет отличаться от минус миллиарда — оно будет отрицательным.
Осталось найти знак всего произведения. Поскольку в первых скобках у нас был плюс, а в последней — минус, получаем следующую конструкцию:
(+) · (+) · (−) = (−)
Итоговый знак — минус! И неважно, чему равно значение самой функции. Главное, что это значение — отрицательное, т.е. на самом правом интервале стоит знак минус. Осталось выполнить четвертый шаг метода интервалов: расставить все знаки. Имеем:
![]()
Исходное неравенство имело вид:
(x − 1)(2 + x)(7 − x) < 0
Следовательно, нас интересуют интервалы, отмеченные знаком минус. Выписываем ответ:
x ∈ (−2; 1) ∪ (7; +∞)
Вот и весь прием, который я хотел рассказать. В заключение — еще одно неравенство, которое решается методом интервалов с привлечением бесконечности. Чтобы визуально сократить решение, я не буду писать номера шагов и развернутые комментарии. Напишу только то, что действительно надо писать при решении реальных задач:
Задача. Решите неравенство:
x(2x + 8)(x − 3) > 0
Заменяем неравенство уравнением и решаем его:
x(2x + 8)(x − 3) = 0;
x = 0;
2x + 8 = 0 ⇒ x = −4;
x − 3 = 0 ⇒ x = 3.
Отмечаем все три корня на координатной прямой (сразу со знаками):
![]()
Справа на координатной оси стоит плюс, т.к. функция имеет вид:
f (x) = x(2x + 8)(x − 3)
А если подставить бесконечность (например, миллиард), получим три положительных скобки. Поскольку исходное выражение должно быть больше нуля, нас интересуют только плюсы. Осталось выписать ответ:
x ∈ (−4; 0) ∪ (3; +∞)
Смотрите также:
- Метод интервалов: случай нестрогих неравенств

- Тест по методу интервалов для строгих неравенств

- Сводный тест по задачам B12 (2 вариант)

- Профильный ЕГЭ-2022, задание 6. Геометрический смысл производной

- Формулы приведения: ускоряем вычисления в тригонометрии

- Задачи B4: перевозка груза тремя фирмами

Суть метода интервалов заключается в том, что при переходе с одного промежутка на другой между корнями функция меняет знак. А решение неравенств – нахождение всех точек, где функция больше или меньше нуля. Это зависит от неравенства.
Решение неравенств методом интервалов удобно, когда видны корни – действительные числа. Вся числовая прямая делится на промежутки. Концами этих промежутков являются корни неравенства. Точки рисуются пустыми если неравенство строгое (больше, меньше) или закрашенными, если не строгое больше или равно, меньше или равно нулю.
Алгоритм решения неравенств:
1. Записать неравенство в стандартном виде. Для этого надо приравнять к нулю функцию и найти корни. Или записать в стандартном виде: (х – х1)(х – х2) …(х – хт) больше, меньше 0
2. Нарисовать числовую прямую. Отметить точки выколотые (или закрашенные) в зависимости от того, принадлежат точки (или нет). То есть строгое или нет неравенство.
3. Выбрать участок с плюсом, если больше нуля, или с минусом, если меньше нуля.
4. Записать ответ.
В ответе использовать круглые скобки, если неравенство строгое, или квадратные если нестрогое (больше или равно, меньше или равно).
Пример 5
Рассмотрим не строгое неравенство (х -3)(х – 2) <= 0
На числовой прямой будут точки 2, 3 – корни уравнения: (х -3)(х – 2) = 0
Считаем знак:
1). На промежутке от минус бесконечности до 2. Возьмём число 1.
Тогда произведение (1 – 3)(1 – 2) положительно, а у нас меньше или равно нулю. Этот участок в ответ не пишем.
2). На интервале (2;3) берём точку 2.5. Считаем знак. Произведение (2.5 – 3)(2.5 – 2) <0. Этот промежуток подходит для решения неравенства.
3). На промежутке от 3 до плюс бесконечности берём точку 4. Считаем знак произведения: (4 – 3)(4-2) >0
Итак, подходит средний промежуток. Так как неравенство не строгое, то в ответе скобки квадратные.
Ответ: 2 <= х <= 3
При решении неравенств с дробями важно учесть, что знаменатель не должен быть равен нулю. Если неравенство строгое, то проблем нет. просто переходим к умножению.
Если неравенство не строгое меньше или равно нулю (или больше или равно нулю), то нужно решить систему и написать, что знаменатель не равен нулю.
Можно написать без системы.
Пример 11.
(х – 1)/(х – 2) больше 0
Пишем произведение: (х – 1)(х – 2) больше 0 и х – 2 не равен 0
х не равно 2.
Отмечаем точки: 1, 2. Считаем знак на числовой прямой.
Берём точку с первого промежутка – 3 и считаем знак произведения:
(-3 -1)(-3-2) >0.
Берём любое число из интервала (1;2) и считаем знак функции:
(1.5 -1)(1.5 – 2) с0,
Последний интервал: из него берём любую точку, например, 4 и считаем знак.
(4-1)(4-2) > 0.
Выбираем промежутки, подходящие к нашему неравенству.
Ответ: (от минус бесконечности;1); (2; плюс бесконечности).
Можно записать ответ по-другому: Х <1; Х>2
Метод интервалов принято считать универсальным для решения неравенств. Иногда этот метод также называют методом промежутков. Применим он как для решения рациональных неравенств с одной переменной, так и для неравенств других видов. В нашем материале мы постарались уделить внимание всем аспектам вопроса.
Что ждет вас в данном разделе? Мы разберем метод промежутков и рассмотрим алгоритмы решения неравенств с его помощью. Затронем теоретические аспекты, на которых основано применение метода.
Особое внимание мы уделяем нюансам темы, которые обычно не затрагиваются в рамках школьной программы. Например, рассмотрим правила расстановки знаков на интервалах и сам метод интервалов в общем виде без его привязки к рациональным неравенствам.
Алгоритм
Кто помнит, как происходит знакомство с методом промежутков в школьном курсе алгебры? Обычно все начинается с решения неравенств вида f(x)<0 (знак неравенства может быть использован любой другой, например, ≤, > или ≥). Здесь f(x) может быть многочленом или отношением многочленов. Многочлен, в свою очередь, может быть представлен как:
- произведение линейных двучленов с коэффициентом 1 при переменной х;
- произведение квадратных трехчленов со старшим коэффициентом 1 и с отрицательным дискриминантом их корней.
Приведем несколько примеров таких неравенств:
(x+3)·(x2−x+1)·(x+2)3≥0,
(x-2)·(x+5)x+3>0 ,
(x−5)·(x+5)≤0,
(x2+2·x+7)·(x-1)2(x2-7)5·(x-1)·(x-3)7≤0 .
Запишем алгоритм решения неравенств такого вида, как мы привели в примерах, методом промежутков:
- находим нули числителя и знаменателя, для этого числитель и знаменатель выражения в левой части неравенства приравниваем к нулю и решаем полученные уравнения;
- определяем точки, которые соответствуют найденным нулям и отмечаем их черточками на оси координат;
- определяем знаки выражения f(x) из левой части решаемого неравенства на каждом промежутке и проставляем их на графике;
- наносим штриховку над нужными участками графика, руководствуясь следующим правилом: в случае, если неравенство имеет знаки < или ≤ изображается, штрихуются «минусовые» промежутки, если же мы работаем с неравенством, имеющим знаки > или ≥, то выделяем штриховкой участки, отмеченные знаком «+».
Четреж, с которым мы будем работать, может иметь схематический вид. Излишние подробности могут перегружать рисунок и затруднять решение. Нас будет мало интересовать маштаб. Достаточно будет придерживаться правильного расположения точек по мере роста значений их координат.
При работе со строгими неравенствами мы будем использовать обозначение точки в виде круга с незакрашенным (пустым) центром. В случае нестрогих неравенств точки, которые соответствуют нулям знаменателя, мы будем изображать пустыми, а все остальные обычными черными.
Отмеченные точки разбивают координатную прямую на несколько числовых промежутков. Это позволяет нам получить геометрическое представление числового множества, которое фактически является решением данного неравенства.
Научные основы метода промежутков
Основан подход, положенный в основу метода промежутков, основан на следующем свойстве непрерывной функции: функция сохраняет постоянный знак на интервале (a, b), на котором эта функция непрерывна и не обращается в нуль. Это же свойство характерно для числовых лучей (−∞, a) и (a, +∞).
Приведенное свойство функции подтверждается теоремой Больцано-Коши, которая приведена во многих пособиях для подготовки к вступительным испытаниям.
Обосновать постоянство знака на промежутках также можно на основе свойств числовых неравенств. Например, возьмем неравенство x-5x+1>0 . Если мы найдем нули числителя и знаменателя и нанесем их на числовую прямую, то получим ряд промежутков: (−∞, −1), (−1, 5) и (5, +∞).
Возьмем любой из промежутков и покажем на нем, что на всем промежутке выражение из левой части неравенства будет иметь постоянный знак. Пусть это будет промежуток (−∞, −1). Возьмем любое число t из этого промежутка. Оно будет удовлетворять условиям t<−1, и так как −1<5, то по свойству транзитивности, оно же будет удовлетворять и неравенству t<5.
Используя оба полученных неравенства и свойство числовых неравенств, мы можем предположить, что t+1<0 и t−5<0. Это значит, что t+1 и t−5 – это отрицательные числа независимо от значения t на промежутке (−∞, −1).
Используя правило деления отрицательных чисел, мы можем утверждать, что значение выражения t-5t+1 будет положительным. Это значит, что значение выражения x-5x+1 будет положительным при любом значении x из промежутка (−∞, −1). Все это позволяет нам утверждать, что на промежутке, взятом для примера, выражение имеет постоянный знак. В нашем случае это знак «+».
Нахождение нулей числителя и знаменателя
Алгоритм нахождения нулей прост: приравниваем выражения из числителя и знаменателя к нулю и решаем полученные уравнения. При возникновении затруднений можно обратиться к теме «Решение уравнений методом разложения на множители». В этом разделе мы ограничимся лишь рассмотрением примера.
Рассмотрим дробь x·(x-0,6)x7·(x2+2·x+7)2·(x+5)3. Для того, чтобы найти нули числителя и знаменателя, приравняем их к нулю для того, чтобы получить и решить уравнения: x·(x−0,6)=0 и x7·(x2+2·x+7)2·(x+5)3=0.
В первом случае мы можем перейти к совокупности двух уравнений x=0 и x−0,6=0, что дает нам два корня 0 и 0,6. Это нули числителя.
Второе уравнение равносильно совокупности трех уравнений x7=0, (x2+2·x+7)2=0, (x+5)3=0. Проводим ряд преобразований и получаем x=0, x2+2·x+7=0, x+5=0. Корень первого уравнения 0, у второго уравнения корней нет, так как оно имеет отрицательный дискриминант, корень третьего уравнения -5. Это нули знаменателя.
0 в данном случае является одновременно и нулем числителя, и нулем знаменателя.
В общем случае, когда в левой части неравенства дробь, которая не обязательно является рациональной, числитель и знаменатель точно также приравниваются к нулю для получения уравнений. Решение уравнений позволяет найти нули числителя и знаменателя.
Определение знаков на интервалах
Определить знак интервала просто. Для этого можно найти значение выражения из левой части неравенства для любой произвольно выбранной точки из данного интервала. Полученный знак значения выражения в произвольно выбранной точке промежутка будет совпадать со знаком всего промежутка.
Рассмотрим это утверждение на примере.
Возьмем неравенство x2-x+4x+3≥0. Нулей числителя выражение, расположенное в левой части неравенства, нулей не имеет. Нулем знаменателя будет число -3. Получаем два промежутка на числовой прямой (−∞, −3) и (−3, +∞).
Для того, чтобы определить знаки промежутков, вычислим значение выражения x2-x+4x+3 для точек, взятых произвольно на каждом из промежутков.
Из первого промежутка (−∞, −3) возьмем −4. При x=−4 имеем (-4)2-(-4)+4(-4)+3=-24 . Мы получили отрицательное значение, значит весь интервал будет со знаком «-».
Для промежутка (−3, +∞) проведем вычисления с точкой, имеющей нулевую координату. При x=0 имеем 02-0+40+3=43. Получили положительное значение, что значит, что весь промежуток будет иметь знак «+».
Можно использовать еще один способ определения знаков. Для этого мы можем найти знак на одном из интервалов и сохранить его или изменить при переходе через нуль. Для того, чтобы все сделать правильно, необходимо следовать правилу: при переходе через нуль знаменателя, но не числителя, или числителя, но не знаменателя мы можем поменять знак на противоположный, если степень выражения, дающего этот нуль, нечетная, и не можем поменять знак, если степень четная. Если мы получили точку, которая является одновременно нулем числителя и знаменателя, то поменять знак на противоположный можно только в том случае, если сумма степеней выражений, дающих этот нуль, нечетная.
Если вспомнить неравенство, которое мы рассмотрели в начале первого пункта этого материала, то на крайнем правом промежутке мы можем поставить знак «+».
Теперь обратимся к примерам.
Возьмем неравенство (x-2)·(x-3)3·(x-4)2(x-1)4·(x-3)5·(x-4)≥0 и решим его методом интервалов. Для этого нам необходимо найти нули числителя и знаменателя и отметить их на координатной прямой. Нулями числителя будут точки 2, 3, 4, знаменателя точки 1, 3, 4. Отметим их на оси координат черточками.
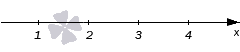
Нули знаменателя отметим пустыми точками.
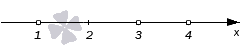
Так как мы имеем дело с нестрогим неравенством, то оставшиеся черточки заменяем обычными точками.
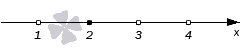
Теперь расставим точки на промежутках. Крайний правый промежуток (4, +∞) будет знак +.
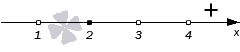
Продвигаясь справа налево будем проставлять знаки остальных промежутков. Переходим через точку с координатой 4. Это одновременно нуль числителя и знаменателя. В сумме, эти нули дают выражения (x−4)2 и x−4. Сложим их степени 2+1=3 и получим нечетное число. Это значит, что знак при переходе в данном случае меняется на противоположный. На интервале (3, 4) будет знак минус.
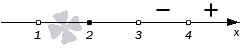
Переходим к интервалу (2, 3) через точку с координатой 3. Это тоже нуль и числителя, и знаменателя. Мы его получили благодаря двум выражениям (x−3)3 и (x−3)5, сумма степеней которых равна 3+5=8. Получение четного числа позволяет нам оставить знак интервала неизменным.
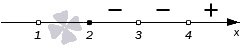
Точка с координатой 2 – это нуль числителя. Степень выражения х-2 равна 1 (нечетная). Это значит, что при переходе через эту точку знак необходимо изменить на противоположный.
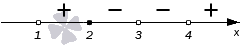
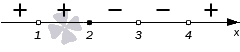
У нас остался последний интервал (−∞, 1). Точка с координатой 1 – это нуль знаменателя. Он был получен из выражения (x−1)4, с четной степенью 4. Следовательно, знак остается прежним. Итоговый рисунок будет иметь вот такой вид:
Применение метода интервалов особенно эффективно в случаях, когда вычисление значения выражения связано с большим объемом работы. Примером может стать необходимость вычисления значения выражения
x+3-343·x2+6·x+112·x+2-34(x-1)2·x-235·(x-12)
в любой точке интервала 3-34,3-24.
Будем считать, что с правилами определения знаков для промежутков мы разобрались. Идем дальше.
Примеры решения неравенств методом интервалов
Теперь займемся применением полученных знаний и навыков на практике.
Решите неравенство (x-1)·(x+5)2(x-7)·(x-1)3≤0 .
Решение
Целесообразно применить для решения неравенства метод интервалов. Находим нули числителя и знаменателя. Нули числителя 1 и -5, нули знаменателя 7 и 1. Отметим их на числовой прямой. Мы имеем дело с нестрогим неравенством, поэтому нули знаменателя отметим пустыми точками, нуль числителя -5 отметим обычной закрашенной точкой.
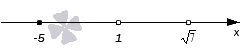
Проставим знаки промежутков, используя правила изменения знака при переходе через нуль. Начнем с крайнего правого промежутка, для которого вычислим значение выражения из левой части неравенства в точке, произвольно взятой из промежутка. Получим знак «+». Перейдем последовательно через все точки на координатной прямой, расставляя знаки, и получим:
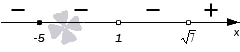
Мы работаем с нестрогим неравенством, имеющим знак ≤. Это значит, что нам необходимо отметить штриховкой промежутки, отмеченные знаком «-».
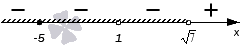
Ответ: (-∞,1)∪(1,7) .
Решение рациональных неравенств в большинстве случаев требует их предварительного преобразования к нужному виду. Только после этого появляется возможность использовать метод интервалов. Алгоритмы проведения таких преобразований рассмотрены в материале «Решение рациональных неравенств».
Рассмотрим пример преобразования квадратных трехчленов в записи неравенств.
Найдите решение неравенства (x2+3x+3)(x+3)x2+2·x-8>0.
Решение
Давайте посмотрим, действительно ли дискриминанты квадратных трехчленов в записи неравенства отрицательны. Это позволит нам определить, позволяет ли вид данного неравенства применить для решения метод интервалов.
Вычислим дискриминант для трехчлена x2+3·x+3: D=32−4·1·3=−3<0. Теперь вычислим дискриминант для трехчлена x2+2·x−8: D’=12−1·(−8)=9>0. Как видите, неравенство требует предварительного преобразования. Для этого представим трехчлен x2+2·x−8 как (x+4)·(x−2), а потом применим метод интервалов для решения неравенства (x2+3·x+3)·(x+3)(x+4)·(x-2)>0 .
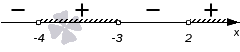
Ответ: (-4,-3)∪(2,+∞) .
Обобщенный метод интервалов
Обобщенный метод промежутков применяется для решения неравенств вида f(x)<0 (≤, >, ≥), где f(x) – произвольное выражение с одной переменной x.
Все действия проводятся по определенному алгоритму. При этом алгоритм решения неравенств обобщенным методом интервалов будет несколько отличаться от того, что мы разобрали ранее:
- находим область определения функции f и нули этой функции;
- отмечаем на координатной оси граничные точки;
- наносим на числовую прямую нули функции;
- определяем знаки промежутков;
- наносим штриховку;
- записываем ответ.
На числовой прямой необходимо отмечать в том числе и отдельные точки области определения. К примеру, областью определения функции служит множество (−5, 1]∪{3}∪[4, 7)∪{10}. Это значит, что нам необходимо отметить точки с координатами −5, 1, 3, 4, 7 и 10. Точки −5 и 7 изобразим пустыми, остальные можно выделить цветным карандашом для того, чтобы отличать их затем от нулей функции.
Нули функции в случае нестрогих неравенств наносятся обычными (закрашенными) точками, строгих – пустыми точками. Если нули совпадают с граничными точками или отдельными точками области определения, то их можно перекрасить в черный цвет, сделав пустыми или закрашенными в зависимости от вида неравенства.
Запись ответа представляет собой числовое множество, которое включает в себя:
- промежутки со штриховкой;
- отдельные точки области определения со знаком плюс, если мы имеем дело с неравенством, знак которого > или ≥ или со знаком минус, если в неравенстве есть знаки < или ≤.
Теперь стало понятно, что тот алгоритм, который мы привели в самом начале темы, является частным случаем алгоритма применения обобщенного метода интервалов.
Рассмотрим пример применения обобщенного метода интервалов.
Решите неравенство x2+2·x-24-34·x-3x-7<0 .
Решение
Вводим функцию f такую, что f(x)=x2+2·x-24-34·x-3x-7 . Найдем область определения функции f:
x2+2·x-24≥0x≠7D(f)=(-∞,-6]∪[4,7)∪(7,+∞) .
Теперь найдем нули функции. Для этого проведем решение иррационального уравнения:
x2+2·x-24-34·x-3=0
Получаем корень x=12.
Для обозначения граничных точек на оси координат используем оранжевый цвет. Точки -6,4 у нас будут закрашенными, а 7 оставляем пустой. Получаем:
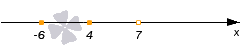
Отметим ноль функции пустой точкой черного цвета, так как мы работаем со строгим неравенством.
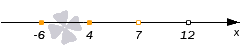
Определяем знаки на отдельных промежутках. Для этого возьмем по одной точке из каждого промежутка, например, 16, 8, 6 и −8, и вычислим в них значение функции f:
f(16)=162+2·16-24-34·16-316-7=264-159>0f(8)=82+2·8-24-34·8-38-7=56-9<0f(6)=62+2·6-24-34·6-36-7=24-152-1==15-2·242=225-962>0f(-8)=-82+2·(-8)-24-34·(-8)-3-8-7=24+3-15<0
Расставляем только что определенные знаки, и наносим штриховку над промежутками со знаком минус:
Ответом будет являться объединение двух промежутков со знаком «-»:(−∞, −6]∪(7, 12).
В ответ мы включили точку с координатой -6. Это не нуль функции, который мы бы не включили в ответ при решении строгого неравенства, а граничная точка области определения, которая входит в область определения. Значение функции в этой точке отрицательное, это значит, что она удовлетворяет неравенству.
Точку 4 мы в ответ не включили, точно также, как не включили весь промежуток [4, 7). В этой точке, точно также, как и на всем указанном промежутке значение функции положительно, что не удовлетворяет решаемому неравенству.
Запишем это еще раз для более четкого понимания: цветные точки необходимо включать в ответ в следующих случаях:
- эти точки являются частью промежутка со штриховкой,
- эти точки являются отдельными точками области определения функции, значения функции в которых удовлетворяют решаемому неравенству.
Ответ: (−∞, −6]∪(7, 12).
Суть метода интервалов
Суть метода в разложении неравенства на множители (повтори тему «Разложение на множители»), определении ОДЗ и знака сомножителей.
Сейчас все поясню.
Возьмем самый простенький пример: ( (x+1)cdot ({x}-2)>0).
Области допустимых значений (ОДЗ) здесь писать не надо, поскольку деления на переменную нет, и радикалов (корней) здесь не наблюдается.
На множители здесь все и так разложено за нас. Но не расслабляйся, это все, чтоб напомнить азы и понять суть!
Допустим, ты не знаешь метода интервалов, как бы ты стал решать это неравенство? Подойди логически и опирайся на то, что уже знаешь.
Во-первых, левая часть будет больше нуля если оба выражения в скобках либо больше нуля, либо меньше нуля, т.к. «плюс» на «плюс» дает «плюс» и «минус» на «минус» дает «плюс», так?
А если знаки у выражений в скобках разные, то в итоге левая часть будет меньше нуля.
А что же нам нужно, чтоб узнать те значения ( x), при которых выражения в скобках будут отрицательными или положительными?
Нам нужно решить уравнение, оно точно такое же как неравенство, только вместо знака «( >)» будет знак «(=)«.
Корни этого уравнения и позволят определить те пограничные значения, при отступлении ( x) от которых множители ( (x+1)) и ( ({x}-2)) будут больше или меньше нуля!
( (x+1)cdot ({x}-2)=0)
( displaystyle left[ begin{array}{l}x=-1\x=2end{array} right.)
А теперь сами интервалы.
Что такое интервал?
Это некий промежуток числовой прямой, то есть все возможные числа, заключенные между двумя какими-то числами – концами интервала. Эти промежутки в голове представить не так просто, поэтому интервалы принято рисовать, сейчас научу.
Рисуем ось ( X), на ней располагается весь числовой ряд от ( -infty ) и до ( +infty ). На ось наносятся точки, те самые так называемые нули функции, значения, при которых выражение равняется нулю.
Эти точки «выкалываются» что означает, что они не относятся к числу тех значений, при которых неравенство верно. В данном случае, они выкалываются, т.к. знак в неравенстве ( >), а не (ge), то есть строго больше, а не больше или равно.
Хочу сказать, что ноль отмечать не обязательно, он без кружочков тут, а так, для понимания и ориентации по оси.
Ладно, ось нарисовали, точки (точнее кружочки) поставили, дальше что, как мне это поможет в решении? – спросишь ты.
Теперь просто…
Возьми значение для икса из интервалов по порядку и подставь их в свое неравенство и смотри, какой знак будет в результате умножения.
Короче, просто берем ( -2) например, подставляем его сюда ( (x+1)cdot ({x}-2)), получится ( 4), а ( 4>0).
Значит на всем промежутке (на всем интервале) от ( -infty ) до ( -1), из которого мы брали ( -2), неравенство будет справедливо.
Иными словами если икс от ( -infty ) до ( -1), то неравенство верно.
То же самое делаем и с интервалом от ( -1) до ( 2), берем ( 0) или ( 1), например, подставляем в ( (x+1)cdot ({x}-2)), определяем знак, знак будет «минус». И так же делаем с последим, третьим интервалом от ( 2) до ( +infty ), где знак получится «плюс».
Такая куча текста вышла, а наглядности мало, правда?
Взгляни еще раз на неравенство ( (x+1)cdot ({x}-2)>0).
Теперь все на ту же ось наносим еще и знаки, которые получатся в результате. Ломаной линией в моем примере обозначаем положительные и отрицательные участки оси.
Смотри на неравенство – на рисунок, опять на неравенство – и снова на рисунок, что-нибудь понятно?
Постарайся теперь сказать на каких промежутках икса, неравенство будет верно.
Правильно, от ( -infty ) до ( -1) неравенство будет справедливо и от ( 2) до ( +infty ).
А на промежутке от ( -1) до ( 2) неравенство ( <) нуля и нас этот промежуток мало интересует, ведь у нас в неравенстве знак ( >) стоит.
Ну, раз ты с этим разобрался, то дело за малым – записать ответ!
В ответ пишем те промежутки, при которых левая часть больше нуля, ( xin (-infty ;-1)cup (2;+infty )), что читается, как икс принадлежит промежутку от минус бесконечности до минус одного и от двух до плюс бесконечности.
Стоит пояснить, что круглые скобки означают, что значения, которыми ограничен интервал не являются решениями неравенства, то есть они не включены в ответ, а лишь говорят о том, что до ( -1), например, но ( -1) не есть решение.
Теперь пример, в котором тебе придется не только интервал рисовать.
Пример №3
( frac{1}{{{x}^{2}}-3x+2}le frac{1}{{x}-2})
Раскладываем на множители и переносим все в одну сторону, нам ведь справа только ноль надо оставить, чтоб с ним сравнивать:
( displaystyle begin{array}{l}frac{1}{({x}-1)cdot ({x}-2)}le frac{1}{{x}-2}\frac{1}{({x}-1)cdot ({x}-2)}-frac{1}{{x}-2}le 0\frac{1-x+1}{({x}-1)cdot ({x}-2)}le 0\frac{-x+2}{({x}-1)cdot ({x}-2)}le 0\frac{{x}-2}{({x}-1)cdot ({x}-2)}ge 0end{array})
Обращаю твое внимание, что в последнем преобразовании, дабы получить в числителе ( displaystyle {x}-2) как и в знаменателе, умножаю обе части неравенства на ( -1).
Помни, что при умножении обеих частей неравенства на ( -1), знак неравенства меняется на противоположный!!!
Пишем ОДЗ:
( left{ begin{array}{l}xne 1\xne 2end{array} right.), иначе знаменатель обратится в ноль, а на ноль, как ты помнишь, делить нельзя!
Согласись, в получившемся неравенства так и подмывает сократить ( {x}-2) в числителе и знаменателе! Этого делать нельзя, можно потерять часть решений или ОДЗ!
Теперь попробуй сам нанести точки на ось.
Замечу лишь, что при нанесении точек надо обратить внимание на то, что точка со значением ( 2), которая исходя из знака ( ge ), казалось бы, должна быть нанесена на ось как закрашенная, закрашенной не будет, она будет выколота!
Почему спросишь ты? А ты ОДЗ вспомни, не собираешься же ты на ноль делить так?
Запомни, ОДЗ превыше всего! Если все неравенство и знаки равенства говорят одно, а ОДЗ – другое, доверяй ОДЗ, великой и могучей!
Ну что, ты построил интервалы, я уверен, что ты воспользовался моей подсказкой по поводу чередования и у тебя получилось вот так (см. рисунок ниже) А теперь зачеркни, и не повторяй эту ошибку больше!
Какую ошибку? – спросишь ты.
Метод интервалов для квадратичной функции
Надеюсь, ты помнишь, как решаются квадратные неравенства? Если нет, прочти тему «Квадратные неравенства».
Напомню общий вид квадратичной функции: ( fleft( x right)=a{{x}^{2}}+bx+c).
Теперь вспомним, какие знаки принимает квадратичная функция.
Ее график – парабола, и функция принимает знак «( +)» при таких ( x), при которых парабола выше оси ( Ox), и «( —)» – если парабола ниже оси ( Ox):
Если у функции есть нули (значения ( x), при которых ( fleft( x right)=0)), парабола пересекает ось ( Ox) в двух точках – корнях соответствующего квадратного уравнения.
Таким образом ось разбивается на три интервала, а знаки функции попеременно меняются при переходе через каждый корень.
Пожалуйста, загляни, если забыл, в статью о том, как использовать графики функций для решения уравнений, неравенств и систем.
А можно ли как-нибудь определить знаки, не рисуя каждый раз параболу?
Вспомним, что квадратный трехчлен можно разложить на множители: ( a{{x}^{2}}+bx+c=aleft( {x}-{{x}_{1}} right)left( {x}-{{x}_{2}} right))
Например: ( 2{{x}^{2}}-7x+3=2left( {x}-frac{1}{2} right)left( {x}-3 right)).
Отметим корни на оси:
Мы помним, что знак функции может меняться только при переходе через корень.
Используем этот факт: для каждого из трех интервалов, на которые ось разбивается корнями, достаточно определить знак функции только в одной произвольно выбранной точке: в остальных точках интервала знак будет таким же.
В нашем примере: при ( x>3) оба выражения в скобках положительны (подставим, например ( x=4): ( 2left( 4-frac{1}{2} right)left( 4-3 right)>0)).
Ставим на оси знак «( +)»:
Далее, ( frac{1}{2}<x<3) (подставь в выражение ( 2left( {x}-frac{1}{2} right)left( {x}-3 right)) любой корень из этого интервала, например, ( x=2)).
Первая скобка положительна, а вторая отрицательна. Значит, все произведение отрицательно: ставим на оси знак «( —)»:
Ну и, при ( x<frac{1}{2}) (подставь, например, ( x=0)) обе скобки отрицательны, значит, произведение положительно:
Случай, когда нулей у функции нет, или он всего один
Если их нет, то и корней нет. А значит, не будет и «перехода через корень». А значит, функция на всей числовой оси принимает только один знак.
Его легко определить, подставив в функцию ( x=0).
Если корень только один, парабола касается оси ( Ox), поэтому знак функции не меняется при переходе через корень. Какое правило придумаем для таких ситуаций?
Если разложить такую функцию на множители, получатся два одинаковых множителя:
( a{{x}^{2}}+bx+c=aleft( {x}-{{x}_{1}} right)left( {x}-{{x}_{1}} right)=a{{left( {x}-{{x}_{1}} right)}^{2}})
А любое выражение в квадрате неотрицательно!
Поэтому знак функции и не меняется. В таких случаях будем выделять корень, при переходе через который знак не меняется, обведя его квадратиком:
Такой корень будем называть кратным.
Пример 6
И еще один очень показательный пример:
( frac{left( {x}-1 right)left( x+3 right){{left( {x}-3 right)}^{2}}{{left( x+2 right)}^{4}}}{left( {x}-2 right){{left( x+3 right)}^{2}}}le 0)
Опять же, мы не сокращаем одинаковые множители числителя и знаменателя, так как, если сократим, нам придется специально запоминать, что нужно выколоть точку ( x=-3).
Дальше, мы видим несколько кратных корней:
- ( x=3): повторяется ( 2) раза;
- ( x=-2): ( 4) раза;
- ( x=-3): ( 3) раза (( 2) в числителе и один в знаменателе).
В случае четного количества поступаем так же, как и раньше: обводим точку квадратиком и не меняем знак при переходе через корень.
А вот в случае нечетного количества это правило не выполняется: знак все равно поменяется при переходе через корень. Поэтому с таким корнем ничего дополнительно не делаем, как будто он у нас не кратный.
Вышеописанные правила относятся ко всем четным и нечетным степеням.
Что запишем в ответе?
