Как найти знак подстановки – Сайт, где вы сможете решить свои вопросы

Знак подстановки

Говорят, что в
данной строке элементы i
и j
составляют инверсию, если i
> j,
но i
стоит в этой строке раньше.

(5
3 4 1 2) – число 5 образует 4 инверсии. Общее
число инверсий в строке равно 8.

Знак
подстановки

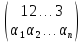
равен
(-1)^a,
где а – число инверсий в строке (α₁,
α₂,
…, α_n)

Пример
3.

Определить
знак подстановки

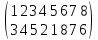
Решение.

Число
инверсий в строке (3 4 5 2 1 8 7 6) равно
2+2+2+1+0+2+1=10

так
как (-1)¹⁰=1,
то данная подстановка является четной.

Знак подстановки
можно определить и другим способом. Для
этого надо разложить подстановку в
произведение независимых циклов.

b
= (k₁-1)+(k₂-1)+…+(k_l-1)=k₁+k₂+…+k_l-S,
(5)

где
k₁
, k₂
, …, k_l
– длины циклов.

Тогда
знак равен (-1)^b

Пусть дана
подстановка n-й
степени и пусть s
есть число независимых циклов в её
разложении плюс число символом,
оставляемых ею на месте. Разность n
– s
называется декрементом этой подстановки.
Декремент равен числу действительно
перемещаемых символов, уменьшенному
на число независимых циклов, входящих
в разложение подстановки и равносилен
b
в формуле (5).

Замечание.
Четность подстановки совпадает с
четностью декремента этой подстановки.

Пример
4.

Определите
знак подстановки

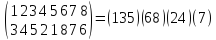
с
помощью разложения подстановки в
произведение независимых циклов.

Решение.

Данная
подстановка раскладывается следующим
образом в произведение независимых
циклов.

b
= 3+2+2+1–4 = 4

(-1)⁴
= 1

Это
четная подстановка.

Умножение подстановок

Определение.
Произведением первой подстановки на
вторую называют последовательное
выполнение двух подстановок n-й
степени, приводящее к некоторой вполне
определенной третьей подстановке n-й
степени.

так,
если даны подстановки четвертой степени

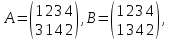
то

Действительно,
при подстановке А символ 1 переходит в
3, но при В символ 3 переходит в 4, поэтому
при АВ символ 1 переходит в 4, и т. д.

Можно перемножить
лишь подстановки одинаковой степени.
Умножение подстановки n-й
степени при n
≥ 3некоммутативно. Действительно, для
рассмотренных выше подстановок А и В
произведение ВА имеет вид

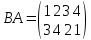
т.
е. подстановка ВА отлична от подстановки
АВ. Такие примеры можно подобрать для
всех n
при n
≥ 3, хотя для некоторых пар подстановок
закон коммутативности случайно может
выполняться.

Умножение подстановок
ассоциативно, т. е. можно говорить о
произведении любого конечного числа
подстановок n-й
степени, взятых (ввиду некоммутативности)
в определенном порядке. В самом деле,
пусть даны подстановки А, В и С и пусть
символ i₁,
1 ≤ i₁
≤ n,
переходит при подстановке А в символ
i₂,
i₂при
подстановке В переходит в символ i₃,
а последний при подстановке С – в символ
i₄.
Тогда при подстановке АВ символ i₁
переходит в i₃,
при подстановке ВС символ i₂
переходит в i₄,
а поэтому как при (АВ)С, так и при А(ВС)
символ i₁
,будет переходить в символ i₄.

Очевидно, что
произведение любой подстановки А на
тождественную подстановку Е, а также
произведение Е на А, равно А:

АЕ=ЕА=А

Назовем,
наконец, обратной для подстановки А
такую подстановку А^-1
той же степени, что

АА^-1
= А^-1А
= Е

Легко
видеть, что обратной подстановкой для
подстановки

служит
подстановка

получающаяся
из А переменой мест верхней и нижней
строк.

Пример 5.

Найти
подстановку, обратную данной

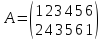
Решение.

Подстановка
А^-1,
обратная подстановке А будет иметь вид

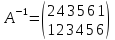
приведем
её к каноническому виду.

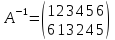
Пример
6.

Найти
порядок указанного элемента в группе
S_n,
n=5

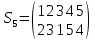
Решение:

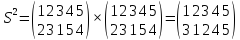
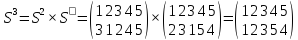
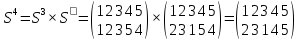
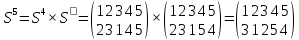
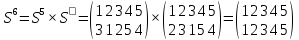
Наконец,
получили тождественную подстановку Е

Ответ:
6

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Макеты страниц

Знак подстановки.

Знак любого рационального числа а определяется следующим образом:

Легко видеть, что для любых рациональных чисел а и b

Это свойство знака, называемое свойством мультипликативности, будет использовано при доказательстве леммы 3.3.

Обозначим через отображение множества в множество определяемое равенством:

Нетрудно видеть, что знак подстановки равен произведению знаков всех чисел соответствующих всевозможным парам различных элементов множества М, т. е.

ЛЕММА 3.3. Знак произведения двух подстановок равен произведению знаков этих подстановок, т. е.

Доказательство. Подстановку можно представить в виде

следовательно, имеем

В силу свойства мультипликативности знака

Поэтому из (2) следует, что

ТЕОРЕМА 3.4. Знак подстановки (функция ) обладает следующими свойствами:

(1) функция мультипликативна, т. е. для любых из

(2) знак транспозиции равен

(3) взаимно обратные подстановки имеют один и тот же знак;

(4) если — транспозиция и — любая подстановка из то

Доказательство. Свойство (1) выполняется в силу леммы 3.3. Свойство (2) непосредственно следует из леммы 3.2. В силу свойства (1)

для любой подстановки . Следовательно, Свойство (4) непосредственно следует из свойств (1) и (2). СЛЕДСТВИЕ 3.5. Произведение двух (или четного числа) подстановок одинаковой четности есть четная подстановка.

СЛЕДСТВИЕ 3.6. Произведение двух подстановок различной четности есть нечетная подстановка.

Источник

Содержание

Подстановки

проверено

Подстановка

Транспозиции и циклы

Определение 3. Циклической подстановкой²⁾, или циклом³⁾ называется такая подстановка $piin S_n$ , что при повторении ее достаточное число раз всякий из действительно перемещаемых ею символов может быть переведен в любой другой из этих символов. Для обозначения цикла используют запись $(iquadpi(i)quadldotsquadpi^{t-1}(i))$ , где $t$ — число действительно перемещаемых символов подстановки, которое называется длиной цикла⁴⁾.

Пример 3. В подстановке

$pi=begin{pmatrix}1 & 2 & 3 & 4 & 5 & 6 & 7 & 8\ 3 & 2 & 6 & 5 & 1 & 4 & 7 & 8end{pmatrix}$

действительно перемещаемыми символами являются 1, 3, 4, 5, 6. Выберем любой из них, например, 3. $pi(3)=6,,pi(6)=4,,pi(4)=5$ , $pi(5)=1,,pi(1)=3$ . Поэтому цикл можно записать как $(3quad 6quad 4quad 5quad 1)$ .

Определение 4. Циклы называются независимыми⁵⁾, если они не имеют общих действительно перемещаемых символов.

Предложение 1. Любая подстановка $pineq e$ из $S_n$ может быть разлжена в произведение попарно независимых циклов. Такое представление определено однозначно с точностью до порядка перемножения циклов.

Пример 4. $begin{pmatrix}1 & 2 & 3 & 4 & 5\ 3 & 5 & 1 & 2 & 4end{pmatrix}=(1quad 3)(2quad 5quad 4)$ — разложение подстановки в произведение попарно независимых циклов.

Определение 5. Цикл длины 2 называется транспозицией⁶⁾.

Предложение 2. Каждая подстановка может быть представлена в виде произведения транспозиций.

В отличие от представления в произведение попарно независимых циклов, представление в виде произведения транспозиций может не быть единственным.

Пример 5. Подстановка $begin{pmatrix}1 & 2 & 3 & 4\ 2 & 3 & 1 & 4end{pmatrix}$ может быть разложена в произведение транспозиций $(1quad 3)(1quad 2)$ или $(1quad 3)(2quad 4)(1quad 2)(1quad 4)$ .

Четность подстановки

См. также

Литература

Наверх

Источник

Определение 5. Подстановкой N-й степени называется взаимно однозначное отображение Множества самого на себя. Обычно подстановку записывают с помощью двух N-перестановок, записанных одна под другой:

, (1)

Где через обозначается число, в которое при подстановке переходит элемент i, т. е. ; i=1,2,…,N.

В записи подстановки можно произвольным образом менять столбцы местами. Например, все три указанные ниже подстановки равны.

. (2)

В частности всякая подстановка N-й степени может быть записана в виде:

При такой форме записи различные подстановки различаются только перестановками, стоящими в нижней строке. Тогда в силу теоремы 1 получили следующее утверждение.

Теорема 4. Число различных подстановок n-й степени равно N.

Определение 6. Числом инверсий в подстановке называется сумма числа инверсий в первой и второй строках подстановки.

Обозначаем число инверсий в подстановке символом . Подстановка называется Четной, если число четное, и называется Нечетной если число нечетное. Знаком подстановки называется число:

Таким образом знак подстановки равен 1 или -1 в зависимости от того четная подстановка или нечетная.

В силу теоремы 2 при перестановке столбцов в подстановке одновременно четности перестановок, стоящих в нижней и верхней строках подстановки, меняются на противоположные. Следовательно, четность перестановки сохраняется. Отсюда и из теоремы 3 получаем, следующие свойства подстановок.

1. Четность и знак подстановки не зависят от формы записи подстановки.

2. При N>1 число четных подстановок N-й степени равно числу нечетных подстановок и равно .

Пример 4. Подстановка (2) нечетная и имеет знак -1, хотя при различных формах записи имеет 3, 7, 5 инверсий.

Покажем, что множество всех подстановок N-й степени образует группу относительно операции умножения подстановок, определенной ниже. Эта группа имеет большое значение в алгебре, называется Симметрической Группой и обозначается символом .

Определение 7. Произведением подстановок и N-й степени называется композиция Этих постановок как отображений, т. е. для любого имеем . Обозначаем

Так как композиция двух биективных отображений биективное отображение, то произведение двух подстановок N-й степени есть подставок N-й степени. При практическом умножении подстановок сначала выполняется правая подстановка, а затем левая. Например,

, .

Теорема 5. Множество всех подстановок n-й степени образует группу относительно операции умножения подстановок.

Доказательство. В силу сказанного выше операция умножения подстановок бинарная алгебраическая операция. Проверим аксиомы группы.

Умножение подстановок ассоциативно. Действительно, пусть . Тогда для любого

И по определению равенства отображений .

Единичным элементом является Тождественная Подстановка

Обратной подстановкой для подстановки Является подстановка

Действительно,

Аналогично показывается, что .

Следовательно, по определению множество группа. Теорема доказана.

Пример выше показывает, что группа некоммутативная, т. е. неабелева.

< Предыдущая		Следующая >

Источник

В результате изучения этой темы читатель

узнает: определение перестановки из n элементов, число всех перестановок из n элементов, определение подстановки, матричный способ записи подстановки, канонический вид записи подстановки, формулировку теоремы о числе подстановок, понятие циклического разложения подстановки, формулировку теоремы о разложении подстановки в произведение непересекающихся циклов, понятие транспозиции, формулировку теоремы о представлении подстановки произведением транспозиций, как задаётся операция умножения подстановок, свойства операции умножения подстановок, символ обозначения симметрической группой подстановок n-ой степени, понятие порядка подстановки, формулировку теоремы о порядке подстановки циклической подгруппы, понятие инверсии, понятия чётной и нечётной подстановок, формулировку о числе чётных подстановка, аксиомы знакопеременной группы;

научится: задавать подстановки через биективное отображение, матрицей, произведение циклов и произведение транспозиций, осуществлять умножение подстановок, определять обратную подстановку для заданной, рассчитывать число k-циклов в симметрической группе подстановок n-ой степени, определять порядок подстановки циклической подгруппы, определять число инверсий, выяснять, является ли заданная подстановка чётной (нечётной).

Итак, в части 1, которая представлена по ссылке [https://dzen.ru/a/Y5PXtxtNyXI4n90Z?share_to=link], определено понятие подстановки n-ой степени и дан ряд определений. связанных с подстановками.

На множестве всех подстановок n-ой степени вводится бинарная операция умножения (произведения) подстановок (указанную операцию также называют композицией или суперпозицией).

Элементы теории алгебры подстановок (часть 2)

Определение операции умножения подстановок n-ой степени

Пример умножения подстановок n-ой степени

Свойства операции умножения подстановок.

Сформулируем ещё несколько свойств операции умножения подстановок.

В результате произведения двух подстановок n-ой степени образуется новая подстановка этой же степени

Операция произведения обладает свойством ассоциативности (в отличие от коммутативности, о которой упоминалось ранее)

Единичная и обратная подстановки n-ой степени

Нахождение обратной подстановки

Проверка, что полученная подстановка является обратной подстановкой для заданной

В качестве Упражнения 1 перемножьте подстановки α на β на γ, представленные в таблице ниже.

Варианты для самостоятельного решения с 1 по 15-ый

Варианты для самостоятельного решения с 16-ого по 30-ый

Пример выполнения практического задания (вариант № 30):

В качестве Упражнения 2 докажите, что подстановка α из таблицы (см. второй столбец) ниже является обратной к подстановке β, указанной в этой же таблице (см. третий столбец).

Варианты для самостоятельного решения с 1 по 15-ый

Варианты для самостоятельного решения с 16-ого по 30-ый

Пример выполнения практического задания (вариант № 30):

Источник

Знак подстановки

Умножение подстановок

Знак подстановки.

Содержание

Подстановки

Подстановка

Транспозиции и циклы

Четность подстановки

См. также

Литература

Вам также может понравиться

Как грамотно составить план текста

Как найти рентабельность заработной платы

Как найти безударные слова в тексте

Добавить комментарий Отменить ответ