Как найти знак произведения

Как найти знак произведения

  • Решение

  •   Видеорешение

Правило

Правило получения знаков при умножении:

(displaystyle times) (displaystyle {Large +}) (displaystyle {Large -})
(displaystyle {Large +}) (displaystyle { +}) (displaystyle { -})
(displaystyle {Large -}) (displaystyle { -}) (displaystyle {+})

Будем находить знаки множителей, опираясь на известный знак множителя и знак произведения.

1. Найдем знак (displaystyle (?)x), опираясь на известные нам знаки множителя (displaystyle -a) и произведения (displaystyle acdot x). Известно, что величина (displaystyle a) имеет знак минус, а произведение (displaystyle -acdot (?)x=acdot x) имеет знак плюс. Тогда (displaystyle ?x) также имеет знак минус, так как только при умножении величины со знаком (displaystyle -) на величину со знаком (displaystyle -)  получается произведение данных величин со знаком (displaystyle +).

Таким образом,

(displaystyle ?x=-x).

2. Найдем знак (displaystyle (?)y), опираясь на известные нам знаки множителя (displaystyle -a) и произведения (displaystyle acdot y). Известно, что величина (displaystyle a) имеет знак минус, а произведение (displaystyle -acdot (?)y=acdot y) имеет знак плюс. Поэтому (displaystyle ?y) имеет знак минус, так как только при умножении величины со знаком (displaystyle -) на величину со знаком (displaystyle -) получается произведение данных величин со знаком (displaystyle +).

Таким образом,

(displaystyle ?y=-y).

Теперь можно использовать полученные результаты для дальнейших рассуждений.

(displaystyle times) (displaystyle a) (displaystyle ?b)
(displaystyle -x) (displaystyle acdot x) (displaystyle -bcdot x)
(displaystyle -y) (displaystyle acdot y) (displaystyle -bcdot y)

3. Найдем знак (displaystyle (?)b), опираясь на известные нам знаки множителя (displaystyle -x) и произведения (displaystyle -bcdot x). Величина (displaystyle x) имеет знак минус, и произведение (displaystyle (?)bcdot (-x)=-bcdot x) имеет знак минус. Поэтому (displaystyle ?b) имеет знак плюс, так как только при умножении величины со знаком (displaystyle +) на величину со знаком (displaystyle -) получается произведение данных величин со знаком (displaystyle -).

Таким образом,

(displaystyle ?b=+b=b).

Следовательно:

(displaystyle times) (displaystyle -a) (displaystyle b)
(displaystyle -x) (displaystyle acdot x) (displaystyle -bcdot x)
(displaystyle -y) (displaystyle acdot y) (displaystyle -bcdot y)
Источник

1) если у множителей два положительных знака, значит произведение имеет положительный знак

Если множители имеют отрицательные знаки, значит и произведение имеет отрицательные знаки

Если один множетель имеет положительный, а другой отрицательный, то произведение отрицательное

2) число × 0 = 0

число × 1 = число

число × -1 = – число

3) что одно из множетелей равен нулю

4) Произведение не меняется от перемены мест множетелей. Значение не меняется, не смотря на то как сгруппированы множетели

5)

Сочетательный закон.

При умножении любых рациональных чисел остается в силе сочетательный закон умножения.

Для любых трех рациональных чисел a, bи с справедливо равенство:

(ab)c = a(bc).

6) Чтобы сумму умножить на число , можно умножить на это число каждое слагаемые и полученные произведения сложить

(a+b) × c = ac × bc

Источник
Умножение
Изображение
Изображается на знак умножения
Обозначение знак умножения
Противоположно деление
Нейтральный элемент 1
Логотип Викисклада Медиафайлы на Викискладе

Умножение 5 яблок на 3, как и умножение 3 яблок на 5, даёт 15 яблок

Умноже́ние — одна из основных математических операций над двумя аргументами, которые называются множителями или сомножителями (иногда первый аргумент называют множимым, а второй множителем). Результат умножения называется их произведением[1].

Для натуральных чисел умножение определяется как многократное сложение[1] — чтобы умножить число a на число b, надо сложить b чисел a (умножение далее обозначено приподнятой точкой между сомножителями):

{displaystyle acdot b=underbrace {a+a+cdots +a} _{b}}.

Умножение можно распространить и на другие типы чисел — на целые, рациональные, вещественные, комплексные путём систематического обобщения[⇨].

В современной математике умножение определяется не только для чисел, оно имеет различный конкретный смысл и соответственно различные определения и свойства для различных математических объектов[2].

Умножение чисел является коммутативной операцией, то есть порядок записи чисел-множителей не влияет на результат их умножения.
Например, умножение чисел 3 и 5 может быть записано как {displaystyle 3cdot 5}, так и 5cdot 3 (произносится также «пятью три», «трижды пять»), и результатом в любом случае является число 15. Проверка через сложение:

{displaystyle underbrace {3+3+3+3+3} _{5}=15},
{displaystyle underbrace {5+5+5} _{3}=15}.

Умножение нечисловых математических, физических и абстрактных величин (например, матриц, векторов, множеств, кватернионов и т. д.) не всегда является коммутативной операцией. При умножении физических величин важную роль играет их размерность[⇨].

Изучение общих свойств операции умножения входит в задачи общей алгебры, в частности теории групп и колец[2].

Формы записи и терминология[править | править код]

Умножение записывается с использованием знака умножения (∙, ×, ∗) между аргументами, такая форма записи называется инфиксной нотацией. В данном контексте знак умножения является бинарным оператором. Знак умножения не имеет специального названия, тогда как, например, знак сложения называется «плюс».

Самый старый из используемых символов — косой крестик (×). Впервые его использовал английский математик Уильям Отред в своём труде «Clavis Mathematicae» 1631 г.
Немецкий математик Лейбниц предпочитал знак в виде приподнятой точки (∙). Этот символ он использовал в письме 1698 года.
Йоханн Ран ввёл звёздочку (∗) в качестве знака умножения, она появилась в его книге «Teutsche Algebra» 1659 г.

В российских учебниках математики в основном используется знак в виде приподнятой точки (∙). Звёздочка (∗) используется, как правило, в текстах компьютерных программ.

Результат записывается с использованием знака равенства «=», например:

{displaystyle acdot b=c}
{displaystyle 6cdot 3=18} («шесть умножить на три равно восемнадцать» или «шестью три — восемнадцать»).

Часто в математических выражениях знак умножения опускается (не записывается), если это не вызывает неоднозначного прочтения. Например вместо {displaystyle y=6cdot x+3cdot z} пишется {displaystyle y=6x+3z}. Как правило, знак умножения опускают, если одним из множителей является однобуквенная переменная, функция или выражение в скобках: {displaystyle b^{2}-4ac}, {displaystyle nsin x}, {displaystyle a(b+c)}.

Традиционно при записи произведения нескольких множителей числа записывают перед переменными,а переменные перед функциями. Так, выражение {displaystyle ncdot sin xcdot 5cdot m} будет записано как {displaystyle 5nmsin x}. Выражения в скобках традиционно записывают последними, то есть выражение {displaystyle xcdot (a+b)cdot 2} будет записано как {displaystyle 2x(a+b)}.

Свойства[править | править код]

Далее описаны основные свойства операция умножения на числовых множествах {displaystyle mathbb {N} ,mathbb {Z} ,mathbb {Q} ,mathbb {R} ,mathbb {C} }.

  • Умножение коммутативно, то есть от перемены мест множителей произведение не меняется. Свойство также известно как переместительный закон умножения[3]:
Коммутативность: {displaystyle acdot b=bcdot a;}
  • Умножение ассоциативно, то есть при последовательном выполнении умножения трёх или более чисел последовательность выполнения операций не имеет значения. Свойство также известно как сочетательный закон умножения[3]:
Ассоциативность: {displaystyle (acdot b)cdot c=acdot (bcdot c);}
  • Умножение дистрибутивно, это свойство согласованности двух бинарных операций, определённых на одном и том же множестве. Свойство также известно как распределительный закон[3]:
Дистрибутивность: {displaystyle xcdot (a+b)=(xcdot a)+(xcdot b),quad forall a,bin A;}
Нейтральный элемент: {displaystyle xcdot 1=1cdot x=x,quad exists !1in A;}
  • Умножение на 1 идемпотентно, то есть повторное применение операции к объекту даёт тот же результат, что и одинарное:
Идемпотентность: {displaystyle x=xcdot 1=(xcdot 1)cdot 1=((xcdot 1)cdot 1)cdot ...cdot 1,quad forall xin A,quad exists !1in A;}
Нулевой элемент: {displaystyle xcdot 0=0cdot x=0,quad exists !0in A.}

Операция умножения чисел, определённых на множествах {displaystyle mathbb {N} ,mathbb {Z} ,mathbb {Q} ,mathbb {R} }, даёт произведение, принадлежащее этому же множеству. Следовательно, операция умножения относится к замкнутым операциям, то есть множества чисел {displaystyle mathbb {Z} ,mathbb {Q} ,mathbb {R} } образуют кольца относительно операции умножения.

На языке общей алгебры вышеперечисленные свойства сложения говорят о том, что {displaystyle mathbb {Z} _{-0},mathbb {Q} _{-0},mathbb {R} _{-0}} являются абелевыми группами относительно операции умножения.

В математических выражениях операция умножения имеет более высокий приоритет по отношению к операциям сложения и вычитания, то есть она выполняется перед ними, но менее высокий приоритет, чем операция возведения в степень.

На множестве вещественных чисел область значений функции умножения графически имеет вид поверхности проходящей через начало координат и изогнутой с двух сторон в виде параболы.

Выполнение умножения[править | править код]

При практическом решении задачи умножения двух чисел необходимо свести её к последовательности более простых операций: «простое умножение», сложение, сравнение и др. Для этого разработаны различные методы умножения, например для чисел, дробей, векторов и др. На множестве натуральных чисел в настоящее время используется алгоритм поразрядного умножения. При этом следует рассматривать умножение как процедуру (в отличие от операции).

Примерный алгоритм процедуры поразрядного умножения двух чисел

Алгоритм умножения.svg

Процедура достаточно сложная, состоит из относительно большого числа шагов и при умножении больших чисел может занять продолжительное время.

Пример пошагового умножения 3 ∙ 3 = 9 на числовой прямой.

«Простое умножение» в данном контексте обозначает операцию умножения одноразрядных чисел, которая может быть легко сведена к сложению. Является гипероператором сложения:

{displaystyle acdot b=operatorname {hyper2} (a,b)=operatorname {hyper} (a,2,b)=a^{(2)}b.}

{displaystyle a{^{(2)}}b=acdot b=underbrace {a+a+dots +a} _{b}.}

где {displaystyle a+a+dots +a} — последовательное сложение b элементов.

Чтобы упростить и ускорить процесс умножения используют табличный метод «простого умножения», для этого заранее вычисляют все комбинации произведений чисел от 0 до 9 и берут готовый результат из этой таблицы[4]:

Таблица для умножения в десятичной системе счисления

* 0 1 2 3 4 5 6 7 8 9
0 0 0 0 0 0 0 0 0 0 0
1 0 1 2 3 4 5 6 7 8 9
2 0 2 4 6 8 10 12 14 16 18
3 0 3 6 9 12 15 18 21 24 27
4 0 4 8 12 16 20 24 28 32 36
5 0 5 10 15 20 25 30 35 40 45
6 0 6 12 18 24 30 36 42 48 54
7 0 7 14 21 28 35 42 49 56 63
8 0 8 16 24 32 40 48 56 64 72
9 0 9 18 27 36 45 54 63 72 81

Данная процедура применима к умножению натуральных и целых (с учётом знака) чисел. Для других чисел используются более сложные алгоритмы.

Умножение чисел[править | править код]

Натуральные числа[править | править код]

Первый вариант определения

Умножением натуральных чисел называется такое соответствие, которое с каждой парой натуральных чисел a и b сопоставляет одно и только одно натуральное число acdot b, обладающее следующими свойствами[5]:

1) {displaystyle acdot 1=a}
2) {displaystyle acdot (b+1)=acdot b+a}.
Второй вариант определения

Воспользуемся определением натуральных чисел mathbb {N} как классов эквивалентности конечных множеств. Обозначим классы эквивалентности конечных множеств {displaystyle C,A,B} порождённых биекциями, с помощью скобок: {displaystyle [C],[A],[B]}. Тогда арифметическая операция «умножение» определяется следующим образом:

{displaystyle [C]=[A]cdot [B]=[Atimes B];}

где: {displaystyle Atimes B={(a,b)mid ain A,bin B}} прямое произведение множеств — множество  C, элементами которого являются упорядоченные пары  (a,b) для всевозможных  {displaystyle ain A,bin B}. Данная операция на классах введена корректно, то есть не зависит от выбора элементов классов, и совпадает с индуктивным определением.

Взаимно однозначное отображение конечного множества A на отрезок {displaystyle N_{a}} можно понимать как нумерацию элементов множества {displaystyle A:quad Asim N_{a}}.

Для умножения натуральных чисел в позиционной системе обозначения чисел применяется поразрядный алгоритм умножения. Если даны два натуральных числа a и b такие, что:

{displaystyle a=a_{n-1}a_{n-2}dots a_{0},quad b=b_{n-1}b_{n-2}dots b_{0},quad forall a_{k},b_{k}in {P},quad forall a_{n-1},b_{n-1}neq 0,quad exists 0in mathbb {N} ;}

где {displaystyle a_{0dots n-1}=a_{k}P^{k},quad b_{0dots n-1}=b_{k}P^{k}};

n — количество цифр в числе {displaystyle nin {1,2,dots ,n}};
k — порядковый номером разряда (позиции), {displaystyle kin {0,1,dots ,n-1}};
P — основание системы счисления;
{displaystyle {P}} множество числовых знаков (цифр), конкретной системы счисления:
{displaystyle {P_{2}}={0,1}},
{displaystyle {P_{10}}={0,1,2,3,4,5,6,7,8,9}},
{displaystyle {P_{16}}={0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}}; тогда:

{displaystyle c=acdot b;quad c_{n-1}c_{n-2}dots c_{0}=a_{n-1}a_{n-2}dots a_{0}cdot b_{n-1}b_{n-2}dots b_{0};}

умножая поразрядно, получаем n промежуточных результатов:

  • {displaystyle t_{n-1,~0}=mod(a_{n-1}cdot b_{0}+r_{n-1},P),quad r_{n}=div(a_{n-1}cdot b_{0}+r_{n-1},P)~,~~t_{0}cdot ~P^{k};}
  • {displaystyle t_{n-1,~1}=mod(a_{n-1}cdot b_{1}+r_{n-1},P),quad r_{n}=div(a_{n-1}cdot b_{1}+r_{n-1},P)~,~~t_{1}cdot ~P^{k};}
  • {displaystyle ...qquad qquad ...qquad qquad qquad qquad qquad qquad ...qquad qquad qquad qquad qquad qquad ...}
  • {displaystyle t_{n-1,~k}=mod(a_{n-1}cdot b_{k}+r_{n-1},P),quad r_{n}=div(a_{n-1}cdot b_{k}+r_{n-1},P)~,~~t_{k}cdot ~P^{k};}

где: r — значение переноса, {displaystyle mod()} — функция нахождения остатка от деления, {displaystyle div()} — функция нахождения неполного частного.

Затем полученные n промежуточных результатов складываем: {displaystyle c=t_{0}+t_{1}+...+t_{k}.}

Таким образом операция умножения сводится к процедуре последовательного простого умножения одноразрядных чисел {displaystyle a_{k}cdot b_{k}}, с формированием переноса при необходимости, которое производится либо табличным методом, либо последовательным сложением. И далее к сложению.

Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и в десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами. При этом нужно пользоваться таблицей умножения, соответствующей данному основанию P системы счисления.

Пример умножения натуральных чисел в двоичной, десятичной и шестнадцатеричной системах счисления, для удобства числа записываются друг под другом соответственно разрядам, перенос пишется сверху:

{displaystyle {begin{array}{ccccccccccc}&&&&&&&&&\&&&&1&1&0&1&1&0\&&&*&&&1&1&0&1\hline &&&&1&1&0&1&1&0\&&&0&0&0&0&0&0&{color {Gray}0}\&&1&1&0&1&1&0&{color {Gray}0}&{color {Gray}0}\+&1&1&0&1&1&0&{color {Gray}0}&{color {Gray}0}&{color {Gray}0}\hline 1&0&1&0&1&1&1&1&1&0end{array}};quad quad {begin{array}{cccccccccc}&&&&_{2}&_{2}&_{3}&_{3}&\&&&&_{1}&_{2}&_{2}&_{2}&\&&&&8&4&5&6&7\&&&*&&&5&4&1\hline &&&0&8&4&5&6&7\&&3&3&8&2&6&8&{color {Gray}0}\+&4&2&2&8&3&5&{color {Gray}0}&{color {Gray}0}\hline &4&5&7&5&0&7&4&7end{array}};quad quad {begin{array}{ccccccccc}&&&&_{8}&_{8}&_{2}\&&&&_{D}&_{D}&_{3}\&&&&6&D&E&4\&&&{*}&&A&1&F\hline &&&6&7&0&5&C\&&0&6&D&E&4&{color {Gray}0}\+&4&4&A&E&8&{color {Gray}0}&{color {Gray}0}\hline &4&5&8&3&6&9&Cend{array}}~~.}

Целые числа[править | править код]

Множество целых чисел — расширение множества натуральных чисел mathbb {N} , получаемое добавлением отрицательных чисел [6] вида -n. Множество целых чисел обозначается mathbb{Z}. Арифметические операции над целыми числами определяются как непрерывное продолжение соответствующих операций над натуральными числами.

Положительное и отрицательное числа на числовой прямой.

Отличие от натуральных чисел состоит в том, что отрицательные числа на числовой прямой направлены в противоположную сторону, это несколько меняет процедуру умножения. Необходимо учитывать взаимное направление чисел, здесь возможны несколько случаев:

Здесь и далее также используется алгоритм поразрядного умножения. Например, рассмотрим выражение: {displaystyle -6cdot 4=-24}; так как у чисел -6 и 4 разные знаки, то выносим минус за скобки: {displaystyle -6cdot 4=-(6cdot 4)}, вычисляя далее получим ответ: {displaystyle -24}.

Рациональные числа[править | править код]

Множество рациональных чисел обозначается mathbb {Q} (от англ. quotient «частное») и может быть записано в таком виде:

{mathbb {Q}}=left{{frac {m}{n}}mid min {mathbb {Z}},nin {mathbb {N}}right}.

Для умножения рациональных чисел в виде обыкновенных (или простых) дробей вида: pm {frac {m}{n}}, следует числители и знаменатели дробей умножить друг на друга.

Если даны два рациональных числа a и b такие, что: {textstyle a={frac {m_{a}}{n_{a}}},b={frac {m_{b}}{n_{b}}}quad forall m_{a},n_{a},m_{b},n_{b}in mathbb {N} quad forall {n_{a}},{n_{b}}neq 0} (дроби не сокращаемые), тогда[7]:

{displaystyle c=acdot b={frac {m_{a}}{n_{a}}}cdot {frac {m_{b}}{n_{b}}}={frac {m_{a}cdot m_{b}}{n_{a}cdot n_{b}}}.}

Пример умножения:

{displaystyle {frac {2}{3}}cdot {frac {1}{5}}={frac {2cdot 1}{3cdot 5}}={frac {2}{15}};quad {frac {3}{7}}cdot {frac {4}{6}}={frac {3cdot 4}{7cdot 6}}={frac {12}{42}}={frac {2}{7}}.}

Арифметическая операция «умножение» над рациональными числами относится к замкнутым операциям.

Вещественные числа[править | править код]

Арифметические операции над вещественными числами представимых бесконечными десятичными дробями определяются как непрерывное продолжение[8] соответствующих операций над рациональными числами.

Если даны два вещественных числа, представимые бесконечными десятичными дробями:

{displaystyle alpha =pm a_{0},a_{1}a_{2}ldots a_{n}ldots ={a_{n}},}
{displaystyle beta =pm b_{0},b_{1}b_{2}ldots b_{n}ldots ={b_{n}},}

определённые соответственно фундаментальными последовательностями рациональных чисел (удовлетворяющие условию Коши), обозначенные как: alpha =[a_{n}] и beta =[b_{n}], то их произведением называют число {displaystyle gamma =[c_{n}]}, определённое произведением последовательностей {a_{n}} и {b_{n}}:

{displaystyle gamma =alpha cdot beta {overset {text{def}}{=}}[a_{n}]cdot [b_{n}]=[a_{n}times b_{n}];}

вещественное число {displaystyle gamma =alpha cdot beta }, удовлетворяет следующему условию:

{displaystyle forall a',a'',b',b''in mathbb {Q} ;~~~~(a'leqslant alpha leqslant a'')land (b'leqslant beta leqslant b'')Rightarrow (a'cdot b'leqslant alpha times beta leqslant a''cdot b'')Rightarrow (a'cdot b'leqslant gamma leqslant a''cdot b'').}

Таким образом произведением двух вещественных чисел  alpha и beta  является такое вещественное число gamma  которое содержится между всеми произведениями вида {displaystyle a'cdot b'} с одной стороны и всеми произведениями вида {displaystyle a''cdot b''} с другой стороны[9].

На практике для того, чтобы умножить два числа alpha и beta , необходимо заменить их с требуемой точностью приближёнными рациональными числами a и b. За приближенное значение произведения чисел alpha cdot beta берут произведение указанных рациональных чисел acdot b. При этом не важно, с какой стороны (по недостатку или по избытку) взятые рациональные числа приближают alpha и beta . Умножение производится по алгоритму поразрядного умножения.

Абсолютная погрешность произведения приближённых чисел: {displaystyle Delta (acdot b)=|b|cdot Delta a+|a|cdot Delta b+Delta acdot Delta bapprox |b|cdot Delta a+|a|cdot Delta b}, абсолютная погрешность числа принимается равной половине последнего знака этого числа. Относительная погрешность произведения равна сумме относительных погрешностей аргументов: {displaystyle delta (acdot b)=delta a+delta b}. Полученный результат округляют до первой верной значащей цифры, значащая цифра приближенного числа является верной, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.

Пример умножения {displaystyle gamma =pi cdot e}, с точностью до 3-го знака после запятой:

График[править | править код]

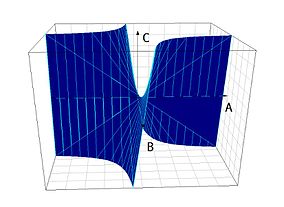
На множестве пар вещественных чисел mathbb {R} ^{2} график функции умножения является проходящим через начало координат гиперболическим параболоидом.

График функции с(a,b)=a*b

Комплексные числа[править | править код]

Множество комплексных чисел с арифметическими операциями является полем и обычно обозначается символом mathbb {C} .

Произведением двух комплексных чисел в алгебраической форме записи, называется комплексное число, равное:

{displaystyle c+fi=(a+di)cdot (b+ei)=(acdot b-dcdot e)+(acdot e+bcdot d)i,}

где: {displaystyle c,a,b,d,e,fin mathbb {R} }, i — мнимая единица.

Для того, чтобы перемножить два комплексных числа в тригонометрической форме записи, нужно перемножить их модули, а аргументы сложить:

{displaystyle c=acdot b=r_{1}(cos varphi _{1}+isin varphi _{1})cdot r_{2}(cos varphi _{2}+isin varphi _{2})=r_{1}cdot r_{2}(cos(varphi _{1}+varphi _{2})+isin(varphi _{1}+varphi _{2})),}

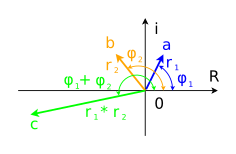
Умножение комплексных чисел на комплексной плоскости.

где: {textstyle r=|z|=|a+ib|={sqrt {a^{2}+b^{2}}};~~~varphi =arg(z)=operatorname {arctg} left({frac {b}{a}}right),} модуль и аргумент комплексного числа.

Умножение комплексного числа {displaystyle a=r_{1}e^{ivarphi _{1}}} в показательной форме, на комплексное число {displaystyle b=r_{2}e^{ivarphi _{2}}} сводится к повороту вектора, соответствующего числу a, на угол  {displaystyle arg(b)} и изменению его длины в {displaystyle |b|} раз. Для произведения комплексных чисел в показательной форме верно равенство:

{displaystyle c=re^{ivarphi }=acdot b=r_{1}e^{ivarphi _{1}}cdot r_{2}e^{ivarphi _{2}}=r_{1}cdot r_{2}cdot e^{i(varphi _{1}+varphi _{2})},}

где: {displaystyle e=2{,}718281828dots } — число e.

Экспоненциальная запись[править | править код]

В экспоненциальной записи числа записываются в виде {displaystyle a=pm xcdot P^{pm n}}, где x — мантисса, {displaystyle P^{n}} — характеристика числа, P — основание системы счисления, nin mathbb{Z } . Для умножения двух чисел, которые записаны в экспоненциальной форме необходимо умножить мантиссы и характеристики: {displaystyle (acdot P^{n})cdot (bcdot P^{k})=(acdot b)cdot P^{n}cdot P^{k}=abcdot P^{n+k}.}

Например:

{displaystyle 2{,}34cdot 10^{-5}cdot 5{,}67cdot 10^{6}=2{,}34cdot 5{,}67cdot 10^{-5}cdot 10^{6}approx 13{,}27cdot 10^{(-5+6)}approx 13{,}27cdot 10^{1}approx 1{,}33cdot 10^{2}.}

Умножение произвольных чисел[править | править код]

При умножении чисел, принадлежащих разным множествам, например {displaystyle 1{,}5(in mathbb {Q} )cdot 5(in mathbb {N} )}, необходимо произвести преобразование (приведение) одного из множителей к типу второго (если существует такая возможность). Для этого число из множества с меньшей мощностью «расширяется» в сторону числа из множества с большей мощностью: {displaystyle mathbb {N} subset mathbb {Z} subset mathbb {Q} subset mathbb {R} subset mathbb {C} subset mathbb {H} }. В данном примере следует воспользоваться тем, что натуральные числа являются подмножеством рациональных и трактовать натуральное число 5 как рациональное число {displaystyle 5{,}0}. Исходное выражение превращается в умножение двух рациональных чисел: {displaystyle 1{,}5(in mathbb {Q} )cdot 5{,}0(in mathbb {Q} )=7{,}5(in mathbb {Q} )}.

Умножение физических величин[править | править код]

Единица измерения физической величины имеет определенное наименование (размерность), например, для длины — метр (м), для времени — секунда (с), для массы — грамм (г) и так далее. Результат измерения той или иной величины представляет собой не просто число, а число с размерностью[10], например, 10 м, 145 с, 500 г. Размерность представляет собой самостоятельный объект, который равноправно участвует в операции умножения. При умножении физических величин умножаются как сами числовые значения, так и их размерности, порождая новое число с новой размерностью. Например, прямоугольник со сторонами 5 м и 3 м обладает площадью, получаемой умножением длин сторон:

5 м · 3 м = 5 · 3 м·м= 15 м·м, или 15 м².

Таким образом, умножение физических величин надо рассматривать как нахождение новой физической величины, отличающейся от величин, которые мы умножаем. Если физически возможно создание такого произведения, например, при нахождении работы, скорости или других величин, то эта величина образует множество, отличное от начальных. В этом случае композиции этих величин  присваивается новое обозначение (новый термин), например: плотность, ускорение, мощность и прочее[11].

Например, если умножить скорость равномерно и прямолинейно движущегося тела, равную 5 м/с, на время, равное 3 с, то получится именованное число (физическая величина), которая называется «длина», или «расстояние» и измеряется в метрах:

5 м/с · 3 с = 15 (м/с) · с = 15 м.

Помимо размерных физических величин существуют безразмерные величины. Безразмерные величины либо просто определяют некоторое количество (измеряются «штуками», «разами» и тому подобное), либо являются отношениями физических величин одной и той же размерности, например, относительная плотность является отношением плотности тела к эталонной плотности (обычно, плотности воды). При умножении величины с размерностью на безразмерную величину результат сохраняет исходную размерность. Например, если взять 5-метровые рейки в количестве 3 штуки, то в результате умножения получим общую длину реек 15 метров:

5 м · 3 = 15 м.

Количество реек (безразмерная величина) здесь не зависит ни от способа их подсчёта, ни от единицы измерения их длины. Например, если измерить длину не в метрах, а в футах, то длина той же рейки составит 16,4 фута, а общая длина трёх реек:

16,4 фута · 3 = 49,2 фута.

Умножение последовательностей[править | править код]

Произведение элементов последовательности может быть компактно записано с помощью специального символа умножения, восходящего к заглавной букве Π (пи) греческого алфавита, как показано в примере:

{displaystyle prod _{i=1}^{4}i=1cdot 2cdot 3cdot 4=24.}

Снизу записывается символ свободной переменной (в данном случае i), называемой «индексом умножения», вместе с начальным значением (в данном случае 1). Сверху записывается конечное значение (в данном случае 4) в виде числа или переменной, либо символ бесконечности infty , если предполагается бесконечное произведение. Такую запись можно «развернуть» в выражение, в котором последовательно подставляются значения индекса умножения от начального до конечного значения:

{displaystyle prod _{i=m}^{n}x_{i}=x_{m}cdot x_{m+1}cdot x_{m+2}cdot ,,cdots ,,cdot x_{n-1}cdot x_{n},}

где m и n есть целые числа или выражения, которые вычисляются в целочисленные значения.

Такая запись обладает следующим свойством[5]:104:

{displaystyle prod _{i=1}^{n+1}a_{i}=(prod _{i=1}^{n}a_{i})a_{n+1}.}

Если значения индекса заданы некоторым множеством, то многократное произведение может быть записано с его помощью, например

{displaystyle prod _{iin A}x_{i}}.

Такая запись означает, что переменная i «пробегает» все значения, принадлежащие множеству A.

См. также[править | править код]

  • Бруски Женая — Люка
  • Деление
  • Возведение в степень

Примечания[править | править код]

  1. ↑ 1 2 Математическая энциклопедия, 1985.
  2. ↑ 1 2 Умножение // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
  3. ↑ 1 2 3 Так это свойство обычно называется в школьных учебниках
  4. ↑ Истомина, 2005, с. 165.
  5. ↑ 1 2 Энциклопедия элементарной математики. Книга 1 (арифметика) / Под ред. П. С. Александров, А. И. Маркушевич, А. Я. Хинчин. — М.-Л., ГТТИ, 1951. 448 с.
  6. ↑ Выгодский, 2003, с. 116—117.
  7. ↑ Гусев, 1988, с. 20.
  8. ↑ Поскольку на множестве вещественных чисел уже введено отношение линейного порядка, то мы можем определить топологию числовой прямой: в качестве открытых множеств возьмём всевозможные объединения интервалов вида {x:alpha <x<beta }
  9. ↑ Ильин, 1985, с. 46.
  10. ↑ Волинская Н. И. Интегрированный урок по физике и математике, Измерение физических величин и их единицы, СШ 7 г. Бреста. brestschool7.iatp.by. Дата обращения: 18 апреля 2016. Архивировано из оригинала 7 августа 2016 года.
  11. ↑ Макаров Владимир Петрович. О «размерности» физических величин. lithology.ru, Литология.РФ. Дата обращения: 18 апреля 2016. Архивировано 6 мая 2016 года.

Литература[править | править код]

  • Барсуков А. Н. Алгебра. Учебник для 6-8 классов.. — Просвещение, 1966. — 296 с.
  • Выгодский М. Я. Справочник по элементарной математике. — М.: АСТ, 2003. — ISBN 5-17-009554-6.
  • Гусев В. А., Мордкович А. Г. Математика. Справочные материалы, книга для учащихся.. — Просвещение, 1988. — 416 с.
  • Ильин В. А. и др. Математический анализ. Начальный курс.. — МГУ, 1985. — 662 с.
  • Эндертон Г. Элементы теории множеств = Elements of Set Theory. — Gulf Professional Publishing, 1977. — 279 с. — ISBN 0-12-238440-7.
  • Иванова О. А. Умножение чисел // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1985. — Т. 5. — С. 495—496. — 1248 с.
  • Истомина Н. Б. Методика обучения математике в начальной школе: Развивающее обучение.. — Ассоциация XXI век, 2005. — 272 с. — ISBN 5-89308-193-5.

Ссылки[править | править код]

  • Умножение: по-японски, по-итальянски и методом майя
Источник

В этом уроке мы узнаем, как перемножать два числа с разными знаками, а также разберемся, как перемножить два отрицательных числа.

Научимся возводить в квадрат как положительные, так и отрицательные числа, и предугадывать знаки результата умножения.

Также мы узнаем, как связаны между собой отрицательные числа и умножение на -1 и как это можно использовать.

Задача:

Кондитерская фабрика выпускает шоколадки по 3000 штук в день.

Фабрика изменила вес одной шоколадки на -10 грамм.

Вопрос: на сколько изменилось количество выпускаемого в день?

Для ответа на этот вопрос необходимо перемножить то, насколько меньше стал вес одной шоколадки, на общее количество шоколадок.

Так мы пришли к тому, что нам необходимо уметь перемножать числа с разными знаками.

Эта информация доступна зарегистрированным пользователям

Правило: чтобы перемножить числа с разными знаками, необходимо посчитать произведение модулей этих чисел и к результату приписать “минус”.

Применим это правило к нашей задаче:

1) Считаем модули:

(mathbf{mid3000mid=3000})

(mathbf{mid-10mid=10})

2) Считаем произведение модулей:

(mathbf{3000cdot10=30000})

3) Приписываем “минус” и получаем ответ: на -30000 грамм.

Как видите, все достаточно просто, приведем еще примеры:

(mathbf{3cdot(-5)=-15})

(mathbf{frac{1}{2}cdot(-2)=-1})

(mathbf{-1frac{1}{3}cdot6=-8})

(mathbf{548cdot(-0.5)=-274})

Заметим, что произведение чисел с разными знаками всегда число отрицательное.

Так происходит потому, что сначала считается произведение модулей, поэтому произведение положительных чисел определенно будет положительным.

Далее мы приписываем к нему минус. А если приписать минус к положительному числу, то получится ни что иное, как число отрицательное.

Эта информация доступна зарегистрированным пользователям

Теперь посмотрим, что делать, если надо перемножить два отрицательных числа.

Эта информация доступна зарегистрированным пользователям

Правило: произведение двух отрицательных чисел равняется произведению их модулей.

Пример:

Необходимо перемножить (mathbf{-15}) и (mathbf{-3})

1) Находим их модули:

(mathbf{mid-15mid=15})

(mathbf{mid-3mid=3})

2) Считаем произведение модулей:

(mathbf{15cdot3=45})

Если записать кратко: (mathbf{-15cdot(-3)=45})

Это и будет ответом.

Даже проще, чем с произведением отрицательных чисел, – не надо приписывать минус.

Пример:

Перемножим (mathbf{-frac{1}{6}cdot(-frac{3}{2})})

1) Посчитаем модули:

(mathbf{mid-frac{1}{6}mid=frac{1}{6}})

(mathbf{mid-frac{3}{2}mid=frac{3}{2}})

2) Считаем их произведение:

(mathbf{frac{1}{6}cdotfrac{3}{2}=frac{1cdot3}{6cdot2}=frac{1}{2cdot2}=frac{1}{4}})

Ответ: (mathbf{frac{1}{4}})

И еще несколько примеров:

(mathbf{-54cdot(-2)=108})

(mathbf{-frac{12}{45}cdot(-frac{15}{4})=frac{12cdot15}{45cdot4}=frac{3cdot15}{45}=frac{45}{45}=1})

(mathbf{-0.002cdot(-0.2)=0.0004})

Заметим, что произведение отрицательных чисел всегда получается больше нуля.

Так происходит потому, что, по правилу, это произведение равняется произведению модулей этих чисел.

Сами модули – числа положительные. Значит, и их произведение является числом положительным.

Все наши примеры это только подтверждают, что произведение отрицательных чисел получается положительным.

Эта информация доступна зарегистрированным пользователям

Эта информация доступна зарегистрированным пользователям

Определение: квадратом числа а называется число (mathbf{a^2}) такое, что (mathbf{a^2=acdot a})

Возможно, у вас уже возник вопрос, почему “квадрат”? Сразу ответим на него.

Чтобы найти площадь прямоугольника, необходимо перемножить длины двух его не противоположных сторон.

А у квадрата все стороны одинаковы, поэтому площадь равняется произведению стороны на саму себя, иными словами, площадь квадрата равняется квадрату длины его стороны.

Мы уже немного ушли в геометрию, которую вы будете изучать позже, а сейчас посмотрим на примеры нахождения квадратов. 

Пример:

Найдем квадрат числа 3.

Считать будем по определению, перемножим 3 само на себя:

(mathbf{3^2=3cdot3=9})

Еще пример на положительное число, найдем квадрат числа 12 :

Точно также нужно перемножить число само на себя:

(mathbf{12^2=12cdot12=144})

И с нулем все также максимально просто: любое число при умножении на 0 дает 0, и сам 0 при умножении на 0 даст 0 :

(mathbf{0^2=0cdot0=0})

Теперь посмотрим, что будет, если мы будем считать квадрат отрицательного числа:

Посчитаем квадрат (mathbf{-4}):

(mathbf{(-4)^2=(-4)cdot(-4)=16})

Заметим, что мы перемножали отрицательные числа – значит, по сути просто взяли квадрат от модуля данного отрицательного числа.

Правило: квадрат отрицательного числа равен квадрату модуля отрицательных чисел.

Также заметим, что квадрат всегда неотрицателен.

Доказательство:

  1. Если число в квадрате положительно, то квадрат положительного числа равен произведению положительных чисел и даст результат больший нуля.
  2. Если число, от которого берется квадрат, равно нулю, то и квадрат равен нулю, что удовлетворяет определению неотрицательности.
  3. Если же число, от которого берется квадрат, отрицательно, квадрат будет являться произведением двух отрицательных чисел, то есть числом положительным.

Таким образом, мы рассмотрели все возможные случаи, и во всех из них квадрат был числом неотрицательным, то есть положительным.

Эта информация доступна зарегистрированным пользователям

Мы уже знаем, что произведение отрицательного числа на положительное даст нам отрицательное число.

А что, если воспользоваться этим в обратную сторону?

Например, имеется отрицательное число (mathbf{-43})

Заметим, что оно равно (mathbf{-1cdot43})

Также заметим, что квадрат от -1 равен 1.

(mathbf{(-1)^2=(-1)cdot(-1)=-(1cdot1)1})

Используя это в случаях с произведением чисел мы можем ловко менять и переставлять знаки.

Например, было такое произведение:

(mathbf{-636cdot(-452)cdot21cdot(-3)})

Преобразовав его можно оставить только один “минус”, смотрите:

(mathbf{-636cdot(-452)cdot21cdot(-3)=(-1)cdot636cdot(-1)cdot452cdot21cdot(-1)cdot3})

Сейчас для больше наглядности мы переставим все -1 в начало, но этого можно и не делать:

(mathbf{(-1)cdot636cdot(-1)cdot452cdot21cdot(-1)cdot3=(-1)cdot(-1)cdot(-1)cdot636cdot452cdot21cdot3})

Каждая пара минус единиц дает единицу. В данном случае минус единиц три штуки, значит, две из них дадут единицу, а третья останется:

(mathbf{(-1)cdot(-1)cdot(-1)cdot636cdot452cdot21cdot3=(-1)cdot636cdot452cdot21cdot3})

Казалось бы, что нам это дало? А дало это нам то, что теперь знак выражения стал более наглядным: мы видим произведение -1 и произведение положительных чисел, являющегося положительным числом.

Вот теперь можно сказать, что ответом будет отрицательное число.

Правило: произведение нескольких чисел является отрицательным, тогда и только тогда, когда из его множителей нечетное количество является отрицательными и ни один множитель не равен нулю.

Оговорка про нуль важна, так как если один из множителей равен нулю, то и все выражение равно нулю, а значит, не является отрицательным.

Иногда -1 уходят полностью. Так происходят в случаях, когда отрицательных множителей четное число.

Пример:

(mathbf{-7cdot2cdot(-3)cdot(-4)cdot(-2)=(-1)cdot(-1)cdot(-1)cdot(-1)cdot7cdot2cdot3cdot4cdot2=7cdot2cdot3cdot4cdot2})

Правило: произведение нескольких чисел является положительным тогда и только тогда, когда из его множителей их четное количество являются отрицательными и ни один множитель не равен нулю.

Отметим еще один момент: -1 можно выносить и заносить в обе стороны.

Эта информация доступна зарегистрированным пользователям

То есть в данном случае мы можем переписать выражение так:

(mathbf{(-1)cdot636cdot452cdot21cdot3=-(636cdot452cdot21cdot3)})

Это же позволит превращать вычитание отрицательного числа в прибавление положительного. В самом деле:

(mathbf{a-(-b)=a+(-(-b))=a+(-1cdot(-b))=a+(-1cdot(-1)cdot b)=a+b})

Эта информация доступна зарегистрированным пользователям

Интересно посмотреть,как развивалась математика в Древней Руси.

В XVIII веке с приходом к власти Петра Первого (1672- 1725) в России появилась система образования, которая постепенно интегрировалась с общемировой и дала множество открытий.

Однако до этого момента тоже существовали математические познания, о которых мы сейчас и расскажем.

Как и в остальном мире, необходимость в математике была вызвана экономикой.

Поэтому одними из первых денежных знаков были домашние животные и шкуры.

Так, например, были резаны (куски шкур), куны (от слова “куница”) и ногаты.

Позже расчеты свели к гривнам: одна гривна, равная примерно 50-ти граммам серебра, равнялась 50-ти резанам, 25-ти кунам или 20-ти ногатам.

И уже позже, только к XIV веку, начали переходить к рублю, представлявшему из себя на тот момент круглый кусок серебра массой 205 грамм.

Меры длины во многих системах, в том числе и древнерусской, были связаны с параметрами человеческого тела:

  • пядь равнялась расстоянию между концами разведенных большого и указательного пальца
  • локоть равнялся расстоянию от кончиков пальца до локтя
  • сажень была косой и маховой: маховая между разведенными с сторону руками, косая между ногой и отведенной вверх рукой

Эта информация доступна зарегистрированным пользователям

Первый свод математических правил встречается в сборнике “Русская правда” (XI век), там опять же говорилось про экономику: штрафы, долги проценты, что лишний раз показывает, что люди уже умели оперировать целыми и дробными числами.

Далее выходили и другие труды, связанные с математикой, которые постепенно входили и в массы.

Книга “Считание удобное, которым всякий человек купующий или продающий, зело удобно изыскати может, число всякие вещи”, которая вышла в 1682 году, своим названием уже намекает на то, что предназначена была не только для ученых или любителей, но и для купечества.

Ну а дальше при Петре I появлялись школы, приглашались зарубежные специалисты, и наука шагнула далеко вперед.

По сей день российские ученые и студенты-математики выигрывают международные конкурсы и награды, решая нерешенные до этого задачи.

Читайте также

Источник

Содержание:

  • Определение произведения чисел
  • Свойства произведения чисел

Определение произведения чисел

Произведение $p$ чисел
$a_{1}, a_{2}, dots, a_{n}$ есть результат умножения этих чисел: $p=a_{1} cdot a_{2} cdot ldots cdot a_{n}$ .
В частности, если умножаются два числа $a$ и $b$, то

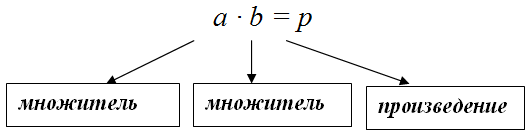
Пример

Задание. Найти произведение чисел:

1)  1.2$cdot 3$   ;   2)  4$cdot 5 cdot 13$ 

Ответ.  

$1,2 cdot 3=3,6$

$4 cdot 5 cdot 13=260$

Свойства произведения чисел

  1. Коммутативность: $n cdot m=m cdot n$

  2. Ассоциативность: $(n cdot m) cdot k=n cdot(m cdot k)$

    На основании этих свойств можем заключить, что при перестановке множителей значение произведения не меняется.

  3. Дистрибутивность: $(n+m) cdot k=n cdot k+m cdot k$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти произведение чисел удобным способом:

1)  5$cdot 17 cdot 2$   ;   2)  7$cdot 2 cdot 15 cdot 5$ 

Решение. По свойства умножения имеем:

$$5 cdot 17 cdot 2=(5 cdot 2) cdot 17=10 cdot 17=170$$

$$7 cdot 2 cdot 15 cdot 5=(7 cdot(2 cdot 15)) cdot 5=(7 cdot 30) cdot 5=210 cdot 5=1050$$

Ответ.  

$5 cdot 17 cdot 2=170$

$7 cdot 2 cdot 15 cdot 5=1050$

Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие
натуральные числа или
десятичные дроби.

Пример

Задание. Найти произведение чисел

1)  156$cdot 32$   ;   2)  $4,71 cdot 3,1$ 

Решение. Запишем умножаемые числа в столбик. Далее умножим сначала единицы второго числа на первое,
полученное произведение запишем под чертой. Затем аналогично умножим десятки второго числа на первое. Результат запишем
под первым произведением только на один разряд левее. В конце найдем сумму полученных произведений по правилу сложения в
столбик

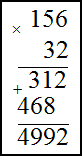
Умножение десятичных дробей во втором примере производится следующим образом: не обращая внимания на запятые, дроби
перемножаются как целые числа; в получившемся произведении отделяют справа число знаков, равное сумме чисел знаков после
запятой у сомножителей. В нашем случае в первом сомножителе два знака после запятой, во втором – один, значит, в ответе
нужно отделить справа три знака:

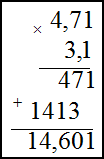
Ответ.  

$156 cdot 32=4992$

$4,71 cdot 3,1=14,601$

Читать дальше: что такое простое число.

Источник

Добавить комментарий