Как найти знак вектора

Определение и обозначение вектора

Вектор в геометрии — это отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом. В некоторых учебниках вектор могут называть направленным отрезком.

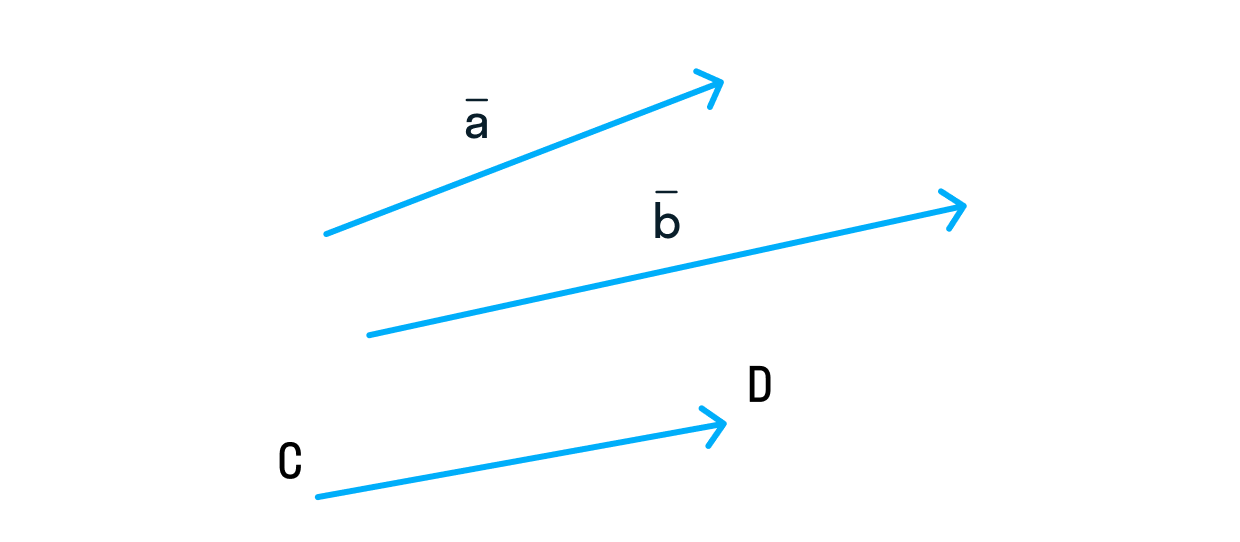
Вектор обозначается одной строчной буквой латинского алфавита или двумя заглавными со стрелкой (в некоторых случаях — прямой линией) сверху.

Интересно, что порядок букв в названии вектора имеет значение! Первая буква отвечает за начало вектора, а последняя — за его конец. Поэтому

и

— абсолютно разные векторы.

Виды векторов

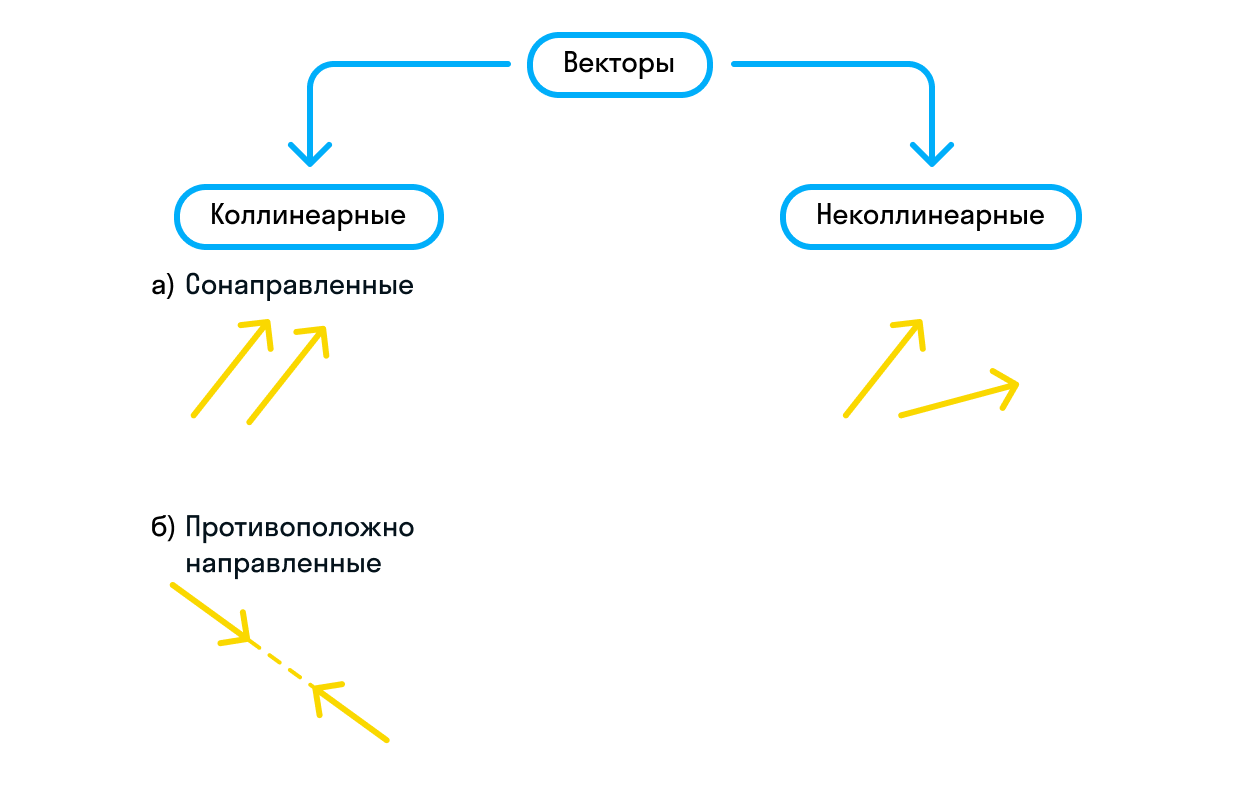
Во-первых, векторы бывают коллинеарными и неколлинеарными.

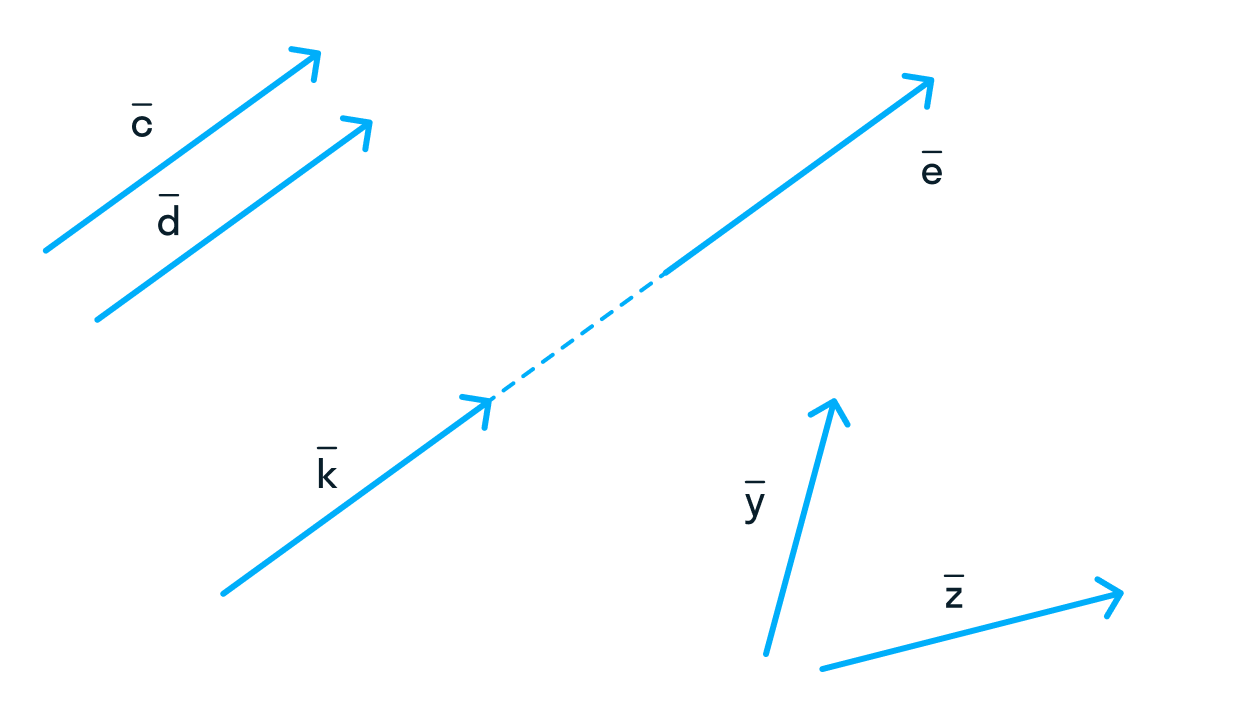
Коллинеарными называют те векторы, которые лежат на одной прямой или параллельных прямых. На рисунке

и

и

являются коллинеарными, а

и

относительно друг друга — нет.

Векторы различаются и по направлению. Если векторы уже являются коллинеарными, они могут быть сонаправленными или противоположно направленными. Сонаправленные векторы обозначаются так:

Если же они противоположно направлены, мы можем записать это следующим образом:

Равными являются те векторы, которые одновременно и коллинеарны, и сонаправлены, а также имеют одинаковую длину.

Нулевой вектор — вектор, длина которого равна нулю. Чаще всего его обозначают так:

Он считается коллинеарным любому вектору.

Иногда в геометрии вводят дополнительные понятия, рассмотрим и их:

• Закреплённый вектор — отрезок с упорядоченными концами: если С — точка начала вектора, а Е — точка конца, тогда

  (это то, что мы понимаем под обычным вектором в школьной геометрии).

• Свободный вектор — вектор, начало и конец которого не закреплены. Его можно перемещать как вдоль прямой, на которой он находится, так и параллельно этой прямой. По сути под свободным вектором понимают множество закреплённых векторов.

Сложение и вычитание векторов

Действия с векторами описываются и в алгебре, и в геометрии. Сегодня мы рассмотрим способы, благодаря которым можно сложить и вычесть векторы, не зная их координат.

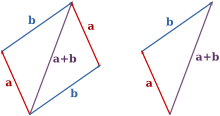
Сложение: метод треугольника

Представим, что в пространстве заданы векторы

и

которые нам необходимо сложить. Эта задача особенно актуальна для физиков, поскольку такие векторные величины, как сила, часто приложены к одному и тому же телу. В таком случае возникает вопрос: а как же рассчитать результирующее действие всех этих сил?

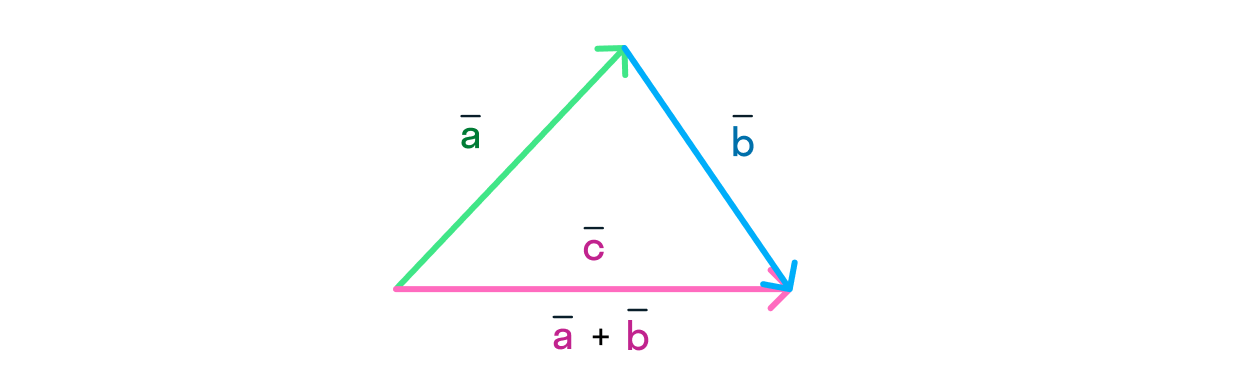
В этом на помощь физикам приходит математика — царица наук! Чтобы сложить два вектора, необходимо:

1. Отложить начало одного вектора от конца другого.

2. Вектор их суммы будет совпадать с вектором

   , который соединяет начало вектора

   с концом вектора

Сложение: метод параллелограмма

Сложить векторы можно и по-другому, используя метод параллелограмма:

1. Совместим между собой начала

   и

2. Отложим от конца

   вектор, равный

3. Отложим от конца

   вектор, равный

4. Благодаря пунктам 2 и 3 мы получили параллелограмм (четырёхугольник, противоположные стороны которого параллельны и равны).

5. Проведём диагональ параллелограмма между

   и

   на которой будет лежать вектор, равный сумме

   и

Задача решена, вы великолепны!

Сложение: метод многоугольника

А что если векторов больше, чем два? На эту проблему математика уже подготовила решение: воспользуемся расширенным методом треугольника, который получил название «метод многоугольника».

Согласно этому методу мы последовательно совмещаем конец и начало векторов, а после изображаем суммирующий вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего. Лучше всего рассмотреть это на чертеже:

Вычитание векторов

Продолжаем проделывать с векторами всевозможные действия, на этот раз вычитание. Математики знают, что вычитание — это по своей сути то же сложение, но с обратным числом.

С векторами работает та же штука: вместо вычитания попробуем прибавить вектор, противоположно направленный исходному:

Изобразим разность векторов с помощью уже знакомого нам правила треугольника:

Боитесь запутаться в векторах сонаправленных и противоположно направленных?
Существует отдельное правило для их вычитания:

1. Отложим один вектор от начала другого.

2. Тогда вектор их разности совпадает с вектором, начало которого совмещено с концом вычитаемого вектора, а конец — с концом уменьшаемого.

Этот метод схож и с методом параллелограмма, но в этом случае мы берём другую диагональ.

Координаты вектора на плоскости и в пространстве

Для выполнения остальных действий с векторами нам необходимо поместить их в такую систему координат, чтобы можно было
определить их положение относительно друг друга. Для этого используют декартову систему координат, которой можно
пользоваться как на плоскости с осями X и Y, так и в пространстве с осями
X, Y, Z.

Тогда, если

находится на плоскости, его координаты можно выразить как

если в пространстве
—

Базисные векторы — это векторы, каждый из которых направлен вдоль своей оси координат, в трёхмерном пространстве их обозначают

Любой вектор в трёхмерном пространстве можно разложить по трём базисным векторам.

с координатами

можно записать так:

Умножение вектора на число

Представьте, что нам необходимо растянуть вектор в два раза или же сжать, но уже в три. За все эти действия отвечает
одна простая задача: умножение вектора на число.

Для того чтобы увеличить или уменьшить вектор в некоторое количество раз, необходимо умножить все координаты вектора
на это число.

Таким образом, если

задан координатами

то

—

Кстати, подобным образом можно перевернуть вектор, направив его в противоположную сторону:

Длина вектора

Длина вектора — одно из основных понятий в этом разделе. И неудивительно, ведь она характеризует его протяженность в
пространстве и выражается числом.

Итак, длина вектора — это расстояние между его началом и концом. Её часто называют модулем, что
отражается и в обозначении. Если нам необходимо найти длину

мы так и запишем:

Длину вектора можно найти разными способами, вот основные:

1. через координаты вектора;

2. через координаты точек начала и конца вектора;

3. через теорему косинусов.

Давайте вместе разберём все методы!

Длина вектора через его координаты

Если

задан через координаты

то его длину можно найти как

Почему мы можем быть уверены, что эта формула правильная? Рассмотрим вектор

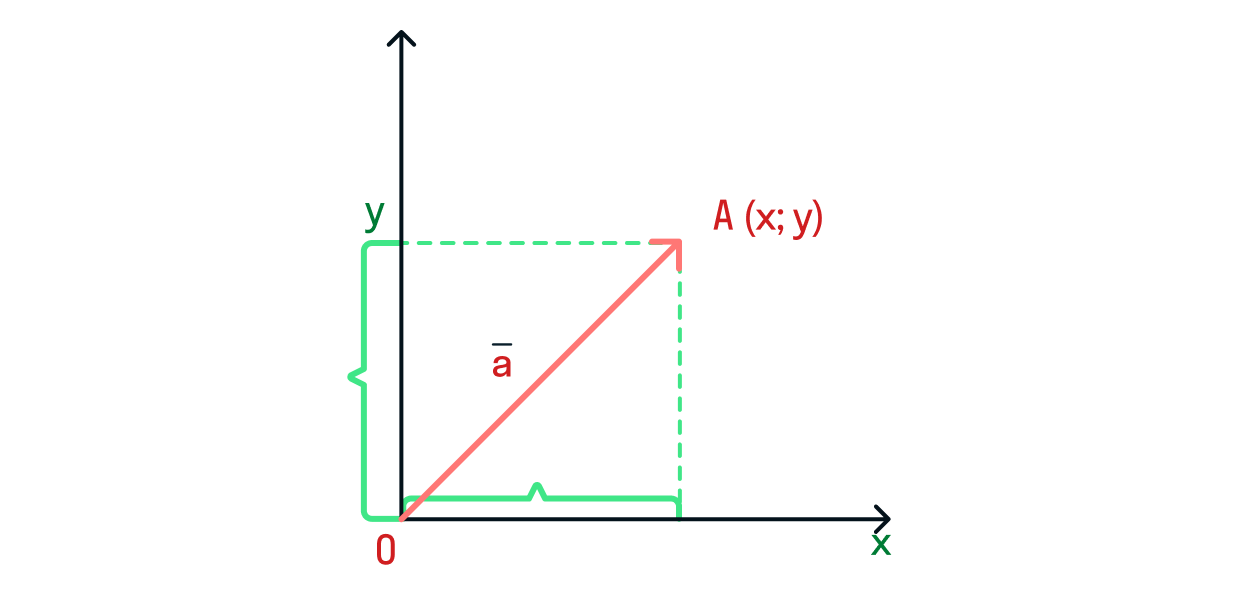
в декартовой системе координат.

Отложим вектор

от точки

с координатами

Тогда этот вектор можно назвать

, и так как мы строили его из
начала координат, координаты вектора могут быть найдены как

Рассчитаем длину

через теорему Пифагора:

Задача 1

Посчитайте, чему равен модуль

, если его координаты

Решение:

Модуль вектора — это его длина, а значит,

Задача 2

Длина

Чему равна координата по оси

, если координата по оси

Решение:

Длина вектора через координаты точек начала и конца

Для начала давайте вспомним, как задать координаты вектора через координаты его начала и конца.

Рассмотрим

где

и

Тогда координаты вектора можно выразить так:

Мы уже знаем, как найти длину вектора через его координаты, поэтому подставим полученное выражение в формулу:

Задача 3

Найдите длину

если

и

Решение:

Задача 4

Рассчитайте координату по

точки

вектора

, если его длина равна

а

Решение:

Остановимся здесь и подставим известные числа в формулу:

или

Длина вектора через теорему косинуса

К сожалению, в задачах не всегда даны координаты точек вектора или его самого. В таком случае мы воспользуемся
теоремой косинуса.
Давайте вспомним её формулировку.

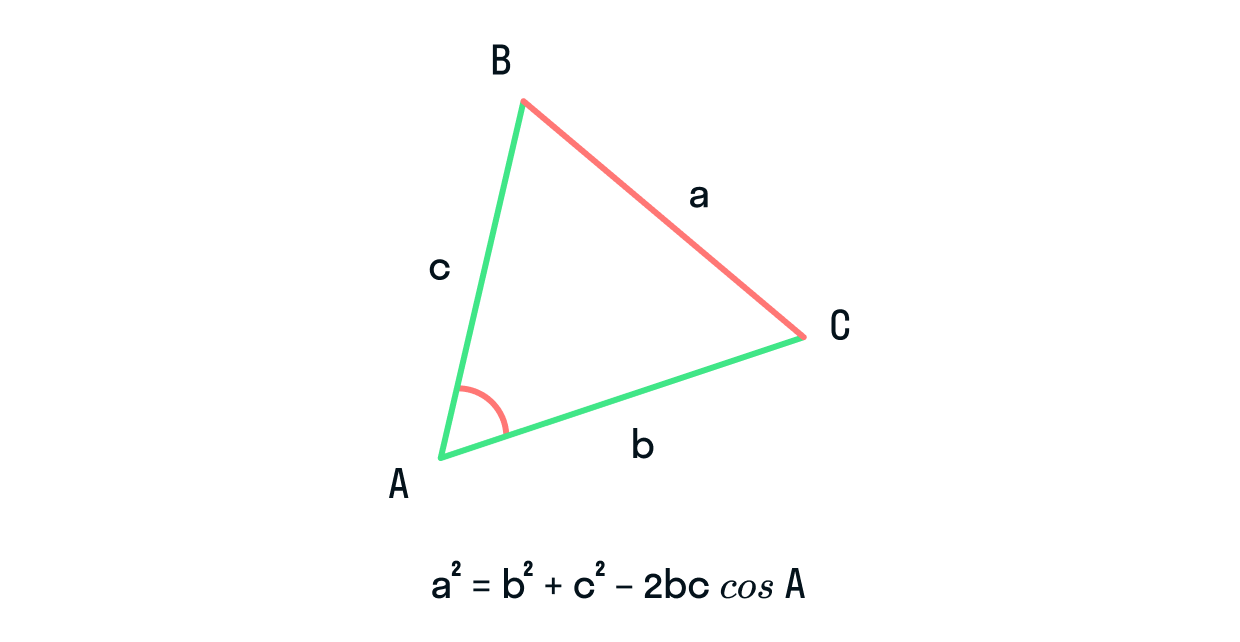
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус
удвоенное произведение этих сторон на косинус угла между ними.

Формула теоремы косинусов:

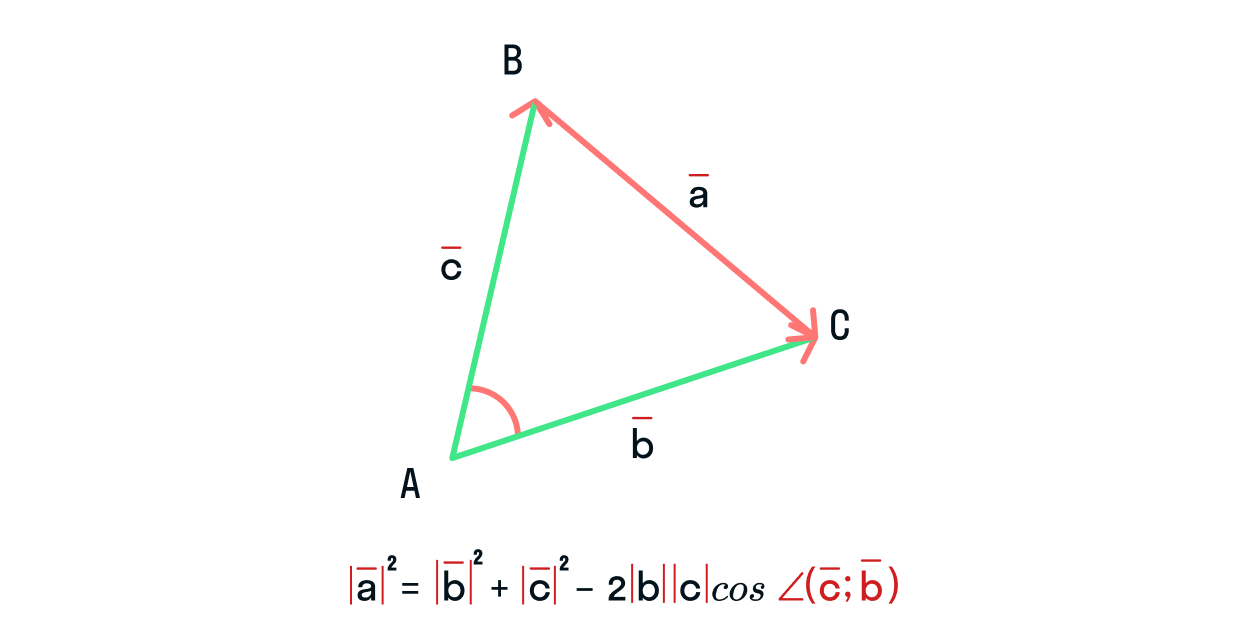
Эту теорему можно применить и в векторной форме. Немного изменим рисунок:

Тогда, чтобы найти длину

, необходимо знать (или иметь возможность вычислить) длины

и

, знать угол между ними, а также уметь рассчитать произведение длин этих векторов.

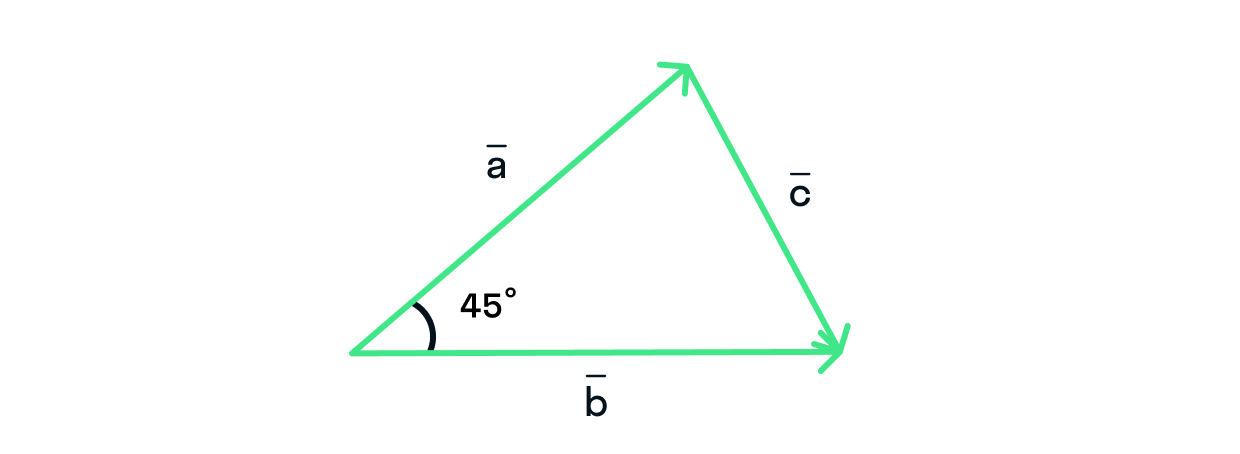
Задача 5

Длины

и

равны 4 и 6 соответственно, а угол между ними равен

Вычислите длину

Решение:

Задача 6

Рассчитайте модуль вектора

в треугольнике, если длина

= 8, длина

= 10, а угол между ними равен

Решение:

Скалярное произведение векторов

Мы практически дошли до финала нашего путешествия по царству векторов. 👑 Нам осталось изучить только скалярное
произведение векторов. Что это?

Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то
есть число,
которое не зависит от выбора системы координат.

Скалярным произведением

и

будет скалярная величина, равная произведению модулей этих векторов, умноженная на
косинус угла между ними:

Вспомним, что в той же физике величины делятся на скалярные (не имеющие направления, например, масса) и векторные
(имеющие направление, например, сила, ускорение, скорость). В математике под вектором подразумевают направленный
отрезок, а понятие скаляра хоть и не равно, но очень близко к понятию числа.

Скалярное произведение показывает, насколько синхронизированы, скоординированы направления векторов. Так, чем больше
угол между векторами, тем меньше согласованности, а значит, скалярное произведение будет уменьшаться с ростом угла:

• Скалярное произведение вектора на само себя равно квадрату его модуля:

  В данном случае значение скалярного произведения является наибольшим из
  возможных.

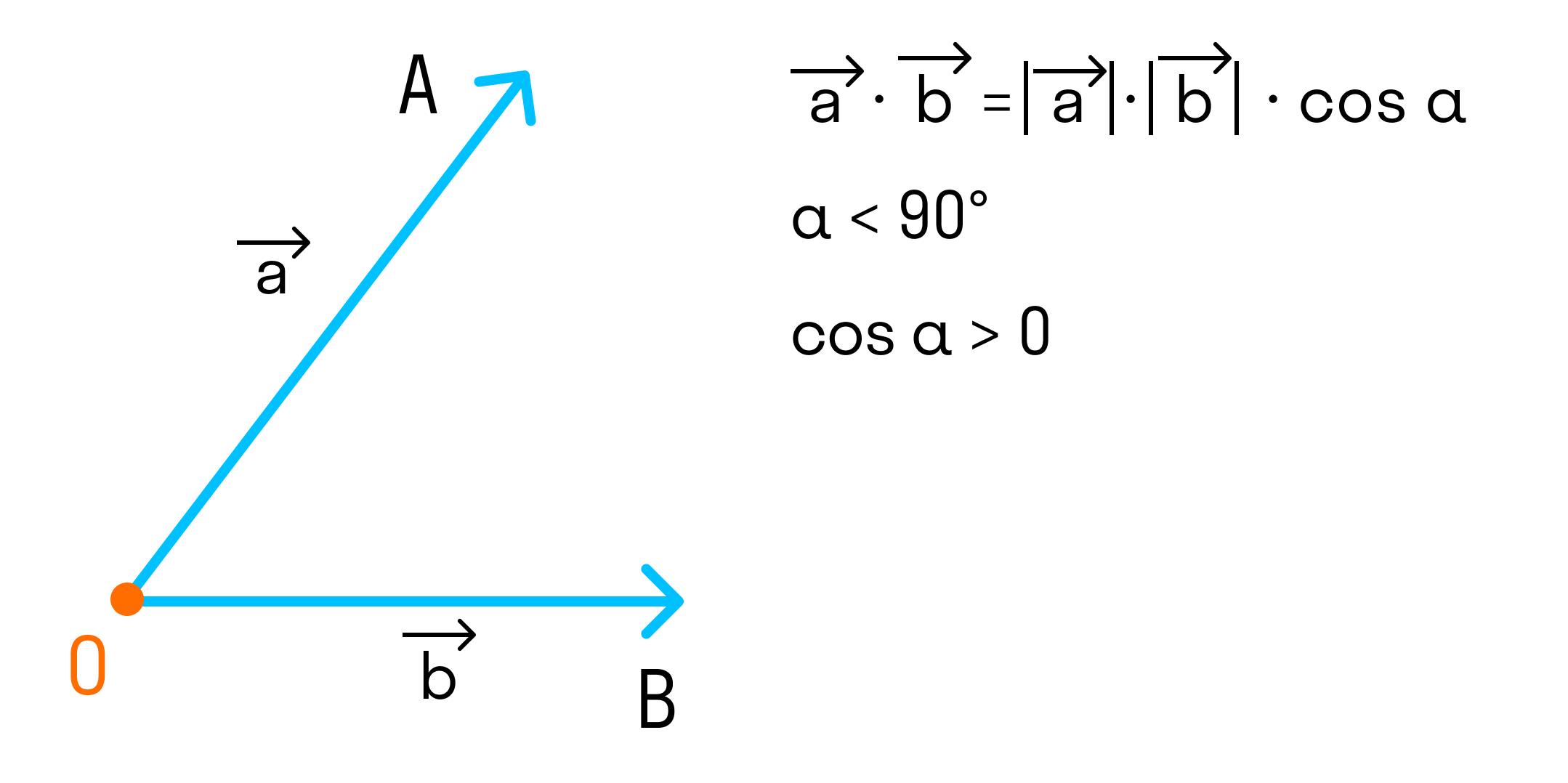
• Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, так как

  

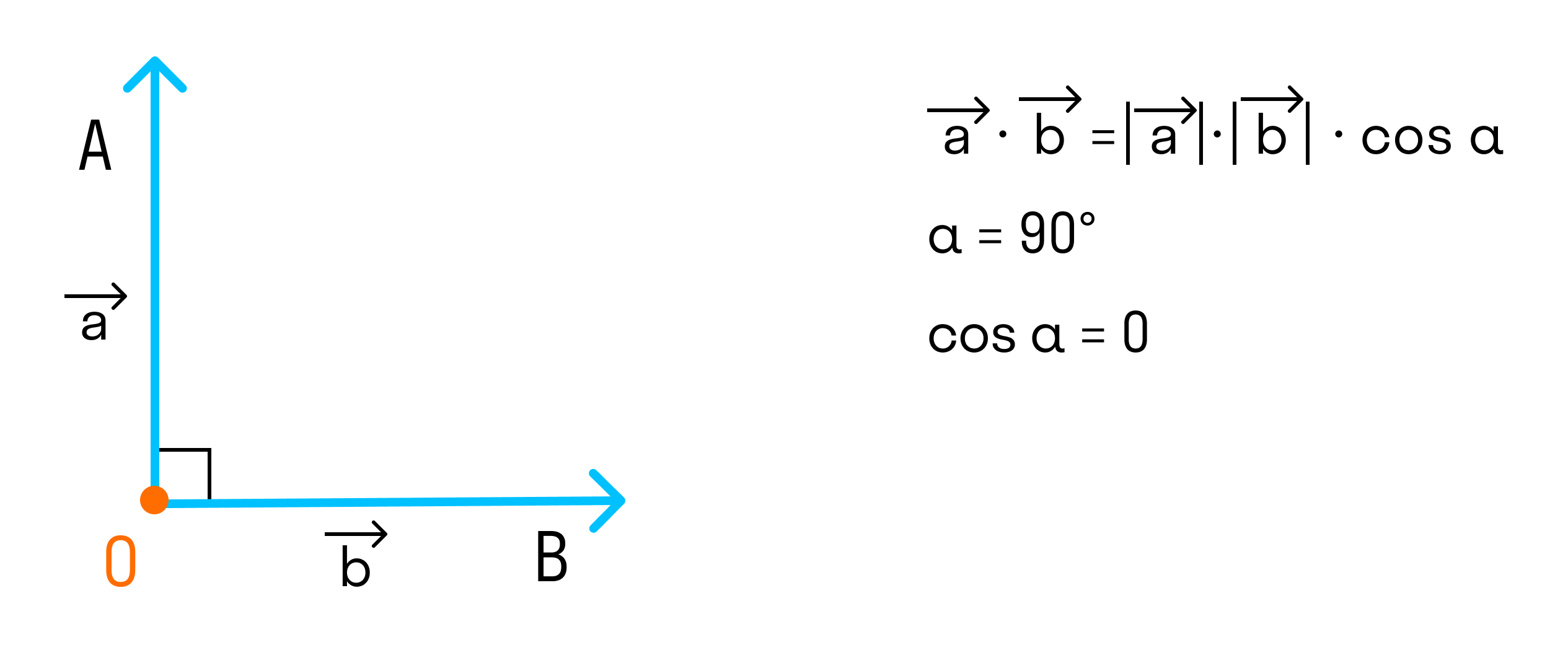
• Если угол между векторами прямой, то скалярное произведение равно 0, так как

  

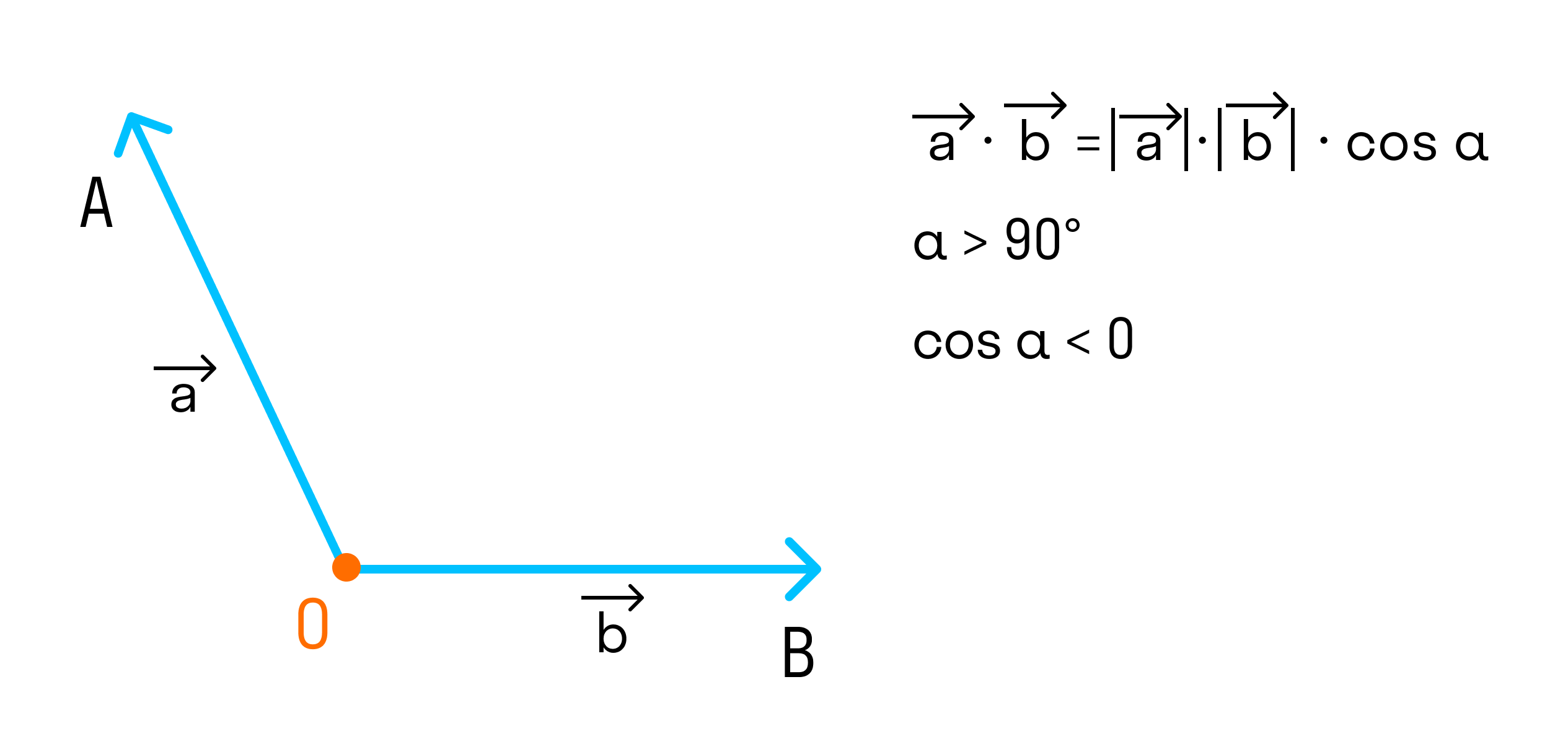
• Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как

  

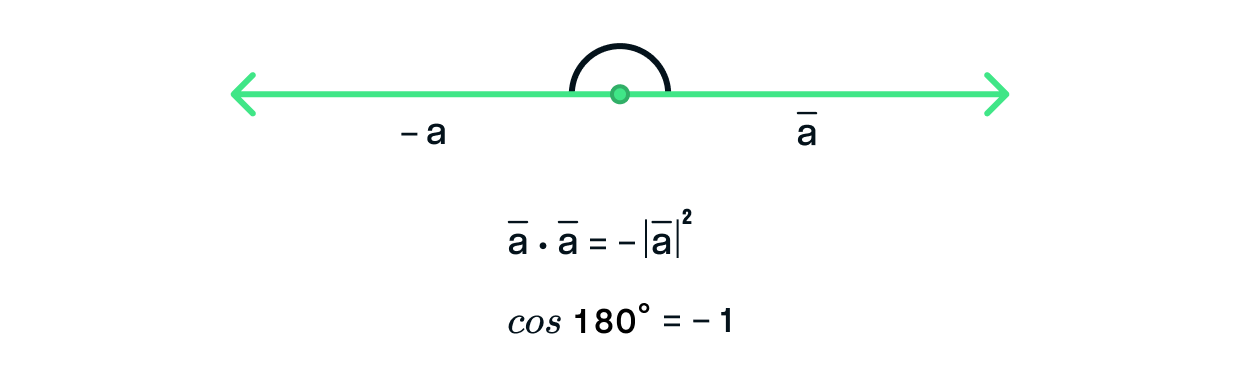
• Cкалярное произведение вектора на противоположно направленный ему вектор равно отрицательному произведению их
  длин . В данном случае значение скалярного произведения является наименьшим из возможных.

  

Конечно, вы можете возразить: «Согласованность направлений отлично показывает угол, для чего нам эти сложные
вычисления?». А всё дело в том, что в пространстве порой очень сложно измерить угол, а вот посчитать скалярное
произведение — просто, особенно если рассмотреть его через координаты.

Если

выражен координатами

а

то скалярное произведение этих векторов описывается формулой:

В пространстве скалярное произведение через координаты векторов будет задаваться так:

Где применяется скалярное произведение? Благодаря ему выполняется большое количество математических операций, таких
как нахождение угла между векторами и любых расстояний, если они заданы через координаты. Благодаря скалярному
произведению можно описать даже характеристику криволинейных поверхностей, но это мы обсудим как-нибудь в другой
раз. 🙂

Чтобы закрепить пройденный материал, нужно больше, чем пара заданий. Поэтом приглашаем на онлайн-уроки математики в
школу Skysmart. За короткое время благодаря особенной платформе и учителям-профессионалам вы сможете улучшить
школьные отметки, подготовиться к экзаменам и олимпиадам, и самое главное — понять и полюбить математику.

Как поставить знак вектора в ворде?

Поставить знак вектора в программе ворд достаточно просто, следуйте следующей инструкции:

Первый шаг. Открываем новый лист программы ворд. На верхней панели настроек находим закладку «Вставка» и активируем. Откроется меню «Вставка», в котором нужно найти блок настроек «Символы» и нажать на иконку с названием «Формуа».

Второй шаг. На экране появиться специальное поле для ввода формул.

Третий шаг. Активируем это поле и переводим курсор на верхнюю панель настроек. В блоке настроек «Структура» находите иконку с названием: «Диакритические знаки» и нажимаете на неё. Перед вами откроется новая панель с различными формулами, в ней отыскиваете иконку с квадратиком в пунктир, над которым есть стрелочка вправо и нажимаете на неё.

Четвертый шаг. На экране отразиться данный квадратик с пунктиром и стрелочкой. Вам нужно курсор поставить вовнутрь этого квадратика.

Пятый шаг. Пишем, например, английскую большую букву «A». И получаем нужный результат.

Видео

Вектор: определение и основные понятия

Определение вектора

рис. 1

Обозначение вектора

Вектор началом которого есть точка А, а концом – точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a .

Длина вектора

Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.

Нулевой вектор

Нулевой вектор обычно обозначается как 0 .

Длина нулевого вектора равна нулю.

Коллинеарные вектора

рис. 2

Сонаправленные вектора

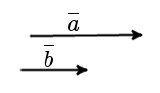рис. 3

Противоположно направленные вектора

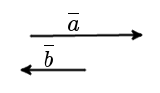рис. 4

Компланарные вектора

рис. 5

Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.

Равные вектора

рис. 6

То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

a = b , если a ↑↑ b и | a | = | b |.

Единичный вектор

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Знакомимся с вектором

Основы линейной алгебры для тех, кого это миновало в универе.

Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.

Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.

⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.

Линейная алгебра

Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.

Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.

Например, мы знаем, что если a + b = c , то a = c − b . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.

Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.

В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.

Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.

Что такое вектор

Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.

Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве

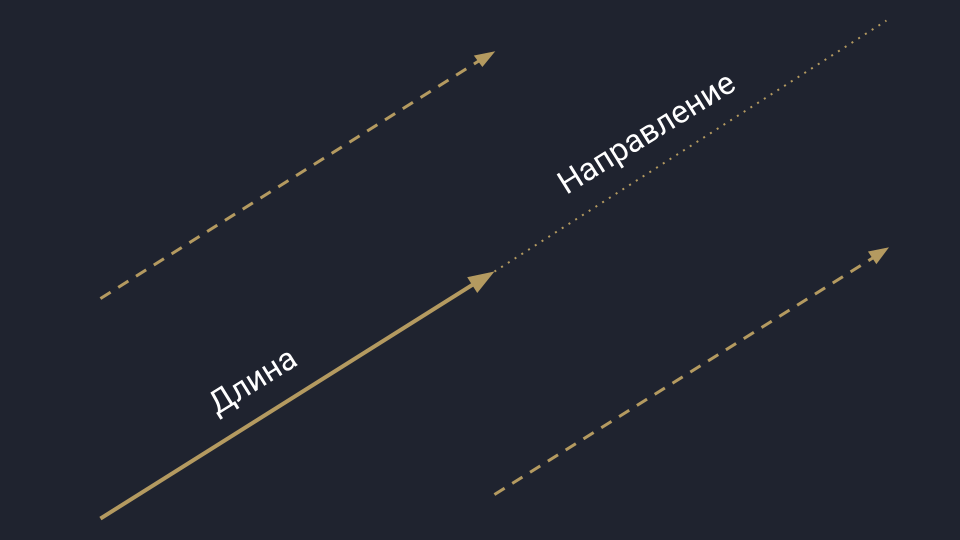
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.

Аналитическое представление вектора: данные можно перевести в числа

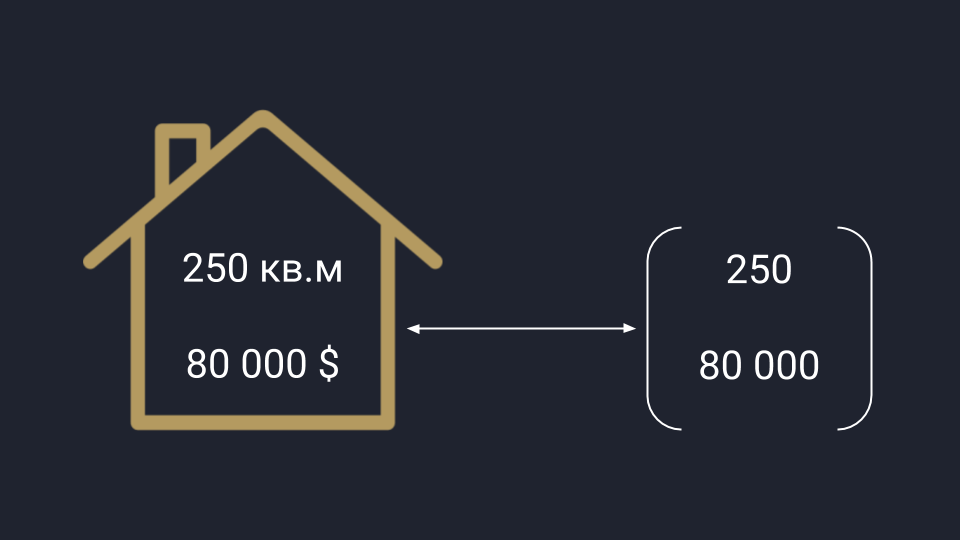
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.

Математическое представление вектора: данные можно перевести в числа или график

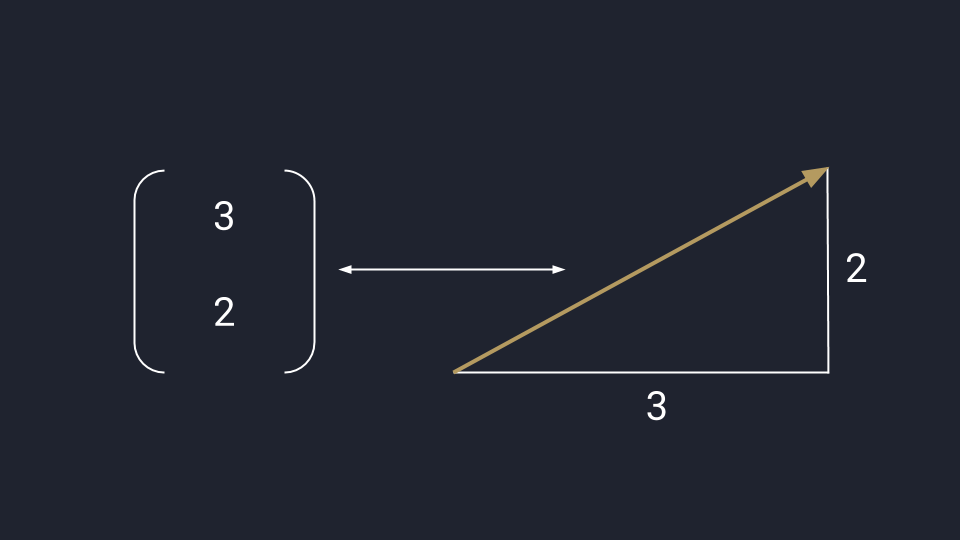
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.

Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат

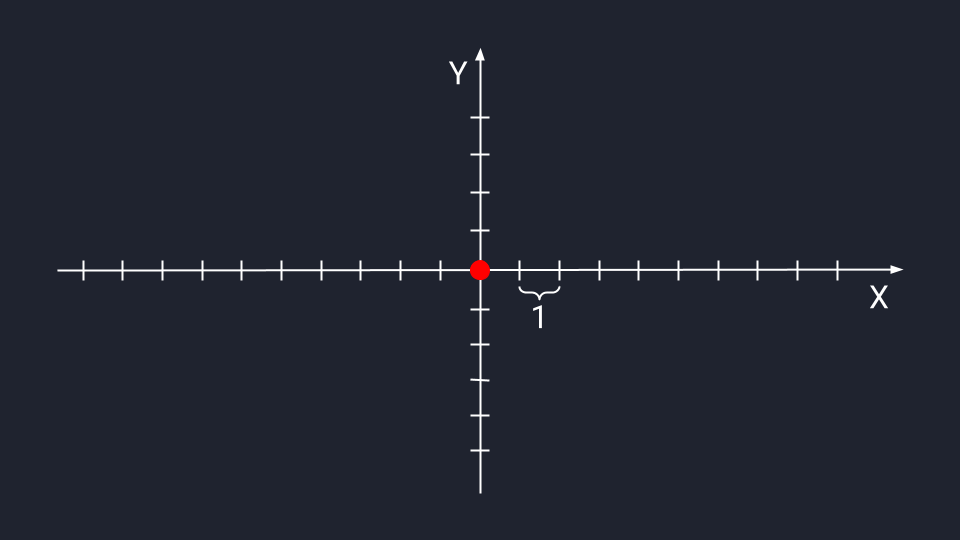
👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.

Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.

Как записывать

Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.

Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.

Способы записи вектора

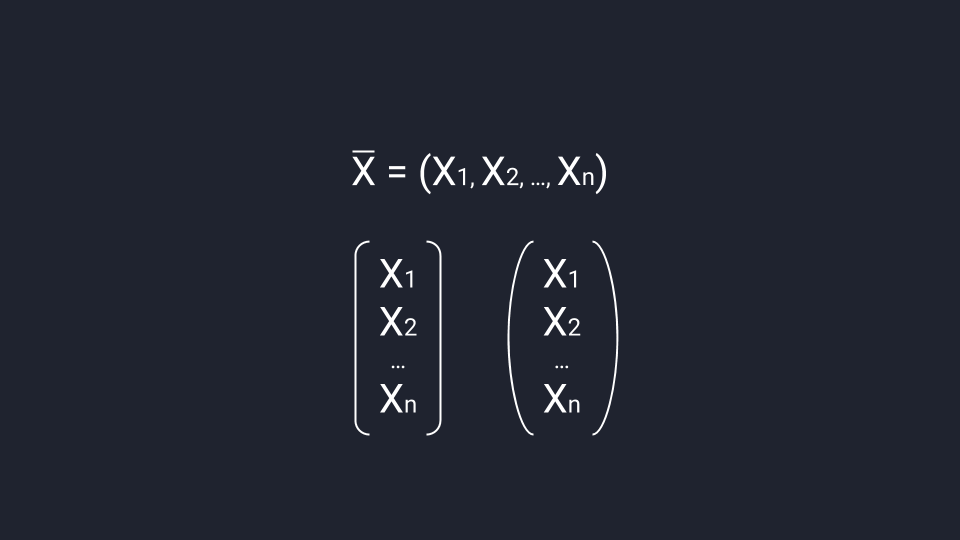
Скаляр

Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.

Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.

Как изображать

Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.

Графическое представление скаляра. Записывается в круглых скобках

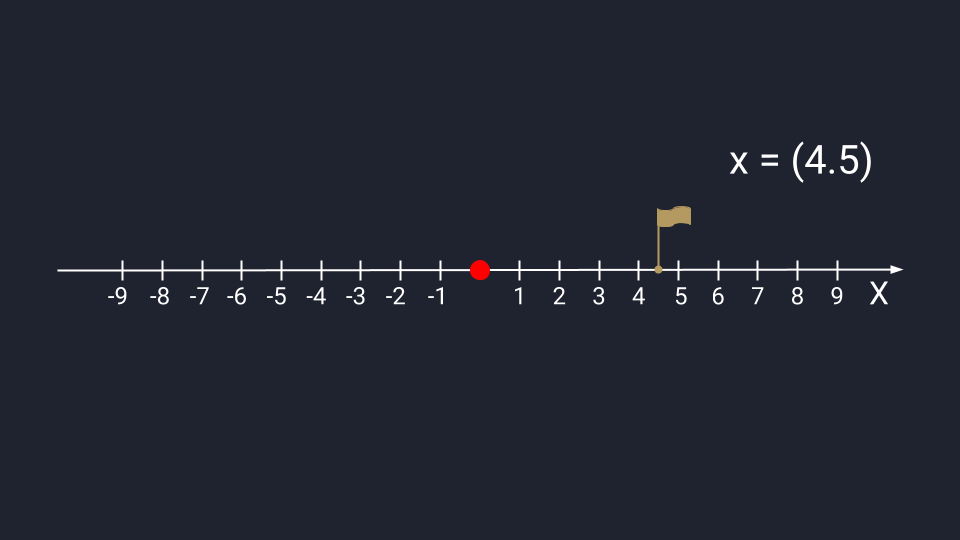
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.

Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.

Графическое представление числового вектора в двух измерениях

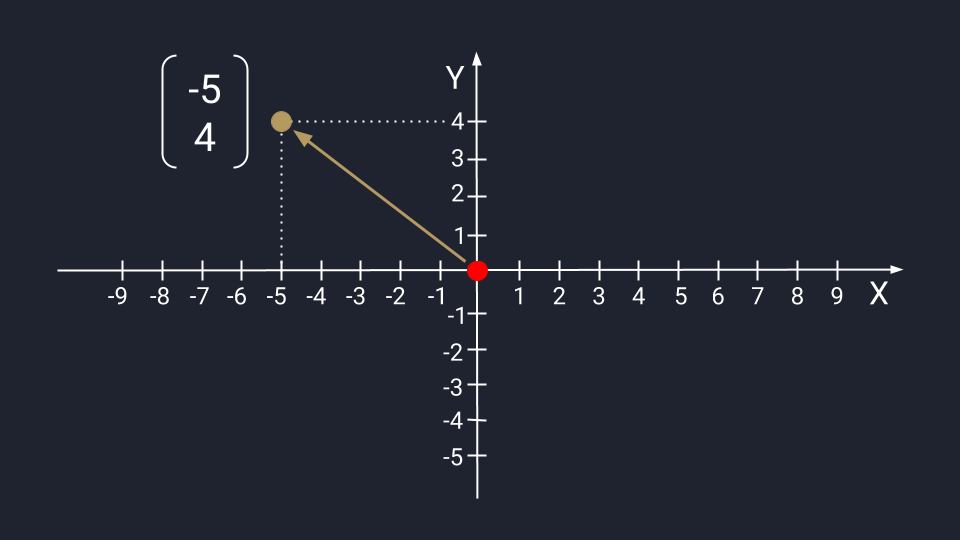
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.

Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.

Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4

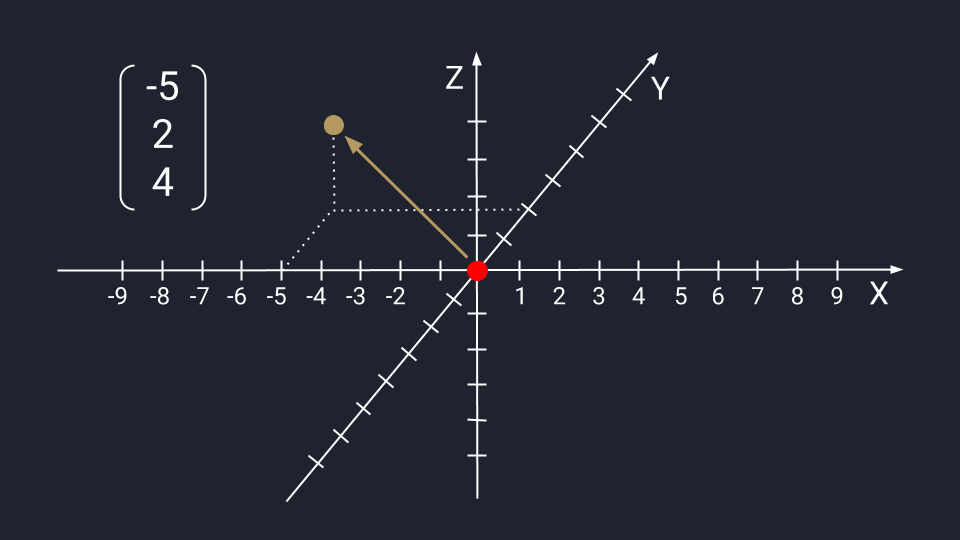
Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.

Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.

И зачем нам это всё

Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:

• На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
• Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.

Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.

И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.

Что дальше

В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.

[spoiler title=”источники:”]

http://ru.onlinemschool.com/math/library/vector/vector-definition/

http://thecode.media/lineynaya-algebra-vektory/

[/spoiler]

Эта статья — о понятии вектора в геометрии. Об общем понятии вектора в математике см. Вектор (математика).

Вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом^[1].

Вектор с началом в точке и концом в точке принято обозначать как . Векторы также могут обозначаться малыми латинскими буквами со стрелкой (иногда — чёрточкой) над ними, например . Другой распространённый способ записи: написание символа вектора прямым жирным шрифтом: .

Вектор в геометрии естественно сопоставляется переносу (параллельному переносу), что, очевидно, проясняет происхождение его названия (лат. vector, несущий). Итак, каждый направленный отрезок однозначно определяет собой какой-то параллельный перенос плоскости или пространства: скажем, вектор естественно определяет перенос, при котором точка перейдёт в точку , также и обратно, параллельный перенос, при котором переходит в , определяет собой единственный направленный отрезок (единственный — если считать равными все направленные отрезки одинакового направления и длины — то есть рассматривать их как свободные векторы; действительно, при параллельном переносе все точки смещаются в одинаковом направлении на одинаковое расстояние, так что в таком понимании ).

Интерпретация вектора как переноса позволяет естественным и интуитивно очевидным способом ввести операцию сложения векторов — как композиции (последовательного применения) двух (или нескольких) переносов; то же касается и операции умножения вектора на число.

Основные понятия[править | править код]

Вектором называется направленный отрезок построенный по двум точкам, одна из которых считается началом, а другая концом.

Координаты вектора определяются как разность координат точек его конца и начала. Например, на координатной плоскости, если даны координаты начала и конца: и , то координаты вектора будут: .

Длиной вектора называется расстояние между двумя точками и , её обычно обозначают

Роль нуля среди векторов играет нулевой вектор, у которого начало и конец совпадают ; ему, в отличие от других векторов, не приписывается никакого направления^[2].

Для координатного представления векторов большое значение имеет понятие проекции вектора на ось (направленную прямую, см. рисунок). Проекцией называется длина отрезка, образованного проекциями точек начала и конца вектора на заданную прямую, причём проекции приписывается знак плюс, если направление проекции соответствует направлению оси, иначе — знак минус. Проекция равна длине исходного вектора, умноженной на косинус угла между исходным вектором и осью; проекция вектора на перпендикулярную ему ось равна нулю.

Применения[править | править код]

Векторы находят широкое применение в геометрии и в прикладных науках, где используются для представления величин, имеющих направление (силы, скорости и т. п.). Применение векторов упрощает ряд операций — например, определение углов между прямыми или отрезками, вычисление площадей фигур. В компьютерной графике векторы-нормали используются, чтобы создать правильное освещение тела. Использование векторов может быть положено в основу метода координат.

Виды векторов[править | править код]

Иногда вместо того, чтобы рассматривать в качестве векторов множество всех направленных отрезков (рассматривая как различные все направленные отрезки, начала и концы которых не совпадают), берут только некоторую модификацию этого множества (фактормножество), то есть, некоторые направленные отрезки рассматривают как равные, если они имеют одинаковое направление и длину, хотя они могут иметь разное начало (и конец), то есть направленные отрезки одинаковой длины и направления считаются представляющими один и тот же вектор; таким образом, каждому вектору оказывается соответствующим целый класс направленных отрезков, одинаковых по длине и направлению, но различающихся началом (и концом).

Так, говорят о «свободных», «скользящих» и «фиксированных» векторах. Эти виды отличаются понятием равенства двух векторов.

• Говоря о свободных векторах, отождествляют любые векторы, имеющие одинаковое направление и длину;
• говоря о скользящих векторах — добавляют, что начала равных скользящих векторов должны совпадать или лежать на одной прямой, на которой лежат изображающие эти векторы направленные отрезки (так что один может быть совмещен с другим перемещением в направлении, им же самим задаваемом);
• говоря о фиксированных векторах — говорят, что равными считаются только векторы, у которых совпадают и направления, и начала (то есть в этом случае факторизации нет: нет двух фиксированных векторов с различными началами, которые считались бы равными).

Формально:

Говорят, что свободные векторы и равны, если найдутся точки и такие, что четырёхугольники и  — параллелограммы.

Говорят, что скользящие векторы и равны, если

Скользящие векторы особо употребимы в механике. Простейший пример скользящего вектора в механике — сила, действующая на твердое тело. Перенос начала вектора силы вдоль прямой, на которой он лежит, не меняет момента силы относительно любой точки; перенос же его на другую прямую, даже если не менять величины и направления вектора, может вызвать изменение его момента (даже почти всегда вызовет): поэтому при вычислении момента нельзя рассматривать силу как свободный вектор, то есть, нельзя её считать приложенной к произвольной точке твердого тела.

Говорят, что фиксированные векторы и равны, если попарно совпадают точки и , и .

Вектором в одном случае называется направленный отрезок, а в других случаях различные векторы — это разные классы эквивалентности направленных отрезков, определяемые неким конкретным отношением эквивалентности. Причем отношение эквивалентности может быть разным, определяя тип вектора («свободный», «фиксированный» итд). Проще говоря, внутри класса эквивалентности все входящие в него направленные отрезки рассматриваются как совершенно равные, и каждый может равно представлять весь класс.

Все операции над векторами (сложение, умножение на число, скалярное и векторное произведения, вычисление модуля или длины, угла между векторами и т. д.) в принципе определены одинаково для всех типов векторов, различие в типах сводится в этом отношении только к тому, что для скользящих и фиксированных наложено ограничение на возможность осуществления операций между двумя векторами, имеющими разное начало (так, для двух фиксированных векторов запрещено — или лишено смысла — сложение, если их начала отличаются; однако для всех случаев, когда эта операция разрешена — или имеет смысл — она такова же, как для свободных векторов). Поэтому часто тип вектора вообще явно не указывается, подразумевается, что он очевиден из контекста. Более того, один и тот же вектор в зависимости от контекста задачи может рассматриваться как фиксированный, скользящий или свободный, например, в механике векторы сил, приложенных к телу, могут суммироваться независимо от точки приложения при нахождении равнодействующей (и в статике, и в динамике при исследовании движения центра масс, изменения импульса и т. п.), но не могут складываться друг с другом без учета точек приложения при вычислении вращающего момента (также и в статике и в динамике).

Отношения между векторами[править | править код]

Два вектора называются коллинеарными, если они лежат на параллельных прямых, либо на одной прямой. Два вектора называются сонаправленными, если они коллинеарны и направлены в одну сторону, противоположно направленными, если коллинеарны и направлены в разные стороны. Есть и другое определение: два ненулевых вектора и называются коллинеарными, если существует некоторое число такое, что ^[3]
Три вектора называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости^[3].

Координатное представление[править | править код]

При работе с векторами часто вводят некоторую декартову систему координат и в ней определяют координаты вектора, раскладывая его по базисным векторам. Разложение по базису геометрически можно представить при помощи проекций вектора на координатные оси. Если известны координаты начала и конца вектора, координаты самого вектора получаются вычитанием из координат конца вектора координат его начала.

За базис часто выбирают координатные орты, обозначаемые , соответственно осям . Тогда вектор можно записать как

Любое геометрическое свойство можно записать в координатах, после чего исследование из геометрического становится алгебраическим и при этом часто упрощается. Обратное, вообще говоря, не совсем верно: обычно принято говорить^[4], что «геометрическое истолкование» имеют лишь те соотношения, которые выполняются в любой декартовой системе координат (инвариантные).

Операции над векторами[править | править код]

Модуль вектора[править | править код]

Модулем вектора называется число, равное длине отрезка . Обозначается, как . Для трёхмерного вектора в декартовой системе координат его можно вычислить как:

Сложение векторов[править | править код]

В координатном представлении вектор суммы получается суммированием соответствующих координат слагаемых:

Для геометрического построения вектора суммы используют различные правила (методы), однако они все дают одинаковый результат. Использование того или иного правила обосновывается решаемой задачей.

Правило треугольника[править | править код]

Правило треугольника наиболее естественно следует из понимания вектора как переноса. Ясно, что результат последовательного применения двух переносов и некоторой точки будет тем же, что применение сразу одного переноса , соответствующего этому правилу.
Для сложения двух векторов и по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной:

Правило трёх точек[править | править код]

Если отрезок изображает вектор , а отрезок изображает вектор , то отрезок изображает вектор .

Правило многоугольника[править | править код]

Начало второго вектора совмещается с концом первого, начало третьего — с концом второго и так далее, сумма же векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом -го (то есть изображается направленным отрезком, замыкающим ломаную). Так же называется правилом ломаной.

Правило параллелограмма[править | править код]

Для сложения двух векторов и по правилу параллелограмма оба эти векторы переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала. (Легко видеть, что эта диагональ совпадает с третьей стороной треугольника при использовании правила треугольника).

Правило параллелограмма особенно удобно, когда есть потребность изобразить вектор суммы сразу же приложенным к той же точке, к которой приложены оба слагаемых — то есть изобразить все три вектора имеющими общее начало.

Модуль суммы двух векторов можно вычислить, используя теорему косинусов:

, где  — косинус угла между векторами и .

Если векторы изображены в соответствии с правилом треугольника и берется угол по рисунку — между сторонами треугольника — что не совпадает с обычным определением угла между векторами, а значит и с углом в приведенной формуле, то последний член приобретает знак минус, что соответствует теореме косинусов в её прямой формулировке.

Для суммы произвольного количества векторов применима аналогичная формула, в которой членов с косинусом больше: по одному такому члену существует для каждой пары векторов из суммируемого набора. Например, для трех векторов формула выглядит так:

Вычитание векторов[править | править код]

Для получения разности в координатной форме надо вычесть соответствующие координаты векторов:

Для получения вектора разности начала векторов соединяются и началом вектора будет конец , а концом — конец . Если записать, используя точки векторов, то .

Модуль разности векторов[править | править код]

Три вектора , как и при сложении, образуют треугольник, и выражение для модуля разности получается аналогичным:

где  — косинус угла между векторами и

Отличие от формулы модуля суммы в знаке перед косинусом, при этом надо хорошо следить, какой именно угол берется (вариант формулы модуля суммы с углом между сторонами треугольника при суммировании по правилу треугольника по виду не отличается от данной формулы для модуля разности, но надо иметь в виду, что тут берутся разные углы: в случае суммы берётся угол, когда вектор переносится к концу вектора , когда же ищется модуль разности, берётся угол между векторами, приложенными к одной точке; выражение для модуля суммы с использованием того же угла, что в данном выражении для модуля разности, отличается знаком перед косинусом).

Умножение вектора на число[править | править код]

Умножение вектора на число , даёт сонаправленный вектор с длиной в раз больше.
Умножение вектора на число , даёт противоположно направленный вектор с длиной в раз больше.
Умножение вектора на число в координатной форме производится умножением всех координат на это число:

Исходя из определения получается выражение для модуля вектора, умноженного на число:

Аналогично как и числами, операции сложение вектора с самим с собой можно записать через умножение на число:

А вычитание векторов можно переписать через сложение и умножение:

Исходя из того, что умножение на не меняет длины вектора, а меняет только направление и учитывая определение вектора, получаем:

Скалярное произведение векторов[править | править код]

Для геометрических векторов скалярное произведение определяется через их геометрические характеристики и вводится следующим образом:

Здесь для вычисления косинуса берётся угол между векторами, который определяется как величина угла, образованного векторами, если приложить их к одной точке (совместить их начала).

Это выражение можно переписать через координаты (здесь формула для трехмерного пространства):

Скалярным квадратом вектора называется его скалярное произведение само на себя и может быть вычислено через модуль вектора:

Векторное произведение векторов[править | править код]

Векторным произведением двух векторов и называется такой вектор , который ортогонален плоскости векторов и , его длина равняется площади параллелограмма, образованного векторами, а направление определяется по правилу правой руки.

Смешанное произведение векторов[править | править код]

Смешанным произведением трёх векторов называется число, определяемое следующим образом:

Модуль этой величины даёт объём параллелепипеда, построенного на векторах .

См. также[править | править код]

• Линейное пространство
• Векторная величина
• Кортеж (математика)

Литература[править | править код]

• Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
  • Переиздание: Изд. АСТ, 2003, ISBN 5-17-009554-6.
• Башмаков М. Что такое вектор? // Квант. — 1976. — № 4. — С. 2—5.
• Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.

Примечания[править | править код]

В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.

• Нахождение координат вектора

• Примеры задач

Нахождение координат вектора

Для того, чтобы найти координаты вектора AB, нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).

Формулы для определения координат вектора

Для плоских задач	AB = {Bx – Ax; By – Ay}
Для трехмерных задач	AB = {Bx – Ax; By – Ay; Bz – Az}
Для n-мерных векторов	AB = {B1 – A1; B2 – A2; … Bn – An}

Примеры задач

Задание 1
Найдем координаты вектора AB, если у его точек следующие координаты: A = (2; 8), B = (5; 12).

Решение:
AB = {5 – 2; 12 – 8} = {3; 4}.

Задание 2
Определим координаты точки B вектора AB = {6; 14}, если координаты точки A = (2; 5).

Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
B_x = AB_x + A_x = 6 + 2 = 8.
B_y = AB_y + A_y = 14 + 5 = 19.

Таким образом, B = (8; 19).

Векторы — основные понятия и формулы

На прошлом занятии мы разобрались с основными определениями кинематики.

И ты наверняка обратил внимание, что некоторые величины имеют только значение (число) – например, путь ((L)).

А некоторые имеют и число, и направление — например, перемещение ((vec{S})).

И сейчас ты узнаешь, почему это настолько важно.

Векторы — коротко о главном

• Существуют скалярные величины: они имеют значение, но не имеют направления;
• Существуют векторные величины. Они имеют как значение, так и направление;
• Значение вектора есть его длина;
• Для большинства операций над векторами необходим пареллельный перенос;
• Вектор можно умножать на скаляр;
• Нулевой вектор – вектор, начало которого совпадает с концом;
• Коллинеарные векторы – векторы, лежащие на одной прямой или на параллельных прямых;
• Коллинеарные векторы, имеющие одинаковую длину и противоположные направления, называются обратными друг другу;
• Векторы можно складывать и вычитать разными методами;
• Правило параллелограмма действует как для сложения, так и для вычитания векторов;
• Векторы можно умножать друг на друга двумя различными способами: скалярным и векторным;
• Проекция вектора на ось — разность между координатами проекций точек конца и начала вектора на ось;
• Если вектор направлен туда же, куда и ось, его проекция положительна. Если вектор направлен в другую сторону, его проекция отрицательна;
• Вектор сам по себе не может быть отрицательным;
• Длина вектора так же не может быть отрицательной;
• Проекция вектора бывает отрицательной;
• Над проекциями тоже можно совершать действия, и это удобнее, чем работать с векторами;
• Проекция суммы векторов равна сумме проекций векторов;
• Проекция разности векторов равна разности проекций векторов;
• С проекцией вектора можно работать как с числом;

Решать задачи с векторами — легко!

Векторы и… Колумб

В 1492 году Колумб приказал кораблям изменить курс на запад-юго-запад, полагая, что он и его команда уже прошли мимо Японии, не заметив ее островов.

Вскоре его экспедиция наткнулась на множество архипелагов, которые ошибочно принимали за земли Восточной Азии. И теперь, спустя века, американцы в октябре отмечают высадку Колумба в Новом Свете.

Кто знает, как повернулась бы история, если бы его корабли не поменяли свое направление?

О направлении

Направление – одна из важнейших характеристик движения.

Подумай, какие из этих величин являются просто числами, а какие тоже являются числами, но имеют еще и направление.

• сила;
• время;
• скорость;
• длина;
• перемещение;
• масса;
• температура;

Наверное, ты без труда заметил, что направление имеют сила, скорость, перемещение, а время, длина, масса и температура – это просто числа.

Так вот, «просто числа» — это скалярные величины (их также называют скалярами).

А «числа с направлением» — это векторные величины (их иногда называют векторы).

В физике существует множество скалярных и векторных величин.

Что такое скалярная величина?

Скалярная величина, в отличие от вектора, не имеет направления и определяется лишь значением (числом)

Это, например, время, длина, масса, температура (продолжи сам!)

Что такое векторная величина?

Векторная величина – это величина, которая определяется и значением, и направлением.

В случае с векторами нам важно, куда мы, например, тянем груз или в какую сторону движемся.

Например, как на этом рисунке изображен вектор силы (нам важно не только с какой силой, но и куда мы тянем груз):

Как обозначаются векторы?

Векторы принято обозначать специальным символом – стрелочкой над названием. Вот, например, вектор перемещения: (vec{S})

Значение вектора – это модуль вектора, то есть его длина.

Обозначить это можно двумя способами: (left| {vec{S}} right|) или (S)

Операции над векторами

Для решения задач необходимо уметь работать с векторами: складывать, вычитать, умножать их.

Давай научимся это делать. Мы пойдем от простого к сложному, но это вовсе не значит, что будет трудно!

Умножение вектора на число

Если вектор умножить на какое-либо число (скаляр), мы просто «растягиваем» вектор, сохраняя его направление. Получившийся вектор сонаправлен начальному, то есть они имеют одинаковое направление.

Это обозначается так: (vec{a}uparrow uparrow vec{b})

(Если направление противоположно, обозначаем так: (vec{a}uparrow downarrow vec{b}))

Рассмотрим на примере, используя клетку для точности построений:

Если вектор умножить на ноль, он станет нулевым.

Обязательно нужно ставить значок вектора над нулем! Нельзя говорить, что векторная величина просто равна скалярной:

(vec{c}=0cdot vec{a}Rightarrow vec{c}=vec{0})

Рассмотрим некоторые свойства нулевого вектора.

Если он нулевой, то его длина равна нулю! Логично, не правда ли?

А это значит, что его начало совпадает с концом, это просто какая-то точка.

Нулевой вектор – вектор, начало которого совпадает с концом.

Нулевой вектор принято считать сонаправленным любому вектору.

Его мы можем получить не только путем умножения вектора на ноль, но и путем сложения противонаправленных векторов:

(vec{a}+(-vec{a})=vec{0})

А если к любому вектору прибавит нулевой, ничего не изменится:

(vec{a}+vec{0}=vec{a})

Если вектор умножают на отрицательное число, он изменит свое направление на противоположное. Такой вектор называется обратным данному.

Но такие векторы должны быть коллинеарны. Звучит как скороговорка, но ничего страшного. Главное – понять суть.

Коллинеарные векторы – векторы, лежащие на одной прямой или на параллельных прямых.

Две прямые параллельны: (qparallel p)

Векторы лежат на одной прямой: они коллинеарны. По направлению видно, что они противонаправлены, это обозначается так:

(vec{a}uparrow downarrow vec{c})

Векторы лежат на параллельных прямых, они коллинеарны. При этом они сонаправлены:

(vec{a}uparrow uparrow vec{b})

Эти двое тоже коллинеарны! Они ведь лежат на параллельных прямых. При этом они противонаправлены:

(vec{b}uparrow downarrow vec{c})

Коллинеарные векторы, имеющие одинаковую длину и противоположные направления, называются обратными друг другу.

Параллельный перенос векторов

Одно из важных свойств вектора, которое очень часто помогает в операциях над ним, – параллельный перенос.

Если передвинуть вектор, не меняя его направления и длины, он будет идентичен начальному. Это свойство –  параллельный перенос.

Сложение векторов по правилу треугольника

Сложение векторов – одна из самых легких и приятных вещей. Предположим, у нас есть два вектора:

Наша цель – найти такой вектор, который будет являться суммой двух данных:

(vec{c}=vec{a}+vec{b})

Для начала нужно сделать так, чтобы конец одного вектора был началом другого. Для этого воспользуемся параллельным переносом:

Теперь достроим до треугольника.

Но как узнать направление нужного нам вектора?

Все просто: вектор суммы идет от начала первого слагаемого к концу второго, мы словно «идём» по векторам:

Это называется правилом треугольника.

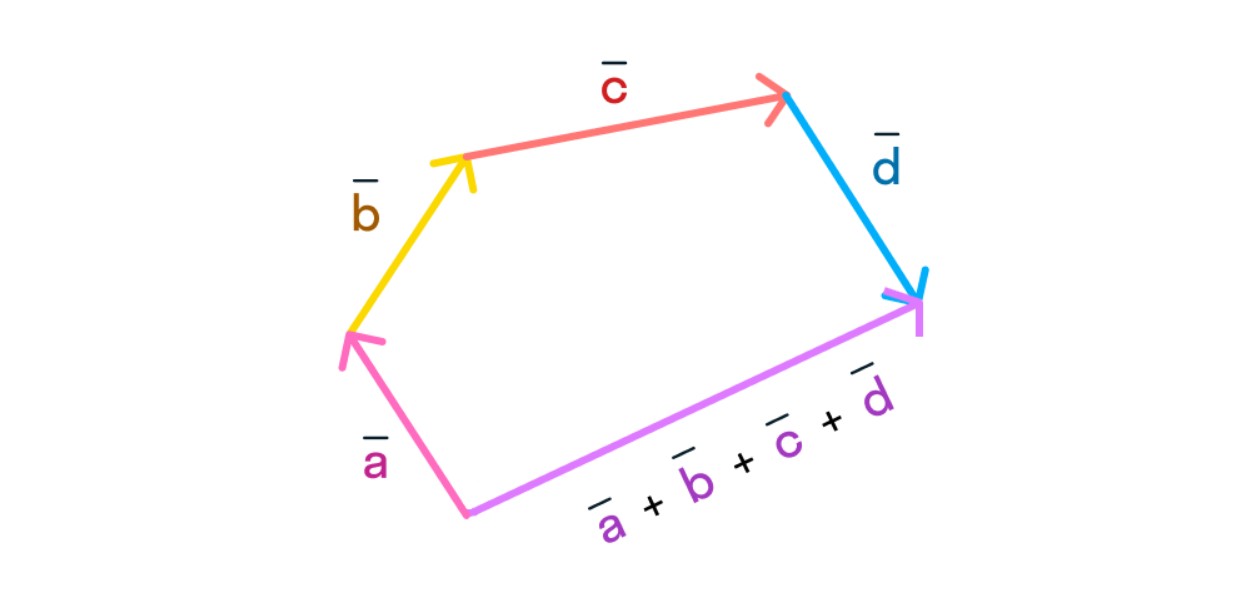
Больше двух слагаемых векторов. Сложение по правилу многоугольника

Но что делать, нам нужно сложить не два, а три, пять векторов или даже больше?

Мы руководствуемся той же логикой: соединяем векторы и «идём» по ним:

(vec{e}=vec{a}+vec{b}+vec{c}+vec{d})

Это называется правилом многоугольника.

Вычитание векторов через сложение

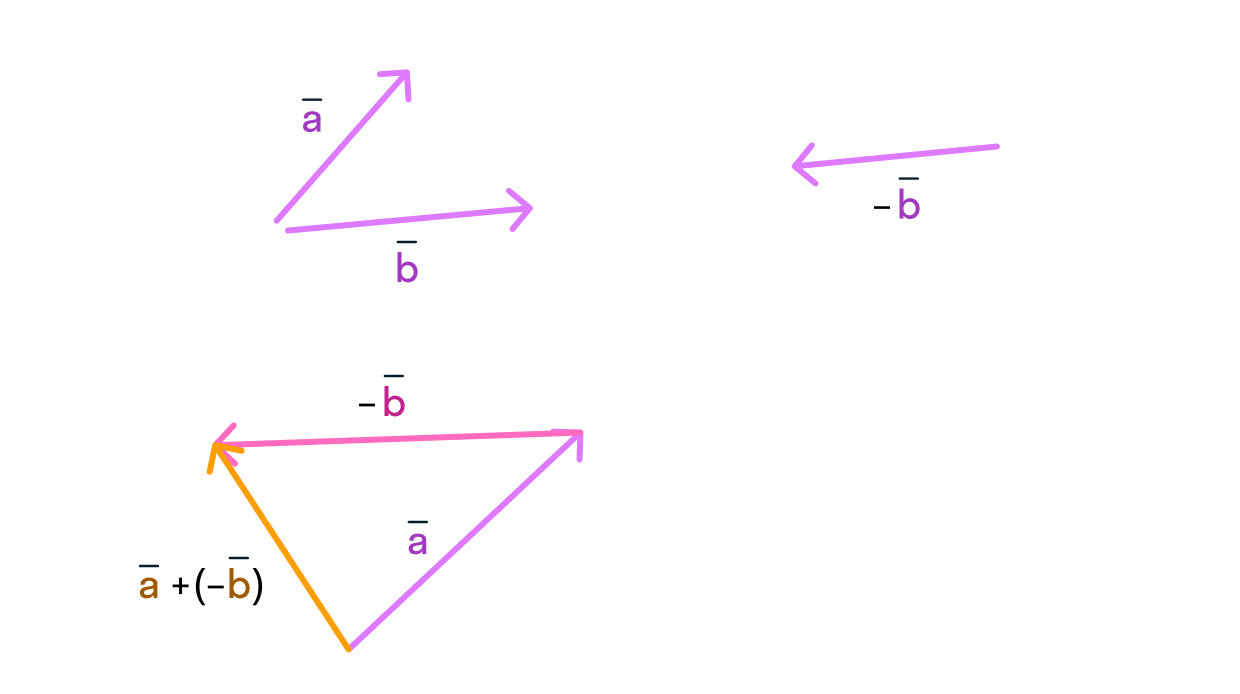
Вычитание векторов не сложнее. Это даже можно сделать через сумму! Для этого нам понадобится понятие обратного вектора. Запишем разность так:

(vec{c}=vec{a}-vec{b}=vec{a}+(-vec{b}))

Тогда нам лишь остается найти сумму с обратным вектором:

А сделать это очень легко по правилу треугольника:

Всегда помни, что вычитание можно представлять сложением, а деление — умножением на дробь.

Вычитание векторов через треугольник

Вычитать векторы можно через треугольник. Основная задача будет состоять в том, чтобы определить направление вектора разности.

Итак, векторы должны выходить из одной точки. Далее мы достраиваем рисунок до треугольника и определяем положение. Рассмотрим два случая:

(vec{c}=vec{a}-vec{b})

(vec{c}=vec{b}-vec{a})

Направление вектора разности зависит от того, из какого вектора мы вычитаем. У них совпадают концы.

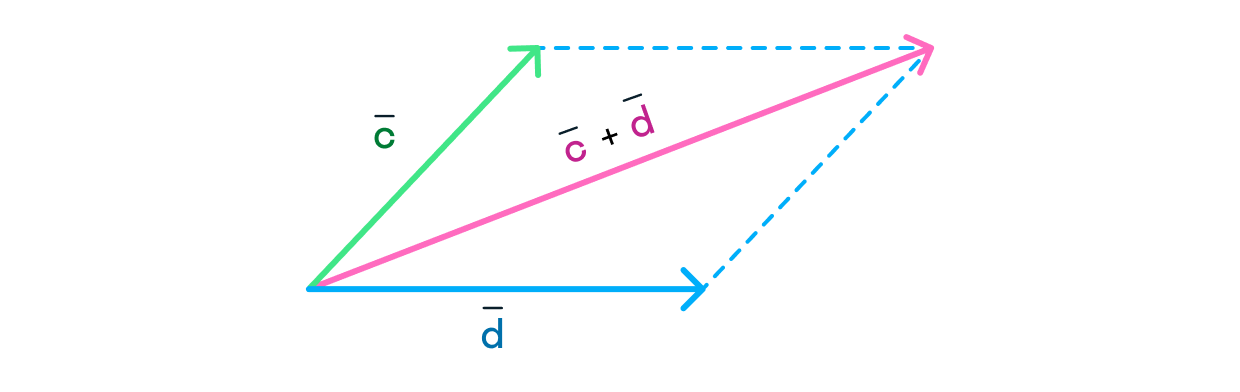
Универсальное правило параллелограмма

Есть еще один способ сложения и вычитания векторов.

Способ параллелограмма наиболее востребован в физике и сейчас ты поймешь, почему. Основа в том, чтобы векторы выходили из одной точки, имели одинаковое начало.

Вот так:

Ничего не напоминает?

Именно! Когда мы делаем чертеж к задачам по физике, все силы, приложенные к телу, мы рисуем из одной точки.

В чем же заключается правило параллелограмма? С помощью параллельного переноса достроим до параллелограмма:

Тогда вектор суммы будет диагональю этой фигуры. Это легко проверяется правилом треугольника. Начало этого вектора совпадает с началом двух слагаемых векторов:

Другая диагональ будет являться разностью этих векторов. Направление определяем так же, как делали раньше.

(vec{c}=vec{a}+vec{b})

(vec{d}=vec{a}-vec{b})

Векторное произведение векторов

Векторное произведение векторов пригодится нам в электродинамике.

Его формула лишь немного отличается от предыдущей:

(vec{a}times vec{b}=left| {vec{a}} right|cdot left| {vec{b}} right|cdot sin varphi )

В отличие от скалярного произведения, результатом его является вектор и его даже можно изобразить!

После параллельного переноса векторов и нахождения угла между ними достроим их до параллелограмма и найдем его площадь. Площадь параллелограмма равна длине вектора произведения:

Этот вектор одновременно перпендикулярен двум другим. Его направление зависит от условного порядка векторов, который либо определен какими-то фактами (когда мы будем изучать силу Лоренца), либо является свободным.

Об этом мы поговорим подробнее, когда будем изучать электродинамику.

Итак, мы разобрали операции с векторами, рассмотрев даже самые сложные из них. Это было не так тяжело, верно? Так происходит не только с векторами, но и со многими другими темами. Идя от легкого к сложному, мы даже не заметили трудностей.

Ведь всегда стоит помнить о том, что даже самое длинное путешествие начинается с первого шага.

Проекции векторов

Что такое проекция вектора и с чем ее едят?

Мы уже выяснили, что над векторами можно проводить множество операций. Здорово, когда можешь начертить векторы, достроить их до треугольника и измерить результат линейкой.

Но зачастую физика не дает нам легких цифр. Наша задача – не отчаиваться и быть умнее, упрощая себе задачи.

Для того, чтобы работать с векторами как с числами и не переживать об их положении и о точности рисунков, были придуманы проекции.

Проекция вектора –  словно тень, которую он отбрасывает на ось координат. И эта тень может о многом рассказать.

Ось координат — прямая с указанными на ней направлением, началом отсчёта и выбранной единицей масштаба.

Ось можно выбрать произвольно. В зависимости от ее выбора можно либо значительно упростить решение задачи, либо сделать его очень сложным.

Именно поэтому необходимо научиться работать с проекциями и осями.

Построение проекции. Определение знака

Возьмем вектор и начертим рядом с ним произвольную ось. Назвать ее тоже можно как угодно, но мы назовем ее осью Х.

Теперь опустим из начала и конца вектора перпендикуляры на эту ось. Отметим координаты начала (Х₀) и конца (Х). Рассмотрим отрезок, заключенный между этими точками.

Казалось бы, мы нашли проекцию. Однако думать, что проекция является простым отрезком, –  большое заблуждение.

Не все так просто: проекция может быть не только положительной. Чтобы найти проекцию, нужно из координаты конца вычесть координату начала:

({{a}_{x}}=x-{{x}_{0}})

Проекция вектора на ось — разность между координатами проекций точек конца и начала вектора на ось.

Проекция обозначается так:
({{a}_{x}}), где a – название вектора, х – название оси, на которую проецируется вектор.

В случае выше определить знак довольно легко. Сразу видим, что координата конца численно больше координаты начала и делаем вывод о том, что проекция положительна:

(x>{{x}_{0}}Rightarrow {{a}_{x}}>0)

Порой работать с буквами трудно. Поэтому предлагаю взять конкретный пример:

Рассмотрим другой случай. В этот раз координата начала больше координаты конца, следовательно, проекция отрицательна:

(x<{{x}_{0}}Rightarrow {{b}_{x}}<0)

Пример на конкретных числах:

Рассмотрим еще один интересный случай.

Давай разместим ось так, чтобы вектор был ей перпендикулярен. Проекции точек начала и конца совпадут и проекция вектора будет равна нулю!

(x={{x}_{0}}Rightarrow {{c}_{x}}=0)

Анализ углов

Рассматривая эти ситуации, можно заметить, что знак, который принимает проекция вектора напрямую зависит от угла между вектором и осью, то есть от его направления!

Из начала вектора проведем луч, параллельный оси и направленный в ту же сторону, что и ось. Получим угол между вектором и осью.

Если угол острый, проекция положительна:

(alpha <{{90}^{o}}Rightarrow {{a}_{x}}>0)

Если угол тупой, проекция отрицательна:

(beta >{{90}^{o}}Rightarrow {{b}_{x}}<0)

Если угол прямой, она равна нулю:

(gamma ={{90}^{o}}Rightarrow {{c}_{x}}>0)

Обрати особое внимание на то, какой именно угол является углом между вектором и осью!

Частные случаи проекции

Настоящий подарок судьбы – тот момент, когда вектор параллелен оси. Это сохраняет драгоценное время при решении множества задач. Рассмотрим эти случаи.

Если вектор параллелен оси, угол между ними либо равен нулю, либо является развернутым (180^О). Это зависит от направления.

При этом длина проекции совпадает с длиной вектора! Смотри!

Как и прежде, если вектор направлен туда же, куда и ось, проекция положительна:

(alpha ={{0}^{o}}Rightarrow {{a}_{x}}=a)

Если вектор направлен в другую сторону, проекция отрицательна:

(alpha ={{180}^{o}}Rightarrow {{a}_{x}}=-a)

Если вектор направлен туда же, куда и ось, его проекция положительна. Если вектор направлен в другую сторону, его проекция отрицательна.

Эти утверждения применимы не только к векторам, которые параллельны оси. Это особенно удобно использовать в тех случаях, когда ось направлена под углом.

Что? Почему раньше не сказал? А… Ну…

Хватит вопросов! Вот тебе пример:

(vec{a}) направлен в ту же сторону, что и ось. Его проекция положительна.

(vec{b}) направлен противоположно оси. Его проекция отрицательна.

Еще один частный случай – работа с обратными векторами.

Давай выясним, как связаны проекции данного вектора и вектора, который является ему обратным. Начертим их и обозначим координаты начал и концов:

Проведем дополнительные линии и рассмотрим два получившихся треугольника. Они прямоугольны, так как проекция строится с помощью перпендикуляра к оси.

Наши векторы отличаются лишь направлением. При этом, если мы просто посмотрим на них как на прямые, мы можем сказать, что они параллельны. Их длины тоже одинаковы.

Прямоугольные треугольники равны по углу и гипотенузе. Это значит, что численно равны и их катеты, в том числе те, которые равны проекциям:

(vec{a}’=-vec{a}) — векторы обратны друг другу;

(left| {vec{a}} right|=left| vec{a}’ right|) — равенство длин векторов;

Мы помним, что обратные векторы всегда коллинеарны. Это значит, что прямые, на которых они расположены, находятся под одним углом к оси:

(alpha =alpha ‘)

Остается лишь определиться со знаками. Данный вектор направлен по оси Х, а обратный ему – против. Значит, первый положителен, а второй отрицателен. Но модули их равны, так как равны их длины.

({{a}_{x}}=-a_{x}^{‘})

Проекции обратных векторов равны по модулю и противоположны по знаку.

Давайте еще раз уточним.

Вектор сам по себе не может быть отрицательным (обратный вектор есть вектор, умноженный на минус единицу).

Длина вектора так же не может быть отрицательной. Длина есть модуль вектора, а модуль всегда положителен.

Проекция вектора бывает отрицательной. Это зависит от направления вектора.

Способы нахождения проекций и векторов с помощью тригонометрии

Зная угол между вектором и осью, можно не прибегать к координатам. Углы, прямоугольные треугольники… Всегда стоит помнить, что, если ты видишь прямоугольный трегольник, тригонометрия протянет тебе руку помощи.

Именно тригонометрия чаще всего применяется в задачах, где требуется работать с проекциями. Особенно она помогает в задачах на второй закон Ньютона.

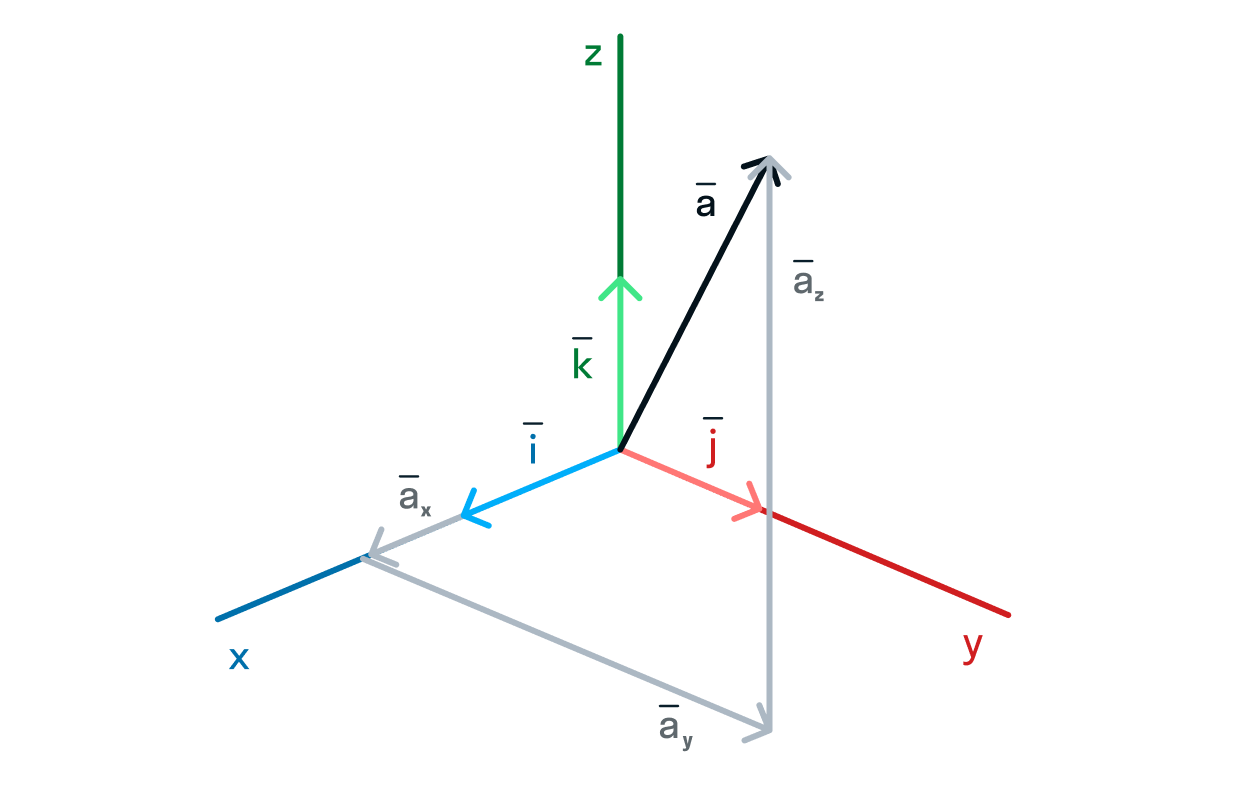
Рассмотрим вектор и его проекции на оси:

Можем заметить, что проекции вектора соответствуют катетам прямоугольного треугольника, который легко можно достроить:

Тогда обозначим прямой угол и угол между вектором и осью:

Зная, что проекции соответствуют катетам, мы можем записать, чему равны синус и косинус угла. Они равны отношению проекций к гипотенузе. За гипотенузу считаем длину данного вектора.

Из этих уравнений легко выражаются проекции.

(sin alpha =frac{{{a}_{y}}}{a})

(cos alpha =frac{{{a}_{x}}}{a})

А еще следует помнить, что из проекций мы можем найти длину данного вектора с помощью теоремы Пифагора:

({{a}^{2}}=a_{x}^{2}+a_{y}^{2})

Зная, как работать с проекциями векторов и часто практикуясь, можно довести свои навыки решения большинства задач механики до совершенства.

Действия над проекциями векторов. Решение задач

Умение применять свои знания на практике невероятно важны. Это касается не только физики.

Мы знаем, что проекции были придуманы для того, чтобы работать не с векторами, а с числами.

Давай попробуем.

Сложение проекций. Доказательство главного свойства

Предположим, у нас есть два вектора и нам нужно найти их сумму. Посчитать по клеткам нам вряд ли удастся:

Спроецируем оба вектора на ось Х. Заметим, что конец одного вектора есть начало второго, то есть их координаты совпадают:

Давай посчитаем проекции векторов и проекцию вектора их суммы:

Мы можем заметить, что сумма проекций двух данных векторов оказалась равна проекции вектора их суммы!

Намного важнее уметь доказывать гипотезы в общем виде.

Тогда никто не сможет упрекнуть тебя в том, что твои утверждения – просто результат совпадения!

Согласно определению проекции, запишем уравнения проекций для двух данных векторов и вектора их суммы:

Заметим, что некоторые точки совпадают. Начало (vec{a}) совпадает с началом (vec{c}). Как мы заметили ранее, конец (vec{a}) совпадает с началом (vec{b}). А конец (vec{b}) совпадает с концом (vec{c}).

Затем запишем, чему равна сумма этих векторов.

Видим, что конец (vec{a}) и начало (vec{b}) одинаковы. Поэтому избавимся от повторов:

У нас остались лишь начало (vec{a}) и конец (vec{b}). А это в свою очередь начало и конец (vec{c})!

Мы доказали нашу гипотезу.

Но что насчет разности?

Все очень просто! Помнишь, как мы считали разность через сумму? Здесь это делается аналогично!

Таким образом,

Проекция суммы векторов равна сумме проекций векторов.

Проекция разности векторов равна разности проекций векторов.

Или можно записать так:

(vec{c}=vec{a}pm vec{b}Rightarrow {{c}_{x}}={{a}_{x}}pm {{b}_{x}})

Простейшие задачи на нахождение проекций

Простейшие задачи на нахождение проекций чаще представлены в виде различных графиков или рисунков.

Давай научимся с ними работать.

Нам даны оси и векторы. Задача: найти проекции каждого из них на обе оси.

Будем делать все по порядку. Для каждого вектора предлагаю сначала определить знак проекций, а затем посчитать их.

В первом случае вектор направлен против оси Х.

Значит, его проекция на эту ось будет отрицательна. Мы убедимся в этом с помощью вычислений.

Сразу бросается в глаза то, что вектор расположен перпендикулярно оси Y. Его проекция на эту ось будет равна нулю, ведь расстояние между проекциями точек начала и конца равно нулю!

Рассмотрим второй вектор.

Он «сонаправлен» оси Y и «противонаправлен» оси Х. Значит, проекция на ось будет положительна, а на ось Х – отрицательна.

Убедимся в этом.

На осях для удобства отметим проекции точек начала и конца вектора, проведя перпендикуляры. Затем проведем вычисления:

Рассмотрим (vec{c}). Заметим, что он является обратным для (vec{b}): их длины равны, а направления противоположны.

Мы помним, что в таком случае их проекции отличаются лишь знаками. И это действительно так:

Поступаем с (vec{d}) так же, как поступали с первым вектором.

Он перпендикулярен оси Х, а значит его проекция (что есть разность между проекциями точки конца и начала!) на эту ось равна нулю.

Проведя перпендикуляры, считаем проекцию на ось Y:

С (vec{e}) работать приятно: он расположен по направлению обеих осей. Обе его проекции будут положительны, остается лишь посчитать их:

Задачи на нахождение вектора и его угла с осью

С помощью проекций можно найти длину вектора и его направление, а также угол, под которым он находится относительно оси.

Давай попробуем это сделать.

Даны проекции вектора на две оси. Для начала нарисуем оси:

Расположить вектор можно как угодно, поэтому произвольно отметим на осях его проекции. Мы помним, что проекции и вектор образуют прямоугольный треугольник. Давай попробуем его составить.

С проекцией на ось Х все понятно, просто поднимаем ее. Но куда поставить проекцию оси Y?

Для этого нам нужно определить направление вектора. Проекция на ось Х отрицательна, значит вектор направлен в другую сторону от оси.

Проекция на ось Y положительна. Вектор смотрит в ту же сторону, что и ось.

Исходя из этого, мы можем нарисовать вектор и получить прямоугольный треугольник:

Теперь нужно найти длину этого вектора. Используем старую добрую теорему Пифагора:

Обозначим угол (alpha ), который необходимо найти, мы учились это делать в начале изучения проекций. Он расположен вне треугольника. Мы ведь не ищем легких путей, верно?

Рассмотрим смежный ему угол (beta ). Его найти гораздо проще, а в сумме они дадут 180 градусов.

Чтобы сделать это, абстрагируемся от векторов, проекций и просто поработаем с треугольником, стороны которого равны 3, 4 и 5. Найдем синус угла (beta ) и по таблице Брадиса (либо с помощью инженерного калькулятора) определим его значение.

Вычитанием угла (beta ) из 180 градусов найдем угол (alpha ):

Главный метод работы с осями и проекциями в решении физических задач

В большинстве задач по физике, когда в условиях нам дают значения векторных величин, например, скорости, нам дают длину вектора.

Поэтому важно научиться искать проекции вектора и связывать их с ней.

Рассмотрим следующий рисунок (вектор F2 перпендикулярен вектору F3):

Чаще всего с подобным расположением векторов мы встречаемся в задачах, где необходимо обозначить все силы, действующие на тело.

Одним из важных этапов решение «векторной части» этих задач является правильный выбор расположения осей. Он заключается в том, чтобы расположить оси так, чтобы как можно большее число векторов оказались им параллельны.

Как правило, оси располагаются под прямым углом друг к другу, чтобы не получить лишней работы с углами.

Сделаем это для данного рисунка:

Мы видим, что остальные векторы расположены к осям под каким-то углом.

Пунктиром проведем горизонтальную линию и отметим этот угол, а затем отметим другие равные ему углы:

Пришло время искать проекции. У нас две оси, поэтому сделаем для удобства табличку:

Мы располагали оси так, чтобы некоторые векторы были расположены параллельно осям, значит их проекции будут равняться их длинам.

Оси перпендикулярны друг другу, поэтому некоторые проекции будут равняться нулю. Запишем это:

Переходим к векторам, которые расположены под углом.

Выглядит страшно, но это не так!

Дальше идет чистая геометрия. Чтобы не запутаться, рассмотрим лишь часть рисунка. А лучше и вовсе перерисовать его часть, могут открыться много новых вещей.

Из конца вектора F1 проведем перпендикуляр к оси Y. Мы получим прямоугольный треугольник, где нам известен угол (альфа) и гипотенуза (вектор).

Обозначим, что является проекцией. Это катет:

Здесь на помощь придет тригонометрия. Этот катет прилежащий к известному углу. Синус угла есть проекция катета, деленная на гипотенузу. Отсюда можно выразить катет (проекцию) и записать ее в таблицу.

Вспомни, когда мы первый раз встретились с тригонометрией, изучая векторы. Мы тоже рассматривали прямоугольный треугольник.

Найдем проекцию на ось Х. Это, кажется, сложнее, ведь мы не знаем угол…

Знаем! Ведь проекция вектора на ось Х – то же самое, что противолежащий катет уже рассмотренного треугольника, смотри:

Значит, проекцию на ось Х можно найти через косинус.

Не забываем смотреть на направления векторов!

Попробуй найти проекции четвертого вектора самостоятельно и сверься с таблицей.

Значит, проекцию на ось Х можно найти через косинус.

Не забываем смотреть на направления векторов!

Попробуй найти проекции четвертого вектора самостоятельно и сверься с таблицей.

Подготовка к ЕГЭ на 90+ в мини-группах

Алексей Шевчук — ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 — WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org — email для записи

• тысячи учеников, поступивших в лучшие ВУЗы страны
• автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
• закончил МФТИ, преподавал на малом физтехе;
• репетиторский стаж — c 2003 года;
• в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
• отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».