Отклонение
расположения
– отклонение реального расположения
рассматриваемого элемента от его
номинального расположения.
Допуск
расположения
– предел, ограничивающий допускаемое
значение отклонения расположения.
Обращаем
внимание, что отклонение расположения
относится не только к поверхностям, но
и к другим геометрическим элементам.
Элемент
– обобщённый термин, под которым в
зависимости от существующих условий
понимается:
-
поверхность
(часть поверхности, плоскость симметрии
нескольких поверхностей); -
линия
(профиль поверхности, линия пересечения
двух поверхностей, ось поверхности или
сечения); -
точка
(точка пересечения поверхностей или
линий, линии и поверхности, центр
окружности или сферы).
Номинальное
расположение
– расположение рассматриваемого
элемента, определяемое номинальными
размерами между ним и базами, или между
рассматриваемыми элементами, если базы
не заданы.
База
–
элемент (или сочетание элементов),
определяющий одну из плоскостей или
осей системы координат, по отношению к
которой задаётся допуск расположения
или определяется отклонение расположения
рассматриваемого элемента.
В
общем виде условные обозначения таких
отклонений на чертежах выглядят следующим
образом:
-
X
Y/Z
W
где
вместо X
указывается условное графическое
обозначение отклонения;
вместо
Y
указывается наибольшая допустимая
величина отклонения (мм);
вместо
Z
указывается величина нормируемого
участка (мм), если отклонение задаётся
не на всём протяжении поверхности, а на
отдельном её участке;
вместо
W
указывается буквенное обозначение
измерительной базы (баз).
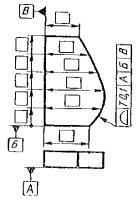
Любое
отклонение взаимного расположения
предполагает базу, относительно которой
задаётся данное отклонение. Базу
обозначают зачернённым треугольником,
который соединяют с рамкой допуска
(рис. 1.3.21, а),
или, чаще всего, обозначают в отдельной
рамке прописной буквой, с указанием той
же буквы в третьем поле рамки допуска
(рис. 1.3.21, б).

Рис.
1.3.21. Примеры обозначения баз на чертежах
Если базой является поверхность или
профиль, то основание зачернённого
треугольника не должно лежать на
продолжении размерной линии (рис. 1.3.22,
а).
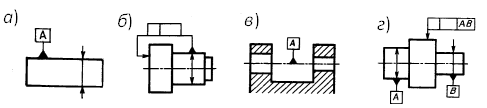
Рис.
1.3.22. Примеры обозначения баз на чертежах
Если же базой является ось или плоскость
симметрии, треугольник должен располагаться
в конце размерной линии соответствующего
размера элемента (рис. 1.3.22, б). Если
базой является общая ось или плоскость
симметрии для нескольких элементов, то
треугольник располагают на общей оси
(рис. 1.3.22, в), или на каждом из элементов
(рис. 1.3.22, г).
Отклонения
расположения
Различают
следующие отклонения расположения.
-
О

тклонение
от параллельности плоскостей (),
или оси
и плоскости,
или двух
осей
– разность наибольшего и наименьшего
расстояний между элементами детали в
пределах нормируемого участка (рис.
1.3.23, а).
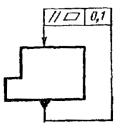
Пример обозначения приведён на рис.
1.3.23, б.
Рис.
1.3.23. Эскиз отклонения от параллельности
плоскостей (а)
и
пример обозначения на чертеже (б)
-
Отклонение
()
от
перпендикулярности
плоскостей,
или плоскости
и оси,
или двух
осей
– отклонение угла между элементами
детали от прямого угла, выраженное в
линейных единицах на длине нормируемого
участка (рис. 1.3.24, а).

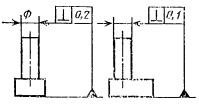
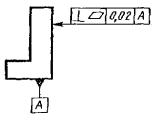
Рис.
1.3.24. Эскиз отклонения от перпендикулярности
плоскостей (а)
и
пример обозначения на чертеже (б)
Пример
обозначения приведён на рис. 1.3.24, б.
-
О

тклонение
()
наклона
элемента относительно базового элемента
– отклонение угла между элементами
детали от номинального угла, выраженное
в линейных единицах на длине нормируемого
участка (рис. 1.3.25, а).
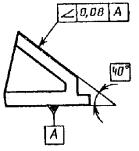
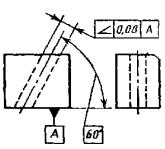
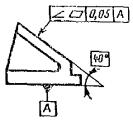
Рис.
1.3.25. Эскиз отклонения наклона плоскости
относительно плоскости (а)
и пример обозначения на чертеже (б)
Угловые
размеры, определяющие номинальное
расположение рассматриваемых элементов
относительно баз или между рассматриваемыми
элементами указывают на чертежах без
предельных отклонений и заключают в
прямоугольные рамки. Пример обозначения
приведён на рис. 1.3.25, б.
-
Отклонение
()
от соосности
относительно оси базовой поверхности
– наибольшее расстояние между осью
рассматриваемой поверхности вращения
и осью базовой поверхности на длине
нормируемого участка (рис. 1.3.26, а).
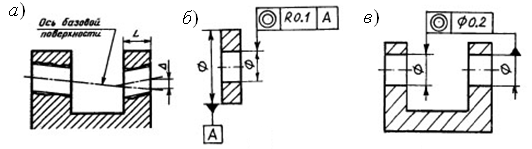
Рис.
1.3.26. Эскиз отклонения от соосности (а)
и примеры обозначений на чертеже (б,
в)
Допуск
соосности может задаваться в диаметральном
(предпочтительно) и радиусном выражении.
Диаметральное выражение есть удвоенное
наибольшее допускаемое значение
отклонения от соосности, и обозначается
знаком .
Радиусное выражение равно половине
диаметрального, и обозначается знаком
R.
В
ранее выпущенной документации встречается
устаревшее графическое обозначение
отклонения от соосности в радиусном
выражении:
Примеры
обозначений приведены на рис. 1.3.26, б,
в.
-
Отклонение
()
от
симметричности относительно базового
элемента
– наибольшее расстояние между плоскостью
симметрии (оси) рассматриваемого
элемента и плоскостью симметрии базового
элемента в пределах нормируемого
участка (рис. 1.3.27, а).

Рис.
1.3.27. Эскизы отклонения от симметричности
(а)
и примеры обозначений на чертеже (б)
Допуск
симметричности может задаваться в
диаметральном (предпочтительно) и
радиусном выражении. Диаметральное
выражение есть удвоенное наибольшее
допускаемое значение отклонения от
симметричности. Оно обозначается знаком
(для поверхностей вращения) или Т
(для остальных поверхностей).
Радиусное
выражение равно половине диаметрального.
Оно обозначается знаком R
(для поверхностей вращения) или Т/2
(для остальных поверхностей).
В
ранее выпущенной документации встречается
устаревшее графическое обозначение
отклонения от симметричности в радиусном
выражении. Примеры обозначений приведены
на рис. 1.3.27, б.
-
Позиционное
отклонение ()
– наибольшее расстояние между реальным
расположением элемента (его центра,
оси или плоскости симметрии) и его
номинальным расположением в пределах
нормируемого участка (рис. 1.3.28, а).

Рис.
3.28. Эскиз позиционного отклонения (а)
и пример обозначения на чертеже (б)
Позиционный
допуск может задаваться в диаметральном
(предпочтительно) и радиусном выражении.
Диаметральное выражение есть удвоенное
наибольшее допускаемое значение
позиционного отклонения элемента, и
обозначается знаком .
Радиусное выражение равно половине
диаметрального, и обозначается знаком
R.
В
ранее выпущенной документации встречается
устаревшее графическое обозначение
позиционного отклонения в радиусном
выражении.
Линейные
размеры, определяющие номинальное
расположение рассматриваемых элементов
относительно баз или между рассматриваемыми
элементами указывают на чертежах без
предельных отклонений и заключают в
прямоугольные рамки. Пример обозначения
приведён на рис. 1.3.28, б.
-
Отклонение
()
от пересечения осей – наименьшее
расстояние между осями, номинально
пересекающимися (рис. 1.3.29, а).
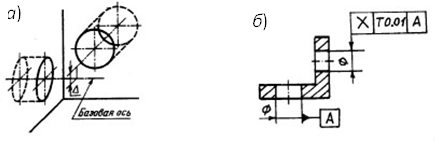
Рис.
1.3.29. Эскиз отклонения от пересечения
осей (а)
и пример обозначения на чертеже (б)
Допуск
пересечения осей может задаваться в
диаметральном (предпочтительно) и
радиусном выражении. Диаметральное
выражение есть удвоенное наибольшее
допускаемое значение отклонения от
пересечения осей, и обозначается знаком
Т.
Радиусное выражение равно половине
диаметрального, и обозначается знаком
Т/2.
Примеры
обозначений приведены на рис. 1.3.29, б.
Суммарные
отклонения формы и взаимного расположения
Суммарное
отклонение формы и расположения
11
– отклонение, являющееся результатом
совместного проявления отклонения
формы и отклонения расположения
рассматриваемой поверхности (или
профиля) относительно заданных баз.
Различают
следующие отклонения формы и взаимного
расположения.
-
Радиальное
биение
()
– разность наибольшего и наименьшего
расстояний от точек реального профиля
поверхности вращения до базовой оси в
сечении плоскостью, перпендикулярной
базовой оси (рис. 1.3.30, а).

Рис.
1.3.30. Эскизы биений радиального (а),
торцового (б)
и в заданном направлении (в)
Данное
отклонение есть результат отклонения
от круглости и отклонения центра сечения
от базовой оси.
-
Торцовое
биение
()
– разность наибольшего и наименьшего
расстояний от точек реального профиля
торцовой поверхности до плоскости,
перпендикулярной базовой оси (рис.
1.3.30, б).
Данное отклонение есть результат
отклонения от плоскостности торца, в
точках измерения, и отклонения от
перпендикулярности торца относительно
базовой поверхности. -
Биение
()
в
заданном направлении
– разность наибольшего и наименьшего
расстояний от точек реального профиля
поверхности вращения в сечении
рассматриваемой поверхности конусом,
ось которого совпадает с базовой осью,
а образующая имеет заданное направление,
до вершины этого конуса (рис. 1.3.30, в).
Обозначения
торцового и радиального биений, а также
биения в заданном направлении, одинаковы
и различаются местоуказанием (рис.
1.3.31).

Рис.
1.3.31. Примеры обозначений биений на
чертежах: радиального (а),
торцового (б)
и в заданном направлении (в)
-
Полное
радиальное биение
()
– разность наибольшего и наименьшего
расстояний от всех точек реальной
поверхности в пределах нормируемого
участка до базовой оси (рис. 1.3.32, а).

Рис.
1.3.32. Эскизы полного радиального (а)
и полного торцового (б)
биений
Полное
радиальное биение относится только к
поверхностям с номинальной цилиндрической
формой и является результатом отклонения
от цилиндричности и отклонения от
соосности.
-
Полное
торцовое биение
()
– разность наибольшего и наименьшего
расстояний от точек всей торцовой
поверхности до плоскости, перпендикулярной
базовой оси (рис. 1.3.32, б).
Полное
торцовое биение относится только к
торцовым поверхностям с номинальной
плоской формой и является результатом
отклонения от плоскостности и от
перпендикулярности.
Обозначения
полного торцового и полного радиального
биений одинаковы и различаются
местоуказанием (рис. 1.3.33).

Рис.
1.3.33. Примеры обозначений биений на
чертежах: полного радиального (а)
и полного торцового (б)
-
Отклонение
()
формы
заданного профиля
– наибольшее отклонение точек реального
профиля от номинального профиля,
определяемое по нормали к номинальному
профилю в пределах нормируемого участка
(рис. 1.3.34, а),
является результатом отклонений
размеров и формы профиля, а также
отклонений расположения его относительно
заданных баз.

Рис.
1.3.34. Эскиз отклонения формы заданного
профиля и пример обозначения на чертеже
Допуск
формы заданного профиля может задаваться
в диаметральном (предпочтительно) и
радиусном выражении.
Диаметральное
выражение есть удвоенное наибольшее
допускаемое значение отклонения формы
заданного профиля, и обозначается знаком
Т.
Радиусное выражение равно половине
диаметрального, и обозначается знаком
Т/2.
Линейные
размеры, определяющие номинальное
расположение рассматриваемых элементов
относительно баз или между рассматриваемыми
элементами указывают на чертежах без
предельных отклонений и заключают в
прямоугольные рамки. Пример обозначения
приведён на рис. 1.3.34, б.
-
Отклонение
()
формы
заданной поверхности
– наибольшее отклонение точек реальной
поверхности от номинальной поверхности,
определяемое по нормали к номинальной
поверхности в пределах нормируемого
участка (рис. 1.3.35, а),
является результатом отклонений
размеров и формы поверхности, а также
отклонений расположения её относительно
заданных баз.
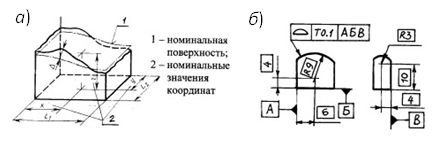
Рис.
1.3.35. Эскиз отклонения формы заданной
поверхности и пример обозначения на
чертеже
Допуск
формы заданной поверхности может
задаваться в диаметральном (предпочтительно)
и радиусном выражении.
Диаметральное
выражение есть удвоенное наибольшее
допускаемое значение отклонения формы
заданной поверхности, и обозначается
знаком Т.
Радиусное
выражение равно половине диаметрального,
и обозначается знаком Т/2.
Линейные
размеры, определяющие номинальное
расположение рассматриваемых элементов
относительно баз или между рассматриваемыми
элементами указывают на чертежах без
предельных отклонений и заключают в
прямоугольные рамки.
Пример
обозначения приведён на рис. 1.3.35, б.
-
Суммарные
отклонения формы и расположения
поверхностей,
для которых не установлены отдельные
графические символы, обозначают знаками
составных отклонений. Сначала идёт
знак отклонения расположения, затем –
знак отклонения формы (рис. 1.3.36).
Например,
знак суммарного отклонения параллельности
и плоскостности (рис. 1.3.36, а);
знак суммарного отклонения перпендикулярности
и плоскостности (рис. 1.3.36, б);
знак суммарного отклонения наклона и
плоскостности (рис. 1.3.36, в).
![]()
Рис.
1.3.36. Примеры обозначений составных
отклонений
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание страницы
- 1. Общие сведения о единой системе допусков и посадок
- 2. Указание на чертежах допусков размеров
- 3. Допуски формы и расположения поверхностей деталей
- 4. Отклонения и допуски расположения
- 5. Указание на чертежах допусков точности деталей
1. Общие сведения о единой системе допусков и посадок
При изготовлении деталей из заготовок необходимо выдерживать определенные геометрические параметры поверхностей — их размеры, форму и относительное расположение. Степень приближения истинного значения рассматриваемого параметра к его теоретическому значению называется точностью.
Размер – это числовое значение линейной величины (диаметра, длины и т.д.), который в машиностроении измеряют в миллиметрах. Размеры подразделяют на номинальные, действительные и предельные.
Номинальный – это размер, относительно которого определяются предельные размеры и который служит также началом отсчета отклонений. Номинальный размер — это основной размер, полученный на основе кинематических, динамических и прочностных расчетов или выбранный из конструктивных, технологических, эксплуатационных, эстетических и других соображений. Номинальные размеры можно классифицировать по назначению на определяющие величину и форму детали, координирующие и сборочные (монтажные). Кроме того, из соображений удобства и точности обработки иногда вводятся технологические размеры. Это тот теоретический размер, к которому как можно ближе должен соответствовать размер готовой детали.
Действительный – это размер, установленный измерением с допустимой погрешностью.
Чтобы изделие считалось годным, т.е. отвечало своему целевому назначению, его действительный размер должен быть выдержан между двумя теоретически допустимыми предельными размерами, разность которых образует допуск. Наибольший предельный размер — это больший из двух предельных, наименьший — это меньший из двух предельных размеров.
Для удобства указывают номинальный размер детали, а каждый из двух предельных размеров определяют по его отклонению от этого номинального размера (рис. 1). Абсолютную величину и знак отклонения получают вычитанием номинального размера из соответствующего предельного размера.
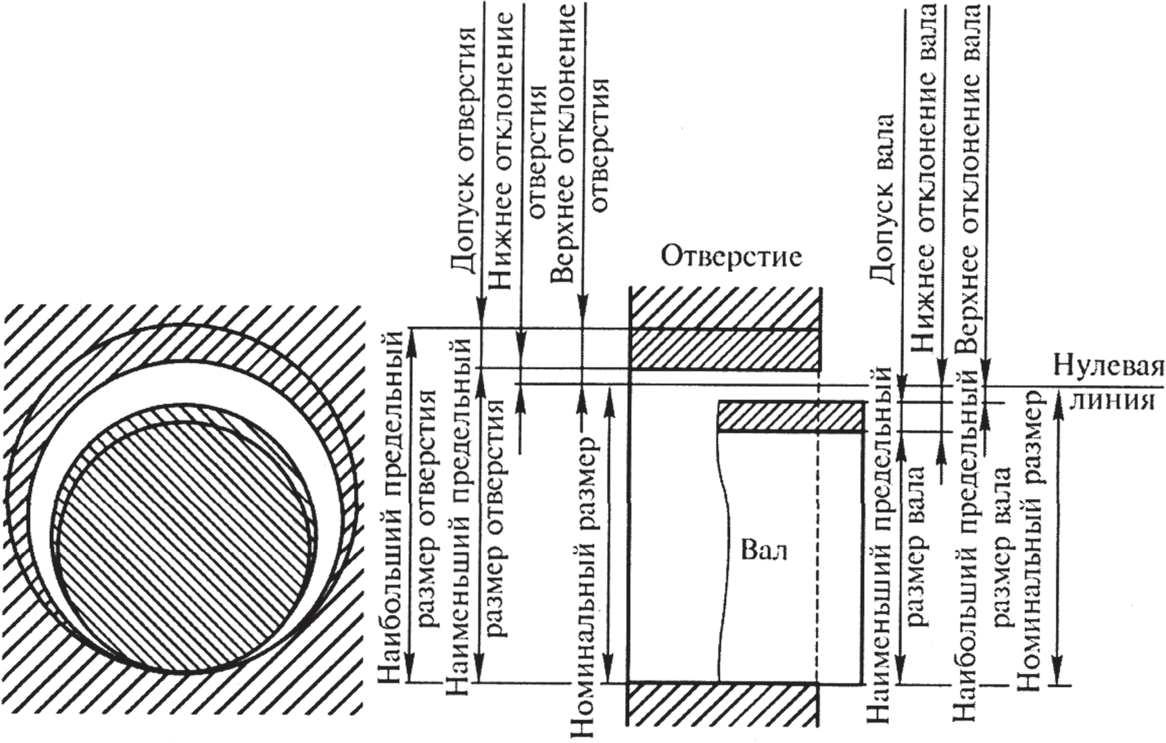
Рис. 1. Формирование отклонений для вала и отверстия относительно нулевой линии номинального размера
Отклонение – это алгебраическая разность между размером (действительным, предельным и т. д.) и соответствующим номинальным размером.
Действительное отклонение — это алгебраическая разность между действительным и номинальным размерами.
Предельное отклонение – это алгебраическая разность между предельным и номинальным размерами. Предельные отклонения подразделяют на верхнее и нижнее.
Верхнее отклонение – это алгебраическая разность между наибольшим предельным и номинальным размерами; нижнее отклонение – это алгебраическая разность между наименьшим предельным и номинальным размерами. Верхнее и нижнее отклонения приводятся в справочных таблицах и измеряются в микрометрах (мкм), а на чертежах указываются в миллиметрах (мм).
Классификацию отклонений по геометрическим параметрам целесообразно рассмотреть на примере соединения вала и отверстия. Термин «вал» применяют для обозначения наружных (охватываемых) элементов деталей, термин «отверстие» — для обозначения внутренних (охватывающих) элементов деталей. Термины «вал» и «отверстие» относят не только к цилиндрическим деталям круглого сечения, но и к элементам деталей другой охватываемой и охватывающей формы (например, ограниченным двумя параллельными плоскостями — шпоночное соединение).
Допуск — это разность между наибольшим и наименьшим предельными размерами или абсолютная величина алгебраической разности между верхним и нижним отклонениями.
Квалитет (степень точности) — совокупность допусков, соответствующих одинаковой степени точности для всех номинальных размеров.
Нулевая линия — это линия, соответствующая номинальному размеру, от которой откладываются отклонения размеров при графическом изображении допусков и посадок. При горизонтальном расположении нулевой линии положительные отклонения откладываются вверх от нее, а отрицательные — вниз.
Поле допуска — это поле, ограниченное верхним и нижним отклонениями. Поле допуска определяется величиной допуска и его положением относительно номинального размера. При графическом изображении поле допуска заключено между двумя линиями, соответствующими верхнему и нижнему отклонениям относительно нулевой линии.
Основное отклонение – одно из двух отклонений (верхнее или нижнее), ближайшее к нулевой линии, используемое для определения положения поля допуска относительно нулевой линии. Основное отверстие — это отверстие, нижнее отклонение которого равно нулю. Основной вал — это вал, верхнее отклонение которого равно нулю.
В зависимости от взаимного расположения полей допусков отверстия и вала различают посадки с зазором, с натягом и переходные, когда возможно получение как зазора, так и натяга (рис. 2).
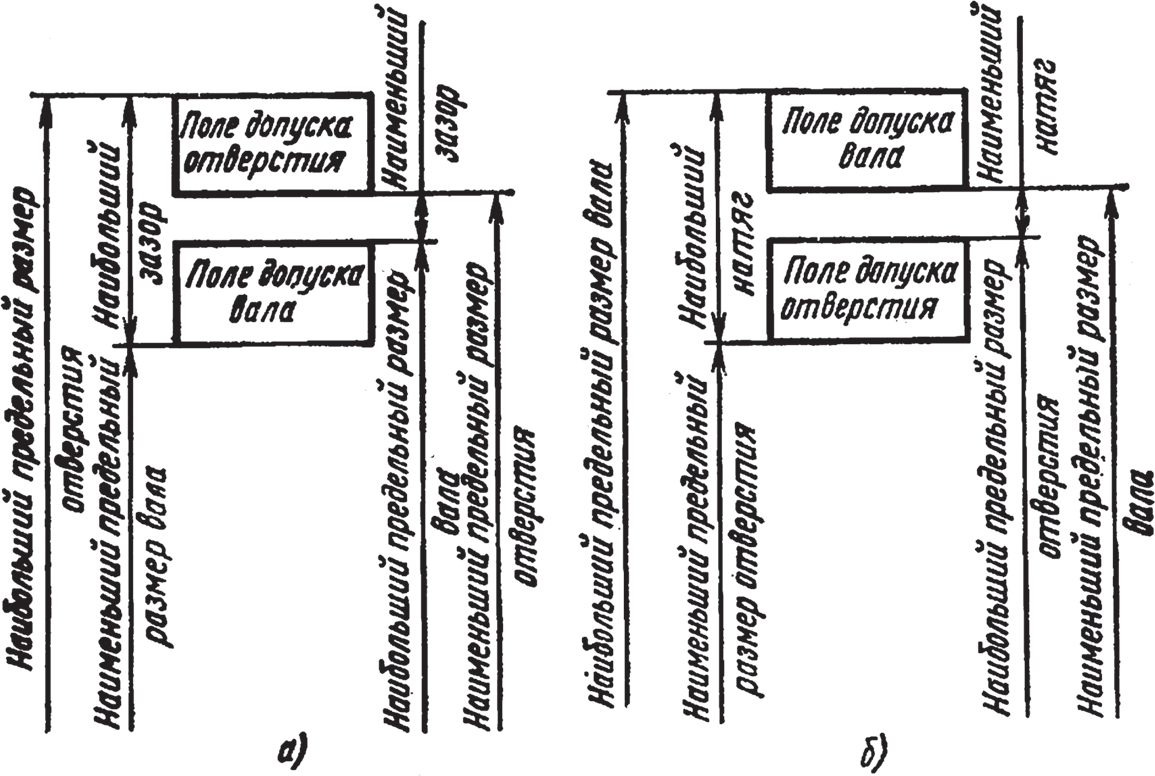
Рис. 2. Типы посадок: а — с зазором; б — с натягом
Номинальным размером посадки называется номинальный размер, общий для отверстия и вала, составляющих соединение. Зазором называется разность размеров отверстия и вала, если размер отверстия больше размера вала.
Посадка с зазором — это посадка, при которой обеспечивается зазор в соединении (поле допуска отверстия расположено над полем допуска вала). К посадкам с зазором относятся также посадки, в которых нижняя граница поля допуска отверстия совпадает с верхней границей поля допуска вала. Поскольку идеально точное изготовление деталей невозможно, то невозможно получить в соединении один и тот же по величине зазор. В связи с этим назначаются два предельных значения — наименьший и наибольший зазоры, между которыми должен находиться зазор в соединении по выбранной посадке.
Натягом называется разность размеров вала и отверстия до сборки, если размер вала больше размера отверстия.
Посадка с натягом — это посадка, при которой обеспечивается натяг в соединении. Поле допуска отверстия расположено под полем допуска вала.
Если после назначения экономически целесообразных допусков на обработку вала и отверстия оказывается, что их поля допусков перекрываются частично или полностью, то такие соединения относят к переходным посадкам.
Переходная посадка — это посадка, при которой возможно получение как зазора, так и натяга.
Для оценки точности соединений (посадок) пользуются понятием «допуск посадки», под которым понимают сумму допусков отверстия и вала, составляющих соединение.
При соединении двух деталей (отверстие и вал) образуется посадка, определяемая разностью их размеров до сборки, т.е. величиной получающихся зазоров или натягов в соединении. Посадка характеризует свободу относительного перемещения соединяемых деталей или степень сопротивления их взаимному смещению.
Различают две равноценные системы образования посадок — система отверстия и система вала (рис. 3).
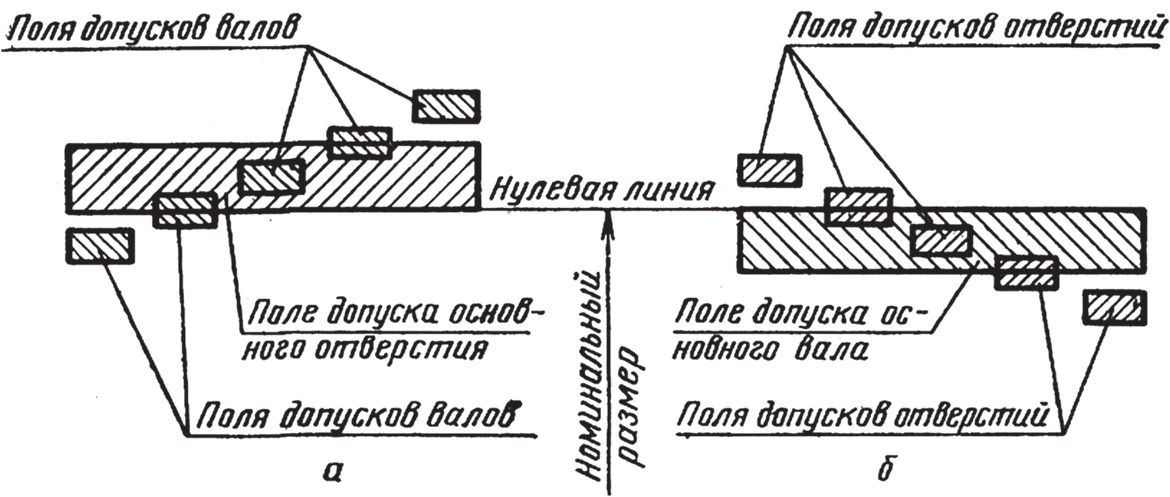
Рис. 3. Примеры посадок в системах: а — отверстия; б — вала
Посадки в системе отверстия – это посадки, у которых различные зазоры и натяги получаются соединением различных валов с основным отверстием. У основного отверстия нижнее отклонение равно нулю или наименьший предельный размер его совпадает с номинальным размером соединения, а верхнее зависит от квалитета.
Посадки в системе вала – это посадки, у которых различные зазоры и натяги получаются соединением различных отверстий с основным валом. У основного вала верхнее отклонение равно нулю или наибольший предельный размер совпадает с номинальным размером соединения, а нижнее зависит от квалитета.
2. Указание на чертежах допусков размеров
Прежде чем назначить предельные отклонения размерам на чертежах определяют характер соединения, возможности ремонта, условия эксплуатации и др.
Предельные размеры с помощью предельных отклонений указывают на чертежах с помощью таблиц несколькими способами:
- числовыми величинами (рис. 4, а), причем отклонение, равное нулю, опускается (рис. 4, д), а одинаковые по абсолютной величине, но противоположные по знаку отклонения указывают один раз со знаками ± (рис. 4, e);
- условными (символическими) обозначениями полей допусков и посадок согласно стандартам (рис. 4, г);
- символическими условными обозначениями полей допусков с указанием справа в скобках их числовых величин (рис. 4, ж).
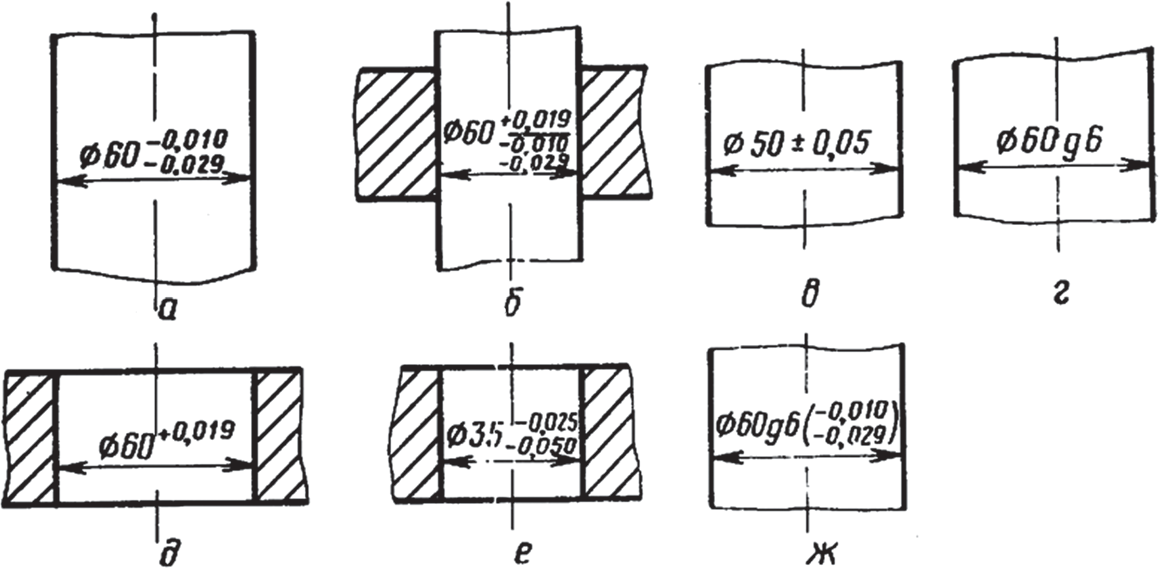
Рис. 4. Нанесение предельных (верхнего и нижнего) отклонений на чертежах
Предельные отклонения размеров деталей, изображенных на чертеже в сборе, указывают также одним из трех перечисленных способов в виде дроби: в числителе представляют предельные отклонения отверстия, в знаменателе — вала (рис. 4, б). На рис. 4, г символ g6 обозначает поле допуска, т.е. два отклонения: верхнее отклонение — 0,010 и нижнее — 0,029 мм. В обозначениях положительных предельных отклонений знак «+» опускать нельзя. Предельные отклонения записывают до последней значащей цифры включительно, выравнивая количество знаков в верхнем и нижнем отклонении добавлением нулей (рис. 4; а,б,е,ж).
Буквенный способ обозначения полей допуска предпочтителен в случае применения предельных калибров для измерения размеров на производстве, так как на калибрах, как правило, маркируются буквенные обозначения полей допусков контролируемых деталей.
Числовые обозначения удобнее при работе на универсальных металлообрабатывающих станках и при контроле изделий универсальными средствами измерений. Смешанные обозначения применяют при неопределенности вопроса о средствах контроля, которые будут использованы на производстве.
3. Допуски формы и расположения поверхностей деталей
В процессе механической обработки деталей под действием сил резания, а также в процессе эксплуатации машины под нагрузкой происходит деформация деталей. В результате нежесткости центров токарного станка или самой заготовки и других причин после обработки деталь может иметь бочкообразный, седлообразный или конусный профиль, т.е. иметь погрешность формы, или иметь радиальное биение наружной поверхности относительно линии центров, т.е. иметь погрешность расположения наружной поверхности относительно осевой линии.
В основу нормирования и систему отсчета отклонений формы и расположения поверхностей положен принцип прилегающих поверхностей и профилей, элементов, деталей, сборочных единиц (узлов).
Под элементом понимается поверхность (часть поверхности, плоскость симметрии нескольких поверхностей), профиль поверхности, линия пересечения двух поверхностей, ось поверхности или сечения (точка пересечения линии, линии и поверхности, центр окружности или сфера).
Различают следующие основные виды прилегающих поверхностей, плоскостей и профилей: номинальная (идеальная) поверхность, номинальная форма, которая задана чертежом или другой технической документацией, и реальная поверхность, ограничивающая деталь и отделяющая ее от окружающей среды.
Профиль — это линия пересечения поверхности с плоскостью или заданной поверхностью. Различают профили номинальной и реальной поверхностей. Прилегающая плоскость и прилегающая прямая — плоскость или прямая, соприкасающаяся с реальной поверхностью или профилем и расположенная вне материала детали так, чтобы отклонение от ее наиболее удаленной точки соответственно реальной поверхности или профиля в пределах нормируемого участка имело минимальное значение (рис. 5, а).
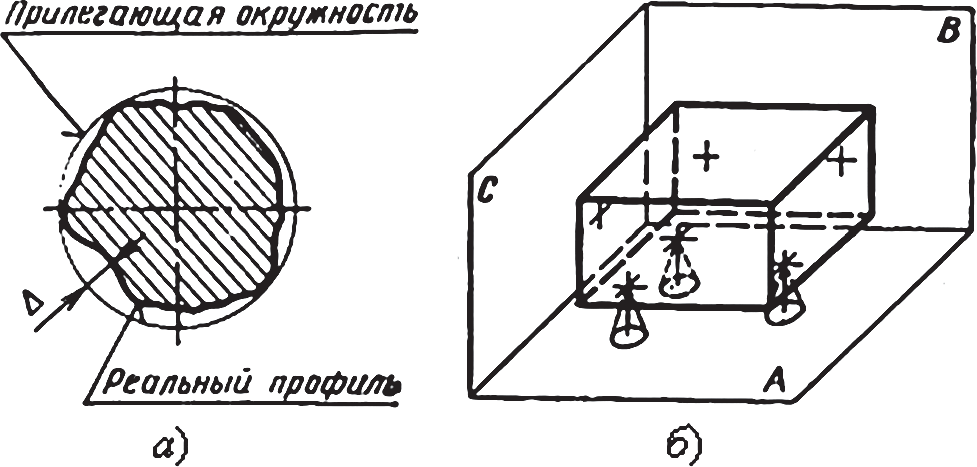
Рис. 5. Номинальные профиль и поверхности: а — прилегающая окружность; б — комплект баз
Нормируемый участок — это участок поверхности или линии, к которому относится допуск или отклонение формы или расположение элемента. Нормируемый участок должен задаваться размерами, определяющими его площадь, длину или угол сектора (в полярных координатах). Если нормируемый участок не задан, то допуск или отклонение формы или расположения должен относиться ко всей поверхности или длине рассматриваемого элемента.
Прилегающая окружность — это окружность минимального диаметра, описания вокруг реального профиля наружной поверхности вращения, или минимального диаметра, вписанная в реальный профиль внутренней поверхности вращения (рис. 5, а).
База — элемент детали (или выполняющее ту же функцию сочетание элементов), определяющий одну из плоскостей или осей системы координат, по отношению к которой задается допуск расположения или определяется отклонение расположения рассматриваемого элемента. Базами могут быть, например, базовая плоскость, базовая ось, базовая плоскость симметрии.
Комплект баз — совокупность двух или трех баз, образующих систему координат, по отношению к которой задается допуск расположения или определяется отклонение расположения рассматриваемого элемента. Базы, образующие комплект баз, различают в порядке убывания числа степеней свободы, лишаемых ими (например, на рис. 5, б база А лишает деталь трех степеней свободы, база В – двух, а база С – одной степени свободы).
Отклонение формы определяется как сумма абсолютных значений наибольших отклонений точки от реальной поверхности, расположенных по обе стороны от средней поверхности. Такой способ оценки получил применение в ряде современных измерительных средств. Разница между отклонениями формы, определенными относительно прилегающей и средней поверхности, практически незначительна.
К отклонениям и допускам формы относятся (рис. 6):
- отклонение от прямолинейности в плоскости и допуск. Частными видами отклонения от прямолинейности являются выпуклость и вогнутость;
- отклонение от прямолинейности оси (или линии) в пространстве и допуск (рис. 6; а, б);
- отклонение от плоскостности и допуск. Частными видами отклонений от плоскостности являются выпуклость и вогнутость (рис. 6; в, г);
- отклонение от круглости и допуск. Частными видами отклонений от круглости являются овальность и огранка (рис. 6; д, е);
- отклонение от цилиндричности и допуск;
- отклонение и допуск профиля продольного сечения цилиндрической поверхности. Частными видами отклонения профиля продольного сечения являются конусообразность, бочкообразность и седлообразность (рис. 6; ж, з, и).
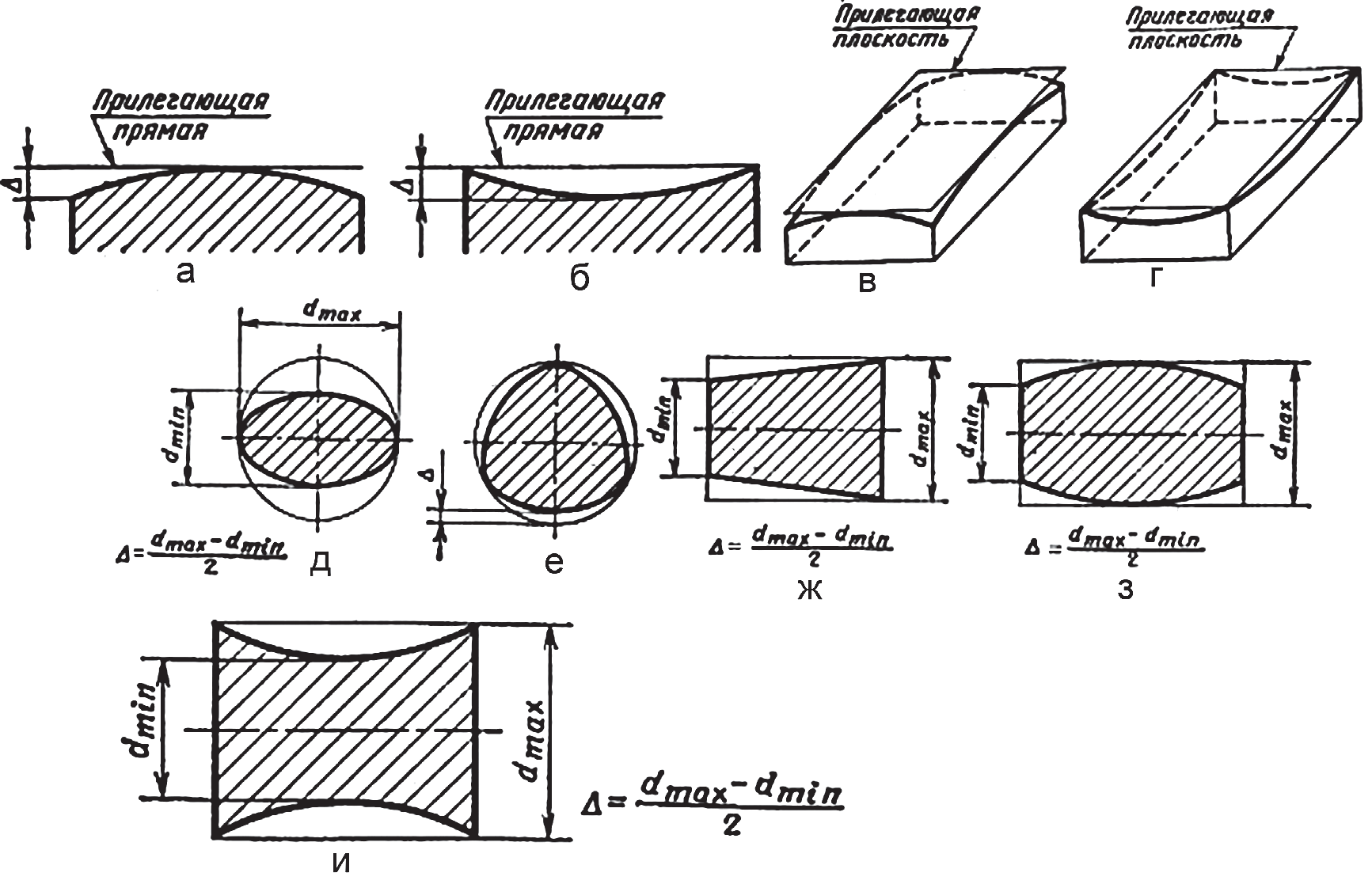
Рис. 6. Отклонения и допуски формы поверхностей изделия
Применять частные виды отклонений — выпуклость, вогнутость, огранку, овальность, конусообразность, бочкообразность, седлообразность для их нормирования следует лишь в обоснованных случаях, когда для обеспечения правильного функционирования изделия важно учитывать и характер отклонения формы.
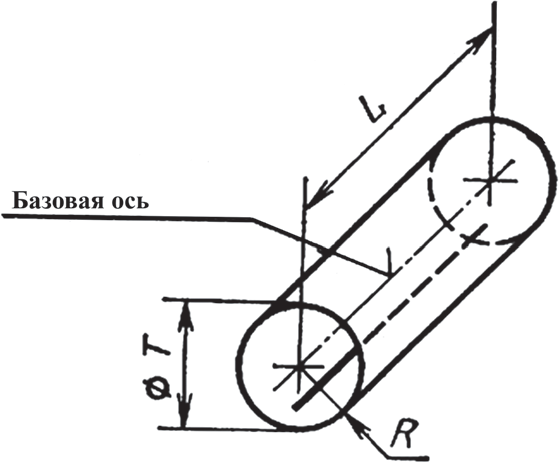
Рис. 7. Поле допуска на соосность
4. Отклонения и допуски расположения
В реальных поверхностях отклонения формы и расположения всегда сочетаются. В работе и при измерениях эти отклонения могут проявляться или раздельно, или совместно. Поэтому установлены собственно отклонения и допуски расположения, предполагающие исключение из рассмотрения отклонений формы путем замены реальных поверхностей прилегающими, и суммарные отклонения и допуски формы и расположения.
Отклонения расположения и допуски определяются относительно баз. Отклонения формы и расположения отдельных баз комплекта могут вызвать неоднозначную оценку геометрических отклонений других поверхностей. Поэтому при назначении комплекта баз важно задать последовательность их выбора, которая должна устанавливаться в порядке убывания числа степеней свободы детали, отнимаемых базами.
Введенный допуск на наклон позволяет нормировать отклонения от любого номинального угла (кроме 0 и 90°) методом, аналогичным методу нормирования допусков на параллельность и перпендикулярность, т.е. в линейной мере.
Допуски на соосность, симметричность, пересечение осей, позиционный допуск можно задавать либо предельным значением отклонения в радиусном выражении, либо диаметром (шириной) поля допуска, что соответствует удвоенному предельному отклонению (допуски в диаметральном выражении). Оба способа выражения допуска показаны на рис. 7 на примере поля допуска на соосность (Т — допуск в диаметральном, R = T/2 — допуск в радиальном выражении).
5. Указание на чертежах допусков точности деталей
На чертежах изделий, как правило, предпочтение отдается условным обозначениям допусков, а не текстовым записям (табл. 1). Записи рекомендуется в основном применять для текстовой документации или в случаях, когда вид допуска или базирования не может быть выражен условным обозначением.
Таблица 1. Условные обозначения допусков
| Группа допусков | Вид допуска | Знак |
| Допуск формы | Допуск прямолинейности | |
| Допуск плоскостности | ||
| Допуск круглости | ||
| Допуск цилиндричности |  |
|
| Допуск профиля продольного сечения | ||
| Допуск расположения | Допуск параллельности | |
| Допуск перпендикулярности | ||
| Допуск наклона | ||
| Допуск соосности |  |
|
| Допуск симметричности | ||
| Позиционный допуск | ||
| Допуск пересечения осей | ||
| Суммарные допуски формы и расположения | Допуск радиального биения Допуск торцового биения
Допуск биения в заданном направлении |
 |
| Допуск полного радиального биения
Допуск полного торцового биения |
 |
|
| Допуск формы заданного профиля | ||
| Допуск формы заданной поверхности |
Опыт применения условных обозначений показал, что они удобны, наглядны, упрощают оформление документации, позволяют избежать разнобоя в текстовых формулировках.
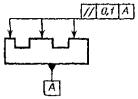
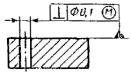
При условном обозначении данные о допусках формы и расположении поверхностей указывают в прямоугольной рамке, разделенной на две части и более (рис. 8), в которых помещают (слева направо): в первой — знак допуска по табл. 1, во второй — числовое значение допуска в миллиметрах, в третьей и последующих — буквенное обозначение базы (баз).

Рис. 8. Указание допусков
Перед числовым значением допуска, который можно задать в радиусном или диаметральном выражениях, должен проставляться символ, указывающий способ выражения. Для допусков в диаметральном выражении применяют символ ø при указании допусков соосности и прецизионных (если поле позиционного допуска круговое или цилиндрическое) — рис. 8, а или символ Т при указании допусков симметричности, пересечения осей, формы заданного профиля и заданной поверхности, позиционного допуска (если поле позиционного допуска ограничено двумя параллельными прямыми или плоскостями) — рис. 8, в. Символ ø применяют также при указании цилиндрических полей допусков прямолинейности, параллельности, перпендикулярности и наклона осей. Для допусков в радиусном выражении используют соответственно символы R или Т/2 (рис. 8; б, г).
Если поле допуска сферическое, пишется слово «сфера» и соответственно символы 0 или Р (рис. 8, д).
Существует правило базирования и указания баз в машиностроении. Буквенные обозначения каждого базового элемента вносятся слева направо в отдельное поле рамки (третье, четвертое и т.д.) в порядке убывания числа степеней свободы детали (например, на рис. 9, а база А лишает деталь трех, база В — двух, а база С — одной степени свободы).
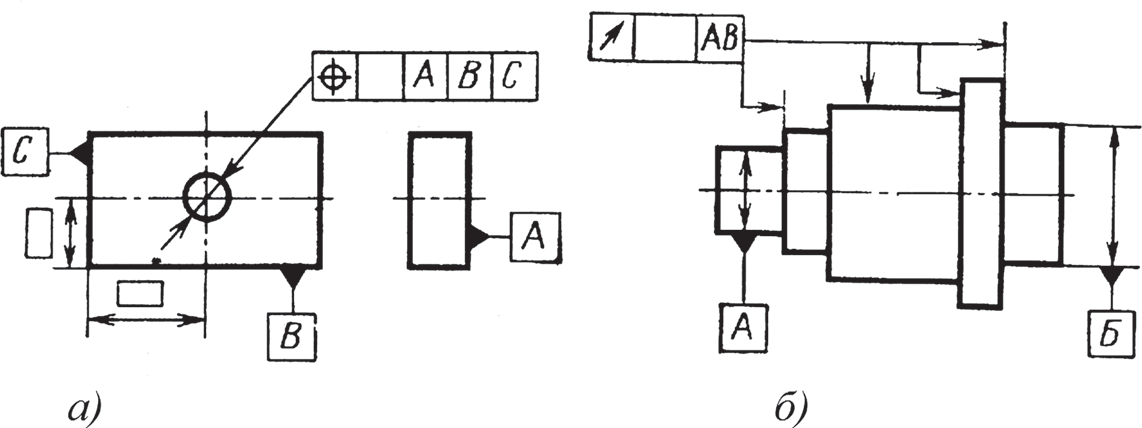
Рис. 9. Обозначение баз: а — буквенное; б — объединенных баз
Если же два или несколько элементов образуют объединенную базу и их последовательность не имеет значения (например, они образуют общую ось), то их буквенные обозначения вписывают вместе в третье поле рамки (рис. 9, б).
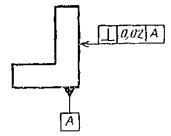
Суммарные допуски формы и расположения поверхностей, для которых не установлены отдельные графические знаки, обозначают знаками составных допусков в такой последовательности: знак допуска расположения, знак допуска формы. Например, рис. 10, а — знак суммарного допуска перпендикулярности и плоскостности поверхности относительно основания 0,02 мм, рис. 10, б — знак суммарного допуска наклона и плоскостности поверхности относительно основания 0,05 мм.
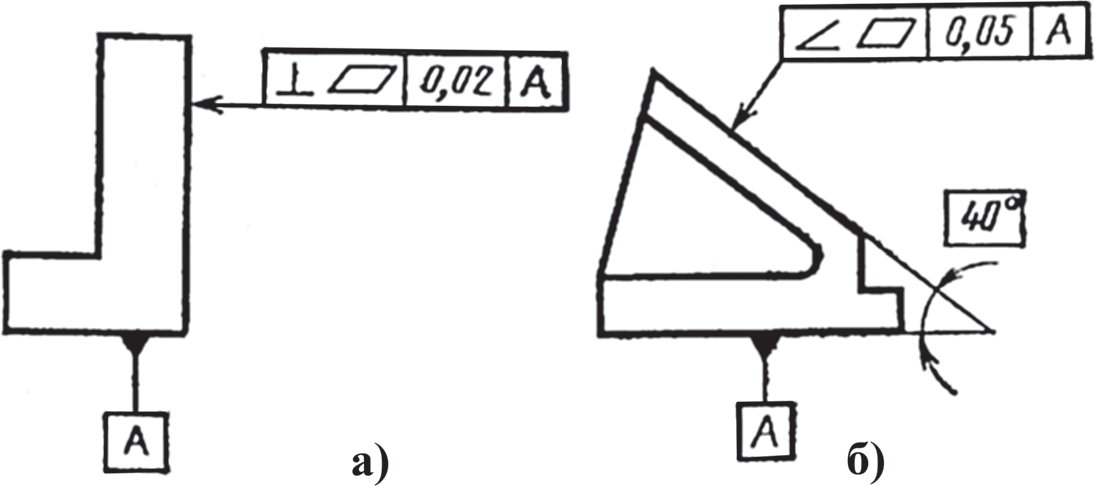
Рис. 10. Суммарные допуски
Отклонения размеров и других параметров готовой детали от указанных в чертеже определяют погрешность обработки, величина которой должна находиться в пределах допуска.
Погрешности подразделяют на систематические и случайные. К систематическим относятся погрешности, которые при обработке партии деталей повторяются на каждой детали. Систематические погрешности по величине больше случайных и определяют точность обрабатываемой детали.
Основными причинами систематических погрешностей обработки являются:
- неточность станка (например, непрямолинейность направляющих станины или неперпендикулярность направляющих оси шпинделя, неточность изготовления шпинделя и его опор и т.д.);
- деформация сборочных единиц (узлов) и деталей станка под действием сил резания и нагрева в процессе работы;
- неточность изготовления режущих инструментов, приспособлений и их износ;
- деформация инструментов и приспособлений под действием сил резания и нагрева в процессе обработки;
- погрешности установки и базирования заготовки на станке;
- деформация обрабатываемой заготовки под действием сил резания и зажима, а также из-за нагрева в процессе обработки;
- погрешности, возникающие при установке инструментов и их настройке на размер;
- погрешности в процессе измерения, вызываемые неточностью измерительных инструментов и приборов, их износом и деформациями, а также ошибкой рабочего при оценке показаний измерительных устройств.
Причины, вызывающие систематические погрешности, можно установить и устранить.
К случайным, непредвиденным относятся погрешности, возникающие вследствие случайных упругих деформаций заготовки, станка, приспособления и режущего инструмента (например, из-за неоднородности обрабатываемого материала).
Метод интервалов: решение простейших строгих неравенств
12 ноября 2017
- Домашнее задание
- Ответы
Для начала — немного лирики, чтобы почувствовать проблему, которую решает метод интервалов. Допустим, нам надо решить вот такое неравенство:
(x − 5)(x + 3) > 0
Какие есть варианты? Первое, что приходит в голову большинству учеников — это правила «плюс на плюс дает плюс» и «минус на минус дает плюс». Поэтому достаточно рассмотреть случай, когда обе скобки положительны: x − 5 > 0 и x + 3 > 0. Затем также рассмотрим случай, когда обе скобки отрицательны: x − 5 < 0 и x + 3 < 0. Таким образом, наше неравенство свелось к совокупности двух систем, которая, впрочем, легко решается:
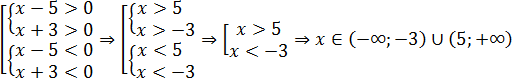
Более продвинутые ученики вспомнят (может быть), что слева стоит квадратичная функция, график которой — парабола. Причем эта парабола пересекает ось OX в точках x = 5 и x = −3. Для дальнейшей работы надо раскрыть скобки. Имеем:
x2 − 2x − 15 > 0
Теперь понятно, что ветви параболы направлены вверх, т.к. коэффициент a = 1 > 0. Попробуем нарисовать схему этой параболы:
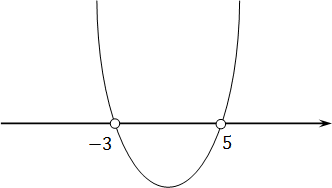
Функция больше нуля там, где она проходит выше оси OX. В нашем случае это интервалы (−∞ −3) и (5; +∞) — это и есть ответ.
Обратите внимание: на рисунке изображена именно схема функции, а не ее график. Потому что для настоящего графика надо считать координаты, рассчитывать смещения и прочую хрень, которая нам сейчас совершенно ни к чему.
Почему эти методы неэффективны?
Итак, мы рассмотрели два решения одного и того же неравенства. Оба они оказались весьма громоздкими. В первом решении возникает — вы только вдумайтесь! — совокупность систем неравенств. Второе решение тоже не особо легкое: нужно помнить график параболы и еще кучу мелких фактов.
Это было очень простое неравенство. В нем всего 2 множителя. А теперь представьте, что множителей будет не 2, а хотя бы 4. Например:
(x − 7)(x − 1)(x + 4)(x + 9) < 0
Как решать такое неравенство? Перебирать все возможные комбинации плюсов и минусов? Да мы уснем быстрее, чем найдем решение. Рисовать график — тоже не вариант, поскольку непонятно, как ведет себя такая функция на координатной плоскости.
Для таких неравенств нужен специальный алгоритм решения, который мы сегодня и рассмотрим.
Что такое метод интервалов
Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f (x) > 0 и f (x) < 0. Алгоритм состоит из 4 шагов:
- Решить уравнение f (x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
- Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
- Выяснить знак (плюс или минус) функции f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней;
- Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется.
Вот и все! После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f (x) > 0, или знаком «−», если неравенство имеет вид f (x) < 0.
На первый взгляд может показаться, что метод интервалов — это какая-то жесть. Но на практике все будет очень просто. Стоит чуть-чуть потренироваться — и все станет понятно. Взгляните на примеры — и убедитесь в этом сами:
Задача. Решите неравенство:
(x − 2)(x + 7) < 0
Работаем по методу интервалов. Шаг 1: заменяем неравенство уравнением и решаем его:
(x − 2)(x + 7) = 0
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:
x − 2 = 0 ⇒ x = 2;
x + 7 = 0 ⇒ x = −7.
Получили два корня. Переходим к шагу 2: отмечаем эти корни на координатной прямой. Имеем:
![]()
Теперь шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000). Получим:
f (x) = (x − 2)(x + 7);
x = 3;
f (3) = (3 − 2)(3 + 7) = 1 · 10 = 10;
Получаем, что f(3) = 10 > 0, поэтому в самом правом интервале ставим знак плюс.
Переходим к последнему пункту — надо отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус.
Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси. Имеем:
![]()
Вернемся к исходному неравенству, которое имело вид:
(x − 2)(x + 7) < 0
Итак, функция должна быть меньше нуля. Значит, нас интересует знак минус, который возникает лишь на одном интервале: (−7; 2). Это и будет ответ.
Задача. Решите неравенство:
(x + 9)(x − 3)(1 − x) < 0
Шаг 1: приравниваем левую часть к нулю:
(x + 9)(x − 3)(1 − x) = 0;
x + 9 = 0 ⇒ x = −9;
x − 3 = 0 ⇒ x = 3;
1 − x = 0 ⇒ x = 1.
Помните: произведение равно нулю, когда хотя бы один из множителей равен нулю. Именно поэтому мы вправе приравнять к нулю каждую отдельную скобку.
Шаг 2: отмечаем все корни на координатной прямой:
![]()
Шаг 3: выясняем знак самого правого промежутка. Берем любое число, которое больше, чем x = 1. Например, можно взять x = 10. Имеем:
f (x) = (x + 9)(x − 3)(1 − x);
x = 10;
f (10) = (10 + 9)(10 − 3)(1 − 10) = 19 · 7 · (−9) = − 1197;
f (10) = −1197 < 0.
Шаг 4: расставляем остальные знаки. Помним, что при переходе через каждый корень знак меняется. В итоге наша картинка будет выглядеть следующим образом:
![]()
Вот и все. Осталось лишь выписать ответ. Взгляните еще раз на исходное неравенство:
(x + 9)(x − 3)(1 − x) < 0
Это неравенство вида f (x) < 0, т.е. нас интересуют интервалы, отмеченные знаком минус. А именно:
x ∈ (−9; 1) ∪ (3; +∞)
Это и есть ответ.
Замечание по поводу знаков функции
Практика показывает, что наибольшие трудности в методе интервалов возникают на последних двух шагах, т.е. при расстановке знаков. Многие ученики начинают путаться: какие надо брать числа и где ставить знаки.
Чтобы окончательно разобраться в методе интервалов, рассмотрим два замечания, на которых он построен:
- Непрерывная функция меняет знак только в тех точках, где она равна нулю. Такие точки разбивают координатную ось на куски, внутри которых знак функции никогда не меняется. Вот зачем мы решаем уравнение f (x) = 0 и отмечаем найденные корни на прямой. Найденные числа — это «пограничные» точки, отделяющие плюсы от минусов.
- Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала. Например, для интервала (−5; 6) мы вправе брать x = −4, x = 0, x = 4 и даже x = 1,29374, если нам захочется. Почему это важно? Да потому что многих учеников начинают грызть сомнения. Мол, что если для x = −4 мы получим плюс, а для x = 0 — минус? А ничего — такого никогда не будет. Все точки на одном интервале дают один и тот же знак. Помните об этом.
Вот и все, что нужно знать про метод интервалов. Конечно, мы разобрали его в самом простом варианте. Существуют более сложные неравенства — нестрогие, дробные и с повторяющимися корнями. Для них тоже можно применять метод интервалов, но это тема для отдельного большого урока.
Теперь хотел бы разобрать продвинутый прием, который резко упрощает метод интервалов. Точнее, упрощение затрагивает только третий шаг — вычисление знака на самом правом куске прямой. По каким-то причинам этот прием не проходят в школах (по крайней мере, мне никто такого не объяснял). А зря — ведь на самом деле этот алгоритм очень прост.
Итак, знак функции на правом куске числовой оси. Этот кусок имеет вид (a; +∞), где a — самый большой корень уравнения f (x) = 0. Чтобы не взрывать мозг, рассмотрим конкретный пример:
(x − 1)(2 + x)(7 − x) < 0;
f (x) = (x − 1)(2 + x)(7 − x);
(x − 1)(2 + x)(7 − x) = 0;
x − 1 = 0 ⇒ x = 1;
2 + x = 0 ⇒ x = −2;
7 − x = 0 ⇒ x = 7;
Мы получили 3 корня. Перечислим их в порядке возрастания: x = −2, x = 1 и x = 7. Очевидно, что наибольший корень — это x = 7.
Для тех, кому легче рассуждать графически, я отмечу эти корни на координатной прямой. Посмотрим, что получится:
![]()
Требуется найти знак функции f (x) на самом правом интервале, т.е. на (7; +∞). Но как мы уже отмечали, для определения знака можно взять любое число из этого интервала. Например, можно взять x = 8, x = 150 и т.д. А теперь — тот самый прием, который не проходят в школах: давайте в качестве числа возьмем бесконечность. Точнее, плюс бесконечность, т.е. +∞.
«Ты че, обкурился? Как можно подставить в функцию бесконечность?» — возможно, спросите вы. Но задумайтесь: нам ведь не нужно само значение функции, нам нужен только знак. Поэтому, например, значения f (x) = −1 и f (x) = −938 740 576 215 значат одно и то же: функция на данном интервале отрицательна. Поэтому все, что от вас требуется — найти знак, который возникает на бесконечности, а не значение функции.
На самом деле, подставлять бесконечность очень просто. Вернемся к нашей функции:
f (x) = (x − 1)(2 + x)(7 − x)
Представьте, что x — это очень большое число. Миллиард или даже триллион. Теперь посмотрим, что будет происходить в каждой скобке.
Первая скобка: (x − 1). Что будет, если из миллиарда вычесть единицу? Получится число, не особо отличающееся от миллиарда, и это число будет положительным. Аналогично со второй скобкой: (2 + x). Если к двойке прибавить миллиард, по получим миллиард с копейками — это положительное число. Наконец, третья скобка: (7 − x). Здесь будет минус миллиард, от которого «отгрызли» жалкий кусочек в виде семерки. Т.е. полученное число мало чем будет отличаться от минус миллиарда — оно будет отрицательным.
Осталось найти знак всего произведения. Поскольку в первых скобках у нас был плюс, а в последней — минус, получаем следующую конструкцию:
(+) · (+) · (−) = (−)
Итоговый знак — минус! И неважно, чему равно значение самой функции. Главное, что это значение — отрицательное, т.е. на самом правом интервале стоит знак минус. Осталось выполнить четвертый шаг метода интервалов: расставить все знаки. Имеем:
![]()
Исходное неравенство имело вид:
(x − 1)(2 + x)(7 − x) < 0
Следовательно, нас интересуют интервалы, отмеченные знаком минус. Выписываем ответ:
x ∈ (−2; 1) ∪ (7; +∞)
Вот и весь прием, который я хотел рассказать. В заключение — еще одно неравенство, которое решается методом интервалов с привлечением бесконечности. Чтобы визуально сократить решение, я не буду писать номера шагов и развернутые комментарии. Напишу только то, что действительно надо писать при решении реальных задач:
Задача. Решите неравенство:
x(2x + 8)(x − 3) > 0
Заменяем неравенство уравнением и решаем его:
x(2x + 8)(x − 3) = 0;
x = 0;
2x + 8 = 0 ⇒ x = −4;
x − 3 = 0 ⇒ x = 3.
Отмечаем все три корня на координатной прямой (сразу со знаками):
![]()
Справа на координатной оси стоит плюс, т.к. функция имеет вид:
f (x) = x(2x + 8)(x − 3)
А если подставить бесконечность (например, миллиард), получим три положительных скобки. Поскольку исходное выражение должно быть больше нуля, нас интересуют только плюсы. Осталось выписать ответ:
x ∈ (−4; 0) ∪ (3; +∞)
Смотрите также:
- Метод интервалов: случай нестрогих неравенств

- Тест по методу интервалов для строгих неравенств

- Сводный тест по задачам B12 (2 вариант)

- Профильный ЕГЭ-2022, задание 6. Геометрический смысл производной

- Формулы приведения: ускоряем вычисления в тригонометрии

- Задачи B4: перевозка груза тремя фирмами

Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.
Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.
Стандартное отклонение обозначается буквой σ (греческая буква сигма).
Стандартное отклонение также называется:
- среднеквадратическое отклонение,
- среднее квадратическое отклонение,
- среднеквадратичное отклонение,
- квадратичное отклонение,
- стандартный разброс.
Использование и интерпретация величины среднеквадратического отклонения
Стандартное отклонение используется:
- в финансах в качестве меры волатильности,
- в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.
Пример:
Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.
| День 1 | День 2 | День 3 | День 4 | |
|---|---|---|---|---|
| Пред.А | 19 | 21 | 19 | 21 |
| Пред.Б | 15 | 26 | 15 | 24 |
В обеих компаниях среднее количество товара составляет 20 единиц:
- А -> (19 + 21 + 19+ 21) / 4 = 20
- Б -> (15 + 26 + 15+ 24) / 4 = 20
Однако, глядя на цифры, можно заметить:
- в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
- в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).
Если рассчитать стандартное отклонение каждой компании, оно покажет, что
- стандартное отклонение компании A = 1,
- стандартное отклонение компании Б ≈ 5.
Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).
Расчет среднеквадратичного (стандартного) отклонения
Формулы вычисления стандартного отклонения

σ — стандартное отклонение,
xi — величина отдельного значения выборки,
μ — среднее арифметическое выборки,
n — размер выборки.
Эта формула применяется, когда анализируются все значения выборки.

S — стандартное отклонение,
n — размер выборки,
xi — величина отдельного значения выборки,
xср — среднее арифметическое выборки.
Эта формула применяется, когда присутствует очень большой размер выборки, поэтому на анализ обычно берётся только её часть.
Единственная разница с предыдущей формулой: “n — 1” вместо “n”, и обозначение “xср” вместо “μ”.
Разница между формулами S и σ (“n” и “n–1”)
Состоит в том, что мы анализируем — всю выборку или только её часть:
- только её часть – используется формула S (с “n–1”),
- полностью все данные – используется формула σ (с “n”).
Как рассчитать стандартное отклонение?
Пример 1 (с σ)
Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.
| День 1 | День 2 | День 3 | День 4 | |
| Пред.Б | 15 | 26 | 15 | 24 |
Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:

Применяем эти шаги:
1. Найти среднее арифметическое выборки:
μ = (15 + 26 + 15+ 24) / 4 = 20
2. От каждого значения выборки отнять среднее арифметическое:
x1 – μ = 15 – 20 = -5
x2 – μ = 26 – 20 = 6
x3 – μ = 15 – 20 = -5
x4 – μ = 24 – 20 = 4
3. Каждую полученную разницу возвести в квадрат:
(x1 – μ)² = (-5)² = 25
(x2 – μ)² = 6² = 36
(x3 – μ)² = (-5)² = 25
(x4 – μ)² = 4² = 16
4. Сделать сумму полученных значений:
Σ (xi – μ)² = 25 + 36+ 25+ 16 = 102
5. Поделить на размер выборки (т.е. на n):
(Σ (xi – μ)²)/n = 102 / 4 = 25,5
6. Найти квадратный корень:
√((Σ (xi – μ)²)/n) = √ 25,5 ≈ 5,0498
Пример 2 (с S)
Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.
У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.
Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.
| Яблоня 1 | Яблоня 2 | Яблоня 3 | Яблоня 4 | Яблоня 5 | Яблоня 6 |
| 9 | 2 | 5 | 4 | 12 | 7 |
Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:

Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.
Применяем практически те же шаги:
1. Найти среднее арифметическое выборки:
Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5
2. От каждого значения выборки отнять среднее арифметическое:
X1 – Xср = 9 – 6,5 = 2,5
X2 – Xср = 2 – 6,5 = –4,5
X3 – Xср = 5 – 6,5 = –1,5
X4 – Xср = 4 – 6,5 = –2,5
X5 – Xср = 12 – 6,5 = 5,5
X6 – Xср = 7 – 6,5 = 0,5
3. Каждую полученную разницу возвести в квадрат:
(X1 – Xср)² = (2,5)² = 6,25
(X2 – Xср)² = (–4,5)² = 20,25
(X3 – Xср)² = (–1,5)² = 2,25
(X4 – Xср)² = (–2,5)² = 6,25
(X5 – Xср)² = 5,5² = 30,25
(X6 – Xср)² = 0,5² = 0,25
4. Сделать сумму полученных значений:
Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5
5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):
(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1
6. Найти квадратный корень:
S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193
Дисперсия и стандартное отклонение
Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).
Дисперсия — в статистике это “среднее квадратов отклонений от среднего”. Чтобы её вычислить нужно:
- Вычесть среднее значение из каждого числа
- Возвести каждый результат в квадрат (так получатся квадраты разностей)
- Найти среднее значение квадратов разностей.
Ещё расчёт дисперсии можно сделать по этой формуле:

S² — выборочная дисперсия,
Xi — величина отдельного значения выборки,
Xср (может появляться как X̅) — среднее арифметическое выборки,
n — размер выборки.
Правило трёх сигм
Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.

Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:
- одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
- двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
- трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).
Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.
Стандартное отклонение в excel
Вычисление стандартного отклонения с “n – 1” в знаменателе (случай выборки из генеральной совокупности):
1. Занесите все данные в документ Excel.

2. Выберите поле, в котором вы хотите отобразить результат.
3. Введите в этом поле “=СТАНДОТКЛОНА(“
4. Выделите поля, где находятся данные, потом закройте скобки.

5. Нажмите Ввод (Enter).

В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.


Коэффициент вариации
Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.
Стандартное отклонение делится на среднее и умножается на 100%.
Можно классифицировать вариабельность выборки по коэффициенту вариации:
- при <10% выборка слабо вариабельна,
- при 10% – 20 % — средне вариабельна,
- при >20 % — выборка сильно вариабельна.
Узнайте также про:
- Корреляции,
- Метод Крамера,
- Метод наименьших квадратов,
- Теорию вероятностей
- Интегралы.
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
|
Единая УКАЗАНИЕ Unified system for design documentation. Representation of limits of |
ГОСТ (CT Взамен |
Постановлением Государственного комитета СССР по стандартам от 4 января
1979 г. № 31 срок введения установлен
с 01.01.80
Настоящий стандарт
устанавливает правила указания допусков формы и расположения поверхностей на
чертежах изделий всех отраслей промышленности.
Термины и
определения допусков формы и расположения поверхностей – по ГОСТ 24642-81.
Числовые
значения допусков формы и расположения поверхностей – по ГОСТ 24643-81.
Стандарт
полностью соответствует СТ СЭВ 368-76.
(Измененная
редакция, Изм. № 1).
1. ОБЩИЕ ТРЕБОВАНИЯ
1.1. Допуски
формы и расположения поверхностей указывают на чертежах условными
обозначениями.
Вид допуска формы и расположения поверхностей должен быть обозначен на
чертеже знаками (графическими символами), приведенными в таблице.
|
Группа |
Вид |
Знак |
|
Допуск формы |
Допуск |
|
|
Допуск плоскостности |
|
|
|
Допуск круглости |
|
|
|
Допуск |
|
|
|
Допуск профиля |
|
|
|
Допуск расположения |
Допуск |
|
|
Допуск |
|
|
|
Допуск наклона |
|
|
|
Допуск соосности |
|
|
|
Допуск |
|
|
|
Позиционный допуск |
|
|
|
Допуск пересечения, |
|
|
|
Суммарные допуски формы и расположения |
Допуск радиального Допуск торцового Допуск биения в |
|
|
Допуск полного Допуск полного торцового |
|
|
|
Допуск формы |
|
|
|
Допуск формы |
|
Формы
и размеры знаков приведены в обязательном приложении 1.
Примеры указания
на чертежах допусков формы и расположения поверхностей приведены в справочном
приложении 2.
Примечание . Суммарные допуски формы и расположения поверхностей, для которых не
установлены отдельные графические знаки, обозначают знаками составных допусков
в следующей последовательности: знак допуска расположения, знак допуска формы.
Например:
![]() – знак суммарного допуска параллельности и
– знак суммарного допуска параллельности и
плоскостности;
![]() – знак суммарного допуска перпендикулярности и плоскостности;
– знак суммарного допуска перпендикулярности и плоскостности;
![]() – знак суммарного допуска наклона и плоскостности.
– знак суммарного допуска наклона и плоскостности.
1.2. Допуск
формы и расположения поверхностей допускается указывать текстом в технических
требованиях, как правило, в том случае, если отсутствует знак вида допуска.
1.3. При указании
допуска формы и расположения поверхностей в технических требованиях текст
должен содержать:
вид допуска;
указание
поверхности или другого элемента, для которого задается допуск (для этого
используют буквенное обозначение или конструктивное наименование, определяющее
поверхность);
числовое
значение допуска в миллиметрах;
указание баз,
относительно которых задается допуск (для допусков расположения и суммарных
допусков формы и расположения);
указание о
зависимых допусках формы или расположения (в соответствующих случаях).
1.4. При
необходимости нормирования допусков формы и расположения, не указанных на
чертеже числовыми значениями и не ограничиваемых другими указанными в чертеже
допусками формы и расположения, в технических требованиях чертежа должна быть
приведена общая запись о неуказанных допусках формы и расположения со ссылкой
на ГОСТ 25069-81 или другие документы, устанавливающие неуказанные допуски
формы и расположения.
Например: 1.
Неуказанные допуски формы и расположения – по ГОСТ 25069-81.
2. Неуказанные
допуски соосности и симметричности – по ГОСТ 25069-81.
(Введен
дополнительно, Изм. № 1).
2. НАНЕСЕНИЕ ОБОЗНАЧЕНИЙ ДОПУСКОВ
2.1. При
условном обозначении данные о допусках формы и расположения поверхностей
указывают в прямоугольной рамке, разделенной на две и более части (черт. 1, 2), в
которых помещают:
в первой – знак
допуска по таблице;
во второй –
числовое значение допуска в миллиметрах;
в третьей и
последующих – буквенное обозначение базы (баз) или буквенное обозначение
поверхности, с которой связан допуск расположения (пп. 3.7; 3.9).
![]()
Черт. 1
![]()
Черт.
2
2.2. Рамки
следует выполнять сплошными тонкими линиями. Высота цифр, букв и знаков,
вписываемых в рамки, должна быть равна размеру шрифта размерных чисел.
Графическое
изображение рамки приведено в обязательном приложении 1.
2.3. Рамку
располагают горизонтально. В необходимых случаях допускается вертикальное
расположение рамки.
Не допускается
пересекать рамку какими-либо линиями.
2.4. Рамку
соединяют с элементом, к которому относится допуск, сплошной тонкой линией,
заканчивающейся стрелкой (черт. 3).
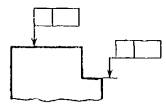
Черт.
3
Соединительная
линия может быть прямой или ломаной, но направление отрезка соединительной
линии, заканчивающегося стрелкой, должно соответствовать направлению измерения
отклонения. Соединительную линию отводят от рамки, как показано на черт. 4.
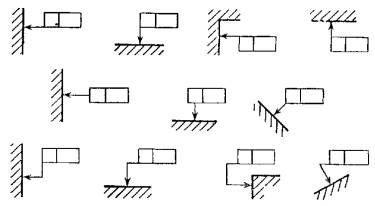
Черт.
4
В необходимых
случаях допускается:
проводить
соединительную линию от второй (последней) части рамки (черт. 5а);
заканчивать
соединительную линию стрелкой и со стороны материала детали (черт. 5б).
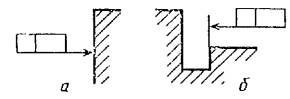
Черт.
5
2.5. Если
допуск относится к поверхности или ее профилю, то рамку соединяют с контурной
линией поверхности или ее продолжением, при этом соединительная линия не должна
быть продолжением размерной линии (черт. 6, 7).
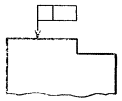
Черт. 6
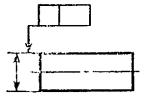
Черт.
7
2.6. Если
допуск относится к оси или плоскости симметрии, то соединительная линия должна
быть продолжением размерной линии (черт. 8а, б). При недостатке
места стрелку размерной линии допускается совмещать со стрелкой соединительной
линии (черт. 8в).
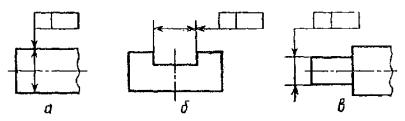
Черт.
8
Если размер элемента уже указан один раз, то
на других размерных линиях данного элемента, используемых для условного
обозначения допуска формы и расположения, его не указывают. Размерную линию без
размера следует рассматривать как составную часть условного обозначения допуска
формы или расположения (черт. 9).
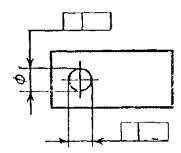
Черт. 9
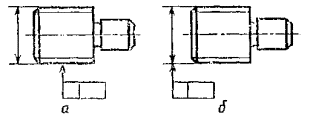
Черт.
10
2.7. Если
допуск относится к боковым сторонам резьбы, то рамку соединяют с изображением в
соответствии с черт. 10а.
Если допуск относится
к оси резьбы, то рамку соединяют с изображением в соответствии с черт. 10б.
2.8. Если
допуск относится к общей оси (плоскости симметрии) и из чертежа ясно, для каких
поверхностей данная ось (плоскость симметрии) является общей, то рамку
соединяют с осью (плоскостью симметрии) (черт. 11а,
б).
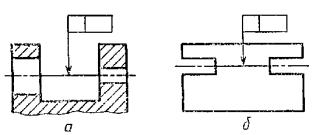
Черт.
11
2.9. Перед
числовым значением допуска следует указывать:
символ Æ , если круговое или цилиндрическое
поле допуска указывают диаметром (черт. 12а);
символ R ,
если
круговое или цилиндрическое поле допуска указывают радиусом (черт. 12б);
символ Т, если
допуски симметричности, пересечения осей, формы заданного профиля и заданной
поверхности, а также позиционные допуски (для случая, когда поле позиционного
допуска ограничено двумя параллельными прямыми или плоскостями) указывают в
диаметральном выражении (черт. 12в);
символ Т/2 для
тех же видов допусков, если их указывают в радиусном выражении (черт. 12г);
слово «сфера» и
символы Æ или R ,
если поле допуска сферическое (черт. 12д).
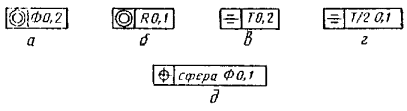
Черт.
12
2.10. Числовое
значение допуска формы и расположения поверхностей, указанное в рамке (черт. 13а),
относится ко всей длине поверхности. Если допуск относится к любому участку
поверхности заданной длины (или площади), то заданную длину (или площадь)
указывают рядом с допуском и отделяют от него наклонной линией (черт. 13 б,
в), которая не должна касаться рамки.
Если необходимо
назначить допуск на всей длине поверхности и на заданной длине, то допуск на
заданной длине указывают под допуском на всей длине (черт. 13г).

Черт.
13
(Измененная
редакция, Изм. № 1).
2.11. Если
допуск должен относиться к участку, расположенному в определенном месте
элемента, то этот участок обозначают штрихпунктирной линией и ограничивают
размерами согласно черт. 14.
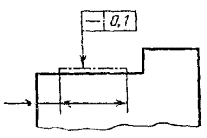
Черт.
14
2.12. Если
необходимо задать выступающее поле допуска расположения, то после числового
значения допуска указывают символ ![]()
Контур
выступающей части нормируемого элемента ограничивают тонкой сплошной линией, а
длину и расположение выступающего поля допуска – размерами (черт. 15).
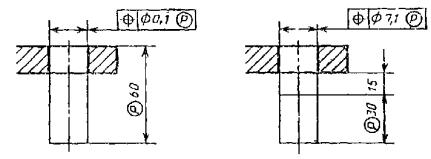
Черт.
15
2.13. Надписи,
дополняющие данные, приведенные в рамке допуска, следует наносить над рамкой под
ней или как показано на черт. 16.
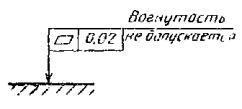
Черт.
16
(Измененная
редакция, Изм. № 1).
2.14. Если для
одного элемента необходимо задать два разных вида допуска, то допускается рамки
объединять и располагать их согласно черт. 17 (верхнее обозначение).
Если для
поверхности требуется указать одновременно условное обозначение допуска формы
или расположения и ее буквенное обозначение, используемое для нормирования
другого допуска, то рамки с обоими условными обозначениями допускается
располагать рядом на соединительной линии (черт. 17, нижнее обозначение).
2.15.
Повторяющиеся одинаковые или разные виды допусков, обозначаемые одним и тем же
знаком, имеющие одинаковые числовые значения и относящиеся к одним и тем же
базам, допускается указывать один раз в рамке, от которой отходит одна
соединительная линия, разветвляемая затем ко всем нормируемым элементам (черт. 18).
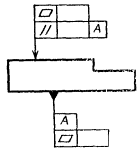
Черт. 17
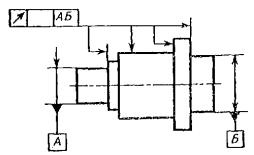
Черт.
18
2.16. Допуски
формы и расположения симметрично расположенных элементов на симметричных
деталях указывают один раз.
3. ОБОЗНАЧЕНИЕ БАЗ
3.1. Базы обозначают
зачерненным треугольником, который соединяют при помощи соединительной линии с
рамкой. При выполнении чертежей с помощью выводных устройств ЭВМ допускается
треугольник, обозначающий базу, не зачернять.
Треугольник,
обозначающий базу, должен быть равносторонним, высотой приблизительно равной
размеру шрифта размерных чисел.
3.2. Если базой
является поверхность или ее профиль, то основание треугольника располагают на
контурной линии поверхности (черт. 19а) или на ее
продолжении (черт. 19б). При этом соединительная линия не
должна быть продолжением размерной линии.
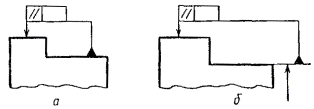
Черт.
19
3.3. Если базой
является ось или плоскость симметрии, то треугольник располагают на конце
размерной линии (черт. 18).
В случае
недостатка места стрелку размерной линии допускается заменять треугольником,
обозначающим базу (черт. 20).
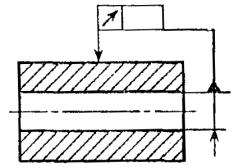
Черт.
20
Если базой
является общая ось (черт. 21а) или плоскость симметрии (черт. 21б)
и из чертежа ясно, для каких поверхностей ось (плоскость симметрии) является
общей, то треугольник располагают на оси.
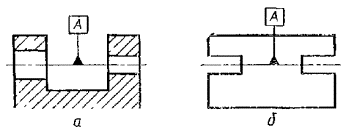
Черт.
21
(Измененная
редакция, Изм. № 1).
3.4. Если базой
является ось центровых отверстий, то рядом с обозначением базовой оси делают надпись
«Ось центров» (черт. 22).
Допускается
обозначать базовую ось центровых отверстий в соответствии с черт. 23.
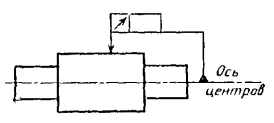
Черт. 22
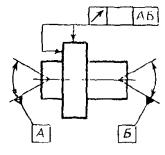
Черт.
23
3.5. Если базой
является определенная часть элемента, то ее обозначают штрихпунктирной линией и
ограничивают размерами в соответствии с черт. 24.
Если базой
является определенное место элемента, то оно должно быть определено размерами
согласно черт. 25.
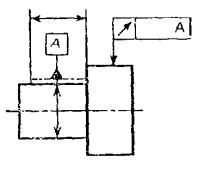
Черт. 24
Черт.
25
3.6. Если нет
необходимости выделять как базу пи одну из поверхностей, то треугольник
заменяют стрелкой (черт. 26б).
3.7.
Если соединение рамки с базой или другой поверхностью, к которой относится
отклонение расположения, затруднительно, по поверхность обозначают прописной
буквой, вписываемой в третью часть рамки. Эту же букву вписывают в рамку,
которую соединяют с обозначаемой поверхностью линией, закапчивающейся
треугольником, если обозначают базу (черт. 27 а ), или стрелкой, если обозначаемая поверхность не является базой (черт.
27 б ). При этом букву следует располагать параллельно основной надписи.
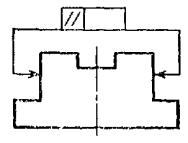
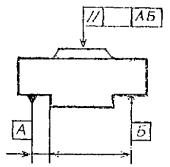
Черт. 26
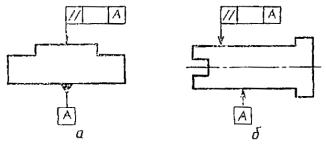
Черт.
27
3.8. Если
размер элемента уже указан один раз, то на других размерных линиях данного
элемента, используемых для условного обозначения базы, его не указывают. Размерную
линию без размера следует рассматривать как составную часть условного
обозначения базы (черт. 28).
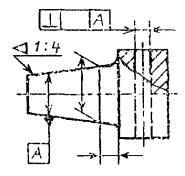
Черт.
28
3.9.
Если два или несколько элементов образуют объединенную базу и их
последовательность не имеет значения (например, они имеют общую ось или
плоскость симметрии), то каждый элемент обозначают самостоятельно и все буквы
вписывают подряд в третью часть рамки (черт. 25 , 29 ).
3.10. Если
необходимо задать допуск расположения относительно комплекта баз, то буквенные
обозначения баз указывают в самостоятельных частях (третьей и далее) рамки. В
этом случае базы записывают в порядке убывания числа степеней свободы, лишаемых
ими (черт. 30).
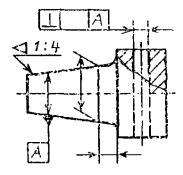
Черт. 29
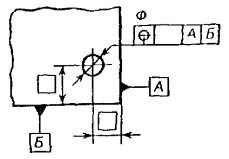
Черт. 30
4. УКАЗАНИЕ НОМИНАЛЬНОГО РАСПОЛОЖЕНИЯ
4.1. Линейные и
угловые размеры, определяющие номинальное расположение и (или) номинальную форму
элементов, ограничиваемых допуском, при назначении позиционного допуска,
допуска наклона, допуска формы заданной поверхности или заданного профиля,
указывают на чертежах без предельных отклонений и заключают в прямоугольные
рамки (черт. 31).
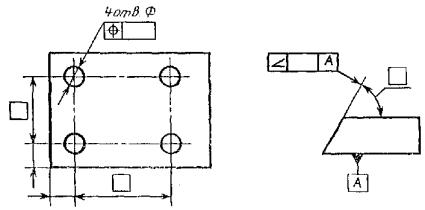
Черт. 31
5. ОБОЗНАЧЕНИЕ ЗАВИСИМЫХ ДОПУСКОВ
5.1. Зависимые
допуски формы и расположения обозначают условным знаком ![]() , который
, который
помещают:
после числового
значения допуска, если зависимый допуск связан с действительными размерами
рассматриваемого элемента (черт. 32а);
после
буквенного обозначения базы (черт. 32б) или без буквенного
обозначения в третьей части рамки (черт. 32г), если
зависимый допуск связан с действительными размерами базового элемента;
после числового
значения допуска и буквенного обозначения базы (черт. 32в) или без буквенного
обозначения (черт. 32д), если зависимый допуск связан с
действительными размерами рассматриваемого и базового элементов.
5.2. Если
допуск расположения или формы не указан как зависимый, то его считают
независимым.
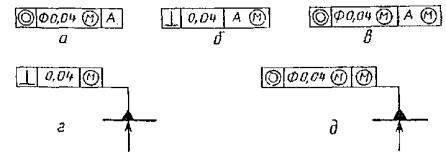
Черт. 32
ПРИЛОЖЕНИЕ 1
Обязательное
ФОРМА
И РАЗМЕРЫ ЗНАКОВ
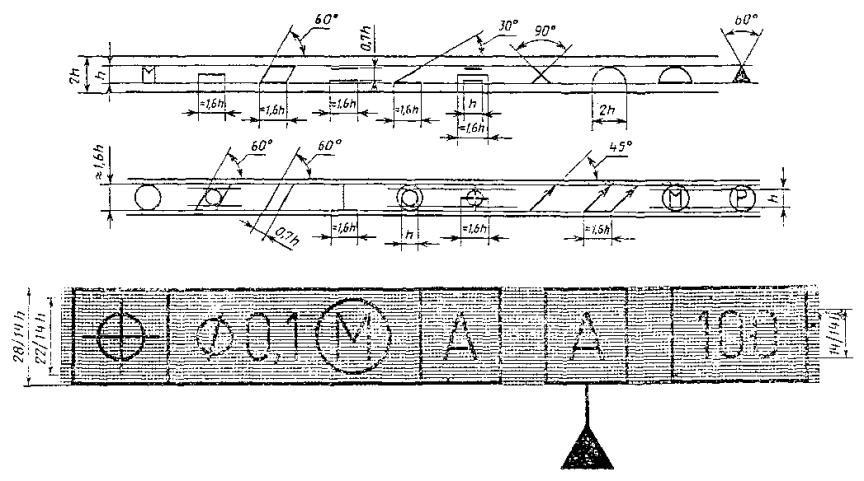
ПРИЛОЖЕНИЕ 2
Справочное
ПРИМЕРЫ УКАЗАНИЯ НА ЧЕРТЕЖАХ ДОПУСКОВ ФОРМЫ И
РАСПОЛОЖЕНИЯ ПОВЕРХНОСТЕЙ
|
Вид |
Указания |
Пояснение |
|
1. Допуск |
|
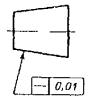
Допуск прямолинейности образующей конуса |
|
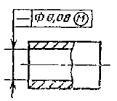
|
Допуск прямолинейности оси отверстия Æ 0,08 мм |
|
|
|
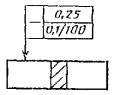
Допуск прямолинейности поверхности 0,25 мм |
|
|
|
Допуск прямолинейности поверхности в |
|
|
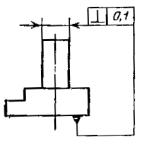
2. Допуск |
|
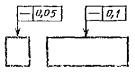
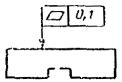
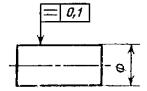
Допуск плоскостности поверхности 0,1 мм. |
|
|
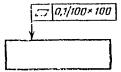
Допуск плоскостности поверхности 0,1 мм на |
|
|
|
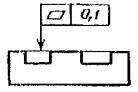
Допуск плоскостности поверхностей |
|
|
|
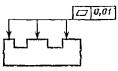
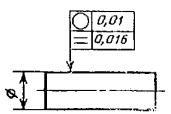
Допуск плоскостности каждой поверхности 0,01 |
|
|
3. Допуск круглости |
|
Допуск круглости вала 0,02 мм. |
|
|
Допуск круглости конуса 0,02 мм. |
|
|
4. Допуск цилиндричности |
|
Допуск цилиндричности вала 0,04 мм. |
|
|
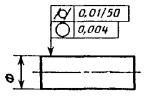
Допуск цилиндричности вала 0,01 мм на длине 50 |
|
|
5. Допуск профиля продольного сечения |
|
Допуск круглости вала 0,01 мм. Допуск профиля продольного сечения вала |
|
|
Допуск профиля продольного сечения вала 0,1 |
|
|
6. Допуск параллельности |
|
Допуск параллельности поверхности |
|
|
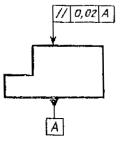
Допуск параллельности общей прилегающей |
|
|
|
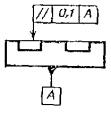
Допуск параллельности каждой поверхности |
|
|
|
Допуск параллельности оси отверстия |
|
|
|
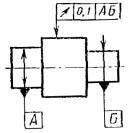
Допуск параллельности осей отверстий в общей Допуск перекоса осей отверстий 0,2 мм. База – ось отверстия А. |
|
|
|
Допуск параллельности оси отверстия |
|
|
7. Допуск перпендикулярности |
|
Допуск перпендикулярности поверхности |
|
|
Допуск перпендикулярности оси отверстия относительно |
|
|
|
Допуск перпендикулярности оси выступа |
|
|
|
Допуск перпендикулярности осп выступа |
|
|
|
Допуск перпендикулярности оси выступа в поперечном База – основание |
|
|
|
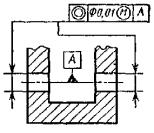
Допуск перпендикулярности оси отверстия |
|
|
8. Допуск наклона |
|
Допуск наклона поверхности относительно поверхности |
|
|
Допуск наклона оси отверстия относительно |
|
|
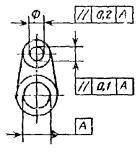
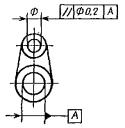
9. Допуск соосности |
|
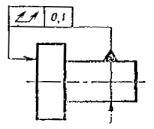
Допуск соосности отверстия относительно |
|
|
Допуск соосности двух отверстий относительно |
|
|
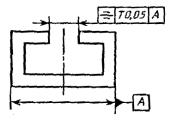
10. Допуск симметричности |
|
Допуск симметричности паза Т 0,05 мм. База – плоскость симметрии поверхностей А |
|
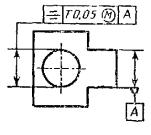
|
Допуск симметричности отверстия Т 0,05 База – плоскость симметрии поверхности А. |
|
|
|
Допуск симметричности осп отверстия |
|
|
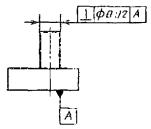
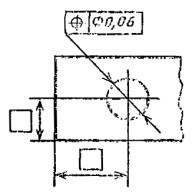
11. Позиционный допуск |
|
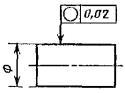
Позиционный допуск оси отверстия Æ 9,06 мм. |
|
|
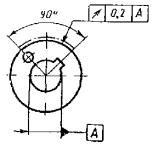
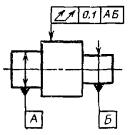
Позиционный допуск осей отверстий Æ 0,2 мм |
|
|
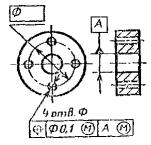
|
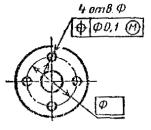
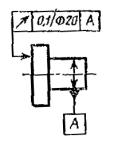
Позиционный допуск осей 4-х отверстий Æ 0,1 мм База – ось отверстия А (допуск |
|
|
|
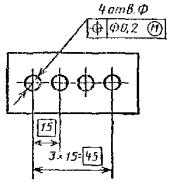
Позиционный допуск 4-х отверстий Æ 0,1 мм |
|
|
|
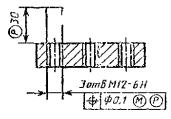
Позиционный допуск 3-х резьбовых отверстий Æ 0,1 мм |
|
|
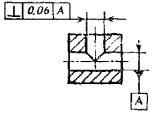
12. Допуск пересечения осей |
|
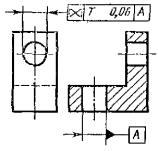
Допуск пересечения осей отверстий Т 0,06 |
|
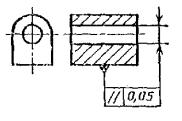
13. Допуск радиального биения |
|
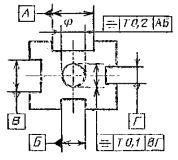
Допуск радиального биения вала относительно |
|
|
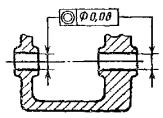
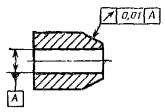
Допуск радиального биения поверхности |
|
|
|
Допуск радиального биения участка поверхности |
|
|
|
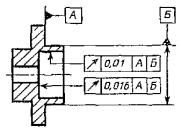
Допуск радиального биения отверстия 0,01 мм Первая база – поверхность Л. Вторая Допуск торцового биения относительно тех же |
|
|
14. Допуск торцового биения |
|
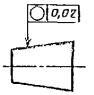
Допуск торцового биения на диаметре 20 мм |
|
15. Допуск биения в заданном направлении |
|
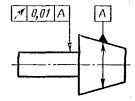
Допуск биения конуса относительно оси |
|
16. Допуск полного радиального биения |
|
Допуск полного радиального биения |
|
17. Допуск полного торцового биения |
|
Допуск полного торцового биения поверхности |
|
18. Допуск формы заданного профиля |
|
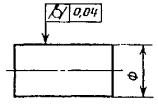
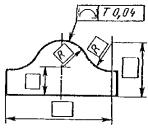
Допуск формы заданного профиля Т 0,04 |
|
19. Допуск формы заданной поверхности |
|
Допуск формы заданной поверхности |
|
20. Суммарный допуск параллельности и плоскостности |
|
Суммарный допуск параллельности и |
|
21. Суммарный допуск перпендикулярности и |
|
Суммарный допуск перпендикулярности и плоскостности |
|
22. Суммарный допуск наклона и плоскостности |
|
Суммарный допуск наклона и плоскостности |
Примечания:
1. В приведенных примерах допуски
соосности, симметричности, позиционные, пересечения осей, формы заданного
профиля и заданной поверхности указаны в диаметральном выражении.
Допускается указывать их в
радиусном выражении, например:
![]()
В ранее выпущенной
документации допуски соосности, симметричности, смещения осей от номинального
расположения (позиционного допуска), обозначенные соответственно знаками ![]() или текстом в технических требованиях,
или текстом в технических требованиях,
следует понимать как допуски в радиусном выражении.
2.
Указание допусков формы и расположения поверхностей в текстовых документах или
в технических требованиях чертежа следует приводить по аналогии с текстом
пояснении к условным обозначениям допусков формы и расположения, приведенным в
настоящем приложении.
При этом поверхности, к которым
относятся допуски формы и расположения или которые приняты за базу, следует
обозначать буквами или проводить их конструкторские наименования.
Допускается вместо слов «допуск
зависимый» указывать знак ![]() и
и
вместо указаний перед числовым значением символов Æ ; R ; Т; Т/2 запись
текстом, например, «позиционный допуск оси 0,1 мм в диаметральном выражении»
или «допуск симметричности 0,12 мм в радиусном выражении».
3. Во вновь разрабатываемой
документации запись в технических требованиях о допусках овальности,
конусообразности, бочкообразности и седлообразности должна быть, например,
следующей: «Допуск овальности поверхности А 0,2 мм (полуразность
диаметров).
В технической документации,
разработанной до 01.01.80, предельные значения овальности, конусообразности,
бочкообразности и седлообразности определяют как разность наибольшего и
наименьшего диаметров.
(Измененная редакция, Изм. № 1).
СОДЕРЖАНИЕ
1. Общие требования . 1
2. Нанесение обозначений допусков . 2
3. Обозначение баз . 6
4. Указание номинального расположения . 9
5. Обозначение зависимых допусков . 9
Приложение 1. Форма и
размеры знаков . 10
Приложение 2. Примеры
указания на чертежах допусков формы и расположения поверхностей . 11