Геометрической прогрессией называют числовую последовательность, каждый следующий член которой получается из предыдущего умножением его на постоянное число, не равное нулю.
Это число называют знаменателем геометрической прогрессии и обозначают буквой (q).
Например, последовательность (3); (6); (12); (24); (48)… является геометрической прогрессией, потому что каждый следующий элемент отличается от предыдущего в два раза (иначе говоря, может быть получен из предыдущего умножением его на два):

Как и любую последовательность, геометрическую прогрессию обозначают маленькой латинской буквой. Числа, образующие прогрессию, называют ее членами (или элементами). Их обозначают той же буквой, что и геометрическую прогрессию, но с числовым индексом, равным номеру элемента по порядку.
Например, геометрическая прогрессия (b_n = {3; 6; 12; 24; 48…}) состоит из элементов (b_1=3); (b_2=6); (b_3=12) и так далее. Иными словами:
|
порядковый номер элемента |
(1) |
(2) |
(3) |
(4) |
(5) |
… |
|
обозначение элемента |
(b_1) |
(b_2) |
(b_3) |
(b_4) |
(b_5) |
… |
|
значение элемента |
(3) |
(6) |
(12) |
(24) |
(48) |
… |
Если вы поняли вышеизложенную информацию, то уже сможете решить большинство задач на эту тему.
Пример (ОГЭ): Геометрическая прогрессия задана условиями (b_1=-2); (q=7). Найдите (b_4).
Решение:
|
|
Зная первый член и знаменатель, последовательно вычисляем элементы, пока не дойдем до нужного. |
|
|
Можно писать ответ. |
Ответ: (-686).
Пример (ОГЭ): Даны первые три члена прогрессии (324); (-108); (36)…. Найдите (b_5).
Решение:
|
|
Чтобы продолжить последовательность, нам нужно знать знаменатель. Найдем его из двух соседних элементов: на что нужно умножить (324), чтоб получилось (-108)? |
|
(324·q=-108) |
Отсюда без проблем вычисляем знаменатель. |
|
(q=-) (frac{108}{324})(=-) (frac{1}{3}) |
Теперь мы легко находим нужный нам элемент. |
|
|
Готов ответ. |
Ответ: (4).
Пример: Прогрессия задана условием (b_n=0,8·5^n). Какое из чисел является членом этой прогрессии:
а) (-5) б) (100) в) (25) г) (0,8) ?
Решение: Из формулировки задания очевидно, что одно из этих чисел точно есть в нашей прогрессии. Поэтому мы можем просто вычислять ее члены по очереди, пока не найдем нужное нам значение. Так как у нас прогрессия задана формулой n-го члена, то вычисляем значения элементов, подставляя разные (n):
(n=1); (b_1=0,8·5^1=0,8·5=4) – такого числа в списке нет. Продолжаем.
(n=2); (b_2=0,8·5^2=0,8·25=20) – и этого тоже нет.
(n=3); (b_3=0,8·5^3=0,8·125=100) – а вот и наш чемпион!
Ответ: (100).
Пример (ОГЭ): Даны несколько идущих последовательно друг за другом членов геометрической прогрессии …(8); (x); (50); (-125)…. Найдите значение элемента, обозначенного буквой (x).
Решение:
|
|
Найти (x), можно, например, умножив (8) на знаменатель прогрессии. Однако мы его не знаем, поэтому сначала найдем знаменатель из двух известных соседних членов. |
|
(50·q=-125) |
|
|
(q=-) (frac{125}{50})(=-)(2,5) |
Теперь вычисляем икс, умножая (8) на (-2,5). |
|
|
Задача решена. |
Ответ: (-20).
Пример (ОГЭ): Прогрессия задана условиями (b_1=7), (b_{n+1}=2b_n). Найдите сумму первых (4) членов этой прогрессии.
Решение:
|
(b_1=7), |
Мы знаем первый элемент и имеем рекуррентное соотношение – формулу для вычисления следующего элемента по предыдущему. |
|
|
(n=1); (b_{1+1}=2b_1 :: ⇔ :: b_2=2·7=14) |
Теперь найдем сумму. |
|
|
(S_4=b_1+b_2+b_3+b_4=) |
Ответ готов. |
Ответ: (105).
Пример (ОГЭ): Известно, что в геометрической прогрессии (b_6=-11), (b_9=704). Найдите знаменатель (q).
Решение:
|
|
Из схемы слева видно, что чтобы «попасть» из (b_6) в (b_9) – мы делаем три «шага», то есть три раза умножаем (b_6) на знаменатель прогрессии. Иными словами (b_9=b_6·q·q·q=b_6·q^3). |
|
(b_9=b_6·q^3) |
Подставим известные нам значения. |
|
(704=(-11)·q^3) |
«Перевернем» уравнение и разделим его на ((-11)). |
|
(q^3=) (frac{704}{-11})(::: ⇔ ::: )(q^3=-) (64) |
Какое число в кубе даст (-64)? |
|
(q=-4) |
Ответ найден. Его можно проверить, восстановив цепочку чисел от (-11) до (704). |
|
|
Все сошлось – ответ верен. |
Ответ: (-4).
Важнейшие формулы
Как видите, большинство задач на геометрическую прогрессию можно решать чистой логикой, просто понимая суть (это вообще характерно для математики). Но иногда знание некоторых формул и закономерностей ускоряет и существенно облегчает решение. Мы изучим две такие формулы.
Формула (n)-го члена: (b_n=b_1·q^{n-1}), где (b_1) – первый член прогрессии; (n) – номер искомого элемента; (q) – знаменатель прогрессии; (b_n) – член прогрессии с номером (n).
С помощью этой формулы можно, например, решить задачу из самого первого примера буквально в одно действие.
Пример (ОГЭ): Геометрическая прогрессия задана условиями (b_1=-2); (q=7). Найдите (b_4).
Решение:
|
(b_4=b_1·q^3) |
Нам нужен четвертый член, вот и вычисляем его сразу, напрямую, не находя всех промежуточных. |
|
|
(b_4=(-2)·7^3=(-2)·343=-686). |
Готов. |
Ответ: (-686).
Этот пример был простым, поэтому формула нам облегчила вычисления не слишком сильно. Давайте разберем задачку чуть посложнее.
Пример: Геометрическая прогрессия задана условиями (b_1=20480); (q=frac{1}{2}). Найдите (b_{12}).
Решение:
|
(b_{12}=b_1·q^{11}) |
Действуем как в предыдущей задаче. |
|
|
(b_4=20480·(frac{1}{2})^{11}=20480·frac{1}{2048}=10.) |
Есть ответ. |
Ответ: (10).
Конечно, возводить (frac{1}{2}) в (11)-ую степень не слишком радостно, но всё же проще чем (11) раз делить (20480) на два.
Сумма (n) первых членов: (S_n=)( frac{b_1·(q^n-1)}{q-1}), где (b_1) – первый член прогрессии; (n) – количество суммируемых элементов; (q) – знаменатель прогрессии; (S_n) – сумма (n) первых членов прогрессии.
Пример (ОГЭ): Дана геометрическая прогрессия (b_n), знаменатель которой равен (5), а первый член (b_1=frac{2}{5}). Найдите сумму первых шести членов этой прогрессии.
Решение:
|
(S_6=)( frac{b_1·(q^6-1)}{q-1}) |
Все данные есть, сразу вычисляем ответ. |
|
(S_6=)( frac{frac{2}{5}·(5^6-1)}{5-1})(=)( frac{frac{2}{5}·15624}{4})(=) |
Ответ готов. |
Ответ: (1562,4).
И вновь мы могли решить задачу «в лоб» – найти по очереди все шесть элементов, а затем сложить результаты. Однако количество вычислений, а значит и шанс случайной ошибки, резко возросли бы.
Для геометрической прогрессии есть еще несколько формул, которые мы не стали рассматривать тут из-за их низкой практической пользы. Вы можете найти эти формулы здесь.
Возрастающие и убывающие геометрические прогрессии
У рассмотренной в самом начале статьи прогрессии (b_n = {3; 6; 12; 24; 48…}) знаменатель (q) больше единицы и поэтому каждый следующий член больше предыдущего. Такие прогрессии называются возрастающими.
Если же (q) меньше единицы, но при этом положителен (то есть, лежит в пределах от нуля до единицы), то каждый следующий элемент будет меньше чем предыдущий. Например, в прогрессии (4); (2); (1); (0,5); (0,25)… знаменатель (q) равен (frac{1}{2}).

Эти прогрессии называются убывающими. Обратите внимание, что ни один из элементов такой прогрессии не будет отрицателен, они просто становятся всё меньше и меньше с каждым шагом. То есть, мы будем постепенно приближаться к нулю, но никогда его не достигнем и за него не перейдем. Математики в таких случаях говорят «стремиться к нулю».
Отметим, что при отрицательном знаменателе элементы геометрической прогрессии будут обязательно менять знак. Например, у прогрессии (5); (-15); (45); (-135); (675)… знаменатель (q) равен (-3), и из-за этого знаки элементов «мигают».

Смотрите также:
Числовая последовательность
Арифметическая прогрессия
Формулы геометрической прогрессии с примерами
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 декабря 2022 года; проверки требуют 37 правок.
У этого термина существуют и другие значения, см. Прогрессия.
Геометри́ческая прогре́ссия — последовательность чисел 





Геометрическая прогрессия называется бесконечно убывающей[2], если знаменатель прогрессии по абсолютной величине меньше единицы.
Произведением первых 



Обозначение: 
Описание[править | править код]
Любой член геометрической прогрессии может быть вычислен по формуле
Если 




Своё название прогрессия получила по своему характеристическому свойству:
то есть модуль любого члена геометрической прогрессии, кроме первого, равен среднему геометрическому (среднему пропорциональному) двух рядом с ним стоящих членов[4].
Примеры[править | править код]

Получение новых квадратов путём соединения середин сторон предыдущих квадратов
- Последовательность площадей квадратов, где каждый следующий квадрат получается соединением середин сторон предыдущего — бесконечная геометрическая прогрессия со знаменателем 1/2. Площади получающихся на каждом шаге треугольников также образуют бесконечную геометрическую прогрессию со знаменателем 1/2, сумма которой равна площади начального квадрата[5]:8—9.
- Геометрической является последовательность количества зёрен на клетках в задаче о зёрнах на шахматной доске.
- 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192 — геометрическая прогрессия со знаменателем 2 из тринадцати членов.
- 50; 25; 12,5; 6,25; 3,125; … — бесконечно убывающая геометрическая прогрессия со знаменателем 1/2.
- 4; 6; 9 — геометрическая прогрессия из трёх элементов со знаменателем 3/2.
,
,
,
— стационарная геометрическая прогрессия со знаменателем 1 (и стационарная арифметическая прогрессия с разностью 0).
- 3; −6; 12; −24; 48; … — знакочередующаяся геометрическая прогрессия со знаменателем −2.
- 1; −1; 1; −1; 1; … — знакочередующаяся геометрическая прогрессия со знаменателем −1.
Свойства[править | править код]
Свойства знаменателя геометрической прогрессии[править | править код]
Знаменатель геометрической прогрессии можно найти по формулам:
Доказательство
По определению геометрической прогрессии.
Свойства членов геометрической прогрессии[править | править код]
- Рекуррентное соотношение для геометрической прогрессии:
Доказательство
По определению геометрической прогрессии.
- Формула общего (
-го) члена:
- Обобщённая формула общего члена:
Доказательство

- Логарифмы членов геометрической прогрессии (если определены) образуют арифметическую прогрессию.
Доказательство
Формула общего члена арифметической прогрессии:

В нашем случае


Доказательство

Пусть
— соответственно
-й,
-й,
-й члены геометрической прогрессии, где
. Тогда для всякой такой тройки выполняется комплементарное свойство геометрической прогрессии, называемое тождеством геометрической прогрессии:

- Произведение членов геометрической прогрессии начиная с k-го члена, и заканчивая n-м членом, можно рассчитать по формуле
Доказательство

- Сумма всех членов убывающей прогрессии:
-
, то
при
, и
при
.
Свойства суммы геометрической прогрессии[править | править код]
где 

Свойства произведения геометрической прогрессии[править | править код]
См. также[править | править код]
- Арифметическая прогрессия
- Арифметико-геометрическая прогрессия
- Числа Фибоначчи
- Показательная функция
- Сумма ряда
Примечания[править | править код]
- ↑ Геометрическая прогрессия Архивная копия от 12 октября 2011 на Wayback Machine на mathematics.ru
- ↑ Это название, хотя и является общепринятым, неудачно, так как бесконечно убывающая геометрическая прогрессия является убывающей, только если и первый член, и знаменатель прогрессии положительны.
- ↑ Геометрическая прогрессия // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- ↑ Если геометрическая прогрессия является конечной последовательностью, то её последний член таким свойством не обладает.
- ↑ Роу С. Геометрические упражнения с куском бумаги. — 2-е изд. — Одесса: Mathesis, 1923. Архивная копия от 19 мая 2017 на Wayback Machine
Геометрическая прогрессия
Кусочек теории.
Геометрическая прогрессия – это последовательность чисел, не равных нулю, в которой каждый следующий член, начиная со второго, в одно и то же количество раз больше (или меньше) предыдущего.
Последовательность чисел 2; 4; 8; 16; 32; 64; … будет являться геометрической прогрессией, причем возрастающей, т.к. каждое следующее число больше предыдущего в 2 раза. В данном случае число 2 является знаменателем этой прогрессии.
Также геометрической прогрессией будет являться последовательность чисел 12; 6; 3; 1,5; 0,75; 0,375; … , причем убывающей, т.к. в ней числа уменьшаются в 2 раза. Но геометрическую прогрессию прежде всего связывают с умножением, поэтому правильнее сказать, что в последовательности числа увеличиваются в 0,5 раз. Здесь знаменателем будет число 0,5.
Знаменатель геометрической прогрессии обозначают буквой q. Если знаменатель не дан, то найти его можно делением текущего члена прогрессии на предыдущий:
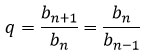
Найти любой по счету член геометрической прогрессии можно, зная ее первый член и знаменатель. Запишем формулу n-ого члена:
![]()
Но необязательно знать именно первый член прогрессии. Пригодится может любое по счету число. Только тогда формула чутка изменится:
![]()
И держи третью формулу для нахождения n-ого члена геометрической прогрессии через предыдущий и последующий члены (правда по модулю)!
![]()
Помимо этих трех формул пригодится еще формула суммы:
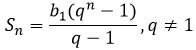
Практика.
Задание 1.

Это задание можно решить без формул. Но если уж так хочется, то можно и по формулам, но мне вот не хочется)
Откинем пока минусы…
Если разделить 125 на 100, то мы увидим во сколько раз следующее число меньше предыдущего: в 1,25 раз. То же самое число получится, если 100 разделить на 80.
Найдем 4-ое число в этой последовательности: 80 : 1,25 = 64.
И 5-ое: 64 : 1,25 = 51,2.
Но не забываем, что знаки у чисел чередуются: четвертое число будет отрицательным, а пятое – положительным.
Ответ: 51,2.
Задание 2.

Опять знаки у чисел чередуются, значит число, спрятанное под иксом, будет отрицательным.
Не будем морочить голову формулами, пойдем задом наперед: разделим 4-ое число на 3-ое (найдем знаменатель прогрессии):
96 : 24 = 4 (знаки у чисел мы откинули временно).
Значит, чтобы найти икс надо 24 разделить на знаменатель 4 и взять результат с минусом.
Ответ: -6.
Задание 3.

По данной нам в условии задаче формуле можно сразу понять, что 2 – знаменатель прогрессии. Если это не понятно – вот доказательство:
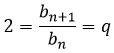
Здесь схитрить не получится, поэтому используем формулу и находим b6.
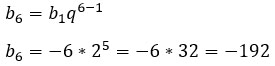
Ответ: -192.
Задание 4.

Каждое следующее число в 4 раза больше предыдущего, значит знаменатель q равен 4.
Зная первый член прогрессии и знаменатель можно найти сумму первых шести членов (n = 6).
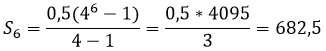
Ответ: 682,5.
Задание 5.
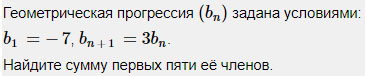
Похожее условие уже встречалось в задании 3. Из данной формулы делаем вывод, что знаменатель q = 3.
Находим сумму:
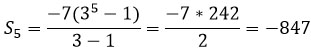
Ответ: -847.
Вот и всё!
С наилучшими пожеланиями, твой персональный препод)
Числовая последовательность
Если ты уже читал тему «Арифметическая прогрессия» ты можешь смело пропускать этот блок и переходить к самой сути.
Если нет, то советую ознакомиться, чтобы иметь общее представление о том, что такое прогрессия в целом и с чем ее едят.
Итак, сядем и начнем писать какие-нибудь числа. Например: ( displaystyle 4,text{ }7,text{ }-8,text{ }13,text{ }-5,text{ }-6,text{ }0,text{ }ldots )
Писать можно любые числа, и их может быть сколько угодно (в нашем случае их ( displaystyle 7)).
Сколько бы чисел мы не написали, мы всегда можем сказать, какое из них первое, какое – второе и так далее до последнего, то есть, можем их пронумеровать. Это и есть пример числовой последовательности:
Числовая последовательность – это множество чисел, каждому из которых можно присвоить уникальный номер.
Например, для нашей последовательности:
Присвоенный номер характерен только для одного числа последовательности. Иными словами, в последовательности нет трех вторых чисел. Второе число (как и ( displaystyle n)-ное число) всегда одно.
Число с номером ( displaystyle n) называетмя ( displaystyle n)-ным членом последовательности.
Всю последовательность мы обычно называем какой-нибудь буквой (например, ( displaystyle a)), и каждый член этой последовательности – той же буквой с индексом, равным номеру этого члена: ( displaystyle {{a}_{1}},text{ }{{a}_{2}},text{ }…,text{ }{{a}_{10}},text{ }…,text{ }{{a}_{n}}).
В нашем случае:
Самые распространенные виды прогрессии это арифметическая и геометрическая. В этой теме мы поговорим о втором виде – геометрической прогрессии.
Ограничения геометрической прогрессии
Первый член {( displaystyle {{b}_{1}})} не равен ( displaystyle 0) и ( displaystyle mathbf{q}text{ }ne text{ }0).
Эти ограничения не случайны!
Допустим, что их нет, и первый член прогрессии все же равен ( displaystyle 0), а q равно, хм.. пусть ( displaystyle 2), тогда получается:
( displaystyle {{b}_{1}}=0)
( displaystyle {{b}_{1}}=0cdot 2=0…) и так далее.
Согласись, что это уже никакая не прогрессия.
Как ты понимаешь, те же самые результаты мы получим, если ( displaystyle {{b}_{1}}) будет каким-либо числом, отличным от нуля, а ( displaystyle q=0).
В этих случаях прогрессии просто не будет, так как весь числовой ряд будут либо все нули, либо одно число, а все остальные нули.
Теперь поговорим поподробнее о знаменателе геометрической прогрессии, то есть о ( displaystyle q).
Знаменатель геометрической прогрессии
Повторим: ( displaystyle q) – это число, во сколько раз изменяется каждый последующий член геометрической прогрессии.
Как ты думаешь, каким может быть ( displaystyle q)? Правильно, положительным и отрицательным, но не нулем (мы говорили об этом чуть выше).
Допустим, что ( displaystyle q) у нас положительное. Пусть в нашем случае ( displaystyle q=3), а ( displaystyle {{b}_{1}}=4).
Чему равен второй член ( displaystyle {{b}_{2}}) и ( displaystyle {{b}_{3}})? Ты без труда ответишь, что:
( displaystyle {{b}_{2}}=4cdot 3=12)
( displaystyle {{b}_{3}}=12cdot 3=36)
Все верно. Соответственно, если ( displaystyle q>0), то все последующие члены прогрессии имеют одинаковый знак – они положительны.
А что если ( displaystyle q) отрицательное? Например, ( displaystyle q=-3), а ( displaystyle {{b}_{1}}=4). Чему равен второй член ( displaystyle {{b}_{2}}) и ( displaystyle {{b}_{3}})?
Это уже совсем другая история
( displaystyle {{b}_{2}}=4cdot -3=-12)
( displaystyle {{b}_{3}}=-12cdot left( -3 right)=36)
Попробуй посчитать ( displaystyle 4) член данной прогрессии. Сколько у тебя получилось? У меня ( displaystyle -108).
Таким образом, если ( displaystyle q<0), то знаки членов геометрической прогрессии чередуются.
То есть, если ты увидишь прогрессию, с чередующимися знаками у ее членов, значит ее знаменатель на ( displaystyle 100%) отрицательный.
Это знание может помочь тебе проверять себя при решении задач на эту тему.
Теперь немного потренируемся:
Пример 1. Попробуй определить, какие числовые последовательности являются геометрической прогрессией, а какие арифметической:
- ( displaystyle 3;text{ }6;text{ }12;text{ }24;text{ }48;text{ }56ldots )
- ( displaystyle 1;text{ }12;text{ }23;text{ }34;text{ }45text{ }ldots )
- ( displaystyle -99;text{ }33;text{ }-11ldots )
- ( displaystyle 5;text{ }7;text{ }9;text{ }11;text{ }13ldots )
- ( displaystyle -6;text{ }5;text{ }17;text{ }28;text{ }39ldots )
- ( displaystyle 64;text{ }16;text{ }4;text{ }1ldots )
- ( displaystyle 2;text{ }4;text{ }8;text{ }18ldots )
Разобрался? Сравним наши ответы:
- Геометрическая прогрессия – 3, 6.
- Арифметическая прогрессия – 2, 4.
- Не является ни арифметической, ни геометрической прогрессиями — 1, 5, 7.
Пример 2. Найти 6-й член прогрессии
Вернемся к нашей последней прогрессии ( displaystyle q=-3), а ( displaystyle {{b}_{1}}=4) и попробуем так же как и в арифметической найти ее ( displaystyle 6) член.
Как ты уже догадываешься, есть два способа его нахождения:
1-й способ. Последовательно умножаем каждый член на ( displaystyle q).
- ( displaystyle {{b}_{1}}=4)
- ( displaystyle {{b}_{2}}=4cdot left( -3 right)=-12)
- ( displaystyle {{b}_{3}}=-12cdot left( -3 right)=36)
- ( displaystyle {{b}_{4}}=36cdot left( -3 right)=-108)
- ( displaystyle {{b}_{5}}=-108cdot left( -3 right)=324)
- ( displaystyle {{b}_{6}}=324cdot left( -3 right)=-972)
Итак, ( displaystyle 6)-ой член описанной геометрической прогрессии равен ( displaystyle -972).
2-й способ. По формуле, которая поможет найти тебе любой член геометрической прогрессии.
( displaystyle {{b}_{6}}={{b}_{1}}cdot q{{ }^{6-1}})
Если нам нужно найти значение числа прогрессии с порядковым номером, то мы умножаем первый член геометрической прогрессии ( displaystyle {{b}_{1}}) на знаменатель ( displaystyle q) в степени, которая на ( displaystyle 1) единицу меньше, чем порядковый номер искомого числа.
( displaystyle {{b}_{6}}=4cdot {{left( -3 right)}^{6-1}}=4cdot {{left( -3 right)}^{5}}=-972)
Попробуем «обезличить» данную формулу – приведем ее в общий вид и получим:
( displaystyle {{b}_{n}}={{b}_{1}}cdot q{{ }^{n-1}}) — уравнение членов геометрической прогрессии, где
- n — порядковый номер члена прогрессии;
- b1 — первый член прогрессии;
- q — знаменатель.
Данная формула верна для всех значений — как положительных, так и отрицательных.
Как найти член геометрической прогрессии, зная два соседних. Формула в общем виде:
( displaystyle {{b}_{n}}=sqrt{{{b}_{n+1}}cdot {{b}_{n-1}}} ), при ( displaystyle n>2)
Не забывай про условие при ( displaystyle n>2)?
Подумай, почему оно важно, например, попробуй самостоятельно просчитать ( displaystyle {{b}_{n}} ), при ( displaystyle n=1). Что получится в этом случае?
Правильно, полная глупость так как формула выглядит так:
( displaystyle {{b}_{1}}=sqrt{{{b}_{1+1}}cdot {{b}_{1-1}}} )
Соответственно, не забывай это ограничение.
Возьмем, к примеру, простую геометрическую прогрессию, в которой нам известны ( displaystyle {{b}_{2}}=6) и ( displaystyle {{b}_{4}}=54).
И посчитаем, чему же равно ( displaystyle {{b}_{3}})
( displaystyle {{b}_{3}}=sqrt{6cdot 54}=sqrt{324}=…)
Правильный ответ – ( displaystyle {{b}_{3}}=pm 18)!
Теперь, когда ты усвоил основные моменты и вывел формулу на свойство геометрической прогрессии, найди ( displaystyle {{b}_{n}} ), зная ( displaystyle {{b}_{n+1}}) и ( displaystyle {{b}_{n-1}})
- ( displaystyle {{b}_{n+1}}=4), ( displaystyle {{b}_{n-1}}=36)
- ( displaystyle {{b}_{n+1}}=-3), ( displaystyle {{b}_{n-1}}=-12)
- ( displaystyle {{b}_{n+1}}=-2), ( displaystyle {{b}_{n-1}}=-32)
Сравни полученные ответы с правильными:
- ( displaystyle {{b}_{n}}=pm 12 )
- ( displaystyle {{b}_{n}}=pm 6 )
- ( displaystyle {{b}_{n}}=pm 8 )
Как найти равноудаленные члены геометрической прогрессии
Как ты думаешь, а если нам были бы даны не соседние с искомым числом значения членов геометрической прогрессии, а равноудаленные от него.
Например, нам необходимо найти ( displaystyle {{b}_{3}} ), а даны ( displaystyle {{b}_{1}} ) и ( displaystyle {{b}_{5}} ). Можем ли мы в этом случае использовать выведенную нами формулу?
Да! Формула работает не только при соседствующих с искомым членах геометрической прогрессии, но и с равноудаленными от искомого членами.
И она приобретает вид:
( displaystyle {{b}_{n}}=sqrt{{{b}_{n+k}}cdot {{b}_{n-k}}} ), при ( displaystyle k<n, kin N)
То есть, если в первом случае мы говорили, что ( displaystyle k=1), то сейчас мы говорим, что ( displaystyle k) может быть равен любому натуральному числу, которое меньше ( displaystyle n).
Главное, чтобы ( displaystyle k) был одинаков для обоих заданных чисел.
Потренируйся на конкретных примерах, только будь предельно внимателен!
Как найти неравноудаленные члены геометрической прогрессии
На самом деле это не так сложно, как кажется! Давай с тобой распишем, из чего состоит каждое данное нам и искомое числа.
( displaystyle {{b}_{3}}={{b}_{1}}cdot {{q}^{2}} )
( displaystyle {{b}_{6}}={{b}_{5}}cdot q={{b}_{1}}cdot {{q}^{5}} )
( displaystyle {{b}_{4}}={{b}_{3}}cdot q={{b}_{1}}cdot {{q}^{3}})
Итак, у нас есть ( displaystyle {{b}_{3}}) и ( displaystyle {{b}_{6}}). Посмотрим, что с ними можно сделать?
Предлагаю разделить ( displaystyle {{b}_{6}}) на ( displaystyle {{b}_{3}}). Получаем:
( displaystyle frac{{{b}_{6}}}{{{b}_{3}}}=frac{{{b}_{1}}cdot {{q}^{5}}}{{{b}_{1}}cdot {{q}^{2}}}={{q}^{3}})
Подставляем в формулу наши данные:
( displaystyle frac{{{b}_{6}}}{{{b}_{3}}}=frac{486}{18}=27)
Следующим шагом мы можем найти ( displaystyle q) – для этого нам необходимо взять кубический корень из полученного числа.
( displaystyle {{q}^{3}}=27 Rightarrow q=sqrt[3]{27}=3)
А теперь смотрим еще раз что у нас есть. У нас есть ( displaystyle {{b}_{3}}), а найти нам необходимо ( displaystyle {{b}_{4}}), а он, в свою очередь равен:
( displaystyle {{b}_{4}}={{b}_{3}}cdot q)
Все необходимые данные для подсчета мы нашли. Подставляем в формулу:
( displaystyle {{b}_{4}}=18cdot 3=54)
Наш ответ: ( displaystyle 54).
Попробуй решить еще одну такую же задачу самостоятельно:
Дано: ( displaystyle {{b}_{3}}=18), ( displaystyle {{b}_{5}}=648)
Найти: ( displaystyle {{b}_{2}})
Сколько у тебя получилось? У меня:
Получим:
( displaystyle {{S}_{n}}q={{b}_{1}}q+{{b}_{2}}q+{{b}_{3}}q+…+{{b}_{n-2}}q+{{b}_{n-1}}q+{{b}_{n}}q)
Посмотри внимательно: что общего в последних двух формулах? Правильно, общие члены, например ( displaystyle {{b}_{2}}={{b}_{1}}q) и так далее, кроме первого и последнего члена. Давай попробуем вычесть из 2-го уравнения 1-ое.
Что у тебя получилось?
( displaystyle {{S}_{n}}q-{{S}_{n}}={{b}_{n}}q-{{b}_{1}})
Теперь вырази ( displaystyle {{b}_{n}}) через формулу члена геометрической прогрессии и подставь полученное выражение в нашу последнюю формулу:
( displaystyle {{S}_{n}}q-{{S}_{n}}={{b}_{1}}{{q}^{n-1}}q-{{b}_{1}}={{b}_{1}}{{q}^{n}}-{{b}_{1}})
Сгруппируй выражение. У тебя должно получиться:
( displaystyle {{S}_{n}}(q-1)={{b}_{1}}({{q}^{n}}-1))
Все, что осталось сделать – выразить ( displaystyle {{S}_{n}}):
( displaystyle {{S}_{n}}=frac{{{b}_{1}}({{q}^{n}}-1)}{q-1}) или ( displaystyle {{S}_{n}}=frac{{{b}_{1}}(1-{{q}^{n}})}{1-q})
Соответственно, в этом случае ( displaystyle qne 1).
А что если ( displaystyle q=1)? Какая формула работает тогда? Представь себе геометрическую прогрессию при ( displaystyle q=1). Что она из себя представляет?
Правильно ряд одинаковых чисел, соответственно формула будет выглядеть следующим образом:
( displaystyle {{S}_{n}}=n{{b}_{1}})
Для начала запишем какую-нибудь геометрическую прогрессию, состоящую из ( displaystyle 5) членов.
Допустим, ( displaystyle {{b}_{1}}=1), а ( displaystyle q=frac{1}{2}), тогда:
- ( displaystyle {{b}_{2}}=1cdot frac{1}{2}=frac{1}{2})
- ( displaystyle {{b}_{3}}=frac{1}{2}cdot frac{1}{2}=frac{1}{4})
- ( displaystyle {{b}_{4}}=frac{1}{4}cdot frac{1}{2}=frac{1}{8})
- ( displaystyle {{b}_{5}}=frac{1}{8}cdot frac{1}{2}=frac{1}{16})
Мы видим, что каждый последующий член меньше предыдущего в ( displaystyle frac{1}{2}) раза, но будет ли какое-либо число ( displaystyle {{b}_{n}}=0)?
Ты сразу же ответишь – «нет». Вот поэтому и бесконечно убывающая – убывает, убывает, а нулем никогда не становится.
Чтобы четко понять, как это выглядит визуально, давай попробуем нарисовать график нашей прогрессии. Итак, для нашего случая формула ( displaystyle {{b}_{n}}={{b}_{1}}cdot q{{ }^{n-1}}) приобретает следующий вид:
( displaystyle {{b}_{n}}=1cdot {{left( frac{1}{2} right)}^{n-1}}={{left( frac{1}{2} right)}^{n-1}})
На графиках нам привычно строить зависимость ( displaystyle x) от ( displaystyle y), поэтому:
( displaystyle {{b}_{n}}=y(x)),
( displaystyle {{left( frac{1}{2} right)}^{n-1}}={{left( frac{1}{2} right)}^{x-1}})
Суть выражения не изменилась.
В первой записи у нас была показана зависимость значения члена геометрической прогрессии от его порядкового номера.
А во второй записи – мы просто приняли значение члена геометрической прогрессии за ( displaystyle y), а порядковый номер обозначили не как ( displaystyle n), а как ( displaystyle x).
Все, что осталось сделать – построить график. Посмотрим, что у тебя получилось. Вот какой график получился у меня:
Видишь?
Функция убывает, стремится к нулю, но никогда его не пересечет, поэтому она бесконечно убывающая.
Отметим на графике наши точки, а заодно и то, что обозначает координата ( displaystyle x) и ( displaystyle y):
Попробуй схематично изобразить график геометрической прогрессии при ( displaystyle q=2), если первый ее член также равен ( displaystyle 1).
Проанализируй, в чем разница с нашим предыдущим графиком?
Справился? Вот какой график получился у меня:
Сумма членов бесконечно убывающей геометрической прогрессии
Итак, для начала посмотрим еще раз на вот этот рисунок бесконечно убывающей геометрической прогрессии из нашего примера:
А теперь посмотрим на формулу суммы геометрической прогрессии, выведенную чуть ранее:
( displaystyle {{S}_{n}}=frac{{{b}_{1}}({{q}^{n}}-1)}{q-1}) или ( displaystyle {{S}_{n}}=frac{{{b}_{1}}(1-{{q}^{n}})}{1-q})
К чему у нас стремится ( displaystyle {{q}^{n}})? Правильно, на графике видно, что оно стремится к нулю.
То есть при ( displaystyle nto infty ), ( displaystyle {{q}^{n}}) будет почти равно ( displaystyle 0), соответственно, при вычислении выражения ( displaystyle 1-{{q}^{n}}) мы получим почти ( displaystyle 1).
В связи с этим, мы считаем, что при подсчете суммы бесконечно убывающей геометрической прогрессии, данной скобкой можно пренебречь, так как она будет равна ( displaystyle 1).
История возникновения геометрической прогрессии
Еще в древности итальянский математик Леонардо из Пизы (более известный под именем Фибоначчи) занимался решением практических нужд торговли.
Перед монахом стояла задача определить, с помощью какого наименьшего количества гирь можно взвесить товар?
В своих трудах Фибоначчи доказывает, что оптимальной является такая система гирь: ( displaystyle 1,text{ }2,text{ }4,text{ }8,text{ }16…)
Это одна из первых ситуаций, в которой людям пришлось столкнуться с геометрической прогрессией, о которой ты уже наверное слышал и имеешь хотя бы общее понятие.
Как только полностью разберешься в теме, подумай, почему такая система является оптимальной?
В настоящее время, в жизненной практике, геометрическая прогрессия проявляется при вложении денежных средств в банк под сложные проценты, или при оценке скорости распространения гриппа (или коронавируса), или при… создании финансовых пирамид!
Интересно? Давай разбираться.
Как быстро Вася заразит весь класс гриппом
Ученик 5 А класса Вася, заболел гриппом, но продолжает ходить в школу. Каждый день Вася заражает двух человек, которые, в свою очередь, заражают еще двух человек и так далее. Всего в классе ( displaystyle 31) человек.
Через сколько дней гриппом будет болеть весь класс?
Решение:
Итак, первый член геометрической прогрессии это Вася, то есть ( displaystyle 1) человек. ( displaystyle 2)-ой член геометрической прогрессии, это те два человека, которых он заразил в первый день своего прихода.
Общая сумма членов прогрессии равна количеству учащихся 5А.
Соответственно, мы говорим о прогрессии, в которой:
( displaystyle begin{array}{l}{{b}_{1}}=1\q=2\{{S}_{n}}=31end{array})
Подставим наши данные в формулу суммы членов геометрической прогрессии:
( displaystyle {{S}_{n}}=frac{{{b}_{1}}({{q}^{n}}-1)}{q-1})
( displaystyle 31=frac{1({{2}^{n}}-1)}{2-1}={{2}^{n}}-1)
( displaystyle begin{array}{l}{{2}^{n}}=31+1\{{2}^{n}}=32\{{2}^{n}}={{2}^{5}}\n=5end{array})
Весь класс заболеет за ( displaystyle 5) дней. Не веришь формулам и числам? Попробуй изобразить «заражение» учеников самостоятельно. Получилось?
Посчитай самостоятельно, за сколько дней ученики заболели бы гриппом, если каждый заражал бы по ( displaystyle 3) человека, а в классе училось ( displaystyle 26) человек.
Какое значение у тебя получилось? У меня получилось, что все начали болеть спустя ( displaystyle 3) дня.
Как ты видишь, подобная задача и рисунок к ней напоминает пирамиду, в которой каждый последующий «приводит» новых людей. Однако, рано или поздно настает такой момент, когда последние не могут никого привлечь.
В нашем случае, если представить, что класс изолирован, ( displaystyle 16) человек из ( displaystyle 31) замыкают цепочку (( displaystyle 51,6%)).
Таким образом, если бы ( displaystyle 31) человек были вовлечены в финансовую пирамиду, в которой деньги давались в случае, если ты приведешь двух других участников, то ( displaystyle 16) человек (( displaystyle {{b}_{5}}={{b}_{1}}{{q}^{4}}) или в общем случае ( displaystyle {{b}_{n}}={{b}_{1}}{{q}^{n}})) не привели бы никого, соответственно, потеряли бы все, что вложили в эту финансовую аферу.
Все, что было сказано выше, относится к убывающей или возрастающей геометрической прогрессии, но, как ты помнишь, у нас есть особый вид – бесконечно убывающая геометрическая прогрессия.
Как же считать сумму ее членов? И почему у данного вида прогрессии есть определенные особенности? Давай разбираться вместе.
Легенда о Сете, создателе шахмат
Узнав, что она изобретена одним из его подданных, царь решил лично наградить его. Он вызвал изобретателя к себе и приказал просить у него все, что он пожелает, пообещав исполнить даже самое искусное желание.
Сета попросил время на размышления, а когда на другой день Сета явился к царю, он удивил царя беспримерной скромностью своей просьбы. Он попросил выдать за первую клетку шахматной доски ( displaystyle 1) пшеничное зерно, за вторую ( displaystyle 2) пшеничных зерна, за третью ( displaystyle -4), за четвертую ( displaystyle -8) и т.д.
Царь разгневался, и прогнал Сета, сказав, что просьба слуги недостойна царской щедрости, но пообещал, что слуга получит свои зерна за все ( displaystyle 64) клетки доски.
А теперь вопрос: используя формулу суммы членов геометрической прогрессии, посчитай, сколько зерен должен получить Сета?
Начнем рассуждать.
Так как по условию за первую клетку шахматной доски Сета попросил ( displaystyle 1) пшеничное зерно, за вторую ( displaystyle 2), за третью ( displaystyle -4), за четвертую ( displaystyle -8) и т.д., то мы видим, что в задаче речь идет о геометрической прогрессии.
Чему равно ( displaystyle q) в этом случае? Правильно.
( displaystyle q=frac{2}{1}=frac{4}{2}=frac{8}{4}=2)
Всего клеток шахматной доски ( displaystyle 64). Соответственно, ( displaystyle n=64).
Все данные у нас есть, осталось только подставить в формулу и посчитать.
( displaystyle {{S}_{n}}=frac{1({{2}^{64}}-1)}{2-1}={{2}^{64}}-1)
Чтобы представить хотя бы приблизительно «масштабы» данного числа, преобразуем ( displaystyle {{2}^{64}}), используя свойства степени:
( displaystyle {{2}^{64}}={{2}^{10}}cdot {{2}^{10}}cdot {{2}^{10}}cdot {{2}^{10}}cdot {{2}^{10}}cdot {{2}^{10}}cdot {{2}^{4}})
Раскроем далее значения ( displaystyle {{2}^{10}}) и ( displaystyle {{2}^{4}}). Как ты знаешь, ( displaystyle {{2}^{10}}=1024), а ( displaystyle {{2}^{4}}=64).
Подставим данное значение в предыдущее выражение:
( displaystyle {{2}^{64}}=1024cdot 1024cdot 1024cdot 1024cdot 1024cdot 1024cdot 64)
Конечно, если ты хочешь, то можешь взять калькулятор и посчитать, что за число в итоге у тебя получится, а если нет, придется поверить мне на слово: итоговым значением выражения будет ( displaystyle 18~ 446~ 744~ 073~ 709~ 551~ 615).
То есть:
( displaystyle 18) квинтильонов ( displaystyle 446) квадрильонов ( displaystyle 744) триллиона ( displaystyle 73) миллиарда ( displaystyle 709) миллионов ( displaystyle 551) тысяч ( displaystyle 615).
Фух) Если желаете представить себе огромность этого числа, то прикиньте, какой величины амбар потребовался бы для вмещения всего количества зерна.
При высоте амбара ( displaystyle 4) м и ширине ( displaystyle 10) м длина его должна была бы простираться на ( displaystyle 300text{ }000text{ }000) км, — т.е. вдвое дальше, чем от Земли до Солнца.
Если бы царь был бы силен в математике, то он мог бы предложить самому ученому отсчитывать зерна, ведь чтобы отсчитать миллион зерен, ему бы понадобилось не менее ( displaystyle 10) суток неустанного счета, а учитывая, что необходимо отсчитать ( displaystyle 18) квинтильонов, зерна пришлось бы отсчитывать всю жизнь.
Задачи на вычисление сложных процентов
Ты наверняка слышал о так называемой формуле сложных процентов. Понимаешь ли ты, что она значит? Если нет, давай разбираться, так как осознав сам процесс, ты сразу поймешь, причем здесь геометрическая прогрессия.
Все мы ходим в банк и знаем, что существуют разные условия по вкладам: это и срок, и дополнительное обслуживание, и процент с двумя различными способами его начисления – простым и сложным.
С простыми процентами все более или менее понятно: проценты начисляются один раз в конце срока вклада.
То есть, если мы говорим о том, что мы кладем 100 рублей на год под ( displaystyle 10%), то ( displaystyle 10%) зачислятся только в конце года.
Соответственно, к окончанию вклада мы получим ( displaystyle 110) рублей.
Сложные проценты — это такой вариант, при котором происходит капитализация процентов, т.е. их причисление к сумме вклада и последующий расчет дохода не от первоначальной, а от накопленной суммы вклада.
Капитализация происходит не постоянно, а с некоторой периодичностью. Как правило, такие периоды равны и чаще всего банки используют месяц, квартал или год.
Допустим, что мы кладем все те же ( displaystyle 100) рублей по ( displaystyle 10%) годовых, но с ежемесячной капитализацией вклада. Что у нас получается?
( displaystyle 1) месяц — ( displaystyle 100cdot left( 1+frac{10}{100cdot 12} right))
Все ли тебе здесь понятно? Если нет, давай разбираться поэтапно.
Мы принесли в банк ( displaystyle 100) рублей. К концу месяца у нас на счете должна появиться сумма, состоящая из наших ( displaystyle 100) рублей плюс процентов по ним, то есть:
( displaystyle 100+100cdot x%)
Согласен?
Мы можем вынести ( displaystyle 100) за скобку и тогда мы получим:
( displaystyle 100+100cdot x%=100cdot left( 1+x% right))
Согласись, эта формула уже больше похожа на написанную нами в начале. Осталось разобраться с процентами
В условии задачи нам сказано про ( displaystyle 10%) годовых. Как ты знаешь, мы не умножаем ( displaystyle 100) на ( displaystyle 10) – мы переводим проценты в десятичные дроби, то есть:
( displaystyle 10%=frac{10}{100})
Верно? Сейчас ты спросишь, а откуда взялось число ( displaystyle 12)? Очень просто!
Повторюсь: в условии задачи сказано про ГОДОВЫЕ проценты, начисление которых происходит ЕЖЕМЕСЯЧНО.
Как ты знаешь, в году ( displaystyle 12) месяцев, соответственно, банк будет начислять нам в месяц ( displaystyle 12) часть от годовых процентов:
( displaystyle 10% ежегодно =frac{10}{100cdot 12} ежемесячно)
Осознал? А теперь попробуй написать, как будет выглядеть эта часть формулы, если я скажу, что проценты начисляются ежедневно.
Справился? Давай сравним результаты:
( displaystyle 10% ежегодно =frac{10}{100cdot 365} ежедневно)
Молодец!
Вернемся к нашей задаче: напиши, сколько будет начислено на наш счет на второй месяц, с учетом, что проценты начисляются на накопленную сумму вклада.
Вот, что получилось у меня:
( displaystyle 100cdot left( 1+frac{10}{100cdot 12} right)cdot left( 1+frac{10}{100cdot 12} right))
Я думаю, что ты уже заметил закономерность и увидел во всем этом геометрическую прогрессию.
Напиши, чему будет равен ее ( displaystyle 12) член, или, иными словами, какую сумму денежных средств мы получим в конце ( displaystyle 12) месяца.
Сделал? Проверяем!
Еще один тип задач на сложные проценты (о прибыли)
Компания «Звезда» начала инвестировать в отрасль в 2000 году, имея капитал ( displaystyle 5000) долларов. Каждый год, начиная с 2001 года, она получает прибыль, которая составляет ( displaystyle 100%) от капитала предыдущего года.
Сколько прибыли получит компания «Звезда» по окончанию 2003 года, если прибыль из оборота не изымалась?
Думаю, ты уже знаешь, как и что считать, но на всякий случай распишу подробно:
( displaystyle {{b}_{1}}=5000) — капитал компании «Звезда» в 2000 году.
( displaystyle {{b}_{2}}=5000cdot left( 1+frac{100%}{100} right)=5000cdot left( 1+1 right)=5000cdot 2=10000) — капитал компании «Звезда» в 2001 году.
( displaystyle {{b}_{3}}=5000cdot left( 1+frac{100%}{100} right)cdot left( 1+frac{100%}{100} right)=5000cdot 4=20000) — капитал компании «Звезда» в 2002 году.
( displaystyle {{b}_{4}}=5000cdot left( 1+frac{100%}{100} right)cdot left( 1+frac{100%}{100} right)cdot left( 1+frac{100%}{100} right)=5000cdot 8=40000) — капитал компании «Звезда» в 2003 году.
Либо мы можем написать кратко:
( displaystyle {{b}_{n}}={{b}_{1}}cdot q{{ }^{n-1}})
Для нашего случая:
( displaystyle {{b}_{1}}=5000)
( displaystyle n=4) — 2000 год, 2001 год, 2002 год и 2003 год.
( displaystyle q =2) — увеличивается на 100%, то есть в 2 раза.
Соответственно:
( displaystyle {{b}_{2003 года}}=5000cdot 2{{ }^{4-1}}=5000cdot {{2}^{3}}=5000cdot 8=40000) рублей
Заметь, в данной задаче у нас нет деления ни на ( displaystyle 12), ни на ( displaystyle 365), так как процент дан ЕЖЕГОДНЫЙ и начисляется он ЕЖЕГОДНО.
То есть, читая задачу на сложные проценты, обрати внимание, какой процент дан, и в какой период он начисляется, и только потом приступай к вычислениям.
Теперь ты знаешь о геометрической прогрессии все.
Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике
Экономические задачи на вклады очень часто требуют знания геометрической прогрессии.
Эти задачи требуют также очень подробного и чёткого описания решения.
По сути, мы составляем математическую модель какой-то жизненной ситуации (например, связанной с банковскими вкладами или кредитами), и важно научиться ничего не пропускать при описании этой модели: описывать словами все введённые обозначения, обосновывать уравнения, которые мы записываем, и всё в таком духе.
Если не написать эти объяснения, вы гарантированно получите 0 баллов даже за правильно найденный ответ!
В этом видео мы узнаем, как работают вклады, научимся решать и, главное, правильно оформлять решение таких задач.
ЕГЭ №17. Экономическая задача. Вклады
Геометрическая прогрессия
- Формула n-го члена
Геометрическая прогрессия – это последовательность чисел, в которой каждое число, начиная со второго, равно предыдущему, умноженному на одно и то же число, отличное от нуля.
Числа, составляющие прогрессию, называются её членами. Число, на которое следует умножить предыдущий член, чтобы получить последующий, называется знаменателем геометрической прогрессии. Знаменатель прогрессии может быть положительным или отрицательным.
Для определения знаменателя данной геометрической прогрессии надо последующий член разделить на предыдущий (например, второй член разделить на первый).
Геометрическую прогрессию можно определить и так: числовая последовательность a1, a2, a3, …, an, … называется геометрической прогрессией, если для любого n
an+1 = an · q,
где q — знаменатель прогрессии, n — порядковый номер члена.
Прогрессия называется возрастающей, если модуль числа |q| > 1, и убывающей, если |q| < 1.
Примеры:
5, 15, 45, 135 — возрастающая прогрессия со знаменателем 3;
4, -2, 1, -0,5 — убывающая прогрессия со знаменателем -0,5.
Формула n-го члена
Если знаменатель прогрессии a1, a2, a3, … равен q, то по определению геометрической прогрессии
a2 = a1 · q;
a3 = a2 · q = (a1 · q) · q = a1 · q2;
a4 = a3 · q = (a1 · q2) · q = a1 · q3;
и так далее. Значит при n > 1
an = a1 · qn-1
n-ый член геометрической прогрессии равен произведению её первого члена на знаменатель прогрессии в степени n-1.
Данная формула называется формулой общего члена геометрической прогрессии. Например, для прогрессии
1, 2, 4, 8, 16, …
a1 = 1, q = 2.
Следовательно,
a10 = a1 · q9 = 1 · 29 = 512.












![{displaystyle q={sqrt[{n-k}]{dfrac {b_{n}}{b_{k}}}},{text{где }}k<n;;forall n,forall kin mathbb {N} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb495b3245f5a775c4432d11c0f5008f819b5d72)







