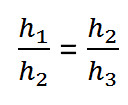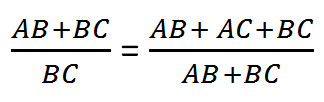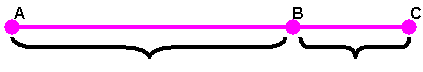Как найти золотое сечение 6 класс

Исследовательская работа ученицы 6 класса “В” ГБОУ Гимназии 1257 Соколовой Ксении.

План

1. I.                  Вступление.
2. II.               Что такое «золотое сечение»?

1.  Определение и построение «золотого сечения».

2.  Число φ и ряд Фибоначчи.

3.  История «золотого сечения».

4.   «Золотое сечение» в природе.

5.  «Золотой прямоугольник».

III.     Практическая часть.

1. Экспериментальное подтверждение красоты и гармонии «золотой пропорции».

    2.  Этот циркуль мы делали вместе с дедушкой.

3.  Коллекция «золотых».

IV. Заключение.

V. Список литературы.

        I.            Вступление.

В учебнике по математике, на странице 145, есть статья про «золотое сечение. Информации в учебнике было очень мало. Используется ли «золотое сечение» в современном мире? Так ли оно гармонично, как утверждают античные философы и ученые?  Чтобы ответить на эти и другие вопросы, я решила подробнее ознакомиться с этой темой.

Цель моей работы: доказательство гармонии «золотого сечения» и его присутствия в окружающем нас мире.

 Гипотеза: мы считаем, что «золотое сечение» действительно гармонично, и  человек в своей деятельности постоянно сталкивается с предметами, имеющими в своей основе «золотые пропорции».

Для выполнения поставленной цели мы решали следующие задачи:

1.      Изучить историю вопроса.

2.      Систематизировать теоретические сведения о золотом сечении.

3.      Создать инструмент для определения «золотых пропорций».

4.      Исследовать присутствие золотого сечения в окружающей жизни.

Методы  исследования:

1.           Работа с учебной и научно-популярной литературой.

2.           Социологический опрос.

3.           Наблюдение, сравнение, анализ, аналогия.

4.           Практическая деятельность. 

Объект исследования: «золотое сечение».

Предмет исследования: золотое сечение в окружающем мире.

Актуальность работы заключается в следующем:

1)      пропорциональность в природе, искусстве, архитектуре и в других сферах окружающей нас жизни означает соблюдение определённых соотношений между отдельными частями и является непременным условием гармонии и красоты;

2)      всеобщий характер исследуемого материала;

3)      богатая и увлекательная история исследуемого материала;

4)      сведения о «золотом сечении» впервые встречаются в учебнике 6 класса; возникает желание углубить свои знания по математике, показать значение математики во всех областях окружающей нас жизни.

        I.            Что такое «золотое сечение» ?

1. 1.     Определение и построение «золотого сечения».

Учение об отношениях и пропорциях успешно развивалось в IV в. до н.э. в Древней Греции. С пропорциями связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке.

Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета.

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему. a : b = b : c или с : b = b : а.

 

Геометрическое изображение золотой пропорции

Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.

 

Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC

Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.

    Как же найти численное выражение «золотой пропорции»?

Пусть х – меньшая часть, тогда кх – большая часть, а(х+кх) – это целый отрезок. Тогда, по определению «золотой пропорции» получим:

х:кх=кх:(х+кх);

Используя основное свойство пропорции, получим:

Разделим обе части равенства на

Приведем уравнение к стандартному виду:

Решение этого уравнения:

Положительный корень уравнения приближенно равен 1,618. Полученное число носит название числа φ (фи).

                      2.   Число φ и ряд Фибинчи.

Это число названо в честь древнегреческого архитектора Фидия, создавшего храм Парфенон в Афинах (по первой букве имени). На самом деле в числе φ бесконечно много знаков после запятой – это бесконечная непериодическая дробь. Можно привести запись этого числа с большим количеством цифр: φ=1,61803398874989484820458683436563811772030917980576286213544…

С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи).

Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:

Месяцы	0	1	2	3	4	5	6	7	8	9	10	11	12	и т.д.
Пары кроликов	0	1	1	2	3	5	8	13	21	34	55	89	144	и т.д.

Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.

Фибоначчи так же занимался решением практических нужд торговли: с помощью какого наименьшего количества гирь можно взвесить товар? Фибоначчи доказывает, что оптимальной является такая система гирь: 1, 2, 4, 8, 16…

                                    3. История «золотого сечения».

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.) .

 Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

В фасаде древнегреческого храма Парфенона, созданного знаменитым древнегреческим архитектором Фидием, присутствуют золотые пропорции.

При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Неаполе, в Национальном музее, хранится пропорциональный циркуль, найденный при раскопках в Помпеях. Пропорциональный циркуль является необходимым атрибутом архитектора. Он состоит из двух равных по длине ножек, скреплённых винтом наподобие ножниц, и позволяет (минуя вычисления!) для любого отрезка получить  отрезок, находящийся с ним в заданном отношении. Так вот, помпейский циркуль наглухо закреплен в отношении золотого сечения.

 В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи  и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.

Лука Пачоли

Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок – бога отца, а весь отрезок – бога духа святого).

Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.

В своих художественных произведениях Леонардо да Винчи конечно же использовал пропорции «золотого сечения». Так например, это соотношение между высотой и шириной лица Моны Лизы на картине «Джоконда».

В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. 

Альбрехт Дюрер. Автопортрет.

Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет: «Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать».

Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица – ртом и т.д.

Великий астроном XVI в. Иоганн Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).

Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».

Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).

В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы «вместе с водой выплеснули и ребенка». Вновь «открыто» золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях «математической эстетикой».

         Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.

Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского.

      

Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона,

      С. Цейзинг

стихотворные размеры.  

Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону.

                            4. Золотое сечение в природе.

Среди придорожных трав растет ничем не примечательное растение – цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок.

 

Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.

В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так относится к длине остального тела, как 62 к 38.

И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы – симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста.

Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.

5.  «Золотой прямоугольник».

Стороны золотого прямоугольника имеют отношение 1,618 к 1. Чтобы построить золотой прямоугольник, начните с квадрата со сторонами, равными двум единицам, потом проведите линию от середины одной стороны квадрата к одной из его вершин, образующих противоположную сторону, как показано на рисунке.

Треугольник EDB является прямоугольным. Около 550 года до Р.Х. Пифагор доказал, что квадрат гипотенузы (X) прямоугольного треугольника равен сумме квадратов двух других его сторон. В данном случае X2 = 22 + I2, или X2 = 5. Длина стороны ЕВ, таким образом, должна быть квадратным корнем из 5. Строя золотой прямоугольник, следующим шагом продлите отрезок CD и постройте на нем отрезок EG, равный квадратному корню из 5, или 2,236 единицы длины, как показано на рис. 3-5. В построенных таким образом прямоугольниках стороны связаны золотым коэффициентом. Таким образом, и прямоугольник AFGC, и прямоугольник BFGD являются золотыми.

Поскольку стороны прямоугольников связаны золотым отношением, следовательно, эти прямоугольники, по определению, являются золотыми прямоугольниками.

                                                     ΙI.            Практическая часть.

                            2.1     Экспериментальное подтверждение красоты и гармонии «золотой пропорции».

Я провела исследование: я нарисовала 7 различных прямоугольников. Среди них я спрятала один прямоугольник, который был сделан по пропорциям «золотого сечения». Затем я расспросила одноклассников, учителей, родных и друзей, какой прямоугольник кажется им наиболее гармоничным?  Всего было опрошено 72 человека. Вот результаты опроса:

Прямоугольник	A	B	C	D	E	F	G
Число голосов	4	3	31	5	9	20	0
Проценты	5,56	4,17	43,06	6,94	12,5	27,78	0

«Золотой прямоугольник» на моем чертеже был подписан буквой С. Как видно из приведенной таблицы, подавляющее большинство опрошенных выбрало «золотой прямоугольник». Мы можем подвести итоги: золотое сечение действительно выглядит гармоничным и радует глаз.

                                   2.2     Этот циркуль мы делали вместе с дедушкой.

Но может быть «золотое сечение» забыто, и в наши дни совсем не используется современными дизайнерами, художниками, архитекторами? Как  же это проверить? Я решила создать свой инструмент для определения «золотой пропорции». Мой циркуль сделан по принципу старинного помпейского циркуля, а помог мне его сделать дедушка.

Вам, наверное, будет интересно узнать, как мы это делали?

Сначала мы взяли 2 одинаковые палки длиной по 146 мм.

Затем мы разделили их на 2 неравные части.

Для того, чтобы циркуль показывал пропорции «золотого сечения» я составила уравнение: Пусть х мм – меньшая часть палки, тогда 1,618х мм – большая часть; (х+1,618х) мм – длина всей палки. Зная, что длина нашей палки 146 мм, получим уравнение

Х+1,618х=146;

2,618х=146;

Х=146:2,618;

Х≈56.

         То есть меньшая часть была 56 мм, а большая часть: 56·1,618≈  90 мм.

Соотношение между двумя сторонами получилось 1,618.

Если раздвинуть ножки циркуля, то он всегда покажет пропорции «золотого сечения». Так как  треугольник АОВ и треугольник СOD называются подобными. В подобных треугольниках все стороны пропорциональны.

Поэтому, если

Теперь с помощью этого циркуля я могла определить, где присутствуют «золотые пропорции».

                                                     2.3     Коллекция «золотых».

Мне стало очень интересно, какие предметы сделаны по принципу «золотого сечения». Я ходила и измеряла всё вокруг. И оказалось, что многие предметы из нашей повседневной жизни сделаны по принципу «золотого сечения».

Первым «открытием» оказался мой пропуск в школу. Я обратила внимание, что все банковские карточки и дисконтные карты магазинов одинакового размера и формы. Таких же размеров мой пропуск в школу. Это очень удобно, все карточки можно положить в один футляр. Но когда я испробовала на моём пропуске свой циркуль, оказалось, что это не просто прямоугольник, а «золотой прямоугольник»!

«Золотым прямоугольником»  оказался и спичечный коробок»!

Куриное яйцо также вписывается в «золотой прямоугольник»!

Упаковки некоторых продуктов, например, представленная на фотографии пачка масла, также представляет собой «золотой прямоугольник».

Исследуя историю вопроса, я поняла, что в Древней Греции золотые пропорции использовались в архитектуре. Интересно, а сейчас при проектировании зданий используют ли архитекторы «золотое сечение»?

Внимательно осмотрев здание нашей школы, я решила «поискать» золотые пропорции в наших окнах.

Я тщательно измерила длину и высоту нашего окна.

Оказалось, что высота нашей оконной рамы 232 см, а ширина 144 см. Разделив 232:144=1,6(1), то есть приближенно наше отношение равно числу ϕ.

IΙΙ  Заключение.

Мне очень понравилось работать над темой, посвященной «золотому сечению». В результате работы подтвердилась наша гипотеза о том, что «золотое сечение» действительно гармонично, и  человек в окружающем мире постоянно сталкивается с предметами, имеющими в своей основе «золотые пропорции».

В ходе работы были решены следующие задачи:

1.      Ознакомились с  историей вопроса.

2.      Систематизировали теоретические сведения о золотом сечении.

3.      Создали инструмент для определения «золотых пропорций» – циркуль по примеру помпейского.

4.      Исследовали присутствие золотого сечения в окружающей жизни, обнаружили, что «золотые пропорции» активно используются в современной жизни: в дизайне упаковок продуктов, в архитектуре и т.д.

Я с удовольствием продолжу изучение этого вопроса в дальнейшем.

                                                                           ΙV  Список литературы:

Волошинов А. В. «Математика и архитектура».- М.: «Просвещение». 2000

Виленкин Н. Я. и д.р. «Математика 6 класс».-М.: «Мнемозина». 2011

В. Лаврус «Золотое сечение».- электронная библиотека. «Наука и техника».

Этап
урока

Содержание

Действия

(слова)
учителя

Действия

(слова)
учеников

№
слайда

Скриншоты
слайдов

с
пояснениями

I. Организацион-ный
момент.

Звенит
звонок

–Здравствуйте, садитесь.

-Начинаем урок  математики

Учащиеся
занимают свои места

1

II.

Сообщение темы и
целей урока.

На слайде записаны слова

– Ребята, напомните, какую главу мы сейчас изучаем? (Математика вокруг
нас).

– Сегодня на
уроке мы попытаемся определить чудо математики, которое встречается в
окружающем нас мире.   Посмотрите на экран и скажите, что вы чувствуете? 
Перед вами фотографии растений, Египетские пирамиды, картина Ивана Ивановича
Шишкина «Корабельная роща», Портрет Моны Лизы (Леонардо да Винчи «Джоконда»).

– С древних времен человек начал разделять вещи на красивые и не
красивые. Уже в Древней Греции античные философы начали выявлять некую
формулу, которая раскрыла тайну того, что мы называем гармонией. Так что же
такое гармония?

– Ребята! Как,
вы, считаете, что же такое гармония? С какими словами у вас ассоциируется
слово “гармония”?

– Если рассматривать цветок вблизи и аналогично другие естественные и
созданные человеком творения, то можно найти единство и порядок, свойственные
всем этим предметам. Этот порядок и единство и есть Гармония, определяющая
Красоту.

Итак, гармония это красота, а красота, как говорили греки, – это
математика, следовательно, гармония это математика.

Из многих пропорций, которыми пользовался человек при создании
живописи, скульптуры, музыки, поэм, самой главной является одна, и именно она
отражает понятие ГАРМОНИИ наилучшим образом. Эту пропорцию называли
по-разному: божественной, золотой, золотым сечением, золотой серединой,
золотым делением, золотым числом.

Мы назовем ее с вами “Золотое сечение”

Иоганн Кеплер
говорил: “Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым
сечением. И если первое из этих двух сокровищ можно сравнить с мерой золота,
то второе с драгоценным камнем”.

– Одно из таких
соотношений получило название «Божественная пропорция» или же по
другому…         

– Откройте
тетради, запишите число и тему урока.

Постановка
целей: – Чему –

мы научимся, изучая эту тему?

Учащиеся отвечают на вопрос

Учащиеся смотрят на слайд и делают
выводы

Обобщаем ответы учащихся

(читает ученик формулировку темы –
«Золотое сечение»).

Записывают в тетрадь.

(читают ученики)

-Познакомиться с понятием «золотое сечение».

-Узнать, где оно применяется.

– Научиться
использовать его в практической деятельности

2

3

    4

5

III.

Устный опрос

На слайде вопросы для устного опроса по
теме «Отношение двух чисел»

– Давайте
посмотрим, как связано это слово с математикой! И в конце урока определим,
верны ли слова ученого Ф. Хауздорда « Есть в математике нечто, вызывающее
человеческий восторг»

Но, сначала
ответим на вопросы:

– Что такое
отношение?

– Что такое
пропорция?

– Основное свойство пропорции?

Учащиеся устно отвечают на вопросы,
размещенные на слайдах

6

IV.

Работа над новой
темой

1.Учащимся дается
определение пропорции, отличное от изученного ранее

1. Историческая справка:

– Учение об
отношениях и пропорциях успешно развивалось в IV
веке до н.э.

В Древней
Греции с пропорциями связывались представления о красоте, порядке и гармонии,
о созвучных аккордах в музыке.

Пропорциональность
в природе, искусстве, архитектуре означает соблюдение определенных
соотношений между размерами отдельных частей растения, скульптуры, здания и
является непременным условием правильного и красивого изображения предмета.

– Давайте же узнаем, что такое «золотое
сечение».

Показать на схеме.

Учащиеся читают определение

Определение: золотое сечение – это такое  пропорциональное деление отрезка на
неравные части, при котором отношение его меньшей части и большей равно
отношению большей к длине всего отрезка.

Дети высказывают свои предположения

7

V.

Закрепление
нового материала

1.Учащиеся опытным путем находят
числовое значение «золотого сечения»

Задание 1. (по группам)

Начертить отрезки: (1 группа)

                          5 см

 

                                                                                                                                                                                                                                   

            2 см               3 см

                         (2
группа)

                 
    8 см

                 

                                                                                                                 

          3
см                5 см 

                    
  (3 группа)

       13 см

                          

                                                                                                                 

        5 см                8 см

– Какую закономерность вы видите? Любое
ли деление отрезка мы можем назвать «золотым сечением»?

– Давайте проверим.

 Рассмотрим пропорцию         

– Какой вывод
вы можете сделать? Какие пропорции относятся к «Золотому сечению»?

Как вы
думаете, где применяется «Золотое сечение»? (ответы детей)      

Учащиеся выполняют в тетрадях и далают
вывод:

(1 группа)

 

Если мы 2 : 3, то получим  ≈ 0,6

а 3 : 5 = 0,6

(2 группа)

Если мы 3 : 5, то получим  ≈ 0,6

а 5 : 8 ≈ 0,6

Если мы 5 : 8, то получим  ≈ 0,6

а 8 : 13 ≈ 0,6

(только те, в
которых в обеих частях получается точно или приближенно 0,6) (вывод
записать).

7

2. Идет демонстрация примеров «золотого
сечения» в архитектуре (практическая работа)

Задание 2. (по группам)

– Скульпторы,
архитекторы, художники использовали и используют золотое сечение в своих
произведениях. Красивейшее произведение древне-греческой архитектуры – храм
Парфенон ( построен в V в. до н.э.) в Афинах.  Он
поражает не своими размерами, а гармоническим совершенством пропор-ции.
Проверим это отношения (высота здания к его длине и она равна 0,6).

 – А теперь рассмотрим другие
произведения архитектуры и проверим пропорции…

 Задание 3. (по группам)

Учащиеся рассматривают слайды с
примерами использования «золотого сечения» и выполняют практическую работу и
делают вывод.

8

3. Идет демонстрация примеров «золотого
сечения» в живописи

Термин «золотое
сечение» ввел великий итальянец Эпохи Возрождения Леонардо да Винчи
доказывал, что пропорции «золотого сечения» свойственны и человеческому телу,
но использовалось и знаменитым русским иконописцем Андреем Рублевым,
применяется в скульптуре.

Задание 4.

– Перед вами репродукция картины Ивана Шишкина “Корабельная роща”.

Самая яркая деталь на этой картине – освещенная солнцем сосна, она
делит картину в отношении «золотого сечения».

Проверьте это! Ярко освещенная солнцем сосна, стоящая на переднем
плане, делит длину картины по горизонтали в «золотом» отношении.

Справа от сосны – освещенный солнцем пригорок. Он делит по «золотому
сечению» правую часть картины по вертикали. Также можно найти мотивы
«золотого сечения» и в других частях картины.

Наличие в картине ярких деталей, делящих ее по «золотому сечению»,
придает картине уравновешенность, чувство спокойствия и гармонии.

Картины великих художников, вызывающие непонятную, притягатель-ную
силу, запоминающиеся, написаны с применением «золотого сечения». Чтобы
создать шедевр, даже в искусстве необходима математика!

 Проверим «Божественную пропорцию» в
живописи.

Учащиеся рассматривают слайды с примерами использования
«золотого сечения» и выполняют практическую работу и делают вывод.

9

10

11

12

VI.

Физминутка.

Звучит фрагмент классического
музыкального произведения. Учащимся предлагается посидеть с закрытыми
глазами, чтобы отдохнуть

-Но «золотое сечение» помогает
сделать красивым не только изображение, но и звуки. Знаменитый мастер
Страдивари изготавливал свои скрипки строго в соответствии с божественной
пропорцией. Послушайте, как прекрасны звуки скрипки

Учащиеся слушают музыкальный фрагмент с
закрытыми глазами

(чтобы включить музыку на слайде надо нажать
на  )

VII. Работа над новой темой (продолжение)

4. Идет демонстрация примеров «золотого
сечения» в природе (практическая работа)

-Золотое сечение нашло свое воплощение
и в живой природе

– Например, рассматривая расположение
листьев на общем стебле растения, можно заметить, что между каждыми двумя
парами листьев третья расположена в месте золотого сечения.

Проверим «Божественную пропорцию» в
природе.

Задание 5.

Учащиеся рассматривают слайд

Учащиеся выполняют вычисления и
сравнивают их с числовым значением золотого сечения

13

14

VIII.

Закрепление
изученного материала.

Просмотр слайдов с различными примерами
золотого сечения

– Золотое сечение называют
божественной мерой красоты, таким образом, золотое сечение это и есть формула
красоты, которую мы искали.

Учащиеся смотрят слайды с 15 по 20 без
комментариев

15

16

17

18

19

20

-Мы с вами также созданы по законам
золотого сечения. Обратите внимание на пропорции лица. Данная схема
представлена у вас в раздаточных материалах. Дома вы можете сравнить
пропорции своего лица с золотым сечением, которое в средневековье считалось
эталоном красоты

Учащиеся рассматривают схему лица

21

IX.

Итог урока.

Итоговое задание «Кроссворд»

-Надеюсь, сегодня вы узнали много
интересного и моя попытка доказать вам всю красоту математики не была
напрасной. А насколько внимательно вы меня слушали, мы вспомним фразу и
ответим « Есть в математике нечто,
вызывающее человеческий восторг»

-А закончу я наш урок  фразой:

“Там, где присутствует золотое
сечение, ощущается красота и гармония”

Вы согласны со мной и неизвестным
автором

Учащиеся высказывают свои мнения

Х.

Домашнее задание.

Запись домашнего задания

1.    Выбрать одну картинку из презентации, постараться найти золотую
пропорцию.

2.    Нарисовать рисунок, используя принцип золотого сечения.

Записывают домашнее задание в дневник

ХI.

Рефлексия.

Выбор фразы.

Учащиеся по очереди
высказываются одним предложением, выбирая начало фразы из рефлексивного
экрана на доске

22

←Вернуться в «Доклады по математике»

Красота, оказывается, порою имеет математическое объяснение.
Пропорции золотого сечения часто используются художниками и скульпторами в соотношениях между
разными элементами картины или скульптуры. Великий Леонардо да Винчи находил соотношение
золотого сечения в пропорциях человеческого тела.

Так чему же равно отношение золотого сечения в математике и как его найти? Разберёмся на примере.

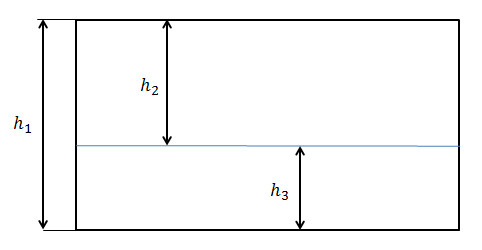
Возьмём лист бумаги и начертим линию горизонта, которая обычно делит небо от земли. Получится,
нечто похожее на рисунок ниже.

Отношение высоты картины h₁ к расстоянию от верхнего края
h₂ равно
отношению расстояния от верхнего края h₂
к расстоянию до нижнего края h₃.
В виде математической записи, это будет выглядеть так:

Найдём числовое значение золотого сечения.

Для этого вернёмся к нашему рисунку. Пусть высота всей картины равна h₁ = 1, а расстояние
от верхнего края до горизонта обозначим за x (h₂ = x). Тогда получим:

=

x² + x − 1 = 0

Положительный корень этого уравнения

≈ 1,618

Это отношение большей части к меньшей в этой пропорции.

Это число равно отношению золотого сечения. Обычно его обозначают греческими буквами
τ (тау) или
φ (фи).
Другие греческие буквы вы можете посмотреть в разделе
«Для учёбы».

Золотое сечение в фигурах

В некоторых фигурах геометрии и стереометрии также присутствует золотое сечение.
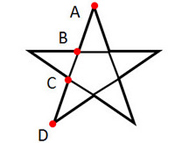
Например, в пятиконечной звезде (пентаграмме).

Точка «B» или «С» делит отрезок
«AD» в пропорциях золотого сечения.
Все остальные стороны звезды также поделены в данном соотношении соответственно.

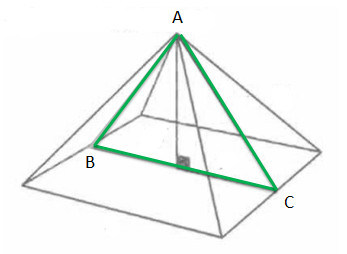
Другой пример золотого сечения был обнаружен в пирамиде Хеопса.

В сечении знаменитого сооружения также заложен принцип золотого сечения.

Сумма двух сторон равнобедренного треугольника «ABC» относится к его основанию
также как сумма всех сторон треугольника к сумме равных сторон. Иными словами:

---

Ваши комментарии

Оставить комментарий:

---

Цель урока:

• познакомить учащихся с понятием “золотое
  сечение”;
• закрепить навык решения уравнений, используя
  основное свойство пропорции;
• расширить кругозор и активизировать
  познавательную деятельность учащихся;
• вовлечь учащихся в исследовательскую
  деятельность.

Ход урока

Урок сопровождается презентацией.

I. Вступительное слово.

С древних времен человек начал разделять вещи
на красивые и не красивые. Уже в Древней Греции
античные философы начали выявлять некую формулу,
которая раскрыла тайну того, что мы называем
гармонией. Так что же такое гармония?

Вопросы к классу: “Ребята! Как, вы, считаете,
что же такое гармония? С какими словами у вас
ассоциируется слово “гармония”?

Обобщаем ответы учащихся (Слайд 1):

Если рассматривать цветок вблизи и аналогично
другие естественные и созданные человеком
творения, то можно найти единство и порядок,
свойственные всем этим предметам. Этот порядок и
единство и есть Гармония, определяющая Красоту.

Итак, гармония это красота, а красота, как
говорили греки, – это математика, следовательно, гармония
это математика.

Из многих пропорций, которыми пользовался
человек при создании живописи, скульптуры,
музыки, поэм, самой главной является одна, и
именно она отражает понятие ГАРМОНИИ наилучшим
образом. Эту пропорцию называли по-разному:
божественной, золотой, золотым сечением, золотой
серединой, золотым делением, золотым числом.
(Слайд 2)

Мы назовем ее с вами “Золотое сечение”

Иоганн Кеплер говорил: “Геометрия владеет
двумя сокровищами – теоремой Пифагора и золотым
сечением. И если первое из этих двух сокровищ
можно сравнить с мерой золота, то второе с
драгоценным камнем”.

Чтобы найти этот драгоценный камень я
предлагаю вам отправиться в экспедицию.

II. Экспедиция.

У каждого учащегося на столе лежат маршрутные
листы (Приложение 1)

Для любого путешествия необходимо собрать
багаж. Давайте пополним наш багаж знаний
определением. Для этого мы отправляемся на
станцию “Теоретическая”.

ТЕОРЕТИЧЕСКАЯ. (Слайд 3)

Золотым сечением называют деление отрезка, при
котором длина его большей части так относится к
длине всего отрезка, как длина меньшей части к
большей.

АВ : АС = ВС : АВ

Это отношение приближённо равно 0,618 или

Итак, багаж упакован, можно отправляться в
экспедицию.

ВИТРУВИЙ (Слайд 3)

Перед вами Витрувианский человек —
рисунок, нарисованный Леонардо Да Винчи примерно
в 1490-92 годах как иллюстрация для книги,
посвящённой трудам античного римского
архитектора Витрувия,
Рисунок является одновременно научным трудом и
произведением искусства, также он служит
примером интереса Леонардо к пропорциям. В
соответствии с сопроводительными записями
Леонардо, он был создан для определения
пропорций (мужского) человеческого тела.

Термин “золотое сечение” был введён именно
Леонардо да Винчи, который использовал золотое
сечение как пропорции “идеального
человеческого тела”.

Известно, что анатомическая особенность
человека описывается золотым сечением. Например:
если мы измерим расстояние от локтя до кончиков
пальцев и разделим получившийся результат на
расстояние от плеча до кончиков пальцев, то
получим отношение !

ЗАДАЧА 1 (Слайд 3, 4)

• Расстояние от локтя до кончиков пальцев у
  человека равно 40 см. Найдите расстояние от плеча
  до кончиков пальцев этого человека.

ЗАДАЧА 2 (Слайд 5)

• Рост человека 160 см. На какой высоте от пола
  должна находиться его талия, чтобы делить тело в
  отношении золотого сечения, т. е. ?

ДНК. (Слайд 6)

Молекула ДНК состоит из двух вертикально
переплетенных между собой спиралей. Отношение
ширины спирали к её длине составляет
приблизительно .

ЗАДАЧА 3.

• Известно, что длина спирали 34 ангстрема, найдите
  ширину спирали. (1 ангстрем = 0,0000001 мм)

ПОДСОЛНУХ. (Слайд 7)

Удивительно, что семена подсолнуха
располагаются по спирали, против часовой
стрелки, и отношение последующего диаметра
спирали к предыдущему равно !

ЗАДАЧА 4. (Слайд 8)

• Диаметр одной спирали семян подсолнечника
  равен 2см. Найдите диаметр предыдущей спирали.

ЗООЛОГИЧЕСКАЯ. (Слайд 9)

Головоногий моллюск наутилус также
подчиняется божественной пропорции, т.е.
соотношение диаметра каждого витка спирали к
последующему равно !

ЗАДАЧА 5 (Слайд 10)

• Первый виток спирали равен 1.2см. Найдите
  размер второго витка спирали.

В ящерице с первого взгляда улавливаются
приятные для нашего глаза пропорции – длина ее
хвоста так относится к длине остального тела, как
!

ЗАДАЧА 6 (Слайд 11)

• Найдите длину всей ящерицы, если длина её
  хвоста 16 см.

ПАРФЕНОН. (Слайд 12)

Парфенон – один из самых величественных храмов
Древней Греции. Отношение высоты здания к его
длине равно !

ЗАДАЧА 7 (Слайд 13)

• Длина Парфенона 69,54 м. Найдите высоту храма,
  если его высота относится к длине по правилу
  “золотого сечения”, т.е. в отношении 5/8.

МУЗЫКАЛЬНАЯ. (Слайд 14)

Любая скрипка сделана по закону золотого
сечения. Длина её части грифа относится к длине
деки, как 5/8!

ЗАДАЧА 8 (Слайд 14)

• Найдите длину скрипки, если длина деки 36 см.

III. Подведем итоги нашей экспедиции. (Слайд 15)

Странная, загадочная, необъяснимая вещь: эта
божественная пропорция мистическим образом
сопутствует всему живому.

Неживая природа не знает, что такое “золотое
сечение”. Но вы непременно увидите эту пропорцию
и в изгибах морских раковин, и в форме цветов, и в
облике жуков, и в красивом человеческом теле.

Все живое и все красивое — все подчиняется
божественному закону, имя которому — “золотое
сечение”.

Так что же такое “золотое сечение”? Что это за
идеальное, божественное сочетание?

Может быть, это закон красоты?

Или все-таки он — мистическая тайна?

Научный феномен или этический принцип?

Ответ неизвестен до сих пор. Точнее — нет,
известен. “Золотое сечение” — это и то, и другое,
и третье. Только не по отдельности, а
одновременно… И в этом его подлинная загадка,
его великая тайна. Так считал Анхель де
Куатьэ

IV. Домашнее задание.

Найти примеры “золотого сечения” в природе,
архитектуре, живописи и т. д. и составить задачи.
Материал желательно оформить в виде презентации.

Примечание: во время решения задач учащиеся
могут работать в парах или группах.