Примеры золотого сечения в архитектуре найти можно везде, когда умеешь его видеть. Выяснить это даже школьнику по силам. В 2013 году ученица 10 класса Сивакова Елена провела собственное исследование зданий 19-20 веков. Проследим, как она это сделала, и научимся видеть и определять его в архитектурных сооружениях за 5 минут. После прочтения статьи не останется вопросов о том, что это такое, и можно ли его необычные свойства использовать в своей жизни.
7+ примеров золотого сечения в архитектуре России
Санкт-Петербург
Здания исторического центра Санкт-Петербурга построены в разных архитектурных стилях, таких как барокко, классицизм, ампир, эклектика, необарокко, неоготика. Подчиняются ли они золотому правилу?
Исаакиевский собор
Придворный архитектор Александра I Огюст Монферран строил этот собор с 1819 по 1858 гг. Стиль позднего классицизма, в котором уже проявлены черты неоренессанса и эклектики. Елена задалась вопросом: «В чём же причина гармонии довольно громоздкого здания?»
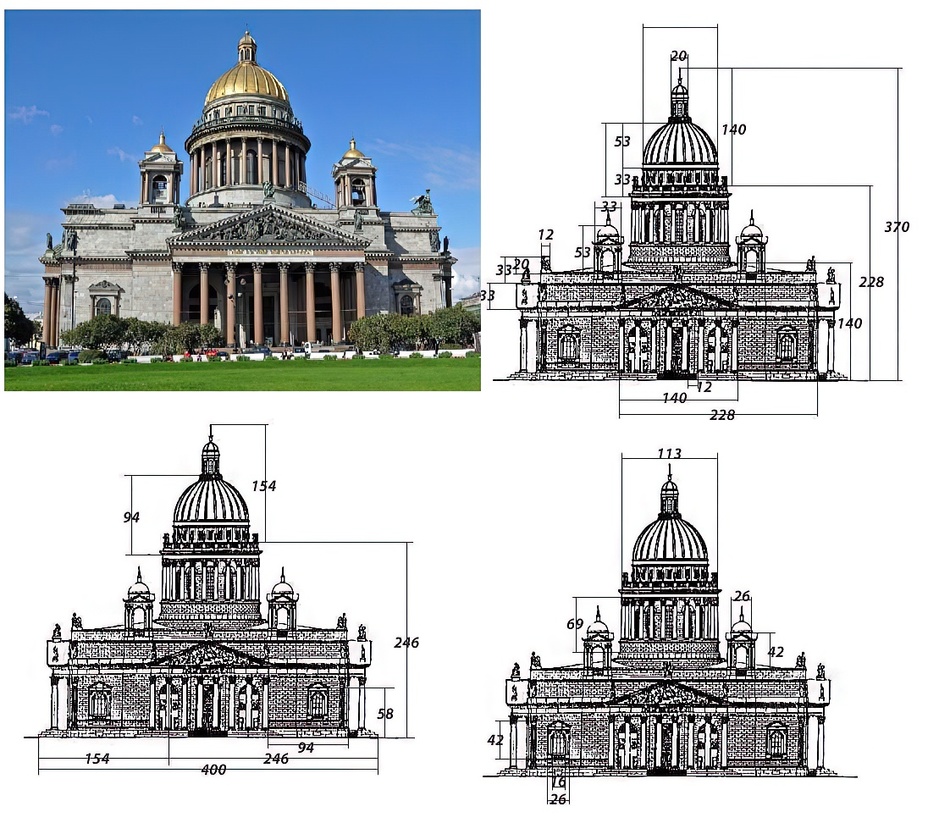
Свой поиск она начала, как рекомендуется в методике профессора Московского архитектурного института Ю.Н.Герасимова, с фасада собора. На чертеже просматриваются три ряда Золотого сечения.

Первый ряд определён шириной здания, которая принята за 400 ед. и представляет такие цифры 400, 247, 153, 94, 58…
Если 400 разделим на число ≈1,618, то получим приблизительно 247; повторяем действие со следующим числом: 247: 1.618≈153.
И так находим все числа. Теперь смотрим на рисунок. Основная часть с колоннами вписывается в прямоугольник со сторонами 400 и 247. Поскольку стороны находятся в соотношении Ф≈1.618, то они образуют Золотой прямоугольник.
Следующий ряд представлен высотой здания: 370, 228, 140, 87, 53, 33, 20, 12. Эти размеры заложены в более мелкие детали. По вертикали Исаакиевский собор делится Золотым сечением у основания купола, что делает соотношение основной части и купола гармоничным.
Третий ряд размеров начинается со 113, и являет ширину основания главного купола: 113, 69, 42, 26, 16. Числа этого ряда встречаются в размерах окон, в высотах колонн и других деталей собора.
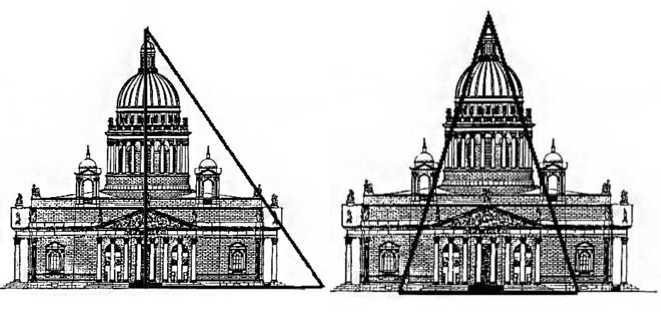
Золотые прямоугольный и равнобедренный треугольники имеют место в здании Исаакиевского собора, как видно из рисунка.
Кунсткамера
На Университетской набережной Васильевского острова стоит здание Кунсткамеры, заложенное в 1718 году под руководством немецкого архитектора Георга Маттарнови: Петровское барокко, два 3-этажных корпуса и сложная многоярусная купольная башня.
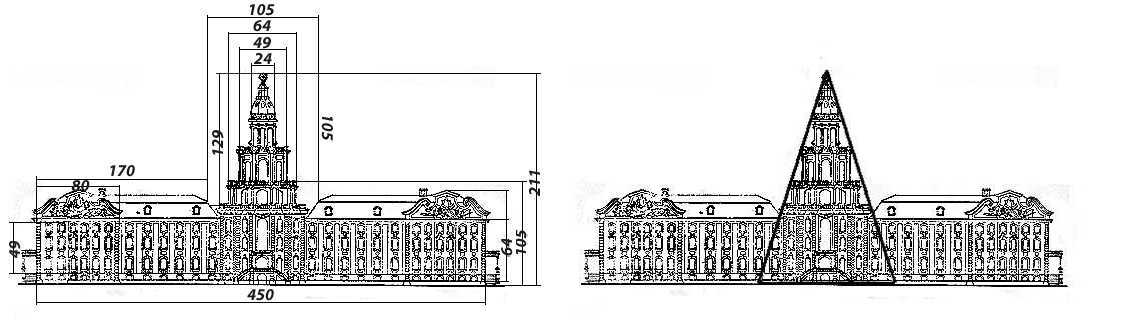
Исследование начинается с главных величин: высоты и длины здания, от которых строится золотой ряд. Длина — 450 ед., далее 277, 170, 105, 65, 40, 24. Такие размеры можно видеть в высоте и широте разных уровней башни, длине корпусов. Сама башенная часть вписана в золотой равнобедренный треугольник от основания до вершины. Золотое сечение просматривается в большей степени именно в этом главном элементе, что правильно с точки зрения архитектуры. Вывод: основа Кунсткамеры подчиняется золотому правилу и сохраняет композиционную гармоничность.
Новый золотой ряд начинает высота здания: 211, 130, 80, 49, 30. Глядя на размеры чертежа, становиться понятно, что выбор трёхэтажного вида корпусов обусловлен соразмерностью с башней.
Торговый дом «Эсдерс и Схейфальс» на пересечении Мойки и Гороховой
Построено в 1907 году по проекту Владимира Александровича Липского и Константина Николаевича де Рошефора (Рошфора). В 1905 г. бельгиец С. Эсдерс и нидерландец Н. Схейфальс подали прошение о разрешении построить пятиэтажное здание с куполом и шпилем на угловой башне для их торгового дома вместо старого.
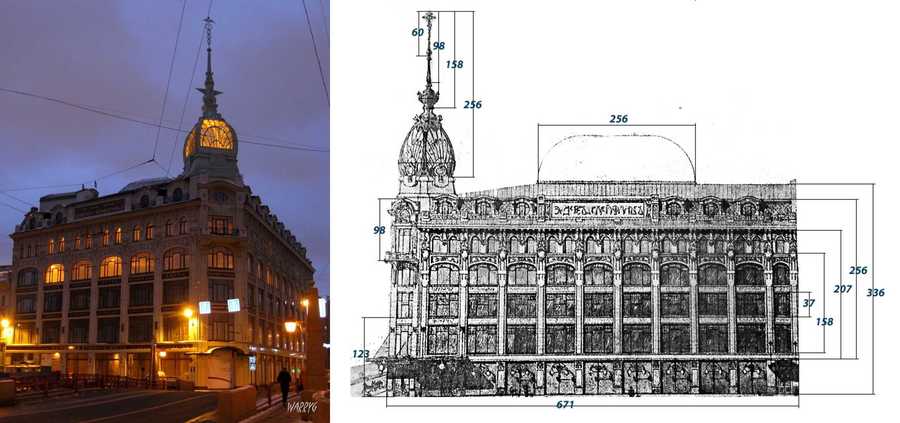
С длины здания в 671 ед. начинается ряд Золотого сечения, наблюдаемого в размерах: 671, 414, 256, 158, 98, 60, 37, 23. Обращаем внимание на основной элемент — шпиль. Убеждаемся, что композиционное решение завершено гармоничным сочетанием высотных величин.
Дом Советов на Московской площади
Построен в 1941г по проекту Ноя Абрамовича Троцкого. Здание советского периода рассматривают как творческую интерпретацию классики. Центральный портик с четырнадцатью колоннами завершает скульптурный ансамбль на тему строительства социализма и гербом Российской Советской Федеративной Социалистической Республики.

По бокам симметрично расположены пятиэтажные корпуса. Длина Дома достигает 1472 ед., из которого методом деления на число Ф получается ряд размеров элементов здания: 1472, 909, 562, 34, 214, 132, 81, 50 (Приложение 21): высоты сооружения, высоты входа и др.
Вершина Золотого равнобедренного треугольника совпадает с вершиной здания, а его стороны проходят через вехние точки главного входа. Прямоугольный золотой треугольник образован вершинами в верхушке здания и в конце внутренней части бокового крыла. Пропорциональность очевидна, хотя и не имеет большой композиционной значимости.

Москва
Московский Государственный Университет на Воробьёвых горах

Над его проектом работал коллектив под управлением Б.М.Иофана, которого позже сместили с должности главного архитектора. Образец послевоенной советской архитектуры выстроен с 1949 по 1953 годы.
Б.М.Иофан предложил композицию из пяти составляющих с центральной башней. В годы строительства это было самое высокое здание в Европе.
Длина здания равна 1472 ед. и начинает ряд: 909, 562, 347, 214, 132, 81, 50. Золотому сечению подчиняются, в основном высотные размеры. Из ширины башни проистекает другой ряд: 538, 332, 205, 126, который видим в широтных размерах.
Золотой прямоугольный треугольник гипотенузой проходит через угол здания и захватывает пристройки.
Таким образом, во всех исследуемых зданиях ученица обнаружила Золотое сечение, сохраняющее гармонию.
5 примеров дополнительно
Чтобы упростить задачу поиска ЗС, можно брать рациональные дроби 3/2; 5/3; 8/5; 13/8; 21/13; 34/21; 55/34; 89/55; и так дальше. Закономерность ясна: 3+2 =5; 5+3=8; 8+5=13… Или ещё проще. Сделайте себе циркуль для определения пропорции по инструкции в видео. Времени уйдет минут 10. Как пользоваться этим циркулем для определения пропорциональности элементов тоже расскажут и покажут.
Применяя этот способ, находим золотую пропорцию русского зодчего Матвея Казакова в кремлёвском здании сената, да и во всех остальных работах: Пречистенском дворце в Москве, Благородном собрании, Голицынской больнице (им. Пирогова)…
Созданный другим великим архитектором Василием Ивановичем Баженовым дом Пашкова в Москве (Российская государственная библиотека) причисляют к образцам совершенных архитектурных памятников, в котором легко определить ЗС.

Ужасный символ Парижа и золотое сечение
 Когда в Париже собирали металлическую Эйфелеву башню, многие французы возмущались. Критики писали о ней, как об «уродстве города», «сраме Парижа», «тощей пирамиде из металлических лестниц». В их числе были Эмиль Золя, Дюма-младший, Ги де Мопассан. Сейчас этот самый посещаемый памятник является гордостью парижан. Может быть виной тому «божественная» пропорция?
Когда в Париже собирали металлическую Эйфелеву башню, многие французы возмущались. Критики писали о ней, как об «уродстве города», «сраме Парижа», «тощей пирамиде из металлических лестниц». В их числе были Эмиль Золя, Дюма-младший, Ги де Мопассан. Сейчас этот самый посещаемый памятник является гордостью парижан. Может быть виной тому «божественная» пропорция?
Она же наблюдается и самом знаменитом французском соборе Нотр-Дам-Де-Пари.
Вся правда о древних строителях
Интуитивно или сознательно великие архитекторы строили здания с учётом этих пропорций? Античные математики знали о золотом сечении со времён Пифагора. Находятся всё новые подтверждения его применения в архитектурных пропорциях. Однако не найти ни одной древней записи с прямой рекомендацией использовать “божественную пропорцию”. Нет таковой и у Витрувия (I век до н. э.), написавшего «Десять книг об архитектуре», в которых он рассматривал пропорциональности в том числе. Странный факт, не правда ли?
Может все выше приведённые исследования являются подгонкой под известный результат? Не так сложно выбрать из множества архитектурных элементов те, которые подтверждают гипотезу, т. к. абсолютной точности никто не требует. Логично задуматься над вопросом: «Что если греки НЕ применяли золотое сечение?»
Собственно говоря, и для Луки Пачоли, написавшего в 1509 году труд «Божественная пропорция», не столь важно было его прикладное значение. Важно было обосновать её мистическую природу. А применять его осознанно стали только с момента издания книги.
Тайна архитектуры Древней Греции
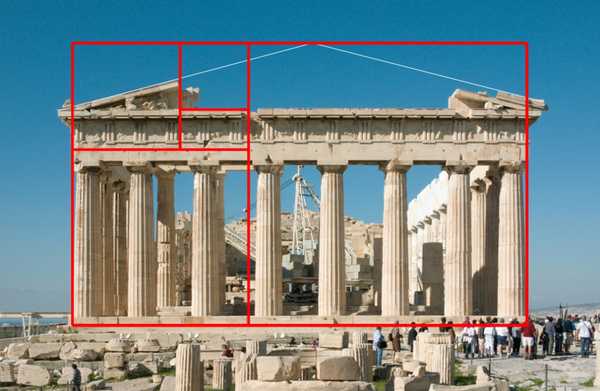
Красивые и гармоничные объекты всегда отвечают правилу ЗС, а при анализе величин определяется эта пропорциональность. Искусствоведы внимательно изучили греческий Парфенон, возведённый в честь победы над персами — храм богини Афины. Отношение длины храма к ширине даёт золотое число с маленькой погрешностью. Если отнять от длины сооружения 14 см и прибавить к ширине, то получится полное совпадение с математической величиной. Фасад здания немного сужается кверху, отклоняется от прямоугольной формы. Учитывая визуальное восприятие, сделано это строителями сознательно. Поэтому считать его прямоугольником золотого сечения не совсем корректно. Но пропорции соблюдаются, так что логично предположить, что архитекторы Иктин и Калликрат умышленно заложили правило в проект?
Мифы и диковинные факты о пирамиде
Пирамида Хеопса также выстроена с учётом этого условия. Не вдаваясь в математическое доказательство наличия золотой формулы, скажем только, что в нём присутствуют прямоугольный золотой треугольник, сторонами которого являются высота и половина стороны основания строения. Ничего удивительного?
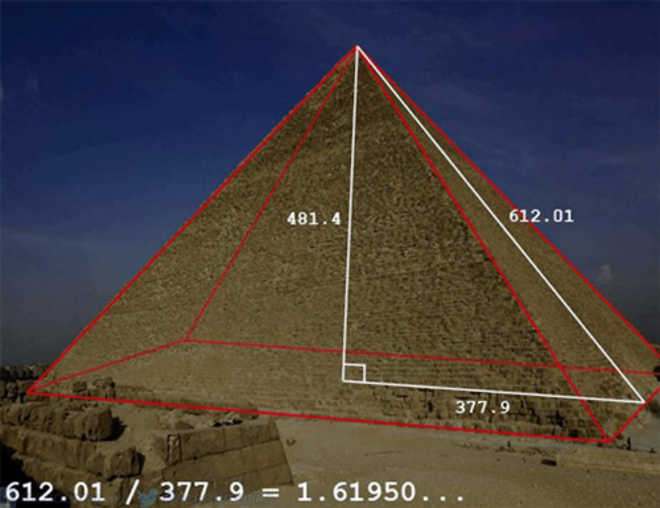
Но тогда возникает вопрос об уровне древнеегипетской математики. Выходит, что теорема Пифагора была им известна за два тысячелетия до рождения самого учёного. Внимание привлекает факт, что наследники Хеопса строили свои пирамиды уже с другими пропорциями. Почему?
Установлено, что сооружения пирамидальной формы с ЗС оказывают на находящихся в них феноменальное воздействие: растения лучше растут, металлы становятся прочнее, вода долго остаётся свежей. Учёные много лет работают с этими загадками, но тайна остаётся.
Замечено, что пирамида приводит структуру пространства в слаженное состояние. Всё, что попадает в зону действия, тоже организуется подобным образом: психоэмоциональное состояние людей улучшается, вредные для человека излучения уменьшаются, исчезают геопатогенные зоны. Интернет утверждает, что если размер фигуры увеличивается в два раза, то влияние пирамиды усиливается в сто раз.
Как же всё-таки построить «Золотой» дом для себя?
Правильное распределение энергий внутри дома, гармоничные конструкции в сочетании с экологией и безопасностью строительных материалов побуждают современных архитекторов и дизайнеров использовать принципы и понятия Золотого сечения. Это увеличивает смету и создаёт впечатление глубокой проработки проекта. Стоимость возрастает на 60-80%.
Для талантливых художников и архитекторов правило сохраняется интуитивно во время творческого процесса. Однако некоторые из них сознательно реализуют это положение.
В природе подобная соразмерность встречается везде. Тот, кто чувствует гармонию пространства, создаст пропорциональное здание без специальных для этого усилий.
Например, наши предки строили хоромы соразмерные человеку. Мерили высоту и длину в саженях, локтях, аршинах, пядях. Никто не возражает, что в человеческом теле соблюдена золотая пропорция? Длина руки от кончиков пальцев до подмышки относится к расстоянию от той же точки до локтя как эта величина к размеру ладони.
Известный французский архитектор Ле Корбюзье для расчёта параметров будущего дома и интерьера использовал в качестве отправной единицы рост хозяина. Все его работы по-настоящему индивидуальны и гармоничны.
5 способов соблюдать правило в интерьере
- В доме, построенном без учёта соотношения, можно сделать перепланировку комнат, чтобы пропорции соответствовали.
- Иногда достаточно переставить мебель или сделать дополнительную перегородку.
- Аналогичным образом меняется высота и длина окон и дверей.
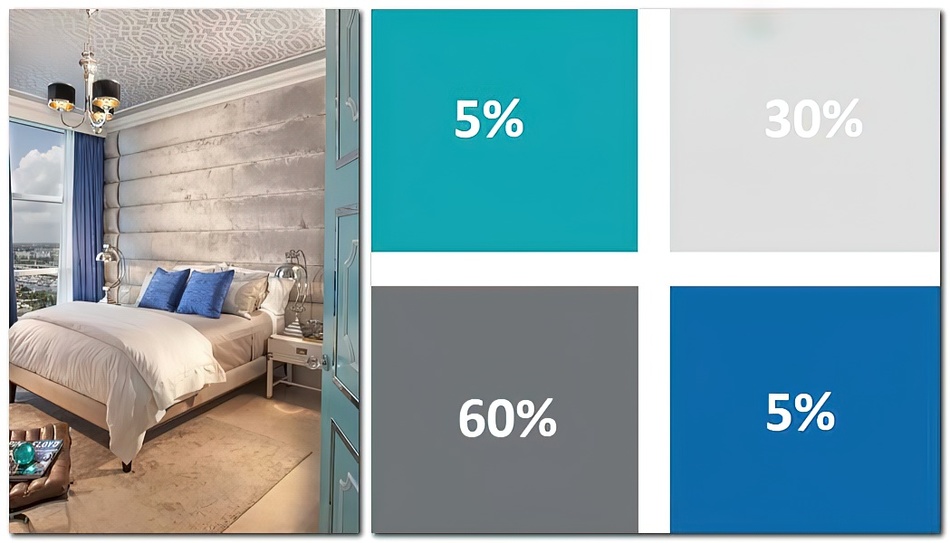
- В цветовом оформлении получение упрощённого соотношения достигается за счёт 60% основного цвета, 30% — оттеняющего, и остальных 10% — усиливающих восприятие тонов.
- Высота и длина мебели должна соизмеряться высотой потолков и шириной простенков.
Приложение этой нормы в интерьере, как архитектурно оформленном пространстве, объединяют с понятиями самоорганизации, рекурсии, асимметрии, красоты.
О золотом сечении простыми словами
Что же это такое? Отрезки золотой пропорции выражаются бесконечной иррациональной дробью, десятичное значение которой равно приближённо числу Ф≈1,618 или Ф≈1,62. Другими словами: если берём целое и делим его на две части так, что одна из них составляет 62%, а другая — 38%, получаем Золотую пропорцию.
Золотой прямоугольник: когда длину большей стороны делим на длину меньшей и получаем число Ф. При делении меньшей на большую получается обратное значение φ ≈ 0,618.
Золотой равнобедренный треугольник: если отношение размера одной боковой стороны и размера основания составляет золотое число Ф; угол между равными сторонами равен 36°.
Золотой прямоугольный треугольник Кеплера объединяет в себе теорему Пифагора и ЗС: соотношение квадратов его сторон составляет 1,618.
Оцените полезность статьи, поделитесь с друзьями и добавьте в закладки, чтобы было легко найти.
Смотрите познавательное видео по теме
Почему нас так привлекают строения древней архитектуры, при виде которых мы испытываем гармонию и умиротворение? Все они были построены на основе золотого сечения, данная зависимость прослеживается и в средневековье, и в современном мире. Математическая пропорция встречается повсеместно: это и ракушки моллюсков, и знаменитые картины художников, и строение человеческого тела, и даже египетские пирамиды. Сегодня расскажем простыми словами, как и, самое главное, зачем нужно использовать божественную гармонию чисел, и как она поможет в строительстве собственного дома и оформлении интерьера.
Просто о сложном: что это такое – правило золотого сечения
Золотое сечение –это правило общей пропорции, которая создает универсальную композицию. Математики называют её формулой божественной гармонии или асимметричной симметрией.
ЭТО ИНТЕРЕСНО! Общее определение правила золотого сечения меньшая величина относится к большей, как большая к целому. Было рассчитано приблизительное число, равное 1,6180339887, это и есто коэфициент золотого сечения. Если смотреть в процентном соотношении, то в одном целом меньшая величина занимает 38%, большая- 62%.
Признано считать, что ЗС пришло к нам еще с древней Греции, но есть и такое мнение, что его греки подсмотрели у египтян. Если проанализировать архитектуру Египта того времени, можно чётко проследить соблюдение математической гармонии. Необычные свойства числовой зависимости стали причиной мистического отношения к золотому сечению:
- практически все живые организмы можно привести к принципу числовой зависимости. Например, тело человека, количество семечек в подсолнухе, структуру ДНК, произведения искусства и вирусную бактерию;
- данная зависимость чисел характерна только для биологических существ и кристаллов, все остальные неживые объекты природы крайне редко обладают золотой пропорцией;
Экскурс в историю: кто придумал золотое сечение
Представление о золотой пропорции имели и древние греки, и египтяне. Но впервые ещё в 1509 году в книге «Божественная Пропорция», иллюстрации к которой принадлежат Леонардо да Винчи, монах Лука Пачоли дал научное определение правилу. Он видел в золотом сечении божественное единство:
- маленький отрезок – это сын;
- большой – отец;
- весь отрезок – это святой дух.
Это интересно. Историки присваивают Леонардо Да Винчи определения термина золотого сечения, поскольку он долгое время изучал божественную закономерность и воплощал ее принцип в своих творениях.
Вторую жизнь ЗС получило в 1855 году благодаря философу Адольфу Цейзингу. Он доработал теорию до абсолютного идеала, и она стала универсальной для всех проявлений. Все это он описал в своей книге «Математическое Естество», на которое в свое время обрушилось много негатива и критики.
Принцип расчета и построения золотого сечения
Примеры пропорции золотого сечения можно видеть при строительстве многих архитектурных сооружений, только нужно знать, как правильно его увидеть. Для этого достаточно посмотреть на строение всего 5 минут.
Как определить число золотого сечения
С пропорцией ЗС связывают астронома из Италии Фибоначчи, он вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Сегодня эта закономерность известна как ряд Фибоначчи:
- 0, 1,1(0+1), 2 (1+1), 3 (1+2), 5 (2+3), 8 (3+5), 13 (5+8), 21 (8+13), 34 (13+21), 55 (21+34), 89 (34+55) и так до бесконечности;
- если выполнить деление последующего числа на предыдущее – получится коэффициент ЗС.
Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленные значения 0,62 и 0,38.
Как рассчитать золотое сечение на простейшем примере
Проще всего объяснить гармонию ЗС можно на примере обычного куриного яйца, точнее на удалении всех точек скорлупы от центра тяжести. Именно форма оболочки, а не её прочность, обеспечила выживаемость птиц столь долгое время и в любых условиях.
Если взять обычный отрезок, который состоит из нескольких маленьких, их длины относятся к большей величине как 0,62. Это показывает, как можно разбить целую линию для получения идеальной пропорции.
Как построить золотое сечение на примере прямоугольника и спирали
Если построить золотой прямоугольник, используя ряд Фибоначчи, он будет выглядеть как единое целое. Рассмотрим зависимость на примере:
- нужно нарисовать квадрат со стороной 1 и рядом ещё один аналогичный;
- над ними разместить квадрат со стороной 2;
- слева гармонично помещается квадрат с гранью 3;
- ниже – квадрат со стороной 5;
- справа пространство займет квадрат с гранью 8;
- площадь прямоугольника 8×13, в котором 13 — это следующее число ряда;
- если разделить на калькуляторе следующее число на предыдущее, получится значение золотого сечения 1,62, причём, чем больше числа, тем меньшая погрешность в их отношении;
- если по этому принципу построить спираль, каждую четверть витка она будет расширяться именно на значение ЗС.
Божественная гармония золотого сечения в архитектуре: фото древних построек и примеры современного строительства
Многие древние здания, которые сохранились до наших времен, подтверждают мнение, что они были построены по правилам идеальной пропорции. Это резиденции королей, церкви, общественные сооружения. Рассмотрим на примерах принцип золотого сечения в разных странах.
Тайны древнеегипетской архитектуры
В архитектуре Древнего Египта по правилам золотой пропорции была построена пирамида Хеопса. Глядя на творение строителей, можно увидеть треугольник с прямым углом, один катет которого является высотой, второй – половиной длины основания. Если взять отношение гипотенузы к меньшей стороне, получим идеальное значение 1,61950 или 1,62.
ЭТО ИНТЕРЕСНО! Форма пирамиды имеет еще одно неоспоримое свойство. В нем сталь становится прочнее, вода дольше сохраняет свежий вкус, и быстрее растут живые растения. Много лет ученые пытаются разгадать этот феномен, но покаего научное решение не найдено.
Было замечено, что пирамида улучшает психоэмоциональное состояние человека, в её области уменьшаются вредоносные излучения, пропадают геопатогенные зоны.
Идеальные пропорции в древней Греции
Идеальная пропорциональность делает архитектурные объекты запоминающимися. Яркий представитель ЗС из древней Греции – Парфенон, который возведен в 5 веке до нашей эры. Если взять отношение его высоты к ширине, получится практически идеальное число 0,618.
Ученые определили, что для абсолютного золотого числа нужно отнять от высоты 14 см и прибавить их к ширине. Учитывая строение сооружения, очень похоже, что это было сделано древними архитекторами Иктином и Калликратом намеренно, поскольку фасад немного сужается в верхней части и отклоняется от золотого прямоугольника. Но общие пропорции ЗС соблюдены.
Памятники архитектуры средневековья
Прекрасным памятником истории архитектуры средневековья, сохранившимся до нашего времени, является собор Парижской Богоматери или Нотр-Дам де Пари.
Архитектура России
Ряд Фибоначчи – это своеобразная матрица, с помощью которой анализируют любое архитектурное сооружение. Чтобы было проще ориентироваться, можно построить на принципе золотого сечения циркуль Фибоначчи.
Золотое сечение в архитектуре Москвы
Выдающееся здание МГУ на Воробьевых горах было построено в послевоенное время. В те годы это было самое высокое строение, состоящее из пяти композиционных групп, которые венчает центральная башня. Здесь чётко прослеживается треугольник с прямым углом, гипотенуза которого захватывает пристройки и проходит через угол здания.
Золотые пропорции прослеживаются и в работах русского зодчего Матвея Казакова
Использовал это прием и архитектор Василий Баженов, его здания причислены к историческим памятникам
Архитектура в Санкт-Петербурге
Живым примером золотого сечения является Исаакиевский собор.
В первую очередь можно проанализировать его ширину, равную 400 единицам:
- при делении числа 400 на значение золотого сечения получим приблизительно 248;
- при дальнейшем делении 248/1,618=153;
основная часть собора вписывается в золотой прямоугольник, длинная сторона которого равна 400, ширина – 248. По высоте здания ЗС можно видеть у купола, благодаря этому внешнее восприятие памятника архитектуры становится гармоничным.
Приведем ещё несколько примеров золотого сечения в архитектуре Санкт-Петербурга.
Кунсткамера
Кунсткамера была построена ещё в 1718 году, руководил строительством немецкий архитектор Георг Маттарнови. Она представляет собой 2 корпуса по 3 этажа, между ними возведена куполообразная многоярусная конструкция в виде башни.Золотое сечение в соотношении сторон можно наблюдать в длине корпусов и в высотах разных уровней.
Торговый дом Эсдерс и Схейфальс
ЗС в здании, возведенном в 1907 году, наблюдается в следующих размерах:
- 671, 414, 256, 98, 60, 37 и 23.
Композиция смотрится гармонично благодаря золотому соблюдению высотных величин.
Дом Советов
Дом Советов был возведен по проекту Троцкого в 1941 году, основной акцент выполняют портик по центру с 14 колоннами и скульптурный ансамбль. По обе стороны расположены два корпуса высотой в 5 этажей. Длина здания – 1472 единицы, если разделить его на значение Ф = 1,618, получим размерный ряд:
1472, 909, 562, 347, 214, 132, 81, 50. К ним относятся высота входа, всего сооружения, различных элементов.
Золотой прямоугольный треугольник идеально вписывается в центр здания, его вершина совпадает с вершиной Дома Советов, а гипотенуза заканчивается в конце бокового крыла. Если построить равнобедренный золотой треугольник, его грани будут проходить через точки в верхней части основного входа.
Примеры золотого сечения в современной архитектуре
Правило золотого сечения при строительстве частного дома
Многие архитекторы, которые разрабатывают проекты частных домов, используют правило золотого сечения. У клиентов создается ощущение, что все детали проработаны для максимально комфортного проживания. При грамотном выборе площадей жильцы на психологическом уровне ощущают умиротворение и успокоение.
Что нужно знать при проектировании фасада
В современном строительстве при проектировании домов кроме ряда Фибоначчи используют ещё один метод, основоположником которого был архитектор из Франции Ле Корбюзье. Он принимал за основу рост будущих владельцев усадьбы и, исходя их этого, рассчитывал параметры строения и комнат. Благодаря такому подходу дом получался не только гармоничный, но и максимально комфортный с индивидуальными чертами хозяев.
Золотое сечение в оформлении интерьера
Даже если дом возведен по типовому проекту, можно внутри его создать интерьер, максимально приближенный к идеальной пропорции 1:1,62. Например, благодаря дополнительным перегородкам или расположению мебельных групп, а также можно изменить дверные или оконные проемы, чтобы соотношение ширины к высоте было в золотом сечении.
Аналогичная ситуация и с цветовым оформлением интерьера, здесь действует упрощенное правило:
- 60% — основная палитра;
- 30% — дополнительный оттенок;
- 10% — близкий тон, который усиливает восприятие основного и дополнительного.
Принцип золотого сечения не является новым в архитектуре, поскольку в прежние времена здания строились не по типовым проектам, а с учетом индивидуальных особенностей будущих владельцев. Такие строения выглядят даже спустя многие года гармоничными и привлекательными. Интерьер, оформленный по правилам идеальной пропорции, позволяет грамотно использовать все площади.
Теперь вы сможете самостоятельно и правильно применить божественную гармонию математических цифр, планируя строительство дома или оформляя свой интерьер. Более того, интересную комбинацию цифр можно использовать и в экономике, и в расчете инвестиций и во всех деталях, с которыми соприкасается человек ежедневно.
Если у вас ещё остались вопросы, предлагаем посмотреть видео, в котором простыми словами разъяснен принцип действия золотого сечения:
На чтение 5 мин. Просмотров 615 Опубликовано 22.03.2023
Содержание
- Что такое золотое сечение?
- Как использовать принцип золотого сечения?
- Наглядные примеры ЗС в архитектуре
- Парфенон, Афины, Греция
- Тадж-Махал, Агра, Индия
- Собор Нотр-Дам, Париж, Франция
- Музей Гуггенхайма, Нью-Йорк, США
- Вилла Савойя, Пуасси, Франция
- Почему в частном домостроении ЗС используется редко?
Золотое сечение — это пропорция, которая часто считается эстетически приятной и гармоничной, и ее можно увидеть во многих известных зданиях и произведениях искусства. В этой статье мы рассмотрим золотое сечение в архитектуре и то, как оно используется для создания красивых и функциональных зданий.
Что такое золотое сечение?

Золотое сечение Фибоначчи — это математическая концепция, которая на протяжении веков использовалась в искусстве, дизайне и архитектуре.
Правило применяется для создания ощущения гармонии и баланса при проектировании зданий. Оно может использоваться для определения различных элементов, таких как высота и ширина окон или расстояние между колоннами.
Использование в архитектуре восходит к Древней Греции, где оно применялось при проектировании таких зданий, как Парфенон. Это соотношение можно найти во многих других известных зданиях, таких как собор Нотр-Дам в Париже и Тадж-Махал в Индии. Сегодня используется в современной архитектуре. Проектировщики часто берут пропорцию в качестве ориентира для определения соотношения различных элементов в проекте здания, но не всегда необходимо или уместно использовать ее в каждом аспекте дизайна.
Как использовать принцип золотого сечения?

Соотношение составляет примерно 1,618, и его часто обозначают греческой буквой phi (Φ). Это число можно встретить во многих природных явлениях, включая спирали раковин, характер роста растений и расположение листьев на стеблях.
Формула Фибоначчи или золотое сечение можно получить, разделив линию на две части так, чтобы большая часть, деленная на меньшую, была равна всей длине, деленной на большую. Математически это соотношение выражается как (a + b)/a = a/b = Φ.
В архитектуре золотое сечение используется для определения идеальных пропорций здания. Например, высота здания может быть разделена на секции в соответствии с концепцией, причем высота каждой секции в 1,618 раза больше, чем высота секции, расположенной ниже. Это может сделать его более эстетически привлекательным.
Одним из самых известных примеров золотого сечения в архитектуре является Парфенон в Афинах, Греция. Парфенон был построен в 5 веке до нашей эры и считается одним из лучших образцов классической архитектуры. Храм основан на системе пропорций, включающей золотое сечение, и считается, что использование этой пропорции является одной из причин, почему здание так радует глаз.
Используется в дизайне, особенно в графическом. Например, размеры изделия могут быть основаны на ЗС, когда ширина в 1,618 раза больше высоты. Это может создать впечатление сбалансированности продукта, а также сделать его более визуально привлекательным.
Наглядные примеры ЗС в архитектуре
Принцип использовался в архитектуре на протяжении всей истории, от древних времен до наших дней. Вот несколько примеров применения.
Парфенон, Афины, Греция

Является одним из самых известных примеров. Построенный в 5 веке до н.э., храм был посвящен греческой богине Афине и служил символом афинской демократии и власти. Фасад Парфенона основан на золотом сечении — ширина здания в 1,618 раза больше его высоты. Колонны здания также спроектированы с учётом этой концепции, их диаметр составляет 1/20 часть высоты колонны.
Архитекторы Парфенона использовали ЗС для создания ощущения гармонии и равновесия в дизайне здания, которое должно было отражать идеалы афинского общества. Несмотря на то, что Парфенон был поврежден в течение веков, он остается одним из самых знаковых строений в архитектуре.
Тадж-Махал, Агра, Индия

Является еще одним примером в архитектуре. Он был построен могольским императором Шах-Джаханом в память о его любимой жене Мумтаз Махал и считается одним из лучших образцов могольской архитектуры.
Тадж-Махал имеет несколько элементов, которые следуют золотому сечению, включая общие пропорции, высоту и ширину центрального купола, а также расположение и размер минаретов. Высота купола также пропорциональна общим размерам здания.
Кроме того, декоративные элементы Тадж-Махала, такие как сложные цветочные узоры и каллиграфия, также расположены в соответствии с концепцией. Симметрия и баланс этих элементов создают ощущение умиротворения.
Собор Нотр-Дам, Париж, Франция

Является классическим примером. Собор был построен в готическом стиле в период с XII по XIV век и включает в себя множество элементов. Одним из наиболее ярких примеров использования ЗС является планировка собора. Общий план здания основан на прямоугольнике. Кроме того, высота собора разделена на секции, которые также пропорциональны.
Другим примером использования является окно в виде розы, расположенное на западном фасаде собора. Использование ЗС в Нотр-Даме, не ограничивается общей планировкой здания и декоративными элементами.
Музей Гуггенхайма, Нью-Йорк, США

Спиральный пандус музея, спроектированный архитектором Фрэнком Ллойдом Райтом, имеет изгиб, повторяющий золотую спираль. Использование такой формы не только служит эстетической цели, но и позволяет посетителям легко ориентироваться в пространстве и рассматривать экспонаты в непрерывном потоке.
Райт был известен использованием органических форм и природных материалов в своих проектах, и Гуггенхайм не является исключением. Внешний облик музея выполнен из бетона и изогнут таким образом, чтобы имитировать форму раковины наутилуса. Использование таких материалов и органических форм в сочетании с точным применением ЗС приводит к созданию гармоничного и визуально потрясающего сооружения.
Вилла Савойя, Пуасси, Франция

Спроектированная Ле Корбюзье, является ярким примером использования золотого сечения в современной архитектуре. Пропорции здания основаны на ЗС, как и внутренние помещения.
Почему в частном домостроении ЗС используется редко?

Хотя правило золотого сечения в архитектуре используется достаточно часто, в частном жилищном строительстве оно встречается относительно редко. Одна из причин этого заключается в том, что частное жилищное строительство часто определяется практическими соображениями, такими как бюджет и функциональность, а не эстетическими соображениями. Кроме того, использование золотого сечения в жилищном строительстве может восприниматься как элитарное или претенциозное, и может не подходить для всех типов жилья.
Концепция пропорций и баланса была важна с ранних времён. На протяжении всей истории архитекторы и дизайнеры использовали различные принципы для достижения гармонии в своих творениях.
Одним из таких принципов является применение концепции, которая наблюдается во множестве произведений искусства и архитектуры. Хотя сама по себе идея остается спорной, ее влияние на мир дизайна и эстетики невозможно отрицать. От древних греков до современных архитекторов стремление к балансу и гармонии в дизайне остается фундаментальным аспектом архитектурной практики.
Наблюдения за природой и попытки раскрыть тайны ее прекрасных созданий принесли немало открытый. Одно из них — золотое сечение. Это некоторая закономерность, которой подчиняется все, что мы называем красивым. Люди, животные, цветы, здания, галактики…
Содержание статьи
- 1 Что такое золотое сечение и как его понимать
- 2 Как построить прямоугольник с идеальными пропорциями
- 3 Как разделить отрезок по правилу золотого сечения
- 4 Идеальный треугольник и пентаграмма
- 5 Применение в строительстве
- 6 Золотое соотношение во внутреннем оформлении
- 7 Золотое сечение в ландшафтном дизайне
Что такое золотое сечение и как его понимать
Часто мы сталкиваемся с домами, предметами, строениями, растениями, которые нас чем-то завораживают. Люди издавна пытались понять, почему одно нам кажется красивым, другое нет, искали закономерности. И вроде нашли. Это некоторое соотношение частей, которое назвали золотым сечением.
О том, кто и когда придумал золотое сечение никто не знает точно. Кто-то приписывает открытие Пифагору, но первое упоминание нашли еще в «Началах» Евклида, а жил он в 3 веке до нашей эры. Так что находка явно давняя. Именно по этому принципу построены древнегреческие и римские храмы. Конечно, это могут быть совпадения, но очень уж странные и очень их много. Так что, скорее всего, они были в курсе идеальных пропорций.

Совершенно точно то, что Леонардо да Винчи искал подтверждение этому принципу в строении человеческого тела. И, что самое интересное, нашел. Те лица и тела, которые кажутся нам красивыми, имеют пропорции, которые как раз и подчиняются закону золотого сечения.
Формальное определение звучит и просто, и сложно. Его связывают с двумя разными по размеру отрезками. Звучит этот принцип примерно так: если отрезок разделить на две неравные части, то это деление будет пропорциональным, если большая часть отрезка относится к целому так же, как и меньшая часть к большему. Будет понятнее, если посмотреть на иллюстрацию и формулу.

На рисунке целый отрезок разделен так, что если а разделить на b, получим 1,1618, та же цифра получается, если целый отрезок разделить на большую часть — a. Это число и есть воплощением идеальной пропорции. Теперь, если посмотрите на картинку с Парфеноном, пропорции этого строения также подчиняются указанному соотношению.
Ту же закономерность можно представить в виде процентов. Может, кому-то так проще. Для того, чтобы деление целого было пропорциональным, части должны составлять 62% и 38%. Возможно, так будет проще запомнить.

Эту закономерность развил дальше математик Фибоначчи. Он разработал числовую последовательность, элементы которой, начиная с девятого, подчиняются тому же закону. Графическое изображение этой последовательности — спираль. Если присмотреться, и в природе, и в архитектуре, и в человеческом теле пропорции красоты присутствуют.
Как построить прямоугольник с идеальными пропорциями
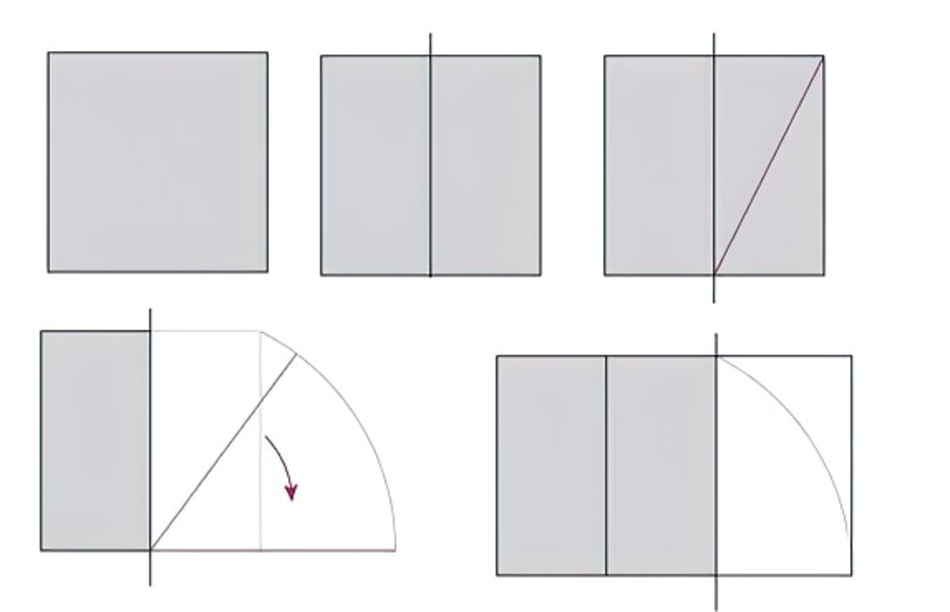
Чтобы применять на практике полученную информацию, надо каким-то образом научиться делить пространство или строить его согласно этому закону. Для начала давайте научимся строить прямоугольник с идеальными пропорциями. За основу берем квадрат.

Квадрат делим пополам, в одном из полученных прямоугольников проводим линию, которая соединяет противоположные углы. Дальше берем циркуль, ставим иголку в центр нижней стороны квадрата, откладываем длину полученной диагонали и отмечаем ее на линии, которая будет продолжением нижней стороны квадрата. Полученный прямоугольник имеет соотношение сторон 1,62 (это как раз то соотношение, которое и дает 62% и 38%).

Что еще интересно, что если вы начнете делить прямоугольник с соотношением сторон 1,62 на квадрат и прямоугольник, вы получите снова прямоугольник с идеальными пропорциями, но меньшего размера. Если вы его снова разделите по тому же принципу, будет еще одна пара квадрат+прямоугольник со сторонами, соотношение которых будет соответствовать золотому сечению. И так до тех пор, пока вы сможете проводить деление. Но что еще интереснее, в это деление отлично вписывается ряд Фибоначчи, который имеет вид раскручивающейся спирали. Иллюстрация на рисунке выше.
Как разделить отрезок по правилу золотого сечения
Это умение пригодится, например, при создании проекта дома, планировки, при разработке дизайна квартиры, расстановке мебели и т.д. Точно также может понадобиться при планировке участка, клумб, высадке растений и т.д. В общем, применяться может практически везде.

Итак, порядок деления отрезка по правилу золотого сечения:
- Берем отрезок, делим его пополам.
- Из одного из концов восстанавливаем перпендикуляр (прямая под углом 90°), который длиной равен половине отрезка. На рисунке это отрезок BC.
- Полученную точку C соединяем прямой с другим концом отрезка (A).
- На отрезке AC ставим точку D. Она находится на расстоянии, равном длине отрезка BС. Проще всего это сделать при помощи циркуля, но можно и линейкой.
- Замеряем длину отрезка AD (снова циркулем, либо линейкой). Такую же длину откладываем на отрезке AB. Получаем точку E.
- Теперь, если измерить длины отрезков AE и EB и разделить их, получим то самое заветное число — 1,62.

Пару раз повторив процедуру, вы научитесь делать все буквально за считанные минуты. Если же вам надо, например, определить высоту окна, его форму, также можно воспользоваться данными пропорциями. По тому же принципу можно определять местоположение всех архитектурных элементов, их размеры. При планировании уже имеющихся объектов, деление проще проводить при помощи процентного соотношения. Тут уже либо считаете в уме, либо используете калькулятор.
Идеальный треугольник и пентаграмма
Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.

Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.
Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.
- Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
- Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D.

- Соединяем точки E и D. При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
- Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.
Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.
https://youtu.be/c3SVIQBXMnA
Применение в строительстве
Как уже говорили, неизвестно кто открыл золотое сечение, но все, что кажется нам красивым, имеет именно такое соотношение сторон. Примеров в природе очень много. Если рассматривать известные здания, то и там тоже есть та же закономерность.

Если вы хотите, чтобы ваш дом внутри и снаружи был привлекательным, запоминался и нравился, при создании или выборе проекта можно просчитать хотя бы основные пропорции. Внести корректировки в пропорции, возможно, не всегда легко, часто связано с дополнительными расходами. Но, если при создании проекта сразу держать в уме золотое сечение, вопросы сами по себе отпадают. На самом деле не так уж это сложно.
Например, вы хотите дом площадью около 100 квадратных метров. Длинную сторону можно принять за 12 метров. Тогда короткая находится как 62% от длинной и составит 7,44 метра. Можно сделать 7 метров или 7,5, можно увеличить до 8. Точное, до сантиметра соблюдение размеров совсем не обязательно. Важно соотношение. А «на глаз» даже в приближении смотрится гармонично. Площадь застройки в таком случае получается несколько меньше — 90-96 квадратов. Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно.

Высота этажа в таком случае принимается как 32% от длинной части. Она составит 12*0,32 = 3,84 метра. В принципе, это соответствует нынешним представлениям о комфортных габаритах помещения, но при желании можно сделать высоту меньше. Примерно также рассчитываются, подбираются все остальные фрагменты дома.
Не стоит забывать, что дом должен вписываться также в ландшафт. Если есть какая-то доминанта — высокий холм, например, то просчитывать надо и соотношение с холмом, и с пропорциями участка. В общем, для создания гармоничной усадьбы очень многие факторы надо учитывать.

По такому же принципу разрабатывают внутреннюю планировку, стараясь по возможности соблюдать требуемое соотношение. Но еще раз повторим: по возможности. Не зацикливайтесь на точном соответствии до сантиметра. Важна общая тенденция.
Золотое соотношение во внутреннем оформлении
Что еще дает золотое сечение кроме визуального наслаждения? Психологи говорят, что в интерьере, созданном по этому правилу человек чувствует себя более комфортно. Это, конечно, субъективно, но можно попробовать. Итак, вот как интерпретируют правило золотого сечения в дизайне интерьеров:
- Если вы собираетесь разделить комнату на зоны, воспользуйтесь правилом. Это значит, что одна из частей должна быть около 62%, вторая — 38%.
- Площадь, занятая предметами мебели, не должна быть больше чем 2/3.
- При подборе мебели руководствуемся правилом: каждый средний предмет по габаритам относится к крупным так же, как маленький к средним.
- При выборе цвета придерживайтесь примерно тех же правил:
- Основной цвет составляет порядка 2/3, все дополнительные и акцентный — 1/3. Цвета выбирают сочетающиеся по определенным правилам.
- Второй вариант: 60% — основной цвет, 30% дополнительные и 10% — это акцентные.

Пример подбора цвета по правилам правильной пропорциональности
- При использовании горизонтального деления стены (панели), высоту панели можно брать 1/3 или 2/3 от общей высоты комнаты. Но при этом мебель подбирается пропорциональной по высоте, а не по длине.
Относительно мебели правило кажется непонятным, но это только на первый взгляд. Например, подбираем группу отдыха. Крупный предмет в этом случае — диван или софа. Средний — журнальный или кофейный столик, кресла. Мелкие — аксессуары. Так вот, размеры журнального столика не должны быть больше длинной стороны дивана, кресла — не больше его короткой стороны. Аксессуары по размерам не больше размеров столика или кресел. В идеале, они соотносятся с ними как 62% и 38%.

Почему не указывается точное соотношение? Потому что, во-первых, найти такие предметы нереально. Во-вторых, золотое сечение — это не только 62% и 38%. Это еще и последовательность Фибоначчи, следование которой также делает оформление гармоничным. Есть люди, у которых следование этой последовательности является «встроенной функцией». Им не надо считать, они выбирают основываясь на чутье и интуиции. Но если проанализировать их выбор, пропорции будут близки к идеальным. Вот так.
Золотое сечение в ландшафтном дизайне
При создании ландшафта на участке, принцип идеальных пропорций применяют, называя его правилом треугольника. В композиции должна быть одна доминанта, остальные ее составляющие лишь подчеркивают, оттеняют ее. Например, на участке есть большое дерево и вы хотите его обыграть. Оно и будет центром композиции — доминантой. Нанесите его на план, расчертите клумбу или рокарий, альпинарий — то, что хотите сделать.

От главенствующего растения или камня, под прямым углом проведите две линии. На этих линиях надо будет высадить более низкие растения. Причем второе по высоте не должно быть выше чем 2/3 от высоты основного объекта. Третий объект — не выше чем 1/3. Дополняют композицию еще более низкорослыми насаждениями. Это коротко о том, как применять золотое сечение в планировке посадок.
Но это не все. Растения надо подбирать по цветам — сочетание зелени разных оттенков, вкрапления цветов и декоративно-лиственных растений — все подчиняется тому же закону. Доминирующий оттенок составляет порядка 60%, дополнительные цвета — 30%, акценты — 10 %. Это если говорить о правилах подбора в одной группе. Но также надо согласовывать и весь план целиком — по размерам, высоте, цветам.
Золотое сечение в архитектуре и дизайне – основные принципы и приложения
Золотое сечение – универсальная математическая формула, которая используется в архитектуре и дизайне для создания гармоничных и пропорциональных объектов. В этой статье вы узнаете, как применять золотое сечение в своих проектах и какие преимущества это дает.
Почему нельзя оторвать взгляд при виде Тадж-Махала, собора Василия Блаженного, египетских пирамид, Золотого Храма в Амритсаре, Шартрского собора, замка Нойшванштайн, Исаакиевского собора? Их строили задолго до появления современных технологий, расчеты вели от руки, без помощи компьютера.
Как Рафаэлю Санти удалось написать мировой шедевр «Сикстинскую Мадонну» так, что столетиями мир удивляется игре красок, пропорциям тела? Что знал Микеланджело Буонаротти, когда писал «Святое семейство»? Почему эти и другие картины так ценятся? В чем их секрет? Может быть, дело в правиле Золотого Сечения, по принципам которого создавались неповторимые здания, картины и даже музыка?
Золотое сечение – что это
За право быть первыми, кто впервые увидел и применил принцип Золотого Сечения, соревнуются древние миры Греции и Египта.
По правилу Золотого Сечения соотношение меньшей величины к большей равно отношению большей величины к целому. В едином целом большая часть составляет 62%, меньшая – 38%. В числовом выражении это 1,6180339887. Эту величину обозначили греческой буквой «фи» (ф). У нее есть другие наименования: Золотая Пропорция, число Бога, число Фи.
По этому правилу создавались не только шедевры архитектуры. Все в мире подчиняется числу Бога. Оно есть в строении ДНК, человеческом теле, растениях и животных. Эволюция на Земле следует этой математической пропорции. Ярким примером Золотой Пропорции можно назвать изящную раковину морского моллюска.

История золотого сечения
Многие древние народы были знакомы с числом Бога. В Египте, Греции, Индии применяли его в жизни. Известно такое определение Божественной Пропорции:
- Маленьким отрезком является Сын
- Большим – Отец
- Целым отрезком – Святой Дух
Так описал Золотое сечение образованный монах Лука Пачоли в 1509 году. Великий Леонардо да Винчи всю жизнь исследовал эту закономерность, применял ее в:
- Живописи
- Механике
- Геометрии
- Математике
- Машиностроении
- Оптике
Определение числа золотого сечения
Достаточно посмотреть 5 минут на здание, чтобы увидеть, применялось ли при его строении число Фи. Для этого нужно знать формулу расчета Золотой Пропорции. Итальянский астроном Фибоначчи определил последовательность чисел. В ней каждое последующее число – это сумма 2 предыдущих чисел.
Это назвали «ряд Фибоначчи»: 0, 1, 1, 2, 3, 5, 8, 13, 21 и далее. Он заметил, что если разделить любое число в ряду на значение предыдущего числа, то получится число Бога. Теперь эту последовательность применяют как матрицу, с помощью которой можно проанализировать архитектурную постройку. Для простоты на основе принципа Золотой Пропорции построили циркуль-разметчик Фибоначчи.
Пример золотого сечения
Утверждение, что число Фи присутствует в природе везде, можно доказать просто. Возьмем обычное куриное яйцо. Почему оно такой формы? Именно она в процессе эволюции гарантировала птицам выживаемость. Потому что природа придала яйцу идеальную форму Золотого Сечения.
Если провести две перпендикулярные линии через центр тяжести яйца, заключить лежащее на боку яйцо в рамки прямоугольника, то каждый полученный маленький отрезок относится к большому, как 0,62.
Как получить золотое сечение
Вот пошаговая инструкция, как можно нарисовать прямоугольник, следуя принципу числа Бога.
- Рисуем 1 квадратик со стороной 1 см, а рядом с ним еще такой же.
- Над двумя квадратиками рисуем квадрат побольше со стороной 2 см.
- Слева от рисунка размещаем квадрат со стороной 3 см.
- Ниже рисуем квадрат 5 х 5 см.
- Справа чертим большой квадрат 8 х 8 см.
Прямоугольник готов. Его площадь составляет 8 х 13 см. Все размеры в соответствии с рядом Фибоначчи: 1, 1, 2, 3, 5, 8, 13. При делении 13 на 8 или 8 на 5 получается число Бога 1,62. Чем большие числа участвуют в делении, тем меньше получается погрешность соотношения. Соединив последовательно дуги в квадратах, получим спираль Золотого сечения.
Почему притягивает взгляд древняя архитектура
Именно потому, что лучшие памятники архитектуры были построены с использованием принципа числа Фи, такими гармоничными выглядят древние храмы, соборы, дворцы, пирамиды. Если изучить пропорции пирамиды Хеопса в Египте, то можно увидеть этот принцип. Катет прямоугольного треугольника служит высотой. Второй катет равен половине значения основания. Соотношение гипотенузы к малому катету равно 1,62.
Известно, что благодаря своей форме египетские пирамиды чудесным образом изменяют свойства помещенных внутрь вещей:
- Сталь обретает прочность
- Долгое время сохраняется свежесть воды
- Ускоряется рост растений
- Улучшается настроение
- Снижается интенсивность вредных излучений
Пока ученые не нашли этому понятного объяснения. Примером использования числа Бога в архитектуре можно считать греческий Парфенон. Высота здания относится к ее ширине, как 0,62. Хотя строили его в V веке до н.э. По этому же принципу в Париже в Средние века построили удивительный собор Парижской Богоматери.

Российская архитектура
Чтобы проанализировать архитектурное сооружение удобно использовать циркуль Фибоначчи. Нужно встать на несколько метров от здания, чтобы оно было полностью хорошо видно, и приложить циркуль. Линии здания, построенного по принципу Золотого Сечения, совпадут с пропорциями циркуля. Такие визуальные исследования могут быть интересными во время путешествий по стране.
Московская архитектура
После Великой Отечественной войны в Москве построили Московский государственный университет. Он стал высочайшим строением в стране, высоты его 5 композиционных групп подчинены правилу Золотого Сечения.
Русский зодчий Матвей Казаков по этому же принципу построил Кремлевское здание сената, Пречистенский дворец, Голицынскую больницу. Число Бога заложил при строительстве дома Пашкова в Москве Василий Баженов. Поэтому здание получило статус исторического памятника.
Архитектура Санкт-Петербурга
Ярким примером архитектурной постройки по правилу Золотой Пропорции является Исаакиевский собор. Его ширина равна 400 единицам. Если разделить 400 на число Бога, получится около 248. Дальше разделим 248 на 1,618 – будет 153.
Таким образом, длина основной части собора составляет 400 при ширине 248 единиц. Золотое Сечение просматривается у основного купола, таким образом, все здание архитектурного памятника абсолютно гармонично.
В XVIII веке в Санкт-Петербурге Георгом Маттарнови построена Кунсткамера. Куполообразная башня, по сторонам которой расположены два трехэтажных корпуса.
Именно этому правилу подчинены длина корпусов и высоты разных уровней. Сама башня представляет собой равнобедренный треугольник, значит, общий принцип постройки соответствует Золотому Сечению.
Высотные величины торгового дома Эсдерс и Схейфальс тоже взяты по этому универсальному правилу архитектуры. Их величины составляют последовательность: 671, 414, 256, 98, 60, 37, 23. Если разделить рядом стоящие значения, то всегда будет число, приблизительно равное 1,62.
В 1941 году был построен Дом Советов. По бокам портика с 14 колоннами и скульптурами располагаются 2 корпуса по 5 этажей. Если разделить общую длину здания 1472 единиц на число Фи, то получается числовой ряд Фибоначчи: 1472, 909, 562, 347, 214, 132, 81, 50. Этим пропорциям соответствуют высота входа, высота здания, высоты других архитектурных элементов. Грани золотого равнобедренного треугольника проходят сквозь точки верха главного входа.

Правила золотого сечения в архитектуре
Архитекторы при разработке проектов частных домов пользуются принципом числа Фи. Их клиенты на себе чувствуют комфорт, потому что прорабатываются все детали:
- Длина и высота здания
- Расположение комнат
- Расстояние до других объектов
- Параметры внутренних помещений
Фасад
Помимо числовой последовательности Фибоначчи, применяют также методику французского архитектора Ле Корбюзье. Он учитывал перспективу роста владельцев дома. Так параметры здания и отдельных комнат получали оптимальное строение. Дом приобретал не только гармоничный вид, но и черты самих хозяев.
Чтобы в перспективе дом радовал грамотным расположением комнат, дверей и окон, лучше сразу определить пропорции. Может быть, где-то внести корректировку.
Например, при строительстве дома площадью 100 м2 длину взять 12 м. Короткая сторона составит от нее 62% – 7,44 м. Не обязательно брать дробное число, можно округлить до 7 или 8 м. Абсолютная точность здесь не важна.
Тогда общая площадь дома выходит меньше, чем планировалось. Значит, стоит увеличить длину до 13 м и снова подсчитать. И так пока не получатся желаемые результаты.
От длины дома высота этажа должна составлять 32%. Умножаем 12 м на 0,32, получаем 3,84 м. В основном это подходящая высота для комфортных габаритов помещений. Но можно изменить по желанию. По такому же принципу рассчитывают другие детали здания.
Также учитывают ландшафт местности, где строится дом. Он должен гармонично соответствовать пропорциям участка, каким-то ориентирам, например:
- Холму
- Пруду
- Маяку
Эти же правила действуют при планировании внутренних помещений, расстановке мебели и бытовой техники.

Интерьер
Принцип числа Бога – это, во-первых, красиво. А во-вторых – это психологический и эмоциональный комфорт. Поэтому так важно его использовать при строительстве и внутреннем обустройстве своего дома. В нем вы будете жить много лет. А значит, все должно нравиться.
Даже внутри типового частного дома можно создать убранство по формуле 62/38. Помочь этому могут дополнительные внутренние перегородки. Особое расположение мебели, реконструкция оконных и дверных проемов. Все это можно соотнести с пропорцией 1:1,62.
Например, жилая комната делится на 2 зоны. Одна большая – на 62% площади, другая – на 38%. Мебель в помещении не должна занимать больше 2/3 площади. Соотношение габаритов крупной мебели к средней должно быть равным соотношению средней к мелкой. Ее высота должна быть в нужной пропорции с параметрами комнат.
Это непонятно только на первый взгляд. Для примера возьмем мебель в гостиной. Самым габаритным предметом будет диван, средними – кресла и низкий столик. Самые мелкие – это полочки, люстра, аквариум, подушки.
Параметры низкого столика не должны превышать длинную сторону дивана. Размеры кресел – не должны быть больше, чем короткая сторона дивана. Мелкие предметы в комнате должны быть меньше кресел и столика. Везде правило 62/38.
В цветовом оформлении хорошо пользоваться формулой:
- 60% основной палитры
- 30% дополнительных оттенков
- 10% похожий тон
Точные пропорции не требуются. Это слишком сложно. Главное – принцип. Есть люди, которые выстраивают свой быт без всяких расчетов, интуитивно. И у них это хорошо получается. Наверное, на подсознательном уровне у них «встроена функция» гармоничного существования.

Создаем ландшафт по методике 62/38
В ландшафтном дизайне это правило получило свое название – «правило треугольника». Любая композиция смотрится хорошо, если есть главная составляющая, все другие ее только подчеркивают. Если на вашем участке уже есть дерево, то оно станет центром композиции.
Вокруг него можно распланировать клумбу или альпийскую горку. Мысленно проведите от верхней его части две линии под прямым углом. В местах пересечения с грунтом высаживают куст с высотой 2/3 от дерева и растение на 1/3 высоты центрального объекта (дерева).
Всю эту группу дополняют еще более низкими растениями. Кроме высоты, обращают внимание на гармонию цвета. Зелень разных оттенков дополняют яркие цветущие растения по принципу числа Фи. Главный цвет на клумбе присутствует на 60%, дополнительные – на 30% плюс цветовой акцент 10%.
По правилу золотого сечения строили с древнейших времен. Поэтому сохранившиеся и построенные недавно всемирно известные архитектурные шедевры всегда интересны туристам из разных стран – это гармония в камне. Зная этот принцип, вы сможете применить его при строительстве своего дома.
