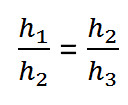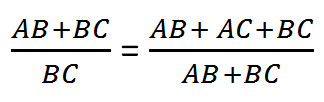| Иррациональные числа ζ(3) — ρ — √2 — √3 — √5 — ln 2 — φ,Φ — ψ — α,δ — e — eπ и π |
|
| Система счисления | Оценка числа Φ |
| Десятичная | 1.6180339887498948482… |
| Двоичная | 1.1001111000110111011… |
| Шестнадцатеричная | 1.9E3779B97F4A7C15F39… |
| Шестидесятеричная | 1; 37 04 55 20 29 39 … |
| Рациональные приближения | 3/2; 5/3; 8/5; 13/8; 21/13; 34/21; 55/34; 89/55; …
|
| Непрерывная дробь | 
|
1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362
Первая тысяча знаков значения Φ[1].
Золотое сечение (золотая пропорция, иначе: деление в крайнем и среднем отношении, гармоническое деление) — отношение частей и целого, при котором отношения частей между собой и наибольшей части к целому равны. Такие отношения наблюдаются в природе, открыты в науке и соблюдаются в искусстве. На «золотых отрезках» основываются различные системы и способы пропорционирования в архитектуре. Соотношение двух величин 


Исторически в древнегреческой математике золотым сечением именовалось деление отрезка 


Число, равное отношению 


Из исходного равенства (например, принимая AB за 1, AC за неизвестную переменную y и BC за x, решая получившуюся систему уравнений x+y=1; x/y=1/x) нетрудно получить квадратное уравнение 


Обратное число, обозначаемое строчной буквой 
Отсюда следует, что
.
Число 
Для практических целей ограничиваются приблизительным значением 

Иллюстрация к определению
Золотое сечение имеет множество замечательных свойств (например, 

История[править | править код]
В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника[6].
Лука Пачоли, современник и друг Леонардо да Винчи, усматривал в этой пропорции «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа[7].
Неизвестно точно, кто и когда именно впервые ввёл в обращение термин «золотое сечение». Несмотря на то, что некоторые авторитетные авторы связывают появление этого термина с Леонардо да Винчи в XV веке[8] или относят появление этого термина к XVI веку[9], самое раннее употребление этого термина находится у Мартина Ома в 1835 году, а именно в примечании ко второму изданию его книги «Чистая элементарная математика»[10], в котором Ом пишет, что это сечение часто называют золотым сечением (нем. goldener Schnitt). Из текста этого примечания следует, что Ом не придумал этот термин сам[11][12], хотя некоторые авторы утверждают обратное[13]. Тем не менее, исходя из того, что в первом издании своей книги Ом уже не употреблял этот термин[14], Роджер Герц-Фишлер делает вывод о том, что этот термин, возможно, появился в первой четверти XIX века[15]. Марио Ливио считает, что он получил популярность в устной традиции около 1830 года.[16] В любом случае именно после Ома термин стал распространён в немецкой математической литературе[17].
Математические свойства[править | править код]
-
- Если угол между диагональю и меньшей стороной прямоугольника, относящейся к большей стороне как 1:2, поделить пополам, то по формуле тангенса половинного угла получится соотношение
- подходящими дробями которой служат отношения последовательных чисел Фибоначчи
. Таким образом,
Отрезание квадрата от прямоугольника, имеющего золотую пропорцию
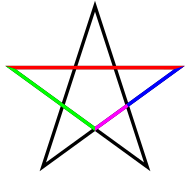
Золотое сечение в пятиконечной звезде
Построение золотого сечения
Другой способ построить отрезок, равный по длине числу золотого сечения
- Другой способ построить отрезок, равный по длине числу золотого сечения, — это начертить квадрат ABCD со стороной 1, после этого одну из сторон, например сторону AD, разделить точкой E пополам, так что AE = DE = 1/2, далее от точки B или C до точки E провести гипотенузу треугольника АВЕ или DCE. Согласно теореме Пифагора
. Затем провести дугу с центром в точке Е от точки В или точки С до прямой, где лежит сторона АD и точка пересечения где будет называться Н. Стороны BE, СЕ и ЕН равны как радиусы окружности. Так как АН = АЕ + ЕН, то отрезок АН длины
и будет результатом. Кроме того, поскольку DH = EH – ED, отрезок DH будет иметь длину
[18].
- где
— биномиальный коэффициент, тогда как
[источник не указан 2670 дней]
Золотое сечение в физике, геометрии, химии[править | править код]
Общее сопротивление этой бесконечной цепи равно 
Золотое число возникает в разных задачах, в том числе в физике. Например, бесконечная электрическая цепь, приведённая на рисунке, имеет общее сопротивление (между двумя левыми концами) 
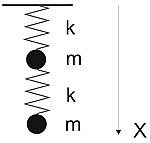
Отношение амплитуд колебаний и частот ~ Ф.
Существуют колебательные системы, физические характеристики которых (отношения частот, амплитуд и др.) пропорциональны золотому сечению. Самый простой пример — система из двух шариков, соединённых последовательно пружинами одинаковой жёсткости (см. рисунок).[20].
Более сложные примеры механических колебаний и их обобщений рассматриваются в этой[прояснить] же книге, в главе «Обобщения одной простой задачи по механике». В книге приведено много примеров проявления и применения золотого сечения в различных областях наук — небесной механике, физике, геофизике, биофизике, физической химии, биологии, Физиологии.
Золотое сечение тесно связано с симметрией пятого порядка, наиболее известными трёхмерными представителями которой являются додекаэдр и икосаэдр. Можно сказать, что всюду, где в структуре проявляются додекаэдр, икосаэдр или их производные, там в описании будет появляться и золотое сечение. Например, в пространственных группировках из Бора: В-12, В-50, В-78, В-84, В-90, …, В-1708, имеющих икосаэдрическую симметрию[21].
Молекула воды, у которой угол расхождения связей Н-О равен 104.70 , то есть близок к 108 градусам (угол в правильном пятиугольнике), может соединяться в плоские и трехмерные структуры с симметрией пятого порядка. Так в разреженной плазме был обнаружен Н+(Н20)21, который представляет собой ион Н30+, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра[22]. В 80-х годах XX века были получены клатратные соединения, содержащие гексааквакомплекс кальция, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра[23]. Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединённых в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды[24].
Золотое сечение и гармония в искусстве[править | править код]
Иллюстрация композиционного значения золотого сечения.
Некоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:
- Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют о том, что при их создании египетские мастера пользовались соотношениями золотого сечения. Меры длины Древнего Египта также были созданы с помощью золотого сечения. Пример: π —
² = 0,5235 м (Локоть царский). Атур обычный = 5,235 км.
- По мнению Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д.
Примеры сознательного использования[править | править код]
Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий И. В. Жолтовский использовал золотое сечение в своих проектах[25].
Иоганн Себастьян Бах в своей трёхголосной инвенции E-dur № 6 BWV 792 использовал двухчастную форму, в которой соотношение размеров частей соответствует пропорциям золотого сечения. 1 часть — 17 тактов, 2 часть — 24 такта (небольшие несоответствия выравниваются за счёт ферматы в 34 такте)[26].
Современными примерами применения золотого сечения может служить мозаика Пенроуза и пропорции государственного флага Того.
Золотое сечение в биологии и медицине[править | править код]
Золотое сечение в природе
Живые системы также обладают свойствами, характерными для «золотого сечения». Например: пропорции тел, спиральные структуры или параметры биоритмов[27][неавторитетный источник?] и др.
См. также[править | править код]
- Божественная пропорция
- Золотая спираль
- Золотой прямоугольник
- Пифагорейский пентакл
- Пропорционирование
- Фибоначчиева система счисления
- Правило третей
- Метод золотого сечения
- Сверхзолотое сечение
- Пластическое число
- Золотой угол
- Канон (искусство)
- Модулор
- Числа Фибоначчи
- Обобщение чисел Фибоначчи
- Обобщённое золотое сечение
Примечания[править | править код]
- ↑ Взята из примера результата компьютерного расчета (1996 года) с гораздо большим числом знаков, чем 1000 Golden ratio 1000 digits Архивная копия от 6 марта 2015 на Wayback Machine
- ↑ 1 2 Савин А. Число Фидия – золотое сечение (рус.) // “Квант” : Научно-популярный физико-математический журнал (издается с января 1970 года). — 1997. — № 6. Архивировано 4 марта 2016 года.
- ↑ Радзюкевич А. В. Красивая сказка о «золотом сечении». Дата обращения: 22 марта 2012. Архивировано 29 декабря 2011 года.
- ↑ Mario Livio, The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number
- ↑ Devlin’s Angle, The Myth That Will Not Go Away
- ↑ Livio, Mario. The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number. — First trade paperback. — New York City : Broadway Books, 2003. — ISBN 978-0-7679-0816-0. Архивная копия от 31 марта 2019 на Wayback Machine
- ↑ В. Лаврус, Золотое сечение. Дата обращения: 18 июля 2004. Архивировано 20 июня 2004 года.
- ↑ François Lasserre. The birth of mathematics in the age of Plato. — American Research Council, 1964-01-01. — 200 с. — P. 76. Архивировано 18 июня 2016 года.
- ↑ Boyer, Carl B. A History of Mathematics (неопр.). — Second Edition. — John Wiley & Sons, Inc., 1991. — С. 50. — ISBN 0-471-54397-7.
- ↑ Martin Ohm. Die reine Elementar-Mathematik. — 2-е изд. — Jonas Verlags-buchhandlung, 1835. — С. 194. — 454 с. Архивировано 23 июля 2016 года.
- ↑ Herz-Fischler, 2013, p. 168.
- ↑ Livio, 2008, p. 6—7.
- ↑ Василенко С. Л. Знак-символ золотого сечения // Академия Тринитаризма. — М., 05.02.2011. — № Эл № 77—6567, публ. 16335. Архивировано 26 ноября 2015 года.
- ↑ Martin Ohm. Die reine Elementar-Mathematik. — 1-е изд.. — Berlin, 1826. — 492 с. — P. 188. Архивировано 30 мая 2016 года.
- ↑ Herz-Fischler, 2013, p. 169.
- ↑ Livio, 2008, p. 7.
- ↑ Herz-Fischler, 2013, p. 169—170.
- ↑ Тони Крилли. Математика: 50 идей, о которых нужно знать = 50 Mathematical Ideas you really need to know. — Phantom Press. — 209 с. — ISBN 9785864716700. Архивировано 18 июня 2016 года.
- ↑ Системы счисления. Дата обращения: 13 ноября 2014. Архивировано 28 ноября 2014 года.
- ↑ Ковалев А.Н. В поисках пятого порядка. — 2017. — 374 с. — ISBN 978-5-4485-3753-0.
- ↑ Современная Кристаллография / под ред. Вайнштейна Б. К.. — Т.2. — М.: Мир, 1979.
- ↑ Holland P. M. Casteiman A. W. A model for the formation and stabilization of chorqed water cluthrates // J. Chem. Phys.. — 1980. — Т. 72, № 1(11). — С. 5984.
- ↑ Электромагнитные поля в биосфере. — Сборник трудов конференции, Т.2. — М., 1984. — С. 22.
- ↑ Зенин С.В. Структурированное состояние воды как основа управления поведением и безопасностью живых систем. — Диссертация докт. биол. наук. — М., 1999.
- ↑ Золотой запас зодчества Архивная копия от 29 января 2009 на Wayback Machine
- ↑ Бах И.С. 15 двухголосных инвенций и 15 трехголосных симфоний. — М.: Музгиз, 1961. — С. 46. — 70 с.
- ↑ Цветков, В. Д. Сердце, золотое сечение и симметрия. — Пущино: ПНЦ РАН, 1997. — 170 с. Дата обращения: 19 февраля 2015. Архивировано 27 сентября 2015 года.
Литература[править | править код]
- на русском языке
- Аракелян Г. Б. Математика и история золотого сечения. — М.: Логос, 2014, 404 с. — ISBN 978-5-98704-663-0.
- Бендукидзе А. Д. Золотое сечение Архивная копия от 11 октября 2004 на Wayback Machine «Квант» № 8, 1973
- Васютинский Н. А. Золотая пропорция. — М.: Молодая гвардия, 1990. — 238[2]c. — (Эврика).
- Власов В. Г. Золотое сечение, или Божественная пропорция // Власов В. Г. Новый энциклопедический словарь изобразительного искусства: В 10 т. — Т.3. — СПб.: Азбука-Классика, 2005. — С.725-732.
- Власов В. Г. Приемы гармонизации пространства в классической архитектуре // Власов В. Г. Искусство России в пространстве Евразии. — Т.3. Классическое искусствознание и «русский мир». — СПб.: Дмитрий Буланин, 2012. — С.156-192.
- Мазель Л. А. Опыт исследования золотого сечения в музыкальных построениях в свете общего анализа форм // Музыкальное образование. — 1930. — № 2. — С. 24-33.
- Сабанеев Л. Л. Этюды Шопена в освещении закона золотого сечения. Опыт позитивного обоснования законов формы // Искусство. — 1925. — № 2. — С. 132—145; 1927. — № 2-3. — С. 32-56.
- Шевелев И.Ш., Марутаев М.А., Шмелев И.Л. Золотое сечение. Три взгляда на природу гармонии. — М.: Стройиздат, 1990. — 343 с. — ISBN 5-274-00197-1.
- Шевелев И.Ш. Геометрическая гармония. Опыт исследования пропорциональности в архитектуре. — Кострома, 1963. — 107 с.
- Шмигевский Н. В. Формула совершенства // Страна знаний. — 2010. — № 4. — С.2-7.
- на других языках
- Mario Livio. The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number. — Crown/Archetype, 2008. — 303 с. — ISBN 9780307485526. Архивная копия от 31 марта 2019 на Wayback Machine Русский перевод в
- Марио Ливио. φ – Число Бога. Золотое сечение – формула мироздания. — Litres, 2015-04-17. — 481 с. — ISBN 9785457762732. Архивная копия от 24 июня 2016 на Wayback Machine
- Roger Herz-Fischler. A Mathematical History of the Golden Number. — Courier Corporation, 2013. — 228 с. — ISBN 9780486152325. Архивная копия от 2 июля 2016 на Wayback Machine
Ссылки[править | править код]
- В. С. Белнин, «Владел ли Платон кодом золотой пропорции? Анализ мифа»
- А. В. Радзюкевич, К вопросу о научном изучении пропорций в архитектуре и искусстве Архивная копия от 3 апреля 2015 на Wayback Machine.
- А. В. Радзюкевич, Критический анализ Адольфа Цейзинга — основоположника гипотезы «золотого сечения». Архивная копия от 19 декабря 2014 на Wayback Machine
- Статья о золотом сечении в изобразительном искусстве, Золотое сечение в изобразительном искусстве
- J. J. O’Connor, E. F. Robertson. Golden ratio. MacTutor History of Mathematics archive. School of Mathematics and Statistics, University of St Andrews, Scotland. Дата обращения: 13 ноября 2015. Архивировано 25 июля 2015 года.
- Функция Фибоначчи Архивная копия от 30 октября 2020 на Wayback Machine в Wolfram alpha
https://ria.ru/20221116/sechenie-1832065968.html
Гармония во всем: что такое золотое сечение и способы его применения
Золотое сечение: что это такое, пропорции, принцип, применение в архитектуре и строительстве
Гармония во всем: что такое золотое сечение и способы его применения
“Божественная гармония” или золотое сечение – правило соотношения частей и целого, универсальное проявление красоты и симметрии. Оно встречается в науке,… РИА Новости, 16.11.2022
2022-11-16T21:08
2022-11-16T21:08
2022-11-16T21:08
общество
европа
греция
ле корбюзье (шарль-эдуар жаннере-гри)
леонардо да винчи
/html/head/meta[@name=’og:title’]/@content
/html/head/meta[@name=’og:description’]/@content
https://cdnn21.img.ria.ru/images/07e6/0b/10/1832031636_0:318:3076:2048_1920x0_80_0_0_74519bda270895480ff99027b7b160ec.jpg
МОСКВА, 16 ноя — РИА Новости. “Божественная гармония” или золотое сечение – правило соотношения частей и целого, универсальное проявление красоты и симметрии. Оно встречается в науке, природе, архитектуре, искусстве. Что такое ряд чисел Фибоначчи, принцип расчета и метод построения на основе пропорций – в материале РИА Новости.Золотое сечение”Определенные пропорции повсеместно используются в дизайне и архитектуре, фотографии и очень часто наблюдаются в естественной природе”, – говорит Ренат Мансуров, профессиональный фотограф, фотохудожник, лауреат и участник международных фотоконкурсов.ИсторияПо словам эксперта, про эту пропорцию писал Ян Чихольд, использовал Малевич, Монферран построил по ней Исаакиевский собор.”Но, как мне кажется, острое желание привязать всё мироздание к одному закону больше говорит о людях прошлого, чем о самом мире. Ум человека плохо переносит множественность, неточность моделей и просто хаос. Из этой особенности и происходит когнитивное “удобство”, когда порядок и закономерность всё-таки находятся”, – отмечает Максим Господинко.Эксперт отмечает, что до Ома это соотношение благодаря трактату монаха францисканца Луки Пачоли, изданному в соавторстве с Леонардо да Винчи, с 1509 года именовали в Европе “божественной пропорцией” (лат. “Divina Proportione”, итал. “Proporzione Divina”).По мнению Сергея Дементьева, “божественная пропорция” (“золотое сечение”) как известная концепция красоты (еще древнегреческий скульптор Поликлет сформировал альтернативные правила красоты, а в 20-м веке модернист архитектор Ле Корбюзье разработал собственную систему пропорционирования) обязана своему появлению упадку веросознания: Эпоха Возрождения в Европе – именно историческая попытка Ренессанса веросознания в новых его формах через умозрение и затем деятельное воплощение в культуре (художественное творчество, архитектура, строительство, парковый, ландшафтный и интерьерный дизайн и т.д.).Пионеры Возрождения Пачоли и Леонардо да Винчи (“Тайная вечеря” и “Мона Лиза” вписаны в геометрические фигуры) обратили свое внимание на античность, где еще в “Началах” Евклид (ок. 300 лет до нашей эры) говорил о делении отрезка в крайнем и среднем отношении (“ἄκρος καὶ μέσος λόγος”), полагая, что на числах построено все мироздание, на идеи Витрувия (ок. 80-70 гг. до нашей эры — после 13 г. до нашей эры), изложенные в “Десяти книгах об архитектуре” (лат. “De architectura libri decem”) о применении математики к искусству архитектуры.Пропорции золотого сеченияО том, как высчитывать золотые пропорции, рассказал эксперт в сфере фотографии Ренат Мансуров.”Если взять для примера линию и разделить ее на две части так, чтобы длинная соотносилась с короткой в такой же пропорции, как вся линия соотносится с длинной, получится золотая пропорция”, – поясняет он. К слову, она равна всегда 1,618, и это так называемое число “фи” обозначается греческой буквой φ — от имени древнегреческого скульптора Фидия.Ренат Мансуров отмечает, что в правильном прямоугольнике соотношение сторон соответствует золотому сечению.”Интересен этот прямоугольник тем, что сколько бы ни отрезали от него квадратов, он всегда будет оставлять после себя кусочек с золотым соотношением сторон и так до бесконечности”, – говорит Ренат Мансуров.Золотое сечение в математикеИтальянский астроном и математик Фибоначчи вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Эта закономерность известна как ряд Фибоначчи.”Если представить два квадрата, поставленных рядом, потом добавить квадрат с удвоенной стороной, то получится квадрат 2 на 2. Далее добавить по спирали против часовой стрелки сумму двух предыдущих квадратов. Получится квадрат с длинной стороны три квадрата, далее добавить к стороне квадрата предыдущую сторону, получится 5, потом 8 потом 13 и 21, каждое последующее число – это сумма сложения с предыдущим, то есть получается такая последовательность, которую и вывел Фибоначчи: 0,1,1,2,3,5,8,13,21 и т.д.”, – поясняет Ренат Мансуров.0, 1,1 (0+1), 2 (1+1), 3 (1+2), 5 (2+3), 8 (3+5), 13 (5+8), 21 (8+13), 34 (13+21), 55 (21+34), 89 (34+55) и до бесконечности. А при делении последующего числа на предыдущее получается коэффициент золотого сечения. По мере возрастания чисел соотношение приближается к 1,618. К примеру, числа 3 и 5, их соотношение равно 1,666, а если взять 13 и 21, то получается уже 1,625. Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленное значение 0,62.А если в каждом квадрате построить дугу из одного угла к другому, то получится так называемая спираль Фибоначчи.Правило золотого сеченияНа практике золотое сечение представляет собой пропорцию, соотношение сторон прямоугольника, отрезков определенной длины, других геометрических форм или сопряженных размерных характеристик реальных объектов.Метод золотого сечения”Если построить прямоугольник, используя метод, указанный выше, и встроить в этот прямоугольник линии, используя числа золотого сечения, то получится разграничение прямоугольника несколькими линиями. И если говорить о композиции, то размещая объекты на линиях или их пересечениях, можно максимально выделить эти объекты как смысловые центры, и наоборот, чем дальше от этих точек, тем труднее будет улавливать смысловой центр”, – поясняет Ренат Мансуров.Если же совместить спираль Фибоначчи и эту сетку, то получится практически инструкция по использованию золотого сечения в фотографии, живописи и дизайне.Где можно увидеть золотое сечениеЕсли разделить обычное куриное яйцо мысленно пополам в самой широкой его части, то получатся правильные золотые пропорции. Пропорции здания Парфенона в Греции, спирали раковин, пропорции тела человека, спиральные галактики и растения, и еще много всего вокруг.ПриродаСвою точку зрения озвучил Максим Господинко.”У растения есть важная задача – наиболее оптимально расположить свои листья или лепестки, для того чтобы уловить больше солнечного света или просто уместить больше семян. В некоторых случаях есть возможность делать это только по плотной спирали (ананас, еловая шишка, подсолнечник). Кажется, что перед таким растением стоит сложная математическая задача – на какой угол сдвинуть следующую семечку или лепесток, но на самом деле вопрос лишь в том, насколько сильное создается отталкивание от уже существующего элемента.И так складывается, что угол отклонения от предыдущего листка действительно очень близок к отношению “фи”, – комментирует эксперт. – Ни одно рациональное отношение не подходит, потому что при повороте под такими углами возникают колонны-лучи с большими дырами, а как мы знаем, семена подсолнечника уложены красивыми спиралями, число которых как раз соответствует числам из ряда Фибоначчи и дыр там никаких нет”.По словам Максима Господинко, ряд Фибоначчи можно легко образовать, взяв ноль и единицу, а каждое последующее за ними получить из суммы двух предыдущих. “Моделировать растение конечно не умеет, насколько мне известно, и не знает количества рядов спиралей, а усилие отталкивания следующего элемента регулируется поколениями и естественным отбором, но в итоге приходит именно к “фи””, – отмечает специалист.ЧеловекПропорции золотого сечения прослеживаются и на примере тела человека. К золотой формуле приравнивается абсолютно все: кости, ладони и пальцы, пропорции участков на лице, расстояние вытянутых рук по отношению к телу. Пропорции таковы:ИскусствоМножество произведений искусства и архитектурных шедевров сделаны по принципам золотого сечения. Египетские и пирамиды Майя, греческий Парфенон и так далее. Картины известных художников тоже выполнены с учетом правил золотого сечения.Прослеживаются такие пропорции и в музыкальных произведениях Шуберта, Моцарта, Баха, Шопена и прочих.”Для дизайнера и художника вопрос о золотом сечении стоит лишь в разрезе более широкой темы – пропорционирования. Не каждый использует этот инструмент, хоть и должен, но часто амбициозный художник, схватившись за “божественную истину”, начинает транслировать лишь её, упуская суть художественного высказывания, передачу образа. Пропорция – лишь инструмент и, очевидно, инструмент не должен идти вперёд задачи. Если образ не понят художником, его невозможно передать”, – говорит Максим Господинко. Но тем не менее, переоценить важность этой пропорции сложно. Часто чувствительный художник сам интуитивно может расположить элементы в соответствии с “фи”, также оно является достаточно простым инструментом, чтобы создать изящную композицию даже в самых простых вещах.Примеры использования в живописи.Примеры использования золотого сечения в дизайне логотипов.Применение золотого сеченияПримеры пропорции золотого сечения можно видеть при строительстве многих архитектурных сооружений и создании проекта дома, в современном дизайне интерьера при планировании и зонировании пространства, расстановки мебели и даже цветовом оформлении, а также в ландшафтном дизайне при выкладке закрученных дорожек, расположении растений на клумбах и других элементов.Так, к примеру, при строительстве квартир и домов отношение самой большой комнаты к площади всей квартиры равно как 0,62 к 1, меньшее помещение делают с таким же соотношением к площади большей комнаты. Так, кухня – к меньшей комнате, прихожая к кухне, санузел к прихожей, а балкон – к санузлу.Кроме того, с помощью золотого сечения подбирают и цветовое оформление. В интерьере применяют соотношение 10-30-60, основанное на золотом сечении. В пространстве используют три основных цвета: первый – доминирующий, охватывает 60% комнаты (стены и пол). Второй оттенок составляет 30% – мебель. И третий, 10%, приходится на декор.По мнению эксперта, теория золотого сечения и “божественных пропорций” довольно популярна, но наука не стоит на месте, и сейчас активно исследуются теории восприятия с научной точки зрения. “То, что работает на практике не одно столетие, однозначно должно напоминать каждый раз о том, что эти пропорции проверены временем и сотнями тысяч творческих людей: фотографы, художники, дизайнеры и архитекторы каждый день работают и используют золотые пропорции в своей работе.Высчитывать миллиметры и микроны в надежде сделать ваше творчество золотым, наверное, не стоит, но и забывать о приятных для глаза пропорциях наверняка не нужно”, – говорит Ренат Мансуров.Как это делать правильно, каждый решает самостоятельно, существует множество приемов композиции и работы с психологией восприятия, которые вместе могут улучшить работу в разы. “Учитесь правильно и не останавливайтесь в изучении художественных и композиционных приемов, и ваше творчество будет сиять оригинальностью и легкостью восприятия”, – советует Ренат Мансуров.Второе золотое сечениеВторое золотое сечение вытекает из основного сечения и дает отношение 44: 56.Максим Господинко отмечает, что золотое сечение – не единственная пропорция, приятная глазу человека, есть “серебряное сечение”. Две величины находятся в “серебряном сечении”, если отношение суммы меньшей и удвоенной большей величины к большей то же самое, что и отношение большей величины к меньшей. Также можно отметить, что порядок разлинованной в клетку тетради приятнее полного хаоса чистого листа (если не брать пропорцию самого его формата за порядок).По словам эксперта, пропорция тетрадки в клетку ничем не хуже золотого сечения, но действие на человека она оказывает иное, как будто организуя простейший порядок – один к одному. “Если бы мы использовали такой поворот угла в подсолнухе, то получили бы одну линию семян, в случае с 1/4 – крест. Каждой задаче – свое решение. В случае с растениями им нужно как раз самое иррациональное число. Примечательно, что именно такое число и прослыло божественным”, – говорит Максим Господинко.Мифы о золотом сечении”Можно спекулировать на тему того, что где-то в глубине восприятия человека лежит именно закономерность ряда Фибоначчи, вероятно, где-то мы так же решали геометрическую задачу поворота на нужный угол по спирали, может быть, всё живое, так или иначе помнит этот опыт. Но чтобы не очаровываться золотым сечением чрезмерно, можно обратить внимание на любовь человека к зигзагам и орнаментам. Далеко не обязательно строить бабушкин ковёр по “фи”, чтобы на него было приятнее смотреть, чем на голую стену, – считает Максим Господинко. – Оказывается, этот вид визуального комфорта обусловлен строением визуального кортекса человеческого мозга, и такие орнаменты, как мы можем увидеть в традиционных культурах, ложатся в него как недостающий кусочек удобного паззла вместо хаотичного визуального потока внешней среды. Резной наличник лучше голых ставень. Кружева лучше минимализма. Природа лучше асфальта. Потому что экономят ресурсы человека, показывая привычные и близкие формы”.
https://ria.ru/20210121/litso-1593906541.html
https://radiosputnik.ria.ru/20220201/piramida-1769426771.html
https://ria.ru/20181111/1532496249.html
европа
греция
РИА Новости
internet-group@rian.ru
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
2022
Новости
ru-RU
https://ria.ru/docs/about/copyright.html
https://xn--c1acbl2abdlkab1og.xn--p1ai/
РИА Новости
internet-group@rian.ru
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
https://cdnn21.img.ria.ru/images/07e6/0b/10/1832031636_345:0:3076:2048_1920x0_80_0_0_d15c886e20acd2d1355969b43de06ca8.jpg
РИА Новости
internet-group@rian.ru
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
общество, европа, греция, ле корбюзье (шарль-эдуар жаннере-гри), леонардо да винчи
Общество, Европа, Греция, Ле Корбюзье (Шарль-Эдуар Жаннере-Гри), Леонардо да Винчи
- Золотое сечение
- История
- Пропорции золотого сечения
- Золотое сечение в математике
- Правило золотого сечения
- Метод золотого сечения
- Где можно увидеть золотое сечение
- Природа
- Человек
- Искусство
- Применение золотого сечения
- Второе золотое сечение
- Мифы о золотом сечении
МОСКВА, 16 ноя — РИА Новости. “Божественная гармония” или золотое сечение – правило соотношения частей и целого, универсальное проявление красоты и симметрии. Оно встречается в науке, природе, архитектуре, искусстве. Что такое ряд чисел Фибоначчи, принцип расчета и метод построения на основе пропорций – в материале РИА Новости.
Золотое сечение
“Определенные пропорции повсеместно используются в дизайне и архитектуре, фотографии и очень часто наблюдаются в естественной природе”, – говорит Ренат Мансуров, профессиональный фотограф, фотохудожник, лауреат и участник международных фотоконкурсов.
История
«
“Первым про золотое сечение писал еще Евклид в “Началах”, которые в свое время были вторые по популярности после Библии. Людям свойственно искать закономерности везде, даже там где их нет, поэтому число “фи” всегда было темой для религиозных спекуляций. Леонардо да Винчи, например, считал, что золотое сечение является выражением божественной сущности Троицы”, – комментирует Максим Господинко, диджитал-художник, дизайнер, основатель Spoils.
По словам эксперта, про эту пропорцию писал Ян Чихольд, использовал Малевич, Монферран построил по ней Исаакиевский собор.
“Но, как мне кажется, острое желание привязать всё мироздание к одному закону больше говорит о людях прошлого, чем о самом мире. Ум человека плохо переносит множественность, неточность моделей и просто хаос. Из этой особенности и происходит когнитивное “удобство”, когда порядок и закономерность всё-таки находятся”, – отмечает Максим Господинко.
«
“Впервые термин “золотое сечение” (“goldener Schnitt”) употребил в эпоху резкого роста европейской секуляризации в примечании ко второму изданию своей “Чистой элементарной математики” в 1835 году доктор философии Мартин Ом. Термин был известен ранее (из текста следует, что Ом не сам его придумал), и в дальнейшем быстро распространился в европейской литературе”, – поясняет Сергей Дементьев, эксперт сервиса meta-luxury недвижимости “Душа объекта”.
Эксперт отмечает, что до Ома это соотношение благодаря трактату монаха францисканца Луки Пачоли, изданному в соавторстве с Леонардо да Винчи, с 1509 года именовали в Европе “божественной пропорцией” (лат. “Divina Proportione”, итал. “Proporzione Divina”).
По мнению Сергея Дементьева, “божественная пропорция” (“золотое сечение”) как известная концепция красоты (еще древнегреческий скульптор Поликлет сформировал альтернативные правила красоты, а в 20-м веке модернист архитектор Ле Корбюзье разработал собственную систему пропорционирования) обязана своему появлению упадку веросознания: Эпоха Возрождения в Европе – именно историческая попытка Ренессанса веросознания в новых его формах через умозрение и затем деятельное воплощение в культуре (художественное творчество, архитектура, строительство, парковый, ландшафтный и интерьерный дизайн и т.д.).
Пионеры Возрождения Пачоли и Леонардо да Винчи (“Тайная вечеря” и “Мона Лиза” вписаны в геометрические фигуры) обратили свое внимание на античность, где еще в “Началах” Евклид (ок. 300 лет до нашей эры) говорил о делении отрезка в крайнем и среднем отношении (“ἄκρος καὶ μέσος λόγος”), полагая, что на числах построено все мироздание, на идеи Витрувия (ок. 80-70 гг. до нашей эры — после 13 г. до нашей эры), изложенные в “Десяти книгах об архитектуре” (лат. “De architectura libri decem”) о применении математики к искусству архитектуры.
Пропорции золотого сечения
О том, как высчитывать золотые пропорции, рассказал эксперт в сфере фотографии Ренат Мансуров.
“Если взять для примера линию и разделить ее на две части так, чтобы длинная соотносилась с короткой в такой же пропорции, как вся линия соотносится с длинной, получится золотая пропорция”, – поясняет он. К слову, она равна всегда 1,618, и это так называемое число “фи” обозначается греческой буквой φ — от имени древнегреческого скульптора Фидия.
Ренат Мансуров отмечает, что в правильном прямоугольнике соотношение сторон соответствует золотому сечению.
“Интересен этот прямоугольник тем, что сколько бы ни отрезали от него квадратов, он всегда будет оставлять после себя кусочек с золотым соотношением сторон и так до бесконечности”, – говорит Ренат Мансуров.
Золотое сечение в математике
Итальянский астроном и математик Фибоначчи вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Эта закономерность известна как ряд Фибоначчи.
“Если представить два квадрата, поставленных рядом, потом добавить квадрат с удвоенной стороной, то получится квадрат 2 на 2. Далее добавить по спирали против часовой стрелки сумму двух предыдущих квадратов. Получится квадрат с длинной стороны три квадрата, далее добавить к стороне квадрата предыдущую сторону, получится 5, потом 8 потом 13 и 21, каждое последующее число – это сумма сложения с предыдущим, то есть получается такая последовательность, которую и вывел Фибоначчи: 0,1,1,2,3,5,8,13,21 и т.д.”, – поясняет Ренат Мансуров.
0, 1,1 (0+1), 2 (1+1), 3 (1+2), 5 (2+3), 8 (3+5), 13 (5+8), 21 (8+13), 34 (13+21), 55 (21+34), 89 (34+55) и до бесконечности. А при делении последующего числа на предыдущее получается коэффициент золотого сечения. По мере возрастания чисел соотношение приближается к 1,618. К примеру, числа 3 и 5, их соотношение равно 1,666, а если взять 13 и 21, то получается уже 1,625. Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленное значение 0,62.
А если в каждом квадрате построить дугу из одного угла к другому, то получится так называемая спираль Фибоначчи.
Правило золотого сечения
На практике золотое сечение представляет собой пропорцию, соотношение сторон прямоугольника, отрезков определенной длины, других геометрических форм или сопряженных размерных характеристик реальных объектов.
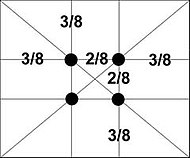
Метод золотого сечения
“Если построить прямоугольник, используя метод, указанный выше, и встроить в этот прямоугольник линии, используя числа золотого сечения, то получится разграничение прямоугольника несколькими линиями. И если говорить о композиции, то размещая объекты на линиях или их пересечениях, можно максимально выделить эти объекты как смысловые центры, и наоборот, чем дальше от этих точек, тем труднее будет улавливать смысловой центр”, – поясняет Ренат Мансуров.
Если же совместить спираль Фибоначчи и эту сетку, то получится практически инструкция по использованию золотого сечения в фотографии, живописи и дизайне.
Где можно увидеть золотое сечение
Если разделить обычное куриное яйцо мысленно пополам в самой широкой его части, то получатся правильные золотые пропорции. Пропорции здания Парфенона в Греции, спирали раковин, пропорции тела человека, спиральные галактики и растения, и еще много всего вокруг.
Природа
«
По словам Рената Мансурова, примеров этих золотых чисел и спиралей найти в природе можно множество. “Распределение семян подсолнуха, спиральные раковины, спиральные галактики, соотношения пропорций человеческого тела, и например, если внимательно посмотреть на нераскрытую еловую шишку или ананас с торца, то можно увидеть эти спирали”, – отмечает эксперт.
Свою точку зрения озвучил Максим Господинко.
“У растения есть важная задача – наиболее оптимально расположить свои листья или лепестки, для того чтобы уловить больше солнечного света или просто уместить больше семян. В некоторых случаях есть возможность делать это только по плотной спирали (ананас, еловая шишка, подсолнечник). Кажется, что перед таким растением стоит сложная математическая задача – на какой угол сдвинуть следующую семечку или лепесток, но на самом деле вопрос лишь в том, насколько сильное создается отталкивание от уже существующего элемента.
И так складывается, что угол отклонения от предыдущего листка действительно очень близок к отношению “фи”, – комментирует эксперт. – Ни одно рациональное отношение не подходит, потому что при повороте под такими углами возникают колонны-лучи с большими дырами, а как мы знаем, семена подсолнечника уложены красивыми спиралями, число которых как раз соответствует числам из ряда Фибоначчи и дыр там никаких нет”.
По словам Максима Господинко, ряд Фибоначчи можно легко образовать, взяв ноль и единицу, а каждое последующее за ними получить из суммы двух предыдущих. “Моделировать растение конечно не умеет, насколько мне известно, и не знает количества рядов спиралей, а усилие отталкивания следующего элемента регулируется поколениями и естественным отбором, но в итоге приходит именно к “фи””, – отмечает специалист.
Названы знаменитости с идеальными пропорциями лица
Человек
Пропорции золотого сечения прослеживаются и на примере тела человека. К золотой формуле приравнивается абсолютно все: кости, ладони и пальцы, пропорции участков на лице, расстояние вытянутых рук по отношению к телу. Пропорции таковы:
- от плеч до макушки к размеру головы = 1:1.618
- от подбородка до верхней губы и от нее до носа = 1:1.618
- от пупка до макушки к отрезку от плеч до макушки = 1:1.618
- от пупка до колен и от колен до ступней = 1:1.618
Искусство
Пирамида Хеопса – единственное сохранившееся классическое чудо света
Множество произведений искусства и архитектурных шедевров сделаны по принципам золотого сечения. Египетские и пирамиды Майя, греческий Парфенон и так далее. Картины известных художников тоже выполнены с учетом правил золотого сечения.
Прослеживаются такие пропорции и в музыкальных произведениях Шуберта, Моцарта, Баха, Шопена и прочих.
“Для дизайнера и художника вопрос о золотом сечении стоит лишь в разрезе более широкой темы – пропорционирования. Не каждый использует этот инструмент, хоть и должен, но часто амбициозный художник, схватившись за “божественную истину”, начинает транслировать лишь её, упуская суть художественного высказывания, передачу образа. Пропорция – лишь инструмент и, очевидно, инструмент не должен идти вперёд задачи. Если образ не понят художником, его невозможно передать”, – говорит Максим Господинко. Но тем не менее, переоценить важность этой пропорции сложно. Часто чувствительный художник сам интуитивно может расположить элементы в соответствии с “фи”, также оно является достаточно простым инструментом, чтобы создать изящную композицию даже в самых простых вещах.
Примеры использования в живописи.
© Public DomainКартина Леонардо Да Винчи “Мона Лиза”
Картина Леонардо Да Винчи “Мона Лиза”
1 из 2
Репродукция картины “Девочка на шаре” 1905 г. работы Пабло Пикассо, выставленная в Государственном музее изобразительных искусств им. А.С. Пушкина.
2 из 2
Картина Леонардо Да Винчи “Мона Лиза”
1 из 2
Репродукция картины “Девочка на шаре” 1905 г. работы Пабло Пикассо, выставленная в Государственном музее изобразительных искусств им. А.С. Пушкина.
2 из 2
Примеры использования золотого сечения в дизайне логотипов.
Логотип социальной сети Twitter на экранах мобильного телефона и компьютера.
1 из 2
Логотип компании Apple на стене фирменного магазине на 5-й авеню в Нью-Йорке.
2 из 2
Логотип социальной сети Twitter на экранах мобильного телефона и компьютера.
1 из 2
Логотип компании Apple на стене фирменного магазине на 5-й авеню в Нью-Йорке.
2 из 2
Применение золотого сечения
Примеры пропорции золотого сечения можно видеть при строительстве многих архитектурных сооружений и создании проекта дома, в современном дизайне интерьера при планировании и зонировании пространства, расстановки мебели и даже цветовом оформлении, а также в ландшафтном дизайне при выкладке закрученных дорожек, расположении растений на клумбах и других элементов.
Так, к примеру, при строительстве квартир и домов отношение самой большой комнаты к площади всей квартиры равно как 0,62 к 1, меньшее помещение делают с таким же соотношением к площади большей комнаты. Так, кухня – к меньшей комнате, прихожая к кухне, санузел к прихожей, а балкон – к санузлу.
Кроме того, с помощью золотого сечения подбирают и цветовое оформление. В интерьере применяют соотношение 10-30-60, основанное на золотом сечении. В пространстве используют три основных цвета: первый – доминирующий, охватывает 60% комнаты (стены и пол). Второй оттенок составляет 30% – мебель. И третий, 10%, приходится на декор.
«
“Существует множество вариантов золотого сечения. Но все они, так или иначе, основаны на числах Фибоначчи. Какие то из них популярны, какие то не очень, но о чем мы говорим сегодня, это то, что выработалось за последние столетия – это явно золотой стандарт, – говорит Ренат Мансуров. – Конечно, нужно понимать, что творчество остается творчеством и отходить от стандарта не возбраняется, но и совсем идти наперекор этим пропорциям не стоит”.
По мнению эксперта, теория золотого сечения и “божественных пропорций” довольно популярна, но наука не стоит на месте, и сейчас активно исследуются теории восприятия с научной точки зрения. “То, что работает на практике не одно столетие, однозначно должно напоминать каждый раз о том, что эти пропорции проверены временем и сотнями тысяч творческих людей: фотографы, художники, дизайнеры и архитекторы каждый день работают и используют золотые пропорции в своей работе.
Реальная Вавилонская башня и первая пирамида: самые старые строения в мире
Высчитывать миллиметры и микроны в надежде сделать ваше творчество золотым, наверное, не стоит, но и забывать о приятных для глаза пропорциях наверняка не нужно”, – говорит Ренат Мансуров.
Как это делать правильно, каждый решает самостоятельно, существует множество приемов композиции и работы с психологией восприятия, которые вместе могут улучшить работу в разы. “Учитесь правильно и не останавливайтесь в изучении художественных и композиционных приемов, и ваше творчество будет сиять оригинальностью и легкостью восприятия”, – советует Ренат Мансуров.
Второе золотое сечение
Второе золотое сечение вытекает из основного сечения и дает отношение 44: 56.
Максим Господинко отмечает, что золотое сечение – не единственная пропорция, приятная глазу человека, есть “серебряное сечение”. Две величины находятся в “серебряном сечении”, если отношение суммы меньшей и удвоенной большей величины к большей то же самое, что и отношение большей величины к меньшей. Также можно отметить, что порядок разлинованной в клетку тетради приятнее полного хаоса чистого листа (если не брать пропорцию самого его формата за порядок).
По словам эксперта, пропорция тетрадки в клетку ничем не хуже золотого сечения, но действие на человека она оказывает иное, как будто организуя простейший порядок – один к одному. “Если бы мы использовали такой поворот угла в подсолнухе, то получили бы одну линию семян, в случае с 1/4 – крест. Каждой задаче – свое решение. В случае с растениями им нужно как раз самое иррациональное число. Примечательно, что именно такое число и прослыло божественным”, – говорит Максим Господинко.
Мифы о золотом сечении
“Можно спекулировать на тему того, что где-то в глубине восприятия человека лежит именно закономерность ряда Фибоначчи, вероятно, где-то мы так же решали геометрическую задачу поворота на нужный угол по спирали, может быть, всё живое, так или иначе помнит этот опыт. Но чтобы не очаровываться золотым сечением чрезмерно, можно обратить внимание на любовь человека к зигзагам и орнаментам. Далеко не обязательно строить бабушкин ковёр по “фи”, чтобы на него было приятнее смотреть, чем на голую стену, – считает Максим Господинко. – Оказывается, этот вид визуального комфорта обусловлен строением визуального кортекса человеческого мозга, и такие орнаменты, как мы можем увидеть в традиционных культурах, ложатся в него как недостающий кусочек удобного паззла вместо хаотичного визуального потока внешней среды. Резной наличник лучше голых ставень. Кружева лучше минимализма. Природа лучше асфальта. Потому что экономят ресурсы человека, показывая привычные и близкие формы”.
←Вернуться в «Доклады по математике»
Красота, оказывается, порою имеет математическое объяснение.
Пропорции золотого сечения часто используются художниками и скульпторами в соотношениях между
разными элементами картины или скульптуры. Великий Леонардо да Винчи находил соотношение
золотого сечения в пропорциях человеческого тела.
Так чему же равно отношение золотого сечения в математике и как его найти? Разберёмся на примере.
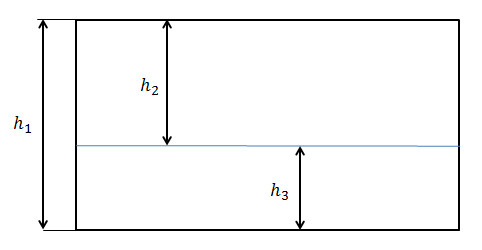
Возьмём лист бумаги и начертим линию горизонта, которая обычно делит небо от земли. Получится,
нечто похожее на рисунок ниже.
Отношение высоты картины h1 к расстоянию от верхнего края
h2 равно
отношению расстояния от верхнего края h2
к расстоянию до нижнего края h3.
В виде математической записи, это будет выглядеть так:
Найдём числовое значение золотого сечения.
Для этого вернёмся к нашему рисунку. Пусть высота всей картины равна h1 = 1, а расстояние
от верхнего края до горизонта обозначим за x (h2 = x). Тогда получим:
=
x2 + x − 1 = 0
Положительный корень этого уравнения
≈ 1,618
Это отношение большей части к меньшей в этой пропорции.
Это число равно отношению золотого сечения. Обычно его обозначают греческими буквами
τ (тау) или
φ (фи).
Другие греческие буквы вы можете посмотреть в разделе
«Для учёбы».
Золотое сечение в фигурах
В некоторых фигурах геометрии и стереометрии также присутствует золотое сечение.
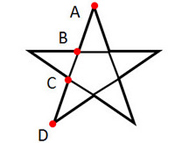
Например, в пятиконечной звезде (пентаграмме).
Точка «B» или «С» делит отрезок
«AD» в пропорциях золотого сечения.
Все остальные стороны звезды также поделены в данном соотношении соответственно.
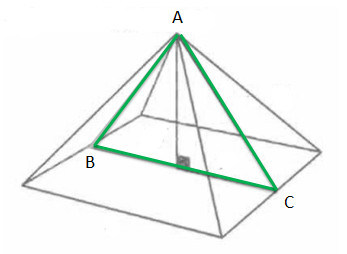
Другой пример золотого сечения был обнаружен в пирамиде Хеопса.
В сечении знаменитого сооружения также заложен принцип золотого сечения.
Сумма двух сторон равнобедренного треугольника «ABC» относится к его основанию
также как сумма всех сторон треугольника к сумме равных сторон. Иными словами:
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Довольно часто говорят, что в математике есть своя красота, но уже к середине V века до н. э. или даже значительно раньше стало известно, что в красоте большое количество математики. Золотое соотношение — это число, у которого, по всей видимости, больше имен, чем у любого другого. Его именуют золотым сечением, божественной пропорцией либо попросту — фи (φ).
Это число обозначает очень приятную — в большинстве случаев — пропорцию, появляющуюся при делении чего-либо на две неравные части. Значительно чаще золотое соотношение возможно встретить при взоре на монументы искусства и архитектуры любого исторического периода. Свое имя число фи взяло в честь греческого архитектора и скульптора Фидия, который, по утверждению некоторых исследователей, деятельно применял данный принцип для украшения самого своего известного творения — Парфенона, возведенного в 440 г. до н. э.
Старейшее сохранившееся до наших дней описание принципа золотого соотношения было сделано Евклидом около 300 г. до н. э. в его труде «Начала». Но самое восхитительное в числе фи — не его настоящее либо кажущееся присутствие в созданных человеком объектах (от кредитных карточек до рисунка Леонардо да Винчи «Витрувианский человек»), но его проявления в природе (рост цветов и ракушек, к примеру).
Вычисление золотого соотношения
Существует большое количество способов математически выразить золотое соотношение, и во всех этих методах имеется своя определенная простота, точность и обаяние. Эвклид обрисовывал его как «сечение в крайнем и среднем отношении». Более «математичное» выражение выглядит так: если золотое соотношение равняется х, то х/1 = 1/(х -1), где x > 1 – есть длина стороны, которая разделена на два неравных отрезка (в простейшем случае больший отрезок равен 1, меньший отрезок получается x – 1 ). Или мы получаем следующее уравнение золотого сечения: х² – х – 1 = 0. Словами же золотое соотношение определяют как пропорцию, в которой «протяженность всей линии относится к большей ее части так же, как та — к меньшей».
Хороший пример золотого сечения — кредитная карточка, имеющая однообразные стандартные размеры во всем мире. В соответствии с правилами золотого соотношения, отношение ее маленькой стороны к длинной такое же, как отношение длинной к сумме длин короткой и длинной сторон. Это делает кредитку золотым прямоугольником. Такая форма была выбрана из-за своего сбалансированного вида — она не кажется ни через чур длинной, ни через чур широкой. Один из способов проверить, есть ли прямоугольник золотым, — расположить два прямоугольника рядом, один «поставив» вертикально на маленькую грань, другой «положив» прикасаясь к первому на долгую. Если диагональ, проходящая через углы расположенного горизонтально прямоугольника, продолжившись, достигнет верхнего угла прямоугольника, расположенного вертикально, прямоугольники являются золотыми. Значительно чаще данный принцип видится в архитектуре. Так, золотым прямоугольником является фасад здания ООН в Нью-Йорке.
Математика в искусстве и природе
В золотом соотношении есть что-то прозаичное — по крайней мере, для тех, кто не владеет математическим складом ума. Речь идет о его численном выражении. Значение х в алгебраическом выражении х² – х – 1 = 0 равняется 1,6180339887… и так без конца. Однако золотое соотношение имеет самое прямое отношение к западному искусству. В большой степени эта связь появилась благодаря трудам Луки Пачоли на рубеже XVI в. Пачоли был современником Леонардо да Винчи, и кое-какие из рисунков маэстро — включая наиболее известное изображение Витрувианского человека — появляются в книге Пачоли De Divina Proportione («Божественная пропорция»), изданной в 1509 г. В данной книге заложены базовые геометрические правила красоты, а вдохновлялся создатель числом фи. Так, в совершенных пропорциях человеческого тела соотношение роста до пупка и полного росту есть золотым. К сожалению, фактические измерения говорят о том, что в действительности «совершенных» тел фактически нет. В ХХ в. золотое соотношение высматривали в естественных формах. Те, кто делал это достаточно упорно, находили его в пропорциях листьев, распределении бутонов на стебле (природные закономерности скорее приблизительно подчиняются принципу последовательности Фибоначчи), кроме того в траектории пикирования охотящегося ястреба. Для кого-то это являлось свидетельством в пользу существования некоего замысла, в соответствии с котором организована сама природа. Для других же это означало, что наше восприятие красоты (либо, по крайней мере, приятной для глаз пропорциональности) продиктовано математикой роста, которая представляет повышение структур в размерах без утраты ими общей формы.
Золотая спираль
Спираль, разворачивающуюся в соответствии с принципом золотого соотношения, возможно выстроить посредством серии золотых прямоугольников. Это частный случай логарифмической спирали, расходящейся от осевой точки под постоянным углом (Математически более верно формулировать так: кривая, касательная к которой образует с радиус-вектором в каждой точке один и тот же угол). Эту спираль соотносят с именем Якоба Бернулли (не смотря на то, что первым обрисовал ее Декарт), главным исследователем ее свойств. Бернулли кроме того захотел, чтобы такую спираль выгравировали на его надгробии, но плохо подкованный в геометрии каменщик воспроизвёл там Архимедову спираль с более пологой траекторией расхождения.
Немного фактов
Интересный факт о золотом сечении №1. Пропорции соседних сегментов раковины моллюска наутилуса приближаются к золотому соотношению.Интересный факт о золотом сечении №2. Не обращая внимания на то, что свое обозначение золотое соотношение взяло в честь Фидия, он не руководствовался этим принципом при разработке проекта Парфенона. Храм немного высоковат чтобы его пропорции строго отвечали стандарту золотого сечения — то ли из-за ошибки в расчетах, то ли вследствие того что Фидию так больше нравилось.
Интересный факт о золотом сечении №3. Золотые прямоугольники возможно поделить на нескончаемое количество уменьшающихся в размерах золотых прямоугольников, «отрезая» от них части по кратчайшей линии. В терминологии греческой школы математиков такое свойство делает золотой прямоугольник гномоном — объектом, способным сохранять форму по мере роста (либо уменьшения).
Интересный факт о золотом сечении №4. Кредитная карточка является примером золотого прямоугольника. Также золотым прямоугольником является фасад здания ООН в Нью-ЙоркеИнтересный факт №5. Фактические измерения говорят о том, что в действительности «совершенных» тел, удовлетворяющих правилу золотого сечения фактически нет.Интересный факт №6. Бернулли хотел, чтобы золотую спираль выгравировали на его надгробии, но плохо подкованный в геометрии каменщик воспроизвёл там Архимедову спираль с более пологой траекторией расхождения.
Наша библиотека в telegram (много книг для физиков, математиков и программистов) : https://t.me/physics_lib
Еще много полезного и интересного вы сможете найти на наших ресурсах:
Physics.Math.Code в контакте (VK)
Physics.Math.Code в telegram
Physics.Math.Code в YouTube
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в Яндекс.Дзен
Число Ф (фи), которое называют золотым сечением или серединой, является одним из самых загадочных терминов в математике и физике. Интересно, что оно часто встречается в повседневной жизни, хотя многие об этом никогда не задумывались. Даже люди, не знакомые с правилом золотого сечения, видят его, сами того не понимая. Проводились эксперименты: испытуемым показывали случайные лица и просили назвать наиболее привлекательные. Таковыми оказывались лица, в которых находили золотые соотношения между различными величинами – шириной лица, глаз, линии бровей, носа. Таким образом, инстинктивно человек видит приближенное к пропорциям, которые считаются идеальными.
Содержание:
- 1 Что такое золотое сечение?
- 2 История золотого сечения
- 3 «Золотые» фигуры
- 4 Золотое сечение в изобразительном искусстве
- 5 Примеры золотого сечения в жизни и в природе
Что такое золотое сечение?
Это пропорция, полученная делением в крайнем и среднем отношении. Также это называют гармоническим делением. Как вычисляется золотая середина? В выражении математическим языком эта величина представляет собой соотношение двух величин a и b, где известно, что а>b, и имеет место такое равенство: a/b=(a+b)/a. Представив, что a и b – это части одного отрезка, можно сказать: отношение меньшей части к большей равно отношению большей части к целому. Золотое сечение обозначают 21-й буквой греческого алфавита – Ф (произносится как «фи»).
Данное число бесконечно, как и Пи, показывающее отношение длины окружности к диаметру. Выглядит оно так: 1.6180339887498948420… Соответственно, округляют Ф до 1,618.
История золотого сечения
У этой величины несколько названий. Среди них – божественная пропорция и асимметричная симметрия. Считается, что в науку метод золотого деления внес Пифагор в VI веке до нашей эры. В свою очередь он узнал об этом у египтян и вавилонян. Ведь то, что они использовали соотношения золотого деления доказывают пропорции пирамид, храмов, барельефов, предметов быта и украшений.
Встречается данное правило и в другой древней архитектуре. Например, пирамида Гизы имеет высоту 146,6 метров, а каждая сторона основания достигает 230,5 метров. Если рассчитать отношение длины стороны к высоте, получаем 1,5717, а это совсем рядом со значением Ф. Греческий скульптор и математик Фидий, живший в V веке до нашей эры с применением правила золотого деления создавал скульптуры для Парфенона. Универсальным связующим звеном математических отношений назвал золотое сечение Платон. А Евклид еще в IV веке до нашей эры увидел золотое сечение в пентаграмме.
С данным понятием непосредственно связана последовательность Фибоначчи. Известный математик создал последовательный ряд чисел, и если взять любые два очередных числа, то их отношение будет очень близко к Ф. При этом по мере возрастания чисел, соотношение всё больше приближается к 1,618. К примеру, если взять 3 и 5, то соотношение равно 1,666, а если 13 и 21, то получается уже 1,625. Равное значению Ф дает отношение 144 и 233.
«Золотые» фигуры
Принцип золотого сечения используется для построения геометрических фигур. И считается, что полученные таким образом фигуры, выглядят наиболее изящными. Это подтверждают многократно проведенные эксперименты. Внимание испытуемых больше привлекают именно такие фигуры.
Самым простым примером является прямоугольник, при вычислении отношения сторон которого получаем значение Ф. Еще один замечательный пример – правильный пятиугольник. Все его диагонали делят друг друга на отрезки, связанные золотой пропорцией, а каждый конец – это золотой треугольник. При вершине такого треугольника образуется угол в 36 градусов, а основание делит боковую сторону в пропорции золотого сечения. Внутри пятиугольника строится пентаграмма.
Древнегреческий ученый Архимед, первым отметил, что если от золотого прямоугольника последовательно отсекать квадраты, соединяя противоположные точки четвертью окружности, получается изящная спираль.
Золотое сечение в изобразительном искусстве
В эпоху Возрождения при создании картин и скульптур великие мастера применяли золотое сечение, чтобы достичь баланс красоты. Наиболее яркими примерами являются творения Леонардо да Винчи. С помощью этого правила художник определял пропорции в работе «Тайная вечеря». Это видно при исследовании размеров стола, стен, элементов интерьера. Также божественная пропорция прослеживается в картинах «Мона Лиза» и «Витрувианский Человек». Такие великие художники, как Микеланджело, Рафаэль, Рембрандт, Сальвадор Дали и другие, использовали золотое сечение при создании своих шедевров.
Примеры золотого сечения в жизни и в природе
Ежедневно мы можем наблюдать идеальные пропорции:
- Грудная и брюшная части тела бабочки соотносятся в золотой пропорции. А при сложенных крыльях это прекрасное создание представляет собой правильный треугольник с равными сторонами.
- У стрекозы длины хвоста и корпуса относятся так же, как общая длина тела к хвосту.
- В пропорциях тела ящерицы также прослеживается данный принцип.
- Большинство яиц птиц можно вписать в золотой прямоугольник.
- Последовательность Фибоначчи видна в развитии растений, в расположении чешуек в шишках, зерен в подсолнухах.
- Спирально растет бараний рог, плетет паутину паук.
- Интересно, что если напугать стадо северных оленей, то животные будут разбегаться по спирали.
- В форме двойной спирали представлена молекула ДНК.
- Цветки разных растений, а также морские звезды имеют форму правильного пятиугольника.
Как видно, примеров с правильными пропорциями в природе и повседневной жизни предостаточно. Не даром золотое сечение называют божественной пропорцией. Вероятно, именно этим правилом руководствовался создатель в процессе заполнения Вселенной живыми и неживыми объектами. То, что соответствует этому правилу, кажется нам наиболее привлекательным.
В мире много интересных вещей, изучение нового делает нас умнее, способствует развитию мозга и мышления. Советуем вам обязательно находить время на познание нового. А чтобы было легче усваивать и запоминать большие объемы информации, рекомендуем тренажеры Викиум. Регулярно используя их для тренировок мозга, вы сможете улучшить память, внимательность, логику и аналитические способности.



![{displaystyle varphi ={frac {1}{Phi }}={frac {{sqrt {5}}-1}{2}}=e^{-0,2ipi }+e^{0,2ipi }=e^{-0,2ln -1}+e^{0,2ln -1}=(-1)^{-0,2}+(-1)^{0,2}={frac {1}{sqrt[{5}]{-1}}}+{sqrt[{5}]{-1}}=2{mathfrak {R}}({sqrt[{5}]{-1}})approx 0,61803}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdc65998e194179675ce0e4dd70cc137c00e6175)