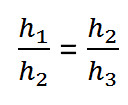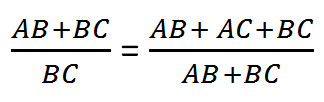Число Ф (фи), которое называют золотым сечением или серединой, является одним из самых загадочных терминов в математике и физике. Интересно, что оно часто встречается в повседневной жизни, хотя многие об этом никогда не задумывались. Даже люди, не знакомые с правилом золотого сечения, видят его, сами того не понимая. Проводились эксперименты: испытуемым показывали случайные лица и просили назвать наиболее привлекательные. Таковыми оказывались лица, в которых находили золотые соотношения между различными величинами – шириной лица, глаз, линии бровей, носа. Таким образом, инстинктивно человек видит приближенное к пропорциям, которые считаются идеальными.
Содержание:
- 1 Что такое золотое сечение?
- 2 История золотого сечения
- 3 «Золотые» фигуры
- 4 Золотое сечение в изобразительном искусстве
- 5 Примеры золотого сечения в жизни и в природе
Что такое золотое сечение?
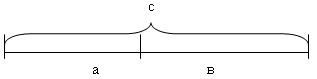
Это пропорция, полученная делением в крайнем и среднем отношении. Также это называют гармоническим делением. Как вычисляется золотая середина? В выражении математическим языком эта величина представляет собой соотношение двух величин a и b, где известно, что а>b, и имеет место такое равенство: a/b=(a+b)/a. Представив, что a и b – это части одного отрезка, можно сказать: отношение меньшей части к большей равно отношению большей части к целому. Золотое сечение обозначают 21-й буквой греческого алфавита – Ф (произносится как «фи»).
Данное число бесконечно, как и Пи, показывающее отношение длины окружности к диаметру. Выглядит оно так: 1.6180339887498948420… Соответственно, округляют Ф до 1,618.
История золотого сечения
У этой величины несколько названий. Среди них – божественная пропорция и асимметричная симметрия. Считается, что в науку метод золотого деления внес Пифагор в VI веке до нашей эры. В свою очередь он узнал об этом у египтян и вавилонян. Ведь то, что они использовали соотношения золотого деления доказывают пропорции пирамид, храмов, барельефов, предметов быта и украшений.
Встречается данное правило и в другой древней архитектуре. Например, пирамида Гизы имеет высоту 146,6 метров, а каждая сторона основания достигает 230,5 метров. Если рассчитать отношение длины стороны к высоте, получаем 1,5717, а это совсем рядом со значением Ф. Греческий скульптор и математик Фидий, живший в V веке до нашей эры с применением правила золотого деления создавал скульптуры для Парфенона. Универсальным связующим звеном математических отношений назвал золотое сечение Платон. А Евклид еще в IV веке до нашей эры увидел золотое сечение в пентаграмме.
С данным понятием непосредственно связана последовательность Фибоначчи. Известный математик создал последовательный ряд чисел, и если взять любые два очередных числа, то их отношение будет очень близко к Ф. При этом по мере возрастания чисел, соотношение всё больше приближается к 1,618. К примеру, если взять 3 и 5, то соотношение равно 1,666, а если 13 и 21, то получается уже 1,625. Равное значению Ф дает отношение 144 и 233.
«Золотые» фигуры
Принцип золотого сечения используется для построения геометрических фигур. И считается, что полученные таким образом фигуры, выглядят наиболее изящными. Это подтверждают многократно проведенные эксперименты. Внимание испытуемых больше привлекают именно такие фигуры.
Самым простым примером является прямоугольник, при вычислении отношения сторон которого получаем значение Ф. Еще один замечательный пример – правильный пятиугольник. Все его диагонали делят друг друга на отрезки, связанные золотой пропорцией, а каждый конец – это золотой треугольник. При вершине такого треугольника образуется угол в 36 градусов, а основание делит боковую сторону в пропорции золотого сечения. Внутри пятиугольника строится пентаграмма.
Древнегреческий ученый Архимед, первым отметил, что если от золотого прямоугольника последовательно отсекать квадраты, соединяя противоположные точки четвертью окружности, получается изящная спираль.
Золотое сечение в изобразительном искусстве
В эпоху Возрождения при создании картин и скульптур великие мастера применяли золотое сечение, чтобы достичь баланс красоты. Наиболее яркими примерами являются творения Леонардо да Винчи. С помощью этого правила художник определял пропорции в работе «Тайная вечеря». Это видно при исследовании размеров стола, стен, элементов интерьера. Также божественная пропорция прослеживается в картинах «Мона Лиза» и «Витрувианский Человек». Такие великие художники, как Микеланджело, Рафаэль, Рембрандт, Сальвадор Дали и другие, использовали золотое сечение при создании своих шедевров.
Примеры золотого сечения в жизни и в природе
Ежедневно мы можем наблюдать идеальные пропорции:
- Грудная и брюшная части тела бабочки соотносятся в золотой пропорции. А при сложенных крыльях это прекрасное создание представляет собой правильный треугольник с равными сторонами.
- У стрекозы длины хвоста и корпуса относятся так же, как общая длина тела к хвосту.
- В пропорциях тела ящерицы также прослеживается данный принцип.
- Большинство яиц птиц можно вписать в золотой прямоугольник.
- Последовательность Фибоначчи видна в развитии растений, в расположении чешуек в шишках, зерен в подсолнухах.
- Спирально растет бараний рог, плетет паутину паук.
- Интересно, что если напугать стадо северных оленей, то животные будут разбегаться по спирали.
- В форме двойной спирали представлена молекула ДНК.
- Цветки разных растений, а также морские звезды имеют форму правильного пятиугольника.
Как видно, примеров с правильными пропорциями в природе и повседневной жизни предостаточно. Не даром золотое сечение называют божественной пропорцией. Вероятно, именно этим правилом руководствовался создатель в процессе заполнения Вселенной живыми и неживыми объектами. То, что соответствует этому правилу, кажется нам наиболее привлекательным.
В мире много интересных вещей, изучение нового делает нас умнее, способствует развитию мозга и мышления. Советуем вам обязательно находить время на познание нового. А чтобы было легче усваивать и запоминать большие объемы информации, рекомендуем тренажеры Викиум. Регулярно используя их для тренировок мозга, вы сможете улучшить память, внимательность, логику и аналитические способности.
Тема урока: «Пропорция. Золотая
пропорция».
Цели урока:
- Знакомство с понятием «пропорция», с
определением «золотая пропорция» и с понятиями,
связанными с ним. - Знакомство с исторической справкой о «золотом
сечении». - Приобретение навыков исследовательской
деятельности. - Приобретение навыков построения «золотой
середины». - Развитие познавательного интереса к
математике. - Воспитание осознанного эстетического вкуса.
Оборудование: карандаши, циркули,
линейки, рулетка; ветка фикуса; репродукции
картин; портреты Пифагора, Леонардо да Винчи,
Баха; презентация (Приложение)
ХОД УРОКА
I. Опрос учащихся по изученной теме
«Отношение»
Что называется ОТНОШЕНИЕМ ДВУХ ЧИСЕЛ?
Найти отношения:
| 124 к 32 | 46 к 92 | 3 к 5 |
| 12,3 к 3 | 14 к 28 | 5 к 8 |
| 0,24 к 12 | 12,46 к 24,92 | 8 к 13 |
| 360 к 240. | 41 к 82 | 34 к 55 |
Ответы:
| 3,875 | 0,5 | 0,6 |
| 4,1 | 0,5 | 0,625 |
| 0,02 | 0,5 | ~0,615 |
| 1,5 | 0,5 | ~0,618 |
– Что показывает отношение двух чисел? (Во
сколько раз первое число больше второго; какую
часть первое число составляет от второго.)
– Какую закономерность вы заметили? (Во втором
столбике получили ответ 0,5, а в третьем ~0,6)
– Подумайте: какие отношения чаще можно
обнаружить в окружающих нас предметах?
II. Изучение нового материала
1) Нахождение отношений, исследуя окружающие
нас предметы.
– Измерим длину и ширину окна; расстояние между
листьями фикуса, находящегося в классной комнате
и найдем соответственные отношения; также
измерим различные части тела ученика (по рисунку
на стр.151 учебника) и также найдем отношения между
полученными результатами измерений.
В тетрадях учащихся записываются результаты
всех измерений и соответственных отношений.
Вывод: Окружающие нас предметы часто
дают примеры «золотых отношений» ~0,6.
2) Учащиеся исследовательской группы знакомят с
материалами своей работы.
Знакомство с понятием «пропорция»
(определение).
Равенство двух отношений называют пропорцией.
или

пропорция» (определение; нахождение «золотой
середины» при помощи 2-у квадратов).
Открытие пропорций принадлежит к заслугам
древневосточной математики, античная же
традиция связывает его с именем выдающегося
философа и математика Пифагора.
Универсальный принцип гармонии и красоты в
пропорциях получил название «золотое сечение»,
которое олицетворяло равновесие знания, чувств и
силы. Золотое сечение возникает при деление
отрезка на две неравные части, таким образом, при
котором весь отрезок относится к большей его
части, как большая к меньшей (0,618).
a : b = b : c или с : b = b : а.
Рис. 1. Геометрическое изображение
золотой пропорции
|
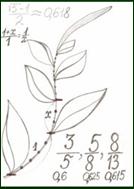
Рис. 2. Расположение листьев фикуса |
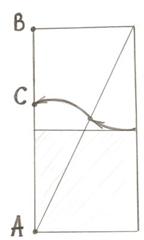
Рис. 3. Нахождение «золотой |
Учащиеся в тетрадях выполняют построения на
нахождение «золотой середины» при помощи двух
квадратов.
Доклад «Как использовали пропорцию для
изображения человеческой фигуры в Древнем
Египте и в Древней Греции» (с иллюстрациями).
Пропорциями называются размерные соотношения
элементов или частей формы между собой, а также
между различными объектами.
Пропорция – это гармонизация формы
художественного произведения,
пропорциональность – её эстетическое качество.
Соразмерность частей образуют красоту формы. В
основе определения пропорций лежит метод
сравнения. Все эти свойства лежат и в основе
грамотного рисунка.
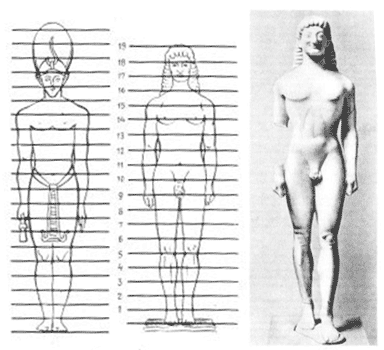
В Древнем Египте для изображений человеческой
фигуры был разработан канон – то есть такая
система пропорций человеческой фигуры, которая
делила изображение на части и позволяла по части
определить целое и по одной части тела
определить другую. Известно, что египтяне
положили в основу деления фигуры 21 ? части. В это
число входили 19 равных частей разделения самой
фигуры, а 2 ? части приходились на изображение
традиционного головного убора.
Египтяне пользовались и специальными сетками
– таблицами, которые наносили на поверхность
каменной плиты или стены для создания рельефа
или росписи. На сохранившихся и дошедших до нас
памятниках можно видеть, что соответствует
членению фигур на части. Были установлены также
определенные размеры для изображения сидящих
фигур и изображения, разных богов. Художнику
необходимо было знать установленные каноном
нормы и научиться вписывать в них изображения,
пользуясь сеткой – таблицей. Единая система
обучения и строгое соблюдение выработанных норм
позволяли выполнять части одного произведения
разными мастерами. Когда такие части составляли
в единую композицию, то они точно сходились, и не
было нарушения пропорций.
Вся история учения о пропорциях связана с
поисками законов гармонии и красоты. В Древней
Грециисистему идеальных пропорций человеческой
фигуры создал скульптор Поликлет в V веке до н. э.
Его теоретическое сочинение на эту тему
называлось «Канон», а выражением в скульптуре
этой системы явилась его статуя «Дорифор», что
означает копьеносец. Мастер изобразил атлета –
юношу, победителя в соревнованиях по метанию
копья, в момент, когда после одержанной победы он
совершает круг почета по стадиону и его
приветствуют восторженные зрители.
Доклад «Золотая пропорция и портрет Монны
Лизы»
Леонардо Да Вини, изучавший и глубоко
анализировавший опыт древних,разрабатывая
правила изображения человеческой фигуры,
пытался на основе литературных сведений
восстановил так называемый «квадрат древних». Он
выполнил рисунок, в котором показана
пропорциональная закономерность в соотношении
частей тела человека.
Портрет Монны Лизы (Джоконды) долгие годы
привлекает внимание исследователей, которые
обнаружили, что композиция рисунка основана на
золотых треугольниках, являющихся частями
правильного звездчатого пятиугольника.
Существует очень много версий об истории этого
портрета. Вот одна из них. Однажды Леонардо да
Винчи получил заказ от банкира Франческо деле
Джокондо написать портрет молодой женщины, жены
банкира, Монны Лизы. Женщина не была красива, но в
ней привлекала простота и естественность облика.
Леонардо согласился писать портрет. Его модель
была печальной и грустной, но Леонардо рассказал
ей сказку, услышав которую, она стала живой и
интересной.
Сказка

один бедный человек, было у него четыре сына: три
умных, а один из них и так, и сяк. И вот пришла за
отцом смерть. Перед тем, как расстаться с жизнью,
он позвал к себе детей и сказал: “Сыны мои, скоро
я умру. Как только вы схороните меня, заприте
хижину и идите на край света добывать себе
счастья. Пусть каждый из вас чему-нибудь
научится, чтобы мог кормить сам себя”. Отец умер,
а сыновья разошлись по свету, договорившись
спустя три года вернуться на поляну родной рощи.
Пришел первый брат, который научился плотничать,
срубил дерево и обтесал его, сделал из него
женщину, отошел немного и ждет. Вернулся второй
брат, увидел деревянную женщину и, так как он был
портной, в одну минуту одел ее: как искусный
мастер он сшил для нее красивую шелковую одежду.
Третий сын украсил женщину золотом и
драгоценными камнями – ведь он был ювелир.
Наконец, пришел четвертый брат. Он не умел
плотничать и шить, он умел только слушать, что
говорит земля, деревья, травы, звери и птицы, знал
ход небесных тел и еще умел петь чудесные песни.
Он запел песню, от которой заплакали
притаившиеся за кустами братья. Песней этой он
оживил женщину, она улыбнулась и вздохнула.
Братья бросились к ней, и каждый кричал одно и то
же: “Ты должна быть моей женой”. Но женщина
ответила: “Ты меня создал – будь мне отцом. Ты
меня одел, а ты украсил – будьте мне братьями. А
ты, что вдохнул в меня душу и научил радоваться
жизни, ты один мне нужен на всю жизнь”.
Кончив сказку, Леонардо взглянул на Монну Лизу,
ее лицо озарилось светом, глаза сияли. Потом,
точно пробудившись от сна, она вздохнула, провела
по лицу рукой и без слов пошла на свое место,
сложила руки и приняла обычную позу. Но дело было
сделано – художник пробудил равнодушную статую;
улыбка блаженства, медленно исчезая с ее лица,
осталась в уголках рта и трепетала, придавая лицу
изумительное, загадочное и чуть лукавое
выражение, как у человека, который узнал тайну и,
бережно ее, храня, не может сдержать торжество.
Леонардо молча работал, боясь упустить этот
момент, этот луч солнца, осветивший его скучную
модель.
Сообщение «О присутствии «золотой
пропорции»в музыке»

музыкальных произведениях есть понятие
размерности. Размерность эта стремится к
«золотой пропорции».
Хроматическая фантазия И. Баха разделена на
первую и вторую части в золотой пропорции.
Чувственное впечатление и рациональный анализ
позволяют приблизиться к сокровенным тайнам
гения. На занятиях в музыкальной школе мы
прослушали это произведение.
Ряд золотого сечения фуги РЕ- МИНОР
хроматической фантазии Баха.
III. Закрепление
Задание классу: В нас окружающих
предметах найти число «фи». Поделиться
результатами.
Заключение исследовательской группы.
С числом «фи» связан ритм сокращений желудочков
сердца человека. В пропорциях человеческого лица
также присутствует число «фи». Если мы соотнесем
длину раковины моллюска с ее диаметром, то
получим все, то же число «фи». При взгляде на
ствол любого растения видно, что каждый лист
растет на ветке под углом, отличным от угла
нижнего листа. Чаще всего угол между
последующими листьями прямо соотносим с числом
«фи». Повсюду куда ни глянешь везде можно
обнаружить присутствие золотого сечения: в
живописи, архитектуре, в музыке, в живой природе.
IV. Итог урока
Итоговая оценка: себе 
Я сегодня
узнал__________________________________________________________________________;
научился
_______________________________________________________________________________.
Мне осталось непонятным
________________________________________________________________.
Моё настроение
V. Домашнее задание: стр.126-128 . № 744,752
,стр.150-151.
Список литературы:
Волошинов А.В. Математика и искусство – М.:
Просвещение, 1992.
Волошинов А.В. Пифагор – М.: Просвещение, 1993.
http://www.ab.ru/~akunb/koluvan/osnova.htm
http://www.koob.ru/vorobyev-nikolay/
http://www.abc-people.com/data/leonardov/zolot_sech-txt.htm
http://goldsech.narod.ru/index.html
http://www.tmn.fio.ru/works/04x/304/index.htm
http://n-t.ru/tp/iz/zs.htm
http://www.log-in.ru/dtSection/news/?id=432
http://www.harunyahya.ru/article_zolotoe_sechenir.php
http://tmn.fio.ru/works/04x/304/p2_21.htm
http://www.abc-people.com/idea/zolotsech/index.htm
←Вернуться в «Доклады по математике»
Красота, оказывается, порою имеет математическое объяснение.
Пропорции золотого сечения часто используются художниками и скульпторами в соотношениях между
разными элементами картины или скульптуры. Великий Леонардо да Винчи находил соотношение
золотого сечения в пропорциях человеческого тела.
Так чему же равно отношение золотого сечения в математике и как его найти? Разберёмся на примере.
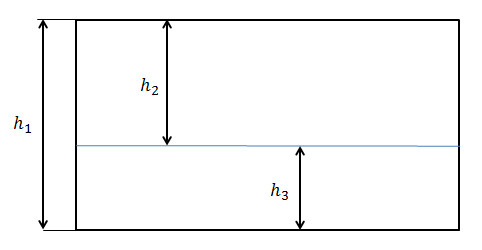
Возьмём лист бумаги и начертим линию горизонта, которая обычно делит небо от земли. Получится,
нечто похожее на рисунок ниже.
Отношение высоты картины h1 к расстоянию от верхнего края
h2 равно
отношению расстояния от верхнего края h2
к расстоянию до нижнего края h3.
В виде математической записи, это будет выглядеть так:
Найдём числовое значение золотого сечения.
Для этого вернёмся к нашему рисунку. Пусть высота всей картины равна h1 = 1, а расстояние
от верхнего края до горизонта обозначим за x (h2 = x). Тогда получим:
=
x2 + x − 1 = 0
Положительный корень этого уравнения
≈ 1,618
Это отношение большей части к меньшей в этой пропорции.
Это число равно отношению золотого сечения. Обычно его обозначают греческими буквами
τ (тау) или
φ (фи).
Другие греческие буквы вы можете посмотреть в разделе
«Для учёбы».
Золотое сечение в фигурах
В некоторых фигурах геометрии и стереометрии также присутствует золотое сечение.
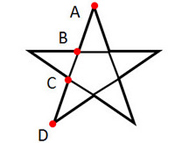
Например, в пятиконечной звезде (пентаграмме).
Точка «B» или «С» делит отрезок
«AD» в пропорциях золотого сечения.
Все остальные стороны звезды также поделены в данном соотношении соответственно.
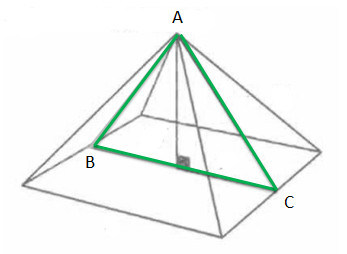
Другой пример золотого сечения был обнаружен в пирамиде Хеопса.
В сечении знаменитого сооружения также заложен принцип золотого сечения.
Сумма двух сторон равнобедренного треугольника «ABC» относится к его основанию
также как сумма всех сторон треугольника к сумме равных сторон. Иными словами:
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Тип урока: урок – практикум с элементами исследования.
Этап
урока
Содержание
Действия
(слова)
учителя
Действия
(слова)
учеников
№
слайда
Скриншоты
слайдов
с
пояснениями
I. Организацион-ный
момент.
Звенит
звонок
–Здравствуйте, садитесь.
-Начинаем урок математики
Учащиеся
занимают свои места
1
II.
Сообщение темы и
целей урока.
На слайде записаны слова
– Ребята, напомните, какую главу мы сейчас изучаем? (Математика вокруг
нас).
– Сегодня на
уроке мы попытаемся определить чудо математики, которое встречается в
окружающем нас мире. Посмотрите на экран и скажите, что вы чувствуете?
Перед вами фотографии растений, Египетские пирамиды, картина Ивана Ивановича
Шишкина «Корабельная роща», Портрет Моны Лизы (Леонардо да Винчи «Джоконда»).
– С древних времен человек начал разделять вещи на красивые и не
красивые. Уже в Древней Греции античные философы начали выявлять некую
формулу, которая раскрыла тайну того, что мы называем гармонией. Так что же
такое гармония?
– Ребята! Как,
вы, считаете, что же такое гармония? С какими словами у вас ассоциируется
слово “гармония”?
– Если рассматривать цветок вблизи и аналогично другие естественные и
созданные человеком творения, то можно найти единство и порядок, свойственные
всем этим предметам. Этот порядок и единство и есть Гармония, определяющая
Красоту.
Итак, гармония это красота, а красота, как говорили греки, – это
математика, следовательно, гармония это математика.
Из многих пропорций, которыми пользовался человек при создании
живописи, скульптуры, музыки, поэм, самой главной является одна, и именно она
отражает понятие ГАРМОНИИ наилучшим образом. Эту пропорцию называли
по-разному: божественной, золотой, золотым сечением, золотой серединой,
золотым делением, золотым числом.
Мы назовем ее с вами “Золотое сечение”
Иоганн Кеплер
говорил: “Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым
сечением. И если первое из этих двух сокровищ можно сравнить с мерой золота,
то второе с драгоценным камнем”.
– Одно из таких
соотношений получило название «Божественная пропорция» или же по
другому…
– Откройте
тетради, запишите число и тему урока.
Постановка
целей: – Чему –
мы научимся, изучая эту тему?
Учащиеся отвечают на вопрос
Учащиеся смотрят на слайд и делают
выводы
Обобщаем ответы учащихся
(читает ученик формулировку темы –
«Золотое сечение»).
Записывают в тетрадь.
(читают ученики)
-Познакомиться с понятием «золотое сечение».
-Узнать, где оно применяется.
– Научиться
использовать его в практической деятельности
2
3
4
5
III.
Устный опрос
На слайде вопросы для устного опроса по
теме «Отношение двух чисел»
– Давайте
посмотрим, как связано это слово с математикой! И в конце урока определим,
верны ли слова ученого Ф. Хауздорда « Есть в математике нечто, вызывающее
человеческий восторг»
Но, сначала
ответим на вопросы:
– Что такое
отношение?
– Что такое
пропорция?
– Основное свойство пропорции?
Учащиеся устно отвечают на вопросы,
размещенные на слайдах
6
IV.
Работа над новой
темой
1.Учащимся дается
определение пропорции, отличное от изученного ранее
1. Историческая справка:
– Учение об
отношениях и пропорциях успешно развивалось в IV
веке до н.э.
В Древней
Греции с пропорциями связывались представления о красоте, порядке и гармонии,
о созвучных аккордах в музыке.
Пропорциональность
в природе, искусстве, архитектуре означает соблюдение определенных
соотношений между размерами отдельных частей растения, скульптуры, здания и
является непременным условием правильного и красивого изображения предмета.
– Давайте же узнаем, что такое «золотое
сечение».
Показать на схеме.
Учащиеся читают определение
Определение: золотое сечение – это такое пропорциональное деление отрезка на
неравные части, при котором отношение его меньшей части и большей равно
отношению большей к длине всего отрезка.
Дети высказывают свои предположения
7
V.
Закрепление
нового материала
1.Учащиеся опытным путем находят
числовое значение «золотого сечения»
Задание 1. (по группам)
Начертить отрезки: (1 группа)
5 см
2 см 3 см
(2
группа)
8 см
3
см 5 см
(3 группа)
13 см
5 см 8 см
– Какую закономерность вы видите? Любое
ли деление отрезка мы можем назвать «золотым сечением»?
– Давайте проверим.
Рассмотрим пропорцию
– Какой вывод
вы можете сделать? Какие пропорции относятся к «Золотому сечению»?
Как вы
думаете, где применяется «Золотое сечение»? (ответы детей)
Учащиеся выполняют в тетрадях и далают
вывод:
(1 группа)
Если мы 2 : 3, то получим ≈ 0,6
а 3 : 5 = 0,6
(2 группа)
Если мы 3 : 5, то получим ≈ 0,6
а 5 : 8 ≈ 0,6
Если мы 5 : 8, то получим ≈ 0,6
а 8 : 13 ≈ 0,6
(только те, в
которых в обеих частях получается точно или приближенно 0,6) (вывод
записать).
7
2. Идет демонстрация примеров «золотого
сечения» в архитектуре (практическая работа)
Задание 2. (по группам)
– Скульпторы,
архитекторы, художники использовали и используют золотое сечение в своих
произведениях. Красивейшее произведение древне-греческой архитектуры – храм
Парфенон ( построен в V в. до н.э.) в Афинах. Он
поражает не своими размерами, а гармоническим совершенством пропор-ции.
Проверим это отношения (высота здания к его длине и она равна 0,6).
– А теперь рассмотрим другие
произведения архитектуры и проверим пропорции…
Задание 3. (по группам)
Учащиеся рассматривают слайды с
примерами использования «золотого сечения» и выполняют практическую работу и
делают вывод.
8
3. Идет демонстрация примеров «золотого
сечения» в живописи
Термин «золотое
сечение» ввел великий итальянец Эпохи Возрождения Леонардо да Винчи
доказывал, что пропорции «золотого сечения» свойственны и человеческому телу,
но использовалось и знаменитым русским иконописцем Андреем Рублевым,
применяется в скульптуре.
Задание 4.
– Перед вами репродукция картины Ивана Шишкина “Корабельная роща”.
Самая яркая деталь на этой картине – освещенная солнцем сосна, она
делит картину в отношении «золотого сечения».
Проверьте это! Ярко освещенная солнцем сосна, стоящая на переднем
плане, делит длину картины по горизонтали в «золотом» отношении.
Справа от сосны – освещенный солнцем пригорок. Он делит по «золотому
сечению» правую часть картины по вертикали. Также можно найти мотивы
«золотого сечения» и в других частях картины.
Наличие в картине ярких деталей, делящих ее по «золотому сечению»,
придает картине уравновешенность, чувство спокойствия и гармонии.
Картины великих художников, вызывающие непонятную, притягатель-ную
силу, запоминающиеся, написаны с применением «золотого сечения». Чтобы
создать шедевр, даже в искусстве необходима математика!
Проверим «Божественную пропорцию» в
живописи.
Учащиеся рассматривают слайды с примерами использования
«золотого сечения» и выполняют практическую работу и делают вывод.
9
10
11
12
VI.
Физминутка.
Звучит фрагмент классического
музыкального произведения. Учащимся предлагается посидеть с закрытыми
глазами, чтобы отдохнуть
-Но «золотое сечение» помогает
сделать красивым не только изображение, но и звуки. Знаменитый мастер
Страдивари изготавливал свои скрипки строго в соответствии с божественной
пропорцией. Послушайте, как прекрасны звуки скрипки
Учащиеся слушают музыкальный фрагмент с
закрытыми глазами
(чтобы включить музыку на слайде надо нажать
на )
VII. Работа над новой темой (продолжение)
4. Идет демонстрация примеров «золотого
сечения» в природе (практическая работа)
-Золотое сечение нашло свое воплощение
и в живой природе
– Например, рассматривая расположение
листьев на общем стебле растения, можно заметить, что между каждыми двумя
парами листьев третья расположена в месте золотого сечения.
Проверим «Божественную пропорцию» в
природе.
Задание 5.
Учащиеся рассматривают слайд
Учащиеся выполняют вычисления и
сравнивают их с числовым значением золотого сечения
13
14
VIII.
Закрепление
изученного материала.
Просмотр слайдов с различными примерами
золотого сечения
– Золотое сечение называют
божественной мерой красоты, таким образом, золотое сечение это и есть формула
красоты, которую мы искали.
Учащиеся смотрят слайды с 15 по 20 без
комментариев
15
16
17
18
19
20
-Мы с вами также созданы по законам
золотого сечения. Обратите внимание на пропорции лица. Данная схема
представлена у вас в раздаточных материалах. Дома вы можете сравнить
пропорции своего лица с золотым сечением, которое в средневековье считалось
эталоном красоты
Учащиеся рассматривают схему лица
21
IX.
Итог урока.
Итоговое задание «Кроссворд»
-Надеюсь, сегодня вы узнали много
интересного и моя попытка доказать вам всю красоту математики не была
напрасной. А насколько внимательно вы меня слушали, мы вспомним фразу и
ответим « Есть в математике нечто,
вызывающее человеческий восторг»
-А закончу я наш урок фразой:
“Там, где присутствует золотое
сечение, ощущается красота и гармония”
Вы согласны со мной и неизвестным
автором
Учащиеся высказывают свои мнения
Х.
Домашнее задание.
Запись домашнего задания
1. Выбрать одну картинку из презентации, постараться найти золотую
пропорцию.
2. Нарисовать рисунок, используя принцип золотого сечения.
Записывают домашнее задание в дневник
ХI.
Рефлексия.
Выбор фразы.
Учащиеся по очереди
высказываются одним предложением, выбирая начало фразы из рефлексивного
экрана на доске
22
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проект по математике Как найти золотую середину?
Содержание
-
1.
Проект по математике Как найти золотую середину? -
2.
Гипотеза – зная определение и правило нахождения -
3.
Цель работы – показать применение понятия «среднее арифметическое нескольких чисел» при решении практических или повседневных задач. -
4.
Задачи1. Найти величины, значения которых могут изменяться.2. -
5.
Среднее арифметическое -
6.
Среднее арифметическое -
7.
Среднее арифметическое -
8.
Среднее арифметическое -
9.
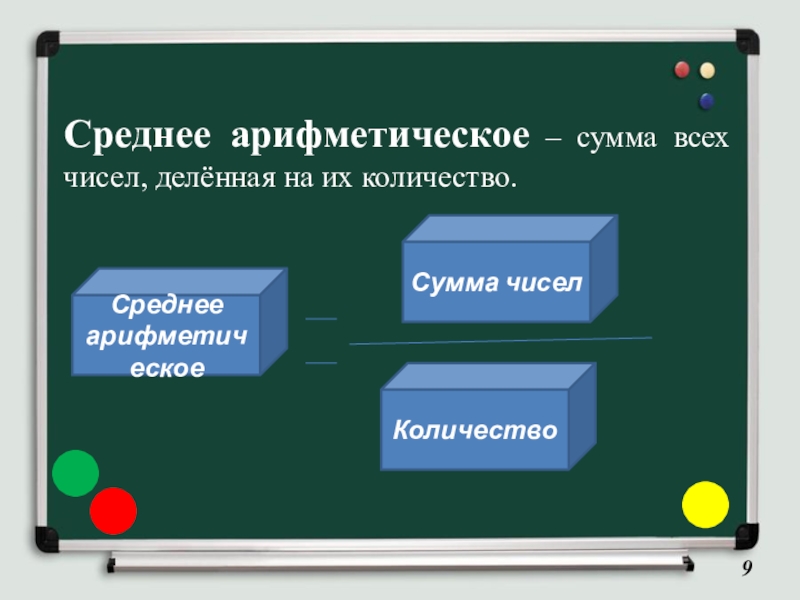
Среднее арифметическое – сумма всех чисел, делённая на их количество.Среднее арифметическоеСумма чиселКоличество -
10.
Средняя зарплата -
11.
Средняя скорость -
12.
Средняя урожайность -
13.
Средний балл -
14.
Какой он ученик 5 «В» класса? -
15.
Какой он ученик 5 «В» класса?14 чел.12 чел. -
16.
Какой он ученик 5 «В» класса?140-145 см -
17.
Какой он ученик 5 «В» класса?30-35 кг -
18.
Какой он ученик 5 «В» класса?А – -
19.
Какой он ученик 5 «В» класса?А – -
20.
Какой он ученик 5 «В» класса?4 – -
21.
Какой он ученик 5 «В» класса?январь – -
22.
Какой он ученик 5 «В» класса?Успеваемостьпо русскому -
23.
Какой он ученик 5 «В» класса?Успеваемостьпо математике«5» – 19 чел.«4» – 5 чел.«3» – 2 чел. -
24.
Слайд 24 -
25.
Слайд 25 -
26.
Я – гражданин России. Моя фамилия начинается -
27.
Спасибо за внимание!
Гипотеза – зная определение и правило нахождения среднего арифметического нескольких чисел, можно найти средние значения различных величин.
Слайд 1Как найти золотую середину?
Выполнила: Фирсова Елизавета, 5 «В» класс
Руководитель: Лазарева
Марина Сергеевна

Слайд 2Гипотеза – зная определение и правило нахождения среднего арифметического нескольких чисел,
можно найти средние значения различных величин.

Слайд 3Цель работы – показать применение понятия «среднее арифметическое нескольких чисел» при
решении практических или повседневных задач.

Слайд 4Задачи
1. Найти величины, значения которых могут изменяться.
2. Определить правила нахождения средних
значений данных величин.
3. Провести исследование на нахождение среднего ученика 5В класса.

Слайд 9Среднее арифметическое – сумма всех чисел, делённая на их количество.
Среднее арифметическое
Сумма
Слайд 15Какой он ученик 5 «В» класса?
14 чел.
12 чел.

Слайд 16Какой он ученик 5 «В» класса?
140-145 см – 4 чел.
146-150 см
– 4 чел.
151-155 см – 9 чел.
156-160 см – 7 чел.
161-165 см – 2 чел.

Слайд 17Какой он ученик 5 «В» класса?
30-35 кг – 1 чел.
36-40 кг
– 11 чел.
41-45 кг – 6 чел.
46-50 кг – 2 чел.
51-55 кг – 1 чел.
56-60 кг – 2 чел.
61-65 кг – 2 чел.
66-70 кг – 1 чел.

Слайд 18Какой он ученик 5 «В» класса?
А – 4; Б – 3;
В – 4;
Д – 3; Е – 5; И – 2;
К – 1; М – 1; Н – 2;
П – 2; С – 1; Т – 1.
Тайна имени

Слайд 19Какой он ученик 5 «В» класса?
А – 1; Б – 3;
В – 3;
Г – 1; Е – 1; К – 3;
Л – 4; М – 3; Н – 1;
П – 1; С – 1; Т – 2;
Ф – 2
Тайна фамилии

Слайд 20Какой он ученик 5 «В» класса?
4 – 1; 5 – 2;
6 – 3;
7 – 1; 8 – 2; 11 – 1;
12 – 2; 15 – 1;
16 – 1; 17 – 1;
18 – 1; 19 – 1;
22 – 2; 23 – 3;
25 – 2; 29 – 2.
Дата рождения

Слайд 21Какой он ученик 5 «В» класса?
январь – 2;
февраль – 3;
март –
2;
апрель – 2; май – 4;
июнь – 1; июль – 3;
август – 3;
октябрь – 1;
ноябрь – 3;
декабрь – 2.
Месяц рождения

Слайд 22Какой он ученик 5 «В» класса?
Успеваемость
по русскому языку
«5» – 7 чел.
«4»

Слайд 23Какой он ученик 5 «В» класса?
Успеваемость
по математике
«5» – 19 чел.
«4» –

Слайд 26Я – гражданин России.
Моя фамилия начинается на букву «И»,
имя
– на букву «Ж».
Средняя дата моего рождения «15.06.2006»,
мне «11» лет.
Мой средний рост составил «153 см»,
средняя масса – «42 кг».
Я – средний ученик 5В класса
средней школы № 38 г. Орска.
Мой средний балл по русскому языку «4»,
а по математике «5».
Я – хороший и послушный ученик, и я – среди вас.
Спасибо за то, что слушали мой рассказ.