Звуковое давление
Звуковое давление – меняющееся избыточное давление, возникающее в упругой среде при прохождении через неё звуковой волны. Уровень звукового давления – измеренное значение звукового давления, относительно опорного давления Рspl = 20 мкПа и соответствующему порогу слышимости звуковой волны частотой 1 кГц. Повышенный уровень звукового давления – причина возникновения шумового загрязнения. Для того, чтобы определить уровень звукового давления и определить мероприятия по его снижению производят специальный расчет:
- выявляют источник (источники) шума и его шумовые характеристики;
- выбирают расчетные точки, определяют допустимый уровень звукового давления в них;
- рассчитывают ожидаемые уровни звукового давления в расчетных точках;
- подсчитывают необходимое снижение шума;
- разрабатывают акустические и архитектурно-строительные меры, обеспечивающие снижение шума.
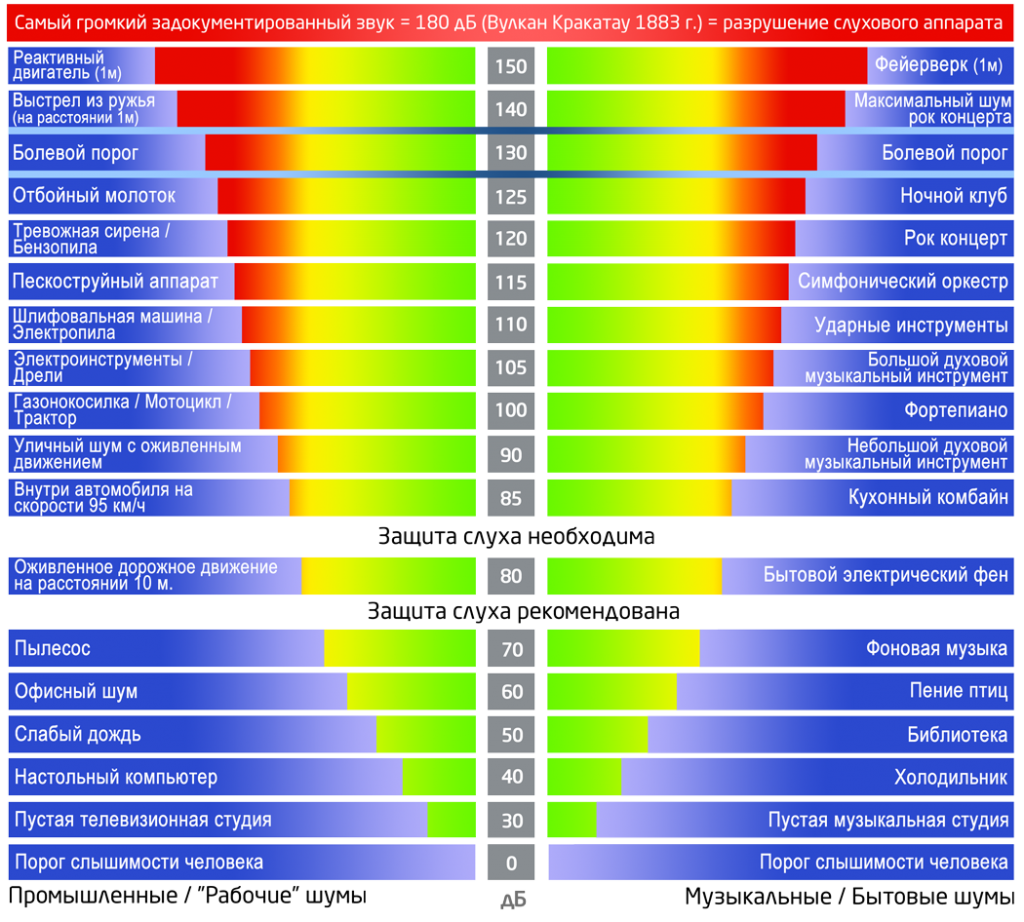
Уровень звукового давления определяют в расчетных точках, выбираемых или на рабочих местах, или в зонах с постоянным пребыванием людей на высоте 1,5 м от пола. Причем в помещении с одним или несколькими одинаковыми источниками две точки, одну – на рабочем месте в зоне прямого звука, вторую – в зоне отраженного звука и в месте постоянного пребывания людей. Если в помещении имеется несколько источников, уровни звуковой мощности которых отличаются на 10 дБ и более, точки выбирают на рабочих местах у источников с максимальными и минимальными уровнями.
Исходные данные для расчета:
- план и разрез помещения с расположением всех типов производственного оборудования и указанием расчетных точек;
- характеристики ограждающих строительных конструкций (материал, толщина, плотность и другие);
- шумовые характеристики и габариты источников шума.
Шумовые характеристики оборудования приведены заводом-изготовителем в документации. Это могут быть: октавные Lw, корректированные LwА, эквивалентные LwАэкв или максимальные LwАмакс корректированные уровни звуковой мощности. Допускаются характеристики в виде октавных уровней звукового давления L или уровней звука на рабочем месте Lд (на определенном расстоянии).
Октавные уровни звукового давления L, дБ, в расчетных точках помещений (с отношением наибольшего к наименьшему размеру не более 5) при работе одного источника шума следует определять по формуле (1) L = Lw +10 lg ((χ Ф)/( Ω r²) + 4/kB), где Lw – октавный уровень звуковой мощности, дБ;
χ – коэффициент, учитывающий влияние ближнего поля в тех случаях, когда расстояние r меньше удвоенного максимального габарита источника (r<2lмакс) (табличные данные);
Ф – фактор направленности источника шума (для источников с равномерным излучением Ф = 1);
Ω – пространственный угол излучения источника, радиан (табличные данные);
r – размер от акустического центра источника шума до расчетной точки, м;
k – коэффициент искажения звукового поля в помещении (табличные данные, в зависимости от среднего коэффициента звукопоглощения αср);
B – акустическая константа помещения, м², определяемая по формуле (2) B = A /(1- αcp),
А – эквивалентная площадь звукопоглощения, м², определяемая по формуле:
![]()
Si -площадь i-й поверхности, м²;
Аj – эквивалентная площадь звукопоглощения j-го искуственного поглотителя, м²;
nj – количество j-ых искуственных поглотителей, шт.;
αcp – средний коэффициент звукопоглощения, определяемый по формуле (4) αcp = A /Sогр,
Sогр – суммарная площадь ограждающих поверхностей помещения, м².
Граничный радиус rгр, м, в помещении с одним источником шума – расстояние от акустического центра источника, на котором плотность энергии прямого звука равна плотности энергии отраженного звука, определяют по формуле (5) rгр =√(B /4 Ω )
Если источник расположен на полу помещения, граничный радиус определяют по формуле (6) rгр=√В/8π =√В/25,12
Расчетные точки на расстоянии до 0,5 rгр считают находящимися в зоне прямого звука. В этом случае октавные уровни звукового давления следует определять по формуле (7) L = Lw +10 lg Ф + 10 lg χ – 20 lg r – 10 lg Ω.
Расчетные точки на расстоянии более 2 rгр считают находящимися в зоне отраженного звука. В этом случае октавные уровни звукового давления следует определять по формуле (8) L = Lw – 10 lg B – 10 lg k + 6.
Октавные уровни звукового давления L, дБ, в расчетных точках помещения с несколькими источниками шума следует определять по формуле:
![]()
где Lwi – октавный уровень звуковой мощности i-го источника, дБ;
χi, Фi, ri -то же, что и в формулах (1) и (6), но для i-го источника;
m – число источников шума, ближайших к расчетной точке (находящихся на расстоянии ri ≤ 5 rмин, где rмин – расстояние от расчетной точки до акустического центра ближайшего источника шума);
n – общее число источников шума в помещении;
k и В – то же, что и в формулах (1) и (8).
Если все n источников имеют одинаковую звуковую мощность Lwi, то
![]()
Если источник шума и расчетная точка расположены в одном помещении, расстояние между ними больше удвоенного максимального размера источника шума и между ними нет препятствий, экранирующих или отражающих шум в направлении расчетной точки, то октавные уровни звукового давления L, дБ, в расчетных точках следует определять: при точечном источнике шума (отдельная установка на территории, трансформатор и т.п.) – по формуле (11)
L = Lw – 20 lg r + 10 lg Ф – βa r/1000 – 10 lg Ω;
при протяженном источнике ограниченного размера (стена производственного здания, цепочка шахт вентиляционных систем на крыше производственного здания, трансформаторная подстанция с большим количеством открыто расположенных трансформаторов) – по формуле (12)
L = Lw – 15 lg r + 10 lg Ф – βa r/1000 – 10 lg Ω;
где Lw, r, Ф, Ω – то же, что и в формулах (1) и (7);
βа – затухание звука в атмосфере, дБ/км (табличные данные).
При расстоянии r ≤ 50 м затухание звука в атмосфере не учитывают.
Октавные уровни звукового давления L, дБ, в расчетных точках в изолируемом помещении, проникающие через ограждающую конструкцию из соседнего помещения с источником (источниками) шума или с территории, следует определять по формуле (13)
L = Lш – R + 10 lg S – 10 lg Bи – 10 lg k,
где Lш – октавный уровень звукового давления в помещении с источником шума на расстоянии 2 м от разделяющего помещения ограждения, дБ, определяют по формулам (1), (8) или (9); при шуме, проникающем в изолируемое помещение с территории, октавный уровень звукового давления Lш снаружи на расстоянии 2 м от ограждающей конструкции определяют по формулам (11) или (12);
R – изоляция воздушного шума ограждающей конструкцией, через которую проникает шум, дБ;
S – площадь ограждающей конструкции, м²;
Ви – акустическая постоянная изолируемого помещения, м²;
k – то же, что и в формуле (1).
Если ограждающая конструкция состоит из нескольких частей с различной звукоизоляцией (например, стена с окном и дверью), R определяют по формуле:
![]()
где Si – площадь i-й части, м²;
Ri – изоляция воздушного шума i-й частью, дБ.
Если ограждающая конструкция состоит из двух частей с различной звукоизоляцией (R1>R2), R определяют по формуле:
![]()
При R1>>R2 и определенном соотношении S1/S2 допускается вместо звукоизоляции ограждающей конструкции R при расчетах по формуле (13) вводить звукоизоляцию слабой части составного ограждения R2 и ее площадь S2.
Эквивалентный и максимальный уровни звука LA, дБ, создаваемого внешним транспортом и проникающего в помещения через наружную стену с окном (окнами), следует определять по формуле (16) L = LA2м – RАтран.о + 10 lg So – 10 lg Bи – 10 lg k,
Где LA2м – эквивалентный (максимальный) уровень звука снаружи на расстоянии 2 м от ограждения, дБ;
RАтран.о – изоляция внешнего транспортного шума окном, дБ;
So – площадь окна (окон), м²;
Bи – акустическая постоянная помещения, м² (в октавной полосе 500 Гц);
k – то же, что и в формуле (1).
Для жилых и административных помещений, гостиниц, общежитий площадью до 25 м² LA, дБ, определяют по формуле (17) LA = LA2м – RАтран.о – 5.
Октавные уровни звукового давления в защищаемом от шума помещении в тех случаях, когда источники шума находятся в другом здании, следует определять в несколько этапов:
1) определяют октавные уровни звуковой мощности шума Lwпр, дБ, прошедшего через наружное ограждение (или несколько ограждений) на территорию, по формуле:
![]()
где Lwi – октавный уровень звуковой мощности i-го источника, дБ;
Bш – акустическая константа помещения с источниками шума, м2;
S – площадь ограждения, м²;
R – изоляция воздушного шума ограждением, дБ;
2) определяют октавные уровни звукового давления для вспомогательной расчетной точки на расстоянии 2 м от наружного ограждения защищаемого от шума помещения по формулам (10) или (11) от каждого из источников шума. При расчете надо учесть, что для расчетных точек в пределах 10° от плоскости стены здания вводится поправка на направленность излучения 10 lg Ф = – 5 дБ;
3) определяют суммарные октавные уровни звукового давления Lсум, дБ, во вспомогательной расчетной точке (на расстоянии 2 м от наружного ограждения защищаемого от шума помещения) от всех источников шума по формуле:
![]()
где Li – уровень звукового давления от i-го источника, дБ;
4) определяют октавные уровни звукового давления L, дБ, в защищаемом от шума помещении по формуле (13), заменив в ней Lш на Lсум.
При непостоянном шуме октавные уровни звукового давления Lj, дБ, в расчетной точке следует определять по формулам (1), (7), (8), (9), (11), (12) или (13) для каждого отрезка времени τJ, мин., в течение которого уровень остается постоянным, заменяя в указанных формулах L на Lj.
Эквивалентные октавные уровни звукового давления Lэкв, дБ, за общее время воздействия T, мин., следует определять по формуле:
![]()
где τJ – время воздействия уровня Lj, мин.;
Lj – октавный уровень за время τJ, дБ.
За общее время воздействия шума T принимают: в производственных и служебных помещениях – продолжительность рабочей смены; в жилых и других помещениях, а также на территориях, где нормы установлены отдельно для дня и ночи, – продолжительность дня 7.00 – 23.00, ночи 23.00 – 7.00 ч.
Допускается в последнем случае принимать за время воздействия T днем – четырехчасовой период с наибольшими уровнями, ночью – одночасовой период с наибольшими уровнями.
Эквивалентные уровни звука непостоянного шума LAэкв, дБ, следует определять по формуле (20), заменяя Lэкв на LAэкв и Lj на LAj.
Также рекомендуем Вам следующий материал:
- “Расчетные параметры наружного воздуха“
- “Подбор воздуховодов по скорости воздуха“
- “Диаграмма Молье“
- “Классификация воздушных фильтров систем вентиляции”
From Wikipedia, the free encyclopedia
| Sound measurements | |
|---|---|
|
Characteristic |
Symbols |
| Sound pressure | p, SPL,LPA |
| Particle velocity | v, SVL |
| Particle displacement | δ |
| Sound intensity | I, SIL |
| Sound power | P, SWL, LWA |
| Sound energy | W |
| Sound energy density | w |
| Sound exposure | E, SEL |
| Acoustic impedance | Z |
| Audio frequency | AF |
| Transmission loss | TL |
|
|
|
|
Sound pressure or acoustic pressure is the local pressure deviation from the ambient (average or equilibrium) atmospheric pressure, caused by a sound wave. In air, sound pressure can be measured using a microphone, and in water with a hydrophone. The SI unit of sound pressure is the pascal (Pa).[1]
Mathematical definition[edit]

Sound pressure diagram:
- silence;
- audible sound;
- atmospheric pressure;
- sound pressure
A sound wave in a transmission medium causes a deviation (sound pressure, a dynamic pressure) in the local ambient pressure, a static pressure.
Sound pressure, denoted p, is defined by
where
- ptotal is the total pressure,
- pstat is the static pressure.
Sound measurements[edit]
Sound intensity[edit]
In a sound wave, the complementary variable to sound pressure is the particle velocity. Together, they determine the sound intensity of the wave.
Sound intensity, denoted I and measured in W·m−2 in SI units, is defined by
where
- p is the sound pressure,
- v is the particle velocity.
Acoustic impedance[edit]
Acoustic impedance, denoted Z and measured in Pa·m−3·s in SI units, is defined by[2]
where
Specific acoustic impedance, denoted z and measured in Pa·m−1·s in SI units, is defined by[2]
where
is the Laplace transform of sound pressure,
is the Laplace transform of particle velocity.
Particle displacement[edit]
The particle displacement of a progressive sine wave is given by
where
It follows that the particle velocity and the sound pressure along the direction of propagation of the sound wave x are given by
where
Taking the Laplace transforms of v and p with respect to time yields
Since 
Consequently, the amplitude of the particle displacement is related to that of the acoustic velocity and the sound pressure by
Inverse-proportional law[edit]
When measuring the sound pressure created by a sound source, it is important to measure the distance from the object as well, since the sound pressure of a spherical sound wave decreases as 1/r from the centre of the sphere (and not as 1/r2, like the sound intensity):[3]
This relationship is an inverse-proportional law.
If the sound pressure p1 is measured at a distance r1 from the centre of the sphere, the sound pressure p2 at another position r2 can be calculated:
The inverse-proportional law for sound pressure comes from the inverse-square law for sound intensity:
Indeed,
where
is the convolution operator,
- z−1 is the convolution inverse of the specific acoustic impedance,
hence the inverse-proportional law:
The sound pressure may vary in direction from the centre of the sphere as well, so measurements at different angles may be necessary, depending on the situation. An obvious example of a sound source whose spherical sound wave varies in level in different directions is a bullhorn.[citation needed]
Sound pressure level[edit]
Sound pressure level (SPL) or acoustic pressure level is a logarithmic measure of the effective pressure of a sound relative to a reference value.
Sound pressure level, denoted Lp and measured in dB,[4] is defined by:[5]
where
- p is the root mean square sound pressure,[6]
- p0 is a reference sound pressure,
- 1 Np is the neper,
- 1 B = (1/2 ln 10) Np is the bel,
- 1 dB = (1/20 ln 10) Np is the decibel.
The commonly used reference sound pressure in air is[7]
p0 = 20 μPa,
which is often considered as the threshold of human hearing (roughly the sound of a mosquito flying 3 m away). The proper notations for sound pressure level using this reference are Lp/(20 μPa) or Lp (re 20 μPa), but the suffix notations dB SPL, dB(SPL), dBSPL, or dBSPL are very common, even if they are not accepted by the SI.[8]
Most sound-level measurements will be made relative to this reference, meaning 1 Pa will equal an SPL of 94 dB. In other media, such as underwater, a reference level of 1 μPa is used.[9] These references are defined in ANSI S1.1-2013.[10]
The main instrument for measuring sound levels in the environment is the sound level meter. Most sound level meters provide readings in A, C, and Z-weighted decibels and must meet international standards such as IEC 61672-2013.
Examples[edit]
The lower limit of audibility is defined as SPL of 0 dB, but the upper limit is not as clearly defined. While 1 atm (194 dB peak or 191 dB SPL)[11][12] is the largest pressure variation an undistorted sound wave can have in Earth’s atmosphere (i.e. if the thermodynamic properties of the air are disregarded, in reality the sound waves become progressively non-linear starting over 150 dB), larger sound waves can be present in other atmospheres or other media, such as underwater or through the Earth.[13]
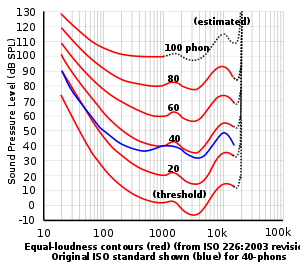
Ears detect changes in sound pressure. Human hearing does not have a flat spectral sensitivity (frequency response) relative to frequency versus amplitude. Humans do not perceive low- and high-frequency sounds as well as they perceive sounds between 3,000 and 4,000 Hz, as shown in the equal-loudness contour. Because the frequency response of human hearing changes with amplitude, three weightings have been established for measuring sound pressure: A, B and C.
In order to distinguish the different sound measures, a suffix is used: A-weighted sound pressure level is written either as dBA or LA. B-weighted sound pressure level is written either as dBB or LB, and C-weighted sound pressure level is written either as dBC or LC. Unweighted sound pressure level is called “linear sound pressure level” and is often written as dBL or just L. Some sound measuring instruments use the letter “Z” as an indication of linear SPL.[13]
Distance[edit]
The distance of the measuring microphone from a sound source is often omitted when SPL measurements are quoted, making the data useless, due to the inherent effect of the inverse proportional law. In the case of ambient environmental measurements of “background” noise, distance need not be quoted, as no single source is present, but when measuring the noise level of a specific piece of equipment, the distance should always be stated. A distance of one metre (1 m) from the source is a frequently used standard distance. Because of the effects of reflected noise within a closed room, the use of an anechoic chamber allows sound to be comparable to measurements made in a free field environment.[13]
According to the inverse proportional law, when sound level Lp1 is measured at a distance r1, the sound level Lp2 at the distance r2 is
Multiple sources[edit]
The formula for the sum of the sound pressure levels of n incoherent radiating sources is
Inserting the formulas
in the formula for the sum of the sound pressure levels yields
Examples of sound pressure[edit]
| Source of sound | Distance | Sound pressure level[a] | |
|---|---|---|---|
| (Pa) | (dBSPL) | ||
| Shock wave (distorted sound waves > 1 atm; waveform valleys are clipped at zero pressure)[11][12] | >1.01×105 | >191 | |
| Simple open-ended thermoacoustic device[14] | [clarification needed] | 1.26×104 | 176 |
| 1883 eruption of Krakatoa[15][16] | 165 km | 172 | |
| .30-06 rifle being fired | 1 m to shooter’s side |
7.09×103 | 171 |
| Firecracker[17] | 0.5 m | 7.09×103 | 171 |
| Stun grenade[18] | Ambient | 1.60×103 …8.00×103 |
158–172 |
| 9-inch (23 cm) party balloon inflated to rupture[19] | At ear | 4.92×103 | 168 |
| 9-inch (23 cm) diameter balloon crushed to rupture[19] | At ear | 1.79×103 | 159 |
| 9-inch (23 cm) party balloon inflated to rupture[19] | 0.5 m | 1.42×103 | 157 |
| 9-inch (23 cm) diameter balloon popped with a pin[19] | At ear | 1.13×103 | 155 |
| LRAD 1000Xi Long Range Acoustic Device[20] | 1 m | 8.93×102 | 153 |
| 9-inch (23 cm) party balloon inflated to rupture[19] | 1 m | 731 | 151 |
| Jet engine[13] | 1 m | 632 | 150 |
| 9-inch (23 cm) diameter balloon crushed to rupture[19] | 0.95 m | 448 | 147 |
| 9-inch (23 cm) diameter balloon popped with a pin[19] | 1 m | 282.5 | 143 |
| Loudest human voice[21] | 1 inch | 110 | 135 |
| Trumpet[22] | 0.5 m | 63.2 | 130 |
| Vuvuzela horn[23] | 1 m | 20.0 | 120 |
| Threshold of pain[24][25][21] | At ear | 20–200 | 120–140 |
| Risk of instantaneous noise-induced hearing loss | At ear | 20.0 | 120 |
| Jet engine | 100–30 m | 6.32–200 | 110–140 |
| Two-stroke chainsaw[26] | 1 m | 6.32 | 110 |
| Jackhammer | 1 m | 2.00 | 100 |
| Traffic on a busy roadway | 10 m | 0.20–0.63 | 80–90 |
| Hearing damage (over long-term exposure, need not be continuous)[27] | At ear | 0.36 | 85 |
| Passenger car | 10 m | 0.02–0.20 | 60–80 |
| EPA-identified maximum to protect against hearing loss and other disruptive effects from noise, such as sleep disturbance, stress, learning detriment, etc.[28] | Ambient | 0.06 | 70 |
| TV (set at home level) | 1 m | 0.02 | 60 |
| Normal conversation | 1 m | 2×10−3–0.02 | 40–60 |
| Very calm room | Ambient | 2.00×10−4 …6.32×10−4 |
20–30 |
| Light leaf rustling, calm breathing[13] | Ambient | 6.32×10−5 | 10 |
| Auditory threshold at 1 kHz[27] | At ear | 2.00×10−5 | 0 |
| Anechoic chamber, Orfield Labs, A-weighted[29][30] | Ambient | 6.80×10−6 | −9.4 |
| Anechoic chamber, University of Salford, A-weighted[31] | Ambient | 4.80×10−6 | −12.4 |
| Anechoic chamber, Microsoft, A-weighted[32][33] | Ambient | 1.90×10−6 | −20.35 |
- ^ All values listed are the effective sound pressure unless otherwise stated.
See also[edit]
- Acoustics
- Phon (unit)
- Loudness
- Sone (unit)
- Sound level meter
- Stevens’s power law
- Weber–Fechner law, especially The case of sound
References[edit]
- ^ “Sound Pressure is the force of sound on a surface area perpendicular to the direction of the sound”. Retrieved 22 April 2015.
- ^ a b Wolfe, J. “What is acoustic impedance and why is it important?”. University of New South Wales, Dept. of Physics, Music Acoustics. Retrieved 1 January 2014.
- ^ Longhurst, R. S. (1967). Geometrical and Physical Optics. Norwich: Longmans.
- ^ “Letter symbols to be used in electrical technology – Part 3: Logarithmic and related quantities, and their units”, IEC 60027-3 Ed. 3.0, International Electrotechnical Commission, 19 July 2002.
- ^ Attenborough K, Postema M (2008). A pocket-sized introduction to acoustics. Kingston upon Hull: The University of Hull. doi:10.5281/zenodo.7504060. ISBN 978-90-812588-2-1.
- ^ Bies, David A., and Hansen, Colin. (2003). Engineering Noise Control.
- ^ Ross Roeser, Michael Valente, Audiology: Diagnosis (Thieme 2007), p. 240.
- ^ Thompson, A. and Taylor, B. N. Sec. 8.7: “Logarithmic quantities and units: level, neper, bel”, Guide for the Use of the International System of Units (SI) 2008 Edition, NIST Special Publication 811, 2nd printing (November 2008), SP811 PDF.
- ^ Morfey, Christopher L. (2001). Dictionary of Acoustics. San Diego: Academic Press. ISBN 978-0125069403.
- ^ “Noise Terms Glossary”. Retrieved 2012-10-14.
- ^ a b Self, Douglas (2020-04-17). Small Signal Audio Design. CRC Press. ISBN 978-1-000-05044-8.
this limit is reached when the rarefaction creates a vacuum, because you can’t have a lower pressure than that. This corresponds to about +194 dB SPL.
- ^ a b Guignard, J. C.; King, P. F.; North Atlantic Treaty Organization Advisory Group for Aerospace Research and Development Aerospace Medical Panel (1972). Aeromedical Aspects of Vibration and Noise. North Atlantic Treaty Organization, Advisory Group for Aerospace Research and Development.
In air at an assumed atmospheric pressure of 1 bar (100,000 N/m2) this occurs theoretically at approximately 191 dB SPL (working with rms values
- ^ a b c d e Winer, Ethan (2013). “1”. The Audio Expert. New York and London: Focal Press. ISBN 978-0-240-82100-9.
- ^ HATAZAWA, Masayasu; SUGITA, Hiroshi; OGAWA, Takahiro; SEO, Yoshitoki (2004-01-01). “Performance of a Thermoacoustic Sound Wave Generator driven with Waste Heat of Automobile Gasoline Engine”. Transactions of the Japan Society of Mechanical Engineers Series B. 70 (689): 292–299. doi:10.1299/kikaib.70.292. ISSN 0387-5016.
- ^ “Krakatoa Eruption – The Loudest Sound”. Brüel & Kjær. Retrieved 2021-03-24.
160 km (99 miles) away from the source, registered a sound pressure level spike of more than 2½ inches of mercury (8.5 kPa), equivalent to 172 decibels.
- ^ Winchester, Simon (2003). Krakatoa: The Day the World Exploded, August 27, 1883. Penguin/Viking. p. 218. ISBN 978-0-670-91430-2.
- ^ Flamme, GregoryA; Liebe, Kevin; Wong, Adam (2009). “Estimates of the auditory risk from outdoor impulse noise I: Firecrackers”. Noise and Health. 11 (45): 223–230. doi:10.4103/1463-1741.56216. ISSN 1463-1741. PMID 19805932.
- ^ Brueck S. E., Kardous C. A., Oza A., Murphy W. J (2014). “NIOSH HHE Report No. 2013-0124-3208. Health hazard evaluation report: measurement of exposure to impulsive noise at indoor and outdoor firing ranges during tactical training exercises” (PDF). Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health.
{{cite web}}: CS1 maint: multiple names: authors list (link) - ^ a b c d e f g “Did You Know How Loud Balloons Can Be?”. Retrieved 8 June 2018.
- ^ “LRAD Corporation Product Overview for LRAD 1000Xi”. Retrieved 29 May 2014.
- ^ a b Realistic Maximum Sound Pressure Levels for Dynamic Microphones – Shure.
- ^ Recording Brass & Reeds.
- ^ Swanepoel, De Wet; Hall III, James W.; Koekemoer, Dirk (February 2010). “Vuvuzela – good for your team, bad for your ears” (PDF). South African Medical Journal. 100 (4): 99–100. doi:10.7196/samj.3697. PMID 20459912.
- ^ Nave, Carl R. (2006). “Threshold of Pain”. HyperPhysics. SciLinks. Retrieved 2009-06-16.
- ^ Franks, John R.; Stephenson, Mark R.; Merry, Carol J., eds. (June 1996). Preventing Occupational Hearing Loss – A Practical Guide (PDF). National Institute for Occupational Safety and Health. p. 88. Retrieved 2009-07-15.
- ^ “Decibel Table – SPL – Loudness Comparison Chart”. sengpielaudio. Retrieved 5 Mar 2012.
- ^ a b William Hamby. “Ultimate Sound Pressure Level Decibel Table”. Archived from the original on 2005-10-19.
- ^ “EPA Identifies Noise Levels Affecting Health and Welfare” (Press release). Environmental Protection Agency. April 2, 1974. Retrieved March 27, 2017.
- ^ ““THE QUIETEST PLACE ON EARTH” – GUINNESS WORLD RECORDS CERTIFICATE, 2005″ (PDF). Orfield Labs.
- ^ Middlemiss, Neil (December 18, 2007). “The Quietest Place on Earth – Orfield Labs”. Audio Junkies, Inc. Archived from the original on 2010-11-21.
- ^ Eustace, Dave. “Anechoic Chamber”. University of Salford.
- ^ “Microsoft lab sets new record for the world’s quietest place”. 2015-10-02. Retrieved 2016-09-20.
The computer company has built an anechoic chamber in which highly sensitive tests reported an average background noise reading of an unimaginably quiet −20.35 dBA (decibels A-weighted).
- ^ “Check out the world’s quietest room”. Microsoft: Inside B87. Retrieved 2016-09-20.
- General
- Beranek, Leo L., Acoustics (1993), Acoustical Society of America, ISBN 0-88318-494-X.
- Daniel R. Raichel, The Science and Applications of Acoustics (2006), Springer New York, ISBN 1441920803.
External links[edit]
 Media related to Sound pressure at Wikimedia Commons
Media related to Sound pressure at Wikimedia Commons- Sound Pressure and Sound Power, Effect and Cause
- Conversion of Sound Pressure to Sound Pressure Level and Vice Versa
- Table of Sound Levels, Corresponding Sound Pressure and Sound Intensity
- Ohm’s Law as Acoustic Equivalent, Calculations
- Relationships of Acoustic Quantities Associated with a Plane Progressive Acoustic Sound Wave
- Sound Pressure and Sound Power, Two Commonly Confused Characteristics of Sound
- How Many Decibels Is Twice as Loud? Sound Level Change and the Respective Factor of Sound Pressure or Sound Intensity
- Decibel (Loudness) Comparison Chart
1.25.
3ВУКОВЫЕ ВОЛНЫ
Понятие
звуковой волны. Скорость звука в различных
средах. Физические характеристики
звука: интенсивность, спектр, высота
тона, громкость, затухание. Ультразвук
и его применение. Эффект Доплера. Ударные
волны.
Звуковые волны.
Важным
видом продольных волн являются звуковые
волны.
Так называются волны с частотами 17 –
20000 Гц. Учение о звуке называется
акустикой. В акустике изучаются волны,
которые распространяются не только в
воздухе, но и в любой другой среде.
Упругие волны с частотой ниже 17 Гц
называются инфразвуком, а с частотой
выше 20000 Гц – ультразвуком.
Звуковые
волны – упругие колебания, распространяющиеся
в виде волнового процесса в газах,
жидкостях, твердых телах.
Избыточное
звуковое давление. Уравнение звуковой
волны.
Уравнение упругой
волны позволяет вычислить смещение
любой точки пространства, по которому
проходит волна, в любой момент времени.
Но как говорить о смещении частиц воздуха
или жидкости от положения равновесия?
Звук, распространяясь в жидкости или
газе, создает области сжатия и разряжение
среды, в которых давление соответственно
повышается или понижается по сравнению
с давлением невозмущенной среды.
Если
![]() –
–
давление и плотность невозмущенной
среды (среды, по которой не проходит
волна), а
![]() –
–
давление и плотность среды при
распространении в ней волнового процесса,
то величина
![]() называется
называется
избыточным
давлением.
Величина
![]() есть
есть
максимальное значение избыточное
давление (амплитуда
избыточного давления).
Изменение избыточного
давления для плоской звуковой волны
(т.е. уравнение плоской звуковой волны)
имеет вид:
 , (30.1)
, (30.1)
где y
– расстояние от источника колебаний
точки, избыточное давление в которой
мы определяем в момент времени t.
Если
ввести величину избыточной плотности
![]() и
и
ее амплитуды
![]() так
так
же, как мы вводили величину избыточного
звукового давления, то уравнение плоской
звуковой волны можно было бы записать
так:
![]() . (30.2)
. (30.2)
С![]() корость
корость
звука
— скорость распространения звуковых
волн в среде. Как правило, в газах
скорость звука меньше, чем в жидкостях,
а в жидкостях
скорость звука меньше, чем в твёрдых
телах. Чем больше плотность, тем больше
скорость звука. Скорость звука в любой
среде вычисляется по формуле:
где β —
адиабатическая
сжимаемость
среды; ρ —
плотность.
Объективные и
субъективные характеристики звука.
Само слово
“звук” отражает два различных, но
взаимосвязанных понятия: 1)звук как
физическое явление; 2)звук – то восприятие,
которое испытывает слуховой аппарат
(человеческое ухо) и ощущения, возникающие
у него при этом. Соответственно
характеристики звука делятся на
объективные,
которые могут быть измерены физической
аппаратурой, и субъективные,
определяемые восприятием данного звука
человеком.
К объективным
(физическим) характеристикам звука
относятся характеристики, которые
описывают любой волновой процесс:
частота, интенсивность и спектральный
состав. В таблицу1. включены сравнительные
данные объективных и субъективных
характеристик.
Таблица1.
|
Субъективные |
Объективные |
|
Высота |
Высота |
|
Тембр |
Тембр |
|
Громкость |
Сила |
Частота
звука
измеряется числом колебаний частиц
среды, участвующих в волновом процессе,
в 1 секунду.
Интенсивность
волны
измеряется энергией, переносимой волной
в единицу времени через единичную
площадь (расположенную перпендикулярно
направлению распространению волны).
Спектральный
состав (спектр)
звука
указывает из каких колебаний состоит
данный звук и как распределены амплитуды
между отдельными его составляющими.
Различают
сплошные
и линейчатые спектры.
Для субъективной оценки громкости
используются величины, называемые
уровнем
силы звука и уровнем громкости.
Таблица
2 -Объективные характеристики механических
волновых процессов.
|
Величина |
Уравнение |
Единица |
Сокращенное |
|
Частота |
|
|
Гц |
|
Звуковое |
|
ньютон на квадратный (паскаль) |
|
|
Плотность |
|
джоуль |
|
|
Поток |
|
ватт |
Вт |
|
Интенсивность |
|
Ватт |
|
Для характеристики
величин, определяющих восприятие звука,
существенными являются не столько
абсолютные значения интенсивности
звука и звукового давления, сколько их
отношение к некоторым пороговым
значениям. Поэтому вводятся понятие
относительных уровней интенсивности
и звукового давления.
Для того,
чтобы звуковая волна воспринималась
на слух, необходимо, чтобы ее интенсивность
превышала бы минимальную величину![]() ,
,
называемую порогом
слышимости.
Величина
![]() различная
различная
для разных частот. Для частоты
![]() порог
порог
слышимости составляет величину порядка![]() .
.
Опытом установлено, что на каждой частоте
есть верхняя граница силы звука
![]() ,
,
при превышении которого у человека
возникают болевые ощущения. Величина
![]() называется
называется
порогом
болевого ощущения.
Уровень
интенсивности
(уровень силы звука) равен десятичному
логарифму отношения интенсивности
звука при данной частоте к интенсивности
звука при той же частоте на пороге
слышимости:
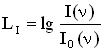 .
.
Громкость
звука
— субъективное восприятие силы звука
(абсолютная величина слухового ощущения).
Громкость главным образом зависит от
звукового
давления
и частоты
звуковых колебаний. Также на громкость
звука влияют его тембр, длительность
воздействия звуковых колебаний и другие
факторы. Уровень
громкости
равен
десятичному логарифму отношения
интенсивности звука при данной частоте
к интенсивности звука при частоте 1000
Гц на пороге слышимости:
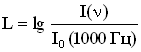 .
.
Единицей
измерения уровня интенсивности является
бел (Б):
![]() .
.
Одна десятая часть бела называется
децибел (дБ): 0,1Б = 1дБ. Формула для
определения уровня интенсивности в
децибелах примет вид:
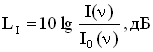 .
.
Если
записать формулу для уровня громкости
в виде
 ,
,
то единицей измерения в СИ при таком
определении величины является, единица,
имеющая название фон. При частоте 1000 Гц
шкала фонов и децибел совпадают, для
других частот они различны.
Уровень
звукового давления
равен произведению 20 на логарифм
отношения звукового давления при данной
частоте к звуковому давлению на пороге
слышимости. Единицей измерения в данном
случае является децибел.
 .
.
Ультразвук:
Механические
волны с частотой колебания, большей
20000Гц, не воспринимаются человеком как
звук.
Ультразвук
представляет собой волнообразно
распространяющееся колебательное
движение частиц среды и характеризуется
рядом отличительных особенностей по
сравнению с колебаниями слышимого
диапазона. В ультразвуковом диапазоне
частот сравнительно легко получить
направленное излучение; ультразвуковые
колебания хорошо поддаются фокусировке,
в результате чего повышается интенсивность
ультразвуковых колебаний в определенных
зонах воздействия. При распространении
в газах, жидкостях и твердых телах
ультразвук порождает уникальные явления,
многие из которых нашли практическое
применение в различных областях науки
и техники.
Прошло чуть более ста лет
с начала исследований в области применения
ультразвуковых колебаний. За это время
в активе человечества появились десятки
высокоэффективных, ресурсосберегающих
и экологически безопасных ультразвуковых
технологий. К их числу относятся:
технологии закалки, лужения и пайки
металлов, предотвращения образования
накипи на теплообменных поверхностях,
сверления хрупких и особо твердых
материалов, сушки термолабильных
веществ, экстрагирования животного и
растительного сырья, растворения,
стерилизации жидких веществ,
мелкодисперсного распыления лекарственных
препаратов, тяжелых топлив, получения
эмульсий и сверхтонких суспензий,
диспергирования красителей, сварки
металлов
и
полимеров, мойки, очистки деталей без
применения горючих и токсичных
растворителей.
В последние годы
ультразвук начинает играть все большую
роль в промышленности и научных
исследованиях. Успешно проведены
теоретические и экспериментальные
исследования в области ультразвуковой
кавитации и акустических течений,
позволившие разработать новые
технологические процессы, протекающие
при воздействии ультразвука в жидкой
фазе. В настоящее время формируется
новое направление химии – ультразвуковая
химия, позволяющая ускорить многие
химико-технологические процессы и
получить новые вещества. Научные
исследования способствовали зарождению
нового раздела акустики – молекулярной
акустики, изучающей молекулярное
взаимодействие звуковых волн с веществом.
Возникли новые области применения
ультразвука: интроскопия, голография,
квантовая акустика, ультразвуковая
фазомерия, акустоэлектроника.
Наряду с
теоретическими и экспериментальными
исследованиями в области ультразвука
выполнено много практических работ.
Разработаны универсальные и специальные
ультразвуковые станки, установки,
работающие под повышенным статическим
давлением, ультразвуковые механизированные
установки для очистки деталей, генераторы
с повышенной частотой и новой системой
охлаждения, преобразователи с равномерно
распределенным полем.
Эхолот-прибор для
определения глубины моря. Ультразвуковой
локатор используется для определения
расстояния до препятствия на пути. При
прохождении ультразвука через жидкость
частицы жидкости приобретают большие
ускорения и сильно воздействуют на
различные тела, помещенные в жидкость.
Это используют для ускорения самых
различных технологических процессов
(например, приготовления растворов.
Отмывки деталей, дубления кож и т.д.).
Ультразвук применяется для обнаружения
дефектов в металлических деталях.В
медицине проводится ультразвуковое
исследование внутренних органов.
Эффектом
Доплера
называется изменение частоты колебаний,
воспринимаемой приемником, при движении
источника этих колебаний и приемника
друг относительно друга.
Для
рассмотрения эффекта Доплера предположим,
что источник и приемник звука движутся
вдоль соединяющей их прямой; vист
и vпр
— соответственно скорости движения
источника и приемника, причем они
положительны, если источник (приемник)
приближается к приемнику (источнику),
и отрицательны, если удаляется. Частота
колебаний источника равна v0.
1.
Источник и приемник покоятся относительно
среды, т. е. vист
= vпр=0.
Если v —
скорость распространения звуковой
волны в рассматриваемой среде, то длина
волны l=vT=v/v0.
Распространяясь в среде, волна достигнет
приемника и вызовет колебания его
звукочувствительного элемента с частотой
![]() (30.3)
(30.3)
Следовательно,
частота v звука, которую
зарегистрирует приемник, равна частоте
v0,
с которой звуковая
волна излучается источником.
2.
Приемник приближается к источнику, а
источник покоится, т.
е. vпр>0,
vист=0.
В данном случае скорость распространения
волны относительно приемника станет
равной v +
vпр.
Так как длина волны при этом не
меняется, то
 (30.4)
(30.4)
т.
е. частота колебаний, воспринимаемых
приемником, в (v+vпр)/v
раз больше частоты колебаний источника.
3.
Источник приближается к преемнику, а
приемник покоится, т.
е. vист
>0, vпр=0.
Скорость
распространения колебаний зависит лишь
от свойств среды, поэтому за время,
равное периоду колебаний источника,
излученная им волна пройдет в направлении
к приемнику расстояние vT
(равное длине волны l)
независимо от того, движется ли источник
или покоится. За это же время источник
пройдет в направлении волны расстояние
vистT
(рис. 224), т. е. длина волны в направлении
движения сократится и станет равной
l‘=l—vистТ=(v—vист)T,
тогда
 (30.5)
(30.5)
т.
е. частота n колебаний,
воспринимаемых приемником, увеличится
в v/(v
– vист)
раз. В случаях 2 и 3, если vист<0
и vпр<0,
знак будет обратным.
4. Источник и
приемник движутся относительно друг
друга. Используя результаты, полученные
для случаев 2 и 3, можно записать выражение
для частоты колебаний, воспринимаемых
приемником:
 (30.6)
(30.6)
причем верхний знак
берется, если при движении источника
или приемника происходит их сближение,
нижний знак — в случае их взаимного
удаления.
Из
приведенных формул следует, что эффект
Доплера различен в зависимости от того,
движется ли источник или приемник. Если
направления скоростей vпр
и vист
не совпадают с проходящей через источник
и приемник прямой, то вместо этих
скоростей в формуле (30.6) надо брать их
проекции на направление этой прямой.
Ударная
волна: поверхность
разрыва,
которая движется относительно
газа/жидкости/твёрдых тел и при пересечении
которой давление,
плотность,
температура
и скорость испытывают скачок.
Ударные
волны возникают при взрывах, детонации,
при сверхзвуковых движениях тел, при
мощных электрич. разрядах и т. д. Например,
при взрыве ВВ образуются высоконагретые
продукты взрыва, обладающие большой
плотностью и находящиеся под высоким
давлением. В начальный момент они
окружены покоящимся воздухом при
нормальной плотности и атмосферном
давлении. Расширяющиеся продукты взрыва
сжимают окружающий воздух, причём в
каждый момент времени сжатым оказывается
лишь воздух, находящийся в определённом
объёме; вне этого объёма воздух остаётся
в невозмущённом состоянии. С течением
времени объём сжатого воздуха возрастает.
Поверхность, которая отделяет сжатый
воздух от невозмущённого, и представляет
собой фронт ударной волны. В ряде случаев
сверхзвукового движения тел в газе
(артиллерийские снаряды, спускаемые
космич. аппараты) направление движения
газа не совпадает с нормалью к поверхности
фронта ударной волны, и тогда возникают
косые ударные волны.
Примером
возникновения и распространения ударной
волны может служить сжатие газа в трубе
поршнем. Если поршень вдвигается в газ
медленно, то по газу со скоростью звука
а
бежит акустич. (упругая) волна сжатия.
Если же скорость поршня не мала по
сравнению со скоростью звука, возникает
ударная волна, скорость распространения
которой по невозмущённому газу больше,
чем скорость движения частиц газа (т.
н. массовая скорость), совпадающая со
скоростью поршня. Расстояния между
частицами в ударной волне меньше, чем
в невозмущённом газе, вследствие сжатия
газа. Если поршень сначала вдвигают в
газ с небольшой скоростью и постепенно
ускоряют, то ударная волна образуется
не сразу. Вначале возникает волна сжатия
с непрерывными распределениями плотности
r и давления р.
С течением времени крутизна передней
части волны сжатия нарастает, т. к.
возмущения от ускоренно движущегося
поршня догоняют её и усиливают, вследствие
чего возникает резкий скачок всех
гидродинамич. величин, т. е. ударная
волна
Ударная
волна в реальных газах. В реальном газе
при высоких температурах происходят
возбуждение молекулярных колебаний,
диссоциация молекул, химические реакции,
ионизация и т. д., что связано с затратами
энергии и изменением числа частиц. При
этом внутренняя энергия e сложным образом
зависит от p
и ρ
и параметры газа за фронтом.
Для
перераспределения энергии газа, сжатого
и нагретого в сильном скачке уплотнения,
по различным степеням свободы требуется
обычно очень много соударений молекул.
Поэтому ширина слоя Dx, в котором происходит
переход из начального в конечное
термодинамически равновесное состояние,
т. е. ширина фронта ударной волны, в
реальных газах обычно гораздо больше
ширины вязкого скачка и определяется
временем релаксации
наиболее медленного из процессов:
возбуждения колебаний, диссоциации,
ионизации и т. д. Распределения

Рис. 25.1
Распределение температуры (a) и плотности
(б) в ударной волне, распространяющейся
в реальном газе.
температуры
и плотности в ударной волне при этом
имеют вид, показанный на рис. 25.1
где вязкий скачок уплотнения изображён
в виде взрыва.
Ударная
волна в твёрдых телах.
Энергия и давление в твёрдых телах имеют
двоякую природу: они связаны с тепловым
движением и с взаимодействием частиц
(тепловые и упругие составляющие). Теория
междучастичных сил не может дать общей
зависимости упругих составляющих
давления и энергии от плотности в широком
диапазоне для разных веществ, и,
следовательно, теоретически нельзя
построить функцию, связывающие (p,ρ)
до и за фронтом ударной волны. Поэтому
расчеты для твёрдых (и жидких) тел
определяются из опыта или полуэмпирически.
Для значительного сжатия твёрдых тел
нужны давления в миллионы атмосфер,
которые сейчас достигаются при
экспериментальных исследованиях. На
практике большое значение имеют слабые
ударные волны с давлениями 104—105
атм. Это давления, которые развиваются
при детонации, взрывах в воде, ударах
продуктов взрыва о преграды и т. д.. В
ряде веществ — железе, висмуте и других
в ударной волне происходят фазовые
переходы — полиморфные превращения.
При небольших давлениях в твёрдых телах
возникают упругие
волны,
распространение которых, как и
распространение слабых волн сжатия в
газах, можно рассматривать на основе
законов акустики.
8
Соседние файлы в папке физика лекцыи
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Отклонение местного давления от окружающего атмосферного давления, вызванное звуковой волной
| Измерения звука | |
|---|---|
| Характеристики | Символы |
| Звуковое давление | p, SPL, L PA |
| Скорость частиц | v, SVL |
| Смещение частиц | δ |
| Интенсивность звука | I, SIL |
| Звуковая мощность | P, SWL, L WA |
| Звуковая энергия | W |
| Плотность звуковой энергии | w |
| Звуковое воздействие | E, SEL |
| Акустическое сопротивление | Z |
| Звуковая частота | AF |
| Потери при передаче | TL |
|
|
|
|
Звуковое давление или акустическое давление – это локальное давление отклонение от окружающего (среднего или равновесного) атмосферного давления, вызванное звуковой волной. В воздухе звуковое давление можно измерить с помощью микрофона, а в воде – с помощью гидрофона. единица СИ звукового давления – это паскаль (Па).
Содержание
- 1 Математическое определение
- 2 Измерения звука
- 2.1 Интенсивность звука
- 2.2 Акустический импеданс
- 2.3 Смещение частиц
- 3 Закон обратной пропорциональности
- 4 Уровень звукового давления
- 4.1 Примеры
- 4.2 Расстояние
- 4.3 Несколько источников
- 5 Примеры звукового давления
- 6 Связь между волнами давления и производством рентгеновских лучей при выбросах в атмосферу
- 7 См. Также
- 8 Ссылки
- 9 Внешние ссылки
Математическое определение
 Диаграмма звукового давления:
Диаграмма звукового давления:
- тишина ;
- звуковой сигнал;
- атмосферное давление;
- звуковое давление
Звуковая волна в среде передачи вызывает отклонение (звуковое давление, динамическое давление) в местном давлении окружающей среды, статическое давление.
Звуковое давление, обозначаемое p, определяется как
- p total = p stat + p, { displaystyle p _ { text {total}} = p _ { text {stat}} + p,}
где
- ptotal – общее давление,
- pstat – статическое давление.
Измерения звука
Интенсивность звука
В звуке волна, дополнительной переменной к звуковому давлению является скорость частицы. Вместе они определяют интенсивность звука волны.
Интенсивность звука, обозначенная I и измеренная в W ·m в единицах СИ, определяется как
- I = pv, { displaystyle mathbf {I} = p mathbf { v},}
где
- p – звуковое давление,
- v- скорость частицы.
Акустический импеданс
Акустический импеданс, обозначенный Z и измеренный в Па · м · с в Единицы СИ, определяются как
- Z (s) = p ^ (s) Q ^ (s), { displaystyle Z (s) = { frac {{ hat {p}} (s)} {{ hat {Q}} (s)}},}
где
- p ^ (s) { displaystyle { hat {p}} (s)}
– это Преобразование Лапласа звукового давления,
- Q ^ (s) { displaystyle { hat {Q}} (s)}
– это преобразование Лапласа для объемного расхода звука.
Удельный акустический импеданс, обозначаемый z и измеряемый в Па · м · с в единицах СИ, определяется как
- z (s) = p ^ (s) v ^ (s), { displaystyle z (s) = { frac {{ hat {p}} (s)} {{ hat {v}} (s)}},}
где
- p ^ (s) { displaystyle { hat {p}} (s)}
– преобразование Лапласа звукового давления,
- v ^ (s) { displaystyle { hat {v}} (s)}
– преобразование Лапласа скорости частицы.
Смещение частицы
Смещение частицы прогрессивной синусоидальной волны задается как
- δ (r, t) знак равно δ м соз (К ⋅ р – ω T + φ δ, 0), { displaystyle delta ( mathbf {r}, t) = delta _ { text {m}} cos ( mathbf {k} cdot mathbf {r} – omega t + varphi _ { delta, 0}),}
где
- δ m { displaystyle delta _ { text {m}}}
– амплитуда смещения частицы,
- φ δ, 0 { displaystyle varphi _ { delta, 0}}
– фазовый сдвиг смещения частицы,
- k- угловой волновой вектор ,
- ω – угловая частота .
Отсюда следует, что скорость частицы и звуковое давление вдоль направления распространения звуковая волна x определяется выражением
- v (r, t) = ∂ δ ∂ t (r, t) = ω δ m cos (k ⋅ r – ω t + φ δ, 0 + π 2) = vm соз (К ⋅ р – ω T + φ v, 0), { displaystyle v ( mathbf {r}, t) = { frac { partial delta} { partial t}} ( mathbf {r }, t) = omega delta _ { text {m}} cos left ( mathbf {k} cdot mathbf {r} – omega t + varphi _ { delta, 0} + { frac { pi } {2}} right) = v _ { text {m}} cos ( mathbf {k} cdot mathbf {r} – omega t + varphi _ {v, 0}),}
- p (r, t) = – ρ c 2 ∂ δ ∂ x (r, t) = ρ c 2 kx δ m cos (k ⋅ r – ω t + φ δ, 0 + π 2) = pm cos ( К ⋅ р – ω T + φ п, 0), { displaystyle p ( mathbf {r}, t) = – rho c ^ {2} { frac { partial delta} { partial x}} ( mathbf {r}, t) = rho c ^ {2} k_ {x} delta _ { text {m}} cos left ( mathbf {k} cdot mathbf {r} – омега t + varphi _ { delta, 0} + { frac { pi} {2}} right) = p _ { text {m}} cos ( mathbf {k} cdot mathbf {r} – omega t + varphi _ {p, 0}),}
где
- vm- амплитуда скорости частицы,
- φ v, 0 { displaystyle varphi _ {v, 0}}
– фазовый сдвиг скорости частицы,
- pm- амплитуда акустического давления,
- φ p, 0 { displaystyle varphi _ {p, 0}}
– фазовый сдвиг акустического давления.
Взятие преобразований Лапласа для v и p относительно времени дает
- v ^ (r, s) = vms cos φ v, 0 – ω sin φ v, 0 s 2 + ω 2, { displaystyle { hat {v}} ( mathbf {r }, s) = v _ { text {m}} { frac {s cos varphi _ {v, 0} – omega sin varphi _ {v, 0}} {s ^ {2} + омега ^ {2}}},}
- p ^ (r, s) = pms cos φ p, 0 – ω sin φ p, 0 s 2 + ω 2. { displaystyle { hat {p}} ( mathbf {r}, s) = p _ { text {m}} { frac {s cos varphi _ {p, 0} – omega sin varphi _ {p, 0}} {s ^ {2} + omega ^ {2}}}.}
Поскольку φ v, 0 = φ p, 0 { displaystyle varphi _ {v, 0 } = varphi _ {p, 0}}
- zm (r, s) = | z (r, s) | = | p ^ (r, s) v ^ (r, s) | = p m v m = ρ c 2 k x ω. { displaystyle z _ { text {m}} ( mathbf {r}, s) = | z ( mathbf {r}, s) | = left | { frac {{ hat {p}} ( mathbf {r}, s)} {{ hat {v}} ( mathbf {r}, s)}} right | = { frac {p _ { text {m}}} {v _ { text { m}}}} = { frac { rho c ^ {2} k_ {x}} { omega}}.}
Следовательно, амплитуда смещения частицы связана с амплитудой акустической скорости и звуковое давление на
- δ m = vm ω, { displaystyle delta _ { text {m}} = { frac {v _ { text {m}}} { omega}},}
- δ m = pm ω zm (r, s). { displaystyle delta _ { text {m}} = { frac {p _ { text {m}}} { omega z _ { text {m}} ( mathbf {r}, s)}}. }
Закон обратной пропорциональности
При измерении звукового давления, создаваемого источником звука, важно также измерить расстояние до объекта, поскольку звуковое давление сферической звуковой волны уменьшается как 1 / r от центра сферы (а не как 1 / r, как интенсивность звука):
- p (r) ∝ 1 r. { displaystyle p (r) propto { frac {1} {r}}.}
Это соотношение является законом обратной пропорциональности.
Если звуковое давление p 1 измеряется на расстоянии r 1 от центра сферы, звуковое давление p 2 при другое положение r 2 может быть вычислено:
- p 2 = r 1 r 2 p 1. { displaystyle p_ {2} = { frac {r_ {1}} {r_ {2}}} , p_ {1}.}
Закон обратной пропорциональности для звукового давления происходит из закона обратных квадратов для интенсивности звука:
- I (r) ∝ 1 r 2. { displaystyle I (r) propto { frac {1} {r ^ {2}}}.}
Действительно,
- I (r) = p (r) v (r) = p (r) [п * г – 1] (г) ∝ п 2 (г), { Displaystyle I (г) = р (г) v (г) = р (г) влево [п * г ^ {- 1} right] (r) propto p ^ {2} (r),}
где
- ∗ { displaystyle *}
– оператор свертки,
- z – это свертка, обратная удельному акустическому импедансу,
, следовательно, закон обратной пропорциональности:
- p (r) ∝ 1 r. { displaystyle p (r) propto { frac {1} {r}}.}
Звуковое давление также может меняться в направлении от центра сферы, поэтому измерения под разными углами могут потребоваться в зависимости от по ситуации. Очевидным примером источника звука, уровень сферической звуковой волны которого изменяется по уровню в разных направлениях, является мегафон.
Уровень звукового давления
Уровень звукового давления (SPL) или уровень акустического давления – это логарифмическая мера эффективного давления звука относительно контрольного значения.
Уровень звукового давления, обозначенный L p и измеренный в дБ, определяется как
- L p = ln (pp 0) Np = 2 log 10 (pp 0) B = 20 log 10 (pp 0) дБ, { displaystyle L_ {p} = ln left ({ frac {p} {p_ {0}}} right) ~ { text {Np}} = 2 log _ {10} left ({ frac {p} {p_ {0}}} right) ~ { text {B}} = 20 log _ {10} left ( { frac {p} {p_ {0}}} right) ~ { text {dB}},}
где
- p – среднеквадратичное звуковое давление,
- p0- эталонное звуковое давление,
- 1 Np – непер,
- 1 B = (1/2 ln 10) Np – bel,
- 1 дБ = (1 / 20 ln 10) Np – децибел.
Обычно используемое эталонное звуковое давление в воздухе
- p0= 20 мкПа,
, которое часто считается порогом человеческого слуха ( примерно звук комара, летящего на расстоянии 3 м). Соответствующие обозначения для уровня звукового давления с использованием этого эталона: L p / (20 мкПа) или L p (re 20 мкПа), но суффиксные обозначения дБ SPL, дБ (SPL), dBSPL или dB SPL очень распространены, даже если они не приняты SI.
Большинство измерений уровня звука будет производиться относительно этого эталона, то есть 1 Па будет равняться SPL 94 дБ. В других средах, таких как под водой, используется контрольный уровень 1 мкПа. Эти ссылки определены в ANSI S1.1-2013.
Основным инструментом для измерения уровней звука в окружающей среде является измеритель уровня звука. Большинство шумомеров обеспечивают показания в децибелах, взвешенных по шкале A, C и Z, и должны соответствовать международным стандартам, таким как IEC 61672-2013.
Примеры
Нижний предел слышимости определяется как SPL 0 дБ, но верхний предел не так четко определен. В то время как 1 атм (пик 194 дБ или 191 дБ SPL) является наибольшим изменением давления, которое неискаженная звуковая волна может иметь в атмосфере Земли, более крупные звуковые волны могут присутствовать в других атмосферы или других сред, например, под водой или сквозь землю.
 Контур равной громкости, показывающий зависимость звукового давления от частоты при различных воспринимаемых уровнях громкости
Контур равной громкости, показывающий зависимость звукового давления от частоты при различных воспринимаемых уровнях громкости
Уши обнаруживают изменения звукового давления. Человеческий слух не имеет плоской спектральной чувствительности (частотной характеристики ) относительно частоты по сравнению с амплитудой. Люди не воспринимают низкочастотные и высокочастотные звуки так же хорошо, как они воспринимают звуки между 3000 и 4000 Гц, как показано на контуре равной громкости. Поскольку частотная характеристика человеческого слуха изменяется с амплитудой, для измерения звукового давления были установлены три взвешивания: A, B и C. A-взвешивание применяется к уровням звукового давления до 55 дБ, B-взвешивание применяется для уровней звукового давления от 55 дБ до 85 дБ, а C-взвешивание предназначено для измерения уровней звукового давления выше 85 дБ.
Для того, чтобы различать различные параметры звука, используется суффикс: A-взвешенное звуковое давление уровень записывается как дБ A или L A. Уровень звукового давления, взвешенный по B, записывается как дБ B или L B, а уровень звукового давления, взвешенный по C, записывается как дБ C или L С. Невзвешенный уровень звукового давления называется «линейным уровнем звукового давления» и часто обозначается как дБ L или просто L. Некоторые инструменты для измерения звука используют букву «Z» как указатель линейного звукового давления.
Расстояние
Расстояние от измерительного микрофона до источника звука часто опускается при цитировании измерений SPL, что делает данные бесполезными из-за неотъемлемого эффекта закона обратных квадратов, в котором вкратце говорится, что удвоение расстояния между источником и приемником приводит к делению измеряемого эффекта на четыре. В случае измерения «фонового» шума в окружающей среде расстояние указывать не нужно, поскольку нет единственного источника, но при измерении уровня шума от конкретной единицы оборудования всегда следует указывать расстояние. Расстояние в один метр (1 м) от источника является часто используемым стандартным расстоянием. Из-за эффектов отраженного шума в закрытом помещении использование безэховой камеры позволяет сопоставить звук с измерениями, проводимыми в условиях свободного поля.
В соответствии с законом обратной пропорциональности, когда уровень звука L p1 измеряется на расстоянии r 1, уровень звука L p2 на расстоянии r 2 равен
- L p 2 = L p 1 + 20 log 10 (r 1 r 2) дБ. { displaystyle L_ {p_ {2}} = L_ {p_ {1}} + 20 log _ {10} left ({ frac {r_ {1}} {r_ {2}}} right) ~ { text {дБ}}.}
Несколько источников
Формула для суммы уровней звукового давления n некогерентных излучающих источников:
- L Σ = 10 log 10 (p 1 2 + p 2 2 +… + pn 2 p 0 2) дБ = 10 log 10 [(p 1 p 0) 2 + (p 2 p 0) 2 +… + (pnp 0) 2] дБ. { displaystyle L _ { Sigma} = 10 log _ {10} left ({ frac {p_ {1} ^ {2} + p_ {2} ^ {2} + ldots + p_ {n} ^ { 2}} {p_ {0} ^ {2}}} right) ~ { text {dB}} = 10 log _ {10} left [ left ({ frac {p_ {1}} {p_ {0}}} right) ^ {2} + left ({ frac {p_ {2}} {p_ {0}}} right) ^ {2} + ldots + left ({ frac { p_ {n}} {p_ {0}}} right) ^ {2} right] ~ { text {dB}}.}
Вставка формул
- (pip 0) 2 = 10 L i 10 дБ, я = 1, 2,…, n { displaystyle left ({ frac {p_ {i}} {p_ {0}}} right) ^ {2} = 10 ^ { frac {L_ { i}} {10 ~ { text {dB}}}}, quad i = 1,2, ldots, n}
в формуле для суммы уровней звукового давления дает
- L Σ = 10 log 10 (10 L 1 10 дБ + 10 L 2 10 дБ +… + 10 L n 10 дБ) дБ. { Displaystyle L _ { Sigma} = 10 log _ {10} left (10 ^ { frac {L_ {1}} {10 ~ { text {дБ}}}} + 10 ^ { frac {L_ {2}} {10 ~ { text {dB}}}} + ldots +10 ^ { frac {L_ {n}} {10 ~ { text {dB}}}} right) ~ { text {дБ}}.}
Примеры звукового давления
| Источник звука | Расстояние | Звуковое давление уровень | |
|---|---|---|---|
| (Pa ) | (dBSPL ) | ||
| Извержение Кракатау 1883 года ; волна давления от третьего взрыва | ~6.32 × 10 | ~ 310 | |
| Кашалот | 6.32 × 10 | 230 | |
| Ударная волна (искаженный звук волны>1 атм ; впадины формы волны отсекаются при нулевом давлении) | >1.01 × 10 | >194 | |
| Простое открытое термоакустическое устройство | 1,26 × 10 | 176 | |
| .30-06 Винтовка стреляет | 1 m to. сбоку стрелка | 7,27 × 10 | 171 |
| Оглушение граната | Ambient | 1.60 ×10….8.00 ×10 | 158–172 |
| 9-дюймовый (23 см) баллон для вечеринок, надутый до разрыва | У уха | 4.92 ×10 | 168 |
| Баллон диаметром 9 дюймов (23 см) раздавлен до разрыва | У уха | 1,79 × 10 | 159 |
| Воздушный шар диаметром 9 дюймов (23 см), выдавленный булавкой | На ухо | 1,13 × 10 | 155 |
| LRAD 1000Xi Акустическое устройство дальнего действия | 1 м | 8,93 × 10 | 153 |
| 9-дюймовый (23 см) баллон для вечеринок, надутый до разрыва | 1 м | 731 | 151 |
| Реактивный двигатель | 1 м | 632 | 150 |
| Баллон диаметром 9 дюймов (23 см) раздавлен до разрыва | 0,95 м | 448 | 147 |
| воздушный шар диаметром 9 дюймов (23 см), выдавленный булавкой | 1 м | 282,5 | 143 |
| Порог боли | В ухе | 63,2–200 | 130–140 |
| Самый громкий человеческий голос | 1 дюйм | 110 | 135 |
| Труба | 0,5 м | 63,2 | 130 |
| Вувузела рог | 1 м | 20,0 | 120 |
| Риск мгновенной потери слуха из-за шума | На ухо | 20,0 | 120 |
| Реактивный двигатель | 100–30 м | 6,32 –200 | 110–140 |
| Двухтактная бензопила | 1 м | 6.32 | 110 |
| отбойный молоток | 1 м | 2,00 | 100 |
| Движение по загруженной дороге | 10 м | 0,20–0,63 | 80– 90 |
| Нарушение слуха (при длительном воздействии, не обязательно продолжаться) | На ухо | 0,36 | 85 |
| Легковой автомобиль | 10 м | 0,02–0,20 | 60–80 |
| EPA -определенный максимум для защиты от потери слуха и других деструктивных эффектов шума, таких как нарушение сна, стресс, нарушение обучения и т. Д.. | Окружающая среда | 0,06 | 70 |
| ТВ (на домашнем уровне) | 1 м | 0,02 | 60 |
| Обычный разговор | 1 м | 2 × 10–0,02 | 40–60 |
| Очень спокойная комната | Окружающая среда | 2.00 ×10….6.32 ×10 | 20–30 |
| Легкий шелест листьев, спокойное дыхание | Окружающий | 6,32 × 10 | 10 |
| Слуховой порог при 1 кГц | На ухе | 2,00 × 10 | 0 |
| Безэховая камера, Orfield Labs, A-взвешенный | Окружающий | 6.80 ×10 | −9,4 |
| Безэховая камера, Университет Солфорда, A- взвешенный | Окружающий | 4,80 × 10 | -12,4 |
| Безэховая камера, Microsoft, A-взвешенный | Окружающий | 1,90 × 10 | −20,35 |
Соотношение между волнами давления a nd образование рентгеновских лучей в воздушных разрядах
Давление и ударные волны, создаваемые электрическими разрядами, способны возмущать окружающий воздух до 80%. Это, однако, имеет немедленные последствия для движения и свойств вторичных стримерных разрядов в возмущенном воздухе: в зависимости от направления (относительно окружающего электрического поля) возмущения воздуха изменяют скорость разряда, способствуют разветвлению или запуску самопроизвольное инициирование встречного разряда. Недавнее моделирование показало, что такие возмущения могут даже способствовать созданию рентгеновского излучения (с энергией в несколько десятков кэВ) от таких стримерных разрядов, которые создаются убегающими электронами через Процесс тормозного излучения.
См. Также
- Акустика
- Фон (единица измерения)
- Громкость
- Сон (единица измерения)
- Измеритель уровня звука
- закон мощности Стивенса
- Закон Вебера-Фехнера, особенно Случай звука
Ссылки
- Общие
- Беранек, Лео Л., Акустика (1993), Акустическое общество Америки, ISBN 0-88318-494-X .
- Дэниел Р. Райчел, Наука и приложения акустики (2006), Springer, Нью-Йорк, ISBN 1441920803 .
Внешние ссылки
- Звуковое давление и звуковая мощность, последствия и причина
- Преобразование звукового давления в уровень звукового давления и наоборот
- Таблица уровней звука, соответствующего звукового давления и интенсивности звука
- Ом Закон как акустический эквивалент, расчеты
- Соотношение акустических величин, связанных с плоской прогрессивной акустической звуковой волной
- Звуковое давление и звуковая мощность, две часто путаемые характеристики звука
- Сколько децибел в два раза громче? Изменение уровня звука и соответствующий коэффициент звукового давления или интенсивности звука
- Децибел (громкость) Сравнительная таблица
| Звуковые измерения | |
|---|---|
|
Характеристика |
Символы |
| Звуковое давление | п, SPL, LPA |
| Скорость частиц | v, SVL |
| Смещение частиц | δ |
| Интенсивность звука | я, SIL |
| Звуковая мощность | п, SWL, LWA |
| Звуковая энергия | W |
| Плотность звуковой энергии | ш |
| Звуковое воздействие | E, SEL |
| Акустический импеданс | Z |
| Частота звука | AF |
| Потеря передачи | TL |
|
|
|
Звуковое давление или же акустическое давление местный давление отклонение от окружающей среды (среднее или равновесное) атмосферное давление, вызванный звуковая волна. В воздухе звуковое давление можно измерить с помощью микрофон, а в воде с гидрофон. В Единица СИ звукового давления – это паскаль (Па).[1]
Математическое определение

Диаграмма звукового давления:
- тишина;
- слышимый звук;
- атмосферное давление;
- звуковое давление
Звуковая волна в среда передачи вызывает отклонение (звуковое давление, динамичный давление) в местном атмосферном давлении, a статический давление.
Звуковое давление, обозначенное п, определяется
куда
- побщий полное давление,
- пстат статическое давление.
Звуковые измерения
Интенсивность звука
В звуковой волне дополнительной переменной к звуковому давлению является скорость частицы. Вместе они определяют интенсивность звука волны.
Интенсивность звука, обозначенный я и измеряется в W ·м−2 в единицах СИ, определяется как
куда
- п это звуковое давление,
- v – скорость частицы.
Акустический импеданс
Акустический импеданс, обозначенный Z и измеряется в Па · м−3· S в единицах СИ, определяется как[2]
куда
это Преобразование Лапласа звукового давления[нужна цитата ],
– преобразование Лапласа объемного расхода звука.
Удельный акустический импеданс, обозначенный z и измеряется в Па · м−1· S в единицах СИ, определяется как[2]
куда
– преобразование Лапласа звукового давления,
– преобразование Лапласа скорости частицы.
Смещение частиц
В смещение частиц из прогрессивный синусоидальная волна дан кем-то
куда
это амплитуда смещения частицы,
это сдвиг фазы смещения частицы,
- k это угловой волновой вектор,
- ω это угловая частота.
Отсюда следует, что скорость частицы и звуковое давление вдоль направления распространения звуковой волны Икс даны
куда
- vм – амплитуда скорости частицы,
– фазовый сдвиг скорости частицы,
- пм – амплитуда акустического давления,
– фазовый сдвиг акустического давления.
Принимая преобразования Лапласа v и п по времени дает
С 
Следовательно, амплитуда смещения частицы связана с амплитудой акустической скорости и звукового давления соотношением
Обратно-пропорциональный закон
При измерении звукового давления, создаваемого источником звука, важно также измерить расстояние до объекта, поскольку звуковое давление сферический звуковая волна уменьшается как 1 /р от центра сферы (а не как 1 /р2, как и интенсивность звука):[3]
Эти отношения обратно пропорциональный закон.
Если звуковое давление п1 измеряется на расстоянии р1 от центра сферы звуковое давление п2 на другой позиции р2 можно рассчитать:
Обратно-пропорциональный закон для звукового давления происходит из закона обратных квадратов для интенсивности звука:
В самом деле,
куда
это свертка оператор
- z−1 – свертка, обратная удельный акустический импеданс,
отсюда обратнопропорциональный закон:
Звуковое давление также может меняться в направлении от центра сферы, поэтому в зависимости от ситуации могут потребоваться измерения под разными углами. Очевидным примером источника звука, сферическая звуковая волна которого изменяется по уровню в разных направлениях, является мегафон.[нужна цитата ]
Уровень звукового давления
Уровень звукового давления (SPL) или уровень акустического давления это логарифмическая мера эффективного давления звука относительно эталонного значения.
Уровень звукового давления, обозначенный Lп и измеряется в дБ, определяется[4]
куда
- п это среднеквадратичное значение звуковое давление,[5]
- п0 это эталонное звуковое давление,
- 1 нп это непер,
- 1 В = (1/2 пер 10) Np это Bel,
- 1 дБ = (1/20 пер 10) Np это децибел.
Обычно используемым эталонным звуковым давлением в воздухе является[6]
- п0 = 20 мкПа,
который часто рассматривается как порог человеческого слуха (примерно звук комара, летящего на расстоянии 3 м). Правильные обозначения уровня звукового давления с использованием этого справочника: Lп/ (20 мкПа) или же Lп (при 20 мкПа), но суффиксные обозначения дБ SPL, дБ (SPL), дБSPL или дБSPL очень распространены, даже если они не приняты СИ.[7]
Большинство измерений уровня звука будет производиться относительно этого эталона, то есть 1 Па будет равняться SPL 94 дБ. В других средствах массовой информации, таких как подводный, эталонный уровень 1 мкПа используется.[8] Эти ссылки определены в ANSI S1.1-2013.[9]
Основным инструментом для измерения уровня звука в окружающей среде является измеритель уровня звука. Большинство шумомеров обеспечивают показания в децибелах, взвешенных по шкале A, C и Z, и должны соответствовать международным стандартам, таким как МЭК 61672-2013.
Примеры
Нижний предел слышимости определяется как SPL 0 дБ, но верхний предел не так четко определен. Пока 1 банкомат (194 дБ пик или же 191 дБ SPL) – это наибольшее изменение давления, которое может иметь неискаженная звуковая волна в Атмосфера Земли, более крупные звуковые волны могут присутствовать в других атмосферы или в других средах, например, под водой или сквозь Землю.[10]

Контур равной громкости, показывая звуковое давление в зависимости от частоты при различных воспринимаемых уровнях громкости
Уши обнаруживают изменения звукового давления. Человеческий слух не имеет квартиры спектральная чувствительность (частотный отклик ) относительно частоты по сравнению с амплитуда. Люди не воспринимают низкочастотные и высокочастотные звуки так же хорошо, как они воспринимают звуки между 3000 и 4000 Гц, как показано на контур равной громкости. Поскольку частотная характеристика человеческого слуха изменяется с амплитудой, для измерения звукового давления были установлены три веса: A, B и C. А-взвешивание применяется к уровням звукового давления до 55 дБ, B-взвешивание применяется к уровням звукового давления между 55 дБ и 85 дБ, а C-взвешивание – для измерения уровней звукового давления выше 85 дБ.[10]
Чтобы различать различные звуковые параметры, используется суффикс: A-взвешенный уровень звукового давления записывается либо как дБА или LА. Уровень звукового давления, взвешенный по шкале B, записывается как дБB или LB, а уровень звукового давления, взвешенный по C, записывается как дБC или LC. Невзвешенный уровень звукового давления называется «линейным уровнем звукового давления» и часто записывается как дБ.L или просто L. В некоторых звукоизмерительных приборах буква «Z» обозначает линейное звуковое давление.[10]
Расстояние
Расстояние от измерительного микрофона до источника звука часто опускается, когда указываются измерения SPL, что делает данные бесполезными из-за внутреннего эффекта закон обратных квадратов, в котором вкратце говорится, что удвоение расстояния между источником и приемником приводит к делению измеряемого эффекта на четыре. В случае измерения «фонового» шума в окружающей среде расстояние указывать не нужно, поскольку нет единственного источника, но при измерении уровня шума от конкретной единицы оборудования всегда следует указывать расстояние. Расстояние один метр (1 м) от источника – часто используемое стандартное расстояние. Из-за эффектов отраженного шума в закрытом помещении использование безэховая камера позволяет сопоставить звук с измерениями, выполненными в условиях свободного поля.[10]
Согласно обратному пропорциональному закону, когда уровень звука Lп1 измеряется на расстоянии р1, уровень звука Lп2 на расстоянии р2 является
Множественные источники
Формула суммы уровней звукового давления п источники некогерентного излучения
Вставка формул
в формуле суммы уровней звукового давления дает
Примеры звукового давления
| Источник звука | Расстояние | Уровень звукового давления[а] | |
|---|---|---|---|
| (Па ) | (дБSPL ) | ||
| 1883 извержение Кракатау; волна давления от третьего взрыва | ~6.32×1010 | ~310 | |
| Кашалот[11] | 6.32×106 | 230 | |
| Ударная волна (искаженные звуковые волны> 1 банкомат; впадины формы сигнала обрезаются при нулевом давлении) | >1.01×105 | >194 | |
| Простой открытый термоакустический устройство[12] | [требуется разъяснение ] | 1.26×104 | 176 |
| .30-06 винтовка уволен | 1 м к сторона стрелка |
7.27×103 | 171 |
| Светошумовая граната[13] | Окружающий | 1.60×103 …8.00×103 |
158–172 |
| 9-дюймовый (23 см) баллон для вечеринок, надутый до разрыва[14] | Слеза | 4.92×103 | 168 |
| Баллон диаметром 9 дюймов (23 см) раздавлен до разрыва[14] | Слеза | 1.79×103 | 159 |
| Воздушный шар диаметром 9 дюймов (23 см), надетый булавкой[14] | Слеза | 1.13×103 | 155 |
| LRAD 1000Xi Акустическое устройство дальнего действия[15] | 1 мес. | 8.93×102 | 153 |
| 9-дюймовый (23 см) баллон для вечеринок, надутый до разрыва[14] | 1 мес. | 731 | 151 |
| Реактивный двигатель[10] | 1 мес. | 632 | 150 |
| Баллон диаметром 9 дюймов (23 см) раздавлен до разрыва[14] | 0,95 м | 448 | 147 |
| Воздушный шар диаметром 9 дюймов (23 см), надетый булавкой[14] | 1 мес. | 282.5 | 143 |
| Порог боли[16][17][18] | Слеза | 63.2–200 | 130–140 |
| Самый громкий человеческий голос[18] | 1 дюйм | 110 | 135 |
| Труба[19] | 0,5 м | 63.2 | 130 |
| Вувузела Рог[20] | 1 мес. | 20.0 | 120 |
| Риск мгновенного потеря слуха из-за шума | Слеза | 20.0 | 120 |
| Реактивный двигатель | 100–30 м | 6.32–200 | 110–140 |
| Двухтактный бензопила[21] | 1 мес. | 6.32 | 110 |
| Отбойный молоток | 1 мес. | 2.00 | 100 |
| Движение на оживленной дороге | 10 м | 0.20–0.63 | 80–90 |
| Нарушение слуха (при длительном воздействии не обязательно быть непрерывным)[22] | Слеза | 0.36 | 85 |
| Легковой автомобиль | 10 м | 0.02–0.20 | 60–80 |
| EPA -определенный максимум для защиты от потери слуха и других негативных последствий шума, таких как нарушение сна, стресс, нарушение обучения и т. д.[23] | Окружающий | 0.06 | 70 |
| Телевизор (установлен на бытовом уровне) | 1 мес. | 0.02 | 60 |
| Нормальный разговор | 1 мес. | 2×10−3–0.02 | 40–60 |
| Очень спокойная комната | Окружающий | 2.00×10−4 …6.32×10−4 |
20–30 |
| Легкий шелест листьев, спокойное дыхание[10] | Окружающий | 6.32×10−5 | 10 |
| Слуховой порог на 1 кГц[22] | Слеза | 2.00×10−5 | 0 |
| Безэховая камера, Орфилд Лабс, A-взвешенный[24][25] | Окружающий | 6.80×10−6 | −9.4 |
| Безэховая камера, Салфордский университет, A-взвешенный[26] | Окружающий | 4.80×10−6 | −12.4 |
| Безэховая камера, Microsoft, A-взвешенный[27][28] | Окружающий | 1.90×10−6 | −20.35 |
- ^ Все перечисленные значения являются эффективным звуковым давлением, если не указано иное.
Связь между волнами давления и образованием рентгеновских лучей в разрядах воздуха
Давление и ударные волны, создаваемые электрическими разрядами, способны возмущать окружающий воздух до 80%.[29][30] Это, однако, имеет непосредственные последствия для движения и свойств вторичных стримерные разряды в возмущенном воздухе: в зависимости от направления (относительно окружающего электрического поля) возмущения в воздухе изменяют скорость разряда, способствуют ветвлению или вызывают спонтанное инициирование встречного разряда. [31] Недавнее моделирование показало, что такие возмущения могут даже облегчить производство Рентгеновские лучи (с энергиями в несколько десятков кэВ) от таких стримерных разрядов, которые создаются убегающими электронами через Тормозное излучение процесс. [32]
Смотрите также
- Акустика
- Телефон (единица измерения)
- Громкость
- Sone (единица измерения)
- Измеритель уровня звука
- Степенной закон Стивенса
- Закон Вебера – Фехнера, особенно Случай звука
Рекомендации
- ^ «Звуковое давление – это сила звука на поверхности, перпендикулярной направлению звука». Получено 22 апреля 2015.
- ^ а б Вулф, Дж. «Что такое акустический импеданс и почему это важно?». Университет Нового Южного Уэльса, факультет физики, музыкальной акустики. Получено 1 января 2014.
- ^ Лонгхерст, Р. С. (1967). Геометрическая и физическая оптика. Норвич: Лонгманс.
- ^ «Буквенные символы для использования в электротехнике – Часть 3: Логарифмические и связанные с ними величины и их единицы», IEC 60027-3 Ed. 3.0, Международная электротехническая комиссия, 19 июля 2002 г.
- ^ Бис, Дэвид А., и Хансен, Колин. (2003). Инженерный контроль шума.
- ^ Росс Рузер, Майкл Валенте, Аудиология: Диагностика (Thieme 2007), стр. 240.
- ^ Томпсон А. и Тейлор Б. Н. Сек. 8.7: «Логарифмические величины и единицы: уровень, непер, бел», Руководство по использованию Международной системы единиц (СИ), издание 2008 г., Специальная публикация NIST 811, 2-е издание (ноябрь 2008 г.), SP811 PDF.
- ^ Морфей, Кристофер Л. (2001). Словарь по акустике. Сан-Диего: Academic Press. ISBN 978-0125069403.
- ^ «Глоссарий терминов по шуму». Получено 2012-10-14.
- ^ а б c d е ж Винер, Итан (2013). «1». Аудио эксперт. Нью-Йорк и Лондон: Focal Press. ISBN 978-0-240-82100-9.
- ^ «Мощные источники звука в океане: кашалоты и военные сонары». Океанский Альянс. Океанский Альянс. Получено 14 октября 2020.
- ^ ХАТАЗАВА, Масаясу; СУГИТА, Хироши; ОГАВА, Такахиро; SEO, Ёситоки (01.01.2004). «Характеристики термоакустического генератора звуковых волн, работающего на отработанном тепле автомобильного бензинового двигателя». Труды Японского общества инженеров-механиков, серия B. 70 (689): 292–299. Дои:10.1299 / kikaib.70.292. ISSN 0387-5016.
- ^ Брюк С. Э., Кардус К. А., Оза А., Мерфи В. Дж. (2014). «Отчет NIOSH HHE № 2013-0124-3208. Отчет об оценке опасности для здоровья: измерение воздействия импульсного шума на внутренних и наружных стрельбищах во время тактических учений» (PDF). Цинциннати, Огайо: Министерство здравоохранения и социальных служб США, Центры по контролю и профилактике заболеваний, Национальный институт профессиональной безопасности и здоровья.CS1 maint: несколько имен: список авторов (связь)
- ^ а б c d е ж “Знаете ли вы, насколько громкими могут быть воздушные шары?”. Получено 8 июн 2018.
- ^ “Обзор продукции корпорации LRAD для LRAD 1000Xi”. Получено 29 мая 2014.
- ^ Нейв, Карл Р. (2006). «Порог боли». Гиперфизика. SciLinks. Получено 2009-06-16.
- ^ Franks, John R .; Стивенсон, Марк Р .; Мерри, Кэрол Дж., Ред. (Июнь 1996 г.). Профилактика потери слуха на рабочем месте – Практическое руководство (PDF). Национальный институт охраны труда и здоровья. п. 88. Получено 2009-07-15.
- ^ а б Реалистичные максимальные уровни звукового давления для динамических микрофонов – Shure.
- ^ Пишущая латунь и язычки.
- ^ Свейнпол, Де Вет; Зал III, Джеймс В .; Koekemoer, Дирк (февраль 2010 г.). «Вувузела – хорошо для вашей команды, плохо для ваших ушей» (PDF). Южноафриканский медицинский журнал. 100 (4): 99–100. Дои:10.7196 / samj.3697. PMID 20459912.
- ^ “Таблица децибел – SPL – Таблица сравнения громкости”. Sengpielaudio. Получено 5 мар 2012.
- ^ а б Уильям Хэмби. «Таблица предельного уровня звукового давления в децибелах». В архиве из оригинала от 19.10.2005.
- ^ «EPA определяет уровни шума, влияющие на здоровье и благополучие» (Пресс-релиз). Агентство по охране окружающей среды. 2 апреля 1974 г.. Получено 27 марта, 2017.
- ^ ““САМОЕ ТИХИЕ МЕСТО НА ЗЕМЛЕ “- СЕРТИФИКАТ МИРОВЫХ РЕКОРДОВ ГИННЕССА, 2005 г.” (PDF). Орфилд Лабс.
- ^ Миддлмисс, Нил (18 декабря 2007 г.). «Самое тихое место на Земле – Лаборатория Орфилда». Audio Junkies, Inc. Архивировано из оригинал 21 ноября 2010 г.
- ^ Юстас, Дэйв. “Безэховая камера”. Солфордский университет.
- ^ «Лаборатория Microsoft устанавливает новый рекорд самого тихого места в мире». 2015-10-02. Получено 2016-09-20.
Компьютерная компания построила безэховую камеру, в которой высокочувствительные тесты показали, что среднее значение фонового шума составляет невообразимо тихо -20,35 дБА (децибелы по шкале А).
- ^ «Оцените самую тихую комнату в мире». Microsoft: внутри B87. Получено 2016-09-20.
- ^ Marode, E .; Bastien, F .; Баккер, М. (1979). «Модель стримера включала искрообразование на основе нейтральной динамики». J. Appl. Phys. 50 (1): 140–146. Bibcode:1979JAP …. 50..140M. Дои:10.1063/1.325697.
- ^ Kacem, S .; и другие. (2013). «Моделирование расширения теплового удара и волн давления, вызванных динамикой стримера в положительных коронных разрядах постоянного тока». IEEE Transactions по науке о плазме. 41 (4): 942–947. Bibcode:2013ITPS … 41..942K. Дои:10.1109 / tps.2013.2249118. S2CID 25145347.
- ^ Köhn, C .; Chanrion, O .; Бабич, Л. П .; Нойберт, Т. (2018). «Свойства стримеров и связанные с ними рентгеновские лучи в возмущенном воздухе». Plasma Sour. Sci. Technol. 27 (1): 015017. Bibcode:2018PSST … 27a5017K. Дои:10.1088 / 1361-6595 / aaa5d8.
- ^ Köhn, C .; Chanrion, O .; Нойберт, Т. (2018). «Выбросы высоких энергий, вызванные колебаниями плотности воздуха при выбросах». Geophys. Res. Латыш. 45 (10): 5194–5203. Bibcode:2018GeoRL..45.5194K. Дои:10.1029 / 2018GL077788. ЧВК 6049893. PMID 30034044.
- Общий
- Беранек, Лев Л., Акустика (1993), Акустическое общество Америки, ISBN 0-88318-494-X.
- Дэниел Р. Райхель, Наука и применение акустики (2006), Springer New York, ISBN 1441920803.
внешняя ссылка
- Звуковое давление и звуковая мощность, следствие и причина
- Преобразование звукового давления в уровень звукового давления и наоборот
- Таблица уровней звука, соответствующего звукового давления и интенсивности звука
- Закон Ома как акустический эквивалент, расчеты
- Соотношения акустических величин, связанных с плоской прогрессивной акустической звуковой волной
- Звуковое давление и звуковая мощность – две часто путаемые характеристики звука
- Сколько децибел в два раза громче? Изменение уровня звука и соответствующий фактор звукового давления или интенсивности звука
- Таблица сравнения децибел (громкости)















propto p^{2}(r),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf101a3713c0641e63e2093d8d2c8f2bb424264d)


![{displaystyle L_{Sigma }=10log _{10}left({frac {p_{1}^{2}+p_{2}^{2}+dots +p_{n}^{2}}{p_{0}^{2}}}right)~{text{dB}}=10log _{10}left[left({frac {p_{1}}{p_{0}}}right)^{2}+left({frac {p_{2}}{p_{0}}}right)^{2}+dots +left({frac {p_{n}}{p_{0}}}right)^{2}right]~{text{dB}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c430352c5808ad08cb5bb81221d3058efd94d2d)


![{ displaystyle L _ { Sigma} = 10 log _ {10} left ( { frac {p_ {1} ^ {2} + p_ {2} ^ {2} + ldots + p_ {n} ^ {2}} {p_ {0} ^ {2}}} right) ~ { text {дБ}} = 10 log _ {10} left [ left ({ frac {p_ {1}} {p_ {0}}} right) ^ {2} + left ({ frac {p_ {2}} {p_ {0}}} right) ^ {2} + ldots + left ({ frac {p_ {n}} {p_ {0}}} right) ^ {2} right] ~ { text {dB}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe9d704c330f25f5c6fd191e56d98df6f89fbe71)

