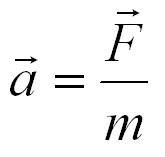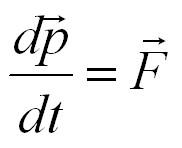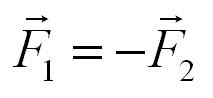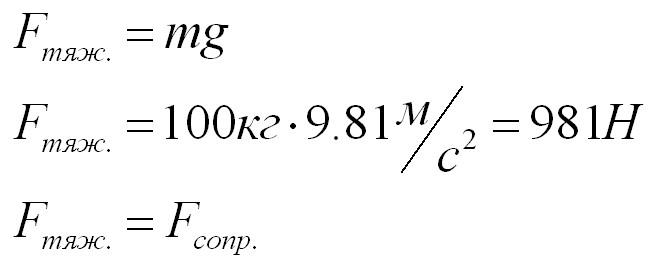Как нашел законы физики ньютон - Сайт, где вы сможете решить свои вопросы

Классическая механика
История…
Фундаментальные понятия Пространство Время Масса Скорость Сила Механическая работа Энергия Импульс
Формулировки Ньютоновская механика Лагранжева механика Гамильтонова механика Формализм Гамильтона — Якоби Уравнения Рауса Уравнения Аппеля Теория Купмана — фон Неймана
Разделы Прикладная механика Небесная механика Механика сплошных сред Геометрическая оптика Статистическая механика
Учёные Галилей Кеплер Ньютон Эйлер Лаплас Д’Аламбер Лагранж Гамильтон Коши
См. также: Портал:Физика

Зако́ны Нью́то́на — три важнейших закона классической механики, которые позволяют записать уравнения движения для любой механической системы, если известны силы, действующие на составляющие её тела. Впервые в полной мере сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год)^[1]^[2]. В ньютоновском изложении механики, широко используемом и в настоящее время, эти законы являются аксиомами, базирующимися на обобщении экспериментальных результатов.

Первый закон Ньютона[править | править код]

Первый закон Ньютона постулирует существование инерциальных систем отсчёта. Поэтому он также известен как закон инерции. Инерция (она же инертность^[3]) — свойство тела сохранять скорость своего движения неизменной по величине и направлению, когда не действуют никакие силы, а также свойство тела сопротивляться изменению его скорости. Чтобы изменить скорость движения тела, необходимо приложить некоторую силу, причём результат действия одной и той же силы на разные тела будет различным: тела обладают разной инерцией (инертностью), величина которой характеризуется их массой.

Современная формулировка[править | править код]

В современной физике первый закон Ньютона принято формулировать в следующем виде^[4]:

Историческая формулировка[править | править код]

Ньютон сформулировал первый закон механики так:

Всякое тело продолжает удерживаться в своём состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» следует заменить термином «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и абсолютного времени, а это представление современная физика отвергает. С другой стороны, в произвольной (например, вращающейся) системе отсчёта закон инерции неверен, поэтому ньютоновская формулировка была заменена постулатом существования инерциальных систем отсчёта.

Второй закон Ньютона[править | править код]

Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО).

Масса материальной точки при этом полагается величиной постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами^[5]^[6]^[7]^[8].

Современная формулировка[править | править код]

В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:

${vec a}={frac {{vec {F}}}{m}},$

где {vec a} — ускорение материальной точки;
— равнодействующая всех сил, приложенных к материальной точке;
— масса материальной точки.

Второй закон Ньютона может быть также сформулирован в эквивалентной форме с использованием понятия импульс:

В инерциальной системе отсчёта скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней внешних сил.

${frac {d{vec p}}{dt}}={vec {F}},$

где — импульс точки, — её скорость, а — время.
При такой формулировке, как и при предшествующей, полагают, что масса материальной точки неизменна во времени^[9]^[10]^[11].

Иногда предпринимаются попытки распространить сферу применения уравнения $frac {d vec p} {dt} = vec{F}$ и на случай тел переменной массы. Однако вместе с таким расширительным толкованием уравнения приходится существенным образом модифицировать принятые ранее определения и изменять смысл таких фундаментальных понятий, как материальная точка, импульс и сила^[12]^[13].

Замечания[править | править код]

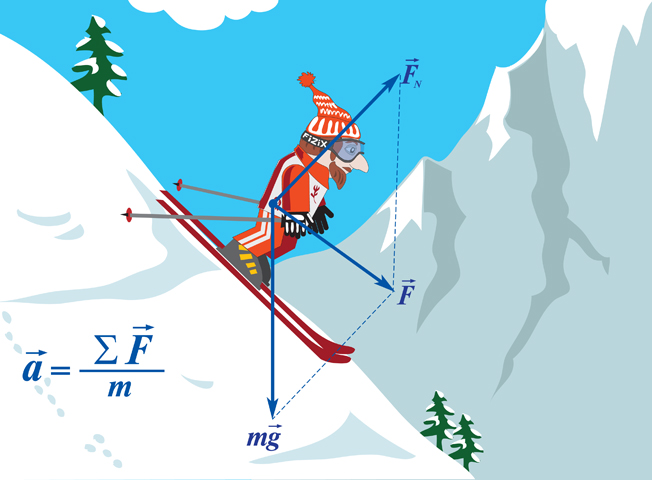
Когда на материальную точку действуют несколько сил, с учётом принципа суперпозиции, второй закон Ньютона записывается в виде

${displaystyle m{vec {a}}=sum _{i=1}^{n}{vec {F_{i}}}quad }$ или ${displaystyle quad {frac {d{vec {p}}}{dt}}=sum _{i=1}^{n}{vec {F_{i}}}.}$

Второй закон Ньютона, как и вся классическая механика, справедлив только для движения тел со скоростями, много меньшими скорости света. При движении тел со скоростями, близкими к скорости света, используется релятивистское обобщение второго закона, получаемое в рамках специальной теории относительности.

Частный случай (при ) второго закона нельзя рассматривать как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.

Историческая формулировка[править | править код]

Исходная формулировка Ньютона:

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Третий закон Ньютона[править | править код]

Этот закон описывает, как взаимодействуют две материальные точки. Пусть имеется замкнутая система, состоящая из двух материальных точек, в которой первая точка может действовать на вторую с некоторой силой ${vec {F}}_{{1to 2}}$ , а вторая — на первую с силой ${vec {F}}_{{2to 1}}$ . Третий закон Ньютона утверждает: сила действия ${vec {F}}_{{1to 2}}$ равна по модулю и противоположна по направлению силе противодействия ${vec {F}}_{{2to 1}}$ .

Третий закон Ньютона является следствием однородности, изотропности и зеркальной симметрии пространства^[14]^[15].

Третий закон Ньютона, как и остальные законы ньютоновской динамики, даёт практически верные результаты лишь только тогда, когда скорости всех тел рассматриваемой системы пренебрежимо малы по сравнению со скоростью света^[16].

Современная формулировка[править | править код]

Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

${vec {F}}_{{2to 1}}=-{vec {F}}_{{1to 2}}.$

Закон утверждает, что силы возникают лишь попарно, причём любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, сила всегда есть результат взаимодействия тел. Существование сил, возникших самостоятельно, без взаимодействующих тел, невозможно^[17].

Историческая формулировка[править | править код]

Ньютон дал следующую формулировку закона^[1]:

Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны.

Для силы Лоренца третий закон Ньютона не выполняется. Лишь переформулировав его как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость^[18]^[19].

Следствия законов Ньютона[править | править код]

Законы Ньютона являются аксиомами классической ньютоновской механики. Из них, как следствия, выводятся уравнения движения механических систем, а также «законы сохранения», указанные ниже. Разумеется, есть и законы (например, всемирного тяготения или Гука), не вытекающие из трёх постулатов Ньютона.

Уравнения движения[править | править код]

Уравнение является дифференциальным уравнением: ускорение есть вторая производная от координаты по времени. Это значит, что эволюцию (перемещение) механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости.

Если бы уравнения, описывающие наш мир, были уравнениями первого порядка, то исчезли бы такие явления, как инерция, колебания, волны.

Закон сохранения импульса[править | править код]

Закон сохранения импульса утверждает, что векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю^[20].

Закон сохранения механической энергии[править | править код]

Если все силы консервативны, то возникает закон сохранения механической энергии взаимодействующих тел: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной^[21].

Законы Ньютона и силы инерции[править | править код]

Использование законов Ньютона предполагает задание некой ИСО. Однако, на практике приходится иметь дело и с неинерциальными системами отсчёта. В этих случаях, помимо сил, о которых идёт речь во втором и третьем законах Ньютона, в механике вводятся в рассмотрение так называемые силы инерции.

Обычно речь идёт о силах инерции двух различных типов^[17]^[22]. Сила первого типа (даламберова сила инерции^[23]) представляет собой векторную величину, равную произведению массы материальной точки на её ускорение, взятое со знаком минус. Силы второго типа (эйлеровы силы инерции^[23]) используются для получения формальной возможности записи уравнений движения тел в неинерциальных системах отсчёта в виде, совпадающем с видом второго закона Ньютона. По определению, эйлерова сила инерции равна произведению массы материальной точки на разность между значениями её ускорения в той неинерциальной системе отсчёта, для которой эта сила вводится, с одной стороны, и в какой-либо инерциальной системе отсчёта, с другой^[17]^[22]. Определяемые таким образом силы инерции силами в истинном смысле слова не являются^[24]^[17], их называют фиктивными^[25], кажущимися^[26] или псевдосилами^[27].

Законы Ньютона в логике курса механики[править | править код]

Существуют методологически различные способы формулирования классической механики, то есть выбора её фундаментальных постулатов, на основе которых затем выводятся законы-следствия и уравнения движения. Придание законам Ньютона статуса аксиом, опирающихся на эмпирический материал, — только один из таких способов («ньютонова механика»). Этот подход принят в средней школе, а также в большинстве вузовских курсов общей физики.

Альтернативным подходом, использующимся преимущественно в курсах теоретической физики, выступает лагранжева механика. В рамках лагранжева формализма имеются одна-единственная формула (запись действия) и один-единственный постулат (тела движутся так, чтобы действие было стационарным), являющийся теоретической концепцией. Из этого можно вывести все законы Ньютона, правда, только для лагранжевых систем (в частности, для консервативных систем). Все известные фундаментальные взаимодействия описываются именно лагранжевыми системами. Более того, в рамках лагранжева формализма можно рассмотреть гипотетические ситуации, в которых действие имеет какой-либо другой вид. При этом уравнения движения станут уже непохожими на законы Ньютона, но сама классическая механика будет по-прежнему применима.

Исторический очерк[править | править код]

Страница «Начал» Ньютона с аксиомами механики

Практика применения машин в мануфактурной промышленности, строительство зданий, кораблестроение, использование артиллерии позволили ко времени Ньютона накопиться большому числу наблюдений над механическими процессами. Понятия инерции, силы, ускорения всё более прояснялись в течение XVII столетия. Работы Галилея, Борелли, Декарта, Гюйгенса по механике уже содержали все необходимые теоретические предпосылки для создания Ньютоном в механике логичной и последовательной системы определений и теорем^[28].

Основные законы механики Исаак Ньютон сформулировал в своей книге «Математические начала натуральной философии»^[1]:

   LEX I
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quantenus a viribus impressis cogitur statum illum mutare.

   LEX II
Mutationem motus proportionalem esse vi motrici impressae et fieri secundum lineam rectam qua vis illa imprimitur.

   LEX III

Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi.

Русский перевод этих формулировок законов см. в предыдущих разделах.

Первый закон (закон инерции), в менее чёткой форме, опубликовал ещё Галилей, допускавший свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений)^[29]. Галилей также сформулировал важнейший принцип относительности, который Ньютон не включил в свою аксиоматику, потому что для механических процессов данный принцип является следствием уравнений динамики. Кроме того, Ньютон считал пространство и время абсолютными понятиями, едиными для всей Вселенной, и явно указал на это в своих «Началах».

Ньютон также дал строгие определения таких физических понятий, как количество движения (не вполне ясно использованное у Декарта^[29]) и сила. Он ввёл в физику понятие массы как меры инертности тела и, одновременно, его гравитационных свойств (ранее физики пользовались понятием вес).

В середине XVII века ещё не существовало современной техники дифференциального и интегрального исчисления. Соответствующий математический аппарат в 1680-е годы параллельно создавался самим Ньютоном (1642—1727), а также Лейбницем (1646—1716). Завершили математизацию основ механики Эйлер (1707—1783) и Лагранж (1736—1813).

Примечания[править | править код]

↑ ¹ ² ³ Исаак Ньютон. Математические начала натуральной философии. Перевод с латинского и примечания А. Н. Крылова / под ред. Полака Л. С.. — М.: Наука, 1989. — С. 40—41. — 690 с. — (Классики науки). — 5000 экз. — ISBN 5-02-000747-1.
↑ Тарг С. М. Ньютона законы механики // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 370. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
↑ Инерция // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 146. — 704 с. — ISBN 5-85270-061-4.
↑ Инерциальная система отсчёта // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1988. — Т. 2. — С. 145. — ISBN 5-85270-034-7.
↑ «Дополнительной характеристикой (по сравнению с геометрическими характеристиками) материальной точки является скалярная величина m — масса материальной точки, которая, вообще говоря, может быть как постоянной, так и переменной величиной. … В классической ньютоновской механике материальная точка обычно моделируется геометрической точкой с присущей ей постоянной массой) являющейся мерой её инерции.» стр. 137 Седов Л. И., Цыпкин А. Г. Основы макроскопических теорий гравитации и электромагнетизма. М: Наука, 1989.
↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 87. — 572 с. «Масса материальной точки считается постоянной величиной, не зависящей от обстоятельств движения».
↑ Голубев Ю. Ф. Основы теоретической механики. — М.: МГУ, 2000. — С. 160. — 720 с. — ISBN 5-211-04244-1. «Аксиома 3.3.1. Масса материальной точки сохраняет своё значение не только во времени, но и при любых взаимодействиях материальной точки с другими материальными точками независимо от их числа и от природы взаимодействий».
↑ Журавлёв В. Ф. Основы теоретической механики. — М.: Физматлит, 2001. — С. 9. — 319 с. — ISBN 5-95052-041-3. «Масса [материальной точки] полагается постоянной, независящей ни от положения точки в пространстве, ни от времени».
↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 254. — 572 с. «…второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем переменного состава требует особого рассмотрения».
↑ «В ньютоновской механике… m=const и dp/dt=ma». Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. — С. 41. — 248 с..
↑ Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 112. — ISBN 0-07-035048-5. Архивировано 17 июня 2013 года. Архивированная копия. Дата обращения: 27 января 2013. Архивировано 17 июня 2013 года. «For a particle in Newtonian mechanics, M is a constant and (d/dt)(Mv) = M(dv/dt) = Ma».
↑ Зоммерфельд А. Механика = Sommerfeld A. Mechanik. Zweite, revidierte auflage, 1944. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 45—46. — 368 с. — ISBN 5-93972-051-X.
↑ Кильчевский Н. А. Курс теоретической механики. Том 1. — М.: Наука, 1977. 480 с.
↑ Жирнов Н. И. Классическая механика. — Серия: учебное пособие для студентов физико-математических факультетов педагогических институтов. — М., Просвещение, 1980. — Тираж 28 000 экз. — с. 38
↑ Тютин И. В. Симметрия в физике элементарных частиц. Часть 1. Пространственно-временные симметрии. // Соросовский образовательный журнал, 1996, № 5, с. 65
↑ Сивухин Д. В. Общий курс физики. Механика. — М., Наука, 1979. — Тираж 50 000 экз. — с. 85
↑ ¹ ² ³ ⁴ Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — 320 с.
↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.
↑ Кычкин И. С., Сивцев В. И. Школьная физика: третий закон Ньютона Архивная копия от 30 мая 2019 на Wayback Machine // Международный журнал экспериментального образования. — 2016. — № 3-2. — С. 191—193.
↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 282. — 416 с. — ISBN 5-06-003117-9.
↑ Савельев И. В. Глава 3. Работа и энергия // Курс общей физики. Механика. — 4-е изд. — М.: Наука, 1970. — С. 89—99. — ISBN 5-17-002963-2. Архивировано 8 сентября 2010 года.
↑ ¹ ² Тарг С. М. Сила инерции // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 494—495. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
↑ ¹ ² Ишлинский А. Ю. К вопросу об абсолютных силах и силах инерции в классической механике // Теоретическая механика. Сборник научно-методических статей. — 2000. — № 23. — С. 3—8. Архивировано 29 октября 2013 года.
↑ «„Силы инерции“ — не силы». Журавлёв В. Ф. Основания механики. Методические аспекты. — М.: ИПМ АН СССР, 1985. — С. 21. — 46 с.
↑ Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 82. — 368 с. — ISBN 5-93972-051-X.
↑ Борн М. Эйнштейновская теория относительности. — М.: «Мир», 1972. — С. 81. — 368 с.
↑ Фейнман Р., Лейтон Р., Сэндс М. Выпуск 1. Современная наука о природе. Законы механики // Фейнмановские лекции по физике. — М.: «Мир», 1965. — С. 225.
↑ Кузнецов Б. Г. Основные принципы физики Ньютона // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 186—197;
↑ ¹ ² Кузнецов Б. Г. Генезис механического объяснения физических явлений и идеи картезианской физики // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 160—161, 169—170, 177;

Литература[править | править код]

Лич Дж. У. Классическая механика. М.: Иностр. литература, 1961.
Спасский Б. И. История физики. М.: «Высшая школа», 1977.
Том 1. Часть 1-я; Часть 2-я
Том 2. Часть 1-я; Часть 2-я
Кудрявцев П. С. Курс истории физики. — М.: Просвещение, 1974.
Crowell, Benjamin (2011), Light and Matter (2011, Light and Matter), especially at Section 4.2, Newton’s First Law, Section 4.3, Newton’s Second Law, and Section 5.1, Newton’s Third Law.
Feynman, R. P.; Leighton, R. B.; Sands, M. The Feynman Lectures on Physics (неопр.). — 2nd. — Pearson/Addison-Wesley, 2005. — Т. Vol. 1. — ISBN 0-8053-9049-9.
Fowles, G. R.; Cassiday, G. L. Analytical Mechanics (неопр.). — 6th. — Saunders College Publishing (англ.) (рус., 1999. — ISBN 0-03-022317-2.
Likins, Peter W. (англ.) (рус.. Elements of Engineering Mechanics (неопр.). — McGraw-Hill Education, 1973. — ISBN 0-07-037852-5.
Marion; Jerry; Thornton, Stephen. Classical Dynamics of Particles and Systems (англ.). — Harcourt College Publishers, 1995. — ISBN 0-03-097302-3.
NMJ Woodhouse. Special Relativity (неопр.). — London/Berlin: Springer, 2003. — С. 6. — ISBN 1-85233-426-6.
Newton, Isaac, «Mathematical Principles of Natural Philosophy», 1729 English translation based on 3rd Latin edition (1726), volume 1, containing Book 1, especially at the section Axioms or Laws of Motion, starting page 19.
Newton, Isaac, «Mathematical Principles of Natural Philosophy», 1729 English translation based on 3rd Latin edition (1726), volume 2, containing Books 2 & 3.
Thomson, W (Lord Kelvin), and Tait, P G, (1867), Treatise on natural philosophy, volume 1, especially at Section 242, Newton’s laws of motion.

Ссылки[править | править код]

Первый закон Ньютона (видеоурок, программа 9 класса)
MIT Physics video lecture on Newton’s three laws
Light and Matter — an on-line textbook
Simulation on Newton’s first law of motion
«Newton’s Second Law» by Enrique Zeleny, Wolfram Demonstrations Project.
Newton’s 3rd Law demonstrated in a vacuum
The Laws of Motion, BBC Radio 4 discussion with Simon Schaffer, Raymond Flood & Rob Iliffe (In Our Time, Apr.3, 2008)

Источник

Мы уже говорили об основах классической механики. Настала пора поговорить о них подробнее и затронуть в обсуждении чуть больше, чем просто основу. В этой статье мы подробно разберем основные законы классической механики. Как вы уже догадались, речь пойдет о законах Ньютона.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Основные законы классической механики Исаак Ньютон (1642-1727) собрал и опубликовал в 1687 году. Три знаменитых закона были включены в труд, который назывался «Математические начала натуральной философии».

Был долго этот мир глубокой тьмой окутан
Да будет свет, и тут явился Ньютон.

(Эпиграмма 18-го века)

Но сатана недолго ждал реванша –
Пришел Эйнштейн, и стало все как раньше.

(Эпиграмма 20-го века)

Что стало, когда пришел Эйнштейн, читайте в отдельном материале про релятивистскую динамику. А мы пока приведем формулировки и примеры решения задач на каждый закон Ньютона.

Первый закон Ньютона

Первый закон Ньютона гласит:

Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано.

Проще говоря, суть первого закона Ньютона можно сформулировать так: если мы на абсолютно ровной дороге толкнем тележку и представим, что можно пренебречь силами трения колес и сопротивления воздуха, то она будет катиться с одинаковой скоростью бесконечно долго.

Инерция – это способность тела сохранять скорость как по направлению, так и по величине, при отсутствии воздействий на тело. Первый закон Ньютона еще называют законом инерции.

До Ньютона закон инерции был сформулирован в менее четкой форме Галилео Галилеем. Инерцию ученый называл «неистребимо запечатленным движением». Закон инерции Галилея гласит: при отсутствии внешних сил тело либо покоится, либо движется равномерно. Огромная заслуга Ньютона в том, что он сумел объединить принцип относительности Галилея, собственные труды и работы других ученых в своих “Математических началах натуральной философии”.

Понятно, что таких систем, где тележку толкнули, а она покатилась без действия внешних сил, на самом деле не бывает. На тела всегда действуют силы, причем скомпенсировать действие этих сил полностью практически невозможно.

Например, все на Земле находится в постоянном поле силы тяжести. Когда мы передвигаемся (не важно, ходим пешком, ездим на машине или велосипеде), нам нужно преодолевать множество сил: силу трения качения и силу трения скольжения, силу тяжести, силу Кориолиса.

Второй закон Ньютона

Помните пример про тележку? В этот момент мы приложили к ней силу! Интуитивно понятно, что тележка покатится и вскоре остановится. Это значит, ее скорость изменится.

В реальном мире скорость тела чаще всего изменяется, а не остается постоянной. Другими словами, тело движется с ускорением. Если скорость нарастает или убывает равномерно, то говорят, что движение равноускоренное.

Если рояль падает с крыши дома вниз, то он движется равноускоренно под действием постоянного ускорения свободного падения g. Причем любой дугой предмет, выброшенный из окна на нашей планете, будет двигаться с тем же ускорением свободного падения.

Второй закон Ньютона устанавливает связь между массой, ускорением и силой, действующей на тело. Приведем формулировку второго закона Ньютона:

Ускорение тела (материальной точки) в инерциальной системе отсчета прямо пропорционально приложенной к нему силе и обратно пропорционально массе.

Если на тело действует сразу несколько сил, то в данную формулу подставляется равнодействующая всех сил, то есть их векторная сумма.

В такой формулировке второй закон Ньютона применим только для движения со скоростью, много меньшей, чем скорость света.

Существует более универсальная формулировка данного закона, так называемый дифференциальный вид.

В любой бесконечно малый промежуток времени dt сила, действующая на тело, равна производной импульса тела по времени.

Третий закон Ньютона

В чем состоит третий закон Ньютона? Этот закон описывает взаимодействие тел.

3 закон Ньютона говорит нам о том, что на любое действие найдется противодействие. Причем, в прямом смысле:

Два тела воздействуют друг на друга с силами, противоположными по направлению, но равными по модулю.

Формула, выражающая третий закон Ньютона:

Другими словами, третий закон Ньютона – это закон действия и противодействия.

Пример задачи на законы Ньютона

Вот типичная задачка на применение законов Ньютона. В ее решении используются первый и второй законы Ньютона.

Десантник раскрыл парашют и опускается вниз с постоянной скоростью. Какова сила сопротивления воздуха? Масса десантника – 100 килограмм.

Решение:

Движение парашютиста – равномерное и прямолинейное, поэтому, по первому закону Ньютона, действие сил на него скомпенсировано.

На десантника действуют сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.

По второму закону Ньютона, сила тяжести равна ускорению свободного падения, умноженному на массу десантника.

Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и противоположна направлена.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

А вот еще одна физическая задачка на понимание действия третьего закона Ньютона.

Комар ударяется о лобовое стекло автомобиля. Сравните силы, действующие на автомобиль и комара.

Решение:

По третьему закону Ньютона, силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.

Другое дело, что действие этих сил на тела сильно отличаются вследствие различия масс и ускорений.

Исаак Ньютон: мифы и факты из жизни

На момент публикации своего основного труда Ньютону было 45 лет. За свою долгую жизнь ученый внес огромный вклад в науку, заложив фундамент современной физики и определив ее развитие на годы вперед.

Он занимался не только механикой, но и оптикой, химией и другими науками, неплохо рисовал и писал стихи. Неудивительно, что личность Ньютона окружена множеством легенд.

Ниже приведены некоторые факты и мифы из жизни И. Ньютона. Сразу уточним, что миф – это не достоверная информация. Однако мы допускаем, что мифы и легенды не появляются сами по себе и что-то из перечисленного вполне может оказаться правдой.

Факт. Исаак Ньютон был очень скромным и застенчивым человеком. Он увековечил себя благодаря своим открытиям, однако сам никогда не стремился к славе и даже пытался ее избежать.
Миф. Существует легенда, согласно которой Ньютона осенило, когда на наго в саду упало яблоко. Это было время чумной эпидемии (1665-1667), и ученый был вынужден покинуть Кембридж, где постоянно трудился. Точно неизвестно, действительно ли падение яблока было таким роковым для науки событием, так как первые упоминания об этом появляются только в биографиях ученого уже после его смерти, а данные разных биографов расходятся.
Факт. Ньютон учился, а потом много работал в Кембридже. По долгу службы ему нужно было несколько часов в неделю вести занятия у студентов. Несмотря на признанные заслуги ученого, занятия Ньютона посещались плохо. Бывало, что на его лекции вообще никто не приходил. Скорее всего, это связано с тем, что ученый был полностью поглощен своими собственными исследованиями.
Миф. В 1689 году Ньютон был избран членом Кембриджского парламента. Согласно легенде, более чем за год заседания в парламенте вечно поглощенный своими мыслями ученый взял слово для выступления всего один раз. Он попросил закрыть окно, так как был сквозняк.
Факт. Неизвестно, как бы сложилась судьба ученого и всей современной науки, если бы он послушался матери и начал заниматься хозяйством на семейной ферме. Только благодаря уговорам учителей и своего дяди юный Исаак отправился учиться дальше вместо того, чтобы сажать свеклу, разбрасывать по полям навоз и по вечерам выпивать в местных пабах.

Дорогие друзья, помните – любую задачу можно решить! Если у вас возникли проблемы с решением задачи по физике, посмотрите на основные физические формулы. Возможно, ответ перед глазами, и его нужно просто рассмотреть. Ну а если времени на самостоятельные занятия совершенно нет, специализированный студенческий сервис всегда к вашим услугам!

В самом конце предлагаем посмотреть видеоурок на тему “Законы Ньютона”.

Источник

Открытия Исаака Ньютона – законы и физика от одного из величайших гениев. Изучите закон всемирного тяготения, три закона движения, гравитация, форма Земли.

Исаак Ньютон (1642-1727) запомнился нам как философ, ученый и математик. Для своего времени он сделал очень много и активно участвовал в научной революции. Интересно, что его взгляды, законы и физика Ньютона будут преобладать еще 300 лет после смерти. По сути, перед нами создатель классической физики.

В последствии слово «ньютоновский» будут вставлять ко всем утверждениям, имеющим связь с его теориями. Исаака Ньютона считают одним из величайших гениев и наиболее влиятельных ученых, чья деятельность охватывала множество научных сфер. Но чем мы ему обязаны и какие открытия совершил?

Три закона движения

Начнем с его знаменитой работы «Математические начала натуральной философии» (1687), в которой раскрывались основы классической механики. Речь идет о трех законах движения, добытых из законов планетарного движения, выдвинутых Иоганном Кеплером.

Первый закон – инерция: объект в состоянии покоя будет оставаться в этом покое, пока на него не повлияет сила, лишенная баланса. Тело в движении продолжит двигаться с изначальной скоростью и в том же направлении, если не столкнется с несбалансированной силой.

Второй: ускорение появляется, когда сила влияет на массу. Чем больше масса, тем больше силы потребуется.

Третий: для каждого действия есть равное противодействие.

Универсальная гравитация

Ньютона стоит поблагодарить за закон всемирного тяготения. Он вывел, что каждая точка массы притягивает другую силой, направленной вдоль линии, пересекающей обе точки (F = G frac{m_1 m_2}{r^2}).

Эти три постулата гравитации помогут ему измерять траектории комет, приливов, равноденствий и прочих явлений. Его доводы разбили последние сомнения касательно гелиоцентрической модели и научный мир принял факт, что Земля не выступает вселенским центром

Все знают, что Ньютон пришел к выводам о гравитации благодаря случаю с яблоком, упавшим ему на голову. Многие думают, что это всего лишь шуточный пересказ, а ученый вывел формулу постепенно. Но в пользу яблочного прорыва говорят записи в дневнике Ньютона и пересказы его современников.

Форма Земли

Исаак Ньютон полагал, что наша планета Земля сформировалась в виде сплющенного сфероида. Позже догадка подтвердится, но в его времена это была важная информация, которая помогла перевести большую часть научного мира с декартовской системы на механику Ньютона.

В математическом поле он обобщил биномиальную теорему, исследовал степенные ряды, вывел собственный метод для аппроксимации корней функции и поделил на классы большинство кривых кубических плоскостей. Также он делился разработками с Готфридом Лейбницем.

Его открытия были прорывными в физике, математике и астрономии, помогавшие при помощи формул разобраться в строении пространства.

Оптика

В 1666 году он все больше углубляется в оптику. Все началось с изучения свойств света, который он измерял сквозь призму. В 1670-1672 гг. исследовал рефракцию света, показывая, как разноцветный спектр перестраивается в одиночный белый свет при помощи линзы и второй призмы.

В итоге, Ньютон понял, что цвет формируется из-за взаимодействия объектов изначально окрашенных. Кроме того заметил, что объектив любого инструмента страдает из-за светового рассеивания (хроматическая аберрация). Ему удалось решить проблемы при помощи телескопа с зеркалом. Его изобретение считается первой моделью отражающего телескопа.

Кроме того…

Также ему принадлежит заслуга в формулировке эмпирического закона охлаждения и изучение скорости звука. С его подачи появился термин «ньютоновская жидкость» – описание любой жидкости, где вязкие напряжения линейно пропорциональны скорости ее трансформации.

Большое количество времени Ньютон посвящал исследованию не только научных постулатов, но и библейской хронологии и внедрялся в алхимию. Однако многие работы появились только после смерти ученого. Так что Исаак Ньютон запомнился не только как талантливый физик, но и философ.

Чем же мы обязаны Исааку Ньютону? Его идеи были прорывными не только для того времени, но и послужили стартовыми точками для всех последующих ученых. Он подготовил плодородную почву для новых открытый и вдохновил на исследование этого мира. Неудивительно, что у Исаака Ньютона появились последователи, развивающие его идеи и теории. Если вам интересно узнать больше, то на сайте есть биография Исаака Ньютона, где представлены дата рождения и смерти (по новому и старому стилю), самые важные открытия, а также интересные факты о величайшем физике.

Источник

Физика > Что открыл Исаак Ньютон?

Три закона движения

Ньютон и его божественный геометр. Автор – Уильям Блейк (1795)

Второй: ускорение появляется, когда сила влияет на массу. Чем больше масса, тем больше силы потребуется.

Третий: для каждого действия есть равное противодействие.

Универсальная гравитация

Известное дерево, вдохновившее Ньютона на мысли о гравитации

Форма Земли

Оптика

Солнечные лучи проходят сквозь призму

Кроме того…

Источник

Ньютон первым обратил внимание на силу, как причину, по которой тела приходят в движение и меняют свою скорость.

Раздел механики, изучающий силы, называется динамикой. По-гречески «динамис», значит «сила».

Что такое сила

Тела действуют друг на друга с помощью сил.

Сила – это мера взаимодействия тел. Измеряя силу, мы измеряем величину взаимного действия тел. В обыденной жизни мы говорим: «как сильно» одно тело действует на другое тело.

Смысл законов Ньютона

Ньютон, в своих законах динамики, хотел сказать следующее:

В I законе: Если сила не действует, скорость не меняется. Импульс тела тоже не меняется.
Во II законе: Если сила действует, скорость меняется. Импульс тела, также, меняется, появляется ускорение.
В III законе: Взаимодействуют два тела — возникают две силы. Они по модулю равны, а по направлению противоположны.

Примечание:

Выражение «векторы равны по модулю», понимаем так: «длины векторов одинаковые».

Перед изучением законов Ньютона рекомендую вспомнить, что такое инерциальные системы отсчета (откроется в новой вкладке).

Первый закон Ньютона

Словесная формулировка первого закона Ньютона:

В инерциальной системе отсчета тело свою скорость не меняет, если на него не действуют другие тела (или действие других тел скомпенсировано).

Формула:

[ large boxed { F = 0 \ a = 0 \ v = const \ p = const } ]

( F = 0 ) – сила на тело не действует (Может быть и так: на тело действуют несколько сил, но их действие компенсируется);

( a = 0 ) – ускорение отсутствует;

( v = const ) – скорость тела не изменяется (остается одной и той же);

( p = const ) – импульс тела не изменяется (остается одним и тем же);

Важно! По первому закону Ньютона, «двигаться с одной и той же скоростью по прямой» и «покоиться» — это равнозначные виды движения.

Значит, если на тело не действуют другие тела (силы), то

тело будет двигаться с одной и той же скоростью по прямой, если оно так двигалось до этого,
или будет продолжать покоиться, если покоилось в прошлом.

Второй закон Ньютона

Сформулируем словами второй закон Ньютона:

Ускорение, приобретаемое телом,
прямо пропорционально
приложенной силе
и обратно пропорционально
массе этого тела.

Формула второго закона Ньютона с пояснениями

[ large boxed { a = frac{F}{m} } ]

( a left( frac{text{м}}{c^{2}} right) ) – ускорение тела

( m left( text{кг} right) ) – масса тела

( F left( H right) ) – сила, которую приложили к телу

Примечание: Ускорение отвечает на вопрос: «Как быстро меняется скорость тела?». Значит, если изменяется хотя бы одна из характеристик вектора скорости, ускорение есть. А если скорость не изменяется, ускорения нет ( vec{ a } = 0 )

Ускорение прямо пропорционально силе:

[ a sim F ]

Чем больше сила, тем больше ускорение тела, тем быстрее тело меняет скорость.

Ускорение обратно пропорционально массе:

[ a sim frac{1}{m} ]

Чем больше месса тела, тем труднее изменить его скорость.

Формулу второго закона часто записывают в векторном виде:

[ vec{ a } = frac{1}{m} cdot vec{ F } ]

Мы можем заменить местами правую и левую части, в таком случае получим:

[ vec{ F } cdot frac{1}{m} = vec{ a } ]

Расшифруем эту запись: Возьмем вектор «F», умножим его на скаляр (1/m) и получим новый вектор «a».

Простыми словами: Векторы ( vec{F} ) и ( vec{a} ) направлены в одну и ту же сторону, а длины у них отличаются.

Дробь ( displaystyle frac{1}{m} ) – это скалярная величина.

( F ) – это вектор.

Примечания:

Вместо слов «направлены в одну и ту же сторону» физики пользуются термином «сонаправлены». Лично мне удобнее пользоваться первой формулировкой.
Часто применяют еще один вид записи, его называют так: «Второй закон Ньютона в импульсной форме».

Третий закон Ньютона

Пусть одно тело действует на второе тело. Тогда это второе тело будет в ответ действовать на первое.

Словами третий закона Ньютона можно сформулировать так:

Силы взаимного действия по модулю равны, а направлены противоположно. Они лежат на прямой, которая соединяет центры тел, действующих друг на друга.

Формула:

[ large boxed { F_{12} = — F_{21} } ]

( F_{12} left( H right) ) – сила, с которой первое тело действует на второе тело.

( F_{21} left( H right) ) – сила, с которой второе тело отвечает первому.

Пояснить формулу можно с помощью такого рисунка:

Рис. 1. Два шара притягиваются. Сила 12 принадлежит черному шару, а сила 21 – красному

Обратите внимание, что длины красного и черного векторов равны.

Не важно, перед каким из векторов находится знак «минус». Этот знак показывает, что векторы направлены в противоположные стороны. Поэтому, формулу третьего закона Ньютона можно записать и так:

[ — F_{12} = F_{21} ]

Примечания:

Если перед каким-либо вектором записан знак «минус», то этот вектор развернут в противоположную от выбранной нами сторону.
Между векторами находится знак равенства. Это значит, что длины векторов одинаковые (векторы по модулю равны).

[ | vec{ F_{12} } | = | vec{ F_{21} } | ]

Советую прочитать еще две статьи. Так как для решения задач кроме знания трех законов Ньютона нужно дополнительно уметь:

находить проекции вектора на оси и
составлять векторные силовые уравнения (ссылки открываются в новых вкладках).

Источник

Первый закон Ньютона[править | править код]

Современная формулировка[править | править код]

Историческая формулировка[править | править код]

Второй закон Ньютона[править | править код]

Современная формулировка[править | править код]

Замечания[править | править код]

Историческая формулировка[править | править код]

Третий закон Ньютона[править | править код]

Современная формулировка[править | править код]

Историческая формулировка[править | править код]

Следствия законов Ньютона[править | править код]

Уравнения движения[править | править код]

Закон сохранения импульса[править | править код]

Закон сохранения механической энергии[править | править код]

Законы Ньютона и силы инерции[править | править код]

Законы Ньютона в логике курса механики[править | править код]

Исторический очерк[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Первый закон Ньютона

Второй закон Ньютона

Третий закон Ньютона

Пример задачи на законы Ньютона

Исаак Ньютон: мифы и факты из жизни

Три закона движения

Универсальная гравитация

Форма Земли

Оптика

Кроме того…

Что такое сила

Смысл законов Ньютона

Первый закон Ньютона

Второй закон Ньютона

Формула второго закона Ньютона с пояснениями

Третий закон Ньютона

Вам также может понравиться

Как найти синус угла правило

Как составить декларацию 3 ндфл ип на усн

Как найти утечку в полипропиленовой трубе

Добавить комментарий Отменить ответ