Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 октября 2021 года; проверки требуют 8 правок.
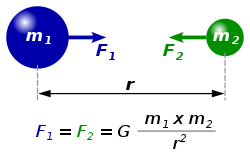
Гравитационная постоянная G лежит в основе закона всемирного тяготения.
Гравитацио́нная постоя́нная, постоянная Ньютона (обозначается обычно G, иногда GN или γ)[1] — фундаментальная физическая постоянная, константа гравитационного взаимодействия.
Согласно Ньютоновскому закону всемирного тяготения, сила гравитационного притяжения F между двумя материальными точками с массами[2] m1 и m2, находящимися на расстоянии r, равна:
Коэффициент пропорциональности G в этом уравнении называется гравитационной постоянной. Численно она равна модулю силы тяготения, действующей на точечное тело единичной массы со стороны другого такого же тела, находящегося от него на единичном расстоянии.
Точность измерений гравитационной постоянной на несколько порядков ниже точности измерений других физических величин[3].
В единицах Международной системы единиц (СИ) рекомендованное Комитетом данных для науки и техники (CODATA) на 2020 год значение гравитационной постоянной[4]:
- G = 6,67430(15)⋅10−11 м3·с−2·кг−1, или Н·м²·кг−2.
Гравитационная постоянная является основой для перевода других физических и астрономических величин, таких, например, как массы планет во Вселенной, включая Землю, а также других космических тел, в традиционные единицы измерения, например, килограммы. При этом из-за слабости гравитационного взаимодействия и результирующей малой точности измерений гравитационной постоянной отношения масс космических тел обычно известны намного точнее, чем индивидуальные массы в килограммах.
Гравитационная постоянная является одной из основных единиц измерения в планковской системе единиц.
История измерения[править | править код]
Гравитационная постоянная фигурирует в современной записи закона всемирного тяготения, однако отсутствовала в явном виде у Ньютона и в работах других ученых вплоть до начала XIX века. Гравитационная постоянная в нынешнем виде впервые была введена в закон всемирного тяготения, по-видимому, только после перехода к единой метрической системе мер. Возможно впервые это было сделано французским физиком Пуассоном в «Трактате по механике» (1809), по крайней мере, никаких более ранних работ, в которых фигурировала бы гравитационная постоянная, историками не выявлено[источник не указан 2081 день].
В 1798 году Генри Кавендиш поставил эксперимент с целью определения средней плотности Земли с помощью крутильных весов, которые предложил использовать для этого Джон Мичелл (Philosophical Transactions 1798). Кавендиш сравнивал маятниковые колебания пробного тела под действием тяготения шаров известной массы и под действием тяготения Земли. Численное значение гравитационной постоянной было вычислено позже на основе значения средней плотности Земли. Точность измеренного значения G со времён Кавендиша увеличилась, но и его результат[5] был уже достаточно близок к современному.
Значение этой постоянной известно гораздо менее точно, чем у всех других фундаментальных физических постоянных, и результаты экспериментов по её уточнению продолжают различаться[6][7].
В то же время известно, что проблемы не связаны с изменением самой постоянной от места к месту и во времени (неизменность гравитационной постоянной проверена с точностью до ΔG/G ~ 10−17), но вызваны экспериментальными трудностями измерения малых сил с учётом большого числа внешних факторов[8]. В будущем, если опытным путём будет установлено более точное значение гравитационной постоянной, то оно может быть пересмотрено[9][10].
В 2013 году значение гравитационной постоянной было получено группой ученых, работавших под эгидой Международного бюро мер и весов:
- G = 6,67554(16)⋅10−11 м3·с−2·кг−1 (стандартная относительная погрешность 25 ppm (или 0,0025 %), первоначальное опубликованное значение несколько отличалось от окончательного из-за ошибки в расчётах и было позже исправлено авторами)[11][12].
В июне 2014 года в журнале «Nature» появилась статья итальянских и нидерландских физиков, где были представлены новые результаты измерения G, сделанные при помощи атомных интерферометров[13]. По их результатам
- G = 6,67191(99)⋅10−11 м3·с−2·кг−1 с погрешностью 0,015 % (150 ppm).
Авторы указывают, что поскольку эксперимент с применением атомных интерферометров основан на принципиально других подходах, он помогает выявить некоторые систематические ошибки, не учитывающиеся в других экспериментах.
В августе 2018 года в журнале «Nature» физиками из Китая и России были опубликованы[14] результаты новых измерений гравитационной постоянной с улучшенной точностью (погрешность 12 ppm, или 0,0012 %). Были использованы два независимых метода — измерение времени качаний торсионного подвеса и измерение углового ускорения, получены значения G, соответственно:
- G = 6,674184(78)⋅10−11 м3·с−2·кг−1;
- G = 6,674484(78)⋅10−11 м3·с−2·кг−1.
Оба результата в пределах двух стандартных отклонений совпадают с рекомендованным значением CODATA, хотя отличаются друг от друга на ~2,5 стандартных отклонения.
По астрономическим данным постоянная G практически не изменялась за последние сотни миллионов лет, скорость её относительного изменения (dG/dt)/G не превышает нескольких единиц на 10−11 в год[15][16][17].
См. также[править | править код]
- Постоянная Гаусса
- Планковские единицы
- Ускорение свободного падения
Примечания[править | править код]
- ↑ В общей теории относительности обозначения, использующие букву G, применяются редко, поскольку там эта буква обычно используется для обозначения тензора Эйнштейна.
- ↑ По определению массы, входящие в это уравнение, — гравитационные массы, однако расхождения между величиной гравитационной и инертной массы какого-либо тела до сих пор не обнаружено экспериментально. Теоретически в рамках современных представлений они вряд ли отличаются. Это в целом было стандартным предположением и со времен Ньютона.
- ↑ Новые измерения гравитационной постоянной еще сильнее запутывают ситуацию Архивная копия от 25 августа 2017 на Wayback Machine // Элементы.ру, 13.09.2013
- ↑ CODATA Internationally recommended values of the Fundamental Physical Constants (англ.). Дата обращения: 7 марта 2020. Архивировано 27 августа 2011 года.
- ↑ Разные авторы указывают разный результат, от 6,754⋅10−11 м²/кг² до (6,60 ± 0,04)⋅10−11м³/(кг·с³) — см. Эксперимент Кавендиша#Вычисленное значение.
- ↑ Gillies G. T. The Newtonian Gravitational Constant Архивная копия от 12 апреля 2019 на Wayback Machine // Sevres (France), Bureau Intern. Poids et Mesures, 1983, 135 p.
- ↑ Ляховец В. Д. Проблемы метрологического обеспечения измерений гравитационной постоянной. // Проблемы теории гравитации и элементарных частиц. Выпуск 17. – М., Энергоатомиздат, 1986. – с. 122-125.
- ↑ Игорь Иванов. Новые измерения гравитационной постоянной ещё сильнее запутывают ситуацию (13 сентября 2013). Дата обращения: 14 сентября 2013. Архивировано 21 сентября 2013 года.
- ↑ Так ли постоянна гравитационная постоянная? Архивная копия от 14 июля 2014 на Wayback Machine Новости науки на портале cnews.ru // публикация от 26.09.2002
- ↑ Brooks, Michael Can Earth’s magnetic field sway gravity? NewScientist (21 сентября 2002). Архивировано 8 мая 2015 года.
- ↑ Quinn Terry, Parks Harold, Speake Clive, Davis Richard. Improved Determination of G Using Two Methods (англ.) // Physical Review Letters. — 2013. — 5 September (vol. 111, no. 10). — ISSN 0031-9007. — doi:10.1103/PhysRevLett.111.101102. Архивировано 29 января 2019 года.
- ↑ Quinn Terry, Speake Clive, Parks Harold, Davis Richard. Erratum: Improved Determination of G Using Two Methods [Phys. Rev. Lett. 111, 101102 (2013)] (англ.) // Physical Review Letters. — 2014. — 15 July (vol. 113, no. 3). — ISSN 0031-9007. — doi:10.1103/PhysRevLett.113.039901. Архивировано 7 октября 2021 года.
- ↑ Rosi G., Sorrentino F., Cacciapuoti L., Prevedelli M., Tino G. M. Precision measurement of the Newtonian gravitational constant using cold atoms (англ.) // Nature. — 2014. — June (vol. 510, no. 7506). — P. 518—521. — ISSN 0028-0836. — doi:10.1038/nature13433. Архивировано 26 мая 2019 года.
- ↑ Li Qing, Xue Chao, Liu Jian-Ping, Wu Jun-Fei, Yang Shan-Qing, Shao Cheng-Gang, Quan Li-Di, Tan Wen-Hai, Tu Liang-Cheng, Liu Qi, Xu Hao, Liu Lin-Xia, Wang Qing-Lan, Hu Zhong-Kun, Zhou Ze-Bing, Luo Peng-Shun, Wu Shu-Chao, Milyukov Vadim, Luo Jun. Measurements of the gravitational constant using two independent methods (англ.) // Nature. — 2018. — August (vol. 560, no. 7720). — P. 582—588. — ISSN 0028-0836. — doi:10.1038/s41586-018-0431-5. Архивировано 31 мая 2019 года.
- ↑ van Flandern T. C. Is the Gravitational Constant Changing (англ.) // The Astrophysical Journal. — IOP Publishing, 1981. — September (vol. 248). — P. 813. — doi:10.1086/159205. — Bibcode: 1981ApJ…248..813V.
Результат: (dG/dt)/G = (−6,4 ± 2,2)×10−11 год−1 - ↑ Verbiest J. P. W., Bailes M., van Straten W., Hobbs G. B., Edwards R. T., Manchester R. N., Bhat N. D. R., Sarkissian J. M., Jacoby B. A., Kulkarni S. R. Precision Timing of PSR J0437−4715: An Accurate Pulsar Distance, a High Pulsar Mass, and a Limit on the Variation of Newton’s Gravitational Constant (англ.) // The Astrophysical Journal. — IOP Publishing, 2008. — 20 May (vol. 679, no. 1). — P. 675—680. — ISSN 0004-637X. — doi:10.1086/529576.
Результат: |Ġ/G| ≤ 2,3 × 10−11 год−1 - ↑ Взрыв звезд доказал неизменность Ньютоновской гравитации в космическом времени. Дата обращения: 24 марта 2014. Архивировано 24 марта 2014 года.
Ссылки[править | править код]
- Гравитационная постоянная // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- Милюков В. К. Гравитационная постоянная // Физическая энциклопедия. — М.: Советская энциклопедия, 1988. — Т. 1. — С. 523.
- Speake C., Quinn T. The search for Newton’s constant // Physics Today. — 2014. — Vol. 67, № 7. — P. 27—33.
- Иванов И. Гравитационная постоянная измерена новыми методами // Элементы. — 22.01.2007.
- Измерение гравитационной постоянной (большой G) как повод для дебатов!
В современной формулировке закона всемирного тяготения присутствует коэффициент , называющийся гравитационной постоянной и стоящий перед формулой особняком. Интересно, что Ньютон, открывший закон притяжения, не использовал явную форму константы, численно она была определена больше века спустя со дня смерти учёного.

Содержание
- Что такое и чему равна гравитационная постоянная
- В чём измеряется гравитационная постоянная
- Как найти гравитационную постоянную – история открытия
- Работы Ньютона
- Как была экспериментально определена гравитационная постоянная – эксперимент Кавендиша
- Измерение гравитационной постоянной
- Современная история изменений гравитационной постоянной
Что такое и чему равна гравитационная постоянная
Формула закона всемирного тяготения, известная по курсу школьной механики:

G – коэффициент пропорциональности или гравитационная постоянная;
m1, m2 – массы двух тел, испытывающих взаимное притяжение;
r – расстояние между ними.
Коэффициент пропорциональности G обозначает силу, с которой притягивается пара килограммовых объектов, расположенных друг от друга на метровом расстоянии. Значение константы обычно принимается равным:

Столь маленькое число объясняет, почему несмотря на постоянное действие гравитации люди, находящиеся рядом, не чувствуют силу тяготения – она проявляется на объектах огромных масс, имеющих высокие порядки, например, массе планет, Солнца, других звёзд.

В чём измеряется гравитационная постоянная
Несмотря на то, что гравитационная постоянная численно равна силе, её единицы измерения не ньютоны. Размерность коэффициента может показаться страшной – 
, но её возникновение легко объясняется.
Согласно Международной системе единиц (системе интернациональной или СИ), сила измеряется в ньютонах, причём

то есть 1 ньютон – сила, изменяющая скорость килограммового объекта на 1 м/с за одну секунду.
После открытия закона тяготения определено: пара килограммовых тел притягивается друг к другу силой со значением, зависящим обратно пропорционально от квадрата расстояния между объектами.
То есть единица измерения гравитационной силы –

и размерность не совпадает с привычной ![]() . Требуется коэффициент, который должен уравнять единицы измерения привычной силы и силы гравитационного взаимодействия.
. Требуется коэффициент, который должен уравнять единицы измерения привычной силы и силы гравитационного взаимодействия.
Проведём математические вычисления самостоятельно.
Нужно уравнять ![]()
и  .
.
Для этого ![]() нужно разделить на 1с2 и 1кг, а также умножить на м3, получим:
нужно разделить на 1с2 и 1кг, а также умножить на м3, получим:

Получилась требуемая размерность.
Следовательно, постоянная имеет размерность ![]() .
.
Как найти гравитационную постоянную – история открытия
Коэффициент G – универсальная константа, измерение которой осуществляется экспериментальным путём. Доподлинно неизвестно, кто открыл значение гравитационной постоянной, первое употребление в «Трактате по механике» Пуассона датируется 1811 годом.
Работы Ньютона
При публикации закона тяготения в трактате Ньютона отсутствовало явное обозначение константы, характеризующее гравитацию и её действие. Коэффициент не появлялся в работах по физике вплоть до конца восемнадцатого века, его точное значение не было вычислено.

Вместо известной сегодня постоянной присутствовал гравитационный параметр:
![]()
M – масса объекта, причём, масса планеты или звезды, так как гравитационный параметр нашёл широкое распространение в астрофизике.
Сегодня для объектов Солнечной системы значение параметра рассчитано точнее, чем гравитационная постоянная G и масса по отдельности, так как она не требует серьёзных экспериментов, вычисляется на основании астрономических наблюдений.
Например:
- для Земли
 ;
; - Луны
 ;
; - Солнца
 .
.
Подробнее о использовании закона всемирного тяготения в астрономии вы можете прочитать в нашей статье.
Как была экспериментально определена гравитационная постоянная – эксперимент Кавендиша
Естествоиспытатель Джон Митчел придумал эксперимент для определения массы Земли при помощи крутильных весов, однако не реализовал его. После его смерти идея опыта и аппаратура перешли к английскому физику и химику Генри Кавендишу, который, усовершенствовав прибор, провёл ряд экспериментов и осуществил задумку своего предшественника.

Главенствующая роль в опытах отводилась установке. На метровой нити из меди подвешивалось коромысло длиной 1,8 метра, на его концах устанавливалась пара свинцовых шариков диаметром 5 сантиметров, массой 775 грамм. Чуть выше крепилась поворотная ферма, причём тщательно соблюдалось требование совпадения оси вращения фермы с медной нитью. На концах поворотной штанги находилось по одному большому свинцовому шару диаметром 20 сантиметров, массой 49,5 килограмм. Чтобы избежать влияния конвекционных воздушных потоков, вся установка накрывалась плотным деревянным кожухом. Вследствие взаимодействия лёгкие шарики притягивались к тяжёлым, закручивая нить и отклоняя коромысло. Угол отклонения фиксировался двумя телескопами, а сила упругости нити приравнивалась гравитационному взаимодействию шаров.

Величина определённой силы притяжения составляла 0,17 микроньютона. Если сравнивать это значение с весом маленького шара, то оно меньше последнего примерно в 45 миллионов раз.
В результате своего эксперимента Генри Кавендиш рассчитал среднюю плотность Земли, причём его эксперимент был точным – погрешность измеренного значения в сравнении с современным значением составляет всего 0,7%. Именно Кавендишу приписывают открытие значения гравитационной постоянной, однако он никогда не задавался подобной целью при проведении своих опытов. Очевидно, величина константы определена на основании результатов его эксперимента, но кто сделал это первым, неизвестно.

Измерение гравитационной постоянной
Значение константы, полученное по измеренной Кавендишем плотности, по разным источникам разнится. Британская энциклопедия называет число, равное ![]() , с каковым некоторые современные физики. Леон Нил Купер утверждает, что экспериментально полученное число равно
, с каковым некоторые современные физики. Леон Нил Купер утверждает, что экспериментально полученное число равно  , а Олег Павлович Спиридонов в сборнике постоянных приводит значение
, а Олег Павлович Спиридонов в сборнике постоянных приводит значение ![]() .
.
Коэффициент пропорциональности определяли после Генри Кавендиша, причём зачастую его установку модернизировали новыми материалами. Например, в 1872 году Корню и Байль для измерения гравитационной постоянной использовали платиновые маленькие шарики и стеклянные, наполненные ртутью, большие. Результаты опыта показали значение
 с относительной погрешностью 5*10-3.
с относительной погрешностью 5*10-3.
Современная история изменений гравитационной постоянной
Гравитационная постоянная – десятичная дробь, её значение постоянно уточняется, причём измерение коэффициента G происходит путём усовершенствования прибора Митчела и улучшения методов наблюдения. Например, в 2018 году учёные из России и Китая проводили опыты на установках разной конструкции. В первой группе применялся метод «time of swing» (TOS), где коэффициент пропорциональности зависит от колебательной частоты весов. Во второй – метод «angular acceleration feedback» (AAF), где угловое ускорение независимо вращающихся коромысел шаров измеряется системой управления с обратной связью, при этом нить поддерживается незакрученной.

По результатам команды первый метод продемонстрировал значение гравитационной постоянной ![]() , второй метод –
, второй метод – ![]() . Относительная погрешность составила 11,6*10-6
. Относительная погрешность составила 11,6*10-6
Комитет по данным для науки и техники (CODATA) рекомендовал на 2020 год значение коэффициента пропорциональности, равное:

Таким образом, гравитационная постоянная всё время уточняется, требуя новые, более точные способы измерения и вычисления.
Сила, которая удерживает нас на поверхности планеты – сила притяжения – не вызывает, на первый взгляд, никаких вопросов: всю свою жизнь мы живем в поле ее действия. Но что это за сила, откуда она берется, как именной действует и чем переносится – для ответов на эти вопросы стоит углубиться в тему более подробно.
Телеграмм-канал Космос нас ждет – больше космоса и красоты. Подписывайтесь!
Закон всемирного тяготения
История открытия
В поместье родителей Исаака Ньютона был прекрасный яблоневый сад. И молодой английский физик любил размышлять, гуляя по нему.
Когда в очередную такую прогулку, ученый увидел, как падает с ветки яблоко (не ему на голову), то у него возник закономерный вопрос: почему яблоко упало именно вниз? Почему не улетело прочь от Земли? Значит, на яблоко, со стороны планеты действует сила, что его притянула.
Этот эпизод произошел в 1666 году. Исааку Ньютону было 23 года.
Тогда получалось, что Луна также подвержена этой силе, ведь она не «улетает» от Земли и вращается вокруг нее. И все остальные предметы на планете тоже «держаться» только благодаря этой силе притяжения.
И только спустя 21 год после прогулки в яблоневом саду, Исаак Ньютон получил вывод формулы для силы, что удерживает Луну и планеты на орбите, а людей на Земле. Свои труды Исаак Ньютон опубликовал в «Математических началах натуральной философии» в 1687.
Запись и формулировка закона
Формулировка Ньютона дошла до наших дней и осталась в первозданном виде:
Из закона всемирного тяготения следует, что между всеми телами, обладающими массой, есть сила притяжения.
Как «представить» гравитацию?
Для наглядного представления, как же именно работает закон всемирного тяготения, представим пространство как резиновую простыню. Она легко прогибается под тяжелыми предметами, если их на нее положить.
Возьмем большой и тяжелый шар для боулинга и положим его на простыню – это наше Солнце. Вокруг него образовалась «воронка». Если теперь рядом с «Солнцем» рассыпать много маленьких шариков – они все скатятся к нему. Так притягиваются планеты к Солнцу и не улетают в свободный полет в космос. Аналогично и Луна около Земли – спутник попал в «гравитационную воронку» нашей планеты и не может из нее выбраться.
Гравитационная постоянная
В формуле закона всемирного тяготения присутствует постоянный коэффициент G – гравитационная постоянная или гравитационная константа. Это фундаментальная величина в современной классической физике, которая является неизменной. Еще она носит название — постоянная Ньютона, хотя в публикациях ученого она не фигурировала.
Чему равна гравитационная постоянная
Значение этого параметра постоянно уточняется, так как гравитационная константа представляет собой десятичную бесконечную дробь.
Современные установки и компьютеры, позволяют измерить значение очень точно. По последним измерения гравитационная постоянная численно равна
Гравитационная постоянная показывает с какой силой притягиваются два тела массой по 1 кг на расстоянии 1 метр.
Именно из-за маленького значения гравитационной постоянной, объясняется тот факт, что мы не ощущаем силу притяжения между предметами. Значение силы становится существенной только при больших массах – звезд и планет.
В чем измеряется гравитационная постоянная.
Если расписать размерность силы – ньютон в Международной системе единиц
то закон всемирного тяготения запишется следующим образом
Сокращая килограммы и выражая G, получим
Эксперимент Генри Кавендиша
Опыт Генри Кавендиша состоялся в 1798 году.
Экспериментальная установка Кавендиша состояла из двух коромысел. На одном коромысле на концах находились массивные шары, на другом маленькие. Масса шаров отличалась почти в 64 раза, размер в 4 раза. Из-за такой большой разницы масс притяжение шаров должно было быть заметно.
Малые шары были подвешены на длинной нити и по повороту коромысла от первоначального положения, можно было определить силу притяжения шаров.
Правда, опыт Кавендиша был нацелен на определение средней плотности Земли, что он и сделал с погрешностью всего лишь в 0,7%. Однако, результаты его эксперимента легли в основу вычисления гравитационной постоянной.
Гравитационный параметр
Вычисление гравитационной постоянной было затруднено, так как все вычисления основывались на движения планет, а сила тяготения, действующая на них со стороны Солнца, зависит от массы самой планеты.В работах Ньютона так же не было упоминания именно гравитационной константы, зато появился гравитационный параметр.
Даже сейчас значение гравитационной постоянной варьируется, а во времена первых открытии найти его было сложно, как и отдельно массы планет. Поэтому гравитационный параметр был более распространен и вычислен для многих планет Солнечной системы.
Ускорение свободного падения
В условиях нашей планеты, мы привыкли оперировать понятие силы тяжести – силы, что действует на объект со стороны планеты.
Сила тяжести выводится из закона всемирного притяжения путем замены величин, не зависящих от массы тела, на одну величину – ускорение свободного падения.
Таким образом, вместо использования многих значений: массы планеты, ее радиуса и гравитационной константы, можно использовать одно.
Чем отличается вес и масса
Эти два понятия перепутались в повседневной жизни и часто заменяют одно другое. Но вес и масса – это две совершенно разных величины.
Масса – это то, сколько килограммов «есть» в теле. Это его характеристика, которая зависит только от свойств самого объекта.
А вес – это сила, с которой объект давит на опору. На горизонтальных поверхностях он равен силе тяжести, на наклонных чуть меньше, но тоже зависит от силы тяжести.
Именно из-за маленькой силы притяжения, космонавты на Луне могли так высоко подпрыгивать, ведь их вес стал значительно меньше, а их масса осталась неизменной.
Открытие планет
По видимой траектории планет и их отклонений от теоретических траекторий, стало возможно расширение Солнечной системы.
Так, в 1781 году была открыта седьмая планета – Уран. Но, ее предсказанный путь вокруг Солнца не совпадал с наблюдаемым. И был сделан вывод, что на Уран гравитацией действует еще один объект за пределами его орбиты. И в 1846 был обнаружен Нептун.
Но и восьмая планета двигалась не в соответствии с теоретическими выводами. Спустя 100 лет, в 1930 году был открыт Плутон, получивший гордое название Девятой планеты, но лишившийся его из-за небольшой массы.
Гравитон — мифическая частица
Гравитация является одним из фундаментальных взаимодействий в современной физике. Вместе с электромагнитным взаимодействием, гравитация описывает весь наш видимый мир. Но в отличие от электромагнитного (его переносчиком является фотон), гравитация не имеет частицы, которая бы являлась переносчиком этого взаимодействия.
Пытаясь «уравнять» эти взаимодействия, ученые предположили, что частица, которая переносит гравитацию может существовать и назвали ее «гравитон».
Однако, экспериментального доказательства ее существования нет.
Предположительно, гравитон не должен обладать массой, электрическим и другими зарядами. Но для того, чтобы выполнять роль переносчика гравитации должен обладать энергией и двигаться со скоростью света.
Таким образом, гравитация, которая формирует галактики и звездные системы таит в себе еще много загадок. Сформулированный в 1687 году закон Ньютона прекрасно описывает движение планет и взаимодействие между телами, но не дает объяснения, так что же такое гравитация и как она «работает».
Сравнительная таблица планет Солнечной системы
«Коэффициент в сравнении с Земным g» показывает, во сколько раз будет отличатся вес на каждой планете. Например, на Марсе наш вес будет составлять только 38% от Земного, а на Юпитере в 2,54 раза больше.
Если Вам понравилось статья:
На чтение 8 мин Просмотров 2.2к.
Наблюдая за перемещением небесных объектов, люди пытались найти объяснение происходящим на небе событиям. У древних людей преобладали версии мистического характера. Но в 17-м веке Исааком Ньютоном было предложено первое научное объяснение перемещению астрономических тел. Теория гравитации совершенствовалась еще несколько столетий, пока не приобрела современный вид.

Однако, несмотря на наблюдения и опыт, в современной астрофизике есть много пробелов и нестыковок, которые ученые затрудняются объяснить. Например, гравитационная константа, значение которой до сих пор не получается определить с достаточной степенью точности. А в последнее время появились предположения, что эта величина не совсем и константа. В этой статье мы и рассмотрим данный вопрос.
Содержание
- Что такое гравитационная постоянная
- Единица измерения гравитационной постоянной
- Как найти гравитационную постоянную, история открытия
- Работы Ньютона
- Экспериментальное определение гравитационной постоянной, эксперимент Кавендиша
- Измерение гравитационной постоянной
- Современная история изменений гравитационной постоянной
Что такое гравитационная постоянная
Гравитационной постоянной (постоянной Ньютона) называют коэффициент, входящий в формулу закона всемирного тяготения. Численное значение константы гравитации (G, GN или g) равно:

Постоянная Ньютона не зависит от характеристик взаимодействующих объектов и внешних критериев. Данный показатель активно используется практиками при вычислении орбит небесных объектов, в геолого-разведывательных процессах, в геодезии и геофизике.
Единица измерения гравитационной постоянной
Сила в физике сила измеряется в ньютонах:

Гравитационная постоянная численно равна силе, но при этом имеет другую размерность:

Данная единица измерения выводится при помощи несложных расчетов. Два тела весом по 1кг будут взаимно притягиваться с силой, обратно пропорциональной квадрату расстояния между ними:

Коэффициент, уравнивающий Н и единицу измерения гравитационной постоянной, вычисляется следующим образом:

Как найти гравитационную постоянную, история открытия
Открытию явления гравитации предшествовали труды многих исследователей. Еще в древней Греции были предложены гипотезы, которые пытались объяснить, почему материальные тела падают на землю, а не летят в произвольном направлении. История открытия гравитации представлена в таблице.
| Николай Коперник | Обосновал модель мира, в которой Солнце занимает центральное место, а остальные объекты вращаются вокруг него (гелиоцентрическая модель). |
| Уильям Гилберт | Высказал предположение, что наша планета и ее спутник являются магнитами друг для друга, при этом магнитная сила Земли больше из-за того, что больше ее масса. |
| Иоганн Кеплер | Сформулировал ряд законов, в том числе 3-й, который был использован при разработке теории гравитации: период обращения планет в квадрате соотносится как большие полуоси орбит в кубе. |
| Галилео Галилей | Обосновал, что если на тело не оказывать никаких воздействий, то оно будет оставаться в бездействии. Сформулировал закон, смысл которого заключался в том, что все тела, независимо от их тяжести, падают вниз с одинаковой скоростью, при этом пройденный путь пропорционален квадрату времени, за которое тело достигло поверхности Земли. |
| Роберт Гук | Сформулировал закон всемирного тяготения для некруговых орбит и предложил Ньютону обосновать его математически. Создал теорию об универсальной силе тяжести. |
| Эдмунд Галлей | Просчитал обратно пропорциональную зависимость силы тяжести и квадрата расстояния. |
| Исаак Ньютон | На основании работ предшественников вывел закон всемирного тяготения. |
| Генри Кавендиш | Собрал приспособление, с помощью которого можно определить величину константы гравитации. |
| Симеон Дени Пуассон | В его трудах впервые появляется понятие гравитационной константы. |
Ньютона интересовало выведение научных правил, а не чистота искомых значений. Экспериментаторы, которые применяли формулу Ньютона на практике, столкнулись с необходимостью введения поправочного коэффициента, который позже получил название ньютоновская константа. Возник вопрос, чему равна гравитационная постоянная. Последовавшие в данном направлении работы показали, что найти гравитационную постоянную можно только опытным путем.
Работы Ньютона
Научная почва для обоснования закона всемирного тяготения была основательно подготовлена предшественниками Ньютона. Большая часть расчетов базировалась на 3-м законе Кеплера. Сила, благодаря которой планеты удерживаются на орбитах, соизмерима с центростремительным ускорением, и должна быть обратно пропорциональна квадрату расстояния от центра планеты до центра Солнца. Сила, вызывающая падение предметов (пресловутого яблока) на землю, была сопоставлена ученым с силой, удерживающей Луну на ее орбите. Кроме того, физик установил центростремительное ускорение Луны относительно Земли.
Ранее опытным путем было установлено значение ускорения свободного падения объектов. Ученый применил удобные для вычислений цифры: дистанция от Луны до центра Земли в 60 раз больше, чем дистанция от объекта, находящегося на поверхности Земли. Если объект направить к центру Земли, то он за 1 секунду пролетит такой же путь, который пройдет Луна за 1 минуту. Эксперименты подтвердили точность теоретических выкладок с погрешностью около 1%. Это указывало на общность природы происхождения сил тяготения.
Из этого можно заключить, что сила обоюдного притяжения должна соответствовать каждой из масс. Также было подтверждено, что гравитация обратно пропорциональна квадрату расстояния между объектами. Исходя из вышесказанного, формула закона всемирного тяготения будет иметь следующий вид:

где F – сила гравитационного тяготения, g – гравитационная постоянная, m1 и m2 – массы объектов, R – расстояние между объектами.
Работы Ньютона внесли вклад в решение следующих вопросов:
- перемещения тел по космическим орбитам;
- ускорение свободного падения;
- приливы океанических вод;
- причины экваториальной выпуклости.
Эйнштейн использовал закон всемирного тяготения при разработке теории относительности. Постоянная гравитационная показывает соотношение между такими характеристиками уравнений поля, как геометрия пространства-времени и тензор энергии-импульса.
Вместо G Ньютон применял в расчетах «гравитационный параметр» µ. Практические наблюдения за космическими телами позволили определить для ряда небесных объектов значение µ с минимальной погрешностью. Рассчитывают µ по формуле:
µ=GM;
где G – константа гравитации, M – масса объекта

В трудах Кеплера также фигурирует гравитационный параметр. В физике с его помощью упрощают некоторые громоздкие формулы.
Экспериментальное определение гравитационной постоянной, эксперимент Кавендиша
Британец Джон Мичелл увековечил свое имя как создатель крутильных весов, с помощью которых впервые смогли определить величину g. Экспериментальное определение гравитационной постоянной не входило в планы исследователя. Он хотел «взвесить» нашу планету. Однако воплотить свои планы Мичелл не успел, и сконструированное им устройство после его кончины досталось Генри Кавендишу.

Кавендиш доработал установку. Конструкция включала шестифутовый стержень, закрепленный на медном волокне длиной 1 м. К плечам коромысла ученый прикрепил два шара из свинца по 775 грамм каждый, соорудив таким образом гантельку. Затем рядом с маленькими шариками он разместил крупные шары по 49,5 кг, что привело к возникновению явления гравитации между объектами. Стержень конструкции отклонился от первоначального положения, что дало возможность найти величину угла поворота гантельки. Опыт Кавендиша оказался успешным: увязав упругие свойства волокна, массу шаров, размер установки и значение угла, он определил массу Земли и ее среднюю плотность. Сегодня эксперимент Кавендиша по-прежнему актуален, исследователями разрабатываются инновационные модификации прибора.
Измерение гравитационной постоянной
С измерением степени точности гравитационной постоянной g сложилась парадоксальная ситуация. Последние многочисленные эксперименты определяют отклонение с точностью 10-4. Это хуже на несколько порядков по сравнению с точностью определения прочих базисных величин. Сравнительно аккуратные результаты можно получить в условиях лаборатории, измеряя силу гравитации между двумя телами с известной массой (модификации эксперимента Кавендиша). Новые атомно-интерферометрические устройства оказались непригодными в измерении гравитационной постоянной в связи с гораздо большей величиной погрешности, чем при эксперименте на механических устройствах.
Современная история изменений гравитационной постоянной
Неординарность ситуации с нахождением точного значения гравитационной константы привела к возникновению догадки, что G не является постоянной в классическом понимании и может с течением времени изменяться. В уравнениях общей теории относительности Эйнштейн увязал гравитационную постоянную и космологическую константу – параметр, который влияет на устойчивость Вселенной.
Хаббл и Фридман обосновали опытным путем модель расширяющейся Вселенной, что противоречило теории стационарной Вселенной Эйнштейна. На долгое время ученые прекратили учитывать при вычислениях космологическую постоянную. В конце 1990-х годов было выявлено и подтверждено ускорение расширения Вселенной. Вновь открытые результаты не вписывались в теорию Хаббла-Фридмана, концепцию пришлось пересматривать, и космологическая постоянная вернулась в физику.
Современная Лямбда-CDM модель Вселенной учитывает космологическую постоянную. Данная концепция объясняет наличие антигравитации, «темной материи», реликтового излучения, и является стандартом в астрофизике с 1998-го года.
Интересно, что Лямбда-CDM модель хорошо коррелирует с космологией черной дыры. Все больше ученых склонны отказываться от Теории большого взрыва, поскольку накопившиеся научные данные противоречат общепринятому взгляду на образование Вселенной. В гипотезу, что видимое нами пространство-время (и мы вместе с ним) бесконечно «падает» в гигантскую черную дыру, отлично вписывается явление ускорения расширения Вселенной, «странности» реликтового излучения, наличие темной материи.
Современная история изменений гравитационной постоянной привела к попыткам астрономов переосмыслить данный физический параметр. Так, Филипп Мангейм считает, что константа g в зависимости от условий ее измерения может менять свое значение. В условиях нашей планеты постоянная g будет иметь известную ученым величину, а вот в космосе значение G будет гораздо меньше.
Космологическая постоянная, описывающая скорость расширения Вселенной, имеет расчетное значение в 10120 раз превосходящее наблюдаемое. Если бы значение g было верным, то галактики не успели бы образоваться. По мнению Мангейма, в расчеты следует ввести новую величину, которая будет пропорциональна произведению космологической и гравитационной констант.
Такой подход позволит устранить существующие противоречия, но у него есть и свои недостатки: подвергаются сомнению основы теории относительности, не объясняется существование реликтового излучения и двойных пульсаров. Преимуществом идеи Мангейма является возможность синтеза теории гравитации и физики элементарных частиц в одну универсальную доктрину.
По вашему мнению, ньютоновская константа – это объективный параметр, или мы просто не все знаем о физических феноменах?
Гравитационная постоянная (также известная как «универсальная гравитационная постоянная», «ньютоновская константа тяготения» или «гравитационная постоянная Кавендиша»), обозначенная буквой GG или малой греческой буквой γγ, является эмпирической физической константой, участвующей в вычислении гравитационных эффектов.
В законе Ньютона она представляет собой коэффициент пропорциональности, связывающий гравитационную силу между двумя телами с результирующей их масс и обратным квадратом их расстояния:
F=γmMR2,F=gamma frac{mM}{{{R}^{2}}},
где γγ – коэффициент пропорциональности, который называют гравитационной постоянной.
В уравнениях поля Эйнштейна она количественно определяет связь между геометрией пространства-времени и тензором энергии-импульса.
Физический смысл γ
Физический смысл γγ нетрудно установить. Для этого в выражении закона притяжения положим m1=m2=1m_1 = m_2 = 1 кг, r=1r = 1 м.
Тогда F=γF = γ, то есть гравитационная постоянная численно равна силе взаимодействия двух материальных точек с массами 1 кг, находящихся на расстоянии 1 м.
Оценка величины γγ на основе предположений о средней плотности Земли показала, что гравитационное притяжение между телами обычных размеров, то есть в лабораторных условиях, очень мало.
Это свидетельствует о том, что для определения γγ нужны достаточно точные и сложные эксперименты.
Опыт Кавендиша
Впервые экспериментально доказал справедливость закона гравитационного притяжения в земных условиях, а также определил гравитационную постоянную γγ английский ученый Г. Кавендиш (1731 – 1810). Для определения были использованы крутильные весы. Основная часть весов – однородный стержень-коромысло длиной ll, подвешенный на тонкой упругой нити аа:
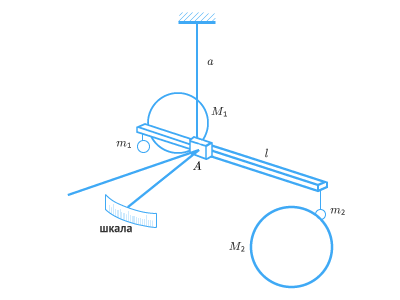
На концах стержня прикрепляли два одинаковых свинцовых шарика, массы которых m1m1 = m2m2 = 730г. С разных сторон этих шариков размещали две другие крупные свинцовые пули, массы которых M1M1 = M2M2 = 158 кг. Вследствие гравитационного взаимодействия между шарами коромысло начинает поворачиваться вокруг оси, проходящей через нить подвеса, на некоторый угол φ. Поскольку длина l стержня значительно больше расстояния между центрами масс шаров m1m1 и M1M1, m2m2 и M2M2, то гравитационным взаимодействием между шарами m1m1 и M2M2, m2m2 и M1M1 можно пренебречь.
Закручивания нити подвеса происходит до тех пор, пока момент пары сил гравитационного взаимодействий не уравновесится моментом упругой силы закручивания нити Μ = kφ.
Угол φφ определяли по отклонению отраженного луча от зеркала А. Модуль кручения kk определили в результате наблюдений за свободными колебаниями коромысла. Чтобы конвекционные потоки воздуха не влияли на результаты измерений, Г. Кавендиш разместил экспериментальную установку в закрытом ящике, который находился в закрытой комнате. Наблюдения и измерения проводились из другого помещения с помощью телескопа. Опыт Кавендиша не раз повторялся в разных вариантах.
Опыт Жолли
Точное значение γγ определено методом, который предложил немецкий физик Ф. Жолли (1809 – 1884). На одном из плеч рычажных весов подвешивали две чаши, между которыми располагали тяжелое свинцовое тело правильной геометрической формы:
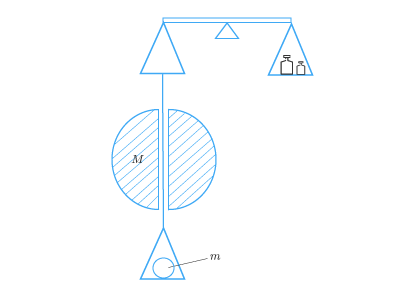
Когда на верхнюю чашу положить тело массой mm, то на него действует сила:
F1=mg+FF1 = mg + F,
где FF – сила гравитационного притяжения между телами массами mm и ММ. Если положить тело массой m в нижнюю чашку, то на него будет действовать сила F2=mg−FF2 = mg – F. Силы F1F1 и F2F2 определяют с помощью грузиков, которые нужны для уравновешивания весов. На основе этих измерений находят γγ:
γ=F1−F22Mmr2gamma =frac{{{F}_{1}}-{{F}_{2}}}{2Mm}{{r}^{2}}
где rr – расстояние между центрами масс mm и ММ.
По современным данным, гравитационная постоянная γγ = 6.67408 · 10-11 м3 кг-1 с-2
Поскольку значение гравитационной постоянной мало, то гравитационное притяжение может быть значительным для тел достаточно больших масс. В результате действия сил гравитационного притяжения осуществляется движение всех небесных тел.
Знание гравитационной постоянной дало возможность определить массу Луны, Солнца и других небесных тел.

