Как измерили массу Луны?
Ученик
(198),
закрыт
15 лет назад
*@ Екатерина @ *
Гений
(86331)
15 лет назад
впервые измерили напрямую (не по параметрам орбит из закона Ньютона) крутильными весами. Луна близко и её сила притяжения очень велика (вспомни приливы) . Так что даже не очень чувствительные весы должны её чувствовать. достаточно сегодняшних точных аналитических весов, чтобы луну взвеситьЧто касается непрямых астрономических методов – можно измерить видимый сдвиг Солнца (и расчитать, насколько смешается Земля, ведь по орбите движется не центр земли а центр масс системы Земля-Луна) . Можно измерить “нутацию”, т. е. отклонение земной оси. Правда оба метода дадут не массу Луны а отношение масс Земли и Луны. Можно измерить отклонение орбит спутников (их то массы известны) .
Вначале рассчитывается, а не измеряется масса Земли. Делается это просто.
Измеряется ускорение свободного падения, измеряется гравитационная постоянная в опытах.
Затем по теории гравитации рассчитывается масса Земли. Ну, а дальше – таким же путем, через закон всемирного тяготения рассчитывается масса Луны.
Используя законы небесной механики и астрономические наблюдений эти данные можно уточнять.
Omen!
Знаток
(269)
15 лет назад
Так же, как и массы других небесных тел (в т.ч. и Земли): по траектории движения в гравитационных полях других небесных тел.
История оценки массы Луны насчитывает уже сотни лет. Ретроспектива этого процесса изложена в статье зарубежного автора Дэвида У. Хьюза. Перевод этой статьи сделан по мере скромных моих познаний в английском и представлен ниже. Ньютон оценил массу Луны значением вдвое большим принятого ныне за правдоподобное. Правда у каждого своя, а истина одна. Точку в этом вопросе могли бы поставить американцы с маятником на поверхности Луны. Они ведь там были😉. То же могли сделать телеметристы по орбитальным характеристикам LRO и прочих ИСЛ. Жаль, что эта информация пока недоступна.
Обсерватория
Vol.122 2002 апрель No.1167
Измерение массы Луны
Обзор к 125-летию Обсерватории
Дэвид У. Хьюз
Кафедра физики и астрономии, Университет Шеффилда
Первая оценка лунной массы была сделана Исааком Ньютоном. Значение этой величины (массы), а также плотность Луны, с тех пор были предметом обсуждения.
Введение
Масса является одной из наиболее неудобных для измерения величин в астрономическом контексте. Обычно мы измеряем силу воздействия неизвестной массы на известную массу, или наоборот. В истории астрономии не было концепции “масс”, скажем, Луны, Земли, и Солнца (MM, МE, МC) до времени Исаака Ньютона (1642 – 1727). После Ньютона, утвердились достаточно точные соотношения масс. Так, например, в первом издании Начал (1687) дано отношение МC/М Е =28700, которое затем увеличивается до МC/М Е =227512 и МC/М Е =169282 во втором (1713) и третьем (1726) изданиях, соответственно, в связи с уточнением астрономической единицы. Эти отношения подчеркнули тот факт, что Солнце было важнее, чем Земля, и оказали значительную поддержку гелиоцентрической гипотезе Коперника.
Данные по плотности (масса/объем) тела помогает оценить его химический состав. Греки более 2200 лет назад получили достаточно точные значения для размеров и объемов Земли и Луны, но массы была неизвестны, а плотности не могли быть рассчитаны. Таким образом, даже при том, что Луна была похожа на сферу из камня, это не могло быть научно подтверждено. Кроме того, не могли быть предприняты первые научные шаги к выяснению происхождения Луны.
Безусловно, лучший метод определения массы планеты сегодня, в космическую эру, опирается на третий (гармонический) закон Кеплера. Если спутник массой m, вращается вокруг Луны массой МM , то
где а это усредненное по времени среднее расстояние между MM и m, G постоянная тяготения Ньютона, и P – период орбиты. Поскольку МM>>m, это уравнение дает значение MM непосредственно.
Если астронавт может измерять ускорение силы тяжести, GM на поверхности Луны, то
где RM – лунный радиус, параметр, который измерял с разумной точностью еще Аристарх Самосский, около 2290 лет назад.
Исаак Ньютон1 не измерял массу Луны непосредственно, но попытался оценить соотношение между солнечной и лунной массой с использованием измерения морских приливов. Даже при том, что многие люди до Ньютона предполагали, что приливы были связаны с положением и влиянием Луны, Ньютон был первым, кто взглянул на предмет с точки зрения гравитации. Он понял, что приливная сила, создаваемая телом массы М на расстоянии d пропорциональна M/d3. Если это тело имеет диаметр D и плотность ρ, эта сила пропорциональна ρD3/d3. И если угловой размер тела, α, мал, приливное сила пропорциональна ρα3 . Так приливообразующая сила Солнца чуть меньше половины лунной.
Осложнения возникли потому, что наибольший прилив был отмечен, когда Солнце было на самом деле в 18.5° от сизигии, а также потому, что лунная орбита не лежит в плоскости эклиптики и имеет эксцентриситет. Принимая все это во внимание, Ньютон на основе своих наблюдений, что “До устья реки Эйвон, в трех милях ниже Бристоля, высота подъема воды в весенних и осенних сизигиях светил (по наблюдениям Samuel Sturmy) составляет около 45 футов, но в квадратурах только 25”, сделал вывод, “что плотность вещества Луны к плотности вещества Земли относится как 4891 к 4000, или как 11 к 9. Следовательно вещество Луны более плотное и более земляное, чем сама Земля”, и “масса вещества Луны будет в массе вещества Земли как 1 в 39.788” (Начала, Книга 3, Предложение 37, Проблема 18).
Поскольку нынешнее значение для соотношения между массой Земли и массы Луны задается как МЕ/MM = 81.300588, ясно, что у Ньютона что-то пошло не так. К тому же значение 3.0 несколько более реалистично, чем 9/5 для отношения высот сизигийного? и квадратурного прилива. Также неточное значение Ньютона для массы Солнца было серьезной проблемой. Обратите внимание, что Ньютон имел очень мало статистической точности, и указание им пяти значащих цифр в значении ME /MM является полностью необоснованным.
Пьер-Симон Лаплас (1749 – 1827) посвятил значительное время для анализа высот приливов (особенно в Бресте), концентрируясь на приливах на четырех основных фазах Луны на обоих солнцестояниях и равноденствиях. Лаплас2 , используя короткие серии наблюдений 18-го века, получил ME /MM значение 59. К 1797 году он уточнил это значение до 58.7. Используя расширенный набор приливных данных в 1825 году, Лаплас 3 получил ME /MM = 75.
Лаплас понял, что приливный подход был одним из многих способов выяснения лунной массы. Тот факт, что вращение Земли осложняет приливные модели, и что конечный продукт расчета был отношение масс Луна / Солнце, явно беспокоило его. Поэтому он сравнил свою приливную силу с результатами измерений, полученными другими методами. Лаплас 4 записывает в дальнейшем коэффициенты МЕ /MM, как 69.2 (с использованием коэффициентов Даламбера), 71.0 (с использованием анализа Маскелина нутации Брэдли и наблюдений параллакса), и 74.2 (с использованием работы Бурга о лунном параллактическом неравенстве). Лаплас, по-видимому, рассматривал каждый результат в равной степени достойным доверия и просто осреднял четыре значения для получения среднего. “La valeur le plus vraisembable de la masse de la lune, qui me parait resulted des divers phenomenes 1/68.5” (ref 4, с. 160). Среднее соотношение МЕ /MM равное 68.5 неоднократно встречается у Лапласа5.
Вполне понятно, что к началу девятнадцатого века, должны были возникнуть сомнения относительно ньютоновского значения 39.788, особенно в умах некоторых британских астрономов, которые были в курсе работ своих французских коллег.
Финлейсон 6 вернулся к приливной методике и при использовании измерения сизигийного? и квадратурного приливов в Дувре за годы 1861, 1864, 1865, и 1866, он получил следующие значения МЕ/MM: 89.870, 88.243, 87.943, и 86.000, соответственно. Феррелом 7 извлечены главные гармоники из девятнадцатилетних приливных данных в Бресте (1812 – 1830) и получено значительно меньшее соотношение МЕ/ МM = 78. Харкнесс 8 приводит приливное значение МЕ/MМ = 78.65.
Так называемый маятниковый метод основан на измерении ускорения от силы тяжести. Возвращаясь к третьему закону Кеплера, с учетом второго закона Ньютона получим
где aМ – усредненное по времени расстояние между Землей и Луной, PM – лунный сидерический период обращения (т.е. длина звездного месяца), gЕ ускорение силы тяжести на поверхности Земли, и RЕ – радиус Земли. Так
Согласно Барлоу и Брайан 9, эта формула была использована Эйри 10 для измерения МЕ/MМ , но была неточна в силу малости этой величины и аккумулировала накопившуюся неопределенность в значениях величин aМ , gЕ , RЕ , и PM.
Когда телескопы стали более совершенными и точность астрономических наблюдений повысилась, стало возможным решить лунное уравнение более точно. Общий центр масс системы Земля /Луна движется вокруг Солнца по эллиптической орбите. И Земля, и Луна вращаются вокруг этого центра масс каждый месяц.
Наблюдатели на Земле, таким образом, видят на протяжении каждого месяца, небольшое смещение на восток и затем небольшое смещение на запад небесной позиции объекта, по сравнению с координатами объекта, которые он имел бы в отсутствии у Земли массивного спутника. Даже с современными инструментами это движение не обнаруживается в случае звезд. Оно может, однако, быть легко измерено для Солнца, Марса, Венеры и астероидов, которые проходят неподалеку, (Эрос, например, в его ближайшей точке находится всего в 60 раз дальше, чем Луна). Амплитуда месячного смещения позиции Солнца составляет около 6,3 секунды дуги. Таким образом
где aC – среднее расстояние между Землей и центром масс системы Земля-Луна (это около 4634 км), и aS – среднее расстояние между Землей и Солнцем. Если среднее расстояние Земля-Луна aM также известно, то
К сожалению, постоянная этого “лунного уравнения”, т.е. 6,3″, это очень маленький угол, который крайне трудно точно измерить. К тому же МЕ/МM зависит от точного знания расстояния Земля-Солнце.
Значение лунного уравнения может быть в несколько раз больше для астероида, который проходит близко с Землей. Гилл 11 использовал 1888 и 1889 позиционных наблюдения астероида 12 Виктория и солнечного параллакса на 8.802″ ± 0.005″ и пришел к выводу, что МЕ/МM =81.702±0.094. Хинкс 12 использовал длинную последовательность наблюдений астероида 433 Эрос и пришел к выводу, что МЕ/МM =81.53±0.047. Затем он использовал обновленное значение солнечного параллакса и исправленные значения для астероида 12 Виктория, сделанные Дэвидом Гиллом и получил исправленное значение МЕ/МM =81.76±0.12.
Используя этот подход, Ньюкомб 13 , из наблюдений Солнца и планет, получил МЕ/МM =81.48±0.20.
Спенсер Джонс14 проанализировал наблюдения за астероидом 433 Эрос, когда он проходил в 26 х 106 км от Земли в 1931 году. Главной задачей было измерение солнечного параллакса, и комиссия Международного астрономического союза была создана в 1928 году с этой целью. Спенсер Джонс обнаружил, что постоянная лунного уравнения равна 6.4390± 0.0015секунды дуги. Это, в сочетании с новым значением для солнечного параллакса, привело к отношению МЕ/МM =81.271±0.021.
Прецессия и нутация также могут быть использованы. Полюс оси вращения Земли прецессирует вокруг полюса эклиптики каждые 26 000 лет или около того, что также проявляется в движения первой точки Овна вдоль эклиптики примерно на 50.2619″ в год.. Прецессия была обнаружена Гиппархом более 2000 лет назад. На это движение накладывается более быстрое, небольшое периодическое движение, известное как нутация, обнаруженная Джеймсом Брэдли (1693 ~ 1762) в 1748 году. Нутация в основном происходит, потому что плоскость лунной орбиты не совпадает с плоскостью эклиптики. Максимальная нутация составляет около 9.23″ и полный цикл занимает около 18.6 лет. Существует также дополнительные нутации производимые Солнцем. Все эти эффекты обусловлены моментами сил, действующими на экваториальные вздутия Земли.
Величина установившейся лунно-солнечной прецессии по долготе, и амплитуды различных периодических нутаций по долготе, являются функциями, среди прочего, массы Луны. Стоун15 отметил, что лунно-солнечная прецессия, L, и постоянная нутации, N, даны так:
где ε=(МM/МS ) (aS/aM )3, aS и aM среднее расстояние Земля-Солнце и Земля-Луна;
eE и eM – эксцентриситеты земной и лунной орбиты, соответственно. Постоянная Делоне представлена как γ. В первом приближении γ есть синус половины угла наклона лунной орбиты к эклиптике. Величина ν это смещение узла лунной орбиты,
в течение Юлианского года, по отношению к линии равноденствий; χ является постоянной, которая зависит от средней возмущающей силы Солнца, момента инерции Земли, и угловой скорости Земли по своей орбите. Обратите внимание, что χ сокращается, если L делится на Н. Стоун подставляя L = 50.378″ и N = 9.223″ получил МЕ/МM = 81.36. Ньюкомб использовал свои собственные измерения L и N и нашел МЕ/МM = 81.62 ± 0.20. Проктор 16 нашел, что МЕ/МM = 80.75.
Движение Луны вокруг Земли было бы точно по эллипсу, если бы Луна и Земля были единственными телами в Солнечной системе. Тот факт, что они таковыми не являются приводит к лунному параллактическому неравенству. В связи с привлечением других тел в Солнечной системе, и Солнца, в частности, орбита Луны чрезвычайно сложна. Три крупнейших неравенства, которые должны быть применены обусловлены эвекцией, вариацией, и годовым уравнением. В контексте настоящей работы вариация является наиболее важным неравенством. (Исторически Седиллот говорит, что лунная вариация была обнаружена Абул-Вафа в 9-м веке; другие приписывают это открытие Тихо Браге).
Лунная вариация вызвана изменением, которое происходит от различия солнечного притяжения в системе Земля-Луна на протяжении синодического месяца. Этот эффект равнен нулю, когда расстояния от Земли до Солнца и Луны до Солнца равны, в ситуации, возникающей очень близко к первой и последней четверти. Между первой четверти (через полнолуние) и последней четвертью, когда Земля находится ближе к Солнцу, чем Луна, и Земля преимущественно оттягивается от Луны. Между последней четвертью (через новолуние) и первой четвертью, Луна находится ближе к Солнцу, чем Земля, и поэтому Луна преимущественно оттягивается от Земли. Полученная остаточная сила может быть разложена на две составляющие, одна касательная к лунной орбите, а другая перпендикулярная к орбите (т.е., в направлении Луна-Земля).
Положение Луны меняется на целых ± 124.97 угловые секунды (согласно Брауэр и Клементс17) по отношению к позиции, которую она имела бы, если бы Солнце было бесконечно далеко. Именно эти 124.9″, известны как параллактическое неравенство.
Поскольку эти 124.97 угловые секунды соответствуют четырем минутам времени, то следует ожидать, что эта величина может быть измерена с достаточной точностью. Наиболее очевидное следствие параллактического неравенства в том, что интервал между новолунием и первой четвертью составляет около восьми минут, т.е. дольше, чем от этой же фазы до полнолуния. К сожалению, точность, с которой эта величина может быть измерена несколько уменьшилась по причине, что лунная поверхность неровная и что различные лунные края должны быть использованы для измерения лунной позиции в различных частях орбиты. (Вдобавок к этому есть также небольшое периодическое изменение в видимом полудиаметре Луны в связи с меняющимся контрастом между яркостью края Луны и неба. Это вносит погрешность, которая изменяется между ± 0.2″ и 2″, см. Кэмпбелл и Нейсон 18).
Рой 19 отмечает, что лунное параллактическое неравенство, P, определяется как
По словам Кэмпбелла и Нейсона18, параллактическое неравенство было установлено как 123.5″ в 1812 году, 122.37″ в 1854 году, 126.46″ в 1854 году, 124.70″ в 1859 году, 125.36″ в 1867 году, и 125.46″ в 1868 году. Таким образом, отношение массы Земли / Луна может быть рассчитано по наблюдениям параллактическим неравенства, если других величин, и особенно солнечного параллакса (т.е. aS), известны. Это привело к дихотомии среди астрономов. Некоторые предполагают, используя массовое соотношение Земля/Луна из параллактического неравенства, оценить среднее расстояние Земля-Солнце. Другие предполагают через последнее оценить первое (см Moulton 20).
Наконец рассмотрим возмущение планетных орбит. Орбиты наших ближайших соседей, Марса и Венеры, которые испытывают гравитационное влияние системы Земля-Луна. В связи с этим действием, орбитальные параметры, такие как эксцентриситет, долгота узла, наклонение, и аргумент перигелия изменяются как функция времени. Точное измерение этих изменений может быть использовано для оценки общей массы системы Земля / Луна, и вычитанием, массы Луны.
Это предложение было впервые сделано Леверье (см. Янг 21). Он подчеркнул тот факт, что движения узлов и перигелиев, хотя и медленные, но непрерывные, и, таким образом, будут известны со все большей точностью с течением времени. Леверье загорелся этой идеей так, что отказался от наблюдений тогдашнего транзита Венеры, будучи убежден, что солнечный параллакс и отношение масс Солнце/Земля в конечном итоге будет найдено гораздо точнее методом возмущений.
Рис. 1. Опубликованное значение для отношения масс Земля / Луна в зависимости от даты.
Самая ранняя точка происходит от Начала Ньютона.
Точность известной лунной массы.
Опубликованное значение для отношения масс Земли/Луны строится как функция даты публикации на рис. 1. Видно, что результаты стали гораздо меньше разниться после приблизительно 1830 года.
Методы измерения можно разделить на две категории. Приливная техника требуется особое оборудование. Вертикальный шест с градуировкой теряется в прибрежной грязи. К сожалению, сложность приливной обстановки вокруг берегов и заливов Европы означала, что полученные значения лунного массы были далеки от точной. Приливная сила, с которой тела взаимодействуют пропорциональна их массе, деленной на куб расстояния. Так следует помнить, что конечный продукт расчета на самом деле соотношение между лунной и солнечной массой. И соотношение между расстояниями до Луны и Солнца должно быть точно известно. Типичные приливные значения МЕ/MМ равны 40 (в 1687 году), 59 (в 1790 году), 75 (в 1825 году), 88 (в 1865 году), и 78 (в 1874 году), подчеркивают трудность, присущую интерпретации данных.
Все остальные методы опирались на точные телескопические наблюдений астрономических позиций. Детальные наблюдения звезд в течение длительных периодов времени привели к получению констант прецессии и нутации оси вращения Земли. Они могут быть интерпретированы в терминах соотношения между лунными и солнечными массами. Точные позиционные наблюдения Солнца, планет и некоторых астероидов, за несколько месяцев, привели к оценке расстоянии Земли от центра масс системы Земля-Луна. Тщательные наблюдения положения Луны в зависимости от времени в течение месяца привели к амплитуде параллактического неравенства. Последние два метода, вместе, опираясь на измерения радиуса Земли, длины звездного месяца, и ускорения силы тяжести на поверхности Земли, привели к оценке величины [1 + (ММ/МE)], а не массы Луны непосредственно. Очевидно, что если [1 + (ММ/МE)] известно лишь с точностью до ± 1%, масса Луны является неопределенной. Чтобы получить соотношение ММ/МE точностью скажем, 1, 0,1, 0,01% требуется величину [1 + (ММ/МE)] измерить с точностью ± 0.012, 0.0012, и 0.00012 %, соответственно.
Оглядываясь на исторический период с 1680 до 2000, можно видеть, что лунная масса была известна ± 50% между 1687 и 1755, ± 10% между 1755 и 1830, ± 3% между 1830 и 1900, ± 0.15 % между 1900 и 1968, и ± 0.0001% между 1968 и по настоящее время. Между 1900 и 1968 два значения были распространены в серьезной литературе. Лунный теория указала, что ME/MM = 81.53, и лунное уравнение и лунной параллактическое неравенство дало несколько меньшую величину ME/MM = 81.45 (см. Гарнетт и Вулли22). Другие значения цитировались исследователями, которые использовали иные значения солнечного параллакса в соответствующих уравнениях. Эта незначительная путаница была удалена когда легкий орбитальный аппарат и командный модуль летали по хорошо известным и точно-измеренным орбитам вокруг Луны в эпоху Apollo. Нынешний значение ME/MM = 81.300588 (см. Зейдельман23), является одной из наиболее точно известных астрономических величин. Наше точное знание фактической лунной массы омрачено неопределенностью в постоянной тяготения Ньютона, G.
Важность лунной массы в астрономической теории
Исаак Ньютон1 сделал очень мало с его новообретенным лунным знанием. Даже при том, что он был первым ученым, измерившим лунную массу, его МЕ/МM = 39.788, казалось бы, заслужили немного современных комментариев. Тот факт, что ответ был слишком мал, почти в два раза, не был реализован в течение более шестидесяти лет. Физически значим только вывод, который Ньютон извлек из ρM/ρE =11/9, состоящий в том, что “тело Луны плотнее и более земное, чем у нашей земли” (Начала, книга 3, предложение 17, следствие 3).
К счастью, этот увлекательный, хотя ошибочный, вывод не приведет добросовестных космогонистов в тупик в попытке объяснить его значение. Примерно в 1830 году стало ясно, что ρM/ρE было 0.6 и МЕ/МM было между 80 и 90. Грант24 отметил, что “это точка, в которой большая точность не взывала к существующим основам науки”, намекая, что точность здесь неважна просто потому, что ни астрономическая теория, ни теория происхождения Луны, не полагались сильно на эти данные. Агнес Клерк25 был более осторожен, отметив, что “лунно-земная система … была особым исключением среди тел находящихся под влиянием Солнца.”
Луна (масса 7,35-1025 г) является пятым в Солнечной системе спутником из десятки (начиная с номера один, это Ганимед, Титан, Каллисто, Ио, Луна, Europa, Кольца Сатурна, Тритон, Титания, и Рея). Актуальный в 16ом и 17ом веках Парадокс Коперника (тот факт, что Луна вращается вокруг Земли, тогда как Меркурий, Венера, Земля, Марс, Юпитер и Сатурн вращается вокруг Солнца) давно забыт. Большой космогонический и селенологический интерес представляло отношение масс “главный / наиболее массивный-вторичный”. Вот список Плутон / Харон, Земля / Луна, Сатурн / Титан, Нептун / Тритон, Юпитер / Каллисто и Уран / Титания, коэффициенты, такие 8.3, 81.3, 4240, 4760, 12800 и 24600, соответственно. Это первое, что указывает на возможное совместное их происхождения по бифуркации путем конденсации жидкости тела (см, например, Дарвин26, Джинс27, и Биндер28). На самом деле, необычное отношение масс Земля / Луна привело Вуд 29 к выводу, что “указывает достаточно четко, что событие или процесс, который создал земную Луну был необычным, и предполагает, что некоторое ослабление нормального отвращение к привлечению специальных обстоятельств, может быть допустимо в этой проблеме”.
Селенология, изучение происхождения Луны, стала «научной» с открытия в 1610 году Галилеем спутников Юпитера. Луна потеряла свой уникальный статус. Тогда Эдмонд Галлей 30 обнаружил, что лунный орбитальный период меняется со временем. Это было не так, однако, до работы Г.Х. Дарвина в конце 1870-х, когда стало ясно, что первоначально Земля и Луна были гораздо ближе друг к другу. Дарвин предположил, что резонансно-индуцированная бифуркация вначале, быстрое вращение и конденсация расплавленной Земли привели к образованию Луны (см Дарвин 26). Осмонд Фишер 31 и В.Х. Пикеринг 32 даже зашел так далеко, что предположил, что бассейн Тихого океана это шрам, который остался, когда Луна откололась от Земли.
Вторым крупным селенологическим фактом было отношение масс Земля/Луна. То, что имелось нарушение значений для дарвиновских тезисов было отмечено А.М. Ляпуновым и Ф.Р. Мултоном (см., например, Moulton33).. Вместе с низким комбинированным угловым моментом системы Земля-Луна, это привело к медленной гибели дарвиновской теории приливов. Затем было предложено, что Луна была просто сформирована в другом месте в Солнечной системе, а затем захвачена в некий сложный процесс трех тел (см., например. Си 34).
Третьим основным фактом была лунная плотность. Ньютоново значение ρM/ρE 1.223 стал 0.61 к 1800г., 0.57 к 1850г., и 0.56 к 1880 (см. Браш35). На заре девятнадцатого века стало ясно, что Луна имеет плотность, которая была около 3.4 г см -3. В конце ХХ века это значение почти не изменилось, и составило 3.3437±0.0016г см-3 (см. Хаббард36). Очевидно, что лунный состав отличался от состава Земли. Эта плотность сходна с плотностью пород на небольшой глубине в мантии Земли и предполагает, что дарвиновская бифуркация произошла в гетерогенной, а не в однородной Земле, в то время, которое наступило после дифференцировки и основного формообразования. Недавно это сходство было одним из основных фактов, способствующих популярности таранной гипотезы лунного образования.
Было отмечено, что средняя плотность Луны была такой же, как у метеоритов (и, возможно астероидов). Гуллемин37 указал плотность Луны в 3.55 раза больше, чем у воды. Он отметил, что “так любопытно было узнать значения 3.57 и 3.54 плотности для некоторых метеоритов, собранных после того, как они попадают на поверхность Земли”. Нэсмит и Карпентер38 отметили, что “удельный вес лунного вещества (3.4) мы можем заметить, это примерно то же самое, что у кремния стекла или алмаза: и как ни странно это почти совпадает с метеоритами, что время от времени мы находим лежащими на земле; следовательно подтверждается теория, что эти тела были изначально фрагментами лунного вещества, и, вероятно, выбрасывались некогда из лунных вулканов с такой силой, что попадали в сферу земного притяжения, и в конечном счете, падали на земную поверхность “.
Юри 39, 40 использовал этот факт, чтобы поддержать свою теорию захвата лунного происхождения, хотя он беспокоился о разнице между лунной плотностью и плотностью определенных хондритовых метеоритов, и других планет земной группы. Эпик 41 счел эти различия несущественными.
Выводы
Масса Луны чрезвычайно нехарактерна. Она слишком велика, чтобы разместить наш спутник комфортно среди групп планетарных захваченных астероидов, как Фобос и Деймос вокруг Марса, групп Гималия и Ананке вокруг Юпитера, и групп Япет и Фиби вокруг Сатурна. Тот факт, что эта масса 1.23% Земли, к сожалению, только незначительная подсказка среди многих в поддержку предлагаемого механизма воздействия-происхождения. К сожалению, сегодняшняя популярная теория типа “тело размером с Марс попадает в недавно дифференцированную Землю и выбивает массу материала” имеет некоторые мелочные проблемы. Даже при том, что этот процесс был признан возможным, это не гарантирует, что он является вероятным. Такие вопросы, как “почему только одна Луна сформировалась в то время?”, “почему другие Луны не образуются в другое время?”, “почему этот механизм сработал на планете Земля, и не коснулся наших соседей Венеры, Марса, и Меркурия?” приходят на ум.
Масса Луны слишком мала, чтобы поместить ее в тот же разряд, что Харон Плутона. 8.3/1 Соотношение между массами Плутона и Харона, коэффициент, который указывает, что пара этих тел образована бифуркацией конденсации, вращением почти жидкого тела, и отстоит очень далеко от значения 81.3/1 отношения массы Земли и Луны.
Мы знаем лунную массу с точностью до одной части от 109. Но не можем избавиться от ощущения, что общий ответ на эту точностью “и что”. В качестве ориентира, или подсказки о происхождении нашего небесного напарника этого знания мало. На самом деле, в одном из последних 555-страничных томов на эту тему 42, индекс даже не включает “лунную массу” в виде записи!
Ссылки.
References
(1) I. Newton, Principia, 1687. Here we are using Sir Isaac Newton’s Mathematical Principles of Natural Philosophy, translated into English by Andrew Motte in 1729; the translation revised and supplied with an historical and explanatory appendix by Florian Cajori, Volume 2: The System of the World (University of California Press, Berkeley and Los Angeles}, 1962.
(2) P.-S. Laplace, Mem. Acad, des Sciences, 45, 1790.
(3) P.-S. Laplace, Traite de Mechanique Celeste, Tome 5, Livre 13 (Bachelier, Paris), 1825.
(4) P.-S. Laplace, Traite de Mechanique Celeste, Tome 3 (rimprimerie de Crapelet, Paris), 1802, p, 156.
(5) P.-S. Laplace, Traite de Mechanique Celeste, Tome 4 (Courcicr, Paris), 1805, p. 346.
(6) H. P. Finlayson, MNRAS, 27, 271, 1867.
(7) W. E, Fcrrel, Tidal Researches. Appendix to Coast Survey Report for 1873 (Washington, D. C) 1874.
(8) W. Harkness, Washington Observatory Observations, 1885? Appendix 5, 1891,
(9) C. W. C. Barlow Sc G. H, Bryan, Elementary Mathematical Astronomy (University Tutorial Press, London) 1914, p. 357.
(10) G. B. Airy, Mem. RAS., 17, 21, 1849.
(11) D. Gill, Annals of the Cape Observatory, 6, 12, 1897.
(12) A. R. Hinks, MNRAS, 70, 63, 1909.
(13) S. Ncwcomb, Supplement to the American Ephemeris for tSy? (Washington, D. C), 1895, p. 189.
(14) H. Spencer Jones, MNRAS, 10], 356, 1941.
(15) E. J. Stone, MNRAS, 27, 241, 1867.
(16) R. A. Proctor, Old and Nets Astronomy (Longmans, Green, and Co., London), [892, p. 213,
(17) D, Brouwer & G. M. Clements, Methods of Celestial Mechanics (Academic Press, New York), 1961.
(18) J. Campbell & E. Neison, MNRAS, 40, 386 and 441, 1880.
(19) A. E. Roy, Orbital Motion, 2nd edition (Adam Hilger, Bristol), 1982, p. 257,
(20) F, R, Moukon, An Introduction w Celestial Mechanics, 2nd revised edition (The Macrnillan Co., New York), 1914, p. 352-
(21) C. A. Young, The Sun (Kegan Paul, Trench, Trubner & Co., London), rSSi, p. 32,
(22) B. L. Gumeire St. R. v, d. R. Woolley, Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac, 3rd impression (Her Majesty’s Stationery Office, London), 1974, p. 4^0.
(23) P. K. Seidelmann (ed,), Explanatory Supplement to the Astronomical Almanac (University Science Books, Mill Valley, California)., 1992, p. 696.
(24) R. Grant, History of Physical Astronomy (Henry G. Bohn, London), 1852, p. 123.
(25) A. M. Clerke, A Popular History of Astronomy during the Nineteenth Century (Adam & Charles Black, Edinburgh), 1885, p. 359.
(26) G. H. Darwin, Phil, Tram. Roy, Soc,, 170, 447, 1879.
(27) J, H, Jeans, Problems of Cosmogony and Stellar Dynamics (Cambridge University Press), 1919.
(28) A. B. Binder, in W. K, Hanmann, R. J. Phillips & G. J. Taylor (eds,), Origin of the Moon (Lunar and Planetary Institutes Houston), 1986, p. 499.
(29) J. A. Wood, in W. K. Hflrtmann, R. J. Phillips & G- J. Taylor (eds,), Origin of the Moon (Lunar and Plane rary Institute, Houston), 1986, p. 19.
(30) E. Halley, Phil. Tram., 17, 913, 1693.
(31) O. Fisher, Nature, 25, 243, 1882.
(32) W. H. Pickering, The Moon: A Summary of the Existing Knowledge of our Satellite (Doublcday Page and Co., New York), 1903, p. 103.
(33) F. R. Moulton, ApJ, 29, 1, 1909.
(34) T. J. J. See, J. Brit. Astr, Assoc, 25, 282, 1915.
(35) S. G. Brush, Nebulous Earth: The (Origin of the Solar System and the Gore of the Earth from Laplace to Jeffreys (Cambridge University Press), 1996, p. 31.
(36) W. B. Hubbard, Planetary Inierion (Van Nosirand Rettihold Co,, New York), 1984, p. T84.
(37) A. Guillemin, La Lune (Hachette, Paris), 1870, p. 189.
(38) J. Nasmyth & J. Carpenter, The Moon, Considered as a Planet, a World, and a Satellita (John Murray, London), 1903, p. 59.
(39) H. C. Urey, The Planets their Origin and Development (Oxford University Press), 1952, p. 204.
(40) H. C. Urey, in Z. Kopal & Z. K. Mikhailov (eds-), The Moon (IAU Symposium 14) (Academic Press), 1962, p, 133.
(41) E. J. Opik, Irish Astr, J., 66, 6c, 1961.
(42) R. M- Canup & K. Righter (eds), Origin of the Earth and Moon (The University of Arizona Press, Tucson), 2000.
Содержание
- – Кто и как измерил массу Луны?
- – Как можно оценить массу звезды?
- – Как найти массу Земли по формуле?
- – В чем особенности Луны?
- – Что видно на земле с Луны?
- – Как люди посчитали массу Земли?
- – Как узнают массу черной дыры?
- – Каким образом можно определить массы небесных тел?
- – Что занимает примерно 40 площади видимой стороны Луны?
- – Как называются низменности на рельефе Луны?
Кто и как измерил массу Луны?
Как измерили
Первым попытался рассчитать массу Луны Ньютон, используя измерения, проведённые во время морских приливов, но получил результат, превышающий истинное значение в два раза. Правильно вычислить массу спутника смогли после того, как Кавендиш экспериментально определил точное значение гравитационной постоянной.
Как можно оценить массу звезды?
Как определяют массу звёзд, планет, комет?
- У звезды выделяют два основных параметра – это температура поверхности (или цвет) и светимость (темп излучения энергии). …
- Если звезда в двойной/тройной системе или в скоплении, то зная параметры орбиты звезд (размер полуоси, период), можно определить массу каждой.
Как найти массу Земли по формуле?
В целом мы будем опираться на второй закон Ньютона F=mg и закон всемирного тяготения F=G*m*M/R^2, где F – сила, с которой Земля притягивает барометр, G – гравитационная постоянная, m – масса барометра, M – искомая масса Земли, R – радиус Земли. В этих обозначениях масса Земли вычисляется по формуле M = g*R^2/G.
В чем особенности Луны?
Луна приблизительно в 3,5 раза меньше Земли. … Луна отличается от других небесных тел огромным количеством кратеров, возникших от столкновения с метеоритами и кометами. Более крупные кратеры появились при прямом попадании космических тел, а мелкие — от обломков, образовавшихся в результате взрывов.
Что видно на земле с Луны?
С Земли на Луне можно увидеть различные селенологические образования — моря, кратеры, горы и горные цепи, разломы, трещины. Морями на Луне называются тёмные области, которые являются относительно ровными участками, покрытыми застывшей лавой.
Как люди посчитали массу Земли?
шариком, Кавендиш сравнил величину этой силы с силой притяжения шарика Землёй и сумел вычислить, во сколько раз масса Земли превышает массу свинцового шара. Таким образом была получена оценка массы Земли (6·10 24 кг) и её ср.
Как узнают массу черной дыры?
Астрономы из США выяснили, что определить массу черной дыры можно по ее взаимосвязи с испускаемым ею светом. Статья ученых с описанием способа опубликована в журнале Science.
Каким образом можно определить массы небесных тел?
Массу небесного тела можно определить: а) из измерений силы тяжести на поверхности данного тела (гравиметрический способ); б) по третьему (уточненному) закону Кеплера; в) из анализа наблюдаемых возмущений, производимых небесным. телом в движениях других небесных тел.
Что занимает примерно 40 площади видимой стороны Луны?
Свыше 40% видимой стороны Луны занимают моря — темные низменные участки, покрытые застывшими лавовыми отложениями.
Как называются низменности на рельефе Луны?
Лунные моря — самые крупные детали лунного рельефа. Это низменности с ровным дном, на котором есть отдельные складки и пики небольших горных вершин, залитых затвердевшей лавой. Она и окрашивает лунные моря в тёмный серовато-коричневатый цвет.
Интересные материалы:
Что надо делать на день рождения домового?
Что надо делать на день рождения умершего?
Что накрыть на стол на день рождения в офисе?
Что не стоит делать в день рождения?
Что нельзя делать в своё день рождения?
Что нужно сделать в день рождения домового?
Что одеть в ресторан на день рождения?
Что означает 3 единицы в дате рождения?
Что означает дата рождения 13 апреля?
Что означают четыре нуля в дате рождения?
|
Фамилия из 6 букв. Используя измерения морских приливов Исаак Ньютон пытался найти соотношение между лунной и солнечной массой, но массу Луны он не измерял. В этом направлении дальше продвинулся Пьер-Симон Лаплас (1749-1827) в основу он взял приливы на обоих равноденствиях и солнцестояниях на четырех основных фазах Луны. В 1861, 1864, 1865 и 1866 годах ученый Финлейсон измерял в Дувре приливы. Точность измерений при помощи измерения только приливных волн привела к результатам, что в 1687-1755 она составляла плюс-минус 50 процентов. Когда ученые начали использовать другие, более точные методы в 1755-1830 годы погрешность уже была плюс-минус 10 процентов. На сегодняшний день погрешность составляет уже плюс-минус 0,0001 процент. Масса Луны составляет 7,3477 на 10 в 22 степени кг, что в 81,3 раза меньше массы нашей планеты Земля автор вопроса выбрал этот ответ лучшим Пашенька 7 лет назад Даже стало интересно, как можно измерить массу планеты, ведь на весы её не положишь и не подвесишь даже. Однако ученым удалось проделать эту работу и мы можем оценить вес и размеры планет с довольно большой точностью. НЬЮТОН Насколько верными были его измерения – это другой вопрос, но первым был НЬЮТОН. Знаете ответ? |
Макеты страниц
В качестве примера того, как определяют массу тел по их ускорениям при взаимодействии, мы найдем массу Лупы по ее взаимодействию с Землей.
О том, что Земля влияет на движение Лупы, известно всем. Все знают, что именно под влиянием Земли Луна движется вокруг Земли по окружности радиусом около 384 000 км.
Обычно считают, что Луна обращается вокруг Земли так, будто центр Земли есть неподвижный центр лунной орбиты. Если бы это было так, то это противоречило бы закону взаимодействия, по которому ускорения получают оба взаимодействующих тела.

Рис. 84

Рис. 85
На самом деле и Луна влияет на Землю, заставляя ее двигаться по окружности и сообщая ей центростремительное ускорение. Но вокруг какого центра?
Астрономические наблюдения показали, что Луна обращается не вокруг центра Земли, а вокруг некоторой точки Р (рис. 84), которая отстоит от центра Земли на 4700 км. (Эта точка находится внутри земного шара.) Вокруг этой же точки Р движется по окружности и центр Земли (рис. 85). Значит, радиусы, соединяющие центры Земли и Луны с точкой Р, движутся с одинаковой угловой скоростью вокруг точки Р. Центр Земли движется по окружности радиусом 





Но отношение ускорении взаимодействующих тел равно, как мы знаем, обратному отношению их масс, поэтому

Так как 


Следовательно, масса Луны в 81 раз меньше массы Земли. Если бы была известна масса Земли, то можно было бы определить массу Луны. Масса Земли действительно была определена (см. гл. 6). Она оказалась равной 


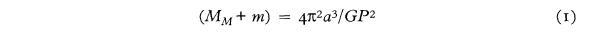
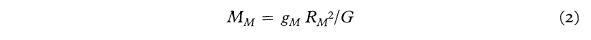
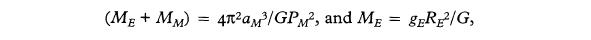

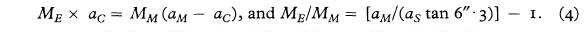
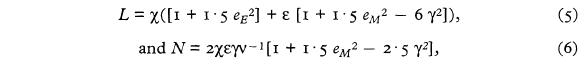
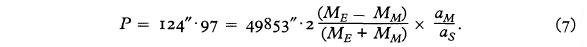
.JPG)


