Содержание
- Как нашли массу планеты земли
- Что такое масса планеты Земля?
- Как нашли массу планеты Земля?
- Результаты
- Как нашли массу планеты земли
- Краткий обзор
- Астрометрия
- Спектроскопия
- Конечные мысли
- Как нашли массу планеты земли
- Как работает поиск землеподобных планет
- В каких местах искали землеподобные планеты
- Что такое масса планеты земли
- Как нашли массу планеты земли
- Влияние массы планеты на жизнь
- Общий итог
Как нашли массу планеты земли
Человечество всегда было обращено к глубинам космоса, интересовалось самыми разнообразными явлениями и встречался с тайнами, которые оставались неизвестными веками. Одной из них была и поиск экзопланет — планет, находящихся за пределами нашей Солнечной системы. Масса планеты Земля всегда была в центре внимания ученых и фанатов космоса. Но как эту массу нашли и что она означает? В этой статье мы разберем все в деталях.
Что такое масса планеты Земля?
Масса Земли — это физическая величина, отражающая количество вещества, из которого состоит планета Земля. Массу Земли можно измерить в килограммах и её значение равно примерно 5,97 * 10^24 кг.

Масса планеты Земля имеет огромное значение в науке и космических исследованиях. Наши существование на этой планете обусловлены многими факторами, и одним из самых важных является её масса. Она влияет на гравитацию Земли и определяет условия для существования нашей атмосферы.
Как нашли массу планеты Земля?

Первые оценки массы Земли были сделаны в 17-18 веках, когда ученые начали изучать гравитационное взаимодействие Земли и Луны. Они использовали законы Ньютона и Сейделя для определения массы Земли, используя данные о гравитационном притяжении Земли и Луны друг к другу.
Однако, точные измерения массы планеты пришли намного позже. С появлением космических технологий в 20 веке стало возможным изучение гравитационного поля Земли с более высокой точностью. С помощью спутников и других средств ученые стали проводить гравиметрические измерения гравитационного поля Земли, чтобы более точно определить её массу.
В 1970-х годах был разработан метод лазерного дальномера, который позволял получать точные измерения расстояний между Землей и луной. Этот метод дал возможность точно измерять изменение расстояния между Землей и Луной, вызванное притяжением Земли. Это, в свою очередь, позволило измерить гравитационное поле Земли и, в конечном итоге, её массу. Именно с помощью этого метода была создана самая точная оценка массы Земли, которая составляет 5,9722 * 10^24 кг.
Результаты
Определение массы Земли было крайне важным достижением науки и космических исследований. Только точное значение массы планеты может дать ученым возможность изучать ее взаимодействие с другими планетами, а также давать возможность оценивать ее влияние на жизнь на Земле. Методы и инструменты проведения измерений массы Земли продолжают улучшаться, и в будущем мы можем ждать более точных и интересных открытий в этой области науки.
Как нашли массу планеты земли
Вселенная — это одна из самых загадочных и таинственных вещей в нашей жизни. Мы изучаем ее уже столетиями, но до сих пор не знаем многих вещей. Одна из таких вещей — это поиск жизни на других планетах в галактике. На протяжении многих лет астрономы и исследователи совершали массу открытий в этой области, но одной из самых важных является нахождение планет, которые могут подобраться к Земле. Но как они это делали?
Краткий обзор
Перед началом мысли о том, как именно нашли массу планет Земли, нужно понимать, что нашли их довольно давно, около полутора века назад. Наши научные инструменты необходимо было развивать и изменять, чтобы улучшить качество фотографий и измерений для открытий.
Первый метод, который использовали ученые, — это было наблюдение за звездами. Они смотрели на транзиты, которые появляются, когда планета проходит перед своей звездой и затем исчезает. Эти транзиты заставили их наблюдать за звездами дольше, что позволяло понимать, как движется звезда на небесной сфере.
Эти наблюдения также помогали исследователям изучить пространственные входы нашей галактики и обнаружить множество возможных планет, которые могут существовать в зоне жизни. После того, как ученые обнаружили позицию на звездном небе, они могли использовать более точные инструменты, чтобы уточнить их расстояние и скорость.
Астрометрия
Астрометрия — это исследование звездного неба и движения звезд. При помощи тех же инструментов, которые мы используем для измерения расстояния до звезды, можно определить гравитационное воздействие планеты на ту же звезду и измерить ее движение. Ученые могли наблюдать изменения в положении звезды на небосводе, когда ее гравитационное воздействие скрывает планеты.
Проблема состояла в том, что астрометрию было очень сложно применять в условиях, которые могли бы познакомить нас с планетами, поскольку эффект, который они оказывают на звезды, настолько слабый.
Спектроскопия
Спектроскопия — это метод изучения света, сочетающий в себе оптику и химию. Используя спектроскопы, астрономы могут изучать свет, который излучает звезда, и определить его состав. Они также могут изучать дополнительные признаки, такие как скорость, с которой движется звезда, и ее перемещение в отношении нас.

Этот метод делает возможным обнаружение планет, которые вращаются вокруг звезды, заставляя ее <<качаться>> слева направо и обратно, поскольку гравитационное воздействие планет оказывает действие на звезду, которое проявляется на спектре. Используя спектроскопические данные для анализа изменений в этом сигнале, ученые могут определить существование планеты и ее массу.
Конечные мысли

Таким образом, наши исследователи используют различные методы, чтобы обнаружить нам наиболее сильно напоминающую Землю планету. Они следят за движением звезд на небосклоне, замеряют скорость звезды, а также используют спектроскопию, чтобы исследовать луч света, который излучает звезда, и получить информацию о возможных планетах.
Поиск «планет-близнецов» продолжается, и нам предстоит провести еще много работ, чтобы найти подходящую планету, но пока любые результаты, которые мы получаем, позволяют нам приблизиться в качественном плане к цели.
- Наблюдение за звездами — это первый и самый важный метод, который использовали ученые.
- Астрометрия — это исследование звездного неба и движения звезд на небосклоне.
- Спектроскопия — это метод изучения света, исследование состава звезды и ее движение.
Главной причиной, по которой мы ищем другие планеты, является наше желание узнать, существует ли другое разумное существо на другой планете во вселенной.
Как нашли массу планеты земли

В поисках второй Земли, люди долгие годы искали другие планеты, на которых можно было бы жить. Именно благодаря массе планеты земли мы можем определить, может ли на ней существовать жизнь.
Как работает поиск землеподобных планет

В настоящее время наша технология позволяет обнаруживать планеты, которые сходны по размеру с Землей и находятся на таком же расстоянии от своей звезды, что и Земля от Солнца. Это позволяет установить, может ли на такой планете существовать жизнь.
Один из методов обнаружения землеподобных планет — это использование телескопов для поиска затенения звезды на фоне которой находится исследуемая планета.
В каких местах искали землеподобные планеты
В первую очередь, исследования проводились на планетах, находящихся внутри Солнечной системы. Но технологии позволяют нам искать планеты и за пределами нашей системы. Например, наш спутник Луну уже исследовали и получили ценные данные для будущих миссий.
Также были созданы космические аппараты, которые отправлялись на расследование околоземных космических объектов. Это позволяло проводить более точные измерения физических параметров и химических соединений.
Что такое масса планеты земли
Масса планеты земли — это ее вес. Она измеряется в килограммах и описывает значение массы всех материальных объектов, находящихся на нашей планете. Чтобы определить, может ли на планете существовать жизнь, необходимо знать ее массу. Таким образом, от массы планеты зависит ее плотность, а следовательно и гравитация, а также атмосфера на поверхности планеты.
Как нашли массу планеты земли
Чтобы определить массу планеты земли, необходимо провести ее измерение. Для этого используется гравитационное притяжение. Метод позволяет с высокой точностью определять массу планет.
Например, если взвеситься на другой планете, то вес будет значительно различаться по сравнению с Землей. Это объясняется различием в гравитации, которая зависит от массы планеты. Таким образом, для определения массы планеты земли необходимо знать ее гравитацию.
Влияние массы планеты на жизнь
Масса планеты имеет огромное влияние на возможность существования на ней жизни. Например, если масса планеты будет слишком мала, то на ней не будет достаточного количества атмосферы, необходимого для сущестования жизни. С другой стороны, если масса планеты будет слишком большой, то ее гравитация будет настолько сильной, что жизнь на ней будет затруднительна.
Также масса планеты влияет на формирование ее физических свойств. Например, на планете с большой массой могут образовываться горы и океаны, что изменит ситуацию с жизнью на такой планете.
Общий итог
Наше понимание массы планеты земли является ключевым фактором в поисках землеподобных планет и в исследовании возможности существования на них жизни. Благодаря технологическим достижениям людей, мы можем лучше понимать планеты, на которых может существовать жизнь.
- масса планеты: главный параметр при поиске землеподобных планет;
- технологии: позволяют исследовать планеты как внутри, так и за пределами Солнечной системы;
- масса планеты влияет на возможность существования жизни на ней: малая масса — не хватает атмосферы, большая масса — затрудняется жизнь из-за гравитации.
«Исследование планет и поиск землеподобных планет — это невероятный путь по пути познания вселенной»
Массу Земли можно измерить при помощи барометра.
В целом мы будем опираться на второй закон Ньютона F=mg и закон всемирного тяготения F=G*m*M/R^2, где F – сила, с которой Земля притягивает барометр, G – гравитационная постоянная, m – масса барометра, M – искомая масса Земли, R – радиус Земли.
В этих обозначениях масса Земли вычисляется по формуле M = g*R^2/G. Осталось только найти величины в правой части формулы.
Сначала измерим ускорение свободного падения g. Для этого нужно сбросить барометр с высокой башни и засечь время падения. Высоту башни, кстати, тоже можно измерить с помощью барометра, но этот вопрос выходит за рамки лекции.
Следующий шаг – определить радиус Земли R. В день летнего солнцестояния, когда Солнце стоит в зените над тропиком рака, нужно измерить длину тени, которую отбрасывает барометр известной нам высоты, находящийся в Москве. Если мы знаем расстояние от Москвы до тропика, то дальше дело техники вычислить радиус Земли.
Самое сложное – вычислить гравитационную постоянную G. Для этого нам потребуется установка, которая называется крутильные весы. Этот прибор позволяет измерить силу, с которой барометр притягивается к тяжёлому свинцовому шару заранее известной массы.
Если мы нигде не схалтурили, мы должны получить значения ускорения свободного падения g=9.8 м/с^2, радиуса Земли R=6371 км и гравитационной постоянной G = 6.67*10^-11 м^3/(кг*с^2).
Следовательно, масса Земли равна примерно 6*10^24 (6 и 24 нуля) килограмм.
Чтобы найти массу других планет, учёные отправляют на эти планеты космонавтов с барометрами.
Источники:
[1] Опыт Галилея со свободным падением: wikipedia.org
[2] Эратосфен и вычисление радиуса Земли: wikipedia.org
[3] Крутильные весы и опыт Кавендиша: wikipedia.org
[4] Второй закон Ньютона: wikipedia.org
[5] Закон всемирного тяготения: wikipedia.org
[6] Измерение высоты здания с помощью барометра: lyceum1502.ru
3,2 K
И всё же, как можно утверждать, что масса именно равна такой, если Земля имеет вещества с разными массами… Читать дальше
Комментировать ответ…Комментировать…
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 12 августа 2022 года; проверки требуют 6 правок.

Ма́сса Земли́ (в астрономии обозначается M⊕, где ⊕ — символ Земли) — масса планеты Земля, в астрономии используется как внесистемная единица массы. 1 M⊕ = (5,9722 ± 0,0006) × 1024 кг[1].
Три других планеты земной группы — Меркурий, Венера и Марс — имеют массу 0,055 M⊕, 0,815 M⊕ и 0,107 M⊕ соответственно.
По сравнению с массой других небесных тел масса Земли составляет:
- 81,3 масс Луны;
- 0,00315 массы Юпитера (масса Юпитера составляет 317,83 M⊕)[2];
- 0,0105 массы Сатурна (масса Сатурна составляет 95,16 M⊕)[3];
- 0,0583 массы Нептуна (масса Нептуна составляет 17,147 M⊕)[4];
- 0,00000300349 массы Солнца (масса Солнца составляет 332946 M⊕).
Формула для определения массы Земли[править | править код]
Согласно закону всемирного притяжения Ньютона сила притяжения между двумя телами:

здесь M — масса земли, m — масса произвольного тела на поверхности Земли, R — расстояние между центрами масс (в данном случае это радиус Земли), G — гравитационная постоянная.
С другой же стороны сила тяжести (притяжения тела к Земле) равна:

m — масса произвольного тела на поверхности Земли, g — ускорение свободного падения.
Поскольку силы одинаковы, то получаем:



Изменение массы Земли[править | править код]
Масса Земли не является постоянной величиной, и в настоящее время потеря массы превышает прирост[5]. На величину массы Земли влияют многочисленные факторы.
Факторы, увеличивающие массу Земли:
- Космическая пыль: метеоры, пыль, кометы и т. д., за счёт неё масса Земли возрастает примерно на 40 тысяч тонн в год[6]
Факторы, уменьшающие массу Земли:
- Диссипация атмосферных газов — водорода (3 кг/сек, или 95000 тонн в год[7]) и гелия (1600 тонн в год[8]). Кроме того, часть электронов атомов атмосферных газов улетучивается быстрее, чем сами атомы;
- Искусственные спутники, которые находятся на удалённых орбитах и могут покинуть околоземное пространство (около 65 тонн в год[9]);
- Уменьшение массы Земли приводит к ослаблению её силы тяжести, и, соответственно, способности удерживать атмосферу;
- Нагрев Земли (за счёт как антропогенных процессов, так и глобального потепления) в сочетании с солнечным излучением может увеличить тепловое движение молекул, что также способствует утечке вещества из атмосферы.
См. также[править | править код]
- Эксперимент Кавендиша
Примечания[править | править код]
- ↑ «2016 Selected Astronomical Constants Архивная копия от 15 февраля 2016 на Wayback Machine» // The Astronomical Almanac Online, USNO–UKHO, <http://asa.usno.navy.mil/> Архивная копия от 24 декабря 2016 на Wayback Machine.
- ↑ Williams, Dr. David R. Jupiter Fact Sheet (недоступная ссылка — история). NASA (2 ноября 2007). Дата обращения: 16 июля 2009. Архивировано 5 октября 2011 года.
- ↑ Solar System Exploration: Saturn: Facts & Figures (недоступная ссылка — история). NASA (28 июля 2009). Дата обращения: 20 сентября 2009. Архивировано 6 октября 2011 года.
- ↑ Solar System Exploration: Neptune: Facts & Figures. NASA (5 января 2009). Дата обращения: 20 сентября 2009. Архивировано из оригинала 14 октября 2007 года.
- ↑ Earth Loses 50,000 Tonnes of Mass Every Year (англ.). SciTech Daily (5 февраля 2012). Дата обращения: 11 апреля 2015. Архивировано 28 марта 2015 года.
- ↑ Herbert A. Zook. Spacecraft Measurements of the Cosmic Dust Flux // Accretion of Extraterrestrial Matter Throughout Earth’s History. — Springer, Boston, MA, 2001. — doi:10.1007/978-1-4419-8694-8_5.
- ↑ Science by Pat Murphy & Paul Doherty (англ.). Fantasy & Science Fiction. Дата обращения: 11 апреля 2015. Архивировано 18 января 2015 года.
- ↑ Earth Loses 50,000 Tonnes of Mass Every Year. Дата обращения: 6 июля 2020. Архивировано 21 апреля 2020 года.
- ↑ Saxena, Shivam; Chandra, Mahesh. Loss in Earth Mass due to Extraterrestrial Space Exploration Missions (англ.) // International Journal of Scientific and Research Publications. — 2013. — May (vol. 3, no. 5). — P. 1.
From Wikipedia, the free encyclopedia
| Earth mass | |
|---|---|

19th-century illustration of Archimedes’ quip of “give me a lever long enough and a fulcrum on which to place it, and I will move the earth”[1] |
|
| General information | |
| Unit system | astronomy |
| Unit of | mass |
| Symbol | M⊕ |
| Conversions | |
| 1 M⊕ in … | … is equal to … |
| SI base unit | (5.9722±0.0006)×1024 kg |
| U.S. customary | ≈ 1.3166×1025 pounds |
An Earth mass (denoted as 

The Earth mass is a standard unit of mass in astronomy that is used to indicate the masses of other planets, including rocky terrestrial planets and exoplanets. One Solar mass is close to 333000 Earth masses. The Earth mass excludes the mass of the Moon. The mass of the Moon is about 1.2% of that of the Earth, so that the mass of the Earth+Moon system is close to 6.0456×1024 kg.
Most of the mass is accounted for by iron and oxygen (c. 32% each), magnesium and silicon (c. 15% each), calcium, aluminium and nickel (c. 1.5% each).
Precise measurement of the Earth mass is difficult, as it is equivalent to measuring the gravitational constant, which is the fundamental physical constant known with least accuracy, due to the relative weakness of the gravitational force. The mass of the Earth was first measured with any accuracy (within about 20% of the correct value) in the Schiehallion experiment in the 1770s, and within 1% of the modern value in the Cavendish experiment of 1798.
Unit of mass in astronomy[edit]
The mass of Earth is estimated to be:
,
which can be expressed in terms of solar mass as:
.
The ratio of Earth mass to lunar mass has been measured to great accuracy. The current best estimate is:[4][5]
| Object | Earth mass MEarth | Ref |
|---|---|---|
| Moon | 0.0123000371(4) | [4] |
| Sun | 332946.0487±0.0007 | [2] |
| Mercury | 0.0553 | [6] |
| Venus | 0.815 | [6] |
| Earth | 1 | By definition |
| Mars | 0.107 | [6] |
| Jupiter | 317.8 | [6] |
| Saturn | 95.2 | [6] |
| Uranus | 14.5 | [6] |
| Neptune | 17.1 | [6] |
| Pluto | 0.0025 | [6] |
| Eris | 0.0027 | |
| Gliese 667 Cc | 3.8 | [7] |
| Kepler-442b | 1.0 – 8.2 | [8] |
The GMEarth product for the Earth is called the geocentric gravitational constant and equals (398600441.8±0.8)×106 m3 s−2. It is determined using laser ranging data from Earth-orbiting satellites, such as LAGEOS-1.[9][10] The GMEarth product can also be calculated by observing the motion of the Moon[11] or the period of a pendulum at various elevations. These methods are less precise than observations of artificial satellites.
The relative uncertainty of the geocentric gravitational constant is just 2×10−9, i.e. 50000 times smaller than the relative uncertainty for MEarth itself. MEarth can be found out only by dividing the GMEarth product by G, and G is known only to a relative uncertainty of 4.6×10−5 (2014 NIST recommended value), so MEarth will have the same uncertainty at best. For this reason and others, astronomers prefer to use the un-reduced GMEarth product, or mass ratios (masses expressed in units of Earth mass or Solar mass) rather than mass in kilograms when referencing and comparing planetary objects.
Composition[edit]
Earth’s density varies considerably, between less than 2700 kg/m3 in the upper crust to as much as 13000 kg/m3 in the inner core.[12] The Earth’s core accounts for 15% of Earth’s volume but more than 30% of the mass, the mantle for 84% of the volume and close to 70% of the mass, while the crust accounts for less than 1% of the mass.[12] About 90% of the mass of the Earth is composed of the iron–nickel alloy (95% iron) in the core (30%), and the silicon dioxides (c. 33%) and magnesium oxide (c. 27%) in the mantle and crust. Minor contributions are from iron(II) oxide (5%), aluminium oxide (3%) and calcium oxide (2%),[13] besides numerous trace elements (in elementary terms: iron and oxygen c. 32% each, magnesium and silicon c. 15% each, calcium, aluminium and nickel c. 1.5% each). Carbon accounts for 0.03%, water for 0.02%, and the atmosphere for about one part per million.[14]
History of measurement[edit]

Pendulums used in Mendenhall gravimeter apparatus, from 1897 scientific journal. The portable gravimeter developed in 1890 by Thomas C. Mendenhall provided the most accurate relative measurements of the local gravitational field of the Earth.
The mass of Earth is measured indirectly by determining other quantities such as Earth’s density, gravity, or gravitational constant. The first measurement in the 1770s Schiehallion experiment resulted in a value about 20% too low. The Cavendish experiment of 1798 found the correct value within 1%. Uncertainty was reduced to about 0.2% by the 1890s,[15] to 0.1% by 1930.[16]
The figure of the Earth has been known to better than four significant digits since the 1960s (WGS66), so that since that time, the uncertainty of the Earth mass is determined essentially by the uncertainty in measuring the gravitational constant. Relative uncertainty was cited at 0.06% in the 1970s,[17] and at 0.01% (10−4) by the 2000s. The current relative uncertainty of 10−4 amounts to 6×1020 kg in absolute terms, of the order of the mass of a minor planet (70% of the mass of Ceres).
Early estimates[edit]
Before the direct measurement of the gravitational constant, estimates of the Earth mass were limited to estimating Earth’s mean density from observation of the crust and estimates on Earth’s volume. Estimates on the volume of the Earth in the 17th century were based on a circumference estimate of 60 miles (97 km) to the degree of latitude, corresponding to a radius of 5,500 km (86% of the Earth’s actual radius of about 6,371 km), resulting in an estimated volume of about one third smaller than the correct value.[18]
The average density of the Earth was not accurately known. Earth was assumed to consist either mostly of water (Neptunism) or mostly of igneous rock (Plutonism), both suggesting average densities far too low, consistent with a total mass of the order of 1024 kg. Isaac Newton estimated, without access to reliable measurement, that the density of Earth would be five or six times as great as the density of water,[19] which is surprisingly accurate (the modern value is 5.515). Newton under-estimated the Earth’s volume by about 30%, so that his estimate would be roughly equivalent to (4.2±0.5)×1024 kg.
In the 18th century, knowledge of Newton’s law of universal gravitation permitted indirect estimates on the mean density of the Earth, via estimates of (what in modern terminology is known as) the gravitational constant. Early estimates on the mean density of the Earth were made by observing the slight deflection of a pendulum near a mountain, as in the Schiehallion experiment. Newton considered the experiment in Principia, but pessimistically concluded that the effect would be too small to be measurable.
An expedition from 1737 to 1740 by Pierre Bouguer and Charles Marie de La Condamine attempted to determine the density of Earth by measuring the period of a pendulum (and therefore the strength of gravity) as a function of elevation. The experiments were carried out in Ecuador and Peru, on Pichincha Volcano and mount Chimborazo.[20] Bouguer wrote in a 1749 paper that they had been able to detect a deflection of 8 seconds of arc, the accuracy was not enough for a definite estimate on the mean density of the Earth, but Bouguer stated that it was at least sufficient to prove that the Earth was not hollow.[15]
Schiehallion experiment[edit]
That a further attempt should be made on the experiment was proposed to the Royal Society in 1772 by Nevil Maskelyne, Astronomer Royal.[21] He suggested that the experiment would “do honour to the nation where it was made” and proposed Whernside in Yorkshire, or the Blencathra-Skiddaw massif in Cumberland as suitable targets. The Royal Society formed the Committee of Attraction to consider the matter, appointing Maskelyne, Joseph Banks and Benjamin Franklin amongst its members.[22] The Committee despatched the astronomer and surveyor Charles Mason to find a suitable mountain.
After a lengthy search over the summer of 1773, Mason reported that the best candidate was Schiehallion, a peak in the central Scottish Highlands.[22] The mountain stood in isolation from any nearby hills, which would reduce their gravitational influence, and its symmetrical east–west ridge would simplify the calculations. Its steep northern and southern slopes would allow the experiment to be sited close to its centre of mass, maximising the deflection effect. Nevil Maskelyne, Charles Hutton and Reuben Burrow performed the experiment, completed by 1776. Hutton (1778) reported that the mean density of the Earth was estimated at 
Cavendish experiment[edit]
Henry Cavendish (1798) was the first to attempt to measure the gravitational attraction between two bodies directly in the laboratory. Earth’s mass could be then found by combining two equations; Newton’s second law, and Newton’s law of universal gravitation.
In modern notation, the mass of the Earth is derived from the gravitational constant and the mean Earth radius by
Where gravity of Earth, “little g”, is
.
Cavendish found a mean density of 5.45 g/cm3, about 1% below the modern value.
19th century[edit]

While the mass of the Earth is implied by stating the Earth’s radius and density, it was not usual to state the absolute mass explicitly prior to the introduction of scientific notation using powers of 10 in the later 19th century, because the absolute numbers would have been too awkward. Ritchie (1850) gives the mass of the Earth’s atmosphere as “11,456,688,186,392,473,000 lbs.” (1.1×1019 lb = 5.0×1018 kg, modern value is 5.15×1018 kg) and states that “compared with the weight of the globe this mighty sum dwindles to insignificance”.[25]
Absolute figures for the mass of the Earth are cited only beginning in the second half of the 19th century, mostly in popular rather than expert literature. An early such figure was given as “14 septillion pounds” (14 Quadrillionen Pfund) [6.5×1024 kg] in Masius (1859). [26] Beckett (1871) cites the “weight of the earth” as “5842 quintillion tons” [5.936×1024 kg].[27] The “mass of the earth in gravitational measure” is stated as “9.81996×63709802” in The New Volumes of the Encyclopaedia Britannica (Vol. 25, 1902) with a “logarithm of earth’s mass” given as “14.600522” [3.98586×1014]. This is the gravitational parameter in m3·s−2 (modern value 3.98600×1014) and not the absolute mass.
Experiments involving pendulums continued to be performed in the first half of the 19th century. By the second half of the century, these were outperformed by repetitions of the Cavendish experiment, and the modern value of G (and hence, of the Earth mass) is still derived from high-precision repetitions of the Cavendish experiment.
In 1821, Francesco Carlini determined a density value of ρ=4.39 g/cm3 through measurements made with pendulums in the Milan area. This value was refined in 1827 by Edward Sabine to 4.77 g/cm3, and then in 1841 by Carlo Ignazio Giulio to 4.95 g/cm3. On the other hand, George Biddell Airy sought to determine ρ by measuring the difference in the period of a pendulum between the surface and the bottom of a mine.[28]
The first tests and experiments took place in Cornwall between 1826 and 1828. The experiment was a failure due to a fire and a flood. Finally, in 1854, Airy got the value 6.6 g/cm3 by measurements in a coal mine in Harton, Sunderland. Airy’s method assumed that the Earth had a spherical stratification. Later, in 1883, the experiments conducted by Robert von Sterneck (1839 to 1910) at different depths in mines of Saxony and Bohemia provided the average density values ρ between 5.0 and 6.3 g/cm3. This led to the concept of isostasy, which limits the ability to accurately measure ρ, by either the deviation from vertical of a plumb line or using pendulums. Despite the little chance of an accurate estimate of the average density of the Earth in this way, Thomas Corwin Mendenhall in 1880 realized a gravimetry experiment in Tokyo and at the top of Mount Fuji. The result was ρ = 5.77 g/cm3.[citation needed]
Modern value[edit]
The uncertainty in the modern value for the Earth’s mass has been entirely due to the uncertainty in the gravitational constant G since at least the 1960s.[29] G is notoriously difficult to measure, and some high-precision measurements during the 1980s to 2010s have yielded mutually exclusive results.[30] Sagitov (1969) based on the measurement of G by Heyl and Chrzanowski (1942) cited a value of MEarth = 5.973(3)×1024 kg (relative uncertainty 5×10−4).
Accuracy has improved only slightly since then. Most modern measurements are repetitions of the Cavendish experiment, with results (within standard uncertainty) ranging between 6.672 and 6.676 ×10−11 m3 / kg / s2 (relative uncertainty 3×10−4) in results reported since the 1980s, although the 2014 NIST recommended value is close to 6.674×10−11 m3 / kg / s2 with a relative uncertainty below 10−4. The Astronomical Almanach Online as of 2016 recommends a standard uncertainty of 1×10−4 for Earth mass, MEarth 5.9722(6)×1024 kg[2]
Variation[edit]
Earth’s mass is variable, subject to both gain and loss due to the accretion of in-falling material, including micrometeorites and cosmic dust and the loss of hydrogen and helium gas, respectively. The combined effect is a net loss of material, estimated at 5.5×107 kg (5.4×104 long tons) per year. This amount is 10−17 of the total earth mass.[citation needed] The 5.5×107 kg annual net loss is essentially due to 100,000 tons lost due to atmospheric escape, and an average of 45,000 tons gained from in-falling dust and meteorites. This is well within the mass uncertainty of 0.01% (6×1020 kg), so the estimated value of Earth’s mass is unaffected by this factor.
Mass loss is due to atmospheric escape of gases. About 95,000 tons of hydrogen per year[31] (3 kg/s) and 1,600 tons of helium per year[32] are lost through atmospheric escape. The main factor in mass gain is in-falling material, cosmic dust, meteors, etc. are the most significant contributors to Earth’s increase in mass. The sum of material is estimated to be 37000 to 78000 tons annually,[33][34] although this can vary significantly; to take an extreme example, the Chicxulub impactor, with a midpoint mass estimate of 2.3×1017 kg,[35] added 900 million times that annual dustfall amount to the Earth’s mass in a single event.
Additional changes in mass are due to the mass–energy equivalence principle, although these changes are relatively negligible. Mass loss due to the combination of nuclear fission and natural radioactive decay is estimated to amount to 16 tons per year.[citation needed]
An additional loss due to spacecraft on escape trajectories has been estimated at 65 tons per year since the mid-20th century. Earth lost about 3473 tons in the initial 53 years of the space age, but the trend is currently decreasing.[citation needed]
See also[edit]
- Abundance of elements in Earth’s crust
- Cavendish experiment
- Earth radius
- Gravitational constant
- Orders of magnitude (mass)
- Planetary mass
- Schiehallion experiment
- Solar mass
- Internal structure of Earth
References[edit]
- ^ Attributed by Pappus of Alexandria (Synagoge [Συναγωγή] VIII, 4th century), as « Δός μοί ποῦ στῶ, καὶ κινῶ τὴν Γῆν ». Engraving from Mechanic’s Magazine (cover of bound Volume II, Knight & Lacey, London, 1824).
- ^ a b c The cited value is the recommended value published by the International Astronomical Union in 2009 (see 2016 “Selected Astronomical Constants” in “The Astronomical Almanac Online”. USNO/UKHO.).
- ^ Lawler, Daniel. “Earth now weighs six ronnagrams: New metric prefixes voted in”. phys.org. Retrieved 21 November 2022.
- ^ a b Pitjeva, E.V.; Standish, E.M. (1 April 2009). “Proposals for the masses of the three largest asteroids, the Moon-Earth mass ratio and the Astronomical Unit”. Celestial Mechanics and Dynamical Astronomy. 103 (4): 365–372. Bibcode:2009CeMDA.103..365P. doi:10.1007/s10569-009-9203-8. S2CID 121374703.
- ^ Luzum, Brian; Capitaine, Nicole; Fienga, Agnès; et al. (10 July 2011). “The IAU 2009 system of astronomical constants: the report of the IAU working group on numerical standards for Fundamental Astronomy”. Celestial Mechanics and Dynamical Astronomy. 110 (4): 293–304. Bibcode:2011CeMDA.110..293L. doi:10.1007/s10569-011-9352-4.
- ^ a b c d e f g h “Planetary Fact Sheet – Ratio to Earth”. nssdc.gsfc.nasa.gov. Retrieved 12 February 2016.
- ^ “The Habitable Exoplanets Catalog”. Planetary Habitability Laboratory @ UPR Arecibo.
- ^ “HEC: Data of Potential Habitable Worlds”.
- ^ Ries, J.C.; Eanes, R.J.; Shum, C.K.; Watkins, M.M. (20 March 1992). “Progress in the determination of the gravitational coefficient of the Earth”. Geophysical Research Letters. 19 (6): 529. Bibcode:1992GeoRL..19..529R. doi:10.1029/92GL00259.
- ^ Lerch, Francis J.; Laubscher, Roy E.; Klosko, Steven M.; Smith, David E.; Kolenkiewicz, Ronald; Putney, Barbara H.; Marsh, James G.; Brownd, Joseph E. (December 1978). “Determination of the geocentric gravitational constant from laser ranging on near-Earth satellites”. Geophysical Research Letters. 5 (12): 1031–1034. Bibcode:1978GeoRL…5.1031L. doi:10.1029/GL005i012p01031.
- ^ Shuch, H. Paul (July 1991). “Measuring the mass of the earth: the ultimate moonbounce experiment” (PDF). Proceedings, 25th Conference of the Central States VHF Society: 25–30. Retrieved 28 February 2016.
- ^ a b See structure of the Earth: inner core volume 0.7%, density 12,600–13,000, mass c. 1.6%; outer core vol. 14.4%, density 9,900–12,200 mass c. 28.7–31.7%. Hazlett, James S.; Monroe, Reed; Wicander, Richard (2006). Physical Geology: Exploring the Earth (6. ed.). Belmont: Thomson. p. 346.
- ^ Jackson, Ian (1998). The Earth’s Mantle – Composition, Structure, and Evolution. Cambridge University Press. pp. 311–378.
- ^ The hydrosphere (Earth’s oceans) account for about 0.02% 2.3×10−4 of total mass, Carbon for about 0.03% of the crust, or 3×10−6 of total mass, Earth’s atmosphere for about 8.6×10−7 of total mass. Biomass is estimated at 10−10 (5.5×1014 kg, see Bar-On, Yinon M.; Phillips, Rob; Milo, Ron. “The biomass distribution on Earth” Proc. Natl. Acad. Sci. USA., 2018).
- ^ a b Poynting, J.H. (1913). The Earth: its shape, size, weight and spin. Cambridge. pp. 50–56.
- ^ P. R. Heyl, A redetermination of the constant of gravitation, National Bureau of Standards Journal of Research 5 (1930), 1243–1290.
- ^ IAU (1976) System of Astronomical Constants
- ^ Mackenzie, A. Stanley, The laws of gravitation; memoirs by Newton, Bouguer and Cavendish, together with abstracts of other important memoirs, American Book Company (1900 [1899]), p. 2.
- ^ “Sir Isaac Newton thought it probable, that the mean density of the earth might be five or six times as great as the density of water; and we have now found, by experiment, that it is very little less than what he had thought it to be: so much justness was even in the surmises of this wonderful man!” Hutton (1778), p. 783
- ^ Ferreiro, Larrie (2011). Measure of the Earth: The Enlightenment Expedition that Reshaped Our World. New York: Basic Books. ISBN 978-0-465-01723-2.
- ^ Maskelyne, N. (1772). “A proposal for measuring the attraction of some hill in this Kingdom”. Philosophical Transactions of the Royal Society. 65: 495–499. Bibcode:1775RSPT…65..495M. doi:10.1098/rstl.1775.0049.
- ^ a b Danson, Edwin (2006). Weighing the World. Oxford University Press. pp. 115–116. ISBN 978-0-19-518169-2.
- ^ a b Hutton, C. (1778). “An Account of the Calculations Made from the Survey and Measures Taken at Schehallien”. Philosophical Transactions of the Royal Society. 68: 689–788. doi:10.1098/rstl.1778.0034.
- ^ Hutton (1778), p. 783.
- ^ Archibald Tucker Ritchie, The Dynamical Theory of the Formation of the Earth vol. 2 (1850), Longman, Brown, Green and Longmans, 1850, p. 280.
- ^ J.G.Mädler in: Masius, Hermann, Die gesammten Naturwissenschaften, vol. 3 (1859), p. 562.
- ^ Edmund Beckett Baron Grimthorpe, Astronomy Without Mathematics (1871), p. 254. Max Eyth, Der Kampf um die Cheopspyramide: Erster Band (1906), p. 417 cites the “weight of the globe” (Das Gewicht des Erdballs) as “5273 quintillion tons”.
- ^ Poynting, John Henry (1894). The Mean Density of the Earth. London: Charles Griffin. pp. 22–24.
- ^ “Since the geocentric gravitational constant […] is now determined to a relative accuracy of 10−6, our knowledge of the mass of the earth is entirely limited by the low accuracy of our knowledge of the Cavendish gravitational constant.” Sagitov (1970 [1969]), p. 718.
- ^ Schlamminger, Stephan (18 June 2014). “Fundamental constants: A cool way to measure big G”. Nature. 510 (7506): 478–480. Bibcode:2014Natur.510..478S. doi:10.1038/nature13507. PMID 24965646. S2CID 4396011.
- ^ “Fantasy and Science Fiction: Science by Pat Murphy & Paul Doherty”.
- ^ “Earth Loses 50,000 Tonnes of Mass Every Year”. SciTech Daily. 5 February 2012.
- ^ Zook, Herbert A. (2001), “Spacecraft Measurements of the Cosmic Dust Flux”, Accretion of Extraterrestrial Matter Throughout Earth’s History, pp. 75–92, doi:10.1007/978-1-4419-8694-8_5, ISBN 978-1-4613-4668-5
- ^ Carter, Lynn. “How many meteorites hit Earth each year?”. Ask an Astronomer. The Curious Team, Cornell University. Retrieved 6 February 2016.
- ^ Durand-Manterola, H. J.; Cordero-Tercero, G. (2014). “Assessments of the energy, mass and size of the Chicxulub Impactor”. arXiv:1403.6391 [astro-ph.EP].
Характеристики планет Солнечной системы были известны еще в средневековье, во времена Кеплера и Галилея. То есть, массу планет приблизительно можно было определить даже простыми методами и инструментами. В современной астрономии есть несколько методов расчета характеристик планет, звезд, скоплений и галактик.
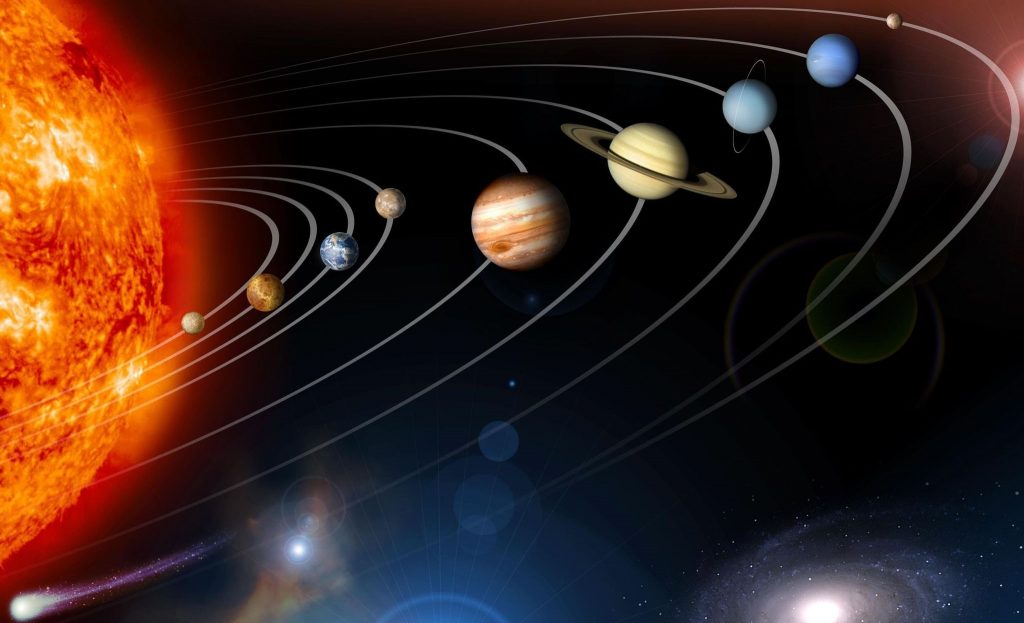
Планеты солнечной системы
Интересный факт: 99,9% всей массы Солнечной системы сосредоточена в самом Солнце. На все планеты вместе взятые приходится не более 0,01%. При этом из этих 0,01%, в свою очередь, 99% массы приходится на газовые гиганты (в том числе 90% только на Юпитер и Сатурн).
Содержание:
- 1 Рассчитываем массу Земли и Луны
- 2 Общие методики определения масс планет
- 3 Значения масс планет Солнечной системы
- 4 Определение масс звезд и галактик
Рассчитываем массу Земли и Луны
Чтобы измерить массу планет солнечной системы, проще всего в первую очередь найти значения для Земли. Как мы помним, ускорение свободного падения определяется по формуле F=mg, где m – масса тела, а F – действующая на него сила.
Параллельно вспоминаем универсальный закон всемирного тяготения Ньютона:

Сопоставив эти две формулы, и зная значение гравитационной постоянной 6,67430(15)·10−11 м³/(кг·с²), можно рассчитать массу Земли. Ускорение свободного падения на Земле мы знаем, 9,8 м/с2, радиус планеты тоже. Подставив все данные на выходе получим приблизительно 5,97 х 10²⁴ кг.

Земля и луна
Зная массу Земли, мы легко рассчитает параметры по другим объектам Солнечной системы – Луна, планеты, Солнце и так далее. С Луной вообще все довольно просто. Здесь достаточно учесть, что расстояния от центров тел до центра масс соотносятся обратно их массам. Подставив эти цифры для Земли и ее спутника получим массу Луны 7.36 × 10²² килограмма.
Перейдем теперь к методикам измерения массы планет земной группы – Меркурий, Венера, Марс. После чего рассмотрим газовые гиганты, и в самом конце – экзопланеты, звезды и галактики.
Общие методики определения масс планет
Наиболее классический способ, как узнать массу планет – расчет при помощи формул третьего закона Кеплера. Он гласит, что квадраты периодов обращения планет соотносятся так же, как кубы больших полуосей орбит. Ньютон немного уточнил этот закон, внеся в формулу массы небесных тел. На выходе получилась такая формула –
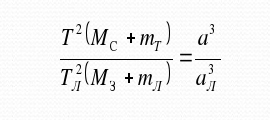
Таким способом можно найти массу всех планет Солнечной системы и самого Солнца.И периоды обращения, и большие полуоси орбит планет Солнечной системы легко измеряются астрономическими методиками, доступными даже без сложных инструментов. А так как массу Земли мы уже рассчитали, можно все цифры подставить в формулу и найти конечный результат.
В отношении же экзопланет и других звезд (но только двойных) в астрономии обычно применяется метод анализа видимых возмущений и колебаний. Он основан на том факте, что все массивные тела “возмущают” орбиты друг друга.
Такими расчетами были открыты планеты Нептун и Плутон, еще до их визуального обнаружения, как говорят “на кончике пера”.
Значения масс планет Солнечной системы
Итак, мы разобрались с общими методиками расчета масс разных небесных тел и посчитали значения для Луны, Земли и Галактики. Давайте теперь составим рейтинг планет нашей системы по их массе.
Возглавляет рейтинг с наибольшей массой планет Солнечной системы – Юпитер, которому не хватило одного порядка чтобы наша система стала двойной. Еще чуть-чуть и у нас могло быть два Солнца, второе вместо Юпитера. Итак, масса этого газового гиганта равняется 1,9 × 10²⁷ кг.
Интересно, что Юпитер – единственная планета нашей системы, центр масс вращения с Солнцем которой расположен вне поверхности звезды. Он отстоит примерно на 7% расстояния между ними от поверхности Солнца.
Вторая по массе планета – Сатурн, его масса 5,7 × 10²⁶ кг. Следующим идет Нептун – 1 × 10²⁶. Четвёртая по массе планета, газовый гигант Уран, масса которого – 8,7 × 10²⁵ кг.
Далее идут планеты земной группы, каменистые тела, в отличие от газовых гигантов с их большим радиусом и относительно малой плотностью.
 Самой тяжелой из этой группы является наша планета, ее массу мы уже рассчитали. Далее идет Венера, масса этой планеты равняется 4,9 × 10²⁴ кг. После нее в рейтинге идет Марс, он почти в 10 раз легче – 6,4 × 10²³кг. И замыкает его, как планета самой маленькой массы, Меркурий – 3,3 × 10²³кг. Что интересно, Меркурий даже легче, чем два спутника в Солнечной системе – Ганимед и Каллисто.
Самой тяжелой из этой группы является наша планета, ее массу мы уже рассчитали. Далее идет Венера, масса этой планеты равняется 4,9 × 10²⁴ кг. После нее в рейтинге идет Марс, он почти в 10 раз легче – 6,4 × 10²³кг. И замыкает его, как планета самой маленькой массы, Меркурий – 3,3 × 10²³кг. Что интересно, Меркурий даже легче, чем два спутника в Солнечной системе – Ганимед и Каллисто.
Определение масс звезд и галактик
Для того чтобы найти характеристики одинарных звездных систем применяется гравиметрический метод. Его суть в измерении гравитационного красного смещения света звезды. Оно измеряется по формуле ∆V=0,635 M/R, где M и R – масса и радиус звезды, соответственно.
Косвенно можно также вычислить массу звезды по видимому спектру и светимости. Сначала определяется ее класс светимости по диаграмме Герцшпрунга-Рассела, а потом вычисляется зависимость масса/светимость. Такой способ не подходит для белых карликов и нейтронных звезд.
Масса галактик вычисляется в основном по скорости вращения ее звезд (или просто по относительной скорости звезд, если это не спиральная галактика). Все тот же всемирный закон тяготения Ньютона нам гласит, что центробежную силу звезд в галактике можно выразить в формуле:

Только в этот раз в формулу мы подставляем расстояние от Солнца до центра нашей галактики и его массу. Так можно рассчитать массу Млечного Пути, которая равняется 2,2 × 10⁴⁴г.
Не забываем, что эта цифра – это масса галактики без учета звезд, орбиты которых располагаются вне орбиты вращения Солнца. Поэтому для более точных расчетов берутся самые внешние звезды рукавов спиральных галактик.
Для эллиптических галактик способ нахождения массы схож, только там берется зависимость между угловым размером, скоростью движения звезд и общей массой.


