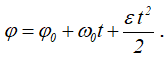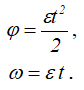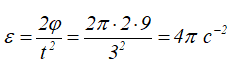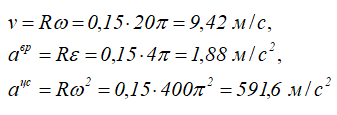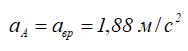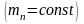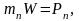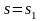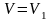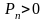GlebPro777
+10
Решено
10 лет назад
Физика
5 – 9 классы
Чему равно ускорение груза массой 500 кг, который опускают с помощью троса, если сила натяжения троса 4000 Н? Сопротивлением воздуха пренебречь.
Смотреть ответ
1
Ответ проверен экспертом
4
(41 оценка)
63
КотикШредингера
5 лет назад
Светило науки – 864 ответа – 7770 раз оказано помощи
Дано:
m = 500 кг
F нат = 4000 Н
Найти: а – ?
а = F/m, где F – равнодействующая F нат и F тяж
Т.к груз опускают вниз, то
F = F тяж – F нат
F тяж = mg
F тяж = 500 кг × 10 Н/кг = 5000 Н
F = 5000 Н – 4000 Н = 1000 Н
Модуль ускорения равен:
а = 1000 Н/500 кг = 2 м/с²
(41 оценка)
https://vashotvet.com/task/314780
Решение.
Покажем силы которые действуют на груз и ускорение. Применим второй закон Ньютона
[ vec{F}={{m}_{1}}cdot vec{a}.{{vec{F}}_{H}}+{{m}_{1}}cdot vec{g}={{m}_{1}}cdot vec{a}.,Oy:,{{m}_{1}}cdot g-{{F}_{H}}={{m}_{1}}cdot a,{{F}_{H}}={{m}_{1}}cdot g-{{m}_{1}}cdot a(1). ]
Рассмотрим барабан. Барабан вращается вокруг своей оси, возникает крутящий момент который равен произведению силы которая действует на барабан на радиус барабана
М = FH∙R (2).
Барабан вращается с угловым ускорением, уравнение динамики вращательного движения имеет вид
М = J∙ε (3).
Где: J – момент инерции цилиндра, ε – угловое ускорение цилиндра.
Момент инерции цилиндра определяется по формуле
[ J=frac{mcdot {{R}^{2}}}{2} (4). ]
Ускорение с которым движется груз, равно тангенциальному ускорению цилиндра, выразим угловое ускорение цилиндра через ускорение груза
[ varepsilon =frac{a}{R}(5). ]
(5) и (4) подставим в (3), (3) подставим в (2) выразим силу натяжения нити, и силу натяжения нити подставим в (1) определим ускорение груза
[ begin{align}
& M=frac{mcdot {{R}^{2}}}{2}cdot frac{a}{R},frac{mcdot {{R}^{2}}}{2}cdot frac{a}{R}={{F}_{H}}cdot R,{{F}_{H}}=frac{mcdot a}{2},frac{mcdot a}{2}={{m}_{1}}cdot g-{{m}_{1}}cdot a, \
& frac{mcdot a}{2}+{{m}_{1}}cdot a={{m}_{1}}cdot g,acdot (frac{m}{2}+{{m}_{1}})={{m}_{1}}cdot g,a=frac{{{m}_{1}}cdot g}{frac{m}{2}+{{m}_{1}}}=frac{2cdot {{m}_{1}}cdot g}{m+2cdot {{m}_{1}}}. \
& a=frac{2cdot 3cdot 10}{12+2cdot 3}=3,33. \
end{align} ]
Ответ: 3,33 м/с2.
Пример решения задачи по определению в заданный момент времени скорости и ускорения точки обода колеса и груза, движущегося равноускоренно из состояния покоя.
Задача
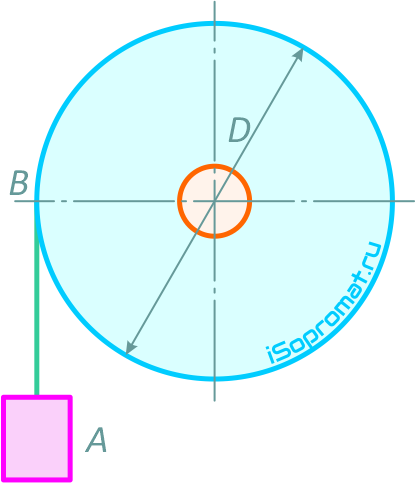
Груз A, подвешенный на нити AB, намотанной на колесо, опускается равноускоренно из состояния покоя, приводя во вращение колесо (рисунок 1.9). За первые 3 секунды колесо совершает 9 оборотов.
Рис. 1.9
Определить в конце 5-й секунды скорость и ускорение точки обода колеса, а также груза A, если диаметр колеса D=30см.
Другие примеры решений >
Помощь с решением задач >
Решение
Колесо вращается равноускоренно согласно уравнению:
При этом угловая скорость ω = ω0 + εt.
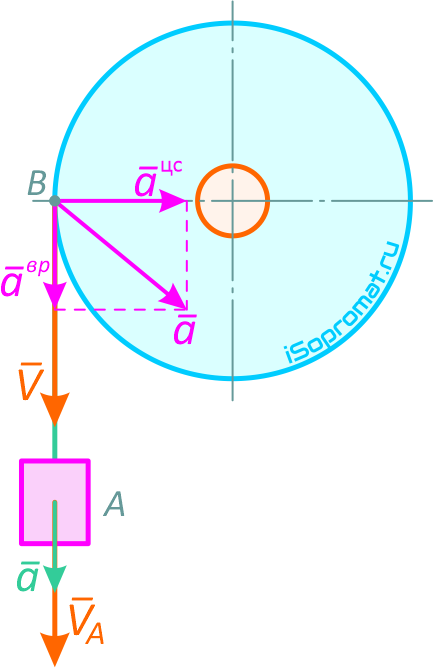
Рис. 1.10
Примем начальные условия: φ0= 0 и ω0= 0, тогда имеем
Определим угловое ускорение:
Угловая скорость колеса в конце 5-й секунды
Определим модули вращательной скорости, вращательного и центростремительного ускорений точки обода колеса в тот же момент времени:
Модуль полного ускорения точки обода колеса
Скорость груза равна скорости точки обода колеса
Ускорение груза равно вращательному ускорению точки обода
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Для определения
скорости
груза 1 воспользуемся теоремой об
изменении кинетической энергии.
Значения Т
из
(16) и
из (32) подставляем в формулу (2), скорость
груза 1 равна:
V1=
4.4 Определение ускорения груза 1
Закон изменения
кинетической энергии для механической
системы можно записать в дифференциальной
форме :
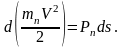
Отсюда легко
находим дифференциальное уравнение
движения системы:
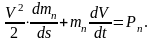
Когда приведенная
масса постоянна
,
будем иметь
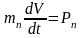
или
где W
– ускорение,
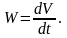
Задача о движении
механической системы сводится к задаче
о движении точки, к которой приведены
масса всей системы и силы, приложенные
к её точкам.
Ускорение при
и
:

W1=
Приведенная к
грузу сила
положительна
Система будет двигаться в выбранном
направлении с ускорением.
Заключение
В результате
расчета установили, что:
а) груз 1 перемещается
в выбранном направлении ускоренно:
так как
;
б) в конце пути
S1=6м
скорость груза V1=
м*с-1;
в) ускорение груза
равно W1=
м*с-2
16
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти ускорение — определение и формулы расчета в физике
Содержание:
-
Что такое ускорение
- Единица измерения
-
Как рассчитать ускорение: формулы
- Для прямолинейного движения
- Для равноускоренного движения
- Для равнозамедленного движения
- Нахождение ускорения через массу и силу
- Мгновенное ускорение
- Максимальное ускорение
- Среднее ускорение
- Проекция ускорения
Что такое ускорение
Ускорение (overrightarrow а) — векторная величина в физике, характеризующая быстроту изменения скорости тела.
Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.
Единица измерения
В СИ (системе интернациональной) ускорение измеряется: ( begin{bmatrix}aend{bmatrix}=frac м{с^2})
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как рассчитать ускорение: формулы
Для прямолинейного движения
Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.
В этом случае ускорение находится по следующим формулам:
(a;=;frac{mathrm V}t)
(a;=;frac{2S}{t^2})
(a;=;frac{V^2}{2S})
Где (a) — достигнутое ускорение тела, (S) — пройденный путь (расстояние), (t) — затраченное время.
Время отсчитывается от начала движения тела.
При прямолинейном равномерном движении ускорение по модулю равняется нулю.
Для равноускоренного движения
Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).
При таком виде движения ускорение определяется по формуле: (a;=;frac{V-V_0}t), где (V_0) и (V) начальная и конечная скорости соответственно, (a) — достигнутое ускорение тела, (t) — затраченное время.
Для равнозамедленного движения
Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).
При таком виде движения ускорение находим по формуле: (a;=-;frac{V-V_0}t), где V0 и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.
Нахождение ускорения через массу и силу
Принцип инерции Галилея:
Если не действовать на тело, то его скорость не будет меняться.
Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.
Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).
II закон Ньютона:
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
или
(overrightarrow a=frac{overrightarrow F}m)
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.
Выражается по формуле:
( overrightarrow a=lim_{trightarrow0}frac{triangleoverrightarrow V}{triangle t})
Максимальное ускорение
(a_{max}=omega v_{max},) где (a_{max}) — максимальное ускорение, (omega) — круговая (угловая, циклическая) частота, (v_{max}) — максимальная скорость.
Среднее ускорение
Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.
(overrightarrow{a_{ср}}=frac{triangleoverrightarrow V}{triangle t}), где (overrightarrow{a_{ср}}) — среднее ускорение, (triangleoverrightarrow V) — изменение скорости, ( triangle t) — изменение времени.
Проекция ускорения
Определение проекции ускорения на ось (х):
(a_x=frac{V_x-V_{0x}}t), где где (a_x) — проекция ускорения на ось (х), (V_x) — проекция текущей скорости на ось (х), (V_{0x}) — проекция начальной скорости на ось (х), (t) или (triangle t) — промежуток времени, за который произошло изменение проекции скорости.
Насколько полезной была для вас статья?
Рейтинг: 1.94 (Голосов: 35)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так