Загрузить PDF
Загрузить PDF
Иногда вычисление площади сводится к простому перемножению двух чисел, но зачастую это вычисление более сложное. Прочтите эту статью для краткого обзора по вычислению площади (или площади поверхности) следующих фигур: четырехугольник, квадрат, параллелограмм, трапеция, треугольник, многоугольник, круг, пирамида, цилиндр, кривая линия.
-
1
Найдите длину двух смежных сторон прямоугольника. Поскольку противоположные стороны прямоугольника равны, нужно найти длины смежных сторон. Обозначьте одну сторону как (b), а другую — как (h).[1]
-
2
Перемножьте значения двух смежных сторон, чтобы найти площадь. Обозначим площадь прямоугольника как (k). Тогда: k = b*h.
- Для более детальных инструкций прочтите статью «Как найти площадь четырехугольника».
Реклама
-
1
Найдите длину стороны квадрата. Поскольку квадраты имеют четыре равные стороны, нужно найти длину всего одной стороны.[2]
-
2
Возведите в квадрат длину стороны. Это и есть площадь квадрата.
- Это верно, потому что квадрат — это прямоугольник, у которого все стороны равны. Так как для прямоугольника k = b*h, а в квадрате b=h, для вычисления площади квадрата просто умножаем его сторону на саму себя.
Реклама
-
1
Выберите одну сторону, на которую будет опущен перпендикуляр. Найдите длину этой стороны.
-
2
Опустите перпендикуляр (высоту) на выбранную ранее сторону и найдите его длину.[3]
- Если нужно, продлите сторону, на которую опускается перпендикуляр, до ее пересечения с перпендикуляром.
-
3
Реклама
-
1
Найдите длины двух параллельных сторон. Обозначьте их как (а) и (b).
-
2
Найдите высоту. Опустите перпендикуляр (высоту (h)) к основанию трапеции.[5]
-
3
Реклама
-
1
Найдите длину одной стороны треугольника (b), на которую будет опущен перпендикуляр (высота) и длину высоты (h).
-
2
Чтобы найти площадь треугольника, подставьте длину соответствующей стороны и длину высоты в формулу: A=0.5b*h
- Для более детальных инструкций прочтите статью «Как найти площадь треугольника».
Реклама
-
1
Найдите длину стороны и длину апофемы (а) (отрезок, соединяющий центр многоугольника и середину любой из его сторон).
-
2
Умножьте длину стороны на количество сторон, чтобы найти периметр многоугольника (р).
-
3
Реклама
-
1
Найдите радиус окружности (r). Это отрезок, соединяющий центр окружности и любую точку на окружности.
-
2
Реклама
-
1
Найдите площадь прямоугольного основания пирамиды с помощью приведенной выше формулы для нахождения площади прямоугольника: k=b*h.
-
2
Найдите площадь каждой треугольной грани пирамиды с помощью приведенной выше формулы для нахождения площади треугольника: A=0.5b*h.
-
3
Сложите все полученные площади для вычисления площади поверхности пирамиды.
Реклама
-
1
Найдите радиус круга в основании цилиндра.
-
2
Найдите высоту цилиндра.
-
3
Найдите площадь круга в основании, используя формулу для вычисления площади круга: А=πr^2.
-
4
Найдите площадь боковой поверхности, умножив высоту цилиндра на периметр основания. Периметр основания равен длине окружности: P = 2πr, поэтому площадь боковой поверхности А= 2πhr.
-
5
Сложите все полученные площади: две площади круговых оснований и площадь боковой поверхности. Таким образом, площадь поверхности цилиндра: SA = 2πr^2 + 2πhr.
- Для более детальных инструкций прочтите статью «Как найти площадь поверхности цилиндра».
Реклама
Допустим, вы хотите найти площадь фигуры, ограниченной кривой линией (описывается функцией f(x)), осью x и значениями функции при x=а и при x=b (то есть область определения [a,b]). Этот метод потребует знаний интегрального исчисления. Если вы не знаете его, этот метод не имеет для вас никакого смысла.
-
1
Определите f(x) через x.
-
2
Возьмите интеграл функции f(x) в интервале [а,b]. По формуле Ньютона-Лейбница: F(x)=∫f(x), ∫abf(x) = F(b) – F(a).
-
3
Подставьте значения а и b в интегральное выражение. Искомая площадь определяется как ∫abf(x). Поэтому, A=F(b)) – F(a).
Реклама
Об этой статье
Эту страницу просматривали 25 303 раза.
Была ли эта статья полезной?
Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников
ABC и
ACD
Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
Содержание:
- Определения
- Формулы площади основных геометрических фигур
Определения
Площадь является одним из основных математических понятий. Она характеризует как плоские, так и поверхностные геометрические объекты.
Определение
Площадью плоской замкнутой фигуры называется величина части плоскости, которая находится внутри указанной фигуры.
Единицей измерения площади плоской фигуры является квадрат со стороной, равной единице. Число, соответствующее
площади некоторой фигуры, состоящей из частей, равно сумме чисел, соответствующих площадям этих частей. Измерение
площадей треугольников и многоугольников основано на возможности построения равновеликих им прямоугольников.
Площадь произвольной ограниченной плоской фигуры определяется как общий предел площадей описанных и
вписанных в нее многоугольников, наибольшие стороны которых по длине стремятся к нулю.
Если фигура имеет площадь, то она называется квадрируемой.
Формулы площади основных геометрических фигур
Площадь треугольника
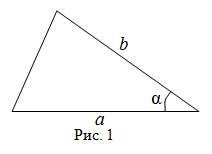
Чтобы найти площадь треугольника, надо найти полупроизведение двух его сторон на синус угла между ними.
То есть если известны длины двух сторон треугольника $ABC$, которые равны
$a$ и $b$, а также угол
$alpha$ между этими сторонами, то искомая площадь:
$$mathrm{S}_{Delta A B C}=frac{1}{2} a b sin alpha$$
Читать дальше: формулы площади треугольника и примеры решений →
Площадь круга
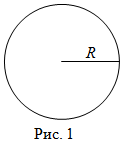
Чтобы найти площадь круга, надо найти произведение числа
$pi$ на квадрат радиуса этого круга, то есть
$$mathrm{S}_{kappa p}=pi R^{2}$$
Читать дальше: формула площади круга и примеры решений →
Площадь квадрата
Чтобы найти площадь квадрата, надо длину его стороны возвести в квадрат, то есть
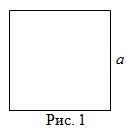
Читать дальше: формула площади квадрата и примеры решений →
Площадь прямоугольника
Чтобы найти площадь прямоугольника, надо его длину умножить на ширину, то есть
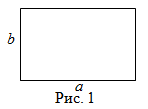
Читать дальше: формула площади прямоугольника и примеры решений →
Площадь параллелограмма
Чтобы найти площадь параллелограмма, нужно найти произведение стороны
$a$ параллелограмма на высоту
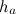, проведенную к этой стороне, то есть
Читать дальше: формулы площади параллелограмма и примеры решений →
Площадь трапеции
Чтобы найти площадь трапеции, нужно длину средней линии
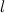умножить на длину высоты
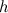, опущенной к основанию:
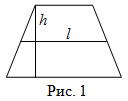
Читать дальше: формулы площади трапеции и примеры решений →
Площадь ромба
Чтобы найти площадь ромба, надо длину стороны умножить на длину высоты, проведенной к этой стороне:
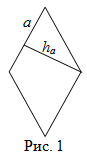
Читать дальше: формулы площади ромба и примеры решений →
Площадь эллипса
Чтобы найти площадь эллипса, нужно найти произведение длин большой и малой полуосей этого эллипса на число
$pi$, то есть
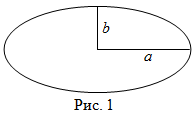
Читать дальше: формула площади эллипса и примеры решений →
- Как найти площадь треугольника
- Как найти площадь ромба
- Как найти площадь эллипса
- Как найти площадь прямоугольного треугольника
- Как найти площадь равнобедренного треугольника
- Как найти площадь равностороннего треугольника
- Как найти площадь круга
- Как найти площадь квадрата
- Как найти площадь прямоугольника
- Как найти площадь параллелограмма
- Как найти площадь трапеции
Download Article
Download Article
There are many different shapes and many reasons why you might want to know their area! Whether you’re doing your homework or trying to figure out how much paint you’ll need to refurbish that living room, wikiHow has your back! Just get started with Step 1 below to learn how to calculate the area of a shape.
-
1
Measure the width and height. You’ll need to start by finding the width and height of the shape (in other words, by finding the measure of two adjoining sides).[1]
- For a parallelogram, you’ll need to use what are called the base and vertical height, but these are the same idea as width and height.
- In the real world, you’ll have to measure for yourself but for your homework your teacher should have these measurements listed with the shape.
-
2
Multiply the sides. Multiply the sides by each other.[2]
For example, if you have a rectangle with a height of 16 in and a width of 42 in, you’ll need to multiply 16 x 42.[3]
- If you’re calculating the area of a square you can actually save yourself some time when using a calculator and just square the side. So, if the side is 4 ft, click 4 and then the square button on your calculator to get the answer. Squaring automatically multiples the number by itself.
Advertisement
-
3
Get your result. The resulting number from the multiplication is the area of your shape, which is written as “square units”. So the area for our rectangle would be 672 square inches.
- This is also sometimes referred to as inches square or written with a small 2 above the text line instead of the word “square”.
Advertisement
-
1
Take your measurements. You’ll need the measurement of the base, the top, and the vertical height. The base and top are the two parallel sides, while the height will be taken on one of the sides with the angle.[4]
- In the real world, you’ll have to measure for yourself but for your homework your teacher should have these measurements listed with the shape.
-
2
Add the top and base measurements.[5]
Let’s say ours has a top that’s 5cm and a base that’s 7cm. That gives us a value of 12. -
3
Multiply that value by 1/2.[6]
That gives us a value of 6. -
4
Multiply that value by the height. For our trapezoid, let’s say that that’s 6cm. That gives us a value of 36.[7]
-
5
Get your result. The resulting number after you multiply the height is the area of the trapezoid. So for our 5x6x7 trapezoid, the area is 36 square cm.
Advertisement
-
1
Find the radius. In order to find the area of a circle, you’ll need to know the radius. This is the measurement of the distance between the center of the circle and the outside edge. You can also find this by taking the diameter, or the measurement of the width of the circle, and dividing it in half.[8]
- In the real world, you’ll have to measure for yourself but for your homework your teacher should have these measurements listed with the shape.
-
2
Square the radius. Multiply the radius times itself. Let’s say we have a radius that is 8 feet. That gives us a value of 64.
-
3
Multiply by pi. Pi (π) is a really big number that is used in lots of calculations. If you’re using a calculator, use the pi function for a really accurate result. If not, you can round pi (ignore some of the numbers) and just multiply by 3.14159. This gives us a value of 201.06176.[9]
-
4
Get your result. The resulting number, 201.06176 in our case, is the area of the circle. So we get a result of 201.06176 square feet.
Advertisement
-
1
Take your measurements. Sectors are portions of a circle, that come out looking a bit like fans. You’ll need to know the radius of the original circle, or one side of your “fan”, as well as the angle of the point. For us, let’s say we have a radius of 14 inches and an angle of 60.[10]
- In the real world, you’ll have to measure for yourself but for your homework your teacher should have these measurements listed with the shape.
-
2
Square the radius. Multiply the radius times itself. This gives us a value of 196 (14×14).
-
3
Multiply by pi. Pi (π) is a really big number that is used in lots of calculations. If you’re using a calculator, use the pi function for a really accurate result. If not, you can round pi (ignore some of the numbers) and just multiply by 3.14159. That gives us a value of 615.75164.[11]
-
4
Divide the angle by 360. Now, you’ll need to take the angle of the point and divide that number by 360 (which is the number of degrees in a circle). For us, we get a value of roughly .166. It’s technically a repeating number, but we’re going to round to make the math easier.[12]
-
5
Multiply the resulting number by the number you got earlier. Multiply the number you get when you divide by 360 by the number you got earlier after you multiply by pi.[13]
For us, this gives a result of about 102.214. -
6
Get your result. This resulting number is the area of your sector, making our sector 102.214 square inches.
Advertisement
-
1
Get your measurements. To get the area of an ellipse, you’ll need to know the two “radio”, which you can think of as the width and the height each divided in half. These are the measurements from the center to the middle of the long side and from the center to the middle of the short side. The measurement lines should form a right angle.
- In the real world, you’ll have to measure for yourself but for your homework your teacher should have these measurements listed with the shape.
-
2
Multiply the two radii.[14]
For us, let’s say that the ellipse is 6 inches wide and 4 inches tall. This gives us radii of 3 inches and 2 inches. Now, we’ll multiply those numbers by each other, giving us 6 (3×2).[15]
-
3
Multiply that number by pi.[16]
Pi (π) is a really big number that is used in lots of calculations. If you’re using a calculator, use the pi function for a really accurate result.[17]
If not, you can round pi (ignore some of the numbers) and just multiply by 3.14159. That gives us a value of 18.84954. -
4
Get your result. That resulting number is the area of your ellipse. For us, that means our ellipse is 18.84954 square inches.
Advertisement
-
1
Find your measurements. You’ll need to know the base measurement of the triangle as well as the height. The base can be any side of the triangle, as long as you can also measure the height. Let’s say that we have a triangle with a base of 3 meters and a height of 1 meter.[18]
- In the real world you’ll have to measure for yourself but for your homework your teacher should have these measurements listed with the shape.
-
2
Multiply the base by the height. For us, this gives a value of 3 (3×1).[19]
-
3
Multiply that value by 1/2.[20]
This gives us a value of 1.5. -
4
Get your result. That resulting value is the area of the triangle. So we get a result of 1.5 square meters.
Advertisement
-
1
Break the shape down into sections. You’ll have to start finding the area for complex shapes by breaking the shape down into geometric shapes, like those discussed above. On homework assignments, it will probably be pretty clear cut what those shapes should be, but in the real world, you might need to break an area up into a lot of shapes in order to get really accurate.[21]
- A good place to start is by looking for right angles and parallel lines. These serve as the basis of many shapes.
-
2
Calculate the area of the separate shapes. Use the instructions above to find the area of the different shapes you find.[22]
-
3
Add the shapes together. Add the resulting areas together in order to get the total area for your shape.[23]
-
4
Use alternative methods. There are other tricks you can try too, depending on the shape. You can also try adding imaginary space in order to make the shape a standard geometric shape, and then subtracting the area of that imaginary space after you get your result, for example.
Advertisement
Add New Question
-
Question
How can I find the square inches of a triangle with a base of 15 inches and the height of 8 inches?
A triangle’s area is equal to one-half its base multiplied by its height. A = (15)(8) ÷ 2 = 60 sq in.
-
Question
A hexagonal prism is 13 cm long and has a volume of 370.5 cm squared. What would be area of the front side?
Divide the volume by the length to get the cross-sectional area. Assuming this is a regular hexagon, use the area formula to solve for the width of a side: A = (0.385)(s²). Multiply the side width thus calculated by the length of the prism. That gives you the area of one side.
-
Question
How can I calculate the area of a parallelogram with a base of 12cm, height of 5 cm, and the inside is 4 cm?
The area of a parallelogram is the base multiplied by the height.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Get help from a friend if you’re having a hard time!
Advertisement
-
Make sure that you keep your units of measurement straight. You don’t want to mix up numbers!
-
It’s a good idea to double check your answer!
Advertisement
References
About This Article
Article SummaryX
To find the area of a square or rectangle, just multiply the width of the shape by its height. To find the area of a circle, start by measuring the distance between the middle of the circle to the edge, which will give you the radius. Then, square the radius and multiply it by pi to find the area. If you need to find the area of a triangle, multiply the base of the triangle by its height. To find the area of a trapezoid, add the top and bottom of the shape together, divide that number in half, and then multiply by the height. To learn how to find the area of other shapes, such as ellipses or shapes that don’t fit one particular category, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 480,712 times.
Reader Success Stories
-
“Having a diagram with step-by-step calculations to follow was really useful!”
