Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Геометрический и физический смысл производной
Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.
Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:

Нам нужно найти скорость в момент времени t=2c. Вычислим производную:

Правила нахождения производных
Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.
Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте.
Пример. Вычислим производную:

Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:

Решение:

Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:

Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:

В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:

Пример:

Решение:

Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Если вы ничего не смыслите в том, что такое производная и какими методами можно её вычислить, то совершенно невозможно решать примеры по математике или задачи по физике. Ведь такое понятие, как производная, является одним из самых важных в математическом анализе.
В этой статье мы расскажем вам, что является производной, какой она имеет геометрический и физический смысл. В общем, мы с вами попытаемся понять производную.
Геометрический и физический смысл производной
Задаём функцию f(x) в интервале (a, b). А точки x и x0 этому интервалу принадлежат. Если изменится x, то и функция тоже изменится. Изменением аргумента является разность его значений x-x0. Записывается эта разность, как дельта икс и имеет название: приращение аргумента. Разность значений функций в двух точках называется приращением или изменением функции. Так каково определение производной?
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Можно записать ещё следующим образом:
Встаёт вопрос, для чего нужно находить такой предел? Вот и ответ:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Ещё в школе нас учили тому, что скорость – это частное пути x=f(t) и времени (t). Вычисляем среднюю скорость за какой-то временной промежуток:
Для того чтобы нам узнать какова скорость движения в момент t0, необходимо вычислить предел:
Сейчас мы разберем один пример, который продемонстрирует вам применение производной на практике. Допустим, тело движется по закону:
Нам необходимо рассчитать скорость в момент времени t=2c. Вычисляем производную:
Правила нахождения производных
Дифференцирование – это процесс нахождения производной. А дифференцируемая функция – это функция, которая имеет производную в данной точке.
Каким образом нам найти саму производную? Нам необходимо составить отношения приращения функции и аргумента, а после вычислить предел при условии стремящегося к нулю приращения аргумента. Но практика показывает, что такой путь вычисления является очень долгим. Всё, что нам необходимо, уже посчитано. И специально для вас, мы подготовили таблицу с производными элементарных функций.
После таблицы мы рассмотрим правила по вычисления производных. Коснёмся мы и вычисления производных сложных функций. Подробно разберём всё на примерах.
Правило первое: выносим константу
Вынести константы можно за знак производной. Причём делать это необходимо! Когда вы решаете примеры по математике, то всегда помните правило – если есть возможность упростить выражение, то делайте это.
Для примера вычислил с вами производную:
Правило второе: производная суммы функций
Производная суммы двух функций равняется сумме производных этих функций. Это касается и производной разности функций.
Сейчас мы с вами на практике рассмотрим пример доказательства этой теоремы.
Найти производную функции:
Решение:
Правило третье: производная произведения функций
По следующей формуле мы сможем вычислить производную произведения двух дифференцируемых функций:
К примеру: необходимо найти производную функции:
Решение:
Необходимо сказать о том, каким образом вычисляются производные сложных функций.
Производная сложной функции равняется произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В примере, который указан выше, мы можем встретить выражение:
В этом примере промежуточным аргументом является 8x в пятой степени. Чтобы нам вычислить производную данного выражения, то для начала необходимо высчитать производную внешней функции по промежуточному аргументу, а после необходимо умножить на производную непосредственно сам промежуточный аргумент по независимой переменной.
Правило четвертое: производная частного двух функций
Ниже приведена формула для того, чтобы определить производную от частного двух функций:
Пример:
Решение:
В данной статье мы попытались рассказать о производных для тех, кто совершенно не знаком с этой темой. Когда вы будете решать примеры, то будьте очень внимательны, ведь в них часто можно встретить ловушки. Эта тема не так уж и проста, какой кажется на первый взгляд.
Вы можете обратиться в наш студенческий сервис по любым вопросам. Мы с удовольствием поможем решить для вас задачи любой сложности. А занимались вы раньше вычислением производных или нет, не имеет никакого значения. Мы помогаем всем!
урок 3. Математика ЕГЭ
Как найти производную от функции
Как считать производные?
Никто не использует определение производной, чтобы ее вычислить. Как же тогда ее посчитать?
Оказывается, существуют специальные формулы, с помощью которых производная от функции вычисляется достаточно просто.
Формулы производной
Выпишем теперь все формулы производной функции и порешаем примеры.
Производная от константы
Производная от любого числа всегда равна (0):
$$(const)^{/}=0;$$
Пример 1
$$(5)^{/}=0;$$
Производная от (x)
Производная просто от (x) равна (1):
$$x^{/}=1;$$
Производная от степени
$$(x^n)^{/}=n*x^{n-1};$$
Пример 2
$$(x^4)^{/}=4*x^{4-1}=4*x^{3};$$
$$(x^{10})^{/}=10*x^{10-1}=10*x^{9};$$
$$(x^{-3})^{/}=-3*x^{-3-1}=-3*x^{-4};$$
$$(x^{frac{1}{3}})^{/}=frac{1}{3}*x^{1-frac{1}{3}}=frac{1}{3}*x^{frac{2}{3}};$$
Производная от квадратного корня
$$(sqrt{x})^{/}=frac{1}{2sqrt{x}};$$
Тут полезно заметить, что формулу производной от квадратного корня можно не учить. Она сводится к формуле производной от степени:
$$(sqrt{x})^{/}=(x^{frac{1}{2}})^{/}=frac{1}{2}*x^{frac{1}{2}-1}=frac{1}{2}*x^{-frac{1}{2}}=frac{1}{2sqrt{x}};$$
Производная от синуса
$$sin(x)^{/}=cos(x);$$
Производная от косинуса
$$cos(x)^{/}=-sin(x);$$
Производная от тангенса
$$tg(x)^{/}=frac{1}{cos^{2}(x)};$$
Производная от котангенса
$$tg(x)^{/}=frac{-1}{sin^{2}(x)};$$
Производная от экспоненты
$$(e^x)^{/}=e^x;$$
Производная от показательной функции
$$(a^x)^{/}=a^x*ln(a);$$
Пример 3
$$(2^x)^{/}=2^{x}*ln(2);$$
Производная от натурального логарифма
$$(ln(x))^{/}=frac{1}{x};$$
Производная от логарифма
$$(log_{a}(x))^{/}=frac{1}{x*ln(a)};$$
Свойства производной
Помимо формул по вычислению производной еще есть свойства производной, их тоже надо выучить.
Вынесение константы за знак производной
$$(alpha*f(x))^{/}=alpha*(f(x))^{/};$$
Пример 4
$$(3*x^5)^{/}=3*(x^5)^{/}=3*5x^4=15x^4;$$
$$(10sin(x))^{/}==10*(sin(x))^{/}=10*cos(x);$$
Производная от суммы и разности двух функций
$$(f(x) pm g(x))^{/}=(f(x))^{/} pm (g(x))^{/};$$
Пример 5
$$(2x^4+x^3)^{/}=?$$
Тут (f(x)=2x^4), а (g(x)=x^3). Тогда по формуле производной от суммы:
$$(2x^4+x^3)^{/}=(2x^4)^{/}+(x^3)^{/}=2*(x^4)^{/}+(x^3)^{/}=2*4x^3+3x^2=8x^3+3x^2;$$
Пример 6
$$(ln(x)+cos(x))^{/}=(ln(x))^{/}+(cos(x))^{/}=frac{1}{x}-sin(x);$$
Пример 7
$$(x^6-e^x)^{/}=(x^6)^{/}-(e^x)^{/}=6x^5-e^x;$$
Производная от произведения двух функций
$$(f(x)*g(x))^{/}=(f(x))^{/}*g(x)+f(x)*(g(x))^{/};$$
Пример 8
$$(x^2*sin(x))^{/}=?$$
$$(x^2*sin(x))^{/}=(x^2)^{/}*sin(x)+x^2*(sin(x))^{/}=2x*sin(x)+x^2*cos(x);$$
Пример 9
$$(ln(x)*e^x)^{/}=(ln(x))^{/}*e^x+ln(x)*(e^x)^{/}=frac{1}{x}*e^x+ln(x)*e^x;$$
Производная от частного двух функций
$$left(frac{f(x)}{g(x)}right)^{/}=frac{(f(x))^{/}*g(x)-f(x)*(g(x))^{/}}{(g(x))^2};$$
Пример 10
$$left(frac{x^3}{sin(x)}right)^{/}=frac{(x^3)^{/}*sin(x)-x^3*(sin(x))^{/}}{(sin(x))^2}=frac{3x^2*sin(x)-x^3*cos(x)}{(sin(x))^2};$$
Примеры нахождения производной
Рассмотрим несколько примеров нахождения производной, чтобы разобраться, как применяются свойства и формулы производной на практике.
Пример 11
$$(5x^3+2cos(x))^{/}=(5x^3)^{/}+(2cos(x))^{/}=$$
$$=5*(x^3)^{/}+2*(cos(x))^{/}=5*3*x^2+2*(-sin(x))=15x^2-2sin(x);$$
Пример 12
$$left(-frac{3x^2}{2x^4+5x}right)^{/}=-frac{(3x^2)^{/}*(2x^4+5x)-3x^2*(2x^4+5x)^{/}}{(2x^4+5x)^2}=$$
$$=-frac{6x*(2x^4+5x)-3x^2*(8x+5)}{(2x^4+5x)^2}=-frac{12x^5-24x^3+15x^2}{(2x^4+5x)^2};$$
Пример 13
$$(2xsqrt{x})^{/}=(2x)^{/}*sqrt{x}+2x*(sqrt{x})^{/}=$$
$$=2*sqrt{x}+2x*frac{1}{2sqrt{x}}=2*sqrt{x}+frac{2x}{2sqrt{x}}=2*sqrt{x}+sqrt{x}=3sqrt{x};$$
Производная сложной функции
Сложная функция – это функция не от аргумента (x), а от какой-то другой функции: (f(g(x))). Например, функция (sin(x^2)) будет сложной функцией: «внешняя» функция синуса берется от «внутренней» функции степени ((x^2)). Так как под синусом стоит аргумент не (x), а (x^2), то такая функция будет называться сложной.
Еще примеры сложных функций:
-
$$ln(3x^4);$$
Внешняя функция: натуральный логарифм; Внутренняя функция: ((3x^4)). -
$$cos(ln(x));$$
Внешняя функция: косинус; Внутренняя функция: ((ln(x))). -
$$e^{2x^2+3};$$
Внешняя функция: экспонента; Внутренняя функция: ((2x^2+3)). -
$$(sin(x))^3;$$
Внешняя функция: возведение в третью степень; Внутренняя функция: (sin(x)).
Чтобы посчитать производную от такой функции, нужно сначала найти производную внешней функции, а затем умножить результат на производную внутренней функции. В общем виде формула выглядит так:
$$f(g(x))^{/}=f^{/}(g(x))*g^{/}(x);$$
Скорее всего, выглядит непонятно, поэтому давайте разберем на примерах.
Пример 14
$$((cos(x))^4)^{/}=?$$
Внешней функцией тут будет возведение в четвертую степень, поэтому сначала считаем производную от степени по формуле ((x^n)^{/}=n*x^{n-1}). А потом умножаем результат на производную внутренней функции, у нас это функция косинуса, по формуле (cos(x)^{/}=-sin(x)):
$$((cos(x))^4)^{/}=underset{text{внешняя производная}}{underbrace{4*(cos(x))^3}}*underset{text{внутренняя производная}}{underbrace{(cos(x))^{/}}}=$$
$$=4*(cos(x))^3*(-sin(x))=-4*(cos(x))^3*sin(x);$$
Пример 15
$$(e^{2x^3+5})^{/}=?$$
Внешняя функция – это экспонента ((e^x)^{/}=e^x), а внутренняя функция – квадратный многочлен ((2x^3+5)):
$$(e^{2x^3+5})^{/}=e^{2x^3+5}*(2x^3+5)^{/}=e^{2x^3+5}*((2x^3)^{/}+5^{/})=e^{2x^3+5}*6x^2.$$
Пример 16
$$(ln((2x^2+3)^6))^{/}=?$$
Внешняя функция – это натуральной логарифм, берем производную от него по формуле ((ln(x))^{/}=frac{1}{x}), и умножаем на производную внутренней функции, у нас это шестая степень: ((x^n)^{/}=n*x^{n-1}). Но и на этом еще не все: под шестой степенью стоит не просто (x), а квадратный многочлен, значит еще нужно умножить на производную от этого квадратного многочлена:
$$ln((2x^2+3)^6)=frac{1}{(2x^2+3)^6}*((2x^2+3)^6)^{/}*(2x^2+3)^{/}=$$
$$=frac{1}{(2x^2+3)^6}*6*(2x^2+3)^5*(4x+0)=frac{1}{(2x^2+3)^6}*6*(2x^2+3)^5*4x=$$
$$=frac{6*(2x^2+3)^5*4x}{(2x^2+3)^6}=frac{24x*(2x^2+3)^5}{(2x^2+3)^6}=frac{24x}{(2x^2+3)^6}.$$
Вывод формул производной функции
Выведем некоторые из этих формул, чтобы было понимание, откуда они берутся. Но перед этим познакомимся с новыми обозначениями. Запись (f(x)) означает, что функция берется от аргумента (x). Например:
$$f(x)=x^3+sin(x);$$
На месте аргумента (x) может стоять все что угодно, например выражение (2x+3). Обозначение такой функции будет (f(2x+3)), а сама функция примет вид:
$$f(2x+3)=(2x+3)^3+sin(2x+3);$$
То есть, везде вместо аргумента (x) мы пишем (2x+3).
И несколько важных замечаний про (Delta f(x)) и (Delta x). Напомню, что значок (Delta) означает изменение некоторой величины. (Delta x) – изменения координаты (x) при переходе от одной точки на графике функции к другой; (Delta f(x)) – разница координат (y) между двумя точками на графике. Подробнее про это можно почитать в главе, где мы вводим понятие производной. Распишем (Delta x) для двух близких точек на графике функции (O) и (B):
$$Delta x=x_B-x_O;$$
Отсюда можно выразить (x_B):
$$x_B=x_O+Delta x;$$
Абсцисса (координата точки по оси (x)) точки (B) получается путем сложения абсциссы точки (O) и (Delta x).
Кстати, функцию (f(x)=x^3+sin(x)) от аргумента (x_B=x_O+Delta x) можно расписать:
$$f(x_B)=f(x_O+Delta x)=(x_O+Delta x)^3+sin(x_O+Delta x);$$

Рис.1. График произвольной функции
И распишем (Delta f):
$$Delta f(x)=f(x_B)-f(x_O)=f(x_O+Delta x)-f(x_O);$$
Тогда определение производной можно записать в виде:
$$f^{/}(x)=frac{Delta f(x)}{Delta x}=frac{f(x_O+Delta x)-f(x_O)}{Delta x} quad при quad Delta x to 0;$$
За (x_O) обычно обозначают точку, в окрестности которой берут производную. То есть, получается (x_O) – это абсцисса начальной точки, а (x_O+Delta x) – абсцисса конечной точки.
Нам это пригодится при выводе формул производной.
Производная квадратичной функции
Выведем теперь формулу производной от (f(x)=x^2), воспользовавшись определением производной:
$$f^{/}(x)=frac{Delta f(x)}{Delta x}=frac{f(x+Delta x)-f(x)}{Delta x} quad при quad Delta x to 0;$$
Распишем числитель (f(x+Delta x)-f(x)) с учетом, что (f(x)=x^2):
$$f(x+Delta x)-f(x)=(x+Delta x)^2-x^2=x^2+2xDelta x+(Delta x)^2-x^2=2xDelta x+(Delta x)^2;$$
Подставим в определение производной:
$$f^{/}(x)=frac{2xDelta x+(Delta x)^2}{Delta x}=frac{Delta x*(2x+Delta x)}{Delta x}=2x+Delta x;$$
Напоминаю, что (Delta x) это бесконечно малая величина:
$$(Delta x)^2 ll 0;$$
Поэтому этим слагаемым можно пренебречь. Вот мы и получили формулу для производной от квадратной функции:
$$f^{/}(x)=(x^2)^{/}=2x;$$
Производная от третьей степени
Аналогичные рассуждения можно провести для функции третьей степени:
$$f(x)=x^3;$$
Воспользуемся определением производной:
$$f^{/}(x)=frac{f(x+Delta x)-f(x)}{Delta x} quad при quad Delta x to 0;$$
$$f(x+Delta x)-f(x)=(x+Delta x)^3-x^3=(x+Delta x-x)((x+Delta x)^2+(x+Delta x)*x+x^2)=$$
$$=Delta x*(x^2+2x*Delta x+(Delta x)^2+x^2+x*Delta x+x^2)=Delta x*(3x^2+3xDelta x);$$
$$f^{/}(x)=frac{f(x+Delta x)-f(x)}{Delta x}=frac{Delta x*(3x^2+3xDelta x)}{Delta x}=3x^2+3xDelta x;$$
Так как при умножении на бесконечно малую величину получается бесконечно малая величина, то слагаемым (3xDelta x) можно пренебречь:
$$f^{/}(x)=(x^3)^{/}=3x^2;$$
Точно таким же способом можно вывести формулы производных для любых степеней:
$$(x^4)^{/}=4x^3;$$
$$(x^5)^{/}=5x^4;$$
$$…$$
$$(x^n)^{/}=n*x^{n-1};$$
Кстати, эта формула справедлива и для дробных степеней.
Вывод остальных формул делается похожим образом, только там может понадобиться знание пределов. Вывод всех формул разбирается в университетском курсе математического анализа.
Что такое производная функции простыми словами? Для чего нужна производная? Определение производной
Как решать задания №7 из ЕГЭ по математике. Анализ графиков при помощи производной. Графики производной и графики функции
Исследуем функцию с помощью производной. Находим точки минимума и максимума, наибольшее и наименьшее значение функции. Точки экстремума. Промежутки возрастания и убывания.
Связь коэффициента наклона и тангенса угла наклона касательной к функции и производной функции в точке касания. Задание №7 в ЕГЭ по математике.
Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.
Производная функции
Процесс нахождения производной функции называется дифференцированием. Производную приходится находить в ряде задач курса математического анализа. Например, при отыскании точек экстремума и перегиба графика функции.
Как найти?
Чтобы найти производную функции нужно знать таблицу производных элементарных функций и применять основные правила дифференцирования:
- Вынос константы за знак производной: $$ (Cu)’ = C(u)’ $$
- Производная суммы/разности функций: $$ (u pm v)’ = (u)’ pm (v)’ $$
- Производная произведения двух функций: $$ (u cdot v)’ = u’v + uv’ $$
- Производная дроби: $$ bigg (frac{u}{v} bigg )’ = frac{u’v – uv’}{v^2} $$
- Производная сложной функции: $$ ( f(g(x)) )’ = f'(g(x)) cdot g'(x) $$
Примеры решения
| Пример 1 |
| Найти производную функции $ y = x^3 – 2x^2 + 7x – 1 $ |
| Решение |
|
Производная суммы/разности функций равна сумме/разности производных: $$ y’ = (x^3 – 2x^2 + 7x – 1)’ = (x^3)’ – (2x^2)’ + (7x)’ – (1)’ = $$ Используя правило производной степенной функции $ (x^p)’ = px^{p-1} $ имеем: $$ y’ = 3x^{3-1} – 2 cdot 2 x^{2-1} + 7 – 0 = 3x^2 – 4x + 7 $$ Так же было учтено, что производная от константы равна нулю. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ y’ = 3x^2 – 4x + 7 $$ |
| Пример 2 |
| Найти производную функции $ y = sin x – ln 3x $ |
| Решение |
|
По правилу производной разности: $$ y’ = (sin x – ln 3x)’ = (sin x)’ – (ln 3x)’ = $$ По таблице интегрирования находим: $$ (sin x)’ = cos x $$ $$ (ln x)’ = frac{1}{x} $$ С учетом того, что аргумент натурального логарифма отличен от $ x $, то нужно домножить ещё на производную самого аргумента: $$ y’ = (sin x)’ – (ln 3x)’ = cos x – frac{1}{3x} cdot (3x)’ = $$ После упрощения получаем: $$ = cos x – frac{1}{3x} cdot 3 = cos x – frac{1}{x} $$ |
| Ответ |
| $$ y’ = cos x – frac{1}{x} $$ |
| Пример 3 |
| Найти производную функции $ y = (3x-1) cdot 5^x $ |
| Решение |
|
В данном примере стоит произведение двух функций, а производная произведения находится по формуле номер 3: $$ (u cdot v)’ = u’v + uv’ $$ $$ y’ = ( (3x-1) cdot 5^x )’ = (3x-1)’ 5^x + (3x-1) (5^x)’ = $$ Производная первой функции вычисляется как разность фунций: $$ (3x-1)’ = (3x)’ – (1)’ = 3(x)’ – (1)’ = 3 $$ Вторая функция является показательной, производная которой находится по формуле: $ (a^x)’ = a^x ln a $: $$ (5^x)’ = 5^x ln 5 $$ Продолжаем решение с учетом найденных производных: $$ y’ = (3x-1)’ 5^x + (3x-1) (5^x)’ = 3 cdot 5^x + (3x-1) 5^x ln 5 $$ |
| Ответ |
| $$ y’ = 3cdot 5^x + (3x-1) 5^x ln 5 $$ |
| Пример 4 |
| Найти производную функции $ y = frac{ln x}{sqrt{x}} $ |
| Решение |
|
Производную дроби найдем по четвертой формуле. Положим $ u = ln x $ и $ v = sqrt{x} $. Тогда их производные по таблице основных элементарных функций равны: $$ u’ = (ln x)’ = frac{1}{x} $$ $$ v’ = (sqrt{x})’ = frac{1}{2sqrt{x}} $$ Используя формулу №4 получаем: $$ y’ = bigg ( frac{ln x}{sqrt{x}} bigg )’ = frac{ frac{1}{x} cdot sqrt{x} – ln x cdot frac{1}{2sqrt{x}} }{x} = $$ Выносим множитель $ frac{1}{2sqrt{x}} $ в числителе за скобку: $$ y’ = frac{2-ln x}{2xsqrt{x}} $$ |
| Ответ |
| $$ y’ = frac{2-ln x}{2xsqrt{x}} $$ |
| Пример 5 |
| Найти производную функции $ y = ln sin 3x $ |
| Решение |
|
Данная функция является сложной, потому производную будем брать по цепочке. Сначала от внешней функции, затем от внутренней. При этом выполняя их перемножение. $$ y’ = (ln sin 3x )’ = frac{1}{sin 3x} cdot (sin 3x)’ = $$ Заметим, что аргумент синуса отличен от $ x $, поэтому тоже является сложной функцией: $$ = frac{1}{sin 3x} cdot cos 3x cdot (3x)’ = frac{1}{sin 3x} cdot cos 3x cdot 3 $$ Учитывая определение котангенса $ ctg x = frac{cos 3x}{sin 3x} $ перепишем полученную производную в удобном компактном виде: $$ y’ = 3ctg 3x $$ |
| Ответ |
| $$ y’ = 3ctg 3x $$ |
Как
найти производную, как взять производную? На
данном уроке мы научимся находить
производные функций. Но перед изучением
данной страницы я настоятельно рекомендую
ознакомиться с методическим
материалом Горячие
формулы школьного курса математики.
Справочное пособие можно открыть или
закачать на страницеМатематические
формулы и таблицы.
Также оттуда нам потребуется Таблица
производных, ее лучше
распечатать, к ней часто придется
обращаться, причем, не только сейчас,
но и в оффлайне.
Есть?
Приступим. У меня для Вас есть две
новости: хорошая и очень хорошая. Хорошая
новость состоит в следующем: чтобы
научиться находить производные совсем
не обязательно знать и понимать, что
такое производная. Если Вас интересует
теоретическое определение производной
функции, математический, физический,
геометрический смысл производной –
поищите в Интернете, информации море.
Наша же задача научиться
находить эти
самые производные. Очень хорошая новость
состоит в том, что научиться брать
производные не так сложно, существует
довольно чёткий алгоритм решения (и
объяснения) этого задания, интегралы или
пределы, например, освоить труднее.
Рекомендую
следующий порядок изучения темы: во-первых,
эта статья. Затем следует прочитать
важнейший урок Производная
сложной функции.
Эти два базовых занятия позволят поднять
Ваши навыки с полного нуля. Далее можно
будет ознакомиться с более сложными
производными в статье Сложные
производные. Логарифмическая производная.
Если планка окажется слишком высока,
то сначала прочитайте вещьПростейшие
типовые задачи с производной.
Помимо нового материала, на уроке
рассмотрены другие, более простые типы
производных, и есть прекрасная возможность
улучшить свою технику дифференцирования.
Кроме того, в контрольных работах почти
всегда встречаются задания на нахождение
производных функций, которые заданы
неявно или параметрически. Такой урок
тоже есть: Производные
неявных и параметрически заданных
функций.
Я попытаюсь в
доступной форме, шаг за шагом, научить
Вас находить производные функций. Вся
информация изложена подробно, простыми
словами.
Собственно, сразу
рассмотрим пример:
Пример 1
Найти
производную функции ![]()
Решение: ![]()
Это
простейший пример, пожалуйста, найдите
его в таблице производных элементарных
функций. Теперь посмотрим на решение и
проанализируем, что же произошло? А
произошла следующая вещь: у нас была
функция
,
которая в результате решения превратилась
в функцию ![]()
.
Говоря
совсем просто, для
того чтобы найти производную функции,
нужно по определенным правилам превратить
её в другую функцию.
Посмотрите еще раз на таблицу производных
– там функции превращаются в другие
функции. Единственным исключением
является экспоненциальная функция ![]()
,
которая превращается сама в себя.Операция
нахождения производной
называется дифференцированием.
Обозначения: Производную
обозначают ![]()
или ![]()
Вернемся
к нашей таблице производных. Из данной
таблицы желательно запомнить
наизусть: правила
дифференцирования и производные
некоторых элементарных функций, особенно:
производную
константы:
![]()
,
где ![]()
–
постоянное число;
производную
степенной функции:
![]()
,
в частности: ![]()
, ![]()
, 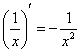
.
Зачем запоминать?
Данные знания являются элементарными
знаниями о производных. И если Вы не
сможете ответить преподавателю на
вопрос «Чему равна производная числа?»,
то учеба в ВУЗе может для Вас закончиться
(лично знаком с двумя реальными случаями
из жизни). Кроме того, это наиболее
распространенные формулы, которыми
приходится пользоваться практически
каждый раз, когда мы сталкиваемся с
производными.
В реальности
простые табличные примеры – редкость,
обычно при нахождении производных
сначала используются правила
дифференцирования, а затем – таблица
производных элементарных функций.
В этой
связи переходим к рассмотрению правил
дифференцирования:
1)
Постоянное число можно (и нужно) вынести
за знак производной
![]()
,
где
–
постоянное число (константа)
Пример 2
Найти
производную функции ![]()
Смотрим
в таблицу производных. Производная
косинуса там есть, но у нас ![]()
.
Решаем:
![]()
Самое время
использовать правило, выносим постоянный
множитель за знак производной:
![]()
А теперь превращаем
наш косинус по таблице:
![]()
Ну и результат
желательно немного «причесать» – ставим
минус на первое место, заодно избавляясь
от скобок:
![]()
Готово.
2)
Производная суммы равна сумме производных
![]()
Пример 3
Найти
производную функции ![]()
Решаем. Как Вы,
наверное, уже заметили, первое действие,
которое всегда выполняется при нахождении
производной, состоит в том, что мы
заключаем в скобки всё выражение и
ставим штрих справа вверху:
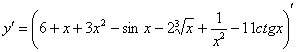
Применяем второе
правило:

Обратите
внимание, что для дифференцирования
все корни, степени нужно представить в
виде ![]()
,
а если они находятся в знаменателе, то
переместить их вверх. Как это сделать
– рассмотрено в моих методических
материалах.
Теперь вспоминаем
о первом правиле дифференцирования –
постоянные множители (числа) выносим
за знак производной:

Обычно в ходе
решения эти два правила применяют
одновременно (чтобы не переписывать
лишний раз длинное выражение).
Все функции,
находящиеся под штрихами, являются
элементарными табличными функциями, с
помощью таблицы осуществляем превращение:

Можно всё оставить
в таком виде, так как штрихов больше
нет, и производная найдена. Тем не менее,
подобные выражения обычно упрощают:

Все
степени вида
желательно
снова представить в виде корней, степени
с отрицательными показателями – сбросить
в знаменатель. Хотя этого можно и не
делать, ошибкой не будет.
Пример 4
Найти
производную функции ![]()
Попробуйте решить
данный пример самостоятельно (ответ в
конце урока)
3)
Производная произведения функций
Вроде
бы по аналогии напрашивается формула ![]()
….,
но неожиданность состоит в том, что:
![]()
Я не буду объяснять,
почему именно так, наша задача научиться
решать производные, а не разбираться в
теории.
Пример 5
Найти
производную функции ![]()
Здесь
у нас произведение двух функций, зависящих
от
.
Сначала
применяем наше странное правило, а затем
превращаем функции по таблице производных:
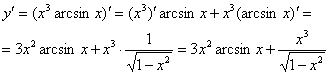
Сложно? Вовсе нет,
вполне доступно даже для чайника.
Пример 6
Найти
производную функции ![]()
В
данной функции содержится сумма ![]()
и
произведение двух функций –
квадратного трехчлена ![]()
и
логарифма ![]()
.
Со школы мы помним, что умножение и
деление имеют приоритет перед сложением
и вычитанием.
Здесь
всё так же. СНАЧАЛА мы
используем правило дифференцирования
произведения:
![]()
Теперь
для скобки ![]()
используем
два первых правила:

В результате
применения правил дифференцирования
под штрихами у нас остались только
элементарные функции, по таблице
производных превращаем их в другие
функции:

Готово.
При
определенном опыте нахождения производных,
простые производные вроде
не
обязательно расписывать так подробно.
Вообще, они обычно решаются устно, и
сразу записывается, что ![]()
.
Пример 7
Найти
производную функции ![]()
Это пример для
самостоятельного решения (ответ в конце
урока)
4)
Производная частного функций
В
потолке открылся люк, не пугайся, это
глюк.
А
вот это вот суровая действительность:

Пример 8
Найти
производную функции ![]()
Чего
здесь только нет – сумма, разность,
произведение, дробь…. С чего бы начать?!
Есть сомнения, нет сомнений, но, В
ЛЮБОМ СЛУЧАЕ для
начала рисуем скобочки и справа вверху
ставим штрих:
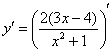
Теперь смотрим на
выражение в скобках, как бы его упростить?
В данном случае замечаем множитель,
который согласно первому правилу
целесообразно вынести за знак производной:
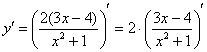
Заодно
избавляемся от скобок в числителе,
которые теперь не нужны.
Вообще
говоря, постоянные множители при
нахождении производной можно и не
выносить, но в этом случае они будут
«путаться под ногами», что загромождает
и затрудняет решение.
Смотрим на наше
выражение в скобках. У нас есть сложение,
вычитание и деление. Со школы мы помним,
что деление выполняется в первую очередь.
И здесь – сначала применяем правило
дифференцирования частного:

Таким образом,
наша страшная производная свелась к
производным двух простых выражений.
Применяем первое и второе правило, здесь
это сделаем устно, надеюсь, Вы уже немного
освоились в производных:

Штрихов больше
нет, задание выполнено.
На
практике обычно (но не всегда) ответ
упрощают «школьными» методами:
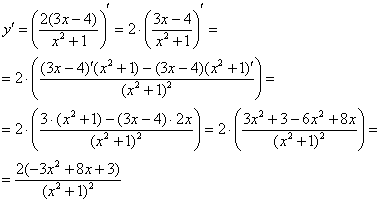
Пример 9
Найти
производную функции ![]()
Это пример для
самостоятельного решения (ответ в конце
урока).
Время от времени
встречаются хитрые задачки:
Пример 10
Найти
производную функции ![]()
Смотрим
на данную функцию. Здесь снова дробь.
Однако перед тем как использовать
правило дифференцирования частного (а
его можно использовать), всегда имеет
смысл посмотреть, а нельзя ли упростить
саму дробь, или вообще избавиться от
нее?
Дело в том, что формула
достаточно
громоздка, и применять ее совсем не
хочется.
В
данном случае можно почленно поделить
числитель на знаменатель.
Преобразуем
функцию:
![]()
Ну вот, совсем
другое дело, теперь дифференцировать
просто и приятно:
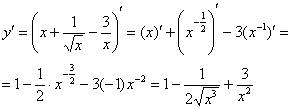
Готово.
Пример 11
Найти
производную функции ![]()
Здесь ситуация
похожа, превратим нашу дробь в произведение,
для этого поднимем экспоненту в числитель,
сменив у показателя знак:
![]()
Произведение
все-таки дифференцировать проще:
![]()
Пример 12
Найти
производную функции ![]()
Это пример для
самостоятельного решения (ответ в конце
урока).
5)
Производная сложной функции
Данное
правило также встречается очень часто.
Но о нём рассказать можно очень много,
поэтому я создал отдельный урок на
тему Производная
сложной функции.
Желаю успехов!
Ответы:
Пример
4: ![]()
.
В ходе решения данного примера следует
обратить внимание, на тот факт, что ![]()
и ![]()
–
постоянные числа, не важно чему они
равны, важно, что это – константы.
Поэтому
выносится
за знак производной, а![]()
.
Пример
7: ![]()
Пример
9: ![]()
Пример
12: ![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
08.02.20157.31 Mб91.rtf
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
