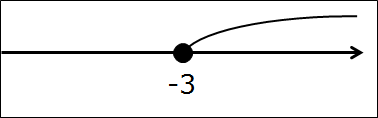
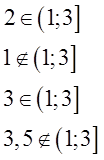Определите вид числового промежутка, составьте его аналитическую и геометрическую модели:
а) (−∞;3];
б) (−9;+∞);
в) (3;7);
г) [−28;0].
reshalka.com
ГДЗ учебник по математике 6 класс Зубарева. 11. Контрольные задания. Номер №1
Решение а
Получай решения и ответы с помощью нашего бота
(−∞;3] − луч, x ≤ 3
Решение б
(−9;+∞) − открытый луч, x > −9
Решение в
(3;7) − интервал, 3 < x < 7
Решение г
[−28;0] − отрезок, −28 ≤ x ≤ 0
Среди множеств чисел имеются множества, где объектами выступают числовые промежутки. При указывании множества проще определить по промежутку. Поэтому записываем множества решений, используя числовые промежутки.
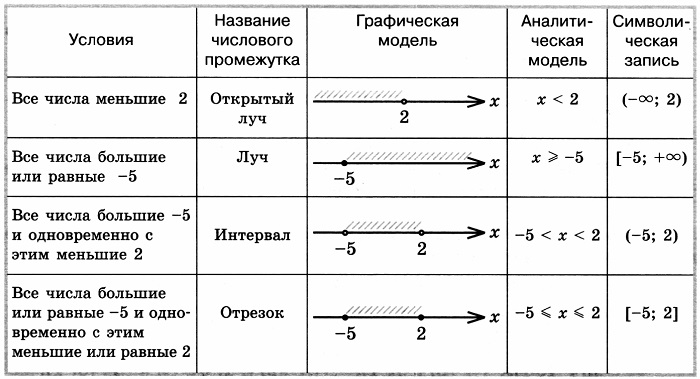
Данная статья дает ответы на вопросы о числовых промежутках, названиях, обозначениях, изображениях промежутков на координатной прямой, соответствии неравенств. В заключение будет рассмотрена таблица промежутков.
Виды числовых промежутков
Каждый числовой промежуток характеризуется:
- названием;
- наличием обычного или двойного неравенства;
- обозначением;
- геометрическим изображением на координатой прямой.
Числовой промежуток задается при помощи любых 3 способов из выше приведенного списка. То есть при использовании неравенства, обозначения, изображения на координатной прямой. Данный способ наиболее применимый.
Произведем описание числовых промежутков с выше указанными сторонами:
- Открытый числовой луч. Название связано с тем, что его опускают, оставляя открытым.
Этот промежуток имеет соответствующие неравенства x<a или x>a, где a является некоторым действительным числом. То есть на такое луче имеются все действительные числа, которые меньше a – (x<a) или больше a – (x>a).
Множество чисел, которые будут удовлетворять неравенству вида x<a обозначается виде промежутка (−∞, a), а для x>a, как (a, +∞).
Геометрический смыл отрытого луча рассматривает наличие числового промежутка. Между точками координатной прямой и ее числами имеется соответствие, благодаря которому прямую называем координатной. Если необходимо сравнить числа, то на координатной прямой большее число находится правее. Тогда неравенство вида x<a включает в себя точки, которые расположены левее, а для x>a – точки, которые правее. Само число не подходит для решения, поэтому на чертеже обозначают выколотой точкой. Промежуток, который необходим, выделяют при помощи штриховки. Рассмотрим рисунк, приведенный ниже.
Из вышеприведенного рисунка видно, что числовые промежутки соответствуют части прямой, то есть лучам с началом в a. Иначе говоря, называется лучами без начала. Поэтому он и получил название открытый числовой луч.
Рассмотрим несколько примеров.
При заданном строгом неравенстве x>−3 задается открытый луч. Эту запись можно представить в виде координат (−3, ∞) . То есть это все точки, лежащие правее, чем -3.
Если имеем неравенство вида x<2,3, то запись (−∞, 2,3) является аналогичной при задании открытого числового луча.
- Числовой луч. Геометрический смысл в том, что начало не отбрасывается, иначе говоря, луч оставляет за собой свою полноценность.
Его задание идет с помощью нестрогих неравенств вида x≤a или x≥a. Для такого вида приняты специальные обозначения вида (−∞, a] и [a, +∞), причем наличие квадратной скобки имеет значение того, что точка включена в решение или в множество. Рассмотрим рисунок, приведеный ниже.
Для наглядного примера зададим числовой луч.
Неравенство вида x≥5 соответствует записи [5, +∞), тогда получаем луч такого вида:
- Интервал. Задавание при помощи интервалов записывается при помощи двойных неравенств a<x<b, где а и b являются некоторыми действительными числами, где a меньше b, а x является переменной. На таком интервале имеется множество точек и чисел, которые больше a, но меньше b. Обозначение такого интервала принято записывать в виде (a, b). Наличие круглых скобок говорит о том, что число a и b не включены в это множество. Координатная прямая при изображении получает 2 выколотые точки.
Рассмотрим рисунок, приведенный ниже.
Пример интервала −1<x<3,5 говорит о том, что его можно записать в виде интервала (−1, 3,5). Изобразим на координатной прямой и рассмотрим.
- Числовой отрезок. Данный промежуток отличается тем, что он включает в себя граничные точки, тогда имеет запись вида a≤x≤b. Такое нестрогое неравенство говорит о том, что при записи в виде числового отрезка применяют квадратные скобки [a, b], значит, что точки включаются во множество и изображаются закрашенными.
Рассмотрев отрезок, получим , что его задание возможно при помощи двойного неравенства 2≤x≤3, которое изображаем в виде 2, 3. На координатной прямой данный точки будут включены в решение и закрашены.
- Полуинтервалы. Это промежуточные интервалы с включением приграничных точек. Они записываются при помощи двойных неравенств вида a<x≤b или a≤b<c, где (a, b] и [a, b). Изобразим на координатной прямой.
Если имеется полуинтервал (1, 3], тогда его обозначение можно в виде двойного неравенства 1<x≤3, при чем на координатной прямой изобразится с точками 1 и 3, где 1 будет исключена, то есть выколота на прямой.
Таблица числовых промежутков
Промежутки могут быть изображены в виде:
- открытого числового луча;
- числового луча;
- интервала;
- числового отрезка;
- полуинтервала.
Чтобы упростить процесс вычисления, необходимо пользоваться специальной таблицей, где имеются обозначения всех видов числовых промежутков прямой.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Числовые промежутки
- Виды числовых промежутков
- Открытый и замкнутый луч
- Отрезок
- Интервал и полуинтервал
Числовые промежутки или просто промежутки — это числовые множества, которые можно изобразить на координатной прямой. К числовым промежуткам относятся лучи, отрезки, интервалы и полуинтервалы.
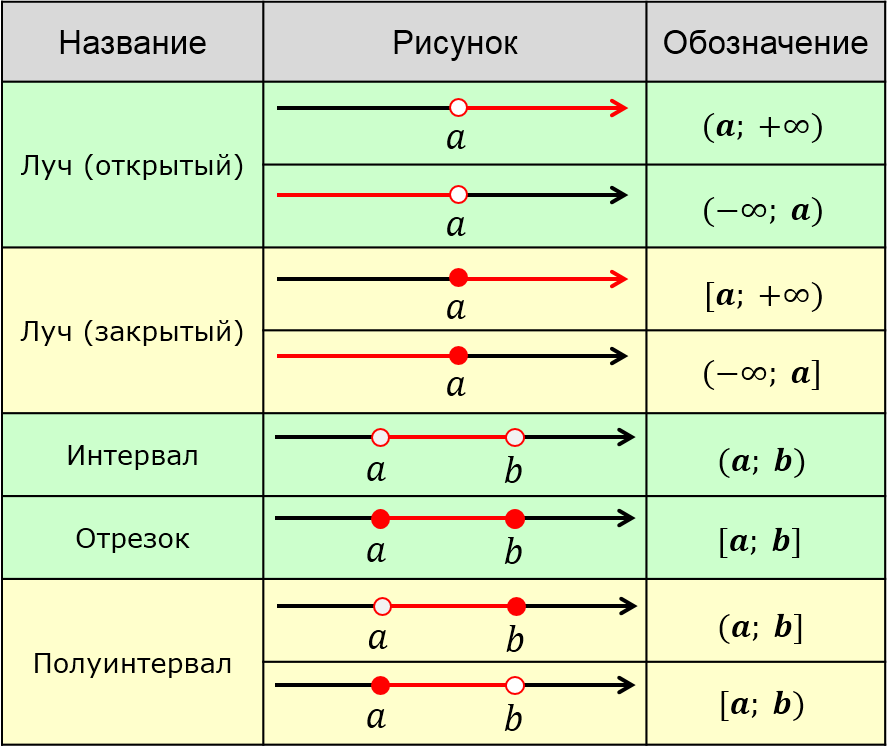
Виды числовых промежутков
| Название | Изображение | Неравенство | Обозначение |
|---|---|---|---|
| Открытый луч |  |
x > a | (a; +∞) |
 |
x < a | (-∞; a) | |
| Замкнутый луч |  |
x ⩾ a | [a; +∞) |
 |
x ⩽ a | (-∞; a] | |
| Отрезок |  |
a ⩽ x ⩽ b | [a; b] |
| Интервал |  |
a < x < b | (a; b) |
| Полуинтервал |  |
a < x ⩽ b | (a; b] |
 |
a ⩽ x < b | [a; b) |
В таблице a и b — это граничные точки, а x — переменная, которая может принимать координату любой точки, принадлежащей числовому промежутку.
Граничная точка — это точка, определяющая границу числового промежутка. Граничная точка может как принадлежать числовому промежутку, так и не принадлежать ему. На чертежах граничные точки, не принадлежащие рассматриваемому числовому промежутку, обозначают незакрашенным кругом, а принадлежащие — закрашенным кругом.
Открытый и замкнутый луч
Открытый луч — это множество точек прямой, лежащих по одну сторону от граничной точки, которая не входит в данное множество. Открытым луч называется именно из-за граничной точки, которая ему не принадлежит.
Рассмотрим множество точек координатной прямой, имеющих координату, большую 2, а, значит, расположенных правее точки 2:
Такое множество можно задать неравенством x > 2. Открытые лучи обозначаются с помощью круглых скобок — (2; +∞), данная запись читается так: открытый числовой луч от двух до плюс бесконечности
.
Множество, которому соответствует неравенство x < 2, можно обозначить (-∞; 2) или изобразить в виде луча, все точки которого лежат с левой стороны от точки 2:
Замкнутый луч — это множество точек прямой, лежащих по одну сторону от граничной точки, принадлежащей данному множеству. На чертежах граничные точки, принадлежащие рассматриваемому множеству, обозначаются закрашенным кругом.
Замкнутые числовые лучи задаются нестрогими неравенствами. Например, неравенства x ⩾ 2 и x ⩽ 2 можно изобразить так:
Обозначаются данные замкнутые лучи так: [2; +∞) и (-∞; 2], читается это так: числовой луч от двух до плюс бесконечности
и числовой луч от минус бесконечности до двух
. Квадратная скобка в обозначении показывает, что точка 2 принадлежит числовому промежутку.
Отрезок
Отрезок — это множество точек прямой, лежащих между двумя граничными точками, принадлежащими данному множеству. Такие множества задаются двойными нестрогими неравенствами.
Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:
Множество точек, из которых состоит данный отрезок, можно задать двойным неравенством -2 ⩽ x ⩽ 3 или обозначить [-2; 3], такая запись читается так: отрезок от минус двух до трёх
.
Интервал и полуинтервал
Интервал — это множество точек прямой, лежащих между двумя граничными точками, не принадлежащими данному множеству. Такие множества задаются двойными строгими неравенствами.
Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:
Множество точек, из которых состоит данный интервал, можно задать двойным неравенством -2 < x < 3 или обозначить (-2; 3). Такая запись читается так: интервал от минус двух до трёх
.
Полуинтервал — это множество точек прямой, лежащих между двумя граничными точками, одна из которых принадлежит множеству, а другая не принадлежит. Такие множества задаются двойными неравенствами:
Обозначаются данные полуинтервалы так: (-2; 3] и [-2; 3). Читается это так: полуинтервал от минус двух до трёх, включая 3
, и полуинтервал от минус двух до трёх, включая минус два
.
Числовые промежутки представляют собой множества чисел на координатной прямой. Это ось, на которой расположены точки или переменные, имеющие определенные координаты. Для нее важно начало отсчета, выбранный единичный отрезок и направление, чтобы обозначать положительные и отрицательные значения.
Знакомство с координатами и числами происходит на уроках математики в 6 классе, но некоторые понятия вводятся уже с 1 класса. Понятия и обозначения используются на протяжении всего курса алгебры и геометрии. Знакомство с азами в средней школе позволит легко справляться со сложными задачами в будущем. Со временем проводятся вычисления со множествами чисел, это касается их пересечения и объединения.
Виды числовых промежутков
На координатной прямой можно выделить несколько видов промежутков. При этом они зависят от одной или двух переменных, расположенных на оси. Они служат границами. Сама прямая имеет координаты (-∞; +∞), то есть от минус бесконечности до плюс бесконечности.
Промежутки позволяют находить значения числовых выражений даже для учащихся младших классов. Выбирается место отсчета и единичный отрезок, что характеризует любую координатную прямую.
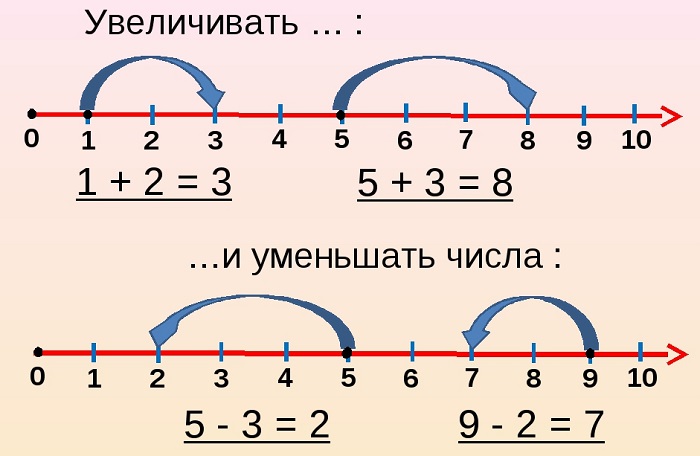
Чтобы выполнить простое арифметическое действие, нужно нарисовать нужное число отрезков. Чтобы сложить «2» и «3», достаточно отмерить сначала два, затем три выбранных единицы и сосчитать полученный результат. Так наглядно представляются простые математические операции для младших школьников.
На координатную прямую можно нанести известные значения и сравнить их, обращая внимание на положение. Так дети наглядно представляют, какое число меньше, а какое больше.
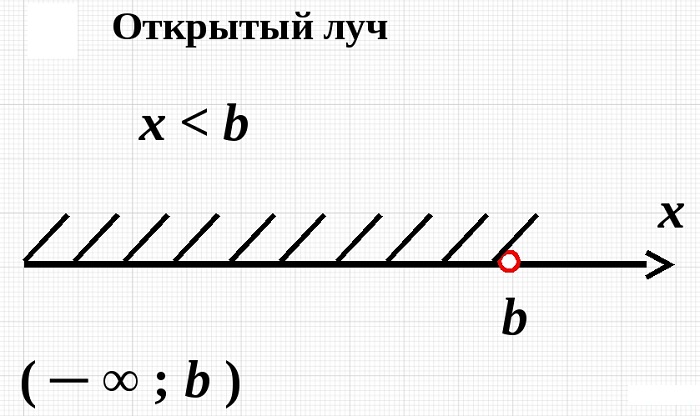
Открытый числовой луч
Открытый луч – интервал с бесконечно большим числом точек. При объяснении понятие «числовой» часто опускается, при этом смысл не меняется.
Точки расположены по одну сторону от определенной переменной, признанной началом координат.
Находиться они могут как с правой, так и с левой стороны. При этом если за основу берется А, то множество обозначается следующим образом:
-
(-∞; А);
-
(А; +∞).
Таким образом указываются координаты. Читается как «от минус бесконечности до А» и «от А до плюс бесконечности».
Также можно охарактеризовать неравенством:
-
х < А;
-
х > А.
Знак зависит от расположения луча относительно А.
Замкнутый числовой луч
Замкнутый луч отличается от открытого тем, что к множеству относится А.
Также ему соответствует условие:
-
х ≤ А (значение меньше или равно А) или (-∞; А], то есть используются квадратные скобки;
-
х ≥ А (значение больше или равно А) или [А; +∞).
При графическом изображении А в этом случае закрашивается, на рисунке она черная.
Что касается открытого луча, то там А остается пустой, еще ее называют выколотой. Она связана с переменной строгим неравенством, не принадлежит к рассматриваемому множеству.
Числовой отрезок
Отрезок – замкнутый, закрытый промежуток или расстояние. Это множество переменных, расположенных на прямой между двумя точками, А и В. При этом они относятся к рассматриваемому множеству и называются концами.
При изображении они будут закрашены. Остальные точки отрезка считаются внутренними.
Обозначается отрезок, например, -7 ≤ х ≤ 3. Запись читается следующим образом: «отрезок от минус семи до трех».
Интервал
Интервал представляет собой открытый отрезок, от которого он отличается тем, что границы к нему не относятся. Интервалу принадлежат исключительно внутренние точки прямой, границы же будут выколоты.
Обозначается, например, 5 < х < 13. Читается запись как «интервал от пяти до тринадцати».
Полуинтервал
Полуинтервал – интервал, при этом одна из точек, его ограничивающих, входит в него. То есть он закрыт с одной стороны. При этом неважно, какая из границ будет принадлежать интервалу, а какая нет.
Обозначаются с помощью двойных неравенств, при этом они называются нестрогими, так как используются знаки «больше или равно» или «меньше или равно». Одна из точек на графике не будет закрашена.
Обозначение может выглядеть, например, так -2 ≤ х < 9, «полуинтервал от минус двух до девяти».
Таблица числовых промежутков
Все промежутки имеют обозначения и неравенства. Данные об этом собраны в таблице. Каждому виду соответствует графическое изображение.
Наглядное изображение поможет восприятию и закреплению материала.
Границы представлены а и b, они так и называются, граничными точками. При этом знаки ≥ и ≤ обозначаются квадратной скобкой. При графическом изображении такая граница закрашивается, это означает, что она входит в множество. Строгие неравенства соответствуют выколотым точкам на графиках.
Промежутки знакомят школьников с простыми неравенствами, строгими и нестрогими, которые необходимы для решения сложных математических задач.
Числовые промежутки
Числовые промежутки или просто промежутки — это числовые множества, которые можно изобразить на координатной прямой. К числовым промежуткам относятся лучи, отрезки, интервалы и полуинтервалы.
Виды числовых промежутков
| Название | Изображение | Неравенство | Обозначение |
|---|---|---|---|
| Открытый луч |  |
x > a | (a; +∞) |
 |
x < a | (-∞; a) | |
| Замкнутый луч |  |
x ⩾ a | [a; +∞) |
 |
x ⩽ a | (-∞; a] | |
| Отрезок |  |
a ⩽ x ⩽ b | [a; b] |
| Интервал |  |
a < x < b | (a; b) |
| Полуинтервал |  |
a < x ⩽ b | (a; b] |
 |
a ⩽ x < b | [a; b) |
В таблице a и b — это граничные точки, а x — переменная, которая может принимать координату любой точки, принадлежащей числовому промежутку.
Граничная точка — это точка, определяющая границу числового промежутка. Граничная точка может как принадлежать числовому промежутку, так и не принадлежать ему. На чертежах граничные точки, не принадлежащие рассматриваемому числовому промежутку, обозначают незакрашенным кругом, а принадлежащие — закрашенным кругом.
Открытый и замкнутый луч
Открытый луч — это множество точек прямой, лежащих по одну сторону от граничной точки, которая не входит в данное множество. Открытым луч называется именно из-за граничной точки, которая ему не принадлежит.
Рассмотрим множество точек координатной прямой, имеющих координату, большую 2, а, значит, расположенных правее точки 2:
Такое множество можно задать неравенством x > 2. Открытые лучи обозначаются с помощью круглых скобок — (2; +∞), данная запись читается так: открытый числовой луч от двух до плюс бесконечности .
Множество, которому соответствует неравенство x < 2, можно обозначить (-∞; 2) или изобразить в виде луча, все точки которого лежат с левой стороны от точки 2:
Замкнутый луч — это множество точек прямой, лежащих по одну сторону от граничной точки, принадлежащей данному множеству. На чертежах граничные точки, принадлежащие рассматриваемому множеству, обозначаются закрашенным кругом.
Замкнутые числовые лучи задаются нестрогими неравенствами. Например, неравенства x ⩾ 2 и x ⩽ 2 можно изобразить так:
Обозначаются данные замкнутые лучи так: [2; +∞) и (-∞; 2], читается это так: числовой луч от двух до плюс бесконечности и числовой луч от минус бесконечности до двух . Квадратная скобка в обозначении показывает, что точка 2 принадлежит числовому промежутку.
Отрезок
Отрезок — это множество точек прямой, лежащих между двумя граничными точками, принадлежащими данному множеству. Такие множества задаются двойными нестрогими неравенствами.
Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:
Множество точек, из которых состоит данный отрезок, можно задать двойным неравенством -2 ⩽ x ⩽ 3 или обозначить [-2; 3], такая запись читается так: отрезок от минус двух до трёх .
Интервал и полуинтервал
Интервал — это множество точек прямой, лежащих между двумя граничными точками, не принадлежащими данному множеству. Такие множества задаются двойными строгими неравенствами.
Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:
Множество точек, из которых состоит данный интервал, можно задать двойным неравенством -2 < x < 3 или обозначить (-2; 3). Такая запись читается так: интервал от минус двух до трёх .
Полуинтервал — это множество точек прямой, лежащих между двумя граничными точками, одна из которых принадлежит множеству, а другая не принадлежит. Такие множества задаются двойными неравенствами:
Обозначаются данные полуинтервалы так: (-2; 3] и [-2; 3). Читается это так: полуинтервал от минус двух до трёх, включая 3 , и полуинтервал от минус двух до трёх, включая минус два .
Числовые промежутки — что такое?
Числовая прямая (или, что то же самое, числовая ось) — понятие нехитрое. Более того, числовая прямая — главный помощник в решении любых заданий с неравенствами! Любых. От примитивных линейных неравенств до сложных показательных или логарифмических неравенств, систем неравенств и метода интервалов. Освоим темку, пока всё просто?)
Что такое числовая прямая? Что такое координатная прямая?
С понятием числовой прямой вы все уже сталкивались, когда изучали такие темы как координаты точек (5-й класс), страшное понятие модуля числа (6-й класс), и особенно когда рисовали графики функций (7-й класс). Вспомним ещё разок?)
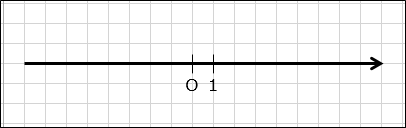
Всё то же самое, ничего нового! Первым делом возьмём и нарисуем в тетрадке самую обычную прямую и дополнительно укажем на ней:
1) Начало отсчёта или начало координат (точку О);
2) Положительное направление (стрелочкой);
3) Масштаб или единицу измерения длины (например, одна тетрадная клетка).
Вот и всё. Про устройство числовой прямой вы тоже давно в курсе (надеюсь). Но на всякий случай напоминаю. Начало координат всегда соответствует числу 0. Все положительные числа изображаются на положительной полуоси справа от нуля, в направлении стрелочки. А все отрицательные — слева от нуля, на отрицательной полуоси. Большее число всегда располагается правее меньшего, а меньшее — левее большего. Элементарно, Ватсон!)
Ну хорошо, прямая и прямая. Но почему — числовая? Ответ очевиден. Каждой точке на прямой соответствует какое-то число. Положительное, отрицательное, целое, дробное, иррациональное — какое угодно. Но — число! Поэтому и прямая — числовая. Это число имеет специальное и вполне научное название — координата точки. Отсюда следует, что числовая прямая — и координатная прямая тоже. Вот так. Два термина в одном флаконе.)
А вот теперь мы с вами колоссально расширяем наши возможности. Начинаем работать с числовой прямой на полную катушку! Готовы?)
Что такое числовой промежуток? Виды числовых промежутков.
В уравнениях было всё просто. Нашли икс, да и записали в ответ. Например, х=2. В неравенствах же ответом обычно служит не одно-два числа, а промежуток. Числовой промежуток. Или даже несколько числовых промежутков. Это и смущает поначалу…) Что это за зверь такой — числовой промежуток?
Числовой промежуток — это просто какой-то кусочек числовой прямой. И всё!
Сейчас начинается самое весёлое. Сейчас мы нашу числовую прямую будем пилить.) Пилить не на дрова, а на… числовые промежутки.)
Вот прям берём числовую прямую и вырезаем из неё какой-то кусочек какими-то точками. Которые, напоминаю, соответствуют каким-то числам. Вот и получаем — числовой промежуток. Разумеется, вырезать конкретный кусочек числовой прямой можно по-разному, да…)
Соответственно, и числовые промежутки в математике бывают разных видов.
Вот они, эти виды (подкрашены красным цветом):
Смотрим на табличку и… мама родная! Какие-то непонятные кружочки (пустые внутри и закрашенные), какой-то странный иероглиф «∞», да ещё и со знаками плюс/минус, круглые и квадратные скобочки.
Вам и вправду страшно? Возможно… Но сейчас вы увидите, насколько всё просто! Читаем дальше.)
Граничные точки
Я разгадала знак бесконечность… (Земфира)
Те точки, которые нам указывают, в каких местах мы выпиливаем кусочек прямой, так и называются — граничные точки. В таблице эти самые граничные точки обозначены буковками a и b. Точка a — левая граница (меньшее число), точка b — правая граница (большее число).
А может ли числовой промежуток в каком-то направлении быть неограниченным?
А почему — нет? Запросто! Можно распилить числовую прямую не в двух точках, а в какой-то одной точке. И забрать себе одну часть — левую или правую. Бесконечную… Или — луч. Только для обозначения этой бесконечной границы буквы или числа не годятся. Зато есть специальный значок «∞«. Значок этот так и называется — «бесконечность». Очевидно, бесконечность бывает двух видов (точнее, двух знаков) — плюс (+∞) или минус (-∞). В зависимости от того, какой именно луч, какая часть прямой, правая или левая, берётся на дальнейшее рассмотрение.
Кружочки и скобочки…
Граничная точка — это, как и намекает название, точка, задающая границу числового промежутка. Слева или справа. Естественно, у думающих тут же возникает вполне логичный и важный вопрос: А куда относить саму граничную точку? Включать её в состав промежутка или нет?
Именно для ответа на этот вопрос нам и служат всякие кружочки и скобочки в обозначениях и на рисунках!
Запоминаем:
Если граничная точка в числовой промежуток НЕ ВХОДИТ, то на числовой прямой она рисуется НЕЗАКРАШЕННОЙ. Т.е. пустой внутри. В математике такие точки называются выколотыми точками. В обозначениях выколотые точки всегда соседствуют с круглыми скобками «(» или «)».
Если же граничная точка в числовой промежуток ВХОДИТ, то на числовой прямой она рисуется ЗАКРАШЕННОЙ, а в записи обозначается квадратной скобкой «[» или «]».
Вот и вся расшифровка.) Кстати говоря, специальные названия промежутков (луч, отрезок, интервал, полуинтервал) запоминать пока не обязательно. Всё равно поначалу будете путаться. Это для общей эрудиции сделано.) На практике обычно не заморачиваются и говорят «числовой промежуток такой-то…», без уточнения вида — луч, отрезок и т.д. А иногда и совсем кратко — просто «промежуток». Если и вы путаетесь — говорите так же. Не ошибётесь! А спецназвания оставим для старших классов. Но если запомнили (и поняли!) названия промежутков — что ж, только респект!)
Теперь можно потренироваться в записи и чтении числовых промежутков. Чтобы не мычать… Ну что, потренируемся?
Читаем числовые промежутки и рисуем их на оси!
С чтением и рисованием числовых промежутков обычно никаких проблем нет. Нужно только чётко понимать, что означают все эти скобочки и кружочки, что разбирались в предыдущем параграфе.
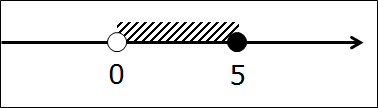
Например, задан числовой промежуток (0; 5].
Словами эта запись звучит так: числовой промежуток от нуля до пяти, не включая ноль и включая пять.
Читаем (и пишем) именно в таком порядке — от левой границы до правой.
Левая граница (т.е. число 0) соседствует с круглой скобкой «(«, о чём нам и говорят слова «не включая». Этот факт означает, что число 0 в наш промежуток не входит. Например, число 0,1 входит, и даже 0,000001 — ещё входит. Хоть чуть-чуть, да больше нуля. А вот ровно ноль — уже нет…
Пятёрка же — напротив, соседствует с квадратной скобкой «]», что говорит нам о том, что сама она также входит в наш промежуток. И отражено словом «включая» в словесной расшифровке.
А теперь нарисуем наш промежуток на оси. Для этого рисуем числовую прямую и отмечаем на ней граничные точки 0 и 5.
Заметили разницу между нулём и пятёркой? Ну да, трудно не заметить! 😉 Точка 0 изображена белой, т.е. незакрашенной. Пустой внутри. Или, по-математически, выколотой точкой. Это, как мы с вами уже выяснили, означает, что ноль — не входит в наш промежуток. В отличие от пятёрки, которая входит в промежуток. И на рисунке, соответственно, нарисованной чёрной. Закрашенной.) Я специально точки такими здоровыми изобразил. Чтобы хорошенько врезались в память…
Итак, мы отметили на оси границы промежутка. Осталось лишь отметить все остальные числа, которые входят в этот промежуток. Вы спросите: Как? Ведь между нулём и пятёркой находится бесконечно много чисел! Это и 1, и 2,5, и 3,14, и 4,9999 и так далее… И что? Все-все отмечать)?
Нет, конечно. Всё гораздо проще!) Сейчас мы с вами отметим на прямой все интересующие нас числа одним махом! Тут есть два варианта. Вариант первый — штриховка. Просто берём и подштриховываем весь кусочек прямой между 0 и 5.
Вариант второй рассмотрим на следующем примере.
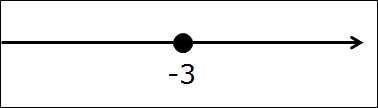
В этот раз дан промежуток такой: [-3; +∞).
Для начала читаем словами название промежутка с гордо поднятой головой: Числовой промежуток от минус трёх до плюс бесконечности, включая минус три!
Вот так. А теперь вопрос на засыпку: почему я оборвал чтение на словах «включая минус три…» и не продолжил мысль гениальными словами «…и не включая плюс бесконечность»?
Всё очень просто. Бесконечность (что плюс, что минус) не может включаться никогда. Это не число, это — символ. Поэтому в подобных записях бесконечность всегда соседствует с круглой скобкой, а в расшифровке говорится просто: «до плюс бесконечности». Или «до минус бесконечности». И всё.
А теперь всё как обычно, рисуем прямую, отмечаем на ней одну единственную точку минус три. Закрашенную, естественно, раз уж скобочка перед минус тройкой — квадратная. Вот так:
И отмечаем все остальные числа, входящие в промежуток от минус тройки до плюс бесконечности. На этот раз я отмечу нужный кусок оси дужкой (от слова дуга) вместо штриховки. Вот так:
Особой разницы между штриховкой и дужками нет. Рисуйте как удобнее. Но в сложных заданиях с неравенствами, где надо постоянно пересекать и объединять много промежутков, дужки предпочтительнее, ибо штриховка куда менее наглядна. Запутаться можно.
Я предпочитаю совмещать оба способа. Получается красиво и наглядно! В следующем уроке, на примерах, сами увидите.)
Вот так рисуются числовые промежутки на оси.
Входит и выходит… ))
А какая нам разница, входит число в указанный промежуток или не входит?
Вопрос смешной. Огромная! Ответ на этот вопрос (входит/не входит) — это ключевой этап в работе с промежутками и с неравенствами вообще! Даже значки специальные придуманы для этого. Вот такие:
За этими странными значками скрываются безобидные слова «принадлежит» и «не принадлежит».
Возьмём, к примеру, промежуток (1; 3].
Входит в этот промежуток, допустим, двойка? Конечно! Раз уж она посерёдке между единичкой и тройкой… А единичка? Э-э-э… Скобка перед ней — круглая! Не входит единичка в наш промежуток. Тройка входит? Попадает на границу, но скобочка — квадратная. Значит, входит! А вот три с половиной — снова не входит. 3,5 строго больше, чем тройка. Выпадает 3,5 из нашего промежутка…
Математически, с помощью значков принадлежности, эти факты можно записать вот так:
А словами можно прочитать вот так:
Два принадлежит промежутку от одного (не включая) до трёх (включая).
Один не принадлежит промежутку от одного (не включая) до трёх (включая).
В этом уроке было простое чтение и рисование промежутков на оси. Пока — цветочки. Переходим к ягодкам. К операциям над числовыми промежутками. Те ещё грабли, да…) Об этом — в следующем уроке.
Какое из данных чисел принадлежит промежутку
Какое из данных чисел принадлежит промежутку N — это задание из ОГЭ под номером 7. Давайте разберемся, как решать такие задачи и решим некоторые из них. В этих задачах вам нужно уметь представлять числовую ось и расположение чисел на ней. А также знать операции и функции, которые при вычислении могут дать искомое число.
Задание 1
Решение: Итак нам даны квадратные корни, которые при извлечении должны нам дать число из указанного промежутка. Каким же должно быть число под корнем? Чтобы ответить на этот вопрос возведем в квадрат границы промежутка:
и
.
То есть, искомое число лежит между 25-ю и 36-ю под корнем. Из представленных вариантов ответов нам подходит только число . Это число под номером 4. Поэтому в ответ мы запишем 4.
Задание 2
Нам снова даны не уже готовые числа, а функции от числа, при выполнении которых получаются какие то числа, одно из них должно попасть в промежуток [6; 7]. Сделаем обратную операцию — возведем в квадрат числа — границы промежутка — и определим в каким пределах находится число под корнем в списке вариантов ответов.
и
Нам подходит число . В перечне ответов оно под номером 3.
Задание 3
Решение: В вариантах ответов даны дроби. Значит частное должно быть числом, в промежутке от 7 до 8. Все дроби в знаменателе имеют 11. Давайте определим числитель, исходя из определения промежутка, в котором он может находиться. То есть умножим числа — границы указанного промежутка — на 11:
и
.
Таким образом, числитель дроби должен быть в промежутке от 77 до 88. Это число 80 и, соответственно, искомое число . Оно стоит под номером 2.
Задание 4
Решение: По аналогии с предыдущим заданием, мы должны определить числитель, умножим границы отрезка на 7.
и
Нам подходит дробь . Она под номером 3. Значит, в ответ мы запишем 3.