Привет, любители математики!
Современная математика без труда умеет вычислять площадь круга через интеграл. Но как с этой задачей справлялась математика во времена, когда интегралов еще не было?..
В школе, нам как данность дают формулу площади круга – пи эр квадрат. Не знаю, возможно, кому то учителя и рассказывают, каким образом эту формулу получили, я вот не помню, честно.
Вопросом вычисления площади круга занимался в свое время мало кому ныне известный Гиппократ Хиосский, о котором я, кстати уже писал. Умный мужик был…
Так вот, этот Гиппократ первым начал утверждать, что площадь круга пропорциональна квадрату его диаметра. Вот только коэффициент пропорциональности ему не давался, уж не знаю почему…
Так вот, круг был действительно проблемой в те времена. Поэтому, решили воспользоваться хитростью.
Было известно, что длина окружности равна:
А что если, разделить окружность на сегменты и попробовать сложить?
И не просто сложить, а вот таким образом:
Хм, а что если разделить на еще большее количество частей? На 8 к примеру…
Таким образом, можно уменьшать эти сегменты до бесконечности, пока не получим прямоугольник!
Получился почти прямоугольник, можно было сделать и 1 градус, но там все в кашу превращалось… Думаю, площадь прямоугольника все умеют находить?..
То что я показал, называется “Доказательство перегруппировкой“. Кем оно было выведено, я так и не понял. Если знаете, поделитесь, будет интересно!
Есть и другие доказательства. Тот же Архимед искал площадь круга через треугольники, но это уже совсем другая история…
Как я и написал в самом начале, доказательство также можно найти с помощью интеграла, это уже более громоздкий способ, но он явно показывает, что древние не ошиблись и пошли по правильному пути.
Многие исследователи считают, что это число было открыто вавилонскими магами и использовалось при строительстве Вавилонской башни и храма Соломона. Число «пи» – отношение длины окружности к диаметру – во многих учениях считалось мистическим, считается, что именно на этом числе древние греки построили свою религию. Так как это отношение немного более 3 и одинаково справедливо для любой окружности, позволяло считать эту величину одной из формообразующих статей (систем).
Можно предположить, что с числом π связано и недавнее происшествие с аварийным запуском ракеты-носителя «Протон-М» с тремя спутниками.
Алгоритм построения квадратуры круга можно вычислить, не прибегая к созданию кривых, как это делал Гиппократ Хиосский, а начать с построения квадрата:
1. Начнем с построения квадрата, отмеряя циркулем 10 равных отрезков на прямой.
2. Строим параллельную прямую (вторую сторону квадрата) которую так же разбиваем на 10 равных отрезков.
3. Соединяем обе параллельные по линиям, полученным в результате разметки. У нас получился квадрат, разбитый на 10 уровней (вертикальную разбивку в данном случае делать не обязательно).
4. Проводим диагональ квадрата из левого нижнего угла в правый верхний угол. Диагональ, проходящая через размеченные уровни квадрата, так же оказывается размеченной на 10 частей.
5. Находим центр квадрата и отмеряем четыре отрезка на диагонали от центра к правому верхнему углу. Этим радиусом из центра квадрата чертим круг. Площадь полученного круга – равновелика площади квадрата из центра, которого вычерчен круг.
Примечания: Данный расчет основан на принципе системного построения, когда
в пифагорейской системе 9-й, уровень является трансформирующим. Приводим теорему Фалеса: Если параллельные прямые пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне. Эти задачи были доказаны древними мастерами, и мы их так же решили с учетом
древних знаний.
Однако отношение науки к решению древних задач заставляет делать соответствующие выводы: Задачи построения квадратуры круга, трисекции угла и удвоения куба решаемы [1].
Отсюда вытекает следствие, – выводы Ванцеля и Линдемана основанные на применении инструментов не участвующих в построении задачи не корректны и не могут утверждать невозможность построения вышеуказанных задач.
1. Радиус круга и его площадь не могут являться атрибутами числа «пи» т.к. это составляющие геометрической фигуры, где число «пи» является всего лишь коэффициэнтом периметра ограничивающего площадь фигуры.
Поэтому теорема Линдемана не может служить доказательством невозможности решения указанных выше задач. Выяснилось, что на сегодняшний день мы не имеем инструмента вычислять площадь круга. Есть трансцендентная π, которая используется до сего дня, и нет постоянной величины, которая должна быть второй компонентой для вычисления площади круга.
Мы даже не знаем, как проверить правильность выполнения этих задач, не применяя никакой цифири, как это требуют условия задачи. Разве только вернуться на две тысячи лет назад к Архимеду (который знал, как это сделать) и его ванне с водой.
И тут возникает мысль: « А вдруг это место еще не занято и никто после того как задачи «запретили» не вычислял нужного числового значения? Маловероятно, но как говорится в таких случаях, это будем мы:
Для начало находим следствие: Вокруг правильного n – угольника можно описать окружность. В каждый правильный многоугольник можно вписать окружность.
Измеряем гипотенузу прямоугольного треугольника со сторонами 10 и 10.
Итак: Нужен корень квадратный из 200, который вычисляем приблизительно до 4-й цифры после нуля, используя тетрадь в клетку и линейку = 14.1422.
Далее вычисляем радиус: 14.1422:10×4=5.65688; тогда r²=5.65688×5.65688=32.000291
Отсюда вычисляем «постоянную»: 100:32.000291=3.12497158228
Проверка: 32.000291×3.12497=99.9999
Возьмем другой прямоугольный треугольник со сторонами 11×11; Вычисляем гипотенузу и находим радиус: 15.55:10×4=6.22; 6.22×6.22×3.12497=120.900; При этом 11×11=121.
Повторим опыт еще раз и возьмем следующий прямоугольный треугольник со сторонами 12×12; Вычисляем гипотенузу и находим радиус: 17:10×4=6.8; 6.8×6.8 ×3.12497=144.49; При этом 12×12=144.
Выводим формулу Sкр.=πкр.r²; где Sкр.- площадь круга; πкр.- постоянная Пифагора (отдадим должное основоположнику математики); r- радиус круга.
Проверяем расчеты со старой и новой формулой на квадрате со сторонами 10×10
Использование формулы Sкр.=πr²: Внешний радиус: 7.0711×7.0711=50.00×3.14=157
Апофема: 5×5=25.00×3.14=78.5
Использование формулы Sкр.=πкр.r²: Внешний радиус: 7.0711×7.0711=50.00×3.12=156
Апофема: 5×5=25.00×3.12=78.00
Две системы уравнений называются равносильными, если эти системы имеют одни и те же решения.
Следствие: Если каждое уравнение системы заменить равносильным уравнением, то получится система, равносильная данной.
Вывод: Постоянная πкр. соответствует требованиям геометрии для построения фигур. В то время как число π трацедентно и в построении точных фигур использоваться не должно т. к это вектор, показывающий наибольшую (раздутую) возможную величину периметра окружности.
В связи с тем, что разница между переменной π =3.14 и вычисленной нами постоянной πкр. = 3.12 составляет 0.02 то в расчетах этого искажения практически не видно. Результат отклонения может сказаться только при вычислении больших орбит и траекторий когда, например ракета, не имеющая дополнительного к расчетному (при экономии горючего) энергетического запаса может не достигнуть нужной высоты полета.
Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.

Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно: Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:

![]() Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.
Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.

Площадь нашей окружности будет равна 50,24 кв. см.
Существует формула площади круга через диаметр. Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения площади треугольника по площади описанной окружности.

![]() Рассмотрим пример расчета площади круга через диаметр, зная его радиус. Пусть дана окружность с радиусом R = 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.
Рассмотрим пример расчета площади круга через диаметр, зная его радиус. Пусть дана окружность с радиусом R = 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.


Теперь используем данные для примера расчета площади круга по приведенной выше формуле:

Как видим, в результате получаем тот же ответ, что и при первых расчетах.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности: 
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности

![]() Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l = 8 см. Подставим значение в выведенную формулу:
Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l = 8 см. Подставим значение в выведенную формулу:

Итого площадь круга будет равна 5 кв. см.
Площадь круга описанного вокруг квадрата

Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора:  отсюда
отсюда  .
.
После того, как найдем диагональ – мы сможем рассчитать радиус:  .
.
И после подставим все в основную формулу площади круга описанного вокруг квадрата: 
![]() Рассмотрим пример расчета площади круга, описанного вокруг квадрата.
Рассмотрим пример расчета площади круга, описанного вокруг квадрата.
Задача: дан квадрат, вписанный в круг. Его сторона a = 4 см. Найдите площадь окружности.
Для начала рассчитаем длину диагонали d.


Теперь подставляем данные в формулу

Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.
Архимед ошибался, когда вычислил площадь круга как произведение квадрата радиуса круга на число Пи=3.14. Проблема этого математика в том, что он не знал цифру 0, которая в “античности” (а это средневековье) не использовалась. Я много раз пояснял, что вся античность создана монахами Ватикана, с целью удревления последнего. Так вот, средневековая Европа 0 не знала.
Вот посмотрите, как действовал Архимед. Он просто разбил круг на сектора, а затем сложил их вот так:

Сочинение Архимеда “Измерение круга”. Это сравнительно простая работа, посвященная длине окружности и площади круга. В ней изложены три теоремы.
Теорема 1
Круг равен треугольнику, основание которого есть окружность, а высота – радиус:
где R – радиус окружности, L – ее длина, S – площадь круга. Доказательство проводится методом исчерпывания, а следовательно, от противного.
В этом первая ошибка Архимеда. Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая. При построении Архимеда в виде сложения секторов нетрудно догадаться, что нарушено главное условие равноудаленности всех точек окружности от ЕДИНОГО центра. Сектора Архимеда имеют каждый свой центр и рассматриваться как единое целое не могут. Каждый последующий центр удален от другого либо на расстояние радиуса, либо на расстояние хорды, соединяющей точки окружности.
Теорема 2
Круг относится к квадрату на диаметре ( приближенно) как 11:14 ,
,
где D – диаметр. Доказательство дано с помощью правильных описанных многоугольников при удвоении числа их сторон.
Интересно посмотреть, каким же было здесь для Архимеда число π. Сначала используем точную формулу площади круга:
Теперь применим приближенную формулу Архимеда
Эти два выражения приравняем. Достаточно приравнять коэффициенты при  :
:
Это хорошее приближение для числа . Приближенное значение π, равное 3
. Приближенное значение π, равное 3 , позднее получило название архимедова числа. Оно удобно тем, что здесь используется дробь
, позднее получило название архимедова числа. Оно удобно тем, что здесь используется дробь с числителем, равным 1, и маленьким знаменателем.
с числителем, равным 1, и маленьким знаменателем.
Простите, но тт число ИРРАЦИОНАЛЬНОЕ, в то время, как приравненная часть выражения РАЦИОНАЛЬНА. Приравнивание рационального и иррационального может происходить только через интегрирование, которого Архимед еще не знал.
Философия традиционно выделяла в акте человеческого познания два его различных вида: чувственное (перцептивное) и рациональное. Первый самоочевидно связан с деятельностью наших органов чувств (зрения, слуха, осязания и пр.). Второй подразумевает работу разума – абстрактно-понятийное мышление, рассудочную деятельность человека.
Иррациональное (от латинского irrationalis – неразумный) – находящееся за пределами разума, алогическое, неинтеллектуальное, несоизмеримое с рациональным мышлением или противоречащее ему. Иррациональное – нечто, находящееся за пределами разума, противоречащее логике. Обычно противопоставляется рациональному как разумному, целесообразному, обоснованному. Понимание иррационального зависит от определения понятия рационального.
Рациональное – знание, постижимое с помощью разума. Исходя из привычки, можно воссоздать особенности того, что мы называем «разумом»; разум – разумно обоснованное, целесообразное – устройство или поступок, которым присуща некоторая цель. Целесообразные поступки и устройства, отправляющиеся от разума, осуществляющие или существующие благодаря разуму.
При интеграции иррационального в рациональное и наоборот, возникает третья форма знания.
Внерациональное знание – знание, не вписывающееся в жесткие каноны научной рациональности, а также представляющее собой способ освоения действительности, отличный от науки.
Вненаучное знание не базируется на критериях научного мышления в полной мере, как это происходит с научным знанием. Вненаучное знание формируется по иным правилам.
Соотношение науки и внерационального знания есть этап разрешения проблемы отграничения научности от вне научного знания, которая не сводится к ошибочному делению знания на истинное или не истинное, правильное или неправильное.
То есть Архимед, сравнивая иррациональное и рациональное применил внерациональное знание, ведь о том, что число тт носит иррациональный характер станет известно гораздо позже.
Кроме того, вам любой математик скажет, что иррациональное число — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде дроби m/n, где m — целое число, n — натуральное число. Иррациональное число может быть представлено ИСКЛЮЧИТЕЛЬНО в виде бесконечной непериодической десятичной дроби. А Архимед применяет дробь типа m/n.
Теорема 3
Ошибка с дробями закрадывается и в третью теорему. Окружность превышает утроенный диаметр меньше чем на  и более чем на
и более чем на диаметра:
диаметра:
Доказательство проводится с помощью правильных вписанных и описанных многоугольников, если число сторон принимает последовательно значение 6, 12, 24, 48, 96.
Выразим из этого неравенства отношение 

Как видите снова к рациональным числам применено иррациональное тт
Почему Архимед ошибался? Да потому, что доказательства иррациональности тт появятся только в 20 веке в трудах Ламберта и Лежандра.
Первая в истории оценка числа сверху и снизу проведена Архимедом ошибочно. Приближенное значение π с избытком, равно 3 . Приближенное значение π с недостатком, по Архимеду, равно 3
. Приближенное значение π с недостатком, по Архимеду, равно 3 Точность расчета самого Архимеда оценим, как: 3
Точность расчета самого Архимеда оценим, как: 3 . Это также хорошее приближение для π, но оно не соответствует условиям применения иррациональных чисел.
. Это также хорошее приближение для π, но оно не соответствует условиям применения иррациональных чисел.
Вы спросите, что я предлагаю? Конечно работать в области естествознания, то есть иметь рациональный взгляд на мир, что позволит нам применить рациональные числа.
И действовать мы будем вот так.
Рис. Разгадка

Далее вычисляем по формуле прямоугольного треугольника, предложенной уже Пифагором (а это отражение Исуса Христа в истории) площадь треугольника АВD. 
Остается сложить 4 площади идентичных прямоугольных и равносторонних треугольников ABD и к к ней добавить 4 площади идентичных сегментов BCD и получим площадь окружности.
S= 4RR arcsin (L/2R)
Теперь действуем еще рациональнее. Берем линейку и замеряем на предложенном мною рисунке “Разгадка” размеры R и L
У меня получилось 4 и 6 условных единицы (в данном случае это сантиметры) соответственно. Подставляем в формулу S= 4RR arcsin (L/2R) = 4х4х4 х arcsin(6/2х4) = 64 х arcsin (6/8) = 64 х arcsin 0,75 = 64 х 0,848062079.
Площадь круга с этими параметрами S= 54,27597306 см. кв.
Теперь применим формулу Архимеда S= πR(2)= 3.14 х 4 х 4 = 3.14 х 16
Площадь круга с этими параметрами S= 50.24 см. кв.
При увеличении параметров числа тт после запятой, в виде бесконечной непериодической десятичной дроби проявляется тенденция роста площади:
3,1415926535 × 16 = 50,26548246
Но посмотрите, КАКАЯ РАЗНИЦА в вычислениях площади по моему методу и по методу Архимеда. Если при использовании arcsin возникает четкое рациональное число, то при использовании числа тт никакой рациональности не наблюдается и в математические вычисления вводится параметр иррациональный, не подвластный разуму, настолько бесконечный, что нам и задумываться над этим не рекомендуют, мол, не вашего ума дело. А для пущей убедительности нашей никчемности, нам предлагают доказать недоказуемое. Например, квадратуру круга.
Квадратура круга — задача, заключающаяся в нахождении способа построения с помощью циркуля и линейки (без шкалы с делениями) квадрата, равновеликого по площади данному кругу. Наряду с трисекцией угла и удвоением куба, является одной из самых известных неразрешимых задач на построение с помощью циркуля и линейки.
Но ведь предложенный мною способ вполне подходит и для этого “сложнейшего” вопроса математики. Я например, совершенно свободно построил такой квадрат, когда понял, что число тт – это функция. Думаю, что и остальные “неразрешимые задачи” не сложнее этой, если к ним подходить рационально и понимать, что круг это тоже функция, созданная вращением любой плоскостной фигуры вокруг своего центра. То есть круг следует считать не геометрической фигурой, а следствием вращения плоских геометрических фигур в плоскости своего нахождения вокруг центра внимания или центра события. Например в математике и физике, центром называется точка пересечения каких-либо осей в геометрической фигуре, точка сосредоточения каких-либо сил в физическом теле. Все это события, на которые мы обращаем внимание.
Центр тяжести — это точка прохождения равнодействующей всех сил тяжести при различных положениях тела относительно вертикали, а также самое важное, существенное значение какого-либо предмета или явления при обсуждении его людьми.
В теории Архимеда, когда он разложил сектора в плоскую фигуру у секторов нет единого центра, а есть то, что ныне именуется реперными точками, то есть такие точки, на которых основывается шкала измерений. Вот только беда этих точек в том, что скажем при измерении температуры тела, они на самом деле измеряют РАСШИРЕНИЕ рабочего тела в градуснике (например, ртути), но не температуру тела.
Математика изучает не реальный мир, а пространственные формы и количественные отношения, тесно связанные с действительностью, но оторванные от материального содержания: числа, величины, линии, фигуры и т. д., то есть абстракции. Но математические абстракции не означают отрыва математики от действительного мира; напротив, чем абстрактнее то или иное понятие, тем больше круг реальных явлений оно охватывает и тем шире применяется. Классический пример – понятие функции.
В основе всей математики лежит чистая теория множеств. Математика изучает структуры, то есть классы множеств с заданным в них операциями и отношениями. Различные области математики тем и отличаются друг от друга, что изучают разные структуры.
Математика возникла из практических нужд людей. В дальнейшем связи ее с практикой сохраняются, но постепенно прямые связи сменяются косвенными – через посредство техники и других наук. В наши дни прикладная математика, разумеется, тесно связана с практикой, понимаемой в широком смысле, а вот чистая, «теоретическая» математика развивается, главным образом, под влиянием своей внутренней логики – необходимостью дальнейшего обобщения накопленных в ней фактов, понятий и теорий.
То, что оставил миру Архимед в вычислении площади круга и своих трех теоремах об этом, появилось под влиянием его внутренней логики. Не будучи знаком с иррациональными числами, Архимед не увидел функциональности числа тт и посчитал его числом рациональным, тем самым вступив в область внерационального знания. Он просто не оценил истинность числа тт, не осознал его функциональность, которая несомненно имеет научное пояснение, просто мы сегодня еще не готовы к его научному пояснению.
Несколько слов о том, что такое arcsin?
Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ) и поэтому, тесно связанная с числом тт. Вспоминайте единый центр окружности, помещенный Архимедом в разные точки: вверху и внизу. График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат.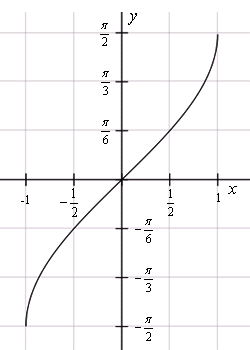
А еще проще, с помощью прямых и обратных тригонометрических функций математики приводят число тт к рациональности. То есть у этого числа существует много рациональных свойств, одно из которых появляется при использовании arcsin в вычислении сегмента. Проще говоря тригонометрические функции это инструменты преобразования числа тт из области теории в область практического применения. Функция арксинус является нечетной:
arcsin(–x) = arcsin(–sin arcsin x) = arcsin(sin(–arcsin x)) = – arcsin x.
Если разделить круг на 4 сектора, а затем сложить их по правилам Архимеда, то вы увидите, что вместо положенных 4 радиусов (а это внешние боковые стороны секторов), на рисунке появится и 5 радиус. А если быть точнее, то он не 5 а 7, потому что мы складываем 4 сектора у трех из которых боковые стороны соприкасаются. Конечно, можно это не замечать, как предпочитают действовать математики, но при условии нахождения секторов в круге, соприкасающихся сторон будет 8, а нарисовано радиусов 4. Это еще одно из доказательств того, что круг и фигура из разложенных секторов НЕ ОДИНАКОВЫ по площади, а нас просто обманывает свой собственный ум. И возникает это при потере единого центра, как это произошло у Архимеда не знавшего нуля.
Вот этот ноль или точка отсчета и дает ОБЛАСТЬ НУЛЯ, которая едина для всех кругов, не зависимо от их радиуса и примерно составляет 4 условные единицы, хорошо заметные на моем примере по рис. Разгадка.
Площадь круга по моим расчетам S= 54,27597306 см. кв. и площадь круга по расчетам Архимеда S= 50.24 см. кв. разнятся на 4 условных единицы и при применении числа тт с бесконечными знаками после запятой, разница ВОЗМОЖНО приблизится к числу 3.14 (и не периодика). То есть, число тт скрыто в “области нуля” и само по себе является нулем, который расширяется в зависимости от радиуса. А это говорит о том, что где бы мы ни начинали точку отсчета, ее значение будет всегда иррациональным и равным числу тт. Кроме момента, когда она является точкой внимания или центром сосредоточения сил.
Ошибка Архимеда в том, что он вынес центр за пределы геометрического тела, совместив его с точкой движения по кривой окружности, а я оставил центр неподвижным и в полагающимся ему месте и назвал то, что прячется в центре – число тт. Число тт и ноль ОДНО И ТО ЖЕ. Иррациональное число тт – это рациональный ноль и наоборот.
Любой календарь, любое линейное и нелинейное измерение с помощью условных единиц иррационально. А вот любое объемное измерение имеет рациональность. Мы живем в трехмерном пространстве и другое понимание, лишь обман нашего мозга.
В старой русской сказке про Емелю, есть сюжет, когда герой одевает на палец кольцо и тут же появляется зубастая щука, которая исполняет его желания. Уж не число ли тт вызывал Емеля для своих чудес?
Вы спросите в чем практичность моих вычислений? Ну, например я могу вам пояснить, что такое бесконечность в двух- и трехмерном пространстве. Это расширение области нуля (числа тт) в зависимости от радиуса круга или сферы.
Эта миниатюра является продолжением работы “Область нуля”
(образование: Московский Государственный Университет им. М.В.Ломоносова, химический факультет)
Приближенное значение числа pi (пи) вычислил еще великий древнегреческий ученый Архимед (287 – 212 гг. до н. э.) в своей работе “Об измерении круга”. Однако П.Бухмиллер в 2011 году заявил, что площадь круга якобы равна полусумме площадей вписанного и описанного квадратов, т.е. якобы равна 3r 2 , а не pi r 2 . ( http://redstar-43.ru )
Вывод числа пи. Опытные данные: pi
Опровергнуть заявление Бухмиллера на опыте элементарно просто. Берете любой цилидрический предмет, например коробку для чистых компакт-дисков, измеряете ее диаметр – около 12,5 см. А затем ниткой или гибкой линейкой измеряете длину ее окружности. Она равна около 39,3 см. Значит, отношение длины окружности к диаметру (определение числа pi) равно:
а не 3. Проведите такой простой опыт самостоятельно. Ведь опыт подтверждает математическую истину, открытую еще Архимедом и опровергает заблуждение Бухмиллера.
Строгий математический вывод числа пи pi
Но математика – наука точная, поэтому ниже представлено, как именно великий Архимед вывел число pi.
Этот текст написан для школьников, интересующихся математикой, лично для Бухмиллера, а также для тех, кто поверил Бухмиллеру.
Итак, Бухмиллер в XXI веке построил вокруг круга описанный и вписанный квадраты и заявил, что, если площадь описанного квадрата равна 4r 2 , а площадь вписаного квадрата равна 2r 2 , то, мол, площадь круга равна 3r 2 . Причем, Бухмиллер даже не попытался доказать это заявление о полусумме.
Архимед же в III веке ДО нашей эры считал умнее. Он построил вокруг круга не только квадраты, но и вписанные и описанные правильные 6-угольники, 8-угольники и так далее вплоть до 96-угольников. И считал их площади. Архимед понимал, что площадь круга S меньше площади описанного правильного многоугольника S O , но больше площади вписанного правильного многоугольника S B :
Так Архимед вывел число pi
Для решения задачи в общем случае рассчитаем площади правильных n-угольников – вписанного в окружность и описанного вокруг нее.
Разделим правильный описанный n-угольник на n равносторонних треугольников и n/2 прямоугольных треугольников с углом a у центра круга (см. рисунок). И вычислим их площади, понимая, что они равны сумме площадей соответствующих треугольников, на которые они разбиты. Очевидно, что:
угол a = 360 o /2n
Площадь треугольника равна bh/2, где b – основание, h – высота. В данном случае для треугольника из описанного многоугольника h = r и b/2 = r tg a и его площадь равна r 2 tg a. А для вписанного – h = r cos a и b/2 = r sin a и его площадь равна r 2 sin a cos a. Площадь многоугольника в n раз больше площади треугольника. Тогда площадь правильного описанного n-угольника равна:
S O = nr 2 tg a = nr 2 tg (360 o /2n)
А площадь правильного вписанного n-угольника равна:
S В = nr 2 sin a cos a
В школьном курсе тригонометрии выводится формула:
sin2a = 2 sin a cos a
Поэтому предыдущее выражение примет вид:
S В = 0,5 nr 2 sin2a = 0,5 nr 2 sin (360 o /n)
А теперь, используя научный калькулятор, подставим n= 100, т.е. площади правильных описанного и вписанного 100-угольников равны:
S O = nr 2 tg (360 o /2n) = 100 r 2 tg (360 o /200) = 100 r 2 tg 1,8 o
S В = 0,5 nr 2 sin (360 o /n) = 50 r 2 sin (360 o /100) = 50 r 2 sin 3,6 o
Следовательно, площадь круга находится в следующих пределах:
3,1395 r 2 3,1426 r 2
и приближенно равна 3,14 r 2 , а число pi
= 3,14. Что и требовалось доказать.
А теперь вычислим более точные значения числа pi. Подставим n= 1000:
S O = 1000 r 2 tg (360 o /2000) = 1000 r 2 tg 0,18 o
S В = 500 r 2 sin (360 o /1000) = 500 r 2 sin 0,36 o
Следовательно, площадь круга находится в следующих пределах:
3,141572 r 2 3,141603 r 2
А теперь, подставим n = 1000 000 = 10 6 для площадей миллион-угольников:
S O = 10 6 r 2 tg 0,00018 o
= 3,1415926536 r 2
S В = 5*10 5 r 2 sin 0,00036 o
= 3,14159265357 r 2
Следовательно, площадь круга находится в следующих пределах:
3,14159265357 r 2 3,1415926536 r 2
= 3,1415926536. Что и требовалось доказать. Как видите, ни о какой полусумме квадратов и речи не идет. И Архимед это понимал.
В качестве домашнего задания вычислите число pi более точно по площадям миллиард-угольников.
Кто открыл площадь окружности
Напомним: число π («пи») определяется как отношение длины окружности к ее диаметру . Это кратко выражается формулой для вычисления длины окружности , или . Другая известная формула, в которой встречается π, – формула площади круга , или . В принципе π можно было бы определить как отношение площади круга к квадрату радиуса. За этими формулами скрываются три нетривиальных математических факта:
| 1) | длина окружности пропорциональна ее диаметру; |
| 2) | площадь круга пропорциональная квадрату радиуса; |
| 3) | коэффициенты пропорциональности в двух последних случаях совпадают. |
Десятичная дробь, выражающая число π, бесконечна, хотя можно вычислить различные конечные дроби – десятичные приближения для π. Наиболее популярное приближение – с точностью до сотых: π ≈ 3,14.
Самое простое приближение для π полагает его равным 3 (несмотря на грубость этого приближения, его ошибка менее 5 %). Такое приближение использовалось, например, в Древнем Вавилоне в III–II вв. до н. э.: длину окружности находили по правилу, которое в современных обозначениях можно записать , площадь круга находили по правилу . Значение π = 3 используется и древними иудеями: библейский автор упоминает, что при строительстве храма при царе Соломоне мастер Хирам из Тира в числе других храмовых украшений «сделал литое из меди море, – от края его до края его десять локтей, – совсем круглое. и шнурок в тридцать локтей обнимал его кругом» (3 Цар 7, 23). Позже для более точных вычислений использовалось геометрическое приближение: от площади квадрата, описанного вокруг круга, отнимались площади треугольников с длиной стороны, равной трети стороны квадрата, получалось довольно точное значение
В Древнем Египте для вычисления площади круга использовалось правило , что соответствует значению . Ошибка при этом составляет менее 1 %. Как получали это правило, неизвестно.
У древнегреческих математиков с их превалирующим интересом к геометрическим построениям и доказательствам, а не к вычислениям, вопрос о численном значении π был не столь важным, нежели проблема квадратуры круга, т. е. построения квадрата, равновеликого данному кругу, если удастся, то с помощью циркуля и линейки, а в противном случае – с помощью каких-то других инструментов. Задача о квадратуре круга имела широкую известность не только среди математиков: например, о ней говорится в комедии Аристофана «Птицы».
Изучая задачу о квадратуре круга, Гиппократ Хиосский (V в. до н. э.) нашел некоторые случаи, когда с помощью циркуля и линейки можно найти квадратуру определенных частей круга, ограниченных кривыми линиями (а именно, двумя окружностями). Такие части называются луночками . Самый простой случай – это луночка между окружностью, описанной около равнобедренного прямоугольного треугольника, и другой окружностью, диаметром которой служит катет этого треугольника.
Нетрудно видеть, что, по теореме Пифагора, , а потому площадь круга, построенного на , равна двум площадям круга, построенного на , а значит, площадь полукруга, построенного на , равна площади четверти круга, построенного на . Поэтому, вырезав из этих фигур их общую часть – сегмент – получим равновеликие фигуры: таким образом, площадь луночки равна площади прямоугольного треугольника .
Древнейшие известные попытки собственно квадратуры круга принадлежат Антифонту и Бризону (V в. до н. э.). Антифонт последовательно вписывал в круг правильные многоугольники, каждый раз удваивая количество сторон, и полагал, что в конце концов многоугольник совпадет с окружностью. Бризон строил два квадрата – вписанный в окружность и описанный вокруг нее – и считал, что площадь квадрата, лежащего между ними, равна площади круга. Разумеется, в буквальном понимании и Антифонт, и Бризон заблуждались. Однако их идеи оказались весьма плодотворными: действительно, вписывая в окружность правильные многоугольники со все большим числом сторон, можно сколь угодно близко подойти к площади круга и длине окружности; смысл есть и в том, чтобы рассматривать не только вписанные, но и описанные многоугольники: при этом площадь круга будет лежать между площадями вписанных и описанных многоугольников, а длина окружности – между периметрами тех и других.
В дальнейшем именно вписанные и описанные правильные многоугольники стали активно применяться как для теоретических исследований, так и для конкретного вычисления числа π. Именно с помощью таких многоугольников было сформулировано строгое доказательство того, что площади кругов относятся как квадраты их диаметров, найденное, по-видимому, Евдоксом и приведенное в «Началах» Евклида. Архимед доказал, что площадь круга равна половине произведения длины окружности на ее радиус. Кроме того, с помощью вычисленных им периметров вписанных и описанных правильных многоугольников (от 6-угольника до 96-угольника) Архимед нашел, что:
или, в десятичных дробях, (подлинное значение ).
Таким образом, он не только нашел приближенные значения π, но и оценил точность этих приближений. Уже найденная Архимедом верхняя оценка, равная 22/7, дает приближение π с точностью 0,04 %. Эту дробь часто называют «архимедовым числом». Клавдий Птолемей, использовав правильный 720-угольник, нашел, что , что составляет приблизительно 3,14167 (ошибка меньше 0,003 %).
Как и для удвоения куба, и для трисекции угла, для квадратуры круга были изобретены методы, использующие свойства различных кривых. Общим свойством этих кривых было их образование путем сочетания двух типов движений – равномерного поступательного (вдоль некоторой прямой) и равномерного вращательного (вокруг некоторой точки или оси). При этом имеет место пропорциональность между углом, на который повернулся вращающийся элемент, и длиной отрезка, пройденной при поступательном движении.
Прежде всего, это была уже упомянутая квадратриса (см. урок, посвященный трисекции угла), которую впервые использовал для квадратуры круга Динострат. Оказывается, если – точка, в которой квадратриса пересекает отрезок , то четверть длины окружности, проходящей через точку , с центром в точке , равна длине отрезка .
Из этого следует, что длина дуги равна , а площадь круга радиуса равна площади прямоугольника со сторонами и ; такой прямоугольник легко построить с помощью циркуля и линейки, если известны отрезки и . Построив прямоугольник, можно построить и равновеликий ему квадрат.
Кроме квадратрисы, для квадратуры круга использовались связанные с ней винтовая линия и спираль Архимеда. Винтовая линия получается при движении точки по поверхности цилиндра, складывающемся из двух движений: во-первых, движения с постоянной скоростью вдоль оси цилиндра, а во-вторых, равномерного вращения по окружности основания цилиндра.
Спираль Архимеда – эта кривая, которую заметает точка , равномерно движущаяся вдоль радиуса , который, в свою очередь, равномерно вращается вокруг точки .
Задача, похожая на квадратуру круга, фигурировала и в Древней Индии. В уже упоминавшейся (см. урок по теореме Пифагора) книге «Шулва-сутра», излагавшей правила строительства алтарей, построение круга, равновеликого данному квадрату , производится так. Вокруг квадрата описывается окружность; пусть перпендикуляр к отрезку , проходящий через центр окружности , пересекает прямую и окружность в точках и , а точка делит отрезок в отношении . Тогда – радиус круга, равновеликого данному квадрату. Если – сторона квадрата, то длина полученного радиуса описанный способ соответствует приближенному значению π
В более поздние времена в Индии использовались приближения для π, равные (т. е. ≈ 3,162 – ошибка менее 1 %); 22/7 и даже 3,1416. Интересно наглядное доказательство предложения «площадь круга равна площади прямоугольника, стороны которого равны полуокружности и радиусу» у математика Ганеши (XVI в.). Как и в доказательстве теоремы Пифагора у Бхаскары, здесь все доказательство состоит из чертежа и слова «смотри». Ганеша делит круг на 12 секторов, а затем разворачивает каждый полукруг, состоящий из 6 секторов, в пилообразную фигуру, основание которой равно полуокружности, а высота – радиусу. Прямоугольник, о котором говорится в условии, получится при вставлении зубьев одной «пилы» в зазоры между зубьями другой. По-видимому, читатель должен был представлять себе, что круг разделен не на 12, а на столь большое число секторов, что эти секторы неотличимы от треугольников, составляющих «пилы».
Значение по-видимому, впервые появилось у китайского астронома и философа Чжан Хена (нач. II в. н. э.); вероятно, из Китая оно перешло к индийцам (Брахмагупта, VII в.) и арабам (ал-Хорезми, IX в.); впрочем, метод получения этого значения нам неизвестен. Лю Хуэй (III–IV вв.) с помощью рассмотрения вписанных и описанных многоугольников (в том числе с 3072 вершинами) пришел к приближению , а Цзу Чун-чжи (V в.) доказал, что
Самаркандский математик ал-Каши в «Трактате об окружности» (1424 г.) поставил себе задачу выразить окружность через диаметр с такой точностью, чтобы погрешность в длине окружности, равной 600 000 диаметров Земли, не превосходила толщины волоса. Рассмотрев правильные многоугольники вплоть до фигуры с 805 306 368 (3 ∙ 2 28 ) вершинами, ал-Каши нашел 16 верных знаков (после запятой) числа π, а именно, приближение (в реальности 17-й знак после запятой – 3 или 4, потому что 18-й – 8). Европейские математики достигли такой точности и превзошли ее лишь в конце XVI в.: в 1597 г. голландец вычислил 17-й знак, для чего применил многоугольник с 1 073 741 824 (2 30 ) вершинами.
В начале XVII в. профессор математических и военных наук Лейденского университета Лудольф ван Цейлен довел количество точных знаков (после запятой) числа π до 35. Современники называли найденное им приближение π «числом Лудольфа». Эти знаки он завещал выбить на надгробном камне. Интересно, что, поскольку в то время привычная нам позиционная запись десятичных дробей еще не вполне прижилась, на надгробии было написано не 3,14159265358979323846264338327960288, а
Еще два голландца XVII в. – В. Снеллиус и Х. Гюйгенс – с помощью некоторых тонких геометрических рассуждений смогли достичь большей точности при меньшем числе сторон рассматриваемых многоугольников. Снеллиус воспроизвел результат Архимеда – три верных знака после запятой – рассматривая не более чем а с помощью получил целых 7 верных знаков. Гюйгенс, доказав некоторые геометрические теоремы, смог вычислить 10 верных знаков с помощью 60-угольника.
Далее метод вписанных и описанных многоугольников уступил место новым методам, разработанным с помощью математического анализа – использованию бесконечных сумм, которые дают приближенные значения числа π нужной точности, если оставить в них достаточно большое, но лишь конечное число членов. В результате число верных знаков быстро возросло: вычислители подбирали формулы поудобнее и соревновались друг с другом в том, кто больше получит этих знаков.
| ГОД | ВЫЧИСЛИТЕЛЬ | ЧИСЛО ТОЧНЫХ ЗНАКОВ |
| 1699 | А. Шарп | 71 |
| 1706 | Дж. Мечин | 100 |
| 1717 | Т. де Ланьи | 112 |
| 1794 | Г. Вега | 136 |
| 1844 | И. М. З. Дазе | 200 |
| 1847 | Т. Клаузен | 248 |
| 1853 | У. Резерфорд | 440 |
Рекорд для XIX в. поставил Уильям Шенкс, нашедший в результате 707 знаков после запятой; в 1-ой половине XX в. эти знаки часто воспроизводили в популярной литературе, а архитекторы даже украшали ими свои сооружения (Дом занимательной науки в Ленинграде, ныне Санкт-Петербург, 1934; Дворец открытий в Париже, 1937). В 1945 г. результаты Шенкса были проверены на компьютере, и оказалось, что из его знаков верны только первые 527. Компьютеры позволили существенно увеличить количество точных цифр в десятичном разложении π, причем, если раньше вычислители тратили на них многие годы, то теперь компьютеры справлялись с этим менее чем за день работы. Этому также способствовало применение более эффективных алгоритмов на основание новых математических формул.
| ГОД | ВЫЧИСЛИТЕЛЬ | КОМПЬЮТЕР | ЧИСЛО ТОЧНЫХ ЗНАКОВ |
| 1949 | Дж. фон Нейман | ENIAC | 2 037 |
| 1958 | Ф. Женюи | IBM 704 | 10 000 |
| 1961 | Д. Шенкс, Дж. Ренч | IBM 7090 | 100 625 |
| 1973 | Ж. Гийу, М. Буйе | CDC-7600 | 1 000 000 |
| 1976 | Д. Х. Бейли | Cray-2 | 29 360 000 |
| 1987 | Я. Канада | NEC SX-2 | 134 217 000 |
| 1989 | Д. и Г. Чудновски | Cray-2, IBM 3090 | 1 011 196 691 |
| 1999 | Я. Канада, Д. Такахаси | HITACHI SR 8000 | 206 158 430 000 |
Само обозначение π для отношения окружности к диаметру было введено в 1706 году У. Джонсом.
Что касается принципиальных математических результатов относительно π, то здесь следует упомянуть, во-первых, доказательство иррациональности этого числа, проведенное в 1766 г. И. Г. Ламбертом (некоторый пробел в доказательстве Ламберта был восполнен в 1800 г. А. М. Лежандром), а во-вторых, доказательство трансцендентности π, осуществленное в 1882 г. К. Ф. Линдеманом. Трансцендентность некоторого числа означает, что оно не может быть корнем никакого уравнения вида с целыми коэффициентами . Из этого следует, что оно не может быть представлено в виде конечной комбинации целых чисел, арифметических действий и знака извлечения корня. Поэтому и квадратура круга не может быть решена с помощью циркуля и линейки, которые позволяют строить лишь отрезки, выражаемые через арифметические действия и квадратные корни.
[spoiler title=”источники:”]
http://ateism.biz/calculation_pi.htm
http://files.school-collection.edu.ru/dlrstore/ee5be68f-68a0-192e-38b9-3cf83a9980dc/00145619808000570.htm
[/spoiler]
