Как по двум векторам найти нормаль - Сайт, где вы сможете решить свои вопросы

Как найти нормаль плоскости

Нормаль плоскости n (вектор нормали к плоскости) – это любой направленный перпендикуляр к ней (ортогональный вектор). Дальнейшие выкладки по определении нормали зависят от способа задания плоскости.

Инструкция

Если задано общее уравнение плоскости – AX+BY+CZ+D=0 или его форма A(x-x0)+B(y-y0)+C(z-z0)=0, то можно сразу записать ответ – n(А, В, С). Дело в том, что это уравнение было получено, как задача определения уравнения плоскости по нормали и точке.

Для получения общего ответа, вам понадобится векторное произведение векторов из-за того, что последнее всегда перпендикулярно исходным векторам. Итак, векторным произведением векторов, является некоторый вектор, модуль которого равен произведению модуля первого (а) на модуль второго (b) и на синус угла между ними. При этом этот вектор (обозначьте его через n) ортогонален a и b – это главное. Тройка этих векторов правая, то есть из конца n кратчайший поворот от a к b совершается против часовой стрелки.
[a,b] – одно из общепринятых обозначений векторного произведения. Для вычисления векторного произведения в координатной форме, используется вектор-определитель (см. рис.1)

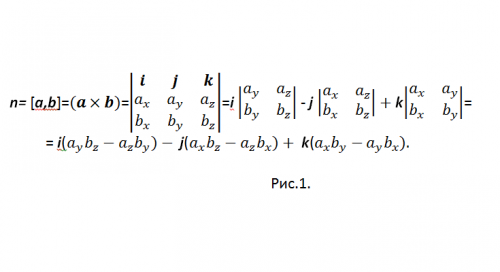
Для того чтобы не путаться со знаком «-», перепишите результат в виде: n={nx, ny, nz}=i(aybz-azby)+j(azbx-axbz)+k(axby-aybx), и в координатах: {nx, ny, nz}={(aybz-azby), (azbx-axbz), (axby-aybx)}.
Более того, дабы не путаться с численными примерами выпишете все полученные значения по отдельности: nx=aybz-azby, ny=azbx-axbz, nz=axby-aybx.

Вернитесь к решению поставленной задачи. Плоскость можно задать различными способами. Пусть нормаль к плоскости определяется двумя неколлинеарными векторами, причем сразу численно.
Пусть даны векторы a(2, 4, 5) и b(3, 2, 6). Нормаль к плоскости совпадает с их векторным произведением и, как только что было выяснено будет равна n(nx, ny, nz),
nx=aybz-azby, ny=azbx-axbz, nz=axby-aybx. В данном случае ax=2, ay=4, az=5, bx=3, by=2, bz=6. Таким образом,
nx=24-10=14, ny=12-15=-3, nz=4-8=-4. Нормаль найдена – n(14, -3, -4). При этом она является нормалью к целому семейству плоскостей.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Уравнения плоскости, компланарной двум неколлинеарным векторам

Напомним, что три или более векторов называются компланарными, если существует плоскость, которой они параллельны. Эту плоскость будем называть компланарной заданным векторам.

Направляющими векторами плоскости называются два неколлинеарных вектора, компланарных этой плоскости, т.е. принадлежащих плоскости или параллельных ей.

Пусть в координатном пространстве Oxyz заданы:

а) точка $M_{0}(x_{0},y_{0},z_{0})$ ;

Направляющие векторы плоскости

б) два неколлинеарных вектора $vec{p}_{1}=a_{1}vec{i}+b_{1}vec{j}+c_{1}vec{k},~vec{p}_{2}=a_{2}vec{i}+b_{2}vec{j}+c_{2}vec{k}$ (рис.4.15).

Требуется составить уравнение плоскости, компланарной векторам $vec{p}_{1},,vec{p}_{2}$ и проходящей через точку $M_{0}(x_{0},y_{0},z_{0}).$

Выберем на плоскости произвольную точку M(x,y,z) . Обозначим vec{r}=overrightarrow{OM}, $vec{r}_{0}=overrightarrow{OM_{0}},$ — радиус-векторы точек и $M_{0}(x_{0},y_{0},z_{0})$ (рис.4.16).

Условие компланарности векторов $overrightarrow{M_{0}M},,vec{p}_{1},,vec{p}_{2}$ (рис.4.16) можно записать, используя свойства смешанного произведения $langleoverrightarrow{M_{0}M},vec{p}_{1},vec{p}_{2}rangle=0.$ Применяя формулу (1.17), получаем уравнение плоскости, проходящей через заданную точку и компланарной двум неколлинеарным векторам:

$begin{vmatrix}x-x_{0}&y-y_{0}&z-z_{0}\a_{1}&b_{1}&c_{1}\a_{2}&b_{2}&c_{2}end{vmatrix}=0,.$

(4.18)

Параметрическое уравнение плоскости

Пусть в координатном пространстве Oxyz заданы:

а) точка $M_{0}(x_{0},y_{0},z_{0})$ ;

б) два неколлинеарных вектора $vec{p}_{1}=a_{1}vec{i}+b_{1}vec{j}+c_{1}vec{k},~vec{p}_{2}=a_{2}vec{i}+b_{2}vec{j}+c_{2}vec{k}$ (рис.4.15).

Требуется составить параметрическое уравнение вида (4.10) плоскости, компланарной векторам $vec{p}_{1},,vec{p}_{2}$ и проходящей через точку $M_{0}(x_{0},y_{0},z_{0}).$

Выберем на плоскости произвольную точку M(x,y,z) . Обозначим vec{r}=overrightarrow{OM}, $vec{r}_{0}=overrightarrow{OM_{0}}$ -радиус-векторы точек и $M_{0}(x_{0},y_{0},z_{0})$ (рис.4.16).

Точка принадлежит заданной плоскости тогда и только тогда, когда векторы $overrightarrow{M_{0}M},$ $vec{p}_{1}$ и $vec{p}_{2}$ компланарны (см. разд. 1.3.2). Запишем условие компланарности: $overrightarrow{M_{0}M}=t_{1}vec{p}_{1}+t_{2}vec{p}_{2},$ где $t_{1},,t_{2}$ — некоторые действительные числа (параметры). Учитывая, что $overrightarrow{M_{0}M}=vec{r}-vec{r}_{0},$ получим векторное параметрическое уравнение плоскости:

$vec{r}=vec{r}_{0}+t_{1}cdotvec{p}_{1}+t_{2}vec{p}_{2}, quad t_{1},t_{2}inmathbb{R},,$

(4.19)

где $vec{p}_{1},,vec{p}_{2}$ — направляющие векторы плоскости, а $vec{r}_{0}$ — радиус-вектор точки, принадлежащей плоскости.

Координатная форма записи уравнения (4.19) называется параметрическим уравнением плоскости:

$begin{cases} x= x_{0}+a_{1}cdot t_{1}+a_{2}cdot t_{2},\ y= y_{0}+b_{1}cdot t_{1}+b_{2}cdot t_{2},\ z= z_{0}+c_{1}cdot t_{1}+c_{2}cdot t_{2}, end{cases}t_{1},t_{2}inmathbb{R},,$

(4.20)

где $a_{1},b_{1},c_{1}$ и $a_{2},b_{2},c_{2}$ — координаты направляющих векторов $vec{p}_{1}$ и $vec{p}_{2}$ соответственно. Параметры $t_{1},,t_{2}$ в уравнениях (4.19),(4.20) имеют следующий геометрический смысл: величины $t_{1},,t_{2}$ пропорциональны расстоянию от заданной точки $M_{0}(x_{0},y_{0},z_{0})$ до точки M(x,y,z), принадлежащей плоскости. При $t_{1}=t_{2}=0$ точка совпадает с заданной точкой $M_{0}$ . При возрастании $t_{1}$ (или $t_{2}$ ) точка перемещается в направлении вектора $vec{p}_{1}$ (или $vec{p}_{2}$ ), а при убывании $t_{1}$ (или $t_{2}$ ) — в противоположном направлении.

Замечания 4.4.

1. Поскольку направляющие векторы плоскости неколлинеарны, то они ненулевые.

2. Любой вектор vec{p}=avec{i}+bvec{j}+cvec{k} , коллинеарный плоскости, ортогонален нормальному вектору vec{n}=Avec{i}+Bvec{j}+Cvec{k} для этой плоскости. Поэтому их скалярное произведение равно нулю:

langlevec{p},vec{n}rangle=acdot A+bcdot B+ccdot C=0.

Следовательно, координаты $a_{1},b_{1},c_{1}$ и $a_{2},b_{2},c_{2}$ направляющих векторов $vec{p}_{1}$ и $vec{p}_{2}$ плоскости и ее нормали связаны однородными уравнениями:

$a_{1}cdot A+b_{1}cdot B+c_{1}cdot C=0, quad a_{2}cdot A+b_{2}cdot B+c_{2}cdot C=0.$

3. Направляющие векторы плоскости определяются неоднозначно.

4. Для перехода от общего уравнения плоскости (4.15) Acdot x+Bcdot y+Ccdot z+D=0 к параметрическому (4.20) нужно выполнить следующие действия:

1) найти любое решение $(x_{0},y_{0},z_{0})$ уравнения Ax+By+Cz+D=0, определяя тем самым координаты точки $M_{0}(x_{0},y_{0},z_{0}),$ принадлежащей плоскости;

2) найти любые два линейно независимых решения $(a_{1},b_{1},c_{1}),$ $(a_{2},b_{2},c_{2})$ однородного уравнения Acdot a+Bcdot b+Ccdot c=0 определяя тем самым координаты решения $(a_{1},b_{1},c_{1})$ и $(a_{2},b_{2},c_{2})$ направляющих векторов $vec{p}_{1}$ и $vec{p}_{2}$ плоскости;

3) записать параметрическое уравнение (4.20).

5. Чтобы перейти от параметрического уравнения плоскости к общему, достаточно либо записать уравнение (4.18) и раскрыть определитель, либо найти нормаль как результат векторного произведения направляющих векторов:

$vec{n}= Bigl[vec{p}_{1},vec{p}_{2}Bigr]= begin{vmatrix} vec{i}&vec{j}&vec{k}\a_{1}&b_{1}&c_{1}\a_{2}&b_{2}&c_{2} end{vmatrix}= underbrace{begin{vmatrix}b_{1}&c_{1}\b_{2}&c_{2}end{vmatrix}}_{A}cdot vec{i}- underbrace{begin{vmatrix}a_{1}&c_{1}\a_{2}&c_{2}end{vmatrix}}_{B}cdot vec{j}+ underbrace{begin{vmatrix}a_{1}&b_{1}\a_{2}&b_{2}end{vmatrix}}_{C}cdot vec{k},,$

и записать общее уравнение плоскости в форме (4.14):

$Acdot(x-x_{0})+Bcdot(y-y_{0})+Ccdot(z-z_{0})=0,.$

6. Векторное параметрическое уравнение плоскости (4.19), полученное в прямоугольной системе координат, имеет тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнении остается прежним.

Пример 4.8. В координатном пространстве Oxyz (в прямоугольной системе координат) заданы точки K(1;2;3) и L(5;0;1) (см. рис.4.11). Требуется:

а) составить параметрическое уравнение плоскости, перпендикулярной отрезку и проходящей через его середину;

б) составить общее уравнение плоскости, проходящей через середину отрезка и компланарной радиус-векторам overrightarrow{OK} и overrightarrow{OL}.

Решение. а) Общее уравнение искомой плоскости было получено в примере 4.5: 2x-y-z-3=0. Составим параметрическое уравнение:

1) находим любое решение уравнения 2x-y-z-3=0 , например, $x_{0}=y_{0}=0,$ $z_{0}=-3,$ следовательно, точка $M_{0}(0;0;-3)$ принадлежит плоскости;

2) находим два линейно независимых (непропорциональных) решения однородного уравнения 2x-y-z=0 например (1;1;1) и (0;1;-1), следовательно, векторы $vec{p}_{1}=vec{i}+vec{j}+vec{k},$ $vec{p}_{2}=vec{j}-vec{k},$ являются направляющими для плоскости;

3) записываем параметрическое уравнение плоскости (4.20):

$begin{cases}x=0+1cdot t_{1}+0cdot t_{2},\ y=0+1cdot t_{1}+1cdot t_{2},\ z=-3+1cdot t_{1}+(-1)cdot t_{2}, end{cases}Leftrightarrow quad! begin{cases}x=t_{1},\ y=t_{1}+t_{2},\ z=-3+t_{1}-t_{2},end{cases} t_{1},t_{2}inmathbb{R},.$

б) Координаты середины M(3;1;2) отрезка были найдены в примере 4.5. Нормаль к искомой плоскости получим как векторное произведение ее направляющих векторов overrightarrow{OK}=vec{i}+2vec{j}+3vec{k}, и overrightarrow{OL}=5vec{i}+vec{k},:

$vec{n}= begin{bmatrix}overrightarrow{OK},overrightarrow{OL}end{bmatrix}= begin{vmatrix}vec{i}&vec{j}&vec{k}\ 1&2&3\ 5&0&1end{vmatrix} = 2cdotvec{i}+14cdotvec{j}-10cdotvec{k},.$

Составляем уравнение (4.14):

2cdot(x-3)+14cdot(y-1)-10cdot(z-2)=0 quad Leftrightarrow quad 2cdot x+14cdot y-10cdot z=0.

Тот же результат можно получить, записывая уравнение (4.18):

$begin{vmatrix}x-3&y-1&z-2\ 1&2&3\ 5&0&1end{vmatrix}=0 quad Leftrightarrow quad 2cdot x+14cdot y-10cdot z=0.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Лекция
9.

Аналитическая
геометрия в пространстве.

Общее
уравнение плоскости.

Определение.
Плоскостью
называется
поверхность, все точки которой
удовлетворяют общему уравнению:

Ax
+ By
+ Cz
+ D
= 0,

где
А, В, С – координаты вектора
-вектор
нормали
к плоскости.

Возможны
следующие частные случаи:

А
= 0 – плоскость параллельна оси Ох

В
= 0 – плоскость параллельна оси Оу

С
= 0 – плоскость параллельна оси Оz

D
= 0 – плоскость проходит через начало
координат

А
= В = 0 – плоскость параллельна плоскости
хОу

А
= С = 0 – плоскость параллельна плоскости
хОz

В
= С = 0 – плоскость параллельна плоскости
yOz

А
= D
= 0 – плоскость проходит через ось Ох

В
= D
= 0 – плоскость проходит через ось Оу

С
= D
= 0 – плоскость проходит через ось Oz

А
= В = D
= 0 – плоскость совпадает с плоскостью
хОу

А
= С = D
= 0 – плоскость совпадает с плоскостью
xOz

В
= С = D
= 0 – плоскость совпадает с плоскостью
yOz

Уравнение
плоскости, проходящей через три точки.

Для
того, чтобы через три какие- либо точки
пространства можно было провести
единственную плоскость, необходимо,
чтобы эти точки не лежали на одной
прямой.

Рассмотрим
точки М₁(x₁,
y₁,
z₁),
M₂(x₂,
y₂,
z₂),
M₃(x₃,
y₃,
z₃)
в декартовой системе координат.

Для
того, чтобы произвольная точка М(x,
y,
z)
лежала в одной плоскости с точками М₁,
М₂,
М₃
необходимо, чтобы векторы

были компланарны т.е. их смешанное
произведение:

()
= 0

Таким
образом,

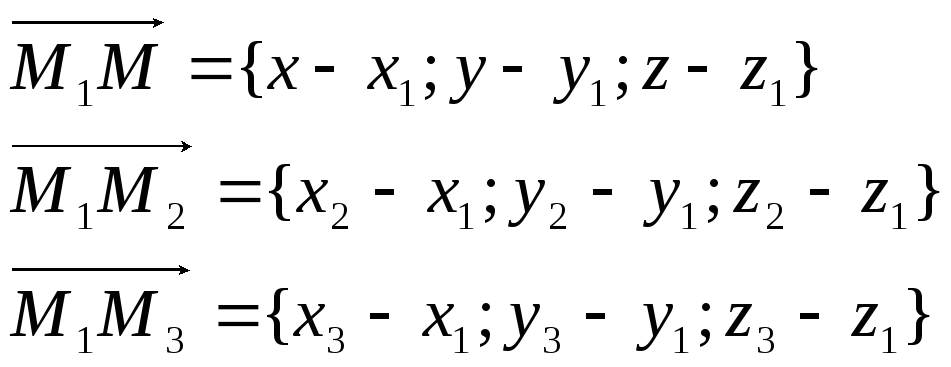
Уравнение
плоскости, проходящей через три точки:

Уравнение
плоскости проходящей через две точки
параллельно вектору.

Пусть
заданы точки М₁(x₁,
y₁,
z₁),
M₂(x₂,
y₂,
z₂)
и вектор
.

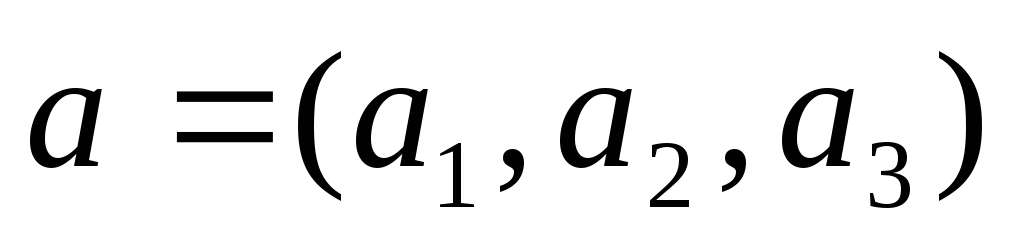Составим
уравнение плоскости, проходящей через
данные точки М₁
и М₂
и произвольную точку М(х, у, z)
параллельно вектору
.

Векторы

и вектор

должны быть компланарны, т.е.

()
= 0

Уравнение
плоскости:

Уравнение
плоскости проходящей через точку
параллельно двум векторам.

Пусть
заданы два вектора

и
,
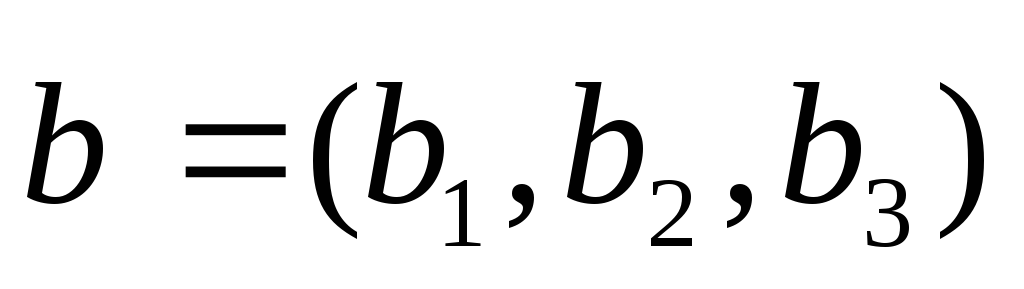коллинеарные плоскости и точка М₁(х₁,
у₁,
z₁).
Тогда для произвольной точки М(х, у, z),
принадлежащей плоскости, векторы

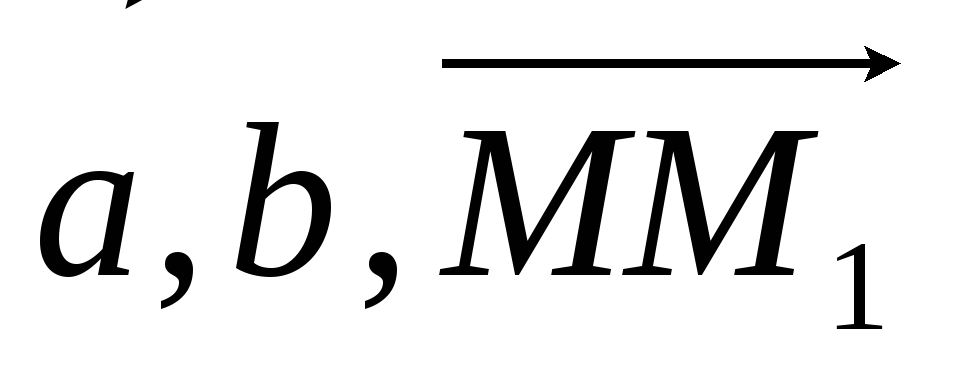
должны быть компланарны.

Уравнение
плоскости:

Уравнение
плоскости проходящей через точку
перпендикулярной вектору.

Теорема.
Если в
пространстве задана точка М₀(х₀,
у₀,
z₀),
то уравнение плоскости, проходящей
через точку М₀
перпендикулярно вектору нормали
(A,
B,
C)
имеет вид:

A(x
– x₀)
+ B(y
– y₀)
+ C(z
– z₀)
= 0.

Доказательство.
Для произвольной точки М(х, у, z),
принадлежащей плоскости, составим
вектор
.
Т.к. вектор

– вектор нормали, то он перпендикулярен
плоскости, а, следовательно, перпендикулярен
и вектору
.
Тогда скалярное произведение

=
0

Таким
образом, получаем уравнение плоскости

Теорема
доказана.

Уравнение
плоскости в отрезках.

Если
в общем уравнении Ах + Ву + Сz
+ D
= 0 поделить обе части на -D

заменив
,
получим уравнение плоскости в отрезках:

Числа
a,
b,
c
отрезки отсекаемые плоскостью при
пересечении соответственно осей х, у,
z
декартовой прямоугольной системы
координат.

Уравнение
плоскости в векторной форме.

где

–
радиус- вектор текущей точки М(х, у, z),

– единичный вектор,
имеющий направление, перпендикуляра,
опущенного на плоскость из начала
координат.

,

и 
– углы, образованные этим вектором с
осями х, у, z.

p
– длина этого перпендикуляра.

В
координатах это уравнение имеет вид:

xcos
+ ycos
+ zcos
– p
= 0.

Параметрическое
уравнение плоскости

Пусть
в пространстве задана точка М₀(х₀,
у₀,
z₀)
и два неколлинеарных вектора

(p₁,
p₂,
p₃)
и
(q₁,
q₂,
q₃).
Пусть М(х, у, z)
текущая точка плоскости. Так как векторы

и

неколлинеарны, то они на плоскости
составляют базис, по которому разложим
вектор
=t+s,
где t,s
– параметры. Поместим произвольно на
плоскость декартову прямоугольную
систему координат так, что бы оси Ох и
Оу лежали в плоскости. Из центра О
проведем в точки М₀
и M
радиусы векторы

и
.
Тогда
=–и

=+t+s
.

Это
параметрическое уравнение плоскости
в векторной форме, а в скалярной форме

x=x₀
+p₁t
+ q₁
s

y=y₀
+p₂t
+ q₂
s

z=z₀
+p₃t
+ q₃
s

Расстояние от
точки до плоскости.

Расстояние
от произвольной точки М₀(х₀,
у₀,
z₀)
до плоскости Ах+Ву+Сz+D=0
равно:

Пример.
Найти уравнение плоскости, зная, что
точка Р(4; -3; 12) – основание перпендикуляра,
опущенного из начала координат на эту
плоскость.

Таким
образом, A
= 4/13; B
= -3/13; C
= 12/13, воспользуемся формулой:

A(x
– x₀)
+ B(y – y₀)
+ C(z – z₀)
= 0.

Пример.
Найти уравнение плоскости, проходящей
через две точки

P(2;
0; -1) и Q(1;
-1; 3) перпендикулярно плоскости 3х + 2у –
z
+ 5 = 0.

Вектор
нормали к плоскости 3х + 2у – z
+ 5 = 0
параллелен
искомой плоскости.

Получаем:

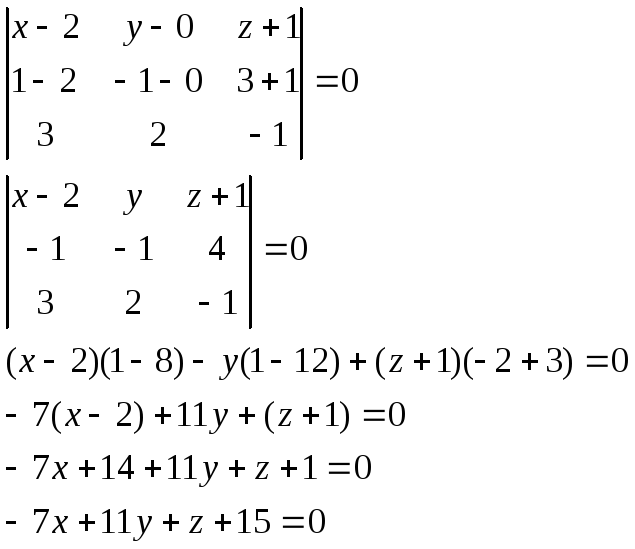
Пример.
Найти уравнение плоскости, проходящей
через точки А(2, -1, 4) и

В(3,
2, -1) перпендикулярно плоскости х
+ у
+ 2z
– 3 = 0.

Искомое
уравнение плоскости имеет вид: Ax
+ By
+ Cz
+ D
= 0, вектор нормали к этой плоскости
(A,
B,
C).
Вектор
(1,
3, -5) принадлежит плоскости. Заданная
нам плоскость, перпендикулярная искомой
имеет вектор нормали
(1,
1, 2). Т.к. точки А и В принадлежат обеим
плоскостям, а плоскости взаимно
перпендикулярны, то

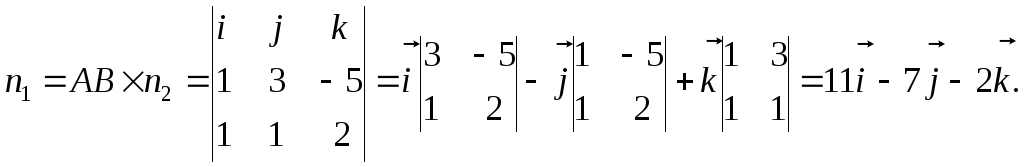
Таким
образом, вектор нормали
(11,
-7, -2). Т.к. точка А принадлежит искомой
плоскости, то ее координаты должны
удовлетворять уравнению этой плоскости,
т.е. 112
+ 71
– 24
+ D
= 0; D
= -21.

Итак,
получаем уравнение плоскости: 11x
– 7y
– 2z
– 21 = 0.

Пример.
Найти уравнение плоскости, зная, что
точка Р(4, -3, 12) – основание перпендикуляра,
опущенного из начала координат на эту
плоскость.

Находим
координаты вектора нормали
=
(4, -3, 12). Искомое уравнение плоскости
имеет вид: 4x
– 3y
+ 12z
+ D
= 0. Для нахождения коэффициента D
подставим в уравнение координаты точки
Р:

16
+ 9 + 144 + D
= 0

D
= -169

Итак,
получаем искомое уравнение: 4x
– 3y
+ 12z
– 169 = 0

Пример.
Даны координаты вершин пирамиды

А₁(1;
0; 3), A₂(2;
-1; 3), A₃(2;
1; 1), A₄(1;
2; 5).

Найти
длину ребра А₁А₂.

Найти
угол между ребрами А₁А₂
и А₁А₄.

Найти
угол между ребром А₁А₄
и гранью А₁А₂А₃.

Сначала
найдем вектор нормали к грани А₁А₂А₃
–
как векторное произведение векторов
и.

=
(2-1;
1-0; 1-3) = (1; 1; -2);

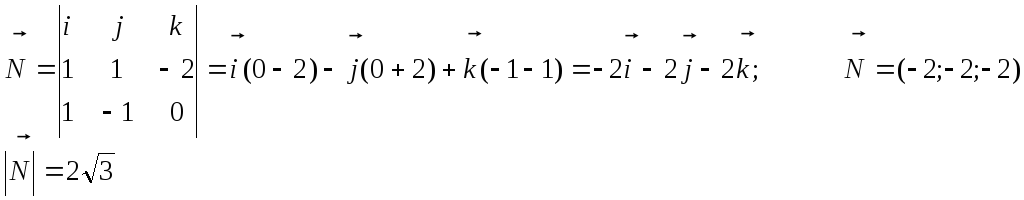
Найдем
угол между вектором нормали и вектором
.

-4
– 4 = -8.

Искомый
угол 
между вектором и плоскостью будет равен

= 90⁰
– .

Найти
площадь грани А₁А₂А₃.

Найти
объем пирамиды.

(ед³).

Найти
уравнение плоскости А₁А₂А₃.

Воспользуемся
формулой уравнения плоскости, проходящей
через три точки.

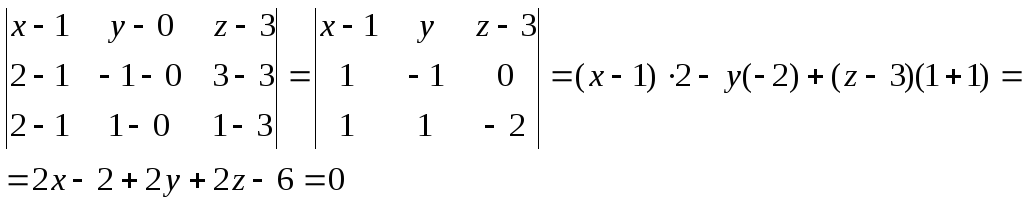
2x
+ 2y
+ 2z
– 8 = 0

x
+ y
+ z
– 4 = 0;

Источник

Вычисление координат вектора нормали. Рассматривая модели отражения света, вы,
наверное, обратили внимание
на то, что нормаль к поверхности — важный элемент. Определение вектора нормали
к поверхности в заданной точке может быть выполнено разными способами. В значительной степени это определяется типом модели
описания поверхности. Для поверхностей,
заданных в аналитической форме, известны методы дифференциальной геометрии,
которые основываются на вычислении частных производных функций описания. Например, если поверхность задана
параметрическими функциями

тогда
координаты вектора нормали можно вычислить так:

В
случае описания поверхности векторно-полигональной моделью для определения
нормалей можно использовать методы векторной алгебры.

Пусть в пространстве задана некоторая многогранная
поверхность. Рассмотрим одну ее плоскую грань, имеющую вид
треугольника (рис. 8.4).

Для
вычисления координат вектора нормали воспользуемся векторным произведением
любых двух векторов, которые лежат в плоскости грани. Такими векторами могут
служить и ребра грани, например, ребра 1-2 и 1-3. Однако формулы для векторного
произведения были определены нами только для
радиус-векторов. Чтобы перейти к радиус-векторам, введем новую систему
координат, центр которой совпадает с вершиной 1, а оси — параллельны осям бывшей системы. Координаты вершин в новой
системе:

Рис. 8.4. Одна грань поверхности
Радиус-векторы

Теперь назовем
ребро (1-2) вектором А, а ребро (1-3) — вектором В, как
показано на рис. 8.4. Таким образом, положение нормали к грани в пространстве будет
описываться радиус-вектором N. Его координаты в системе (х’, у’, г’) выразим
формулами для векторного произведения

Плоская грань
может быть изображена в разных ракурсах. В каждой конкретной ситуации необходимо выбирать направление нормали,
которое соответствует видимой стороне грани. Если плоская грань может быть видна с обратной
стороны, то тогда в расчетах отраженного света необходимо выбирать для нормали обратный
вектор, то есть (-N).

Если
полигональная поверхность имеет не треугольные грани, а, например, плоские четырехугольные, то расчет нормали можно выполнять
по любым трем вершинам грани.

Источник

5.2.3. Вектор нормали плоскости (нормальный вектор)

Вектор нормали плоскости – это вектор, который перпендикулярен данной плоскости. Очевидно, что у любой плоскости бесконечно много нормальных векторов.

Но для решения задач нам будет хватать и одного: если плоскость задана общим уравнением в прямоугольной (!) системе координат, то вектор является нормальным вектором данной плоскости.

Просто до безобразия! – всё, что нужно сделать – это «снять» коэффициенты из уравнения плоскости. И чтобы хоть как-то усложнить практику рассмотрим тоже простую, но очень важную задачу, которая часто встречается, причём, не только в геометрии:

Задача 134

Найти единичный нормальный вектор плоскости .

Решение: принципиально ситуация выглядит так:

Сначала из уравнения плоскости «снимем» вектор нормали: .

И эту задачку мы уже решали: для того чтобы найти единичный вектор , нужно каждую координату вектора разделить на длину вектора .

Вычислим длину вектора нормали:

Таким образом:

Контроль: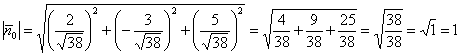, ОК

Ответ:

Вспоминаем, что координаты этого вектора – есть в точности направляющие косинусы вектора : .

И, как говорится, обещанного три страницы ждут 🙂 – вернёмся к Задаче 130, чтобы выполнить её проверку. Напоминаю, что там требовалось построить уравнение плоскости по точке и двум векторам , и в результате решения мы получили уравнение .

Проверяем:

Во-первых, подставим координаты точки в полученное уравнение:

– получено верное равенство, значит, точка лежит в данной плоскости.

На втором шаге из уравнения плоскости «снимаем» вектор нормали: . Поскольку векторы параллельны плоскости, а вектор ей перпендикулярен, то должны иметь место следующие факты: . Ортогональность векторов элементарно проверяется с помощью скалярного произведения: