В этом уроке будем учиться строить эпюры для балок, работающих на поперечный изгиб — эпюры поперечных сил и изгибающих моментов. Важно уметь правильно построить и проанализировать эти эпюры, потому что большинство современных инженерных сооружений состоят из элементов, которые работают на изгиб.
В статье рассмотрим 2 примера: один попроще — консольная балка, загруженная сосредоточенными силами и моментом, другой посложнее — двухопорная балка, загруженная распределённой нагрузкой.
Чтобы освоить материал этого урока, уже нужно знать, как определяются опорные реакции. Умеешь — отлично, но если же нет, то можешь изучить этот урок.
Подробно рассматривать в этом уроке нахождения реакций не будем, я буду приводить только их расчёт.
Поперечные силы и изгибающие моменты
При поперечном изгибе, в поперечных сечениях балки, возникает два внутренних силовых фактора (ВСФ) – поперечная сила (Q) и изгибающий момент (Mизг).
Наша задача, научиться определять их и строить эпюры. Чтобы потом, используя полученные эпюры, можно было проводить различные расчёты. Например, подбирать размеры поперечных сечений балки или проверять прочность балки, если эти размеры уже заданы и т. д.
Поперечные силы и изгибающие моменты определяются с помощью метода сечений. Когда балка мысленно рассекается на две части. Затем действие частей балки друг на друга заменяется внутренними силовыми факторами (ВСФ) – поперечными силами и изгибающими моментами. Потом путём рассмотрения равновесия одной из частей находятся ВСФ.
Если пока не очень понятно — это нормально, когда начнём это всё делать на практике, ты обязательно всё поймёшь!
Обозначения поперечных сил и изгибающих моментов
Теперь поговорим по поводу обозначений для поперечных сил и изгибающих моментов. Как правило, задачи в сопромате, и механике в целом, решаются относительно каких-то координатных осей. А поперечные силы и изгибающие моменты, имеют индексы в зависимости от выбранной системы координат.
Например, если выбрать следующие обозначения для координатных осей:
То, поперечная сила, будет обозначаться, как Qy (параллельна оси y), а изгибающий момент, как Mx (поворачивает относительно оси x). Это наиболее частый вариант. Однако, можно встретить обозначения – Qy, Mz или Qz, Mx. Самые ленивые, предпочитают подписывать данные величины, как просто Q и M. Как видишь, здесь всё зависит от предпочтений твоего преподавателя. Чтобы изучая этот урок, ты не привыкал (- а) к каким-то индексам, т. к. твой преподаватель тебя всё равно будет учить по-своему, я решил использовать в статье для поперечной силы, просто букву – Q, а для изгибающего момента – Mизг. Такое обозначение изгибающего момента, тоже используется часто, а сам индекс «изг» нужен, чтобы не путать внутренний – изгибающий момент, с внешними моментами, которые почти всегда подписываются просто буквой – M.
Расчётная схема балки
Также нужно понимать, что когда мы рассчитываем поперечные силы и изгибающие моменты, мы считаем их непросто для какой-то линии:
А подразумеваем, что мы рассчитываем некоторый элемент конструкции — балку, которая обязательно имеет некоторую форму, либо для которой впоследствии будет рассчитана эта форма, в зависимости от целей расчёта.
К примеру, балка может иметь прямоугольное поперечное сечение:
Если в расчётах эпюр при растяжении (сжатии) или кручении, форма стержня указывалась явно, и в этом был определённый смысл, так как те стержня имели ступенчатую форму – разную жёсткость на участках. То здесь, как правило, балки имеют одинаковое сечение, по всей длине, поэтому для экономии времени, балку показывают в виде такой линии. Затем, после построения эпюр, традиционно, для балки либо подбирается поперечное сечение из условия прочности, либо проверяется прочность уже заданного сечения.
Правила знаков для поперечных сил и изгибающих моментов
В этом разделе поговорим о правилах знаков для поперечных сил и изгибающих моментов. Для примера возьмём самую простую расчётную схему — консольную балку, загруженную сосредоточенной силой (F).
Расчётная схема
Предположим, что нужно определить поперечную силу и изгибающий момент в каком-то поперечном сечении. Пока не будем строить никаких эпюр, а просто поставим перед собой простейшую задачу — рассчитать внутренние силовые факторы (Q и Мизг) для одного, конкретного сечения. Например, рассмотрим сечение в заделке (А).
Чтобы вычислить внутренние силовые факторы для этого сечения, нужно учесть всю внешнюю нагрузку, либо справа от сечения, либо слева. Если учитывать нагрузку справа — нужно учесть силу F, а если учитывать нагрузку слева — нужно учесть тогда реакции в заделке. Чтобы не вычислять реакции, пойдём по короткому пути и учтём всю нагрузку — справа.
Правило знаков для поперечных сил
Поперечная сила в сечении будет равна алгебраической сумме всех внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
А знаки внешних сил определяются следующим образом — если внешняя сила, относительно рассматриваемого сечения, стремится повернуть:
• ПО часовой стрелке, то её нужно учесть с «плюсом»;
• ПРОТИВ часовой стрелки — учитываем её с «минусом».
Таким образом, для нашего случая, поперечная сила в сечении A будет равна:
Правило знаков для изгибающих моментов
Изгибающий момент в сечении будет равен алгебраической сумме всех моментов внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
Перед тем как поговорить о правилах знаков для изгибающих моментов. Необходимо понять ещё одну особенность — когда на балку действует какая-то внешняя нагрузка, балка деформируется. При деформации балки принято различать «верхние волокна» и «нижние волокна», относительно линии (нейтральной оси), проходящей через центр тяжести поперечного сечения балки.
Одни волокна при поперечном изгибе, будут растягиваться, а другие сжиматься.
В нашем случае, «верхние волокна», как видишь, будут растянуты, а нижние – сжаты.
На основании этой особенности, часто используется следующее правило для изгибающих моментов — если момент силы стремится растянуть:
• верхние волокна, то учитываем его с «минусом»;
• нижние волокна, то нужно учесть его с «плюсом».
Не забываем, что мы ведём расчёт моментов, поэтому все силы нужно умножать на соответствующие плечи.
Таким образом, в нашем случае, изгибающий момент в сечении A будет равен:
Если на балку действуют сосредоточенные моменты, то правило знаков аналогичное:
Сосредоточенные моменты, конечно, уже не нужно ни на что умножать. Например, для верхней схемы, изгибающий момент в сечении A будет равен:
Как построить эпюры поперечных сил и изгибающих моментов ?
В пределах участков, и эпюра Q и эпюра M меняются по определённому закону. Границами участков являются точки приложения сил, моментов, а также начало и конец распределённой нагрузки (будем рассматривать во второй задаче). Поэтому, чтобы построить эпюры в пределах участка, сначала необходимо написать уравнения, которые будут описывать изменение поперечных сил и изгибающих моментов в пределах участка. А затем, подставляя в уравнения координаты начала и конца участка, получить значения на эпюрах в характерных точках, и построить эпюры на участке. Рассчитав таким образом все участки, можно построить эпюры для балки.
Чувствую, опять перегрузил тебя информацией…давай лучше, наконец, посмотрим, как это всё делается на практике 😉
Построение эпюр для консольной балки
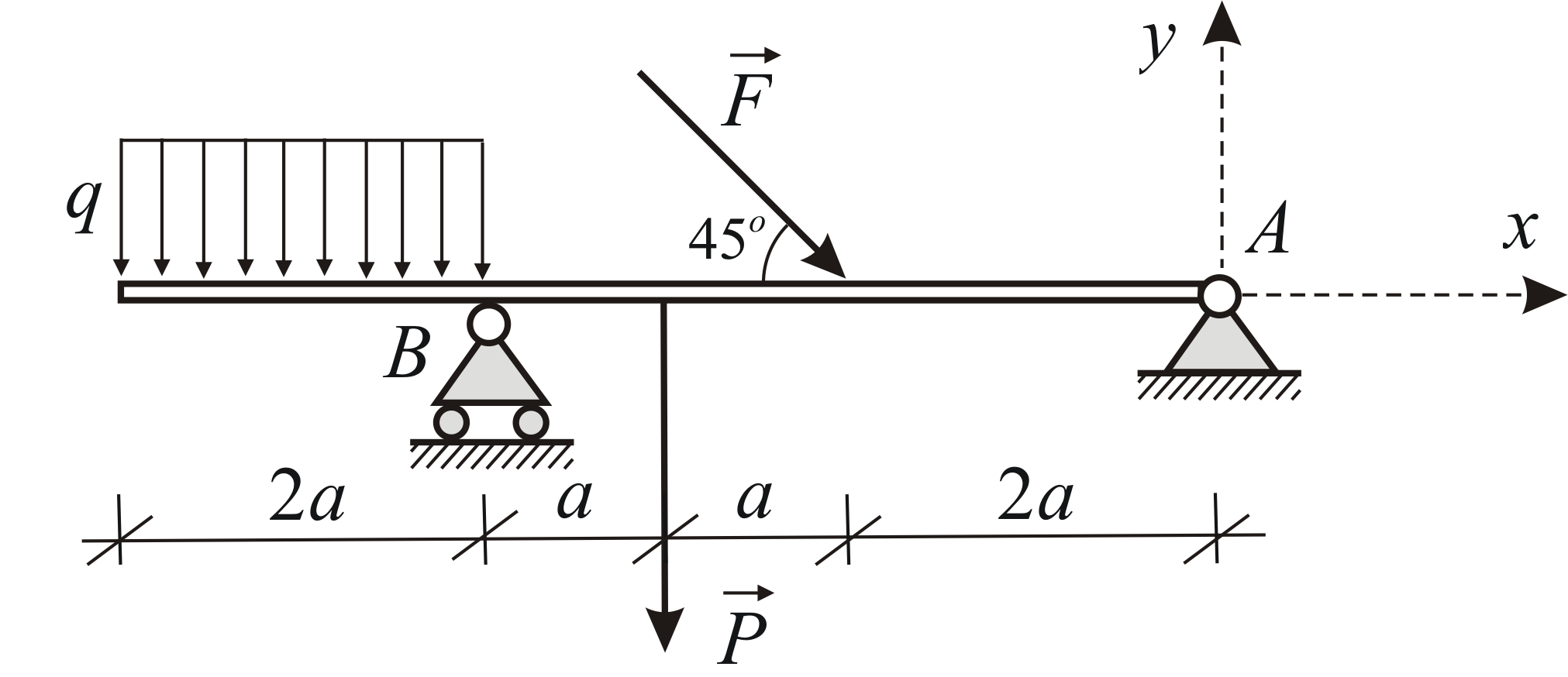
В качестве первого примера, возьмём консольную балку, жёстко закреплённую с левого торца и загруженной следующим образом:
Будем рассчитывать балку справа налево.
Рассмотрим первый участок
Обозначим некоторое сечение 1-1 на расстоянии x1, от свободного торца балки, при этом x1 будет находиться в диапазоне: 0 ≤ x1 ≤ 4м.
Так как расчёт выполняется справа налево, то в уравнениях необходимо учесть всю нагрузку, которая находится правее рассматриваемого сечения. Как видишь, на этом участке действует всего лишь одна сила F. Её и будем учитывать.
Поперечные силы на первом участке
Сила F, относительно сечения 1-1, поворачивает ПО часовой стрелке, поэтому с учётом правила знаков, записываем её с «плюсом»:
Как видишь, поперечная сила будет постоянна на первом участке:
Уже можем отразить это на эпюре поперечных сил:
Изгибающие моменты на первом участке
Теперь запишем уравнение для изгибающих моментов. Сила F растягивает верхние волокна, поэтому с учётом правила знаков, нужно учесть момент силы F со знаком «минус»:
Здесь уже изгибающие моменты будут меняться по линейному закону. Как я уже писал, чтобы построить эпюру изгибающих моментов на участке, нужно вычислить значения на границах участка:
Откладываем полученные значения:
Расчёт второго участка
Переходим ко второму участку. Также будем рассматривать некоторое сечение 2-2, на расстоянии x2 от начала участка (0 ≤ x2 ≤ 6м). Здесь также нужно учесть ВСЮ нагрузку, которая находится справа от сечения 2-2.
Поперечные силы на втором участке
Теперь на участке будут действовать 2 силы (сосредоточенный момент — M, никак не влияет на эпюру поперечных сил), учитываем их с учётом правила знаков:
Теперь можем показать окончательную эпюру поперечных сил:
Изгибающие моменты на втором участке
Для изгибающих моментов, с учётом правила знаков, второе уравнение будет выглядеть следующим образом:
Вычисляем значения на границах второго участка:
Показываем окончательную эпюру изгибащих моментов:
Проверка построенных эпюр
Балку можно рассчитать и слева направо. При этом очевидно, должны получаться те же эпюры. Давай проверим себя и рассчитаем эту балку с другой стороны.
Определение реакций в жёсткой заделке
Первым делом, нам потребуется определить реакции в заделке:
Расчёт эпюр поперечных сил и изгибающих моментов
Рассчитываем все участки теперь слева направо:
Ожидаемо, получили те же эпюры поперечных сил и изгибающих моментов:
Причём не обязательно считать все участки балки только слева направо или справа налево. Можно считать балку с разных сторон:
Такой подход позволяет минимизировать расчёт: когда балка имеет много расчётных участков. Как раз так и будем считать вторую двухопорную балку.
Эпюра моментов со стороны растянутых или сжатых волокон
По построенной эпюре можно явно сказать, какие волокна балки будут растянуты, а какие сжаты. Это очень полезная информация, при проведении прочностных расчётов.
Причем сама эпюра была построенна со стороны растянутых волокон:
Однако, студентов некоторых специальностей учат строить эпюры, с другой стороны – со стороны сжатых волокон:
Как видишь, в первом случае, отрицательные значения на эпюре моментов откладываются выше нулевой линии, а во втором – ниже. При этом правила знаков для расчета эпюр и сами расчёты не меняются. Обычно эпюры «на растянутых волокнах» строят студенты — строители, а эпюры «на сжатых волокнах» строятся студентами машиностроительных специальностей. В конечном счёте с какой стороны ты будешь строить эпюры, будет зависеть от твоего преподавателя, как он учит. В своих уроках я буду строить эпюры моментов со стороны растянутых волокон.
Учёт распределённой нагрузки
Перед тем как пойдём дальше и рассмотрим вторую задачу – двухопорную балку, нужно научиться работать с распределённой нагрузкой.
Давай рассмотрим ещё одну простенькую схему — консольную балку, загруженную распределённой нагрузкой:
Определение поперечной силы и изгибающего момента в сечении A
Чтобы определить поперечную силу в сечении A, первым делом нужно «свернуть» распределённую нагрузку (q) до сосредоточенной силы. Для этого нужно интенсивность нагрузки (q) умножить на длину участка действия нагрузки.
После чего получим силу — ql, приложенную ровно посередине участка, на котором действует распределённая нагрузка:
Тогда поперечная сила QA будет равна:
Изгибающий момент Mизг, A будет равен:
Расчёт эпюр поперечных сил и изгибающих моментов
Для написания уравнений для расчёта эпюр рассмотрим сечение 1-1:
Уравнение для поперечных сил будет следующее:
Рассчитаем значения на эпюре поперечных сил:
Уравнение для изгибающих моментов будет следующее:
Тогда значения на эпюре будут такими:
На участке с распределённой нагрузкой, на эпюре изгибающих моментов всегда будет либо выпуклость, либо вогнутость. Так как эпюра на этом участке будет меняться по квадратичному закону.
Если эпюра моментов откладывается со стороны растянутых волокон, распределённая нагрузка будет направлена «внутрь вогнутости» (выпуклости) эпюры изгибающих моментов:
Если же эпюра моментов откладывается со стороны сжатых волокон, то наоборот:
Построение эпюр для двухопорной балки
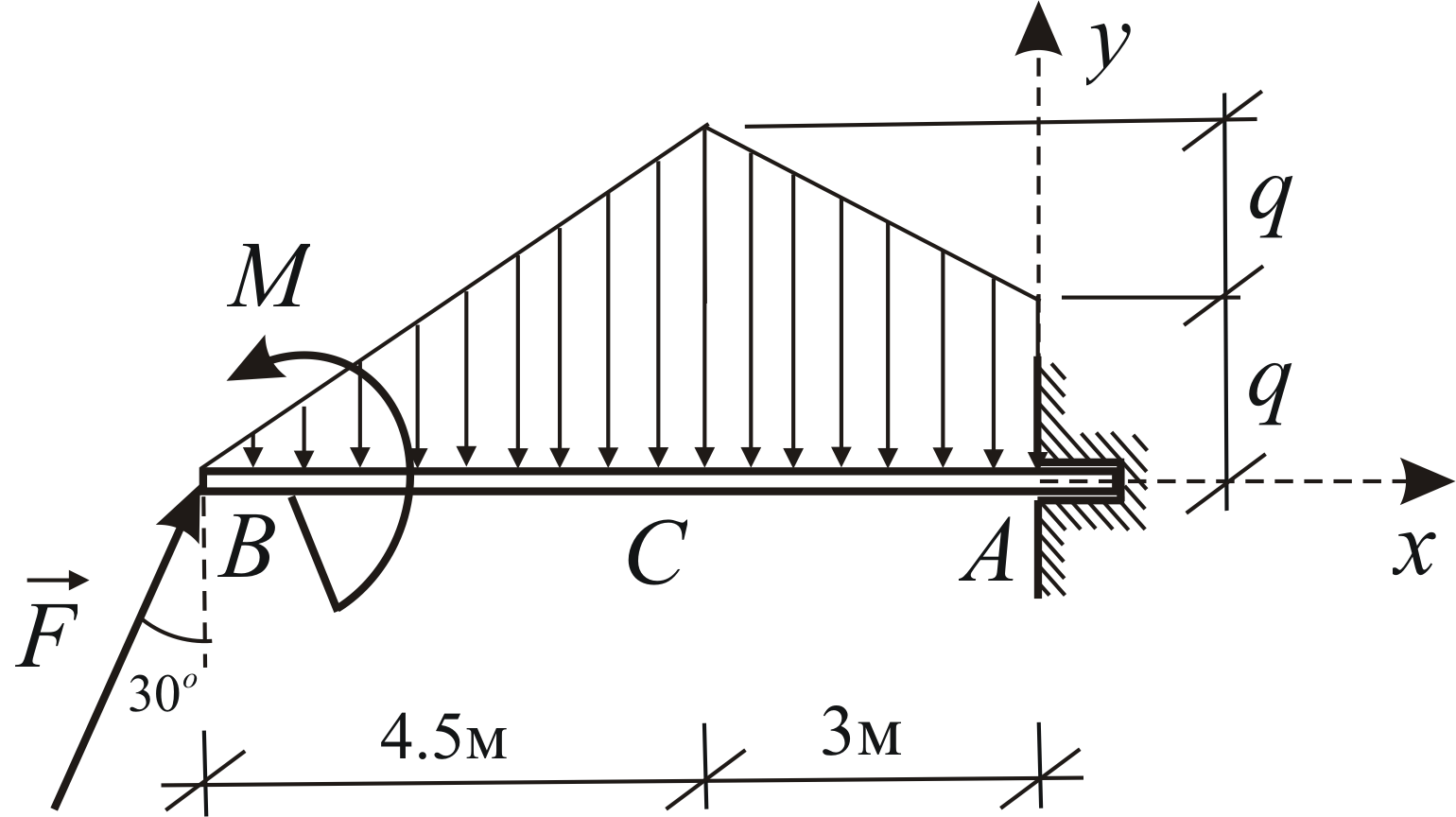
А теперь давай рассмотрим более сложную схему – двухопорную балку, загруженную всеми типами нагрузок:
Определим реакции опор:
Рассчитываем первый участок:
Строим эпюры на первом участке:
Определение экстремума на эпюре моментов
Так как эпюра поперечных сил пересекает нулевую линию на первом участке, это значит, что в месте пересечения — на эпюре изгибающих моментов будет экстремум — точка, в которой эпюра моментов часто имеет наибольшее значение. Это значение, обязательно следует рассчитывать, потому — что экстремумы часто являются не только максимальными значениями в пределах участка, но и для всей балки в целом. Поэтому так важно, вычислять это значение, для дальнейшего проведения прочностных расчётов.
Чтобы найти экстремум, сначала нужно найти координату, где эпюра поперечных сил пересекает нулевую линию. Для этого уравнение для поперечных сил нужно приравнять к нулю:
Отсюда найти значение координаты:
Затем подставить это значение в уравнение для изгибающих моментов:
Теперь можем указать экстремум на эпюре:
Расчет эпюр на остальных участках
Расчёты остальных участков не вижу смысла комментировать, потому что здесь будет применяться всё то, о чём я уже рассказывал по ходу урока. Поэтому просто приведу решение:
Определение экстремума:
Оценка правильности построенных эпюр поперечных сил и изгибающих моментов
И напоследок хочу рассказать как можно проверить себя – оценить правильность построенных эпюр визуально. Собственно так, как проверяют эпюры — преподаватели, ведь они не проверяют у всех студентов каждое уравнение, каждый знак или цифру, т.к. это бы занимало слишком много времени.
Вот несколько признаков, правильно построенных эпюр:
- На эпюре поперечных сил, в местах приложения сосредоточенных сил, должны быть скачки на величину этих сил.
- На эпюре изгибающих моментов, в местах приложения сосредоточенных моментов, должны быть скачки на величину этих моментов.
- Эпюра поперечных сил, на участках без распределённой нагрузки, должна быть постоянна. А на участках, где действует распределённая нагрузка – меняться по линейному закону.
- Эпюра изгибающих моментов, на участках без распределённой нагрузки, должна меняться по линейному закону или быть постоянна (если действуют только сосредоточенные моменты). А на участках, где действует распределённая нагрузка – иметь вогнутость или выпуклость.
Правила построения эпюр поперечных сил и изгибающих моментов
Озвучим правила построения эпюр, вытекающие из метода сечений, и являющиеся следствием дифференциальных и интегральных зависимостей, некоторые из которых справедливы при обходе эпюр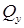 
и 
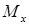слева направо. Зная правила построения эпюр, можно быстро найти грубую ошибку только по внешнему виду эпюр.
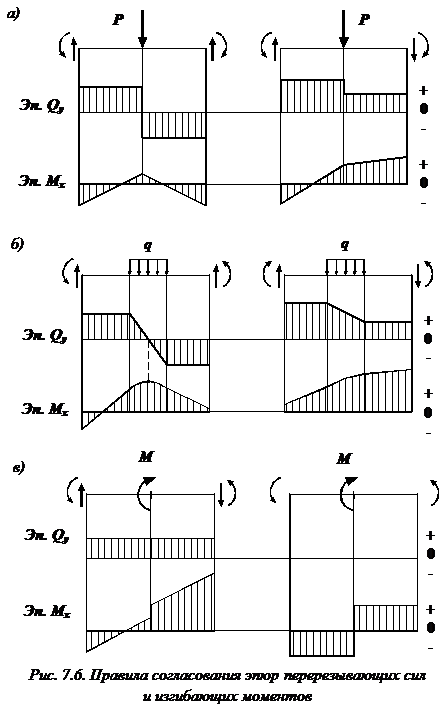
Правило построения эпюр – отсутствующая распределенная нагрузка
Если на участке балки отсутствует распределенная нагрузка (
), то эпюра поперечных сил на этом участке представляет собой прямую, параллельную оси балки (рис. 7.6). По дифференциальной зависимости распределенной нагрузки и поперечной силы: поскольку , то и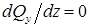 
. Следовательно, 
.
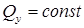Эпюра изгибающих моментов на участке, где 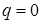, – прямая линия. Причем, если 
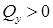, то прямая идет вверх, а если 
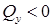, прямая идет вниз. Если 
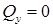, то изгибающий момент постоянен, поскольку 
.
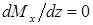Правило построение эпюр – скачки и изломы
Под сосредоточенной силой (P) на эпюре поперечных сил 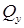(рис. 7.6, а) имеется скачок на величину этой силы и по ее направлению, а на эпюре изгибающих моментов 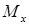– излом, угол которого направлен навстречу нагрузке.
Правило построение эпюр – присутствует распределенная нагрузка
Если на участке балки имеется равномерно распределенная нагрузка: эпюра поперечных сил 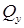представляет собой наклонную прямую (рис. 7.6, б), идущую вниз, если нагрузка 
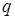направлена вниз (и наоборот). Эпюра 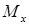на этом участке, согласно третьей формуле дифференциальных зависимостей, изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке.
Правило построение эпюр – экстремум
Если эпюра поперечной силы проходит через нулевое значение, то в этом сечении балки на эпюре изгибающих моментов 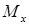имеется экстремум (последнее вытекает из дифференциальной зависимости 
). В точках, соответствующих началу и концу участка, в пределах которого действует распределенная нагрузка, параболическая и прямолинейная части эпюры 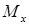переходят одна в другую плавно (без излома).
Правило построение эпюр – внешний момент
Сосредоточенный внешний момент M (рис. 7.6, в) никак не отражается на эпюре 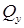. На эпюре в месте приложения этого момента имеется скачок на его величину.
Заметим, что построение эпюр поперечных сил и изгибающих моментов ввел в практику расчета балок на изгиб французский ученый Жан Антуан Шарль Бресс (1822 – 1883 гг.) в 1859 г.
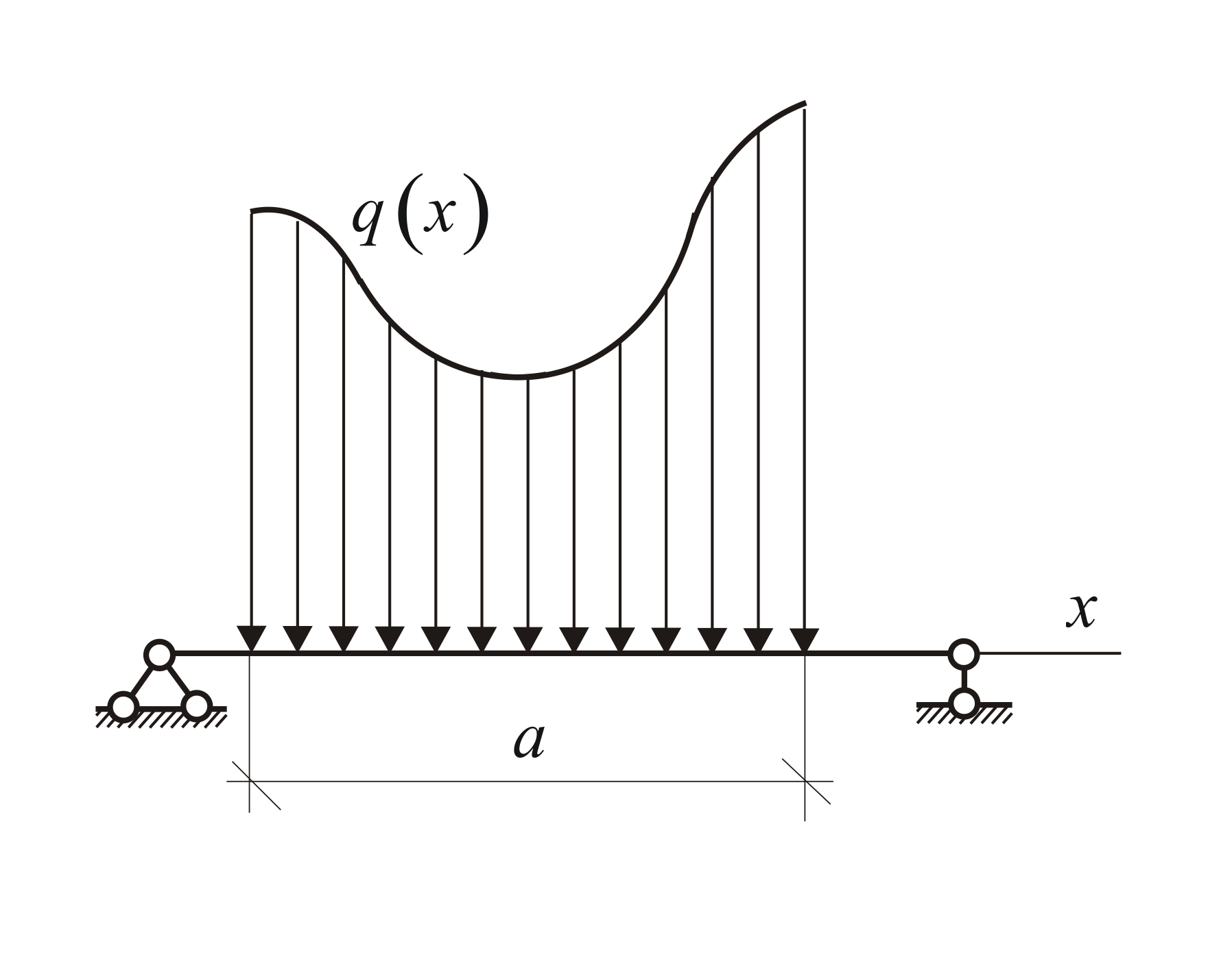
Поверхностные и объёмные силы
представляют собой нагрузку, распределённую
по некоторой поверхности или объёму.
Такая нагрузка задаётся интенсивностью
,
которая представляет собой силу,
приходящуюся на единицу некоторого
объёма, или некоторой площади, или
некоторой длины.
Особое место при решении ряда
практически интересных задач занимает
случай плоской распределённой нагрузки,
приложенной по нормали к некоторой
балке. Если вдоль балки направить ось
,
то интенсивность будет функцией
координаты
и измеряется в Н/м. Интенсивность
представляет собой силу, приходящуюся
на единицу длины.
Плоская фигура, ограниченная балкой
и графиком интенсивности нагрузки,
называется эпюрой распределённой
нагрузки (Рис. 1.28). Если по характеру
решаемой задачи можно не учитывать
деформации, т.е. можно считать тело
абсолютно твёрдым, то распределённую
нагрузку можно (и нужно) заменить
равнодействующей.
|
|
|
|
|
Рис. 1.28 |
Рис. 1.29 |
|
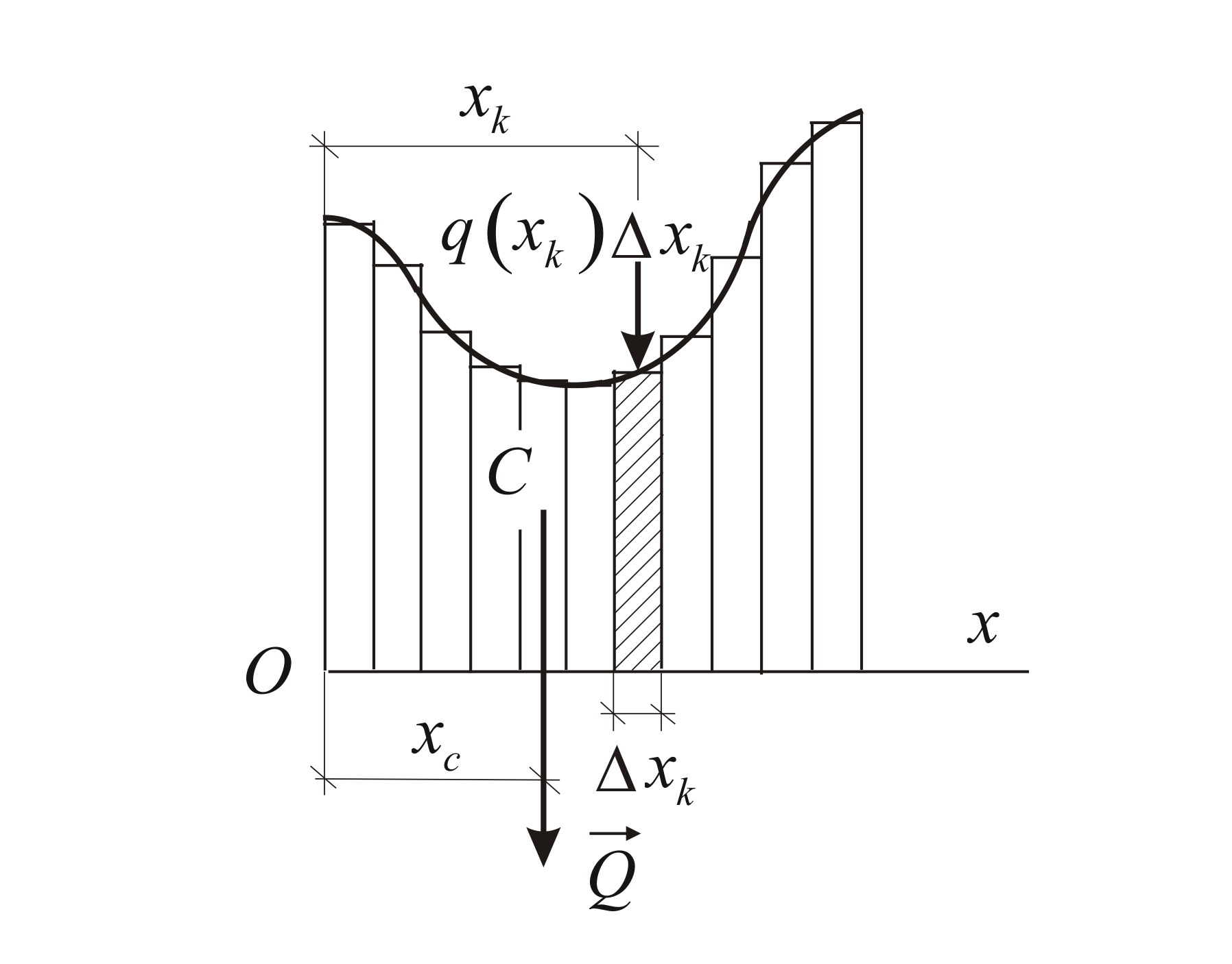
Разобьём балку на
отрезков длиной
,
на каждом из которых будем считать
интенсивность постоянной и равной
,
где
–координата отрезка
.
При этом кривая интенсивности заменяется
ломаной линией, а нагрузка, приходящаяся
на отрезок
,
заменяется сосредоточенной силой
,
приложенной в точке
(Рис. 1.29). Полученная система параллельных
сил имеет равнодействующую, равную
сумме сил, действующих на каждый из
отрезков, приложенную в центре
параллельных сил.
Понятно, что такое представление
тем точнее описывает реальную ситуацию,
чем меньше отрезок
,
т.е. чем больше число отрезков
.
Точный результат получаем, переходя к
пределу при длине отрезка
,
стремящейся к нулю. Предел, получаемый
в результате описанной процедуры,
представляет собой интеграл. Таким
образом, для модуля равнодействующей
получаем:
Для определения координаты точки
приложения равнодействующей используем
теорему Вариньона:
если система сил имеет равнодействующую,
то момент равнодействующей относительно
любого центра (любой оси) равен сумме
моментов всех сил системы относительно
этого центра (этой оси)
Записывая эту теорему для системы сил
в проекциях на ось
и переходя к пределу при длине отрезков,
стремящейся к нулю, получаем:
Очевидно, модуль равнодействующей
численно равен площади эпюры распределённой
нагрузки, а точка её приложения совпадает
с центром тяжести однородной пластины,
имеющей форму эпюры распределённой
нагрузки.
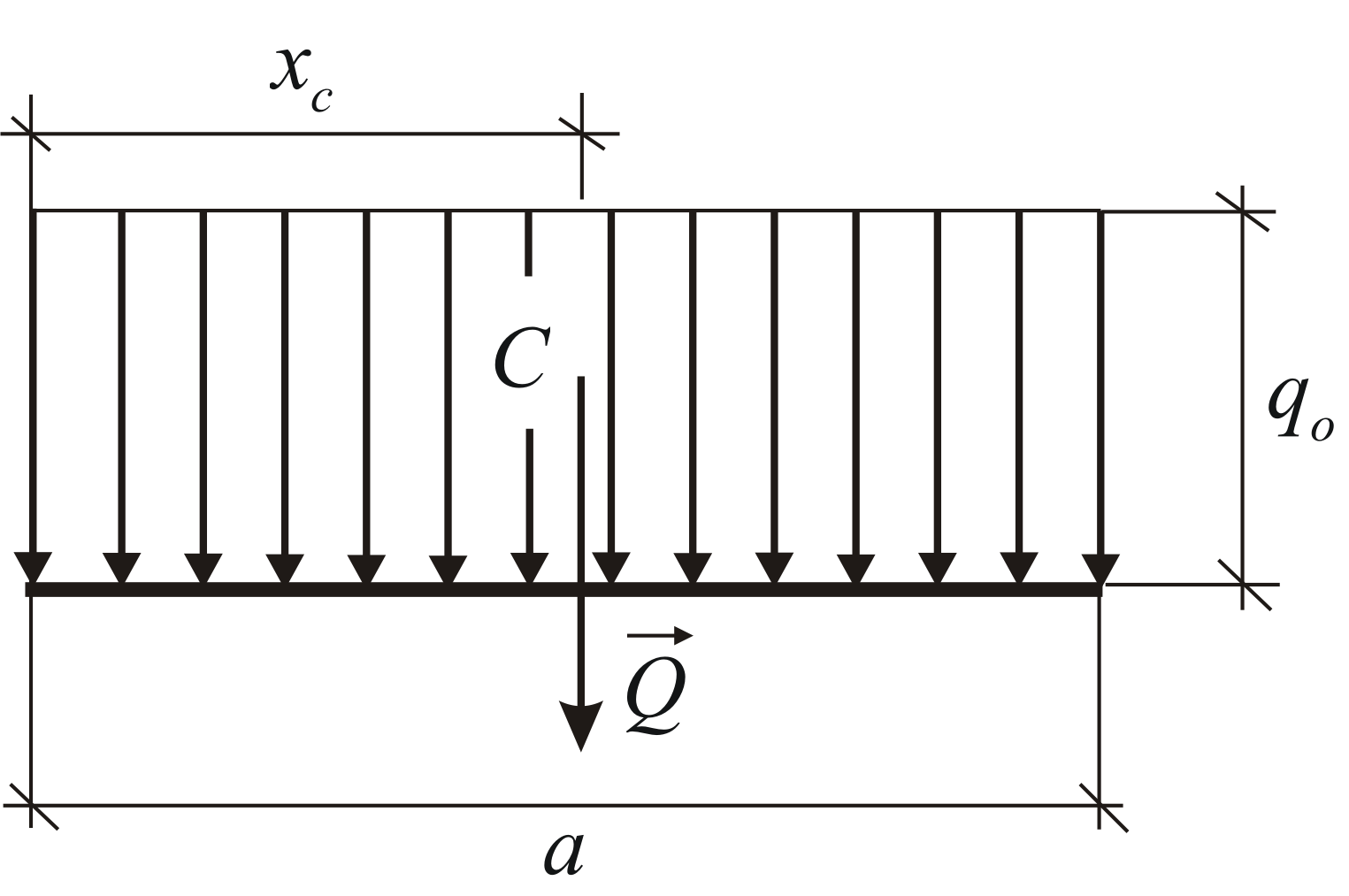
Отметим два часто встречающихся случая.
Равномерно распределённая нагрузка,
(Рис. 1.30). Модуль равнодействующей и
координата её точки приложения
определяются по формулам:
В инженерной практике такая нагрузка
встречается довольно часто. Равномерно
распределённой в большинстве случаев
можно считать весовую и ветровую
нагрузку.
|
|
|
|
|
Рис. 1.30 |
Рис. 1.31 |
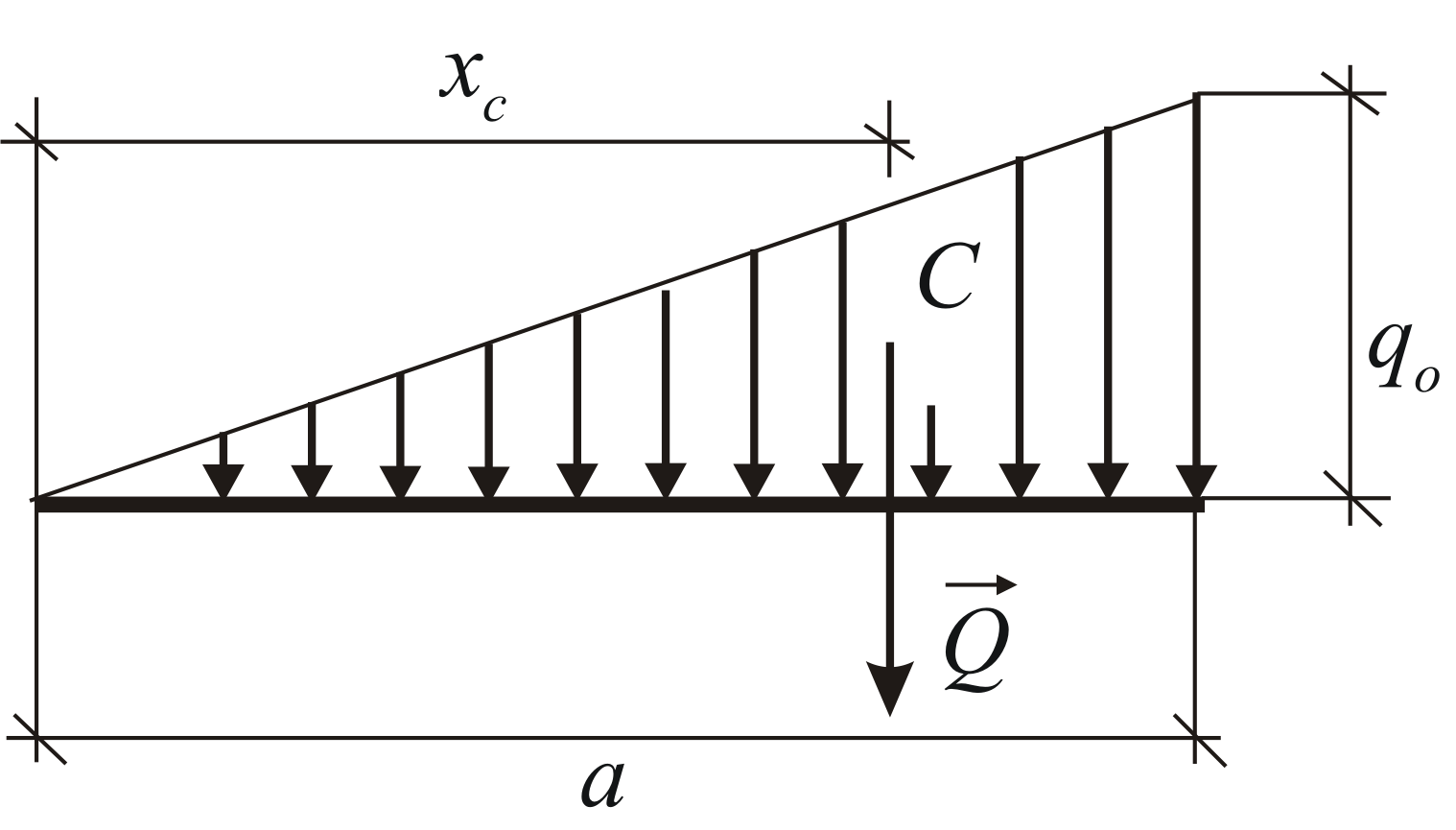
Линейно
распределённая нагрузка,
(Рис. 1.31). В этом случае:
В
частности, давление воды на вертикальную
стенку прямо пропорционально глубине
.
Пример
1.5
Определить реакции опор
и
балки, находящейся под действием двух
сосредоточенных сил и равномерно
распределённой нагрузки. Дано:
|
|
|
Рис. 1.32 |
Найдём равнодействующую распределённой
нагрузки. Модуль равнодействующей равен
плечо силы
относительно точки
равно
Рассмотрим равновесие балки. Силовая
схема представлена на Рис. 1.33.
|
|
|
Рис. 1.33 |
Условия
равновесия в рассматриваемом случае
имеют вид:
Пример
1.6
Определить реакцию заделки консольной
балки, находящейся под действием
сосредоточенной силы, пары сил и
распределённой нагрузки (Рис. 1.34).
Дано:
Заменим распределённую нагрузку тремя
сосредоточенными силами. Для этого
разобъём эпюру распределённой нагрузки
на два треугольника и прямоугольник.
Находим
Силовая схема представлена на Рис. 1.35.
|
|
|
|
|
Рис. 1.34 |
Рис. 1.35 |
Вычислим
плечи равнодействующих относительно
оси
Условия
равновесия в рассматриваемом случае
имеют вид:
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:
1. Что
называется интенсивностью распределённой
нагрузки?
2. Как
вычислить модуль равнодействующей
распределённой нагрузки?
3. Как
вычислить координату точки приложения
равнодействующей распределённой
нагрузки?
4. Чему
равен модуль и какова координата точки
приложения равномерно распределённой
нагрузки?
5. Чему
равен модуль и какова координата точки
приложения линейно распределённой
нагрузки?
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из
сборника задач И.В.Мещерского: 4.28;
4.29; 4.30; 4.33; 4.34.
Из
учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА –
теория и практика»: комплекты СР-2; СР-3.
ПРАКТИЧЕСКИЕ
ЗАНЯТИЯ № 4-5
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.2015560.03 Кб15PSY – recommendation.pdf
- #
- #
В этой статье будут рассмотрены основные нюансы расчета прогибов, методом начальных параметров, на примере консольной балки, работающей на изгиб. А также рассмотрим пример, где с помощью универсального уравнения, определим прогиб балки и угол поворота.
Равномерно и неравномерно распределенная нагрузка на балку
Распределение сил, которые лежат в одной плоскости, задается равномерно распределенной тяжестью. Основным обозначением является интенсивность q — предельная тяга, несущая равнодействующую на единицу длины нагруженного участка АВ длиной а.
Единицы измерения распределённой нагрузки [Н/м].
Её также можно заменить на величину Q, которая приложена в середину AB.
Составим формулу: Q = q∗a
Неравномерно распределённую нагрузку чаще всего упрощают, приводя её к эквивалентной равномерно распределенной, чтобы упростить расчеты.
При построении также следует учитывать максимальный прогиб балки, её прочность, расчетную опорную реакцию и моментальную опору.
Методика выполнения расчета на прогиб
Прежде чем приступать к расчету, нужно будет вспомнить некоторые зависимости из теории сопротивления материалов и составить расчетную схему. В зависимости от того, насколько правильно выполнена схема и учтены условия нагружения, будет зависеть точность и правильность расчета.
Используем простейшую модель нагруженной балки, изображенной на схеме. Простейшей аналогией балки может быть деревянная линейка, фото.
В нашем случае балка:
- Имеет прямоугольное сечение S=b*h, длина опирающейся части составляет L;
- Линейка нагружена силой Q, проходящей через центр тяжести изгибаемой плоскости, в результате чего концы поворачиваются на небольшой угол θ, с прогибом относительно начального горизонтального положения, равным f;
- Концы балки опираются шарнирно и свободно на неподвижных опорах, соответственно, не возникает горизонтальной составляющей реакции, и концы линейки могут перемещаться в произвольном направлении.
Для определения деформации тела под нагрузкой используют формулу модуля упругости, который определяется по соотношению Е=R/Δ, где Е – справочная величина, R— усилие, Δ— величина деформации тела.
Вычисляем моменты инерции и сил
Для нашего случая зависимость будет выглядеть так: Δ = Q/(S·Е). Для распределенной вдоль балки нагрузки q формула будет выглядеть так: Δ = q·h/(S·Е).
Далее следует наиболее принципиальный момент. Приведенная схема Юнга показывает прогиб балки или деформацию линейки так, если бы ее раздавливали под мощным прессом. В нашем случае балку изгибают, а значит, на концах линейки, относительно центра тяжести, приложены два изгибающих момента с разным знаком. Эпюра нагружения такой балки приведена ниже.
Чтобы преобразовать зависимость Юнга для изгибающего момента, необходимо обе части равенства умножить на плечо L. Получаем Δ*L = Q·L/(b·h·Е).
Если представить, что одна из опор жестко закреплена, а на второй будет приложен эквивалентный уравновешивающий момент сил Mmax = q*L*2/8, соответственно, величина деформации балки будет выражаться зависимостью Δх = M·х/((h/3)·b·(h/2)·Е). Величину b·h2/6 называют моментом инерции и обозначают W. В итоге получается Δх = M·х/(W·Е) основополагающая формула расчета балки на изгиб W=M/E через момент инерции и изгибающий момент.
Чтобы точно выполнить расчет прогиба, потребуется знать изгибающий момент и момент инерции. Величину первого можно посчитать, но конкретная формула для расчета балки на прогиб будет зависеть от условий контакта с опорами, на которых находится балка, и способа нагружения, соответственно для распределенной или концентрированной нагрузки. Изгибающий момент от распределенной нагрузки считается по формуле Mmax = q*L2/8. Приведенные формулы справедливы только для распределенной нагрузки. Для случая, когда давление на балку сконцентрировано в определенной точке и зачастую не совпадает с осью симметрии, формулу для расчета прогиба приходится выводить с помощью интегрального исчисления.
Момент инерции можно представить, как эквивалент сопротивления балки изгибающей нагрузке. Величину момента инерции для простой прямоугольной балки можно посчитать по несложной формуле W=b*h3/12, где b и h – размеры сечения балки.
Из формулы видно, что одна и та же линейка или доска прямоугольного сечения может иметь совершенно разный момент инерции и величину прогиба, если положить ее на опоры традиционным способом или поставить на ребро. Недаром практически все элементы стропильной системы крыши изготавливаются не из бруса 100х150, а из доски 50х150.
Реальные сечения строительных конструкций могут иметь самые разные профили, от квадрата, круга до сложных двутавровых или швеллерных форм. При этом определение момента инерции и величины прогиба вручную, «на бумажке», для таких случаев становится нетривиальной задачей для непрофессионального строителя.
Формулы для практического использования
На практике чаще всего стоит обратная задача – определить запас прочности перекрытий или стен для конкретного случая по известной величине прогиба. В строительном деле очень сложно дать оценку запасу прочности иными, неразрушающими методами. Нередко по величине прогиба требуется выполнить расчет, оценить запас прочности здания и общее состояние несущих конструкций. Мало того, по выполненным измерениям определяют, является деформация допустимой, согласно расчету, или здание находится в аварийном состоянии.
Совет! В вопросе расчета предельного состояния балки по величине прогиба неоценимую услугу оказывают требования СНиПа. Устанавливая предел прогиба в относительной величине, например, 1/250, строительные нормы существенно облегчают определение аварийного состояния балки или плиты.
Например, если вы намерены покупать готовое здание, простоявшее достаточно долго на проблемном грунте, нелишним будет проверить состояние перекрытия по имеющемуся прогибу. Зная предельно допустимую норму прогиба и длину балки, можно безо всякого расчета оценить, насколько критическим является состояние строения.
Строительная инспекция при оценке прогиба и оценке несущей способности перекрытия идет более сложным путем:
- Первоначально измеряется геометрия плиты или балки, фиксируется величина прогиба;
- По измеренным параметрам определяется сортамент балки, далее по справочнику выбирается формула момента инерции;
- По прогибу и моменту инерции определяют момент силы, после чего, зная материал, можно выполнить расчет реальных напряжений в металлической, бетонной или деревянной балке.
Вопрос – почему так сложно, если прогиб можно получить, используя для расчета формулу для простой балки на шарнирных опорах f=5/24*R*L2/(E*h) под распределенным усилием. Достаточно знать длину пролета L, высоту профиля, расчетное сопротивление R и модуль упругости Е для конкретного материала перекрытия.
Ответ прост — необходимо непросто рассчитать, но и сохранить на бумаге ход выполнения проверочного расчета, чтобы сделанные выводы о состоянии перекрытия можно было проверить и перепроверить по всем этапам проверки.
Совет! Используйте в своих расчетах существующие ведомственные сборники различных проектных организаций, в которых в сжатом виде сведены все необходимые формулы для определения и расчета предельного нагруженного состояния.
Проверка сечения балки по касательным напряжениям
Так как Qmax = 68 кН, то
Построение эпюр нормальных σ и касательных τ напряжений в неблагоприятном сечении балки:
Построение эпюры нормальных напряжений
Построение эпюры касательных напряжений
В отношении главных напряжений неблагоприятным является сечение над левой опорой, в котором:
М = -32 кНм и Q = 68 кН.
Значение напряжений в различных точках по высоте двутавра сведены в таблицу 1
Таблица 1
Результаты расчета в примере
Изобретение относится к области неразрушающего контроля и мониторинга прогиба балок. Объект изобретения предназначен для строительных конструкций, находящихся в стадии эксплуатации.
Причины возрастания прогиба балки
1) деградация материалов;
2) дефекты и образование неисправностей (трещины, коррозия, гниение в древесине и т.д.);
3) увеличение нагрузки.
Прогибы балок зданий и сооружений можно измерить различными способами.
Известен [1, с.52] способ измерения прогиба балок в различное время их эксплуатации, заключающийся в том, что с помощью двух планок с делениями, одна из которых закреплена неподвижно в бетонном или железобетонном основании, а другая планка закреплена на балке, и по их взаимному смещению судят о прогибе балки. Полный прогиб складывается из прогиба от собственного веса балки и существующей на ней нагрузки. Полный прогиб измеряют с помощью высокоточной рейки и нивелира.
Данный способ обладает рядом недостатков:
— малая точность измерений прогиба балки;
— необходимость устройства опорного железобетонного основания;
— заполняется пространство под балкой, что нарушает технологический процесс;
— нет дистанционного управления; затруднен мониторинг прогиба балки.
Известен [1, с.54] способ измерения прогибов балки прогибомерами систем Максимова и ЦНИИСК, заключающийся в том, что к испытываемой конструкции в месте, где требуется измерить прогиб, прикрепляют стальную проволоку диаметром 0,25 мм так, чтобы она дважды обматывала барабан прогибомера со шкалой, и к концу ее подвешивают груз весом 1,5 кг. При прогибе конструкции проволока вращает барабан, соединенный со стрелкой, которая движется по циферблату. На циферблате имеется также счетчик оборотов с ценой деления 0,1 см. Прибор крепится к неподвижному предмету специальной металлической струбциной.
Недостатками этого способа являются потребность неподвижной опоры (предмета) для крепления прибора, который вместе с проволокой закрывает пространство под балкой на время измерения прогиба балки; отсутствие дистанционного управления измерениями прогиба; требуется присутствие работника на этапе измерений; затруднен мониторинг прогиба; на результаты измерений оказывает влияние температура и другие природные явления (ветер, дождь, снег и т.д.); неточность измерений, вызванная изменением места наибольшего прогиба балки, вызванного изменением свойств материала балки с течением времени, положением нагрузки и т.д.
Наиболее близким к заявленному способу измерений прогибов балок и плит является известный [1, с.59] способ измерения прогибов (перемещений) электромеханическим прибором со штоком, упругим элементом и тензорезисторами, наклеенными на упругие элементы, заключающийся в том, что прибор устанавливают на неподвижную опору под балкой в месте наибольшего прогиба, шток упирают в балку непосредственно или через дополнительную связь, балка прогибается под нагрузкой в результате деградации материала и других причин в течение времени, прогибы регистрируют косвенно через электрические сопротивления тензорезисторов ΔR, по которым через переводной коэффициент определяется прогиб балки.
Недостатками этого способа является низкая точность измерения прогиба балки, вызванная тем, что измерение производится без учета возможного изменения места наибольшего прогиба по длине балки, которое вызвано различными непредвиденными причинами; необходимость опорного устройства для крепления прибора и связи с балкой прибора, что приводит к ограничению использования пространства под балкой или над балкой на время измерений; необходимость устройства защиты прибора от различных природных воздействий и его охраны, особенно в зимнее время при непрерывном измерении, что затрудняет мониторинг прогиба балки.
Целью предлагаемого способа определения прогиба балок является повышение точности измерений наибольших прогибов балок; проведение мониторинга прогиба балки; измерение прогибов с дистанционным управлением без нарушения технологических процессов над балкой и под балкой в период измерения прогибов в любых условиях окружающей среды.
Способ заключается в следующем.
Существующими средствами измерения, например, с помощью высокоточной геодезической рейки и нивелира, устанавливают значение наибольшего начального прогиба балки Δ0 в любой момент времени эксплуатации балки и тем самым устанавливают места наибольшего прогиба балки.
Определяют значение постоянного коэффициента r, значение которого определяют по формулам в зависимости от расчетной схемы балки методами строительной механики из [2], который входит в расчетную формулу прогиба балки.
На фиг.1 показана условная схема подключения тензорезисторов на балке, где 1 — провода, 2 — рабочие тензорезисторы, 3 — компенсационные тензорезисторы, 4 — балка, 5 — тензостанция. Проводами 1 соединятся рабочие 2 и компенсационные 3 тензорезисторы, размещенные на обоих поясах балки 4 на участке в месте наибольшего прогиба на подготовленную поверхность, при этом рабочие крепятся вдоль главных напряжений σ, а компенсационные — перпендикулярно им в промежутках между рабочими тензорезисторами. Все провода 1 соединены с измерительным прибором электрического (омического) сопротивления в виде многоканальной тензостанции 5.
Подготовка к работе включает в себя следующие действия. Изолируют тензорезисторы эпоксидной смолой, монтируют известные из работы [2] мостовые схемы для каждой пары рабочих 2 и компенсационных тензорезисторов 3 в одном сечении балки R1 и R2, подключают провода 1 с тензостанцией 5 и определяют R0 — начальное электрическое (омическое) сопротивление всех рабочих тензорезисторов. Тензорезисторы наклеивают на участках поясов балки длиной 15-20 см по одному тензорезистору на каждые 5 см длины пояса, как показано на фиг.1, при базе тензорезисторов 10-30 мм, так как на этой длине может попадать сечение балки с наибольшим прогибом. Число рабочих тензорезисторов принимают от 3 до 5 в том и другом поясе балки исходя из вероятности смещения наибольшего прогиба балки от тех или иных причин в процессе эксплуатации балки в пределах 15-20 см длины балки, так как на длине 15-20 см можно разместить от 3 до 5 рабочих и компенсационных тензорезисторов с базой (длиной) 10-30 мм и шириной (компенсационных) 10 мм.
Весь процесс измерения происходит следующим образом:
1) при увеличении прогиба изменяется омическое сопротивление тензорезисторов, и по соединительным проводам вся информация об этом поступает на тензостанцию;
2) полный прогиб определяют по формуле
Δ(t)=Δ0+r·(|ΔR1(t)|+|ΔR2(t)|),
где Δ0 — начальный прогиб в момент начала наблюдений при t=0, измеренный нивелиром и высокоточной геодезической рейкой;
r — постоянный коэффициент, зависящий от расчетной схемы балки.
Известно из [1], что и ,
где k — коэффициент тензочувствительности тензорезисторов, тогда имеем эпюру ΔR подобной эпюре ε, как показано на фиг.2 и фиг.3, на которых изображены однопролетные балки с сосредоточенной нагрузкой в середине и равномерно распределенной нагрузкой по всей длине пролета, где ε1 и ε2 — деформации, ΔR1 и ΔR2 — омические (электрические) сопротивления, Δ — наибольший прогиб, L — длина пролета, F — сосредоточенная сила, h — высота сечения, b — ширина сечения.
Из эпюры ΔR имеем при и ΔR2 по абсолютному значению. Отсюда , где ус — расстояние от нейтральной оси балки до верхнего или нижнего края балки с симметричным поперечным сечением балки, как показано на фиг.2 и фиг.3. Известно из работы [2], что для однопролетной балки с сосредоточенной нагрузкой в середине пролета наибольший прогиб . С учетом J=W·yc и значением yc имеем:
— для однопролетной балки с шарнирными опорами и сосредоточенной силой в середине пролета балки по фиг.2 имеем
где для балки любого симметричного поперечного сечения высотой h имеем , k — коэффициент тензочувствительности тензорезисторов, Е — модуль упругости материала;
— для однопролетной балки с шарнирными опорами и равномерно распределенной нагрузкой по всей длине пролета по фиг.3 и имеем
где , |ΔR1(t)| и |ΔR2(t) — приращение электрических (омических) сопротивлений тензорезисторов в момент времени t, взятых по абсолютной величине, в омах. Для других расчетных схем находят значение r методами строительной механики;
3) проводят предварительный контроль достоверной работы мостовой схемы из тензорезисторов путем сравнения средних значений измерений от контрольной нагрузки F0, полученных прямыми механическими измерениями прогиба Δ1=Δ(F0), например геодезической высокоточной рейкой и нивелиром и по результатам измерений омических сопротивлений (ΔR1 и ΔR2) по формуле
Δ2=r·(|ΔR1|+|ΔR2|),
должно соблюдаться равенство Δ1=Δ2, с отличием не более 5%;
4) дальнейшие измерения прогиба балки в любой момент времени t осуществляют только по показаниям измерения сопротивления тензорезисторов по расчетной формуле
Δ(t)=Δ0+r·(|ΔR1(t)|+|ΔR2(t)|),
для значений r, зависящих от расчетных схем балок.
На основании результатов измерений f и Δ, приведенных в сводной таблице, построены графики зависимости прогибов f и Δ от нагрузки, представленные на фиг.4, где показаны результаты лабораторных испытаний балки с измерением прогибов индикатором часового типа и измерением сопротивлений ΔR1 и ΔR2.
1. Землянский А.А. Обследование и испытание зданий и сооружений: учебное пособие. — М: Изд-во АСВ, 2001. — 240 с., с ил.
2. Писаренко Г.С., Яковлев А.П., Матвеев В.В. Справочник по сопротивлению материалов. Изд-во «Наукова Думка», Киев, 1975. — 703 с.
Способ неразрушающего измерения прогиба балок в строительных конструкциях на стадии эксплуатации, заключающийся в том, что на поверхностях верхнего и нижнего поясов балки в месте наибольшего прогиба Δ, устанавливаемого с помощью высокоточной геодезической рейки и нивелира, наклеивают тензорезисторы с одинаковыми характеристиками непосредственно на подготовленную поверхность верхнего и нижнего поясов балки, отличающийся тем, что рабочие и компенсационные тензорезисторы наклеивают в количестве от 3 до 5 штук в каждом поясе на участке длиной от 15 до 25 см с наибольшим прогибом Δ, при этом рабочие тензорезисторы крепят вдоль главных напряжений σ вдоль балки, а компенсационные — между рабочими тензорезисторами поперек балки; защищают их от различных воздействий эпоксидной смолой, монтируют мостовые схемы для каждой пары тензорезисторов (рабочих и компенсационных) и соединяют провода от них с тензостанцией; измеряют начальное сопротивление R рабочих тензорезисторов, при этом прогиб балки Δ(t) в любой момент времени t определяют по формуле:Δ(t)=Δ+r·(|ΔR(t)|+|ΔR(t)|),где Δ — начальный наибольший прогиб балки в момент времени t=0, измеренный с помощью высокоточной геодезической рейки и нивелира до наклейки тензорезисторов; r — постоянный коэффициент, зависящий от расчетных схем и размеров балки, определяемый методами строительной механики:для балки с равномерно распределенной нагрузкой: ;для балки с сосредоточенной нагрузкой в середине пролета: ,где k — коэффициент тензочувствительности, l — длина пролета балки, h — высота балки;|ΔR(t)| и |ΔR(t)| — наибольшие приращения электрических (омических) сопротивлений из всех рабочих тензорезисторов, измеренных с помощью многоканальной тензостанции, вызванных изменением прогиба балки, различными причинами, измеряемые постоянно или периодически в отдельные моменты времени или в процессе эксплуатации балки при мониторинге прогиба балки.
Пример расчета прогиба балки
Для закрепления пройденного материала, предлагаю рассмотреть пример с заданными численными значениями всех параметров балки и нагрузок. Возьмем также консольную балку, которая жестко закреплена с правого торца. Будем считать, что балка изготовлена из стали (модуль упругости E = 2·105 МПа), в сечении у нее двутавр №16 (момент инерции по сортаменту I = 873 см4). Рассчитывать будем прогиб свободного торца, находящегося слева.
Подготовительный этап
Проводим подготовительные действия, перед расчетом прогиба: помечаем базу O, с левого торца балки, проводим координатные оси и показываем реакции, возникающие в заделке, под действием заданной нагрузки:
В методе начальных параметров, есть еще одна особенность, которая касается распределенной нагрузки. Если на балку действует распределенная нагрузка, то ее конец, обязательно должен находиться на краю балки (в точке наиболее удаленной от заданной базы). Только в таком случае, рассматриваемый метод будет работать. В нашем примере, нагрузка, как видно, начинается на расстоянии 2 м. от базы и заканчивается на 4 м. В таком случае, нагрузка продлевается до конца балки, а искусственное продление компенсируется дополнительной, противоположно-направленной нагрузкой. Тем самым, в расчете прогибов будет уже учитываться 2 распределенные нагрузки:
Распределенная нагрузка
Распределенной нагрузкой называют внешние или внутренние усилия, которые приложены не в одной точке твердого тела (т.е. не сосредоточены в одной точке), а равномерно, случайным образом или по заданному закону распределены по его определенной длине, площади (поверхности) или объему.
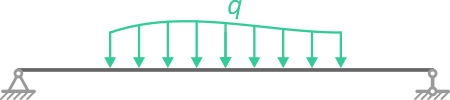
Рассмотрим виды распределенных нагрузок q: линейную, равномерную, треугольную (возрастающую или убывающую), трапециевидную, нелинейную, наклонную (направленную под углом) и замену их результирующей сосредоточенной силой — равнодействующей Q (Rq)
Воздействие на детали, конструкции, элементы механизмов может быть задано распределенными нагрузками: в плоской системе задается интенсивность действия по длине конструкции, в пространственной системе – по площади.
Это может быть собственный вес элемента конструкции, давление газа или воды, распределенный вес сыпучих материалов, ветровая нагрузка и тому подобное.
Обозначение распределенной нагрузки — q
Размерность:
- линейной нагрузки — Н/м,
- нагрузки распределенной по площади — Н/м2,
- объемной (например при учете собственного веса элементов конструкции) — Н/м3.
или кратные им, например кН/м.
Равнодействующая распределенной нагрузки
При решении некоторых задач технической и теоретической механики, распределенную нагрузку удобно заменять её равнодействующей, обозначаемой Q или Rq, которая для линейного случая распределения, определяется произведением интенсивности нагрузки q на её длину AB.
Равнодействующая распределенной нагрузки действует в точке, расположенной в центре тяжести фигуры, ограниченной профилем её распределения.
Рассмотрим способы замены распределенных нагрузок их равнодействующей.
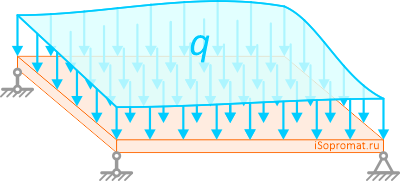
Равномерно распределенная нагрузка
Равномерно распределенная по длине AB нагрузка интенсивностью q, измеряемая в Н/м
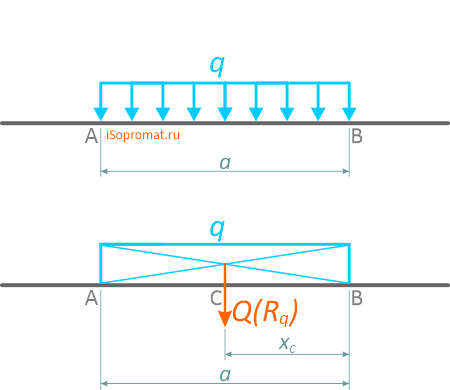
может быть заменена сосредоточенной силой Q (Rq)
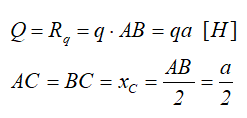
приложенной в центре (на пересечении диагоналей) прямоугольника, середине отрезка AB.
Линейно изменяющаяся (треугольная) нагрузка
Треугольная, линейно изменяющаяся убывающая (возрастающая) нагрузка
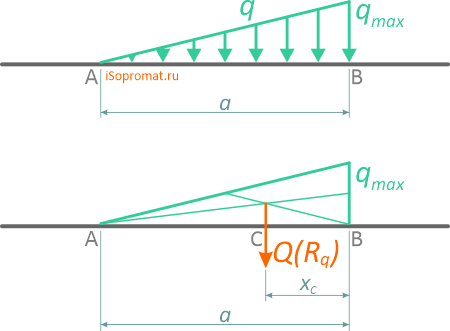
может быть заменена равнодействующей силой, приложенной в точке C
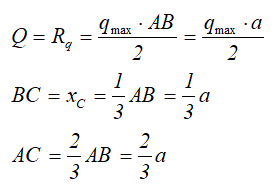
Отметим, что центр тяжести треугольника находится на пересечении его медиан, на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин.
Трапециевидная распределенная нагрузка
Трапециевидная, равномерно убывающая или возрастающая нагрузка характеризуется длиной и двумя значениями интенсивности распределения нагрузки: минимальной qmin и максимальной qmax
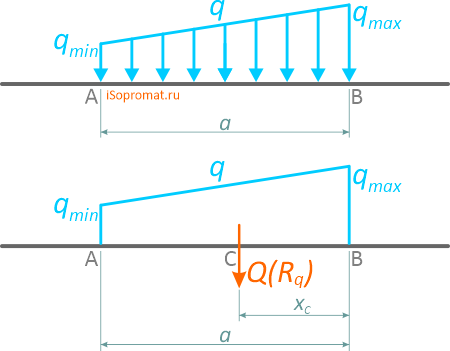
Профиль такой нагрузки представляет собой трапецию.
Величина и положение равнодействующей Q в данном случае определяется по выражениям
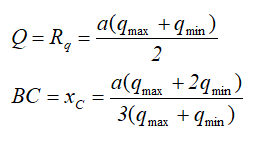
Нелинейная распределенная нагрузка
В произвольном общем случае, интенсивность распределения нагрузки по её длине может описываться одной или несколькими функциями.
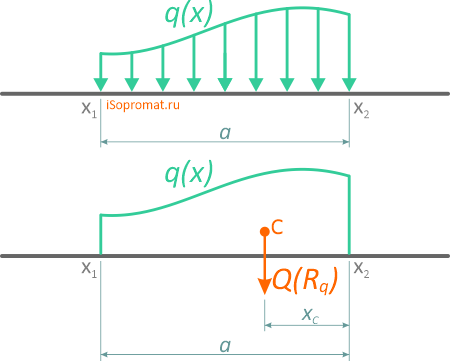
Зная функцию q(x), сосредоточенная эквивалентная (равнодействующая) сила рассчитывается по формуле
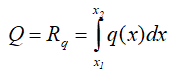
Эта сила также приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x).
Для расчета точки приложения равнодействующей нагрузки необходимо вычислить координату положения центра тяжести фигуры, образуемой нагрузкой.
Наклонная распределенная нагрузка
В случаях, когда распределенная нагрузка приложена под определенным углом, величина равнодействующей определяется аналогично ранее описанным способам.
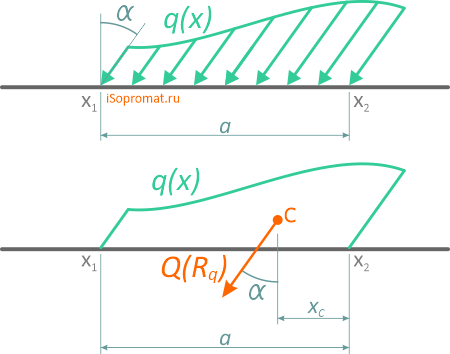
При этом угол наклона самой силы будет равен углу наклона нагрузки q.
Например, линия действия равнодействующей наклонной равномерно распределенной нагрузки будет пересекать ось балки ровно посередине между крайними точками её приложения.
Величина равнодействующей будет равна площади параллелограмма, образованного профилем нагрузки.
Как рассчитывается момент распределенной нагрузки
Распределенная нагрузка от давления
Примером распределенной нагрузки от давления может служить расчет усилий, разрывающих стенки баллона со сжатым газом.
Определим результирующую силу давления в секторе трубы при интенсивности q [Н/м];
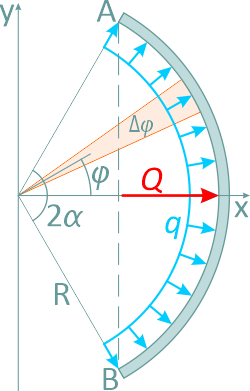
где:
R – радиус трубы,
2α – центральный угол,
ось Ox – ось симметрии.
Выделим элемент сектора с углом ∆φ и определим силу ∆Q, действующую на плоский элемент дуги:
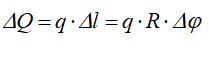
Проекция этой силы на ось Ox будет
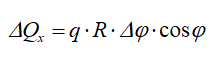
В силу симметрии элемента трубы (с дугой AB) относительно оси Ox проекция результирующей силы на ось Oy:
Qy = 0, т.е. Q = Qx,
Тогда
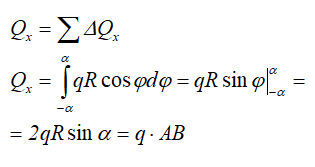
где АВ – хорда, стягивающая концы дуги.
Для цилиндрической емкости высотой h и внутренним давлением P на стенки действует равномерно распределенная нагрузка интенсивностью q = p [Н/м2].
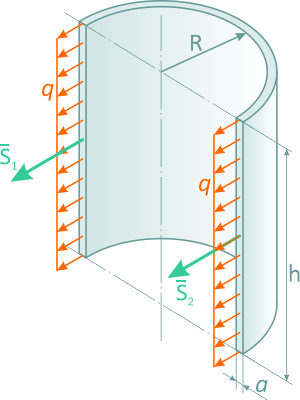
Если цилиндр рассечен по диаметру, то равнодействующая этих сил равна
F = q ∙ d ∙ h
где, d – внутренний диаметр, или
F = p ∙ 2R ∙ h.
Тогда, разрывающие баллон по диаметру усилия:
S1 = S2 = S;
2S = F;
S = p∙h∙R.
Если принять что a – толщина стенки, то (пренебрегая усилиями в крышке и дне цилиндра) растягивающее напряжение в стенке равно
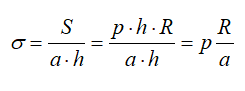
Примеры решения задач >
Уравнения равновесия системы сил >
