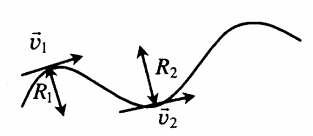
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости
Линейная скорость
Определение и формулы
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
![]()
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость
Определение и формулы
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Полезные факты
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:
![]()
Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:
![]()
Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Определение и формула
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с2). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙103 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙106. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Задание EF18273
Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно…
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17763
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза
б) уменьшить в 2 раза
в) увеличить в 4 раза
г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
- Радиус окружности R1 = R.
- Радиус окружности R2 = 4R.
- Центростремительное ускорение: aц.с. = a1 = a2.
Найти нужно ν2.
Центростремительное ускорение определяется формулой:
![]()
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:
![]()
Или:

Отсюда:

Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 21.6k
Частота вращения (обращения) — это физическая величина, равная количеству оборотов, которые тело совершает за единицу времени (1 секунду).
Чтобы найти частоту вращения надо количество оборотов разделить на время совершения этих оборотов:
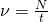
Частота вращения – величина, обратная периоду вращения:
Частота вращения показывает, сколько оборотов совершается за 1 с.
За единицу частоты вращения в СИ принимают частоту вращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: [1/с] или [с-1] (читается: секунда в минус первой степени). Единица частоты в СИ называется Герц [Гц].
Обозначения:
T — период обращения
ν — частота обращения
N — число оборотов
t — время, за которое тело совершило N оборотов по окружности
Как посчитать количество оборотов в минуту?
Один оборот в минуту равен обороту в секунду, делённому на 60: 1 об/мин = 1/мин = 1/(60 с) = 1/60 об/с ≈ 0,01667 об/с. Обратно: один оборот в секунду равен 60 оборотам в минуту.
Как найти число оборотов n в физике?
Число полных оборотов за единицу времени называют частотой вращения. Частота измеряется в герцах (Гц). Частота вращения обозначается буквой ν (читается «ню») и вычисляется по формуле: ν = n t .
Как рассчитать число оборотов шпинделя?
пр = 1000 ·Vр /p·D, где 1000 – коэффициент перевода миллиметров в метры, Vр – расчетная скорость резания, м/мин; D – диаметр заготовки по обрабатываемой поверхности при точении и диаметр фрезы или сверла при фрезеровании или сверлении, мм; p = 3,14. Расчетная частота вращения шпинделя корректируется по паспорту станка.
Как найти угловую скорость вращения?
Формулы угловой скорости
- ω=dφ/dt=φ’, рад/с; с-1 (2.3)
- ω=1,5 с-1=9,42 рад/с.
- ω=n2π/60=nπ/30 рад/с; с-1.
Какая скорость при 3000 оборотов?
При 3000 оборотах: на 5й — 120кмчас.
Как посчитать количество оборотов двигателя?
Общее число пазов статора разделите на число пазов, приходящихся на одну секцию обмотки одной из фаз. Если получится 2, то перед вами двигатель с двумя полюсами — с одной парой полюсов. Следовательно синхронная частота составляет 3000 оборотов в минуту или примерно 2910 с учетом скольжения.
Что такое период обращения в физике?
Период обращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот. Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток.
Как найти число вращения?
Уравнение равномерного вращательного движения можно представить так: N = nt, где N — в оборотах, n — об/мин и t — в мин. Находим число оборотов маховика: N = 152,8 ∙ 5 = 764 оборота.
Какая скорость вращения шпинделя лучше?
Самая оптимальная скорость вращения — это 7200 оборотов в минуту (обычно, используют следующее обозначение — 7200 rpm).
Как найти угловое ускорение тела?
Другими словами: ω = dΘ/dt. Вычислите угловое ускорение. Напомним, что угловое ускорение – это быстрота изменения угловой скорости. Таким образом, угловое ускорение равно производной от угловой скорости.
Что показывает угловое ускорение?
| Угловое ускорение | |
|---|---|
| СИ | рад/с2 |
| СГС | рад/с2 |
| Примечания | |
| псевдовектор |
Можно ли долго ехать на 3000 оборотах?
Большинство экспертов и автомастеров рекомендуют оптимальные обороты двигателя на уровне 2500-3000 оборотов в минуту.
Сколько должно быть оборотов при скорости 120 км?
на трассе при скорости 120 км в час- обороты 1800-2000 об/мин.
Сколько полюсов у двигателя 3000 оборотов?
Если в обозначении асинхронного двигателя два полюса (2Р), то его номинальная частота вращения вала три тысячи оборотов в минуту (3000 об/мин).
Что такое период обращения?
Период обращения время одного полного оборота. В СИ период измеряется в секундах: . Период может быть рассчитан по формуле , где количество оборотов за время . Частота обращения количество оборотов в единицу времени.
Что такое частота обращения и каковы его единицы?
Частота вращения — это физическая величина, равная числу полных оборотов за единицу времени. Единица частоты вращения — секунда в минус первой степени (с−1, s−1), оборот в секунду. Часто используются такие единицы, как оборот в минуту, оборот в час и т. д.
Как найти угловое ускорение?
Другими словами: ω = dΘ/dt. Вычислите угловое ускорение. Напомним, что угловое ускорение – это быстрота изменения угловой скорости. Таким образом, угловое ускорение равно производной от угловой скорости.
Вращательное движение (Движение тела по окружности)
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α
Вращательное движение, характеристики
| Вращательное движение | Угловая скорость | Угловое ускорение |
|---|---|---|
| Равномерное | Постоянная | Равно нулю |
| Равномерно ускоренное | Изменяется равномерно | Постоянно |
| Неравномерно ускоренное | Изменяется неравномерно | Переменное |
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).
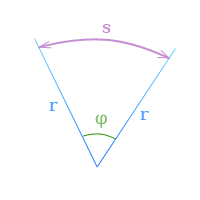
Если
φ — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана
[
φ = frac{s}{r}
]
Соотношение между единицами угла
[ frac{φ_{рад}}{φ_{°}} = frac{π}{180°} ]
|
$ 1 enspace рад = 57.3° $ |
$ 1° = 17.45 enspace мрад $ |
$ 1´ = 291 enspace мкрад $ |
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t).
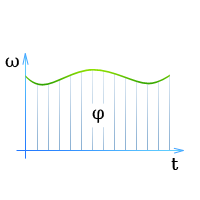
Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
[ [n] = [f] = frac{Обороты}{Секунда} = frac{(об)}{с} = frac{1}{c} = Герц ]
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
ω — угловая частота,
то
Период
[
T = frac{1}{f} = frac{1}{n}
]
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2π:
[
φ = 2 π N
]
Угловая скорость
Из формулы для одного оборота следует:
[
ω = 2 π f = frac{2π}{T}
]
Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.
Вращательное движение (движение тела по окружности) |
стр. 422 |
|---|
Содержание:
Вращательное движение тела:
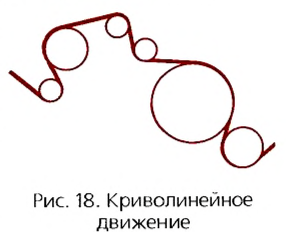
До сих пор мы изучали прямолинейное движение тел, хотя в природе и технике часто совершаются более сложные движения тел — криволинейные, когда траекторией тела является кривая линия. Любую кривую линию всегда можно представить как совокупность дуг окружностей разных радиусов (рис. 18). 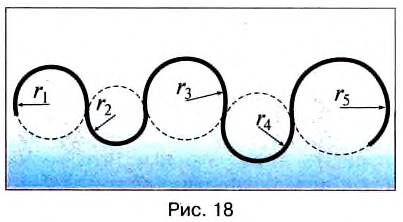
Поэтому, изучив движение материальной точки по окружности, сможем в дальнейшем изучать и любые другие криволинейные движения. Кроме того, из всех возможных криволинейных движений в технике широко применяется вращательное движение деталей машин и механизмов, например вращение шестерён машин и станков, деталей, обрабатываемых на токарных станках, валов двигателей, колес машин, фрез, свёрл и т. п. Любая точка этих деталей движется по окружности. Эти две особенности и обусловили обязательное изучение движения по окружности, а именно — равномерное движение тела по окружности.
Движение материальной точки по круговой траектории с постоянной по значению, но изменяющейся по направлению скоростью, называют равномерным движением по окружности.
Предположим, что тело равномерно движется по окружности из точки А в точку В (рис. 19). Тогда пройденный им путь — это длина дуги 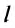
где 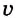 — скорость движения тела по окружности;
— скорость движения тела по окружности; 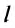 — пройденный телом путь (длина дуги);
— пройденный телом путь (длина дуги); 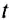 — время движения тела.
— время движения тела.
Направление скорости проще всего определить на опыте.
Опыт:
К вращающемуся точильному кругу, прикоснемся железным стержнем. Увидим, что искры из-под стержня летят по касательной к окружности этого круга (рис. 20).
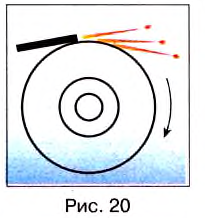
Результат будет таким же в любой точке этого круга. Но каждая искра — это раскалённая частичка, оторвавшаяся от круга и летящая с такой же скоростью, какую она имела в последний момент движения вместе с кругом.
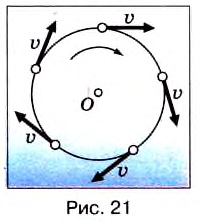
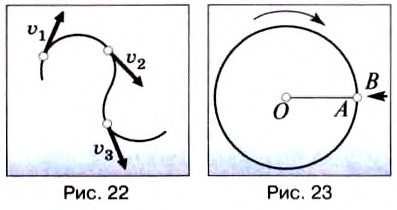
Итак, скорость материальной точки при движении по окружности направлена по касательной к ней в любой точке круга (рис. 21), а с учётом представления кривой на рисунке 18 этот вывод можно распространить на любые криволинейные движения (рис. 22).
Опыт:
Закрепим на горизонтальной оси О фанерный диск (рис. 23), на котором проведен радиус ОА. Напротив точки А поставим указатель В и будем медленно и равномерно вращать диск. Увидим, что точка А с каждым оборотом диска снова появляется напротив указателя В, т. е. совершает движение, повторяющееся через определенный интервал времени.
Движения, при которых определенные положения материальной точки повторяются через одинаковые интервалы времени, называют периодическими движениями.
Равномерное движение по окружности — это периодическое движение. Периодическое движение характеризуют такими величинами, как период обращения и частота обращения.
Период обращения – это интервал времени, в течение которого материальная точка совершает один оборот при равномерном движении по окружности.
Обозначается период обращения большой латинской буквой Т.
Если за время 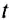 материальная точка при равномерном движении по окружности совершает N оборотов, то период обращения определяется формулой:
материальная точка при равномерном движении по окружности совершает N оборотов, то период обращения определяется формулой:
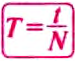
Единицей периода обращения в СИ является одна секунда (1 с).
Если период обращения равняется 1 с, то материальная точка при равномерном движении по окружности осуществляет один оборот за 1 с.
Частота обращения определяется числом оборотов, которое материальная точка совершает за единицу времени при равномерном движении по окружности
Обозначается частота обращения малой латинской буквой 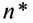 .
.
* В научной и учебной литературе частоту обращения еще обозначают малой греческой буквой 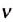 (ню).
(ню).
Если за время  материальная точка совершила N оборотов, то, чтобы определить частоту обращения
материальная точка совершила N оборотов, то, чтобы определить частоту обращения 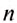 , нужно N поделить на
, нужно N поделить на  , т. е.:
, т. е.:
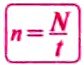 а так как
а так как  = ТN , то
= ТN , то  .
.
Из последней формулы видно, что частота обращения и период обращения связаны обратно пропорциональной зависимостью, а для определения единицы частоты обращения нужно единицу разделить на единицу периода обращения, т. е. на секунду.
Единицей частоты обращения в СИ является единица, разделённая на секунду 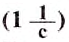 .
. 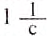 это частота обращения, при котором за 1 с материальная точка совершает 1 полный оборот, двигаясь равномерно по окружности. В технике такую единицу иногда называют одним оборотом в секунду
это частота обращения, при котором за 1 с материальная точка совершает 1 полный оборот, двигаясь равномерно по окружности. В технике такую единицу иногда называют одним оборотом в секунду 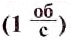 , часто применяют также единицу один оборот в минуту
, часто применяют также единицу один оборот в минуту 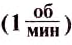 .
.
Движение точки по окружности
Движения, происходящие в природе и технике, могут отличаться по изменению значения скоростей и по изменению направления скоростей. Так, например, при движении точки вдоль прямой линии в одном направлении направление скорости не меняется, хотя ее значение может быть различным. В этом случае движение считается неравномерным.
Но движения могут быть и криволинейными, например, точки могут двигаться по окружностям. На рисунке 18 изображена траектория движения точек нити или ленты между круглыми барабанами. Такие траектории можно представить в виде отрезков прямых линий и окружностей разных размеров. Понятно, что такие движения могут быть и равномерными, каждая точка все время будет иметь одинаковую скорость по значению, хотя направление скорости от точки к точке траектории может меняться.
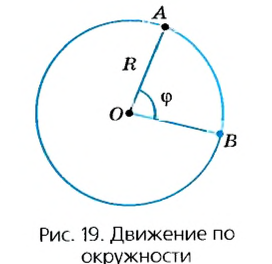
Рассмотрим движение материальной точки по окружности, когда это движение равномерно, т. е. значение скорости остается постоянным (рис. 19). Точка, двигаясь по окружности радиуса R, за определенное время 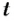 переходит из точки А в точку В. При этом отрезок OA поворачивается на угол
переходит из точки А в точку В. При этом отрезок OA поворачивается на угол  – угловое перемещение точки. Такое движение можно характеризовать угловой скоростью:
– угловое перемещение точки. Такое движение можно характеризовать угловой скоростью:

где 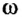 (греческая буква «омега») – угловая скорость;
(греческая буква «омега») – угловая скорость;  (греческая буква «фи») – угловое перемещение.
(греческая буква «фи») – угловое перемещение.
Угловое перемещение определяется в радианах (рад.). 1 радиан — это такое перемещение, когда траектория движения точки – длина дуги окружности АВ – равна длине радиуса R.
Единицей угловой скорости является радиан в секунду (рад/с).
1 рад/с равен угловой скорости такого равномерного движения по окружности, при котором за 1 с осуществляется угловое перемещение 1 рад.
При определении угловой скорости слово «рад» обычно не пишут, а просто обозначают 1/с (имеется в виду рад/с).
Движение точки по окружности (и вращение твердого тела) характеризуют также такие величины, как период и частота вращения.
Период вращения (Т) – это время, на протяжении которого точка (тело) совершает один полный оборот по окружности. Период вращения:

где t — время вращения, N — количество выполненных оборотов.
Период вращения Т измеряется в секундах. Период равен 1 с, если точка (тело) осуществляет один оборот в секунду. Частота вращения (вращательная частота):

где N — количество совершенных оборотов за время t .
Частота вращения измеряется в оборотах за секунду (об/с).
Частота вращения  определяет количество оборотов точки (тела) вокруг центра (оси вращения) за 1 с.
определяет количество оборотов точки (тела) вокруг центра (оси вращения) за 1 с.
Еще Архимед установил, что для всех окружностей любого радиуса отношение длины окружности к его диаметру является величиной постоянной. это число обозначили греческой буквой 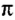 («пи»).
(«пи»).
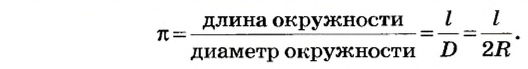
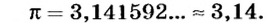
Таким образом, длина окружности 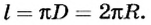
За один оборот материальная точка осуществляет угловое перемещение 2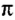 рад.
рад.
Движение по окружности характеризуется привычным для нас понятием скорости как пути, который проходит точка за единицу времени. В данном случае эта скорость называется линейной. Если учитывать, что за один оборот (время Т) точка проходит путь 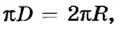 то линейная скорость равномерного движения точки по окружности
то линейная скорость равномерного движения точки по окружности 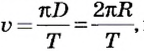 или
или 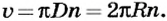
Вращение твердого тела
Твердые тела состоят из большого количества частичек. Абсолютно твердыми наукой считаются тела, расстояние между точками которых не изменяется во время явлений, которые с ними происходят. Однако следует иметь в виду, что абсолютно твердых тел в природе нет.
Как упоминалось в § 3, движения твердых тел бывают поступательные и вращательные. Твердые тела могут вращаться вокруг любых осей, в том числе и тех, которые проходят через их центры.
В случае а (рис. 20) ось вращения проходит через центр шара (например, вращаются колеса транспортных средств или Земля в своем суточном вращении вокруг оси). В случае в ось проходит через край шара. В случае в шар находится на определенном расстоянии от оси (например, Земля движется вокруг Солнца или Луна вокруг Земли). В некоторых случаях даже Землю и Луну можно считать материальными точками, а в некоторых случаях это сделать невозможно. Подумайте, в каких?
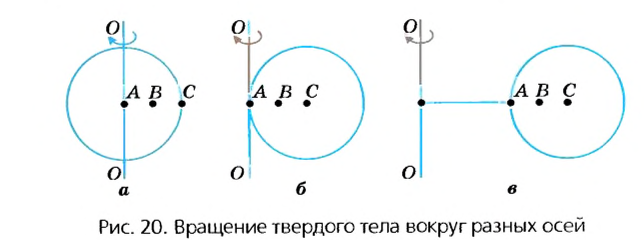
Что же является наиболее характерным для вращательного движения твердых тел? Очевидно, что при этом все точки этих тел в своем движении описывают окружности, центры которых находятся на осях вращения.
Понятно также, что разные точки тел за одно и то же время проходят по своим траекториям разные расстояния – чем дальше от оси вращения лежат точки, тем больше эти расстояния. Но за одно и то же время угловое перемещение  всех точек одинаково. Следовательно, и угловая скорость
всех точек одинаково. Следовательно, и угловая скорость 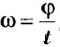 для всех точек данного тела также будет одинаковой.
для всех точек данного тела также будет одинаковой.
Для характеристики вращательного движения твердых тел используют такие же понятия, что и для движения точки по окружности: период вращения Т – время одного полного вращения; вращательная частота (частота вращения) 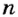 — количество полных вращений за единицу времени; угловая скорость со. Кроме основной единицы частоты вращения об/с, используют об/мин, об/ч и т. п.
— количество полных вращений за единицу времени; угловая скорость со. Кроме основной единицы частоты вращения об/с, используют об/мин, об/ч и т. п.
Период вращения Земли вокруг- Солнца равен в среднем 365 суток, а период вращения Луны вокруг Земли в среднем 28 суток. Изучая физику, астрономию, вы узнаете, что небесные тела, например планеты Солнечной системы, движутся не по окружностям, а по так называемым эллипсам.
Динамика вращательного движения
При просмотре фильмов-боевиков вы могли наблюдать, что при резком вращении руля автомобиля машина опрокидывается. В цирке мотоциклисты катаются по поверхности стен.
Проведем такой опыт. Нальем воду в ведро и раскрутим его в вертикальной плоскости. При определенной скорости вращения вода не выливается из ведра.
Из приведенных выше примеров можно сделать заключение, что существует сила, которая опрокинет машину при резком повороте, удержит мотоциклиста на стене и не даст вылиться воде из ведра при вращении.
Откуда появляется эта сила? От чего зависит ее величина?
Для этого вспомним о возникновении центростремительной силы в теле при равномерном вращательном движении:

По третьему закону Ньютона:
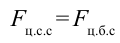
и при вращении появляется также центробежная сила. 
Вот эта центробежная сила опрокинет резко разворачивающуюся машину, удержит воду в ведре при вращении и т.д.
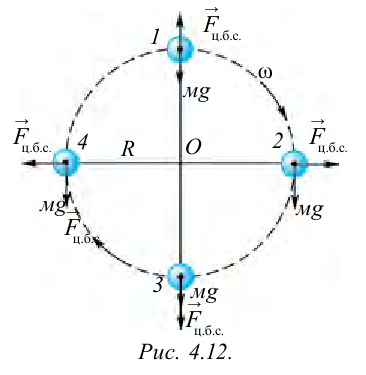
На рисунке 4.12 показаны силы, действующие на тело, которое совершает вращательные движения по кругу радиусом  . В точке 1, из-за того что центробежная сила
. В точке 1, из-за того что центробежная сила  направлена противоположно силе тяжести
направлена противоположно силе тяжести 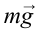 , вес тела уменьшается:
, вес тела уменьшается:
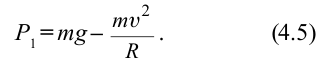
В точке 3 сила тяжести тела и центробежная сила направлены вниз, т.е. в одном направлении. В этом случае вес тела растет:

Центробежную силу нужно учитывать при вращении тела и в случаях поворота в ходе движения.
Кроме того, на поворотах дороги под воздействием центробежной силы наблюдается отклонение тела от вертикального положения. Чтобы это не приводило к авариям, велосипедисты или мотоциклисты должны двигаться с небольшим уклоном в сторону от центра вращения (рис. 4.13а).
Для уравновешивания этой силы специально для автомобилей на поворотах строят участки дороги с уклоном с одной стороны (рис. 4.13б). Для трамваев и поездов рельсы на поворотах дороги с внешней стороны круга делаются чуть выше.

- Заказать решение задач по физике
Пример
При движении по кругу тело опускается вниз. При каком радиусе круга тело не упадет с точки 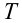 . Скорость тела в точке
. Скорость тела в точке 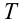 равна 30 м/с.
равна 30 м/с.
Дано:
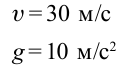
Найти:
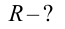
Решение:
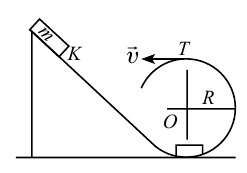
Чтобы тело не упало из точки 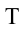 должно
должно 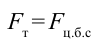 выполняться следующее условие:
выполняться следующее условие: 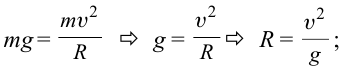
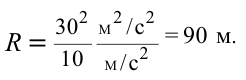
Ответ: 90 м.
Кинематика вращательного движения
При криволинейном движении материальной точки ее мгновенная скорость направлена по касательной к траектории в данной точке.
Движение тела (МТ) по окружности является частным случаем криволинейного движения по траектории, лежащей в одной плоскости.
Одним из простейших и широко распространенных видов такого движения является движение по окружности с постоянной по модулю скоростью. Это такое движение, при котором тело (МТ) за любые равные промежутки времени описывает одинаковые дуги. Подчеркнем, что при подобном движении скорость точки постоянно меняет свое направление.
Для описания движения по окружности используется ряд физических величин. Рассмотрим некоторые из них.
Удобным параметром для определения положения материальной точки М, совершающей движение по окружности радиусом R с центром в начале координат, является угол поворота 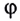 (рис. 25)
(рис. 25)
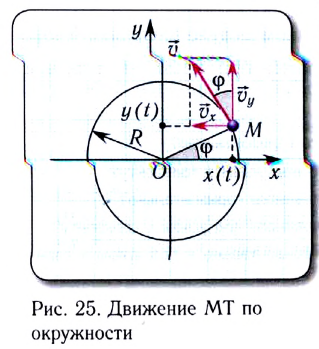
радиус-вектора точки М. Он отсчитывается от оси Ох против хода часовой стрелки и связан с декартовыми координатами соотношениями:

По теореме Пифагора можно найти, что координаты х и у материальной точки в декартовой системе координат удовлетворяют соотношению
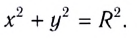
Скорость  с которой материальная точка движется по окружности, называется линейной скоростью (рис. 26).
с которой материальная точка движется по окружности, называется линейной скоростью (рис. 26).
Проходимый точкой путь s (длина дуги окружности) равен, как и для всякого равномерного движения, произведению модуля скорости v и промежутка времени движения 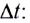
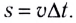
Модуль угловой скорости 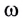 — это отношение угла поворота
— это отношение угла поворота 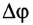 к промежутку времени
к промежутку времени 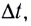 за который этот поворот произошел:
за который этот поворот произошел:
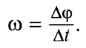
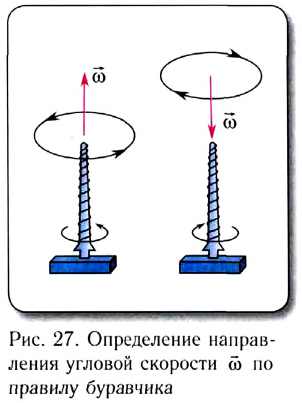
Угловая скорость  со является величиной векторной. Она направлена вдоль оси вращения материальной точки, и ее направление определяется по правилу буравчика, т. е. совпадает с направлением поступательного движения конца буравчика, рукоятка которого вращается в том же направлении, что и тело (рис. 27).
со является величиной векторной. Она направлена вдоль оси вращения материальной точки, и ее направление определяется по правилу буравчика, т. е. совпадает с направлением поступательного движения конца буравчика, рукоятка которого вращается в том же направлении, что и тело (рис. 27).
Единица угловой скорости в СИ — радиан в секунду 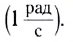
При движении по окружности с постоянной по модулю скоростью v угловая скорость 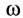 является величиной постоянной и ее модуль равен отношению угла поворота
является величиной постоянной и ее модуль равен отношению угла поворота 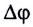 к промежутку времени
к промежутку времени 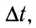 за который этот поворот произошел:
за который этот поворот произошел:
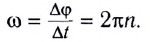
Здесь n — частота вращения — физическая величина, численно равная числу оборотов N материальной точки в единицу времени:
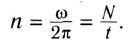
Единица частоты вращения в СИ — секунда в минус первой степени 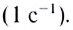 Время совершения одного оборота называется периодом вращения Т.
Время совершения одного оборота называется периодом вращения Т.
Следовательно,

В СИ период измеряется в секундах (1с).
При совершении полного оборота 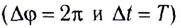 период определяется по формуле
период определяется по формуле

Модуль постоянной линейной скорости тела (МТ), движущегося по окружности, вычисляется по формуле

Проекции скорости 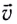 (см. рис. 25) с течением времени изменяются по закону
(см. рис. 25) с течением времени изменяются по закону
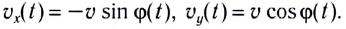
Модуль угловой скорости определяется соотношением
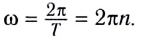
Следовательно, соотношение между модулями линейной и угловой скорости имеет вид

Поскольку 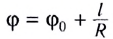 (докажите самостоятельно), где
(докажите самостоятельно), где 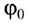 — угол поворота радиус-вектора в момент начала движения, то кинематический закон движения МТ но окружности имеет вид
— угол поворота радиус-вектора в момент начала движения, то кинематический закон движения МТ но окружности имеет вид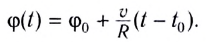
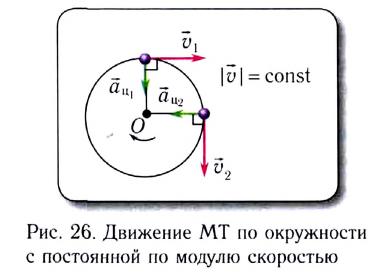
При движении МТ по окружности с постоянной по модулю скоростью ее направление непрерывно изменяется и, следовательно, движение МТ происходит с ускорением, которое называется центростремительным 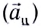 или нормальным
или нормальным 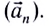 Ускорение направлено по радиусу к центру окружности и характеризует быстроту изменения направления скорости
Ускорение направлено по радиусу к центру окружности и характеризует быстроту изменения направления скорости 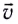 с течением (см. рис. 26). Его модуль определяется формулой
с течением (см. рис. 26). Его модуль определяется формулой
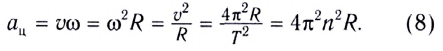
Нормальное ускорение 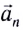 в любой момент времени перпендикулярно скорости
в любой момент времени перпендикулярно скорости 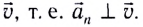
Как и при прямолинейном равноускоренном движении, ускорение 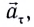 называемое тангенциальным (касательным), совпадает с направлением скорости
называемое тангенциальным (касательным), совпадает с направлением скорости 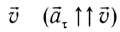 или направлено противоположно ей
или направлено противоположно ей 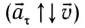 и поэтому изменяет только модуль скорости. Следовательно, при движении по окружности с непостоянной по модулю скоростью (например, математический маятник) или при любом криволинейном движении полное ускорение
и поэтому изменяет только модуль скорости. Следовательно, при движении по окружности с непостоянной по модулю скоростью (например, математический маятник) или при любом криволинейном движении полное ускорение 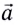 можно представить в виде векторной суммы нормального ускорения
можно представить в виде векторной суммы нормального ускорения 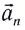 и тангенциального ускорения
и тангенциального ускорения 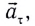 направленного по касательной к окружности в данной точке (рис. 28):
направленного по касательной к окружности в данной точке (рис. 28):
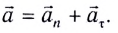
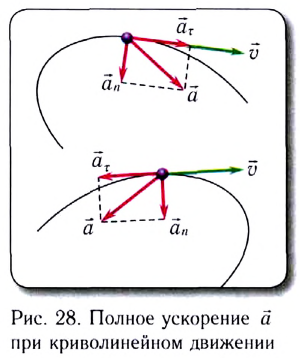
Полное ускорение 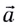 всегда направлено в сторону вогнутости траектории (см. рис. 28).
всегда направлено в сторону вогнутости траектории (см. рис. 28).
Модуль полного ускорения находится по теореме Пифагора:

где 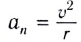 – нормальное ускорение, с которым точка двигалась бы по дуге
– нормальное ускорение, с которым точка двигалась бы по дуге
окружности радиусом r, заменяющей траекторию в окрестности рассматриваемой точки. Этот радиус r называют радиусом кривизны траектории.
- Равномерное движение материальной точки по окружности
- Колебательное движение
- Физический и математический маятники
- Пружинные и математические маятники
- Поступательное движение
- Равномерное и неравномерное движение
- Равномерное движение
- Неравномерное движение
