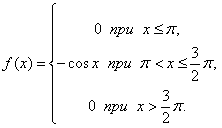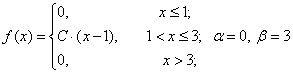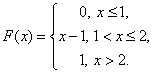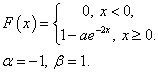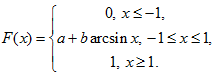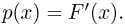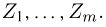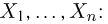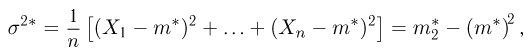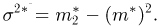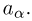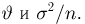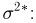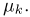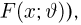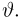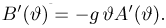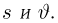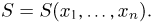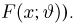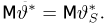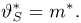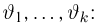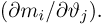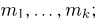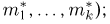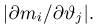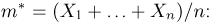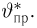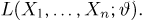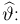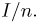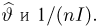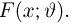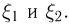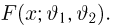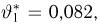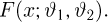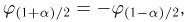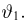Функция распределения случайной величины
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Пусть
– действительное число. Вероятность события,
состоящего в том, что
примет значение, меньшее
, то есть вероятность
события
обозначим через
. Разумеется, если
изменяется, то, вообще говоря, изменяется и
, то есть
– функция от
.
Функцией распределения называют функцию
, определяющую вероятность
того, что случайная величина
в результате испытания примет значение,
меньшее
, то есть:
Геометрически
это равенство можно истолковать так:
есть вероятность того, что случайная величина примет
значение, которое изображается на числовой оси точкой, лежащей левее точки
.
Иногда
вместо термина «функция распределения» используют термин «интегральная
функция».
Функцию
распределения дискретной случайной величины
можно представить следующим соотношением:
Это
соотношение можно переписать в развернутом виде:
Функция
распределения дискретной случайной величины есть разрывная ступенчатая функция,
скачки которой происходят в точках, соответствующих возможным значениям
случайной величины и равны вероятностям этих значений. Сумма всех скачков
функции
равна 1.
Свойства функции распределения
Свойство 1.
Значения
функции распределения принадлежат отрезку
:
Свойство 2.
– неубывающая функция, то есть:
,
если
Свойство 3.
Если возможные значения случайной величины
принадлежат интервалу
,
то:
1)
при
;
2)
при
Свойство 4.
Справедливо равенство:
Свойство 5.
Вероятность того, что непрерывная случайная
величина
примет одно определенное значение, равна нулю.
Таким образом, не представляет интереса говорить о
вероятности того, что непрерывная случайная величина примет одно определенное
значение, но имеет смысл рассматривать вероятность попадания ее в интервал,
пусть даже сколь угодно малый.
Заметим, что было бы неправильным думать, что
равенство нулю вероятности
означает, что событие
невозможно (если, конечно, не ограничиваться
классическим определением вероятности). Действительно, в результате испытания
случайная величина обязательно примет одно из возможных значений; в частности,
это значение может оказаться равным
.
Свойство 6.
Если возможные значения непрерывной случайной величины
расположены на всей оси
,
то справедливы следующие предельные соотношения:
Свойство 7.
Функция распределения непрерывная слева, то есть:
Смежные темы решебника:
- Дискретная случайная величина
- Непрерывная случайная величина
- Математическое ожидание
- Дисперсия и среднее квадратическое отклонение
Примеры решения задач
Пример 1
Дан ряд
распределения случайной величины
:
|
|
1 | 2 | 6 | 8 |
|
|
0,2 | 0,3 | 0,1 | 0,4 |
Найти и изобразить ее функцию распределения.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Будем задавать различные значения
и находить для них
1. Если
,
то, очевидно,
в том числе и при
2. Пусть
(например
)
Очевидно, что и
3. Пусть
(например
);
Очевидно, что и
4. Пусть
Очевидно, что и
5. Пусть
Итак:
График функции распределения
Пример 2
Случайная
величина
задана функцией распределения:
Найти
вероятность того, что в результате испытания
примет значение:
а) меньше
0,2;
б) меньше
трех;
в) не
меньше трех;
г) не
меньше пяти.
Решение
а) Так
как при
функция
, то
то есть
при
б)
в)
События
и
противоположны, поэтому
Отсюда:
г) сумма
вероятностей противоположных событий равна единице, поэтому
Отсюда, в
силу того что при
функция
, получим:
Пример 3
Задана
непрерывная случайная величина X своей плотностью
распределения вероятностей f(x). Требуется:
1)
определить коэффициент A;
2) найти
функцию распределения F(x);
3)
схематично построить графики функций f(x) и F(x);
4)
вычислить математическое ожидание и дисперсию X;
5)
определить вероятность того, что X примет значение из
интервала (a,b).
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
1)
Постоянный параметр
найдем из
свойства плотности вероятности:
В
нашем случае эта формула имеет вид:
Получаем:
2)
Функцию распределения
найдем из
формулы:
Учитывая
свойства
, сразу можем отметить,
что:
и
Остается
найти выражение для
, когда х принадлежит интервалу
:
Получаем:
3) Построим графики функций:
График плотности распределения
График функции распределения
4) Вычислим
математическое ожидание:
В нашем случае:
Вычислим дисперсию:
Искомая дисперсия:
5) Вероятность того, что
примет значение из интервала
:
Задачи контрольных и самостоятельных работ
Задача 1
Закон
распределения случайной величины X задан таблицей.
Найти ее
математическое ожидание, дисперсию и значение функции распределения в заданной
точке.
F(1)=
M[X]=
D[X]=
Задача 2
Случайная
величины X задана функцией распределения
Найти
плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить графики дифференциальной и интегральной функций.
Найти вероятность попадания случайной величины X в интервалы (1,2; 1,8),
(1,8; 2,3)
Задача 3
Дискретная
случайная величина X задана рядом распределения. Найти:
1)
функцию распределения F(x) и ее график;
2)
математическое ожидание M(X);
3)
дисперсию D(X).
|
|
-5 | 5 | 25 | 45 | 65 |
|
|
0.2 | 0.15 | 0.3 | 0.25 | 0.1 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
В задаче
дискретная случайная величина задана рядом распределения.
Найти
; M(X), D(X), P(0≤X≤2); F(x).
Начертить график F(x)
Задача 5
В задаче
непрерывная случайная величина X задана функцией
распределения F(x).
Найти a; f(x); M(X); D(X); P(X<0.2)
Начертить
графики функций f(x);F(x).
Задача 6
Функция
распределения непрерывной случайной величины X (времени безотказной работы
некоторого устройства) равна
(
). Найти вероятность безотказной
работы устройства за время x больше либо равно T.
Задача 7
Функция
распределения непрерывной случайной величины задана выражением:
Найдите:
1)
параметр a;
2)
плотность вероятностей;
4) P(0<x<1)
Постройте
графики интегральной и дифференциальной функции распределения.
Задача 8
Дана
интегральная функция распределения. Найти: дифференциальную функцию f(x),M(X),σ(X),D(X).
Задача 9
Дана
функция распределения F(х) случайной величины Х.
Найти плотность
распределения вероятностей f(x), математическое ожидание M(X),
дисперсию D(X) и вероятность попадания X на
отрезок [a,b]. Построить графики
функций F(x) и f(x).
Задача 10
НСВ X имеет
плотность вероятности (закон Коши)
Найти:
а)
постоянную C=const;
б)
функцию распределения F(x);
в)
вероятность попадания в интервал -1<x<1
г)
построить графики f(x), F(x).
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Непрерывная случайная величина
Ранее мы представили примеры решений задач о дискретной случайной величине, теперь переходим к непрерывной. Формально в задачах требуется найти тоже самое: вычислить числовые характеристики, начертить графики, определить неизвестные параметры, найти вероятности событий.
Но формулы-то совсем другие (в силу непрерывности СВ), поэтому стоит разобраться в них хорошенько. Надеемся, наши примеры вам помогут (а если нет времени, закажите решение).
Ниже вы найдете примеры решений на самые разные законы распределений непрерывных случайных величин: законы $arcsin$ и $arctan$, тригонометрические и логарифмические функции, показательный, равномерный закон распределения, законы Коши, Симпсона, Лапласа и т.д.
Примеры для других НСВ: Нормальный закон, Равномерный закон, Показательный закон.
Спасибо за ваши закладки и рекомендации
Примеры решений
Задача 1. Случайная величина X задана дифференциальной функцией распределения
1) Определить вероятность попадания случайной величины X в интервал $[pi, 5/4 pi]$.
2) Найти математическое ожидание и дисперсию случайной величины X.
Задача 2. Случайная величина X задана плотностью вероятности:
Требуется:
а) найти коэффициент C;
б) найти функцию распределения F(x);
в) найти M(X), D(X), σ(X)
г) найти вероятность P(α < X < β);
д) построить графики f(x) и F(x).
Задача 3. Случайная величина Х задана функцией распределения F(x).
А) является ли случайная величина Х непрерывной?
Б) имеет ли случайная величина Х плотность вероятности f(X)? Если имеет, найти ее.
В) постройте схематично графики f(X) и F(X).
Задача 4. Дана функция распределения F(x) непрерывной случайной величины X.
1. Найти значения параметров a,b
2. Построить график функции распределения F(x)
3. Найти вероятность P(α < X < β)
4. Найти плотность распределения p(x) и построить ее график.
Задача 5. Время в годах безотказной работы прибора подчинено показательному закону, т.е. плотность распределения этой случайной величины такова: f(t)=2e-2t при t ≥ 0 и f(t)=0 при t<0.
1) Найти формулу функции распределения этой случайной величины.
2) Определить вероятность того, что прибор проработает не более года.
3) Определить вероятность того, что прибор безотказно проработает 3 года.
4) Определить среднее ожидаемое время безотказной работы прибора.
Задача 6. Функция распределения вероятностей случайной величины $X$ имеет вид:
А) найти $a$ и $b$;
Б) найти плотность $f(x)$;
В) нарисовать график $F(x)$;
Г) нарисовать график $f(x)$;
Д) найти $M[X]$;
Е) найти $D[X]$.
Задача 7. Функция распределения вероятностей случайной величины $X$ имеет вид:
$$F(x)=A+B arctan (x/2), -infty lt x lt infty $$ (закон Коши).
А) определить постоянные $A$ и $B$;
Б) найти плотность распределения вероятностей
В) найти $P(-1 lt X lt 1)$;
Г) нарисовать график $F(x)$;
Д) нарисовать график $f(x)$.
Задача 8. Случайная величина $X$ имеет распределение Парето с плотностью вероятности $f(x)=4/23(23/x)^5$
при $23 le x$ и $f(x)=0$ при $x lt 23$.
Найдите $M(X)$ и $P(23lt X lt 27)$.
Задача 9. Непрерывная случайная величина задана интегральной функцией (функцией распределения) $F(x)$. Найти:
А) вероятность попадания случайной величины $X$ в интервал $(a;b)$.
Б) дифференциальную функцию (функцию плотности вероятностей) $f(x)$.
В) математическое ожидание, дисперсию и среднее квадратическое отклонение величины $X$.
Г) построить графики функций $F(x)$ и $f(x)$.
Задача 10. Случайная величина $X$ подчинена закону Лапласа $p(x)=acdot e^{-lambda |x|}$, $lambda gt 0.$ Найти $a$, $M(x)$, $D(x)$ и $F(x)$. Построить графики $p(x)$ и $F(x)$.
Задача 11. Случайная величина $X$ задана функцией распределения $F(x)$. Найти:
5) дифференциальную функцию $f(x)$ (плотность распределения),
6) математическое ожидание $M(X)$, дисперсию $D(X)$, среднее квадратическое отклонение $sigma(X)$.
7) Моду $Mo$ и медиану $Me$,
8) $P(1/2 lt X lt 2).$
Построить графики функции и плотности распределения.
Задача 12. Случайная величина $Х$ подчинена закону Симпсона (закону равнобедренного треугольника) на участке от $-a$ до $+a$.
а) Написать выражение для плотности распределения.
б) Построить график функции распределения.
в) Определить числовые характеристики случайной величины Х.
Мы отлично умеем решать задачи по теории вероятностей
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
Тема 23. Функция и плотность распределения непрерывной случайной величины
Пренебрежение различием между близкими значениями случайной величины широко используется для упрощения описания и изучения случайных величин. В связи с этим вводится следующее определение.
Случайные величины, значения которых заполняют непрерывные интервалы, т.е. бесконечно мало отличаются друг от друга, называются непрерывными
случайными величинами.
Из этого определения следует, что непрерывные случайные величины могут принимать сколько угодно много разных близких значений и их нельзя задавать законом распределения. Для задания непрерывных случайных величин используются функции распределения и плотности распределения.
Напомним, что функцией распределения (как для дискретной, так и для непрерывной) случайной величины называют функцию F (x) , определяющую ве-
роятность того, что случайная величина X в результате испытания примет зна-
|
чение, меньшее x , т.е.: |
|
|
F (x) = P( X < x) |
(5.1) |
На рис. 2.8 представлен график функции распределения непрерывной случайной величины.
F(x)
1
Рис. 2.8. График функции распределения непрерывной случайной величины
Плотностью распределения случайной величины X называется произ-
водная от ее функции распределения FX (x) . Плотность распределения обозна-
|
чается |
f X (x) . Следовательно, согласно определению: |
|||
|
f (x) = |
dF (x) |
(5.2) |
||
|
dx |
||||
|
Для непрерывной случайной величины функция F (x) и плотность |
f (x) |
|||
|
распределения удовлетворяют следующим условиям: |
||||
|
1) |
при всех действительных x справедливо: |
|||
|
f (x) ≥ 0 ; |
(5.3) |
63

2) для любых a < b справедливо равенство:
|
P(a ≤ X < b) = ∫b |
f (x)dx = F(b) − F(a) ; |
(5.4) |
|
a |
||
|
3) |
||
|
F(+∞) = ∫∞ f (x)dx =1; |
(5.5) |
|
|
−∞ |
4) вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.
Эти свойства вытекают из определения плотности распределения и свойств функции распределения. Неотрицательность выводится из того, что функция распределения всегда не убывает. Второе свойство определяется на основе основного свойства функции распределения. Последнее свойство есть важный частный случай второго и выполняется потому, что значения случайной величины всегда удовлетворяют условию: −∞ < X < ∞. Оно называется условием нормировки.
Геометрически (рис. 2.9) основные свойства плотности распределения означают, что:
1)вся кривая плотности распределения лежит не ниже оси абсцисс;
2)площадь криволинейной трапеции, ограниченной сверху графиком функции плотности распределения, снизу осью абсцисс, слева и справа прямыми x = a
иx = b , равна вероятности попадания случайной величины в интервал a < X < b ;
3)полная площадь, ограниченная кривой плотности распределения и осью абсцисс, равна единице.
f(x)
Рис. 2.9. График плотности распределения непрерывной случайной величины
Зная плотность распределения f (x) , можно найти функцию распределения F (x) по формуле:
|
F(x) = ∫x |
f (x)dx |
(5.6) |
|
−∞ |
64

Приведем несколько примеров, в которых используются плотности распределения.
Пример 1. При каких значениях параметра a функция
|
0, |
если |
x ≤ −2 |
|||
|
2 |
, |
если − 2 < x ≤ 0 |
|||
|
f (x) = ax |
|||||
|
0, |
eссл |
x > 0 |
|||
будет являться плотностью распределения вероятности случайной величины X ?
Решение. По условию, заданная функция всюду неотрицательна, если a положительно. Остается только найти его значение. Воспользуемся последним
свойством плотности распределения – ∫∞ f (x)dx =1.
−∞
В данном случае подынтегральная функция не равна нулю только тогда, когда − 2 ≤ x ≤ 0 , и, следовательно, интеграл равен нулю при интегрировании по тем областям, в которых не выполняется условие − 2 ≤ x ≤ 0 . А по условию, на
интервале − 2 ≤ x ≤ 0 заданная функция равна ax2 . Значит, должно выполняться равенство:
|
∫0 ax2dx =1. |
||||||||||||
|
Вычисление интеграла дает: |
−2 |
|||||||||||
|
0 |
||||||||||||
|
0 |
||||||||||||
|
x3 |
03 |
(−2)3 |
8a |
|||||||||
|
∫ax |
2 |
. |
||||||||||
|
dx = a 3 |
= a 3 − a |
3 = |
3 =1 |
|||||||||
|
−2 |
−2 |
|||||||||||
Следовательно, при значении параметра a = 83 заданная функция является
плотностью распределения вероятности случайной величины X . Пример 2. Дана плотность распределения:
|
0, |
если x ≤ −1 |
|
|
если −1 < x ≤1 |
||
|
f (x) = a(x +1), |
||
|
0, |
если x >1 |
|
Определить: а) параметр a ; б) вероятность того, что значение случайной величины попадает в интервал (0.5, 1.5) ; в) функцию распределения.
Решение. В условии этой задачи сказано, что заданная функция является плотностью распределения случайной величины. Эта функция равна нулю при всех значениях x , которые меньше -1 и больше 1. Поэтому все значения случай-
ной величины удовлетворяют x <1. Для того чтобы найти значение параметра a , так же как и в предыдущем примере воспользуемся последним свойством
65

|
плотности распределения – |
∫∞ f (x)dx =1. Запишем это условие, учитывая задан- |
|||||||||||||||||||||||||
|
−∞ |
||||||||||||||||||||||||||
|
ный вид плотности распределения: |
||||||||||||||||||||||||||
|
∫1 a(x +1)dx =1. |
||||||||||||||||||||||||||
|
−1 |
||||||||||||||||||||||||||
|
После интегрирования получаем: |
||||||||||||||||||||||||||
|
1 |
2 |
1 |
1 |
2 |
(−1) |
2 |
1 |
1 |
||||||||||||||||||
|
x |
+ (−1) |
= a( |
+1 |
− |
+1) |
= 2a =1 |
||||||||||||||||||||
|
∫a(x +1)dx = a |
+ x |
= a |
+1 |
− a |
||||||||||||||||||||||
|
−1 |
2 |
−1 |
2 |
2 |
2 |
2 |
||||||||||||||||||||
|
Следовательно, a = |
1 |
. |
||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||
Поскольку плотность распределения есть производная функции распределения, интеграл от плотности является функцией распределения. В данной задаче функция распределения должна равняться нулю при всех x < −1 и единице, при всех x >1. Если −1 < x <1, интегрирование плотности дает:
|
x |
1 |
x |
1 |
x2 |
x |
||||||||||||||||||||
|
F(x) = f (x)dx = |
(x +1)dx = |
+ x |
= |
||||||||||||||||||||||
|
∫ |
2 |
∫ |
2 |
||||||||||||||||||||||
|
2 |
−1 |
||||||||||||||||||||||||
|
−∞ |
−1 |
2 |
|||||||||||||||||||||||
|
1 |
x2 |
1 |
(−1) |
2 |
x2 |
+1 + 2x |
x +1 |
||||||||||||||||||
|
+ x |
− |
+ |
(−1) |
= |
= |
||||||||||||||||||||
|
2 |
2 |
2 |
4 |
2 |
|||||||||||||||||||||
|
2 |
Подчеркнем специально, что найденное выражение справедливо только при условии x <1. Таким образом, функция распределения есть:
|
0, |
если |
x ≤ −1 |
|||
|
2 |
|||||
|
x +1 |
|||||
|
F(x) = |
если |
−1 < x ≤1 |
|||
|
2 |
|||||
|
если |
x >1 |
||||
|
1, |
|||||
Теперь найдем вероятность того, что выполняется условие 0.5 < X <1.5 . Проще всего использовать найденную функцию распределения. Получаем:
|
P(0.5 < X <1.5) = F(1.5) − F(0.5) |
3 |
2 |
7 |
||||
|
=1 |
− |
= |
|||||
|
4 |
16 |
||||||
Пример 3. Функция распределения непрерывной случайной величины X имеет вид:
|
0, |
если |
x ≤ 0 |
||
|
Аx |
2 |
+ В, |
если 0 < x ≤1 |
|
|
F(x) = |
||||
|
1, |
если |
x >1 |
||
66

Определить параметры A и B . Найти вероятность того, что случайная величина X примет значение: а) меньше 0.5; б) больше, чем -0.5; в) в интервале (1.5, 5). Определить плотность распределения случайной величины X .
Решение. Для решения надо так подобрать параметры A и B , чтобы функция распределения была непрерывной, так как по условию X – непрерывная случайная величина. Это значит, что при x = 0 она должна равняться нулю. По-
|
этому A 02 + B = 0 и B = 0 . Аналогично, |
при x =1 функция распределения |
||||
|
должна равняться единице. Следовательно, |
A 12 + B =1 и A =1. Таким образом, |
||||
|
функция распределения непрерывной случайной величины Х есть: |
|||||
|
0, |
если |
x ≤ 0 |
|||
|
2 |
, |
если 0 < x ≤1 |
|||
|
F(x) = x |
|||||
|
если |
x >1 |
||||
|
1, |
|||||
|
Теперь найдем вероятность того, |
что значение X < 0.5 . Для этого доста- |
точно вычислить F (0.5) . Получаем P( X < 0.5) = F(0.5) = 0.52 = 0.25. По усло-
вию задачи, все значения случайной величины X неотрицательны и не больше, чем 1. Поэтому P( X > −0.5) =1 − F (−0.5) =1. Аналогично, P( X >1.5) = 0 .
Пример 4. Функция распределения непрерывной случайной величины Х имеет вид:
|
0, |
если |
x ≤1 |
|||
|
Аx |
2 |
+ В, если1 |
< x ≤ 3 |
||
|
F(x) = |
|||||
|
1, |
если |
x > 3 |
|||
Определить параметры A и B . Найти вероятность того, что случайная величина X примет значение: а) меньше 1.5; б) больше, чем 1.5, но меньше, чем 2.5. Определить плотность распределения случайной величины X .
Решение. Так как по условию X − непрерывная случайная величина, для решения надо так подобрать параметры A и B , чтобы функция распределения была непрерывной. Значит, при x =1 она должна равняться нулю, а при x = 3 функция распределения должна равняться единице. Следовательно, имеем систему двух линейных алгебраических уравнений с двумя неизвестными A и B :
A + B = 0
9A + B =1
Эта система имеет единственное решение A =1 / 8 , B = −1/ 8 .
Таким образом, функция распределения непрерывной случайной величины
|
X есть: |
0, |
если |
x ≤1 |
|||
|
1 |
2 |
|||||
|
F(x) = |
(x |
−1), |
если |
1 < x ≤ 3 |
||
|
8 |
1, |
если |
x > 3 |
|||
Теперь вероятность того, что значение X <1.5 , равна значению функции распределения при значении x =1.5 , т.е.:
67

|
P( X <1.5) = F(1.5) = |
1.52 |
−1 |
= |
1.25 |
= 0.15625 |
||||||||
|
8 |
8 |
||||||||||||
|
Аналогично, получаем: |
|||||||||||||
|
2.52 |
1.52 |
||||||||||||
|
P(1.5 < X < 2.5) = F(2.5) − F(1.5) = |
−1 |
− |
−1 |
= |
5.25 −1.25 |
= 0.5 |
|||||||
|
8 |
8 |
8 |
|||||||||||
По определению плотности распределения случайной величины, она равна производной от функции распределения. Поэтому, вычисляя производную, получаем:
|
(0)′, |
если |
x ≤1 |
0, |
если |
x ≤ 1 |
|||||||
|
′ |
1 |
|||||||||||
|
x2 −1 |
||||||||||||
|
f ( x) = |
, |
если |
1 < x ≤ |
3 = |
x, |
если |
1 < x ≤ 3 |
|||||
|
8 |
4 |
|||||||||||
|
0, |
если |
x > 3 |
||||||||||
|
(1)′, |
если |
x > 3 |
||||||||||
Задачи для самостоятельного решения
|
Задача 1. Может ли функция |
|||||
|
0, |
если |
x ≤ 0 |
|||
|
F(x) = |
2 |
, |
если 0 < x ≤1 |
||
|
x |
|||||
|
если |
x > 2 |
||||
|
1, |
являться функцией распределения случайной величины?
Задача 2. Функция распределения случайной величины X имеет вид:
|
0, |
если |
x ≤1 |
|
|
Аx + В, |
если1 < x ≤ 3 |
||
|
F(x) = |
|||
|
1, |
если |
x > 3 |
|
Определить параметры A и B . Найти вероятность того, что случайная величина X примет значение: а) меньше –2; б) меньше 4; в) больше 3; г) больше 3; д) в интервале (-2, 2); е) в интервале (-1, 0); ж) в интервале (-3, 5).
Задача 3. Функция распределения случайной величины X имеет вид:
|
0, |
если |
x ≤ 0 |
|||
|
2 |
, |
если 0 |
< x ≤ 2 |
||
|
F(x) = Ax |
|||||
|
1, |
если |
x > 2 |
|||
Определить параметр A и плотность распределения случайной величины. Задача 4. Функция распределения случайной величины X имеет вид:
|
0, |
если |
x ≤ 0 |
|
|
если 0 < x ≤1 |
|||
|
F(x) = Ax, |
|||
|
1, |
если |
x >1 |
|
Определить параметр A и вероятность попадания значения случайной величины в интервал (-1, 0.5).
68

Задача 5. Функция распределения случайной величины X имеет вид:
|
0, |
если |
x ≤1 |
|
|
А(x −1)2 , |
если1 < x ≤ 3 |
||
|
F(x) = |
|||
|
1, |
если |
x > 3 |
|
Определить параметр A и построить график функции распределения. Задача 6. Функция распределения случайной величины имеет вид:
|
0, |
если |
x ≤ −2 |
||
|
F(x) = |
0.25(x + 2)2 , |
если − 2 < x ≤ 0 |
||
|
1, |
если |
x > 0 |
||
Найти плотность распределения случайной величины и вероятность того, что значение Х больше, чем -1.5, но меньше, чем -0.5.
Задача 7. Функция распределения случайной величины имеет вид:
|
0, |
если |
x ≤1 |
||
|
Аx |
2 |
+ В, |
если1 < x ≤ 4 |
|
|
F(x) = |
||||
|
1, |
если |
x > 4 |
||
Определить параметры A и B . Найти вероятность того, что случайная величина X примет значение: а) меньше 0.5; б) больше -0.5; в) в интервале (1.5, 3) . Определить плотность распределения случайной величины X .
|
Задача 8. Дана плотность распределения: |
||
|
0, |
если |
x ≤ −1 |
|
если −1 |
< x ≤1 |
|
|
f (x) = a, |
||
|
если |
x >1 |
|
|
0, |
Определить: а) параметр a ; б) вероятность попадания в интервал (0.5, 1.5) ; в) функцию распределения.
Тема 24. Математическое ожидание и дисперсия непрерывной случайной величины
Математическое ожидание дискретных случайных величин, введенное выше, определялось законом распределения случайной величины и использовалось при предельном переходе от биномиального распределения к распределению Пуассона. Для непрерывных случайных величин, математическое ожидание и дисперсия выражаются через плотности распределения согласно следующему определению.
Математическим ожиданием непрерывной случайной величины X с
|
плотностью распределения f (x) называется: |
|
|
M ( X ) = ∫∞ xf (x)dx |
(5.7) |
|
−∞ |
69

Это определение представляет собой обобщение определения для дискретных случайных величин.
Пример 5. Найти M ( X ) , если случайная величина X имеет плотность рас-
|
пределения: |
|||
|
0, |
если |
x ≤1 |
|
|
f (x) = 0.25, |
если1 < x ≤ 5 |
||
|
0, |
если |
x > 5 |
Решение. По определению математического ожидания, получаем:
|
∞ |
1 |
5 |
+∞ |
|||||||
|
M ( X ) = ∫xf (x)dx = |
∫xf (x)dx + ∫xf (x)dx + ∫xf (x)dx = |
|||||||||
|
−∞ |
−∞ |
1 |
5 |
|||||||
|
5 |
1 |
x2 |
5 |
52 − |
1 |
|||||
|
= ∫x |
dx = |
= |
= 3 |
|||||||
|
4 |
8 |
8 |
||||||||
|
1 |
1 |
|||||||||
Здесь учтено, что по условию плотность распределения равна нулю всюду вне интервала (1;5) и равна 0.25 только внутри интервала (1;5).
Пример 6. Найти M ( X ) , если случайная величина X имеет плотность распределения:
|
0, |
если |
x ≤1 |
||||
|
− x |
2 |
+8x −7 |
||||
|
f (x) = |
, |
если1 < x ≤ 7 |
||||
|
36 |
||||||
|
если |
x > 7 |
|||||
|
0, |
||||||
Решение. Учитывая, что так же, как в предыдущем примере, при вычислении математического ожидания надо найти интеграл только по той области, где плотность распределения отлична от нуля, получаем:
|
7 x(−x |
2 +8x −7) |
1 |
x4 |
8x |
3 |
7x2 |
7 |
|||||||||||||||||||||||||||||||||||
|
M ( X ) = |
∫ |
dx = |
− |
+ |
− |
= |
||||||||||||||||||||||||||||||||||||
|
36 |
36 |
4 |
3 |
2 |
||||||||||||||||||||||||||||||||||||||
|
1 |
||||||||||||||||||||||||||||||||||||||||||
|
1 |
4 |
7 |
3 |
7 7 |
2 |
4 |
3 |
2 |
49 35 +13 |
|||||||||||||||||||||||||||||||||
|
1 |
7 |
8 |
||||||||||||||||||||||||||||||||||||||||
|
1 |
8 1 |
7 1 |
||||||||||||||||||||||||||||||||||||||||
|
= |
− |
+ |
− |
− |
− |
+ |
− |
= |
= 4 |
|||||||||||||||||||||||||||||||||
|
36 |
4 |
3 |
2 |
4 |
3 |
2 |
36 12 |
|||||||||||||||||||||||||||||||||||
Математическое ожидание обладает следующими свойствами:
1.Постоянный множитель можно выносить за знак математического ожидания, т.е. M (cX ) = cM ( X ) , где c – любое постоянное число.
2.Математическое ожидание постоянной величины равно этой постоянной.
3.Математическое ожидание суммы конечного числа случайных величин равно сумме их математических ожиданий.
Эти свойства вытекают из определения математического ожидания. Например, первое свойство имеет место потому, что все значения случайной величины
70

Y = cX получаются из значений случайной величины Х умножением на множитель c, а вероятности соответствующих значений новой случайной величины никак не изменяются.
Еще раз подчеркнем, что математическое ожидание есть усредненная характеристика случайной величины. Оно всегда определяется только одним числом, которое находится на интервале между наименьшим и наибольшим из возможных значений случайной величины. В отличие от функции и плотности распределения, которые дают полную информацию о случайной величине и позволяют находить вероятности ее значений или вероятности того, что они находятся в любом интервале, знание математического ожидания недостаточно для определения таких вероятностей.
Дисперсия случайных величин характеризует средний разброс квадрата отклонений значений случайной величины X от ее математического ожидания M ( X ) . Аналогично тому, как это было для дискретных случайных величин,
вводится следующее определение.
Дисперсией случайной величины X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
|
D( X ) = M (( X − M ( X ))2 ) |
(5.8) |
Поэтому размерность D(X ) равна квадрату размерности X . Удобнее D( X ) является среднее квадратичное отклонение σ = D( X ) . Дисперсии случайных
величин удовлетворяют следующим свойствам:
1. Дисперсия постоянной величины C равна нулю:
D(C) = 0
2. Постоянный множитель выносится за знак дисперсии в квадрате, т.е.:
D(cX ) = c2 D( X )
3. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий, т.е.:
D( X +Y ) = D( X ) + D(Y )
|
4. Для вычисления D( X ) удобнее использовать равенство |
|
|
D( X ) = M (X 2 )−(M ( X ))2 |
(5.9) |
Заметим, что отклонение случайной величины X от числа, равного ее математическому ожиданию M ( X ) , т.е. Z = X − M ( X ) – также случайная вели-
чина. При этом M (Z ) всегда равно нулю, т.е. M (X − M (X )) = 0 . Действительно, используя свойства (1) – (3), получаем:
M (Z) = M ( X ) − M (M ( X )) = M ( X ) − M (X ) = 0
|
Именно по этой причине разброс значений X относительно M ( X ) |
харак- |
|
теризуется дисперсией D( X ) и средним квадратичным уклонением σ = |
D(X ) . |
Пример 7. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины X , которая имеет плотность распределения:
71

|
0, |
если x ≤1 |
|
|
если1 < x ≤ 6 |
||
|
f (x) = 0.2, |
||
|
0, |
если x > 6 |
|
Решение. По определению математического ожидания, получаем:
|
∞ |
6 |
1 |
1 |
6 |
1 |
35 |
7 |
||||||||||
|
M ( X ) = ∫xf (x)dx = ∫x |
dx = |
x2 |
= |
(62 |
−1) = |
= |
. |
||||||||||
|
5 |
10 |
1 |
10 |
10 |
2 |
||||||||||||
|
−∞ |
1 |
Здесь учтено, что, по условию, плотность распределения равна нулю всюду вне интервала (1,6) и равна 0.2 только внутри интервала (1,6) .
Для того чтобы найти дисперсию X , воспользуемся формулой (5.9) и найдем сначала:
|
∞ |
6 |
1 |
1 |
6 |
1 |
215 |
43 |
|||||||||||||||||||||
|
M ( X 2 ) = ∫x2 f (x)dx = ∫x2 |
dx = |
x3 |
= |
(63 −1) = |
= |
|||||||||||||||||||||||
|
1 |
. |
|||||||||||||||||||||||||||
|
5 |
15 |
15 |
15 |
3 |
||||||||||||||||||||||||
|
−∞ |
1 |
|||||||||||||||||||||||||||
|
Поэтому: |
2 |
|||||||||||||||||||||||||||
|
D( X ) = M ( X 2 ) −(M ( X )2 |
43 |
7 |
43 |
4 − 49 3 |
172 |
−147 |
25 |
|||||||||||||||||||||
|
= |
− |
= |
= |
= |
||||||||||||||||||||||||
|
3 |
12 |
12 |
12 |
|||||||||||||||||||||||||
|
2 |
|
σ = |
D( X ) = |
25 |
= |
5 |
3 |
||
|
12 |
2 |
||||||
|
Пример 8. Найти математическое ожидание, дисперсию и среднеквадрати- |
|||||||
|
ческое отклонение случайной величины X , заданной плотностью распределения: |
|||||||
|
0, |
если |
x ≤1 |
|||||
|
− x |
2 |
+8x −7 |
|||||
|
f (x) = |
, |
если1 < x ≤ 7 |
|||||
|
36 |
|||||||
|
если |
x > 7 |
||||||
|
0, |
|||||||
Решение. При вычислении математического ожидания надо найти интеграл только по той области, где плотность распределения отлична от нуля, получаем:
|
7 |
x(−x2 +8x |
−7) |
1 |
x4 |
8x3 |
7x2 |
7 |
49 35 +13 |
|||||||||||||||||||||||||||||||
|
М( Х) = |
∫ |
dx = |
− |
+ |
− |
= |
= 4. |
||||||||||||||||||||||||||||||||
|
36 |
36 |
4 |
3 |
2 |
36 12 |
||||||||||||||||||||||||||||||||||
|
1 |
|||||||||||||||||||||||||||||||||||||||
|
1 |
|||||||||||||||||||||||||||||||||||||||
|
Аналогично, получаем: |
7 |
||||||||||||||||||||||||||||||||||||||
|
М( Х2 ) = |
7 |
x2 (−x2 +8x −7) |
1 |
x5 |
8x4 |
7x3 |
7 |
4 4 +8 |
|||||||||||||||||||||||||||||||
|
dx = |
− |
+ |
− |
= |
=17.8 |
||||||||||||||||||||||||||||||||||
|
∫ |
|||||||||||||||||||||||||||||||||||||||
|
36 |
36 |
5 |
4 |
3 |
36 15 |
||||||||||||||||||||||||||||||||||
|
1 |
|||||||||||||||||||||||||||||||||||||||
|
1 |
|||||||||||||||||||||||||||||||||||||||
|
Поэтому по формуле (5.9): |
|||||||||||||||||||||||||||||||||||||||
|
D( X ) =17.8 − 42 =1.8, |
σ = |
1.8 ≈1.4 |
Существуют различные распределения непрерывных случайных величин. Плотности распределений непрерывных случайных величин называют также законами распределений. Далее будут рассмотрены равномерно распределенные и нормально распределенные случайные величины.
72

Задачи для самостоятельного решения
Найти математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины
Задача 9. Плотность распределения:
|
0, |
если |
x ≤ −1 |
|
|
1 |
, |
если −1 < x ≤ 1 |
|
|
f ( x) = |
2 |
||
|
если |
x > 1 |
||
|
0, |
Задача 10. Плотность распределения:
|
0, |
если |
x ≤ 0 |
||||||||||||||
|
3 |
(2 x − x2 ), |
|||||||||||||||
|
f ( x) = |
если 0 < x ≤ 2 |
|||||||||||||||
|
4 |
||||||||||||||||
|
0, |
если |
x > 2 |
||||||||||||||
|
Задача 11. Плотность распределения: |
||||||||||||||||
|
0, |
если |
x ≤ −1 |
||||||||||||||
|
если −1 < x ≤1 |
||||||||||||||||
|
f (x) = 0.75(1 − x2 ), |
||||||||||||||||
|
0, |
если |
x >1 |
||||||||||||||
|
Задача 12. Плотность распределения: |
||||||||||||||||
|
0, |
если |
x ≤ −2 |
||||||||||||||
|
3 |
(4 − x2 ), |
|||||||||||||||
|
f ( x) = |
если − 2 < x ≤ 2 |
|||||||||||||||
|
32 |
||||||||||||||||
|
0, |
если |
x > 2 |
||||||||||||||
|
Задача 13. Плотность распределения: |
||||||||||||||||
|
0, |
если |
x ≤1 |
||||||||||||||
|
3 |
( x2 |
|||||||||||||||
|
f ( x) = − |
− 6 х + 5), |
если 1 < x ≤ 5 |
||||||||||||||
|
32 |
||||||||||||||||
|
0, |
если |
x > 5 |
||||||||||||||
|
Задача 14. Плотность распределения: |
||||||||||||||||
|
0, |
если |
x ≤ −5 |
||||||||||||||
|
3 |
( x2 |
|||||||||||||||
|
f ( x) = − |
+ 6 x + 5), |
если − 5 < x ≤ −1 |
||||||||||||||
|
32 |
||||||||||||||||
|
0, |
если |
x > −1 |
||||||||||||||
|
Задача 15. Плотность распределения: |
||||||||||||||||
|
0, |
если |
x ≤ −2 |
||||||||||||||
|
2 |
+ 4 |
х) |
||||||||||||||
|
3(12 − x |
||||||||||||||||
|
f ( x) = |
, |
если − 2 < x ≤ 6 |
||||||||||||||
|
256 |
||||||||||||||||
|
если |
x > 6 |
|||||||||||||||
|
0, |
||||||||||||||||
|
Задача 16. Плотность распределения: |
||||||||||||||||
|
0, |
если |
x ≤ 1 |
||||||||||||||
|
2 |
( x2 − 5x + 4), |
если 1 < x ≤ 4 |
||||||||||||||
|
f ( x) = − |
9 |
|||||||||||||||
|
0, |
если |
x > 4 |
||||||||||||||
73
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Так же как и теория вероятностей, математическая статистика имеет свои ключевые понятия, к которым относятся: генеральная совокупность, теоретическая функция распределения, выборка, эмпирическая функция распределения, статистика. Именно с определения этих понятий, а также с установления связи между ними и объектами, изучаемыми в теории вероятностей, мы начнем изложение математической статистики, предварительно дав краткое описание задач, которые собираемся решать. Кроме того, в последнем параграфе главы остановимся на некоторых распределениях, наиболее часто встречающихся в математической статистике.
Задачи математической статистики
Математическая статистика, являясь частью общей прикладной математической дисциплины «Теория вероятностей и математическая статистика», изучает, как и теория вероятностей, случайные явления, использует одинаковые с ней определения, понятия и методы и основана на той же самой аксиоматике А.Н. Колмогорова.
Однако задачи, решаемые математической статистикой, носят специфический характер. Теория вероятностей исследует явления, заданные полностью их моделью, и выявляет еще до опыта те статистические закономерности, которые будут иметь место после его проведения. В математической статистике вероятностная модель явления определена с точностью до неизвестных параметров. Отсутствие сведений о параметрах компенсируется тем, что нам позволено проводить «пробные» испытания и на их основе восстанавливать недостающую информацию.
Попытаемся показать различие этих двух взаимосвязанных дисциплин на простейшем примере — последовательности независимых одинаковых испытаний, или схеме Бернулли (часть 1, гл.4). Схему Бернулли можно трактовать как подбрасывание несимметричной монеты с вероятностью выпадения «герба» (успеха) р и «цифры» (неудачи) 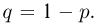
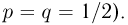
часть 1, гл.4, параграфы 2-4) и т.д. В математической статистике значения р и q неизвестны заранее, но мы можем произвести серию подбрасываний монеты. Цель проведения испытаний как раз и заключается либо в определении р и q, либо в проверке некоторых априорных суждений относительно их значений. Таким образом, судя уже по этому простейшему примеру, задачи математической статистики являются в некотором смысле обратными задачам теории вероятностей.
В математической статистике обычно принято выделять два основных направления исследований.
Первое направление связано с оценкой неизвестных параметров. Возвращаясь к нашему примеру, предположим, что мы произвели п подбрасываний монеты и установили, что в 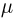
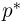
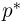
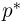
Второе направление в математической статистике связано с проверкой некоторых априорных предположений, или статистических гипотез. Так, до опыта мы можем предположить, что монета симметрична, т.е. высказать гипотезу о равенстве 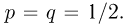
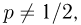
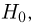
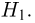
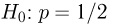
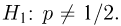
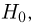
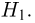
на ошибки первого и второго рода. Ошибка первого рода состоит в том, что мы принимаем конкурирующую гипотезу 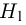
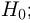
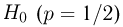
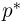
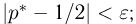
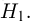
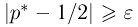
Далее мы увидим, что задача проверки статистических гипотез наиболее полно решается для случая двух простых гипотез. Можно поставить и задачу проверки нескольких гипотез (в примере с монетой можно взять, например, три гипотезы: 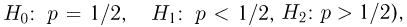
Условно математическую статистику можно подразделить на исследование байесовских и небайесовских моделей.
Байесовские модели возникают тогда, когда неизвестный параметр является случайной величиной и имеется априорная информация о его распределении. При байесовском подходе на основе опытных данных априорные вероятности пересчитываются в апостериорные. Применение байесовского подхода фактически сводится к использованию формулы Байеса (см. часть 1, гл. 3, параграф 5), откуда, собственно говоря, и пошло его название. Байесовский подход нами будет применяться только как вспомогательный аппарат при доказательстве некоторых теорем.
Небайесовские модели появляются тогда, когда неизвестный параметр нельзя считать случайной величиной и все статистические выводы приходится делать, опираясь только на результаты «пробных» испытаний. Именно такие модели мы будем рассматривать в дальнейшем изложении.
В заключение этого параграфа отметим, что в математической статистике употребляют также понятия параметрических и непараметрических моделей. Параметрические модели возникают тогда, когда нам известна с точностью до параметра (скалярного или векторного) функция распределения наблюдаемой характеристики и необходимо по результатам испытаний определить этот параметр (задача оценки неизвестного параметра) или проверить гипотезу о принадлежности его некоторому заранее выделенному множеству значений (задача проверки статистических гипотез). Все приведенные выше примеры с подбрасыванием монеты представляют собой параметрические модели. Примеры непараметрических моделей мы рассмотрим позже.
Основные понятия математической статистики
Основными понятиями математической статистики являются: генеральная совокупность, выборка, теоретическая функция распределения.
Генеральная совокупность. Будем предполагать, что у нас имеются N объектов, каждому из которых присуще определенное значение некоторой числовой характеристики X. Характеристика X, вообще говоря, может быть и векторной (например, линейные размеры объекта), однако для простоты изложения мы ограничимся только скалярным случаем, тем более что переход к векторному случаю никаких трудностей не вызывает. Совокупность этих N объектов назовем генеральной совокупностиью.
Поскольку все наши статистические выводы мы будем делать, основываясь только на значениях числовой характеристики X, естественно абстрагироваться от физической природы самих объектов и отождествить каждый объект с присущей ему характеристикой X. Таким образом, с точки зрения математической статистики генеральная совокупность представляет собой N чисел, среди которых, конечно, могут быть и одинаковые.
Выборка. Для того чтобы установить параметры генеральной совокупности, нам позволено произвести некоторое число п испытаний. Каждое испытание состоит в том, что мы случайным образом выбираем один объект генеральной совокупности и определяем его значение X. Полученный таким образом ряд чисел 

Заметим, что сам процесс выбора можно осуществлять различными способами: выбрав объект и определив его значение, изымать этот объект и не допускать к последующим испытаниям (выборка без возвращения); после определения его значения объект возвращается в генеральную совокупность и может полноправно участвовать в дальнейших испытаниях (выборка с возвращением) и т.д.
Разумеется, если бы мы смогли провести сплошное обследование всех объектов генеральной совокупности, то не нужно было бы применять никакие статистические методы и саму математическую статистику можно было бы отнести к чисто теоретическим наукам. Однако такой полный контроль невозможен по следующим причинам. Во-первых, часто испытание сопровождается разрушением испытуемого объекта; в этом случае мы имеем выборку без возвращения. Во-вторых, обычно необходимо исследовать весьма большое количество объектов, что просто невозможно физически. Наконец, может возникнуть такое положение, когда многократно измеряется один и тот же объект, но каждый замер производится со случайной ошибкой, и цель последующей статистической обработки заключается именно в уточнении характеристик объекта на основе многократных наблюдений; при этом результат каждого наблюдения надо считать новым объектом генеральной совокупности (простейшим примером такой ситуации является многократное подбрасывание монеты с целью определения вероятности выпадения «герба»). Следует помнить также, что выборка обязательно должна удовлетворять условию репрезентативности или, говоря более простым языком, давать обоснованное представление о генеральной совокупности.
С ростом объема N генеральной совокупности исчезает различие между выборками с возвращением и без возвращения. Мы, как обычно это делается в математической статистике, будем рассматривать случай бесконечно большого объема генеральной совокупности и поэтому, употребляя слово «выборка», не будем указывать, какая она — с возвращением или без него.
Теоретическая функция распределения. Пусть 
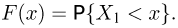
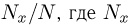
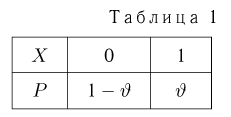
В случае выборки 
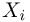


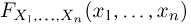

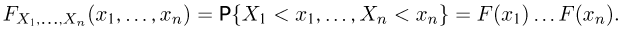
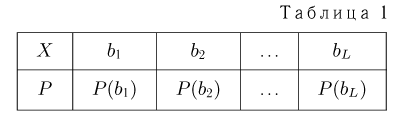
В дальнейшем, как правило, мы будем предполагать, что F(x) является функцией распределения либо дискретной, либо непрерывной наблюдаемой случайной величины X. В первом случае будем оперировать рядом распределения случайной величины X, записанным в виде табл. 1, а во втором — плотностью распределения
Простейшие статистические преобразования
Прежде чем переходить к детальному анализу наблюденных статистических данных, обычно проводят их предварительную обработку. Иногда результаты такой обработки уже сами по себе дают наглядную картину исследуемого явления, в большинстве же случаев они служат исходным материалом для получения более подробных статистических выводов.
Вариационный и статистический ряды. Часто бывает удобно пользоваться не самой выборкой 
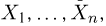
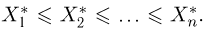

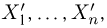
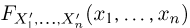
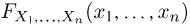
Для 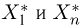
Пример 1. Измерение проекции вектора скорости молекул водорода на одну из осей координат дало (с учетом направления вектора) результаты 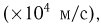
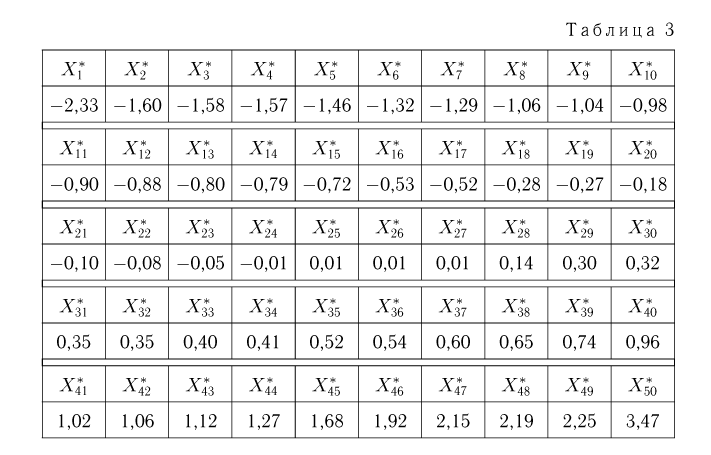
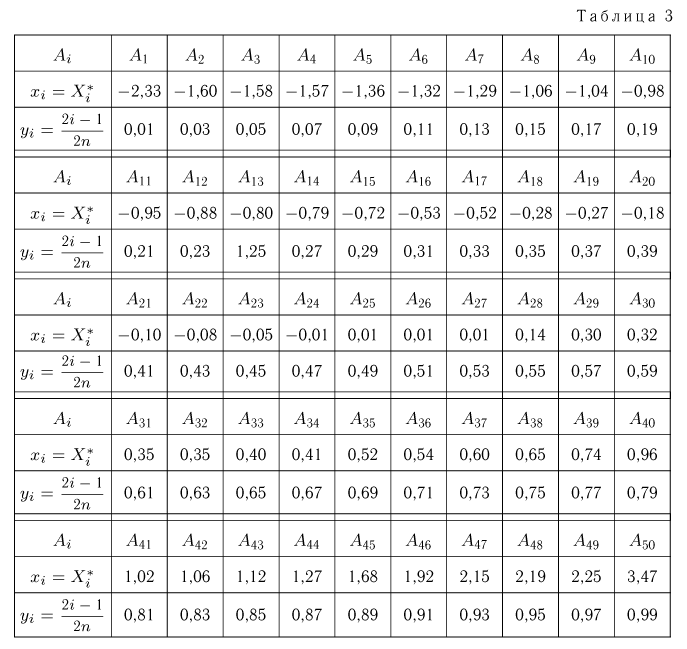
Вариационный ряд этой выборки приведен в табл. 3. Крайними членами вариационного ряда 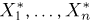
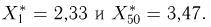
Если среди элементов выборки 
ряда (табл.4), в котором 
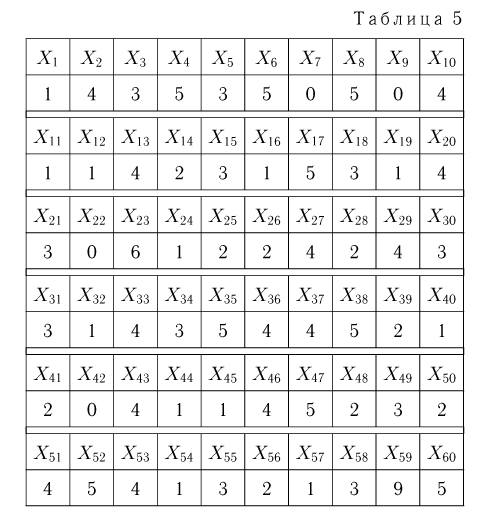
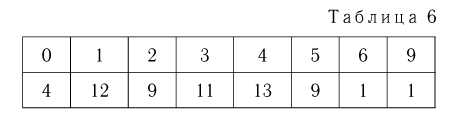
Пример 2. В течение минуты каждую секунду регистрировалось число попавших в счетчик Гейгера частиц. Результаты наблюдений приведены в табл. 5.
Статистический ряд выборки представлен в табл. 6.

Статистики. Для получения обоснованных статистических выводов необходимо проводить достаточно большое число испытаний, т.е. иметь выборку достаточно большого объема п. Ясно, что не только использование такой выборки, но и хранение ее весьма затруднительно. Чтобы избавиться от этих трудностей, а также для других целей, полезно ввести понятие статистики, общее определение которой формулируется следующим образом. Назовем статистикой 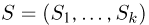
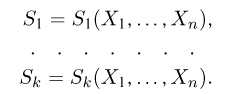
Как функция от случайного вектора 
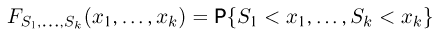
определяется для дискретной наблюдаемой случайной величины X формулой
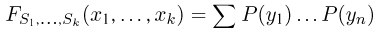
и для непрерывной — формулой
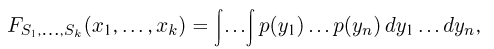
где суммирование или интегрирование производится по всем возможным значениям 
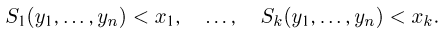
Пример 3. Пусть выборка 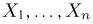
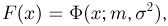
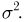
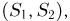
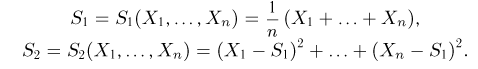
Тогда
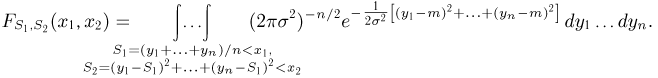
Мы, однако, не будем вычислять записанный интеграл, а воспользуемся тем фактом (см. пример 29, часть 1, гл.6, параграф 7), что любое линейное преобразование переводит нормально распределенный вектор в вектор, снова имеющий нормальное распределение, причем ортогональное преобразование переводит вектор с независимыми координатами, имеющими одинаковые дисперсии, в вектор с также независимыми и имеющими те же самые дисперсии координатами.
Из курса теории вероятностей известно, что статистика 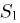
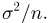
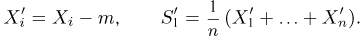
Очевидно, что
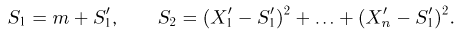
Пусть теперь А — линейное ортогональное преобразование пространства 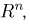
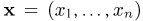
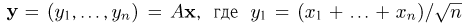
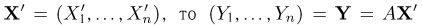
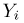
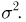
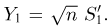
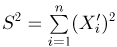
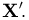
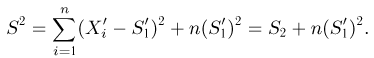
С другой стороны, в силу ортогональности преобразования А
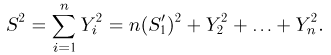
Отсюда, в частности, следует, что
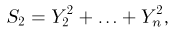
т.е. 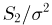
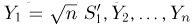
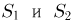
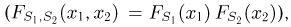
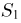
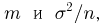
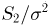
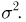
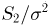
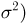
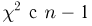
Отметим, что проведенные рассуждения будут нами постоянно использоваться в гл. 4, посвященной статистическим задачам, связанным с нормально распределенными наблюдениями.
Важный класс статистик составляют так называемые достаточные статистики. Не давая пока строгого математического определения, скажем, что статистика S является достаточной, если она содержит всю ту информацию относительно теоретической функции распределения F(x), что и исходная выборка 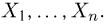
Эмпирическая функция распределения. Пусть мы имеем выборку 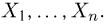
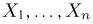
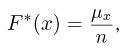
где 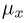
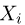
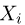
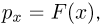
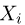
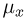
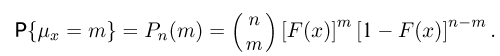
Функция 

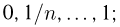


Построение эмпирической функции распределения 
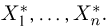

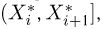
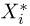
Пример 4. График эмпирической функции распределения, построенной по вариационному ряду из табл. 3, приведен на рис. 1.
Если выборка задана статистическим рядом (см. табл. 4), то эмпирическая функция распределения также постоянна на интервалах 
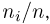
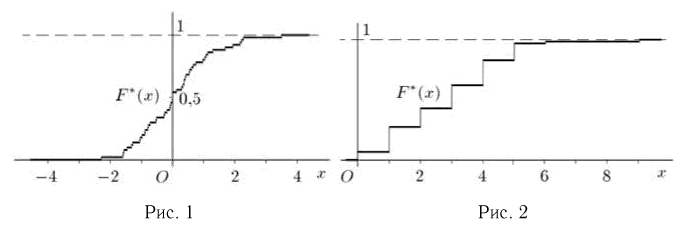
Пример 5. График эмпирической функции распределения, построенной по статистическому ряду из табл. 6, приведен на рис. 2.
Гистограмма, полигон. Для наглядности выборку иногда преобразуют следующим образом. Всю ось абсцисс делят на интервалы 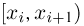
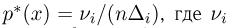
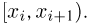
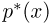
При наблюдении дискретной случайной величины вместо гистограммы часто используют полигон частот. Для этого по оси абсцисс откладывают все возможные значения 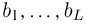


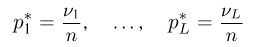
(полигон относительных частот). Для большей наглядности соседние точки соединяются отрезками прямой.
Для непрерывной наблюдаемой случайной величины полигоном относительных частот иногда называют ломаную линию, соединяющую середины отрезков, составляющих гистограмму.
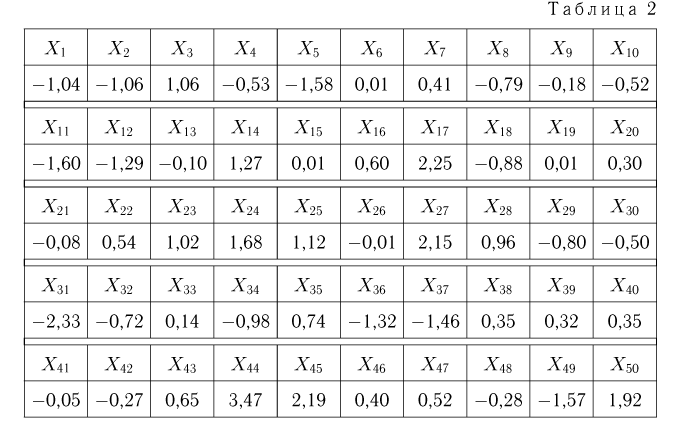
Пример 6. Построим гистограмму и полигон относительных частот выборки, представленной в табл. 2. Для этого выберем интервалы одинаковой длины 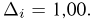
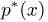
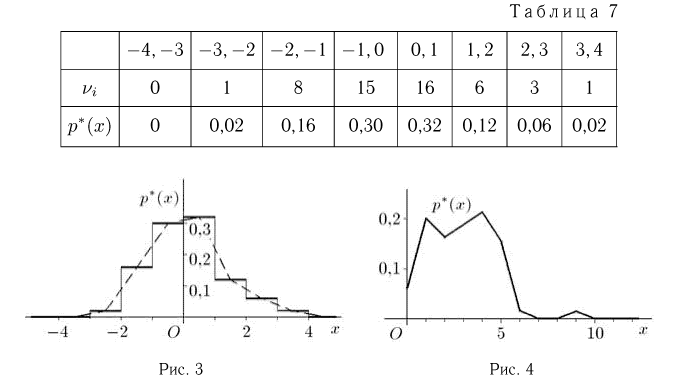
Пример 7. Построим полигон относительных частот выборки, приведенной в табл. 5. Возможные значения наблюдаемой случайной величины X (числа частиц, попавших в счетчик Гейгера) представляют собой неотрицательные целые числа. Воспользовавшись статистическим рядом из табл. 6, получаем полигон относительных частот, изображенный на рис. 4.
Предельное поведение эмпирической функции распределения.
Предположим, что по выборке 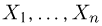
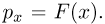
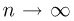
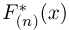
Теорема Гливенко-Кантелли. При 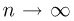
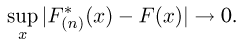
Смысл теоремы Гливенко-Кантелли заключается в том, что при увеличении объема выборки п у эмпирической функции распределения исчезают свойства случайности и она приближается к теоретической функции распределения.
Аналогично, если п велико, то значение гистограммы 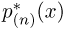
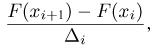
где 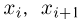
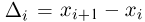
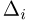
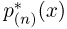
Выборочные характеристики. Эмпирическая функция распределения 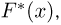
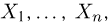
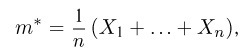
второй момент
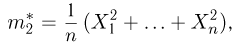
дисперсию
момент k-го порядка
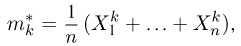
центральный момент k-го порядка
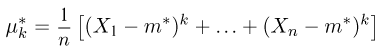
и т.д. Соответствующие характеристики называются выборочными (выборочное среднее, выборочный второй момент, выборочная дисперсия и т.п.). Ясно, что выборочные характеристики как функции от случайных величин 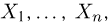
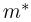
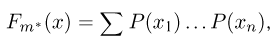
где суммирование ведется по всем 
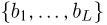
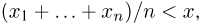
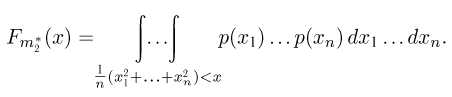
Наряду с выборочной дисперсией 
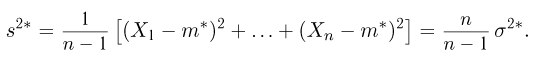
Характеристику 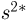
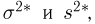
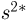

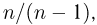
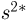
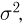

Пример 8. Подсчитаем выборочное среднее и выборочные дисперсии для выборки, приведенной в табл. 2:
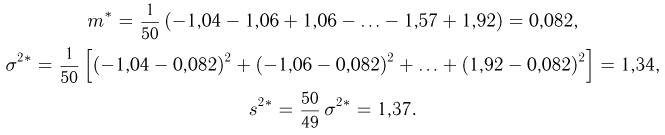
Для подсчета выборочной дисперсии 
Основные распределения математической статистики
Наиболее часто в математической статистике используются: нормальное распределение, 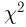
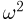
Нормальное распределение. Одномерное стандартное нормальное распределение (стандартный нормальный закон) задается своей плотностью распределения (см. часть 1, гл.5, параграф 4)
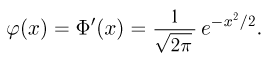
Значения функции Ф(x) и плотности 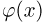
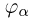
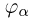
Общее одномерное нормальное распределение характеризуется двумя параметрами: средним (математическим ожиданием) т и дисперсией 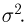
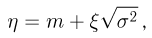
где случайная величина 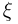
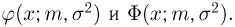
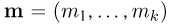

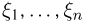
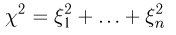
носит название 

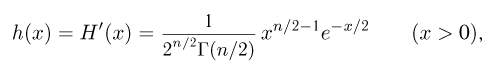
где 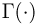
Значения функции 

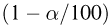
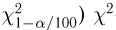

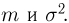
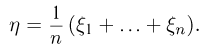
Тогда случайная величина
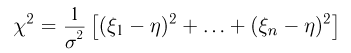
имеет 
Еще одна схема, в которой появляется 
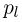
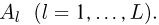
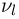
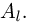
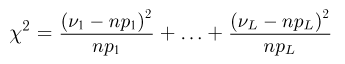
при 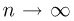
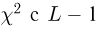
t-распределение. Пусть 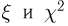
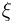


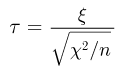
называется t-распределением с п степенями свободы, t-распределение имеет плотность распределения
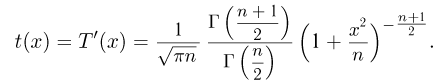
Значения функции t-распределения и 
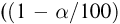
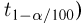
Далее, пусть 
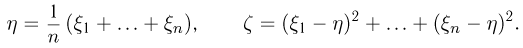
Тогда случайные величины 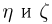
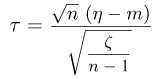
имеет t-распределение с n-1 степенями свободы (доказательство этого см. в примере 3).
F-распределение. Пусть 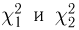
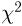
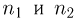
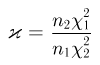
носит название F-распределения с параметрами 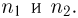
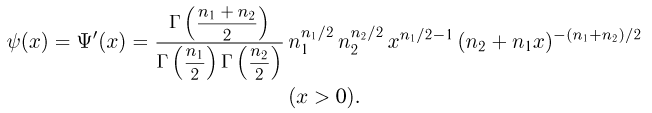
Значения 
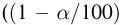
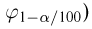
Распределение Колмогорова. Функция распределения Колмогорова имеет вид
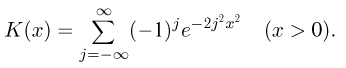
Распределение Колмогорова является распределением случайной величины
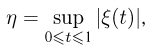
где 
Значения функции распределения Колмогорова приведены в [1], табл.6.1. Квантили распределения Колмогорова будем обозначать через


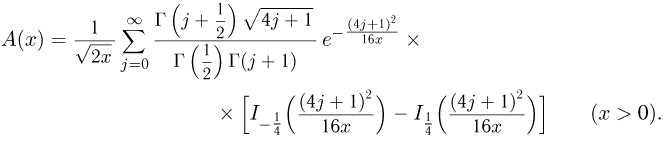
Здесь 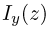

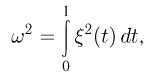
где 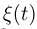
Значения функции 

Оценки неизвестных параметров
Как уже говорилось в гл. 1, одним из двух основных направлений в математической статистике является оценивание неизвестных параметров. В этой главе мы дадим определение оценки, опишем те свойства, которые желательно требовать от оценки, и приведем основные методы построения оценок. Завершается глава изложением метода построения доверительных интервалов для неизвестных параметров.
Статистические оценки и их свойства
Предположим, что в результате наблюдений мы получили выборку 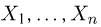
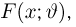


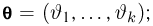
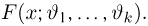
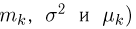

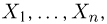
Оценкой неизвестного параметра 
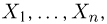
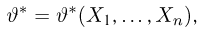
зависящую только от выборки 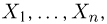
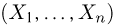
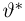
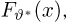
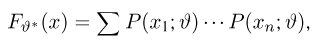
где суммирование ведется по всем переменным 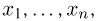
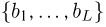
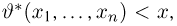
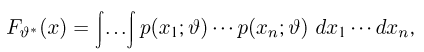
где интегрирование ведется по области, выделяемой неравенством 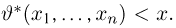


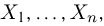

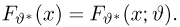
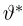
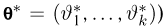
Пример:
Предположим, что проведено п испытаний в схеме Бернулли с неизвестной вероятностью успеха 
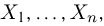
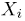
В качестве оценки 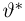
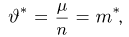
где
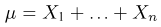
представляет собой суммарное число успехов в п испытаниях Бернулли. Статистика 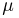

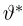

Пример:
Выборка 
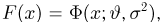


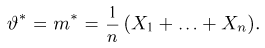
Функция распределения 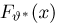
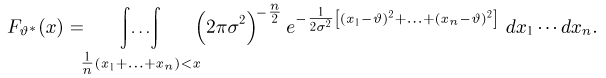
Однако вместо непосредственного вычисления написанного n-мерного интеграла заметим, что статистика
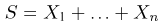
распределена по нормальному закону с параметрами 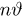
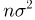
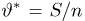
Разумеется, на практике имеет смысл использовать далеко не любую оценку.
Пример:
Как и в примере 1, рассмотрим испытания в схеме Бернулли. Однако теперь в качестве оценки неизвестной вероятности успеха 
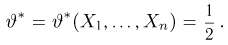
Такая оценка будет хороша лишь в том случае, когда истинное значение 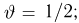

Приведенный пример показывает, что желательно употреблять только те оценки, которые по возможности принимали бы значения, наиболее близкие к неизвестному параметру. Однако в силу случайности выборки в математической статистике мы, как правило, не застрахованы полностью от сколь угодно большой ошибки. Значит, гарантировать достаточную близость оценки 

Опишем теперь те свойства, которые мы хотели бы видеть у оценки.
Главное свойство любой оценки, оправдывающее само название «оценка», — возможность хотя бы ценой увеличения объема выборки до бесконечности получить точное значение неизвестного параметра 


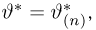
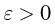

Отметим, что правильнее было бы говорить о состоятельности последовательности оценок 
Пример:
Оценка 

Пример:
Пусть выборка 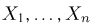
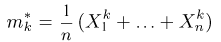
сходится к теоретическому моменту 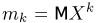
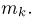
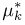
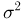
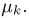
Пример:
Выборка 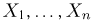
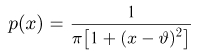
с неизвестным параметром 



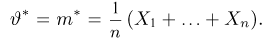
Однако 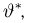


Из курса теории вероятностей известно (см. часть 1, гл.7, параграф 1), что мерой отклонения оценки 

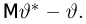
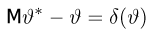
называется смещением оценки 
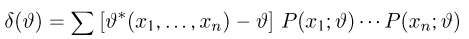
в дискретном случае и
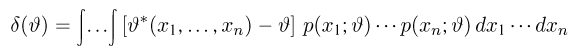
в непрерывном, где суммирование или интегрирование ведется по всем возможным значениям
Оценка 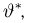
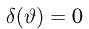
при всех 
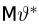
Пример:
Оценка 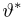

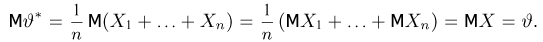
Пример:
Выборочные моменты 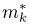
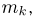
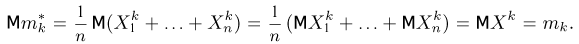
Вычислим теперь математическое ожидание выборочной дисперсии
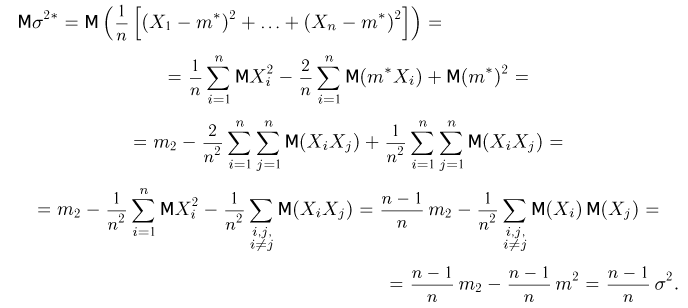
Таким образом, 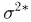
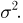
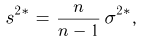
то
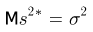
и 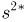
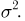
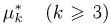
Пример:
Пусть 
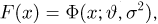

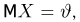
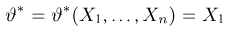
является несмещенной. Очевидно, однако, что она не является состоятельной.
Примеры 8 и 9 показывают, что состоятельная оценка может быть сметенной и, наоборот, несмещенная оценка не обязана быть состоятельной.
Рассматривая несколько оценок неизвестного параметра 

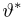
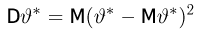
(дисперсия, как и распределение оценки, зависит от неизвестного параметра 
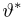

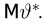
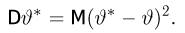
Имеется несколько подходов к нахождению несмещенных оценок с минимальной дисперсией. Это связано с тем, что такие оценки существуют не всегда, а найти их бывает чрезвычайно сложно. Здесь мы изложим понятие эффективности оценки, основанное на неравенстве Рао-Крамера.
Теорема:
Неравенство Рао-Крамера. Пусть 

где 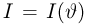
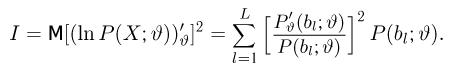
а в непрерывном — формулой
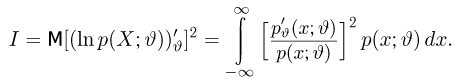
Прежде чем переходить к доказательству теоремы, заметим, что по неравенству Рао-Крамера дисперсия любой несмещенной оценки не может быть меньше 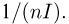
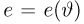

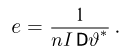
Ясно, что эффективность любой оценки 



Несмещенная оценка 
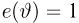
Доказательство теоремы 1. Доказательство этой и всех остальных теорем будем проводить (если не сделано специальной оговорки) для непрерывного случая. Это связано с тем, что непрерывный случай, как правило, более сложен, и читатель, усвоивший доказательство для непрерывного случая, легко проведет его для дискретного.
Как мы увидим из хода доказательства, условия регулярности семейства 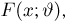
функция 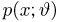

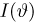
Приступим теперь к собственно доказательству теоремы. Заметим прежде всего, что, дифференцируя тождество
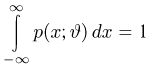
(в силу сформулированного условия это можно делать), получаем
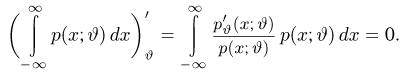
Далее, в силу несмещенности оценки 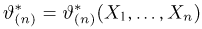
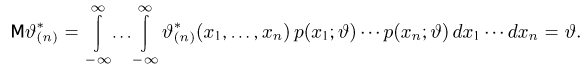
Дифференцируя это равенство по 
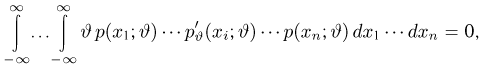
полученное из (1) и (2), находим
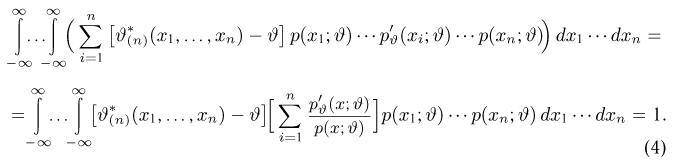
Воспользовавшись неравенством Коши-Буняковского
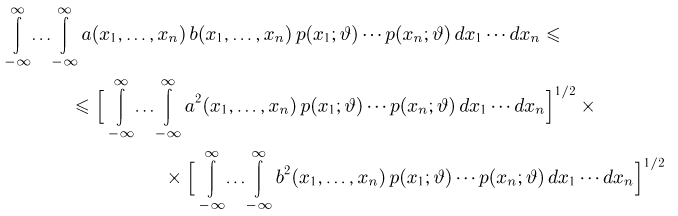
при
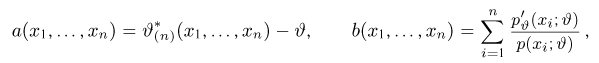
имеем
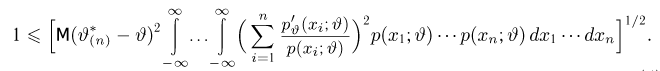
Заметим теперь, что в силу тождества (2)
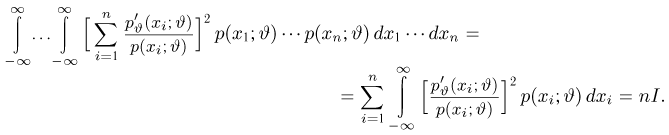
Тогда неравенство (5) можно переписать в виде 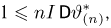
Замечание:
Для превращения используемого при доказательстве теоремы 1 неравенства Коши-Буняковского, в равенство необходимо и достаточно существование таких функций 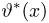
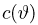

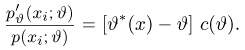
При этом оценка 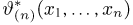
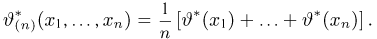
Обозначая
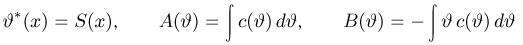
и интегрируя уравнение (6), получаем, что необходимым условием существования эффективной оценки является возможность представления плотности распределения 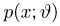
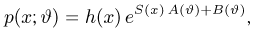
где 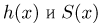
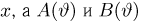
Аналогичное представление для ряда распределения 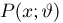
Экспоненциальные семейства играют в математической статистике важную роль. В частности, как мы показали, только для этих семейств могут существовать эффективные оценки, которые к тому же определяются формулой
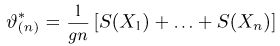
(появление множителя 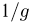
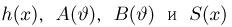
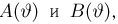
Замечание:
Неравенство Рао-Крамера можно обобщить на случай смещенных оценок:
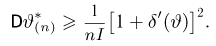
И в этом случае неравенство превращается в равенство только тогда, когда семейство распределений экспоненциально.
Пример:
Рассмотрим оценку 


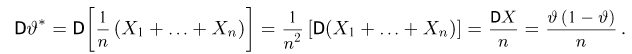
Найдем информацию Фишера (напомним, что в данном случае наблюдаемая величина X принимает всего два значения 0 и 1 с вероятностями 
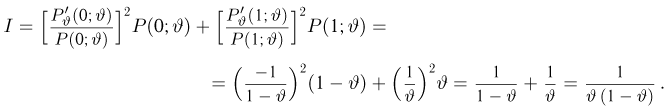
Таким образом, 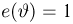

Пример:
Рассмотрим оценку 
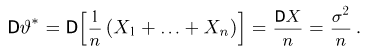
Далее,
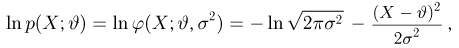
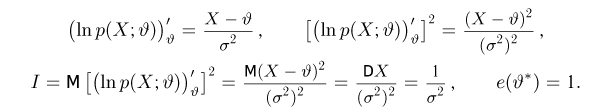
И в этом примере оценка 
Пример:
Оценим неизвестную дисперсию 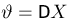
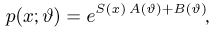
где
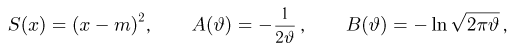
т.е. по отношению к неизвестной дисперсии 


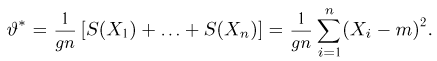
С другой стороны, нетрудно видеть, что 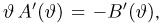
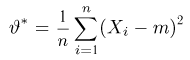
и, значит, ее эффективность. Впрочем, эффективность оценки 
Пусть теперь мы оцениваем не дисперсию, а среднее квадратичное отклонение 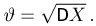
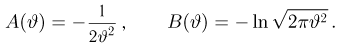
Поэтому равенство 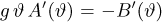
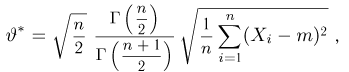
равную корню квадратному из оценки дисперсии с точностью до постоянного множителя 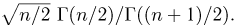


Пример:
Пусть выборка 
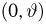

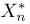

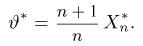
Функция распределения 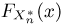
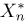
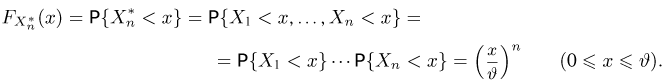
Тогда
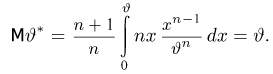
Значит, оценка 
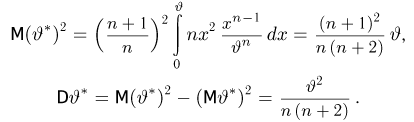
Мы видим, что дисперсия оценки 
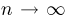
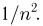
В заключение этого параграфа отметим, что эффективные по Рао-Крамеру оценки существуют крайне редко. Правда, как мы увидим в параграфе 4, эффективность по Рао-Крамеру играет существенную роль в асимптотическом анализе оценок, получаемых методом максимального правдоподобия. Кроме того, существуют обобщения неравенства Рао-Крамера (например, неравенство Бхаттачария [7]), позволяющие доказывать оптимальность более широкого класса оценок.
В следующем параграфе мы рассмотрим другой подход к определению оценок с минимальной дисперсией, базирующийся на достаточных статистиках.
Наиболее распространенные методы нахождения оценок приводятся в параграфах 3-6.
Наконец, в параграфе 7 описан подход к построению доверительных интервалов для неизвестных параметров.
Достаточные оценки
Первый шаг в поисках другого (не основанного на неравенстве Рао-Крамера) принципа построения оценок с минимальной дисперсией состоит во введении понятия достаточной статистики (отметим, что достаточные статистики играют в современной математической статистике весьма важную роль, причем как при оценке неизвестных
параметров, так и при проверке статистических гипотез). Назовем k-мерную статистику
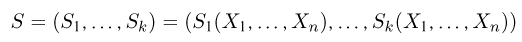
достаточной для параметра 
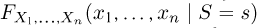
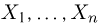
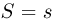
Пример:
Пусть 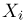
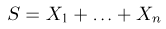
— общее число успехов в п испытаниях Бернулли. Покажем, что она является достаточной для вероятности успеха 
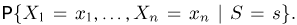
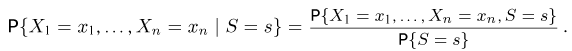
Если 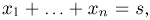
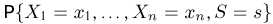
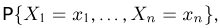
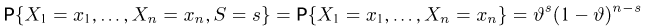
(напомним еще раз, что каждое 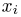
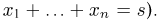
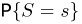
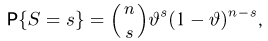
то из (9) получаем, что
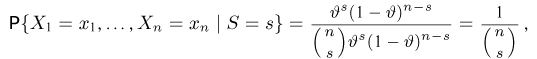
т. е. не зависит от 
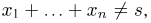
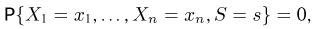
откуда
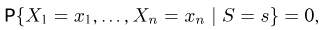
т. е. опять-таки не зависит от 
Очевидно, что использовать приведенное выше определение для проверки достаточности конкретных статистик весьма сложно, особенно в непрерывном случае. Простой критерий достаточности задается следующей теоремой.
Теорема:
Факторизационная теорема Неймана-Фишера. Для того чтобы статистика 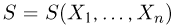

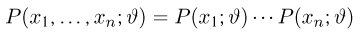
в дискретном случае или плотность распределения
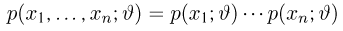
в непрерывном случае выборки 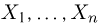
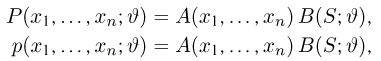
где функция 
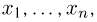
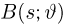
Доказательство:
Для простоты изложения ограничимся только дискретным случаем. По определению условной вероятности,
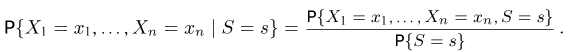
Очевидно, что числитель в правой части (II) совпадает с вероятностью 
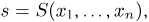
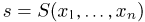
Теперь, если S — достаточная статистика, то левая часть (12) не зависит от 
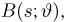
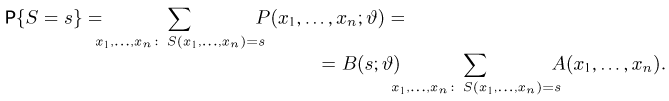
Подставляя последнее равенство в (12), имеем
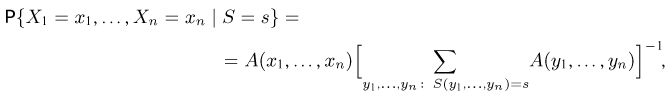
т.е. не зависит от 
Замечание к теореме 2. Очевидно, что представление (10) справедливо с точностью до функции 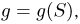
Пример:
Пусть 
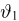
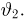
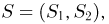
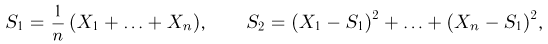
является достаточной для (двумерного) параметра 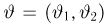
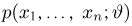

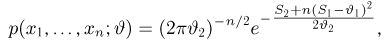
т.е. имеет вид (10), где
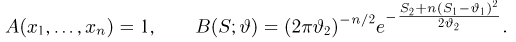
Пример:
Пусть 
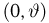
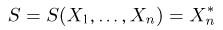
является (одномерной) достаточной статистикой для 
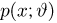
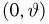
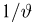
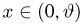

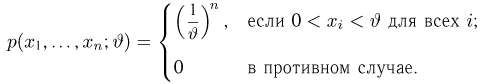
В частности, область изменения каждого аргумента 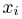
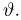
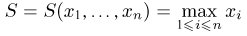
и положим
С учетом введенных функций.
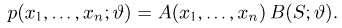
Здесь уже при определении функции 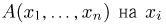
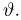



является достаточной для параметра
Пример:
Покажем, что для экспоненциального семейства (7) существует одномерная достаточная статистика. Этот факт легко установить, если подставить выражение (7) в формулу для плотности распределения выборки
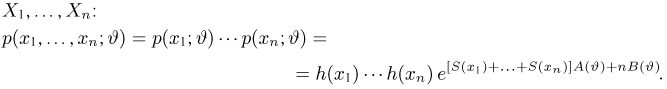
Полагая теперь
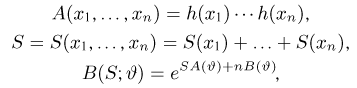
видим, что одномерная статистика
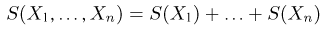
является достаточной для параметра 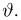
Как уже говорилось в гл. 1, смысл достаточной статистики S заключается в том, что она включает в себя всю ту информацию о неизвестном параметре 


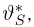
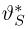
Начиная с этого момента и до конца параграфа будем для простоты предполагать, что неизвестный параметр 
Пусть имеется некоторая оценка 
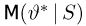

Теорема:
Улучшение оценки по достаточной статистике. Пусть S — достаточная статистика, а 
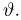
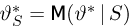
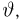
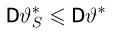
при всех
Доказательство:
В силу достаточности статистики 5 условное распределение, а значит, и условное математическое ожидание оценки 


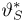
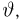
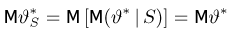
для условного математического ожидания немедленно следует несмещенность оценки
Наконец,
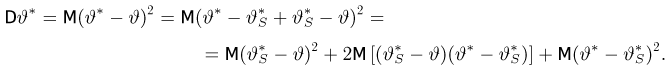
Используя опять свойство условного математического ожидания, получаем
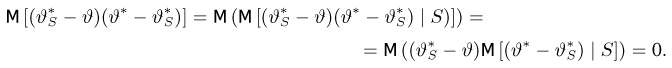
Поэтому
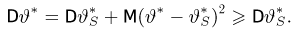
Замечание:
Неравенство (13) превращается для некоторого 
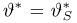
Замечание:
Утверждение теоремы остается в силе и для смещенной оценки 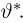
Смысл теоремы 3 заключается в том, что взятие условного математического ожидания, т. е. переход к оценке 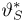

Пример:
Пусть 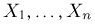

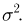
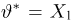

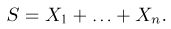
Нетрудно показать, что статистика S является достаточной для параметра 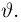
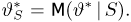
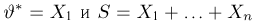

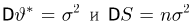
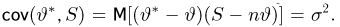

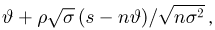
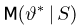
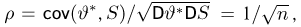

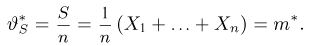
Иными словами, мы из совсем плохой оценки 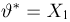
Рассмотренный пример приоткрывает нам те возможности, которые несет с собой теорема 3. Однако, прежде чем сделать последний шаг, введем еще одно определение. Назовем статистику 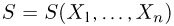
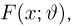
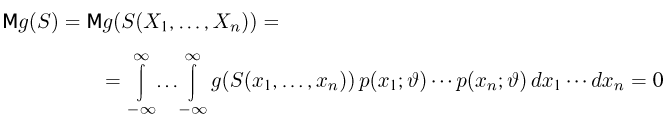
при всех 
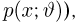
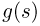
Теорема:
Минимальность дисперсии оценки, зависящей от полной достаточной статистики. Пусть S — полная достаточная статистика, 
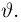
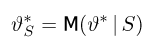
является единственной несмещенной оценкой с минимальной дисперсией.
Доказательство теоремы немедленно вытекает из предыдущих результатов. Действительно, в силу теоремы 3 оценка с минимальной дисперсией обязательно должна находиться среди оценок, зависящих только от достаточной статистики S; в противном случае ее можно было бы улучшить с помощью условного математического ожидания. Но среди оценок, зависящих только от S, может быть максимум одна несмещенная. В самом деле, если таких оценок две: 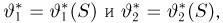
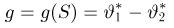
имеет при всех значениях 
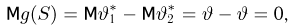
что в силу полноты статистики S влечет за собой равенство 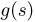
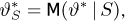
Перейдем к обсуждению полученных результатов.
Условие полноты статистики S, как мы видим, сводится к единственности несмещенной оценки 
Сравнение размерностей полной статистики S и оцениваемого параметра 




Сформулируем очевидное следствие из теоремы 4. которое удобно применять во многих частных случаях.
Следствие из теоремы 4. Если оценка 
Пример:
Пусть 
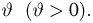
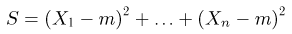
является достаточной для параметра 
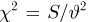
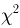
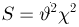
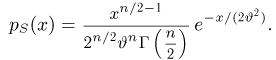
Пусть теперь 
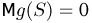
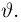
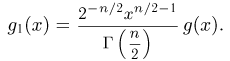
Тогда
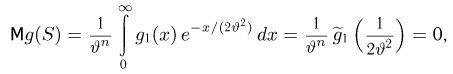
что 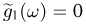
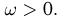
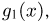
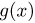
Рассмотрим теперь оценку
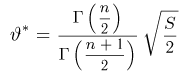
(см. пример 12) неизвестного среднего квадратичного отклонения 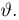
Пример:
Рассмотрим оценку
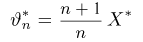
параметра 
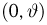
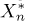
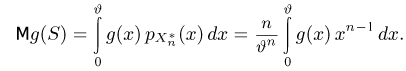
Отсюда, в частности, следует, что если 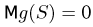
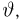
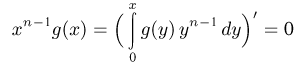
при всех х. Поэтому 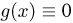
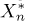
Таким образом, в силу следствия из теоремы 4 и в этом примере оценка 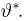
Метод моментов
Пусть мы имеем выборку 
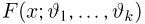
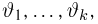
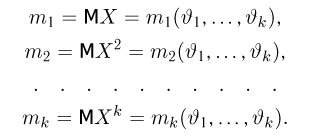
Суть метода моментов заключается в следующем: так как выборочные моменты являются состоятельными оценками теоретических моментов (см. пример 8), мы можем в написанной системе равенств при большом объеме выборки п теоретические моменты 
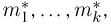
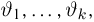
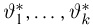

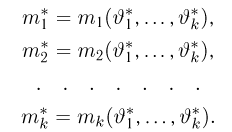
Можно показать, что при условии непрерывной зависимости решения этой системы от начальных условий 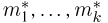
Теорема:
Асимптотическая нормальность оценок, полученных методом моментов. При некоторых условиях, наложенных на семейство 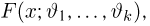
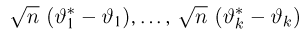
при 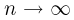

Доказательство:
Будем полагать, что выполнены следующие условия: а) параметры 
б) существует теоретический момент 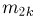
в) функция
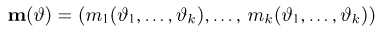
дифференцируема по 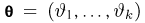
Доказательство теоремы проведем для одномерного случая, предоставляя общий случай читателю. Оно является комбинацией следующих результатов: теоремы о дифференцируемости обратного отображения и центральной предельной теоремы. Действительно, поскольку существует дисперсия DX, то при каждом истинном значении 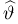
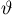
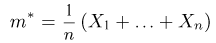
асимптотически при 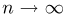
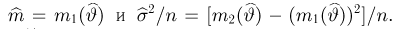

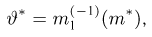
где 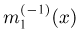
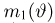
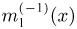
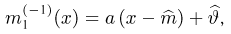
причем 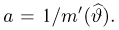
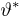
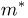
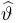
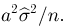
Пример:
Найдем методом моментов оценку неизвестной вероятности успеха 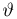
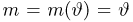
Итак, оценка 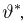
Пример:
Выборка 
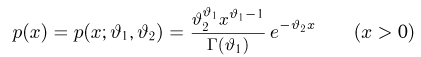
с двумя неизвестными параметрами 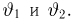
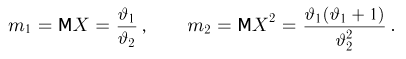
Отсюда для определения оценок 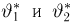
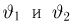
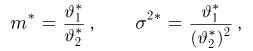
решение которой имеет вид
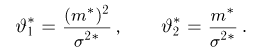
Вообще говоря, в методе моментов не обязательно использовать первые k моментов. Более того, можно рассматривать моменты не обязательно целого порядка. Иногда для использования в методе моментов привлекают более или менее произвольные функции 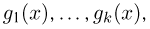
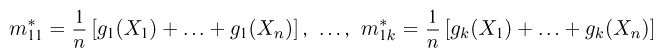
функций 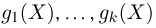
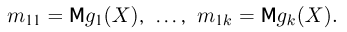
Пример:
Пусть выборка 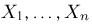
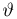
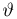
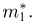
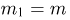
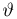
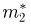
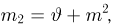
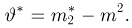
Следует отметить, что оценки, полученные методом моментов, обычно имеют эффективность существенно меньше единицы и даже являются смещенными. Иногда из-за своей простоты они используются в качестве начального приближения для нахождения более эффективных оценок.
Метод максимального правдоподобия
Метод максимального правдоподобия является наиболее распространенным методом нахождения оценок. Пусть по-прежнему выборка 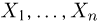
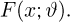
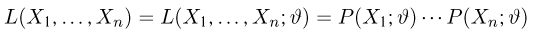
в дискретном случае и
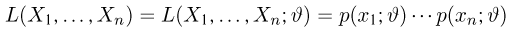
в непрерывном называется функцией правдоподобия. Отметим,что в функции правдоподобия 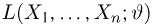





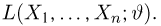
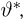
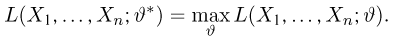
При практической реализации метода максимального правдоподобия удобно пользоваться не самой функцией правдоподобия, а ее логарифмом.
Уравнением правдоподобия называется уравнение
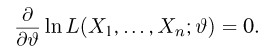
Если функция правдоподобия дифференцируема по 
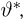


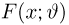
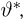
Пример:
Найдем оценку неизвестной вероятности успеха 
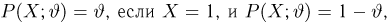
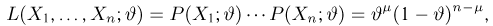
где 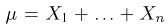
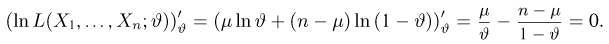
Решая это уравнение, имеем
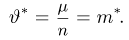
Поскольку
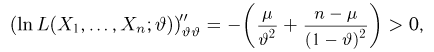
то 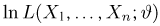

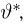
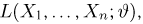
Оказывается, имеется тесная связь между эффективными оценками и оценками, полученными методом максимального правдоподобия. А именно, справедлива следующая теорема.
Теорема:
Совпадение эффективной оценки с оценкой максимального правдоподобия. Если (естественно, при условиях регулярности теоремы 1) существует эффективная оценка 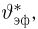
Доказательство теоремы 6 представляет собой дальнейшее уточнение доказательства теоремы 1. Действительно, как следует из замечания 1 к теореме 1, из существования эффективной оценки 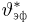
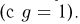
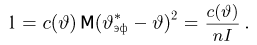
Поэтому из условия строгой положительности информации I вытекает строгая положительность 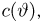
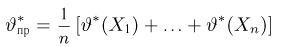
уравнения правдоподобия
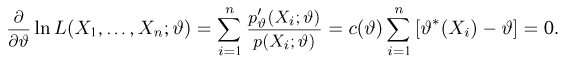
Это решение совпадает с эффективной оценкой 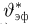
В общем случае оценка максимального правдоподобия может быть не только неэффективной, но и смещенной. Тем не менее она обладает свойством асимптотической эффективности в следующем смысле.
Теорема:
Асимптотическая эффективность оценки максимального правдоподобия. При некоторых условиях на семейство 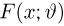
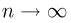

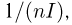
Доказательство:
Сначала сформулируем условия теоремы (см. [9]), которые, как мы увидим далее, гарантируют возможность дифференцируемости под знаком интеграла и разложения 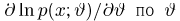
а) для (почти) всех х существуют производные
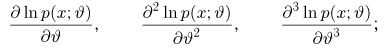
б) при всех 
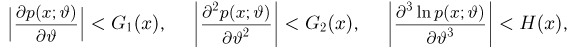
где функции 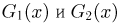
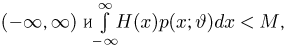
в) информация I конечна и положительна для всех
Обозначим через 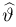
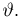
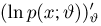
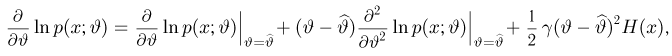
причем 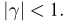
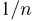
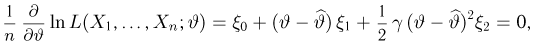
где случайные величины 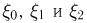
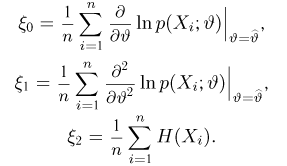
Рассмотрим поведение 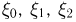
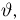
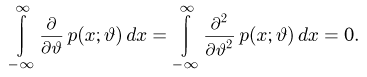
Поэтому
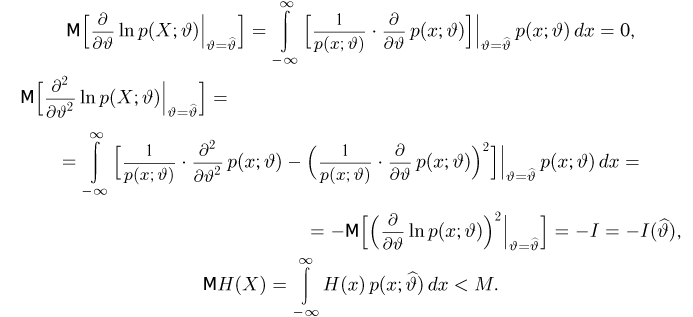
Вернемся к уравнению (14) и воспользуемся сначала тем фактом, что при 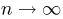
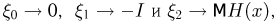
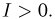
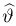
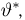
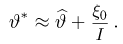
Величина 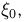
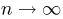
Поэтому оценка 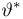
Замечание:
Доказанная теорема гарантирует, что среди всех решений уравнения правдоподобия существует по крайней мере одно 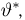
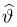
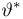
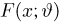
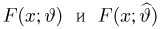
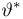
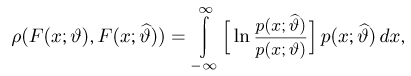
поскольку в силу закона больших чисел именно к расстоянию Кульбака-Лейблера при 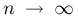
здесь 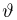
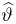
В случае, когда семейство 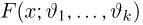
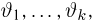
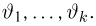
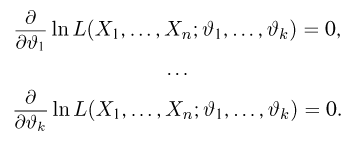
Пример:
Выборка 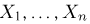
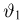
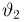
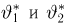
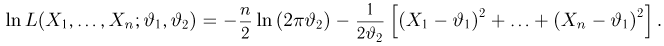
Система уравнений правдоподобия имеет вид
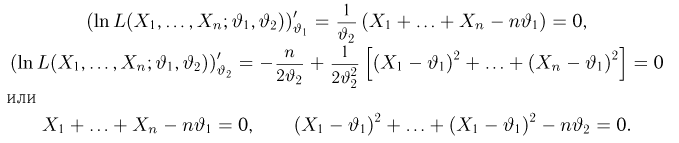
Таким образом,
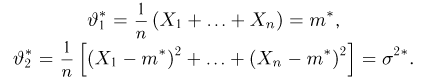
Читателю предлагается самостоятельно показать, что 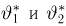
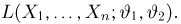
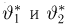
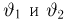
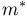
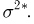
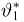
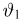
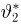
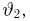
Оказывается, однако, что если мы в качестве оценки параметра 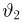
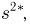
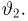
Метод минимального расстояния
Суть этого метода заключается в следующем. Предположим, что любым двум функциям распределения 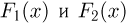
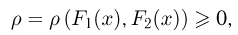
называемое расстоянием, причем 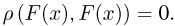
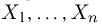
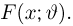
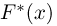
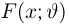
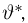
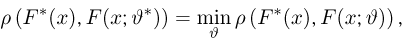
т. е. такое значение 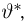
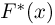
Приведем примеры некоторых наиболее часто встречающихся в математической статистике расстояний.
Равномерное расстояние (расстояние Колмогорова) определяется формулой
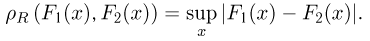
Расстояние 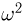
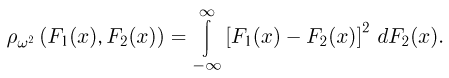
Расстояние 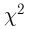
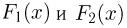
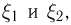
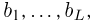
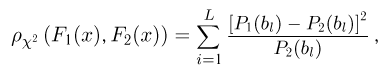
где вероятности 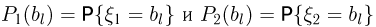
Использование приведенных выше расстояний для получения оценок весьма сложно в вычислительном плане, и поэтому они употребляются крайне редко. Здесь мы упомянули об этих расстояниях только потому, что применение оценок, полученных с их помощью, позволяет упростить вычисление уровней значимости критериев при проверке сложных непараметрических статистических гипотез, поскольку такие оценки естественным образом связаны с соответствующими критериями (см. параграф 5 гл. 3).
Метод номограмм
Еще одним методом, позволяющим, пользуясь только номограммами (специальным образом разлинованными листами бумаги, которые в математической статистике носят название вероятностной бумаги), весьма просто и быстро оценить неизвестные параметры, является метод номограмм. Его сущность состоит в следующем. Пусть мы имеем выборку 
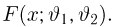
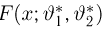
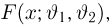
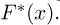
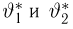
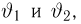
Казалось бы, мы пришли к не менее сложной задаче: найти «чрезвычайно простой» способ приближения эмпирической функции распределения функцией распределения из семейства 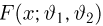
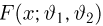
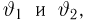
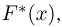
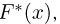
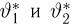
Практическая реализация метода номограмм происходит следующим образом. Сначала выборку 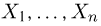
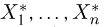
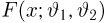
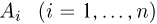
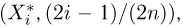
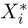
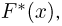
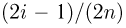
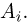
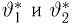
Пример 26. Предполагая в примере 1 из гл. 1, что проекция вектора скорости молекул водорода распределена по нормальному закону, оценим с помощью метода номограмм неизвестное математическое ожидание 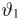
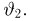
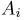
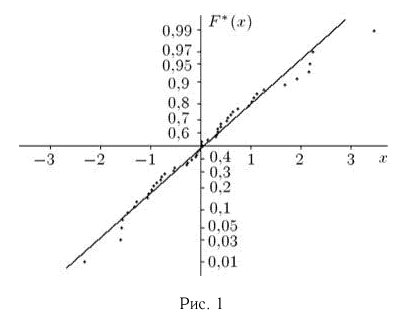
Оценка 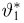
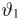
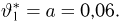
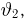
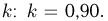
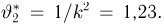
правдоподобия (см. пример 18, а также пример 8 из гл. 1): 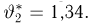
Следует отметить, что с помощью метода номограмм можно судить также о правильности выбора семейства 
Доверительные интервалы
Полученные в предыдущих параграфах оценки неизвестных параметров естественно называть точечными, поскольку они оценивают неизвестный параметр одним числом или точкой. Однако, как мы знаем, точечная оценка не совпадает с оцениваемым параметром и более разумно было бы указывать те допустимые границы, в которых может находиться неизвестный параметр 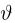
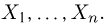

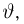

Доверительной вероятностью назовем такую вероятность 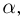
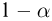
Задавшись доверительной вероятностью 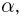

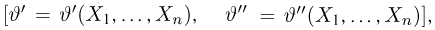

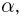


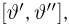
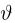
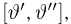
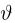

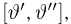
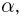
Доверительные интервалы определим, следуя Ю. Нейману, опираясь на точечные оценки. По заданной оценке 
Итак, пусть у нас имеется выборка 
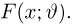

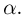

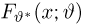

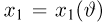
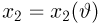
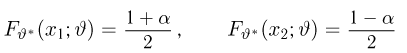
(напомним, что 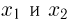
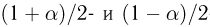
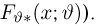


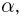
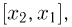

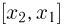
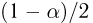

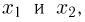
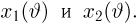
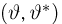
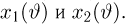

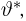

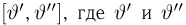

Именно интервал 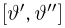
Пример 27. Построим симметричный доверительный интервал доверительной вероятности а для неизвестной вероятности успеха 

где 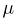
При малом объеме выборки п процедура построения доверительных интервалов трудоемка, поскольку она практически сводится к перебору значений неизвестного параметра. Поэтому существуют специальные таблицы (см. [1], табл. 5.2), которые по наблюденным значениям числа успехов 

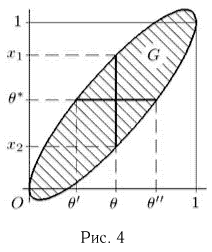
При больших объемах выборки п пользуются тем фактом, что в силу интегральной теоремы Муавра-Лапласа оценка 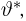

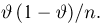
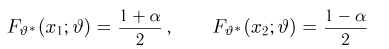
связаны с 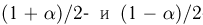
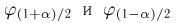
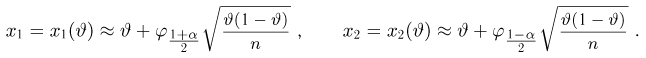
Учитывая, что 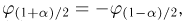
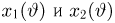
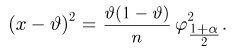
Последнее уравнение, как нетрудно видеть, представляет собой уравнение эллипса (рис. 4) (физически непонятный выход эллипса за полосу 

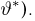
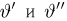
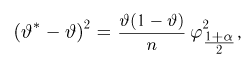
откуда окончательно получаем
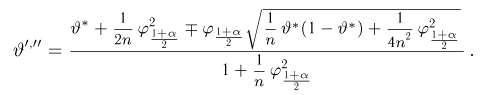
Пример:
Построим симметричный доверительный интервал доверительной вероятности а для неизвестного среднего 
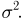
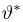

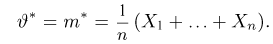
Оценка 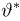
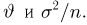
т.е. 
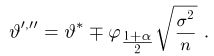
Пример:
Как и в предыдущем примере, предположим, что выборка 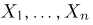
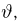
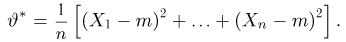
Тогда случайная величина 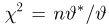
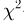
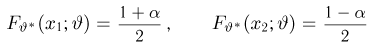
определяются формулами
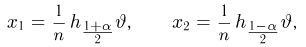
где 
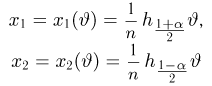
представляют собой уравнения двух лучей, исходящих из начала координат (рис.6), и, значит, границы симметричного доверительного интервала доверительной вероятности а для неизвестной дисперсии 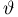
Пример:
Рассмотрим, наконец, случай, когда в выборке из нормальной генеральной совокупности неизвестны оба параметра: среднее 
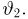
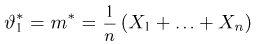
и выборочной дисперсией
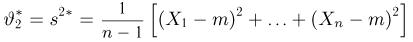
(см. пример 25).
Построение доверительного интервала 
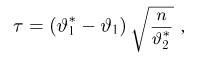
которая, как говорилось в параграфе 4 гл. 1, имеет t-распределение с п — 1 степенями свободы. Обозначим через 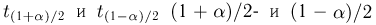
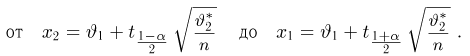
Продолжая рассуждения, как и в случае известной дисперсии, и учитывая равенство 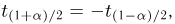
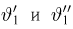
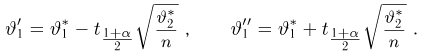
Доверительный интервал 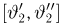
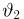
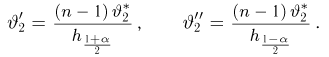
При этом нужно учитывать, что квантили 
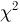
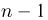
В заключение отметим, что в современной математической статистике доверительные интервалы строят так же, основываясь на критериях значимости.
Решение заданий и задач по предметам:
- Теория вероятностей
- Математическая статистика
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Генеральная совокупность
Непрерывные распределения вероятностей и их параметры
- Общие свойства непрерывного распределения
- Функция распределения непрерывной случайной величины
- Числовые характеристики непрерывного распределения
- Таблица непрерывных распределений, их параметров и числовых характеристик
- Примеры
п.1. Общие свойства непрерывного распределения
Если случайная величина x может принимать любые значения в интервале (a;b), она называется непрерывной случайной величиной.
Функция (p(x)) от значения случайной величины, равная вероятности получения этого значения в испытании, называется плотностью распределения.
Свойства плотности распределения: begin{gather*} p(x)geq 0\ int_{-infty}^{+infty}p(x)dx=1 text{(условие нормировки)} end{gather*}
Например:
Пусть случайная величина равномерно распределена на отрезке (xin [a;b]), т.е. (p(x)=c=const). Из условия нормировки получаем: $$ int_{-infty}^{+infty}p(x)dx=int_{a}^{b}ccdot dx=ccdot x|_{a}^{b}=c(b-a)=1Rightarrow c=frac{1}{b-a} $$ Плотность равномерного непрерывного распределения: $$ p(x)= begin{cases} frac{1}{b-a}, xin [a;b]\ 0, xnotin [a;b] end{cases} $$
п.2. Функция распределения непрерывной случайной величины
Функцией распределения непрерывной случайной величины называют функцию, которая определяет вероятность, что значение случайной величины x не превышает граничное значение t: $$ F(t)=P(xleq t)=int_{-infty}^t p(x)dx $$ Вероятность для случайной величины попасть в интервал (cleq xleq d) определяется интегралом от плотности вероятности: $$ P(cleq xleq d)=int_{c}^d p(x)dx=F(d)-F(c) $$ и равна разности значений функции распределения на концах интервала.
Для непрерывной случайной величины график (F(x)) является монотонно возрастающей гладкой кривой. Область значений (F(x)in [0;1]).
Предел (F(x)) слева равен 0, предел справа равен 1: $$ lim_{xrightarrow -infty}F(x)=0; lim_{xrightarrow +infty}F(x)=1 $$ Например:
Найдем функцию распределения для равномерного распределения с плотностью: $$ p(x)= begin{cases} frac{1}{b-a}, xin [a;b]\ 0, xnotin [a;b] end{cases} $$ Для всех (xlt a) $$ F(x)=int_{-infty}^a p(x)dx=int_{-infty}^acdot dx=0 $$ Для всех (aleq xleq b) begin{gather*} F(t)=0+int_{a}^t p(x)dx=int_{a}^tfrac{1}{b-a}cdot dx=frac{1}{b-a}cdot x|_{a}^t=frac{t-a}{b-a}\ F(x)=frac{x-a}{b-a} end{gather*} Для всех (xgt b) begin{gather*} F(x)=F(b)+int_{b}^{+infty} p(x)dx=1+0=1 end{gather*} Получаем: $$ F(x)= begin{cases} 0, xlt a\ frac{x-a}{b-a}, xin [a;b]\ 1, xgt b end{cases} $$ Графики плотности распределения и функции распределения для равномерно распределенной непрерывной величины:
п.3. Числовые характеристики непрерывного распределения
Числовыми характеристиками непрерывного распределения являются математическое ожидание, дисперсия и среднее квадратичное отклонение (СКО).
Если для дискретных распределений числовые характеристики определяются через суммы (см. §62 данного справочника), то для непрерывных распределений для этого используются интегралы.
Математическое ожидание непрерывной случайной величины (x) с плотностью распределения (p(x)) равно интегралу: $$ M(X)=int_{-infty}^{+infty}xcdot p(x)dx $$
Дисперсия непрерывной случайной величины (x) с плотностью распределения (p(x)) равна интегралу: $$ D(X)=int_{-infty}^{+infty}(x-M(x))^2cdot p(x)dx=int_{-infty}^{+infty}x^2cdot p(x)dx-M^2(x) $$
Среднее квадратичное отклонение (СКО) непрерывной случайной величины – это корень квадратный от дисперсии: $$ sigma(X)=sqrt{D(X)} $$
Например:
Найдем числовые характеристики равномерного распределения. $$ p(x)= begin{cases} frac{1}{b-a}, xin [a;b]\ 0, xnotin [a;b] end{cases} $$ Мат. ожидание: begin{gather*} M(x)=int_{-infty}^{+infty} xcdot p(x)dx=int_{a}^{b} xcdotfrac{1}{b-a}dx=frac{1}{b-a}cdotfrac{x^2}{2}|_{a}^{b}=frac{b^2-a^2}{2(b-a)}=\ =frac{(b-a)(b+a)}{2(b-a)}=frac{a+b}{2} end{gather*} Т.е., среднее значение (центр тяжести) равномерного распределения – это середина отрезка.
Дисперсия: begin{gather*} D(x)=D(X)=int_{-infty}^{+infty}x^2cdot p(x)dx-M^2(x)=D(X)=int_{a}^{b}x^2cdotfrac{1}{b-a}dx-left(frac{a+b}{2}right)^2=\ =frac{1}{b-a}cdotfrac{x^3}{3}|_{a}^{b}-left(frac{a+b}{2}right)^2=frac{b^3-a^3}{3(b-a)}-frac{b^3-a^3}{3(b-a)}-frac{(a+b)^2}{4}=frac{a^2+ab+b^2}{3}-frac{a^2+2ab+b^2}{4}=\ =frac{a^2-2ab+b^2}{12}=frac{(b-a)^2}{12} end{gather*} СКО: $$ sigma(x)=sqrt{D(x)}=frac{b-a}{2sqrt{3}} $$
п.4. Таблица непрерывных распределений, их параметров и числовых характеристик
| Название | Принятое обозначение |
Плотность распределения |
Мат. ожидание |
Дисперсия |
| Непрерывное равномерное | (U(a,b)) | begin{gather*} p(x)=frac{1}{b-a}\ xinleft[a;bright] end{gather*} | (frac{a+b}{2}) | (frac{(b-a)^2}{12}) |
| Нормальное (Гаусса) | (N(mu,sigma^2)) | begin{gather*} p(x)=frac{1}{sqrt{2pisigma^2}}e^{-frac{(x-mu)^2}{2sigma^2}}\ xinmathbb{R} end{gather*} | (mu) | (sigma^2) |
| Экспоненциальное | (Exp(lambda)) | begin{gather*} p(x)=lambda e^{-lambda x}\ lambdagt 0, xgeq 0 end{gather*} | (frac1lambda) | (frac{1}{lambda^2}) |
п.5. Примеры
Пример 1. Непрерывная случайная величина x задана плотностью распределения: $$ p(x)= begin{cases} Ax^2, xin [0;2]\ 0, xnotin [0;2] end{cases} $$ Найдите множитель A, функцию распределения, мат. ожидание, дисперсию и СКО случайной величины x. Постройте графики плотности распределения и функции распределения. Чему равна вероятность, что случайная величина окажется в интервале (frac12leq xleq 1)?
Находим множитель A из условия нормировки: begin{gather*} int_{-infty}^{+infty}p(x)dx=int_{0}^{2}Ax^2dx=1\ Acdotfrac{x^3}{3}|_{0}^{2}=frac{A}{3}(2^3-0)=frac{8A}{3}=1Rightarrow A=frac38\ p(x)= begin{cases} frac38 x^2, xin [0;2]\ 0, xnotin [0;2] end{cases} end{gather*} График плотности распределения:
Функция распределения (F(x)) для (xlt 0) равна 0, для (xgt 2) равна 1.
Найдем (F(x)) в интервале (xinleft[0;2right]): begin{gather*} F(t)=int_{0}^{t}p(x)dx=frac38int_{0}^{t}x^2dx=frac38cdotfrac{x^3}{3}|_{0}^{t}=frac{t^3}{8}Rightarrow F(x)=frac{x^3}{8}\ F(x)= begin{cases} 0, xlt 0\ frac{x^3}{8}, xin [0;2]\ 1, xgt 2 end{cases} end{gather*} График функции распределения:
Найдем математическое ожидание: begin{gather*} M(x)=int_{-infty}^{+infty}xcdot p(x)dx=int_{0}^{2}xcdotfrac38 x^2dx=frac38int_{0}^{2}x^3dx=frac38cdotfrac{x^4}{4}|_{0}^{2}=frac{3}{32}cdot 2^4=1,5 end{gather*} Найдем дисперсию: begin{gather*} D(x)=int_{-infty}^{+infty}x^2cdot p(x)dx-M^2(x)=int_{0}^{2}x^2cdotfrac38 x^2dx-1,5^2=frac38int_{0}^{2}x^4dx-1,5^2=\ =frac38cdotfrac{x^5}{5}|_{0}^{2}-1,5^2=frac{3}{40}cdot 2^5-1,5^2=2,4-2,25=0,15 end{gather*} Найдем СКО: $$ sigma(x)=sqrt{D(x)}=sqrt{0,15}approx 0,387 $$ Вероятность для x оказаться в интервале (frac12leq xleq 1) равна: $$ Pleft(frac12leq xleq 1right)=F(1)-Fleft(frac12right)=frac{1^3}{8}-frac{left(frac12right)^3}{8}=frac{7}{64} $$
Пример 2. Непрерывная случайная величина x задана функцией распределения: $$ F(x)= begin{cases} 0, xlt c\ frac{(x+2)^2}{4}, cleq xleq d\ 1, xgt d end{cases} $$ Найдите границы интервала c и d, плотность распределения, мат. ожидание, дисперсию и СКО случайной величины x. Постройте графики плотности распределения и функции распределения. Чему равна вероятность, что случайная величина окажется в интервале (-1leq xleq -frac12)
Границы интервала ищем из условий: begin{gather*} F(c)=frac{(c+2)^2}{4}=0Rightarrow c=-2\ F(d)=frac{(d+2)^2}{4}=1Rightarrow d=0 end{gather*} Получаем: begin{gather*} F(x)= begin{cases} 0, xlt -2\ frac{(x+2)^2}{4}, -2leq xleq 0\ 1, xgt 0 end{cases} end{gather*} График функции распределения:
Плотность распределения равна производной от функции распределения: $$ p(x)=F'(x) $$ Для (xlt -2cup xgt 0) получим (p(x)=0), т.к. производная от постоянной равна 0.
На значащем интервале: $$ p(x)=left(frac{(x+2)^2}{4}right)=frac{2(x+2)}{4}=frac{x+2}{2} $$ Получаем: begin{gather*} p(x)= begin{cases} frac{x+2}{2}, -2leq xleq 0\ 0, xlt -2cup xgt 0 end{cases} end{gather*} График плотности распределения:
Найдем математическое ожидание: begin{gather*} M(x)=int_{-infty}^{+infty}xcdot p(x)dx=int_{-2}^{0}xcdotfrac{x+2}{2}dx=frac12int_{-2}^{0}(x^2+2x)dx=frac12cdotleft(frac{x^3}{3}+x^2right)|_{-2}^{0}=\ =frac12left(0-left(frac{-8}{3}+4right)right)=-frac23 end{gather*} Найдем дисперсию: begin{gather*} D(x)=int_{-infty}^{+infty}x^2cdot p(x)dx-M^2(x)=int_{-2}^{0}x^2cdotfrac{x+2}{2}dx-left(-frac23right)^2=\ =frac12int_{-2}^{0}(x^3+2x^2)dx-frac49=frac12cdotleft(frac{x^4}{4}+frac{2x^3}{3}right)|_{-2}^{0}-frac49=frac12left(0-left(frac{16}{4}-frac{2cdot 8}{3}right)right)-frac49=\ =frac23-frac49=frac29 end{gather*} Найдем СКО: $$ sigma(x)=sqrt{D(x)}=frac{sqrt{2}}{3} $$ Вероятность для x оказаться в интервале (-1leq xleq -frac12) равна: $$ Pleft(-1leq xleq -frac12right)=Fleft(-frac12right)-F(-1)=frac{left(-frac12+2right)^2}{4}-frac{(-1+2)^2}{4}=frac{1,5^2-1^2}{4}=frac{9}{16} $$