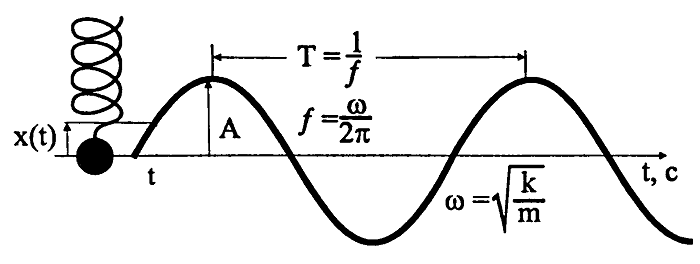
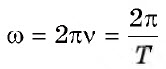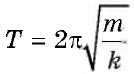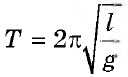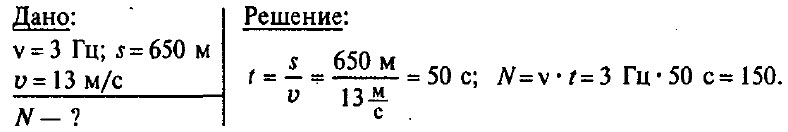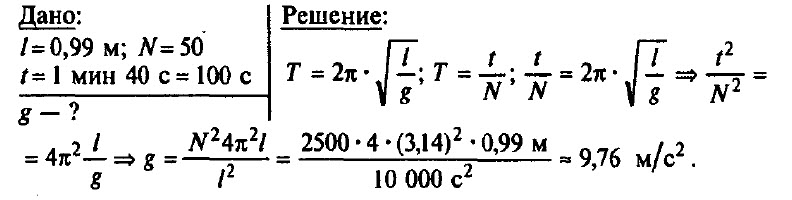Как по графику найти амплитуду амплитуда колебаний - Сайт, где вы сможете решить свои вопросы

Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):

амплитуда,
период,
частота,
циклическая частота,
фаза,
начальная фаза.

Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза

Такие величины, как амплитуду и период, можно определить по графику колебаний.

Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.

Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.

А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.

Что такое амплитуда

Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.

Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.

В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.

Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.

К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.

Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».

С помощью графика амплитуду можно определить так (рис. 2):

Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды

Что такое период

Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.

Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.

( large T left( c right) ) – период колебаний.

Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.

Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.

Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике

Период – это время одного полного колебания.

На графике период найти удобнее одним из таких способов (рис. 4):

Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами

Что такое частота

Обозначают ее с помощью греческой буквы «ню» ( large nu ).

Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».

Поэтому, размерность частоты — это единицы колебаний в секунду:

( large nu left( frac{1}{c} right) ).

Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).

Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.

Одно колебание в секунду соответствует частоте в 1 Герц.

[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]

Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:

[ large boxed{ nu = frac{1}{T} }]

Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду

Что такое циклическая частота

Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.

Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:

( large displaystyle omega left( frac{text{рад}}{c} right) )

Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).

Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».

Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:

[ large boxed{ omega = 2pi cdot nu }]

Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.

Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.

Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).

И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.

Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.

Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).

Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд

Что такое начальная фаза и как определить ее по графику колебаний

Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.

Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).

(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).

Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рис. 7. Угол отклонения качелей перед началом колебаний

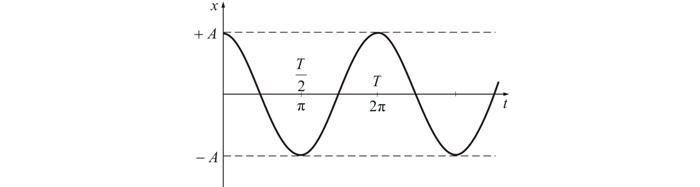
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.

Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.

Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой

Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.

Определим угол (large varphi_{0} ) с помощью графика колебаний.

Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).

Как вычислить начальный угол по интервалу смещения

Алгоритм нахождения начального угла состоит из нескольких несложных шагов.

Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.

[large T = 5 – 1 = 4 left( text{сек} right)]

Из графика следует, что период T = 4 сек.

Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):

[large frac{Delta t }{T} = frac{1}{4} ]

Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.

Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.

Для этого используем формулу:

[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]

(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )

Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.

В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.

Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:

[large varphi_{0} = — frac{pi }{2} ]

Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».

Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).

Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».

А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».

Примечания:

Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.

Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.

Что такое фаза колебаний

Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.

Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний

В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).

Различия между фазой и начальной фазой

Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.

Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.

Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой

Как на графике колебаний отметить фазу

На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.

На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.

Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике

А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.

Как определить фазу с помощью формулы

Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.

Время колебаний t будет величиной переменной.

Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:

[large boxed{ varphi = omega cdot t + varphi_{0} }]

Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.

Что такое разность фаз

Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.

Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.

Обозначим их:

( large varphi_{01}) – для первого процесса и,

( large varphi_{02}) – для второго процесса.

Рис. 12. Для двух колебаний можно ввести понятие разности фаз

Определим разность фаз между первым и вторым колебательными процессами:

[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]

Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.

Как связаны характеристики колебаний — формулы

Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.

Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.

Связь между периодом, количеством колебаний и общим временем колебательного процесса:

[large boxed{ T cdot N = t }]

( large T left( c right) ) – время одного полного колебания (период колебаний);

( large N left( text{шт} right) ) – количество полных колебаний;

( large t left( c right) ) – общее время для нескольких колебаний;

Период и частота колебаний связаны так:

[large boxed{ T = frac{1}{nu} }]

(large nu left( text{Гц} right) ) – частота колебаний.

Количество и частота колебаний связаны формулой:

[large boxed{ N = nu cdot t}]

Связь между частотой и циклической частотой колебаний:

[large boxed{ nu cdot 2pi = omega }]

(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.

Фаза и циклическая частота колебаний связаны так:

[large boxed{ varphi = omega cdot t + varphi_{0} }]

(large varphi_{0} left( text{рад} right) ) — начальная фаза;

(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;

Между фазой и количеством колебаний связь описана так:

[large boxed{ varphi = N cdot 2pi }]

Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:

[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]

(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.

Источник

Задачи на Механические колебания с решениями

Формулы, используемые на уроках «Задачи на Механические колебания».

Название величины	Обозначение	Единица измерения	Формула
*Амплитуда колебаний*	A	м
*Период колебаний*	T	с	T = 1 / v ; T = t / N
*Частота колебаний*	v	Гц	*v = 1 / T ;* *v = N / t*
*Число колебаний за какое-то время*	N		*N = t /T ;* *N = vt*
*Время*	t	с	t = NT ; t = N / v
*Циклическая частота колебаний*	ω	Гц
*Период колебаний пружинного маятника*	T	c
*Период колебаний математического маятника*	T	c
*Уравнение гармонических колебаний*			x(t) = Asin(ωt+φ₀)

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
Шарик на нити совершил 60 колебаний за 2 мин. Определите период и частоту колебаний шарика.

Задача № 2.
На рисунке изображен график зависимости координаты от времени колеблющегося тела.

По графику определите: 1) амплитуду колебаний; 2) период колебаний; 3) частоту колебаний; 4) запишите уравнение координаты.

Задача № 3.
Амплитуда незатухающих колебаний точки струны 2 мм, частота колебаний 1 кГц. Какой путь пройдет точка струны за 0,4 с? Какое перемещение совершит эта точка за один период колебаний?

Задача № 4.
Пользуясь графиком изменения координаты колеблющегося тела от времени, определить амплитуду, период и частоту колебаний. Записать уравнение зависимости x(t) и найти координату тела через 0,1 и 0,2 с после начала отсчета времени.

Задача № 5.
Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с².

Задача № 6.
Груз массой 400 г совершает колебания на пружине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.

Задача № 7.
Частота колебаний крыльев вороны в полете равна в среднем 3 Гц. Сколько взмахов крыльями сделает ворона, пролетев путь 650 м со скоростью 13 м/с?

Задача № 8.
Гармоническое колебание описывается уравнением
Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?

Задача № 9.
Математический маятник длиной 0,99 м совершает 50 полных колебаний за 1 мин 40 с. Чему равно ускорение свободного падения в данном месте на поверхности Земли? (Можно принять π² = 9,87.)

Задача № 10.
ОГЭ
Как и во сколько раз изменится период колебаний пружинного маятника, если шарик на пружине заменить другим шариком, радиус которого вдвое меньше, а плотность — в два раза больше?

Задача № 11.
ЕГЭ
Два математических маятника за одно и то же время совершают — первый N₁ = 30, а второй — N₂ = 40 колебаний. Какова длина каждого из них, если разность их длин Δl = 7 см?

Краткая теория для решения Задачи на Механические колебания.

Это конспект по теме «ЗАДАЧИ на Механические колебания». Выберите дальнейшие действия:

Перейти к теме: ЗАДАЧИ на
Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
Вернуться к списку конспектов по Физике.
Проверить свои знания по Физике.

Источник

Амплитуда колебаний – это максимальное значение отклонения от нулевой точки. В физике данный процесс анализируется в разных разделах.

Он изучается при механических, звуковых и электромагнитных колебаниях. В перечисленных случаях амплитуда измеряется по-разному и по своим законам.

Амплитуда колебаний

Амплитудой колебания называют максимальную отдаленную точку нахождения тела от положения равновесия. В физике она обозначается буквой А и измеряется в метрах.

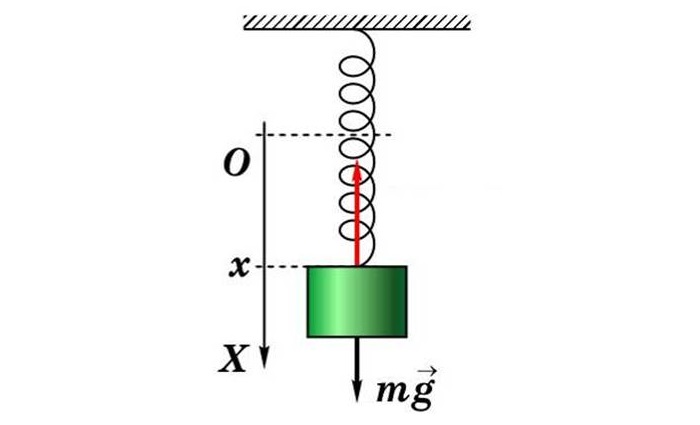
За амплитудой можно наблюдать на простом примере пружинного маятника.

В идеальном случае, когда игнорируется сопротивление воздушного пространства и трение пружинного устройства, устройство будет колебаться бесконечно. Описание движения выполняется с помощью функций cos и sin:

x(t) = A * cos(ωt + φ0) или x(t) = A * sin(ωt + φ0),

где

величина А – это амплитуда свободных движений груза на пружине;
(ωt + φ0) – это фаза свободных колебаний, где ω – это циклическая частота, а φ0 – это начальная фаза, когда t = 0.

002

В физике указанную формулу называют уравнением гармонических колебаний. Данное уравнение полностью раскрывает процесс, где маятник движется с определенной амплитудой, периодом и частотой.

Период колебаний

Результаты лабораторных опытов показывают, что циклический период движения груза на пружине напрямую зависит от массы маятника и жесткости пружины, но не зависит от амплитуды движения.

В физике период обозначают буквой Т и описывают формулами:

Исходя из формул, период колебаний – это механические движения, повторяющиеся через определенный промежуток времени. Простыми словами периодом называют одно полное движение груза.

Частота колебаний

Под частотой колебаний следует понимать количество повторений движения маятника или прохождения волны. В разных разделах физики частота обозначается буквами ν, f или F.

Данная величина описывается выражением:

v = n/t – количество колебаний за промежуток времени,

где

n – это единица колебаний;
t – отрезок времени.

В Международной системе измерений частоту измеряют в Гц (Герцах). Она относится к точным измеряемым составляющим колебательного процесса.

Например, наукой установлена частота вращения Солнца вокруг центра Вселенной. Она равна -10³⁵ Гц при одинаковой скорости.

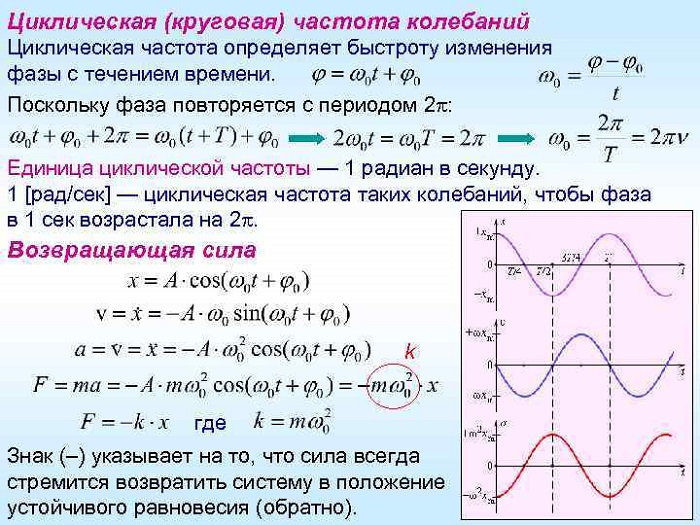
Циклическая частота

В физике циклическая и круговая частота имеют одинаковое значение. Данная величина еще называется угловой частотой.

Обозначают ее буквой омега. Она равна числу собственных колебательных движений тела за 2π секунд времени:

ω = 2π/T = 2πν.

Данная величина нашла свое применение в радиотехнике и, исходя из математического расчета, имеет скалярную характеристику. Ее измерения проводят в радианах на секунду. С ее помощью значительно упрощаются расчеты процессов в радиотехнике.

Например, резонансное значение угловой частоты колебательного контура рассчитывают по формуле:

WLC = 1/LC.

Тогда как обычная циклическая резонансная частота выражается:

VLC = 1/2π*√ LC.

В электрике под угловой частотой следует понимать число полных трансформаций ЭДС или число оборотов радиуса – вектора. Здесь ее обозначают буквой f.

Как определить амплитуду, период и частоту колебаний по графику

Для определения на графике составляющих колебательного механического процесса или, например, колебания температуры, нужно разобраться в терминах этого процесса.

К ним относят:

расстояние испытываемого объекта от исходной точки – называют смещением и обозначают х;
наибольшее отклонение – амплитуда смещения А;
фаза колебания – определяет состояние колебательной системы в любой момент времени;
начальная фаза колебательного процесса – когда t = 0, то φ = φ₀.

402

Из графика видно, что значение синуса и косинуса может меняться от -1 до +1. Значит, смещение х может быть равно –А и +А. Движение от –А до +А называют полным колебанием.

Построенный график четко показывает период и частоту колебаний. Стоить отметить, что фаза не воздействует на форму кривой, а только влияет на ее положение в заданный промежуток времени.

Источник

Характеристики колебаний

амплитуда,
период,
частота,
циклическая частота,
фаза,
начальная фаза.

Такие величины, как амплитуду и период, можно определить по графику колебаний.

Что такое амплитуда

Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.

Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.

К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_ <0>) обозначают амплитуду колебаний этой величины.

С помощью графика амплитуду можно определить так (рис. 2):

Что такое период

Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.

( large T left( c right) ) – период колебаний.

Период – это время одного полного колебания.

На графике период найти удобнее одним из таких способов (рис. 4):

Что такое частота

Обозначают ее с помощью греческой буквы «ню» ( large nu ).

Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».

Поэтому, размерность частоты — это единицы колебаний в секунду:

( large nu left( frac<1> right) ).

Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^ <-1>right) ), потому, что по свойствам степени ( large displaystyle frac<1> = c^ <-1>).

Одно колебание в секунду соответствует частоте в 1 Герц.

Что такое циклическая частота

( large displaystyle omega left( frac<text<рад>> right) )

Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).

Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».

Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:

Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.

Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.

Затем, воспользоваться формулой ( large displaystyle nu = frac<1> ) и вычислить частоту ( large nu ).

И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.

Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.

Что такое начальная фаза и как определить ее по графику колебаний

Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_ <0>).

(large varphi_ <0>left(text <рад>right) ) — начальная фаза, измеряется в радианах (или градусах).

Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рассмотрим теперь, как величина (large varphi_ <0>) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.

Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_ <0>) будет отличаться от нулевого значения.

Определим угол (large varphi_ <0>) с помощью графика колебаний.

Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_ <0>) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_ <0>).

Как вычислить начальный угол по интервалу смещения

Алгоритм нахождения начального угла состоит из нескольких несложных шагов.

Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.

[large T = 5 – 1 = 4 left( text <сек>right)]

Из графика следует, что период T = 4 сек.

Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac<Delta t >):

Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.

Для этого используем формулу:

(large displaystyle frac<1> <4>cdot 2pi = frac<pi > <2>=varphi_ <0>)

Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac<pi > <2>) – это начальная фаза для красной кривой на рисунке.

В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.

Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:

Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac<pi > <2>) имеет знак «плюс».

Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_ <0>= 0 ).

Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».

А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_ <0>) записываем со знаком «-».

Примечания:

Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
На графике колебаний начальная фаза ( varphi_<0>) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.