Для изучения зависимости электрических параметров соберём электрическую цепь, изображённую на схеме (рис.(1)).
Состав схемы (по часовой стрелке по ходу электрического тока):
- источник электрического напряжения (тока);
- электрический ключ для размыкания;
- последовательно подключённый амперметр для измерения силы тока в цепи;
- сопротивление (спираль никелиновой проволоки);
- вольтметр, подключённый параллельно к сопротивлению.

Рис. (1). Первая схема электрической цепи
При замыкании цепи отметим показания приборов. Используя регулятор напряжения на источнике, изменим напряжение в два раза. При этом показания вольтметра и амперметра также изменятся в два раза. Продолжим увеличивать напряжение на источнике. Наблюдения показывают, что при увеличении напряжения в (3) раза, вольтметр покажет увеличение напряжения на спирали в три раза. Во столько же раз увеличится и сила тока.
Опыт показывает зависимость изменения силы тока от приложенного напряжения.
Сила тока в проводнике прямо пропорциональна напряжению на концах проводника: (Ibacksim U).
Эту зависимость можно изобразить графически:
Рис. (2). График зависимости силы тока в проводнике от напряжения между концами этого проводника
При включении в электрическую цепь источника тока различных проводников и амперметров увидим, что для разных проводников показания амперметров различны, значит, сила тока для каждого проводника отличается.

Рис. (3). Электрическая схема с набором различных сопротивлений (AB), (CD), (EF)
Графики тоже будут отличаться.

Рис. (4). Графики зависимости силы тока от напряжения для сопротивлений (AB), (CD), (EF)
Вольтметр подключим поочерёдно к концам этих проводников. Увидим равные значения напряжения. Значение силы тока на участке цепи пропорционально разности потенциалов на его концах и зависит от рода вещества проводника. Отличие электрических параметров (U) и (I) связано с тем, что проводники имеют разное электрическое сопротивление.
Сопротивление проводника равно (1) Ом, если в проводнике при напряжении на концах (1) вольт протекает сила тока (1) ампер:
([R]=1) Ом;
(R=frac{U}{I});
Единицы измерения применяют с кратными приставками: миллиом (мОм), килоом (кОм), мегаом (МОм).
(1) мОм = (0,001) Ом;
(1) кОм = (1000) Ом;
(1) МОм = (1 000 000) Ом.
Почему существует сопротивление? Движению электронов под действием поля мешают ионы кристаллической решётки металла.
Электрический ток — направленное движение заряженных частиц.
В середине (XIX) века Джеймс Кларк Максвелл объединил исследования Вольта, Эрстеда, Ампера, Ома, Фарадея в классическую электродинамику. Учёные придерживались гипотезы, что электричество переносят положительные частицы. Все законы строились на этом предположении.
За направление электрического тока принимают движение положительно заряженных частиц.
(29) апреля (1897) года Джозеф Джон Томсон выступил на заседании Королевского общества с докладом о катодных лучах, что и считается датой открытия электрона.
Электронный ток — направленное движение электронов.
В металлах электрический ток переносится электронами. Положительные ионы, связанные узлами кристаллической решётки, перемещаться не могут. Электроны, перемещаясь между ионами, сталкиваются с ними, отскакивают обратно, что уменьшает общий поток электронов.
Электрическое сопротивление — физическая величина, отражающая свойство проводника препятствовать электронному току.
(R=frac{U}{I});
([R]=1~frac{В}{А}=1~Ом).
Чтобы узнать, как зависит сила тока в цепи от сопротивления, обратимся к опыту (рис.(4)).

Рис. (5). Электрическая цепь с аккумулятором
На рисунке изображена электрическая цепь, источником тока в которой является аккумулятор.
- Напряжение (2) В на концах резисторов постоянно. Это подтверждают показания вольтметра, подключенного параллельно к резистору.
- Используются три постоянных резистора сопротивлениями (1), (2) и (4) Ом, которые подключаются в цепь поочерёдно.
- Сила тока в цепи измеряется амперметром, который подключен последовательно с резистором.
Таблица (1). Результаты опыта
| Напряжение на концах проводника, В | Сопротивление проводника, Ом | Сила тока в цепи, А |
|
(2) |
(1) |
(2) |
|
(2) |
(2) |
(1) |
|
(2) |
(4) |
(0,5) |
По опытным данным (табл.(1)) прослеживается закономерность, которую обнаружил ещё в (1827) году Георг Ом.
Сила тока в проводнике обратно пропорциональна сопротивлению проводника: (Ibacksim frac{1}{R}).
В честь этого ученого открытый им закон называют его именем — закон Ома для участка цепи.
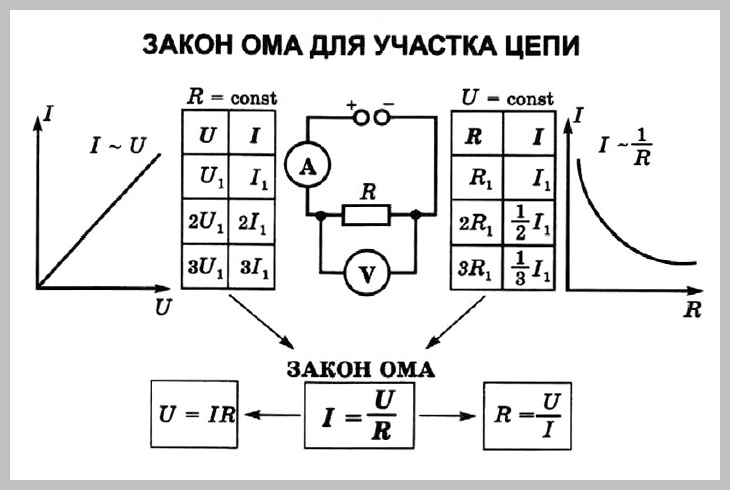
Сила тока на участке цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению участка цепи:
где I — сила тока, U — напряжение, R — сопротивление.
При изменяющемся сопротивлении и постоянном напряжении на участке зависимость силы тока от сопротивления будет гиперболической:

Рис. (6). График зависимости силы тока от сопротивления проводника
Определить сопротивление проводника можно несколькими способами:
1. при помощи амперметра и вольтметра;
2. при помощи омметра;
3. при помощи мультиметра, который эксплуатируется в режиме омметра.
Таблица (2). Способы измерения сопротивления
|
амперметр и вольтметр |
омметр |
мультиметр в режиме омметра |
|
Рис. 7. Амперметр и вольтметр |
Рис. 8. Омметр |
Рис. 9. Мультиметр |
|
|
|
|

Рис. 10. Обозначение омметра в цепи (или мультиметра в режиме измерения сопротивления)
Источники:
Рис. 2. График зависимости силы тока в проводнике от напряжения между концами этого проводника. © ЯКласс.
Рис. 4. Графики зависимости силы тока от напряжения для сопротивлений AB, CD, EF. © ЯКласс.
Рис. 6. График зависимости силы тока от сопротивления проводника. © ЯКласс.
Рис. 7. Старые советские измерительные приборы, Creative Commons Zero 1.0 License, https://openclipart.org/detail/205486/voltmeter-and-ammeter.
Рис. 8. Автор: Сергин Владимир Александрович – Собственный фотоснимок автора, Общественное достояние, https://commons.wikimedia.org/w/index.php?curid=4353228.
Рис. 9. Мультиметр. © ЯКласс.
Рис. 10. Указание авторства не требуется: 2021-06-07, бесплатно для коммерческого использования, https://clck.ru/VLDy3/.
Как определить сопротивление по графику зависимости силы тока от напряжения
Решение задач на уроках физики в 10-11 классах и при подготовке к ЕГЭ смотрите в следующих конспектах:
Задачи на Закон Ома.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
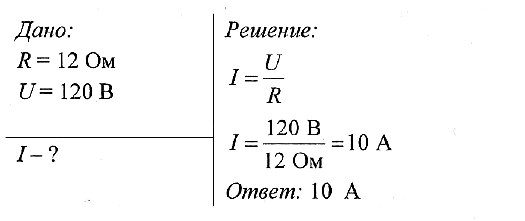
Задача № 1. Какова сила тока в резисторе, если его сопротивление 12 Ом, а напряжение на нем 120 В?
Задача № 2. Сопротивление проводника 6 Ом, а сила тока в нем 0,2 А. Определите напряжение на концах проводника.

Задача № 3. Определите сопротивление проводника, если при напряжении 110 В сила тока в нем 2 А.

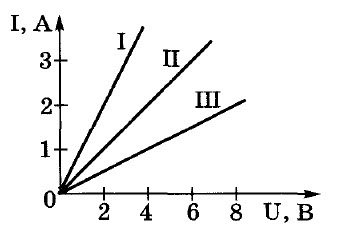
Задача № 4. По графикам зависимости силы тока от напряжения определите сопротивление каждого проводника.

Задача № 5. Чему равна сила тока в электрической лампе карманного фонаря, если сопротивление нити накала 16,6 Ом и лампа подключена к батарейке напряжением 2,5 В?

Задача № 6. Электрический утюг включен в сеть с напряжением 220 В. Какова сила тока в нагревательном элементе утюга, если сопротивление его равно 48,4 Ом?
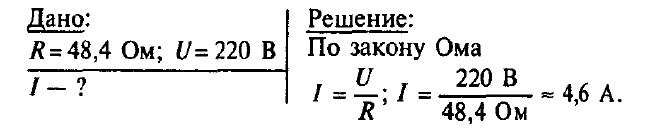
Задача № 7. При напряжении 110 В, подведенном к резистору, сила тока в нем равна 5 А. Какова будет сила тока в резисторе, если напряжение на нем увеличить на 10 В?
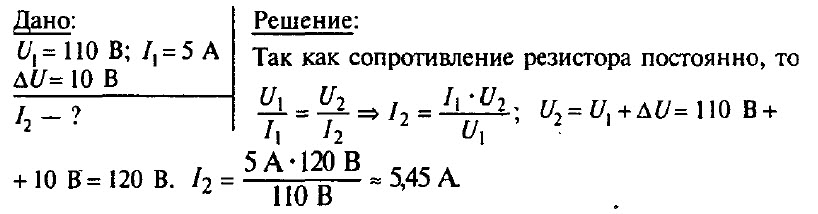
Задача № 8. Чему равно сопротивление спирали электрической лампы в рабочем состоянии, у которой на цоколе написано 6,3 В, 0,22 А?
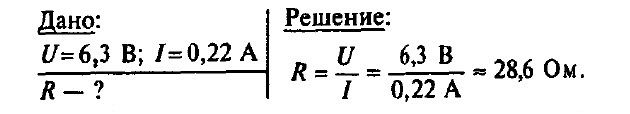
Задача № 9. Показание вольтметра, присоединенного к горящей электрической лампе накаливания, равно 120 В, а амперметра, измеряющего силу тока в лампе, 0,5 А. Чему равно сопротивление лампы? Начертите схему включения лампы, вольтметра и амперметра.

Задача № 10. ОГЭ Источник постоянного тока с ЭДС E = 12 В и внутренним сопротивлением г = 1 Ом замкнут на внешнее сопротивление R = 9 Ом. Определить силу тока в цепи I, падение напряжения UR на внешнем участке и падение напряжения Ur на внутреннем участке цепи.

Краткая теория для решения Задачи на Закон Ома.
Это конспект по теме «ЗАДАЧИ на Закон Ома». Выберите дальнейшие действия:
Источник
Задание 14 ЕГЭ по физике
Электричество. Закон сохранения электрического заряда,
закон Кулона, конденсатор, сила тока,
закон Ома для участка цепи, последовательное и параллельное соединение
проводников, работа и мощность тока,
В задании 14 проверяются знания по теме «Постоянный электрический ток». Это задание базовому уровня. Задачи носят, в основном, расчетный характер. Их решение основывается на знаниях законов и закономерностей постоянного электрического тока, умении «читать» электрические схемы, работать с графическими зависимостями.
1. На графике показана зависимость силы тока I в проводнике от времени t. Определите заряд, прошедший через проводник за Δt = 60 с с момента начала отсчёта времени.

Ответ: _____________________ Кл.
Используя зависимость силы тока от времени, электрический заряд можно определить как площадь геометрической фигуры под графиком. В данной задаче требуется рассчитать площадь трапеции Применяя геометрическую формулу площади трапеции и подставляя значения физических величин, получим (Кл).
Секрет решения. Подобный прием нахождения значения физической величины через площадь под графиком применяется во многих разделах физики: в «Механике», «МКТ и термодинамике», «Электродинамике». Здесь важно правильно выделить геометрическую фигуру, так как иногда требуется найти площадь не всей фигуры, а только ее части. Как всегда, в расчетах требует особого внимания система единиц (СИ). Пренебрежение одним из перечисленных моментов приведет к потере «легкого» балла.
2. Пять одинаковых резисторов с сопротивлением 3 Ом соединены в электрическую цепь, через которую течёт ток I (см. рисунок). Идеальный вольтметр показывает напряжение 9 В. Чему равна сила тока I?

Ответ: __________________________ А.
Резисторы, подключенные к вольтметру, соединены между собой последовательно. Отсюда следует, что сумма напряжений на каждом резисторе равна значению напряжения, которое показывает вольтметр. Запишем это в виде формулы Используя закон Ома, выразим значения напряжений и
Здесь учтено, что в указанной точке (см. схему) ток I разделяется на две равные части из-за равенства сопротивлений в разветвленных частях цепи.

Деление силы тока на две равные части
Подставляя численные значения, получим
Секреты решения. В задачах со схемами необходимо уметь выделять виды соединения проводников. После этого можно использовать известные закономерности для силы тока, напряжения и сопротивления. Ввиду того, что в задачах может быть большое количество проводников, решение в общем виде бывает громоздким, что может привести к математической ошибке. Поэтому лучше подставлять численные значения на ранних этапах решения.
3. На плавком предохранителе счётчика электроэнергии указано: «15 А, 380 В». Какова максимальная суммарная мощность электрических приборов, которые можно одновременно включать в сеть, чтобы предохранитель не расплавился?
Формулы для расчета мощности электрического тока имеют вид:
В зависимости от условия задачи, надо применять ту или иную формулу. Так как в задаче дается сила тока и напряжения, необходимо воспользоваться формулой
Подставляя численные значения, проведем расчет:
Секреты решения.
Формулы для расчета мощности лучше изучать как следствия формул для расчета работы тока или количества теплоты, выделяющейся в проводнике с током.
При делении этих формул на время t получим формулы для расчета мощности.
Источник
Зависимость силы тока от напряжения — формула, график и законы
Фундаментальной связью в электричестве является зависимость силы тока от напряжения. Благодаря этому закону, экспериментально установленном Омом в 1826 году, созданы различные измерительные приборы. Удалось исследовать физику короткого замыкания. Формулу можно применять для систем, которые зависят от электросопротивления. Пожалуй, разработка любой электрической сети невозможна без использования этого открытия.

Общие сведения
Любое физическое тело состоит из молекул и атомов. Эти частицы взаимодействуют между собой. Они могут притягиваться друг к другу или отталкиваться. В изолированной системе элементарные частицы являются носителями заряда. В спокойном состоянии, то есть когда на тело не оказывается внешнего воздействия, алгебраическая сумма энергии частиц всегда постоянная величина. Это утверждение называется законом сохранения электрического заряда.

Частицы хаотично могут перемещаться по кристаллической решётке, но их движение компенсируется. Поэтому ток не возникает. Но если к телу приложить внешнюю силу, то свободные электроны начинают двигаться в одну сторону. Это упорядоченное движение заряженных частиц и называют электрическим током. Количественно его можно описать через силу.
Упорядочено заряды заставляет двигаться электрическое поле, вдоль линий которого и происходит перемещение. Впервые этот термин ввёл Фарадей. Он сумел выяснить, что вокруг любого носителя существует особый вид материи, влияющий на поведение других частиц. За силовую характеристику электрического поля было взято отношение действующей силы к величине заряда, помещённого в данную точку: E = F / q. Назвали эту характеристику напряжённостью.
Изучение поля позволило экспериментально открыть принцип суперпозиции. То есть установить, что напряжённость поля, созданного системой зарядов, равна геометрической сумме величин, существующих у отдельных носителей: E = Σ E1 + E2 +…+ En. Напряжённость прямо пропорциональна напряжению, которое, в свою очередь, равняется разности потенциалов между двумя точками.
По сути, это работа электрического поля, совершаемая для переноса единичного заряда из одного места в другое: U = A / q = E * d, где d – расстояние между точками. Значение напряжения зависит от нескольких факторов:
- строения тела;
- температуры;
- сопротивления.
Самое большее влияние оказывает последняя величина. Именно она характеризует способность материала препятствовать прохождению тока, то есть определяет проводимость. Сопротивление зависит от длины проводника и его сечения: R = (p * l) / S, где p – параметр обратный удельной проводимости (справочное значение). Он численно равняется сопротивляемости однородного проводника единичной длины и площади сечения.
Подтверждение закона Ома
Бум исследования электрических явлений пришёлся на конец XVIII – начало XIX веков. Такие учёные, как Фарадей, Ампер, Вольт, Эрстед, Кулон, Лачинов, Ом провели ряд экспериментов, которые позволили Максвеллу создать теорию электромагнитных явлений.

Огромную роль в открытии новых знаний сыграл опыт Ома исследовавшего, от чего зависит сила тока в цепи. Немецкий физик ставил опыты над проводимостью различных материалов. Для этого он использовал электрическую цепь, в разрыв которой подключал проводники разной длины и замерял силу тока.
Изначально учёный не смог установить закономерность. Всё дело в том, что для своих опытов Ом использовал химическую батарею. Друг учёного Поггендорф предложил взять термоэлектрический источник тока. В итоге физик смог проследить зависимость. Описал он её так: частное от a, разделённого на l + b, где b определяет интенсивность воздействия на проводника длиною l, причём a и b — постоянные, зависящие соответственно от действующей силы и сопротивления элементов цепи.
Обычно при изучении закона в седьмом классе средней школы учитель демонстрирует эту зависимость на практических уроках. Для этого чтобы ученики удостоверились в справедливости утверждения, преподаватель собирает электрическую цепь, в состав которой входят:
- вольтметр – прибор для измерения напряжения, включается параллельно измеряемому проводнику;
- амперметр – устройство для замера тока, подключается последовательно с измеряемым телом;
- регулируемый источник электродвижущей силы (ЭДС).
Суть опыта заключается в подключении проводников с разной длиной. Измеренные результаты заносят в таблицу. Она должна иметь примерно следующий вид:
| Первое тело | Второе тело | Третье тело | |||
| U, В | I, А | U, В | I, А | U, В | I, А |
| 1 | 0,5 | 1 | 0,4 | 1 | 0,2 |
| 2 | 1 | 2 | 0,6 | 2 | 0,3 |
| 3 | 1,5 | 3 | 0,8 | 3 | 0,4 |
| 4 | 2 | 4 | 1 | 4 | 0,5 |
Проведя анализ таблицы, можно сделать вывод. Если для любого тела напряжение разделить на соответствующую ему силу тока, то получится одно и то же число. Следовательно, это отношение является свойством проводника. Для первого оно равно двум, второго – пяти, а третьего – десяти. При одинаковых токах в третьем случае число больше, значит, это тело оказывает большее сопротивление току.
Полученные значения по факту и являются величинами, обратными проводимости. Обозначают их буквой R (resistance).
График зависимости
По результатам эксперимента Ом построил график зависимости силы тока от сопротивления, который напоминает собой левую часть параболы. Современная запись закона Ома имеет вид: I = U / R. Звучит она следующим образом: ток прямо пропорционален напряжению и обратно пропорционален электрическому сопротивлению.
Но при разработке приборов или исследовании участка цепи перед учёными и инженерами стоит задача, прежде всего, выяснить зависимость тока от напряжения. Поэтому ими строится график, в котором по оси абсцисс откладывают значение потенциала, а ординат — силы тока. В итоге если отложить соответствующие точки, то должна получиться прямая линия. Это говорит о том, что зависимость величин линейная. То есть во сколько раз увеличивается напряжение, во столько же возрастает сила тока.

Такого вида график называется вольт-амперной характеристикой (ВАХ). Но при реальных измерениях изменение ток зависит ещё от температуры. Установлено, что при нагреве сопротивление проводника увеличивается. Поэтому прямая на ВАХ будет иметь меньший угол наклона. Кроме того, ток может быть двух видов:
- постоянный – сила не изменяется от времени;
- переменный – изменяющийся по синусоидальному закону.
Поток носителей заряда для второго вида описывается гармоническим законом: I(t) = Im * cos (wt + f), где: w – циклическая частота, f – сдвиг фаз относительно напряжения, Im – наибольшее значение тока. Тогда изменение напряжения во времени можно записать так: U(t) = Um * cos (wt). В этом случае закон Ома примет вид: I = U / Z, где Z – полное сопротивление цепи.

График зависимости силы тока от времени, впрочем, как и напряжения, будет представлять собой синусоиду. Если отложить их на одном рисунке, то при активном сопротивлении (резистор) фазы величин будут совпадать друг с другом. В схеме, содержащей реактивные составляющие, а это ёмкость, и индуктивность, фаза тока соответственно будет опережать и отставать от напряжения. Угол изменения составит девяносто градусов.
Графики зависимости позволяют определить мощность. Сделать это можно, воспользовавшись формулой: P = U * I * cos(f). Чтобы построить график мощности, нужно аппроксимировать на ось t точки синусоиды I(t) и U(t), в которых параметры изменяют свой знак.
Характеристика P(t) будет также описываться по гармоническому закону. Причём в каждой этой точке линя изменит направление.
Простейшие задачи
Зависимость, установленную экспериментальным путём, широко используют при проектировании электронных схем различных устройств. С помощью закона Ома рассчитывают нужное сопротивление резисторов для той или иной цепи, вычисляют значение тока при определённом напряжении.
Вот некоторые из таких заданий:


Следует отметить, что в школьных задачах не учитываются характеристики источника тока.
По умолчанию считают, что он имеет бесконечно малое внутреннее сопротивление. Но на самом деле это не так. Электродвижущая сила генератора электрической энергии затрачивается как на внутренние, так и внешние потери. Поэтому формула закона Ома для полной цепи имеет вид: I = (U0 + U) / R + r, где: U0 – внутреннее падение напряжения, r0 – сопротивление источника.
Источник
Используя график зависимости тока от напряжения (рис. 104), найдите сопротивление.
Для решения задачи применяем формулу закона Ома.
Ответ: сопротивление 2 Ом.
Похожие записи:
При напряжении на концах проводника 2 В сила тока в проводнике 0,5 А. Какой будет сила тока в провод…
Электронная теория утверждает, что в металлических проводниках свободно передвигаться могут только э…
Как можно проверить правильность показаний амперметра с помощью другого амперметра, точность показан…
Укажите ошибку на схеме рисунка 98.
На
прошлых уроках мы с вами познакомились с понятиями «сила электрического тока» и
«напряжение». Давайте вспомним, что силой тока называется физическая
величина, численно равная электрическому заряду, протекающему через поперечное
сечение проводника за единицу времени.
Напряжение
— это физическая величина, характеризующая работоспособность электрического
поля.
Таким
образом, сила тока и напряжение характеризуют
электрический ток и его действия. Значит, сила тока должна каким-то образом
зависеть от напряжения. Давайте установим эту зависимость. Для чего
воспользуемся установкой, представленной на рисунке.
В качестве потребителя тока в цепи используется резистор — это металлический проводник в виде спирали. Параллельно резистору подключён вольтметр, измеряющий напряжение
на этом участке цепи. Остальная часть цепи состоит из источника тока, ключа и
амперметра. В качестве источника тока будем использовать устройство, которое
позволяет регулировать напряжение на концах проводника.
Будем
изменять напряжение на резисторе и следить за соответствующими изменениями силы
тока в цепи, а все измерения заносить в таблицу:
Уже из этих данных следует, что сила тока в проводнике прямо
пропорциональна напряжению на проводнике: I ~ U.
Подключим
теперь к источнику тока другую спираль, например, спираль осветительной лампы и
повторим опыт.
Как
видим, при тех же значениях напряжения, что и в первом случае, мы получили
другие значения силы тока. Однако и в этом проводнике сила тока прямо
пропорциональна напряжению.
Наблюдаемую
нами зависимость силы тока в проводнике от напряжения между концами этого
проводника можно изобразить графически. На таком графике в условно выбранном
масштабе по оси абсцисс откладывается напряжение, а по оси ординат — сила тока.
Такой
график в физике называют вольт-амперной характеристикой проводника.
Теперь,
по результатам проведённых опытов, вычислим отношение напряжения к силе тока
для каждого из измерений:
Как
видим, оно постоянно для каждого из проводников, но имеет разное значение для разных
проводников.
Следовательно,
существует физическая величина, характеризующая свойства проводника, по
которому течёт электрический ток. Эту величину называют электрическим
сопротивлением проводника или просто сопротивлением. Обозначают
сопротивление латинской буквой R.
За единицу сопротивления принимают ом. Она
получила своё название в честь немецкого учёного Г. Ома, открывшего основной закон электрической
цепи.
1
Ом — это сопротивление проводника, в котором при напряжении 1 В проходит ток
силой 1 А.
Это
небольшое сопротивление. У спиралей обычных электроламп оно составляет сотни
ом, поэтому сопротивление часто выражают в кратных единицах:
Попытаемся
теперь объяснить, почему проводник обладает электрическим сопротивлением.
Вспомните, что электрический ток в металлах представляет собой направленное
движение свободных электронов. Движущиеся под действием электрического поля
электроны взаимодействуют с атомами и ионами кристаллической решётки металла. Следовательно,
атомы и ионы препятствуют движению электронов, то есть оказывают
сопротивление их движению. Это ведёт к уменьшению скорости направленного
движения электронов, а значит, и силы тока в проводнике.
Электрическое
сопротивление можно сравнить с трением, которое всегда препятствует движению.
Как мы знаем, любое тело быстрее скатится с гладкой поверхности, чем с
шершавой.
Подобно
этому, электроны в плохом проводнике двигаются медленнее, чем в хорошем. В диэлектриках,
электрическое сопротивление бесконечно большое, поэтому они и не проводят ток.
Таким
образом, новая величина — сопротивление — отражает противодействие среды
движению в ней свободных носителей заряда. В соединительных проводах это
противодействие, как правило, незначительно, что позволяет сопротивлением
соединительных проводов при решении большинства задач пренебречь.
Определённым
сопротивлением обладают и измерительные приборы. При включении последовательно
в цепь амперметра его сопротивление добавляется к полному сопротивлению цепи.
Это вызывает нежелательное уменьшение силы тока. Чтобы этого не случилось,
сопротивление амперметра должно быть мало́. Идеальным был бы амперметр без
сопротивления. Именно таким мы и будем считать сопротивление амперметра в
задачах.
Наоборот,
добавление вольтметра параллельно некоторому прибору создаёт току ещё один
«обходной» путь, что также резко изменяет параметры цепи. Чтобы избежать этих
нежелательных последствий, надо применять вольтметры с максимально больши́м
сопротивлением.
И
ещё об очень важном. При слишком малом сопротивлении цепи сила тока в ней может
принять недопустимо большое значение. При замыкании цепи, представленной на
рисунке, ток в ней пройдёт, фактически не испытывая сопротивления. Это — короткое
замыкание.
В
таком режиме могут быть испорчены и прибор, и источник тока, а перегрев
проводов может привести к пожару.
Пример
решения задачи.
Задача. Когда
напряжение увеличили на 3 В, сила тока в цепи возросла вдвое, и ток за 1 с
совершил работу 3 Дж. Найдите значения силы тока после увеличения напряжения.
Закон Ома назван в честь своего открывателя это ученый Георг Симон Ом. Свои эксперименты в области электричества он начал вдохновляясь опытами Фурье. Ом проводил свои опыты с различными материалами и изучение их электропроводности. Так была разработана знаменитая формула, которая стала краеугольной в современной физике, которая вошла в школьные учебники: I=U/R. Сила тока пропорциональна величине напряжения и имеет обратную пропорциональность сопротивлению.
В статье подробно разобраны области теории и практического применения принципов закона Ома в современной электротехнике. В качестве дополнения, в материале содержатся два обучающих видеоролика и один научный материал на тему статьи.
Закон Ома
Закон Ома показывает отношения между напряжением (U), током (I) и сопротивлением (R). Записано это может быть тремя разными способами:
U = I × R
или
I = V/R
или
R = V/I
Где:
- V – напряжение в вольтах (В);
- I – сила тока в амперах (А);
- R – сопротивление в омах (Ом);
Для большинства схем амперы – слишком большие величины, а омы – слишком маленькие. Поэтому в формулу можно подставлять миллиамперы и килоомы. Если силу тока подставлять в миллиамперах (мА), то сопротивление обязательно должно быть в килоомах (кОм) и наоборот. Напряжение – всегда в вольтах.
Чтобы проще запомнить три разные версии определения Закона Ома, можно воспользоваться «VIR-треугольником».
- Если надо вычислить напряжение, закрываем пальцем V. У нас остаются I и R. Они на одном уровне, значит между ними ставим знак умножения. Получается: V = I × R .
- Если вычисляем ток, закрываем пальцем I. У нас остаётся V над R. Значит напряжение делится на сопротивление: I = V/R .
- Аналогичным образом поступаем при вычислении сопротивления. Закрываем R. Остаётся V над I. Значит: R = V/I .
Закон Ома, определение: Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Есть также частный случай – Закон Ома для участка цепи – сила тока в участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению этого участка.
Закон Ома для цепи
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
φ1-φ2=I*R, где
- I – ток, протекающий по участку цепи.
- R – сопротивление этого участка.
- φ1-φ2 – разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:
Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Для полной цепи
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Для переменного тока
Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).
Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.
Для замкнутой цепи
На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.
Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.
Формула для расчета падения напряжения на индуктивном сопротивлении:
U = I ⋅ ωL
Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).
Формула для расчета падения напряжения на емкостном сопротивлении:
U = I / ω ⋅ С
С – емкость реактивного сопротивления.
Эти две формулы – частные случаи закона Ома для переменных цепей.
Полный же будет выглядеть следующем образом:
I = U / Z
Здесь Z – полное сопротивление переменной цепи известное как импеданс.
Сфера применения
Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:
- Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
- В сверхпроводниках;
- Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
- В вакуумных и газовых радиолампах;
- В диодах и транзисторах.
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I1= I2 ;
- U = U1+ U2 ;
- R = R1+ R2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I1+ I2 … ;
- U = U1= U2 … ;
- 1 / R = 1 / R1+ 1 / R2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.



