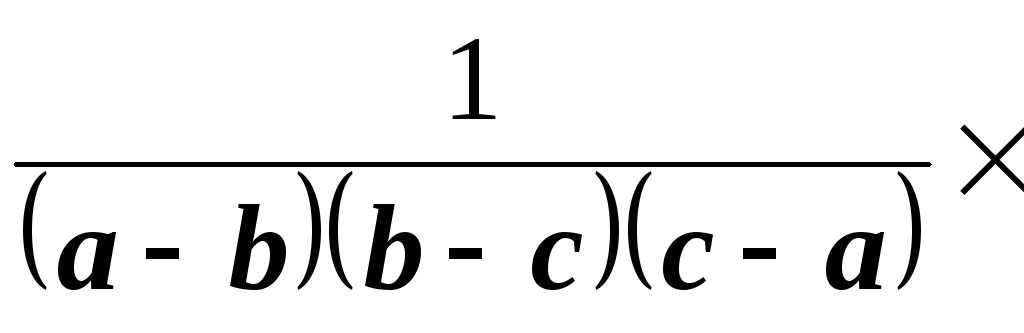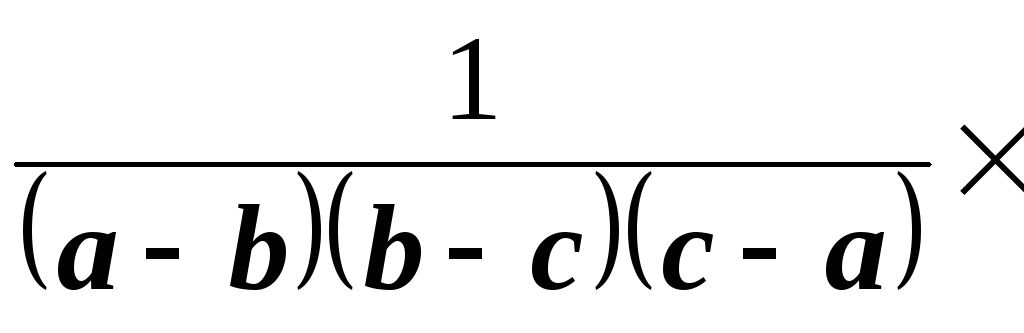Рассмотрим
простейшие приемы нахождения оригинала
по известному изображению. Один из них
основан на использовании таблицы
изображений, которая в этом случае
рассматривается в обратном порядке, и
правил операционного исчисления. В
первую очередь это относится к теореме
смещения, интегрированию и дифференцированию
изображения и изображению свертки
функций.
Пример
12.
Найти оригинал f(t),
если
.
Решение.
Исходным можно взять соответствие
.
Операции
смещения на а
в области изображений соответствует
операция домножения на
в области оригиналов. Поэтому при а=1
имеем
.
Операции
домножения на
в области изображений соответствует
запаздывание на =2
в области оригиналов. Следовательно,
Пример
13.
Найти оригинал изображения
.
Решение.
Выделим в знаменателе полный квадрат
.
Воспользуемся
равенством
,
а также теоремой смещения. В результате
получим
.
Пример
14.
Найти оригинал, соответствующий
изображению
.
Решение.
Можно поступить так: за исходное взять
соотношение
.
Затем
воспользуемся тем, что делению на р
в области изображений соответствует
операция интегрирования в области
оригиналов:
.
Это же свойство
применим повторно:
.
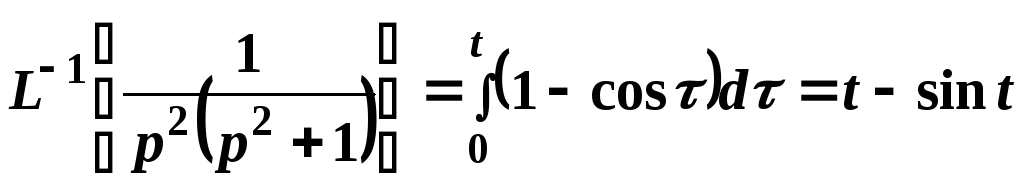Заметим,
что оригинал указанного изображения
проще можно было бы найти, если разложить
его на простейшие дроби:
.
Согласно
свойству линейности имеем
.
Пример
15.
Найти оригинал изображения
.
Решение.
Представим изображение в виде
.
Произведению
изображений
и
соответствует свертка их оригиналов
и
.
Поэтому
.
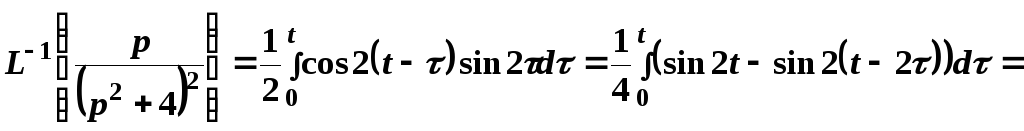
Для
этого изображения оригинал можно найти
проще, если воспользоваться тем, что
операции дифференцирования в области
изображений соответствует операция
домножения на (-t)
в области оригиналов. Поэтому
.
Очень
часто при решении практических задач
возникает необходимость нахождения
оригиналов изображений, которые
представляются в виде дробно рациональной
функции
,
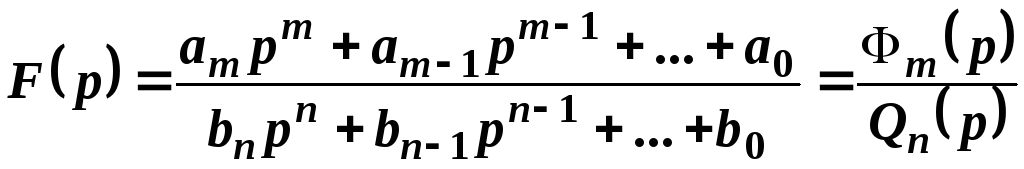в
которой старшая степень числителя
меньше старшей степени знаменателя
переменной р.
При
нахождении оригинала такой дроби
разлагают ее на сумму простых дробей с
помощью метода неопределенных
коэффициентов, известного из интегрального
исчисления. Затем находят оригиналы
для каждой простой дроби.
Пример
16.
Найти оригинал, соответствующий
изображению
.
Решение.
Разложим данную дробь на сумму простейших
дробей. Для этого, прежде всего, найдем
корни знаменателя, решив уравнение
.
Проверкой убеждаемся, что
один из его корней. Разделим кубический
многочлен
на двучлен р+1.
В частном получим
.
Дискриминант этого трехчлена –
отрицательный, на действительные
множители он не разлагается. Разложение
данного изображения на простейшие дроби
имеет вид:
.
Отсюда
.
Полагая
в этом равенстве
,
находим
.
Затем приравниваем коэффициенты при
одинаковых степенях р:
,
.
Таким
образом,
.
В
знаменателе второй дроби выделим полный
квадрат, а в числителе – двучлен
:
.
Используя
свойство линейности , переходим в область
оригиналов. Получим
.
Заметим,
что в данном случае, прежде чем приступать
к разложению изображения на простейшие
дроби, было бы полезно воспользоваться
теоремой смещения. Для этого в исходном
изображении выделим двучлен
:
.
Тогда
.
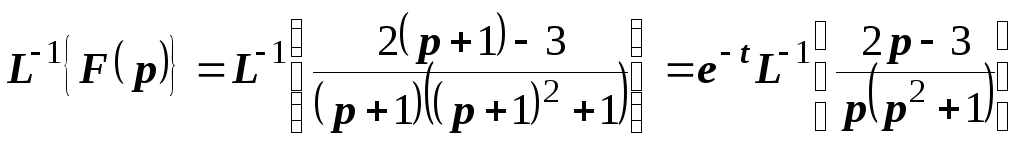Разложение
полученного изображения на простейшие
дроби проще, чем исходного:
;
; 
; 
.
Оригиналом
будет функция
или
.
Задача
нахождения оригиналов, соответствующих
дробно-рациональным изображениям
упрощается, если воспользоваться
следующей краткой таблицей (табл. 3).
Таблица 3 –
Изображение – оригинал
|
№ |
Изображение |
Оригинал |
|||
|
1 |
2 |
3 |
|||
|
1 |
|
|
|||
|
2 |
|
|
|||
|
3 |
|
|
|||
|
4 |
|
|
|||
|
5 |
|
|
|||
|
6 |
|
|
|||
|
7 |
|
|
|||
|
8 |
|
|
|||
|
9 |
|
|
|||
|
1
0 |
|
|
Продолжение табл.
3
|
1 |
2 |
3 |
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Примеры решений задач по операционному исчислению (преобразованию Лапласа)
Операционное (символическое) исчисление – это один из методов математического анализа, позволяющий в
некоторых случаях свести исследование и решение дифференциальных, псевдодифференциальных, интегральных уравнений, к более простым алгебраическим задачам.
Изучая преобразование Лапласа, мы вводим оригинал функции $f(t)$ и ее изображение $F(p)$, находимое по формуле:
$$F(p) = int_0^infty f(t) e^{-pt}dt$$
Для быстроты и удобства решения задач составлена таблица изображений и оригиналов, которая, наряду с теоремами (линейности, подобия, смещения, запаздывания), свойствами и правилами дифференцирования и интегрирования изображения/оригинала, постоянно используется в решении примеров.
В этом разделе вы найдете готовые задания разного типа: восстановление оригинала или изображения функции, нахождение свертки функций, решение ДУ, систем ДУ или интегральных уравнений с помощью преобразования Лапласа и т.д.
Полезная страница? Сохрани или расскажи друзьям
Как найти изображение функции
Задача 1. Найти изображение данного оригинала, или оригинала, удовлетворяющего данному уравнению
$$f(t)=frac{e^{2t}-e^{-3t}}{t}.$$
Задача 2. Пользуясь определением, найти изображение функции $f(t)=3^t$.
Задача 3. Найти изображение функции: $int_0^t cos tau cdot e^{-3tau}dtau. $
Задача 4. Найти изображение оригинала $f(x)$ двумя способами:
1) Вычислив интеграл $F(p) = int_0^infty f(x) e^{-px}dx$;
2) Воспользовавшись таблице изображений и свойствами преобразования Лапласа.
Оригинал задается формулой (курсочно-линейная функция, см. файл).
Как найти оригинал функции
Задача 5. Найти оригинал изображения $F(p)$, где
$$F(p)=frac{2p-1}{(p^2-4p+13)^2}.$$
Задача 6. Найти оригинал изображения
$$F(p)=frac{15p^2+3p+34}{(p^2+4p+8)(p^2-6p+5)}.$$
Задача 7. Найти оригинал для функции с помощью вычетов
$$F^*(p)=frac{1}{e^{4p}-625}.$$
Как решить ДУ (систему ДУ) операционным методом
Задача 8. Найти частное решение дифференциального уравнения с заданными начальными условиями операторным методом
$$x’+x=4e^t, x(0)=2.$$
Задача 9. Найти решение задачи Коши методами операционного исчисления
$$x”+2x’+2x=te^{-t}, quad x(0)=0, x'(0)=0.$$
Задача 10. Методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.
$$x’=x-y,\
y’=x+y,\
x(0)=2, y(0)=1.$$
Задача 11. Методом операционного исчисления найти решение задачи Коши для ДУ 3-го порядка
$$x”’+x”-2x’-5x=5e^t, quad x(0)=0, x'(0)=1, x”(0)=2.$$
Задача 12. Решите задачу Коши для системы дифференциальных уравнений с помощью преобразования Лапласа.
$$frac{dx}{dt}=x-2y,\
frac{dy}{dt}=x+3y,\
x(0)=0, y(0)=1. $$
Задача 13. C помощью формулы Дюамеля найти решение уравнения
$$x”’+x’=tg t, quad x(0)=x'(0)=x”(0)=0.$$
Задача 14. Решить систему ДУ с помощью преобразования Лапласа
$$
x’=-y+z,\
y’=z, quad x(0)=1, \
z’=-x+z;\
y(0)=z(0)=1/2.
$$
Как решить интегральное уравнение
Задача 15. Методом операционного исчисления найти решение интегрального уравнения
$$ y(t)=cos t +int_0^t (t-tau)^2 y(tau)d tau. $$
Задача 16. Решить интегральное уравнение
$$ int_0^t ch (tau) x(t-tau)d tau = t. $$
Как найти свертку функций
Задача 17. Найти свертку функций $f(t)=1$ и $phi(t)=sin 5t$.
Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей, оформление производится в Word, срок от 1 дня.
Подробнее о решении заданий с преобразованием Лапласа
Дополнительная информация
- Онлайн-помощь по математическому анализу
- Дифференциальные уравнения – задачи с решениями
- Как решать ДУ с помощью операционного исчисления
Содержание
Отыскание оригинала по изображению
Рассмотрим два способа для нахождения оригинала по заданному изображению:
-
Разложение изображения на сумму элементарных дробей, оригиналы для которых можно найти по таблице.
-
Применение теорем разложения.
Разложение $F(p)$ на сумму элементарных дробей и применение основных теорем операционного исчисления
Пример 1.
Найти оригинал $f(t)$ для заданного изображения $F(p)$.
begin{equation*}
begin{split}
F(p)&=displaystylefrac{1}{p(p-1)(p^2+4)}= \
&=-frac{1}{4p}+frac{1}{5(p-1)}+frac{p-4}{20(p^2+4)}=\
&=-frac{1}{4p}+frac{1}{5(p-1)}+frac{p}{20(p^2+4)}-frac{1}{10}frac{2}{(p^2+4)}\
&\
f(t)&=-frac14+frac15e^t+frac{1}{20}mbox{cos},2t-frac{1}{10}mbox{sin},2t.
end{split}
end{equation*}
Пример 2.
Найти оригинал $f(t)$ для заданного изображения $F(p)$.
begin{equation*}
F(p)=displaystylefrac{1}{p^3-8}.
end{equation*}
begin{equation*}
begin{split}
F(p)&=displaystylefrac{1}{p^3-8}= \
&=frac{1}{12(p-2)}-frac{p+4}{12(p^2+2p+4)}=\
&=frac{1}{12(p-2)}-frac{p+4}{12((p+1)^2+3^2)}=\
&=frac{1}{12(p-2)}-frac{1}{12}cdotfrac{p+1}{(p+1)^2+(sqrt{3})^2}-frac{sqrt{3}}{12}cdotfrac{sqrt{3}}{(p+1)^2+(sqrt{3})^2}.\
&\
f(t)&=frac{1}{12}e^{2t}-frac{1}{12}e^{-t}(mbox{cos},tsqrt{3}+sqrt{3},mbox{sin},tsqrt{3}).
end{split}
end{equation*}
Пример 3.
Найти оригинал $f(t)$ для заданного изображения $F(p)$.
begin{equation*}
begin{split}
F(p)&=displaystylefrac{1}{p+2p^2+p^3}=displaystylefrac{1}{p(p+1)^2}.
end{split}
end{equation*}
Можно разложить на сумму элементарных дробей, а можно использовать теорему об интегрировании оригинала. Воспользуемся теоремой:
begin{equation*}
t,e^{-t}risingdotseq frac{1}{p^2+1},, Rightarrow ,, intlimits_0^ttau,e^{-tau},dtaurisingdotseq frac{1}{p (p+1)^2}.
end{equation*}
Вычислим интеграл и запишем оригинал $f(t)$:
begin{equation*}
intlimits_0^ttau,e^{-tau},dtau = -(t+1)e^{-t}+1 ,, Rightarrow ,,
end{equation*}
begin{equation*}
displaystylefrac{1}{p(p+1)^2} risingdotseq -(t+1)e^{-t}+1.
end{equation*}
Пример 4.
Найти оригинал $f(t)$ для заданного изображения $F(p)$.
begin{equation*}
F(p)=displaystylefrac{e^{-p}}{p+1}.
end{equation*}
Воспользуемся теоремой запаздывания.
begin{equation*}
frac{1}{p+1} risingdotseq e^{-t},, Rightarrow ,,
end{equation*}
begin{equation*}
frac{e^{-p}}{p+1}=frac{e^{-1cdot p}}{p+1} risingdotseq e^{-(t-1)}cdoteta(t-1).
end{equation*}
Применение теорем разложения
Первая теорема разложения
Пусть $F(p)$ — аналитическая в окрестности $z=infty$ функция и в этой окрестности раскладывается в ряд Лорана:
begin{equation*}
F(p)=sumlimits_{k=1}^{infty}displaystylefrac{c_k}{p^k}.
end{equation*}
Тогда
begin{equation*}
F(p)risingdotseq f(t)=sumlimits_{k=1}^{infty}displaystylefrac{c_k}{(k-1)!}t^{k-1}.
end{equation*}
Вторая теорема разложения
Пусть $F(p)$ — дробно-рациональная функция и $p_1, ldots p_n$ — ее полюсы (простые или кратные).
Тогда
begin{equation*}
F(p)risingdotseq f(t)=sumlimits_{k=1}^{n}mbox{res}left(F(p_k)e^{p_kt}right).
end{equation*}
Пример 5.
Найти оригинал $f(t)$ для заданного изображения $F(p)$.
begin{equation*}
F(p)=displaystylefrac{p}{(p+1)(p+2)(p+3)(p+4)}
end{equation*}
Обозначим
$$H(p)=F(p)e^{pt}.$$
Все особые точки $H(p)$ — простые полюсы:
$$p_1=-1,,, p_2=-2,,, p_3=-3,,, p_4=-4.$$
begin{equation*}
begin{split}
mbox{res}left(H(p_1)right)&=-frac16e^{-t}, \
mbox{res}left(H(p_2)right)&=e^{-2t}, \
mbox{res}left(H(p_3)right)&=-frac32e^{-3t}, \
mbox{res}left(H(p_4)right)&=frac23e^{-4t}.
end{split}
end{equation*}
Тогда по второй теореме разложения получаем:
begin{equation*}
f(t)=-frac16e^{-t}+e^{-2t}-frac32e^{-3t}+frac23e^{-4t}.
end{equation*}
Пример 6.
Найти оригинал $f(t)$ для заданного изображения $F(p)$.
begin{equation*}
F(p)=displaystylefrac{1}{(p-a)(p-b)^2}
end{equation*}
По второй теореме разложения:
begin{equation*}
f(t)=frac{te^{bt}}{b-a}-frac{e^{bt}}{(b-a)^2}+frac{e^{at}}{(b-a)^2}.
end{equation*}
Пример 7.
Найти оригинал $f(t)$ для заданного изображения $F(p)$.
begin{equation*}
F(p)=displaystylefrac{p^3}{(p^2+1)^2}
end{equation*}
Обозначим
$$H(p)=F(p)e^{pt}.$$
Особые точки $H(p)$ — полюсы второго порядка:
$$p_1=i,,, p_2=-i.$$
begin{equation*}
begin{split}
mbox{res}left(H(p_1right))&=frac{e^{it}(2+it)}{4}, \
mbox{res}left(H(p_2right))&=frac{e^{-it}(2-it)}{4}.
end{split}
end{equation*}
Тогда по второй теореме разложения:
begin{equation*}
f(t)=frac14left(2e^{it}+2e^{-it}+i,te^{it}-i,te^{-it}right)=mbox{cos},t-frac12,t,mbox{sin},t.
end{equation*}
Пример 8.
Найти оригинал $f(t)$ для заданного изображения $F(p)$.
begin{equation*}
F(p)=displaystylefrac{p}{p^2+1}.
end{equation*}
Разложим $F(p)$ в ряд Лорана в окрестности $z=infty$:
begin{equation*}
F(p)=frac{p}{p^2}sumlimits_{n=0}^{infty}displaystylefrac{(-1)^n}{p^{2n}}=sumlimits_{n=0}^{infty}displaystylefrac{(-1)^n}{p^{2n+1}}.
end{equation*}
И по первой теореме разложения получим:
begin{equation*}
f(t)=sumlimits_{n=0}^{infty}displaystylefrac{(-1)^nt^{2n}}{(2n)!}=mbox{cos},t.
end{equation*}
Пример 9.
Найти оригинал $f(t)$ для заданного изображения $F(p)$.
begin{equation*}
F(p)=displaystylefrac{1}{p^2}mbox{cos}displaystylefrac{1}{p}.
end{equation*}
Разложим $F(p)$ в ряд Лорана в окрестности $z=infty$:
begin{equation*}
F(p)=frac{1}{p^2}sumlimits_{n=0}^{infty}displaystylefrac{(-1)^n}{(2n)!p^{2n}}=sumlimits_{n=0}^{infty}displaystylefrac{(-1)^n}{(2n)!p^{2n+2}}.
end{equation*}
По первой теореме разложения:
begin{equation*}
f(t)=sumlimits_{n=0}^{infty}displaystylefrac{(-1)^n}{(2n)!(2n+1)!}t^{2n+1}.
end{equation*}
Свойства преобразования Лапласа
Находить изображения, пользуясь только определением изображения, не всегда просто и удобно. Свойства преобразования Лапласа существенно облегчают задачу нахождения изображений для большого числа разнообразных функций, а также задачу отыскания оригиналов по их изображениям.
Линейность
Линейной комбинации оригиналов соответствует такая же линейная комбинация изображений, т. е. есл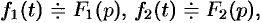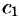и 
, 
и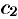 
— постоянные числа, то 
.
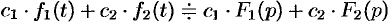Используя свойства интеграла, находим
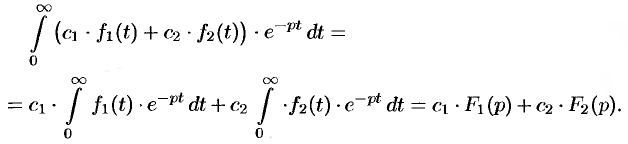
Пример №78.4.
Найти изображения функций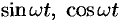 
(
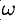— любое число), 
.
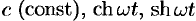Решение:
Пользуясь свойством линейности, формулой (78.3), находим:
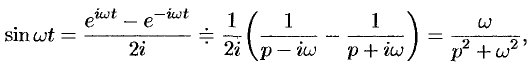
т.е.
Аналогично получаем формулу
Далее,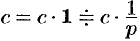 
, т. е.
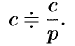
Наконец,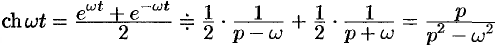 
, т.е.
Аналогично получаем формулу
Подобие
Если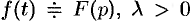 
, то 
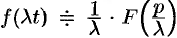, т. е. умножение аргумента оригинала на положительное число 
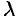приводит к делению изображения и его аргумента на это число.
По формуле (78.1) имеем
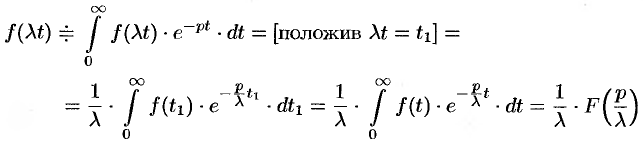
(так как безразлично, какой буквой обозначена переменная интегрирования).
Например, пусть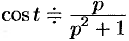 
. Тогда
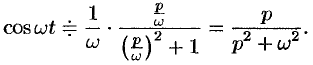
Смещение (затухание)
Если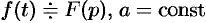 
, то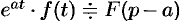 
, т. е. умножение оригинала на функцию 
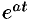влечет за собой смещение переменной 
.
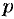В силу формулы (78.1) имеем
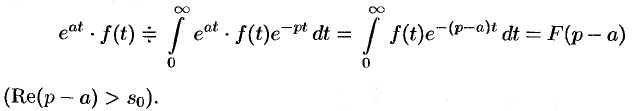
Благодаря этому свойству можно расширить таблицу соответствия между оригиналами и их изображениями:
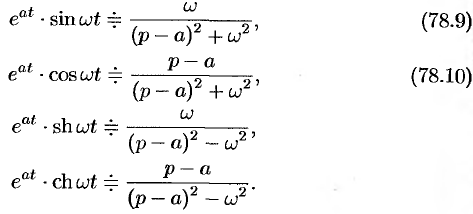
Пример №78.5.
Найти оригинал по его изображению
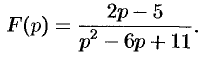
Решение:
Преобразуем данную дробь так, чтобы можно было воспользоваться свойством смещения:
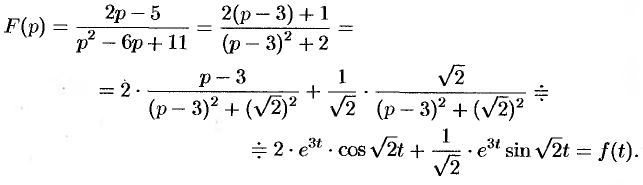
(См. формулы (78.9), (78.10) и свойство линейности.)
Запаздывание
Если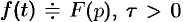 
, то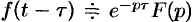 
, т. е. запаздывание оригинала на положительную величину 
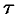приводит к умножению изображения оригинала без запаздывания на 
.
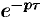Положив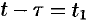 
, получим
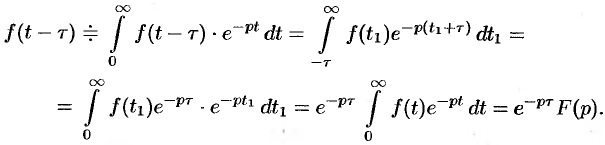
Поясним термин «запаздывание». Графики функци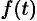и 
и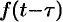 
имеют одинаковый вид, но график функции 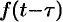сдвинут на 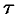единиц вправо (см. рис. 304). Следовательно, функци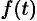и и 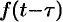описывают один и тот же процесс, но процесс, описываемый функцией 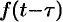, начинается с опозданием на время .
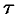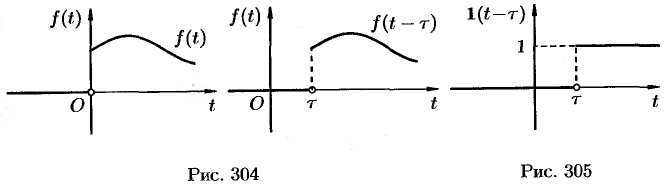
Свойство запаздывания удобно применять при отыскании изображения функций, которые на разных участках задаются различными аналитическими выражениями; функций, описывающих импульсные процессы.
Функция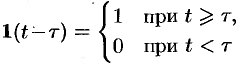 
называется обобщенной единичной функцией (см. рис 305).
Так как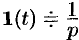 
, то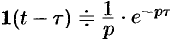 
.
Запаздывающую функцию
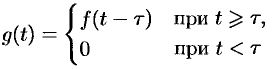
можно записать так: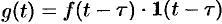 
.
Пример №78.6.
Найти изображение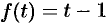 
.
Решение:
Для того чтобы быть оригиналом, функция 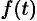должна удовлетворять условиям 1-3 (см. п. 78.1). В этом смысле исходную задачу можно понимать двояко.
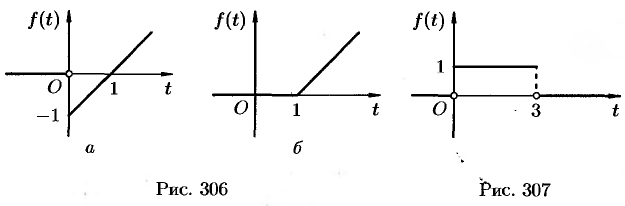
Если понимать функцию 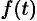как
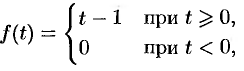
т. е.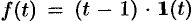 
(см. рис. 306, а), то, зная, что 
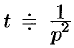(см. формулу (78.4)), 
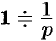и, используя свойство линейности, находим
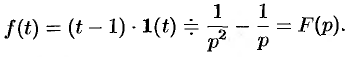
Если же понимать функцию 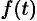как
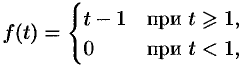
т. е.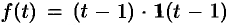 
(см. рис. 306, б), то, используя свойство запаздывания, находим 
.
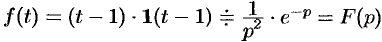Пример №78.7.
Найти изображение функции
Решение:
Данная функция описывает единичный импульс (см. рис. 307), который можно рассматривать как разность двух оригиналов: единичной функции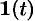 
и обобщенной единичной функции 
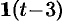. Поэтому 
.
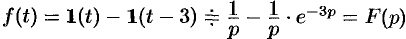Пример №78.8.
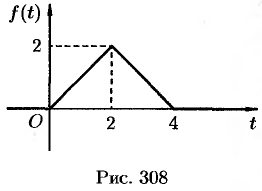
Найти изображение функции
Решение:
Функция-оригинал изображена на рис. 308. Запишем ее одним аналитическим выражением, используя функции Хевисайда 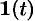и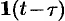 
:
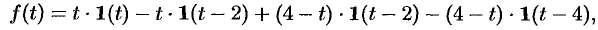
т.е.
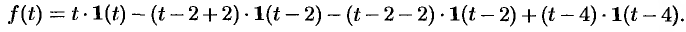
Раскроем скобки и приведем подобные слагаемые:
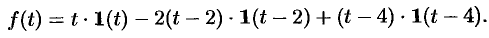
Изображение функции 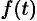будет равно
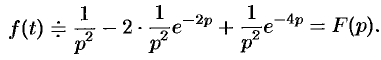
Замечания.
- Изображение периодического оригинала с периодом, равным
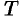, есть 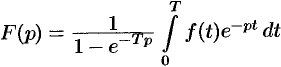. - Свойство опережения
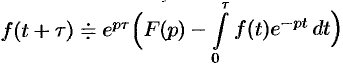
применяется значительно реже.
, есть 
.
Дифференцирование оригинала
Если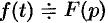 
и функции 
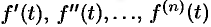являются оригиналами, то
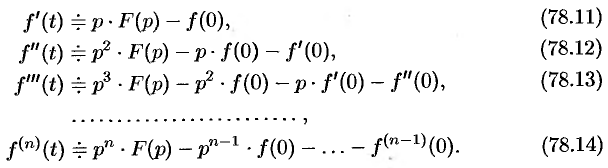
По определению изображения находим
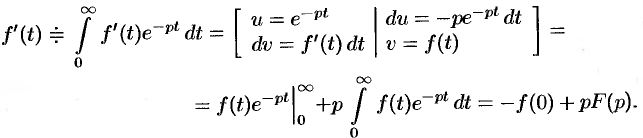
Итак,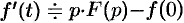 
. Пользуясь полученным результатом, найдем изображение второй производной 
:
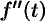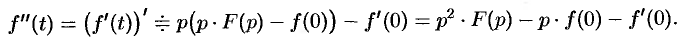
Аналогично найдем изображение третьей производной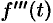 
:
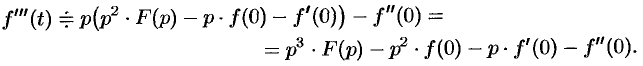
Применяя формулу (78.11)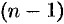 
раз, получим формулу (78.14).
Замечание. Формулы (78.11)—(78.14) просто выглядят при нулевых начальных условиях: если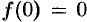 
, то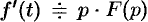 
; если 
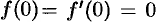, то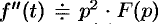 
, и, наконец, если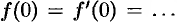 
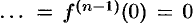, то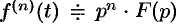 
, т. е. дифференцированию оригинала соответствует умножение его изображения на .
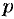Рассмотренное свойство дифференцирования оригинала вместе со свойством линейности широко используется при решении линейных дифференциальных уравнений.
Пример №78.9.
Найти изображение выражения
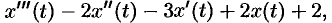
если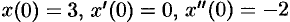 
.
Решение:
Пусть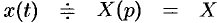 
. Тогда, согласно формулам (78.11) — (78.13), имеем
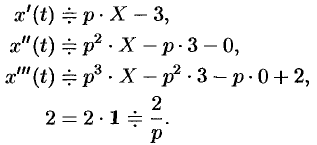
Следовательно,
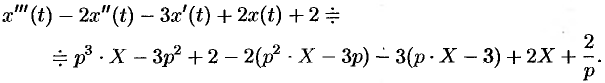
Дифференцирование изображения
Если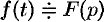 
, то
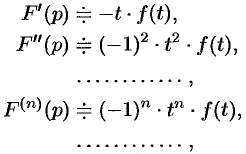
т. e. дифференцированию изображения соответствует умножение его оригинала на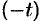 
.
Согласно теореме 78.1 существования изображения,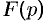 
является аналитической функцией в полуплоскости 
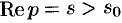. Следовательно, у нее существует производная любого порядка. Дифференцируя интеграл (78.1) по параметру 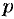(обоснование законности этой операции опустим), получим
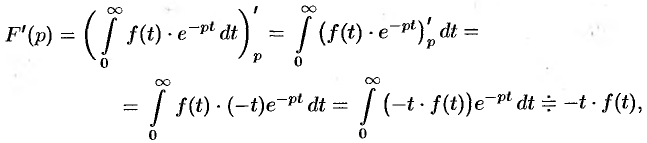
т.е.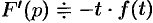 
. Тогда 
, 
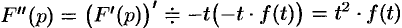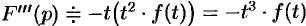и вообще 
.
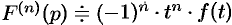Пример №78.10.
Найти изображения функций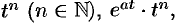 
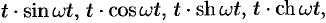
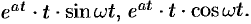
Решение:
Так как 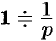, то, в силу свойства дифференцирования изображения, имеем 
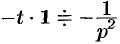, т. е.
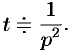
Далее находим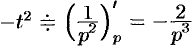 
, т.е. 
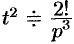. Продолжая дифференцирование, получим
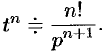
С учетом свойства смещения получаем
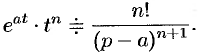
Согласно формуле (78.5),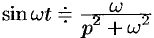 
. Следовательно,
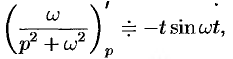
т. e.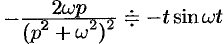 
, или
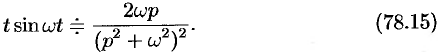
Аналогично, используя формулы (78.6), (78.7) и (78.8), находим
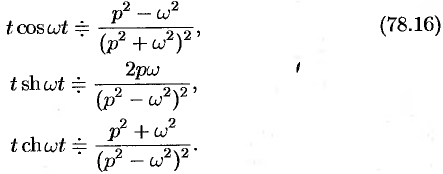
С учетом свойства смещения и формул (78.15) и (78.16), получаем
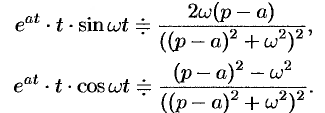
Интегрирование оригинала
Если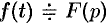 
, то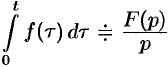 
, т. е. интегрированию оригинала от 0 до 
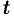соответствует деление его изображения на .
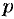Функция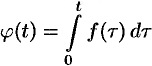 
является оригиналом (можно проверить).
Пусть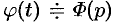 
. Тогда по свойству дифференцирования оригинала имеем
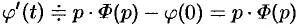
(так как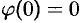 
). А так как
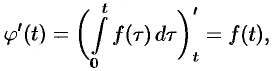
то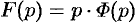 
. Отсюда 
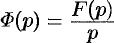, т. е. 
.
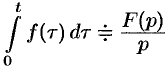Интегрирование изображения
Если 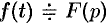и интеграл 
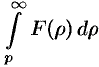сходится, то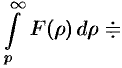 
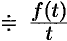, т. e. интегрированию изображения от 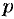до 
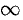соответствует деление его оригинала на .
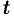Используя формулу (78.1) и изменяя порядок интегрирования (обоснование законности этой операции опускаем), получаем
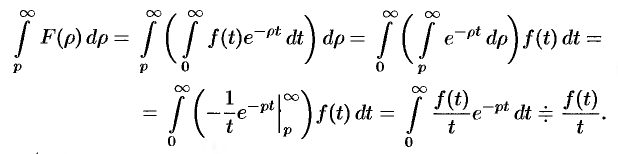
Пример №78.11.
Найти изображение функции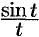 
; найти изображение интегрального синуса 
.
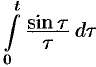Решение:
Так как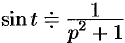 
, то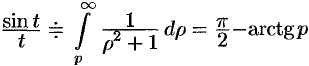 
, т.е. 
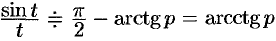. Применяя свойство интегрирования оригинала, получаем 
.
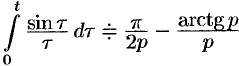Умножение изображений
Если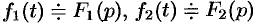 
, то
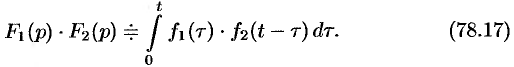
Можно показать, что функция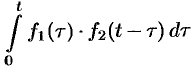 
является оригиналом.
Используя преобразование Лапласа (78.1), можно записать
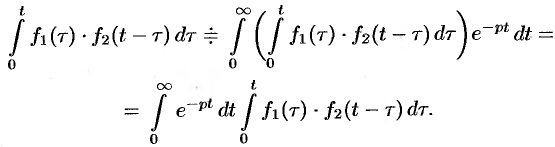
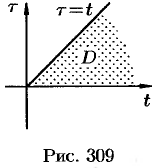
Область 
интегрирования полученного двукратного интеграла определяется условиями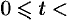 
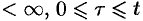(см. рис. 309).
Изменяя порядок интегрирования и полагая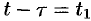 
, получим
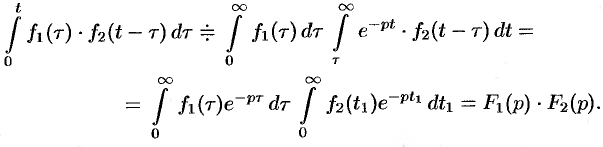
Интеграл в правой части формулы (78.17) называется сверткой функци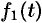и 
и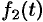 
и обозначается символом 
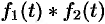, т. е.
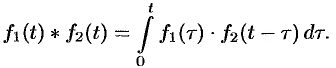
Можно убедиться (положив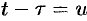 
), что свертывание обладает свойством переместительности, т. е. 
.
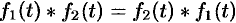Итак, умножение оригиналов равносильно их свертыванию, т. е.
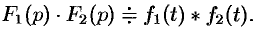
Пример №78.12.
Найти оригинал функций
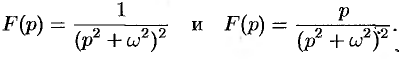
Решение:
Так как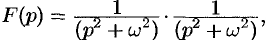 
и 
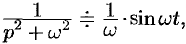то
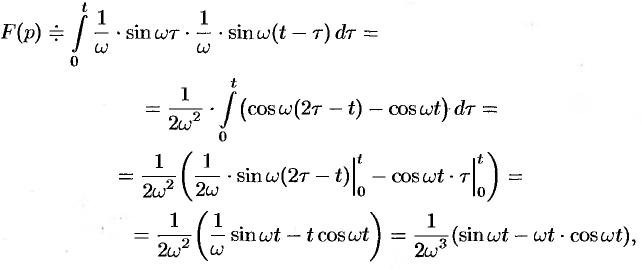
т.е.
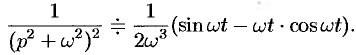
Аналогично получаем
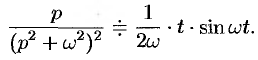
Следствие 78.2. Есл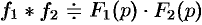и 
и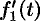 
также является оригиналом, то
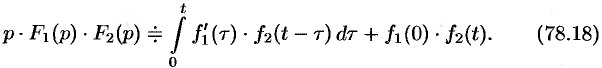
Запишем произведение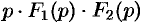 
в виде
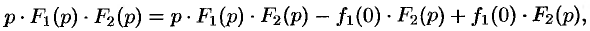
или
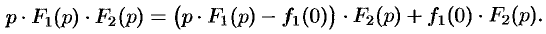
Первое слагаемое в правой части есть произведение изображений, соответствующих оригиналам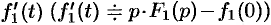 
и 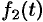. Поэтому на основании свойства умножения изображений и линейности можно записать 
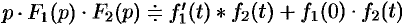или
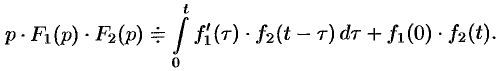
Формула (78.18) называется формулой Дюамеля.
На основании свойства переместительности свертки формулу Дюамеля можно записать в виде
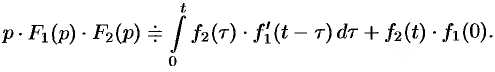
Формулу Дюамеля можно применять для определения оригиналов по известным изображениям.
Пример №78.13.
Найти оригинал, соответствующий изображению
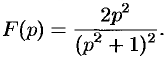
Решение:
Так как
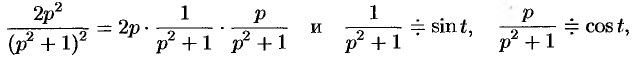
то на основании формулы Дюамеля (78.18) имеем
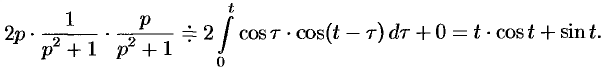
Умножение оригиналов
Если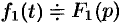 
и 
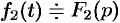, то
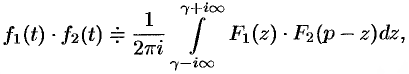
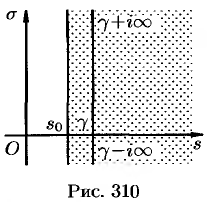
где путь интегрирования — вертикальная прямая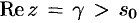 
(см. рис. 310) (примем без доказательства).
Резюме
Рассмотренные свойства преобразования Лапласа представляют собой основные правила (аппарат) операционного исчисления. Для удобства пользования перечислим эти свойства.
- Линейность: .
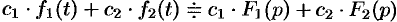- Подобие: .
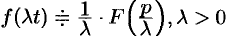- Смещение: .
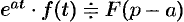- Запаздывание: .
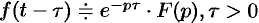- Дифференцирование оригинала:
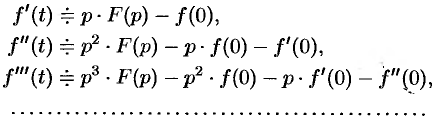
- Дифференцирование изображения
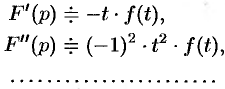
- Интегрирование оригинала: .
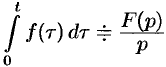- Интегрирование изображения: .
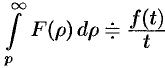- Умножение изображений: .
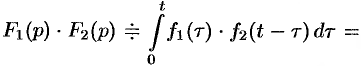
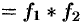- Умножение оригиналов: .
.
.
.
.
.
.
.
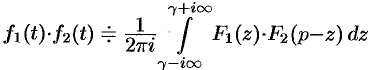.Таблица оригиналов и изображений
Составим краткую таблицу, устанавливающую соответствие между некоторыми оригиналами (часто встречающимися на практике) и их изображениями. Достаточно полная таблица оригиналов и изображений, позволяющая по заданному оригиналу находить изображение и наоборот, есть, в частности, в книге «Справочник по операционному исчислению» (авторы В. А. Диткин и П. И. Кузнецов).
Таблица оригиналов и изображений
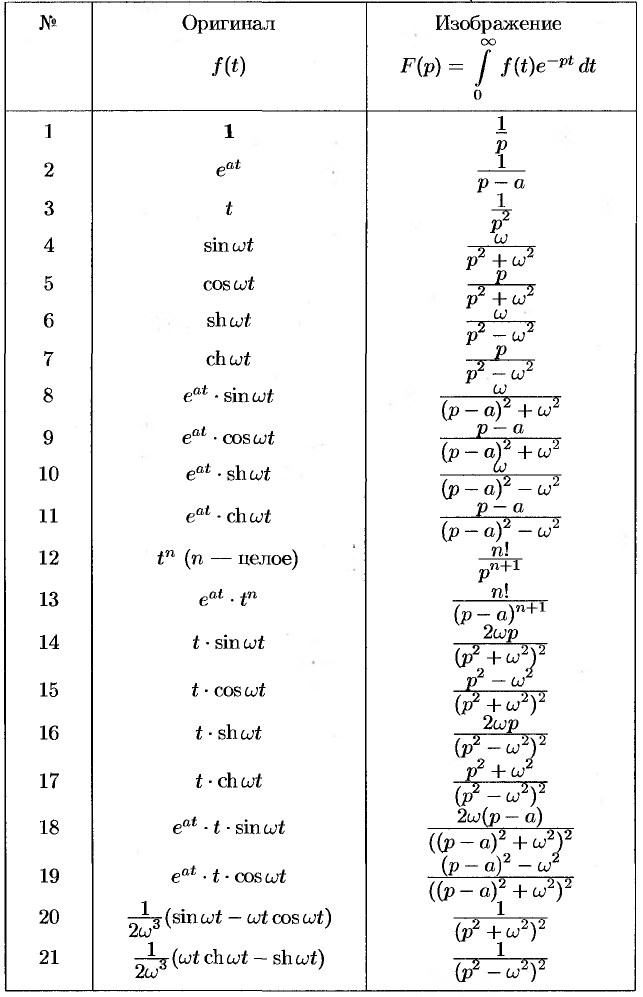
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:
